Abstract
Coordination is essential for establishing and sustaining teamwork. Agents in a team must agree on their tasks and plans, and thus, group decision-making techniques are necessary to reach agreements in teams. For instance, to agree on a joint task, the agents can provide their preferences for the alternative tasks, and the best alternative could be selected by majority. Previous works assumed that agents only provide their preferences for the alternatives. However, when selecting a joint task for teamwork, it is essential to consider not only the preferences of the agents, but also the probability of the agents being able to execute the task if it is selected. In this paper, we propose a novel model, the decIsion-MAking under Group commItmeNt modEl (IMAGINE), for computing the optimal decision for a team considering several parameters. Each agent provides: (1) the utility of each alternative for the team, (2) the associated cost for the agent by executing the alternative, and (3) the probability that the agent will be able to execute the alternative task. The IMAGINE gathers these data from the agents, as well as the requisite quorum for each alternative task, which is the minimum number of agents required to complete the task successfully. Given this information, the IMAGINE determines the optimal decision for the group. We evaluated the IMAGINE by comparing it to a baseline method that does not consider the quorum requirement. We show that the IMAGINE generally comes up with a better decision than the baseline method and that the higher the quorum, the better the decisions the IMAGINE makes are.
1. Introduction
Coordination is key in establishing and maintaining teamwork ([1]). Team members must be aware of their capabilities and how they can fulfill the roles required by the team’s high-level plan. For that, agents in a team must agree on their tasks and plans ([2]). Kaminka and Frenkel [3] presented different techniques to reach agreements in teams. In most of them, there is a set of available alternatives, and the goal is to agree on the “best” alternative. The agents, in this case, provide their preferences for the alternatives, and the output is the most preferred alternative for the group. For instance, in the Bar Ilan Teamwork Engine (BITE), robots use decision-making in order to govern a coordinated activity ([4]). Dery et al. [5] used voting for decision-making to schedule a meeting in a group of agents, with the minimal number of agents’ preferences ([6]) and, later, with the preferences that were learned from the social network of each agent ([7]).
In teamwork, agents may commit the group while providing their preferences. If, for instance, the alternatives are possible tasks and the agents should decide on a joint task to execute, the agents should commit the group to execute the chosen task. Specifically, assume a group of scout robots that should decide on which minefield to scout among three alternative fields. Each agent provides its preferences for the alternative minefields; however, once they agree on the minefield, all the agents commit to scout the chosen minefield. This is different from voting on a task in which the agents do not take part in executing it. For instance, Guttmann and Zukerman [8] presented the ETAPP framework that applies a voting policy to choose an agent to execute a task. Only the selected agent commits to executing the task while the rest of the agents do not commit.
Once the group has chosen an alternative (e.g., a task), individual agents may unexpectedly not participate in executing it, due to, for example, other commitments or physical limitations. However, an alternative task may depend on the number of participating agents to be executed successfully. This number is called “quorum”. Moreover, even before agreeing on a joint alternative, an agent may have uncertainty about its ability to execute an alternative. For example, a robot may be hesitant about scouting a specific minefield because its mechanical condition may prevent it from reaching the field. In another domain, where a group of personal digital assistants (PDAs) attempt to agree on a time slot for a joint meeting, an agent may be uncertain as to a time slot due to prior commitments. Thus, when reaching an agreement about the chosen alternative, the probability of each agent to commit to executing the alternative should be taken into consideration, especially when a quorum is required.
Previous works ([9,10]) assumed that agents only provide their preference values for the alternatives. However, in systems where the agents commit a group, agents should take into consideration not only their preferences, but also the probability of executing the alternative successfully. For instance, in the scout robot example, every robot should (1) scale the minefields according to it utility for the group (e.g., its strategic importance) and (2) provide the probability of participating in scouting each minefield (e.g., based on its mechanical condition). Using the given probability of the agents participating in the different alternative tasks, we can estimate the probability of a quorum for each of the alternatives. This may influence the selection of the best joint decision. For instance, if a quorum requirement states that at least four scout robots of the group must join the task, then in order to select the preferred minefield, we should take into consideration the probability of reaching the required quorum based on the agents’ probability of participating.
In this paper, we propose a novel probabilistic voting model (IMAGINE) in which the agents provide three values for each alternative: (1) the utility of the alternative for the group if the execution is successful (similar to the meaning of the preference value in regular decision-making problems) (2) the cost to the agent of executing the alternative, and (3) the agent’s probability of participating in executing the alternative. The decision-making function determines the best decision given this information under a quorum requirement.
We evaluated the IMAGINE in a simulated domain based on the example of minefields. We compared it to a baseline algorithm that finds a winner without considering the quorum. Through the experiments, we show that in about of the cases, the IMAGINE recommends a different decision than the baseline method; in about of these cases, the IMAGINE’s decision is better. Furthermore, the higher the quorum, the deeper the gap between the IMAGINE and the baseline is. However, when the requirement of the quorum is low, the baseline is almost as good as the IMAGINE.
The first contribution of this paper is to propose a novel decision-making model (IMAGINE) that determines the optimal decision given the information from the agents under the quorum requirement. The second contribution is to propose a dynamic programming algorithm to compute the probability that at least q agents will execute the alternative. The third contribution is evaluating the IMAGINE against a baseline mechanism that does not consider the quorum.
2. Related Work
Multi-agent decision-making is a wide field ([11,12]). One of the main challenges in multi-agent decision-making is designing mechanisms for the group to reach an agreement, i.e., consensus [13,14,15]. Voting is a central mechanism for reaching an agreement ([16]). The decision-making mechanism presented in this paper is close to the voting mechanism. In both mechanisms, agents provide their preferences for some alternatives. Nevertheless, a main difference is that voting procedures do not consider the probability of the agents performing the alternatives, as well as their cost.
Gelain et al. [17] proposed to interpret the preference values as probabilities ranging from zero to one. Moreover, a predefined probability distribution of the votes was assumed by [18]. The winning probability of each candidate was evaluated using the Plurality, Borda, and Copeland protocols ([10]). The authors also showed the theoretical bounds for the ability to calculate the probability of an outcome. Bachrach et al. [19] proposed an algorithm for computing the probability of a candidate winning, assuming a voting rule that is computable in polynomial time (such as range voting) and assuming a uniform random distribution of the voters’ choice of candidates. However, while these papers focused on calculating the winning probability for each candidate, their voting rule considered only the probabilities of the preferences of the agents rather than the probability of the agents to commit to performing as the candidates, as we consider in this paper. In addition, these papers did not consider a quorum requirement.
A number of studies have looked at agents’ commitment in group decision-making. Ziotti and Leoneti [20] presented a study to assess the likelihood of group decision-making commitment, modeled by a multicriteria method based on game theory. Moreover, they evaluated the group decision-making commitment in terms of the players’ satisfaction and feeling of fairness. They discovered that mathematical methods may encourage collective decision-making, resulting in better levels of the sense of justice and satisfaction, as well as a higher likelihood of commitment to the agreements reached. Núncio [21] investigated the significance and ramifications of the ability to express empathy in the workplace. The work wanted to understand how team cooperation is influenced by perceived leader empathy under monetary constraints, as well as the impact of participants’ cooperation, group commitment, and individualism in this relationship. Novelli and Spina [22] showed that some level of commitment allows the group to benefit from the use of systematic approaches to decision-making. Although it appears from these studies that commitment is a significant aspect in group decision-making, no previous research has looked into how to make a group decision while considering the agents’ commitment to the decision.
3. Decision-Making under the Group Commitment Model (IMAGINE)
Let be a group of agents, a set of alternatives, and q a required quorum, i.e., a minimum number of agents that must participate in the execution of the alternative. Every agent provides three values for each alternative considering its execution and success:
- Utility: the utility of the alternative for the group. For example, the utility for the group by selecting a certain minefield is affected by its strategic importance;
- Cost: the cost of the alternative to the agent. For example, the cost incurred by a certain agent voting for a certain minefield is affected by the time and energy it spends on reaching the minefield;
- Probability: the probability that the agent will be able to execute the alternative. For instance, the probability that an agent will be able to scout a certain minefield is affected by its time constraints and by its mechanical condition.
The utility reflects the preference of the agents for the alternatives, similar to other group decision-making problems. For instance, if a group of personal digital assistants (PDAs) attempts to agree on a time slot for a joint meeting, the utility reflects the preference of the agent for the alternative time slots. The preferences could be obtained by the human user in advance or could be learned by the agent from the previous time slots of the user. In other domains of multirobot systems, the utility could be estimated by the agents, using a predefined function over the environmental parameters, sensed by each agent. For instance, in the minefield example, each alternative minefield is affected by the estimated strategic importance to the group. This could be influenced by the information gathered by each agent on the minefields.
The cost of each alternative to an individual agent could be estimated as well. In the multirobot domain, it could be formalized in a predefined function, as the utility. For instance, in the minefield example, each alternative minefield is affected by the estimated time and energy required to reach the minefield. In the PDA domain, the cost could be estimated by the expected workload of the candidate day, based on previous meetings, or by predefined labeling marked by the human user.
Obtaining probabilities is the most challenging and may be domain dependent. The obtaining of the probabilities by the user is both time consuming and impractical. It could, however, be estimated based on the cost provided by the user or learned by the agent. The higher the cost of an alternative to an agent, the less likely it is that the agent is able to execute that alternative. Alternatively, if the agent has collected historical data about the user’s behavior, the agent could predict the probability of each alternative using a learned prediction model.
We can describe our problem as an optimization problem. Given a set of alternatives C, a required quorum to commit to the alternatives q, and a set of agents A, which provide the utility, cost, and probability for the alternatives, the goal is to find the alternative that optimizes the overall gain of the group under a quorum requirement. We propose to address this challenge with a decision-making procedure. Agents in a group provide their utilities, costs, and probabilities over the alternatives. The decision-making function finds the alternative that has the highest expected total gain for the group. The decision-making function takes into consideration the preferences of the agents as follows:
- Group utility: This value is considered only if the alternative is successfully executed. For example, the utility by selecting a certain minefield is counted only if eventually the minefield is successfully scouted;
- Agent cost: This cost is considered only for agents who execute it even if the execution fails. For example, the cost is considered even if eventually the scouting is not performed due to a low number of participants (the quorum is not met). The reason is that the agents who arrived at the minefield still incur the cost of the time and energy involved in reaching the minefield.
Table 1 summarizes the differences between the attributes the agents provide for the alternatives. The Successful column displays whether or not the alternative must be successful in order for the attribute to be considered. The Execute column represents whether or not the agent must participate in the execution of the alternative in order for the attribute to be considered. The utility (first row) is considered if eventually the alternative was executed successfully, but even if the agent has not executed it. The cost (second row) is considered only for agents that have executed it, even if eventually the alternative was not executed successfully.

Table 1.
Differences between the attributes in terms of success and execution.
Let us formalize the IMAGINE. First, we define the utility set, cost set, and probability set, which contain the utilities, costs, and probabilities (respectively) of the alternatives given by the agents:
Definition 1.
The
utility set is a set of the utilities of alternative given by agents , respectively, where represents the utility of alternative given by agent .
Definition 2.
The
cost set is a set of the costs of alternative provided by agents , respectively, where represents the cost of alternative given by agent .
Definition 3.
The
probability set is a set of the probabilities of alternative provided by agents , respectively, where represents the probability of alternative given by agent .
Example 1.

Assume a group of three agents and four alternatives . The utilities, costs, and probabilities of the alternatives given by the agents are presented in Table 2. The three values of an alternative are represented by a tuple . For instance, the tuple of alternative given by agent is presented in the second column of the first row.

Table 2.
Utilities, costs, and probabilities of the alternatives given by agents .
The utility set of alternative based on the first row in Table 2 is ; its cost set is ; its probability set is .
Now, we can present the utility and probability of alternative to the group. The group utility of an alternative is the sum of its utilities given by the agents.
Definition 4.
The group utility of alternative is the sum of the utilities of given by the agents in group A:
The probability of executing an alternative by the group depends on a quorum:
Definition 5.
The group probability of alternative is the probability that at least q agents will execute alternative :
Example 2.
The group utility of alternative is . ’s group probability is (this will be explained in the next section).
The cost of executing an alternative by an agent is taken into consideration even if eventually the alternative is not executed successfully. Thus, we multiply it solely by the individual probability.
Definition 6.
The agent expected cost of agent by executing alternative is the product of ’s cost and probability .
The expected utility of the group considers the alternative’s group utility and probability under the quorum requirement.
Definition 7.
The group expected utility of alternative is the product of ’s group utility and probability .
Finally, the expected gain by choosing alternative subtracts the expected cost from the group expected utility.
Definition 8.
The expected gain of alternative is:
Example 3.
We compute for . The first part is the product of the group’s utility and probability: .
The second part is the expected cost:
The total sum of the expected costs is: .
The expected gain by choosing alternative is: .
Once the expected gain is computed for all the alternatives, IMAGINE can determine the best decision by selecting the alternative with the highest expected gain.
Definition 9.
The chosen alternative is the alternative that maximizes the expected gain:
Example 4.
In our example, the expected gain of each alternative, given a required quorum of two, is as follows:
As a result, alternative will be selected by the group.
4. Algorithm and Complexity
Computing the group probability under the quorum requirement has a major effect on the complexity of the expected gain. We present a dynamic programming algorithm to find the probability that at least q agents will execute the alternative (Definition 5). Our dynamic programming algorithm relies on the fact that the problem of computing the probabilities that x and of y agents will execute the alternative are subproblems of computing the probability that of agents will execute the alternative.
For instance, assume a group of eight agents, and assume the dynamic algorithm has already computed the probability of five and six of them executing the alternative. These probabilities are and , correspondingly. Now, assume a new agent in the group with the probability of executing the alternative. We want to compute the probability of six of the nine agents executing the alternative. We can use the probabilities that we have already computed for eight agents as follows. There are two cases in which we can consider six of nine agents: (1) five of the first eight agents with the ninth new agent will execute it—this will occur with a probability of ; or (2) six of the first eight agents will execute it, while the ninth will not execute it—this will occur with a probability of . The total probability that six of nine agents will execute the alternative is the sum of both cases: .
We describe this process in Algorithm 1. We begin with the information solely about the probability of the first agent. In Line 3, we initialize the probability that it will not execute the alternative (its complement probability) and the probability that it will execute the alternative (Line 4). The main loop (Lines 5–11) adds information in every iteration about the probability of one more agent. This computation relies on the probabilities computed in the previous subproblems. Finally, in Lines 12–14, we sum up the probabilities of each subgroup that are greater than the quorum.
| Algorithm 1 COMPUTE_GROUP_PROBABILITY |
|
Example 5.
We use an example to describe Algorithm 1. Assume the input of the algorithm is and . In Lines 3–4, we initialize the array with the probability that the first agent will not execute alternative (the complement of the first probability) and the probability that it will execute the alternative (). Then, in the main loop, we consider the next probability (), and we compute the probability that 0 agents will execute , 1 agent will execute it, and 2 agents will execute it:
p(0 agents execute):
p(1 agent executes):
p(1 agent executes):
p(2 agents execute):
In the next iteration, we compute the new probabilities based on (1) the probabilities of the first two agents in the array and (2) the probability of the third agent ():
p(0 agents execute):
p(1 agent executes):
p(1 agent executes):
p(2 agents execute):
p(2 agent executes):
p(3 agents execute):
Finally, the probability that at least agents will execute the alternative is the sum of the probabilities that two agents will execute () and that three agents will execute it (0.252) (Lines 12–14). The algorithm returns the sum: 0.766.
The complexity of the algorithm COMPUTE_GROUP_PROBABILITY is , where n is the number of agents. Thus, the complexity of the decision-making model (IMAGINE) (Definition 9) is: , where m is the number of alternatives. m for the computation of the expected gain for each one of the alternatives, and for the computation of the group probability for each agent.
5. Evaluation
In this section, we present an evaluation of the IMAGINE. We built a simulation of the minefield domain. Each one of the minefield alternatives in the simulation was characterized by its location, level of danger, and strategic importance. The group utility of a minefield is affected by its level of danger and strategic importance. The higher the strategic importance, the higher its utility is, and the higher the level of danger, the lower the utility is. We set the group utility as the product of these parameters. We simulated the estimate of each robot for the group utility by drawing a value out of a normal distribution with a mean value equal to the simulated group utility. The probability and the cost of a robot scouting a minefield were linearly affected by the distance between a robot and a minefield. The further the minefield from the location of the robot, the lower the probability of the robot to scout it is, and the higher the cost of the robot to scout it is. We simulated these numbers by randomly locating the minefields and the scout robots in a two-dimensional grid.
We ran experiments for groups consisting of 3, 10, 20, 30, and 40 agents. In addition, we varied the number of minefield alternatives: 3, 10, 20, 30, 40, and 50. Finally, we varied the quorum requirement, the percentage of the robots that have to participate in the scouting: 40%, 50%, 60%, 70%, 80%, 90%, and 100%. We repeated each experiment (a combination of the group’s size, the amount of minefields, and the quorum) 50 times.
A quorum of robots is required to complete an alternative task. When the decision-maker, the IMAGINE computes the expected gain of each alternative, it takes into account the agents’ probabilities of completing each alternative task (as obtained by the agents). It chooses the alternative with the highest expected gain based on this and the given required quorum. In practice, however, the required quorum for the chosen alternative may not be met. There is a cost for the agents in this case, but no utility. Obviously, if the robots had known this beforehand, they would not have chosen that option. An oracle algorithm, as the name implies, knows this in advance, and thus would have chosen in this case an alternative that is guaranteed to be executed by the required number of robots, even if it has a lower group utility. This explains why an oracle decision-maker is only used as an upper bound to normalize the results and not as a realistic alternative algorithm to the IMAGINE. For instance, in our example, if an oracle knows that a quorum of two agents will not be finally achieved, it will make a decision that requires a quorum of one. In this case, the best alternative is rather than the best alternative in a quorum of two. Thus, an oracle decision-maker is guaranteed to achieve the highest gain. We measured the quality of the IMAGINE by calculating the ratio between the gain of the chosen minefield and the gain of minefield chosen by the oracle algorithm.
We emphasized in the Related Work that prior publications did not take into account the probability of the agents committing to performing their preferred candidates, as we did in this paper. Furthermore, previous papers made no mention of a quorum requirement. As a result, we were unable to compare our algorithm to past methods; however, we compared the IMAGINE to a baseline heuristic that does not consider the quorum. The total value of an alternative was computed as the expectation of the difference between the utility and cost provided by the agents:
In our example, based on Table 2:
In this case, the baseline will select as the best candidate, rather than , which was selected by the IMAGINE.
Our main findings were: (1) almost all the experiments showed (93%) that the quality of the winner found by the IMAGINE was equal or higher than the winners found by the baseline; (2) the quality of the winner in the IMAGINE was almost the same as the winner found by the oracle; (3) the quorum requirement was a key factor that significantly influenced the quality of the winner. We present some results that support these findings. Other results also showed the same trends.
We show the influence of the percentage of the quorum in Figure 1, where the number of agents is 30 and the number of alternatives is 30. The x-axis is the percentage of the quorum, and the y-axis is the ratio between the gain of the chosen minefield and the gain of the minefield chosen by the oracle algorithm. We call this ratio the quality of the algorithm. We can see that independent of the quorum, the IMAGINE was close to optimal. By comparing the IMAGINE to the baseline method, we can see that the greater the quorum, the greater the gap between the IMAGINE and the baseline method was. The reason is that the baseline method does not consider the quorum as the IMAGINE does, but only the expected gain. Therefore, when the percentage of the quorum was high, it was more difficult to find a winner without considering the influence of the quorum.
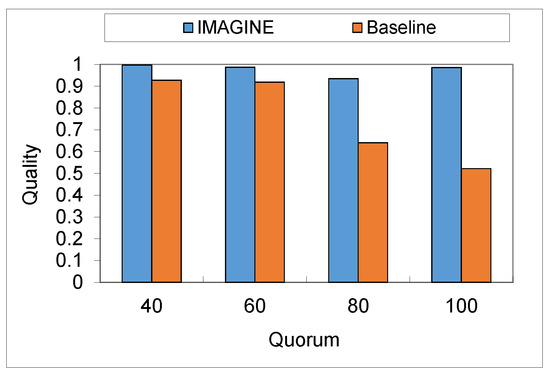
Figure 1.
Uniform distribution: quality over quorum (the group size is 30, and the number of alternatives is 30).
Figure 2 presents the quality (y-axis) as a function of the number of agents (x-axis), where the number of alternatives is 20 and the quorum is 60%. As we can see, the IMAGINE was better than the baseline. Nevertheless, the size of the group did not significantly influence the quality of the algorithms. We can see similar results in Figure 3, which presents the quality as a function of the number of alternatives, where the size of the group is 30 and the quorum is . Here, again, we can see that the number of alternatives was not a significant factor in determining the quality.
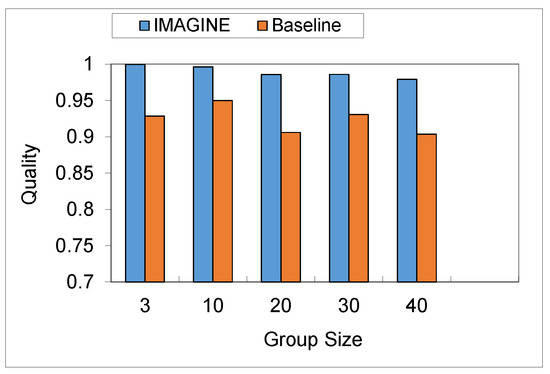
Figure 2.
Quality over group size (the number of alternatives is 20, and the quorum is 60%).
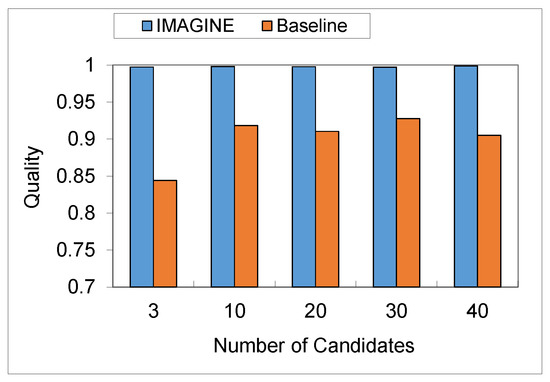
Figure 3.
Quality over number of alternatives (the number of agents is 30, and the quorum is 40%).
In order to show the advantage of the IMAGINE over the baseline method, we checked the number of tests in which the winner found by the IMAGINE was better than the winners found by the baseline method. We found that in 62% of the tests, the IMAGINE and the baseline found different winners; in 95% of these cases, the winner found by the IMAGINE surpassed the winner chosen by the baseline.
To summarize, the IMAGINE found better winners than the baseline method. The quality of the winners, found by the baseline method, was affected mainly by the quorum.
6. Conclusions
6.1. Summary
In this paper, we presented an optimization problem of finding the best alternative among m alternatives by agents in a group, with a quorum requirement. We proposed a decision-making model under a group commitment for teamwork (IMAGINE) in which agents provide three values for each alternative instead of one: the utility of the alternative for the group, the cost of the agent in executing the alternative, and the probability of the agent executing the alternative. Moreover, a quorum was required to carry out the alternatives. This is a critical technique, in particular for teams of collaborating agents who must commit to the entire group.
We evaluated the IMAGINE by comparing it to a baseline method that does not consider the required quorum. We showed that the IMAGINE finds better winners than the baseline method. The IMAGINE’s results were close to optimal. The baseline method was affected mainly by the quorum factor. In low quorums, it presented results close to the results achieved by the IMAGINE, but in high quorums, the winners it found were far from optimal.
6.2. Discussion
In this study, we assumed that the agents would be able to give utility, cost, and probability. In some cases, this assumption is justified. In a group of personal digital assistants (PDAs) or in the minefield example, we illustrated how to obtain these parameters. They could be collected in advance by the human user or learned by the agent based on past data. However, we believe that in some domains, the agents may find it difficult to offer some of these parameters. Indeed, in earlier similar research, the utility and cost were assumed to be known, but the probability of the agents executing the alternative has never been assumed before; therefore, it is more difficult to estimate.
The evaluation of the algorithms is a limitation of this work. We created a simulation of the minefield localization problem and evaluated the performance of the various algorithms on a variety of parameters. However, assessing the algorithms with real-world scenarios in a real-world setting could improve the experiments. We leave this for future work.
6.3. Future Work
Our model can be easily extended in two possible directions. The first is to determine different quorum requirements for different alternatives. The importance of this direction is for domains where every alternative has a different quorum. For instance, different minefields might have different sizes, which require a different number of agents to scout. The second direction is to determine weights for the voters in which the quorum requirement should consider these weights. This is essential when there are key agents that execute the alternative. For instance, certain agents are required to attend a meeting. In the future, we plan to examine the IMAGINE in more domains with varied distributions. In addition, we plan to use learning algorithms to enable the agents to provide only one value, which is more intuitive, and yet choose a winner with a similar quality to the one selected by the IMAGINE.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Tambe, M. Towards Flexible Teamwork. J. Artif. Intell. Res. 1997, 7, 83–124. [Google Scholar] [CrossRef] [Green Version]
- Sycara, K.; Sukthankar, G. Literature review of teamwork models. Robot. Instit. Carnegie Mellon Univ. 2006, 31, 31. [Google Scholar]
- Kaminka, G.A.; Frenkel, I. Towards flexible teamwork in behavior-based robots. In Proceedings of the Fourth International Joint Conference on Autonomous Agents and Multiagent Systems, Utrecht, The Netherlands, 25–29 July 2005; pp. 1355–1356. [Google Scholar]
- Kaminka, G.A.; Frenkel, I. Integration of coordination mechanisms in the BITE multirobot architecture. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 2859–2866. [Google Scholar]
- Dery, L.N.; Kalech, M.; Rokach, L.; Shapira, B. Reaching a joint decision with minimal elicitation of voter preferences. Inf. Sci. 2014, 278, 466–487. [Google Scholar] [CrossRef]
- Naamani-Dery, L.; Kalech, M.; Rokach, L.; Shapira, B. Reducing preference elicitation in group decision-making. Exp. Syst. Appl. 2016, 61, 246–261. [Google Scholar] [CrossRef]
- Lesser, O.; Naamani-Dery, L.; Kalech, M.; Elovici, Y. Group decision support for leisure activities using voting and social networks. Group Decis. Negotiat. 2017, 26, 473–494. [Google Scholar] [CrossRef]
- Guttmann, C.; Zukerman, I. Voting Policies That Cope with Unreliable Agents. In Proceedings of the Fourth International Joint Conference on Autonomous Agents and Multiagent Systems, AAMAS ’05; ACM: New York, NY, USA, 2005; pp. 365–372. [Google Scholar] [CrossRef] [Green Version]
- Endriss, U. Trends in Computational Social Choice; Lulu Press: Morrisville, NC, USA, 2017. [Google Scholar]
- Aziz, H.; Brandt, F.; Elkind, E.; Skowron, P. Computational social choice: The first ten years and beyond. In Computing and Software Science; Springer: New York, NY, USA, 2019; pp. 48–65. [Google Scholar]
- Bulling, N. A survey of multi-agent decision-making. KI-Künstliche Intell. 2014, 28, 147–158. [Google Scholar] [CrossRef]
- Rizk, Y.; Awad, M.; Tunstel, E.W. Decision making in multiagent systems: A survey. IEEE Trans. Cogn. Dev. Syst. 2018, 10, 514–529. [Google Scholar] [CrossRef]
- Qin, J.; Ma, Q.; Shi, Y.; Wang, L. Recent advances in consensus of multi-agent systems: A brief survey. IEEE Trans. Ind. Electron. 2016, 64, 4972–4983. [Google Scholar] [CrossRef]
- Li, Y.; Tan, C. A survey of the consensus for multi-agent systems. Syst. Sci. Control Eng. 2019, 7, 468–482. [Google Scholar] [CrossRef] [Green Version]
- Bannikova, M.; Dery, L.; Obraztsova, S.; Rabinovich, Z.; Rosenschein, J.S. Reaching consensus under a deadline. Auton. Agents Multi. Agent. Syst. 2021, 35, 9. [Google Scholar] [CrossRef]
- Alfurhood, B.S.; Silaghi, M.C. A Survey of Group Decision Making Methods and Evaluation Techniques. In Proceedings of the Thirty-First International Flairs Conference, Melbourne, FL, USA, 21–23 May 2018. [Google Scholar]
- Gelain, M.; Pini, M.S.; Rossi, F.; Venable, K.B. Dealing with incomplete preferences in soft constraint problems. In Proceedings of the International Conference on Principles and Practice of Constraint Programming, Providence, RI, USA, 23–27 September 2007; Springer: New York, NY, USA, 2007; pp. 286–300. [Google Scholar]
- Hazon, N.; Aumann, Y.; Kraus, S.; Wooldridge, M. On the evaluation of election outcomes under uncertainty. Artif. Intell. 2012, 189, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Bachrach, Y.; Betzler, N.; Faliszewski, P. Probabilistic Possible Winner Determination. In Proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence, AAAI’10, Atlanta, GA, USA, 11–15 July 2010; pp. 697–702. [Google Scholar]
- Ziotti, V.C.; Leoneti, A.B. Improving commitment to agreements: The role of group decision-making methods in the perception of sense of justice and satisfaction as commitment predictors. Pesqui. Oper. 2020, 40. [Google Scholar] [CrossRef]
- Núncio, A.T.S. The Effects of Leader’S Perceived Empathy, Group Commitment and Individualism on Team Cooperation, under “Public Goods Game”. Ph.D. Thesis, Universidade Católica Portuguesa, Lisbon, Portugal, 2020. [Google Scholar]
- Novelli, E.; Spina, C. The value of Commitment for Strategic Decision-Making: Evidence from a Field Experiment. In Academy of Management Proceedings; Academy of Management: Briarcliff Manor, NY, USA, 2021; Volume 2021, p. 13808. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).