Abstract
The efficient operation of emergency medical services is critical for any society. Typically, optimisation and simulation models support decisions on emergency ambulance stations’ locations and ambulance management strategies. Essential inputs for such models are the spatiotemporal characteristics of ambulance trips. Access to data on the movements of ambulances is limited, and therefore modelling efforts often rely on assumptions (e.g., the Euclidean distance is used as a surrogate of the ambulance travel time; the closest available ambulance is dispatched to a call; or the travel time estimates, offered by application programming interfaces for ordinary vehicles, are applied to ambulances). These simplifying assumptions are often based on incomplete data or common sense without being fully supported by the evidence. Thus, data-driven research to model ambulance trips is required. We investigated a unique dataset of global positioning system-based measurements collected from seventeen emergency ambulances over three years. We enriched the data by exploring external sources and designed a rule-based procedure to extract ambulance trips for emergency cases. Trips were split into training and test sets. The training set was used to develop a series of statistical models that capture the spatiotemporal characteristics of emergency ambulance trips. The models were used to generate synthetic ambulance trips, and those were compared with the test set to decide which models are the most suitable and to evaluate degrees to which they fit the statistical properties of real-world trips. As confirmed by the low values of the Kullback–Leibler divergence (–) and by the Kolmogorov–Smirnov test at the significance level of , we found a very good fit between the probability distributions of spatiotemporal properties of synthetic and real trips. A reasonable modelling choice is a model where the exponential dependency on the population density is used to locate emergency cases, emergency cases are allocated to hospitals following empirical probabilities, and ambulances are routed using the fastest paths. The models we developed can be used in optimisations and simulations to improve their validity.
1. Introduction
Rapid responses to medical emergencies depend on the proper design and management of emergency medical services (EMS). Traditionally, to design EMS that fit the local conditions, mathematical optimisation and simulation models are used. There are several drawbacks of earlier models, such as the necessity to rely on simplifying assumptions for fundamental issues, e.g., coverage of emergency cases, relocation of ambulances, and busy probabilities [1]. Many models ignore patient survivability [2], uncertainties linked with travel times, or route choice [3].
The need to apply simplifying assumptions arises due to the lack of data and to make underlying optimisation problems more tractable. More recently, due to improvements in sensing and communication technologies, access to data has been significantly improved, opening new pathways for data-centric approaches. This paper explores a unique dataset of global positioning system (GPS)-based measurements collected from seventeen emergency ambulances that extends over three years. Based on the data, we developed a series of models that can be used to generate synthetic ambulance trips that fit reasonably well with the spatiotemporal properties of real emergency ambulance trips. We gave priority to models that are simple to use, and together with the models, we also present the parameter values; so the models can be directly applied by other researchers or practitioners. In particular, this study focuses on mountainous regions and medium-sized cities and their neighbourhoods. The case study included the data from the Žilina region in Slovakia; however, some of the parameters could also be transferable to other similar areas. Moreover, this paper describes a methodology that can be applied to similar data from different types of geographical areas. The developed models can inform optimisations and simulations of EMS and improve their validity.
1.1. Literature Review
In this section, we start by providing a short overview of the literature covering EMS modelling that concerns optimisation, simulation, and data-centric methodologies. Further, we introduce several selected studies based on optimisation or simulation techniques while highlighting some typical modelling assumptions that can be replaced with data on ambulance trips. Next, we discuss data-centric and mixed (optimisation, simulation, and data) approaches. We conclude the section by overviewing papers that exploited GPS-based measurements from ambulances to demonstrate the novelty of our approach to such data.
Over the last few decades, several monographs discussed the optimisation of EMS. The foundations and historical evolution of location science were thoroughly documented in [4], and an overview of applications, including emergency response to traffic accidents and preventive healthcare, was given in [5]. Several review papers addressed some selected modelling aspects. The location and relocation models were summarised in [6]. Problems were covered in [7], and location problems with multiple criteria in [8]. Comprehensive taxonomy and an overview of available literature on EMS-related location problems were given in [9]. A more recent review of successive model innovations of location models for emergency services was given in [10]. Despite an abundance of literature on EMS optimisation, only a few review papers have considered the full range of EMS systems. Review [11], argues in favour of a holistic and user-centric approach to EMS that follows the whole path of a patient through the EMS. Regarding the modelling, the paper emphasises the need to incorporate realistic information, sources of uncertainty, and forecasting methods.
Optimisation approaches to emergency systems are dominant in the literature, and the assumptions regarding spatiotemporal characteristics of emergency trips are central in the methodology. The bi-objective spatial optimisation model, integrating coverage and median objectives, was proposed by [12]. The problem is solved in two stages; first, the number of fire stations is minimised; second, the number of fire stations is constrained, and the total weighted travel time is minimised. The Euclidean distance is considered in the objective as a surrogate for travel time. Similarly, [13] proposed a methodology for reorganising a network of volunteer fire departments while estimating travel times of emergency vehicles with the Euclidean distances and a constant travel speed. The Euclidean distance has been commonly considered as a satisfactory surrogate of network travel time in the literature [14,15,16]. Another approach is to approximate travel time from road segment speed limits. For instance, it has been used when looking for the optimal locations of healthcare centres with a modified p-median model [17] and when developing a versatile framework for solving location-allocation problems applicable to public service systems [18]. An extension of this approach was introduced in [19], where uncertainties in delays, travel time, and ambulance availability derived from EMS calls were considered to maximise the expected coverage, subject to the limited number of ambulances. Travel times were estimated using the road network data and by taking into account acceleration at the beginning and deceleration at the end of the trip. The higher availability of services based on several APIs (Google Maps APIs, TomTom Maps APIs, etc.) has provided new modelling opportunities. The problem of optimising preventive healthcare facility locations to maximise the participation of patients was addressed by [20]. Distances and travel times were estimated using Google Maps. The paper [21] proposed an approach on how to maximise the overall expected survival probabilities of multiple classes of patients. In numerical experiments, the travel time was again estimated using Google Maps. The drawback of such an approach is that models behind the API do not consider the driving characteristics of emergency vehicles that may differ from those of ordinary traffic. Modelling assumptions also concern the composition of emergency trips (e.g., after the treatment of a patient at the scene, the ambulance may return back to the station or the patient is transported to a hospital). Focusing on rural regions, the authors in [22] proposed dynamic relocation strategies in which ambulances are proactively redeployed throughout the region. The proposed theoretical framework considers the different compositions of trips; however, in numerical analysis, none of the patients was transported to a hospital. Another type of assumption concerns the allocation of ambulances to emergency cases. Paper [23] proposes a methodology for evaluation of the performances of response time thresholds in terms of the resulting patient survival rate. In the model, the closest available ambulance is always dispatched to a call. If two ambulances are equidistant from the call, one is randomly selected. Possible strategies for assignment of ambulances to incidents were investigated in [24], confirming that the choice of the strategy affects the fraction of late arrivals. Mixed simulation and optimisation approaches tend to apply similar modelling assumptions regarding emergency trips. A discrete event simulator for the Singapore Emergency Medical system was developed to investigate alternative actions regarding how to improve ambulance response time [25]. The destination hospital is decided based on the proximity to the incident scene, and travel times are deduced from speed limits of roads, without explicitly considering intersection delays, traffic congestion, acceleration, and deceleration. A historical emergency call database is used to deduce correction factors for the travel time. An optimisation model, to determine better ambulance base locations, and a simulation model, to observe dynamic behaviour of the systems, were proposed in [26]. The travel time was estimated based on Euclidean distances, considering a fixed correction factor and constant speeds for different periods of the day. Agent-based simulation applied to the modelling of travel time in the health service domain was presented in [27]. Assuming a constant travel time for each type of landscape, travel times are estimated in the form of a travel time grid. Simplifying assumptions related to the spatiotemporal characteristics of ambulance trips are often based on incomplete data or common sense without being fully supported by data. This is a consequence of the limited access to detailed and sufficiently large datasets on ambulance trips. Hence, data-driven research to model ambulance trips is required.
The majority of data-driven approaches in the area of EMS are concerned only with the temporal characteristics of trips. The spatial characteristics are left behind, as the emergency calls database is the most typical data source. Among temporal characteristics, the greatest focus is on the response time. An early paper [28] provided estimates of ambulance and fire truck speeds. In the analysis, road classes, time of day (rush hours and non-rush hours), and season (summer and winter) were considered. High priority call data were used to explore ambulance travel times in [29]. The travel time was modelled by a probability distribution, and the paper demonstrated how it can be used to create coverage maps. The paper highlighted the importance of going beyond the constant average speed assumption. EMS and fire-related calls were examined by [30] to explore the dependence between EMS response time and weather conditions. They found that the presence of snow is important for predictions. Apart from call data, response records constitute a precious source of information about response times. For example, they were used in [31] to study the spatial variation in ambulance response time for out-of-hospital cardiac arrests in the city-state of Singapore. The ambulance response time was found to be associated with traffic conditions, weekends, distance from the nearest station, and off-peak driving hours. Whether a longer response time can be attributed to poorer neighbourhoods was investigated in [32]. The data did not support such a hypothesis. A model predicting the ambulance arrival time based on historical records was proposed in [33]. The analyses of significant features confirmed that the use of blue lights and sirens shortened the travel time, an estimate of transport time based only on a street network significantly underestimated the transport time, and the wet weather increased the transport times.
It is sensible to combine data-centric and modelling approaches; however, such approaches are relatively rare in the literature. EMS call data were explored by [34]. They found that demand for ambulances significantly varies. The dependency discovered in data was used in combination with a mixed-integer optimisation model to explore how the reallocation of ambulances could compensate for the time-dependent demand. In [35], EMS cases for a 5-year interval from 2020 to 2050 were predicted by correlating current EMS cases with demographic factors and considering expected population changes. Next, the genetic algorithm was used to find the optimal future locations of ambulance stations, which were contrasted with the current design. A similar approach was presented in [36], where an artificial neural network was used to predict emergency cases combined with the p-center problem to locate facilities. The study shows that the combination of a predictive model and optimisation model (i.e., prescriptive optimisation) may bring significant improvements.
Ambulances have been equipped with information technologies based on GPS and the Global System for Mobile Communications (GSM) for more than 20 years [37]; however, only limited research efforts have been made to exploit the information contained in this data to facilitate modelling and planning efforts. After a thorough literature review, we discovered only a few papers that worked with GPS-based data that came from ambulances. Motivated by the issue of the redeployment of ambulances, the authors of [38] used a GPS-based vehicle locator data to predict the most likely ambulance speeds. The speed profile was estimated for each road segment while separately considering weekdays and weekends, with the mean average error reaching 15 km/h. Predictions of travel times together with routes of ambulances with blue lights and sirens activated were conducted by [39]. The GPS-based measurements were map-matched onto the road segments that were associated with weights. Considering the weights, the shortest path algorithm was used to predict the route and the travel time. The best results were achieved by amending the weights by using a simple regression model and correcting for deviations between the estimates and real data. A probabilistic prediction approach to estimate the distribution of travel times on each road segment was elaborated by [40]. The Bayesian model was shown to outperform other approaches (e.g., the harmonic mean of speeds on the road segment, maximum likelihood estimates from the log-normal distribution of travel speeds, and the method proposed by [29]); however, it is computationally exceedingly demanding. An improvement of the Bayesian model was presented in [41]. The travel time is modelled at the trip level and not the link level, and it depends on explanatory variables such as the time of day and day of the week. The proposed model is computationally more tractable on large networks and provides estimates comparable to [40]. As another use case for GPS-based ambulance data, the paper [42] presented a procedure for preparing a travel time coverage map for emergency journeys. Hence, research papers exploiting GPS-based measurements in unison focus on travel time, which is just a single aspect concerning the modelling of ambulance trips.
Similar ideas and methods that we used in our work can be found in the below-mentioned papers. The processing of raw GPS data is described in [40]. Discussion of appropriate thresholds for identifying stops of the trips is available in [43]. We used similar methods for extracting the trips from GPS data as in [44]. A description of travel time modelling (from station to patient) can be found in [29]. The model of the dependency of travel time on distance was introduced in [45]. Simulation tools intended for the analysis of EMS were used in [46,47]. Our pursuit of improving those tools inspired us to prepare this work.
1.2. The Scientific Contributions and Structure of the Paper
The need for undertaking research that aims to contribute to current EMS efficiency improvements is perpetual. The rapid construction of new highways and road infrastructure, the arrival of large companies attracting workers from distant areas, suburbanization (i.e., a shift of population from urban to close suburbs), ageing of the population, etc., all of which have been witnessed in the Žilina region and many other Slovak regions in the last few years, lead to changes that make the current EMS design inefficient. For example, by combining the p-median-like approaches with computer simulations, it was estimated by [46] that redesign of the existing EMS in Slovakia could reduce the average response time by 47 s, leading to an additional 121 patients who could be saved every year. Thus, there is the potential to bring non-negligible benefits with mathematical modelling efforts.
As the literature review demonstrated, these modelling activities are typically informed by emergency call data or emergency response reports while focusing on the temporal characteristics of ambulance trips. The operation of emergency ambulances is to a greater extent described by GPS-based data; however, such data are less accessible for research purposes. In previous studies, GPS data were mostly used for ambulance travel time predictions and travel time analysis. Consequently, there is a lack of scientific literature offering comprehensive models to inform EMS modelling activities about the spatiotemporal characteristics of ambulance trips.
This paper, through its primary contribution, will impact the state-of-the-art, and provides some secondary contributions. The primary contribution is a comprehensive set of spatiotemporal models. To the best of the authors’ knowledge, this is the first application of GPS-based measurements to modelling, in one paper, all spatiotemporal characteristics of emergency ambulance trips that are necessary to generate complete synthetic trips. To achieve this goal, we put together linear and nonlinear regression models, histograms, a graphical representation of the road network with the concept of shortest/fastest paths, and fitted a combination of standard probability distribution functions to data. Secondary contributions are as follows: (i) we developed a new rule-based method that enables us to extract emergency ambulance trips from GPS-based data whose novelty resides in the combination of existing methods; (ii) we compared modelling alternatives to choose the most suitable models, and (iii) we validated the proposed models by comparing the properties of trips generated by models with real trips in the test set.
The paper is organised as follows. The data processing is described in Section 2. Section 4 presents the results. Section 4.1 introduces the modelling concept. Models of ambulance trips are developed in Section 4.2 and they are validated in Section 4.3. The paper is concluded in Section 5.
2. Materials
Falck Dataset
The geo-referenced ambulance data used in this research were provided by the company Falck Záchranná a.s. In the early 2019, Falck Záchranná a.s. operated 107 out of 270 ambulance stations in Slovakia while covering approximately 39% of the geographical area of Slovakia. Falck Záchranná a.s. has been monitoring its fleet of ambulances by using GPS-based units, and all historical geo-referenced data have been stored on the web portal www.webdispecink.sk. Altogether, we received permission to extract the geo-referenced data of 17 ambulances (hereafter referred to as the Falck dataset). On the web portal, the raw data are organised into two tables. The first table contains car floating data, and it is composed of rows that represent individual measurements of the ambulance position characterised by the time stamp, latitude, longitude, speed, and status (on or off) of the siren and the blue lights. The second table characterises each ambulance trip by providing the from-address and to-address, start and end time, mileage, and fuel status at the end of the trip. The selected ambulances are serving the region of Žilina located in the northern part of Slovakia, which is composed of three counties: Žilina, Čadca and Kysucké Nové Mesto. The area is 1749 km and has a residential population of 281,000 inhabitants.
Typically, the ambulance crew waits at an ambulance station to be assigned a task from the operation centre. The operation centre handles emergency calls and distributes tasks to the ambulance crews. The geographical locations of 12 ambulance stations, where the crews of the 17 vehicles are based, and the frequency of measurements of the car floating data are shown in Figure 1. The frequency of measurements is evaluated by analysing the time between two consecutive measurements allocated to the same trip. Typically, measurements are taken each 5 to 25 s. Such a frequency is sufficient to model the ambulance trips, as it enables us to trace vehicle trajectories reliably at the level of road segments and to measure travelled distances and travel times.
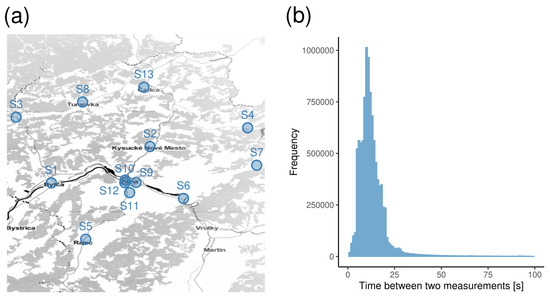
Figure 1.
(a) The geographical area of the Žilina region with the marked positions showing ambulance stations where the crews of the observed emergency vehicles are based. Four ambulance stations, S9–S12 are located within the city of Žilina, and ambulance stations S1–S8 and S13 are distributed in the neighbouring small towns and villages. (b) The frequency of measurements of the car floating data.
3. Methods
3.1. Data Pre-Processing Workflow
The purpose of the data pre-processing was to extract from the Falck dataset individual trips of ambulances. A presented method is a combination of existing methods. An ambulance engine is typically switched off while waiting for an emergency call at the station and it can be switched on or off a couple of times during a trip. Hence, the definition of trips based on switching the ambulance engine on or off, which is provided by the system archiving GPS-based positions of vehicles, does not fit the purpose of the paper. Unfortunately, the detailed reports on ambulance trips or annotated data that could be used to supervise a learning algorithm were not available to us. Therefore, we designed a simple rule-based approach and a workflow shown in Figure 2 to extract the trips of emergency vehicles from the Falck dataset.
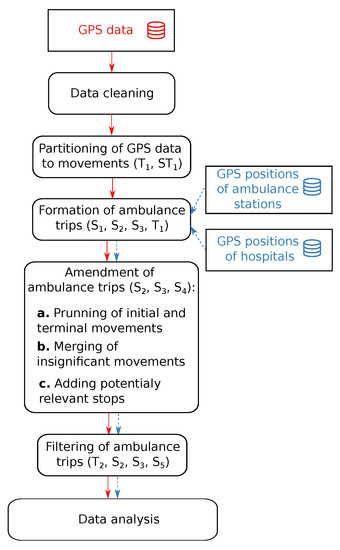
Figure 2.
A schematic illustrating the workflow applied to GPS-based data. Symbols enclosed in brackets indicate spatial and temporal characteristics used the in rules applied by the workflow. For the explanation of symbols please see the text.
Typically, an ambulance is located at a station, and the crew is waiting for an assignment from the emergency operation centre. Then, the crew drives the ambulance to the desired destination point(s), delivers the required aid, and returns back to the ambulance station. Occasionally, the returning part of the trip is used to refuel the ambulance or to get supplies of medical material. Hence, we consider a trip to be an ordered sequence of movements between points of interest (e.g., station(s), patient(s), hospital(s), etc.). Each trip is expected to be initialised and terminated at the same station.
Phases of the workflow and the rules applied when extracting trips have been derived from the above-mentioned assumptions. We aimed to develop a rule-based workflow that results in a reasonable set of ambulance trips and depends on a minimum number of parameters. To construct the rules, we considered temporal characteristics:
- Time between two consecutive GPS-based measurements ();
- Overall duration of the trip ();
Spatial characteristics:
- Aerial distance between two consecutive GPS-based measurements ();
- Aerial distance between an initial (terminal) GPS-based measurements of a movement and a hospital ();
- Aerial distance between an initial (terminal) GPS-based measurements of a movement and an ambulance station ();
- Length of a movement ();
- Overall length of a trip ();
A spatiotemporal characteristic:
- Instantaneous speed ().
In Figure 2, we use symbols assigned to characteristics to indicate their usage in phases of the workflow. The initial design of data processing steps was evaluated by inspecting the large sample of trip trajectories and trip stops displayed on the map, and by analysing basic statistical properties of the resulting trips (e.g., the numbers of movements constituting trips, lengths and durations of movements, frequencies of trip patterns, etc.). According to the findings, the initial workflow was amended, and finally, we obtained the following phases:
- Data cleaning: In this phase, typical data problems such as empty, unexpected, or redundant values were handled. Whenever possible, the data problems were fixed; e.g., values of categorical features such as the state of the blue lights and siren were unified. Problematic data, such as redundant table rows, were eliminated. As the data analysis focuses only on three administrative districts located in the Žilina region, the records corresponding to the ambulance leaving the area of the Slovak Republic were eliminated. Similarly, whenever we identified from the data that an ambulance was operated from a station in a different Slovak region, we excluded the corresponding records from the analysis. This occurred when the operator decided to allocate an ambulance to another area temporarily. Moreover, we analysed the average velocities between consecutive GPS measurements. Only a few records were identified as outliers and eliminated. For our purposes, every measurement was represented by ordered tuple , where t was the date and time (expressible in seconds) of the measurement, p was the position (longitude and latitude) of the vehicle, and v was the instantaneous velocity of the vehicle.
- Partitioning of GPS measurements to movements: For each ambulance, the GPS measurements were sorted by the time stamps. Hence, we obtained a sequence of measurements for each vehicle, where n was the number of measurements of a vehicle after data cleaning, and . The sorted sequence of GPS measurements was cut into subsequences (referred to as movements) by adding a dividing point between two consequent GPS measurements if at the time when the measurements were taken, the instantaneous velocity of the ambulance was 0 km/h (i.e., the ambulance did not move), and the time difference between those GPS measurements was at least 120 s. This value was empirically selected as a sufficient value for minimising the chance that a short stop due to the traffic situation or for other reasons (e.g., waiting at intersections) would be recognised as a significant stop during a trip. A formal description of the movement can be done as follows: let be a subsequence of indices such that k is a member of this subsequence if and only if km/h and s. We remark that is an appropriate natural number. Movement is a sequence of measurements with times
- Formation of ambulance trips: We define a trip of an ambulance as a sequence of co-located movements, and this sequence is initiated and terminated at an ambulance station, where is a subsequence of indices such that i is a member of this subsequence if and only if the aerial distance between the points and p is not larger than 300 m. (We remark that p is a position of ambulance station and is an appropriate natural number.) Two consecutive movements and are considered to be co-located if the aerial distance between the terminal point of the first movement and the initial point of the second movement is less than 200 m and the time difference is not larger than 2 h. Initial and terminal points of a movement were associated with an ambulance station or hospital if the aerial distance between them was less than or equal to 300 m (for an illustration, see Figure 3). GPS positions of ambulance stations and hospitals that are deployed across the Slovak Republic were kindly provided to us by the authors of the work [46]. Trips were assembled by processing the created movements (movement by movement) in the order of timestamps associated with the initial GPS measurements. The process of building an ambulance trip was initiated when the first GPS measurement of the movement was associated with an ambulance station. A trip was grown by appending co-located movements until a movement was found with the terminal point associated with the initial emergency station. Hence, a trip was a closed-loop initiated and terminated at the position of an ambulance station. If a pair of movements that were not collocated was encountered while an ambulance trip was being formed, the forming process was cancelled, and the next movement with the first GPS point associated with an ambulance station was used to initiate the process of trip building. The formation process continued until all movements were processed.
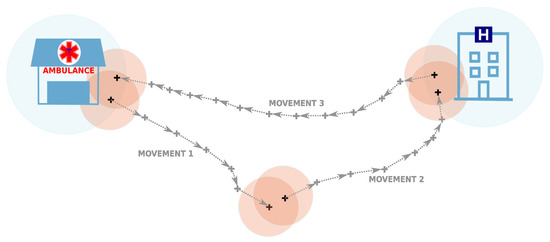 Figure 3. An illustration of a trip that originates and terminates at the ambulance station and is formed by three co-located movements. First, GPS measurements should be combined to form movements; secondly, a trip should be constituted from a sequence of co-located movements.
Figure 3. An illustration of a trip that originates and terminates at the ambulance station and is formed by three co-located movements. First, GPS measurements should be combined to form movements; secondly, a trip should be constituted from a sequence of co-located movements. - Amendment of ambulance trips: By evaluating a sample set of ambulance trips visualised on the map, we concluded that the majority of extracted trips were proper and ready for analysis. However, some flaws that repeated multiple times were identified:
- –
- Some trips contained very short movements, which appeared to be insignificant. Often, it was initial or terminal movement located within the area of an ambulance station.
- –
- Some trips approached a hospital or an ambulance station, but the movement was not split into two movements (i.e., the potential stop was not recognised).
- –
- Some trips were very short in length and in time.
- –
- Some trips were very long and very complex to interpret (taking a long time and having many stops till the ambulance returned back to the initial ambulance station).
To mitigate these problems, additional procedures were implemented:- –
- Pruning of initial and terminal movements: When the initial and terminal movements of a trip were very short and took place within the close surroundings of an ambulance station, they were insignificant for the trip. Therefore, a sequence of initial (terminal) movements was eliminated from the trip if their terminal (initial) point was closer than 300 metres from the ambulance station.
- –
- Merging of insignificant inner movements: In further analyses, we considered inner movements of a trip only in the context of hospitals, ambulance stations, and potential locations of patients that could be associated with the initial and terminal points of inner movements. Therefore, short inner movements (no longer than 500 m) were merged with the preceding or the following movements belonging to the same trip if either the endpoint of both movements was associated with the same ambulance station (and/or hospital) or both endpoints were not associated with any known point of interest (ambulance station or hospital).
- –
- The addition of potentially relevant stops: To not miss a potentially relevant stop of an ambulance at an ambulance station or a hospital, all movements were scanned by inspecting all inner GPS measurements. If an inner GPS measurement with the instantaneous velocity equal to zero was detected, it was checked whether it could have been associated (i.e., it was located closer than 300 m) with an ambulance station or hospital different from the ambulance station(s) or hospital(s) the initial and terminal points of a given movement were associated with. If there was more than one such inner point, the inner point which was closest to a given ambulance station or hospital was found. The movement was cut at an identified inner point, and two movements were formed.
- Filtering of emergency ambulance trips: Finally, to obtain an interpretable set of trips, we applied a set of simple filters. Trips composed of two movements were always selected. Trips consisting of more than two movements were selected only if at least 50% of initial and terminal points of inner movements were associated either with a hospital or with an ambulance station. To prevent the selection of trips that were too short or too complex for further analysis, we evaluated the overall lengths and durations of trips. We only selected trips longer than 1 km (to exclude short technical trips typically done within the area of an ambulance station) and shorter than 500 km (the distance that should be sufficient to accommodate trips to major Slovak hospitals located in the cities of Bratislava and Košice). For similar reasons, we considered only trips taking more than 15 min and less than six h.
The reported values of thresholds were obtained empirically by running a grid search and evaluating samples of the trips visually and by evaluating some simple quantities, such as lengths, durations, and the number of movements.
4. Results
4.1. Extraction of Emergency Ambulance Trips
The workflow presented in Section 3.1 was implemented in R while using dplyr, geosphere, HereR, scales, factoextra, OpenStreetMap, and ggplot2 libraries. We built 59,020 trips by applying the methodology described in Section 3. After applying the filtering where too short or too complex trips were excluded, 44,166 ambulance trips remained. Considering only ambulance stations where at least 100 trips were initialised, the total number of trips used in the analyses reached 44,099. In Figure 4, we analyse their basic properties. Ambulances are statically assigned to ambulance stations; however, on a long time scale, the assignments may change due to organisational reasons. Consequently, we found several stations (e.g., S1, S6, and S7), which are typically served by the same ambulance, and some ambulance stations (e.g., S3, S9, and S13) served by more than one ambulance. Similarly, we found some ambulances typically serving one station, and some other ambulances being used by multiple stations. In Figure 4, we report the ambulances’ numbers and dates from when the data were available. Not all vehicles were in operation from March 2016, when the recording of GPS traces was introduced. In all cases, the analysis included data collected until March 2019.
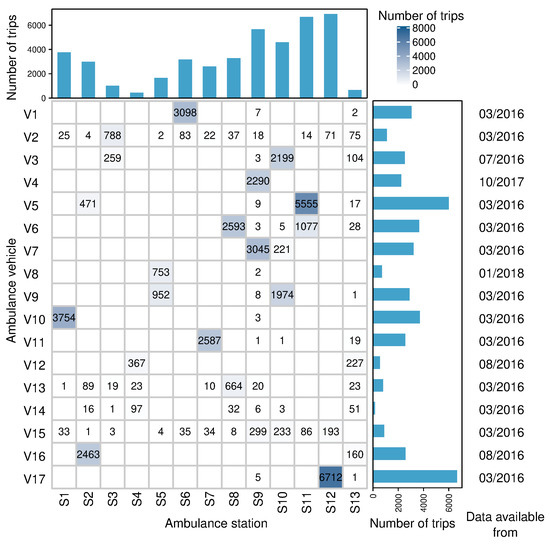
Figure 4.
Number of trips extracted from the Falck dataset for each ambulance and initial ambulance station. For each ambulance, we report the start date of the time period for which the data were available for analysis.
4.2. Modelling of Ambulance Trips
We used trips extracted from the Falck dataset to build a series of models that capture and reproduce the main characteristics of emergency ambulance trips. Simultaneously, models should be parsimonious to be easily used by other researchers utilising publicly available data. Thus, we searched for a reasonable trade-off between the accuracy of models, data requirements, and simplicity. The modelling workflow is visualised in Figure 5. In the following subsections, we target the spatial—and afterwards temporal—characteristics of trips.
Figure 5.
Flowchart of the workflow to model characteristics of emergency ambulance trips.
4.2.1. Trip Patterns
During the data pre-processing (phase “Formation of ambulance trips”), some initial and terminal points of movements were assigned to one of these two geographic categories: an emergency ambulance station or a hospital. The unassigned points were considered locations where treatment was provided to patients. We encoded each of these three locations with a character: “s” stands for an emergency ambulance station, “h” represents a hospital, and “p” symbolises a stop associated with the treatment of a patient. Then, we represent each trip by a string that describes the assignment of the initial and terminal points of movements that compose a trip. Figure 6 shows the frequencies of ten most frequent trip patterns. The great majority of trips were composed of two or three movements, and the number of movements exceeded ten only very rarely (see inset of Figure 6). By far, the two most common trip categories were “sphs” and “sps”, which together represent 77.5% of all extracted trips. These two categories involve visiting of a patient, which is, in the case of a trip category “sphs”, followed by the transport of the patient to a hospital. Less frequent trips involve pattern “shs”, corresponding either to the transport of a patient who came to the ambulance station on his own to the hospital, or a technical trip involving a visit to a hospital. Other categories involve combined trips when the ambulance was assigned to another trip before returning to the ambulance stations (“sphphs”), transport of a patient between two hospitals (“shhs”), and other relatively rare categories of complex trip patterns.
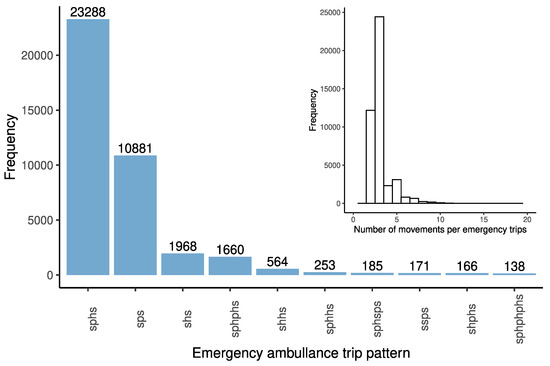
Figure 6.
Frequencies of emergency ambulance trip patterns. The characters encode the visit of an ambulance station (“s”), hospital (“h”), and patient “p”. The inset shows the frequencies of movement counts that constitute a trip. The empirical probability of observing a trip of a given pattern can be calculated by dividing the frequency by the total number of trips, 44,099.
4.2.2. Locations of Emergency Cases
The likelihood of the occurrence of emergency cases within a certain geographic area is frequently assumed to be proportional to the population [18,48]. This is a practical modelling assumption due to the high availability of population data. We used the population raster, shown in Figure 7b, providing the information on the 2018 residential population which is available in the resolution of m [49]. By using the same raster geometry, we counted the emergency cases extracted from the Falck dataset taking place within each raster cell.
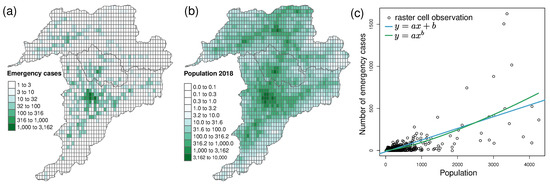
Figure 7.
(a) Counts of emergency cases (only “sps” and “sphs” trips were considered) in Žilina, Kysucké Nové mesto, and Čadca districts. (b) Residential population in 2018. In both cases, a raster with the cell size m was used. (c) Scatter plot of the number of emergency cases versus the population. Each point in the plot corresponds to a grid cell in panels (a,b). Lines show the fit to the data with linear and power functions, respectively.
To characterise the locations of emergency cases, we built regression models using the numbers of emergency cases (y) and the populations (x) of raster cells. We explored four different sizes of raster cells, , , , and and linear and power functions (see Table 1). As expected, while enlarging the cell size, the quality of the fit between the regression models and the number of emergency cases increased, at the expense of the precision, by which we modelled the locations of emergency cases. The values of adjusted suggest that the fit we started observing with the cell sizes 1500 and bigger was satisfactory, despite the fact that some residuals are relatively large (see also Figure 7c). This was confirmed by comparing the lengths and durations of synthetic and real trips. Thus, cell size is sufficient to identify locations of emergency cases at the level of municipality. We repeated the same procedure while using ambient population raster [50]; however, we found very similar results, with slightly worse fits by the models.

Table 1.
Functional forms, values of parameters, and adjusted obtained when modelling the dependency between the number of emergency cases and the residential population while using differently sized raster cells.
Functional forms in Table 1 can be used to determine locations of emergency cases when generating synthetic ambulance trips. By using them, we determined the expected number of emergency cases in each cell based on the population count. The probabilities of observing an emergency case in each raster cell were calculated by normalising obtained values. Probabilities were used to decide a grid cell randomly, and an emergency case’s exact location within the cell was determined with a uniform probability.
4.2.3. Allocation of Emergency Cases to Stations and Hospitals
Frequently, the allocation of an emergency case to a station is derived from its proximity. We applied a probabilistic approach considering the allocation of emergency cases to the closest, second closest, or farthest emergency station [17,20,24]. In Figure 8, we show the empirical probability distributions extracted from the data when considering Euclidean distances. We show a separate distribution for each selected range of the distance between the emergency case location and the nearest emergency ambulance station. The results show that the probability distribution changes significantly with the distance. As the distance increased, it became more likely that an emergency case was allocated to the closest emergency station. Such behaviour reflects the difference between urban and rural areas. In urban areas, the density of EMS stations is larger, and thus it is not so critical to allocate an emergency case to the closest station. When using road network distances, we obtained only slightly different probability distributions (see Figure S1 of the Supplementary Information (SI) File).
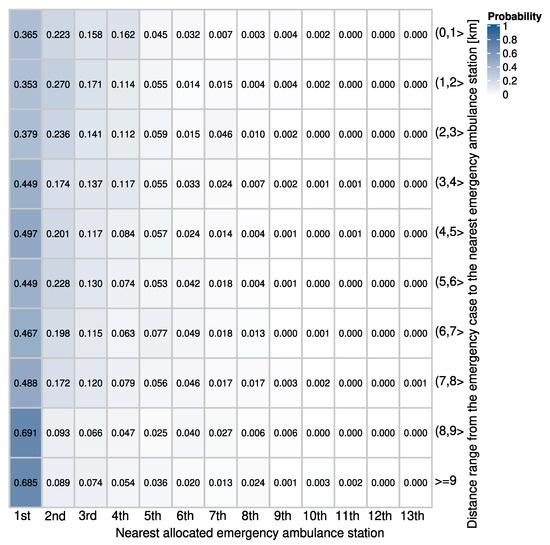
Figure 8.
The empirical probability distributions of emergency cases to be allocated to the k-th nearest ambulance station (in each row, we present the distribution for a range of the distance from an emergency case location to the nearest emergency ambulance station). In the evaluations, we used the Euclidean distances.
We applied a similar approach to model the allocation of emergency cases to hospitals. The values of empirical probabilities for hospitals are displayed in Figure 9. Again, the differences between Euclidean and road network distances are small, making the Euclidean distances a more practical approach, as they are computationally less demanding. When modelling a trip, an emergency case can be allocated to a station (hospital) following the reported empirical probabilities. Comparing the allocation of emergency cases to stations with hospitals revealed that a small number of hospitals was considered in each case, and most frequently, the closest hospital was selected. It can be explained by the significantly higher spatial density of stations.
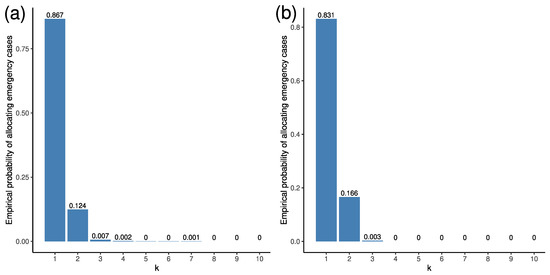
Figure 9.
The empirical probabilities of emergency cases to be allocated to the k-th closest hospitals. (a) We used the Euclidean distances. (b) We used the road network distances. In the analyses only “sphs” and “sps” trips were considered.
4.2.4. Routing of Emergency Ambulances
It is plausible to assume that ambulances take efficient paths, especially when heading towards an emergency case location or transporting a patient to a hospital. We explored two candidate models, the shortest (i.e., the path between two locations in the road network with the smallest sum of road segment lengths) and the fastest (i.e., the path with the smallest sum of travel time estimates of its constituent road segments) paths, and evaluated their correlations with the real paths taken by emergency ambulances. It is also not equally essential to model with high precision a part of the trip when an ambulance is transporting a patient to the hospital or when it is returning without a patient to a station. To explain these situations, we evaluated the routing at the level of movements.
We selected random samples of movements belonging to “sps” and “sphs” trip types from the training set, for each “sp”, “ph”, “hs”, and “ps” movement type. To find the shortest and fastest paths connecting initial and terminal points of movements, we used the HERE REST API [51]. To evaluate the agreement between the lengths and the durations of the movements and the estimated lengths and durations of the shortest and fastest paths, we used the following indicators:
where denotes the actual sample value of the length or duration, is the estimated value of the length or duration for either the shortest or the fastest path i, and represents the average of values , for . The values of indicators are presented in Table 2.

Table 2.
An evaluation of the agreement between the lengths and durations of real movements and the shortest and the fastest paths connecting the same origins and destinations.
Though the lengths of shortest and fastest paths differed only slightly, we can conclude that the fastest paths modelled the lengths of movements better than the shortest paths. The fastest paths constituted a very good model for the routing of “sp” (see Figure 10a), “ph” (see Figure 10b), and “hs” type movements, due to high values of the Pearson correlation coefficient and low values of MAPE and RMSE. As expected, the error was mostly caused by underestimating the lengths of movements when using the fastest paths. The lengths of “ps” movements were captured by the fastest paths less precisely (see Figure 10c). As the ambulance is returning to the station, the crew is sometimes refuelling the vehicle or visiting the main station. Consequently, routing efficiency decreases. Somewhat surprisingly, we did not observe a similar effect for the “hs”-type movements, which might be related to the difficulties with inferring the positions of “p” stops from GPS data, whereas “h” stops were identified more reliably, as we knew the exact geographical locations of hospitals.
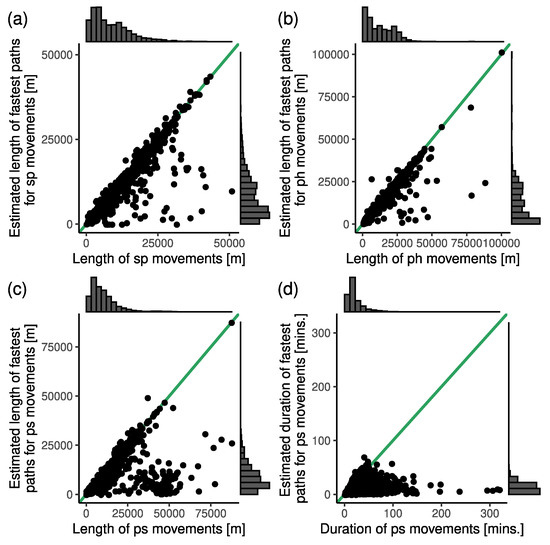
Figure 10.
The scatter plots of observed and estimated parameters of movements. (a) The lengths of “sp”-type movements. (b) The lengths of “ph”-type movements. (c) The lengths of “ps”-type movements. (d) The duration of “ps”-type movements. To facilitate the comparison, we display a diagonal line with slope in each plot, and we show the histogram for each quantity.
When making the HERE REST API requests, we set the initial date and time of departure. We activated a parameter that enabled us to consider the real-time traffic situation when calculating the shortest and fastest paths. Nevertheless, Table 2 and Figure 10d show that the estimated durations using shortest and fastest paths provided by the HERE REST API [51] were not good estimates of travel time. For this reason, we devised a specific model to estimate the travel time, which is presented in Section 4.2.5.
4.2.5. Travel Time
We developed a simple model to provide sufficiently accurate predictions of travel time. We consider the most common trips “sps” and “sphs”, and five types of movements: “sps_sp” (the first part of the string indicates the type of trip, and the second part indicates the type of the movement; in this case, the first movement of the trip was heading from the ambulance station “s” to the patient location “p”), “sps_ps”, “sphs_sp”, “sphs_ph”, and ”sphs_hs”. We prepared a model for each type of movement. We derived the travel time T from the dependency on the movement length d. By adopting the approach proposed by [29], where the ambulance movements from station to patient (i.e., ”sps_sp” and “sphs_sp”) are considered, we introduce the model
where and are the following functions:
with model parameters a, b, , , , c, , and . Numerical experiments on the Falck dataset resulted in values of close to zero. Hence, we simplified the modelling function to the following form:
For the travel time in minutes and the distance d in metres, we obtained parameter values reported in Table 3. The data and the obtained functions are presented in panels (a)–(e) of Figure 11. The linear part of the function was computed by linear regression, and parameter c was given by a continuity requirement for . Parameter was computed numerically to minimise the standard deviation. During the data processing, we used the Cook distance to identify and discard the outliers, while following recommendations given in the reference [52] (p. 112).

Table 3.
Parameter values of the travel time models given by Equation (6) fitted on the Falck dataset.
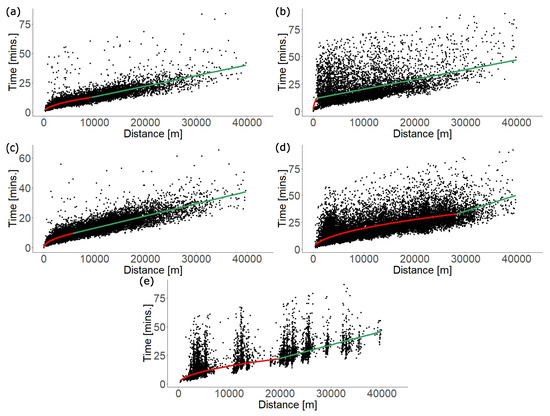
Figure 11.
The dependence of travel time on the travelled distance for (a) “sps_sp”, (b) “sps_ps”, (c) “sphs_sp”, (d) “sphs_ph”, and (e) “sphs_hs” movements. The function is displayed by red on interval and by green on interval , 40,000⟩.
We can observe that movements “sps_sp” and “sphs_sp” led to similar results as those reported in the reference [29]. For other movements, the data exhibit more variance. For “sphs_ph” movements, we obtained significantly different values of parameters, and the breaking point was at a higher value of . We suppose that this was caused by conditions involved during patient transport. In the case of “sphs_hs” movements, we observed specific clusters of data that were caused by fixed distances between hospitals and ambulance stations. In the case of “sps_ps” and “sphs_hs” movements, the great dispersion of data can be explained by the fact that the ambulance drivers take various detours or make stops.
4.2.6. Provision Times
Provision times, i.e., durations of stops at patients’ locations or hospitals, constitute important parts of the trip duration. In Figure 12, we introduce the empirical distribution of provision times for the “sps” and “sphs” trips. Distributions of provision times are bimodal. Most likely, short provision times correspond to cases when patients are immediately loaded into the ambulance. In contrast, longer provision times correspond to emergency cases when treatment of the patient at the scene is required. We model the density functions by the weighted sum of two gamma distributions:
where is the weight, , for are parameters that need to be fitted to data, and represents the provision time (i.e., we considered provision times longer than or equal to two minutes due to data processing reasons). The symbol denotes the gamma function. For the fitting, we used a grid search while evaluating the quadratic error function. The values of parameters are presented in Table 4 and the corresponding density functions are visualised in Figure 12a–c. Interestingly, by comparing panels (a) and (b), we see that the distribution of provision times for “sps” trips is slightly wider than for “sphs” trips.
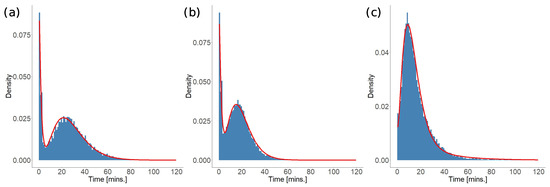
Figure 12.
The empirical distribution of provision times. (a) Durations of patient treatments in “sps” trips. (b) Durations of patient treatments in the “sphs” trips. (c) Durations of stops at hospitals in the “sphs” trips. The red line indicates the fit to the data given by Equation (7).

Table 4.
Parameter values of the distribution function (7) fitted on the Falck dataset.
The quality of the fit was validated by the Kolmogorov–Smirnov (KS) test. The test was successful if it output the value of the statistic D which was lower than the critical value (where is the level of significance). We considered as the level of significance. The results of the KS test, presented in Table 5, confirmed the significance of all obtained distribution functions.

Table 5.
Results of the Kolmogorov–Smirnov test.
4.2.7. Modelling the Start Times of Ambulance Trips
In simulation models of EMS, could be necessary to model the occurrence of emergency ambulance trips in time. We considered three relevant time scales for ambulance trips: time of day, day of week, and month of the year. In Figure 13, we evaluate the empirical probabilities of an ambulance trip to be initiated within a given period. During the day, the probability fluctuates, but we can observe two peaks: first, at approximately 9.00 a.m. and second at 7.00 p.m. Emergency cases were approximately uniformly distributed over the days of the week and months of the year. We considered the trip types “sps” and “sphs” separately, finding very similar results. Hence, we report only figures summarising all trips of these two types.
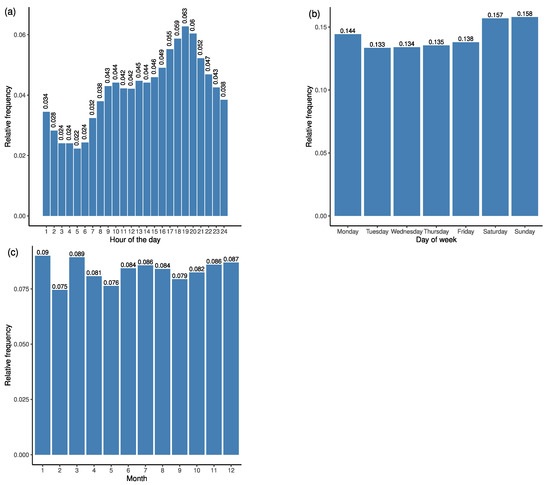
Figure 13.
Empirical probabilities of the initial time of emergency ambulance trips evaluated at three different time scales. (a) The time scale of hours. (b) The time scale of weekdays. (c) The time scale of months. The analysis was done on “sps” and “sphs” trips. To avoid the bias caused by different availability of data from ambulances, in panel (c), we considered only trips that took place in 2018, as the data from all vehicles were available for that complete year.
Determining the total number of trips that needed be generated for a given area based on our dataset (e.g., per unit of time and per capita) was difficult, as we analysed data from only one service provider. Falck Záchranná a.s. was the major service provider in this period for the given area; however, we cannot exclude that emergency medical services were also provided by some other providers, e.g., ambulances operated by hospitals.
Considering the total number of trips of patterns of “sps” and “sphs” types reported in Figure 6 and the overall period in which the data was collected, we calculated the average number of trips per month; see Table 6. Thus, these numbers apply to the ambulances and stations considered in this paper, and if needed, these numbers can be recalculated per ambulance or per ambulance station. Nevertheless, these numbers were used to evaluate the system from the perspective of one service provider only.

Table 6.
The total number and the average number of trips per month and per trip pattern.
4.3. Validation of Models
We validated models derived from data by using them to generate ambulance trips and comparing them with real trips. We split data into training and test sets, which is a standard approach in statistical and machine learning to test the generalisation abilities of models [53]. First, we split the trips of types “sps” and “sphs” randomly into two groups: training set (8646 and 18,555 trips of types “sps” and “sphs”, respectively, which is about 80% of trips) and test data (2235 and 4733 trips of types “sps” and "sphs", respectively, which is about 20% of trips). To create the models presented in Section 4.2.2, Section 4.2.3, Section 4.2.4, Section 4.2.5 and Section 4.2.6, we used only the training data. Second, using models presented in Section 4.2.2, Section 4.2.3, Section 4.2.4, Section 4.2.5 and Section 4.2.6, we generated 2235 and 4733 trips of types “sps” and “sphs”, respectively, and in this section we compare them with the trips in the test set.
The process of generating a trip is initiated by drawing a start time (hour of the day) from the empirical distribution presented in Section 4.2.7. As concluded from the analyses, the probabilities of observing an ambulance trip as a function of the month of year or day of the weak are close to uniform. Thus, the day when an ambulance trip took place was chosen with uniform probability from the interval 1 March 2016 to 30 April 2019, which is the period when the data were collected.
To generate the spatial characteristics of a trip, we started by selecting the location of an emergency case by using a model presented in Section 4.2.2. Next, the location was assigned to an emergency station, and if it was an “sphs” trip, to a hospital by applying the strategies presented in Section 4.2.3. To find routing for all movements, the approaches discussed in Section 4.2.4 were utilised while using HereR library [51] and considering the start times, to account for traffic. The provision times at the emergency locations and at the hospitals were drawn from empirical distributions presented in Section 4.2.6). Finally, travel time was set based on models presented in Section 4.2.5.
To validate the proposed models and evaluate which strategies lead to the most realistic spatial characteristics of trips, we compared the distribution of movements length and duration of generated trips with the trips in the test set. Preliminary evaluations indicated that the largest impacts on the obtained density functions were the locations of emergency cases, the allocation of cases to hospitals, and the routing. Thus, no modelling alternatives were considered for the empirical probabilities that characterise the allocation of emergency cases to stations presented in Figure 8. We generated several sets of trips while considering the following modelling options:
- Location of an emergency case (see Section 4.2.2):
- —default: By exponential model to identify a grid cell and then choose a location within a cell with uniform probability.
- —alternative: By the linear model to choose a grid cell and then find a location within a cell with uniform probability.
- —alternative: To choose a grid cell with empirical probabilities (derived from data) and then find a location within a cell with uniform probability. Comparison of this option with and enables us to evaluate the models locating the emergency cases based on the proposed models that depend on the population density.
- Allocation of an emergency case (see Section 4.2.3):
- –default: To a hospital following the empirical probabilities of allocating a station to the 1st, 2nd, 3rd, and so on closest hospital;
- —alternative: To the closest hospital;
- —alternative: To a hospital following the closest-hospital-specific empirical probability distribution to allocate a station to the 1st, 2nd, 3rd, and so on closest hospital.
- Routing (see Section 4.2.4):
- —default: Following the fastest path in the road network;
- —alternative: Following the shortest path in the road network.
4.3.1. Validation of Spatial Characteristics
To evaluate the above-mentioned modelling options, we compare the probability density function of movement length with the default settings (i.e., ) and test data in Figure 14. Models fit the test data for both movements (“sp” and “ps”) of “sps” trips and the “sp” movements of “sphs” trips well. Models fit less satisfactorily the movements heading towards the hospital, as the distribution was multimodal for that phase. This effect was even more pronounced with the movements returning from the hospital to the ambulance station. In the latter case, this was caused by detours (e.g., often related to visits to petrol stations or destinations other than home emergency stations) that ambulances often take. Detours add to the complexity of movements and are difficult to predict. Movements when an ambulance is returning back to the emergency station are not so critical for the EMS, as they have a limited impact on the quality of service provided to the patients. For this reason, we did not put a high priority on these movements.
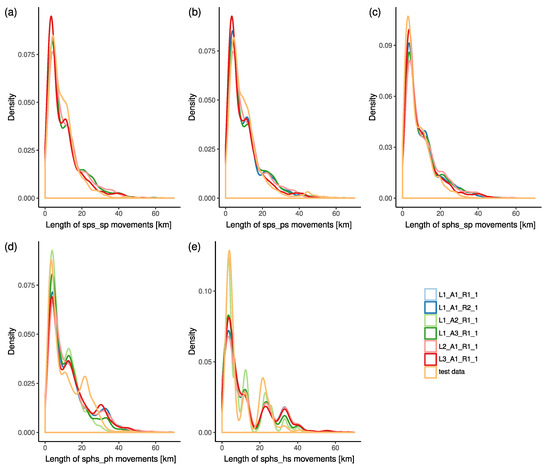
Figure 14.
The probability density functions of movements’ lengths for “sps” and “sphs” trips. Each panel (a–e) corresponds to a different movement type of “sps” and “sphs” trips (indicated by the x-axis label). The default settings, i.e., , are compared with test data, a linear model (), empirical probabilities (), the allocation of emergency cases to the closest hospital (), closest hospital-specific empirical probability distributions (), and the shortest path’s routing ().
By comparing the modelling options with the trips in the test sets, we validated the models. To facilitate the comparison, we present in Table 7 the values of the Kullback–Leibler () divergence [54].
where is the distribution corresponding to the test dataset and is the distribution corresponding to a model. The divergence is a measure of a distance between two density functions. Values of are non-negative. Larger values indicate larger differences between distributions and if and only if the distributions are identical.

Table 7.
The values of the KL divergence measuring the distances between probability density functions of movement lengths obtained by models and trips in the test dataset. In column , the row averages of values are presented.
To understand the impact of randomness on the density functions, we generated five independent sets of trips (i.e., –) for the default settings (i.e., ) while varying the seed that affects the sequence of numbers produced by random number generators. A comparison of the first five rows in Table 7 with other rows confirms that the variance due to the randomisation was smaller than the differences between models. Instances of random numbers had only minor effects on the distribution, confirming that the test set constitutes a sufficiently large sample of data (see also Figure S2 of the Supplementary Information File). Overall, the differences between models and the test data are small. No model fit the test data in the best way for all types of movement. According to (the row average of values), the lengths of movements are approximated the best by the model. The values of for the , , and models are similar as well. Hence, modelling options and , presented in Section 4.2.2 are valid alternatives for .
4.3.2. Validation of Temporal Characteristics
Analogously to the previous section, here we compare the temporal characteristics of trips with the test set. Figure 15 presents the probability density functions of the duration of movements determined by models presented in Section 4.2.5. The initial movements (“sps_sp” and “sphs_sp”) agree very well with the test data. The dependency of the duration of outbound movements from a patient’s location on distance is associated with higher variability (see panels (b) and (d) of Figure 11). Consequently, the estimates of movement duration (panels (b) and (d) in Figure 15) were less precise. Similar to lengths, the density function of the duration of return movements to the station of the trip type “sphs” is multimodal (see panel (e) of Figure 15). It is difficult to fit with models such complex shapes exactly; nevertheless, the overall trend was well captured. Again, it is worth noting that return movements to the ambulance station are not so critical for the quality of service provided by the EMS and are often combined with various types of poorly predictable detours. To gain better insights into the differences in the performance of models, we calculated values of the KL divergence, ; see Table 8. At the movement level, values confirm that initial movements (“sps_sp” and “sphs_sp”) were fitted by models better than other movements. No model performed the best for all types of movements, and the performances of the models were very similar. Moreover, the values for the models are comparable to the values obtained for randomisations of the default model, –. In Figure 16, we compare the probability density functions of the durations of entire trips resulting from models with the test data. The models fit the test data very well. The values of the KL divergence in Table 8 confirm the good fit.
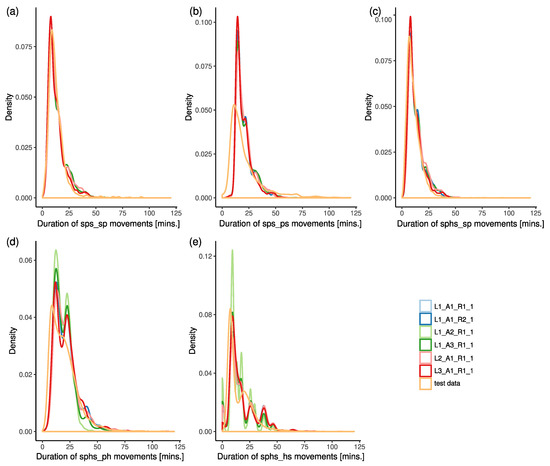
Figure 15.
The probability density functions of movement duration. Each panel (a–e) corresponds to a different movement type of “sps” and “sphs” trips (indicated by the x-axis label). The default settings, i.e., , are compared with test data, a linear model (), empirical probabilities (), the allocation of emergency cases to the closest hospital (), closest hospital-specific empirical probability distributions (), and shortest path routing ().

Table 8.
Values of the divergence measuring the differences between the probability density functions of duration for generated movements (left) and generated trips (right), and trips in the test dataset. The row averages of values for movements are presented in column .
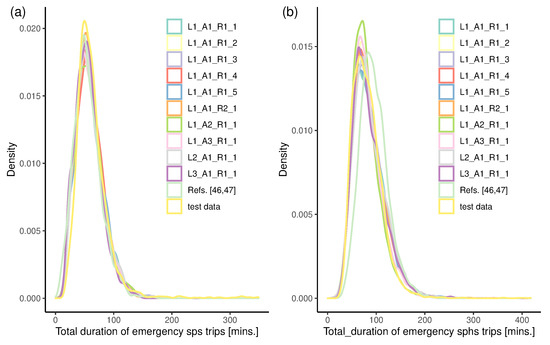
Figure 16.
The probability density functions of trip duration. Panel (a) corresponds to “sps” and panel (b) to “sphs” trips. Five randomisations of default settings, i.e., to , are compared with linear model (), empirical probabilities (), the allocation of emergency cases to the closest hospital (), closest hospital-specific empirical probability distributions (), shortest path routing (), the model presented in [46,47], and test data.
In addition, we applied the Kolmogorov–Smirnov (K-S) test to investigate the hypothesis that values of the lengths and durations of movements and trips fit such values in the test dataset. The results of the K-S test are presented in Tables S1–S5 of the Supplementary Information File. In the majority of cases, the hypothesis was not rejected. The rejected cases are associated with the times during movements when the ambulance was returning to the station. For the model , the hypothesis was also rejected for the times during movements where a patient was being transported to the hospital.
Overall, regarding the length and the duration, the differences between models’ variants are small. Hence, the best choice appears to be a simple and less data-demanding model. From this perspective, the default model is a reasonable choice.
4.4. Use of the Data Models in Simulations and Optimisations
Researchers and practitioners can use the proposed modelling framework in optimisations and simulations of EMS to improve the validity of models. The benefits of the proposed model against assumptions applied in optimisation and simulation models of EMS were visible in several comparisons presented in the paper. For example, Figure 10d shows a weak correlation between the travel times of movements and estimated travel times provided by HERE REST API. Hence, we can expect that travel time estimates provided by HERE REST API would lead to pure models. In [22], visits of hospitals were excluded in numerical analysis. Similarly, optimisation models based on the p-median approach excluded hospital visits [17,18]. In Figure 6, we showed that trips that included visits to hospitals were dominant. Excluding the visits to hospitals when modelling ambulance trips would undoubtedly lead to a significant difference in the distributions of the durations and lengths of movements (trips), as is visible in Figure 14, Figure 15 and Figure 16. In Figure 16, we added a comparison with the state-of-the-art model presented in [46,47]. We found a good fit for “sps” trips; the model [46,47] only very slightly overestimated the number of trips with very short durations. For “sphs” trips, model [46,47] systematically overestimated the duration. Thus, this comparison confirmed the superiority of our models. Hence, we recommend EMS researchers to apply (if possible) valid models derived from data, rather than models based on assumptions derived from incomplete data or common sense.
In simulations, realistic ambulance trips that well fit the spatiotemporal properties of real trips can be generated in the same way as validation trips in Section 4.3. Several components of the modelling framework can be used in optimisation models. In the p-median or p-centre-based optimisation models [4], the costs associated with the assignment of patients to ambulance stations or hospitals can be more precisely estimated by considering the probabilities of the most frequent trip patterns presented in Section 4.2.1. Furthermore, descriptions of the dependencies of emergency occurrences in the population, introduced in Section 4.2.2, can be used to estimate the spatial distribution of the EMS demand better. Empirical probability distributions describing allocation of ambulances to emergency cases (Section 4.2.3) can be used to model such allocations realistically for location optimisations. Analyses of the routing (Section 4.2.4) and travel time (Section 4.2.5) can be used in the coverage type of optimisation models, where valid estimates of times required to reach patients are crucial.
5. Conclusions
A modelling framework able to reproduce some statistical spatiotemporal characteristics of emergency ambulance trips was proposed in this paper. More specifically, a unique GPS-based dataset describing the operation of ambulances was collected. A rule-based procedure was designed and applied to extract a set of ambulance trips from GPS-based measurements. A series of models capturing the main spatiotemporal characteristics of ambulance trips was created and fitted on the training dataset. Selected modelling alternatives were compared and evaluated using the test dataset. The results of numerical experiments demonstrated that the models satisfactorily capture the statistical distributions describing the lengths and durations of ambulance trips. The Kullback–Leibler divergence reached values in the range from to for travelled distances and from to for travel times. The K-S test at the significance level of accepted the fit in the vast majority of cases.
The differences between model variants were small; hence, the best choice appears to be a simple and less data-demanding model. Thus, a reasonable choice is the default model , and applying the following modelling choices: exponential dependency on the population density to locate emergency cases; emergency cases being allocated to hospitals following the empirical probabilities of allocating a station to the 1st, 2nd, and 3rd closest hospitals (etc.); and ambulances being routed using fastest paths. This is an important contribution that opens new research perspectives, as spatiotemporal characteristics of emergency trips represent an important input to pursue the operational excellence of EMS systems.
The proposed models are dependent on publicly available tools and data, and hence are simple to use. Together with models, we also presented the parameter values. Thus, models can be easily used by other researchers or practitioners to support modelling efforts in the EMS domain. Generated ambulance trips can be used to optimise the operation of the EMS or assess the suitability of the EMS design, e.g., to determine a suitable number of ambulances, the scheduling of ambulance crew shifts, or the appropriate number of ambulance stations and their locations.
Limitations and Future Research
Several important limitations are inherited from our modelling assumptions. The majority of operations (e.g., transport and provision of the service) are considered to be independent, and possible dependencies—e.g., the dependence of the provision time on the ambulance crew—are neglected. To keep the models easily applicable, some possibly relevant determinant factors (e.g., the use of blue lights and sirens) were been considered in this paper. All the data were collected in the Žilina region, where only several medium-sized and small municipalities are located. The whole area is mountainous, and only valleys are inhabited. This has a profound impact on the shape of the road network and thus on emergency trips. Both urban and rural areas are present and served by ambulances. Thus, the presented results are primarily applicable to similar landscapes—e.g., Bolzano (Italy), Arecibo (Portoriko), and Medford (USA, Oregon). Our results should not be generalised to flatlands, highly urbanised areas, or other types of high-density population areas. Nevertheless, the applied modelling techniques are universal and can be applied to data from an arbitrary region.
Our models will bring direct practical benefits, as they will be implemented in a simulation model of EMS [46,47] that has been previously used in several applications. An important part of further investigations should be quantifying improvements resulting from data-centric modelling by using optimisation and simulation models. Future work will involve using determinant factors and modelling techniques to better predict locations of emergency cases. In addition, future work will explore which modelling techniques can provide the best predictions of ambulance trajectories and ambulance travel times. Further research could focus on the exploration of possibilities regarding how to design data-centric approaches to optimise the structure of EMS, or on the study of delays of ambulances at signalised and unsignalised intersections from GPS-based measurements. Point processes could be applied, e.g., to destinations, or other components, to model the spatial characteristics of ambulance trips.
Supplementary Materials
The following are available at https://www.mdpi.com/article/10.3390/math9172165/s1.
Author Contributions
Conceptualisation, Ľ.B.; methodology, Ľ.B. and P.C.; software, Ľ.B. and P.C.; validation, Ľ.B. and P.C.; investigation, Ľ.B. and P.C.; resources, Ľ.B.; data curation, Ľ.B.; writing—original draft preparation, Ľ.B. and P.C.; writing—review and editing, Ľ.B. and P.C.; visualization, Ľ.B. and P.C.; project administration, Ľ.B.; funding acquisition, Ľ.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Slovak Research and Development Agency under contracts SK-IL-RD-18-005, “ICT and smart cars for efficient emergency response and traffic management”, and APVV-19-0441, “Allocation of limited resources to public service systems with conflicting quality criteria”; in part by projects VEGA 1/0216/21, “Design of emergency systems with conflicting criteria with the tools of artificial intelligence”, and VEGA 1/0089/19 “Data analysis methods and decisions support tools for service systems supporting electric vehicles”; and in part by the Operational Program Integrated Infrastructure 2014–2020 “Innovative Solutions for Propulsion, Power, and Safety Components of Transport Vehicles” through the European Regional Development Fund under grant ITMS313011V334.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Acknowledgments
We thank Tomáš Blázy for his support with GPS-based data extraction from www.webdispecink.sk and Falck Záchranná a.s., namely, Miloslav Váňa and Jozef Sudický, for enabling access to GPS-based data for research purposes. We thank Shima Rahmani for valuable comments and suggestions. Finally, we thank Peter Jankovič for sharing with us data from his simulation model and three anonymous reviewers who helped us to improve the paper.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| EMS | Emergency Medical Services |
| GPS | Global Positioning System |
| API | Application Programming Interface |
| GSM | Global System for Mobile Communications |
| sps | station-patient-station drive |
| sphs | station-patient-hospital-station drive |
| MAPE | Mean Percentage Absolute Error |
| RMSE | Root Mean Square Error |
| KS | Kolmogorov–Smirnov |
| KL | Kullback–Leibler |
References
- Zaffar, M.A.; Rajagopalan, H.K.; Saydam, C.; Mayorga, M.; Sharer, E. Coverage, survivability or response time: A comparative study of performance statistics used in ambulance location models via simulation–optimization. Oper. Res. Health Care 2016, 11, 1–12. [Google Scholar] [CrossRef]
- Erkut, E.; Ingolfsson, A.; Erdogan, G. Ambulance location for maximum survival. Nav. Res. Logist. 2008, 55, 42–58. [Google Scholar] [CrossRef]
- Zhang, Z.; He, Q.; Gou, J.; Li, X. Analyzing travel time reliability and its influential factors of emergency vehicles with generalized extreme value theory. J. Intell. Transp. Syst. Technol. Plan. Oper. 2019, 23, 1–11. [Google Scholar] [CrossRef]
- Eiselt, H.A.; Marianov, V. Foundations of Location Analysis; Business and Economics ed.; Springer: Boston, MA, USA, 2012. [Google Scholar]
- Eiselt, H.A.; Marianov, V. Applications of Location Analysis; Business and Economics ed.; Springer: Boston, MA, USA, 2015; Volume 232. [Google Scholar] [CrossRef]
- Brotcorne, L.; Laporte, G.; Semet, F. Ambulance location and relocation models. Eur. J. Oper. Res. 2003, 147, 451–463. [Google Scholar] [CrossRef]
- Farahani, R.Z.; Asgari, N.; Heidari, N.; Hosseininia, M.; Goh, M. Covering problems in facility location: A review. Comput. Ind. Eng. 2012, 62, 368–407. [Google Scholar] [CrossRef]
- Farahani, R.Z.; SteadieSeifi, M.; Asgari, N. Multiple criteria facility location problems: A survey. Appl. Math. Model. 2012, 34, 1689–1709. [Google Scholar] [CrossRef]
- Basar, A.; Catay, B.; Unluyurt, T. A taxonomy for emergency service station location problem. Optim. Lett. 2012, 6, 1147–1160. [Google Scholar] [CrossRef] [Green Version]
- Marianov, V. Location Models for Emergency Service Applications. 2017. Chapter 11. pp. 237–262. Available online: https://pubsonline.informs.org/doi/abs/10.1287/educ.2017.0172 (accessed on 14 September 2020).
- Aringhieri, R.; Bruni, M.; Khodaparasti, S.; van Essen, J. Emergency medical services and beyond: Addressing new challenges through a wide literature review. Comput. Oper. Res. 2017, 78, 349–368. [Google Scholar] [CrossRef]
- Yao, J.; Zhang, X.; Murray, A.T. Location optimization of urban fire stations: Access and service coverage. Comput. Environ. Urban Syst. 2019, 73, 184–190. [Google Scholar] [CrossRef]
- Degel, D.; Wiesche, L.; Rachuba, S.; Werners, B. Reorganizing an existing volunteer fire station network in Germany. Socio-Econ. Plan. Sci. 2014, 48, 149–157. [Google Scholar] [CrossRef]
- Cudnik, M.T.; Yao, J.; Zive, D.; Newgard, C.; Murray, A.T. Surrogate markers of transport distance for out-of-hospital cardiac arrest patients. Prehosp. Emerg. Care 2012, 16, 266–272. [Google Scholar] [CrossRef]
- Murray, A.T. Optimising the spatial location of urban fire stations. Fire Saf. J. 2013, 62, 64–71. [Google Scholar] [CrossRef]
- Murray, A.T. Fire Station Siting; Springer International Publishing: Cham, Switzerland, 2015; pp. 293–306. [Google Scholar]
- Jia, T.; Tao, H.; Qin, K.; Wang, Y.; Liu, C.; Gao, Q. Selecting the optimal healthcare centers with a modified p-median model: A visual analytic perspective. Int. J. Health Geogr. 2014, 13, 42. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cebecauer, M.; Buzna, Ľ. A versatile adaptive aggregation framework for spatially large discrete location-allocation problems. Comput. Ind. Eng. 2017, 111, 364–380. [Google Scholar] [CrossRef]
- Ingolfsson, A.; Budge, S.; Erkut, E. Optimal ambulance location with random delays and travel times. Health Care Manag. Sci. 2008, 11, 262–274. [Google Scholar] [CrossRef]
- Gu, W.; Wang, X.; McGregor, S.E. Optimization of preventive health care facility locations. Int. J. Health Geogr. 2010, 18, 9–17. [Google Scholar] [CrossRef] [Green Version]
- Knight, V.; Harper, P.; Smith, L. Ambulance allocation for maximal survival with heterogeneous outcome measures. Omega 2012, 40, 918–926. [Google Scholar] [CrossRef]
- Van Barneveld, T.C.; Bhulai, S.; van der Mei, R.D. A dynamic ambulance management model for rural areas. Health Care Manag. Sci. 2017, 20, 165–186. [Google Scholar] [CrossRef]
- McLay, L.A.; Mayorga, M.E. Evaluating emergency medical service performance measures. Health Care Manag. Sci. 2010, 13, 124–136. [Google Scholar] [CrossRef]
- Jagtenberg, C.J.; Bhulai, S.; van der Mei, R.D. Dynamic ambulance dispatching: Is the closest-idle policy always optimal? Health Care Manag. Sci. 2017, 20, 517–531. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lam, S.S.W.; Zhang, Z.C.; Oh, H.C.; Ng, Y.Y.; Wah, W.; Ong, M.E.H. Reducing ambulance response times using discrete event simulation. Prehosp. Emerg. Care 2014, 18, 207–216. [Google Scholar] [CrossRef]
- Nogueira, L.C.; Pinto, L.R.; Silva, P.M.S. Reducing emergency medical service response time via the reallocation of ambulance bases. Health Care Manag. Sci. 2016, 19, 31–42. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.; Lassa, J. Interactive, open source, travel time scenario modelling: Tools to facilitate participation in health service access analysis. Int. J. Health Geogr. 2017, 16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Erkut, E.; Fenske, R.; Kabanuk, S.; Gardiner, Q.; Davis, J. Improving the emergency service delivery in St. Albert. INFOR Inf. Syst. Oper. Res. 2001, 39, 416–433. [Google Scholar] [CrossRef]
- Budge, S.; Ingolfsson, A.; Zerom, D. Empirical analysis of ambulance travel times: The case of Calgary emergency medical services. Manag. Sci. 2010, 56, 716–723. [Google Scholar] [CrossRef]
- McLay, L.A.; Boone, E.L.; Brooks, J.P. Analyzing the volume and nature of emergency medical calls during severe weather events using regression methodologies. Socio-Econ. Plan. Sci. 2012, 46, 55–66. [Google Scholar] [CrossRef]
- Earnest, A.; Ong, M.E.H.; Shahidah, N.; Ng, W.M.; Foo, C.; Nott, D.J. Spatial analysis of ambulance response times related to prehospital cardiac arrests in the city-state of Singapore. Prehosp. Emerg. Care 2012, 16, 256–265. [Google Scholar] [CrossRef]
- Seim, J.; Glenn, M.J.; English, J.; Sporer, K. Neighborhood poverty and 9-1-1 ambulance response time. Prehosp. Emerg. Care 2018, 22, 436–444. [Google Scholar] [CrossRef] [Green Version]
- Fleischman, R.J.; Lundquist, M.; Jui, J.; Newgard, C.D.; Warden, C. Predicting ambulance time of arrival to the emergency department using global positioning system and google maps. Prehospital Emerg. Care 2013, 17, 458–465. [Google Scholar] [CrossRef] [Green Version]
- Degel, D.; Wiesche, L.; Rachuba, S.; Werners, B. Time-dependent ambulance allocation considering data-driven empirically required coverage. Health Care Manag. Sci. 2015, 18, 444–458. [Google Scholar] [CrossRef]
- Sasaki, S.; Comber, A.J.; Suzuki, H.; Brunsdon, C. Using genetic algorithms to optimise current and future health planning - the example of ambulance locations. Int. J. Health Geogr. 2010, 9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grekousis, G.; Liu, Y. Where will the next emergency event occur? predicting ambulance demand in emergency medical services using artificial intelligence. Comput. Environ. Urban Syst. 2019, 76, 110–122. [Google Scholar] [CrossRef]
- Derekenaris, G.; Garofalakis, J.; Makris, C.; Prentzas, J.; Sioutas, S.; Tsakalidis, A. Integrating gis, gps and gsm technologies for the effective management of ambulances. Comput. Environ. Urban Syst. 2001, 25, 267–278. [Google Scholar] [CrossRef]
- Phan, A.; Ferrie, F.P. Interpolating sparse gps measurements via relaxation labeling and belief propagation for the redeployment of ambulances. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1587–1598. [Google Scholar] [CrossRef]
- Poulton, M.; Noulas, A.; Weston, D.; Roussos, G. Modeling metropolitan-area ambulance mobility under blue light conditions. IEEE Access 2019, 7, 1390–1403. [Google Scholar] [CrossRef]
- Westgate, B.S.; Woodard, D.B.; Matteson, D.S.; Henderson, S.G. Travel time estimation for ambulances using Bayesian data augmentation. Ann. Appl. Stat. 2013, 7, 1139–1161. [Google Scholar] [CrossRef] [Green Version]
- Westgate, B.S.; Woodard, D.B.; Matteson, D.S.; Henderson, S.G. Large-network travel time distribution estimation for ambulances. Eur. J. Oper. Res. 2016, 252, 322–333. [Google Scholar] [CrossRef]
- Piorkowski, A. Construction of a dynamic arrival time coverage map for emergency medical services. Open Geosci. 2018, 10, 67–173. [Google Scholar] [CrossRef]
- Van Dijk, J. Identifying activity-travel points from GPS-data with multiple moving windows. Comput. Environ. Urban Syst. 2018, 70, 84–101. [Google Scholar] [CrossRef]
- Koháni, M.; Czimmermann, P.; Váňa, M.; Cebecauer, M.; Buzna, Ľ. Location-scheduling optimization problem to design private charging infrastructure for electric vehicles. In Operations Research and Enterprise Systems; Revised Selected Papers; Communications in Computer and Information Science; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Kolesar, P.; Walker, W.; Hausner, J. Determining the relation between fire engine travel times and travel distances in New York City. Oper. Res. 1975, 23, 614–627. [Google Scholar] [CrossRef] [Green Version]
- Jánošíková, Ľ.; Kvet, M.; Jankovič, P.; Gábrišová, L. An optimization and simulation approach to emergency stations relocation. Cent. Eur. J. Oper. Res. 2019, 27, 737–758. [Google Scholar] [CrossRef]
- Jánošíková, Ľ.; Jankovič, P.; Kvet, M.; Zajacová, F. Coverage versus response time objectives in ambulance location. Int. J. Health Geogr. 2021, 20, 32. [Google Scholar] [CrossRef] [PubMed]
- Janáček, J.; Jánošíková, Ľ.; Buzna, Ľ. Optimized design of large-scale social welfare supporting systems oncomplex networks. In Optimization in Complex Networks: Theory and Applications; Springer Science + Business Media: New York, NY, USA, 2012; pp. 337–361. ISBN 978-1-4614-0753-9. e-ISBN 978-1-4614-0754-6. [Google Scholar]
- WorldPop, “Gridded Residential Population Data”. 2020. Available online: https://www.worldpop.org (accessed on 14 September 2020).
- Oak Ridge National Laboratory. Landscan Dataset. 2020. Available online: https://landscan.ornl.gov/landscan-datasets (accessed on 14 September 2020).
- HERE Platform. Landscan Dataset. 2021. Available online: https://developer.here.com/ (accessed on 25 February 2021).
- Chatterjee, S.; Hadi, A.S. Regression Analysis by Example; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).