Metamaterial Acoustics on the (2 + 1)D Einstein Cylinder ^†

Abstract

The Einstein cylinder is the first cosmological model for our universe in modern history. Its geometry not only describes a static universe—a universe being invariant under time reversal—but it is also the prototype for a maximally symmetric spacetime with constant positive curvature. As such, it is still of crucial importance in numerous areas of physics and engineering, offering a fruitful playground for simulations and new theories. Here, we focus on the implementation and simulation of acoustic wave propagation on the Einstein cylinder. Engineering such an extraordinary device is the territory of metamaterial science, and we will propose an appropriate tuning of the relevant acoustic parameters in such a way as to mimic the geometric properties of this spacetime in acoustic space. Moreover, for probing such a space, we derive the corresponding wave equation from a variational principle for the underlying curved spacetime manifold and examine some of its solutions. In particular, fully analytical results are obtained for concentric wave propagation. We present predictions for this case and thereby investigate the most significant features of this spacetime. Finally, we produce simulation results for a more sophisticated test model which can only be tackled numerically.

1. Introduction

Shortly after concluding with the formulation of the general theory of relativity in 1916, Einstein moved on to devise relativistic models of the universe, applying his new theory to the realm of physical cosmology. Assuming uniformity and isotropy for a universe on a very large scale was a natural assumption for his time, and he produced a simple cosmological model of a finite, static universe with constant spherical curvature, currently called the Einstein cylinder [1,2,3].

Such spaces of constant curvature represent maximally symmetric geometries. This property explains its fundamental importance in many physics and engineering applications, e.g., in the description of uncharged, perfect relativistic fluids [4] and other standard cosmological models [5] (p. 59). Moreover, in the past years, quantum mechanical phenomena in spaces of constant curvature have attracted the focus of intense investigation [6], raising critical questions beyond their possible experimental verification. Nonetheless, the simulation of acoustic phenomena [7] in such spaces has so far been vastly neglected.

In this work, we explore the possibilities of simulating acoustics on the Einstein cylinder with the help of acoustic metamaterials—materials which enable researchers and engineers to contrive extraordinary devices with exceptional properties, exceeding the limits established by nature. These metamaterials offer researchers and engineers unique opportunities to design and build novel artificial devices with exceptional characteristics (see, e.g., [7,8,9,10]). For recent remarkable advances in this field of metamaterials acoustic, we refer to [11], where a special type of multifunctional acoustic lens is designed by only using isotropic material parameters. Furthermore, in [12], acoustic metamaterial devices are constructed that are reconfigurable by using untethered physical stimuli, i.e., avoiding mechanisms such as compression or pneumatic actuators.

Modeling acoustic wave propagation with particular geometries can be shown to result from a simple variational principle for the acoustic potential, a framework developed in [13] and then extended to various other spacetime geometries [14,15,16,17,18]. This approach yields a wave equation in the form of a partial differential equation for the acoustic potential, connected to a harmonic time dependence and to a Sturm–Liouville problem for the radial isotropic coordinates, which then can be treated analytically.

The same framework also permits one to determine the acoustic parameters corresponding to the postulated spacetime via the so-called constitutive equations [13]. It is this acoustic fine-tuning which exactly implements the acoustic wave propagation for the curved background spacetime under consideration.

The paper is organized as follows: Section 2 introduces the essential differential-geometric framework for setting up and working with the spacetime at hand. In the last part of the same section, the geometric features of the Einstein cylinder are linked to the physical properties and conditions of this spacetime. This formalism is also required to derive the corresponding wave equation for the acoustic analogue model.

Section 3 briefly details the prescription on how to implement the spacetime geometry of the $(2+1)$D Einstein cylinder in its acoustic analogue space. In this process of metamaterial tuning, the relevant acoustic parameters (the scalar bulk modulus and the density tensor) have to be selected appropriately in order to engineer in the laboratory a suitable device which mimics the geometric features of the Einstein cylinder acoustically.

Section 4 centers on the actual wave propagation on this curved spacetime. We show how a general variational principle on the $(2+1)$D Lorentzian manifold derives the relevant wave equation for the acoustic scalar field. In order to examine the significant features of this acoustic analogue space, monochromatic (i.e., having fixed frequency) and concentrically traveling test waves are used to probe the metamaterial. In this case, fully analytical results are obtained—specifically for the non-trivial radial dependence of the wave propagation. Another interesting example presents entirely numerical estimates. It describes a test scenario with an asymmetric wave distribution from the very beginning of the laboratory setup.

Section 5 concludes this discussion, offering a very short summary with an outlook.

2. Spacetime Geometry of the Einstein Cylinder

For this model, we consider the special case of constant positive curvature, $a>0$, for two dimensions. Naturally, it will be the 2-sphere $S^2\left(a\right)$, which we then embed into $(2+1)$D spacetime with Lorentzian signature. This is the prototype model of a homogeneous and isotropic spacetime. The $(2+1)$-dimensional Einstein cylinder, $M={\mathbb{R}}_{+}\times S^2\left(a\right)$, is defined in local coordinates by the following metric tensor (see, e.g., [3]):

$$\mathit{g}=-\left(cdt\right)\otimes \left(cdt\right)+\left(ad{\mathsf{\Omega }}_2\right)\otimes \left(ad{\mathsf{\Omega }}_2\right),$$

(1)

where ${\mathsf{\Omega }}_2$ denotes the familiar solid angle for $S^2$. Therefore it is $d{\mathsf{\Omega }}_2\otimes d{\mathsf{\Omega }}_2=d\vartheta \otimes d\vartheta +{sin}^2\vartheta d\phi \otimes d\phi$, where $\vartheta$ and $\phi$ are the polar and azimuthal angles, respectively. Furthermore, the time coordinate comes with constant speed $c>0$, and the fixed value $a>0$ intrinsically represents a natural scale factor for length. Observe that the symbol ‘⊗’ in Equation (1) denotes the conventional tensor product (see [3] (Section I.3)).

At this point, it is convenient to use isotropic radial coordinates, which are quite commonly used in the description of spherically symmetric spacetimes. They are defined by introducing the radius $r=asin\vartheta$, so that $0\le r<a$ for $0\le \vartheta <\pi /2$. Additionally, as usual, the azimuthal angle takes values $0\le \phi <2\pi$. Now, with this choice of isotropic radial coordinates, the original metric of Equation (1) is straightforwardly recast into the more suitable form

$$\mathit{g}=-\left(cdt\right)\otimes \underset{{\displaystyle {\theta }^0}}{\underbrace{\left(\phantom{(}cdt\right)}}+\frac{dr}{\sqrt{1-r^2/a^2}}\otimes \underset{{\displaystyle {\theta }^1}}{\underbrace{\frac{dr}{\sqrt{1-r^2/a^2}}}}+\left(rd\phi \right)\otimes \underset{{\displaystyle {\theta }^2}}{\underbrace{\left(\phantom{(}rd\phi \right)}},$$

(2)

where the local coframe with dual base ${\theta }^{\mu }\in T_p^{*}M$ ($\mu =0,1,2$) is then given by

$${\theta }^0=cdt,{\theta }^1=\frac{dr}{\sqrt{1-r^2/a^2}},{\theta }^2=rd\phi .$$

(3)

By construction, this frame $({\theta }^0,{\theta }^1,{\theta }^2)$ possesses local flatness. Moreover, orthogonality holds, such that $\mathit{\eta }=-{\theta }^0\otimes {\theta }^0+{\theta }^1\otimes {\theta }^1+{\theta }^2\otimes {\theta }^2,$ where $\eta$ is the Minkowski metric.

In the following, we will employ Cartan’s structure equations as an efficient mathematical formalism which facilitates the calculation of the corresponding curvature tensors in pseudo-Riemannian geometry. The final results for curvature are well-known but not presented this way in the literature, so that here we proceed with a brief derivation (brief within this formalism) for illustrative purposes and completeness of the exposition.

Cartan’s first structure equations involve the computation of the exterior covariant derivatives of the basis 1-forms given in Equation (3) by using the wedge symbol ‘∧’ for the product of exterior calculus (see [3] (Section I.3)). The requirement for vanishing torsion, $D{\theta }^{\mu }=0$, immediately yields

$$D{\theta }^2=\frac{\sqrt{1-r^2/a^2}}{r}{\theta }^1\wedge {\theta }^2+{\omega }^2{}_{\nu }\wedge {\theta }^{\nu }=0,$$

(4)

so that the corresponding connection 1-forms, ${\omega }^{\mu }{}_{\nu }$, for the given orthogonal frame (Equation (3)) are

$${\omega }^2{}_1=\frac{\sqrt{1-r^2/a^2}}{r}{\theta }^2=-{\omega }^1{}_2.$$

(5)

All other connections ${\omega }^{\mu }{}_{\nu }$ are zero. Next, Cartan’s second structure equations serve to determine the curvature 2-forms ${\mathsf{\Omega }}^{\mu }{}_{\nu }$. With Equation (5), the only relevant contribution is

$${\mathsf{\Omega }}^1{}_2=d{\omega }^1{}_2=-\frac{\partial }{\partial r}\left(\frac{\sqrt{1-r^2/a^2}}{r}\right)dr\wedge {\theta }^2-\frac{\sqrt{1-r^2/a^2}}{r}d{\theta }^2=\frac{1}{a^2}{\theta }^1\wedge {\theta }^2.$$

(6)

Identifying ${\displaystyle {\mathsf{\Omega }}^1{}_2=d{\omega }^1{}_2=\frac{1}{2}{\widehat{R}}^1{}_{2\mu \nu }{\theta }^{\mu }\wedge {\theta }^{\nu }}$, it is straightforward to observe that the only non-zero and independent component of the Riemann curvature tensor in the coframe is

$${\widehat{R}}^1{}_{212}=\frac{1}{a^2}.$$

(7)

Accordingly, in the same frame, the components of the Ricci tensor, ${\widehat{R}}_{\mu \nu }$, and the curvature scalar, R, are given by

$${\widehat{R}}_{00}=0,{\widehat{R}}_{11}={\widehat{R}}_{22}=\frac{1}{a^2},R=\frac{2}{a^2}.$$

(8)

Now, we are in a position to connect the geometric properties, that is, the curvature of the manifold $M={\mathbb{R}}_{+}\times S^2\left(a\right)$, to the physical features of the underlying spacetime. It is the Einstein tensor with its field equation which precisely provides this link.

Using Equation (8) in ${\displaystyle {\widehat{G}}_{\mu \nu }={\widehat{R}}_{\mu \nu }-\frac{1}{2}{\eta }_{\mu \nu }R}$, the only non-vanishing component of the Einstein tensor, ${\widehat{G}}_{\mu \nu }$, is the 00-component:

$${\widehat{G}}_{00}=\frac{1}{a^2}=G_{00}.$$

(9)

Note that the result is the same in the local coframe and coordinate frame, denoted by $G_{00}$. This is true because it is ${\theta }^0=cdt$, and also ${\widehat{G}}_{\mu \nu }=0$ for all components except ${\widehat{G}}_{00}$.

Substituting Equation (9) into the Einstein field equations immediately implies for the energy-matter density ${\rho }_0$:

$$\underset{{\displaystyle 1/a^2}}{\underbrace{G_{00}}}=\frac{8\pi G}{c^4}\underset{{\displaystyle {\rho }_0{c}^2}}{\underbrace{T_{00}}}\Rightarrow {\rho }_0=\frac{c^2}{8\pi G{a}^2}>0,$$

(10)

where G is the gravitational constant. Thus, a universe filled uniformly with energy-matter will implement the static model of a $(2+1)$D Einstein cylinder. In the following section, we will discuss how to implement this model within metamaterial acoustics, the gravity analogue model which investigates analogues of general relativistic spacetimes in acoustics (see, e.g., [7,8,9,10]).

3. Acoustic Space and Metamaterial Tuning

The prescription for a constant energy–matter density throughout the Einstein cylinder, viz., Equation (10), in the general theory of relativity has its counterpart in acoustic theory. More precisely, there exists a one-to-one correspondence between the metric of a given spacetime metric and the acoustic parameters of the metamaterial which will display analogous properties. This relationship was derived in [13].

Accordingly, the acoustic engineer who wishes to implement a spacetime $(M,\mathbf{g})$ in the laboratory environment (physical space) has to fine-tune the mass-density tensor $\varrho$ and bulk modulus $\kappa$ in such a manner that it will produce the desired acoustic wave propagation in the corresponding acoustic space (virtual space).

In explicit form, both spaces—physical and virtual space—are linked by the constitutive relations [13], and in the case of the Einstein cylinder, a straightforward calculation shows that the bulk modulus $\kappa$ and the density tensor $\rho$ have to be

$${\displaystyle \kappa =\frac{1}{\sqrt{1-r^2/a^2}},{\rho }_0{\rho }^{ij}=\sqrt{1-r^2/a^2}\left(\begin{array}{cc}1& 0\\ 0& 1/r^2\end{array}\right),}$$

(11)

where $0<r<a$ and $i,j=r,\phi$. Recall that $\sqrt{1-r^2/a^2}=cos\vartheta$, and the variables are restricted to a domain without coordinate singularities.

The constitutive equations, Equation (11), describe the acoustic model at hand and provide the corresponding bulk modulus and the full symmetric matrix of density of the metadevice. As such, they fully encapsulate the structure of the underlying metamaterial for acoustics on the $(2+1)$D Einstein cylinder. For a general approach to retrieving all effective acoustic properties of an acoustic fluid material (the scalar bulk modulus and all $n(n+1)/2$ components of the density tensor in n spatial dimensions) see [19].

4. Wave Propagation and Its Simulation

The fundamental law which governs acoustic wave propagation within a curved spacetime background is dictated by a variational principle, similar to Fermat’s principle of least time in theoretical optics (see, e.g., [20] (Appendix I, Example 11)).

According to this principle, for a given spacetime M with metric g, the action is stationary with respect to variations of the acoustic potential $\varphi :M\to \mathbb{R}$, such that [13]:

$$\frac{\delta }{\delta \varphi }\underset{\mathsf{\Omega }\subseteq M}{\int }d{\mathrm{vol}}_{\mathit{g}}g(\nabla \varphi ,\nabla \varphi )=0.$$

(12)

The spacetime domain $\mathsf{\Omega }\subseteq M$ is bounded, and $d{\mathrm{vol}}_g$ is its differential volume form. The covariant derivative ∇, acting here on the acoustic scalar field $\varphi$, is just the conventional partial derivative, so that in local coordinates $\nabla \varphi =g^{\mu \nu }{\varphi }_{,\mu }{\partial }_{\nu }$, where all ${\partial }_{\mu }\in T_{p}M$ form a basis (see, e.g., [21] (Section 1.2.3)). As usual, spacetime indices such as $\mu$ or $\nu$ which are preceded by a comma stand for partial derivatives with respect to $x^{\mu }$ or $x^{\nu }$, respectively.

As a consequence of Equation (12), the corresponding physical propagation law will have its equivalent in equations of motion with self-adjoint differential operators acting on the related field variables [22] (p. 351). This produces separable partial differential equations which are Sturm–Liouville problems for one of the field variables supplying analytical or at least semi-analytical solutions. (Here, semi-analytical solutions are separable solutions where some functional dependencies of the variables under consideration can be factored out in analytical form.) In fact, Equation (12) corresponds to the Euler–Lagrange equation, ${\Delta }_M\varphi =0$, which contains the Laplace–Beltrami operator ${\Delta }_M=d\delta +\delta d$ on manifold M acting on the acoustic scalar field $\varphi$. Here, d denotes the exterior derivative and $\delta$ its adjoint operator (see, e.g., [23] (Section 4.2)). In local coordinates, the Euler–Lagrange equation takes the following form:

$${\Delta }_M\varphi =\frac{1}{\sqrt{-g}}{\left(\sqrt{-g}{g}^{\mu \nu }{\varphi }_{,\mu }\right)}_{,\nu }=0$$

(13)

where $g=det\mathit{g}<0$. The Einstein summation convention for repeated upper and lower indices is implied.

For acoustic wave propagation on the Einstein cylinder, we use the spacetime metric introduced by Equation (2), such that Equation (13) converts to

$$-\frac{1}{c^2}\frac{{\partial }^2\varphi }{\partial t^2}+\left[\left(1-\frac{r^2}{a^2}\right)\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\left(1-\frac{2r^2}{a^2}\right)\frac{\partial }{\partial r}\right]\varphi +\frac{{\partial }^2\varphi }{\partial {\phi }^2}=0.$$

(14)

This is exactly the wave equation which governs acoustic wave propagation on the Einstein cylinder, engineered and enforced by the acoustic parameters determined by Equation (11).

Next, we turn to solutions of Equation (14) in order to probe the spacetime properties of the Einstein cylinder. For this purpose, we will choose concentric radial waves moving away from the origin:

$$\varphi (t,r,\phi )=A^{+}{e}^{i\omega t}{\varphi }_1\left(r\right).$$

(15)

The amplitude is $A^{+}>0$, and the frequency is $\omega >0$. Function ${\varphi }_1\left(r\right)$ represents the radial dependency in the full expression of the acoustic potential

$$\varphi (t,r,\phi )={\varphi }_0\left(t\right){\varphi }_1\left(r\right){\varphi }_2\left(\phi \right).$$

(16)

Applying the separation of variables method as the standard procedure, it is straightforward to recognize that the time dependence in Equation (16) displays a simple harmonic behavior, i.e., ${\varphi }_0\left(t\right)=e^{i\omega t}$. Because of the radial symmetry of the concentric prototype waves, the angular factor ${\varphi }_2\left(\phi \right)$ in Equation (16) is just a constant which can be absorbed into the amplitude $A^{+}$ in Equation (15).

Hence, after substituting into the wave equation, Equation (14), the expressions Equations (15) and (16) with conditions $\partial \varphi /\partial \phi =0$ and ${\partial }^2\phi /\partial t^2=-{\omega }^2\varphi$, we readily arrive at

$$\left(1-\frac{r^2}{a^2}\right){\varphi }_1^{″}+\frac{1}{r}\left(1-\frac{2r^2}{a^2}\right){\varphi }_1^{\prime }+\frac{{\omega }^2}{c^2}{\varphi }_1=0.$$

(17)

Thus, ultimately, all of the non-trivial behavior for the wave propagation will be contained in the radial contribution ${\varphi }_1\left(r\right)$. An elementary analysis shows that the second-order linear differential equation determining ${\varphi }_1\left(r\right)$, Equation (17), has three regular singular points at $r=0,a$, and ∞. The canonical forms for differential equations with such characteristics are either Gauss’s differential equation or the generalized hypergeometric equation [24,25].

A suitable transformation rule for converting Equation (17) into canonical form is given by

$$\left\{\begin{array}{cc}\hfill {\varphi }_1\left(r\right)& ={\left.\phantom{|}y\left(x\right)\right|}_{x=r^2/a^2},\hfill \\ \hfill {\varphi }_1^{\prime }\left(r\right)& {\displaystyle =\frac{2r}{a^2}{y}^{\prime }\left(x\right),}\hfill \\ \hfill {\varphi }_1^{″}\left(r\right)& {\displaystyle =\frac{2}{a^2}\left(\frac{2r^2}{a^2}{y}^{″}\left(x\right)+y^{\prime }\left(x\right)\right),}\hfill \end{array}\right.$$

(18)

which after some simplification produces

$$x(1-x)y^{″}+\left(1-\frac{3}{2}x\right)y^{\prime }+\frac{a^2}{4}\frac{{\omega }^2}{c^2}y=0.$$

(19)

Now, comparing Equation (19) with Gauss’s equation defined by

$$x(1-x)y^{″}+\left[\gamma -(\alpha +\beta +1)x\right]y^{\prime }-\alpha \beta y=0$$

(20)

yields the solution in terms of the hypergeometric function

$${}_2{F}_1\left(\left.\begin{array}{ccc}\alpha & & \beta \\ & \gamma \end{array}\right|x\right),\mathrm{with}\alpha ,\beta ,\gamma \in \mathbb{R},$$

(see [26] (p. 207, Theorem 9.3)). In the case of Equation (19), the parameters are

$$\left\{\begin{array}{c}\alpha =\frac{1}{4}\left(1+\sqrt{1+4a^2\frac{{\omega }^2}{c^2}}\right),\hfill \\ \beta =\frac{1}{4}\left(1-\sqrt{1+4a^2\frac{{\omega }^2}{c^2}}\right),\hfill \\ \gamma =1.\hfill \end{array}\right.$$

(21)

This completes the computation of the first solution.

In order to find the second independent solution, we now consider the generalized hypergeometric equation defined by the following homogeneous linear differential equation of degree: $\max (p,q)$, $p,q\in \mathbb{N}$:

$$\left[{(-1)}^{p}x\prod _{i=1}^p\left(x\frac{d}{dx}-a_i+1\right)-\prod _{j=1}^q\left(x\frac{d}{dx}-b_j\right)\right]G\left(x\right)=0,$$

(22)

which has the subsequent Meijer G-function as solution (see [25] (p. 13, Section 1.5) or [27] (p. 867, Equation (12)))

$$G\left(x\right)=G_{p,q}^{2,0}\left(\left.\begin{array}{cccc}{a}_1\hfill & a_2\hfill & \cdots \hfill & a_p\hfill \\ b_1\hfill & b_2\hfill & \cdots \hfill & b_q\hfill \end{array}\right|x\right).$$

(23)

To obtain a second-order equation, we choose $p=q=2$ and further assume that $b_1=b_2=0$. After some lengthy but straightforward calculation, Equation (22) reduces to

$$x(1-x)G^{″}+\left[1-\left(3-a_1-a_2\right)x\right]G^{\prime }-\left(1-a_1-a_2+a_1{a}_2\right)G=0.$$

(24)

The comparison with Equation (19) yields, for the parameters of the solution Equation (23) with $p=q=2$, the explicit values

$$\left\{\begin{array}{c}{a}_1=\frac{1}{4}\left(3+\sqrt{1+4a^2\frac{{\omega }^2}{c^2}}\right),\hfill \\ a_2=\frac{1}{4}\left(3-\sqrt{1+4a^2\frac{{\omega }^2}{c^2}}\right).\hfill \end{array}\right.$$

(25)

This completes the computation of the second solution.

In summary, the individual solutions provided by Equations (21) and (25) for the hypergeometric function ${}_2{F}_1$ and the Meijer G-function $G_{2,2}^{2,0}$, respectively, add up, giving the following general solution for the radial dependence ${\varphi }_1$ of the concentric prototype waves, Equation (15), in fully analytic form:

$$\begin{array}{cc}\hfill {\varphi }_1\left(r\right)=C_1& {}_2{F}_1\left({\displaystyle \left.\begin{array}{ccc}\frac{1}{4}\left(1+\sqrt{1+4a^2\frac{{\omega }^2}{c^2}}\right)& & \frac{1}{4}\left(1-\sqrt{1+4a^2\frac{{\omega }^2}{c^2}}\right)\\ & 1\end{array}\right|\frac{r^2}{a^2}}\right)\hfill \\ \hfill +C_2& G_{2,2}^{2,0}\left({\displaystyle \left.\begin{array}{ccc}\frac{1}{4}\left(3+\sqrt{1+4a^2\frac{{\omega }^2}{c^2}}\right)& & \frac{1}{4}\left(3-\sqrt{1+4a^2\frac{{\omega }^2}{c^2}}\right)\\ 0& & 0\end{array}\right|\frac{r^2}{a^2}}\right).\hfill \end{array}$$

(26)

Both hypergeometric and Meijer G-functions are well defined functions, implemented with high precision on many mathematical software systems.

Given the precise analytical result for concentric wave propagation, viz., Equation (15) with Equation (26), we may now proceed with numerical wave simulations to further explore the properties of the underlying acoustic space possessing all analogue features of the spacetime of the Einstein cylinder ${\mathbb{R}}_{+}\times S^2\left(a\right)$. Apart from the time-harmonic dependence of the wave potential, only the non-trivial radial dependence is of interest.

For the numerical evaluation of ${\varphi }_1\left(r\right)$, we normalize the amplitude $A^{+}=1$ and choose the fixed frequency $\omega =1/2\pi$, as well as a length scale $a=100$ and a constant speed $c=1$. In the graphical representations, Figure 1, we select several distinct boundary conditions, allowing for different configurations to exhibit the propagation behavior for the concentric prototype waves traveling on the Einstein cylinder. The radial dependence will be examined in the interval from $r=0$ to $r=a=100$. Thus, the boundary conditions are conveniently chosen on the radial positions $r=1$ and $r=99$ in order to avoid the two singular points at $r=0$ and $r=a$ of the underlying differential equation, Equation (17).

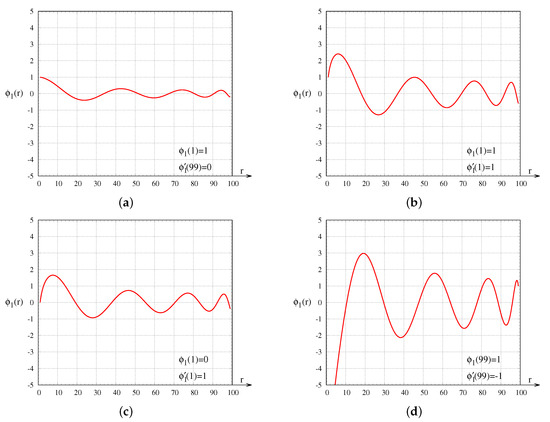
Figure 1a assumes the boundary conditions ${\varphi }_1\left(1\right)=1$, meaning that the starting amplitude is assigned a unit value. The second condition is ${\varphi }_1^{\prime }\left(99\right)=0$. The particle velocity of the acoustic wave is $\mathit{v}=\mathsf{\nabla }\varphi$, where the boldface nabla symbol refers to the classical spatial gradient, so that $\mathsf{\nabla }\varphi =g^{ij}{\varphi }_{,i}{\partial }_j$, with $i,j=1,2$ (see [13,28]). This latter condition physically enforces a vanishing velocity as the wave reaches the characteristic length. In Figure 1b, we allow the wave to launch with initial velocity ${\varphi }_1^{\prime }\left(1\right)=1$. As a direct result of this adjustment, the wave amplitude now modulates considerably more than before over the given test interval. Figure 1c maintains the initial velocity ${\varphi }_1^{\prime }\left(1\right)=1$ but starts off at a zero amplitude. Clearly, a change in amplitude appears to qualitatively preserve all features of the previous configuration with different initial amplitude. Ultimately, Figure 1d completely alters the acoustic setup by considering a wave which travels inwards with unit amplitude from the outer radial position $r=99$ having velocity ${\varphi }_1^{\prime }\left(1\right)=-1$.

In the first three cases of Figure 1a–c, we observe an essential damping of the wave amplitude. Physically, this is explained by the stretching of the coordinate scale related to ${\theta }^1$ (see Equation (2)), which occurs as the isotropic radius approaches the equator at $r=a$. On the other hand, in the case of Figure 1d, where the wave is traveling inwards—traveling from the equator to the origin—a significant amplification of the wave materializes.

As the last example, we will consider the boundary-value problem by imposing the set of conditions for the acoustic potential given in Figure 2. The objective is to perform a full wave simulation. For this purpose, we carry out a finite element analysis (FEA) for the complete potential, directly using the wave equation, Equation (14).

The initial wave distribution at $t=0$ is an exponential “blob” represented by

$$\varphi (0,r,\phi )=e^{-10{(r-2)}^2-20{\left(\phi -\frac{\pi }{2}\right)}^4},$$

which evidently makes an analytical treatment intractable. Again, the constant speed is $c=1$. The characteristic length is now $a=4$ in order to improve the graphical visualization, and the time interval ends at $T=4\pi$. The two remaining boundary conditions require that the acoustic pressure either vanishes at instant $t=0$ or at position $r=a$. Note that the acoustic pressure is determined by $p={\rho }_0\partial \varphi /\partial t$, where ${\rho }_0>0$ is the ambient density (see [13] (Equation (3)) and [28] (p. 13)). The actual numerical implementation, coded in Mathematica [29], requires no further assumptions—symmetry obviously is violated, and the sound waves in general possess variable frequency.

Figure 3 directly shows in graphical form the numerical results for the boundary-value problem of the wave equation on the Einstein cylinder, Figure 2. With final time $T=4\pi$, the snapshots which examine the waves during the time $[0,T]$ are computed at each multiple of $T/50$. Figure 3 depicts the nine frames $9,10,11,\dots ,17$.

A graphical animation (using 50 frames in total, similar to Figure 3) is available for download at [https://drive.google.com/file/d/1bR06XZAMxqz5sh4o1BKi2WRTHPUwsxNC/view?usp=sharing]. Accessed date is 28 July 2021. The video visualizes damping of the amplitude as the waves approach the equator at $r=a$. The effect becomes more pronounced as the waves reach this limit.

In the first examples, Figure 1a–d, fully analytical results were derived and then applied for numerical computation, concentrating on the relevant non-trivial dependence of the isotropic radial coordinate and exploiting symmetry for probing the underlying acoustic spacetime. The last example implements entirely numerical scenarios by direct integration of the partial differential equation, Equation (14), the equation (together with its boundary/initial conditions) which controls all wave properties on ${\mathbb{R}}_{+}\times S^2\left(a\right)$. Of course, other numerical scenarios are conceivable and may be tackled by diverse numerical integrator software. Alternatively, in a different approach, software such as COMSOL Multiphysics ${}^{\circledR }$ [30] may be used for physically simulating all wave phenomena with finite-element methods in a virtual laboratory by only using the necessary acoustic parameters provided in Equation (11).

5. Conclusions

In this work, we presented an analysis of acoustic wave propagation on the Einstein cylinder. This spacetime geometry stands out by being maximally symmetric and having constant positive curvature. For this reason, it was our candidate of choice for modeling within metamaterial acoustics.

In order to engineer such an analogue spacetime with the tools of metamaterials, we provided the corresponding acoustic parameters for future implementations in a laboratory setting, thus making it subject to challenging experiments.

For a concise description and derivation of all wave properties on this curved spacetime manifold, we built up a differential-geometric formalism, which eventually allowed us to derive the central wave equation from a variational principle.

Next, using concentric waves for probing significant features of this spacetime, a detailed study led us to fully analytic results. In this case, we found that the non-trivial radial dependence of the wave propagation may be expressed in terms of hypergeometric functions and Meijer G-functions. Various different scenarios served as an illustration—in particular, we observed an appreciable damping as the waves approach the equator, i.e., as the waves reach the characteristic length scale of the Einstein cylinder with respect to the origin. As another interesting test case, we examined the evolution of a wave with an initial asymmetric configuration, namely an exponential “blob”. This entirely numerical simulation again demonstrates the typical damping for outwards traveling waves. Conversely, for inwards traveling waves, an amplification of their amplitude is detected.

It is our hope that the variational approach for simulating metamaterials within transformation acoustics, and that the application of the corresponding constitutive relations for engineering analogue acoustic devices, will prove themselves as valuable tools in this area of research.