An Optimized Triggering Algorithm for Event-Triggered Control of Networked Control Systems
Abstract
1. Introduction
1.1. Literature Review
1.2. Main Contributions
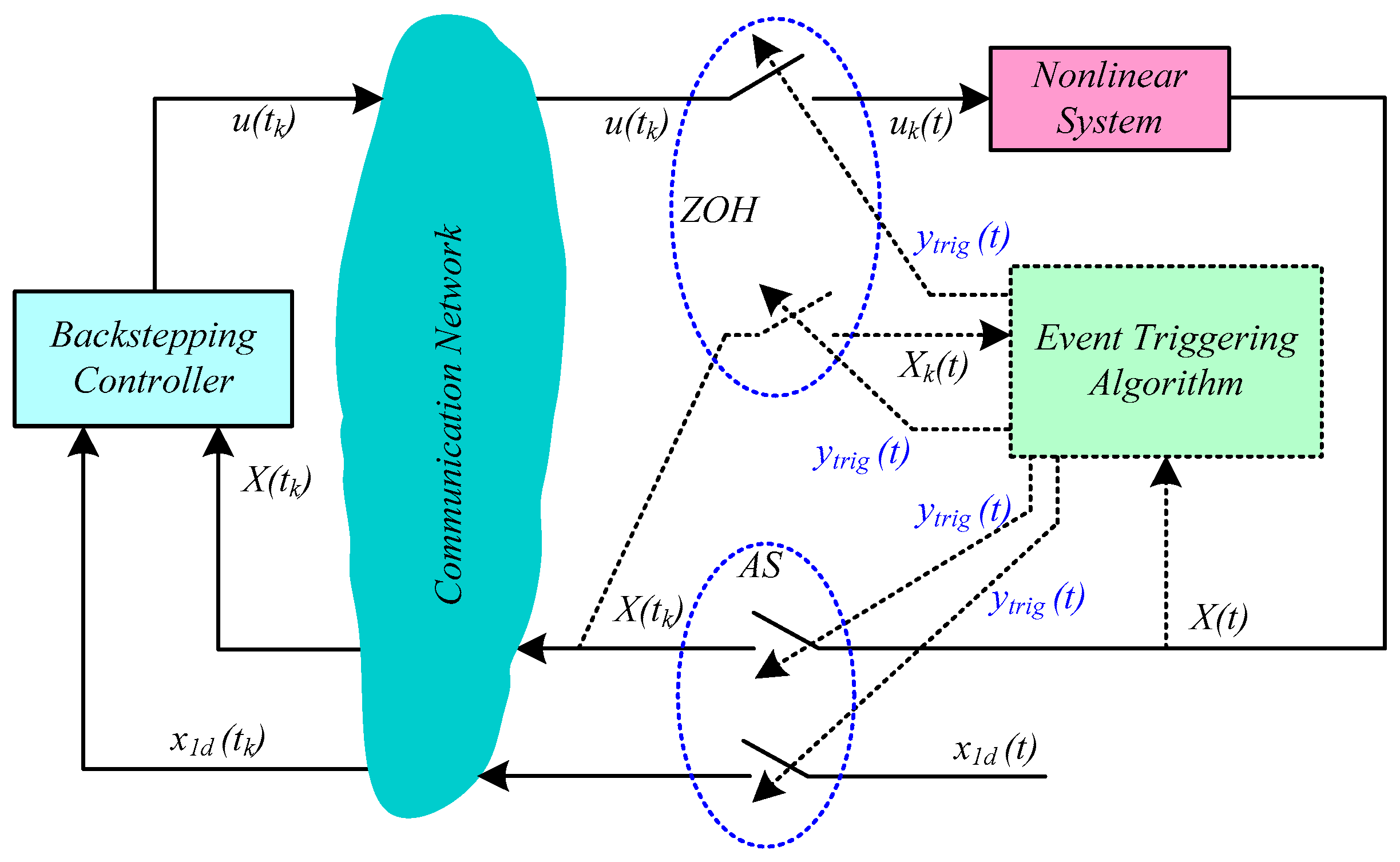
2. Description of ETC for NCS and Control Problem Statement
3. Design of Backstepping Controller and ETC Scheme
3.1. Backstepping Controller Design
3.2. ETC Scheme with Backstepping Controller
| Algorithm 1. Event Triggering Algorithm |
| if or |
| (i) an event is triggered () and |
| (ii) control command is updated |
| else |
| (i) no event triggering () and |
| (ii) control command is on hold at its previous value |
| end |
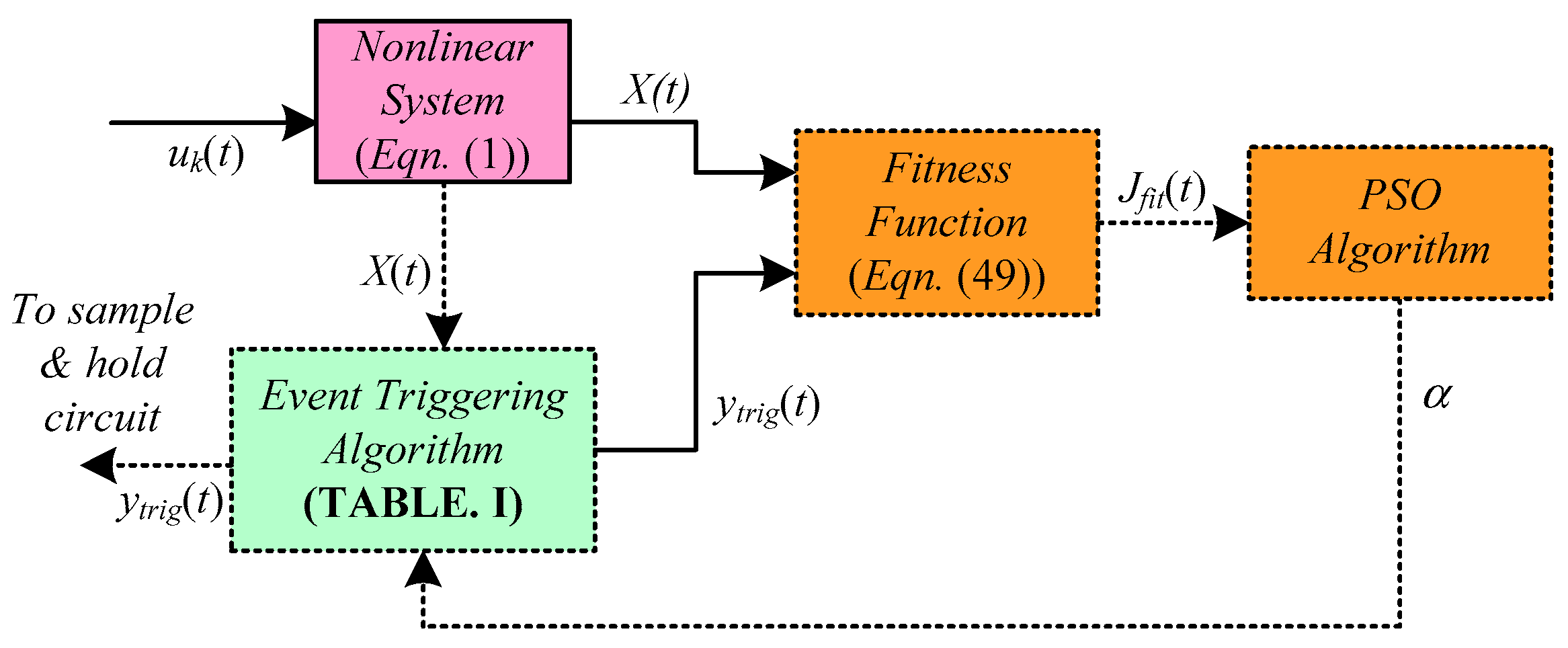
3.3. Design of Optimized Event Triggering Algorithm
3.4. Case Study 1: Stabilization of Inverted Pendulum System
3.5. Case Study 2: Stabilization of Single-Link Robot System
4. Simulation Results
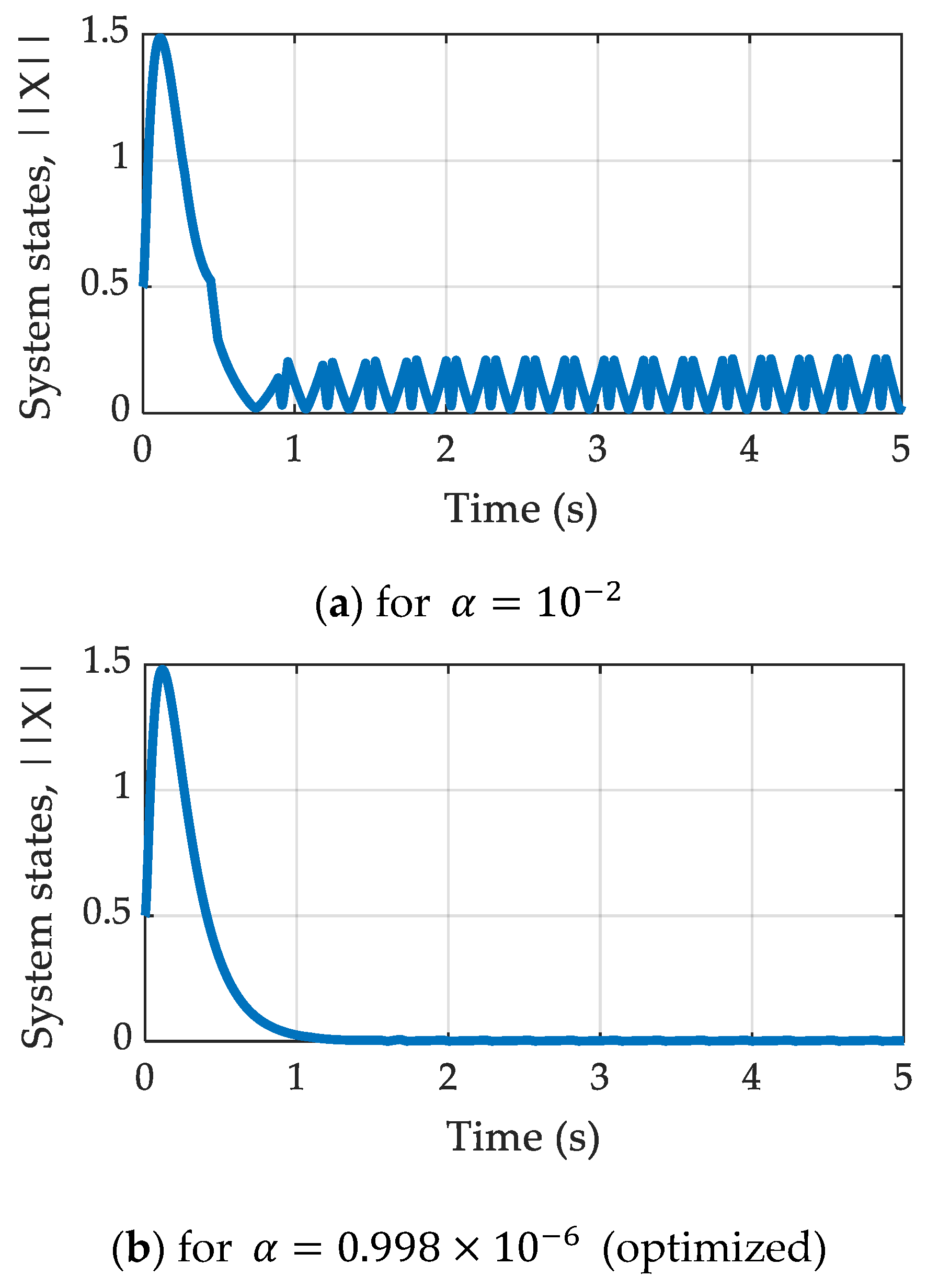
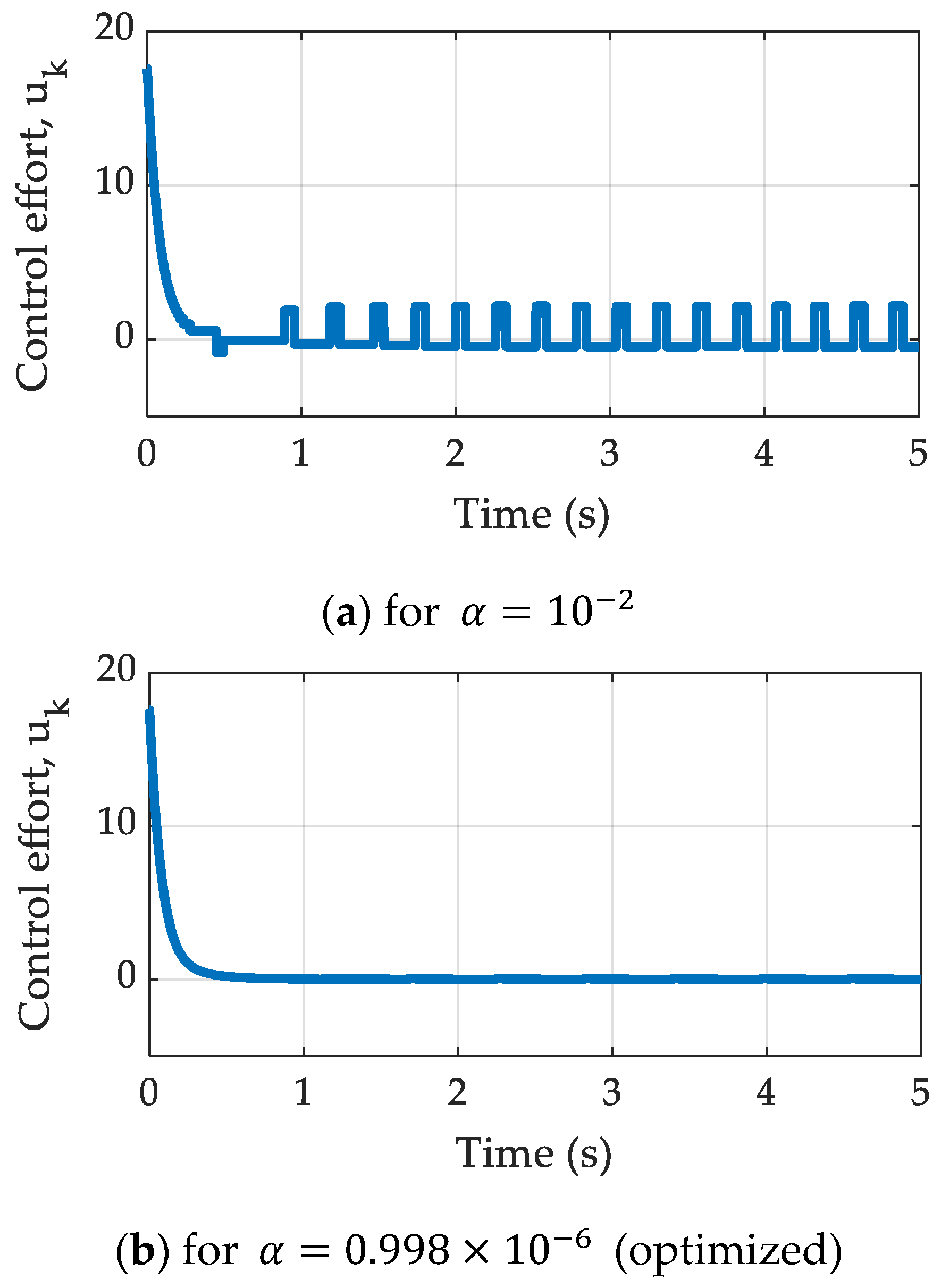
4.1. Case Study 1: Stabilization of Inverted Pendulum System
4.2. Case Study 2: Stabilization of Single-Link Robot System
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Åarzén, K.-E. A Simple Event-Based PID Controller. IFAC Proc. Vol. 1999, 32, 8687–8692. [Google Scholar] [CrossRef]
- Heemels, W.P.M.H.; Sandee, J.H.; Van Den Bosch, P.P.J. Analysis of Event-Driven Controllers for Linear Systems. Int. J. Control 2008, 81, 571–590. [Google Scholar] [CrossRef]
- Vamvoudakis, K.G. Event-Triggered Optimal Adaptive Control Algorithm for Continuous-Time Nonlinear Systems. IEEE/CAA J. Autom. Sin. 2014, 1, 282–293. [Google Scholar] [CrossRef]
- Sahoo, A.; Xu, H.; Jagannathan, S. Neural Network-Based Event-Triggered State Feedback Control of Nonlinear Continuous-Time Systems. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 497–509. [Google Scholar] [CrossRef]
- Yu, H.; Hao, F. Input-to-State Stability of Integral-Based Event-Triggered Control for Linear Plants. Automatica 2017, 85, 248–255. [Google Scholar] [CrossRef]
- Wang, A.; Liu, L.; Qiu, J.; Feng, G. Event-Triggered Robust Adaptive Fuzzy Control for a Class of Nonlinear Systems. IEEE Trans. Fuzzy Syst. 2019, 27, 1648–1658. [Google Scholar] [CrossRef]
- Lu, W.; Yin, X.; Fu, Y.; Gao, Z. Observer-Based Event-Triggered Predictive Control for Networked Control Systems under Dos Attacks. Sensors 2020, 20, 6866. [Google Scholar] [CrossRef] [PubMed]
- Mazo, M.; Tabuada, P. Special Issue Technical Notes and Correspondence: Decentralized Event-Triggered Control over Wireless Sensor/Actuator Networks. IEEE Trans. Automat. Control 2011, 56, 2456–2461. [Google Scholar] [CrossRef]
- Tripathy, N.S.; Kar, I.N.; Paul, K. An Event-Triggered Based Robust Control of Robot Manipulator. In Proceedings of the 2014 13th International Conference on Control Automation Robotics and Vision, ICARCV, Singapore, 10–12 December 2014; pp. 425–430. [Google Scholar] [CrossRef]
- Bhadu, M.; Tripathy, N.S.; Kar, I.N.; Senroy, N. Event-Triggered Communication in Wide-Area Damping Control: A Limited Output Feedbackbased Approach. IET Gener. Transm. Distrib. 2016, 10, 4094–4104. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; Sabih, M. Networked Event-Triggered Control: An Introduction and Research Trends. Int. J. Gen. Syst. 2014, 43, 810–827. [Google Scholar] [CrossRef]
- Gautam, M.K.; Pati, A.; Mishra, S.K.; Appasani, B.; Kabalci, E.; Bizon, N.; Thounthong, P. A Comprehensive Review of the Evolution of Networked Control System Technology and Its Future Potentials. Sustainability 2021, 13, 2962. [Google Scholar] [CrossRef]
- Behera, A.K.; Bandyopadhyay, B. Self-Triggering-Based Sliding-Mode Control for Linear Systems. IET Control Theory Appl. 2015, 9, 2541–2547. [Google Scholar] [CrossRef]
- Behera, A.K.; Bandyopadhyay, B. Event-Triggered Sliding Mode Control for a Class of Nonlinear Systems. Int. J. Control 2016, 89, 1916–1931. [Google Scholar] [CrossRef]
- Behera, A.K.; Bandyopadhyay, B. Robust Sliding Mode Control: An Event-Triggering Approach. IEEE Trans. Circuits Syst. II Express Briefs 2017, 64, 146–150. [Google Scholar] [CrossRef]
- Postoyan, R.; Tabuada, P.; Nesic, D.; Anta, A. Event-Triggered and Self-Triggered Stabilization of Distributed Networked Control Systems. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 2565–2570. [Google Scholar] [CrossRef]
- Abdelrahim, M.; Postoyan, R.; Daafouz, J.; Nešić, D. Stabilization of Nonlinear Systems Using Event-Triggered Output Feedback Controllers. IEEE Trans. Automat. Control 2016, 61, 2682–2687. [Google Scholar] [CrossRef]
- Jiao, J.; Wang, G. Event Driven Tracking Control Algorithm for Marine Vessel Based on Backstepping Method. Neurocomputing 2016, 207, 669–675. [Google Scholar] [CrossRef]
- Li, Y.X.; Yang, G.H. Model-Based Adaptive Event-Triggered Control of Strict-Feedback Nonlinear Systems. IEEE Trans. Neural Networks Learn. Syst. 2018, 29, 1033–1045. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.X.; Yang, G.H. Event-Triggered Adaptive Backstepping Control for Parametric Strict-Feedback Nonlinear Systems. Int. J. Robust Nonlinear Control 2018, 28, 976–1000. [Google Scholar] [CrossRef]
- Mishra, S.K.; Purwar, S.; Kishor, N. Event-Triggered Nonlinear Control of OWC Ocean Wave Energy Plant. IEEE Trans. Sustain. Energy 2018, 9, 1750–1760. [Google Scholar] [CrossRef]
- Mishra, S.K.; Appasani, B.; Jha, A.V.; Garrido, I.; Garrido, A.J.; Costa Castelló, R. Centralized Airflow Control to Reduce Output Power Variation in a Complex OWC Ocean Energy Network. Complexity 2020. [Google Scholar] [CrossRef]
- Zhang, C.H.; Yang, G.H. Event-Triggered Control for a Class of Strict-Feedback Nonlinear Systems. Int. J. Robust Nonlinear Control 2019, 29, 2112–2124. [Google Scholar] [CrossRef]
- Huang, J.; Wang, Q.G. Event-Triggered Adaptive Control of a Class of Nonlinear Systems. ISA Trans. 2019, 94, 10–16. [Google Scholar] [CrossRef] [PubMed]
- Xing, L.; Wen, C.; Liu, Z.; Su, H.; Cai, J. Event-Triggered Output Feedback Control for a Class of Uncertain Nonlinear Systems. IEEE Trans. Automat. Control 2019, 64, 290–297. [Google Scholar] [CrossRef]
- Li, T.; Wen, C.; Yang, J.; Li, S.; Guo, L. Event-Triggered Tracking Control for Nonlinear Systems Subject to Time-Varying External Disturbances. Automatica 2020, 119. [Google Scholar] [CrossRef]
- Xu, B.; Liu, X.; Wang, H.; Zhou, Y. Event-Triggered Control for Nonlinear Systems via Feedback Linearisation. Int. J. Control 2020, 1–11. [Google Scholar] [CrossRef]
- Hu, X.; Yu, H.; Hao, F. Lyapunov-Based Event-Triggered Control for Nonlinear Plants Subject to Disturbances and Transmission Delays. Sci. China Inf. Sci. 2020, 63. [Google Scholar] [CrossRef]
- Zou, K.; Cai, Y.; Chen, L.; Sun, X. Event-Triggered Nonlinear Model Predictive Control for Trajectory Tracking of Unmanned Vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021. [Google Scholar] [CrossRef]
- Cui, L.; Zhang, Y.; Wang, X.; Xie, X. Event-Triggered Distributed Self-Learning Robust Tracking Control for Uncertain Nonlinear Interconnected Systems. Appl. Math. Comput. 2021, 395. [Google Scholar] [CrossRef]
- Su, X.; Wen, Y.; Shi, P.; Wang, S.; Assawinchaichote, W. Event-Triggered Fuzzy Control for Nonlinear Systems via Sliding Mode Approach. IEEE Trans. Fuzzy Syst. 2021, 29, 336–344. [Google Scholar] [CrossRef]
- Mishra, S.K.; Pati, A.; Appasani, B.; Jha, A.V.; Kumar, M.R.; Pal, V.C.; Gautam, M.K. Event-Triggered Fractional-Order PID Control of Fractional-Order Networked Control System. In Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2021; Volume 690, pp. 205–216. [Google Scholar] [CrossRef]
- Clerc, M. Particle Swarm Optimization; ISTE Ltd.: London, UK, 2010. [Google Scholar] [CrossRef]
- Wang, J.J. Simulation Studies of Inverted Pendulum Based on PID Controllers. Simul. Model. Pract. Theory 2011, 19, 440–449. [Google Scholar] [CrossRef]
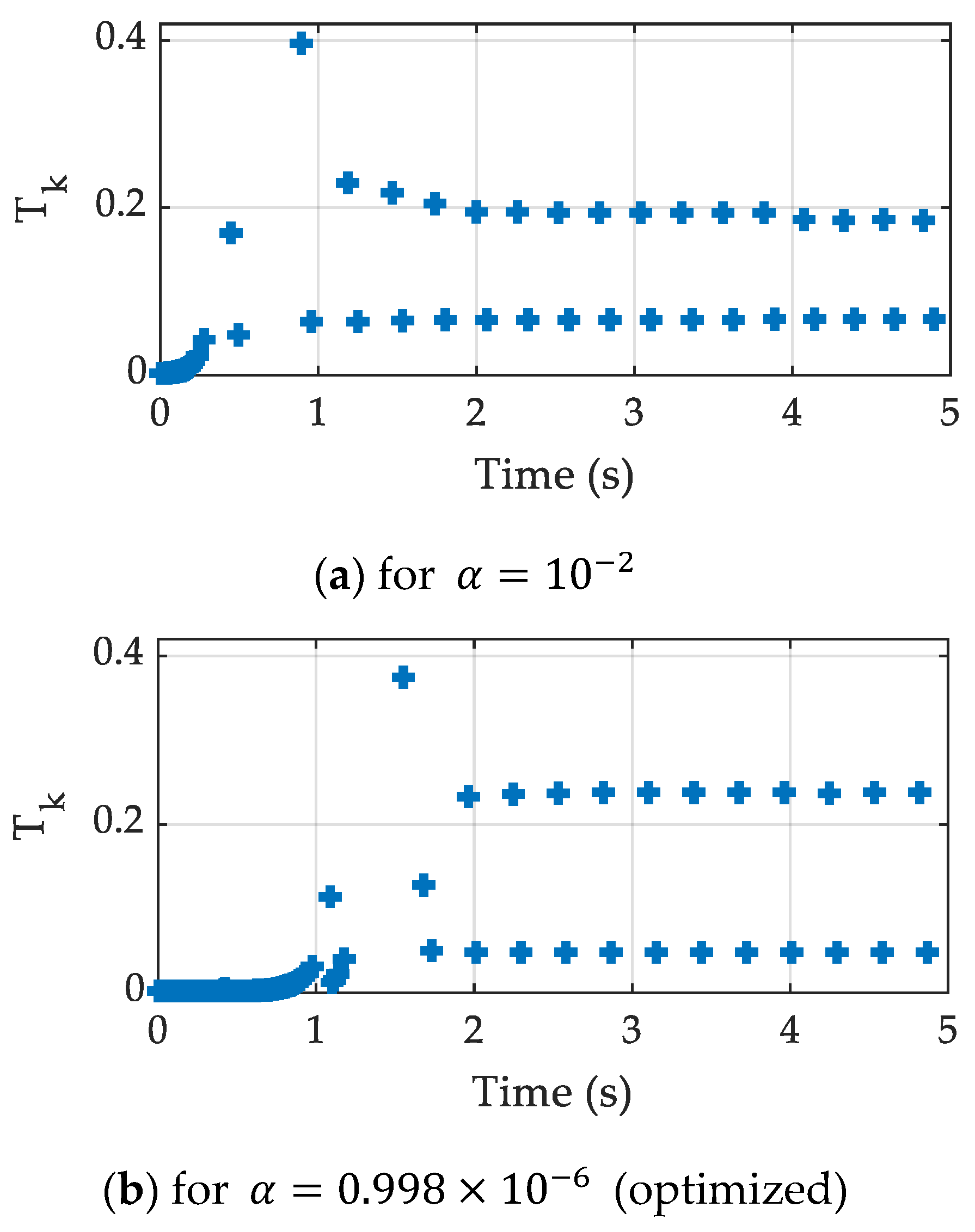
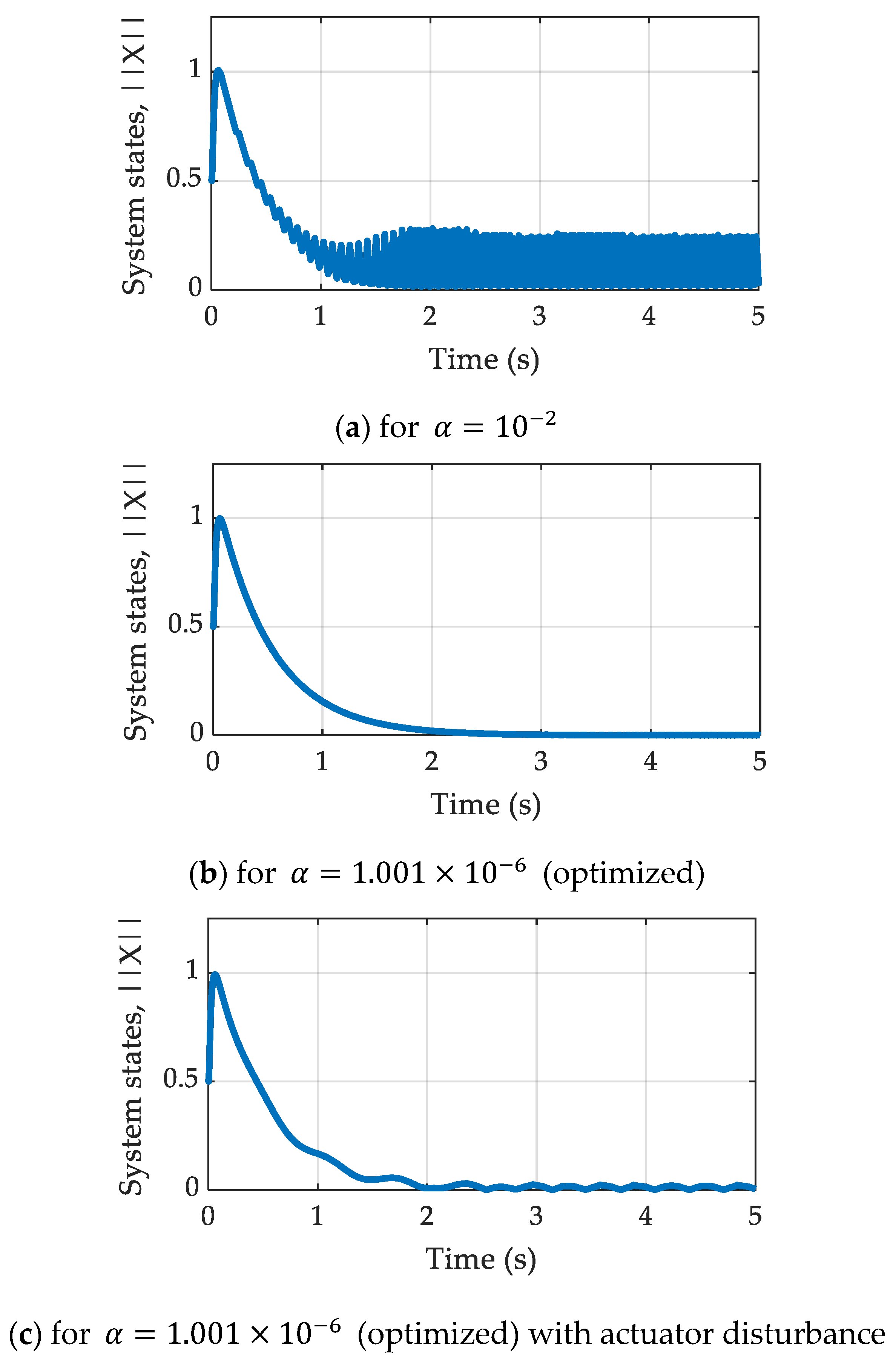

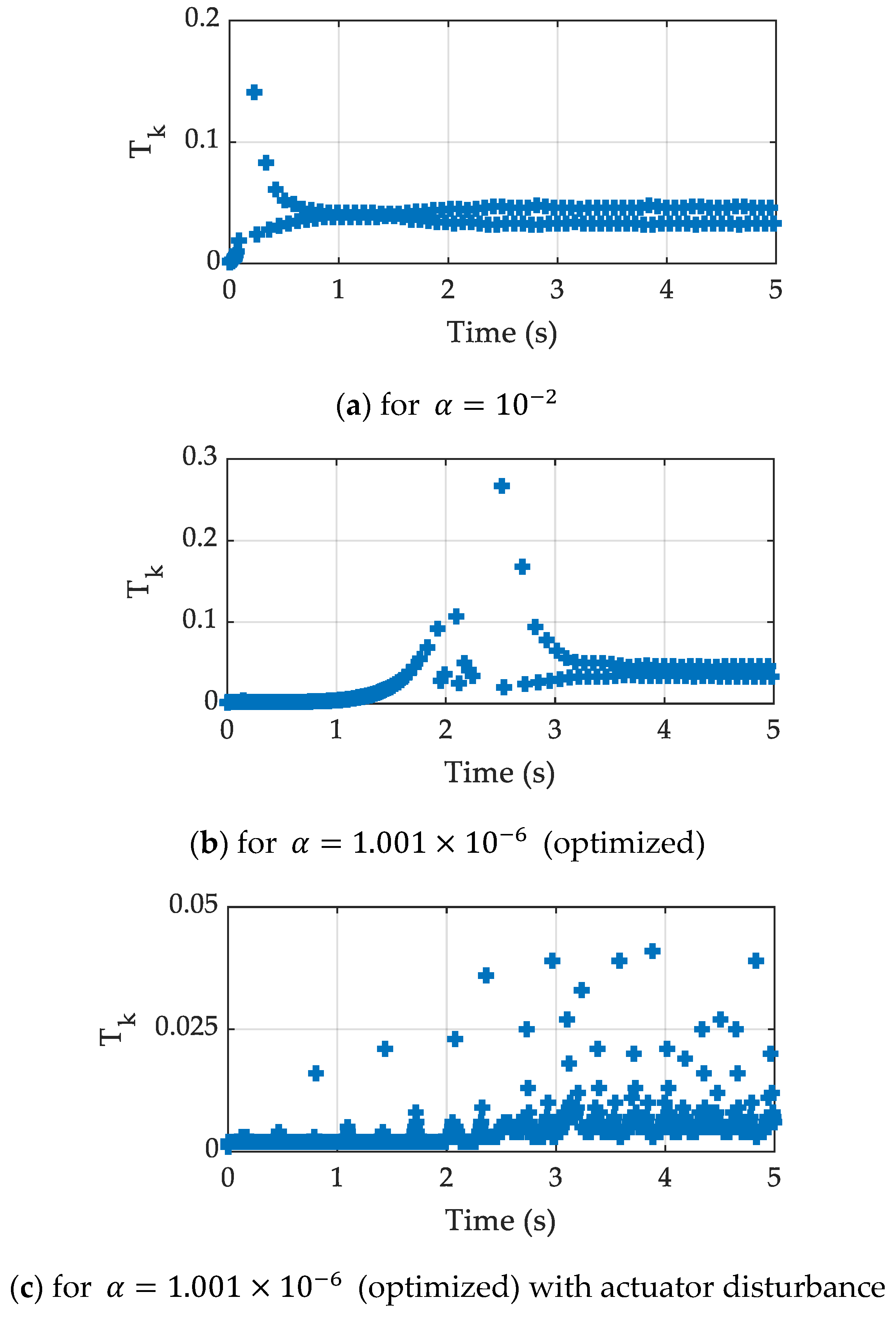
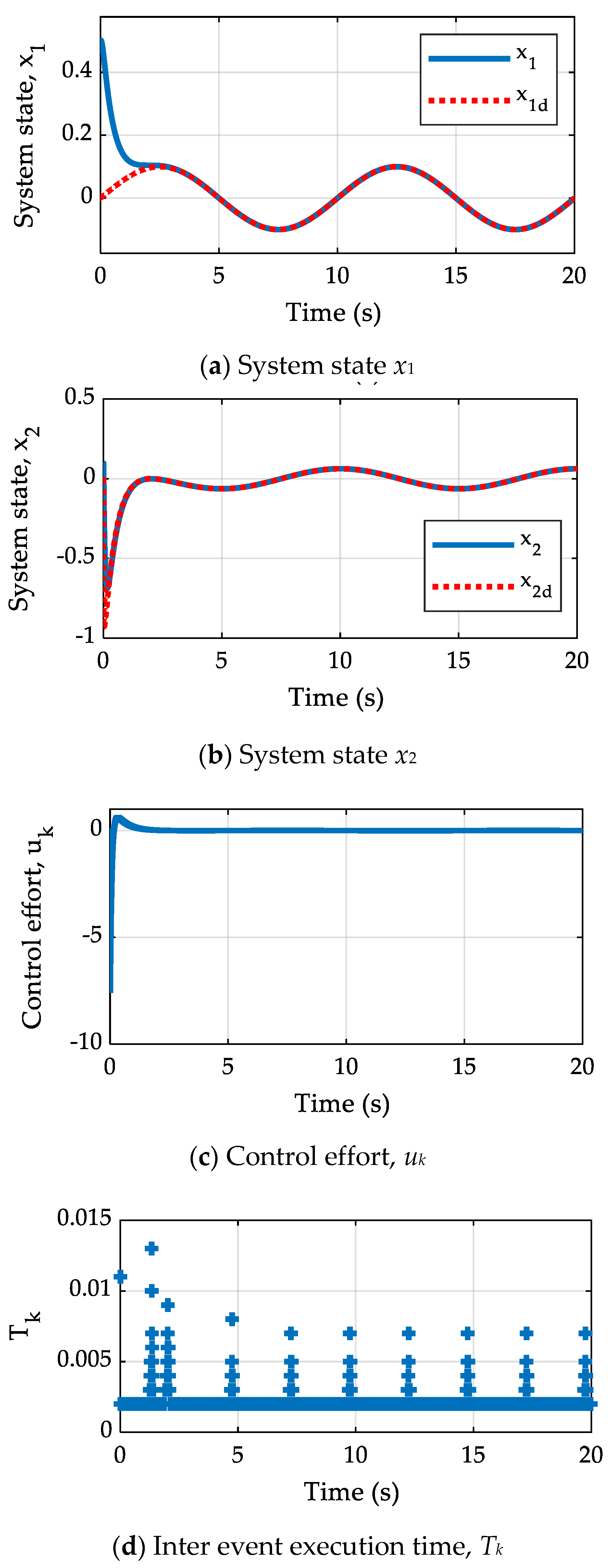
| M (Kg) | m (Kg) | l (m) | g (m/s2) | k1 | k2 | η |
|---|---|---|---|---|---|---|
| 1 | 0.1 | 0.3 | 9.8 | 5 | 5 | 1 |
| Value of α | Fitness Function Jfit (t) | Number of Samples |
|---|---|---|
| 10−1 | 72.13 | 147 |
| 10−2 | 22.92 | 211 |
| 10−3 | 8.15 | 276 |
| 10−4 | 2.70 | 335 |
| 10−5 | 1.21 | 394 |
| 10−6 | 0.85 | 508 |
| 10−7 | 0.86 | 630 |
| 10−8 | 0.91 | 736 |
| 10−9 | 1.01 | 866 |
| 10−10 | 1.12 | 969 |
| 0.998 × 10−6 | 0.8369 | 501 |
| J | m (Kg) | l (m) | g (m/s2) | k1 | k2 | η |
|---|---|---|---|---|---|---|
| 0.5 | 0.1 | 0.3 | 9.8 | 2 | 10 | 1 |
| Value of α | Fitness Function Jfit (t) | Number of Samples |
|---|---|---|
| 10−1 | 78.33 | 509 |
| 10−2 | 25.47 | 521 |
| 10−3 | 8.56 | 538 |
| 10−4 | 3.287 | 556 |
| 10−5 | 1.71 | 693 |
| 10−6 | 1.49 | 971 |
| 10−7 | 1.60 | 1240 |
| 10−8 | 1.82 | 1511 |
| 10−9 | 2.09 | 1782 |
| 10−10 | 2.35 | 2057 |
| 1.001 × 10−6 | 1.488 | 968 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mishra, S.K.; Jha, A.V.; Verma, V.K.; Appasani, B.; Abdelaziz, A.Y.; Bizon, N. An Optimized Triggering Algorithm for Event-Triggered Control of Networked Control Systems. Mathematics 2021, 9, 1262. https://doi.org/10.3390/math9111262
Mishra SK, Jha AV, Verma VK, Appasani B, Abdelaziz AY, Bizon N. An Optimized Triggering Algorithm for Event-Triggered Control of Networked Control Systems. Mathematics. 2021; 9(11):1262. https://doi.org/10.3390/math9111262
Chicago/Turabian StyleMishra, Sunil Kumar, Amitkumar V. Jha, Vijay Kumar Verma, Bhargav Appasani, Almoataz Y. Abdelaziz, and Nicu Bizon. 2021. "An Optimized Triggering Algorithm for Event-Triggered Control of Networked Control Systems" Mathematics 9, no. 11: 1262. https://doi.org/10.3390/math9111262
APA StyleMishra, S. K., Jha, A. V., Verma, V. K., Appasani, B., Abdelaziz, A. Y., & Bizon, N. (2021). An Optimized Triggering Algorithm for Event-Triggered Control of Networked Control Systems. Mathematics, 9(11), 1262. https://doi.org/10.3390/math9111262









