Two-Agent Pareto-Scheduling of Minimizing Total Weighted Completion Time and Total Weighted Late Work

Abstract

We investigate the Pareto-scheduling problem with two competing agents on a single machine to minimize the total weighted completion time of agent A’s jobs and the total weighted late work of agent B’s jobs, the B-jobs having a common due date. Since this problem is known to be NP-hard, we present two pseudo-polynomial-time exact algorithms to generate the Pareto frontier and an approximation algorithm to generate a $(1+ϵ)$-approximate Pareto frontier. In addition, some numerical tests are undertaken to evaluate the effectiveness of our algorithms.

1. Introduction

Problem description and motivation: Multi-agent scheduling has attracted an ever-increasing research interest due to its extensive applications (see the book of Agnetis et al. [1]). Among the common four problem-versions (including lexical-, positive-combination-, constrained-, and Pareto-scheduling, as shown in Li and Yuan [2]) for a given group of criteria for multiple agents, Pareto-scheduling has the most important practical value, since it reflects the effective tradeoff between the actual and (usually) conflicting requirements of different agents.

Our considered problem is formally stated as follows. Assume that two agents (A and B) compete to process their own sets of independent and non-preemptive jobs on a single machine. The set of the $n_X$ jobs from agent $X\in \{A,B\}$ is ${\mathcal{J}}_X=\{J_1^X,J_2^X,\cdots ,J_{n_X}^X\}$ with ${\mathcal{J}}_A\cap {\mathcal{J}}_B=\varphi$. For convenience, we call a job from agent X an X-job. All jobs are available at time zero, and are scheduled consecutively without idle time due to the regularity of the objective functions as shown later. Each job $J_j^X$ has a processing time $p_j^X$ and a weight $w_j^X$. In addition, each B-job $J_j^B$ has also a common due date d. We assume that all parameters $p_j^X$, $w_j^X$ and d are known integers.

Let $\sigma$ be a schedule. We use $C_j^X\left(\sigma \right)$ to denote the completion time of job $J_j^X$ in $\sigma$. The objective function of agent A is the total weighted completion time, denoted by $\sum w_j^A{C}_j^A\left(\sigma \right)$, while the objective function of agent B is the total weighted late work, denoted by $\sum w_j^B{Y}_j^B\left(\sigma \right)$. Here, the late work $Y_j^B\left(\sigma \right)$ of job $J_j^B$ indicates the amount processed after the due date d, specifically,

$$Y_j^B\left(\sigma \right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{if} C_j\left(\sigma \right)\le d,\hfill \\ C_j^B\left(\sigma \right)-d,\hfill & \mathrm{if} d<C_j^B\left(\sigma \right)\le d+p_j^B,\hfill \\ p_j^B,\hfill & \mathrm{if} C_j^B\left(\sigma \right)>d+p_j^B.\hfill \end{array}\right.$$

(1)

Following Hariri et al. (1995) [3], job $J_j^B$ is said to be early, partially early, and late in $\sigma$, if $Y_j^B\left(\sigma \right)=0$, $0<Y_j^B\left(\sigma \right)<p_j^B$, and $Y_j^B\left(\sigma \right)=p_j^B$, respectively.

Falling into the category of Pareto-scheduling, the problem studied in this paper aims at generating all Pareto-optimal points (PoPs) and the corresponding Pareto-optimal schedules (PoSs) (the definitions of PoPs and PoSs will be given in Section 2) of all jobs with regard to $\sum w_j^A{C}_j^A$ and $\sum w_j^B{Y}_j^B$). Using the notations in Agnetis et al. [1], our studied scheduling problem can be denoted by $1|d_j^B{=d|}^{\#}(\sum w_j^A{C}_j^A,\sum w_j^B{Y}_j^B)$. For this problem, we will devise some efficient approximate algorithms.

Our considered scheduling model arises from many practical scenarios. For example, in a factory, two concurrent projects (A and B), each containing a certain amount of activities with distinct importance, have to share a limited resource. The former focuses on the mean completion time of its activities. In contrast, the latter requires its activities to be completed before the due date as much as possible, since, otherwise, the shortcomings of some key technical forces after the due date will occur and result in irretrievable loss. It is necessary to model the goal of project B as the weighted late work, that is, minimizing the parts left unprocessed before the due date. In addition, two projects naturally have to negotiate to seek a trade-off method of utilizing the common resource.

For another example, in a distribution center, two categories (A- and B-) goods are stored in a warehouse, in which the former comprises common goods and the latter comprises fresh goods with a shelf life. It is hoped that the shipping preparations for the A-goods will be completed as soon as possible. However, due to their limited shelf life, if they are transported after a certain time, the B-goods will not be fresh enough when they reach the customers. Therefore, it is reasonable to respectively model the goals of A-goods and B-goods by minimizing the total weighted completion time and the total weighted late work, and seek an efficient transportation method.

Related works and our contribution: Numerous works have addressed multi-agent scheduling problems in the literature. With the aim of this paper, we only summarize briefly some related results. Wan et al. [4] provided a strongly polynomial-time algorithm for the two-agent Pareto-scheduling problem on a single machine to minimize the number of the tardy A-jobs and the maximum cost of the B-jobs. Later, Wan et al. [5] investigated two Pareto-scheduling problems on a single machine with two competing agents and a linear-deterioration processing time: ${1\left|\right|}^{\#}(E_{max}^A,E_{max}^B)$ and ${1\left|\right|}^{\#}(\sum E_j^A,E_{max}^B)$, where $\sum E_j^A$ is the total earliness of the A-jobs and $E_{max}^X$ is the maximum earliness of the X-jobs. For these two problems, they respectively proposed a polynomial-time algorithm. Gao and Yuan [6] showed that the following two Pareto-scheduling problems with a positional due index and precedence constraints are both polynomially solvable: ${1\left|\right|}^{\#}(\sum C_j^A,f_{max}^B)$ and ${1\left|\right|}^{\#}(f_{max}^A,f_{max}^B)$, where $f_{max}^X$ indicates the maximum cost of the X-jobs. He et al. [7] extensively considered the versions of the problems in Gao and Yuan [6] with deteriorating or shortening processing times and without positional due indices and precedence constraints, and devised polynomial-time algorithms. Yuan et al. [8] showed the single-machine preemptive problem $1|r_j{,pmtn|}^{\#}(L_{max}^a:L_{max}^b)$ can be solved in a polynomial time, where $L_{max}^X$ indicates the maximum lateness of the X-jobs. Wan [9] investigated the single-machine two-agent scheduling problem to minimize the maximum costs with position-dependent jobs, and developed a polynomial-time algorithm.

While most results on Pareto-scheduling concentrate on devising exact algorithms to obtain the Pareto frontier, there are also some methods (such as [10,11,12,13,14]) of developing approximate algorithms to generate the approximate Pareto frontier. Dabia et al. [10] adopted the trimming technique to derive the approximate Pareto frontier for some multi-objective scheduling problems. Yin et al. [15] considered two just-in-time (JIT) scheduling problems with two competing agents on unrelated parallel machines, in which the one agent’s criterion is to maximize the weighted number of its JIT jobs, and another agent’s criterion is either to maximize its maximum gains from its JIT jobs or to maximize the weighted number of its JIT jobs. They showed that the two problems are both unary NP-hard when the machine number is not fixed, and proposed either a polynomial-time algorithm or a fully polynomial-time approximation scheme (FPTAS) when the machine number is a constant. Yin et al. [16] also considered similar problems in the setting of a two-machine flow shop, and provided two pseudo-polynomial-time exact algorithms to find the Pareto frontier. Chen et al. [17] studied a multi-agent Pareto-scheduling problem in a no-wait flow shop setting, in which each agent’s criterion is to maximize its own weighted number of JIT jobs. They showed that it is unary NP-hard when the number of agents is arbitrary, and presented pseudo-polynomial time algorithms and an $(1,1-ϵ,\dots ,1-ϵ)$-approximation algorithm when the number of agents is fixed.

From the perspective of methodology, as a type of optimization problem, the multi-agent scheduling problem’s solution algorithms potentially allow for exploiting the optimal robot path planning by a gravitational search algorithm (Purcaru et al. [18]) and optimization based on phylogram analysis (Soares et al. [19]).

In the prophase work (Zhang and Yuan [20]), we proved that the constrained scheduling problem of minimizing the total late work of agent A’s jobs with equal due dates subject to the makespan of agent B’s jobs not exceeding a given upper bound, is NP-hard even if agent B has only one job. It implies the NP-hardness of our considered problem in this paper. Thus we limit the investigation to devising pseudo-polynomial-time exact algorithms and an approximation algorithm to generate the approximate Pareto frontier.

In addition, in our recent work (Zhang et al. [21]), we considered several three-agent scheduling problems under different constraints on a single machine, in which the three agents’ criteria are to minimize the total weighted completion time, the weighted number of tardy jobs, and the total weighted late work. Among those problems, there are two questions related to this paper: $1|p_j^A\uparrow \downarrow w_j^A{|}^{\#}(\Sigma w_j^A{C}_j^A,\Sigma w_j^B{Y}_j^B)$, which is solved in $O(n_A{n}_B^2{U}^A{U}^B)$, and $1|p_j^A\uparrow \downarrow w_j^A,d_j^B\uparrow \downarrow w_j^B{|}^{\#}(\Sigma w_j^A{C}_j^A,\Sigma w_j^B{Y}_j^B)$, which is solved in $O(n_A{n}_B{U}^A{U}^B)$. The notation $p_j^A\uparrow \downarrow w_j^A$ represents that the jobs of the first agent have inversely agreeable processing times and weights, i.e., the smaller the processing time for a job, the greater its weight, and the notation $d_j^B\uparrow \downarrow w_j^B$ represents that the jobs of agent B have inversely agreeable due dates and weights. $U^A$ and $U^B$ are the upper bounds on the criteria $\Sigma w_j^A{C}_j^A$ and $\Sigma w_j^B{Y}_j^B$, respectively. In contrast to Zhang et al. [21], in this article we remove the constraint $p_j^A\uparrow \downarrow w_j^A$ and turn to the optimization problem of B-jobs having a common due date.

The remainder of the paper is organized as follows. In Section 2, some preliminaries are provided. In Section 3 and Section 4, we present two dynamic programming algorithms and an FPTAS. In Section 5, some numeral tests are undertaken to show the algorithms’ efficiency. Section 6 concludes the paper and suggests the future research direction.

2. Preliminaries

For self-consistency, in this section we describe some notions and properties related to Pareto-scheduling, and we present other useful notations in the description of the algorithms in the following sections.

Definition 1.

Consider two m-vectors $\mathit{u}=(u_1,u_2,\dots ,u_m)$ and $\mathit{v}=(v_1,v_2,\dots ,v_m)$.

(i) We say that $\mathit{u}$ dominates $\mathit{v}$, denoted by $\mathit{u}⪯\mathit{v}$, if $u_i\le v_i$ for $i=1,2,\dots ,m$.

(ii) We say that $\mathit{u}$ strictly dominates $\mathit{v}$, denoted by $\mathit{u}\prec \mathit{v}$, if $\mathit{u}⪯\mathit{v}$ and $\mathit{u}\ne \mathit{v}$.

(iii) Given a constant $ϵ>0$, we say that $\mathit{u}$ $ϵ$-dominates $\mathit{v}$, denoted by $\mathit{u}{⪯}_{ϵ}\mathit{v}$, if and only if $u_i\le (1+ϵ)v_i$ for $i=1,2,\dots ,m$.

Definition 2.

Given two agents’ criteria ${\gamma }^A(\sigma )$ and ${\gamma }^B(\sigma )$, a feasible schedule σ is called Pareto-optimal and the corresponding objective vector $({\gamma }^A(\sigma ),{\gamma }^B(\sigma ))$ is called a Pareto-optimal point, if no other feasible schedule π satisfies $({\gamma }^A(\pi ),{\gamma }^B(\pi ))\prec ({\gamma }^A(\sigma ),{\gamma }^B(\sigma ))$. All the Pareto-optimal points form the Pareto frontier, denoted by $\mathit{P}$.

Let $\mathbf{R}$ be the set of the objective vectors of all feasible schedules, and $\mathbf{Q}$ be a subset of $\mathbf{R}$.

Definition 3.

A vector $\mathit{u}\in \mathit{Q}$ is called non-dominated in $\mathit{Q}$, if there exists no other vector $\mathit{v}\in \mathit{Q}$ such that $\mathit{v}\prec \mathit{u}$.

It is not difficult to see that, for the above definitions, the latter is an extension of the former, and especially when $\mathbf{Q}$ is exactly equal to $\mathbf{R}$, all the non-dominated vectors in $\mathbf{Q}$ compose the Pareto-optimal frontier. The following lemma establishes the relationship between sets $\mathbf{P}$ and a subset $\mathbf{Q}\subseteq \mathbf{R}$.

Lemma 1.

For any set $\mathit{Q}$ with $\mathit{P}\subseteq \mathit{Q}\subseteq \mathit{R}$, if $\mathit{O}$ is the set including all the non-dominated vectors in $\mathit{Q}$, then $\mathit{O}=\mathit{P}$.

Proof. 

By Definition 2, for each Pareto-optimal point $\mathbf{u}\in \mathbf{P}$, there is no other vector $\mathbf{v}\in \mathbf{R}$ such that $\mathbf{v}\prec \mathbf{u}$, and naturally, such a fact also holds for the set $\mathbf{Q}$, since $\mathbf{Q}\subseteq \mathbf{R}$. Then, it follows that $\mathbf{P}\subseteq \mathbf{O}$ by the definition of the set $\mathbf{O}$. Next we show that $\mathbf{O}\subseteq \mathbf{P}$. If not, we pick up one vector $\mathbf{w}$ from $\mathbf{O}\backslash \mathbf{P}$. Again by Definition 2, there is some vector $\mathbf{w}\in \mathbf{P}$ such that $\mathbf{w}\prec \mathbf{u}$. Nevertheless, this is impossible, since $\mathbf{w}\in \mathbf{P}\subseteq \mathbf{Q}$ leads to no existence of such a vector $\mathbf{w}$ in $\mathbf{Q}$ by the assumption of $\mathbf{w}$ and Definition 3. Thus $\mathbf{O}=\mathbf{P}$. □

From Lemma 1, to generate the Pareto frontier $\mathbf{P}$, an alternative is to first determine a set $\mathbf{Q}$ with $\mathbf{P}\subseteq \mathbf{Q}\subseteq \mathbf{R}$, and then delete the dominated vectors in $\mathbf{Q}$. Throughout the reminder of this paper, such a subset $\mathbf{Q}$ is called an intermediate set. Obviously, $\mathbf{R}$ is also an intermediate set.

Definition 4.

For a given constant $ϵ>0$, a $(1+ϵ)$-approximate Pareto frontier, denoted by ${\mathit{P}}_{ϵ}$, is a set of the objective vectors satisfying, for any $({\gamma }^A(\sigma ),{\gamma }^B(\sigma ))\in \mathit{P}$, there exists at least one objective vector $({\gamma }^A({\sigma }^{\prime }),{\gamma }^B({\sigma }^{\prime }))\in {\mathit{P}}_{ϵ}$ such that $({\gamma }^A({\sigma }^{\prime }),{\gamma }^B({\sigma }^{\prime })){⪯}_{ϵ}({\gamma }^A(\sigma ),{\gamma }^B(\sigma ))$.

Definition 5.

A family of algorithms $\{{\mathcal{A}}_{ϵ}:ϵ>0\}$ is called afully polynomial-time approximation scheme(FPTAS) if, for each $ϵ>0$, ${\mathcal{A}}_{ϵ}$ generates a $(1+ϵ)$-approximate Pareto frontier with a running time in the polynomial in the instance size and $1/ϵ$.

Besides those already mentioned in Section 1, the following notations will also be used later:

• $\mathcal{J}$${}_j^X:$ indicates the set of the first j jobs in $\mathcal{J}$${}^X$, namely, $\mathcal{J}$${}_j^X=\{J_1^X,J_2^X,\cdots ,J_j^X\}$.
• $J_i^X{\prec }_{\sigma }{J}_j^{X^{\prime }}$ indicates that job $J_i^X$ immediately precedes $J_j^{X^{\prime }}$ in schedule $\sigma$, where $X,X^{\prime }\in \{A,B\}$.
• $s_j^X(\sigma )$ indicates the starting time of job $J_j^X$ in $\sigma$.
• $P_{\mathrm{sum}}^X={\sum }_{j=1}^{n_X}{p}_j^X$ indicates the total processing time of all X-jobs.
• $P_{\mathrm{sum}}$ indicates the total processing time of all jobs, and $P_{\mathrm{sum}}=P_{\mathrm{sum}}^A+P_{\mathrm{sum}}^B$.
• $W_{\mathrm{sum}}^X={\sum }_{j=1}^{n_X}{w}_j^X$ indicates the total weight of all X-jobs.
• $W_{\mathrm{sum}}$ indicates the total weight of all jobs, and $W_{\mathrm{sum}}=W_{sum}^A+W_{sum}^B$.
• $p_{max}^X$ indicates the maximum processing time of the X-jobs, namely, $p_{max}^X=max\{p_j^X:1\le j\le n_X\}$.
• $w_{max}^X$ indicates the maximum weight of the X-jobs, namely, $w_{max}^X=max\{w_j^X:1\le j\le n_X\}$.

3. An Exact Algorithm

In this section a dynamic programming algorithm for problem $1|d_j^B{=d|}^{\#}(\sum w_j^A{C}_j^A,\sum w_j^B{Y}_j^B)$ is presented. For description convenience, for a given schedule $\sigma$, the job set $\mathcal{J}$ is divided into the following four subsets: ${\mathcal{J}}^{A_1}(\sigma )=\{J_j^A:C_j^A(\sigma )\le d\}$, ${\mathcal{J}}^{A_2}(\sigma )=\{J_j^A:C_j^A(\sigma )>d\}$, ${\mathcal{J}}^{B_1}(\sigma )=\{J_j^B:s_j^B(\sigma )<d\}$, and ${\mathcal{J}}^{B_2}(\sigma )=\{J_j^B:s_j^B(\sigma )\ge d\}$. Obviously, such a partition of the job set is well defined for a given schedule.

The following lemma establishes the structural properties of the Pareto-optimal schedule.

Lemma 2.

For each Pareto-optimal point $(C,Y)$ of problem $1|d_j^B{=d|}^{\#}(\sum w_j^A{C}_j^A,\sum w_j^B{Y}_j^B)$, there is a Pareto-optimal schedule σ such that

(i) ${\mathcal{J}}^{A_1}(\sigma ){\prec }_{\sigma }{\mathcal{J}}^{B_1}(\sigma ){\prec }_{\sigma }{\mathcal{J}}^{A_2}(\sigma ){\prec }_{\sigma }{\mathcal{J}}^{B_2}(\sigma )$.

(ii) the jobs in ${\mathcal{J}}^{B_1}(\sigma )$ are sequenced in the non-increasing order of their weights and the jobs in ${\mathcal{J}}^{B_2}(\sigma )$ are sequenced arbitrarily.

(iii) the jobs in ${\mathcal{J}}^{A_1}(\sigma )$ and ${\mathcal{J}}^{A_2}(\sigma )$ are sequenced according to the weighted shortest processing time (WSPT) rule.

Proof. 

In Lemma 2, statement (i) can easily be observed, since the jobs in ${\mathcal{J}}^{B_2}(\sigma )$ are late and this will not result in any increase in their total late work when moving them to the end of the schedule, and as many A-jobs as possible can be positioned before the B-jobs in ${\mathcal{J}}^{B_1}(\sigma )$, provided that the last job in ${\mathcal{J}}^{B_1}(\sigma )$ is not late. The left two statements in Lemma 2 can easily be proved by an interchange argument and the detail is omitted here. □

Lemma 2 allows us only to consider the feasible schedules simultaneously satisfying the conditions (i)-(iii). To this end, we re-number the $n_A$ jobs in ${\mathcal{J}}^A$ in the WSPT order and the $n_B$ B-jobs in the maximum weight first (MW) order so that

$$\frac{p_1^A}{w_1^A}\le \frac{p_2^A}{w_2^A}\le \cdots \le \frac{p_{n_A}^A}{w_{n_A}^A}.$$

(2)

$$w_1^B\ge w_2^B\ge \cdots \ge w_{n_B}^B.$$

(3)

Such a sorting takes $O(nlogn)$ time.

According to Lemma 1, the algorithm to be described adopts the strategy of first finding the intermediate set dynamically and then deleting the dominated points in it. It is necessary to mention that in the proposed algorithm we appropriately relax the conditions to find a modestly larger intermediate set. For briefly describing the dynamic programming algorithm, we introduce the following terminologies and notations.

• an $ABAB$-schedule is defined to be a schedule $\pi$ for $\mathcal{I}\subseteq \mathcal{J}$ satisfying (i) $\pi ={\pi }_1\prec {\pi }_2\prec {\pi }_3\prec {\pi }_4$, where among the four mutually disjointed subschedules ${\pi }_1,{\pi }_2,{\pi }_3,and{\pi }_4$, the A-jobs are included in ${\pi }_1$ and ${\pi }_3$, and the B-jobs are included in ${\pi }_2$ and ${\pi }_4$; (ii) no idle time exists between the jobs in each subschedule, but this is not necessarily so between two subschedules. Moreover, the idle time between ${\pi }_3$ and ${\pi }_4$ is supposed to be long enough; (iii) the jobs in each subschedule are sequenced in the increasing order of their indices.
• an $(\overrightarrow{x},\overleftarrow{y})$-schedule is defined to be an $ABAB$-schedule $\pi$ for ${\mathcal{J}}_x^A\cup ({\mathcal{J}}^B\backslash {\mathcal{J}}_{y-1}^B)$ with no idle time existing between subschedules ${\pi }_2$ and ${\pi }_3$, where $x\in \{1,2,\dots ,n_A\}$ and $y\in \{1,2,\dots ,n_B\}$.
• a vector $(t_1,t_2,t_3,C,Y)$ is introduced to denote a state of $(\overrightarrow{x},\overleftarrow{y})$, in which $t_1,t_2,t_3,C$, and Y, respectively, stand for the end point of ${\pi }_1$, the start point of ${\pi }_2$, the end point of ${\pi }_3$, the total weighted completion time of the A-jobs of ${\mathcal{J}}_x^A$, and the total weighted late work of the B-jobs of ${\mathcal{J}}^B\backslash \{{\mathcal{J}}_{y-1}^B\}$. Note that a state of $(\overrightarrow{x},\overleftarrow{y})$ at least corresponds to some $(\overrightarrow{x},\overleftarrow{y})$-schedule.
• $\Gamma (\overrightarrow{x},\overleftarrow{y})$ denotes the set of all the states of $(\overrightarrow{x},\overleftarrow{y})$.
• $\tilde{\Gamma }(\overrightarrow{x},\overleftarrow{y})$ denotes the set obtained from $\Gamma (\overrightarrow{x},\overleftarrow{y})$ by deleting the vectors $(t_1,t_2,t_3,C,Y)$, for which there is another vector $(\overline{t_1},\overline{t_2},\overline{t_3},\overline{C},\overline{Y})$ with $t_1\le \overline{t_1},t_2\ge \overline{t_2},t_3\le \overline{t_3},C\le \overline{C}$, and $Y\le \overline{Y}$.
• Let ${\mathbf{Q}}_1=\{(C,Y):(t_1,t_2,t_3,C,Y)\in \tilde{\Gamma }(\overrightarrow{n_A},\overleftarrow{1})\}$, and let $\widetilde{{\mathbf{Q}}_1}$ be the set of the non-dominated vectors in ${\mathbf{Q}}_1$.

To solve problem $1|d_j^B{=d|}^{\#}(\sum w_j^A{C}_j^A,\sum w_j^B{Y}_j^B)$, we have to first compute $\tilde{\Gamma }(\overrightarrow{n_A},\overleftarrow{1})$ and then obtain the Pareto-frontier $\widetilde{{\mathbf{Q}}_1}$. This can be realized by dynamically computing the sets $\Gamma (\overrightarrow{x},\overleftarrow{y})$ for all the possible choices of the tuple $(x,y)$. Note that each $(\overrightarrow{x},\overleftarrow{y})$-schedule can be obtained either by adding job $J_x^A$ to some $(\overrightarrow{x-1},\overleftarrow{y})$-schedule, or by adding job $J_y^B$ to some $(\overrightarrow{x},\overleftarrow{y+1})$-schedule. Therefore, we can informally describe our dynamic programming algorithm as follows.

Initially, set $\Gamma (\overrightarrow{0},\overleftarrow{n_B+1})=\{(0,t_0,t_0,0,0):d-p_{max}^A+1\le t_0\le d+p_{max}^B-1\}$ and $\Gamma (\overrightarrow{x},\overleftarrow{y})=\varnothing$ if $(x,y)\ne (0,n_B+1)$. Then we recursively generate all the state sets $\Gamma (\overrightarrow{x},\overleftarrow{y})$ from the previously-generated sets $\Gamma (\overrightarrow{x-1},\overleftarrow{y})$ and $\Gamma (\overrightarrow{x},\overleftarrow{y+1})$. Specifically,

• For each state $(t_1,t_2,t_3,C,Y)\in \Gamma (\overrightarrow{x-1},\overleftarrow{y})$ with $\Gamma (\overrightarrow{x-1},\overleftarrow{y})\ne \varphi$, add two states $(t_1^{\prime },t_2^{\prime },t_3^{\prime },C^{\prime },Y^{\prime })$ and $(t_1^{″},t_2^{″},t_3^{″},C^{″},Y^{″})$ to the set $\Gamma (\overrightarrow{x},\overleftarrow{y})$, with

  $$(t_1^{\prime },t_2^{\prime },t_3^{\prime },C^{\prime },Y^{\prime })=(t_1+p_x^A,t_2,t_3,C+w_x^A(t_1+p_x^A),Y),$$

  and

  $$(t_1^{″},t_2^{″},t_3^{″},C^{″},Y^{″})=(t_1,t_2,t_3+p_x^A,C+w_x^A(t_3+p_x^A),Y).$$

These two states respectively correspond to the newly obtained $(\overrightarrow{x},\overleftarrow{y})$-schedules by scheduling job $J_x^A$ immediately following the subschedule ${\pi }_1$ and immediately following the subschedule ${\pi }_3$, in some $(\overrightarrow{x-1},\overleftarrow{y})$ schedule $\pi$ that corresponds to the state $(t_1,t_2,t_3,C,Y)$. Note that the first case occurs only when $t_1+p_x^A\le t_2$ is satisfied.

• For each state $(t_1,t_2,t_3,C,Y)\in \Gamma (\overrightarrow{x},\overleftarrow{y+1})$, also add two two states $(t_1^{\prime },t_2^{\prime },t_3^{\prime },C^{\prime },Y^{\prime })$ and $(t_1^{″},t_2^{″},t_3^{″},C^{″},Y^{″})$ to the set $\Gamma (\overrightarrow{x},\overleftarrow{y})$, with

  $$(t_1^{\prime },t_2^{\prime },t_3^{\prime },C^{\prime },Y^{\prime })=(t_1,t_2-p_y^B,t_3,C,Y+w_y^{B}max\{t_2-d^B,0\}),$$

  and

  $$(t_1^{″},t_2^{″},t_3^{″},C^{″},Y^{″})=(t_1,t_2,t_3,C,Y+w_y^B{p}_y^B).$$

These two states respectively correspond to the newly obtained $(\overrightarrow{x},\overleftarrow{y})$-schedules by scheduling job $J_y^B$ immediately preceding the subschedule ${\pi }_2$ and immediately following the subschedule ${\pi }_4$, in some $(\overrightarrow{x},\overleftarrow{y+1})$ schedule $\pi$ that corresponds to the state $(t_1,t_2,t_3,C,Y)$. Note that the first case occurs only when $t_1\le t_2-p_y^B<d^B$ is satisfied.

Note that, if in the above state-generation procedures we replace sets $\Gamma (\overrightarrow{x-1},\overleftarrow{y})$ and $\Gamma (\overrightarrow{x},\overleftarrow{y+1})$ with sets $\tilde{\Gamma }(\overrightarrow{x-1},\overleftarrow{y})$ and $\tilde{\Gamma }(\overrightarrow{x},\overleftarrow{y+1})$, then the resulting set of new states, denoted by ${\Gamma }^{\prime }(\overrightarrow{x},\overleftarrow{y})$, may be different from $\Gamma (\overrightarrow{x},\overleftarrow{y})$. Recall that, when deleting those dominated vectors in the sets $\Gamma (\overrightarrow{x},\overleftarrow{y})$ and ${\Gamma }^{\prime }(\overrightarrow{x},\overleftarrow{y})$, the newly obtained sets are respectively denoted by $\tilde{\Gamma }(\overrightarrow{x},\overleftarrow{y})$ and $\widetilde{{\Gamma }^{\prime }}(\overrightarrow{x},\overleftarrow{y})$, which will be shown to be identical in the following lemma.

Lemma 3.

$\tilde{\Gamma }(\overrightarrow{x},\overleftarrow{y})=\widetilde{{\Gamma }^{\prime }}(\overrightarrow{x},\overleftarrow{y})$.

Proof. 

Since $\tilde{\Gamma }(\overrightarrow{x-1},\overleftarrow{y})\subseteq \Gamma (\overrightarrow{x-1},\overleftarrow{y})$ and $\tilde{\Gamma }(\overrightarrow{x},\overleftarrow{y+1})\subseteq \Gamma (\overrightarrow{x},\overleftarrow{y+1})$, it follows that ${\Gamma }^{\prime }(\overrightarrow{x},\overleftarrow{y})\subseteq \Gamma (\overrightarrow{x},\overleftarrow{y})$ by the generation procedure of the new states as described previously. If $\Gamma (\overrightarrow{x},\overleftarrow{y})={\Gamma }^{\prime }(\overrightarrow{x},\overleftarrow{y})$, then naturally $\tilde{\Gamma }(\overrightarrow{x},\overleftarrow{y})=\widetilde{{\Gamma }^{\prime }}(\overrightarrow{x},\overleftarrow{y})$. In the following, suppose that $\Gamma (\overrightarrow{x},\overleftarrow{y})\backslash {\Gamma }^{\prime }(\overrightarrow{x},\overleftarrow{y})\ne \varnothing$. We next show that each state $(t_1^{\prime },t_2^{\prime },t_3^{\prime },C^{\prime },Y^{\prime })\in \Gamma (\overrightarrow{x},\overleftarrow{y})\backslash {\Gamma }^{\prime }(\overrightarrow{x},\overleftarrow{y})$ is dominated by a state $(\overline{t_1},\overline{t_2},\overline{t_3},\overline{C},\overline{Y})\in {\Gamma }^{\prime }(\overrightarrow{x},\overleftarrow{y})$, namely, $\overline{t_1}\le t_1^{\prime },\overline{t_2}\ge t_2^{\prime },\overline{t_3}\le t_3^{\prime },\overline{C}\le C^{\prime },\overline{Y}\le Y^{\prime }$.

Let ${\pi }^{\prime }$ be an $(\overrightarrow{x},\overleftarrow{y})$-schedule corresponding to $(t_1^{\prime },t_2^{\prime },t_3^{\prime },C^{\prime },Y^{\prime })$. According to the above discussion, there are four possibilities of deriving ${\pi }^{\prime }$ from some schedule $\pi$, which is assumed to correspond to the state $(t_1,t_2,t_3,C,Y)$ in $\Gamma (\overrightarrow{x-1},\overleftarrow{y})$ or $\Gamma (\overrightarrow{x},\overleftarrow{y+1})$.

Case 1.${\pi }^{\prime }$ is obtained from $\pi$ by scheduling job $J_x^A$ directly after subschedule ${\pi }_1$. Then $(t_1,t_2,t_3,C,Y)\in \Gamma (\overrightarrow{x-1},\overleftarrow{y})$ with $t_1+p_x^A\le t_2$, and there is a state $(\widetilde{t_1},\widetilde{t_2},\widetilde{t_3},\tilde{C},\tilde{Y})\in \tilde{\Gamma }(\overrightarrow{x-1},\overleftarrow{y})$ such that $\widetilde{t_1}\le t_1,\widetilde{t_2}\ge t_2,\widetilde{t_3}\le t_3,\tilde{C}\le C$, and $\tilde{Y}\le Y$. Let $\tilde{\pi }$ be an $(\overrightarrow{x-1},\overleftarrow{y})$-schedule corresponding to $(\widetilde{t_1},\widetilde{t_2},\widetilde{t_3},\tilde{C},\tilde{Y})$, and let $\overline{\pi }$ be the $(\overrightarrow{x},\overleftarrow{y})$-schedule obtained from $\tilde{\pi }$ by scheduling $J_x^A$ directly after schedule ${\tilde{\pi }}_1$. Let $(\overline{t_1},\overline{t_2},\overline{t_3},\overline{C},\overline{Y})$ be the state corresponding to $\overline{\pi }$. Note that the above operation to get $\overline{\pi }$ is feasible since $\widetilde{t_1}+p_x^A\le t_1+p_x^A\le t_2\le \widetilde{t_2}$. Then we have $(\overline{t_1},\overline{t_2},\overline{t_3},\overline{C},\overline{Y})=(\widetilde{t_1}+p_x^A,\widetilde{t_2},\widetilde{t_3},\tilde{C}+w_x^A(\widetilde{t_1}+p_x^A),\tilde{Y}).$ Combining with the fact that $(t_1^{\prime },t_2^{\prime },t_3^{\prime },C^{\prime },Y^{\prime })=(t_1+p_x^A,t_2,t_3,C+w_x^A(t_1+p_x^A),Y)$, we have

$$\left\{\begin{array}{c}\overline{t_1}=\widetilde{t_1}+p_x^A\le t_1+p_x^A=t_1^{\prime },\\ \overline{t_2}=\widetilde{t_2}\ge t_2=t_2^{\prime },\\ \overline{t_3}=\widetilde{t_3}\le t_3=t_3^{\prime },\\ \overline{C}=\tilde{C}+w_x^A(\widetilde{t_1}+p_x^A)\le C+w_x^A(t_1+p_x^A)=C^{\prime },\\ \overline{Y}=\tilde{Y}\le Y=Y^{\prime }.\end{array}\right.$$

(4)

Case 2.${\pi }^{\prime }$ is obtained from $\pi$ by scheduling $J_x^A$ directly after schedule ${\pi }_3$. Then $(t_1,t_2,t_3,C,Y)\in \Gamma (\overrightarrow{x-1},\overleftarrow{y})$, and there is a state $(\widetilde{t_1},\widetilde{t_2},\widetilde{t_3},\tilde{C},\tilde{Y})\in \tilde{\Gamma }(\overrightarrow{x-1},\overleftarrow{y})$ such that $\widetilde{t_1}\le t_1,\widetilde{t_2}\ge t_2,\widetilde{t_3}\le t_3,\tilde{C}\le C$, and $\tilde{Y}\le Y$. Let $\tilde{\pi }$ be an $(\overrightarrow{x-1},\overleftarrow{y})$-schedule corresponding to $(\widetilde{t_1},\widetilde{t_2},\widetilde{t_3},\tilde{C},\tilde{Y})$, and let $\overline{\pi }$ be the $(\overrightarrow{x},\overleftarrow{y})$-schedule obtained from $\tilde{\pi }$ by scheduling $J_x^A$ directly after schedule ${\tilde{\pi }}_3$. Let $(\overline{t_1},\overline{t_2},\overline{t_3},\overline{C},\overline{Y})$ be the state corresponding to $\overline{\pi }$. Then we have $(\overline{t_1},\overline{t_2},\overline{t_3},\overline{C},\overline{Y})=(\widetilde{t_1},\widetilde{t_2},\widetilde{t_3}+p_x^A,\tilde{C}+w_x^A(\widetilde{t_3}+p_x^A),\tilde{Y}).$ Combining with the fact that $(t_1^{\prime },t_2^{\prime },t_3^{\prime },C^{\prime },Y^{\prime })=(t_1,t_2,t_3+p_x^A,C+w_x^A(t_3+p_x^A),Y)$, we have

$$\left\{\begin{array}{c}\overline{t_1}=\widetilde{t_1}\le t_1=t_1^{\prime },\\ \overline{t_2}=\widetilde{t_2}\ge t_2=t_2^{\prime },\\ \overline{t_3}=\widetilde{t_3}+p_x^A\le t_3+p_x^A=t_3^{\prime },\\ \overline{C}=\tilde{C}+w_x^A(\widetilde{t_3}+p_x^A)\le C+w_x^A(t_3+p_x^A)=C^{\prime },\\ \overline{Y}=\tilde{Y}\le Y=Y^{\prime }.\end{array}\right.$$

(5)

Case 3.${\pi }^{\prime }$ is obtained from $\pi$ by scheduling $J_y^B$ directly before schedule ${\pi }_2$. Note that in this case, the condition $t_1\le t_2-p_y^B<d^B$ must be satisfied. Then $(t_1,t_2,t_3,C,Y)\in \Gamma (\overrightarrow{x},\overleftarrow{y+1})$, and there is a state $(\widetilde{t_1},\widetilde{t_2},\widetilde{t_3},\tilde{C},\tilde{Y})\in \tilde{\Gamma }(\overrightarrow{x},\overleftarrow{y+1})$ such that $\widetilde{t_1}\le t_1,\widetilde{t_2}\ge t_2,\widetilde{t_3}\le t_3,\tilde{C}\le C$, and $\tilde{Y}\le Y$. Let $\tilde{\pi }$ be an $(\overrightarrow{x},\overleftarrow{y+1})$-schedule corresponding to $(\widetilde{t_1},\widetilde{t_2},\widetilde{t_3},\tilde{C},\tilde{Y})$, and let $\overline{\pi }$ be the $(\overrightarrow{x},\overleftarrow{y})$-schedule obtained from $\tilde{\pi }$ by scheduling $J_y^B$ directly before schedule ${\pi }_2$. Let $(\overline{t_1},\overline{t_2},\overline{t_3},\overline{C},\overline{Y})$ be the state corresponding to $\overline{\pi }$. The above operation to obtain $\overline{\pi }$ is feasible. In fact, $\widetilde{t_1}\le t_1\le t_2-p_y^B$, which means there are enough spaces for $J_y^B$ to be scheduled in. In the following we will illustrate that the condition $\widetilde{t_2}-p_y^B<d$ is satisfied.

Claim 1.If $\widetilde{t_2}\ne t_2$, then $\widetilde{t_2}\le d$.

Suppose to the contrary that $\widetilde{t_2}>d$, then $J_y^B$ is partially early or late in $\overline{\pi }$, implying that $J_{y+1}^B,J_{y+2}^B,\dots ,J_{n_B}^B$ are all late in $\tilde{\pi }$, i.e., there is no job in ${\tilde{\pi }}_2$, which further suggests that ${\sum }_{j=1}^x{p}_j^A=\widetilde{t_1}+\widetilde{t_3}-\widetilde{t_2}$. What is more, since $\tilde{Y}\le Y$, the jobs $J_{y+1}^B,J_{y+2}^B,\dots ,J_{n_B}^B$ are also late in $\pi$, which also indicates that $\tilde{Y}=Y$ and ${\sum }_{j=1}^x{p}_j^A=t_1+t_3-t_2$. From $\widetilde{t_1}+\widetilde{t_3}-\widetilde{t_2}=t_1+t_3-t_2$, $\widetilde{t_1}\le t_1$, $\widetilde{t_2}\ge t_2$, and $\widetilde{t_3}\le t_3$ we know that $\widetilde{t_2}=t_2$ contradicts $\widetilde{t_2}\ne t_2$. Thus, $\widetilde{t_2}\le d^B$. Claim 1 follows.

If $\widetilde{t_2}-p_y^B\ge d^B$, then $\widetilde{t_2}\ne t_2$. From Claim 1 we have $\widetilde{t_2}\le d<d+p_y^B$, i.e., $\widetilde{t_2}-p_y^B<d$, which is a contradiction. Thus the condition $\widetilde{t_2}-p_y^B<d^B$ is satisfied and the operation to get $\overline{\pi }$ is feasible. Then we have $(\overline{t_1},\overline{t_2},\overline{t_3},\overline{C},\overline{Y})=(\widetilde{t_1},\widetilde{t_2}-p_y^B,\widetilde{t_3},\tilde{C},\tilde{Y}+w_y^{B}max\{\widetilde{t_2}-d,0\}).$ Combining with the fact that $(t_1^{\prime },t_2^{\prime },t_3^{\prime },C^{\prime },Y^{\prime })=(t_1,t_2-p_y^B,t_3,C,Y+w_y^{B}max\{t_2-d,0\})$, we have

$$\left\{\begin{array}{c}\overline{t_1}=\widetilde{t_1}\le t_1=t_1^{\prime },\\ \overline{t_2}=\widetilde{t_2}-p_y^B\ge t_2-p_y^B=t_2^{\prime },\\ \overline{t_3}=\widetilde{t_3}\le t_3=t_3^{\prime },\\ \overline{C}=\tilde{C}\le C=C^{\prime }.\end{array}\right.$$

(6)

Next we prove that $\overline{Y}\le Y^{\prime }$. In fact, if $\widetilde{t_2}=t_2$, then $\overline{Y}=\tilde{Y}+w_y^{B}max\{\widetilde{t_2}-d,0\}\le Y+w_y^{B}max\{t_2-d,0\}=Y^{\prime }$. If $\widetilde{t_2}\ne t_2$, then from Claim 1 we know that $\widetilde{t_2}\le d$, and then $t_2-d<0$. Thus we have $\overline{Y}=\tilde{Y}\le Y=Y^{\prime }$.

Case 4.${\pi }^{\prime }$ is obtained from $\pi$ by scheduling $J_y^B$ directly after schedule ${\pi }_4$. Then $(t_1,t_2,t_3,C,Y)\in \Gamma (\overrightarrow{x},\overleftarrow{y+1})$, and there is a state $(\widetilde{t_1},\widetilde{t_2},\widetilde{t_3},\tilde{C},\tilde{Y})\in \tilde{\Gamma }(\overrightarrow{x},\overleftarrow{y+1})$ such that $\widetilde{t_1}\le t_1,\widetilde{t_2}\ge t_2,\widetilde{t_3}\le t_3,\tilde{C}\le C$, and $\tilde{Y}\le Y$. Let $\tilde{\pi }$ be an $(\overrightarrow{x},\overleftarrow{y+1})$-schedule corresponding to $(\widetilde{t_1},\widetilde{t_2},\widetilde{t_3},\tilde{C},\tilde{Y})$, and let $\overline{\pi }$ be the $(\overrightarrow{x},\overleftarrow{y})$-schedule obtained from $\tilde{\pi }$ by scheduling $J_x^A$ directly after schedule ${\tilde{\pi }}_3$. Let $(\overline{t_1},\overline{t_2},\overline{t_3},\overline{C},\overline{Y})$ be the state corresponding to $\overline{\pi }$. Then we have $(\overline{t_1},\overline{t_2},\overline{t_3},\overline{C},\overline{Y})=(\widetilde{t_1},\widetilde{t_2},\widetilde{t_3},\tilde{C},\tilde{Y}+w_y^B{p}_y^B).$ Combining with the fact that $(t_1^{\prime },t_2^{\prime },t_3^{\prime },C^{\prime },Y^{\prime })=(t_1,t_2,t_3,C,Y+w_y^B{p}_y^B)$, we have

$$\left\{\begin{array}{c}\overline{t_1}=\widetilde{t_1}\le t_1=t_1^{\prime },\\ \overline{t_2}=\widetilde{t_2}\ge t_2=t_2^{\prime },\\ \overline{t_3}=\widetilde{t_3}\le t_3=t_3^{\prime },\\ \overline{C}=\tilde{C}\le C=C^{\prime },\\ \overline{Y}=\tilde{Y}+w_y^B{p}_y^B\le Y+w_y^B{p}_y^B=Y^{\prime }.\end{array}\right.$$

(7)

The result follows. □

Theorem 1.

Algorithm 1 solves the Pareto-frontier scheduling problem $1|d_j^B{=d|}^{\#}(\Sigma w_j^A{C}_j^A,\Sigma w_j^B{Y}_j^B)$ in $O(n_A{n}_{B}d{P}_{sum}{U}^A{U}^B)$ time.

Algorithm 1: For problem $1|d_j^B{=d|}^{\#}(\sum w_j^A{C}_j^A,\sum w_j^B{Y}_j^B)$

Proof. 

The correctness of Algorithm 1 is guaranteed by Lemma 2, Lemma 1, and Lemma 3. Here we only analyze its time complexity. The initialization step takes $O(P_{\mathrm{sum}}+n_A{n}_B)$ time, which is dominated by the final time complexity of Algorithm 1. In the implementation of Algorithm 1, we guarantee that $\Gamma (\overrightarrow{x},\overleftarrow{y})=\tilde{\Gamma }(\overrightarrow{x},\overleftarrow{y})$. Note that $0\le t_1\le d^B$ and $d^B-p_{max}^A+1\le t_3\le P_{\mathrm{sum}}$, then each state set $\Gamma (\overrightarrow{x},\overleftarrow{y})$ contains $O(d^B{P}_{\mathrm{sum}}{U}^A{U}^B)$ states. Moreover, $\Gamma (\overrightarrow{x},\overleftarrow{y})$ is obtained by performing at most two (constant) operations on the states in $\Gamma (\overrightarrow{x-1},\overleftarrow{y})\bigcup \Gamma (\overrightarrow{x},\overleftarrow{y+1})$ for $x=0,1,\dots ,n_A$, $y=n_B+1,n_B,\dots ,1$. Note that the upper bounds of $\Sigma w_j^A{C}_j^A$ and $\Sigma w_j^B{Y}_j^B$ are given by $U^A={\sum }_{j=1}^{n_A}{w}_j^A{P}_{\mathrm{sum}}$ and $U^B={\sum }_{j=1}^{n_B}{w}_j^B{p}_j^B$, respectively. Thus, the overall running time of Algorithm 1 is $O(n_A{n}_{B}d{P}_{\mathrm{sum}}{U}^A{U}^B)$. □

4. An FPTAS

In this section, for problem $1|d_j^B{=d|}^{\#}(\sum w_j^A{C}_j^A,\sum w_j^B{Y}_j^B)$, we first give another dynamic programming algorithm, and then turn it into an FPTAS by the trimming technique. As for Algorithm 1, we first introduce the following terminologies and notations.

• An $(x,y)$-schedule is defined to be an ABAB-schedule $\pi$ for ${\mathcal{J}}_x^A\cup {\mathcal{J}}_y^B$ with no idle time existing between subschedules ${\pi }_1$, ${\pi }_2$ and ${\pi }_3$, where $x\in \{1,2,\dots ,n_A\}$ and $y\in \{1,2,\dots ,n_B\}$.
• A vector $(t_1,t_2,t_3,W,k(\pi ),C,Y)$ is introduced to denote a state of $(x,y)$, in which $t_1,t_2,t_3,W,k,C$ and Y, respectively, stand for the end point of ${\pi }_1$, the end point of ${\pi }_2$, the end point of ${\pi }_3$, the total weight of the jobs in ${\pi }_3$, the index of the last B-job in ${\pi }_2$, the total weighted completion time of the A-jobs of ${\mathcal{J}}_x^A$, and the total weighted late work of the B-jobs of ${\mathcal{J}}_y^B$. Note that a state of $(x,y)$ at least corresponds to some $(x,y)$-schedule.
• $\Gamma (x,y)$ denotes the set of all the states of $(x,y)$.
• $\tilde{\Gamma }(x,y)$ denotes the set obtained from $\Gamma (x,y)$ by deleting the vectors $(\overline{t_1},\overline{t_2},\overline{t_3},\overline{W},k,\overline{C},\overline{Y})$, for which there is another vector $(t_1,t_2,t_3,W,k,C,Y)$ with $t_1\le \overline{t_1},t_2\le \overline{t_2},t_3\le \overline{t_3},W\le \overline{W},C\le \overline{C},Y\le \overline{Y}$.
• Let ${\mathbf{Q}}_2=\{(C,Y):(t_1,t_2,t_3,W,k,C,Y)\in \tilde{\Gamma }(n_A,n_B)\}$, and let $\widetilde{{\mathbf{Q}}_2}$ be the set of the non-dominated vectors in ${\mathbf{Q}}_2$.

Clearly, ${\mathbf{Q}}_2$ is an intermediate set. Similarly to the discussion for Algorithm 1, we can generate all the $\Gamma (x,y)$ for all the possible choices of the tuple $(x,y)$ dynamically in the following way.

Initially, set $\Gamma (0,0)=\{(0,0,0,0,0,0,0)\}$ and $\Gamma (x,y)=\varnothing$ if $(x,y)\ne (0,0)$. Then we recursively generate all the state sets $\Gamma (x,y)$ from the previously generated sets $\Gamma (x-1,y)$ and $\Gamma (x,y-1)$. Specifically,

• For each state $(t_1,t_2,t_3,W,k,C,Y)\in \Gamma (x-1,y)$ with $\Gamma (x-1,y)\ne \varnothing$, add two states $(t_1^{\prime },t_2^{\prime },t_3^{\prime },W^{\prime },$$k^{\prime },C^{\prime },Y^{\prime })$ and $(t_1^{″},t_2^{″},t_3^{″},W^{″},k^{″},C^{″},Y^{″})$ to the set $\Gamma (x,y)$, with

  $$\begin{array}{c}(t_1^{\prime },t_2^{\prime },t_3^{\prime },W^{\prime },k^{\prime },C^{\prime },Y^{\prime })=(t_1+p_x^A,t_2+p_x^A,t_3+p_x^A,W,k,C+w_x^A(t_1+p_x^A)+W{p}_x^A,Y\hfill \\ +w_k^{B}max\{min\{t_2+p_x^A-d^B,p_x^A\},0\}),and(t_1^{″},t_2^{″},t_3^{″},W^{″},k^{″},C^{″},Y^{″})\hfill \\ =(t_1,t_2,t_3+p_x^A,W+w_x^A,k,C+w_x^A(t_3+p_x^A),Y).\hfill \end{array}$$

These two states respectively correspond to the newly obtained $(x,y)$-schedules by scheduling job $J_x^A$ immediately following the subschedule ${\pi }_1$ and immediately following the subschedule ${\pi }_3$, in some $(x-1,y)$ schedule $\pi$ that corresponds to the state $(t_1,t_2,t_3,W,k,C,Y)$. Note that the first case occurs only when $t_1+p_x^A\le t_2$ is satisfied.

• For each state $(t_1,t_2,t_3,W,k,C,Y)\in \Gamma (x,y-1)$, also add two two states $(t_1^{\prime },t_2^{\prime },t_3^{\prime },W^{\prime },k^{\prime },C^{\prime },Y^{\prime })$ and $(t_1^{″},t_2^{″},t_3^{″},W^{″},k^{″},C^{″},Y^{″})$ to the set $\Gamma (x,y)$, with

  $$(t_1^{\prime },t_2^{\prime },t_3^{\prime },W^{\prime },k^{\prime },C^{\prime },Y^{\prime })=(t_1,t_2+p_y^B,t_3+p_y^B,W,y,C+W{p}_y^B,Y+w_y^{B}max\{t_2+p_y^B-d^B,0\}),$$

  and

  $$(t_1^{″},t_2^{″},t_3^{″},W^{″},k^{″},C^{″},Y^{″})=(t_1,t_2,t_3,W,k,C,Y+w_y^B{p}_y^B).$$

These two states respectively correspond to the newly obtained $(x,y)$-schedules by scheduling job $J_y^B$ immediately after ${\pi }_2$ and immediately following the subschedule ${\pi }_4$, in some $(x,y-1)$ schedule $\pi$ that corresponds to the state $(t_1,t_2,t_3,W,k,C,Y)$. Note that the first case occurs only when $t_2<d^B$ is satisfied.

Note that, if in the above state-generation procedures we replace sets $\Gamma (x-1,y)$ and $\Gamma (x,y-1)$ with sets $\tilde{\Gamma }(x-1,y)$ and $\tilde{\Gamma }(x,y-1)$, then the resulting set of new states, denoted by ${\Gamma }^{\prime }(x,y)$, may be different from $\Gamma (x,y)$. Recall that, when deleting those dominated vectors in the sets $\Gamma (x,y)$ and ${\Gamma }^{\prime }(x,y)$, the newly obtained sets are respectively denoted by $\tilde{\Gamma }(x,y)$ and $\widetilde{{\Gamma }^{\prime }}(x,y)$, which will be shown to be identical in the following lemma, and its proof is similar to that of Lemma 3.

Lemma 4.

$\tilde{\Gamma }(x,y)=\widetilde{{\Gamma }^{\prime }}(x,y)$.

Theorem 2.

Algorithm 2 solves $1|d_j^B{=d|}^{\#}(\sum w_j^A{C}_j^A,\sum w_j^B{Y}_j^B)$ in $O(n_A{n}_B^{2}d{P}_{sum}{W}_{sum}^A{U}^A{U}^B)$ time.

Algorithm 2: For solving $1|d_j^B{=d|}^{\#}(\sum w_j^A{C}_j^A,\sum w_j^B{Y}_j^B)$

Proof. 

The correctness of Algorithm 2 is guaranteed by the discussion above. Next we only analyze its time complexity. The initialization step takes $O(n_A{n}_B)$ time, which is dominated by the final time complexity of Algorithm 2. In the implementation of Algorithm 2, we guarantee that $\Gamma (x,y)=\tilde{\Gamma }(x,y)$. Note that $0\le t_1\le d^B$ and $d-p_{max}^A+1\le t_3\le P_{\mathrm{sum}}$, $0\le k\le n_B$ and $0\le W\le W_{\mathrm{sum}}^A$, then each state set $\Gamma (x,y)$ contains $O(n_{B}d{P}_{\mathrm{sum}}{W}_{\mathrm{sum}}^A{U}^A{U}^B)$ states. Moreover, $\Gamma (x,y)$ is obtained by performing at most two (constant) operations on the states in $\Gamma (x-1,y)\bigcup \Gamma (x,y-1)$ for $x=0,1,\dots ,n_A$, $y=0,1,\dots ,n_B$. Thus, the overall running time of Algorithm 2 is $O(n_A{n}_B^2{d}^B{P}_{\mathrm{sum}}{W}_{\mathrm{sum}}^A{U}^A{U}^B)$. □

Next we turn Algorithm 2 into an FPTAS in the following way. Set $\Delta =1+\frac{ϵ}{2n}$, $L^1=\lceil lo{g}_{\Delta }d\rceil$, $L^3=\lceil lo{g}_{\Delta }(P_{\mathrm{sum}})\rceil$, $L^W=\lceil lo{g}_{\Delta }(W_{\mathrm{sum}}^A)\rceil$, $L^A=\lceil lo{g}_{\Delta }(U^A)\rceil$ and $L^B=\lceil lo{g}_{\Delta }(U^B)\rceil$. Set $I_i^1=[{\Delta }^{(i-1)},{\Delta }^i]$ for $i=1,2,\dots ,L^1$, $I_i^3=[{\Delta }^{(i-1)},{\Delta }^i]$ for $i=1,2,\dots ,L^3$, $I_i^W=[{\Delta }^{(i-1)},{\Delta }^i]$ for $i=1,2,\dots ,L^W$, $I_i^A=[{\Delta }^{(i-1)},{\Delta }^i]$ for $i=1,2,\dots ,L^A$ and $I_i^B=[{\Delta }^{(i-1)},{\Delta }^i]$ for $i=1,2,\dots ,L^B$. For $x=0,1,\dots ,n_A$ and $y=0,1,\dots ,n_B$, $\widehat{\Gamma }(x,y)$ is obtained from $\Gamma (x,y)$ by the following operation: for any two states $(t_1,t_2,t_3,W,k,C,Y)$ and $(\overline{t_1},\overline{t_2},\overline{t_3},\overline{W},k,C,Y)$ in $\Gamma (x,y)$, if $(t_1,t_3,W,C,Y)$ and $(\overline{t_1},\overline{t_3},\overline{W},\overline{C},\overline{Y})$ fall into the same box $I_u^1\times I_v^3\times I_w^W\times I_p^A\times I_q^B$ for $u=1,2,\dots ,L^1$, $v=1,2,\dots ,L^3$, $w=1,2,\dots ,L^W$, $p=1,2,\dots ,L^A$ and $q=1,2,\dots ,L^B$ with $t_2\le \overline{t_2}$, remaining the first one. Note that it takes $O(L^1{L}^3{L}^W{L}^A{L}^B)$ time to partition the boxes. Moreover, we define

$${\mathbf{Q}}_3=\{(C,Y):(t_1,t_2,t_3,W,k,C,Y)\in \widehat{\Gamma }(n_A,n_B)\}$$

(8)

and let $\widetilde{{\mathbf{Q}}_3}$ be the set of non-dominated vectors in ${\mathbf{Q}}_3$.

Theorem 3.

Algorithm 3 is an FPTAS for solving $1|d_j^B{=d|}^{\#}(\sum w_j^A{C}_j^A,\sum w_j^B{Y}_j^B)$.

Algorithm 3: For solving $1|d_j^B{=d|}^{\#}(\sum w_j^A{C}_j^A,\sum w_j^B{Y}_j^B)$

Proof. 

By induction on $z=x+y$, We prove that, for any state $(t_1^{\prime },t_2^{\prime },t_3^{\prime },W^{\prime },k^{\prime },C^{\prime },Y^{\prime })\in \Gamma (x,y)$, there is a state $(\overline{t_1},\overline{t_2},\overline{t_3},\overline{W},k^{\prime },\overline{C},\overline{Y})\in \widehat{\Gamma }(x,y)$ such that $\overline{t_1}\le {\Delta }^z{t}_1^{\prime }$, $\overline{t_2}\le t_2^{\prime }$, $\overline{t_3}\le {\Delta }^z{t}_3^{\prime }$, $\overline{W}\le {\Delta }^z{W}^{\prime }$, $\overline{C}\le {\Delta }^z{C}^{\prime }$ and $\overline{Y}\le {\Delta }^z{Y}^{\prime }$.

This is obviously true for $z=0$. Inductively suppose that it holds up to $z-1$. Next we show that it also holds for z. Recall that each state $(t_1^{\prime },t_2^{\prime },t_3^{\prime },W^{\prime },k^{\prime },C^{\prime },Y^{\prime })\in \Gamma (x,y)$ is derived from some state $(t_1,t_2,t_3,W,k,C,Y)$ in $\Gamma (x-1,y)$ or $\Gamma (x,y-1)$. Let ${\pi }^{\prime }$ be an $(x,y)$-schedule corresponding to $(t_1^{\prime },t_2^{\prime },t_3^{\prime },W^{\prime },k^{\prime },C^{\prime },Y^{\prime })$, and let $\pi$ be a schedule corresponding to the state $(t_1,t_2,t_3,W,k,C,Y)$. Using the induction hypothesis, there is a state $(\widehat{t_1},\widehat{t_2},\widehat{t_3},\widehat{W},k,\widehat{C},\widehat{Y})$ in $\widehat{\Gamma }(x-1,y)$ or $\widehat{\Gamma }(x,y-1)$ such that $\widehat{t_1}\le {\Delta }^{z-1}{t}_1,\widehat{t_2}\le t_2,\widehat{t_3}\le {\Delta }^{z-1}{t}_3,\widehat{W}\le {\Delta }^{z-1}W,\widehat{C}\le {\Delta }^{z-1}C$, and $\widehat{Y}\le {\Delta }^{z-1}Y$. Let $\widehat{\pi }$ be an $(x-1,y)$-schedule or $(x,y-1)$-schedule corresponding to $(\widehat{t_1},\widehat{t_2},\widehat{t_3},\widehat{W},k,\widehat{C},\widehat{Y})$, and if it is feasible, let $\tilde{\pi }$ be the $(x,y)$-schedule obtained from $\widehat{\pi }$ by performing the same operation that we perform on $\pi$ to get ${\pi }^{\prime }$. Let $(\widetilde{t_1},\widetilde{t_2},\widetilde{t_3},\tilde{W},\tilde{k},\tilde{C},\tilde{Y})$ be the state corresponding to $\tilde{\pi }$. Furthermore, there is a state $(\overline{t_1},\overline{t_2},\overline{t_3},\overline{W},\tilde{k},\overline{C},\overline{Y})\in \widehat{\Gamma }(x,y)$ in the same box with $(\widetilde{t_1},\widetilde{t_2},\widetilde{t_3},\tilde{W},\tilde{k},\tilde{C},\tilde{Y})$ such that $\overline{t_1}\le \Delta \widetilde{t_1}$, $\overline{t_2}\le \widetilde{t_2}$, $\overline{t_3}\le \Delta \widetilde{t_3}$, $\overline{W}\le \Delta \tilde{W}$, $\overline{C}\le \Delta \tilde{C}$ and $\overline{Y}\le \Delta \tilde{Y}$. There are four possible ways to get ${\pi }^{\prime }$ from $\pi$.

Case 1.${\pi }^{\prime }$ is obtained from $\pi$ by scheduling $J_x^A$ directly after schedule ${\pi }_1$. Note that in this case, the condition $t_2+p_x^A-d^B<p_k^B$ must be satisfied. Then $(t_1,t_2,t_3,W,k,C,Y)\in \Gamma (x-1,y)$, and the operation to get $\tilde{\pi }$ is feasible since $\widehat{t_2}+p_x^A-d^B\le t_2+p_x^A-d^B<p_k^B$. Then we have $(\widetilde{t_1},\widetilde{t_2},\widetilde{t_3},\tilde{W},\tilde{k},\tilde{C},\tilde{Y})=(\widehat{t_1}+p_x^A,\widehat{t_2}+p_x^A,\widehat{t_3}+p_x^A,\widehat{W},k,\widehat{C}+w_x^A(\widehat{t_1}+p_x^A)+\widehat{W}{p}_x^A,\widehat{Y}+w_k^{B}max\{min\{\widehat{t_2}+p_x^A-d^B,p_x^A\},0\}).$ Combining with the fact that $(t_1^{\prime },t_2^{\prime },t_3^{\prime },W^{\prime },k^{\prime },C^{\prime },Y^{\prime })=(t_1+p_x^A,t_2+p_x^A,t_3+p_x^A,W,k,C+w_x^A(t_1+p_x^A)+W{p}_x^A,Y+w_k^{B}max\{min\{t_2+p_x^A-d^B,p_x^A\},0\})$, we have

$$\left\{\begin{array}{c}\overline{t_1}\le \Delta \widetilde{t_1}=\Delta (\widehat{t_1}+p_x^A)\le {\Delta }^z(t_1+p_x^A)={\Delta }^z{t}_1^{\prime },\\ \overline{t_2}\le \widetilde{t_2}=\widehat{t_2}+p_x^A\le t_2+p_x^A=t_2^{\prime },\\ \overline{t_3}\le \Delta \widetilde{t_3}=\Delta (\widehat{t_3}+p_x^A)\le {\Delta }^z(t_3+p_x^A)={\Delta }^z{t}_3^{\prime },\\ \overline{W}\le \Delta \tilde{W}=\Delta \widehat{W}\le {\Delta }^{z}W={\Delta }^z{W}^{\prime },\\ \tilde{k}=k=k^{\prime },\\ \overline{C}\le \Delta \tilde{C}=\Delta (\widehat{C}+w_x^A(\widehat{t_1}+p_x^A)+\widehat{W}{p}_x^A)\le {\Delta }^z(C+w_x^A(t_1+p_x^A)+W{p}_x^A)={\Delta }^z{C}^{\prime },\\ \overline{Y}\le \Delta \tilde{Y}=\Delta (\widehat{Y}+w_k^{B}max\{min\{\widehat{t_2}+p_x^A-d^B,p_x^A\},0\})\le {\Delta }^z(Y+w_k^{B}max\{min\{t_2+p_x^A-d^B,p_x^A\},0\})={\Delta }^{z}Y.\end{array}\right.$$

(9)

Case 2.${\pi }^{\prime }$ is obtained from $\pi$ by scheduling $J_x^A$ directly after schedule ${\pi }_3$. Then $(t_1,t_2,t_3,W,k,C,Y)\in \Gamma (x-1,y)$, and $\tilde{\pi }$ is clearly a feasible schedule. Then we have $(\widetilde{t_1},\widetilde{t_2},\widetilde{t_3},\tilde{W},\tilde{k},\tilde{C},\tilde{Y})=(\widehat{t_1},\widehat{t_2},\widehat{t_3}+p_x^A,\widehat{W}+w_x^A,k,\widehat{C}+w_x^A(\widehat{t_3}+p_x^A),\widehat{Y}).$ Combining with the fact that $(t_1^{\prime },t_2^{\prime },t_3^{\prime },W^{\prime },k^{\prime },C^{\prime },Y^{\prime })=(t_1,t_2,t_3+p_x^A,W+w_x^A,k,C+w_x^A(t_3+p_x^A),Y)$, we have

$$\left\{\begin{array}{c}\overline{t_1}\le \Delta \widetilde{t_1}=\Delta \widehat{t_1}\le {\Delta }^z{t}_1={\Delta }^z{t}_1^{\prime },\\ \overline{t_2}\le \widetilde{t_2}=\widehat{t_2}\le t_2=t_2^{\prime },\\ \overline{t_3}\le \Delta \widetilde{t_3}=\Delta (\widehat{t_3}+p_x^A)\le {\Delta }^z(t_3+p_x^A)={\Delta }^z{t}_3^{\prime },\\ \overline{W}\le \Delta \tilde{W}=\Delta (\widehat{W}+w_x^A)\le {\Delta }^z(W+w_x^A)={\Delta }^z{W}^{\prime },\\ \tilde{k}=k=k^{\prime },\\ \overline{C}\le \Delta \tilde{C}=\Delta (\widehat{C}+w_x^A(\widehat{t_3}+p_x^A))\le {\Delta }^z(C+w_x^A(t_3+p_x^A))={\Delta }^z{C}^{\prime },\\ \overline{Y}\le \Delta \tilde{Y}=\Delta \widehat{Y}\le {\Delta }^{z}Y={\Delta }^z{Y}^{\prime }.\end{array}\right.$$

(10)

Case 3.${\pi }^{\prime }$ is obtained from $\pi$ by scheduling $J_y^B$ directly after schedule ${\pi }_2$. Note that in this case, the condition $t_2<d^B$ must be satisfied. Then $(t_1,t_2,t_3,W,k,C,Y)\in \Gamma (x,y-1)$, and the operation to get $\tilde{\pi }$ is feasible since $\widehat{t_2}\le t_2<d^B$. Then we have $(\widetilde{t_1},\widetilde{t_2},\widetilde{t_3},\tilde{W},\tilde{k},\tilde{C},\tilde{Y})=(\widehat{t_1},\widehat{t_2}+p_y^B,\widehat{t_3}+p_y^B,\widehat{W},y,\widehat{C}+\widehat{W}{p}_y^B,\widehat{Y}+w_y^{B}max\{\widehat{t_2}+p_y^B-d^B,0\}).$ Combining with the fact that $(t_1^{\prime },t_2^{\prime },t_3^{\prime },W^{\prime },k^{\prime },C^{\prime },Y^{\prime })=(t_1,t_2+p_y^B,t_3+p_y^B,W,y,C+W{p}_y^B,Y+w_y^{B}max\{t_2+p_y^B-d^B,0\})$, we have

$$\left\{\begin{array}{c}\overline{t_1}\le \Delta \widetilde{t_1}=\Delta \widehat{t_1}\le {\Delta }^z{t}_1={\Delta }^z{t}_1^{\prime },\\ \overline{t_2}\le \widetilde{t_2}=\widehat{t_2}+p_y^B\le t_2+p_y^B=t_2^{\prime },\\ \overline{t_3}\le \Delta \widetilde{t_3}=\Delta (\widehat{t_3}+p_y^B)\le {\Delta }^z(t_3+p_y^B)={\Delta }^z{t}_3^{\prime },\\ \overline{W}\le \Delta \tilde{W}=\Delta \widehat{W}\le {\Delta }^{z}W={\Delta }^z{W}^{\prime },\\ \tilde{k}=y=k^{\prime },\\ \overline{C}\le \Delta \tilde{C}=\Delta (\widehat{C}+\widehat{W}{p}_y^B)\le {\Delta }^z(C+W{p}_y^B)={\Delta }^z{C}^{\prime },\\ \overline{Y}\le \Delta \tilde{Y}=\Delta (\widehat{Y}+w_y^{B}max\{\widehat{t_2}+p_y^B-d^B,0\})\le {\Delta }^z(Y+w_y^{B}max\{t_2+p_y^B-d^B,0\})={\Delta }^z{Y}^{\prime }.\end{array}\right.$$

(11)

Case 4.${\pi }^{\prime }$ is obtained from $\pi$ by scheduling $J_y^B$ directly after schedule ${\pi }_4$. Then $(t_1,t_2,t_3,W,k,C,Y)\in \Gamma (x,y-1)$, and $\tilde{\pi }$ is clearly a feasible schedule. Then we have $(\widetilde{t_1},\widetilde{t_2},\widetilde{t_3},\tilde{W},\tilde{k},\tilde{C},\tilde{Y})=(\widehat{t_1},\widehat{t_2},\widehat{t_3},\widehat{W},k,\widehat{C},\widehat{Y}+w_y^B{p}_y^B).$ Combining with the fact that $(t_1^{\prime },t_2^{\prime },t_3^{\prime },W^{\prime },k^{\prime },C^{\prime },Y^{\prime })=(t_1,t_2,t_3,W,k,C,Y+w_y^B{p}_y^B)$, we have

$$\left\{\begin{array}{c}\overline{t_1}\le \Delta \widetilde{t_1}=\Delta \widehat{t_1}\le {\Delta }^z{t}_1={\Delta }^z{t}_1^{\prime },\\ \overline{t_2}\le \widetilde{t_2}=\widehat{t_2}\le t_2=t_2^{\prime },\\ \overline{t_3}\le \Delta \widetilde{t_3}=\Delta \widehat{t_3}\le {\Delta }^z{t}_3={\Delta }^z{t}_3^{\prime },\\ \overline{W}\le \Delta \tilde{W}=\Delta \widehat{W}\le {\Delta }^{z}W={\Delta }^z{W}^{\prime },\\ \tilde{k}=k=k^{\prime },\\ \overline{C}\le \Delta \tilde{C}=\Delta \widehat{C}\le {\Delta }^{z}C={\Delta }^z{C}^{\prime },\\ \overline{Y}\le \Delta \tilde{Y}=\Delta (\widehat{Y}+w_y^B{p}_y^B)\le {\Delta }^z(Y+w_y^B{p}_y^B)={\Delta }^z{Y}^{\prime }.\end{array}\right.$$

(12)

Thus, for each state $(C^{\prime },Y^{\prime })$ in $\widetilde{{\mathbf{Q}}_2}$, there is a state $(\overline{C},\overline{Y})$ in ${\mathbf{Q}}_3$ such that $\overline{C}\le {\Delta }^n{C}^{\prime }\le (1+ϵ)C^{\prime }$ and $\overline{Y}\le {\Delta }^n{Y}^{\prime }\le (1+ϵ)Y^{\prime }$.

Next we analyze its time complexity. The initialization step takes $O(n_A{n}_B)$ time, which is dominated by the final time complexity of Algorithm 3. In the implementation of Algorithm 3, we guarantee that $\Gamma (x,y)=\widehat{\Gamma }(x,y)$. Note that there are $O(L^1{L}^3{L}^W{L}^A{L}^B)$ distinct boxes and $0\le k\le n_B$, then there are at most $O(n_B{L}^1{L}^3{L}^W{L}^A{L}^B)$ different states $(t_1,t_2,t_3,W,k,C,Y)$ in $\Gamma (x,y)$. Moreover, $\Gamma (x,y)$ is obtained by performing at most two (constant) operations on the states in $\Gamma (x-1,y)\bigcup \Gamma (x,y-1)$ for $x=0,1,\dots ,n_A$, $y=0,1,\dots ,n_B$. Thus, the overall running time of Algorithm 3 is $O(n_A{n}_B^2{L}^1{L}^3{L}^W{L}^A{L}^B)$. □

5. Numerical Results

In this section some numerical results are provided to show the efficiency of our proposed algorithms. For running our optimization algorithms, we need to input the following parameters relative with the job instances: the numbers of A-jobs and B-jobs, the processing times and weights of all the jobs, and the common due date of B-jobs. By running Algorithms 1 and 2, we get the Pareto frontier. To use Algorithm 3, we need to choose the value of $ϵ$ (>0) to get a $(1+ϵ)$-approximate Pareto frontier. Note that for the same instance, the Pareto frontiers obtained by Algorithms 1 and 2 are the same, except that the running time of Algorithm 1 is theoretically faster than that of Algorithm 2. The closer the $(1+ϵ)$-approximate Pareto frontier obtained by Algorithm 3 is to the curve obtained by Algorithms 1 and 2, the closer it is to the optimal solution.

We randomly generate some job instances, in which the numbers of the jobs are set to be $n=4$ ($n_A=n_B=2$), $n=6$ ($n_A=n_B=3$), and $n=10$ ($n_A=n_B=5$). The processing times and the weights of the jobs are randomly generated between 1 and 2. The common due date of B-jobs is set to be 5. What is more, we set $ϵ=1$. We ran our algorithms on these instances in a Matlab R2016b environment on an Intel(R) Core(TM) CPU, 2.50 GHz, 4 GB of RAM computer. In fact, when the number of the jobs is small, the Pareto frontier or the approximate Pareto frontier can be found relatively quickly, but when the number of the jobs increases, the running time will increase hugely. The following three Figure 1, Figure 2 and Figure 3 present the Pareto frontier and $(1+ϵ)$-approximate Pareto frontier generated by Algorithms 1–3. As can be seen from the three figures, the results obtained by Algorithms 1 and 2 are exactly the same. The results of Algorithm 3 are consistent with those of Algorithms 1 and 2, which may be due to the coincidence caused by the small size of the instance we chose and the few choices in the sizes of the jobs. In fact, considering that the problem we studied is NP-hard, our algorithm can only reach pseudo-polynomial-time theoretically. Therefore, our algorithm is theoretically more suitable for small-scale instances, where the sizes of the jobs are relatively uniform, which fits with the nature of such problems in real life, such as in logistics distribution centers where we use boxes of fixed sizes.

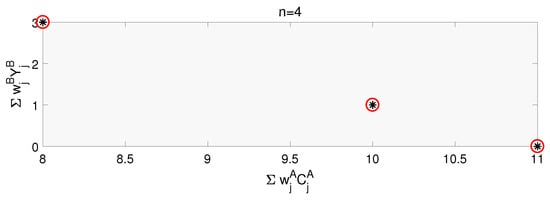
Figure 1. The black stars are the points generated by Algorithms 1 and 2, the red circles are points generated by Algorithm 3.

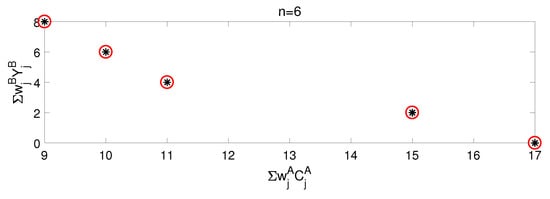
Figure 2. The black stars are the points generated by Algorithms 1 and 2, the red circles are points generated by Algorithm 3.

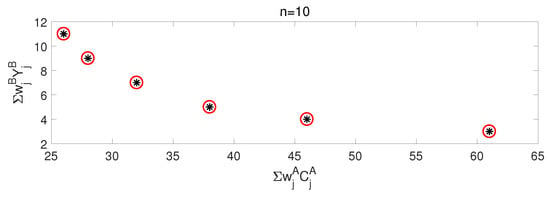
Figure 3. The black stars are the points generated by Algorithms 1 and 2, the red circles are points generated by Algorithm 3.

6. Conclusions

In this paper we investigated a Pareto-optimal problem of scheduling two agents’ jobs on a single machine to minimize one agent’s total weighted completion time and the other’s total weighted late work. For this problem, we devised two dynamic programming algorithms to obtain the Pareto frontier, and an FPTAS to generate an approximate Pareto frontier. Some numerical results were also provided. Compared with the two problems $1|p_j^A\uparrow \downarrow w_j^A{|}^{\#}(\Sigma w_j^A{C}_j^A,\Sigma w_j^B{Y}_j^B)$ and $1|p_j^A\uparrow \downarrow w_j^A,d_j^B\uparrow \downarrow w_j^B{|}^{\#}(\Sigma w_j^A{C}_j^A,\Sigma w_j^B{Y}_j^B)$ studied in Zhang et al. [20], the constraint $p_j^A\uparrow \downarrow w_j^A$ was removed from the problem considered in this paper and we turned to the optimization problem under the condition that B-jobs had a common due date. Table 1 lists the computational complexity of the above three problems. As we can see from Table 1, the condition $p_j^A\uparrow \downarrow w_j^A$ seems to have a greater impact on the complexity result of the problem. In future research, we can try to devise more efficient approximation algorithms for our considered problem with a constant performance-ratio, and we can also study two-agent problems with other combinations of objective functions.

Table 1. Complexity of three problems.

Problems	Complexity	Reference
$1|p_j^A\uparrow \downarrow w_j^A{|}^{\#}(\Sigma w_j^A{C}_j^A,\Sigma w_j^B{Y}_j^B)$	$O(n_A{n}_B^2{U}^A{U}^B)$	Zhang et al. [20]
$1|p_j^A\uparrow \downarrow w_j^A,d_j^B\uparrow \downarrow w_j^B{|}^{\#}(\Sigma w_j^A{C}_j^A,\Sigma w_j^B{Y}_j^B)$	$O(n_A{n}_B{U}^A{U}^B)$	Zhang et al. [20]
$1|d_j^B{=d|}^{\#}(\Sigma w_j^A{C}_j^A,\Sigma w_j^B{Y}_j^B)$	$O(n_A{n}_{B}d{P}_{\mathrm{sum}}{U}^A{U}^B)$	Theorem 1