Time-Reversible Synchronization of Analog and Digital Chaotic Systems
Abstract
1. Introduction
2. Materials and Methods
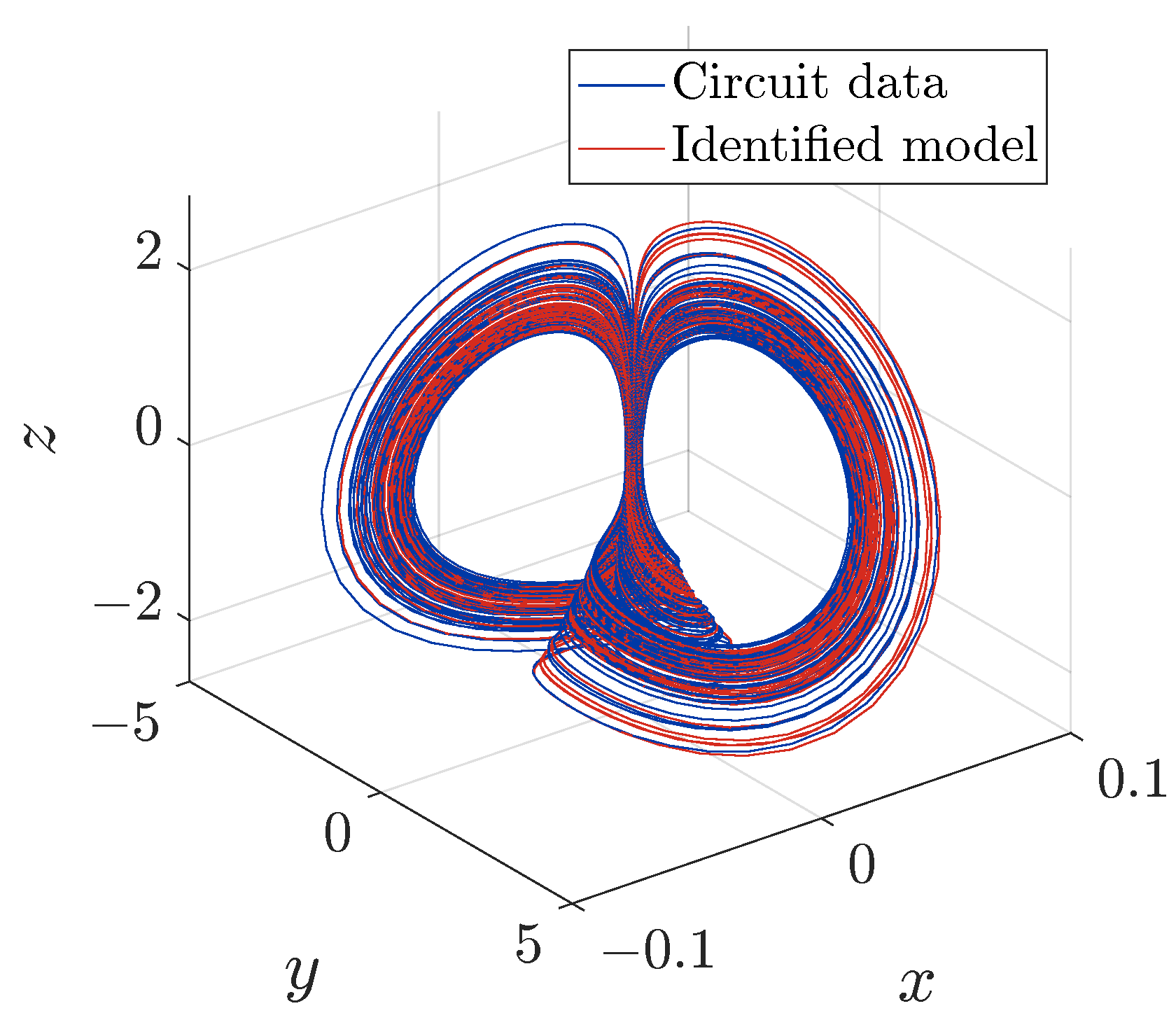
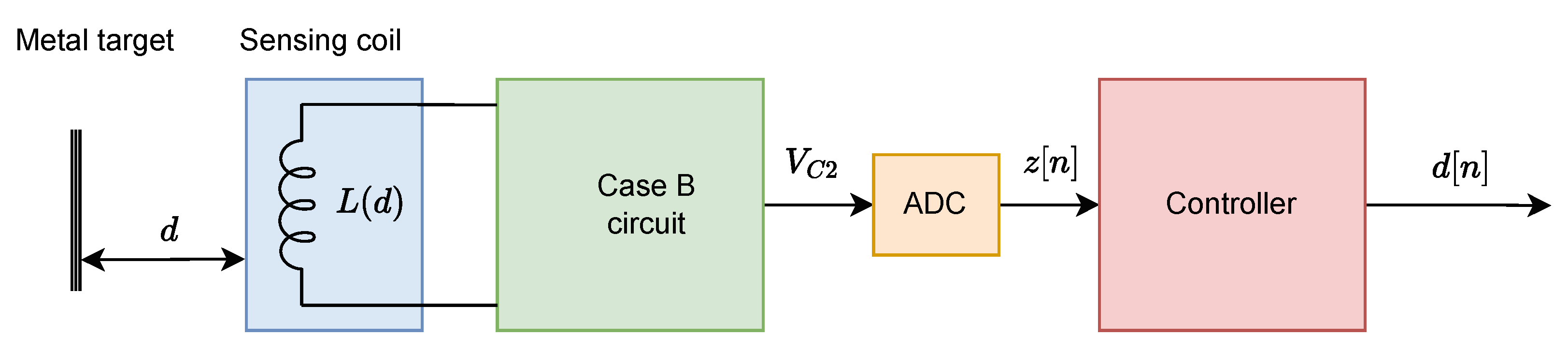
2.1. Circuit Implementation and Identification
2.2. Time-Reversible Synchronization
 |
 |
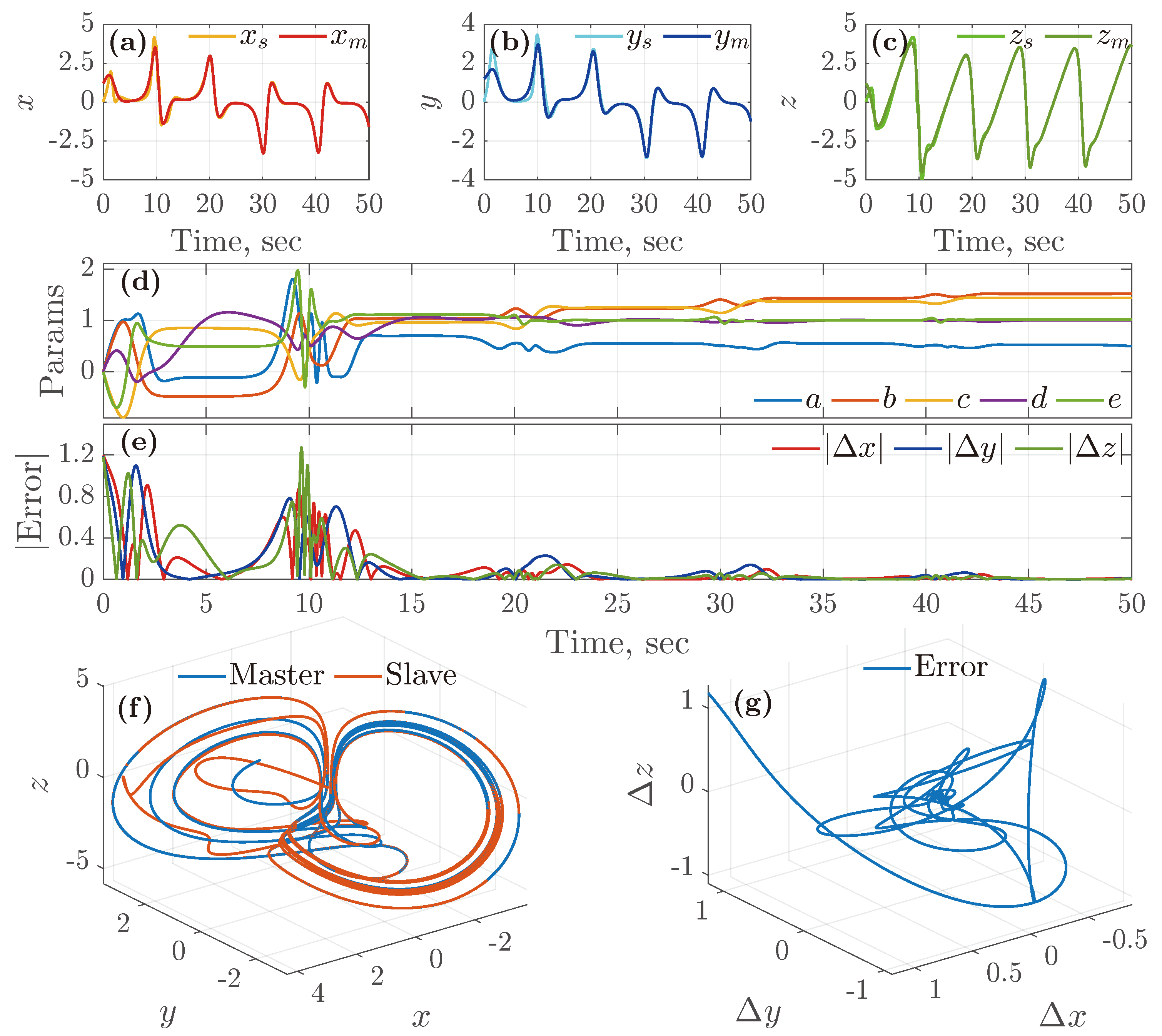
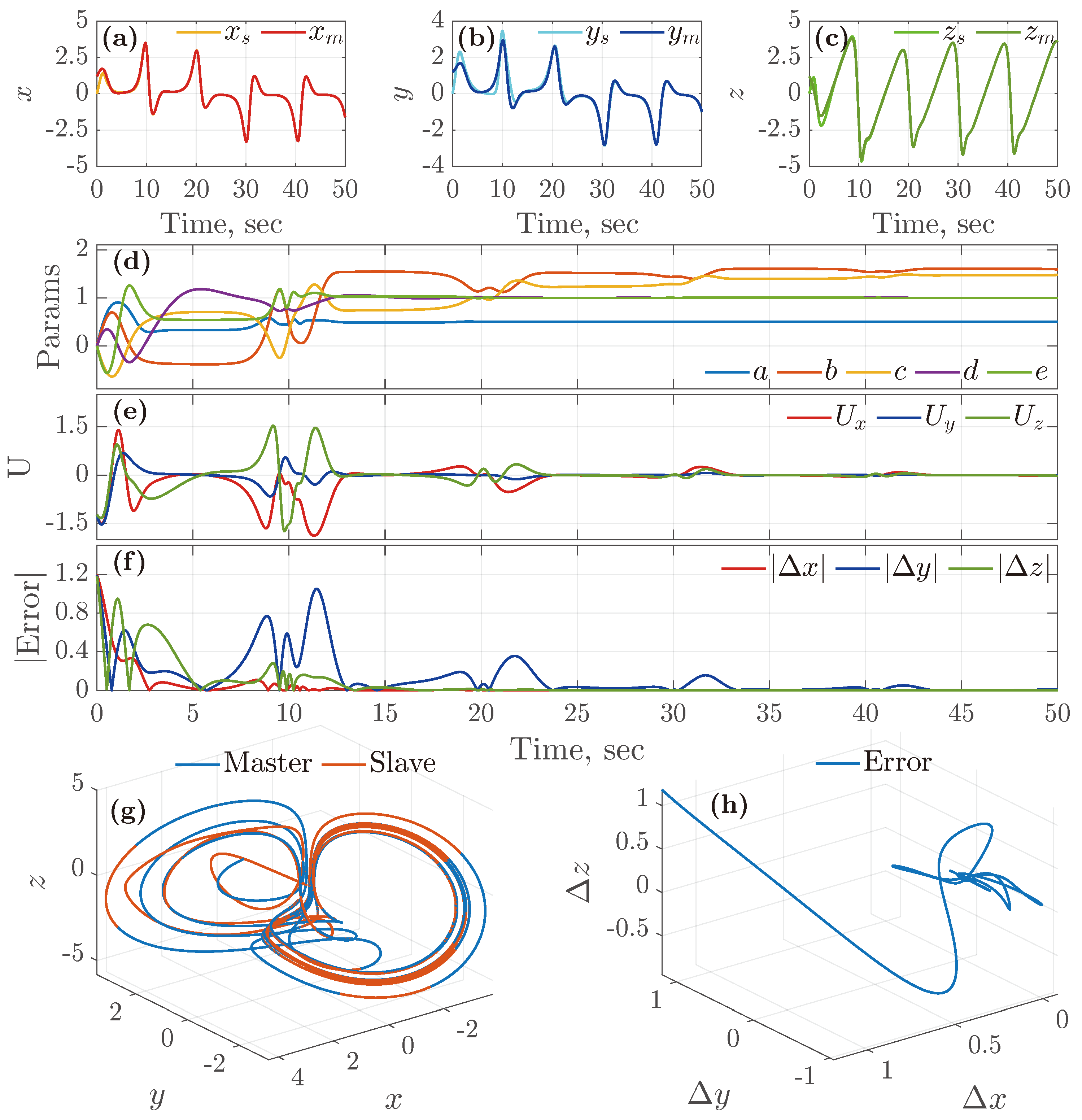
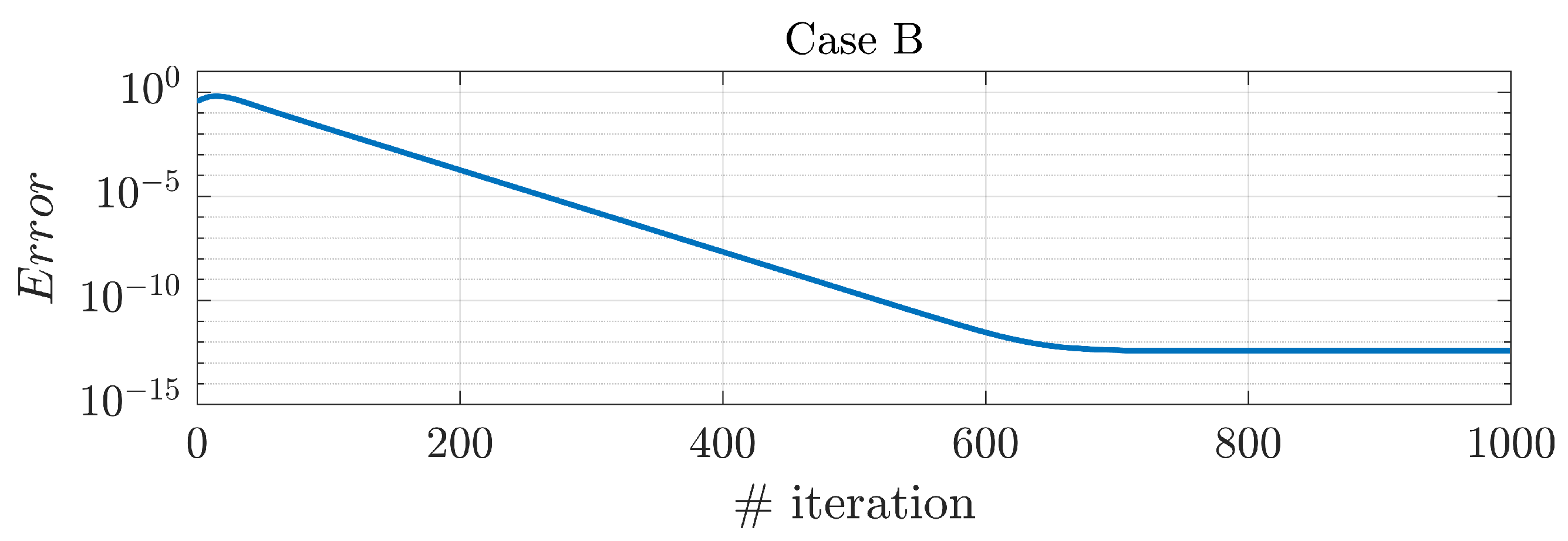
3. Experimental Results
3.1. Numerical Experiments
3.2. Physical Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef] [PubMed]
- Tsimring, L.S.; Sushchik, M.M. Multiplexing chaotic signals using synchronization. Phys. Lett. A 1996, 213, 155–166. [Google Scholar] [CrossRef]
- Dmitriev, A.; Hasler, M.; Panas, A.; Zakharchenko, K. Basic principles of direct chaotic communications. In Synchronization: Theory and Application; Springer: Berlin/Heidelberg, Germany, 2003; pp. 41–63. [Google Scholar]
- Babajans, R.; Cirjulina, D.; Capligins, F.; Kolosovs, D.; Litvinenko, A. Synchronization of Analog-Discrete Chaotic Systems for Wireless Sensor Network Design. Appl. Sci. 2024, 14, 915. [Google Scholar] [CrossRef]
- Klein, E.; Mislovaty, R.; Kanter, I.; Kinzel, W. Public-channel cryptography using chaos synchronization. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005, 72, 016214. [Google Scholar] [CrossRef]
- Andreev, A.V.; Maksimenko, V.A.; Pisarchik, A.N.; Hramov, A.E. Synchronization of interacted spiking neuronal networks with inhibitory coupling. Chaos Solitons Fractals 2021, 146, 110812. [Google Scholar] [CrossRef]
- Hsiao, F.H.; Chang, S.W. Integrating rc6 stream cipher to a chaotic synchronization system. IEEE Access 2024, 12, 26308–26323. [Google Scholar] [CrossRef]
- Karawanich, K.; Chimnoy, J.; Khateb, F.; Marwan, M.; Prommee, P. Image cryptography communication using FPAA-based multi-scroll chaotic system. Nonlinear Dyn. 2024, 112, 4951–4976. [Google Scholar] [CrossRef]
- Feng, W.; Yang, J.; Zhao, X.; Qin, Z.; Zhang, J.; Zhu, Z.; Wen, H.; Qian, K. A novel multi-channel image encryption algorithm leveraging pixel reorganization and hyperchaotic maps. Mathematics 2024, 12, 3917. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, J.; Chen, Y.; Qin, Z.; Zhang, Y.; Ahmad, M.; Woźniak, M. Exploiting robust quadratic polynomial hyperchaotic map and pixel fusion strategy for efficient image encryption. Expert Syst. Appl. 2024, 246, 123190. [Google Scholar] [CrossRef]
- Alexan, W.; Youssef, M.; Hussein, H.H.; Ahmed, K.K.; Hosny, K.M.; Fathy, A.; Mansour, M.B.M. A new multiple image encryption algorithm using hyperchaotic systems, SVD, and modified RC5. Sci. Rep. 2025, 15, 9775. [Google Scholar] [CrossRef]
- Nithya, C.; Lakshmi, C.; Thenmozhi, K.; Harshavardhan, M.; Kumaran, R.; Meikandan, P.V.; Mahalingam, H.; Amirtharajan, R. Secure gray image sharing framework with adaptive key generation using image digest. Sci. Rep. 2025, 15, 8854. [Google Scholar] [CrossRef] [PubMed]
- Ye, C.; Tan, S.; Wang, J.; Shi, L.; Zuo, Q.; Feng, W. Social Image Security with Encryption and Watermarking in Hybrid Domains. Entropy 2025, 27, 276. [Google Scholar] [CrossRef]
- Aljuhni, A.; Aljaedi, A.; Alharbi, A.R.; Mubaraki, A.; Alghuson, M.K. Hybrid Dynamic Galois Field with Quantum Resilience for Secure IoT Data Management and Transmission in Smart Cities Using Reed–Solomon (RS) Code. Symmetry 2025, 17, 259. [Google Scholar] [CrossRef]
- Wang, S.; He, J. Design of new chaotic system with multi-scroll attractor by using variable transformation and its application. Phys. Scr. 2025, 100, 025230. [Google Scholar] [CrossRef]
- Zhou, S.; Cheng, Z.; Huang, G.; Zhu, R.; Chai, Y. Synchronization evaluation of memristive photosensitive neurons in multi-neuronal systems. Chaos Solitons Fractals 2024, 187, 115470. [Google Scholar] [CrossRef]
- Kusch, L.; Breyton, M.; Depannemaecker, D.; Petkoski, S.; Jirsa, V.K. Synchronization in spiking neural networks with short and long connections and time delays. Chaos Interdiscip. J. Nonlinear Sci. 2025, 35. [Google Scholar] [CrossRef]
- Rumbaugh, L.K.; Dunn, K.J.; Bollt, E.M.; Cochenour, B.; Jemison, W.D. An underwater chaotic lidar sensor based on synchronized blue laser diodes. In Proceedings of the Ocean Sensing and Monitoring VIII, Baltimore, MD, USA, 19–20 April 2016; SPIE: Bellingham, WA, USA, 2016; Volume 9827, pp. 128–138. [Google Scholar]
- Karimov, A.; Rybin, V.; Kopets, E.; Karimov, T.; Nepomuceno, E.; Butusov, D. Identifying empirical equations of chaotic circuit from data. Nonlinear Dyn. 2023, 111, 871–886. [Google Scholar] [CrossRef]
- Mohadeszadeh, M.; Pariz, N. An application of adaptive synchronization of uncertain chaotic system in secure communication systems. Int. J. Model. Simul. 2022, 42, 143–152. [Google Scholar] [CrossRef]
- Liu, J.; Chen, G.; Zhao, X. Generalized synchronization and parameters identification of different-dimensional chaotic systems in the complex field. Fractals 2021, 29, 2150081. [Google Scholar] [CrossRef]
- Lahav, N.; Sendiña-Nadal, I.; Hens, C.; Ksherim, B.; Barzel, B.; Cohen, R.; Boccaletti, S. Topological synchronization of chaotic systems. Sci. Rep. 2022, 12, 2508. [Google Scholar] [CrossRef]
- Hramov, A.E.; Koronovskii, A.A. An approach to chaotic synchronization. Chaos Interdiscip. J. Nonlinear Sci. 2004, 14, 603–610. [Google Scholar] [CrossRef]
- Brown, R.; Kocarev, L. A unifying definition of synchronization for dynamical systems. Chaos Interdiscip. J. Nonlinear Sci. 2000, 10, 344–349. [Google Scholar] [CrossRef] [PubMed]
- Min, F. Chua System Synchronization and Implementation. In Discontinuous Dynamics and System Synchronization; Springer: Berlin/Heidelberg, Germany, 2024; pp. 113–149. [Google Scholar]
- Sun, Y.J. Exponential synchronization between two classes of chaotic systems. Chaos Solitons Fractals 2009, 39, 2363–2368. [Google Scholar] [CrossRef]
- Butusov, D.; Rybin, V.; Karimov, A. Fast time-reversible synchronization of chaotic systems. Phys. Rev. E 2025, 111, 014213. [Google Scholar] [CrossRef] [PubMed]
- Sprott, J.C. Some simple chaotic flows. Phys. Rev. E 1994, 50, R647. [Google Scholar] [CrossRef]
- Karimov, T.; Nepomuceno, E.G.; Druzhina, O.; Karimov, A.; Butusov, D. Chaotic oscillators as inductive sensors: Theory and practice. Sensors 2019, 19, 4314. [Google Scholar] [CrossRef]
- Boccaletti, S.; Kurths, J.; Osipov, G.; Valladares, D.; Zhou, C. The synchronization of chaotic systems. Phys. Rep. 2002, 366, 1–101. [Google Scholar] [CrossRef]
- Hu, W. An improved chaotic detection system for metal detectors. In Proceedings of the Journal of Physics: Conference Series, Dublin, Ireland, 19–23 July 2021; IOP Publishing: Bristol, UK, 2021; Volume 2087, No. 1. p. 012065. [Google Scholar]
- Efremova, E.; Dmitriev, A.; Kuzmin, L.; Petrosyan, M. Wireless distance measurement by means of ultra-wideband chaotic radio pulses. In Proceedings of the ITM Web of Conferences, Cluj-Napoca, Romania, 9–12 October 2019; EDP Sciences: London, UK, 2019; Volume 30, p. 12005. [Google Scholar]
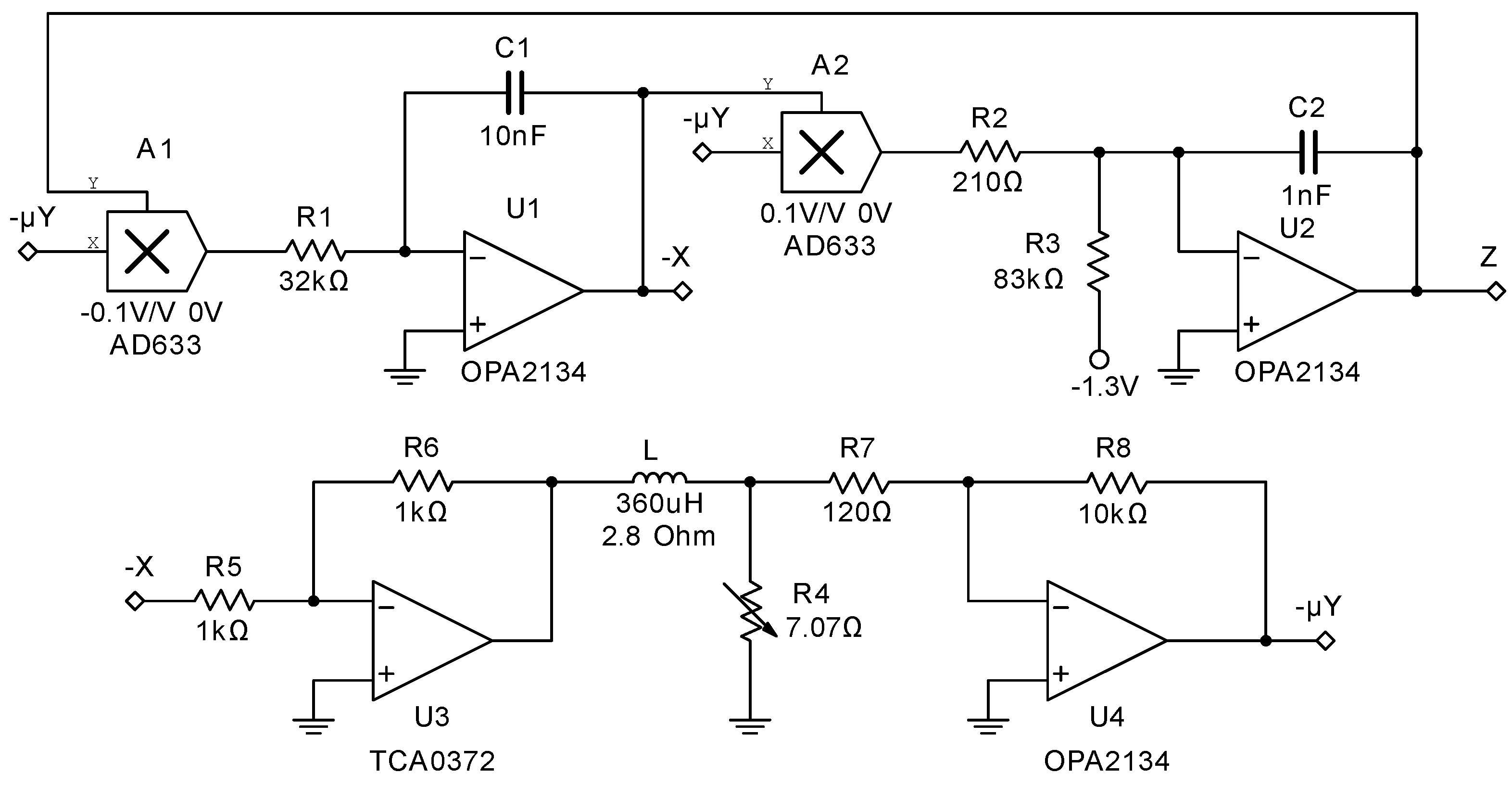

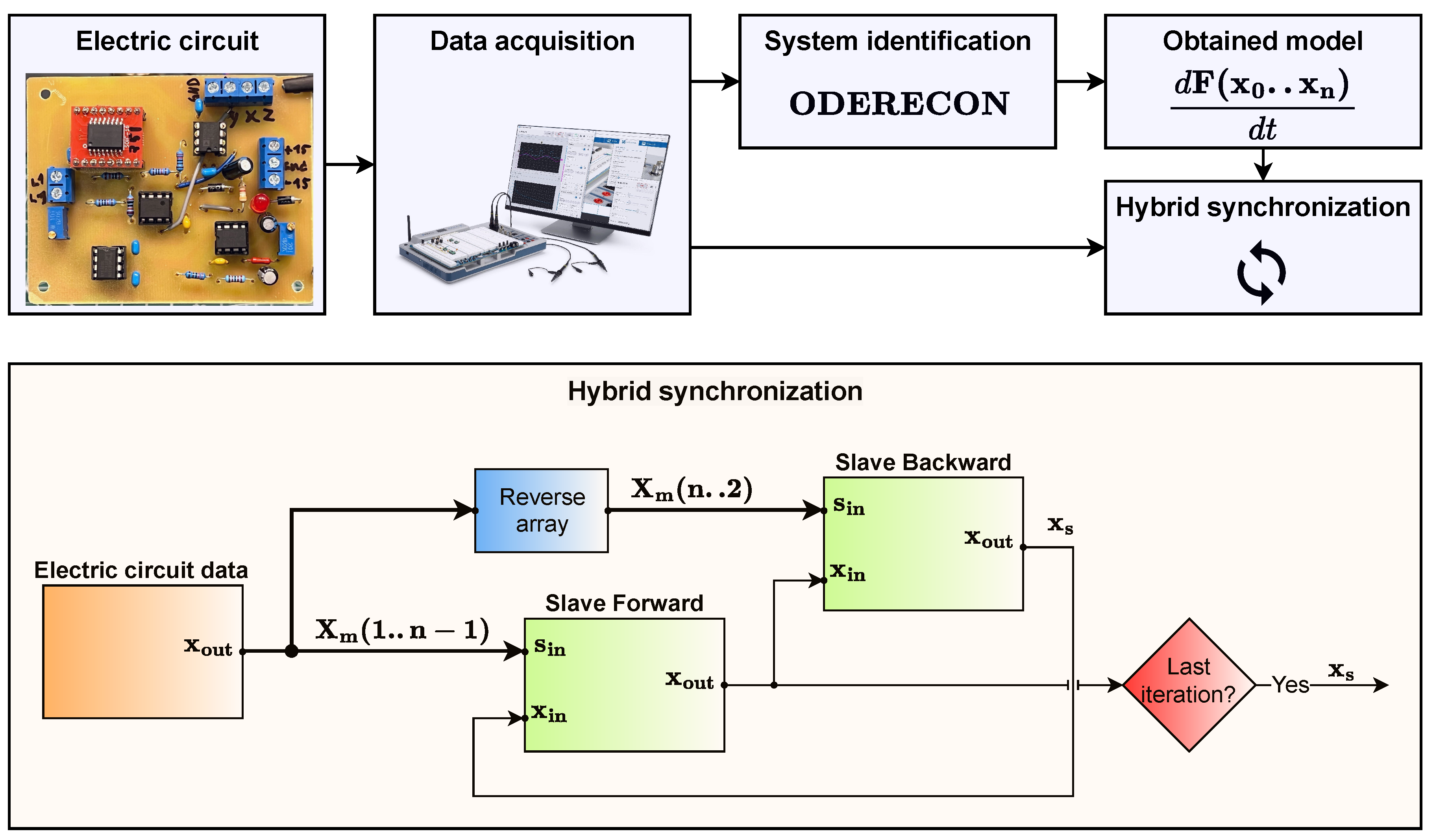
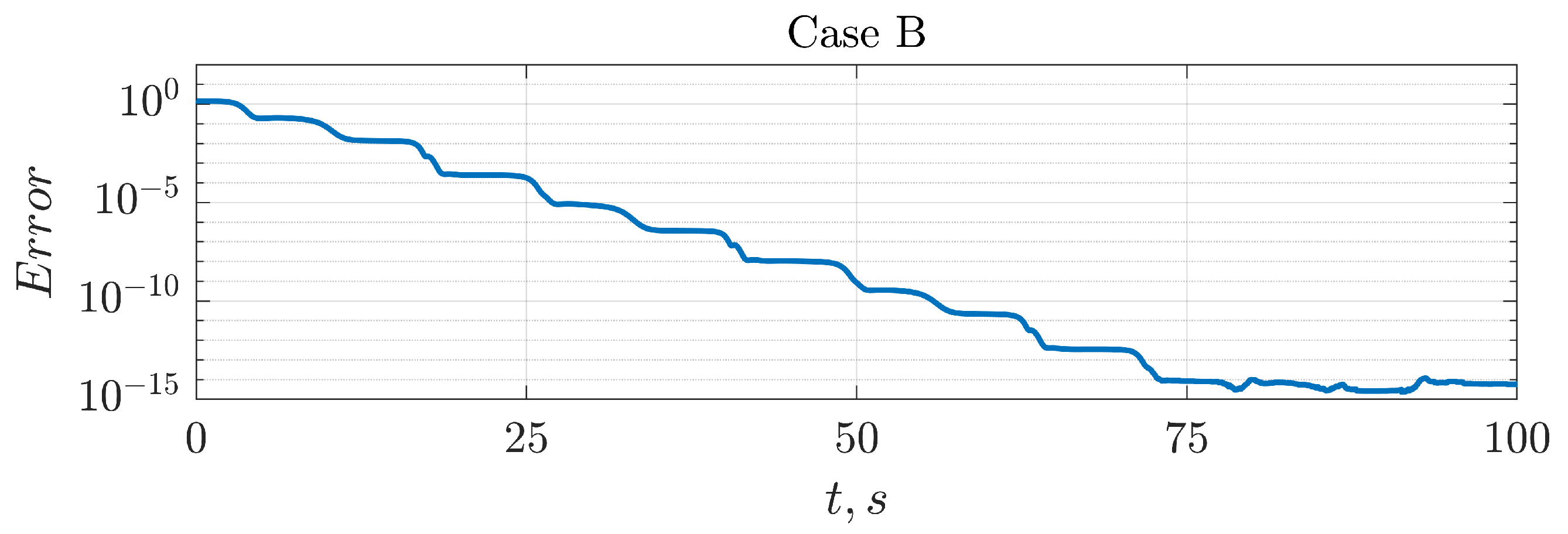
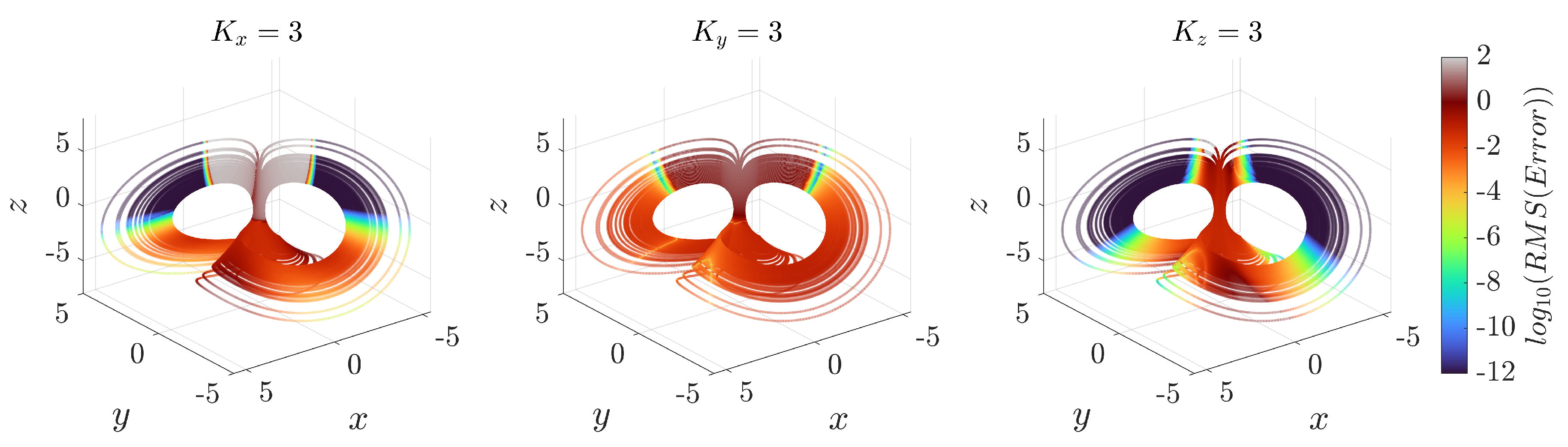

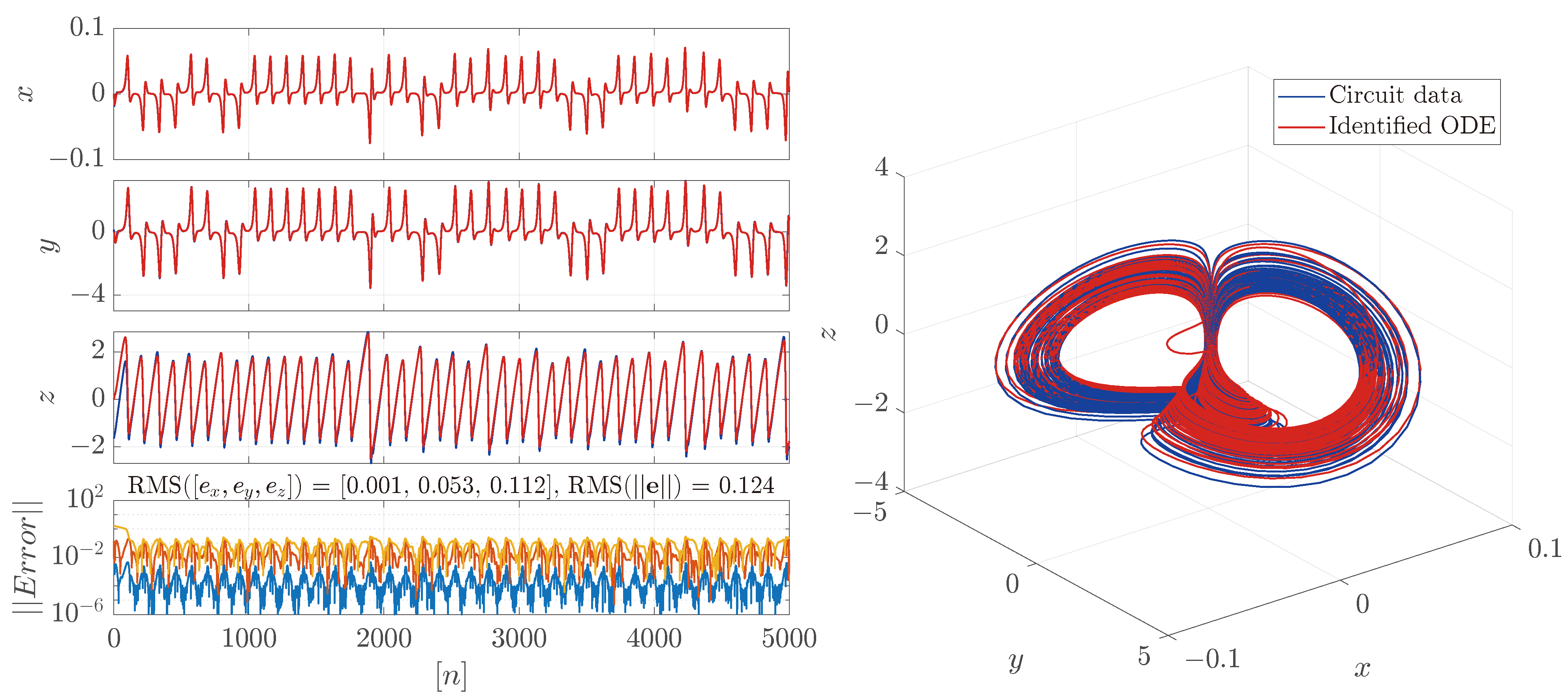
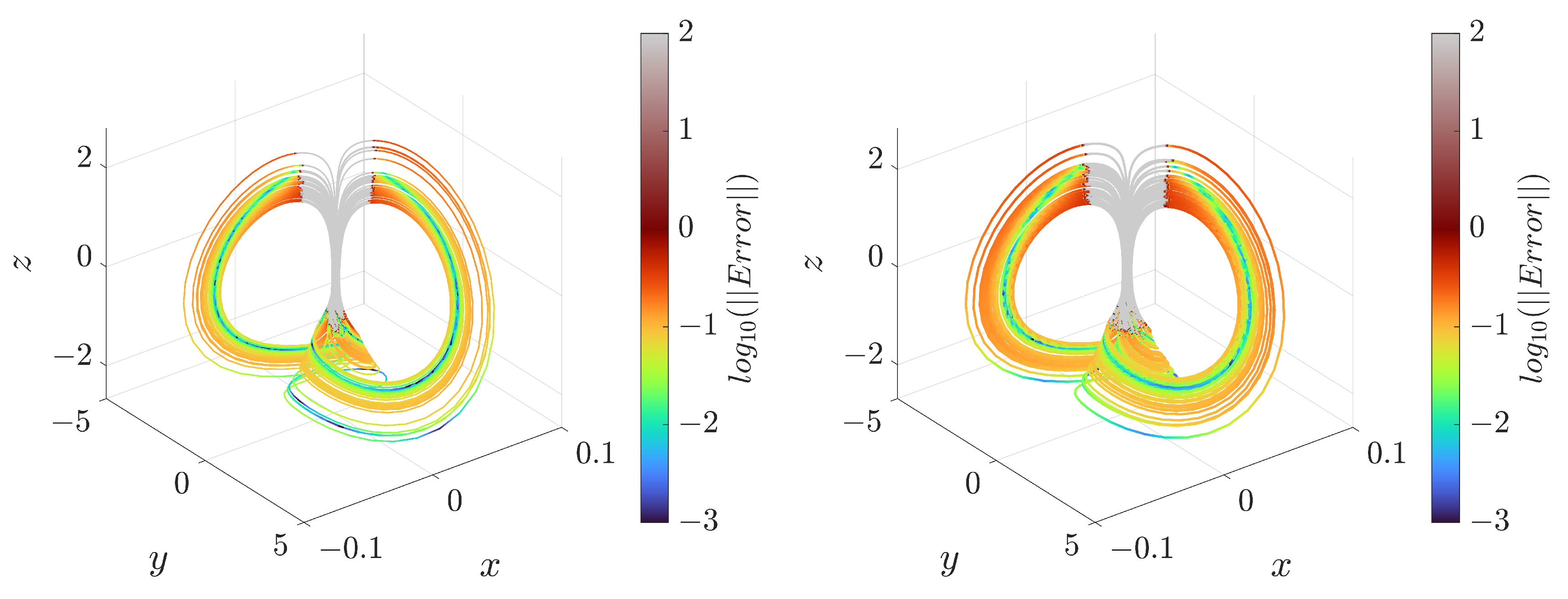
| Type | Iterations | N Points | ||
|---|---|---|---|---|
| 15 | 30 | 100 | ||
| Pecora–Carroll | − | 1.787 | 1.491 | 0.681 |
| Adaptive | − | 1.016 | 0.803 | 0.606 |
| Reversible | 10 | 0.889 | 0.896 | 0.596 |
| 100 | 0.836 | 0.532 | 0.018 | |
| 1000 | 0.45 | 0.027 | 3.962 × 10−13 | |
| Monomial | |||
|---|---|---|---|
| Constants | |||
| 1 | 0.56584 | −1889.7719 | 7294.8977 |
| Linear terms | |||
| x | 525.8895 | 1,631,650.7934 | −15,674.7009 |
| y | −19.1559 | −28,145.5863 | 1030.2079 |
| z | −1.062 | −36.5299 | −314.1264 |
| Quadratic terms | |||
| 1863.194 | −428,705.5214 | −3,107,210.5065 | |
| 20.2827 | 20,185.9366 | −300,112.975 | |
| −509.3423 | −36,035.4457 | −20,384.6695 | |
| −0.13808 | −394.7372 | −604.5916 | |
| 282.167 | 289.9596 | 684.9051 | |
| −0.24937 | 10.7169 | −116.461 | |
| Qubic terms | |||
| −23,687.6184 | −217,773.3151 | 19,662.5142 | |
| −509.2357 | −986.8019 | −1,050,985.1787 | |
| 265.0119 | 12,758.1406 | 752.5436 | |
| 160.1033 | −7751.9336 | −4795.2182 | |
| 9.2083 | −196.1558 | −33.2336 | |
| −7.5831 | 409.9541 | 218.3688 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karimov, A.; Rybin, V.; Babkin, I.; Karimov, T.; Ponomareva, V.; Butusov, D. Time-Reversible Synchronization of Analog and Digital Chaotic Systems. Mathematics 2025, 13, 1437. https://doi.org/10.3390/math13091437
Karimov A, Rybin V, Babkin I, Karimov T, Ponomareva V, Butusov D. Time-Reversible Synchronization of Analog and Digital Chaotic Systems. Mathematics. 2025; 13(9):1437. https://doi.org/10.3390/math13091437
Chicago/Turabian StyleKarimov, Artur, Vyacheslav Rybin, Ivan Babkin, Timur Karimov, Veronika Ponomareva, and Denis Butusov. 2025. "Time-Reversible Synchronization of Analog and Digital Chaotic Systems" Mathematics 13, no. 9: 1437. https://doi.org/10.3390/math13091437
APA StyleKarimov, A., Rybin, V., Babkin, I., Karimov, T., Ponomareva, V., & Butusov, D. (2025). Time-Reversible Synchronization of Analog and Digital Chaotic Systems. Mathematics, 13(9), 1437. https://doi.org/10.3390/math13091437







