Abstract
Full terms, which serve as tools for classifying algebras into subclasses, can be studied using an algebraic approach. For a natural number n, this paper introduces the algebra of order-preserving full terms under the -superposition operation satisfying the superassociativity using mappings on the set of all order-preserving transformations on a finite chain . We prove the freeness property of such algebra with respect to the variety of superassociative algebras. Additionally, binary operations on the powerset of order-preserving full terms whose elements are called tree languages are discussed. To define order-preserving identities and order-preserving varieties, the left-seminearring of full hypersubstitutions is determined. The required characteristics for any identity to be an order-preserving identity are considered. Furthermore, we also discuss the homomorphism of full hypersubstitutions with other algebraic structures.
MSC:
08A05; 08A35; 20M07; 20M05
1. Introduction
Recall from [1] that a full term, a term in which all of the operations of the given signature are allowed and the structure is unrestricted, is one of the generalizations of the words that are constructed from an alphabet for a natural number and a given signature, also known as operation symbols. Basically, we consider two concrete examples. In a Boolean algebra, if we consider the Boolean algebra signature , is a full term because it uses the binary operations ∨ and ∧, the unary operation ¬, and the variables . In contrast, is not a full term because it does not use , or 1. Another example is the expression on a group G with the signature , where · is a binary associative operation on G, e is the identity, and −1 denotes inversion. On the other hand, is not a full term.
By definition, for a type with for all n-ary operation symbols indexed by some non-empty set I, the set of all n-ary full terms of type is the smallest set closed under finite application of the following inductive steps: (1) is an n-ary full term of type where is a mapping on a finite set and is an operation symbol of type and (2) is an n-ary full term of type where are n-ary full terms of type and is an n-ary operation symbol of type . For more details, we refer the reader to the comprehensive monograph [2]. It is known that an algebra consisting of the set and the superposition of arity satisfies the axiom of superassociativity and is a member of a variety of superassociative algebras [3,4,5,6]. The monograph [2] provides interesting facts in the study of superassociative algebras of multiplace functions. Furthermore, algebralization of terms in various classes has been revealed in many papers; for instance, see [7,8].
Actually, full terms always play a crucial rule in solid varieties, which are closed varieties of algebras under hypersubstitutions. In essence, hypersubstitutions modify terms by systematically replacing the operation symbols with corresponding terms. This provides a way to study the behavior of the terms under structural changes or transformations. When applying a hypersubstitution, the full terms are transformed, and their behavior determines whether certain algebraic identities or properties hold in the corresponding algebraic system. For instance, on a group G with the signature , a hypersubstitution defined by and can transform a full term into another one. In fact, by using the superposition operation, the extension of turns into another term. Particularly, we call a hypersubstitution whose images are full terms a full hypersubstitution of type . Algebraically, the set of all full hypersubstitutions forms a monoid under a binary operation and an identity mapping defined by . Recent trends in this domain can be found in [9,10].
Although a full term is defined by a transformation in a full transformation semigroup under the usual composition where , there are other possibilities of applying other classes of transformation semigroups for subclasses of full terms. The following are some developments in this line. The set of all strongly full terms induced by an identity transformation is a subalgebra of the set of full terms. In [11], a subsemigroup for constructing an n-ary -full term of type . . Thus, the set of all order-decreasing full terms of type is examined. Full terms determined by transformations with a restricted range are discussed in [12]. In 2023, Kumduang and Sriwongsa introduced a full term preserving a partition. The algebra for the quantifier-free formulas generated by such a term is constructed. See the paper [9] for this topic. Recently, for a fixed subset Y of , has been defined as a transformation semigroup with a fixed set. A full term constructed from transformations with a fixed set called a -full term is presented using such a transformation. See [13] for more information.
Recall that a transformation is called an order-preserving transformation if , and then for all . The symbol stands for the set of all order-preserving transformations on , i.e.,
for all . Refer to [14,15,16,17,18,19] for more details pertaining to order-preserving transformations. This paper aims to apply order-preserving transformations to the set to define a novel class of full terms and study several algebraic properties. The presentation of this paper is organized as follows. In Section 2, the algebra of n-ary order-preserving full terms of type , together with the appropriate operation, is established. We also study the free algebra for full terms constructed from order-preserving transformations. In Section 3, we consider tree languages over the set of all order-preserving full terms of type . Moreover, we define the binary operations on the set of all n-ary order-preserving full terms of type derived from the superposition operation and demonstrate that these operations possess the associative property. Algebras of mapping whose images are order-preserving full terms, which include an identity element, are constructed and investigated in Section 4. Subclasses of identities arising from order-preserving full terms and varieties of algebras that satisfy these identities are examined. Finally, we discuss the homomorphisms of the algebras of the order-preserving full terms.
2. The Superassociative Algebra of Full Terms Defined by Order-Preserving Transformations
In this section, we aim to construct a novel algebra which satisfies the superassociative law using the concept of order-preserving transformations. Firstly, we inductively define the set of n-ary order-preserving full terms of type as follows:
Definition 1.
Let n be a positive integer. An n-ary order-preserving full term of type is inductively defined by
- (1)
- is an n-ary order-preserving full term of type if is an n-ary operation symbol and α is an order-preserving transformation on .
- (2)
- is an n-ary order-preserving full term of type if is an n-ary operation symbol and are n-ary order-preserving full terms of type .
The set of all n-ary order-preserving full terms of type , closed under finite applications of (2), is denoted by .
Some examples of n-ary order-preserving full terms of type are shown in the following examples.
Example 1.
Consider a type with a ternary operation g. Since , then . On the other hand, because .
Example 2.
Let be a type with a quaternary operation symbol f. Then, we have whereas
It turns out that for a fixed , each order-preserving full term of type can be drawn using a tree diagram, which means that when a type is finitary, i.e., the number of each operation symbol is finite, each order-preserving full term t has a tree representation. From Example 1, a tree representation of
can be shown in the following Figure 1.
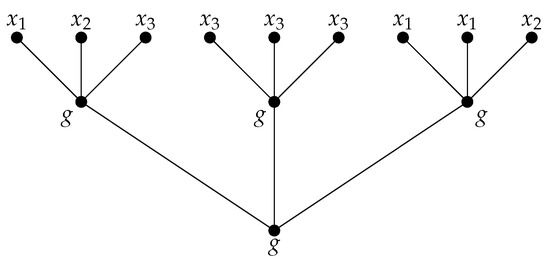
Figure 1.
A tree representation of .
We remark that an order-preserving full term t is a completely expanded term given in [8] because the maximum depth of all of the variables in t is equal and equals 2.
Now, we observe that where n is a positive integer.
For the set of all n-ary order-preserving full terms of type , we define the superposition operation
by
- (1)
- ;
- (2)
Consider the following example.
Example 3.
Let be an order-preserving transformation on . If we set , and as ternary order-preserving full terms of type , then we have
On the other hand,
We now obtain the following algebra of type :
Recall from [3] that a superassociative algebra of rank n, where , sometimes called a Menger algebra of rank n, is a pair of the form where G is a non-empty set and ∘ is an -ary operation defined on G which satisfies the axiom of superassociative law, i.e.,
for all .
Then, we prove the following theorem.
Theorem 1.
is a superassociative algebra of rank n.
Proof.
We prove that satisfies the superassociative law by induction on the complexity of the order-preserving full term t such that the equation
holds. Firstly, if where , then
Inductively, assume that such that satisfy (1). Then,
which completes the proof. □
The generating system of the algebra is denoted by and constructed by
Let be the variety of all algebras of type that satisfy the superassociativity. For the free algebra generated by with respect to , where Z is an alphabet of variables indexed by the set , the operation on will be represented by .
As a consequence, the following theorem is the main result in this section, which provides the freeness property of the algebra .
Theorem 2.
The algebra is free with respect to the variety of superassociative algebra of rank n, freely generated by the set .
Proof.
We claim that is isomorphic to . To ensure that this claim is true, we inductively define the mapping
by and
Clearly, the mapping is a surjection. In fact, we let . Then, an order-preserving full term of type exists such that .
To show that the mapping is injective, let and be order-preserving transformations on a finite chain . Suppose that . Then, , which implies that and . Thus, , which proves the injectivity.
Now, we prove by induction on the complexity of an order-preserving full term t that is a homomorphism, i.e.,
for all .
If , then
Now, let and assume that for all ,
Then, we obtain
Similarly, given the fact that
for all where is an identity mapping on , we then have
Due to the superassociativity of , we conclude that and are equal. □
3. Algebras of Languages Induced by the Set
In the first part of this section, as follows from [2], we define the tree languages over the powerset of order-preserving full terms of type . The symbol stands for the set of all non-empty subsets of order-preserving full terms of type . Each element in is called a language of order-preserving full terms.
Example 4.
It is straightforward to see from Example 1 that on the set ,
are some elements in .
Recall from [2] that the non-deterministic superposition operation on the set of all n-ary full terms of type is a mapping
given by
- (1)
- if where ;
- (2)
- if ;
- (3)
- if T is an arbitrary non-empty subset of ;
- (4)
- if or for some
where are in .
The following example demonstrates the process of computation of languages with respect to the operation for some n.
Example 5.
On the set described in Example 4, let , and . According to the definition of the operation , is equal to , and equals
and .
Thus, is the set
belonging to .
Some properties of the superposition are discussed.
Proposition 1.
If , then
Proof.
Let be non-empty subsets of the set of all order-preserving full terms of type . There are three cases to consider. Firstly, if where β is an order-preserving transformation, then . For the next case, let be such that for all . Consider
On another side, we obtain
From our assumption, in this case, we conclude that the set equals .
Suppose that . Because , then . □
Proposition 2.
If , then
Proof.
Using Proposition 1, we have
Let . Firstly, let where . Consider . According to Proposition 1, we obtain .
Now, let and suppose that
for all Consider
Finally, if T is an arbitrary non-empty subset of the set of all order-preserving full terms of type , we then have . □
Now, the relationship between the set of all full terms and the set of all order-preserving full terms of the same type is shown by the following theorem.
Theorem 3.
is a subalgebra of .
Proof.
Clearly, . For , we show on a characteristic of a set A that is an element in . There are three cases to consider. If where , then is an element in . For the second case, let . Assume that for all . Consider . Through this assumption, we obtain , belonging to the set . For the last case, if A is an arbitrary non-empty subset of , then . Since each is already in , then The proof is completed. □
The second aim of this section is to define and study the binary operations on and .
Now, let . The binary operation + is defined as follows.
by
We define the binary operation on the Cartesian product of n-tuples of order-preserving full terms of type as follows. For all , define
by
Naturally, for , we define the binary operation on by
On the Cartesian product , the binary operation
is defined by
for all .
The following theorem presents the connection between and
Theorem 4.
The semigroup is embedded into
Proof.
We first show that is a semigroup. To this end, let be the elements in Then, according to the superassociativity of , we obtain . Therefore, is a semigroup. For the associativity of *, let . Consider
Thus, is a semigroup.
Now, for any , we define a mapping by . Assume that . Consider
Since ψ is injective, we can conclude that is embedded into □
Moreover, we yield the following relationship.
Theorem 5.
is embedded into
Proof.
Clearly, reasoning dual to the proof of Theorem 4 shows that the mapping
is a monomorphism from the semigroup to
. □
Other embeddabilities are described as follows:
Theorem 6.
The following statements hold:
- (1)
- embeds into
- (2)
- embeds into
Proof.
Let t be an n-ary order-preserving full term. We define a mapping by . It is clear that is injective. Moreover, For (2), we define a mapping by . Obviously, is injective. Additionally, is also a homomorphism. That means Thus, the proof is completed. □
4. A Variety of Algebras Satisfying the Identities Induced by Order-Preserving Transformations
In this section, our objective is to construct a novel associative algebra that includes an identity element. Each element of this algebra will be applied to defining a class of identity called an order-preserving hyperidentity, and a variety of algebras satisfies such identity. First, we achieve this by defining a mapping that assigns each operation symbol of type to the set of all n-ary order-preserving full terms of type as follows.
An order-preserving full hypersubstitution of type or an -full hypersubstitution of type is a mapping
that assigns each n-ary operation symbol of type to the set of all n-ary order-preserving full terms of the same type. The set of all -full hypersubstitutions of type is denoted by .
For and , we define the order-preserving full terms arising from a mapping as follows.
- (1)
- If , then ;
- (2)
- If , then .
It is observed that if t is an order-preserving full term of type , then is an order-preserving full term of type for all .
Any -full hypersubstitution of type can be extended to a mapping
defined as follows
- (1)
- ;
- (2)
- .
For , we define the binary operation by where ∘ is the usual composition of functions.
We give some properties of such a hypersubstitution.
Lemma 1.
Let α be an order-preserving transformation on . For any , the equation
holds.
Proof.
Let and . There are two cases to consider: Case 1: If where , then
Case 2: Let and assume that
for all and . According to the definition of a term arising from , we obtain
□
Through Lemma 1, we have the following theorem.
Theorem 7.
The extension of each -full hypersubstitution of type is an endomorphism on the superassociative algebra .
Proof.
We will show by induction on the complexity of that for any ,
Firstly, if where is an order-preserving transformation, then according to Lemma 1, we have
Assume such that
for all . Then, we consider the left-hand side of (2), i.e.,
For the right-hand side of 2, we have
Applying the fact that the operation is superassociative given in Theorem 1, we conclude that □
Proposition 3.
Let and . Then,
Proof.
We give a proof by induction on the complexity of the term t. If where α is an order-preserving transformation, then Let and assume that for all . Then, Here, the proof is completed. □
According to Proposition 3, we obtain the following result, which shows that the extensions of the product of two order-preserving full hypersubstitutions with respect to and the product of two extensions are the same thing.
Proposition 4.
Let and be the extensions of -full hypersubstitutions of type . Then,
Proof.
We prove by induction on the complexity of the order-preserving full term t. First, if where α is an order-preserving transformation, according to the definition of the full terms arising from another mapping on the set , we obtain Let and assume that where . Then,
On the other hand,
Applying the fact that each order-preserving full hypersubstituion is an endomorphism on the algebra proved in Theorem 7, thus equals □
Having Proposition 4 at hand, notice that . Indeed, due to the associative property of the composition ∘ of functions, . As a result, is a monoid where is the identity hypersubstitution which is defined by .
Our next aim is to define the second binary operation on . A binary operation on is defined by
We notice that is an element in . Furthermore, because of the satisfaction of in the superassociative law, is associative, and thus forms a semigroup.
By , we mean an order-preserving hypersubstitution that maps any operation symbol to a term t.
Proposition 5.
The semigroup embeds into .
Proof.
Let t be an order-preserving full term of type . It is not difficult to prove that a mapping is an injective homomorphism. □
The relationship between two associative binary operations and + is now discussed.
Theorem 8.
forms a left-seminearring.
Proof.
It is enough to show the left distributive law, i.e., , is satisfied. In fact, according to Theorem 7, we have
□
Unfortunately, the right distributivity, i.e., , is not true, as shown in the following counterexample.
Example 6.
Let I be a singleton index set and with a binary operation symbol f. Assume that are elements in defined by
Consider
and
Since we know that and , a term does not equal . Hence, , which means that the right distributivity does not hold.
Since the algebra is generated by the set
then any mapping
is called an -full substitution. Let be the set of all -full substitutions. Each -full substitution can be uniquely extended to an endomorphism
Define for all where ∘ is the usual composition. Let be an identity mapping on . We note that the equation holds due to an application of Theorem 2. Hence, we find that is a monoid.
Theorem 9.
can be embedded into .
Proof.
Let . Then, according to Theorem 7, is an endomorphism of . Since the algebra is generated by the generating set , we obtain as an -full substitution with
To show that the mapping defined by
is a monomorphism, let . Obviously, is an injection. Given the fact that the extension of the product of two hypersubstitutions is the composite mapping between each extension of the hypersubstitution, as proven in Proposition 4, then Therefore, is a homomorphism. □
Consider a variety of algebras V of type , and let be the set of all identities in V. Now, define as the set of identities in V where both s and t are order-preserving full terms of type . In other words,
It is well known that forms a congruence on the absolutely free algebra . However, this is not generally the case for . The theorem below demonstrates that is a congruence on .
Theorem 10.
is a congruence on .
Proof.
Assume that We will prove that Firstly, we will prove using induction on the complexity of the term that
If where , it follows given that is compatible with the operations of the absolutely free algebra and given the definition of the order-preserving full terms that
That is,
And
Suppose that such that for all ,
Thus,
Moreover,
This means . So, we have the claim.
Given , then
□
Using the concept of -full hypersubstitutions, the notions of an -full closed identity and an -full closed variety are introduced.
Definition 2.
Let V be a variety of type .
- (1)
- An identity is called an-full closed identity (or an order-preserving identity) of V if for all ;
- (2)
- A variety V is called -full closed (or an order-preserving variety) if every identity in is an -full closed identity.
A necessary condition for any variety V to be -full closed is provided.
Theorem 11.
Let V be a variety of type . If is a fully invariant congruence on , then V is -full closed.
Proof.
Assume that is a fully invariant congruence on . If and , then according to Theorem 7, acts as an endomorphism on . Consequently, , meaning that V is -full closed.
□
For a variety V of type , is a congruence on according to Theorem 10. We then form the quotient algebra
The quotient algebra obtained belongs to . Note that we have a natural homomorphism
such that
Finally, we prove the following theorem.
Theorem 12.
Every is an -full closed identity of a variety V of algebras of type .
Proof.
Assume that and . According to Theorem 7, we find that is an endomorphism on the algebra . Thus,
is a homomorphism. By assumption,
That is,
Thus,
That is,
Therefore, is an -full closed identity of V. □
5. Homomorphisms of Algebras of Full Terms Induced by Order-Preserving Full Terms
In this section, we discuss several kinds of homomorphisms on algebras of full terms induced by order-preserving full terms. The first result shows the homomorphism property of the superassociative algebra and the algebra of term operations on an arbitrary algebra.
Let be an algebra of type , and let t be an n-ary order-preserving full term of type over an alphabet . Then, t induces an n-ary operation on through the following steps:
- (1)
- If where is a mapping in ,then ;
- (2)
- If is an n-ary order-preserving full term of type , and are the term operations which are induced by then where is defined by for every .
Consequently, is called the order-preserving full term operation induced by t on the algebra . The set of all n-ary order-preserving full term operations on will be denoted by .
On the set , an -ary operation can be defined by
- (1)
- ;
- (2)
Normally, the algebra
is constructed.
To show that is a homomorphic image of the algebra , the following lemma is needed.
Lemma 2.
.
Proof.
We give a proof on a characteristic of s. Assume that where . Then, we obtain
We now inductively suppose that and for every . Then, we have
□
As a consequence, we prove the following:
Theorem 13.
For every algebra of type , the algebra is homomorphic to .
Proof.
For , we define the mapping by
for every order-preserving full term t. Obviously, is well defined. Indeed, from , we obtain , which gives . To prove that is a homomorphism, we let be the order-preserving full terms of type . In fact, Lemma 2 implies that and are equal, which means that Alternatively, we say that is a homomorphic image of . □
Our next purpose is to show another homomorphism of the algebra of order-preserving full terms. For this, we apply the notion of the complexity of terms given in [20] to an order-preserving full term.
Definition 3.
The maximum depth of an order-preserving full term t, denoted by , is the longest distance from the first operation symbol that appears in t (from the left) to the variables. It can be inductively defined by
- (1)
- if ;
- (2)
- if .
We produce a formula for counting the maximum depth of order-preserving full terms under the superposition operation.
Theorem 14.
Let . Then,
Proof.
We give a proof by induction on the maximum depth of an order-preserving full term s. If , then where is a mapping on and with each , having arity n. It follows from the superposition that
Since and from (3), we conclude that
Now, let , and the formula is already satisfied for . Since we know that
then we have
This completes the proof. □
As a corollary, the formula for the maximum depth of in terms of the maximum depth t when t is an arbitrary order-preserving full term and is an order-preserving hypersubstitution is obtained.
Corollary 1.
Let be a type and . Then,
Proof.
If t is an order-preserving full term of the form where , then according to the definition of the extension of , we have Inductively, assume that and the formulas are satisfied for . Then, we obtain
□
Moreover, the maximum depth of order-preserving full hypersubstitutions is now defined.
Definition 4.
The maximum depth of , denoted by , is the greatest value of the maximum depth of each order-preserving full term for , i.e.,
For example, let be a type with the ternary operation symbols f and g. If we set using
It can be seen that and . As a consequence, .
We close this section with the connection between and the set of natural numbers with respect to the usual addition and usual multiplication in sense of a homomorphism.
Theorem 15.
On the left-seminearrings and , the mapping
defined by is an epimorphism.
Proof.
It is obvious that the mapping is well defined. For every natural number n, there is an order-preserving full hypersubstitution such that . Thus, is surjective. To show that the mapping preserves the operations, we show that the following two equations are satisfied:
and
for every In fact, applying Corollary 1, we have
which shows that Equation (4) holds. Moreover, it follows from Theorem 14 that
which proves (5). It is not difficult to show that the mapping sends an identity mapping on to a natural number 1 acting as an identity with respect to a usual multiplication · on . Indeed, from Corollary 1, we can conclude that □
Author Contributions
Conceptualization: K.W. and T.K. Methodology: K.W. and T.K. Formal Investigation: K.W. and T.K. Writing—Original Draft Preparation: K.W. and T.K. Writing—review and editing: K.W. and T.K. Visualization: K.W. Project Administration: K.W. Funding Acquisition: K.W. and T.K. All authors have read and agreed to the published version of the manuscript.
Funding
The first author acknowledges the support from the National Research Council of Thailand (NRCT) (Grant No. N42A670860) and Rajamangala University of Technology Lanna, Thailand. The second author was supported by Rajamangala University of Technology Rattanakosin, Thailand.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors thank the anonymous referees for their valuable comments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Denecke, K.; Jampachon, P. Clones of full terms. Algebra Discret. Math. 2004, 4, 1–11. [Google Scholar]
- Denecke, K. Partial Clones of Terms: An Algebraic Approach to Trees, Formulas and Languages; Eliva Press: Chisinau, Moldova, 2024. [Google Scholar]
- Dudek, W.A.; Trokhimenko, V.S. Algebras of Multiplace Functions; De Gruyter: Berlin, Germany, 2012. [Google Scholar]
- Dudek, W.A.; Trokhimenko, V.S. Menger algebras of k-commutative n-place functions. Georgian Math. J. 2021, 28, 355–361. [Google Scholar] [CrossRef]
- Dudek, W.A.; Trokhimenko, V.S. On σ-commutativity in Menger algebras of n-place functions. Comm. Algebra 2017, 45, 4557–4568. [Google Scholar] [CrossRef]
- Kumduang, T.; Sriwongsa, S. Representations of superassociative algebras by commutative functions with different types. Asian-Eur. J. Math. 2023, 16, 2350204. [Google Scholar] [CrossRef]
- Phusanga, D.; Koppitz, J. The semigroup of linear terms. Asian-Eur. J. Math. 2020, 13, 2050005. [Google Scholar] [CrossRef]
- Wattanatripop, K.; Kumduang, T. The partial clone of completely expanded terms. Asian-Eur. J. Math. 2024, 17, 2450063. [Google Scholar] [CrossRef]
- Kumduang, T.; Sriwongsa, S. Superassociative structures of terms and formulas defined by transformations preserving a partition. Commun. Algebra 2023, 51, 3203–3220. [Google Scholar] [CrossRef]
- Wattanatripop, K.; Changphas, T. The Menger algebra of terms induced by order-decreasing transformations. Commun. Algebra 2021, 49, 3114–3123. [Google Scholar] [CrossRef]
- Wattanatripop, K.; Changphas, T. The clone of K*(n,r)-full terms. Discuss. Math. Gen. Alg. Appl. 2019, 39, 277–288. [Google Scholar]
- Phuapong, S.; Kumduang, T. Menger algebras of terms induced by transformations with restricted range. Quasigroups Relat. Syst. 2021, 29, 255–268. [Google Scholar]
- Wattanatripop, K.; Changphas, T.; Kumduang, T. Algebras of full terms constructed from transformations with fixed set. Discuss. Math. Gen. Alg. Appl. 2024, 44, 127–146. [Google Scholar]
- Korkmaz, E.; Ayik, H. Ranks of nilpotent subsemigroups of order-preserving and decreasing transformation semigroups. Turk. J. Math. 2021, 45, 11. [Google Scholar] [CrossRef]
- Abusarris, H.; Darweesh, M.; Ayik, G. On the rank of generalized order-preserving transformation semigroups. Turk. J. Math. 2023, 47, 10. [Google Scholar] [CrossRef]
- Ayık, H.; Ayık, G.; Dağdeviren, A. On the semigroup of all injective orientation-preserving and order-decreasing partial transformations on a finite chain. Commun. Algebra 2025, 1–15. [Google Scholar] [CrossRef]
- Ayık, G.; Ayık, H.; Koc, M. Combinatorial results for order-preserving and order decreasing transformations. Turk. J. Math. 2011, 35, 617–625. [Google Scholar] [CrossRef]
- Fernandes, V.H. On the monoid of order-preserving transformations of a finite chain whose ranges are intervals. Semigroup Forum 2024, 109, 336–346. [Google Scholar] [CrossRef]
- Koppitz, J.; Worawiset, S. Ranks and presentations for order-preserving transformations with one fixed point. Turk. J. Math. 2022, 46, 23. [Google Scholar] [CrossRef]
- Denecke, K.; Wismath, S.L. Complexity of terms, composition and hypersubstitution. Int. J. Math. Math. Sci. 2003, 15, 959–969. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).