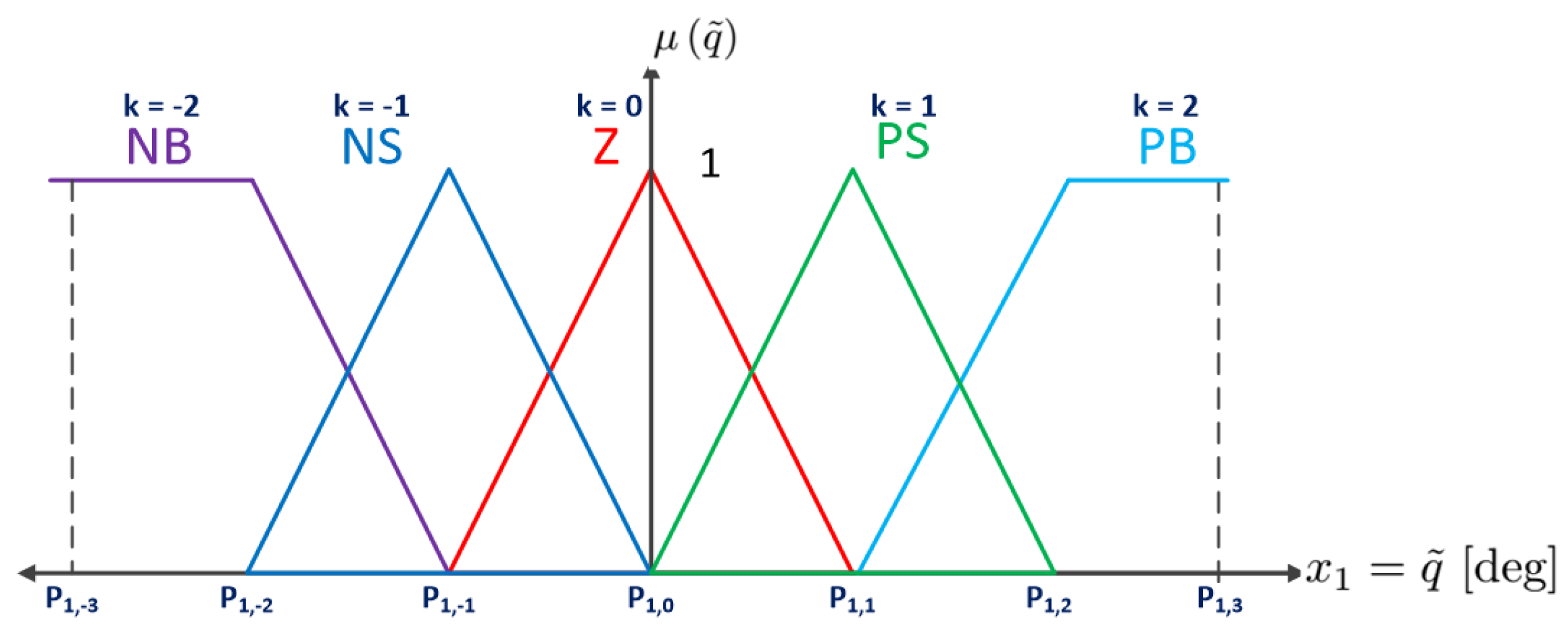
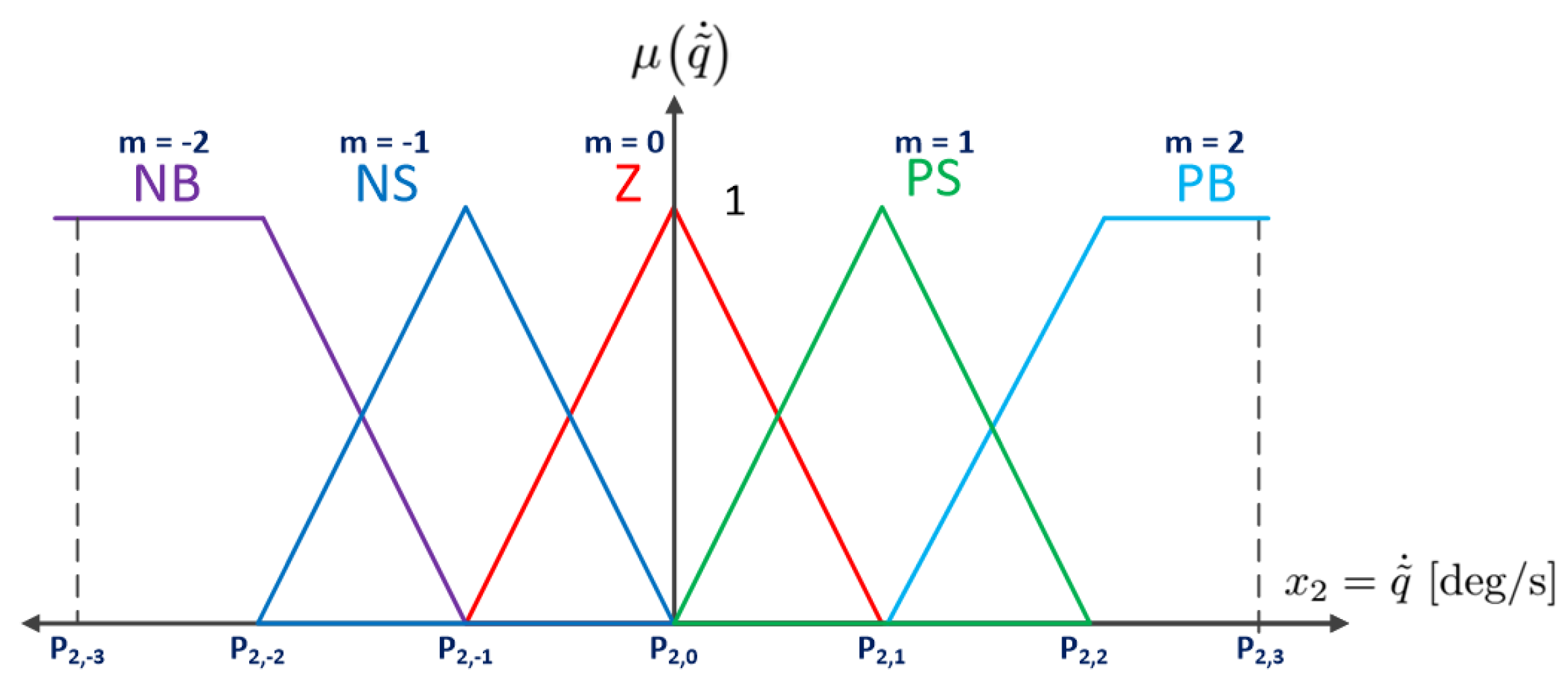
Since Calcev published his papers outlining a guideline for the design of fuzzy controllers to be input and output strictly as passive sectorial fuzzy controllers [
3,
4], several approaches using this type of controller applied to the motion control of robotic manipulators, both for regulation and trajectory tracking, have been presented in different instances, showing excellent results [
5,
6]. Furthermore, in [
7], a sectorial fuzzy controller using non-Lipschitz membership functions was used in a computed torque control array to achieve finite-time convergence for joint angular position errors of a robotic arm, with the advantage of not using discontinuous functions. Fuzzy control has yielded very good results in the control of flexible joint robotic manipulators. The paper by [
8] employs fuzzy descriptions to represent uncertainty bounds and system performance. The stability proof is carried out using Lyapunov theory, and an implementation example is given via simulations.
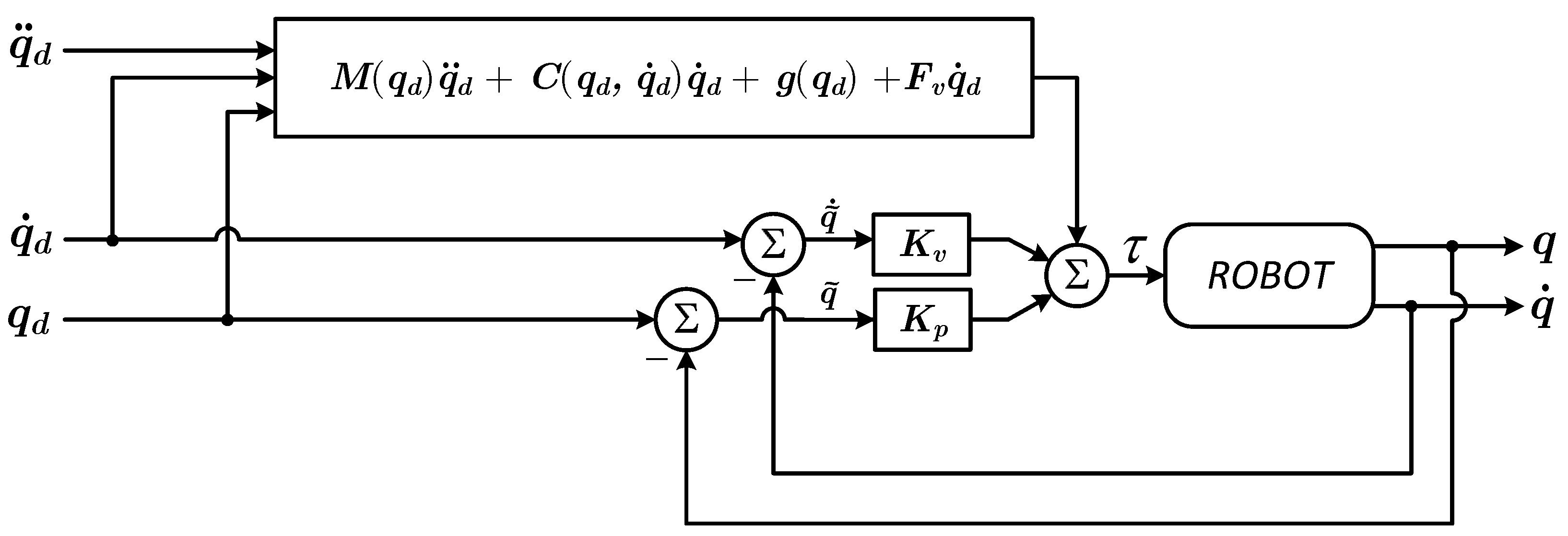
An important approach to the control of robot manipulators is model feedforward control. This simple strategy uses the inverse dynamics of a system, evaluated along reference signals, as the control law [
9]. However, implementing this control strategy requires precise values of the robot model’s parameters. An enhancement to this strategy is represented by the PD model plus a feedforward control compensation scheme, which was analyzed and tested in [
1]. They reported a stability analysis and experimental results for robot motion control using a PD plus feedforward controller, achieving performance comparable to the popular computed-torque control law. Recently, this approach has been extended to its fuzzy implementation in [
10], where Global Uniform Asymptotic Stability (GUAS) for
n-link serial robot manipulators has been formally proven, showing its good performance both in simulation and real-time experiments. To effectively utilize the excellent performance of PD control along with a feedforward controller, feedforward compensation is often implemented in an adaptive manner to address model uncertainties or disturbances. Artificial neural networks (ANNs), both feedforward-fixed and recurrent (adaptive) types, are the so-called battle horse of all current applications in Machine Learning for Robotic Control Systems, where they are extensively used to implement these types of systems [
11]. In the work presented in [
12], a fixed NN is applied to optimize the parameters of a Proportional–Integral–Derivative (PID) controller used in the tracking motion control of a Two-Degrees-of-Freedom (DOF) robotic arm. The NN yielded better results than those obtained via Genetic Algorithms or the cuckoo search algorithm. Performance comparisons were carried out with the PID parameter values obtained by the different optimization algorithms, demonstrating that their proposal showed the best results in terms of transient response and disturbance rejection. Adaptive neural networks have been extensively utilized in robot manipulators since the first successful approach introduced in [
13]. This approach is illustrated in the work of [
14], where an NN is used adaptively to model the desired dynamics of a robotic manipulator. This method is used in conjunction with a nonlinear PD controller to manage the motion trajectories of robot manipulators. Similarly, ref. [
15] introduced a wavelet NN to control a deicing robot manipulator used on farm transmission lines. In this controller, the neural network was responsible for estimating the disturbances and unmodeled dynamics of the robot. A radial-basis adaptive NN was used to control a robotic arm with a unified objective bound in [
16], showing satisfactory performance results. This unified objective bound includes all type of constraints related to various robotic manipulation tasks, such as transient performances, speed limits, and power consumption. However, the robot used only moved parallel to the horizontal plane such that no gravity vector was involved. Also, the control law used some discontinuous functions whose nature was not considered in the stability proof. In recent years, this approach has been expanded upon, as demonstrated by [
17], who proposed an adaptive controller based on neural networks to address uncertainties and input saturation in robotic manipulators. In a study by [
18], an adaptive NN controller was developed for
n-serial robotic systems with time-varying state constraints. The researchers demonstrated the controller’s stability and achieved promising results in simulations. Additionally, in [
19], the authors introduced a controller for an
n-link constrained robotic arm, utilizing a radial-basis adaptive NN. They considered actuator dynamics, along with state and input constraints, as well as unknown time-varying delays, all at the same time. Time-varying barrier Lyapunov functions were employed, proving Semiglobally Uniformly Ultimately Bounded (SGUUB) closed-loop stability. Saturation functions and Lyapunov–Krasovskii functionals were used to eliminate the effects of actuator saturation and time delays. They validated their proposal via simulation studies. Also, in [
20], a radial-basis NN is used in two parts to model and control a 6-DOF robotic arm. The article shows the whole procedure followed to construct the robot, along with the kinematic modeling and the controller design. The controller design uses a previous model of the robot estimated using a fixed radial-basis NN, and then an adaptive radial basis to control the trajectory tracking of their robot. The stability analysis is developed by applying Lyapunov theory. The controller performance is assessed by both simulation and experimental experiments, yielding excellent results with almost zero angular position errors and very minimal adaption time. In [
21], a very similar control scheme to [
14] is applied, combining feedback linearization (FDL) with a multilayer NN-based observer. Its stability is proven using Lyapunov’s second method. The authors carry out several simulations to test their proposed controller versus the FDL and PID approaches, considering both parametric uncertainties and strong external disturbances. An NN controller applied to the regulation of the position of a 3-DOF robot manipulator is described in [
22]. In this work, a three-layer B-spline ANN is used to control the robotic arm using only the angular position errors at each joint as inputs to the NN. The paper includes both the development of the robot’s kinematic model and a comparative assessment of the new proposal versus a PID controller, with and without parameter deviations. The new controller shows acceptable angular position errors.
In the current work, using the new properties of sectorial fuzzy controllers (SFCs) presented in [
10], which led to the discovery of strict Lyapunov functions that allowed us to conclude that GUAS should be utilized for sectorial fuzzy control (SFC) plus model feedforward compensation control of robot manipulators, a controller composed of an SFC in the feedback loop plus an adaptive NN in a feedforward array is proposed. This type of control proposal compensates for disturbances and parameter deviation, guaranteeing global uniform asymptotic motion trajectory tracking for robot manipulators of
n-link at the same time. The adaptive NN is made up of three actual layers that require the calculation of two independent sets of weights, which is an initial step to implement this adaptive NN as a deep NN composed of a larger number of layers, as shown in [
23]. Furthermore, formal stability analysis through Lyapunov functions and a LaSalle–Yoshizawa corollary for systems with discontinuities [
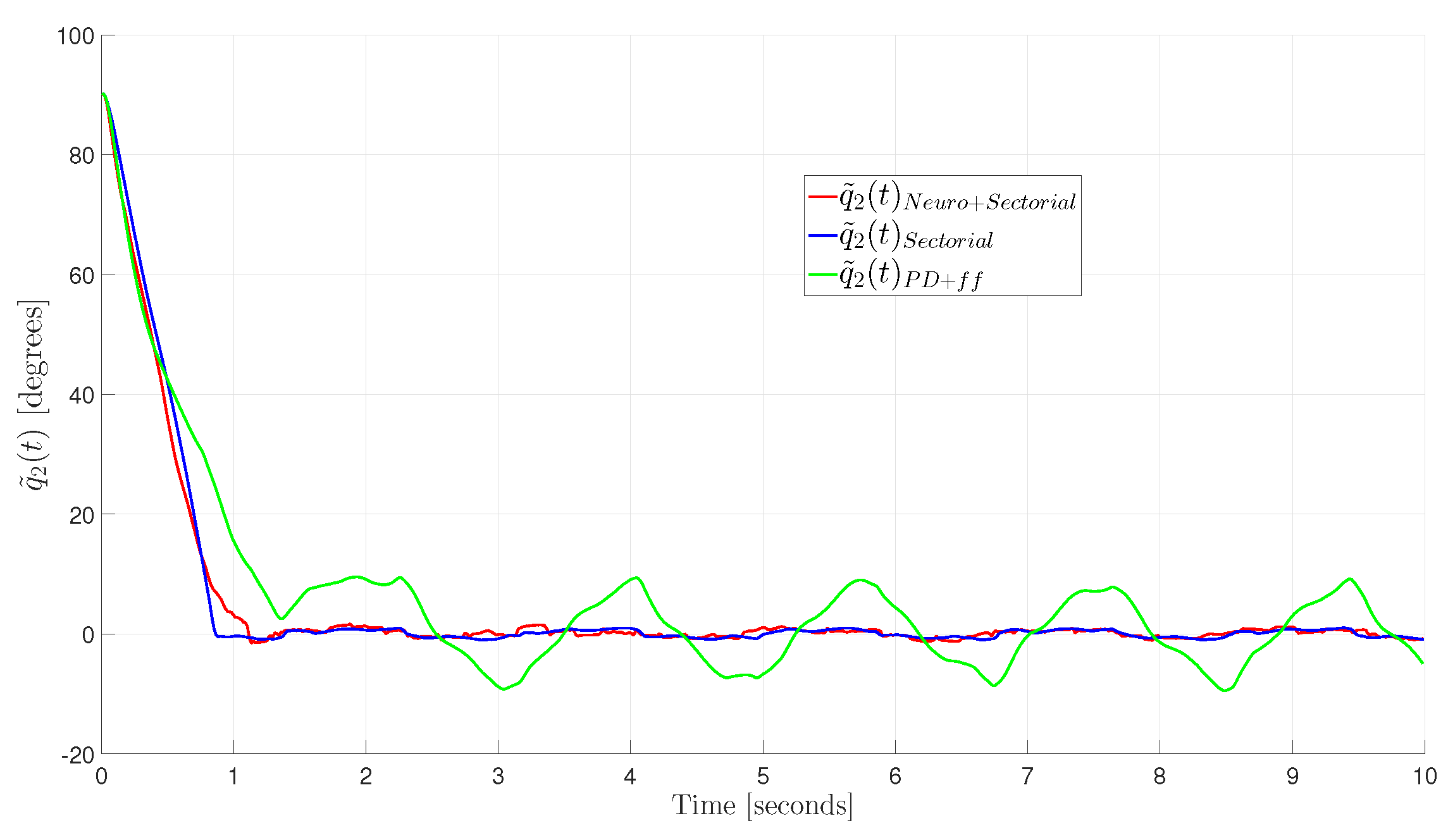
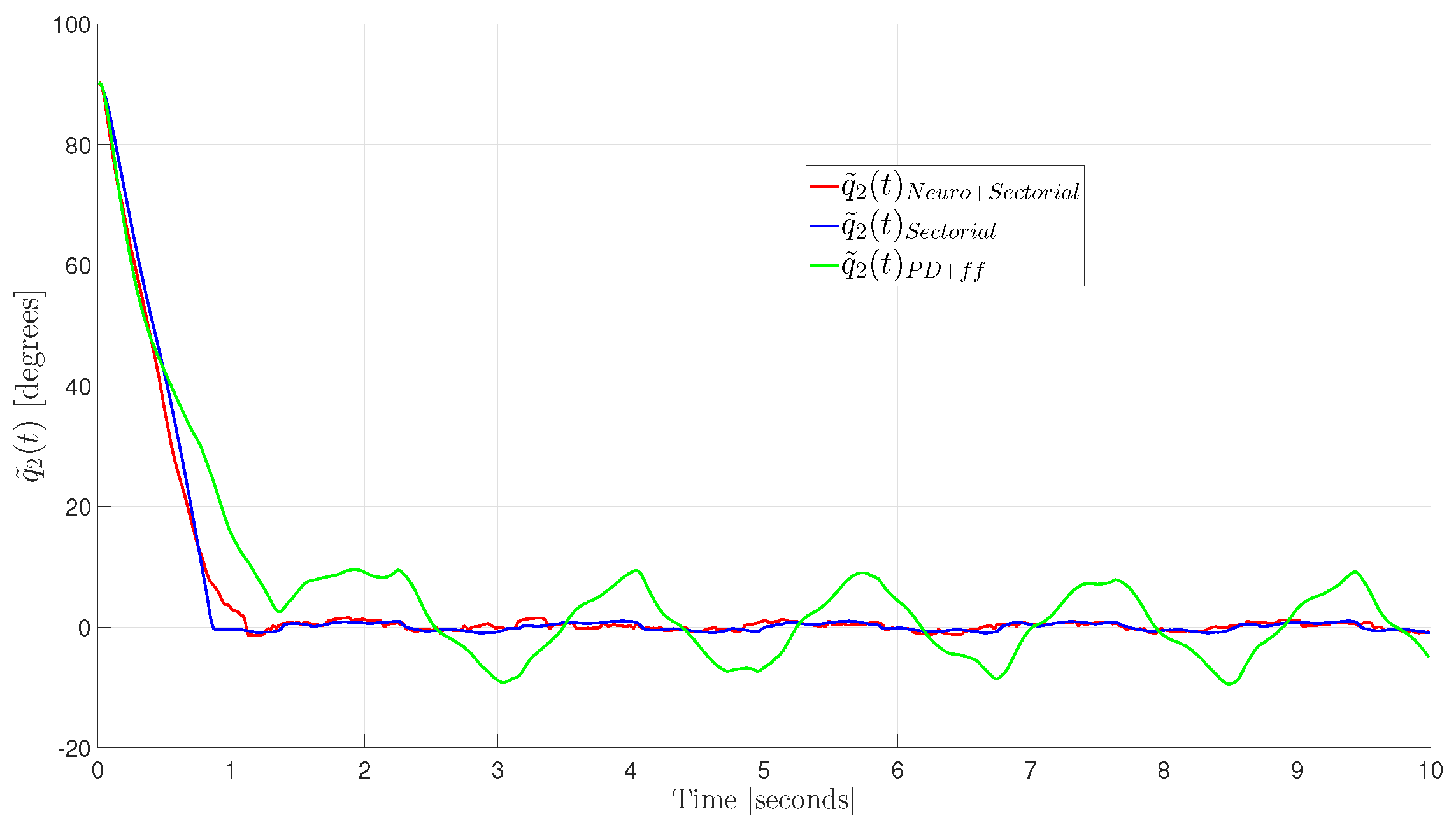
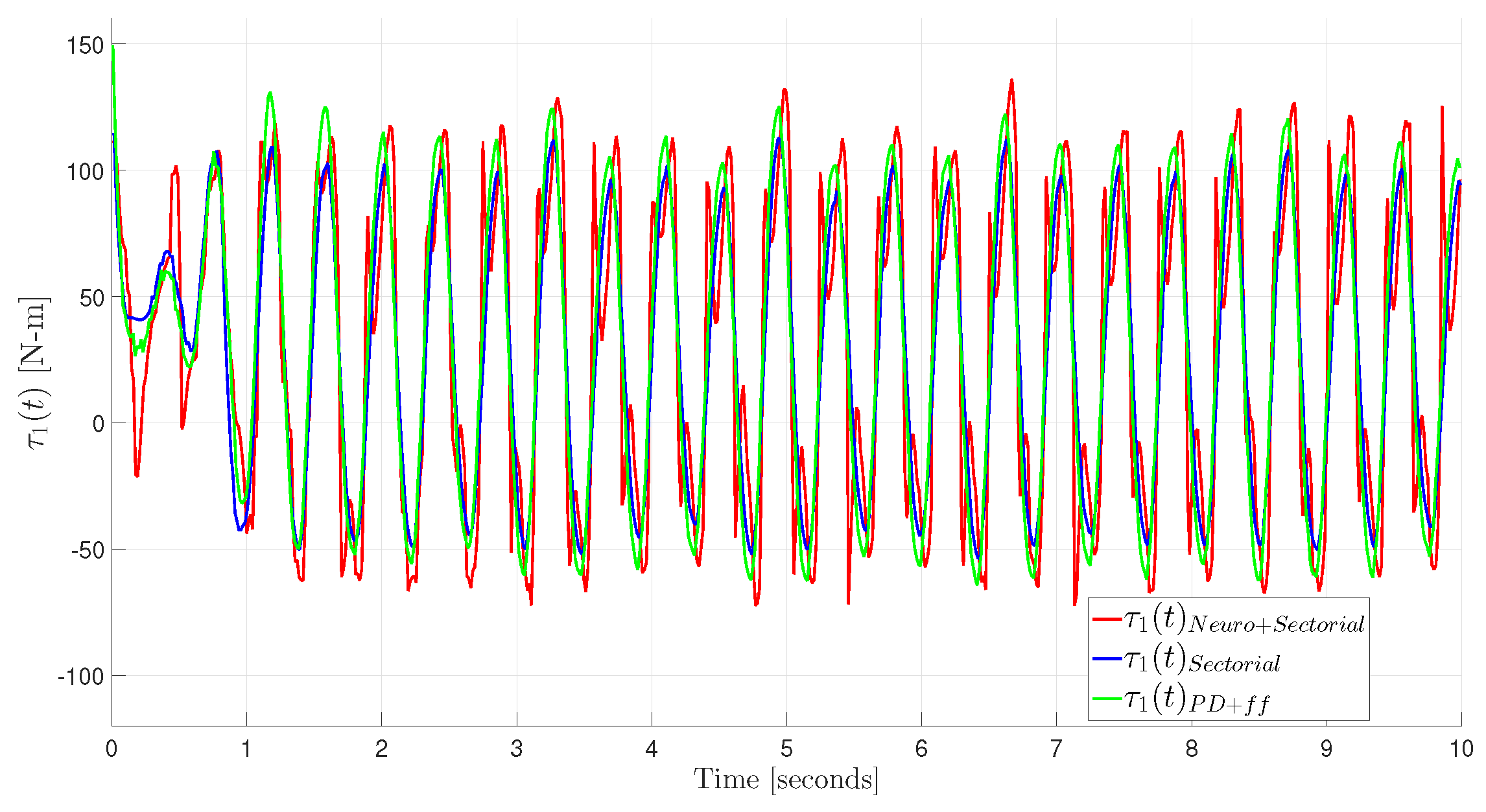
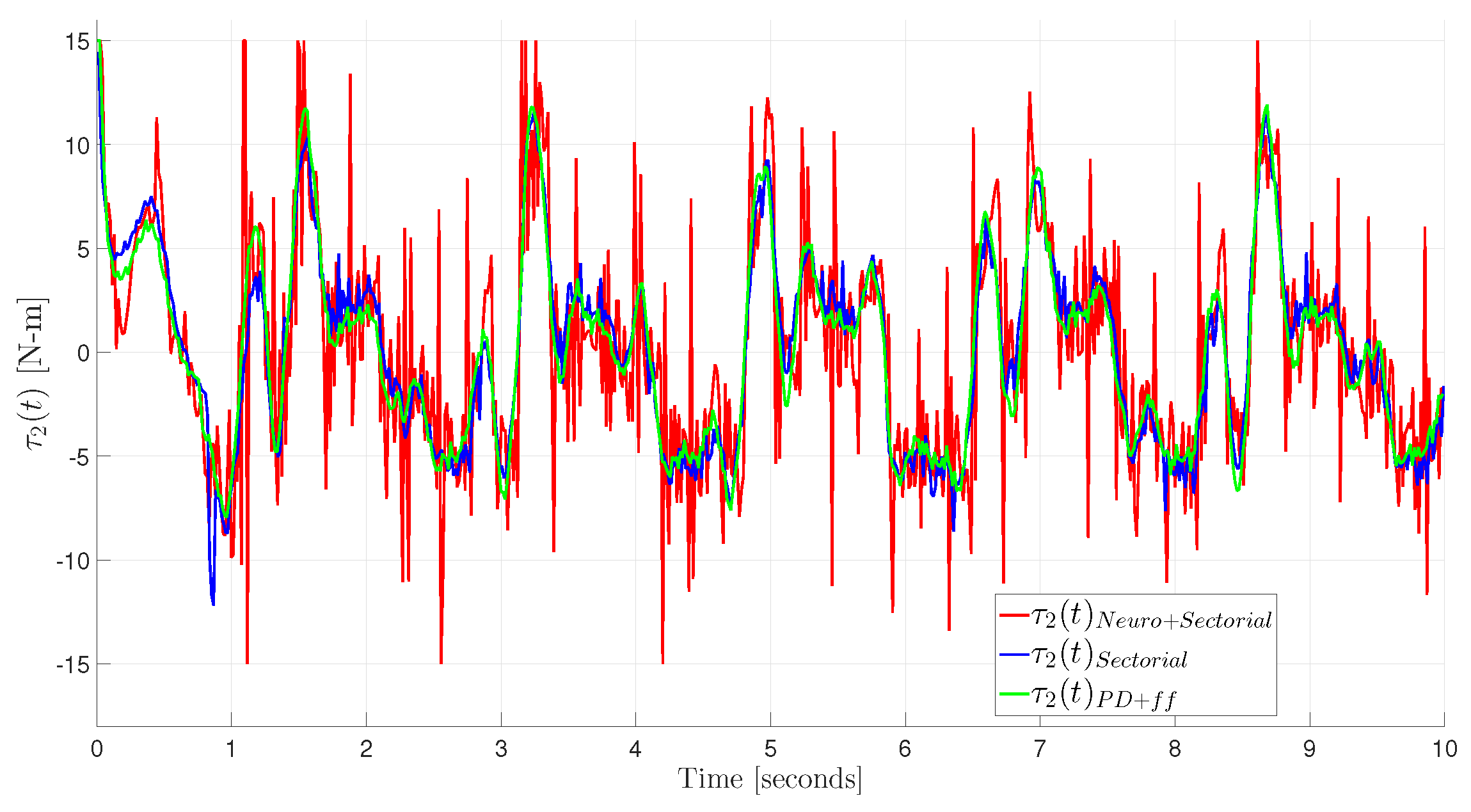
24], which were not used in previous approaches, demonstrate that the proposed controller leads to global uniform convergence of position and velocity errors to zero, keeping all of its signals bounded. To the best of the authors’ knowledge, this proposed controller is the first motion trajectory controller for robot manipulators based on an SFC for a feedback loop with adaptive feedforward NN compensation that does not need knowledge of robot dynamics to achieve the control objective. Finally, intensive real-time experimental tests are carried out and compared with the angular position error performance achieved by two previously published motion controllers, where, in general, the best performance is achieved by the proposed SFC with an adaptive feedforward NN compensation controller.
The remainder of this paper is structured as follows:
Section 2 presents a review of robot dynamics focused on its useful properties for stability analysis, along with a brief introduction to ANNs for modeling approximation, and the PD control plus feedforward compensation that our new proposal improves.
Section 3 presents the SFC, listing its main properties used for stability analysis.
Section 4 introduces our new approach, the sectorial fuzzy controller with Adaptive NN compensation, its control law, and the adaptive dynamics for the NN weights. A stability analysis of the closed-loop error dynamics of our new control approach, applying a corollary of the LaSalle–Yoshizawa theorem for nonsmooth systems and Lyapunov stability theory, is presented in depth in
Section 5.
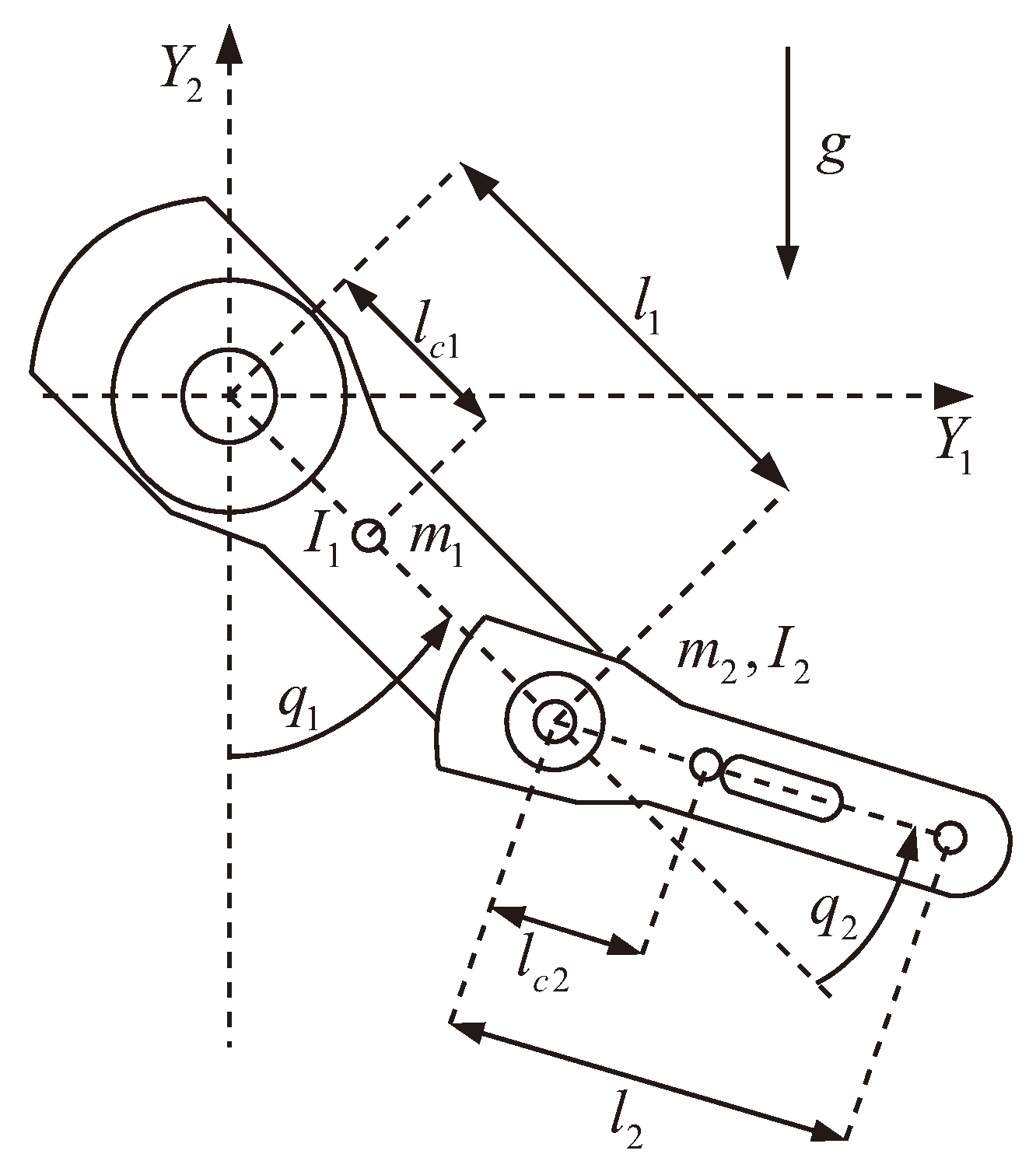
Section 6 shows the main characteristics of the 2-DOF robot that is used as the plant for all the controllers, and includes all the design information, numerical simulation information, and real-time experiments, as well as a performance comparison of our new proposed controller versus the other two previously published controllers. In
Section 7, we present the main conclusions obtained from the comparative analysis of the simulation and real-time implementation of our proposal with respect to previous approaches.