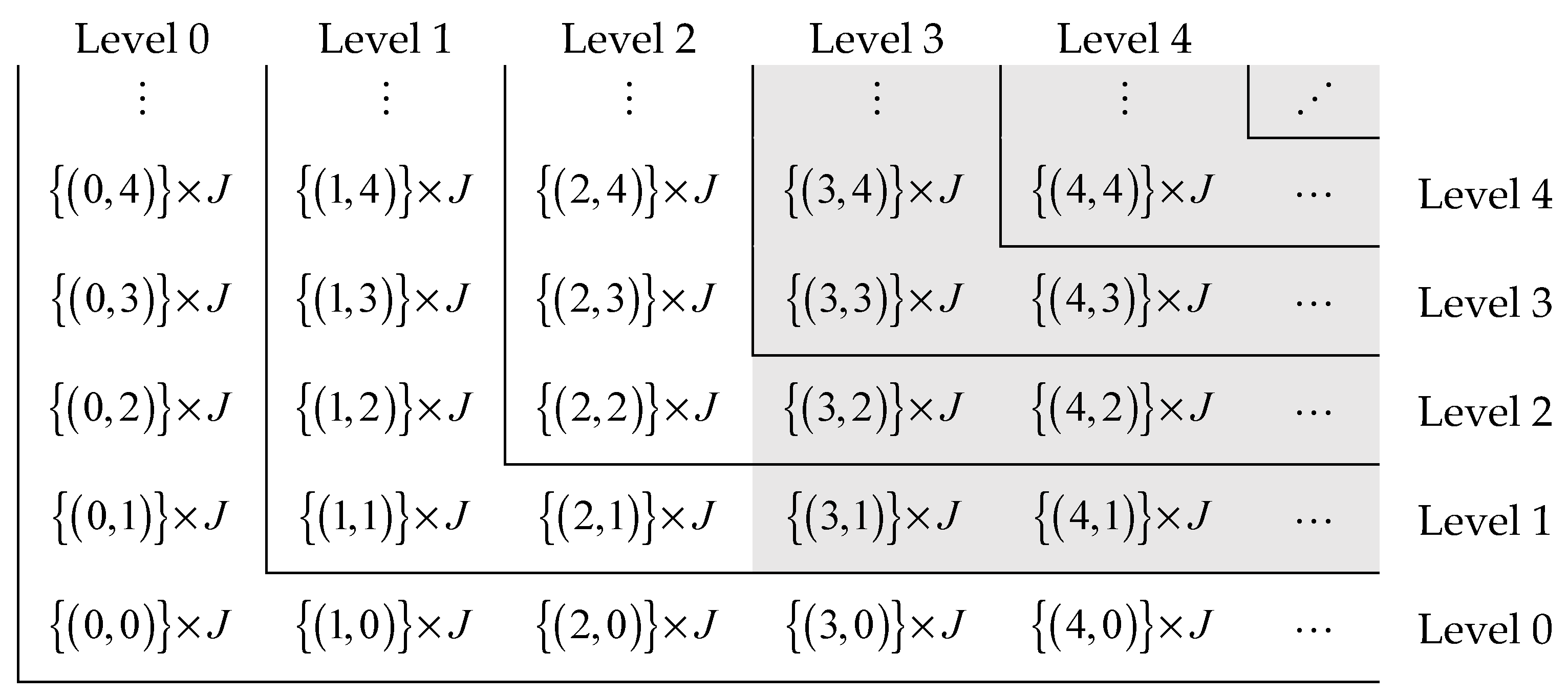1. Introduction
Multi-dimensional Markov chains of M/G/1 type (
Md-M/G/1) are the natural extensions of the classical Markov chains of M/G/1 type [
1,
2]. They are discrete-time Markov processes with state space
, where
is the set of nonnegative integers and
[
3,
4,
5,
6]. The number
of the elements in the set
can be finite or infinite. The probability of transition from a state
with
to states
may depend on
, and
but not on the specific values of
and
The one-step transitions of
Md-M/G/1 processes from a state
are limited to states
such that
where the vector
consists of all 1s. Md-QBD processes are a specific type of multi-dimensional Markov chain of M/G/1 type, where one-step transitions from
to states
are allowed only if
[
3,
5,
6,
7].
Md-M/G/1 processes are Markov chains of M/G/1 type with the level
consisting of states
, for which condition
holds.
The matrix
is a key characteristic of Markov chains of M/G/1 type. Each element of this matrix represents the conditional probabilities that, starting from a specific state at a given level, the process will first appear at a lower level in a particular state. It has been shown in [
8] that the matrix
can be expressed in terms of matrices of order
, called the sector exit probabilities. A system of equations was created for these matrices, and an algorithm to find its minimal nonnegative solution was proposed.
For the
Md-M/G/1 processes, the concept of the state sectors has been introduced in [
8]. It has been shown that the matrix
can be expressed in terms of matrices of order
representing the sector exit probabilities. A system of equations was developed for these matrices, and an algorithm for solving it was proposed. However, it remains unclear whether the set of matrices of sector exit probabilities constitutes the minimal nonnegative solution to this system.
This study builds upon the work presented in [
8]. We demonstrate that the family of matrices representing the sector exit probabilities is the minimal nonnegative solution to the system established in [
8]. Additionally, we introduce a new iterative algorithm for computing blocks of order
of the matrix
.
Section 2 reviews the relevant results obtained in [
8].
Section 3 focuses on the joint distribution of the sector exit times and the number of sectors crossed.
Section 4 establishes the minimality property of the matrices of the sector exit probabilities. In
Section 5, we introduce our new iterative algorithm for computing the matrix
Finally,
Section 6 presents our concluding remarks.
We use bold capital letters to denote matrices and bold lowercase letters to denote vectors. Unless otherwise stated, all vectors in this paper have integer components and the length . For any vector , we use the notation for the component of . For vectors and , means that for all , and means that for all . Functions and are defined, respectively, as and . Given a vector , we define sets and as , , and . We refer to the sets of the form as the sectors.
2. Multi-Dimensional Process of M/G/1 Type
Let
be an irreducible multi-dimensional Markov chain of M/G/1 type on the state space
, and
denote the probability of a one-step transition from
to
. We assume that the transition probability matrix
, partitioned into blocks
(
, for all
, satisfies the following properties:
where
,
, are nonnegative square matrices such that
is a stochastic matrix. Process
is the Markov chain of M/G/1 type, with the level
consisting of states
such that
. We refer to this process as an
M-dimensional Markov chain of M/G/1 type
.
The level
of a multi-dimensional process of M/G/1 type consists of states
such that
. For instance, consider the state space
of a
process, which is divided into subsets
,
, as illustrated in
Figure 1. Solid lines represent the boundaries of the process levels. The states of the sector
belong to the gray-colored subsets.
The transition matrix of a multi-dimensional Markov chain of M/G/1 type has a block Hessenberg form
where blocks
and
are nonnegative square matrices, such that
and
are stochastic matrices. Each state
of a level
can be characterized by the triple
, where
is an element of the set
defined as
Hence, entries of the matrices
and
can be indexed by the elements of the set
. As it follows from (1), the matrices
, partitioned into blocks
of order
, can be represented as
For any level
, the entry
of the matrix
represents the probability that, starting from the state
of the level
, the chain will first appear at the level
in state
. The matrix
is the minimal nonnegative solution to the equation ([
1])
Equation (3) can be transformed into the following system for the blocks
of the matrix
:
Let the set
be defined as
For any vectors
and
, the entry
of the matrix of the sector exit probabilities
represents the probability that, starting in the state
, the process
reaches the set
by hitting the state
([
8]). It implies that the matrix
is substochastic.
The family of matrices
,
, and the matrix
uniquely define each other, since we have the following equalities
where
is the set of all
v−tuples
satisfying
…,
,
.
As shown in [
8], the matrices
,
, satisfy the following system:
We will demonstrate that the family
,
, is the minimal nonnegative solution to the system (8) in the set of families
,
, of nonnegative matrices.
3. The Joint Distribution of the Sector Exit Times and the Number of Sectors Crossed
Let us define the sequence of passage times as follows:
We say that at time
, the process
is in the sector
if conditions
and
are met. The difference
represents the time the process spends in the sector
. We define the sector
exit time as the moment
when the process leaves the sector
,
Additionally, we define the number of sectors visited along a path to
as
If an initial state
of the process belongs to
, then we have
and
. If
with
, then at the first hitting time of
, the process exits the sector
and enters the sector
, which implies equality
. The set
is reached at the moment of transition from the set
to the state
.
For vectors , , and , we define matrices , , , and as follows.
The element
of the matrix
is the conditional probability that the process
, starting in the state
, reaches the set
by hitting the state
after passing through exactly
sectors,
The element
of the matrix
is the conditional probability that the process
will eventually hit the set
in the state
, given that it starts in the state
,
The element
of the matrix
is the conditional probability that the process
, starting in the state
, reaches the set
by hitting the state
after no more than
transition steps, and passing through exactly
sectors,
The element
of the matrix
is the conditional probability that the process
will hit the set
in the state
after no more than
transition steps, given that it starts in the state
,
It is easy to see that the matrices
,
,
, and
satisfy the following relations
For each
, any path of
leading from a state
to a state
must successively visit sets
, which will require visiting at least
sectors. Therefore, we have
for all
,
, and
. Additionally, it is impossible to visit
sectors without taking at least
transition steps, which implies that
for all
,
, and
.
The transition probabilities away from the boundary are spatially homogeneous, indicating that for any vector
and any vector
, the probabilities
may depend on
, and
, but not on the specific values of
,
and
, i.e.,
This means that the matrices
and
may be expressed as
Here, for vectors
and
, the matrices
and
are defined as
independently of the vector
. Vectors
and
in (17) satisfy conditions
and
. Therefore, the index
of matrices
and
is a nonnegative vector and its index
belongs to the set
. We refer to the matrices
as the matrices of the first passage probabilities.
It was demonstrated in [
8] that for all
and
, the matrices
satisfy the system
In the next theorem, we obtain a similar property for the matrices
.
Theorem 1. The matrices satisfy the system Proof of Theorem 1. We will initially demonstrate the validity of the following formulae for all values of
and
:
The first formula, in (19), is straightforward. The second formula adheres to the law of total probability, accounting for all possible process states following the first transition. Consider two states:
and
. The state
can be reached from the state
after a single transition, which contributes the term
to the second formula in (19). Additionally, the first transition can lead the process to some state
with
. To reach the set
from state
, the process
must necessarily hit the state
within no more than
transition steps. This contributes to the second term on the right-hand side of (19). Equation (18) for the matrices
is derived from (19) using Formulas (1) and (17). □
4. Minimality Property of the Sector Exit Probabilities
Matrices of the sector exit probabilities were defined in [
8] as the
,
. Entries of the matrix
determine the transition probabilities of the embedded Markov chain
, since for
, we have
We define matrices
,
, as
. These matrices determine the transition probabilities of the Markov process
as
for all
and
. From (20) and (21), it follows that the matrices
and
are related as
As a direct consequence of Theorem 1, we can derive the following property of the matrices
:
Neuts has demonstrated in [
1] that in one-dimensional cases—when the equality
holds—the matrix
is the minimal nonnegative solution of (3). We will show that similar results are also held in multi-dimensional cases. The proof is based on inequalities that we will derive in Lemma 1.
Lemma 1. The matrices satisfy the following inequalities Proof of Lemma 1. For any vectors
,
, and
, the element
of the matrix
is the conditional probability that the process
, starting in the state
, reaches the set
by hitting the state
after no more than
transition steps and passing through exactly
sectors. To hit the set
, starting in a state
and passing through exactly one sector is only possible if that single crossed sector is the set
. Therefore, we have the equalities
Let the sets
be defined as the set of all
tuples
satisfying
,
,…,
,
. Hitting the set
after no more than
transition steps is only possible if the total number of steps taken in the crossed sectors does not exceed
. It implies the following inequality
Let us introduce, in (26), new variables
,
,
,
, …,
. Since
, it is clear that the v-tuple (
) belongs to the set
. Using these variables and Formula (17), we can obtain from (26) the inequality
The statement of Lemma 1 follows from (23) and (27). □
Let matrices
,
,
, be defined as
It has been shown in [
8] that for each
, the sequence
,
, entry-wise monotonically converges to matrix
. The family of matrices
, is the minimal solution of system (8) in the set of families
,
, of nonnegative matrices. In the following theorem, we will demonstrate that the equality
holds for all
.
Theorem 2. The family of matrices of the sector exit probabilities , , is the minimal solution of the system (8) in the set of families of nonnegative matrices , . For each , the sequence , , entry-wise monotonically converges to matrix .
Proof of Theorem 2. At first, we prove by induction that matrices
defined by (28)–(29) satisfy
for all
and for all
. Since
and
, we know that
. Let us assume that
for some
and for all
Then, using (29), we obtain
which proves the induction step. The sequence
,
, entry-wise monotonically converges to matrix
and the sequence
,
, converges to matrix
[
8]. This implies the following inequalities for limiting matrices
and
:
Since both families
,
, and
,
, are solutions of the system (8), and the family
, is the minimal nonnegative solution of (8), and the inequalities
hold for all
we necessarily have equality
for all
. □
5. Computing the Matrix G
Any vector
can be represented as
, where
and
It was shown in [
8] that the matrices of the first passage probabilities possess the following properties
In Theorem 3 we show that decomposition (32) is a special case of more general results for nonnegative matrices of the form (31).
Theorem 3. Let , , be a family of nonnegative matrices such that for all and let each entry of the matrix seriesbe convergent. Then, matrices satisfy the following systemFor each vector such that ,
matrices , , can be decomposed as Proof of Theorem 3. It was shown in [
7] (Lemma 1), that for
and
, the sets
,
can be decomposed in terms of the cartesian products of sets
,
,
as
It follows from (33) and (35) that the matrix
can be represented as follows:
After applying (33) to each sum inside the square brackets in (37), we obtain
which can be rewritten as (35).
It follows from the definition of the set
, that isolating in (33) the first component of the
-tuple
, the matrix
can be transformed as
From here, using Formula (35), we obtain
which proves Formula (34). □
Let us define matrices
as
For each
, the sequence
,
, is entry-wise monotonically increasing and converges to the matrix
([
8]). This implies that for all
, the sequence
, is also entry-wise monotonically increasing and converges to the matrix
given by (7).
It follows from Theorem 3 that matrices
satisfy the system
Using decomposition (35), we can rewrite Equation (29) as
When using the iterative algorithm (28) and (29) to solve the system (8), a key challenge is the enumeration of elements of the set . In the subsequent theorem, we will show how to avoid these calculations.
Theorem 4. Let matrices , , and , , , be defined asThen, for each , matrices and satisfy the following inequalities Proof of Theorem 4. The proof is based on the fact that the sequences , , and , , are entry-wise monotonically increasing.
First, we will demonstrate that for all vectors
and
, the sequences
and
,
, satisfy
,
. Since
and
we know that
and
. Let us assume that
and
for some
and for all
,
. Then, it follows from (42) and (40) that the following inequality holds:
Using (43), inequality (45), and (39), we obtain
which proves the induction step. Therefore,
and
for all
and for all
,
.
Let us demonstrate that for all
and
, the sequences
, and
,
, satisfy
,
. Since
and
we know that
and
. Let us assume that
and
for some
and for all
,
. The following inequality follows from (42) and (40):
By applying this inequality along with the equalities (43) and (39), we can derive the following results:
which prove the induction step. Thus,
and
for all
and for all
,
. □
Given that the sequences
,
, and
, are entry-wise monotonically increasing, we can derive the following inequalities based on Theorem 4:
for all
, and
for all
. Since the sequence
,
, converges to the matrix
, and the sequence
, converges to the matrix
, the inequalities (46) and (47) lead to the conclusion presented in Corollary 1.
Corollary 1. For each , the sequence , , is entry-wise monotonically increasing and converges to the matrix . For each , the sequence , is entry-wise monotonically increasing and converges to the matrix .
Consequently, Theorem 4 outlines the new algorithm for computing the matrices of the sector exit probabilities and the matrix . Passing in the equalities (42) and (43) to the limit as tends to infinity, and using Corollary 1, we obtain a system of equations for matrices and .
Corollary 2. Matrices and satisfy the following system: Please note, if , all sums in Equation (49) will equal zero, since for all . Therefore, in these cases, Equation (49) has the form , . Consequently, Equations (48) and (49) outline the relationships between the blocks , , of the matrix and all its other blocks.
6. Conclusions
Matrices of the sector exit probabilities
were introduced in [
8] as a means of calculating the matrix
of multi-dimensional processes of M/G/1 type using matrices of order
. A system of Equations (28) and (29) for the matrices
was obtained, and an algorithm for calculating its minimal nonnegative solution was proposed. However, the question remained whether the family of matrices
,
, was a minimal nonnegative solution to the system (28) and (29). In Theorem 2, we gave a positive answer to this question. The algorithm proposed in [
8] was difficult to apply due to the need to enumerate the elements of the set
. In
Section 5, we demonstrated that the matrices
and blocks
of the matrix
satisfied the system (48) and (49), and provided an algorithm outlined in Equations (41) and (43) for solving this system. This algorithm successfully avoided the challenges associated with the enumeration of the elements of the set
in the algorithm introduced in [
8].
In multi-dimensional cases, both families of the matrices and are infinite, leading to a system with infinitely many equations. Managing systems with infinitely many equations and unknown infinite matrices is not feasible. Therefore, future research should concentrate on developing a method for selecting an appropriate truncation approximation.