Queues with Working Vacations: A Survey
Abstract
1. Introduction
2. Markovian Systems
2.1. Generic Model
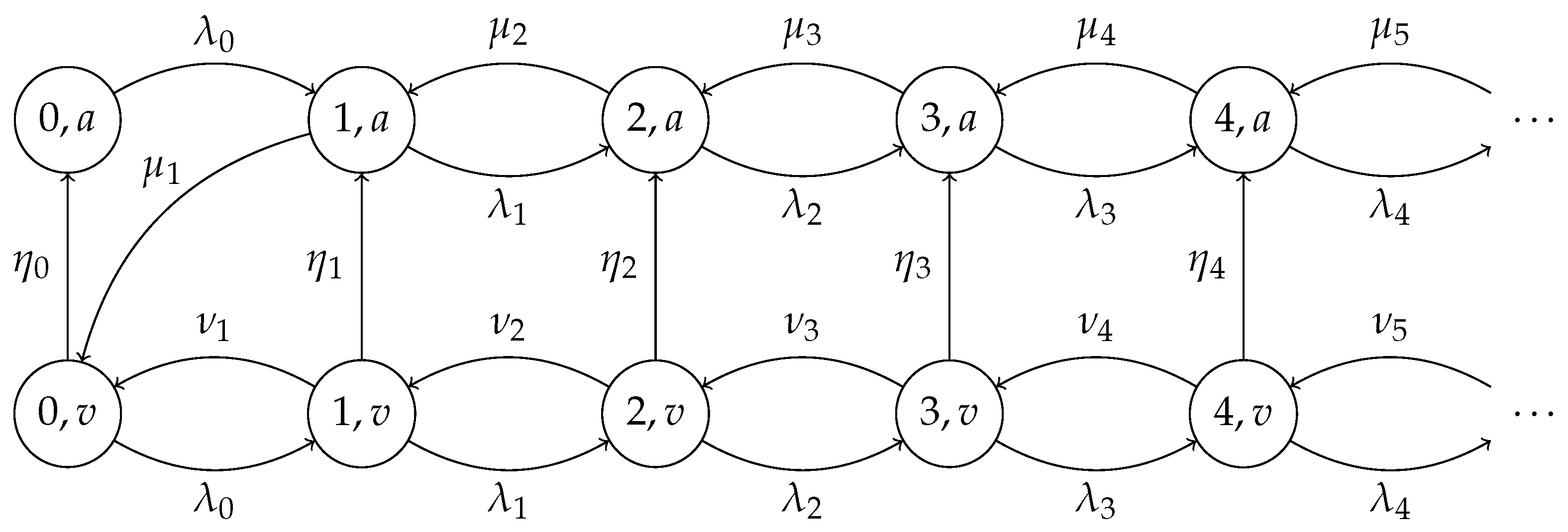
2.2. Queue with Working Vacations
2.3. M/M/c Queue with Synchronised Working Vacations
2.4. Further Comments
3. Quasi-Birth–Death Queues
3.1. Balance Equations
3.2. Homogenous QBD
3.3. Non-Homogenous QBD
3.4. Examples
3.4.1. MAP/M/1 Single-Working Vacation Queue
3.4.2. Multiserver Queue with Working Vacations
3.5. Retrial Queue with Vacation Interruptions
4. General Service Times
4.1. Queue
- We assume that the consecutive service times constitute a sequence of independent and identically distributed random variables, with common distribution function () and corresponding Laplace–Stieltjes transform . During working vacations, the server slows down and takes time units to finish a single unit of service time. Here, is a constant multiplier. Let denote the probability-generating function of the number of arrivals during a service time that starts when the server is active. By conditioning on the length of the service time, we find thatHere, denotes the probability mass function of a Poisson random variable with mean x:When service starts during a working vacation, the server may or may not be active during the service time. We, therefore, consider both the (partial) probability-generating functions and of the number of arrivals during a service time when the server remains on vacation or returns to the active mode, respectively. By conditioning on the length of the service time and the remaining length of the working vacation, we find that
- Alternatively, we assume that the distribution of the service time depends on the server state at the start of the service. Let and denote the Laplace–Stieltjes transforms of the service times when the server is active and on vacation, respectively. With , and defined as above and by conditioning on the end of the working vacation during the service time, we find that
4.2. Further Comments
5. General Interarrival Times
5.1. G/M/1 Queue
5.2. Further Comments
6. Other Queueing Systems with Working Vacations
6.1. Retrial Queues with Working Vacations
6.2. Working Server Breakdowns
6.3. Discrete-Time Working Vacation Queues
6.4. Fluid Queues
7. Queueing Games
7.1. The Game with Multiple Working Vacations
7.2. Customer Heterogeneity
7.3. Further Remarks
8. Applications
8.1. Ethernet Passive Optical Networks
8.2. Power-Saving Protocols
8.2.1. WirelessNetworks
8.2.2. Data Centres
8.2.3. Peer-to-Peer Networking
8.3. Manufacturing and Service Systems
9. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Takagi, H. Queueing Analysis: Vacation and Priority Systems; North-Holland: Amsterdam, The Netherlands, 1991; Volume 1. [Google Scholar]
- Tian, N. Vacation Queueing Models: Theory and Applications; Springer: Cham, Switzerland, 2006. [Google Scholar]
- Doshi, B. Queueing Systems with vacations: A survey. Queueing Syst. 1986, 1, 29–66. [Google Scholar] [CrossRef]
- Tian, N.; Xu, X.; Ma, Z.; Jin, S.; Sun, W. A Survey for stochastic decomposition in vacation queues. In Stochastic Models in Reliability, Network Security and System Safety: Essays Dedicated to Professor Jinhua Cao on the Occasion of His 80th Birthday; Springer: Singapore, 2019; pp. 134–158. [Google Scholar] [CrossRef]
- Servi, L.D.; Finn, S.G. M/M/1 queues with working vacations (M/M/1/WV). Perform. Eval. 2002, 50, 41–52. [Google Scholar] [CrossRef]
- Chandrasekaran, V.M.; Indhira, K.; Saravanarajan, M.C.; Rajadurai, P. A survey on working vacation queueing models. Int. J. Pure Appl. Math. 2016, 106, 33–41. [Google Scholar]
- Li, J.; Tian, N. The M/M/1 queue with working vacations and vacation interruptions. J. Syst. Sci. Syst. Eng. 2007, 16, 121–127. [Google Scholar] [CrossRef]
- Liu, W.; Xu, X.; Tian, N. Stochastic decompositions in the M/M/1 queue with working vacations. Oper. Res. Lett. 2007, 35, 595–600. [Google Scholar] [CrossRef]
- Hui, X.; Chen, H.; Tian, N.; Donghua, L. Study on N-Policy Working Vacation Polling System for WDM. In Proceedings of the International Conference on Communication Software and Networks, Chengdu, China, 27–28 February 2009; pp. 508–511. [Google Scholar] [CrossRef]
- Wang, K.H.; Chen, W.L.; Yang, D.Y. Optimal management of the machine repair problem with working vacation: Newton’s method. J. Comput. Appl. Math. 2009, 233, 449–458. [Google Scholar] [CrossRef]
- Yue, D.; Yue, W.; Xu, G. Analysis of customers’ impatience in an M/M/1 queue with working vacations. J. Ind. Manag. Optim. 2012, 8, 895–908. [Google Scholar] [CrossRef]
- Selvaraju, N.; Goswami, C. Impatient customers in an M/M/1 queue with single and multiple working vacations. Comput. Ind. Eng. 2013, 65, 207–215. [Google Scholar] [CrossRef]
- Laxmi, P.V.; Jyothsna, K. Impatient customer queue with Bernoulli schedule vacation interruption. Comput. Oper. Res. 2015, 56, 1–7. [Google Scholar] [CrossRef]
- Li, J.; Cheng, B. Threshold-policy analysis of an M/M/1 queue with working vacations. J. Appl. Math. Comput. 2016, 50, 117–138. [Google Scholar] [CrossRef]
- Wang, J.; Gao, S.; Do, T.V. Performance analysis of a two-node computing cluster. Comput. Ind. Eng. 2016, 93, 227–235. [Google Scholar] [CrossRef]
- Bouchentouf, A.A.; Yahiaoui, L. On feedback queueing system with reneging and retention of reneged customers, multiple working vacations and Bernoulli schedule vacation interruption. Arab. J. Math. 2017, 6, 1–11. [Google Scholar] [CrossRef]
- Majid, S.; Manoharan, P. Analysis of a M/M/c queue with single and multiple synchronous working vacations. Appl. Appl. Math. Int. J. 2017, 12, 671–694. [Google Scholar]
- Manoharan, P.; Majid, S. Stationary analysis of a multiserver queue with multiple working vacation and impatient customers. Appl. Appl. Math. Int. J. 2017, 12, 658–670. [Google Scholar]
- Sudhesh, R.; Azhagappan, A.; Dharmaraja, S. Transient analysis of M/M/1 queue with working vacation, heterogeneous service and customers’ impatience. RAIRO Oper. Res. 2017, 51, 591–606. [Google Scholar] [CrossRef]
- Majid, S.; Manoharan, P. Impatient customers in an M/M/c queue with single and multiple synchronous working vacations. Pak. J. Stat. Oper. Res. 2018, 14, 571–594. [Google Scholar]
- Majid, S.; Manoharan, P. Analysis of an M/M/1 queue with working vacation and vacation interruption. Appl. Appl. Math. Int. J. 2019, 14, 19–33. [Google Scholar]
- Sun, W.; Li, S.; Wang, Y.; Tian, N. Comparisons of exhaustive and nonexhaustive M/M/1/N queues with working vacation and threshold policy. J. Syst. Sci. Syst. Eng. 2019, 28, 154–167. [Google Scholar] [CrossRef]
- Shekhar, C.; Varshney, S.; Kumar, A. Optimal control of a service system with emergency vacation using bat algorithm. J. Comput. Appl. Math. 2020, 364, 112332. [Google Scholar] [CrossRef]
- Majid, S. Analysis of customer’s impatience in queues with Bernoulli schedule server working vacations and vacation interruption. Afr. Mat. 2022, 33, 1. [Google Scholar] [CrossRef]
- Lv, S.; Wen, J.; Yang, M. The M/M/1 working vacation queueing system with N-policy and different arrival rates. Eng. Lett. 2023, 31, 1–7. [Google Scholar]
- Jyothsna, K.; Kumar, P.V.; Laxmi, P.V. Bat algorithm for optimizing a working vacation queue with impatient clients and secondary service. OPSEARCH 2024, 62, 777–796. [Google Scholar] [CrossRef]
- Latouche, G. Introduction to Matrix Analytic Methods in Stochastic Modeling; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1999. [Google Scholar]
- Wolf, D. Approximation of the invariant probability measure of an infinite stochastic matrix. Adv. Appl. Probab. 1980, 12, 710–726. [Google Scholar] [CrossRef]
- Do, T.V. Comments on “multi-server system with single working vacation”. Appl. Math. Model. 2009, 33, 4435–4437. [Google Scholar] [CrossRef]
- Bertsimas, D.; Nakazato, D. The distributional Little’s law and its applications. Oper. Res. 1995, 43, 298–310. [Google Scholar] [CrossRef]
- Indra; Ruchi. Transient analysis of two-dimensional state Markovian queueing model with working vacation and breakdown. Int. J. Agric. Stat. Sci. 2010, 6, 571–584. [Google Scholar]
- Sudhesh, R.; Raj, L.F. Computational Analysis of Stationary and Transient Distribution of Single Server Queue with Working Vacation. In Proceedings of the 4th ObCom International Conference on Recent Trends in Computing, Communication and Information Technology, Vellore, India, 9–11 December 2011; Volume 269, pp. 480–489. [Google Scholar]
- Yang, D.; Wu, Y. Analysis of a finite-capacity system with working breakdowns and retention of impatient customers. J. Manuf. Syst. 2017, 44, 207–216. [Google Scholar] [CrossRef]
- Ye, Q.; Liu, L. Analysis of MAP/M/1 queue with working breakdowns. Commun. Stat. Theory Methods 2018, 47, 3073–3084. [Google Scholar] [CrossRef]
- Azhagappan, A.; Deepa, T. Variant impatient behavior of a Markovian queue with balking reserved idle time and working vacation. RAIRO Oper. Res. 2020, 54, 783–793. [Google Scholar] [CrossRef]
- Shekhar, C.; Kumar, N.; Gupta, A.; Kumar, A.; Varshney, S. Warm-spare provisioning computing network with switching failure, common cause failure, vacation interruption, and synchronized reneging. Reliab. Eng. Syst. Saf. 2020, 199, 106910. [Google Scholar] [CrossRef]
- Azhagappan, A.; Deepa, T. Transient behavior of a single-server Markovian queue with balking and working vacation interruptions. J. Oper. Res. Soc. China 2021, 9, 321–341. [Google Scholar] [CrossRef]
- Ayyappan, G.; Archana, G. Analysis of MAP/PH1, PH2/2 queueing model with working breakdown, repairs, optional service and balking. Appl. Appl. Math. Int. J. 2023, 18, 1. [Google Scholar]
- Baba, Y. The M/PH/1 queue with working vacations and vacation interruption. J. Syst. Sci. Syst. Eng. 2010, 19, 496–503. [Google Scholar] [CrossRef]
- Sreenivasan, C.; Chakravarthy, S.R.; Krishnamoorthy, A. MAP/PH/1 queue with working vacations, vacation interruptions and N policy. Appl. Math. Model. 2013, 37, 3879–3893. [Google Scholar] [CrossRef]
- Choudhary, A.; Chakravarthy, S.R.; Sharma, D.C. Analysis of MAP/PH/1 queueing system with degrading service rate and phase type vacation. Mathematics 2021, 9, 2387. [Google Scholar] [CrossRef]
- Arulmozhi, N. Analysis of MAP/PH/1 queueing model subject to two-stage vacation policy with imperfect service, setup time, breakdown, delay time, phase type repair and reneging customer. Appl. Appl. Math. Int. J. 2023, 18, 3. [Google Scholar]
- Thakur, S.; Jain, A.; Ahuja, A. Analysis of MAP/PH/1 model with working vacation, working breakdown and two-phase repair. Arab. J. Sci. Eng. 2024, 49, 7431–7451. [Google Scholar] [CrossRef]
- Lin, C.H.; Ke, J.C. Multi-server system with single working vacation. Appl. Math. Model. 2009, 33, 2967–2977. [Google Scholar] [CrossRef]
- Wu, C.H.; Wang, K.H.; Ke, J.C.; Ke, J.B. A heuristic algorithm for the optimization of M/M/s queue with multiple working vacations. J. Ind. Manag. Optim. 2012, 8, 1–17. [Google Scholar] [CrossRef]
- Tian, N.; Li, J.; Zhang, Z. Matrix analytic method and working vacation queues: A survey. Int. J. Inf. Manag. Sci. 2009, 20, 603–633. [Google Scholar]
- Bini, D.A.; Latouche, G.; Meini, B. Numerical Methods for Structured Markov Chains; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Li, T.; Zhang, L.; Gao, S. Performance of an M/M/1 retrial queue with working vacation interruption and classical retrial policy. Adv. Oper. Res. 2016, 2016, 4538031. [Google Scholar] [CrossRef]
- Li, J.; Tian, N.; Zhang, Z.G.; Luh, H.P. Analysis of the M/G/1 queue with exponentially working vacations-a matrix analytic approach. Queueing Syst. 2009, 61, 139–166. [Google Scholar] [CrossRef]
- Wu, D.A.; Takagi, H. M/G/1 queue with multiple working vacations. Perform. Eval. 2006, 63, 654–681. [Google Scholar] [CrossRef]
- Murugan, S.P.B.; Santhi, K. An M/G/1 queue with server breakdown and multiple working vacation. Appl. Appl. Math. Int. J. 2015, 10, 678–693. [Google Scholar]
- Kleiner, I.; Frostig, E.; Perry, D. Busy periods for queues alternating between two modes. Methodol. Comput. Appl. Probab. 2023, 25, 60. [Google Scholar] [CrossRef]
- Afanasyev, G.A. A vacation queue M/G/1 with close-down times. Theory Probab. Its Appl. 2021, 66, 1–14. [Google Scholar] [CrossRef]
- Zhang, M.; Hou, Z. Performance analysis of M/G/1 queue with working vacations and vacation interruption. J. Comput. Appl. Math. 2010, 234, 2977–2985. [Google Scholar] [CrossRef]
- Zhang, M.; Hou, Z. Performance analysis of MAP/G/1 queue with working vacations and vacation interruption. Appl. Math. Model. 2011, 35, 1551–1560. [Google Scholar] [CrossRef]
- Gao, S.; Liu, Z. An M/G/1 queue with single working vacation and vacation interruption under Bernoulli schedule. Appl. Math. Model. 2013, 37, 1564–1579. [Google Scholar] [CrossRef]
- Lee, D.H.; Kim, B.K. A note on the sojourn time distribution of an M/G/1 queue with a single working vacation and vacation interruption. Oper. Res. Perspect. 2015, 2, 57–61. [Google Scholar] [CrossRef][Green Version]
- Saffer, Z.; Telek, M. M/G/1 Queue with Exponential Working Vacation and Gated Service. In Proceedings of the 18th International Conference on Analytical and Stochastic Modeling Techniques and Applications (ASMTA 2011), Venice, Italy, 20–22 June 2011; Lecture Notes in Computer Science 6751. pp. 28–42. [Google Scholar]
- Gao, S.; Yao, Y. An M-X/G/1 queue with randomized working vacations and at most J vacations. Int. J. Comput. Math. 2014, 91, 368–383. [Google Scholar] [CrossRef]
- Luo, C.; Li, W.; Yu, K.; Ding, C. The matrix-form solution for Geo(X)/G/1/N working vacation queue and its application to state-dependent cost control. Comput. Oper. Res. 2016, 67, 63–74. [Google Scholar] [CrossRef]
- Kleiner, I.; Frostig, E.; Perry, D. A decomposition property for an MX/G/1 queue with vacations. Indag. Math. 2023, 34, 973–989. [Google Scholar] [CrossRef]
- Xu, X.L.; Liu, M.X.; Zhao, X.H. The bulk input M[X]/M/1 queue with working vacations. J. Syst. Sci. Syst. Eng. 2009, 18, 358–368. [Google Scholar] [CrossRef]
- Laxmi, P.V.; Rajesh, P.; Kassahun, T.W. Performance measures of variant working vacations on batch arrival queue with server breakdowns. Int. J. Manag. Sci. Eng. Manag. 2019, 14, 53–63. [Google Scholar] [CrossRef]
- Ye, Q. The analysis of M-X/M/1 queue with two-stage vacations policy. Commun. Stat. Theory Methods 2019, 48, 4492–4510. [Google Scholar] [CrossRef]
- Bouchentouf, A.A.; Guendouzi, A. The M-X/M/c Bernoulli feedback queue with variant multiple working vacations and impatient customers: Performance and economic analysis. Arab. J. Math. 2020, 9, 309–327. [Google Scholar] [CrossRef]
- Baba, Y. Analysis of a GI/M/1 queue with multiple working vacations. Oper. Res. Lett. 2005, 33, 201–209. [Google Scholar] [CrossRef]
- Banik, A.D.; Gupta, U.C.; Pathak, S.S. On the GI/M/1/N queue with multiple working vacations—Analytic analysis and computation. Appl. Math. Model. 2007, 31, 1701–1710. [Google Scholar] [CrossRef]
- Chae, K.C.; Lim, D.E.; Yang, W.S. The GI/M/1 queue and the GI/Geo/1 queue both with single working vacation. Perform. Eval. 2009, 66, 356–367. [Google Scholar] [CrossRef]
- Li, J.; Tian, N. Performance analysis of a GI/M/1 queue with single working vacation. Appl. Math. Comput. 2011, 217, 4960–4971. [Google Scholar] [CrossRef]
- Zhang, M.; Hou, Z. Steady state analysis of the GI/M/1/N queue with a variant of multiple working vacations. Comput. Ind. Eng. 2011, 61, 1296–1301. [Google Scholar] [CrossRef]
- Goswami, V. Study of customers’ impatience in a GI/M/1/N queue with working vacations. Int. J. Manag. Sci. Eng. Manag. 2015, 10, 144–154. [Google Scholar] [CrossRef]
- Yang, D.; Cho, Y. Analysis of the N-policy GI/M/1/K queueing systems with working breakdowns and repairs. Comput. J. 2019, 62, 130–143. [Google Scholar] [CrossRef]
- Li, J.H.; Tian, N.S.; Ma, Z.Y. Performance analysis of GI/M/1 queue with working vacations and vacation interruption. Appl. Math. Model. 2008, 32, 2715–2730. [Google Scholar] [CrossRef]
- Tao, L.; Liu, Z.; Wang, Z. The GI/M/1 queue with start-up period and single working vacation and Bernoulli vacation interruption. Appl. Math. Comput. 2011, 218, 4401–4413. [Google Scholar] [CrossRef]
- Laxmi, P.V.; Demie, S. Performance analysis of renewal input (a, c, b) policy queue with multiple working vacations and change over times. J. Ind. Manag. Optim. 2014, 10, 839–857. [Google Scholar] [CrossRef]
- Tamrakar, G.K.; Banerjee, A.; Gupta, U.C. Analysis of batch size-dependent bulk service queue with multiple working vacation. Int. J. Comput. Math. Comput. Syst. Theory 2022, 7, 149–171. [Google Scholar] [CrossRef]
- Panda, G.; Banik, A.D.; Guha, D. Stationary analysis and optimal control under multiple working vacation policy in a GI/M ((a,b))/1 queue. J. Syst. Sci. Complex. 2018, 31, 1003–1023. [Google Scholar] [CrossRef]
- Ouazine, S.; Abbas, K. Development of computational algorithm for multiserver queue with renewal input and synchronous vacation. Appl. Math. Model. 2016, 40, 1137–1156. [Google Scholar] [CrossRef]
- Do, T.V. M/M/1 retrial queue with working vacations. Acta Inform. 2010, 47, 67–75. [Google Scholar] [CrossRef]
- Tao, L.; Liu, Z.; Wang, Z. M/M/1 retrial queue with collisions and working vacation interruption under N-policy. RAIRO Oper. Res. 2012, 46, 355–371. [Google Scholar] [CrossRef]
- Tao, L.; Zhang, L.; Gao, S. M/M/1 retrial queue with working vacation interruption and feedback under N-policy. J. Appl. Math. 2014, 2014, 414739. [Google Scholar] [CrossRef]
- Li, J.; Li, T. An M/M/1 retrial queue with working vacation, orbit search and balking. Eng. Lett. 2019, 27, 97–102. [Google Scholar]
- Manoharan, P.; Murugan, S.P.B.; Sobanappriya, A. Analysis of a Markovian retrial queue with working vacation under N-control pattern. Commun. Math. Appl. 2022, 13, 851–863. [Google Scholar] [CrossRef]
- Gao, S.; Wang, J.; Li, W.W. An M/G/1 retrial queue with general retrial times, working vacations and vacation interruption. Asia-Pac. J. Oper. Res. 2014, 31, 1440006. [Google Scholar] [CrossRef]
- Murugan, S.P.B.; Santhi, K. An M/G/1 retrial queue with single working vacation. Appl. Appl. Math. Int. J. 2017, 12, 1–22. [Google Scholar]
- Li, T.; Zhang, L.; Gao, S. An M/G/1 retrial queue with single working vacation under Bernoulli schedule. RAIRO Oper. Res. 2020, 54, 471–488. [Google Scholar] [CrossRef]
- Liu, T.H.; Chiou, K.C.; Chen, C.M.; Chang, F.M. Multiserver retrial queue with two-way communication and synchronous working vacation. Mathematics 2024, 12, 1163. [Google Scholar] [CrossRef]
- Ayyappan, G.; Thamizhselvi, P.; Somasundaram, B. Analysis of M-[X1],M-[X2]/G(1),G(2)/1 retrial queueing system with priority services, working breakdown, collision, Bernoulli vacation, immediate feedback, starting failure and repair. Appl. Appl. Math. Int. J. 2019, 14, 1–18. [Google Scholar]
- Murugan, S.P.B.; Vijaykrishnaraj, R. A Bulk Arrival Retrial Queue with Second Optional Service and Exponentially Distributed Multiple Working Vacation. In Proceedings of the International Conference on Applications of Fluid Dynamics (ICAFD), Miyagi, Japan, 6–8 November 2019; Volume 2177. [Google Scholar] [CrossRef]
- Jain, M.; Kumar, A. Unreliable server M[X]/G/1 retrial feedback queue with balking, working vacation and vacation interruption. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2023, 93, 57–73. [Google Scholar] [CrossRef]
- Majid, S.; Bouchentouf, A.A.; Guendouzi, A. Analysis and optimisation of a M/M/1/WV queue with Bernoulli schedule vacation interruption and customer’s impatience. Acta Univ. Sapientiae 2021, 13, 367–395. [Google Scholar] [CrossRef]
- Liu, T.H.; Hsu, H.Y.; Ke, J.C.; Chang, F.M. Preemptive priority Markovian queue subject to server breakdown with imperfect coverage and working vacation interruption. Computation 2023, 11, 89. [Google Scholar] [CrossRef]
- Kalidass, K.; Kasturi, R. A queue with working breakdowns. Comput. Ind. Eng. 2012, 63, 779–783. [Google Scholar] [CrossRef]
- Liu, Z.; Song, Y. The M-X/M/1 queue with working breakdown. RAIRO Oper. Res. 2014, 48, 399–413. [Google Scholar] [CrossRef]
- Liou, C. Markovian queue optimisation analysis with an unreliable server subject to working breakdowns and impatient customers. Int. J. Syst. Sci. 2015, 46, 2165–2182. [Google Scholar] [CrossRef]
- Yang, D.Y.; Chung, C.H.; Wu, C.H. Sojourn times in a Markovian queue with working breakdowns and delayed working vacations. Comput. Ind. Eng. 2021, 156, 107239. [Google Scholar] [CrossRef]
- Seenivasan, M.; Chandiraleka, S. Single Server Queueing Model with Multiple Working Vacation and with Breakdown. In Proceedings of the 2nd International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 21–22 April 2022. [Google Scholar] [CrossRef]
- Jeyakumar, S.; Senthilnathan, B. Modelling and analysis of a bulk service queueing model with multiple working vacations and server breakdown. RAIRO Oper. Res. 2017, 51, 485–508. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, W.; Hu, L. Performance evaluation and analysis of a discrete queue system with multiple working vacations and non-preemptive priority. J. Ind. Manag. Optim. 2020, 16, 1135–1148. [Google Scholar] [CrossRef]
- Li, J.H.; Tian, N.S.; Liu, W.Y. Discrete-time GI/Geo/1 queue with multiple working vacations. Queueing Syst. 2007, 56, 53–63. [Google Scholar] [CrossRef]
- Lim, D.E.; Lee, D.H.; Yang, W.S.; Chae, K.C. Analysis of the GI/Geo/1 queue with N-policy. Appl. Math. Model. 2013, 37, 4643–4652. [Google Scholar] [CrossRef]
- Laxmi, P.; Suchitra, V. Discrete-time renewal input state dependent queue with working vacations and change over time. OPSEARCH 2015, 52, 285–306. [Google Scholar] [CrossRef]
- Yi, X.W.; Kim, J.D.; Choi, D.W.; Chae, K.C. The Geo/G/1 queue with disasters and multiple working vacations. Stoch. Model. 2007, 23, 537–549. [Google Scholar] [CrossRef]
- Li, J.H.; Liu, W.Q.; Tian, N. Steady-state analysis of a discrete-time batch arrival queue with working vacations. Perform. Eval. 2010, 67, 897–912. [Google Scholar] [CrossRef]
- Li, J.H. Analysis of the discrete-time Geo/G/1 working vacation queue and its application to network scheduling. Comput. Ind. Eng. 2013, 65, 594–604. [Google Scholar] [CrossRef]
- Cheng, J.; Tang, Y.; Yu, M. The discrete-time bulk-service Geo/Geo/1 queue with multiple working vacations. J. Appl. Math. 2013, 2013, 587269. [Google Scholar] [CrossRef]
- Goswami, V.; Panda, G. Synchronized abandonment in discrete-time renewal input queues with vacations. J. Ind. Manag. Optim. 2022, 18, 4373–4391. [Google Scholar] [CrossRef]
- Goswami, C.; Selvaraju, N. The discrete-time MAP/PH/1 queue with multiple working vacations. Appl. Math. Model. 2010, 34, 931–946. [Google Scholar] [CrossRef]
- Ye, Q. Algorithmic computation of MAP/PH/1 queue with finite system capacity and two-stage vacations. J. Ind. Manag. Optim. 2020, 16, 2459–2477. [Google Scholar] [CrossRef]
- Wang, S.; Xu, X. Equilibrium strategies of the fluid queue with working vacation. Oper. Res. 2021, 21, 1211–1228. [Google Scholar] [CrossRef]
- Cai, S.J.; Ye, Q.Q.; Liu, Y.F. Equilibrium strategies in a fluid queue with working vacations. J. Oper. Res. Soc. China 2023, 1–25. [Google Scholar] [CrossRef]
- Xu, X.; Geng, J.; Liu, M.; Guo, H. Stationary analysis for the fluid model driven by the M/M/c working vacation queue. J. Math. Anal. Appl. 2013, 403, 423–433. [Google Scholar] [CrossRef]
- Vijayashree, K.V.; Anjuka, A. Fluid queue driven by an M/M/1 queue subject to Bernoulli-schedule-controlled vacation and vacation interruption. Adv. Oper. Res. 2016, 2016, 2673017. [Google Scholar] [CrossRef]
- Yu, S.; Liu, Z.; Wu, J. Fluid queue driven by a multi-server queue with multiple vacations and vacation interruption. RAIRO Oper. Res. 2017, 51, 931–944. [Google Scholar] [CrossRef]
- Vijayashree, K.V.; Anjuka, A. Fluid Queue Driven by an M/M/1 Queue Subject to Working Vacation and Impatience. In Proceedings of the 3rd International Conference on Computational Intelligence, Cyber Security, and Computational Models (ICC3), Coimbatore, India, 14–16 December 2017; Communications in Computer and Information Science 844. pp. 172–182. [Google Scholar] [CrossRef]
- Vijayashree, K.V.; Anjuka, A. Stationary analysis of a fluid queue driven by an M/M/1 queue with working vacation. Qual. Technol. Quant. Manag. 2018, 15, 187–208. [Google Scholar] [CrossRef]
- Xu, X.; Wang, X.; Song, X.; Li, X. Fluid model modulated by an M/M/1 working vacation queue with negative customer. Acta Math. Appl. Sin. Engl. Ser. 2018, 34, 404–415. [Google Scholar] [CrossRef]
- Xu, X.; Wang, H. Analysis of fluid model modulated by an M/PH/1 working vacation queue. J. Syst. Sci. Syst. Eng. 2019, 28, 132–140. [Google Scholar] [CrossRef]
- Li, L.; Wang, J.; Zhang, F. Equilibrium customer strategies in Markovian queues with partial breakdowns. Comput. Ind. Eng. 2013, 66, 751–757. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, J.; Liu, B. Equilibrium balking strategies in Markovian queues with working vacations. Appl. Math. Model. 2013, 37, 8264–8282. [Google Scholar] [CrossRef]
- Sun, W.; Li, S. Equilibrium and optimal behavior of customers in Markovian queues with multiple working vacations. TOP 2014, 22, 694–715. [Google Scholar] [CrossRef]
- Sun, W.; Li, S.; Li, Q. Equilibrium balking strategies of customers in Markovian queues with two-stage working vacations. Appl. Math. Comput. 2014, 248, 195–214. [Google Scholar] [CrossRef]
- Li, K.; Wang, J.; Ren, Y.; Chang, J. Equilibrium joining strategies in M/M/1 queues with working vacation and vacation interruptions. RAIRO Oper. Res. 2016, 50, 451–471. [Google Scholar] [CrossRef]
- Tian, R.; Hu, L.; Wu, X. Equilibrium and optimal strategies in M/M/1 queues with working vacations and vacation interruptions. Math. Probl. Eng. 2016, 2016, 9746962. [Google Scholar] [CrossRef]
- Panda, G.; Goswami, V.; Banik, A.D. Equilibrium behaviour and social optimization in Markovian queues with impatient customers and variant of working vacations. RAIRO Oper. Res. 2017, 51, 685–707. [Google Scholar] [CrossRef]
- Sun, W.; Li, S.; Tian, N. Equilibrium and optimal balking strategies of customers in unobservable queues with double adaptive working vacations. Qual. Technol. Quant. Manag. 2017, 14, 94–113. [Google Scholar] [CrossRef]
- Ma, Q.; Li, J.; Liu, W. Social optimization in M/M/1 queue with working vacation and N-policy. RAIRO Oper. Res. 2018, 52, 439–452. [Google Scholar] [CrossRef]
- Xu, B.; Xu, X. Equilibrium strategic behavior of customers in the M/M/1 queue with partial failures and repairs. Oper. Res. 2018, 18, 273–292. [Google Scholar] [CrossRef]
- Lee, D.H. Equilibrium balking strategies in Markovian queues with a single working vacation and vacation interruption. Qual. Technol. Quant. Manag. 2019, 16, 355–376. [Google Scholar] [CrossRef]
- Ma, Q.; Zhao, Y.Q.; Liu, W.; Li, J. Customer strategic joining behavior in Markovian queues with working vacations and vacation interruptions under Bernoulli schedule. Asia-Pac. J. Oper. Res. 2019, 36, 1950003. [Google Scholar] [CrossRef]
- Wang, H.; Xu, X.; Wang, S. Equilibrium customers strategies in the Markovian working vacation queue with setup times. Int. J. Comput. Sci. Math. 2019, 10, 443–458. [Google Scholar] [CrossRef]
- Do, N.H.; Do, T.V.; Melikov, A. Equilibrium customer behavior in the M/M/1 retrial queue with working vacations and a constant retrial rate. Oper. Res. 2020, 20, 627–646. [Google Scholar] [CrossRef]
- Tian, R.; Wang, Y. Optimal strategies and pricing analysis in M/M/1 queues with a single working vacation and multiple vacations. RAIRO Oper. Res. 2020, 54, 1593–1612. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, R. Strategic analysis in Markovian queues with a single working vacation and multiple vacations. Int. J. Innov. Comput. Inf. Control 2020, 16, 349–366. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, L.; Shao, Y.; Zhao, Y.Q. Joining strategies under two kinds of games for a multiple vacations retrial queue with N-policy and breakdowns. AIMS Math. 2021, 6, 9075–9099. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J. Strategic joining and information disclosing in Markovian queues with an unreliable server and working vacations. Qual. Technol. Quant. Manag. 2021, 18, 298–325. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, X. Equilibrium analysis of cloud user request based on the Markov queue with variable vacation and vacation interruption. RAIRO Oper. Res. 2021, 55, 2807–2825. [Google Scholar] [CrossRef]
- Panda, G.; Goswami, V. Equilibrium joining strategies of positive customers in a Markovian queue with negative arrivals and working vacations. Methodol. Comput. Appl. Probab. 2022, 24, 1439–1466. [Google Scholar] [CrossRef]
- Tian, R.; Zhang, Z.G.; Su, S. On Markovian queues with single working vacation and Bernoulli interruptions. Probab. Eng. Inf. Sci. 2022, 36, 616–643. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, L.; Zhao, Y.Q.; Li, L.; Xu, W. Joining strategies of noncooperative and cooperative in a single server retrial queue with N-policy and multiple server vacations. Commun. Stat. Theory Methods 2023, 52, 1076–1100. [Google Scholar] [CrossRef]
- Sun, W.; Xie, X.; Zhang, Z.; Li, S. Equilibrium balking behavior of customers and regulation measures in a multi-server queue with threshold policy. Qual. Technol. Quant. Manag. 2024, 22, 526–552. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Zhang, G. The effect of information on the strategic behavior in a Markovian queue with catastrophes and working vacations. Qual. Technol. Quant. Manag. 2024, 21, 688–721. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, X.; Liu, M. Optimal strategy analysis of a Markovian queue with variable vacation and vacation interruptions under unobservable cases. Qual. Technol. Quant. Manag. 2024, 21, 556–586. [Google Scholar] [CrossRef]
- Yu, M.; Alfa, A.S. Strategic queueing behavior for individual and social optimization in managing discrete time working vacation queue with Bernoulli interruption schedule. Comput. Oper. Res. 2016, 73, 43–55. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, P.; Yue, W. Performance analysis and optimization of a pseudo-fault Geo/Geo/1 repairable queueing system with N-policy, setup time and multiple working vacations. J. Ind. Manag. Optim. 2017, 13, 1467–1481. [Google Scholar] [CrossRef]
- Guha, D.; Goswami, V.; Banik, A.D. Equilibrium balking strategies in renewal input batch arrival queues with multiple and single working vacation. Perform. Eval. 2015, 94, 1–24. [Google Scholar] [CrossRef]
- Panda, G.; Goswami, V.; Banik, A.D.; Guha, D. Equilibrium balking strategies in renewal input queue with Bernoulli-schedule controlled vacation and vacation interruption. J. Ind. Manag. Optim. 2016, 12, 851–878. [Google Scholar] [CrossRef]
- Xu, F.; Tian, R.; Shao, Q. Optimal pricing strategy in an unreliable M/G/1 retrial queue with Bernoulli preventive maintenance. RAIRO Oper. Res. 2023, 57, 2639–2657. [Google Scholar] [CrossRef]
- Li, J.; Tiam, N.; Chen, H.; Lu, D. Adaptive Service Analysis for EPON Base on Working Vacation Queueing Model. In Proceedings of the 11th IEEE Singapore International Conference on Communication Systems, Guangzhou, China, 19–21 November 2008; pp. 693–697. [Google Scholar] [CrossRef]
- Zhu, Y.; Ma, Y.; Zheng, D.; Zhao, L.; Han, X. Research on Passive Optical Network Based on Ant Colony Algorithms for Bandwidth Distribution in Uplink Direction. In Proceedings of the International Conference on Web Information Systems and Mining, Shanghai, China, 7–8 November 2009; Lecture Notes in Computer Science 5854. pp. 320–327. [Google Scholar]
- Guha, D.; Banik, A.D. On the renewal input batch-arrival queue under single and multiple working vacation policy with application to EPON. INFOR Inf. Syst. Oper. Res. 2013, 51, 175–191. [Google Scholar] [CrossRef]
- Phung-Duc, T. Single-Server Systems with Power-Saving Modes. In Proceedings of the Analytical and Stochastic Modelling Techniques and Applications (ASMTA 2015), Albena, Bulgaria, 26–29 May 2015; Lecture Notes in Computer Science 9081. pp. 158–172. [Google Scholar] [CrossRef]
- Yu, X.; Ma, Z.; Guo, S.; Chen, L. Performance analysis of wireless communication networks with threshold activation process and interference signals. Int. J. Commun. Netw. Distrib. Syst. 2020, 25, 78–94. [Google Scholar] [CrossRef]
- Ma, Z.; Yu, X.; Guo, S.; Zhang, Y. Analysis of wireless sensor networks with sleep mode and threshold activation. Wirel. Netw. 2021, 27, 1431–1443. [Google Scholar] [CrossRef]
- Shapique, A.M.; Sudhesh, R.; Dharmaraja, S. Transient analysis of a modified differentiated vacation queueing system for energy-saving in WiMAX. Methodol. Comput. Appl. Probab. 2024, 26, 23. [Google Scholar] [CrossRef]
- Ouyang, Y.; Chiang, Y.; Hsu, C.; Yi, G. An optimal control policy to realize green cloud systems with SLA-awareness. J. Supercomput. 2014, 69, 1284–1310. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Do, T.V. A Model for a Computing Cluster with Two Asynchronous Servers. In Proceedings of the Advanced Computational Methods for Knowledge Engineering (ICCSAMA 2017), Berlin, Germany, 30 June–1 July 2017; Volume 629, pp. 197–211. [Google Scholar] [CrossRef]
- Sahoo, C.N.; Goswami, V. Cost and energy optimisation of cloud data centres through dual VM modes—Activation and passivation. Int. J. Commun. Netw. Distrib. Syst. 2017, 18, 371–389. [Google Scholar] [CrossRef]
- Qin, B.; Jin, S.; Zhao, D. Energy efficient virtual machine scheduling strategy with semi-sleep mode on the cloud platform. Int. J. Innov. Comput. Inf. Control 2019, 15, 337–349. [Google Scholar] [CrossRef]
- Guo, S.; Ma, Z.; Yu, X.; Chen, L. An energy saving strategy based on M/M/c queueing model with preemptive priority and asynchronous working vacation. Int. J. Auton. Adapt. Commun. Syst. 2022, 15, 106–125. [Google Scholar] [CrossRef]
- Liu, F.; Ma, Z.; Si, Q.; Yan, M. Performance analysis of peer-to-peer networks based on two-phase service queuing theory. Int. J. Commun. Netw. Distrib. Syst. 2021, 27, 349–365. [Google Scholar] [CrossRef]
- Wang, S.; Ma, Z.; Wang, R.; Fang, W. Performance analysis of a queueing system based on working vacation with repairable fault in the P2P network. J. Supercomput. 2023, 79, 12902–12923. [Google Scholar] [CrossRef]
- Shen, Y.; Ma, Z.; Jiang, Z.; Li, Y.; Qin, G. Performance analysis of P2P network based on differentiated service Geo/Geo/1 + 1 queue. Clust. Comput. 2024, 27, 9837–9849. [Google Scholar] [CrossRef]
- Yang, D.; Tsao, C. Reliability and availability analysis of standby systems with working vacations and retrial of failed components. Reliab. Eng. Syst. Saf. 2019, 182, 46–55. [Google Scholar] [CrossRef]
- Gao, S.; Wang, J.; Zhang, J. Reliability analysis of a redundant series system with common cause failures and delayed vacation. Reliab. Eng. Syst. Saf. 2023, 239, 109467. [Google Scholar] [CrossRef]
- Yang, D.Y.; Wu, C.H. Evaluation of the availability and reliability of a standby repairable system incorporating imperfect switchovers and working breakdowns. Reliab. Eng. Syst. Saf. 2021, 207, 107366. [Google Scholar] [CrossRef]
- Ambika, K.; Vijayashree, K.V.; Janani, B. Modelling and analysis of production management system using vacation queueing theoretic approach. Appl. Math. Comput. 2024, 479, 128856. [Google Scholar] [CrossRef]
- Kumar, P.; Jain, M.; Meena, R.K. Transient analysis and reliability modeling of fault-tolerant system operating under admission control policy with double retrial features and working vacation. ISA Trans. 2023, 134, 183–199. [Google Scholar] [CrossRef]
- Harini, R.; Indhira, K. Stochastic modelling and meta heuristic optimization of a batch production system. J. King Saud Univ. Sci. 2024, 36, 103308. [Google Scholar] [CrossRef]
- Janani, B.; Vijayashree, K.V. Analysis of an unreliable server with soft failures and working vacations and its application in a smart healthcare system. Results Control Optim. 2023, 10, 100211. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fiems, D. Queues with Working Vacations: A Survey. Mathematics 2025, 13, 1894. https://doi.org/10.3390/math13111894
Fiems D. Queues with Working Vacations: A Survey. Mathematics. 2025; 13(11):1894. https://doi.org/10.3390/math13111894
Chicago/Turabian StyleFiems, Dieter. 2025. "Queues with Working Vacations: A Survey" Mathematics 13, no. 11: 1894. https://doi.org/10.3390/math13111894
APA StyleFiems, D. (2025). Queues with Working Vacations: A Survey. Mathematics, 13(11), 1894. https://doi.org/10.3390/math13111894






