Basins of Attraction for Third-Order Sigmoid Beverton Holt Difference Equation
Abstract
1. Introduction
2. Preliminaries
- 1.
- f is increasing in each of its arguments.
- 2.
- f satisfies the negative feedback condition:for all .
- i.
- There exists a fixed point of T in .
- ii.
- If T is strongly order preserving, then there exists a fixed point in , which is stable relative to .
- iii.
- If there is only one fixed point in , then it is a global attractor in and therefore asymptotically stable relative to .
- i.
- The function ϕ is continuous.
- ii.
- .
- iii.
- consists of non-comparable points.
- iv.
- If T is differentiable on R and such that the n-th column of has positive entries for , then ϕ is Lipschitz on .
3. Local Dynamics
- Ifthen is the unique equilibrium. Also, , so the equilibrium is locally and asymptotically stable.
- If , then there are two equilibrium points, and . Then is locally asymptotically stable, and is the non-hyperbolic equilibrium point.
- Ifthen there are three equilibrium points,and
4. Global Dynamics
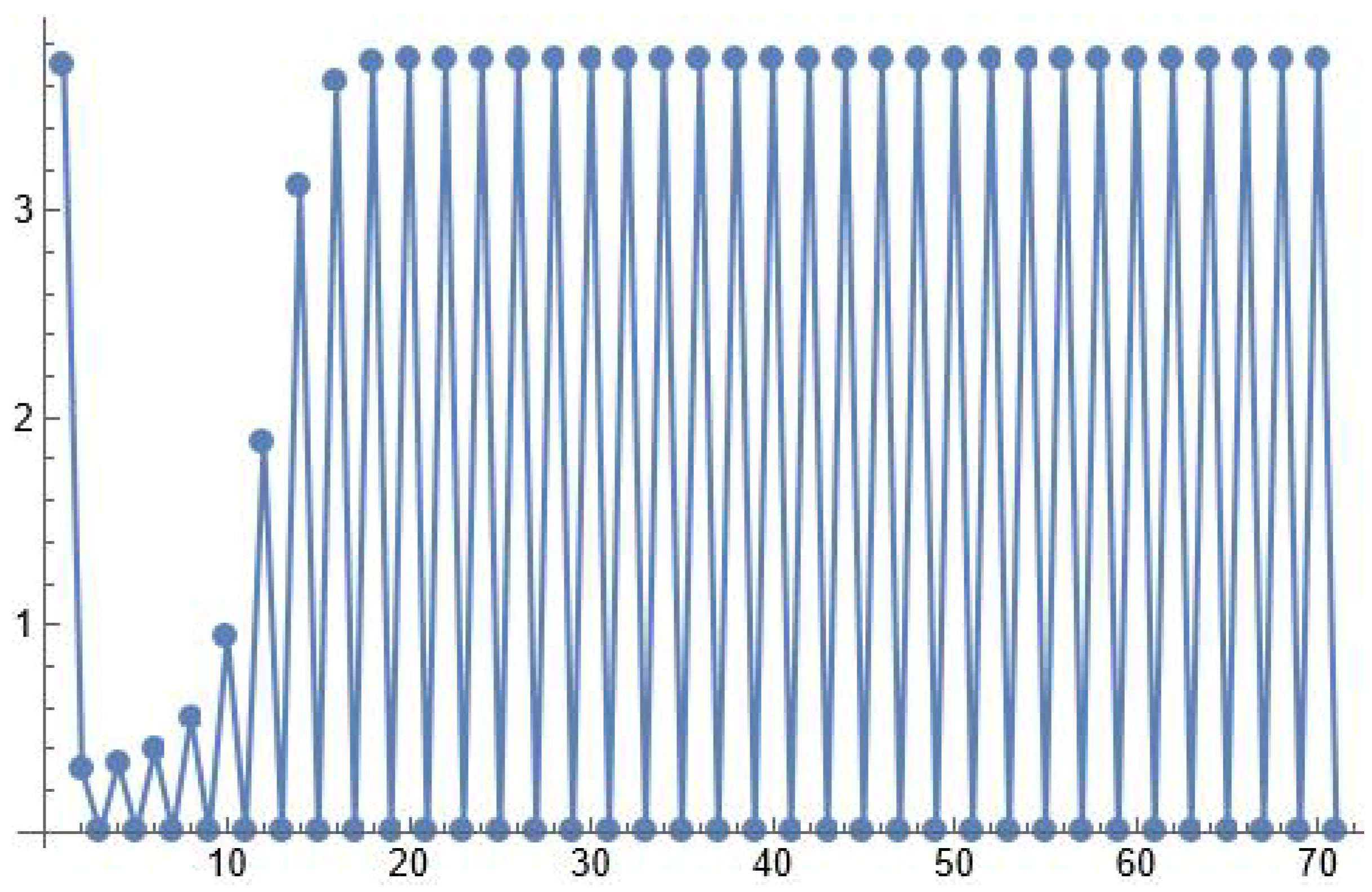
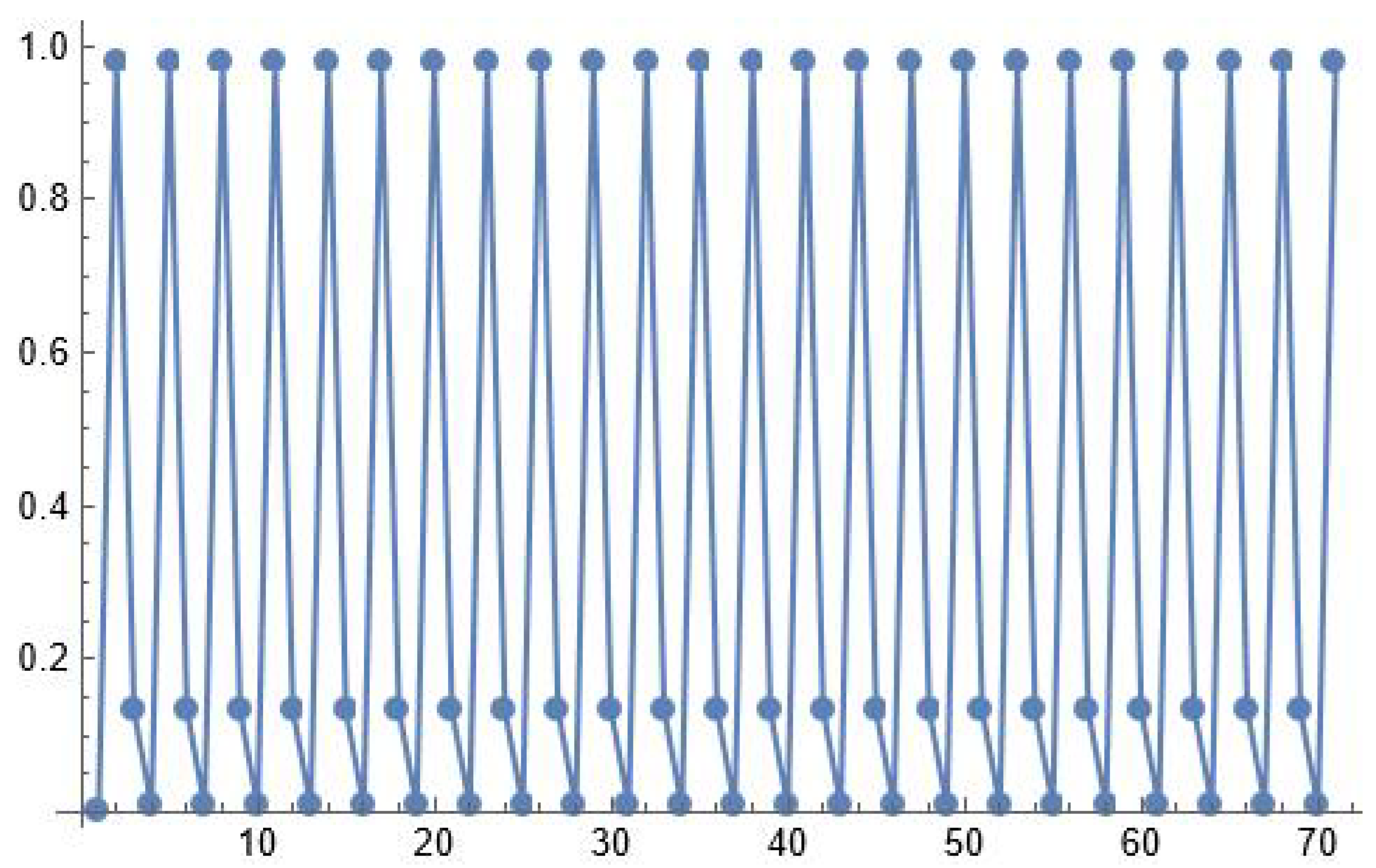
5. Existence of Periodic Solutions of Periods Two and Three
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bilgin, A.; Kulenović, M.R.S.; Pilav, E. Basins of Attraction of Period-Two Solutions of Monotone Difference Equations. Adv. Differ. Equ. 2016, 2016, 25. [Google Scholar] [CrossRef]
- Allen, L. An Introduction to Mathematical Biology; Pearson: Boston, MA, USA, 2006. [Google Scholar]
- Thieme, H.R. Mathematics in Population Biology; Princeton Series in Theoretical and Computational Biology; Princeton University Press: Princeton, NJ, USA, 2003; xx+543p. [Google Scholar]
- Camouzis, E.; Ladas, G. Dynamics of Third-Order Rational Difference Equations with Open Problems and Conjectures; Advances in Discrete Mathematics and Applications; Chapman & Hall/CRC: Boca Raton, FL, USA, 2008; Volume 5. [Google Scholar]
- Elaydi, S.N.; Cushing, J.M. Discrete Mathematical Models in Population Biology–Ecological, Epidemic, and Evolutionary Dynamics; Springer Undergraduate Texts in Mathematics and Technology; Springer: Cham, Switzerland, 2024; xiv+481p. [Google Scholar]
- Camouzis, E.; Ladas, G.; Quinn, E.P. On third-order rational difference equations. II. J. Differ. Equ. Appl. 2004, 10, 1041–1047. [Google Scholar]
- Camouzis, E.; Chatterjee, E.; Ladas, G.; Quinn, E.P. On third-order rational difference equations. III. J. Difference Equ. Appl. 2004, 12, 1119–1127. [Google Scholar]
- Camouzis, E.; Ladas, G. On third-order rational difference equations. V. J. Differ. Equ. Appl. 2005, 11, 553–562. [Google Scholar] [CrossRef]
- Camouzis, E.; Ladas, G.; Quinn, E.P. On third-order rational difference equations. VI. J. Differ. Equ. Appl. 2005, 11, 759–777. [Google Scholar] [CrossRef]
- Camouzis, E.; Ladas, G. On third-order rational difference equations. I. J. Difference Equ. Appl. 2008, 14, 333–343. [Google Scholar]
- Kulenović, M.R.S.; Nurkanović, Z. Global behavior of a three-dimensional linear fractional system of difference equations. J. Math. Anal. Appl. 2005, 310, 673–689. [Google Scholar] [CrossRef][Green Version]
- Hess, P. Periodic-Parabolic Boundary Value Problems and Positivity; Pitman Research Notes in Mathematics Series; Longman Scientific and Technical, Harlow; John Wiley and Sons, Inc.: New York, NY, USA, 1991; Volume 247. [Google Scholar][Green Version]
- Hirsch, M.W.; Smith, H. Competitive and Cooperative Systems: Mini-Review. In Positive Systems (Rome, 2003); Lecture Notes in Control and Information Science; Springer: Berlin/Heidelberg, Germany, 2003; Volume 294, pp. 183–190. [Google Scholar][Green Version]
- Hirsch, M.W.; Smith, H. Monotone maps: A review. J. Differ. Equ. Appl. 2005, 11, 379–398. [Google Scholar] [CrossRef]
- Hirsch, M.W.; Smith, H. Monotone Dynamical Systems. In Handbook of Differential Equations: Ordinary Differential Equations; Elsevier B.V.: Amsterdam, The Netherlands, 2005; Volume II, pp. 239–357. [Google Scholar]
- Cima, A.; Gasull, A.; Manosa, V. Asymptotic Stability for Block Triangular Maps. Sarajevo J. Math. 2022, 18, 25–44. [Google Scholar] [CrossRef]
- Elaydi, S. An Introduction to Difference Equations, 3rd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Hale, J.K.; Kocak, H. Dynamics and Bifurcations; Texts in Applied Mathematics; Springer: New York, NY, USA, 1991; Volume 3. [Google Scholar]
- Kocić, V.; Ladas, G. Global Behavior of Nonlinear Difference Equations of Higher Order with Applications; Mathematics and its Applications; Kluwer Academic Publishers Group: Dordrecht, The Switzerland, 1993; Volume 256. [Google Scholar]
- Lakshmikantham, V.; Trigiante, D. Theory of Difference Equations: Numerical Methods and Applications, 2nd ed.; Monographs and Textbooks in Pure and Applied Mathematics; Marcel Dekker, Inc.: New York, NY, USA, 2002; Volume 251. [Google Scholar]
- Robinson, C. Stability, Symbolic Dynamics, and Chaos; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Wiggins, S. Introduction to Applied Nonlinear Dynamical Systems and Chaos, 2nd ed.; Texts in Applied Mathematics; Springer: New York, NY, USA, 2003; Volume 2. [Google Scholar]
- Kulenović, M.R.S.; Marcotte, J.; Merino, O. Cones for Coordinate-wise Monotone Functions and Dynamics of Monotone Maps. J. Differ. Equ. Appl. 2025. submitted. [Google Scholar]
- Janowski, E.J.; Kulenović, M.R.S. Attractivity and global stability for linearizable difference equations. Comput. Math. Appl. 2009, 57, 1592–1607. [Google Scholar] [CrossRef][Green Version]
- Cushing, J.M. An evolutionary Beverton-Holt model. In Theory and Applications of Difference Equations and Discrete Dynamical Systems; Springer Proc. Math. Stat., 102; Springer: Berlin/Heidelberg, Germany, 2014; pp. 127–141. [Google Scholar][Green Version]
- Cushing, J.M. One Dimensional Maps as Population and Evolutionary Dynamic Models. In Applied Analysis in Biological and Physical Sciences; Springer Proceedings in Mathematics & Statistics; Springer: New Delhi, India, 2016; Volume 186, pp. 41–62. [Google Scholar][Green Version]
- Cushing, J.M. Difference equations as models of evolutionary population dynamics. J. Biol. Dyn. 2019, 13, 103–127. [Google Scholar] [CrossRef] [PubMed]
- Clark, C.W. A delayed recruitment model of population dynamics with an application to baleen whale populations. J. Math. Biol. 1976, 3, 381–391. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kulenović, M.R.S.; Sullivan, R. Basins of Attraction for Third-Order Sigmoid Beverton Holt Difference Equation. Mathematics 2025, 13, 2990. https://doi.org/10.3390/math13182990
Kulenović MRS, Sullivan R. Basins of Attraction for Third-Order Sigmoid Beverton Holt Difference Equation. Mathematics. 2025; 13(18):2990. https://doi.org/10.3390/math13182990
Chicago/Turabian StyleKulenović, Mustafa R. S., and Ryan Sullivan. 2025. "Basins of Attraction for Third-Order Sigmoid Beverton Holt Difference Equation" Mathematics 13, no. 18: 2990. https://doi.org/10.3390/math13182990
APA StyleKulenović, M. R. S., & Sullivan, R. (2025). Basins of Attraction for Third-Order Sigmoid Beverton Holt Difference Equation. Mathematics, 13(18), 2990. https://doi.org/10.3390/math13182990






