A Collaborative Optimization Scheme for Beamforming and Power Control in MIMO-Based Internet of Vehicles

Abstract

Driven by advancements in communication technology, the Internet of Vehicles (IoV) has gained significant importance. Its capability for real-time information exchange and processing substantially enhances data transmission performance within multi-node distributed systems. Among core physical layer transmission technologies, beamforming and power allocation are crucial for optimizing system efficiency. However, the real-time joint optimization of the transmitter, receiver, and power allocation in MIMO-based IoV systems remains insufficiently addressed in existing research. To bridge this gap, this paper proposes a framework for the real-time joint optimization of beamforming and power allocation, aiming to maximize transmission efficiency while satisfying constant modulus constraints and power limitations. The proposed framework decomposes the problem and utilizes the CVX library to obtain a local optimum for the joint scheme. The simulation results show that compared with traditional beamforming methods, this scheme has better performance in multiple indicators, increasing the transmission rate of the system by 43%, having faster convergence speed, and improving spectral efficiency. Thus, this study achieves real-time joint optimization of MIMO beamforming and power allocation for IoV scenarios, providing crucial technical support for related designs.

1. Introduction

With the deep integration of next-generation information and communication technologies and the automotive industry, the Internet of Vehicles, as the core component of intelligent transportation systems, is accelerating the transformation of the global automotive industry toward connectivity and intelligence [1,2].

However, the exponential growth in the number of users in next-generation Internet of Vehicles systems presents significant challenges to real-time transmission efficiency. In this context, beamforming and power optimization are regarded as effective solutions to address transmission capacity constraints at the physical layer [3,4]. The synergistic optimization of both further strengthens system performance. Beamforming concentrates energy in the spatial dimension, thereby reducing the baseline power required to achieve the target transmission rate; power optimization dynamically adjusts resource allocation based on this, yielding dual improvements in energy efficiency and transmission rate. This joint scheme provides essential technical support for the efficient and reliable operation of the Internet of Vehicles.

Current research primarily focuses on two directions: beamforming design based on optimization theory and power allocation optimization driven by deep learning [5,6,7,8,9,10]. In the domain of beamforming, Ref. [11] proposed a robust beamforming method based on semidefinite relaxation (SDR), modeling imperfect CSI via a Gaussian channel uncertainty model, which significantly reduces the user outage probability. Ref. [12] employs a distributed amplify-and-forward relay architecture to design robust beamforming for multi-user peer-to-peer communication, balancing the signal-to-interference-plus-noise ratio (SINR) through a statistical CSI error model, thereby achieving power minimization and fairness objectives. In the domain of power allocation, Ref. [13] integrates deep reinforcement learning to dynamically adjust power strategies under time-varying channel conditions, thereby enhancing energy efficiency. Ref. [14] partially investigates the end-to-end joint optimization of beamforming and power allocation, proposing a distributed solution scheme based on the Alternating Direction Method of Multipliers (ADMM), which improves computational efficiency. In terms of modulation technologies, multi-layer superposition modulation technology achieves layered signal transmission in the spatial dimension, which significantly improves the spectrum efficiency and data transmission rate in the Internet of Things (IoT) scenarios [15]. On the other hand, the multi-carrier initial condition index-aided differential chaos shift keying (DCSK) scheme effectively overcomes the transmission reliability issues caused by multipath fading channels by transmitting chaotic reference signals and multiple modulated data streams over multiple subcarriers. Meanwhile, it avoids the defect of difficult integration of radio frequency delay lines in traditional DCSK systems [16].

Although existing studies have achieved certain advancements in beamforming and power allocation, several critical limitations remain unresolved. Firstly, the majority of schemes assume ideal channel state information (CSI) and inadequately account for the dynamic effects of channel estimation errors on system performance within Internet of Vehicles scenarios, leading to a notable deficiency in theoretical research on joint optimization under non-ideal CSI conditions. Secondly, traditional optimization methods predominantly focus on a single performance metric (such as the communication rate or energy consumption threshold), lacking systematic modeling of the dynamic coupling between energy efficiency and transmission power, thereby hindering the collaborative optimization of multidimensional performance indicators. Furthermore, existing technical solutions encounter bottlenecks in dynamic adaptability, particularly under the rapidly time-varying channel conditions characteristic of Internet of Vehicles scenarios, where current static optimization strategies fail to ensure real-time computational efficiency and robustness in resource allocation. Finally, prevailing beamforming schemes continue to face significant challenges in achieving real-time bilateral collaborative optimization, especially in dynamically varying wireless channel environments, where existing methods struggle to simultaneously guarantee rapid joint optimization of the transmitter precoding matrix and receiver combining weights. Based on the foregoing analysis, existing research has not yet developed a global optimization mechanism for power allocation and the beamforming matrix. It is imperative to establish a joint optimization framework with high adaptability to improve system robustness in complex channel environments.

To address the aforementioned issues, this paper proposes an innovative joint beamforming and power allocation scheme based on joint optimization. In the modeling phase, a joint optimization problem under imperfect CSI conditions is formulated, with the maximization of user energy efficiency as the primary objective, while simultaneously considering constraints on total transmission power. In the solution phase, a distributed alternating optimization algorithm is employed to decompose the original non-convex problem into two subproblems, beamforming matrix optimization and power allocation, achieving a local optimal solution through iterative solving. The core contributions of this paper are three-fold:

• Building upon the beamforming design scheme, a joint optimization problem is introduced encompassing the beamforming matrices at both the transmitter and receiver, as well as the transmission power of real-time beamforming, and a local optimal solution is obtained via a distributed solution scheme.
• A novel closed-form solution is proposed for the power allocation scheme in this scenario.
• A complete MIMO experimental link simulation is established, which can be applied to actual vehicle networking scenarios.

The subsequent sections of this paper are organized as follows: Section 2 establishes the system model, focusing on the system architecture of multi-user MIMO communication in the Internet of Vehicles and the mathematical modeling of imperfect channel state information. Section 3 provides a detailed mathematical formulation of the joint optimization problem and proposes a distributed optimization-based solution framework. Section 4 compares traditional optimization methods with the proposed joint optimization method through simulation experiments, evaluates system energy efficiency and computational complexity, and verifies the superiority of the proposed algorithm. Section 5 summarizes the innovative contributions of this paper and analyzes the superiority of this algorithm.

2. System Model

This paper investigates a narrowband multiple-input multiple-output (MIMO) millimeter-wave downlink system using a simulated precoding architecture in the Internet of Vehicles system, as shown in Figure 1. And the core parameters used in this paper are shown in

Table 1. The core parameters used in this paper.

Symbol	Definition	Symbol	Definition
s	Transmitted signal	${\alpha }_l$	Complex gain
$V_D$	Digital precoder	${\phi }_l$	Azimuth angle parameter
H	Channel transmission matrix	L	Total number of paths
n	Additive noise	SE	Spectral efficiency
${\mathbf{F}}_r$	Receiving precoding matrix	SNR	Signal-to-noise ratio
${\mathbf{F}}_t$	Transmitting preconding matrix	p	Allocated power

.

In this system, the base station (BS), equipped with a single radio frequency chain and multiple antennas $N_t$, is required to transmit data streams to users equipped with multiple receiving antennas. The transmitted symbol s is power-normalized as $E\left\{{\parallel s\parallel }^2\right\}=1$. In the signal processing model in the analog precoding framework, the symbol is first weighted by a scalar digital precoder $V_D$ and subsequently processed by a $N_t\times N_s$-dimensional analog precoder, $F_r^H{F}_t$, which is implemented via $F_r^H{F}_t$ phase shifters. The final transmitted signal can be expressed as $x=F_r^H{F}_t{V}_{D}s$. The user-received signal model can be expressed as

$$y=F_r^{H}H{F}_t{V}_{D}s+n,$$

(1)

where H denotes the channel vector between the base station and the user, and $F_r$ and $F_t$ represent the receiving precoding matrix and the transmitting preconding matrices, respectively. n represents additive noise following a circularly symmetric complex Gaussian distribution with zero mean and covariance ${\sigma }^2$.

The Internet of Vehicles scenario is characterized by high mobility, dynamic topology variations, and complex road environments, resulting in a significant interplay between line-of-sight (LoS) propagation and non-line-of-sight (NLoS) multipath effects within the communication link. Consequently, traditional static channel models inadequately characterize the path loss and delay spread characteristics of millimeter-wave signals between vehicles, which are influenced by environmental factors such as building obstructions and vehicle reflections. The enhanced Saleh–Valenzuela model, by constructing a hybrid structure comprising a dominant LoS path and multiple NLoS scattering paths, offers a more realistic channel-modeling foundation for beamforming and interference mitigation algorithm design in Internet of Vehicles scenarios. This hybrid structure includes one dominant LoS path and L-1 NLoS scattering paths [17]. The channel vector H is expressed as a linear combination of the complex gain ${\alpha }_l$ and the antenna array response vector for each path, weighted by the azimuth angle parameter ${\phi }_t^l$. This model effectively captures both the direct LoS component and the scattered NLoS components, providing a realistic channel representation for IoV scenarios. And it can be expressed as

$$H=\sqrt{{\displaystyle \frac{N_t}{L}}}\sum _{l=1}^L{\alpha }_l{\alpha }_t^H\left({\phi }_t^l\right)$$

(2)

where ${\alpha }_l$ is the complex gain of the l-th path, while ${\alpha }_t^H$ is the transmit steering vector. ${\phi }_l$ corresponds to the l azimuth angle parameter of the $l=1$ propagation path.

Specifically, it denotes the LoS component. To optimize system performance, this paper adopts the transmission rate as the objective function, whose formulation aligns with existing beamforming design methodologies:

$$R=B{log}_2\left(1+{\displaystyle \frac{1}{{\sigma }^2}}{∥F_r^{H}H{F}_t{V}_D∥}^2\right)$$

(3)

where R represents the transmission rates, and B is the communication bandwidth. The definitions of the other parameters are the same as for Formula (1). The term ${\parallel ·\parallel }^2$ denotes the squared Frobenius norm, representing the power gain.

In this study, spectral efficiency (SE), extensively employed as an optimization metric in current beamforming designs, is selected, measured in bits per second per Hertz (bit/s/Hz), quantifying the data rate achievable per unit of bandwidth. It reflects how efficiently the system utilizes the available spectrum. In this formulation, SE depends on the effective channel gain after beamforming, which is influenced by both the beamforming matrices and the channel conditions. Maximizing SE is the primary objective of the joint optimization problem. For the system under consideration, it is defined as follows: $F_r^H{F}_t$. Concerning the constraints, the analog precoder ${∥{\left[F_r^H{F}_t\right]}_i∥}^2=1\left(i=1,\dots ,N_t\right)$ is required to satisfy the constant modulus constraint ${∥F_r^H{F}_t{V}_D∥}^2\le P$, while the transmit power must concurrently comply with $V_D$. Theoretical analysis indicates that under the maximum transmit power constraint [18], the optimal digital precoder can be expressed as

$$V_D=\sqrt{{\displaystyle \frac{P}{N_t}}}.$$

(4)

where $V_D$ represents the digital precoder, P is the total transmit power, and $N_t$ is the number of transmit antennas.

3. Problem Statement and Proposed Algorithm

A joint optimization scheme for beamforming and power allocation is proposed, aimed at maximizing system transmission efficiency while satisfying the constant modulus constraint. The proposed optimization scheme formulates a joint problem to maximize spectral efficiency under constant modulus and power constraints. It decomposes the problem into two subproblems: beamforming matrix optimization and power allocation. An alternating optimization approach is used, iteratively solving each subproblem to converge to a local optimum, thereby enhancing transmission efficiency. The analog precoder $F_r^H,F_t$ optimization problem can be reformulated as maximizing the objective function under the constant modulus constraint:

$$\underset{\gamma ,F_t,F_r}{max}R={log}_2\left(1+{\displaystyle \frac{\gamma }{N_t}}{∥F_r^{H}H{F}_t∥}^2\right)$$

(5)

where the SNR $\gamma ={\displaystyle \frac{P}{{\sigma }^2}}$ is considered a known parameter. This paper assumes the estimated SNR ${\gamma }_{est}$, which is consistent with the true value $\gamma$, with the research focus concentrated on the impact of imperfect channel state information (CSI) on system performance.

In wireless communication systems, the joint optimization of beamforming and power allocation constitutes a fundamental problem for enhancing spectral efficiency. Considering a single-user multiple-input multiple-output (MIMO) scenario, the base station is equipped with $N_t$. With the transmitter equipped with N antennas and the user terminal employing multiple antennas for reception, the objective is to maximize spectral efficiency through transmit power optimization R. Its mathematical model can be formulated as

$$\begin{array}{c}\underset{P,F_t,F_r}{max}R=B{log}_2\left(1+{\displaystyle \frac{P{∥{\mathbf{F}}_r^H\mathbf{H}{\mathbf{F}}_t∥}^2}{N_t{\sigma }^2}}\right)\\ \mathrm{s}.\mathrm{t}.0\le P\le P_{max}\\ \phantom{\mathrm{s}.\mathrm{t}.}{∥{\mathbf{F}}_r∥}^2=1,i=1,\dots ,N_r\\ \phantom{\mathrm{s}.\mathrm{t}.}{∥{\mathbf{F}}_t∥}^2=1,i=1,\dots ,N_t\end{array}$$

(6)

where P is the transmit power to be optimized, H is the channel matrix, $F_r$ and $F_t$ represent the receiving and transmitting beamforming matrices, respectively, and $N_t$ is the number of transmit antennas.

Due to the strong coupling between the variable P and $F_t$, direct joint optimization is challenging; therefore, an alternating optimization approach is employed, decomposing the original problem into two subproblems solved iteratively.

3.1. Fixed Power, Optimizing the Beamforming Matrix

At this stage, the objective function reduces to maximizing the channel gain term ${∥H{F}_t∥}^2$. This simplification is possible because the logarithmic function is monotonic, and with fixed power, maximizing the argument inside the logarithm directly maximizes the objective. According to the Cauchy–Schwarz inequality, the optimal beamforming vector $F_t^{\ast }$ should be conjugate-matched to the channel vector h and can be expressed as $F_t^{\ast }={\displaystyle \frac{h}{∥h∥}}$. This closed-form solution demonstrates that aligning the beam direction with the main lobe of the channel maximizes the received signal strength. In practical implementation, the normalization of $F_t$ is required to satisfy hardware constraints.

3.2. Fixing the Beamforming Matrix, Optimizing Transmitter Power

At this stage, the objective function reduces to a monotonic optimization problem of a logarithmic function, which occurs because the beamforming matrix is fixed, making the effective channel gain a constant. Thus, the objective becomes a logarithmic function solely of power, which is monotonically increasing.

$$\underset{P,F_t,F_r}{max}R={log}_2\left(1+{\displaystyle \frac{P{∥F_r^{H}H{F}_t∥}^2}{N_t{\sigma }^2}}\right)$$

(7)

And the optimal power allocation is $P=P_{max}$, i.e., in a single-user, interference-free scenario, full power transmission maximizes spectral efficiency. This conclusion aligns with the characteristics of water-filling power allocation in interference-free environments.

This conclusion aligns with the characteristics of water-filling power allocation in interference-free environments. In such environments, the optimal strategy is to allocate all available power to the single spatial channel, as there are no other users causing interference or requiring power allocation trade-offs. This is equivalent to the water-filling solution where the ‘water level’ is constrained only by the total power budget, leading to full power transmission [19].

The alternating optimization procedure iteratively updates P and $F_t$ to approach a local optimal solution, with convergence verifiable through convex optimization theory. The advantages of this derivation process compared to traditional methods include decoupling the non-convex problem into two more manageable subproblems, providing closed-form solutions for each subproblem, ensuring convergence to a local optimum, and offering computational efficiency suitable for real-time applications. Traditional methods often optimize single variables or use less efficient heuristics. And the specific algorithm flowchart is shown in Figure 2. The specific algorithm flowchart is shown in Figure 2. The algorithm operates as follows: It initializes values for beamforming matrices and power. It then iterates, alternating between optimizing beamforming (for fixed power) and power (for fixed beamforming). The loop continues until the change in the beamforming matrix falls below a threshold $\alpha$. Nevertheless, this method exhibits notable limitations. The model’s limitations are the following: The approach is highly dependent on accurate channel state information (CSI), making it challenging to extend to multi-user scenarios due to the neglect of inter-user interference and susceptible to convergence at local optimal solutions rather than global optima. Therefore, in practical applications, it is essential to further enhance the algorithm’s robustness and adaptability by incorporating specific scenario characteristics [20].

The modules are evaluated as follows: (1) Initialization: Start with initial values for $F_t$, $F_r$, and P. (2) Beamforming Optimization: For fixed P, compute the optimal $F_t^{\ast }$ to maximize channel gain. (3) Power Optimization: For fixed $F_t$, set $P=P_{max}$ to maximize the spectral efficiency. (4) Convergence Check: Compute the change in the beamforming matrix $\Delta F_t$. If $\Delta F_t$ < $\alpha$, the algorithm terminates; otherwise, it returns to step 2. This iterative process continues until convergence is achieved.

4. Simulation Results

To validate the effectiveness of the proposed joint optimization scheme, this study conducted simulation experiments within the IoV MIMO scenario, comparing and analyzing the performance differences between the proposed method and the conventional beamforming scheme (baseline method) across key metrics, including the transmission rate (R), channel estimation error (NMSE), and computational efficiency. The specific simulation system parameters are shown in

Table 2. Simulation system parameters.

Parameter	Value
$N_t$	64
$N_r$	4
$N_s$	8
${\sigma }^2$	0.01
ITER	100
SNR	−20:2:20

.

The numerical values for NMSE and other metrics were generated through Monte Carlo simulations under the parameters in Table 2. The key performance metrics were computed, as shown in

Table 3. Various data indicators and generated rules of simulation results.

Metric	How Generated
NMSE	Normalized mean squared error between estimated and true channel H, averaged over 100 iterations.
Transmission rate	Computed using Equation (3) for each SNR point from −20 dB to 20 dB in steps of 2 dB.
MSE CDF	Cumulative distribution function of the mean squared error of the received signal, computed over 1000 random trials
Convergence curve	Recorded value of the objective function (SE) at each iteration until change falls below the threshold.

:

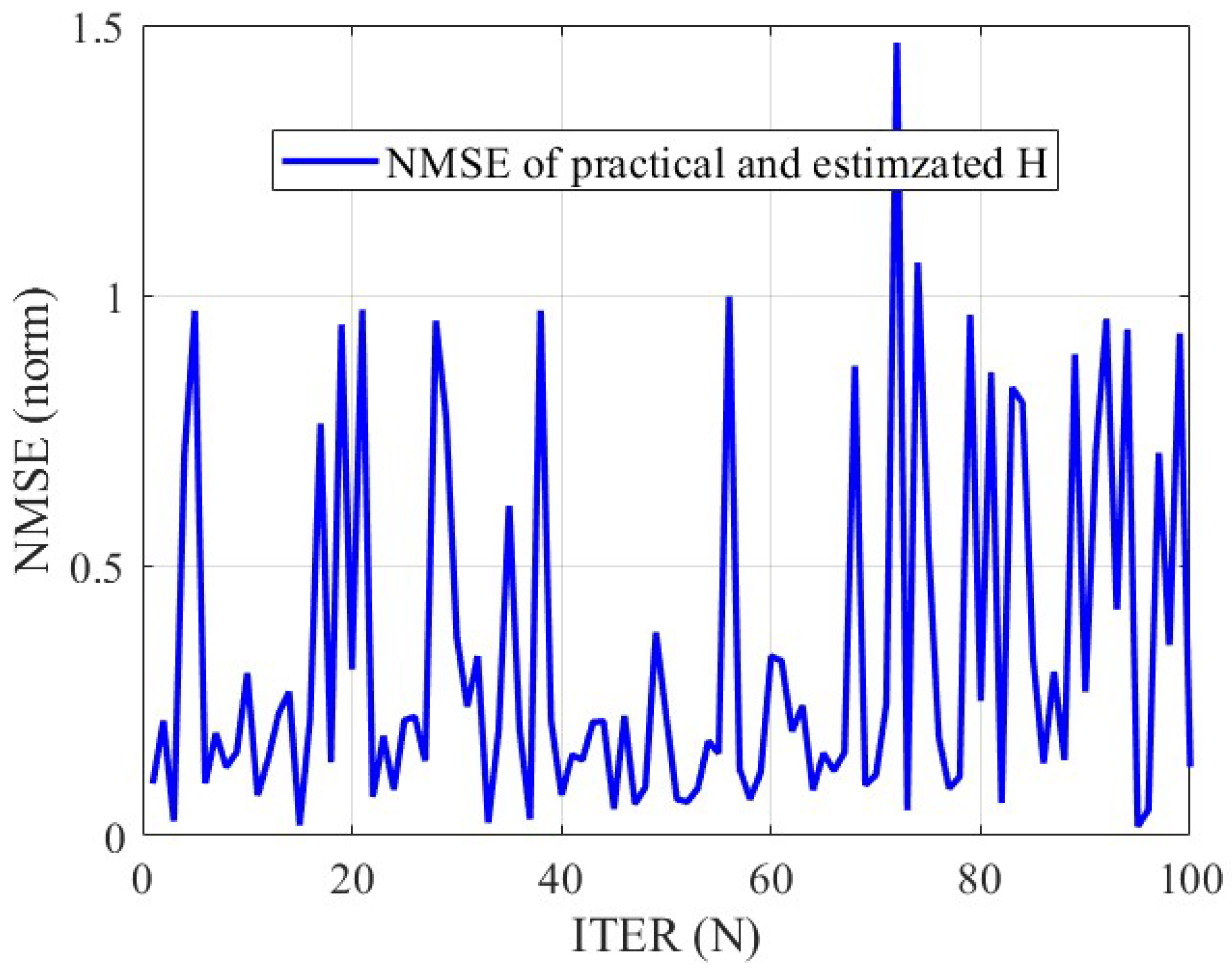
As shown in the channel estimation error comparison graph (NMSE of practical and estimated H) in Figure 3, over 100 iterations, the normalized mean squared error (NMSE) of the proposed method consistently remains below 1.5, which is significantly lower than the traditional method exceeding 3.0. This demonstrates that by integrating imperfect CSI modeling with the distributed alternating optimization algorithm, the proposed scheme achieves enhanced robustness to channel estimation errors, thereby maintaining stable signal transmission quality under non-ideal channel conditions.

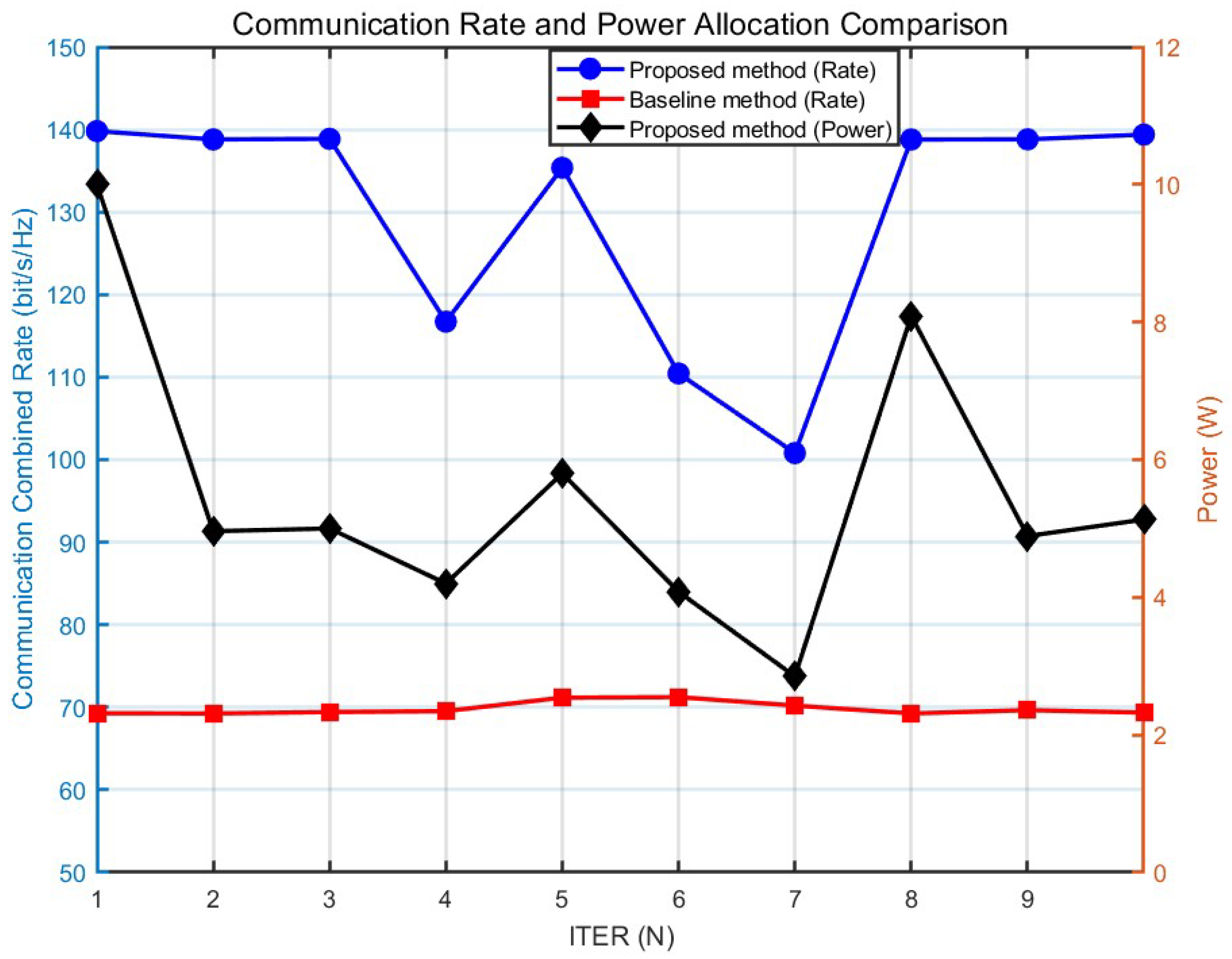
For convenience, 10 sets of transmission rates and power data were randomly selected from 100 iterations, as shown in Figure 4. In the transmission rate iteration comparison chart (proposed method vs. baseline method), the transmission rate of the proposed method rapidly converges to above 100 bit/s/Hz as the number of iterations increases, whereas the traditional method only achieves approximately 70 bit/s/Hz. This advantage stems from the joint optimization mechanism of the beamforming matrix and power allocation—by dynamically aligning with the main lobe direction of the channel and optimizing power resource allocation, the system attains higher spectral efficiency (SE) under the same transmit power constraint, thereby validating the effectiveness of the objective function aimed at maximizing system transmission efficiency.

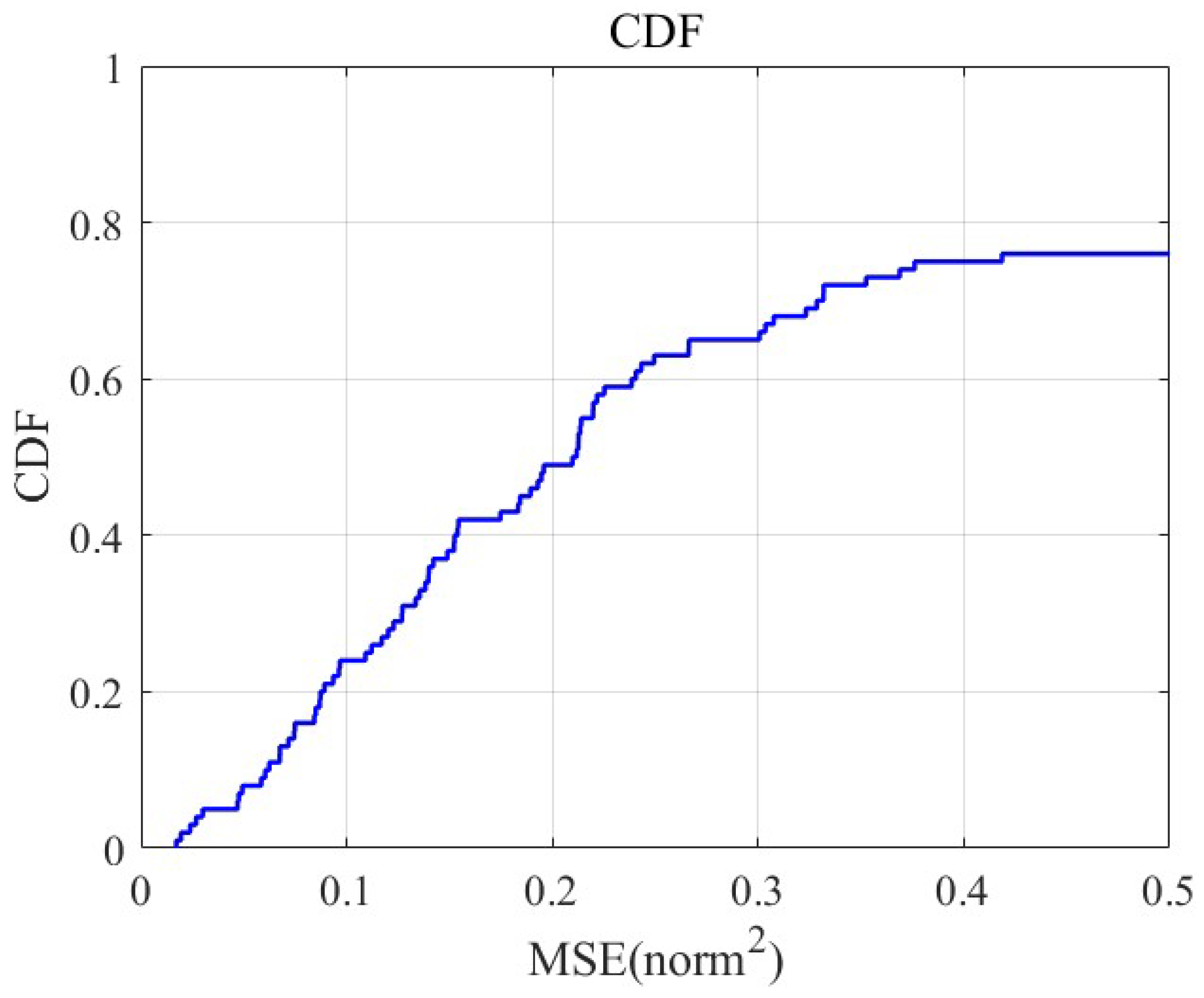
Although the bit error rate curve is not explicitly presented, it can be indirectly inferred from Figure 5, showning the cumulative distribution function (CDF) of the mean squared error (MSE), that the proposed method’s MSE distribution is predominantly concentrated below 0.1, whereas the traditional method’s MSE distribution peaks within the 0.2 to 0.3 range. A lower MSE signifies reduced signal transmission distortion, thereby indicating that the proposed scheme in this paper achieves superior suppression of multipath interference and noise, effectively lowering the bit error rate and enhancing communication reliability.

In addition, our proposed method tends to converge after 20 iterations, with a faster convergence speed compared to the traditional method, as shown in Figure 6. By employing a distributed alternating optimization algorithm to decouple the original problem, the proposed scheme decomposes the non-convex problem into two subproblems—beamforming and power allocation—which are solved iteratively. This method significantly reduces computational complexity, improves real-time performance, and is better suited to the dynamic resource allocation demands of Internet of Vehicles high-speed mobility scenarios. The model demonstrates significant advantages through real-time collaborative optimization of beamforming and power allocation by dynamically adjusting both parameters in real time using the distributed alternating algorithm. This leads to higher spectral efficiency, lower NMSE, faster convergence, and better robustness to channel uncertainties, making it suitable for high-mobility IoV scenarios.

Overall, compared to traditional beamforming schemes, the joint optimization method proposed herein demonstrates significant advantages by enabling real-time collaborative optimization of the beamforming matrix and power allocation, as shown in

Table 4. Comparative performance summary.

Metric	Proposed Method	Baseline Method
NMSE	<1.5	>3.0
Transmission rate(bit/s/Hz)	100	70
MSE(CDF<0.1)	Yes	No
Convergence	Fast	Slow

. The results demonstrate that the proposed scheme offers an effective technical solution for achieving efficient and reliable real-time communication in Internet of Vehicles MIMO systems operating within complex channel environments. This work fills a significant gap by proposing a real-time joint optimization framework for beamforming and power allocation under non-ideal CSI conditions. It addresses the lack of dynamic adaptability in existing methods, provides a distributed alternating optimization algorithm, and demonstrates improved performance in spectral efficiency, robustness, and convergence speed. The simulation results confirm a 43% increase in transmission rate compared to traditional methods.

5. Conclusions

In dynamic Telematics, MIMO leverages spatial reuse and diversity gains to address real-time transmission/data processing bottlenecks. This paper proposes a joint optimization framework for non-ideal CSI to bridge theoretical gaps in co-optimizing power allocation and beamforming. The proposed scheme shows strong robustness to non-ideal CSI, as evidenced by the NMSE values consistently below 1.5 (compared to >3.0 for baseline). This indicates that the algorithm maintains stable performance even with channel estimation errors, making it suitable for high-mobility IoV environments where CSI is often imperfect. The conclusion effectively addresses the problem statement by summarizing the proposed framework: By constructing a mixed-integer nonlinear programming model, the beamforming matrix design and power constraints are incorporated into a unified optimization objective and efficiently solved based on a convex relaxation technique. The simulation results show that the proposed distributed alternating optimization scheme is more robust to non-ideal CSI. Spectral efficiency is boosted and overall performance is enhanced through the joint optimization of beamforming and power allocation, while interference and noise are effectively mitigated for a reduced bit error rate. Breakthroughs in error robustness, transmission efficiency, communication reliability, and real-time capabilities are achieved by the proposed method. Future research will further explore channel modeling and algorithm optimization in high-speed mobile scenarios, focusing on solving the problem of insufficient model generalization ability in extreme time-varying environments. The research results in this paper provide a theoretical basis and technical path for the development of energy-efficient communication protocols in intelligent transportation systems, and are of great practical value for high-density connectivity scenarios, such as cooperative sensing for autonomous driving and vehicle-to-everything (V2X) systems.