Appointment Scheduling Considering Outpatient Unpunctuality Under Telemedicine Services
Abstract
1. Introduction
2. Literature Review
2.1. Traditional Outpatient Appointment Scheduling
2.2. Appointment Scheduling Incorporating Telemedicine
2.3. Appointment Scheduling with Mathematical Programming Methods
3. Problem Formulation
4. Solution Approach
5. Numerical Studies
5.1. Data Settings
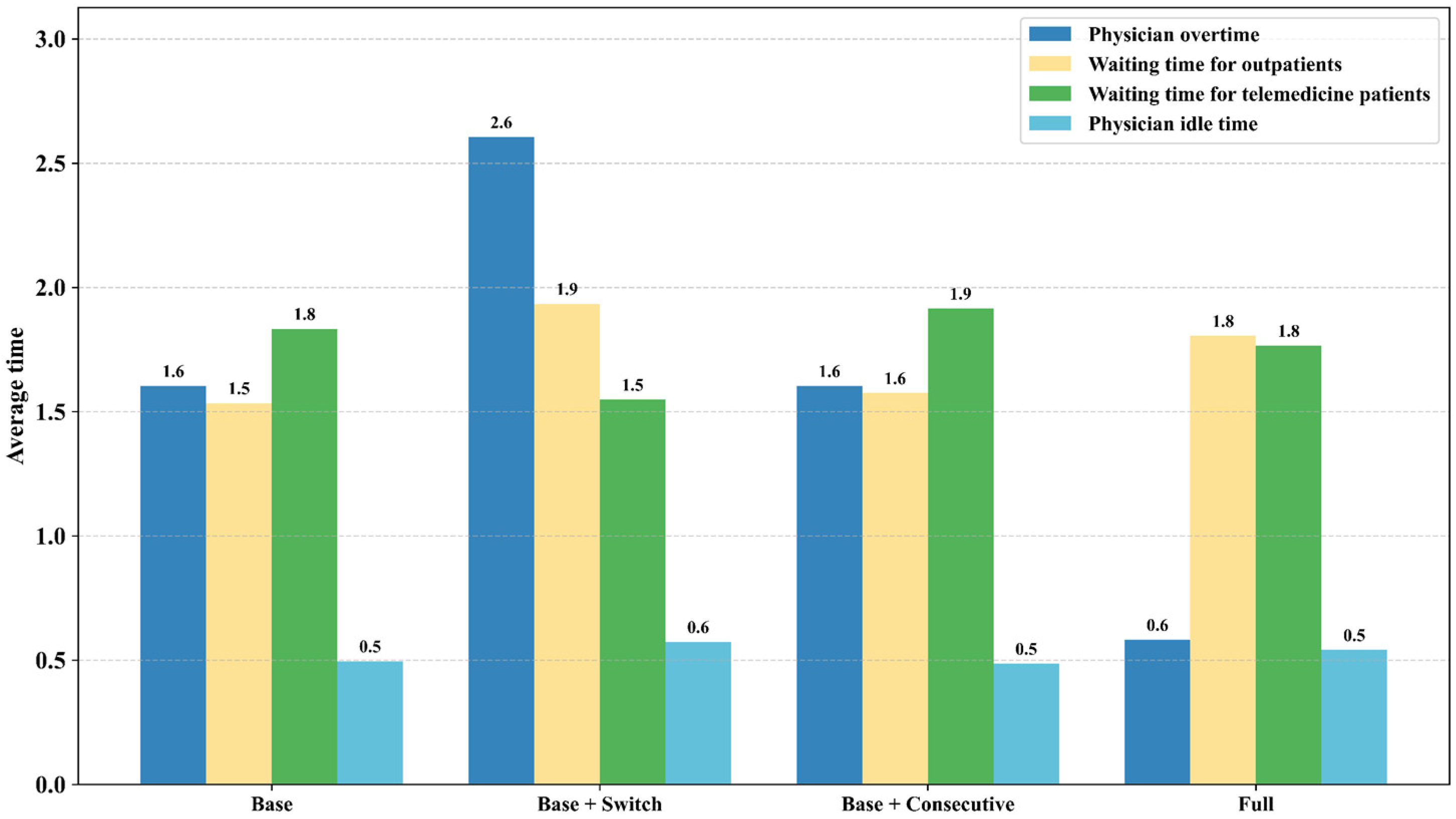
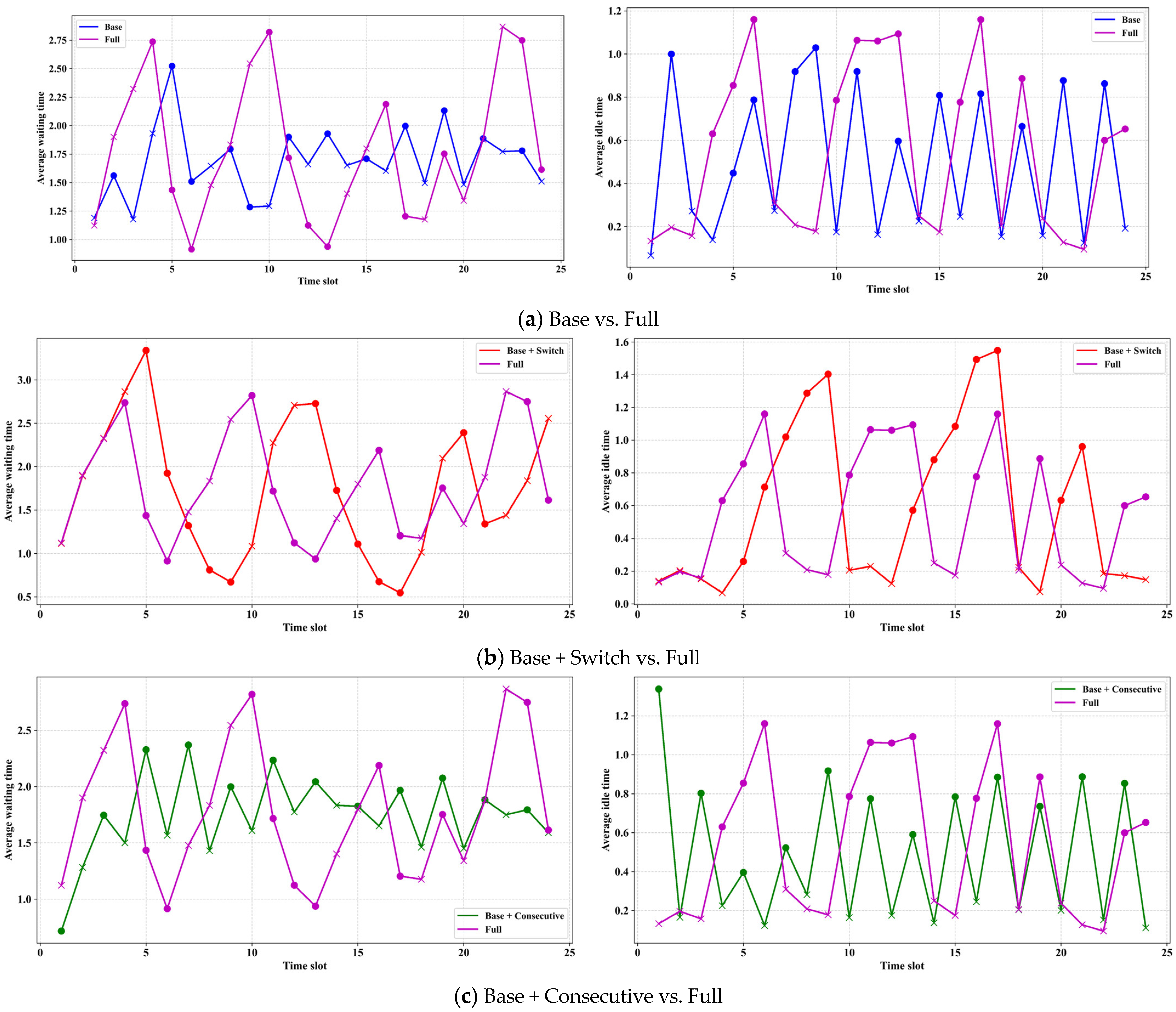
5.2. Ablation Study
5.3. Sensitivity Analysis
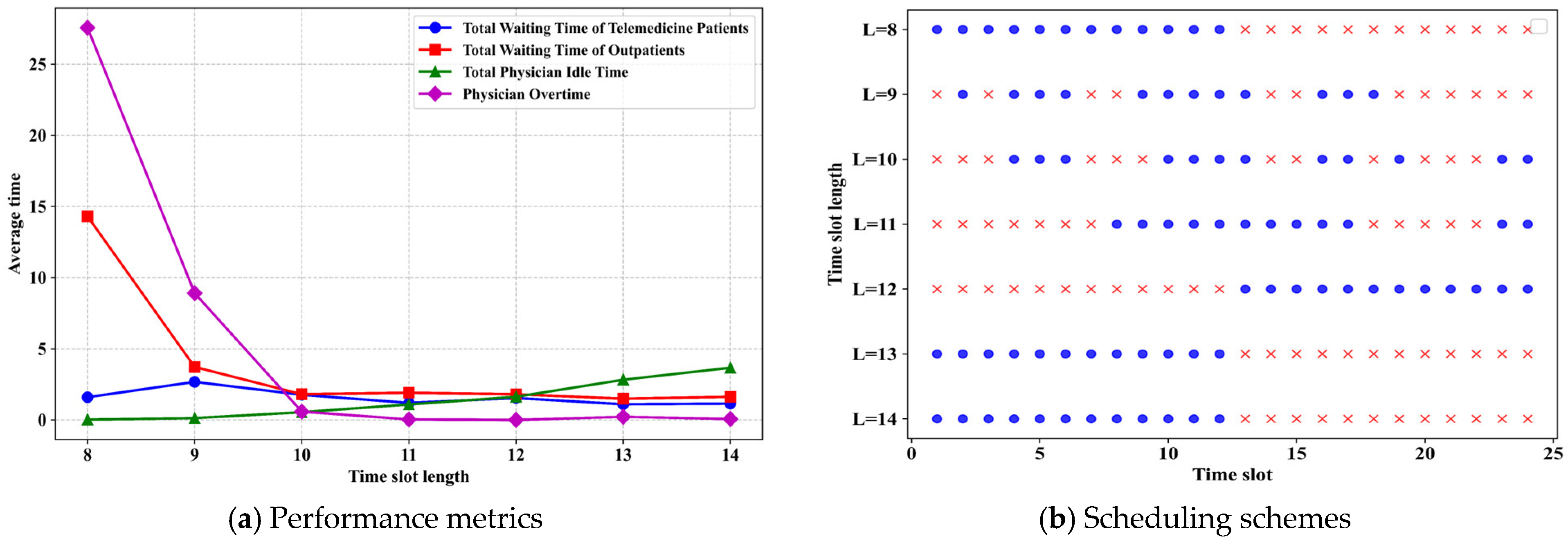
5.3.1. Impact of Time Slot Length
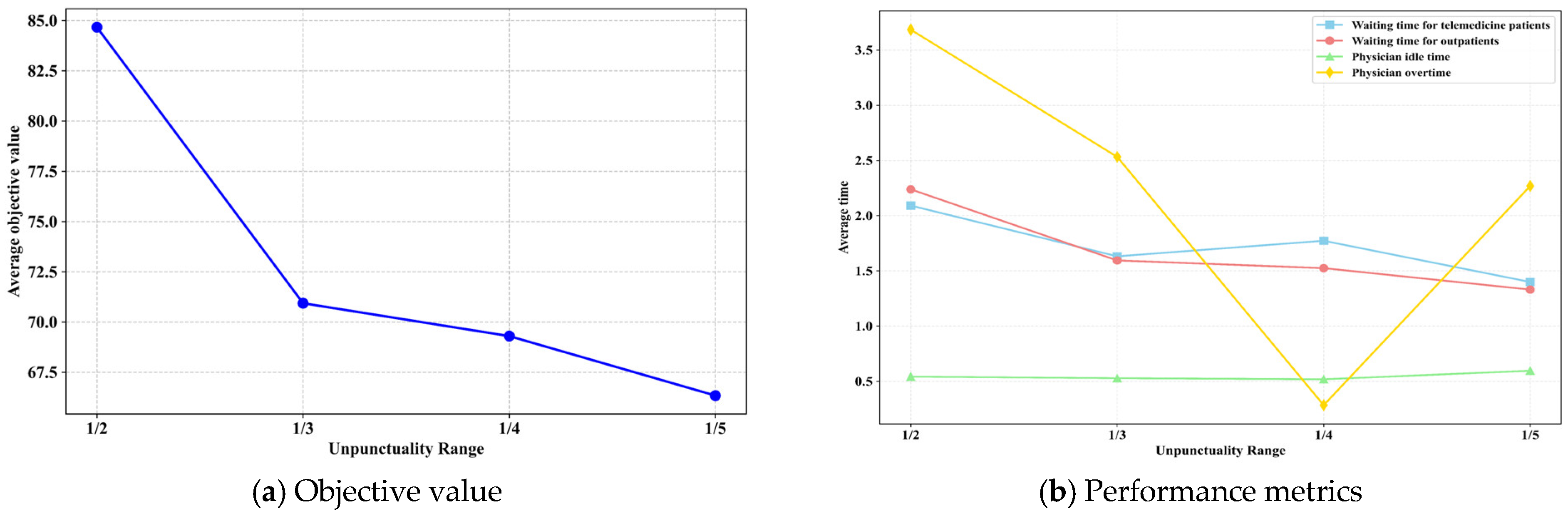
5.3.2. Impact of Unpunctuality Range
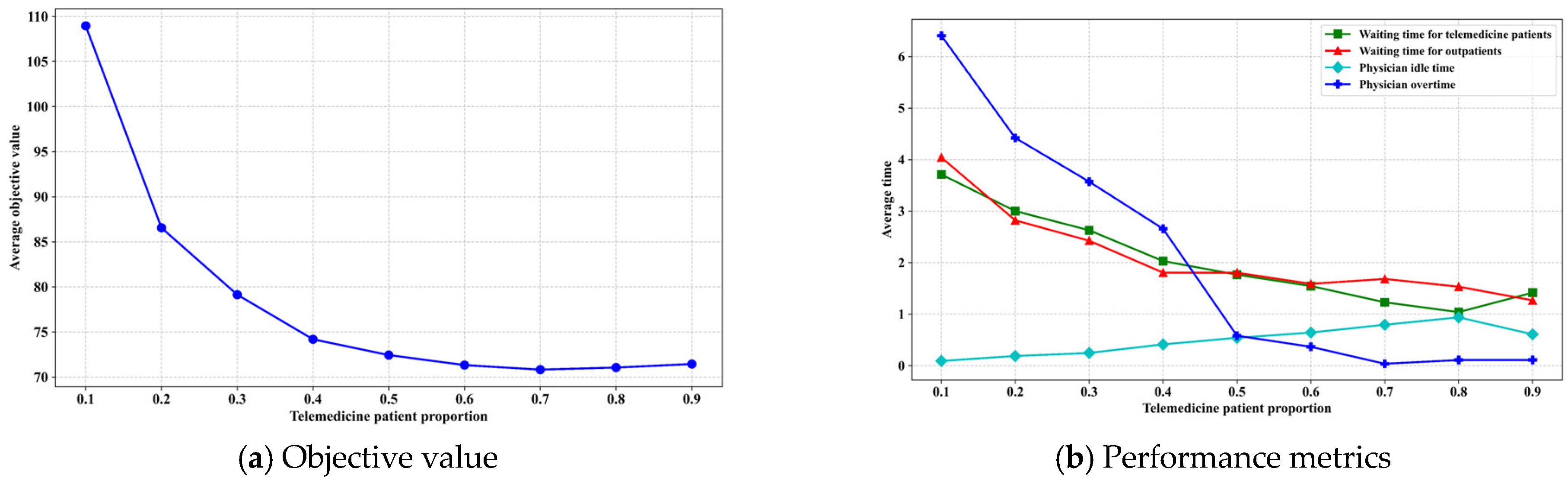
5.3.3. Impact of Telemedicine Patient Proportion
5.3.4. Impact of Weighting Coefficients
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Stochastic Mixed-Integer Programming | |
| Mixed-Integer Linear Programming | |
| Sample Average Approximation | |
| Standard Deviation | |
| PHA | Progressive Hedging Algorithm |
References
- Jackson, L.E.; Danila, M.I. Healthcare disparities in telemedicine for rheumatology care. Curr. Opin. Rheumatol. 2022, 34, 171–178. [Google Scholar] [CrossRef]
- Jose, A.P.; Kaushik, A.; Tange, H.; van der Weijden, T.; Pandey, N.; Sharma, A.; Sheikh, R.; Ali, N.; Kushwaha, S.; Kondal, D.; et al. Redesigning telemedicine: Preliminary findings from an innovative assisted telemedicine healthcare model. BMC Prim. Care 2024, 25, 380. [Google Scholar] [CrossRef]
- Chen, W.; Chen, L.; Shen, X.; Wang, X.L.; Zhang, Y.T. Data-Driven Optimization of Physician Allocation for Online Consultation in Internet Hospitals. SSRN 2025. [Google Scholar] [CrossRef]
- Cai, Y.; Song, H.Q.; Wang, S. Managing appointment-based services with electronic visits. Eur. J. Oper. Res. 2024, 315, 863–878. [Google Scholar] [CrossRef]
- Cayirli, T.; Veral, E. Outpatient scheduling in health care: A review of literature. Prod. Oper. Manag. 2003, 12, 519–549. [Google Scholar] [CrossRef]
- Gupta, D.; Denton, B. Appointment scheduling in health care: Challenges and opportunities. IIE Trans. 2008, 40, 800–819. [Google Scholar] [CrossRef]
- Min, D.; Yih, Y. A simulation study of registration queue disciplines in an outpatient clinic: A two-stage patient flow model. Eur. J. Ind. Eng. 2009, 3, 127–145. [Google Scholar] [CrossRef]
- Mak, H.Y.; Rong, Y.; Zhang, J. Appointment scheduling with limited distributional information. Manag. Sci. 2015, 61, 316–334. [Google Scholar] [CrossRef]
- Ahmadi-Javid, A.; Jalali, Z.; Klassen, K.J. Outpatient appointment systems in healthcare: A review of optimization studies. Eur. J. Oper. Res. 2017, 258, 3–34. [Google Scholar] [CrossRef]
- Salzarulo, P.A.; Mahar, S.; Modi, S. Beyond patient classification: Using individual patient characteristics in appointment scheduling. Prod. Oper. Manag. 2016, 25, 1056–1072. [Google Scholar] [CrossRef]
- Deceuninck, M.; Fiems, D.; De Vuyst, S. Outpatient scheduling with unpunctual patients and no-shows. Eur. J. Oper. Res. 2018, 265, 195–207. [Google Scholar] [CrossRef]
- Zhu, H.; Chen, Y.H.; Leung, E.; Liu, X. Outpatient appointment scheduling with unpunctual patients. Int. J. Prod. Res. 2018, 56, 1982–2002. [Google Scholar] [CrossRef]
- Xiao, F.; Lai, K.K.; Lau, C.K.; Ram, B. Robust Overbooking for no-shows and cancellations in healthcare. Mathematics 2024, 12, 2563. [Google Scholar] [CrossRef]
- Sun, B.; Xu, Z.; Wei, M.; Wang, X. A study on the strategic behavior of players participating in air-rail intermodal transportation based on evolutionary games. J. Air Transp. Manag. 2025, 126, 102793. [Google Scholar] [CrossRef]
- Jiang, B.W.; Tang, J.F.; Yan, C.J. A stochastic programming model for outpatient appointment scheduling considering unpunctuality. Omega 2019, 82, 70–82. [Google Scholar] [CrossRef]
- Homem-de-Mello, T.; Kong, Q.; Godoy-Barba, R. A simulation optimization approach for the appointment scheduling problem with decision-dependent uncertainties. Inf. J. Comput. 2022, 34, 2845–2865. [Google Scholar] [CrossRef]
- Dogru, A.K.; Melouk, S.H.; Çapar, İ.; Weida, T.J. Managing interruptions in appointment schedules via patient notification. Comput. Oper. Res. 2023, 159, 106352. [Google Scholar] [CrossRef]
- Li, C.; Yang, Z.; Yang, F.J.; Wang, F. A novel and efficient real-time sequencing strategy for appointment scheduling with unpunctual patients. J. Sched. 2024, 27, 135–149. [Google Scholar] [CrossRef]
- Zhou, S.H.; Pang, S.; Zhao, Y.N.; Shi, Y.T. Sequencing and scheduling appointments with weighted completion time minimization and waiting time tolerance. Comput. Oper. Res. 2025, 176, 106948. [Google Scholar] [CrossRef]
- Lokkerbol, J.; Adema, D.; Cuijpers, P.; Reynolds III, C.F.; Schulz, R.; Weehuizen, R.; Smit, F. Improving the cost-effectiveness of a healthcare system for depressive disorders by implementing telemedicine: A health economic modeling study. Am. J. Geriatr. Psychiatry 2014, 22, 253–262. [Google Scholar] [CrossRef] [PubMed]
- Jue, J.S.; Spector, S.A.; Spector, S.A. Telemedicine broadening access to care for complex cases. J. Surg. Res. 2017, 220, 164–170. [Google Scholar] [CrossRef]
- Ellimoottil, C.; Boxer, R.J. Bringing surgical care to the home through video visits. JAMA Surg. 2018, 153, 177–178. [Google Scholar] [CrossRef]
- DeNicola, N.; Marko, K. Connected health and mobile apps in obstetrics and gynecology. Obstet. Gynecol. Clin. 2020, 47, 317–331. [Google Scholar] [CrossRef]
- Gadzinski, A.J.; Ellimoottil, C. Telehealth in urology after the COVID-19 pandemic. Nat. Rev. Urol. 2020, 17, 363–364. [Google Scholar] [CrossRef]
- Qiao, Y.; Ran, L.; Li, J.L.; Zhai, Y.K. Design and comparison of scheduling strategy for teleconsultation. Technol. Health Care 2021, 29, 939–953. [Google Scholar] [CrossRef] [PubMed]
- Ji, M.L.; Wang, S.S.; Peng, C.; Li, J.L. Two-stage robust telemedicine assignment problem with uncertain service duration and no-show behaviours. Comput. Ind. Eng. 2022, 169, 108226. [Google Scholar] [CrossRef]
- Huang, J.Y.; Morrice, D.; Bard, J. Coordinated scheduling for in-clinic and virtual medicine patients in a multi-station network. IISE Trans. 2024, 56, 437–457. [Google Scholar] [CrossRef]
- Shen, X.X.; Li, N.; Xie, X.Q. Multiserver time window allowance schedules for virtual visits with uncertain time-dependent no-shows and service times. Adv. Eng. Inform. 2024, 59, 102252. [Google Scholar] [CrossRef]
- Guo, H.N.; Xie, Y.; Jiang, B.W.; Tang, J.F. When outpatient appointment meets online consultation: A joint scheduling optimization framework. Omega 2024, 127, 103101. [Google Scholar] [CrossRef]
- Bragin, M.A. Survey on Lagrangian relaxation for MILP: Importance, challenges, historical review, recent advancements, and opportunities. Ann. Oper. Res. 2024, 333, 29–45. [Google Scholar] [CrossRef]
- Wang, W.J.; Tian, G.D.; Luo, M.Q.; Zhang, H.H.; Yuan, G.; Niu, K.J. More mixed-integer linear programming models for solving three-stage remanufacturing system scheduling problem. Comput. Ind. Eng. 2024, 194, 110379. [Google Scholar] [CrossRef]
- Wu, X.Q.; Zhou, S.H. Sequencing and scheduling appointments on multiple servers with stochastic service durations and customer arrivals. Omega 2022, 106, 102523. [Google Scholar] [CrossRef]
- Shen, X.X.; Du, S.C.; Sun, Y.N.; Sun, P.Z.; Law, R.; Wu, E.Q. Advance scheduling for chronic care under online or offline revisit uncertainty. IEEE Trans. Autom. Sci. Eng. 2023, 21, 5297–5310. [Google Scholar] [CrossRef]
- Shen, X.X.; Frigerio, N.; Du, S.C.; Matta, A. Production Planning and Allocation of Re-Entrance Flows with Stochastic Quality. In Proceedings of the 2024 IEEE 20th International Conference on Automation Science and Engineering (CASE), Bari, Italy, 28 August–1 September 2024; pp. 2943–2948. [Google Scholar]
- Ju, L.H.; Jiang, J.; Wu, L.F.; Sun, J.B. A Sample Average Approximation Approach for Stochastic Optimization of Flight Test Planning with Sorties Uncertainty. Mathematics 2024, 12, 3024. [Google Scholar] [CrossRef]
- Poss, M. Robust combinatorial optimization with variable budgeted uncertainty. 4OR 2013, 11, 75–92. [Google Scholar] [CrossRef]
- Pelletier, S.; Jabali, O.; Laporte, G. The electric vehicle routing problem with energy consumption uncertainty. Transp. Res. Part B Methodol. 2019, 126, 225–255. [Google Scholar] [CrossRef]
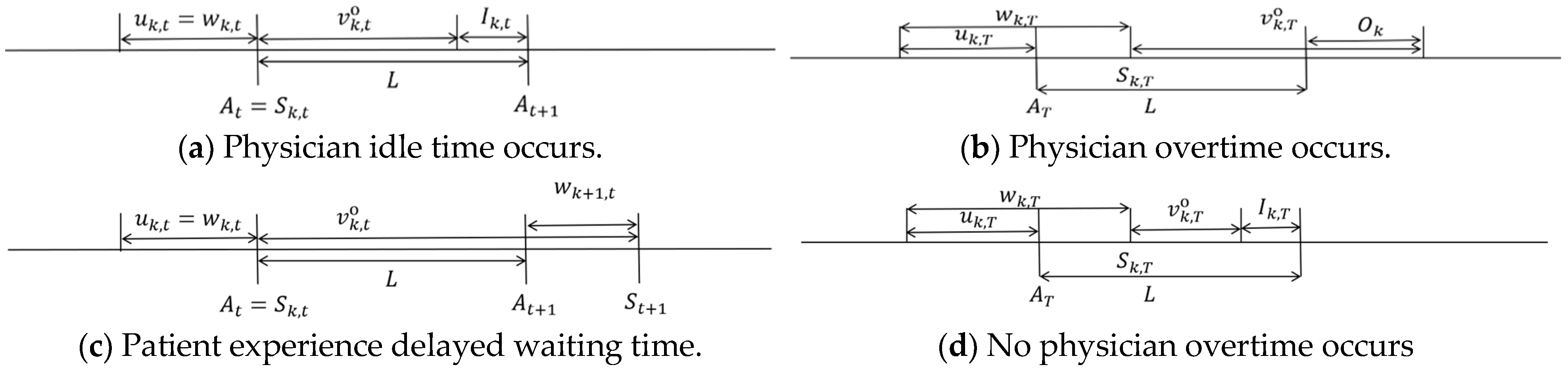
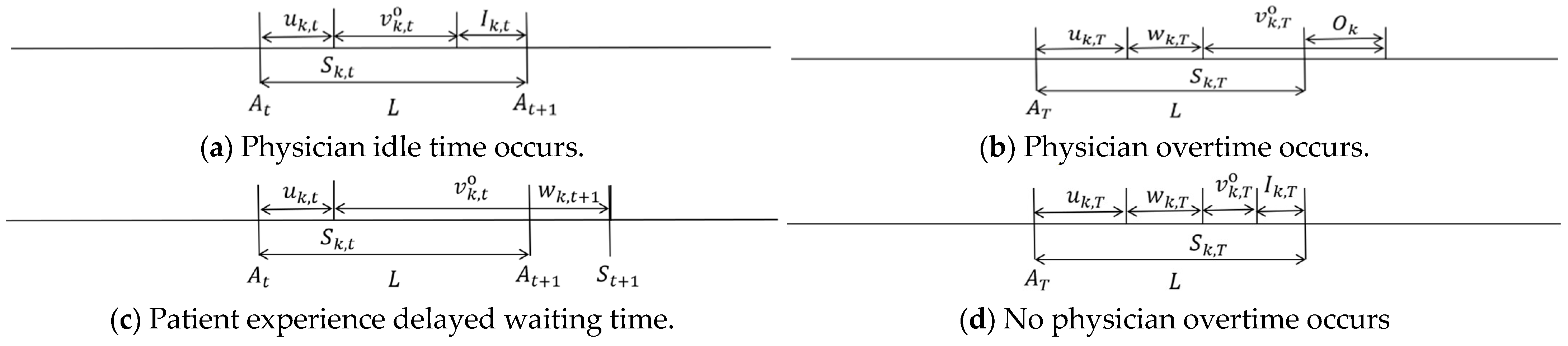
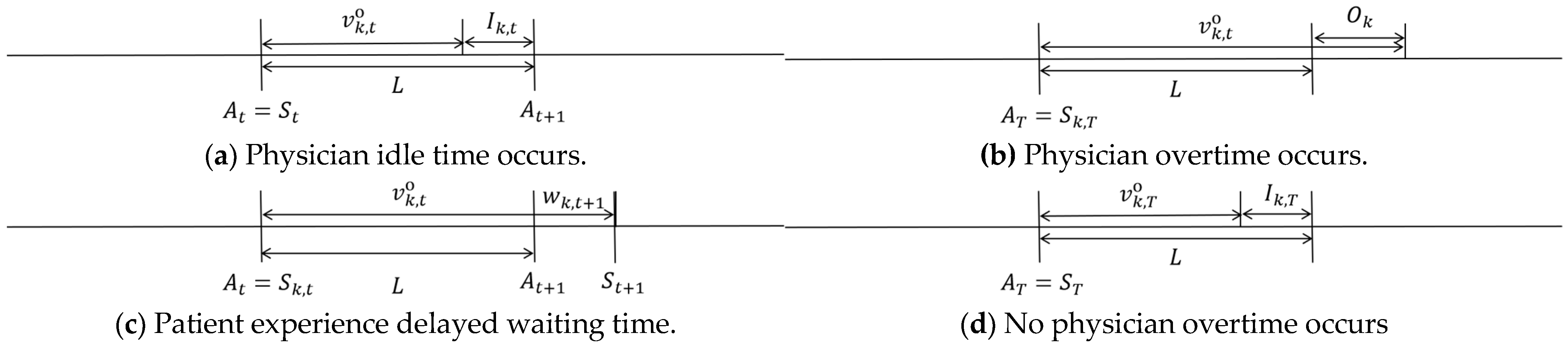
| Sets and Parameters | Description |
| Set of time slots | |
| Set of scenarios | |
| Fixed length of a time slot | |
| Planned start time of the -th time slot | |
| Proportion of telemedicine patients scheduled | |
| Proportion of outpatients scheduled | |
| Service time for telemedicine patient assigned to slot in scenario | |
| Service time for outpatient assigned to slot in scenario | |
| Unpunctuality of outpatient assigned to slot in scenario | |
| Weight coefficients | |
| Decision Variables | Description |
| Binary variable, 1 if slot assigned to telemedicine patient, else 0 | |
| Binary variable, 1 if slot assigned to outpatient, else 0 | |
| Continuous variable, actual service start time for patient in slot , scenario | |
| Continuous variable, waiting time of telemedicine patient in slot , scenario | |
| Continuous variable, waiting time of outpatient in slot , scenario | |
| Continuous variable, physician idle time in slot , scenario | |
| Continuous variable, physician overtime in scenario | |
| Binary variable, 1 if the service status switches between time slots and , else 0 | |
| Binary variable, 1 if both slots and are assigned to telemedicine patients, else 0 |
| Sample Size (K) | Objective Value | Solution Time |
|---|---|---|
| 20 | 67.15 | 1.6 |
| 30 | 68.03 | 4.4 |
| 40 | 69.60 | 7.3 |
| 50 | 70.79 | 14.7 |
| 60 | 70.30 | 21.8 |
| 70 | 71.72 | 35.7 |
| 80 | 70.33 | 23.8 |
| 90 | 72.11 | 76.4 |
| 100 | 71.32 | 41.6 |
| 110 | 71.49 | 151.4 |
| 120 | 71.75 | 158.7 |
| 130 | 71.09 | 179.8 |
| 140 | 71.45 | 299.2 |
| 150 | 71.92 | 300.9 |
| 160 | 71.13 | 317.1 |
| 170 | 71.55 | 398.9 |
| 180 | 71.45 | 416.9 |
| Weighting Coefficients | Objective Value | ||||
|---|---|---|---|---|---|
| 72.44 | 21.2 | 21.7 | 13.0 | 0.6 | |
| 44.07 | 32.2 | 24.9 | 0.0 | 0.5 | |
| 105.73 | 15.1 | 17.7 | 19.7 | 2.5 | |
| 62.24 | 14.0 | 19.7 | 20.2 | 2.5 | |
| 72.52 | 32.0 | 23.4 | 0.0 | 1.1 | |
| 71.42 | 17.1 | 22.3 | 14.4 | 3.1 | |
| 73.30 | 22.1 | 21.3 | 12.1 | 0.4 | |
| 66.01 | 22.9 | 19.8 | 11.3 | 0.6 | |
| 78.32 | 16.3 | 25.4 | 15.2 | 3.4 | |
| 68.39 | 18.4 | 22.5 | 14.4 | 2.6 | |
| 77.74 | 23.1 | 20.4 | 11.6 | 0.6 | |
| 43.80 | 21.3 | 22.7 | 13.0 | 0.5 | |
| 128.20 | 19.6 | 19.1 | 14.0 | 2.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Chen, L.; Shen, X.; Zhang, Y.; Wang, X. Appointment Scheduling Considering Outpatient Unpunctuality Under Telemedicine Services. Mathematics 2025, 13, 2591. https://doi.org/10.3390/math13162591
Chen W, Chen L, Shen X, Zhang Y, Wang X. Appointment Scheduling Considering Outpatient Unpunctuality Under Telemedicine Services. Mathematics. 2025; 13(16):2591. https://doi.org/10.3390/math13162591
Chicago/Turabian StyleChen, Wei, Liang Chen, Xiaoxiao Shen, Yutao Zhang, and Xiulai Wang. 2025. "Appointment Scheduling Considering Outpatient Unpunctuality Under Telemedicine Services" Mathematics 13, no. 16: 2591. https://doi.org/10.3390/math13162591
APA StyleChen, W., Chen, L., Shen, X., Zhang, Y., & Wang, X. (2025). Appointment Scheduling Considering Outpatient Unpunctuality Under Telemedicine Services. Mathematics, 13(16), 2591. https://doi.org/10.3390/math13162591






