Abstract
This paper explores the strategic implications of technological adoption within shipping logistics service supply chains, with a particular focus on blockchain technology (BCT). When integrating new technologies, supply chain stakeholders evaluate associated risks alongside complexity, profitability, and operational challenges, which influence their strategic behaviors. Anchored in the concept of technology trust, this study examines how different risk preferences affect BCT adoption decisions and freight rate strategies. A game-theoretic model is constructed using a mean-variance utility framework to analyze interactions between shipping companies and freight forwarders under three adoption scenarios: no adoption (NN), partial adoption (BN), and full adoption (BB). The results indicate that risk-seeking agents are more likely to adopt BCT early but face greater freight rate volatility in the initial stages. As the technology matures, strategic variability declines and the influence of adaptability on pricing becomes less pronounced. In contrast, risk-neutral and risk-averse participants tend to adopt more conservatively, resulting in slower but more stable pricing dynamics. These findings offer new insights into how technology trust and risk attitudes shape strategic decisions in digitally transforming supply chains. The study also provides practical implications for differentiated pricing strategies, BCT adoption incentives, and collaborative policy design among logistics stakeholders.
Keywords:
blockchain technology; technology trust; risk disposition; shipping logistics; supply chain strategy; mean-variance analysis MSC:
91-10
1. Introduction
1.1. Background and Motivation
The rapid evolution of Internet technology underscores the strategic imperative of integrating next-generation information technologies with traditional industries to drive the digital transformation of industrial chains [1]. An integral component of the traditional industrial chain, the shipping logistics service supply chain within the shipping industry has emerged as a crucial focal point for transformation [2]. In this context, numerous stakeholders within the port and shipping domains have successively formulated digital development strategies [3]. Notably, blockchain technology (BCT) has been increasingly integrated into shipping logistics services to accelerate operational digitalization [4]. BCT has boundless possibilities to improve supply chain functions, from supply chain provenance to business process reengineering and security enhancement [5,6]. For instance, COSCO Shipping, in collaboration with Shanghai Customs and Shanghai International Port (Group) Co., Ltd. (headquartered in Shanghai, China), has instituted a cross-border trade management big data platform grounded in BCT.
Performing as a key component, freight forwarders often face procedural inefficiencies, including slow, offline quotation and booking procedures, excessive reliance on manual operations, and information lags. the freight forwarding enterprise actively employs BCT to realize the digital transformation. In response, these enterprises have begun implementing BCT-enabled digital solutions. For instance, Maersk partnered with IBM in 2020 to launch TradeLens, introducing the electronic Bill of Lading (eBL). In 2021, MSC followed suit by implementing an eBL service through WAVE BL, achieving a paperless documentation workflow [7]. The challenges associated with freight forwarding business processes are no longer confined solely to freight forwarding enterprises. As the digital transformation accelerates, shipping companies have increasingly extended their reach into the freight forwarding sector. For example, in 2020, Maersk successfully concluded the assimilation of Damco’s business. Utilizing its proprietary freight forwarding enterprise, Maersk proactively engaged cargo proprietors for spatial transactions, launching a portal to technologically elevate the reservation procedure, markedly diminishing the temporal requisites for container bookings. These initiatives signify the shipping conglomerate’s endeavor to bypass intermediary freight forwarding entities and engage in direct transactions with shippers, thereby fostering a homogeneous competition with extant freight forwarding enterprises. The vertical competition between shipping entities and freight forwarders has intensified [8], leading to increased volatility in freight forwarding service pricing, particularly in the wake of the novel coronavirus pandemic, consequently exerting influence on the market demand and profitability of the parties [9].
While BCT plays an increasingly prominent role in supply chain visibility and coordination [10,11], its adoption remains uneven and facing significant uncertainty. A case in point is the discontinuation of TradeLens in November 2022, when Maersk and IBM jointly announced the termination of the platform [12]. This event serves as a reminder that while BCT has the potential to enhance the optimization of maritime logistics service supply chain resource allocation and improve supply chain operations, numerous uncertainties regarding its widespread adoption and application persist within the shipping industry and among member enterprises in the supply chain [13,14].
BCT stands as a nascent technology, and its comprehensive application remains in the realm of experimentation, contributing to a diminishing level of technical reliance among members of the shipping logistics service supply chain. Stated differently, stakeholders within the supply chain exhibit varying risk preferences concerning the adoption of BCT. During the exploratory phase of BCT implementation to enhance operational processes, supply chain participants must consider the stakeholders involved in traditional and blockchain-based operational paradigms. This consideration can mitigate the potential divergence in service quality, thereby averting declines in customer satisfaction and operational stability [15,16].
In the context of blockchain applications still being in an exploratory phase, enterprises within the shipping logistics service supply chain exhibit markedly different strategic responses toward BCT adoption. These differences are closely related to their risk preferences. Risk-tolerant firms are more inclined to adopt BCT early to gain competitive advantages, while risk-averse firms may adopt a wait-and-see strategy due to limited resources, insufficient understanding of new technologies, or high transition costs [17,18]. Such strategic divergence not only affects the extent to which firms can leverage supply chain transparency, but also has profound implications for their freight rate decision-making, market responsiveness, and bargaining power within the supply chain.
Despite the growing attention to the integration of BCT in logistics, extant research has primarily focused on technical implementation, traceability enhancement, or information security [19,20,21]. However, little is known about how freight rate decisions are affected by BCT-enabled transparency, especially when decision-makers differ in their risk preferences. Moreover, existing models often assume homogenous behaviors regarding technology adoption, neglecting the strategic divergence between early adopters and conservative actors. The lack of analytical frameworks capturing competitive freight rate dynamics under asymmetric BCT adoption and heterogeneous risk attitudes represents a significant gap in the literature.
To address this gap, this study incorporates blockchain adoption behavior and risk preference heterogeneity into a mean-variance-based game-theoretic framework, aiming to investigate how strategic competition and risk attitudes jointly influence pricing decisions in a partially digitalized shipping logistics service supply chain. Against this backdrop, this study incorporates blockchain adoption behavior and risk preference heterogeneity into the analytical framework by developing a mean-variance-based game model. The model aims to investigate how firms with different risk attitudes make freight rate decisions under varying degrees of supply chain transparency enabled by BCT. It further explores the strategic interplay between freight rate optimization and blockchain adoption decisions, providing insights into the pricing dynamics and competitive positioning of firms in a partially digitalized shipping logistics service supply chain.
1.2. Research Questions and Contributions
Amidst the peril posed by technological applications in digitally transforming the supply chain of shipping logistics services, this manuscript formulates a game-theoretic model grounded in the research milieu of competitive dynamics within freight forwarding services involving shipping entities and freight forwarders. Its objective is to examine the impact of business rivalry, the inclination of supply chain constituents to embrace BCT, and the responsiveness of service providers to BCT on the pricing determinations of service providers, contingent upon their distinct risk inclinations.
The paper poses three principal research inquiries:
- Q1:
- How do heterogeneous risk preferences affect freight rate decision-making in competitive logistics settings?
- Q2:
- What is the role of blockchain-induced transparency in shaping pricing strategies?
- Q3:
- How do shipping companies and freight forwarders respond strategically under different adoption scenarios (no adoption (NN), partial adoption (BN), and full adoption (BB))?
Although prior research has largely concentrated on horizontal or vertical relationships within the shipping market [22,23], limited attention has been paid to the strategic interactions and competitive dynamics between maritime carriers and freight forwarders—two key yet distinct actors within the shipping logistics service supply chain [9]. This gap underscores the need for analytical models that can capture their interdependent decision-making under emerging digital technologies such as blockchain. This paper examines the impact of competition between two constituents within the supply chain on service pricing from the vantage point of freight agency services. Subsequently, examining the impact of risk attitudes among participants in the shipping logistics service supply chain on freight rates and profitability is conducted to provide the theoretical basis for stakeholders engaged in risk management. Lastly, a scarcity of content on the adaptability of BCT exists within the realm of academic inquiry. This study examines the application of BCT, offering theoretical recommendations for supply chain members.
This study contributes to the literature by (1) integrating mean-variance utility with a game-theoretic model in blockchain-enabled logistics; (2) modeling heterogeneous risk preferences in freight rate decisions under partial or full BCT adoption; and (3) offering insights into risk-sharing mechanisms and investment coordination for improving supply chain resilience.
The subsequent sections of the paper are structured as follows. Section 2 undertakes an examination of the most pertinent literature. Section 3 formulates the foundational game-theoretic model describing the interactions between shipping enterprises and freight forwarding entities. Concurrently, we determine and analyze the equilibrium prices. Section 4 and Section 5 explores the ramifications of pricing dynamics and the promotional interventions of BCT on the market structure. Section 6 encompasses numerical experiments and sensitivity analyses. Finally, Section 7 provides a summary of the research and its conclusions.
2. Literature Review
This study explores the following predominant research avenues: (1) freight rate competition in shipping logistics service chains, (2) supply chain risk, and (3) the adoption of BCT. Presented below are several pertinent studies in this domain.
(1) Freight rate competition in shipping logistics service chains
Freight rate competition is a critical factor in determining market share within the shipping logistics service supply chain, particularly in the face of volatile global trade and fluctuating transport costs [11,24]. A number of studies have investigated pricing mechanisms in this context. Zhou and Lee [25] analyzed optimal pricing for container transportation, incorporating repositioning costs for empty containers. Yin and Kim [26] explored freight rate design when carriers provide transportation services to freight forwarders, considering volume discounts, penalty pricing, and price breakpoints. Xu et al. [27] extended this framework to a three-tier supply chain consisting of a carrier, two forwarders, and multiple shippers, proposing a Stackelberg game model to derive optimal joint pricing and cost-sharing strategies. Chen et al. [28] examined pricing behavior under duopoly and monopoly market structures, showing how market conditions significantly affect freight rate decisions.
While these works provide valuable insights into freight pricing, they largely focus on horizontal competition among carriers, overlooking the increasingly relevant interaction between shipping companies and freight forwarders. This study addresses this gap by modeling non-cooperative freight rate strategies between shipping companies and forwarders, taking into account the influence of blockchain technology and business model evolution in the digital era.
(2) Risk Attitudes in Shipping Services
Beyond singular research on freight competition, scholars have also established a nexus between risk attitudes and pricing determinations. Value-at-risk (VaR) [29], conditional VaR (CVaR) [30], and mean-variance (MV) methods [31] have been employed to scrutinize the risk disposition of decision-makers. Scant literature on risk attitudes exists within the realm of the shipping industry. For instance, Zheng et al. [32] contemplated the competition between a risk-neutral, non-capacity-constrained shipping company and a risk-averse yet capacity-constrained counterpart. Their discourse delves into the ramifications of risk aversion on the pricing strategy of shipping companies in a competitive milieu. Chiu et al. [33] adopted the MV approach to examine the impact of risk attitudes and demand uncertainty on pricing, showing that higher risk tolerance increases price volatility and demand variability. Bai et al. [34] employed a copula-GARCH model to investigate the correlation between freight rates and income across six clean product transportation routes. They conducted CoVaR measurements to test the value at risk among different routes. Li et al. [35] further extended this line of research by adopting an evolutionary game-theoretic approach to show that disruptions like COVID-19 exacerbate strategic risks in maritime logistics, where asymmetric cost and benefit structures among supply chain members—particularly between shipping companies, forwarders, and ports—play a decisive role in shaping dynamic pricing and cooperation behavior. In maritime risk research, scholarly attention has predominantly focused on ship operations [36], accident-related risks [37], extreme weather, geopolitical tensions [38], and market uncertainties [39], reflecting the complex and multifaceted nature of risk in the shipping industry.
Despite these contributions, the existing literature seldom investigates how risk attitudes affect shipping companies’ strategic expansion into downstream services such as freight forwarding, nor does it consider the operational risk associated with emerging technologies like blockchain. This study integrates both market-based price fluctuation risks and the operational risks of blockchain adoption, providing a more comprehensive perspective on risk-embedded pricing behavior.
(3) Blockchain Adoption in Shipping Logistics Supply Chains
In terms of shipping services, numerous intricate stakeholders are required to manage an extensive array of transportation documents, which impede the seamless conveyance of goods between parties [40]. Moreover, challenges such as the arduousness of data sharing, inadequate data confidentiality, suboptimal traceability, and a deficiency in cohesion and trust among diverse public and private stakeholders hinder the realization of integrated supply chains. Consequently, the shipping domain has advocated the utilization of BCT as a remedy for extant challenges [41]. Currently, blockchain research centers focus predominantly on supply chain decision-making. Scholarly investigations into BCT concentrate on the financial sector and supply chain management. For instance, Fan and Zhang [42] applied BCT to securities trading systems to address data tampering risks. Liu et al. [43] incorporated CVaR-based profit-sharing mechanisms in blockchain-enhanced supply chains, highlighting the role of information transparency and risk aversion.
In maritime contexts, Hirata [44] emphasized that early adoption of BCT can facilitate strategic entry. Kim and Shim [45] demonstrated that BCT can increase visibility and reduce administrative bottlenecks, while Jain et al. [46] showed its value in expediting customs clearance. Carlan et al. [47] evaluated blockchain’s role in supply chain integration, identifying both efficiency gains and barriers.
Several studies have applied game-theoretic models to blockchain adoption. Zhong et al. [48] used Cournot and Stackelberg frameworks to analyze pricing during early BCT deployment. Zhao et al. [49] examined blockchain services offered by ports, and Wang [50] investigated how technology investment affects firm strategy, consumer welfare, and equilibrium outcomes. Li et al. [51] adopt a Hotelling model to analyze how competing shipping platforms determine blockchain investment strategies under user single-homing and multi-homing behaviors. Liu et al. [4] use a two-stage Stackelberg game to examine how a shipping firm selects between blockchain and traditional sales channels when facing multiple shippers with heterogeneous preferences.
Nevertheless, most existing works assume uniform adoption and overlook heterogeneous willingness and adaptation capabilities among firms. Moreover, few studies explicitly consider how blockchain adoption risk interacts with pricing and profitability. This paper addresses these gaps by modeling how the willingness and adaptability of shipping companies and freight forwarders toward BCT influence their strategic and pricing behavior under competition.
In summary, three key streams emerge from the literature: (1) freight rate competition, mainly focused on horizontal dynamics among carriers; (2) risk attitudes, often considered in isolation from technology adoption; and (3) blockchain implementation, primarily addressed at a functional or macro level. However, few studies explore the interplay of these factors, especially in the context of strategic rivalry between shipping companies and forwarders. This paper contributes to the literature by (1) shifting the focus from carrier-to-carrier competition to non-cooperative dynamics between shipping companies and freight forwarders; (2) integrating risk attitudes and blockchain adoption risks into a unified freight rate decision framework; and (3) modeling how firms’ heterogeneous willingness and adaptability toward BCT adoption affect pricing, market power, and profitability under competition.
3. Model Hypothesis and Solution
3.1. Model Hypothesis
Within the domain of shipping logistics services, the primary entity offering agency services for the shipper is the freight forwarder company. However, with the evolution and progress of shipping companies, a scenario of homogeneous competition has emerged between the shipping company and the freight forwarder. This paper intentionally excludes considerations of cooperative relationships between freight forwarders and shipping companies to underscore the competitive dynamics between these entities. It posits a scenario wherein a competitive relationship prevails between the two entities. The model is streamlined by assuming the market comprises two shipping logistics service supply chains. One is characterized by the freight forwarder acting as the contract carrier, and the other is dominated by the shipping company. Both entities offer agency services. The shipping company wields greater monopoly power within the shipping market [52]. Therefore, this paper posits that the inception and control of the blockchain alliance are attributed to the shipping company. The shipping company cannot compel blockchain adoption, and the freight forwarder retains the discretion to abstain from participation in the blockchain alliance.
BCT further amplifies this strategic tension. On one hand, BCT adoption allows firms to improve supply chain credibility and information utilization, which may translate into stronger pricing power and higher market share. On the other hand, early adopters face technological and market risks, such as sunk investment costs, uncertain user acceptance, and potential interoperability issues [15,16]. Therefore, firms with different risk preferences are likely to adopt different BCT strategies: risk-tolerant firms may become early adopters to secure first-mover advantages, while risk-averse firms may delay adoption or opt out altogether.
To capture this heterogeneity in adoption behavior, this study adopts a mean-variance (MV) utility framework. The MV approach is widely used in economics and operations research to model decision-making under uncertainty, particularly when both expected returns and risk levels influence strategic choices [53,54]. In the context of BCT, expected utility corresponds to revenue outcomes under enhanced transparency, while variance captures the uncertainty in realizing such benefits.
Moreover, this study is principally structured around three models: (1) The scenario where neither of the service providers engages in the blockchain alliance, denoted as the NN model. (2) The situation in which all service providers embrace the blockchain alliance, denoted as the BB model. (3) The circumstance where the shipping logistics service supply chain dominated by freight forwarding abstains from the blockchain alliance, and solely the shipping logistics service supply chain governed by shipping companies aligns with the blockchain alliance.
According to the research content, referring to Chen et al.’s [55,56] article, the following models are modeled, and the following hypotheses are proposed:
- (1)
- In the shipping market, freight rates are generally positively correlated with transport demand and negatively correlated with the supply of shipping capacity [57]. Numerous scholars have pointed out that under a functioning market economy, greater seller credibility and effective utilization of supply chain information can enable sellers within the supply chain to command higher prices [58]. As commonly done in the literature of market demand, we have employed the classic market demand function, which is linearly influenced by three factors: it decreases with price increases and rises with greater credibility and information utilization.
- (2)
- With the growth of international trade, shipping logistics has rapidly expanded, handling 90% of global transportation and becoming the backbone of trade [59]. Since 2008, the shipping market has generally been in a state of oversupply [60,61]. Thus, we assume sufficient cargo supply to meet carrier operational needs.
- (3)
- In the traditional shipping logistics service supply chain, the information asymmetry between the two chains leads to freight forwarder and shipping company not knowing each other’s actual strategies and the low information exchange efficiency of each supply chain link. After joining the blockchain alliance, the nodes between the supply chains record information in the blockchain to ensure the authenticity and validity of the information and improve the efficiency of information interaction [62,63].
The following models are presented based on the model assumptions described above, and the parameters involved in this paper are shown in Table 1. All parameters involved are positive.

Table 1.
Meanings of notations and parameters.
(1) Base model–No Blockchain Cooperation (NN model)
We define two supply chains: the shipping logistics service supply chain dominated by shipping companies and acting as an agent service provider is s, and the shipping logistics service supply chain dominated by freight forwarding and acting as an agent service provider is h. Figure 1 illustrates the transactional relationships among the entities in the supply chain.
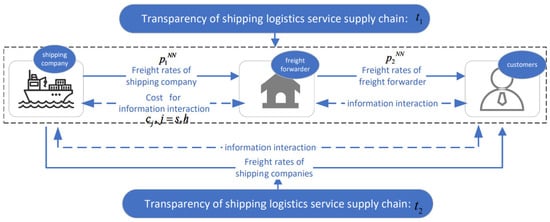
Figure 1.
The operational processes of NN model.
The utility of the shipper choosing s is . The utility of the shipper choosing h is .
According to consumer preferences, the market demand function of consumers for shipping companies or freight forwarders can be obtained as follows:
At this time, the profit function of the shipping company is . The expected profit of the shipping company is . The standard deviation of profit is . The profit function of the freight forwarder is . The expected profit of the freight forwarder is . The standard deviation of profit is .
We use the MV theory to determine the average risk utility function of the shipping company is . The average risk utility function of the freight forwarder is .
denotes risk sensitivity coefficient. When , it denotes that the shipping company or freight forwarder exhibits a risk-seeking disposition, with its utility ascending alongside profit augmentation and profit uncertainty. When , it signifies that the shipping enterprise or freight forwarder manifests risk aversion, with its efficacy escalating concomitantly with profit increments and diminishing in tandem with heightened profit uncertainty. When , it indicates that the shipping company or freight forwarder maintains a risk-neutral stance, wherein its utility surges in tandem with profit escalation, irrespective of the degree of profit uncertainty.
(2) Both Blockchain (BB model)
We assume the shipper’s inclination to opt for a shipping logistics service supply chain that applies BCT is . Among them, 1 and 2 represent the initial and middle stages of blockchain application. Figure 2 depicts the transactional relationships among supply chain entities during the initial phase of blockchain implementation. Figure 3 illustrates the transactional structure among supply chain participants during the intermediate phase of blockchain implementation.
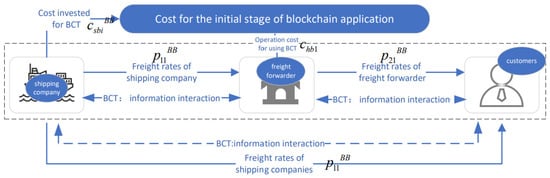
Figure 2.
The operational processes of BB model—initial stages.
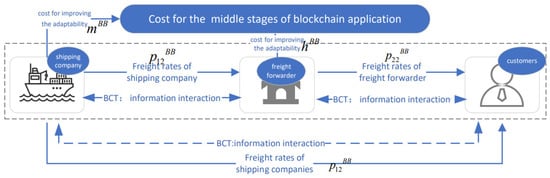
Figure 3.
The operational processes of BB model—middle stages.
The utility of the shipper choosing s is . The utility of the shipper choosing h is . Among them, , .
In accordance with consumer preferences, the market demand function for shipping companies or freight forwarders can be derived as follows:
At this time, the profit function of the shipping company is . The expected profit of the shipping company is . The standard deviation of profit is . The profit function of the freight forwarder is . The expected profit of the freight forwarder is , and the standard deviation of profit is . We use MV theory to determine the average risk utility function of the shipping company is . The average risk utility function of the freight forwarder is .
(3) Only Shipping Company joins BC alliance (BN model)
We assume that the utility of the shipper choosing s is . The utility of the shipper choosing h is , where .
The market demand function of consumers for shipping companies or freight forwarders can be obtained according to consumer preferences as follows:
At this time, the profit function of the shipping company is . Among them, . The expected profit of the shipping company is . The standard deviation of profit is . The profit function of the freight forwarder is . The expected profit of the freight forwarder is , and the standard deviation of profit is .
We use MV theory to know the average risk utility function of the shipping company is . The average risk utility function of the freight forwarder is .
3.2. Model Solution
This study contemplates three models. The equilibrium solution is elucidated using the NN model as an illustrative instance. The determinations of decision variables under the BB and BN models are expounded in Appendix A. The fixation of freight rates by shipping companies and freight forwarders is executed through profit maximization. The first order condition for maximizing the profit of the shipping company is . The first-order condition for maximizing the profit of the freight forwarder is . The second derivative of the maximum value is , . We can determine the optimal freight rate is .
The derived optimal freight rate is incorporated into the anticipated profit and standard deviation for the shipping company and the freight forwarder:
4. Equilibrium Price Analysis
4.1. Shipper Preference Analysis
Corollary 1.
The analysis of the three models indicates that when , , otherwise . If other factors, such as , , , when , , otherwise .
Proof.
(1) NN model. From the obtained optimal freight rate, the price difference between the shipping company and the freight forwarder is . Obviously, , .
The pricing set by the shipping company surpasses that of the freight forwarder; conversely, the pricing of the shipping company falls below that of the freight forwarder. This observation indicates that when the shipper’s inclination is more pronounced, the pricing by the service provider exceeds that of the competitor. This pronounced inclination is attributable to the heightened willingness of the shipper, resulting in a larger market share for the service provider and increased market demand. Observation shows that the shipper’s inclination is correlated with risk disposition and the transparency of the shipping logistics service supply chain. Moreover, the threshold represented by diminishes with an augmentation in and dwindles with an escalation in .
(2) In the BB model, analogously, based on the derived optimal freight rate, the initial stage price differential between the shipping company and the freight forwarder in implementing BCT is denoted as
When , . On the contrary, .
The price difference between the shipping company and the freight forwarder in the medium term of BCT application is
When , , otherwise, . Aligned with the NN model, whether during the initial or intermediate phase of BCT application, a direct correlation prevails, and the larger the market share, the more elevated the freight rates set by service providers compared to their competitors. In the BB model, the transparency of the supply chain is fixed at 1 because of the implementation of BCT. During this period, the magnitude of the threshold is dependent on the risk disposition of the service provider and the investment cost incurred by the service provider for the assimilation of BCT.
(3) BN model
Consistent with the abovementioned models, an overarching trend prevails: the greater the market share, the more elevated the freight rate. Simultaneously, the threshold during this juncture is interconnected with the risk disposition of the service provider and the extent of assimilation of BCT. □
Corollary 1 explains the existence of a threshold demarcating the segmentation of the shipping logistics service market into two scenarios. Specifically, a corresponding increase in market share occurs when the shipper’s consumer willingness is heightened. The proof process further reveals a substantial correlation between the magnitude of the threshold and the prevailing risk disposition. The threshold decreases with the increase of and decreases with the increase of , indicating that when the service provider pursues risk, its freight rate is higher than that of competitors.
This corollary highlights the importance of understanding consumer preference distribution when designing freight rate strategies. Shipping companies with stronger brand influence or contractual leverage are justified in charging higher prices, especially under symmetric blockchain adoption. Risk sensitivity parameters further nuance this strategy, suggesting that managers should evaluate their competitors’ risk attitudes when setting pricing benchmarks.
A practical example is Maersk’s early adoption of the TradeLens platform. As a market leader with strong customer loyalty, Maersk was able to maintain premium pricing in its blockchain-enabled offerings. In contrast, many smaller freight forwarders adopted a wait-and-see approach due to perceived implementation risk and uncertain payoffs, validating the model’s implication that higher baseline market preference correlates with more favorable pricing power under blockchain adoption.
This result suggests that full blockchain adoption leads to a more predictable and balanced pricing environment. For supply chain managers, encouraging both shipping companies and freight forwarders to adopt blockchain jointly can mitigate pricing volatility and foster stable contractual relationships.
4.2. Risk Attitude Analysis
Discussing the influence of equilibrium price on risk attitude, Corollarys 2 and 3 can be obtained.
Corollary 2.
(1) The equilibrium price of the service provider diminishes with the escalation of its risk sensitivity coefficient and that of the competitor. When the service provider pursues high risk (for example, in the NN model, , , the augmentation of the equilibrium price amplifies the propensity of the shipping company (or freight forwarder) to cover associated costs. Conversely, in instances where service providers are averse to risk, the ascent in price diminishes the willingness of the shipping company to shoulder risk-related costs. Conversely, in cases where service providers are risk-averse, the price rise diminishes the shipping company’s willingness to assume the costs associated with risk.
Proof.
Examine the influence of risk disposition on freight rate determination across the three models. As indicated in Section 3.1, specifically in the NN model, the optimal freight rate for the shipping company and the freight forwarder can be determined by differentiating the first derivative:
□
Similarly, within the BB and BN models, the freight rates set by shipping companies and freight forwarders exhibit a decline with an augmentation in the risk sensitivity coefficient of the shipping company and the risk sensitivity coefficient of its competitors. Observing Corollary 2: (1) In the NN model, the freight rates established by shipping companies and freight forwarders decrease when their individual risk sensitivity coefficient and that of their competitors are augmented. This observation implies that when the shipping company and the freight forwarder bear a heightened risk, a predisposition to perceive market demand as volatile and the market as contracting exists. Consequently, the freight rate is diminished to capture a larger market share. The shipping company or freight forwarder mitigates prices in scenarios where competitors shoulder increased risks, which can be attributed to the higher risk of competitors leading to a concurrent reduction in their pricing, thereby decreasing the equilibrium price in the agency service market. (2) When the shipper’s inclination to choose is intensified, the shipping company and the shipping agent amplify the freight rate in tandem with a pursuit of elevated risk. When shipping companies and freight forwarders embrace heightened risk, the inverse correlation emerges: the more pronounced the willingness to bear the cost of information sharing, the steeper the decrease in pricing with an escalation in willingness. Conversely, when shipping companies and freight forwarders opt for risk aversion, a positive correlation surfaces: the diminished willingness to bear the cost of information sharing corresponds to escalated pricing. This phenomenon arises from the perspective that heightened risk among shipping companies and freight forwarders is associated with a belief that greater information sharing enhances market demand, prompting an escalation in freight rates to attain market stability.
Corollary 2 suggests that risk-sensitive firms may reduce prices to mitigate market uncertainty or defensively secure market share. This is particularly relevant in competitive environments where rival firms exhibit high levels of risk aversion, prompting aggressive price reductions. Online freight marketplaces like Freightos allow for real-time rate adjustment based on competitive intelligence and risk assessments [64]. Firms utilizing these platforms can dynamically adjust pricing in response to perceived competitor behavior, reflecting the model’s insight that risk attitudes directly affect pricing strategy in digital logistics ecosystems.
The BN model leads to asymmetrical pricing power, favoring the blockchain adopter. This finding highlights the risk of unilateral technology investment in competitive settings. Managers should pursue bilateral blockchain adoption or implement contracts that ensure information reciprocity to prevent strategic disadvantage.
Corollary 3.
(1) In instances where the service provider adopts a risk-averse stance, its expected profit ascends with an augmentation in its risk attitude coefficient; conversely, the expected profit diminishes with an increase in the risk attitude coefficient. (2) In scenarios where there is a contrast in risk attitudes between the shipping company and the freight forwarder, such as when the freight forwarder embraces heightened risk, the shipping company attains the maximum expected profit solely when risk is either avoided or prudently pursued.
Proof.
(1) NN model. The derivative of the expected profit concerning the risk attitude coefficient can be obtained by solving the equilibrium price as follows:
The second derivative shows that when , or , and that is a convex function.
Hence, when the shipping company leans towards risk aversion, the anticipated profit of the shipping company escalates with an augmentation in the risk attitude coefficient of the shipping company. When , is a convex function.
Nevertheless, the anticipated profit of the shipping company declines with an increase in the risk attitude coefficient of the shipping company. From , the risk attitude coefficient of the shipping company is correlated with the risk attitude of the freight forwarder, displaying an ascending trajectory.
When , or when , is a convex function. Hence, when the freight forwarder exhibits a low inclination for high risk or pursues risk aversion, its anticipated profit diminishes with an increase in the risk attitude coefficient of the freight forwarder.
When , the freight forwarder pursues high risk, its expected profit increases with the increase of the freight forwarding risk attitude coefficient. If the shipping company chooses risk aversion, and , the risk coefficient of the freight forwarder is related to the risk attitude of the shipping company, indicating an upward trend.
(2) BB model. Similarly, in the early stage of the application of BCT, when . In this formula, , and when , , is a convex function. In essence, when the freight forwarder opts for risk avoidance or exhibits a lesser inclination for high risk, the expected profit function of the shipping company diminishes with an increase in its risk attitude coefficient. Conversely, in instances where the freight forwarder actively pursues high risk, the expected profit of the shipping company rises with an augmentation in its risk attitude coefficient.
When , the risk attitude coefficient of the shipping company increases with the increase of the risk attitude coefficient of the freight forwarder. When .
In this formula, if , then , and when , is a convex function, indicating that when the shipping company adopts a risk-averse stance or exhibits a diminished inclination for high risk, the expected profit of the freight forwarder rises with an increase in the risk attitude coefficient of the freight forwarder. The freight forwarder is more willing to pursue high risk in such instances. Conversely, suppose the shipping company’s propensity for high-risk pursuits is heightened. In that case, the expected profit of the freight forwarder declines with an increase in the risk attitude coefficient of the freight forwarder, signifying a greater inclination of the freight forwarder to avoid risks.
In the middle of the application of BCT,
.
In this formula, when , , and is a convex function. In essence, when the shipping company actively pursues high risk, the expected profit of the freight forwarder rises with the increase in the risk attitude coefficient of the freight forwarder, and the freight forwarder avoids risk. Conversely, when the shipping company is risk-averse or exhibits a limited willingness to pursue high risk, the expected profit of the freight forwarder diminishes with an increase in the risk attitude coefficient of the freight forwarder, and the freight forwarder leans towards pursuing high risk.
(3) BN model. When the freight forwarder actively pursues high risk, the expected profit of the shipping company increases with the increase in the risk attitude coefficient of the shipping company. Conversely, when the freight forwarder avoids risk, the expected profit of the shipping company diminishes with an increase in the risk attitude coefficient of the shipping company. In instances where the shipping company pursues high risk, the expected profit of the freight forwarder increases with an augmentation in the risk attitude coefficient of the freight forwarder while accounting for the risk aversion of the freight forwarder. On the contrary, when the shipping company is risk-averse, the expected profit of the freight forwarder declines with an increase in the risk attitude coefficient of the freight forwarder, and the freight forwarder leans towards pursuing high risk. □
The equilibrium result of Corollary 3 shows that under the NN model, the game becomes more intense, with both parties more likely to adopt aggressive pricing strategies to capture market share. This reflects a “prisoner’s dilemma” scenario, where the absence of a trust mechanism (such as blockchain) causes a cooperative game to devolve into a non-cooperative, self-interested competition. When neither party adopts blockchain, aggressive competition emerges, reducing overall profits. This underscores the strategic cost of non-adoption. Practitioners should view blockchain not only as a technical upgrade but also as a cooperative tool to prevent value erosion in logistics networks.
Corollary 3 implies that misalignment in risk preferences between supply chain partners can lead to intensified competition or suboptimal profit outcomes. Managers must strive for strategic coordination and risk alignment through joint investments, contracts, or digital governance mechanisms to prevent volatility and value erosion. This dynamic closely parallels the freight rate war during early 2020, when many carriers refrained from blockchain-enabled coordination amid COVID-19 disruptions. Without trusted information-sharing mechanisms, players sacrificed margins to capture transient market share, leading to collective value erosion—a pattern directly predicted by the model.
5. Impact of the Application of BCT
5.1. Impact on Freight Rate Decision-Making
The shipper’s inclination towards implementing BCT and the service provider’s capacity to incorporate BCT are assessed to analyze the determination of freight rates.
Corollary 4.
(1) When , the freight rate of the service provider increases with the shipper’s willingness to apply BCT, and as the value of increases, the freight rate of the service provider decreases with the increase of willingness. (2) When , , .
The shipper’s inclination to adopt BCT exerts the most significant influence on the freight rate of the shipping company within the BB model. It has the most pronounced impact on the change in freight rates within the BN model. Conversely, if , the shipper’s willingness to adopt BCT has the least consequential effect on the freight rate of the shipping company in the BN model.
Proof.
First, after comparing the NN and the BB models, the shipping company and freight forwarder’s freight rates change. By comparing the freight rates of the initial shipping companies and freight forwarders, we determine that , .
The relationship between freight rate change and risk attitude is analyzed. The risk coefficient of the shipping company and the freight forwarder is obtained for the price difference and is obtained. Corollary 3 shows that when the service provider pursues high risk appropriately, that is, , the profit of the service provider is maximized, and , . That is, the freight rate after the application of BCT is higher than that without the application of BCT and increases with the increase of the willingness to apply technology.
We then compare the price changes in the NN model and the BN model period. In the early stage of the application of BCT, the freight rate difference of the shipping company is , and the freight rate difference of the freight forwarder is . Combined with Corollary 3, we can determine that , , and , .
Following the implementation of BCT, the freight rate of the shipping company increases with the increase in the shipper’s willingness. In contrast, the freight rate of the freight forwarder diminishes with an increase in the shipper’s willingness.
Finally, the freight rates of the BB and the BN models are compared. Taking the initial application of BCT as an example, the price difference between the two models is , .
Similarly, combined with Corollary 3, it can be seen that when the service provider properly pursues high risk, , , and , . Therefore, the freight rates of shipping companies and freight forwarders in the BB model are higher than those in the BN model, and the difference in freight rates decreases as the shipper’s willingness to use BCT increases. □
Corollary 4 (1) delineates that adopting new technologies is dependent on the shipper’s receptivity to the technology, influencing the freight rate determination of the service provider. The propensity for a higher willingness to adopt BCT corresponds to a more substantial increase in the freight rate of the service provider post-implementation of BCT. (2) When the market demand of the service provider is more sensitive to alterations in the pricing of the other party, the freight rate of the shipping company experiences a more pronounced impact from the shipper’s willingness during the application of BCT.
This corollary measures the impact of different risk preference coefficients on optimal pricing, demonstrating the pattern that greater risk aversion leads to more conservative strategies. It highlights the importance of behavioral economics in supply chain pricing, especially during the early stages of digital transformation. Higher risk aversion results in more conservative pricing strategies. This finding suggests that understanding partner firms’ risk profiles is crucial. Supply chain managers should incorporate behavioral assessments when negotiating freight contracts, especially under technological uncertainty. Corollary 4 confirms that customer readiness and digital maturity significantly shape the pricing impact of blockchain adoption. Service providers should evaluate their clients’ willingness to engage with BCT-enabled processes before implementing aggressive pricing strategies linked to digital services. For example, MSC’s phased deployment of blockchain-based eBL services illustrates a targeted rollout approach aligned with market readiness. On select trade lanes, MSC coordinated with shippers that demonstrated higher digital capabilities, reducing adoption resistance and maximizing value capture.
Corollary 5.
(1) After the application of BCT, the equilibrium price increases with an augmentation in the adaptation coefficient to the blockchain. (2) The primary and immediate factor influencing the adaptability of the blockchain on the freight rate of the service provider is the investment cost borne by the service provider. A greater investment in unit cost corresponds to a more pronounced impact on the difference in freight rates attributable to adaptability.
Proof.
According to the equilibrium price solution, for the first derivative, we can obtain , , , , .
It is evident that when the shipping company adopts BCT, the augmentation in the degree of adaptation to the blockchain increases its freight rate. Similarly, if the freight forwarder embraces BCT, an elevation in the degree of adaptation to the blockchain corresponds to an increase in the freight rate of the freight forwarder. Conversely, in scenarios where only the shipping company adopts BCT, and the freight forwarder does not, the freight rate of the freight forwarder decreases with an increase in the service provider’s adaptation to the blockchain. This scenario underscores that a heightened degree of adaptation to the blockchain exerts a more substantial impact on the freight rate decision of the service provider. The freight rate changes in the NN and the BB models are compared. First, the freight rate in the initial application of the BB model is compared with that in the NN model. From Corollary 4, we know that . Second, compared with the BB model in the middle of the application, the freight rate changes of the shipping company and the freight forwarder, we can obtain the following: , .
The foregoing analysis clearly shows that when the shipping company and the freight forwarder adopt BCT, the growth rate of the initial freight rate difference is consistent, increasing at the rate of . In the interim application phase, the growth rate of the freight rate difference is contingent on the unit adaptation cost h, m, with a higher investment in cost resulting in a faster increase in freight rates. Specifically, when only the shipping company adopts BCT, the freight rate difference increases with the increase in adaptability to the blockchain. In contrast, the freight rate difference of the freight forwarder diminishes with increased adaptability to the blockchain. A heightened degree of adaptation to the blockchain corresponds to an elevated freight rate in the service provider’s decision-making. Compared to the freight rate decision when both parties exhibit a high degree of adaptation to BCT, the shipping company commands a higher freight rate when the freight forwarder refrains from adopting BCT. □
Corollary 5 reveals that when the risk preference coefficient is relatively small, the weight of expected returns dominates the decision-making process, leading to more aggressive pricing behavior. This aligns with real-world observations where risk-seeking firms tend to set higher prices in pursuit of greater returns, but such behavior also increases the likelihood of price wars and volatility in the logistics market. When firms exhibit high risk-seeking behavior, the resulting freight rates tend to be more aggressive, potentially leading to volatility in the logistics market. Managers should monitor partners’ risk-seeking behavior and establish hedging or stabilization mechanisms—especially in environments lacking price regulation. This is consistent with Hapag-Lloyd’s digital booking platform upgrades, which enabled early adaptability to eBL systems and yielded selective pricing advantages. The BN scenario highlights the penalty for asymmetric adaptability—when the freight forwarder lags in technology integration, its rate declines relative to the shipping company. These findings emphasize that adaptability investment must be bilateral to avoid pricing imbalance and market power asymmetry.
5.2. Impact on Profit
The financial performance of service providers before and after engaging in BCT is suboptimal, prompting an analysis of the impact of BCT application on profits.
Corollary 6.
(1) When , the profit function of the service provider decreases with the increase of , and when and the profit function of the service provider increases with the increase of . (2) Compared with the NN model, when , the profit margin of service providers in the BB and the BN models increases with the increase of , and when , the profit margin of service providers in the BB and the BN models decreases with the increase of .
Proof.
In the BB model, in the early application of BCT,
,
,
, .
In the middle of the application of BCT, we can know that
, .
has an extreme value, and the profit function of the service provider is concave, that is, when , the profit function of the service provider decreases with the increase of , and when , the profit function of the service provider increases with the increase of .
Similarly, in the BN model, has a minimum value, and the profit function of the service provider is concave, that is, when , the profit function of the service provider decreases with the increase of , and when , the profit function of the service provider increases with the increase of .
We compare the profit difference between the service providers in the NN and the BB models. From Section 4.1, ,
, . The above formula shows the existence of a threshold, when , is a monotonically decreasing function. In other words, when the willingness to adopt BCT increases, the profit difference of the shipping company between the two models diminishes. Conversely, when , the profit difference of the shipping company increases with the augmentation of the willingness to apply BCT.
Similarly, , . When , is a monotonically decreasing function, that is, when the profit difference of freight forwarders in the two models decreases with the increase of the willingness to apply BCT. On the contrary, when , the profit difference of freight forwarders increases with the increase of the willingness to apply BCT. It can be seen that the profit of freight forwarders also increases with the increase of the application of BCT.
Secondly, the profits of the NN and the BN models are compared. Similarly, we know that the profit margin of the shipping company under the BN model and the NN model is . When , is a monotone decreasing function, that is, when the profit difference of the shipping companies in the two models decreases with the increase of the willingness to apply BCT. On the contrary, when , the profit margin of the shipping company increases with the increase of the willingness to apply BCT. The profit difference of the freight forwarder is . When , A is a monotonically decreasing function, that is, when the profit difference of freight forwarding in the two models decreases with the increase of the willingness to apply BCT. On the contrary, when , the profit difference of freight forwarding increases with the increase of the willingness to apply BCT. □
Corollary 6 demonstrates that even when two firms adopt the same level of blockchain technology, differing risk preferences may lead to divergent pricing outcomes, and vice versa. This indicates that strategic alignment requires not only technological coordination but also behavioral compatibility. Both dimensions must be considered jointly to achieve true strategic synergy in supply chain partnerships. The interaction between blockchain adoption status and risk preference significantly affects price dispersion between firms. Managers should consider not only technology alignment but also behavioral compatibility when forming partnerships or alliances.
Corollary 7.
(1) When , the profit of the service provider decreases with the increase of the initial service provider’s adaptation to the blockchain. When , the profit of the service provider increases with the increase of the initial service provider’s adaptation to the blockchain. (2) In the later stage of BCT, when , , the profit of the service provider decreases with the increase of the service provider’s adaptation to the blockchain; on the contrary, the profit of the service provider increases with the increase of the service provider’s adaptation to the blockchain. The proof of Corollary 7 is similar to that of Corollary 6.
Corollary 7 shows that the relationship between supply chain transparency (e.g., enhanced by blockchain) and profit is not linear. Instead, it exhibits diminishing marginal returns beyond a certain threshold. This supports empirical observations that excessive transparency may lead to information redundancy or excessive costs, suggesting the need for a cost–benefit evaluation in blockchain investments. Profit does not increase linearly with transparency; instead, it shows diminishing returns beyond a certain point. Managers should be cautious about overinvesting in blockchain visibility and should evaluate marginal gains against implementation costs.
These corollaries jointly demonstrate that blockchain adoption and freight rate decisions are deeply shaped by asymmetric preferences, digital maturity, and coordination readiness across the supply chain. Firms must align technological investments with partner capabilities and market receptivity to fully realize the strategic benefits predicted by the model.
6. Data Analysis
The data analysis segment examines the variations in influential factors affecting the market demand trend of two shipping logistics service supply chains under the state of blockchain application. The subsequent section delineates the assignment of model parameters: , , , , , , , .
6.1. Equilibrium Price and Expected Profit Analysis
(1) Table 2 shows the equilibrium price analysis reveals three critical patterns in stakeholder dominance.

Table 2.
Equilibrium prices and dominant stakeholders.
NN Model Dominance by Freight Forwarders. Under all risk attitudes, freight forwarders consistently maintain lower equilibrium prices () and capture larger market shares. Without blockchain, traditional information asymmetry favors forwarders’ operational flexibility. Risk aversion () further amplifies this advantage, as forwarders reduce prices by 4.2% (from 115 to 110 when ) to attract shippers.
BB Model: Shipping Companies’ Blockchain Premium. When both parties adopt blockchain and pursue risk (), shipping companies command a 3.7% price premium ( vs. ). Blockchain integration enhances shipping companies’ credibility (captured by in utility functions), allowing them to leverage scale advantages. Risk-seeking behavior further increases their willingness to invest in BCT adaptability, boosting prices. The higher premium under risk-seeking reflects investments like Maersk’s significant early spending on TradeLness, betting on long-term dominance.
BN Model: Asymmetric Adoption Penalty. If freight forwarders avoid blockchain () while shipping companies adopt it, a 28% price gap emerges ( vs. ). Forwarders’ resistance to BCT erodes shipper trust (reflected in ), forcing them to cut prices to retain demand. This scenario closely reflects the position of smaller freight forwarders following the initial rollout of TradeLens (prior to its termination). As major carriers such as Maersk launched blockchain-enabled digital booking platforms, traditional forwarders experienced a decline in perceived trustworthiness. Lacking comparable technological capabilities, many responded with aggressive price cuts, resulting in substantial margin compression—particularly for mid-sized firms struggling to maintain differentiation. The failure of TradeLens in 2022, partly due to limited participation from rival carriers and forwarders, underscores the strategic dilemma captured by our BN model: unilateral adoption may distort market dynamics, while non-adoption risks competitive marginalization.
Blockchain adoption shifts market power. Shipping companies dominate when BCT is widely adopted (BB) or unilaterally implemented (BN), while forwarders lead only in traditional (NN) settings. Risk-seeking attitudes amplify this divergence.
(2) Figure 4 shows the equilibrium profit from the standpoint of risk attitude and the shipper’s preference. The remaining influencing factors are assigned, , , , .

Figure 4.
Equilibrium profit under risk attitudes.
The graph shows that as the consumer preference value diminishes, approaching tending to 0, the expected profit of the shipping company increases more rapidly. In contrast, the expected profit of the freight forwarder sees a more gradual increase. Following the application of BCT, with lower consumer preference, the expected profit of the shipping company increases faster than that of the freight forwarder. Among these observations, the closer the expected profit-risk attitude of the shipping company approaches 0, the more rapid the profit increase in the later stages of BCT application compared to the early stages, indicating a greater inclination towards risk aversion by the shipping company. Similarly, the expected profit of freight forwarding exhibits a stronger propensity towards risk aversion in the later stages of blockchain application. In scenarios where consumer preference is high, the expected profit growth rate for the shipping company is lower than that of the freight forwarder. However, both shipping companies and freight forwarders still display a prevailing inclination towards risk aversion. In cases where only freight forwarders do not adopt BCT, a higher consumer preference leads to a more consistent trajectory in the expected profit growth or decline of the shipping company’s service. In the intermediate stages of BCT application by shipping companies, the higher the risk aversion of the freight forwarder, the greater the expected profit. When it reaches the threshold , the expected profit increases with the increase of the risk attitude coefficient when pursuing risk. Obviously, with higher consumer preference, the shipping company’s application of BCT is associated with a lower inclination towards risk. Conversely, in the case of freight forwarding, where only the shipping company adopts BCT, there is a greater likelihood of pursuing the benefits of high risk.
Freight rates under the BB scenario are consistently higher than those under BN and NN scenarios. This aligns with practical observations in digital container shipping platforms such as Maersk’s TradeLens and COSCO’s Global Shipping Business Network (GSBN), where bilateral BCT adoption facilitates information transparency and process automation, enabling premium pricing. In contrast, NN scenarios resemble low-coordination conditions during early pandemic phases or Red Sea crises, where lack of shared trust and visibility induced price volatility and competition-driven rate suppression.
6.2. Impact of Shipper’S Willingness to Use BCT on Expected Profit
As in Section 6.1, other influencing factors are assigned, , , .
As shown in Figure 5, there is a threshold that allows the shipping company to avoid risks, and when , its expected profit increases with the shipper’s willingness to use BCT. On the contrary, when the shipping company pursues risk, and when , its expected profit decreases with the increase in the shipper’s willingness to use the blockchain.
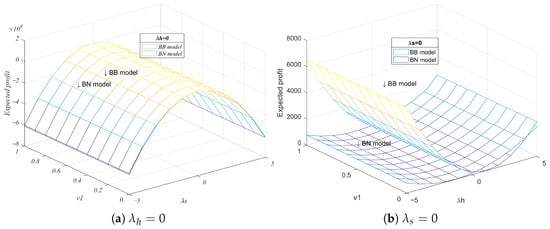
Figure 5.
Expected profit change of the shipping company.
Similarly, a threshold emerges when the shipping company adopts a risk-neutral stance while freight forwarding pursues risk. In the BB model, the expected profit of the shipping company rises with an increase in the shipper’s willingness to use BCT. The more minimal the increase, the more substantial the expected profit increase when the freight forwarding risk is avoided. In the BN model, the increment in the shipper’s willingness to use BCT leads to a less substantial increase in the expected profit of the shipping company.
Conversely, as shown in Figure 6a, in the BN model, when the shipping company pursues high risk, the expected profit of the freight forwarder rises with an increase in the shipper’s willingness to use BCT. In the BB model, when the shipping company embraces high risk, the expected profit of the freight forwarder declines with an increase in the shipper’s willingness to use BCT. As shown in Figure 6b, when the shipping company is risk-neutral, the expected profit of the freight forwarder diminishes with its pursuit of high risk or risk aversion while increasing with an elevation in the shipper’s willingness to use blockchain technology. Notably, the expected profit of the freight forwarder under the BN model surpasses that under the BB model.
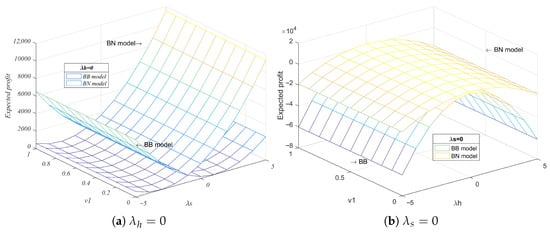
Figure 6.
Expected profit change of the freight forwarder.
The consumer preference coefficient directly affects pricing power, especially for shipping companies under the BB model. This outcome is evident in the premium-tier strategies of Maersk and CMA CGM, where brand-recognized BCT-enabled services appeal to shippers with higher digital affinity. In contrast, less digitally mature clients—such as those in Africa or South America—may push equilibrium towards the BN or NN model’s pricing zone.
6.3. The Impact of Blockchain Adaptation on Expected Profit
Assign values to the remaining influencing factors, , , , .
The impact of on the expected profit in the initial stage of blockchain application is examined. As depicted in Figure 7a, when both the shipping company and the freight forwarder exhibit risk neutrality, the expected profit of the service provider increases with an augmentation in the service provider’s adaptability to the blockchain. However, in comparison with the BB model, the most substantial increase is observed in the expected profit of the freight forwarder in the BN model. Moreover, the expected profit in the BB model tends to decrease with the elevation of the service provider’s adaptability to the blockchain. When = = 0, freight forwarders in BN models gain more higher profits than BB models.
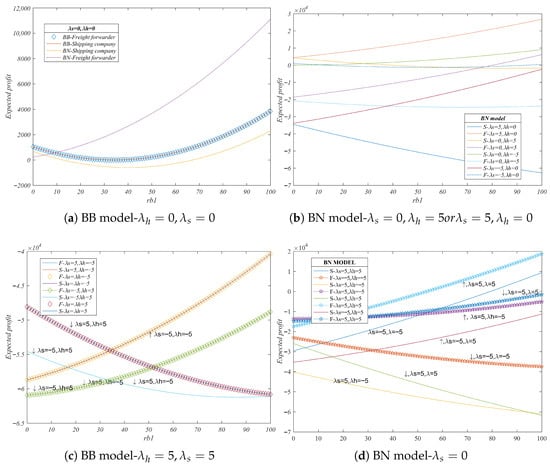
Figure 7.
Profit sensitivity to blockchain adaptability .
In Figure 7b, it can be found that only when the shipping company is risk-averse and the freight forwarding is risk-neutral, the expected profit of the shipping company in the BN model will increase with the increase of . In other cases, as long as one party is risk-neutral, the expected profit of the shipping company will decrease with the increase of .
Figure 7c,d illustrate the influence of on the expected profit of service providers in the BB and BN models when freight forwarders and shipping companies are in a state of risk aversion or risk pursuit, respectively. Under the influence of , shipping companies display a greater inclination to avoid attaining profits, while freight forwarders exhibit a heightened willingness to pursue risks to enhance their profits. As risk aversion increases (higher ), both shipping and freight rates decrease, particularly in the BB scenario. This indicates that risk-averse firms adopt more conservative pricing strategies, and the stabilizing effect of blockchain is more pronounced when both parties adopt it. This validates the conservative pricing strategies adopted during high-risk events like the 2021 Suez Canal blockage or COVID-19 lockdowns. In these cases, even digitally capable carriers lowered their rates to maintain service continuity and mitigate capacity uncertainty, a behavioral pattern the model effectively captures.
Figure 8 shows that in the BB model, when the risk attitude of the service provider is not considered, the expected profit of the service provider increases with the increase of , . When the freight forwarder pursues risk, the expected profit of the shipping company decreases with the increase of , . When the freight forwarder is risk-averse or risk-neutral, the expected profit of the shipping company increases with the increase of , , and the increase of the expected profit of the shipping company is the highest when the shipping company pursues risk. Similarly, when the shipping company pursues risk, the expected profit of the freight forwarder decreases with the increase of , . When the shipping company is risk-neutral or risk-averse, the expected profit of the freight forwarder increases with the increase of , , and the expected profit growth rate is greater when the shipping company is risk-averse. Comparing NN, BN, and BB scenarios under varying levels, the BB case consistently yields the highest total profit and the most stable price structure. BN shows asymmetry, with freight forwarders gaining more benefit due to early transparency advantage.
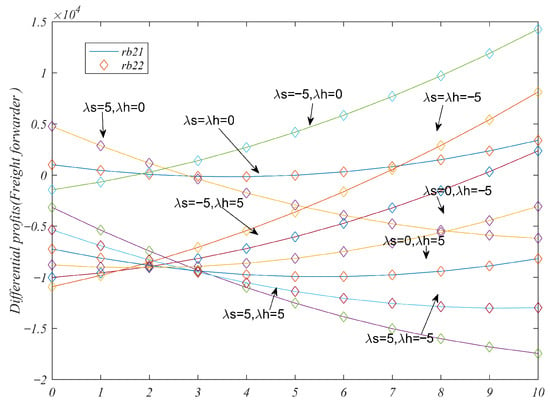
Figure 8.
Total profit comparison across blockchain scenarios.
Figure 9 shows that in the BN model, the expected profit of the service provider increases with the increase of . For the shipping company, a heightened degree of adaptation of the service provider to the blockchain corresponds to an elevated expected profit when the freight forwarding risk is avoided. In the case of freight forwarding, when the shipping company embraces risk, its expected profit is most significantly influenced by the adaptability of blockchain. The freight forwarder’s profit is highly sensitive to the shipping company’s adaptability, especially if the forwarder is risk-seeking. This mirrors the dependency of non-adopting forwarders on the quality and integration ease of carriers’ blockchain systems. A poorly adapted or closed system forces forwarders into inefficient manual workarounds, harming profit. This underscores the risk for forwarders staying out of blockchain alliances if major carriers drive adoption.
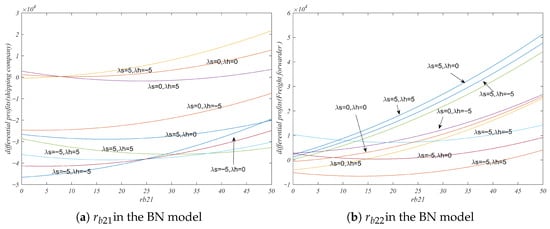
Figure 9.
Sensitivity of the expected profit of service provider to , in the BN model.
The consistent result is that the BB scenario (full adoption) yields the highest and most stable total system profit (Figure 8). This strongly supports industry moves towards collaborative blockchain consortia like GSBN, which focuses on trusted data exchange between carriers, terminals, and customs, improving efficiency and reducing disputes, aligning with the BB model’s profit potential through system-wide transparency and coordination. The lower and more volatile profits in the NN scenario reflect the well-documented inefficiencies of the traditional, paper-based, siloed shipping processes, plagued by delays, errors, fraud risks, and intense, margin-eroding price competition—problems blockchain specifically aims to solve.
The results suggest that in partial adoption settings (BN), freight forwarders tend to benefit more due to unilateral transparency advantages. However, in full adoption (BB), both parties share the gains, suggesting the importance of mutual commitment. In contrast, the NN scenario reflects a situation where both lose with intensified price competition. Therefore, coordinating the timing of BCT adoption and promoting symmetric information sharing are crucial for achieving mutual benefit.
This study has several limitations. First, the use of mean-variance utility simplifies real-world decision-making behavior and may not capture nonlinear or bounded rationality effects (e.g., loss aversion). Second, blockchain adoption is modeled as a binary choice, while in practice, adoption may be partial, phased, or hybrid. Third, the model abstracts away from multi-party interactions involving regulators, port authorities, or customs agents, which may affect decision outcomes. Lastly, the analysis is based on numerical simulations with stylized parameters; future work could empirically calibrate the model using real data or validate it through case studies in port logistics environments.
7. Conclusions
This paper analyzes the risk attitude in the competitive landscape of shipping logistics service supply chains employing three distinct applications of blockchain technology. It concludes by analyzing the competition between shipping companies and freight forwarders. The discussion encompasses freight competition among service providers under varying risk attitudes, the adaptability of service providers to the blockchain, and the impact of supply chain members’ willingness to use BCT on equilibrium price and profit. This study addressed four central research questions. It was found that risk attitudes substantially affect freight rate strategies in both competitive and cooperative settings. Blockchain transparency mitigates information asymmetry, but its effect varies with adoption scope. The NN scenario results in a prisoner’s dilemma, while BB leads to joint gains. Moreover, when one party adopts blockchain alone (BN), imbalance emerges. These findings highlight that pricing strategies in digital logistics are co-determined by behavioral risk profiles and technological trust structures. The following key findings are deduced:
(1) In the absence of a BCT application, when service providers opt for high-risk strategies, the equilibrium price experiences a decrease. In scenarios where the risk attitude of one party contradicts that of competitors, the service provider will lower its price to maintain market stability.
The equilibrium price is observed to influence the willingness to bear the cost. Pursuing high risk reduces the equilibrium price, diminishing the willingness of service providers to incur the cost of information sharing. Conversely, when avoiding risks, the equilibrium price elevates the willingness of service providers to share information.
As to the expected profit of service providers, choosing to avoid risks leads to an increase in expected profit with an escalation in the risk coefficient, while pursuing risks results in a decrease in expected profits with an increase in the risk coefficient.
(2) After the implementation of BCT by the service provider, when the service provider adopts a risk-pursuing strategy, the freight rate decreases with an increase in the shipper’s willingness to use BCT. In the BB model, the shipper’s willingness to use BCT exerts a greater impact on the shipping company’s freight rate than on the freight forwarding rate. In contrast, in the BN model, the shipper’s willingness to use BCT has a more pronounced effect on the freight forwarding rate. In the BB model, when the shipper’s willingness is greater, the freight forwarder must significantly avoid risks to enhance its expected profit. The higher the risk the shipping company pursues, the slower the expected profit increases with the shipper’s willingness. In scenarios where competitors pursue high risk, with an increase in the shipper’s willingness, the freight forwarder’s expected profit growth rate in the BN model surpasses the expected profit growth rate in the BB model.
(3) The greater the adaptability of service providers to BCT, the more rapidly the equilibrium price increases. In the BN model, with an increase in the service provider’s adaptability to BCT, the shipping company’s freight rate experiences a gradual increase. In contrast, the freight rate of freight forwarding decreases. In the BB model, the growth rate of the shipping company’s freight rate surpasses that of freight forwarding.
As the initial service provider’s adaptation to the blockchain increases, the shipping company’s expected profit rises when it avoids risks. When freight forwarders pursue risks, their expected profits increase with the initial service provider’s adaptation to the blockchain. In the later stages of blockchain application, shipping companies and freight forwarders invest more time and manpower in adapting to the blockchain to ensure profit growth.
In the BB model, when competitors are risk-neutral or risk-averse, their expected profits increase with the service provider’s adaptation to the blockchain. In the BN model, the shipping company’s expected profit increases with the service provider’s adaptation to the blockchain. At the same time, the freight forwarding company maximizes benefits only when the shipping company pursues high risk.
In summary, this paper proposes the following recommendations for the risk management of shipping companies and freight forwarders in a competitive environment:
(1) In the agency service market competition, when the shipper’s preference is higher and competitors pursue high risk, the service provider can consider lowering the freight rate, and competitors should adjust the price upwards when avoiding risks.
(2) In cases where both sides of the competition apply BCT, if the shipper’s willingness to use BCT is greater, the shipping company should consider pursuing risks to maximize profits. At the same time, the freight forwarder should lean towards risk avoidance to ensure their profits.
(3) When only the shipping company applies BCT, it should adopt a risk-averse strategy and accelerate adaptation to BCT to enhance profits. If the shipping company pursues risks, the freight forwarder should work on increasing the shipper’s willingness to use BCT without investing heavily in the human and time costs of BCT to maximize profits.
From a managerial perspective, firms should align blockchain adoption timing and risk preference assessment to design more stable and collaborative pricing strategies. Port authorities and regulators can play a facilitative role by offering blockchain subsidies, risk-sharing contract templates, or creating a sandbox environment for testing decentralized logistics solutions. Public–private coordination is essential to minimize adoption gaps and reduce system-wide inefficiencies during the digital transition.
Theoretically, this study enriches the literature by integrating mean-variance analysis with game theory to jointly account for heterogeneous risk preferences and blockchain-driven transparency in logistics pricing. It contributes to the behavioral operations field by modeling how bounded rationality and digital trust interact under competitive pressure in supply chain contexts. Future research could expand this model to encompass multi-agent settings, including port authorities, regulatory bodies, and customs actors. Such extensions may help examine complex coalitions or platform-based blockchain consortia. Moreover, empirical validation through case studies in large logistics hubs (e.g., Ningbo, Rotterdam) could assess whether the simulated strategies align with real-world firm behavior. Governments or regulators might also be surveyed or modeled to explore incentive schemes (e.g., tax credits or regulatory sandboxes) for accelerating blockchain standardization and adoption across logistics networks.
Author Contributions
Conceptualization, methodology, writing—original draft preparation Y.C.; writing—review and editing, Y.C. and J.M.; conceptualization, methodology, writing—review and editing, supervision, project administration, B.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Ningbo Philosophy and Social Science Research Base Project grant number JD6-284 and the Scientific Research Start-up Fund of Ningbo University of Technology Project grant number 2023KQ097. and The APC was funded by Yujing Chen.
Institutional Review Board Statement
Not applicable for studies not involving humans or animals.
Informed Consent Statement
Written informed consent has been obtained from the patient(s) to publish this paper.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
(1) BB model
Initial application of blockchain:
The mid-term application of blockchain:
(2) BN model
Initial application of blockchain:
The mid-term application of blockchain:
References
- Lu, B.; Xu, X. Digital transformation and port operations: Optimal investment under incomplete information. Transp. Policy 2024, 151, 134–146. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, C.; Zhang, J.; Chen, Z.; Liu, M.; Aziz, F.; Kurniawan, T.A.; Yap, P.-S. Digitalization and innovation in green ports: Areview of current issues, contributions and the way forward in promoting sustainable ports and maritime logistics. Sci. Total. Environ. 2024, 912, 169075. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Liu, J.; Qi, S. Incentive policy for rail-water multimodal transport: Subsidizing price or constructing dry port? Transp. Policy 2024, 150, 219–243. [Google Scholar] [CrossRef]
- Liu, M.; Xin, X.; Wang, X.; Zhang, T.; Chen, K. Dual-channel slot sales strategy for container liner shipping companies with blockchain technology adoption. Transp. Policy 2025, 162, 200–220. [Google Scholar] [CrossRef]
- Cao, Y.; Shen, B. Adopting blockchain technology to block less sustainable products’ entry in global trade. Transp. Res. Part E Logist. Transp. Rev. 2022, 161, 102695. [Google Scholar] [CrossRef]
- Schmidt, C.G.; Wagner, S.M. Blockchain and supply chain relations: A transaction cost theory perspective. J. Purch. Supply Manag. 2019, 25, 100552. [Google Scholar] [CrossRef]
- Kim, H.; Xiao, Z.; Zhang, X.; Fu, X.; Qin, Z. Rethinking Blockchain Technologies for the Maritime Industry: An Overview of the Current Landscape. Future Internet 2024, 16, 454. [Google Scholar] [CrossRef]
- Saeed, N. Cooperation among freight forwarders: Mode choice and intermodal freight transport. Res. Transp. Econ. 2013, 42, 77–86. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, C.; Zhang, C.; Wang, S. Upstream encroachment and downstream outsourcing in competing shipping supply chains. Int. J. Prod. Econ. 2023, 255, 108655. [Google Scholar] [CrossRef]
- Dutta, P.; Choi, T.M.; Somani, S.; Butala, R. Blockchain technology in supply chain operations: Applications, challenges and research opportunities. Transp. Res. Part Logist. Transp. Rev. 2020, 142, 102067. [Google Scholar] [CrossRef] [PubMed]
- Chang, J.A.; Katehakis, M.N.; Shi, J.J.; Yan, Z. Blockchain-empowered Newsvendor optimization. Int. J. Prod. Econ. 2021, 238, 108144. [Google Scholar] [CrossRef]
- Iyer, L.S. AI enabled applications towards intelligent transportation. Transp. Eng. 2021, 5, 100083. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, J.; Hu, X. Servitization with blockchain in the maritime supply chain. Ocean. Coast. Manag. 2022, 225, 106195. [Google Scholar] [CrossRef]
- Zheng, S.; Jiang, C. Consortium blockchain in shipping: Impacts on industry and social welfare. Transp. Res. Part A Policy Pract. 2024, 183, 104071. [Google Scholar] [CrossRef]
- Balci, G.; Surucu Balci, E. Blockchain adoption in the maritime supply chain: Examining barriers and salient stakeholders in containerized international trade. Transp. Res. Part E Logist. Transp. Rev. 2021, 156, 102539. [Google Scholar] [CrossRef]
- Nguyen, S.; Chen, P.S.L.; Du, Y. Blockchain adoption in container shipping: An empirical study on barriers, approaches, and recommendations. Mar. Policy 2023, 155, 105724. [Google Scholar] [CrossRef]
- Kersten, W.; Seiter, M.; von See, B.; Hackius, N.; Maurer, T. Trendsand Strategies in Logistics and Supply Chain Management-Digital. Transformation Opportunities; BVL: Bremen, Germany, 2017. [Google Scholar]
- Hackius, N.; Petersen, M. Blockchain in logistics and supply chain: Trickortreat? In Proceedings of the Hamburg International Conference of Logistics (HICL), Hamburg, Germany, 12–13 October 2017. [CrossRef]
- Alanazi, F. The future of transportation: Blockchain-powered solutions. Transp. J. 2024, 64, e12032. [Google Scholar] [CrossRef]
- Rahman, M.H.; Menezes, B.C.; Baldacci, R. Exploring the role of blockchain technology, warehouse automation, smart routing, and cloud computing in logistics performance. Prod. Manuf. Res. 2024, 12, 2393614. [Google Scholar] [CrossRef]
- Idrissi, Z.K.; Lachgar, M.; Hrimech, H. Blockchain, IoT and AI in logistics and transportation: A systematic review. Transp. Econ. Manag. 2024, 2, 275–285. [Google Scholar] [CrossRef]
- Xu, L.; Wei, Y.Q.; Chen, J.H.; Luo, Y.Q. Carrier channel encroachment and forwarder order sequence: An equilibrium analysis of shipping service supply chain. Int. J. Shipp. Transp. Logist. 2013, 42, 77–86. [Google Scholar] [CrossRef]
- Xu, L.; Luo, Y.; Chen, J.; Zhou, S. Capacity prioritization allocation and credit financing option in shipping freight forwarding market. Comput. Ind. Eng. 2024, 189, 109987. [Google Scholar] [CrossRef]
- Boyaci, T.; Gallego, G. Supply chain coordination in a market with customer service competition. Prod. Oper. Manag. 2004, 13, 3–22. [Google Scholar] [CrossRef]
- Zhou, W.H.; Lee, C.Y. Pricing and competition in a transportation market with empty equipment repositioning. Transp. Res. Part B Methodol. 2009, 43, 677–691. [Google Scholar] [CrossRef]
- Yin, M.; Kim, K.H. Quantity discount pricing for container transportation services by shipping lines. Comput. Ind. Eng. 2012, 63, 313–322. [Google Scholar] [CrossRef]
- Xu, L.; Govindan, K.; Bu, X.; Yin, Y. Pricing and balancing of the sea–cargo service chain with empty equipment repositioning. Comput. Oper. Res. 2015, 54, 286–294. [Google Scholar] [CrossRef]
- Chen, R.; Dong, J.X.; Lee, C.Y. Pricing and competition in a shipping market with waste shipments and empty container repositioning. Transp. Res. Part B Methodol. 2016, 85, 32–55. [Google Scholar] [CrossRef]
- Tapiero, C.S. Value at risk and inventory control. Eur. J. Oper. Res. 2005, 163, 769–775. [Google Scholar] [CrossRef]
- Wu, J.; Yue, W.; Yamamoto, Y.; Wang, S. Risk analysis of a pay to delay capacity reservation contract. Optim. Methods Softw. 2006, 21, 635–656. [Google Scholar] [CrossRef]
- Choi, T.; Chung, S.; Zhuo, X. Pricing with risk sensitive competing container shipping lines: Will risk seeking do more good than harm? Transp. Res. Part B Methodol. 2020, 133, 210–229. [Google Scholar] [CrossRef]
- Zheng, W.; Li, B.; Song, D.P. Effects of risk-aversion on competing shipping lines’ pricing strategies with uncertain demands. Transp. Res. Part B Methodol. 2017, 104, 337–356. [Google Scholar] [CrossRef]
- Chiu, C.H.; Choi, T.M. Supply chain risk analysis with mean-variance models: A technical review. Ann. Oper. Res. 2013, 240, 489–507. [Google Scholar] [CrossRef]
- Bai, X.; Lam, J.S.L. Pricing and Freight rate co-movement and risk spillovers in the product tanker shipping market: A copula analysis. Transp. Res. Part E Logist. Transp. Rev. 2021, 149, 102315. [Google Scholar] [CrossRef]
- Li, G.; Ren, Y.; Jiang, C.; Wang, W.; Guo, Y. Coordinated evolution game of marine supply chain from the perspective of sustainable development based on system dynamics. Ocean. Coast. Manag. 2024, 254, 107195. [Google Scholar] [CrossRef]
- Zhou, K.; Xing, W.; Wang, J.; Li, H.; Yang, Z. A data-driven risk model for maritime casualty analysis: A global perspective. Reliab. Eng. Syst. Saf. 2024, 244, 109925. [Google Scholar] [CrossRef]
- Deng, W.; Ma, X.; Qiao, W. Resilience-oriented safety barrier performance assessment in maritime operational risk management. Transp. Res. Part D Transp. Environ. 2025, 139, 104581. [Google Scholar] [CrossRef]
- Kandel, R.; Baroud, H. A data-driven risk assessment of Arctic maritime incidents: Using machine learning to predict incident types and identify risk factors. Reliab. Eng. Syst. Saf. 2024, 243, 109779. [Google Scholar] [CrossRef]
- Sui, C.; Wang, S.; Zheng, W. Sentiment as a shipping market predictor: Testing market-specific language models. Transp. Res. Part E-Logist. Transp. Rev. 2024, 189, 103651. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Wang, F.; Yue, X. Blockchain technology for port logistics capability: Exclusive or sharing. Transp. Res. Part B Methodol. 2021, 21, 635–656. [Google Scholar] [CrossRef]
- Yang, C.S. Maritime shipping digitalization: Blockchain-based technology applications, future improvements, and intention to use. Transp. Res. Part E Logist. Transp. Rev. 2019, 131, 108–117. [Google Scholar] [CrossRef]
- Fan, H.B.; Zhang, J. Research on the application of block chain technology in asset backed securitization. J. Intell. Fuzzy Syst. 2018, 35, 2847–2854. [Google Scholar] [CrossRef]
- Liu, L.; Li, F.T.; Qi, E.S. Research on Risk Avoidance and Coordination of Supply Chain Subject Based on Blockchain technology. Sustainability 2019, 11, 2182. [Google Scholar] [CrossRef]
- Hirata, E. Contestability of Container Liner Shipping Market in Alliance Era. The Asian Journal of Shipping and Logistics. Transp. Res. Part E Logist. Transp. Rev. 2017, 33, 27–32. [Google Scholar]
- Kim, K.H.; Shim, J.H. Application and policy direction of blockchain in logistics and distribution industry. J. Int. Bus. Stud. 2018, 9, 77–85. [Google Scholar] [CrossRef]
- Jain, A.S.; Jain, A.; Chauhan, N.; Singh, V.; Thakur, N. Seguro digital storage of documents using blockchain. Int. J. Eng. Sci. 2018, 5, 4–951. [Google Scholar]
- Carlan, V.; Coppens, F.; Sys, C.; Vanelslander, T. Blockchain technology as key contributor to the integration of maritime supply chain? In Maritime Supply Chains; Elsevier: Amsterdam, The Netherlands, 2020; pp. 229–259. [Google Scholar]
- Zhong, H.; Zhang, F.; Gu, Y. A Stackelberg game based two-stage framework to make decisions of freight rate for container shipping lines in the emerging blockchain-based market. Transp. Res. Part E Logist. Transp. Rev. 2021, 149, 102303. [Google Scholar] [CrossRef]
- Zhao, H.D.; Ye, Z.N.; Liu, C.J. Reducing the bullwhip effect to enhance maritime service resilience: The power of blockchain technology for cutting down the market uncertainty in the maritime supply chain. Ocean. Coast. Manag. 2023, 244, 106824. [Google Scholar] [CrossRef]
- Wang, H.; Wang, C.; Li, M.; Xie, Y. Blockchain technology investment strategy for shipping companies under competition. Ocean. Coast. Manag. 2023, 243, 106696. [Google Scholar] [CrossRef]
- Li, H.; Gao, J.; Li, X. Blockchain adoption strategy of two-sided shipping platforms connecting forwarder and liner company. Ocean. Coast. Manag. 2024, 247, 106932. [Google Scholar] [CrossRef]
- Lee, H.; Boile, M.; Theofanis, S.; Choo, S. Modeling the Oligopolistic and Competitive Behavior of Carriers in Maritime Freight Transportation Networks. Procedia Soc. Behav. Sci. 2012, 54, 1080–11054. [Google Scholar] [CrossRef][Green Version]
- Zhuo, W.; Shao, L.; Yang, H. Mean–variance analysis of option contracts in a two-echelon supply chain. Eur. J. Oper. Res. 2018, 271, 535–547. [Google Scholar] [CrossRef]
- Sun, Z.M.; Shi, B.L.; Liu, J.R. Pricing, emission reduction and coordination for maritime supply chain with risk-averse members in the blockchain era. Environ. Dev. Sustain. 2025. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, B. Analysis on the evolution of shipping logistics service supply chain market structure under the application of Blockchain Tech-nology. Adv. Eng. Inform. 2022, 53, 101714. [Google Scholar] [CrossRef]
- Yujing, C.; Bin, Y. Cooperative Decision Making of Supply Chain Members of Shipping Logistics Services Under the Background of Blockchain. Asia-Pac. J. Oper. Res. 2021, 39, 2140018. [Google Scholar]
- Fransoo, J.C.; Lee, C.Y. The critical role of ocean container transport in global supply chain performance. Prod. Oper. Manag. 2023, 22, 253–268. [Google Scholar] [CrossRef]
- Radojicic, V.; Radonjic, V.; Markovic, G. A New Competitive Model Based on Trade-Of Between Credibility and Price. Econ. Comput. Econ. Cybern. Stud. Res. 2012, 46, 231–242. [Google Scholar]
- Leckie, C.; Dwivedi, A.; Johnson, L.W. Credibility and price premium-based competitiveness for industrial brands. J. Retail. Consum. Serv. 2023, 74, 103418. [Google Scholar] [CrossRef]
- Cui, K.; Chi, M.; Zhao, Y.; Liu, Z. Evolutionary Game-Based Regulatory Strategy Optimization for Information Transmission Prices in Integrated Energy Systems. Energies 2025, 18, 1452. [Google Scholar] [CrossRef]
- UNCTAD. Review of Maritime Transport 2023. Available online: https://unctad.org/publication/review-maritime-transport-2023 (accessed on 27 September 2023).
- Farah, M.B.; Ahmed, Y.; Mahmoud, H.; Shah, S.A.; Al-Kadri, M.O.; Taramonli, S.; Bellekens, X.; Abozariba, R.; Idrissi, M.; Aneiba, A. A survey on blockchain technology in the maritime industry: Challenges and future perspectives. Future Gener. Comput. Syst. 2024, 157, 618–637. [Google Scholar] [CrossRef]
- Xu, P.; Lee, J.; Barth, J.R. Rocert Glenn Richery. Blockchain as supply chain technology: Considering transparency and security. Int. J. Phys. Distrib. Logist. Manag. 2021, 51, 305–324. [Google Scholar] [CrossRef]
- Yang, C.C.; Chen, L.; Xia, Q. Freight insurance pricing strategy based on an online freight platform. Ind. Manag. Data Syst. 2023, 123, 2929–2945. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).