Consistency of Restricted Maximum Likelihood Estimators in High-Dimensional Kernel Linear Mixed-Effects Models with Applications in Estimating Genetic Heritability

Abstract

Restricted maximum likelihood (REML) estimators are commonly used to obtain unbiased estimators for the variance components in linear mixed models. In modern applications, particularly in genomic studies, the dimension of the design matrix with respect to the random effects can be high. Motivated by this, we first introduce high-dimensional kernel linear mixed models, derive the REML equations, and establish theoretical results on the consistency of REML estimators for several commonly used kernel matrices. The validity of the theories is demonstrated via simulation studies. Our results provide rigorous justification for the consistency of REML estimators in high-dimensional kernel linear mixed models and offer insights into the application of estimating genetic heritability. Finally, we apply the kernel linear mixed models to estimate genetic heritability in a real-world data application.

1. Introduction

Heritability, particularly narrow-sense heritability, refers to the proportion of phenotypic variance explained by additive genetic variance. For example, it is well-known that the estimated heritability of human height is roughly 0.8 [1,2]. However, early identified genes could only explain a small fraction of height heritability. More recently, large-scale genome-wide association studies (GWASs) involving 5.4 million individuals have identified 12,111 height-related single-nucleotide polymorphisms (SNPs). It has been shown that common SNPs can explain 40–50% of the phenotypic variation in human height [3]. Therefore, the previously observed “missing heritability” can be attributed to the small effect sizes of individual SNPs. Furthermore, because a classical GWAS relies on linear models and multiple testing procedures, a SNP must meet stringent criteria at the whole-genome level (e.g., p-value < ${10}^{-8}$) to be considered significant. As a result, many SNPs with small yet meaningful effects remain undetectable using classical GWAS methods.

The idea that heritability is spread across multiple SNPs that contribute to phenotypic traits, also known as polygenicity, has been widely accepted over the past few decades. As a result, rather than estimating the individual effect of each SNP, state-of-the-art models in GWASs estimate the cumulative effect of multiple SNPs in a genetic region, such as all SNPs in a gene, a pathway, or even a chromosome. For quantitative traits, linear mixed-effects models are commonly used to model the cumulative effect of multiple SNPs. It was shown that, using a linear mixed model, known as genome-wide complex trait analysis (GCTA) [4], 45% of the variance in human height could be explained by all common SNPs [5]. This finding has since been supported by the large-scale GWAS mentioned above.

Linear mixed-effects models (LMMs) provide powerful alternatives in GWASs, and various studies have explored LMMs in the high-dimensional setting. In Li et al. [6], the authors proposed inference methods for linear mixed models using techniques similar to the debiased LASSO method [7,8], achieving an estimator of the fixed effects with the optimal convergence rate and valid inferential procedures. However, their framework assumes that the cluster size of the random effects is large, which is generally not true in genetic studies where linear mixed-effects models are commonly applied. Similarly, Law and Ritov [9] proposed methods for constructing asymptotic confidence intervals and hypothesis tests for the significance of random effects. In both studies, however, high dimensionality resides in the fixed effects, while the dimension of the random effects is assumed to be low. This limits their applicability to genetic studies, where the SNP matrix is often treated as the design matrix for random effects [4,10].

Therefore, it is of greater interest to investigate the properties of variance component estimators when the random effects are high-dimensional. Jiang et al. [11] provided theoretical guarantees for the consistency of the restricted maximum likelihood (REML) estimator under the setting where the random-effects design matrix is high-dimensional and random in the so-called linear regime ($n/p\to \tau$ for some $0<\tau \le 1$). These techniques have since been extended to construct confidence intervals for variance components [12] and to establish the asymptotic normality of heritability estimators based on GWAS summary statistics [13].

Currently, the most commonly used LMMs in GWASs, as studied in Jiang et al. [11], for a polygenetic quantitative trait can be expressed via the following additive model:

$$y_i={\mu }_i+\sum _{j\in \mathcal{C}}{G}_{ij}{u}_j+{ϵ}_i,i=1,\dots ,n,$$

(1)

where ${\mu }_i$ is the fixed effect of the ith individual, which is typically of the form ${\mu }_i={\mathit{x}}_i^T\mathit{\beta }$, and ${\mathit{x}}_i$ are covariates (e.g., age, gender, and race group) of the ith individual; $\mathcal{C}$ is a set of SNPs; and $G_{ij}$ is the genotype of the jth SNP of the ith individual. $u_j$ is the effect of the jth SNP, which typically follows a normal distribution $u_1,\dots ,u_{\left|\mathcal{C}\right|}\sim \mathrm{i}.\mathrm{i}.\mathrm{d}.\mathcal{N}(0,{\sigma }_u^2)$ with $\left|\mathcal{C}\right|$ being the cardinality of the set $\mathcal{C}$. ${ϵ}_i$ is the random error or other possible environmental effects, which are typically modeled by a normal distribution ${ϵ}_1,\dots ,{ϵ}_n\sim \mathrm{i}.\mathrm{i}.\mathrm{d}.\mathcal{N}(0,{\sigma }_{ϵ}^2)$. By writing $g_i={\sum }_{j\in \mathcal{C}}{G}_{ij}{u}_j$, model (1) can be written as

$$y_i={\mu }_i+g_i+{ϵ}_i,i=1,\dots ,n,$$

or in a vector form

$$\mathit{y}=\mathit{\mu }+\mathit{g}+\mathit{ϵ},$$

(2)

where $\mathit{y}={[y_1,\dots ,y_n]}^T$, $\mathit{\mu }={[{\mu }_1,\dots ,{\mu }_n]}^T$, and $\mathit{ϵ}={[{ϵ}_1,\dots ,{ϵ}_n]}^T$. Under the distributional assumptions in Model (1), the distributions of $\mathit{g}$ and $\mathit{ϵ}$ are

$$\mathit{g}\sim {\mathcal{N}}_n(\mathbf{0},{\sigma }_u^2{\mathit{GG}}^T),\mathit{ϵ}\sim {\mathcal{N}}_n(\mathbf{0},{\sigma }_{ϵ}^2{\mathit{I}}_n),$$

(3)

where the matrix $\mathit{G}$ is an $n\times \left|\mathcal{C}\right|$-matrix containing SNPs in region $\mathcal{C}$.

An underlying assumption in Model (1) or (2) is that the genetic effect associated with the quantitative trait of interest is linear. This may not be a reasonable assumption in reality, as generally the relationships between genotypes and phenotypes are rather complex. Therefore, the following semi-parametric models could be more appropriate.

$$y_i={\mu }_i+h(G_{i1},\dots ,G_{i\left|\mathcal{C}\right|})+{ϵ}_i,i=1,\dots ,n,$$

(4)

where $h\in \mathcal{H}$ and $\mathcal{H}$ is some function space. In particular, let $\mathcal{H}$ be a reproducing kernel Hilbert space (RKHS) associated with a kernel function $K(·,·)$. The representer theorem [14] shows that when ${\mu }_i={\mathit{x}}_i^T\mathit{\beta }$, the estimating equation for $\mathit{\beta }$ and $\mathit{h}={[h(G_{11},\dots ,G_{1\left|\mathcal{C}\right|}),\dots ,h(G_{n1},\dots ,G_{n\left|\mathcal{C}\right|})]}^T$ under penalized least squares is equivalent to the Henderson mixed model equation, which is often used to obtain the BLUP in a linear mixed model. In this case, the linear mixed model is given as

$$\mathit{y}=\mathit{X}\mathit{\beta }+\mathit{a}+\mathit{ϵ},$$

(5)

where $\mathit{a}\sim {\mathcal{N}}_n(\mathbf{0},{\sigma }_a^2\mathit{K})$ with $\mathit{K}$ being a kernel matrix, $\mathit{ϵ}\in {\mathcal{N}}_n(\mathbf{0},{\sigma }_{ϵ}^2{\mathit{I}}_n)$, $\mathit{a}$ and $\mathit{ϵ}$ are independent.

In this paper, we study the consistency of the REML estimator for variance components in a high-dimensional kernel linear mixed-effects model. Such models have also been widely used in spatial statistics [15], as well as in identifying significant genetic variants [10,16] and predicting genetic risk for diseases [17]. The results established in this paper extend the work by Jiang et al. [11] from linear kernels to other commonly used kernels that capture nonlinear genetic effects, thereby providing theoretical justification for the successful application of kernel LMMs in genetic studies.

The rest of the paper is organized as follows: Section 2 provides the formulation of the REML equations for kernel linear mixed-effects models and the main consistency results for the REML estimators. The main results rely heavily on random matrix theories (RMTs), and a brief review of the RMTs is also given in Section 2. Simulation studies are given in Section 3 to verify the theoretical results, followed by a real-world data application.

Notations : Throughout this paper, bold alphabetic or Greek letters are used for vectors, while bold capital alphabetic or Greek letters are used for matrices. For an $n\times n$ matrix $\mathit{A},\mathit{B}$, $\mathit{A}\ge 0$ means that $\mathit{A}$ is positive and semi-definite, while $\mathit{A}\ge \mathit{B}$ means that $\mathit{A}-\mathit{B}\ge 0$. For a vector $\mathit{x}$, $\left|\mathit{x}\right|=\sqrt{{\sum }_{i=1}^n{x}_i^2}$ denotes its Euclidean norm, and we use $∥\mathit{A}∥$ to denote the operator norm of a matrix $\mathit{A}$; that is, $∥\mathit{A}∥=\sqrt{{\lambda }_{max}\left({\mathit{A}}^T\mathit{A}\right)}$. When $\mathit{A}$ is symmetric and positive semi-definite, this is the same as the largest eigenvalue of $\mathit{A}$. $\det \left(\mathit{A}\right)$ is used to denote the determinant of a squared matrix $\mathit{A}$. For two matrices $\mathit{A},\mathit{B}$ of the same size, $\mathit{A}\circ \mathit{B}$ denotes the Hadamard product; i.e., ${[\mathit{A}\circ \mathit{B}]}_{ij}={\mathit{A}}_{ij}{\mathit{B}}_{ij}$. Moreover, if $f:\mathbb{R}\to \mathbb{R}$ is a univariate function and $\mathit{A}$ is a matrix, then $f\left[\mathit{A}\right]$ denotes a matrix of the same size as $\mathit{A}$ and ${\left[f\left(\mathit{A}\right)\right]}_{ij}=f\left(A_{ij}\right)$.

2. Materials and Methods

2.1. The REML Equations for Variance Components

Let q be the rank of the fixed-effects design matrix $\mathit{X}$ and $\mathit{A}\in {\mathbb{R}}^{n\times (n-q)}$ such that ${\mathit{A}}^T\mathit{X}=\mathbf{0}$ and ${\mathit{A}}^T\mathit{A}={\mathit{I}}_{n-q}$. Then, by multiplying ${\mathit{A}}^T$ on both sides of Equation (5), we obtain

$$\tilde{\mathit{y}}=\tilde{\mathit{a}}+\widetilde{\mathit{ϵ}},$$

(6)

where $\tilde{\mathit{y}}={\mathit{A}}^T\mathit{y}$ and

$$\begin{array}{cc}\hfill \tilde{\mathit{a}}={\mathit{A}}^T\mathit{a}& \sim {\mathcal{N}}_n\left(\mathbf{0},{\sigma }_a^2{\mathit{A}}^T\mathit{KA}\right),\hfill \\ \hfill \widetilde{ϵ}={\mathit{A}}^T\mathit{ϵ}& \sim {\mathcal{N}}_n\left(\mathbf{0},{\sigma }_{ϵ}^2{\mathit{I}}_{n-q}\right).\hfill \end{array}$$

Let $f\left(\tilde{\mathit{y}}\right|\mathit{\theta })$ be the probability density function of $\tilde{\mathit{y}}$. Then the restricted log-likelihood of $\mathit{\theta }:={[{\sigma }_a^2,{\sigma }_{ϵ}^2]}^T$ is

$$\begin{array}{cc}\hfill {\ell }_r\left(\mathit{\theta }\right)& =logf\left(\tilde{\mathit{y}}\right|\mathit{\theta })\propto -{\displaystyle \frac{1}{2}}log\det \left({\sigma }_a^2{\mathit{A}}^T\mathit{KA}+{\sigma }_{ϵ}^2{\mathit{I}}_{n-q}\right)-{\displaystyle \frac{1}{2}}{\tilde{\mathit{y}}}^T{\left({\sigma }_a^2{\mathit{A}}^T\mathit{KA}+{\sigma }_{ϵ}^2{\mathit{I}}_{n-q}\right)}^{-1}\tilde{\mathit{y}}\hfill \\ \hfill & =-{\displaystyle \frac{1}{2}}log\det \left({\sigma }_{ϵ}^2(\gamma {\mathit{A}}^T\mathit{KA}+{\mathit{I}}_{n-q})\right)-{\displaystyle \frac{1}{2{\sigma }_{ϵ}^2}}{\tilde{\mathit{y}}}^T{\left(\gamma {\mathit{A}}^T\mathit{KA}+{\mathit{I}}_{n-q}\right)}^{-1}\tilde{\mathit{y}}\hfill \\ \hfill & =-{\displaystyle \frac{n-q}{2}}log{\sigma }_{ϵ}^2-{\displaystyle \frac{1}{2}}log\det \left(\gamma {\mathit{A}}^T\mathit{KA}+{\mathit{I}}_{n-q}\right)-{\displaystyle \frac{1}{2{\sigma }_{ϵ}^2}}{\tilde{\mathit{y}}}^T{\left(\gamma {\mathit{A}}^T\mathit{KA}+{\mathit{I}}_{n-q}\right)}^{-1}\tilde{\mathit{y}},\hfill \end{array}$$

where $\gamma ={\sigma }_a^2/{\sigma }_{ϵ}^2$ is the ratio between two variance components. With slight abuse of notation, let $\mathit{\theta }={[\gamma ,{\sigma }_{ϵ}^2]}^T$ in what follows.

A well-known result for REML estimators is that they are independent of the choice of $\mathit{A}$, which is based on the following identity [18]

$$\mathit{A}{(\gamma {\mathit{A}}^T\mathit{KA}+{\mathit{I}}_{n-q})}^{-1}{\mathit{A}}^T={\mathit{V}}_{\gamma }^{-1}-{\mathit{V}}_{\gamma }^{-1}\mathit{X}{\left({\mathit{X}}^T{\mathit{V}}_{\gamma }^{-1}\mathit{X}\right)}^{-1}{\mathit{X}}^T{\mathit{V}}_{\gamma }^{-1},$$

where ${\mathit{V}}_{\gamma }={\mathit{I}}_n+\gamma \mathit{K}$. Also, let ${\mathbf{\Sigma }}_{\gamma }={\mathit{I}}_{n-q}+\gamma {\mathit{A}}^T\mathit{KA}$, then

$${\mathit{P}}_{\gamma }:=\mathit{A}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T={\mathit{V}}_{\gamma }^{-1}-{\mathit{V}}_{\gamma }^{-1}\mathit{X}{\left({\mathit{X}}^T{\mathit{V}}_{\gamma }^{-1}\mathit{X}\right)}^{-1}{\mathit{X}}^T{\mathit{V}}_{\gamma }^{-1}.$$

Therefore, ${\tilde{\mathit{y}}}^T{\left(\gamma {\mathit{A}}^T\mathit{KA}+{\mathit{I}}_{n-q}\right)}^{-1}\tilde{\mathit{y}}={\mathit{y}}^T\mathit{A}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{y}={\mathit{y}}^T{\mathit{P}}_{\gamma }\mathit{y}$, and the restricted log-likelihood function can be written as

$${\ell }_r\left(\mathit{\theta }\right)\propto -{\displaystyle \frac{n-q}{2}}log{\sigma }_{ϵ}^2-{\displaystyle \frac{1}{2}}log\det \left({\mathbf{\Sigma }}_{\gamma }\right)-{\displaystyle \frac{1}{2{\sigma }_{ϵ}^2}}{\mathit{y}}^T{\mathit{P}}_{\gamma }\mathit{y}.$$

(7)

By taking the derivatives with respect to $\gamma$ and ${\sigma }_{ϵ}^2$ and letting them equal to zero, we know that the REML estimators of $\gamma$ and ${\sigma }_{ϵ}^2$ satisfy the following REML equations:

$$\left\{\begin{array}{c}{\widehat{\sigma }}_{ϵ}^2={\displaystyle \frac{1}{n-q}}{\mathit{y}}^T{\mathit{P}}_{\gamma }\mathit{y}\hfill \\ {\displaystyle \frac{{\mathit{y}}^T{\mathit{P}}_{\gamma }{\mathit{KP}}_{\gamma }\mathit{y}}{\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)}}={\displaystyle \frac{{\mathit{y}}^T{\mathit{P}}_{\gamma }\mathit{y}}{n-q}}\hfill \end{array}\right.$$

(8)

2.2. A Review on Random Matrix Theory

In this section, we briefly review the theory of random matrices. For more details on the application of random matrix theory in statistics, we refer interested readers to Bai and Silverstein [19] and Paul and Aue [20]. Let $\mathit{A}$ be an $m\times m$ matrix with eigenvalues ${\lambda }_j,j=1,2,\dots ,m$. The empirical spectral distribution (ESD) of the matrix $\mathit{A}$ is defined to be

$$F_m^{\mathit{A}}\left(x\right)={\displaystyle \frac{1}{m}}\sum _{j=1}^m{\mathbb{I}}_{\{{\lambda }_j\le x\}},x\in \mathbb{R}.$$

For a double array of i.i.d. random variables $\{g_{jk}:j,k=1,2,\dots \}$ with a mean of 0 and a variance of ${\sigma }^2$, write $\mathit{G}=[{\mathit{g}}_1,\dots ,{\mathit{g}}_p]=\left[\begin{array}{c}{{\mathit{g}}^{\mathbf{\prime }}}_1^T\\ ⋮\\ {{\mathit{g}}^{\mathbf{\prime }}}_n^T\end{array}\right]$ with ${\mathit{g}}_j={(g_{1j},\dots ,g_{nj})}^T$ and ${{\mathit{g}}^{\mathbf{\prime }}}_j={(g_{j1},\dots ,g_{jp})}^T$. It is well known that the ESD of the sample covariance matrix $\mathit{S}={\displaystyle \frac{1}{p}}{\mathit{GG}}^T$ converges almost surely in distribution to the Marchenko–Pastur (M-P) law.

Theorem 1.

(Marchenko–Pastur Law). Suppose that $\left\{g_{ij}\right\}$ are i.i.d. random variables with a mean of 0 and a variance of ${\sigma }^2$. Also assume that $n/p\to \tau \in (0,\infty )$ as $n,p\to \infty$. Then, with a probability of 1, $F^{\mathit{S}}$ tends toward the M-P law having density

$${\phi }_{\tau }\left(x\right)=\left\{\begin{array}{cc}{\left(2\pi {\sigma }^2\tau x\right)}^{-1}\sqrt{(b_{+}\left(\tau \right)-x)(x-b_{-}\left(\tau \right))}\hfill & \mathit{if} x\in [b_{-}\left(\tau \right),b_{+}\left(\tau \right)]\hfill \\ 0\hfill & \mathit{otherwise}.\hfill \end{array}\right.,$$

and has a point mass $1-1/\tau$ at the origin if $\tau >1$, where $b_{\pm }\left(\tau \right)={\sigma }^2{(1\pm \sqrt{\tau })}^2$.

The following corollary is by Jiang et al. [11], which is a consequence of convergence in distribution and will be frequently used.

Corollary 1.

Under the assumptions of Theorem 1, for the integer l,

$$n^{-1}\mathit{tr}\left({\mathit{S}}^l\right)\to {\int }_{b_{-}\left(\tau \right)}^{b_{+}\left(\tau \right)}{x}^l{\phi }_{\tau }\left(x\right)dx, \mathit{as}p\to \infty .$$

In general, the assumptions on i.i.d. can be reduced. The following theorem is Theorem 4.3 in Bai and Silverstein [19].

Theorem 2.

Suppose that the entries of $\mathit{G}\in {\mathbb{R}}^{n\times p}$ are random variables that are independent of each n and identically distributed for all n and satisfy $\mathbb{E}\left[\right|g_{11}-\mathbb{E}\left[g_{11}\right]{|}^2]=1$. Also assume that $\mathit{T}=\mathit{diag}\{{\tau }_1,\dots ,{\tau }_p\}$, ${\tau }_i$ is real, and that the empirical distribution function of $\{{\tau }_1,\dots ,{\tau }_p\}$ converges a.s. to a probability distribution function H as $n\to \infty$. The entries of both $\mathit{G}$ and $\mathit{T}$ may depend on n. Set

$$\mathit{B}=\mathit{A}+{\displaystyle \frac{1}{n}}\mathit{G}\mathit{T}{\mathit{G}}^T,$$

where $\mathit{A}\in {\mathbb{R}}^{n\times n}$ is symmetric and satisfies $F^{\mathit{A}}\to H$ almost surely, where H is a distribution (possibly defective) on the real line. Assume that $\mathit{G}$, $\mathit{T}$, and $\mathit{A}$ are independent. When $p/n\to y>0$ as $n\to \infty$, then the ESD of $\mathit{B}$ and $F^{\mathit{B}}$ converges almost surely as $n\to \infty$ to a nonrandom distribution function F.

The limiting spectral behaviors of $p^{-1}{\mathit{GG}}^T$ have not only been studied, but the limiting spectral behaviors of inner-product kernel matrices $f\left[p^{-1}{\mathit{GG}}^T\right]$ have also been studied. Here we quote Theorem 2.1 in El Karoui [21].

Theorem 3.

(Spectrum of Inner-Product Kernel Random Matrices). Let us assume that we observe n i.i.d. random vectors ${{\mathit{g}}^{\prime }}_i\in {\mathbb{R}}^p$. Consider the kernel matrix $\mathit{K}$ with entries

$$K_{ij}=f\left({\displaystyle \frac{{{\mathit{g}}^{\prime }}_i^T{\mathit{g}}_j^{\prime }}{p}}\right).$$

Assume that

1. 

$n\asymp p$; that is, $n/p$ and $p/n$ remain bounded as $p\to \infty$.

2. 

${\mathbf{\Sigma }}_p$ is a positive definite $p\times p$ matrix and $∥{\mathbf{\Sigma }}_p∥$ remains bounded in p; that is, there exists $C>0$ such that $∥{\mathbf{\Sigma }}_p∥\le C$ for all p.

3. 

${\mathbf{\Sigma }}_p/p$ has a finite limit; that is, there exists $l\in \mathbb{R}$ such that ${lim}_{p\to \infty }\mathit{tr}\left({\mathbf{\Sigma }}_p\right)/p=l$.

4. 

${{\mathit{g}}^{\prime }}_i={\mathbf{\Sigma }}_p^{1/2}{\mathbf{\Gamma }}_i$.

5. 

The entries of ${\mathbf{\Gamma }}_i$, a p-dimensional random vector, are i.i.d. Also, as denoted by ${\mathbf{\Gamma }}_i\left(k\right)$, the kth entry of ${\mathbf{\Gamma }}_i$, we assume that $\mathbb{E}\left[{\mathbf{\Gamma }}_i\left(k\right)\right]=0$, $\mathit{Var}\left[{\mathbf{\Gamma }}_i\left(k\right)\right]=1$, and $\mathbb{E}\left[|{\mathbf{\Gamma }}_{\mathit{i}}\left(\mathit{k}\right){|}^{4+\eta }\right]<\infty$ for some $\eta >0$.

6. 

f is a $C^1$ function in the neighborhood of $l={lim}_{p\to \infty }\mathit{tr}\left({\mathbf{\Sigma }}_p\right)/p$ and a $C^3$ function in the neighborhood of 0.

Under these assumptions, the kernel matrix $\mathit{K}$ can (in probability) be approximated consistently in the operator norm when p and n tend to ∞ by the matrix $\mathit{M}$, where

$$\mathit{M}=\left(f\left(0\right)+f^{″}\left(0\right){\displaystyle \frac{\mathit{tr}\left({\mathbf{\Sigma }}_p^2\right)}{2p^2}}\right){\mathbf{1}}_n{\mathbf{1}}_n^T+f^{\prime }\left(0\right){\displaystyle \frac{{\mathit{GG}}^T}{p}}+v_p{\mathit{I}}_n,$$

(9)

where

$$v_p=f\left({\displaystyle \frac{\mathit{tr}\left({\mathbf{\Sigma }}_p\right)}{p}}\right)-f\left(0\right)-f^{\prime }\left(0\right){\displaystyle \frac{\mathit{tr}\left({\mathbf{\Sigma }}_p\right)}{p}}.$$

In other words,

$$∥\mathit{K}-\mathit{M}∥\stackrel{p}{\to }0, \mathit{when} p\to \infty .$$

El Karoui [21] also studied the behaviors of the spectrum of Euclidean distance kernel random matrices or, in other words, radial basis kernel matrices. The following result is from Theorem 2.2 from El Karoui [21].

Theorem 4.

(Spectrum of Euclidean Distance Kernel Random Matrices). Consider the $n\times n$ kernel matrix $\mathit{K}$ with entries

$$K_{ij}=f\left({\displaystyle \frac{∥{\mathit{g}}_i^{\prime }-{\mathit{g}}_j^{\prime }∥}{p}}\right).$$

Let us call

$$\tau =2{\displaystyle \frac{\mathit{tr}\left({\mathbf{\Sigma }}_p\right)}{p}}.$$

Let us call ψ the vector with the ith entry ${\psi }_i={∥{\mathit{g}}_i^{\prime }∥}_2^2/p-\mathit{tr}\left({\mathbf{\Sigma }}_p\right)/p$. Suppose that the assumptions of Theorem 3 hold, but that conditions 5 and 6 are replaced by

(5’) 

The entries of ${\mathbf{\Gamma }}_i$, a p-dimensional random vector, are i.i.d. Also, as denoted by ${\mathbf{\Gamma }}_i\left(k\right)$ the kth entry of ${\mathbf{\Gamma }}_i$, we assume that $\mathbb{E}\left[{\mathbf{\Gamma }}_i\left(k\right)\right]=0$, $\mathit{Var}\left[{\mathbf{\Gamma }}_i\left(k\right)\right]=1$, and $\mathbb{E}\left[\right|{\mathbf{\Gamma }}_i\left(k\right){|}^{5+\eta }]<\infty$ for some $\eta >0$.

(6’) 

f is $C^3$ in a neighborhood of τ.

Then $\mathit{K}$ can be approximated consistently in the operator norm (and in probability) by the matrix $\mathit{M}$, which is defined by

$$\begin{array}{cc}\hfill \mathit{M}& =f\left(\tau \right){\mathbf{1}}_n{\mathbf{1}}_n^T+f^{\prime }\left(\tau \right)\left[{\mathbf{1}}_n{\mathit{\psi }}^T+\mathit{\psi }{\mathbf{1}}_n^T-2{\displaystyle \frac{{\mathit{GG}}^T}{p}}\right]+\hfill \\ \hfill & {\displaystyle \frac{f^{″}\left(\tau \right)}{2}}\left[{\mathbf{1}}_n{(\mathit{\psi }\circ \mathit{\psi })}^T+(\mathit{\psi }\circ \mathit{\psi }){\mathbf{1}}_n^T+2\mathit{\psi }{\mathit{\psi }}^T+4{\displaystyle \frac{\mathit{tr}\left({\mathbf{\Sigma }}_p^2\right)}{p^2}}{\mathbf{1}}_n{\mathbf{1}}_n^T\right]+v_p{\mathit{I}}_n,\hfill \end{array}$$

(10)

where $v_p=f\left(0\right)+\tau f^{\prime }\left(\tau \right)-f\left(\tau \right)$. In other words,

$$∥\mathit{K}-\mathit{M}∥\stackrel{p}{\to }0, \mathit{when} p\to \infty .$$

The following lemma provides a useful bound for the variance of a quadratic form, and its proof is given in Appendix A.

Lemma 1.

Suppose that $\mathit{y}=\mu +\mathit{e}$, with μ being a fixed vector; $\mathbb{E}\left[\mathit{e}\right]=0$; $\mathbb{E}\left[{\mathit{ee}}^T\right]=\mathbf{\Sigma }$; and $\mathbb{E}\left[\right|\mathit{e}{|}^4]<\infty$. Then

$$\mathit{Var}[{\mathit{y}}^T\mathbf{\Gamma }\mathit{y}]\le 2\mathit{Var}[{\mathit{e}}^T\mathbf{\Gamma }\mathit{e}]+8{\mathit{\mu }}^T{\mathbf{\Gamma }}^T\mathbf{\Sigma }\mathbf{\Gamma }\mathit{\mu }.$$

2.3. Consistency of REML Estimators in Kernel LMMs

In this section, we will show the main results on the consistency of REML estimators for kernel linear mixed models under three commonly used classes of kernel matrices in genetic data analysis. The first one is the weighted product kernel, which is a natural generalization of the product kernel and is the kernel matrix used in a sequence kernel association test (SKAT) [10] in genetic association studies. The other two classes are the inner-product-based kernel matrices and the Euclidean distance-based kernel matrices. An example of an inner-product-based kernel is the polynomial kernel, and an example of a Euclidean distance-based kernel is a Gaussian kernel. Proofs of all results in this section can be found in Appendix A.

2.3.1. Weighted Product Kernel

The following theorem serves as a natural extension of the result by Jiang et al. [11] to the case of a weighted product kernel. It guarantees the consistency of REML estimators of the variance components in kernel linear mixed models when the entries in $\mathit{G}$ are i.i.d. and have a finite fourth moment, and the weights in the diagonal matrix $\mathit{W}$ are upper and lower bounded.

Theorem 5.

For $\mathit{K}=p^{-1}{\mathit{GWG}}^T$ with entries in $\mathit{G}\in {\mathbb{R}}^{n\times p}$ and $\mathit{W}\in {\mathbb{R}}^{p\times p}$,

1. 

$G_{ij}$ are i.i.d. with $\mathbb{E}\left[G_{ij}\right]=0$, $\mathbb{E}\left[G_{ij}^2\right]=1$, and $\mathbb{E}\left[G_{ij}^4\right]<\infty$;

2. 

$\mathit{W}=\mathit{diag}\{w_1,\dots ,w_p\}$ with

$$\underset{1\le i\le p}{max}|w_i|\le 1,\underset{1\le i\le p}{min}\left|w_i\right|\ge \delta ,$$

(11)

for some $\delta >0$.

Then as $n/p\to \tau \in (0,1)$ and $n,p\to \infty$, we have

$$\begin{array}{c}\hfill \widehat{\gamma }\stackrel{p}{\to }{\gamma }_0,{\widehat{\sigma }}_{ϵ}^2\stackrel{p}{\to }{\sigma }_{ϵ}^2,\end{array}$$

where ${\gamma }_0$ is the true value for γ.

In addition, the same result still holds when $\mathit{G}$ is replaced by its column standardized version $\tilde{\mathit{G}}$ as given in the following corollary. The proofs of the theorem and the following corollary are very similar to the proofs in Jiang et al. [11], and they can be found in Appendix A.

Corollary 2.

Let $\mathit{G}$ be a random matrix whose elements are i.i.d. with $\mathbb{E}\left[G_{ij}\right]=0$, $\mathbb{E}\left[G_{ij}^2\right]=1$, and $\mathbb{E}\left[G_{ij}^4\right]<\infty$. Let $\tilde{\mathit{G}}$ be the matrix that is obtained by column standardizing the matrix $\mathit{G}$; i.e.,

$$\tilde{\mathit{G}}=(\mathit{G}-\overline{\mathit{g}}\otimes {\mathbf{1}}_n){\mathit{D}}_s^{-1},$$

where $\overline{\mathit{g}}=[{\overline{g}}_1,\dots ,{\overline{g}}_p]$ with ${\overline{g}}_j=n^{-1}{\sum }_{i=1}^n{G}_{ij}$, $j=1,\dots ,p$, and ${\mathit{D}}_s=\mathit{diag}\{s_1,\dots ,s_p\}$ with $s_j^2={(n-1)}^{-1}{\sum }_{i=1}^n{(G_{ij}-{\overline{g}}_j)}^2$. Let $\mathit{W}\in {\mathbb{R}}^{p\times p}$ be the weight matrix satisfying Equation (11). Then for $\tilde{\mathit{K}}=p^{-1}\tilde{\mathit{G}}\mathit{W}{\tilde{\mathit{G}}}^T$, as $n/p\to \tau \in (0,1)$ and $n,p\to \infty$, we have

$$\begin{array}{c}\hfill \widehat{\gamma }\stackrel{p}{\to }{\gamma }_0,{\widehat{\sigma }}_{ϵ}^2\stackrel{p}{\to }{\sigma }_{ϵ}^2,\end{array}$$

where ${\gamma }_0$ is the true value for γ.

The i.i.d. assumption on the entries of $\mathit{G}$ in Theorem 5 and Corollary 2 may limit their applicability in genetic studies, where SNPs are often correlated due to linkage disequilibrium (LD). However, it is worth noting that the correlation among SNPs does not necessarily hinder the application of these results. This is because the theoretical guarantees rely on the validity of the Marchenko–Pastur law, which was originally established for random matrices with i.i.d. entries having a mean of zero and unit variance. Importantly, the i.i.d. assumption on the entries can be relaxed: the Marchenko–Pastur law still holds for random matrices with i.i.d. rows, as long as each row has a mean of zero and unit variance and satisfies a light tail condition (e.g., sub-Gaussian) [22]. Therefore, as long as the SNP vectors from each individual are i.i.d., we expect that the results in Theorem 5 and Corollary 2 remain valid.

2.3.2. Inner-Product Kernel Matrices

Inner-product kernels, including the linear kernel and the polynomial kernel, are commonly used in practice. Generally, an inner-product-based kernel matrix has the form $\mathit{K}=f\left[p^{-1}{\mathit{GG}}^T\right]$. The first thing that needs to be addressed is the positive definiteness of $\mathit{K}$. In fact, based on Hiai [23], a necessary and sufficient condition for $\mathit{K}$ to be positive definite is when f is real analytic and $f^{\left(k\right)}\left(0\right)\ge 0$ for all $k\ge 0$. In this subsection, we will implicitly assume that this condition is satisfied.

Theorem 6.

For $\mathit{K}=f\left[p^{-1}{\mathit{GG}}^T\right]$ with entries in $\mathit{G}\in {\mathbb{R}}^{n\times p}$ and the function f,

1. 

$n\asymp p$.

2. 

$G_{ij}$ are i.i.d. with $\mathbb{E}\left[G_{ij}\right]=0$, $\mathbb{E}\left[G_{ij}^2\right]=1$, and $\mathbb{E}\left[\right|G_{ij}{|}^{4+\eta }]<\infty$ for some $\eta >0$.

3. 

f is a $C^1$ function in the neighborhood of 1 and a $C^3$ function in the neighborhood of 0.

Then as $n/p\to \tau \in (0,1)$ as $n,p\to \infty$, we have

$$\widehat{\gamma }\stackrel{p}{\to }{\gamma }_0,{\widehat{\sigma }}_{ϵ}^2\stackrel{p}{\to }{\sigma }_{ϵ}^2,$$

where ${\gamma }_0$ is the true value for γ.

2.3.3. Euclidean Distance Kernel Matrices

Another commonly used kernels in practice are the Euclidean distance-based kernels, such as the Gaussian kernel. Similar to the case in the inner-product kernel matrices, the positive definiteness of $\mathit{K}$ is the first issue to be addressed. According to Wendland [24], f being completely monotone is a necessary and sufficient condition for a Euclidean distance kernel matrix to be positive semi-definite. In other words, the function f needs to satisfy $f\in C^{\infty }\left([0,\infty )\right])$ and ${(-1)}^k{f}^{\left(k\right)}\left(r\right)\ge 0$ for all $r>0$ and $k=0,1,2,\dots$. Throughout Section 2.3.3, it will be implicitly assumed that f is completely monotone.

Theorem 7.

Let $\mathit{K}$ be a kernel matrix with entries $K_{ij}=f\left(p^{-1}{∥{\mathit{g}}_i^{\prime }-{\mathit{g}}_j^{\prime }∥}_2^2\right)$. Suppose that the entries in $\mathit{G}\in {\mathbb{R}}^{n\times p}$ and the function f satisfying

1. 

$n\asymp p$.

2. 

$G_{ij}$ are i.i.d. with $\mathbb{E}\left[G_{ij}\right]=0$, $\mathbb{E}\left[G_{ij}^2\right]=1$ and $\mathbb{E}\left[\right|G_{ij}{|}^{5+\eta }]<\infty$ for some $\eta >0$.

3. 

f is a $C^3$ function in a neighborhood of 2.

Then as $n/p\to \tau \in (0,1)$ and $n,p\to \infty$, we have

$$\widehat{\gamma }\stackrel{p}{\to }{\gamma }_0,{\widehat{\sigma }}_{ϵ}^2\stackrel{p}{\to }{\sigma }_{ϵ}^2,$$

where ${\gamma }_0$ is the true value for γ.

Remark 1.

Both Theorems 6 and 7 rely on the approximation of inner-product kernel matrices or Euclidean distance kernel matrices by linear kernels, identity matrices, and some low-rank matrices. Based on the proofs in El Karoui [21], the approximation rate for inner-product kernel matrices is $o_p\left(p^{-\delta /2}\right)$ for some $\delta <{\displaystyle \frac{1}{2}}$, while for a Gaussian kernel with entries with $exp\{-{∥{\zeta }_{\mathit{i}}-{\zeta }_{\mathit{j}}∥}^2/2\}$, the approximation rate is $nexp\{-p^{1/2+2/m+\delta }\}$ with $p^{1/2+2/m+\delta }$ being the rate that $\mathit{tr}\left(\mathit{Var}\right[\zeta \left]\right)$ grows to infinity, and this is an extremely fast rate.

3. Results

3.1. Simulation Studies

3.1.1. Weighted Product Kernel

We follow an idea similar to that by Jiang et al. [11]; we simulated the genotype for each SNP. Specifically, the minor allele frequencies (MAFs) for p SNPs $\{f_1,f_2,\dots ,f_p\}$ were generated from the uniform distribution $\mathrm{Unif}[0.05,0.5]$, where $f_j$ is the allele for the jth SNP. In the simulation, the number of SNPs is set to $p=2n$. For the weight matrix $\mathit{W}$, the jth element $w_j$ is defined to be

$$w_j={\displaystyle \frac{-{log}_{10}{f}_j}{{max}_{1\le j\le p}-{log}_{10}{f}_j}}.$$

The logarithm of MAF, which was defined in Li et al. [25], is one of the commonly used weights to detect effects from common variants and also takes the contributions from rare variants into account. To simulate the genotype matrix $\tilde{\mathit{G}}\in {\{0,1,2\}}^{n\times p}$, the Hardy–Weinberg equilibrium was assumed. Specifically, for the j SNP, the genotype value of each individual was sampled from $\{0,1,2\}$ according to the probabilities ${(1-f_j)}^2,2f_j(1-f_j)$, and $f_j^2$, respectively. Given the simulated genotypes, column standardization was applied to each column in $\tilde{\mathit{G}}$, and the resulting genotype matrix was denoted as $\mathit{G}$. The weighted kernel matrix is defined as

$$\mathit{K}=p^{-1}{\mathit{GWG}}^T.$$

The responses are simulated based on the following equation:

$$\mathit{y}=\mathit{X}\mathit{\beta }+\mathit{a}+\mathit{ϵ},$$

(12)

where the fixed-effect design matrix $\mathit{X}=[{\mathbf{1}}_n,\tilde{\mathit{X}}]\in {\mathbb{R}}^{n\times 3}$ and the elements in $\tilde{\mathit{X}}$ were generated from a standard normal distribution. We set $\mathit{\beta }={[1,2,-1]}^T$. The random effect $\mathit{a}\sim {\mathcal{N}}_n(\mathbf{0},0.6\mathit{K})$, and the random noise $\mathit{ϵ}\sim {\mathcal{N}}_n(\mathbf{0},2{\mathit{I}}_n)$. The choice of the variance component for the random effects is the same as in Jiang et al. [11] under their dense scenario. On the other hand, genetic data is often noisy, and the signal-to-noise ratio is low. To mimic the real situation, we set the variance of the random error to be two. In the simulation, we selected 100, 200, 400, 600, 800, and 1000 as the sample sizes. A total of 1000 Monte Carlo replications were conducted to evaluate the performance of the REML estimators for the variance components in the simulation model.

Figure 1 provides the boxplots for the REML estimators of the variance components in the simulation model (12). As shown from both panels, the REML estimators converge to the true values, which justifies the theoretical results developed in the previous sections. The mean and standard deviation of the REML estimators of the variance components are given in Table 1.

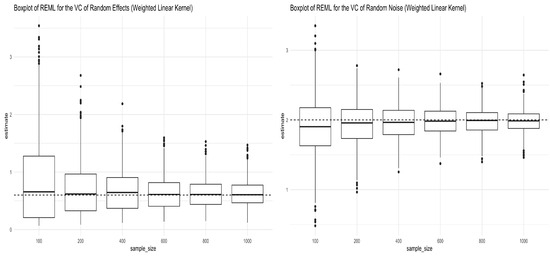
Figure 1. Boxplots for REML estimators of variance components obtained from Simulation (12) under the weighted linear kernel. The left panel shows the boxplots for the REML estimator of ${\sigma }_a^2$ (truth = 0.6), and the right panel shows the boxplots for the REML estimator of ${\sigma }_{ϵ}^2$ (truth = 2) under different sample sizes.

Table 1. Mean and standard deviations (values in the parenthesis) of REML estimators for ${\sigma }_a^2$ and ${\sigma }_{ϵ}^2$ based on 1000 Monte Carlo simulations under the weighted linear kernel.

Sample Size	${\widehat{\mathit{\sigma }}}_{\mathit{a}}^{\mathbf{2}}$	${\widehat{\mathit{\sigma }}}_{\mathit{ϵ}}^{\mathbf{2}}$
100	0.837 (0.709)	1.895 (0.415)
200	0.698 (0.451)	1.941 (0.302)
400	0.668 (0.344)	1.959 (0.237)
600	0.634 (0.286)	1.977 (0.204)
800	0.631 (0.247)	1.979 (0.182)
1000	0.631 (0.231)	1.985 (0.162)

3.1.2. Inner Product Kernel

We followed the same procedures mentioned in Section 3.1.1 to simulate the genotype matrix $\mathit{G}$, and Equation (12) was used to generate the response, except that in this case the kernel matrix is $\mathit{K}={(1+p^{-1}{\mathit{GG}}^T)}^2$, with the polynomial kernel having an order of 2. In the expression, power means the elementwise power. Figure 2 shows the simulation results for the REML estimators of the two variance components in Equation (12). As we can see from both panels in Figure 2, the REML estimators converge to the true values as anticipated. The mean and standard deviation of the REML estimators of the variance components are given in Table 2.

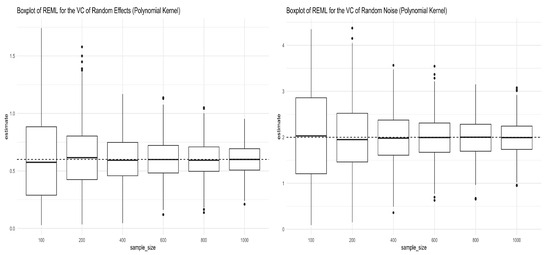
Figure 2. Boxplots for REML estimators of variance components obtained from Simulation (12) under the polynomial kernel with a degree of 2. The left panel shows the boxplots for the REML estimator of ${\sigma }_a^2$ (truth = 0.6), and the right panel shows the boxplots for the REML estimator of ${\sigma }_{ϵ}^2$ (truth = 2) under different sample sizes.

Table 2. Mean and standard deviations (values in the parenthesis) of REML estimators for ${\sigma }_a^2$ and ${\sigma }_{ϵ}^2$ based on 1000 Monte Carlo simulations under the polynomial kernel with a degree of 2.

Sample Size	${\widehat{\mathit{\sigma }}}_{\mathit{a}}^{\mathbf{2}}$	${\widehat{\mathit{\sigma }}}_{\mathit{ϵ}}^{\mathbf{2}}$
100	0.606 (0.375)	2.004 (1.021)
200	0.618 (0.284)	1.974 (0.790)
400	0.603 (0.206)	1.985 (0.561)
600	0.604 (0.172)	1.992 (0.469)
800	0.603 (0.152)	1.995 (0.416)
1000	0.601 (0.130)	1.996 (0.364)

3.1.3. Euclidean Distance Kernel

In this section, we investigated the consistency of REML estimators of the variance components when the kernel used to generate data in Equation (12) is the Gaussian kernel. When applying the Gaussian kernel $K(\mathit{u},\mathit{v})=exp\{-{\displaystyle \frac{{∥\mathit{u}-\mathit{v}∥}^2}{2\varphi }}\}$, the tuning parameter $\varphi$ is chosen to be the sample variance of the Euclidean distance between each pair. Figure 3 shows the simulation results for the REML estimators of the two variance components in Equation (12). The REML estimators converge to the true values as shown in both panels in Figure 3. The mean and standard deviation of the REML estimators of the variance components are given in Table 3.

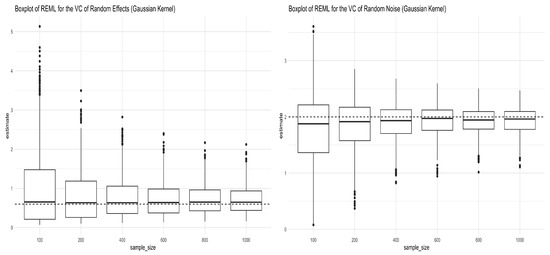
Figure 3. Boxplots for REML estimators of variance components obtained from Simulation (12) under the Gaussian kernel. The left panel shows the boxplots for the REML estimator of ${\sigma }_a^2$ (truth = 0.6), and the right panel shows the boxplots for the REML estimator of ${\sigma }_{ϵ}^2$ (truth = 2) under different sample sizes.

Table 3. Mean and standard deviations (values in parentheses) of REML estimators for ${\sigma }_a^2$ and ${\sigma }_{ϵ}^2$ based on 1000 Monte Carlo simulations under the Gaussian kernel.

Sample Size	${\widehat{\mathit{\sigma }}}_{\mathit{a}}^{\mathbf{2}}$	${\widehat{\mathit{\sigma }}}_{\mathit{ϵ}}^{\mathbf{2}}$
100	1.000 (0.955)	1.774 (0.631)
200	0.818 (0.650)	1.853 (0.432)
400	0.755 (0.483)	1.900 (0.320)
600	0.715 (0.406)	1.934 (0.262)
800	0.717 (0.363)	1.929 (0.229)
1000	0.707 (0.335)	1.938 (0.215)

3.2. Real Data Analysis

To check the performance of Restricted Maximum Likelihood (REML) estimators in high-dimensional kernel linear mixed models, we conducted a real data analysis similar to that by Jiang et al. [11]. The Study of Addiction: Genetics and Environment (SAGE) (dbGap Study Accession: phs000092.v1.p1) dataset was used to estimate the heritability of body mass index (BMI) based on kernel linear mixed models. To check the consistency of heritability estimation across different traits, we also include height and weight as the phenotypes.

After removing individuals without height or weight measures, a total of $n=1985$ individuals of European ancestry remain. We also performed a quality control process similar to that by Jiang et al. [11] to avoid bias in the estimation. Specifically, SNPs with a missing rate of >1%, a minor allele frequency (MAF) of <5%, and a p-value of <0.001 from the Hardy–Weinberg equilibrium test were excluded from the analysis. After the quality control process, p = 4,898,519 SNPs remained for analysis.

As in Jiang et al. [11], for the fixed-effect design matrix $\mathit{X}$, besides the intercept, the first 10 principal component scores computed from the product kernels were included. Kernel LMMs with the product kernel $\mathit{K}=p^{-1}{\mathit{GG}}^T$, a second-order polynomial kernel, and a Gaussian kernel were used to estimate the variance components and hence the heritability. The results are summarized in Table 4. The heritability obtained by the linear kernel is 20.35%, which is very close to the one (19.6%) obtained in Jiang et al. [11]. It can be seen from the table that the heritability estimation of BMI is higher when the polynomial kernel $\mathit{K}={\left(p^{-1}{\mathit{GG}}^T\right)}^2$ or the Gaussian kernel $K(\mathit{u},\mathit{v})=exp\{-{\displaystyle \frac{{∥\mathit{u}-\mathit{v}∥}^2}{2\varphi }}\}$ with $\varphi =1$ is used. The heritability obtained by the polynomial kernel is 50.08%, while the one obtained by the Gaussian kernel is 34.29%.

Table 4. Heritability estimation for BMI, height, and weight under different kernel matrices.

	Product	Polynomial	Gaussian
BMI	20.35%	50.08%	34.29%
Height	10.21%	49.93%	17.97%
Weight	8.46%	37.02%	16.31%

It is believed that the BMI is highly heritable, and recent twin studies have demonstrated large variation in BMI heritability, ranging from 31% to 90% [26]. Based on the previous results, the heritability estimation obtained using the product kernel is below this range, while the estimations using the Gaussian kernel and the polynomial kernel are within this range. The trend that estimated heritability using the polynomial kernel is the highest among the three choices of kernel and is consistent among the other two phenotypes.

In addition, we also experimented with different values of the constant c in the polynomial kernel, ranging from 0 to 1. Table 5 summarizes the heritability estimates under these choices. The results show that the performance of heritability estimation is sensitive to the choice of kernel hyperparameters. In particular, Table 5 reveals a general pattern: as the value of c increases, the estimated heritability tends to decrease. One explanation is that ${\left(c+{\displaystyle \frac{1}{p}}{\mathit{GG}}^T\right)}^2=c^2{\mathit{J}}_n+{\displaystyle \frac{2c}{p}}{\mathit{GG}}^T+{\left({\displaystyle \frac{1}{p}}{\mathit{GG}}^T\right)}^2$ so that the largest eigenvalue of the ${\left(c+{\displaystyle \frac{1}{p}}{\mathit{GG}}^T\right)}^2$ is lower bounded by ${\lambda }_{max}\left(c^2{\mathit{J}}_n\right)=n{c}^2$, which means that when c becomes larger, the rank-one matrix $c^2{\mathit{J}}_n$ dominates the spectrum of the polynomial kernel matrix. Consequently, the kernel matrix carries less informative structure for estimating the variance component in the random effects, resulting in a smaller estimate of ${\widehat{\sigma }}_a^2$.

Table 5. Heritability estimation for BMI, height, and weight under different kernel matrices.

	BMI	Height	Weight
0	50.08%	49.93%	37.02%
0.2	64.93%	16.23%	16.39%
0.4	31.26%	10.54%	8.82%
0.6	21.01%	7.95%	6.05%
0.8	15.92%	6.41%	4.67%
1	12.85%	5.39%	3.87%

4. Discussion

Kernel methods have been widely used in machine learning to capture nonlinear relationships between features and responses. In this paper, we demonstrate that when kernels are correctly specified, the REML estimators for the variance components in high-dimensional kernel linear mixed models are consistent across three classes of kernel functions. Simulation studies validate the theoretical results on consistency.

In addition, we would like to highlight a few directions for future work. First, as we have mentioned, the consistency of the REML estimators for variance components in kernel LMMs is established under the assumption that the kernels are correctly specified. In practice, the underlying data-generating process and the appropriate kernel are often unknown. Misspecifying the kernel in a kernel LMM could lead to inconsistent variance component estimators, resulting in biased estimates of heritability. Therefore, it is worth exploring a data-driven approach to identify the appropriate kernel function and evaluate its performance in estimating genetic heritability compared to commonly used kernels.

Second, the theories in this paper are established under the high-dimensional linear regime, where the sample size grows linearly with the number of SNPs. One reason for this assumption is that random matrix theory is widely used to derive theoretical results, and most existing work in random matrix theory focuses on the linear regime. Therefore, it is worthwhile to extend random matrix theory beyond the linear regime. Recently, Ghorbani et al. [27] and Mei et al. [28] developed theories for random kernel matrices under the polynomial regime, where $n\asymp p^{\lambda }$ with $\lambda <1$. However, in genetic studies, the number of SNPs is often much larger than the sample size. Thus, it is worthwhile to extend the results in this paper to scenarios where $n\asymp p^{\lambda }$ and $\lambda >1$ and to develop the corresponding theories for random kernel matrices under this regime.

Last but not least, as demonstrated in the real data analyses, the performance of kernel LMMs depends heavily on the choice of the kernel matrix. In practice, researchers often lack prior knowledge about which kernel is most appropriate. Therefore, developing a data-driven method for kernel selection would be highly desirable. One widely used strategy is multiple kernel learning [29], in which a single kernel matrix is replaced by a convex combination of several kernel matrices, where the weights of the kernel matrices are also learning by minimizing a loss function (e.g., mean squared error in the regression setting). Extending the current work to accommodate kernel matrices constructed via multiple kernel learning would be a valuable direction for future research.

Appendix A.1. Proof of Lemma 1

Proof. 

Let $Q={\mathit{y}}^T\mathbf{\Gamma }\mathit{y}$ and note that

$$\begin{array}{cc}\hfill \mathbb{E}\left[Q\right]& =\mathbb{E}[{\mathit{y}}^T\mathbf{\Gamma }\mathit{y}]=\mathbb{E}\left[{(\mathit{\mu }+\mathit{e})}^T\mathbf{\Gamma }(\mathit{\mu }+\mathit{e})\right]\hfill \\ \hfill & ={\mathit{\mu }}^T\mathit{A}\mathit{\mu }+\mathbb{E}\left[{\mathit{e}}^T\mathbf{\Gamma }\mathit{e}\right],\hfill \end{array}$$

we can obtain

$$\begin{array}{cc}\hfill Q-\mathbb{E}\left[Q\right]& ={(\mathit{\mu }+\mathit{e})}^T\mathbf{\Gamma }(\mathit{\mu }+\mathit{e})-{\mathit{\mu }}^T\mathbf{\Gamma }\mathit{\mu }-\mathbb{E}[{\mathit{e}}^T\mathbf{\Gamma }\mathit{e}]\hfill \\ \hfill & ={\mathit{e}}^T\mathbf{\Gamma }\mathit{e}-\mathbb{E}[{\mathit{e}}^T\mathbf{\Gamma }\mathit{e}]+2{\mathit{e}}^T\mathbf{\Gamma }\mathit{\mu }.\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill \mathrm{Var}\left[Q\right]& =\mathbb{E}\left[{(Q-\mathbb{E}\left[Q\right])}^2\right]\hfill \\ \hfill & =\mathbb{E}\left[{\left({\mathit{e}}^T\mathbf{\Gamma }\mathit{e}-\mathbb{E}[{\mathit{e}}^T\mathbf{\Gamma }\mathit{e}]+2{\mathit{e}}^T\mathbf{\Gamma }\mathit{\mu }\right)}^2\right]\hfill \\ \hfill & \le \mathbb{E}\left[2{({\mathit{e}}^T\mathbf{\Gamma }\mathit{e}-\mathbb{E}[{\mathit{e}}^T\mathbf{\Gamma }\mathit{e}])}^2+8{\mathit{\mu }}^T{\mathbf{\Gamma }}^T{\mathit{ee}}^T\mathbf{\Gamma }\mathit{\mu }\right]\hfill \\ \hfill & =2\mathrm{Var}[{\mathit{e}}^T\mathbf{\Gamma }\mathit{e}]+8{\mathit{\mu }}^T{\mathbf{\Gamma }}^T\mathbf{\Sigma }\mathbf{\Gamma }\mathit{\mu }\hfill \end{array}$$

□

Appendix A.2. Proof of Theorem 5

Proof. 

Let ${\mathbf{\Sigma }}_{\gamma }={\mathit{A}}^T{\mathit{V}}_{\gamma }\mathit{A}$. Then according to the well-known identity (see for example, Searle et al. [18]), we have

$$\begin{array}{cc}\hfill {\mathit{P}}_{\gamma }& ={\mathit{V}}_{\gamma }^{-1}-{\mathit{V}}_{\gamma }^{-1}\mathit{X}{\left({\mathit{X}}^T{\mathit{V}}_{\gamma }^{-1}\mathit{X}\right)}^{-1}{\mathit{X}}^T{\mathit{V}}_{\gamma }^{-1}\hfill \\ \hfill & =\mathit{A}{\left({\mathit{A}}^T{\mathit{V}}_{\gamma }\mathit{A}\right)}^{-1}{\mathit{A}}^T\hfill \\ \hfill & =\mathit{A}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T.\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill |\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)|& =|\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}\right)|\hfill \\ \hfill & =|\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\left(p^{-1}{\mathit{GWG}}^T\mathit{A}\right)\right)|\hfill \\ \hfill & \le {\lambda }_{max}\left({\mathbf{\Sigma }}_{\gamma }^{-1}\right)p^{-1}\mathrm{tr}\left({\mathit{A}}^T{\mathit{GWG}}^T\mathit{A}\right).\hfill \end{array}$$

Under the assumptions of $\mathit{W}$, we have ${\mathit{I}}_p-\mathit{W}\ge 0$, and hence

$${\mathit{A}}^T{\mathit{GG}}^T\mathit{A}\ge {\mathit{A}}^T{\mathit{GWG}}^T\mathit{A},$$

which further implies that

$$\mathrm{tr}\left({\mathit{A}}^T{\mathit{GG}}^T\mathit{A}\right)\ge \mathrm{tr}\left({\mathit{A}}^T{\mathit{GWG}}^T\mathit{A}\right).$$

As a consequence,

$$\begin{array}{cc}\hfill |\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)|& \le {\lambda }_{max}\left({\mathbf{\Sigma }}_{\gamma }^{-1}\right)p^{-1}\mathrm{tr}\left({\mathit{A}}^T{\mathit{GG}}^T\mathit{A}\right)\hfill \\ \hfill & ={\lambda }_{min}^{-1}\left({\mathbf{\Sigma }}_{\gamma }\right)p^{-1}\mathrm{tr}\left({\mathit{A}}^T{\mathit{GG}}^T\mathit{A}\right)\hfill \\ \hfill & \le p^{-1}\mathrm{tr}\left({\mathit{A}}^T{\mathit{GG}}^T\mathit{A}\right)={\mathcal{O}}_p\left(n\right),\hfill \end{array}$$

where the last equality follows from Corollary 1.

Now we define

$$\begin{array}{cc}\hfill \Delta =\Delta \left(\gamma \right)& ={\mathit{y}}^T\mathit{B}\left(\gamma \right)\mathit{y}\hfill \\ \hfill \mathit{B}=\mathit{B}\left(\gamma \right)& ={\displaystyle \frac{{\mathit{P}}_{\gamma }{\mathit{KP}}_{\gamma }}{\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)}}-{\displaystyle \frac{{\mathit{P}}_{\gamma }}{n-q}}\hfill \\ \hfill & ={\displaystyle \frac{\mathit{A}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T}{\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)}}-{\displaystyle \frac{\mathit{A}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T}{n-q}}\hfill \\ \hfill & =\mathit{A}({\mathit{C}}_1-{\mathit{C}}_2){\mathit{A}}^T,\hfill \end{array}$$

with

$$\begin{array}{cc}\hfill {\mathit{C}}_1& ={\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}/\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)\hfill \\ \hfill {\mathit{C}}_2& ={\mathbf{\Sigma }}_{\gamma }^{-1}/(n-q).\hfill \end{array}$$

Next, we write $\Delta =\mathbb{E}[\Delta |\mathit{G}]+\Delta -\mathbb{E}[\Delta \left|\mathit{G}\right]$, and we are going to show that $\mathit{E}[\Delta |\mathit{G}]$ converges to some constant limit, and $\Delta -\mathbb{E}[\Delta |\mathit{G}]=o_p\left(1\right)$. We first show that $\Delta -\mathbb{E}[\Delta |\mathit{G}]=o_p\left(1\right)$. Based on Lemma 1,

$$\begin{array}{cc}\hfill \mathrm{Var}[\Delta |\mathit{G}]& =\mathrm{Var}\left[{\mathit{y}}^T\mathit{A}({\mathit{C}}_1-{\mathit{C}}_2){\mathit{A}}^T\mathit{y}|\mathit{G}\right]\hfill \\ \hfill & =\mathrm{Var}\left[{\tilde{\mathit{y}}}^T({\mathit{C}}_1-{\mathit{C}}_2)\tilde{\mathit{y}}|\mathit{G}\right]\hfill \\ \hfill & \le 2{\sigma }_{ϵ}^2\mathrm{tr}\left(({\mathit{C}}_1-{\mathit{C}}_2){\mathbf{\Sigma }}_0({\mathit{C}}_1-{\mathit{C}}_2){\mathbf{\Sigma }}_0\right)\hfill \\ \hfill & =2{\sigma }_{ϵ}^2\left[\mathrm{tr}\left({\left({\mathit{C}}_1{\mathbf{\Sigma }}_0\right)}^2\right)+\mathrm{tr}\left({\left({\mathit{C}}_2{\mathbf{\Sigma }}_0\right)}^2\right)-2\mathrm{tr}\left({\mathit{C}}_1{\mathbf{\Sigma }}_0{\mathit{C}}_2{\mathbf{\Sigma }}_0\right)\right]\hfill \end{array}$$

(A1)

where $\tilde{\mathit{y}}={\mathit{A}}^T\mathit{y}\sim {\mathcal{N}}_{n-q}(\mathbf{0},{\sigma }_{ϵ}^2{\mathit{A}}^T{\mathit{V}}_0\mathit{A})={\mathcal{N}}_{n-q}(\mathbf{0},{\sigma }_{ϵ}^2{\mathbf{\Sigma }}_0)$ and ${\mathit{V}}_0$ and ${\mathbf{\Sigma }}_0$ are the corresponding matrices of ${\mathit{V}}_{\gamma }$ and ${\mathbf{\Sigma }}_{\gamma }$ with the truth ${\gamma }_0$. We now consider each term in the right hand side of Equation (A1). First note that

$$\mathrm{tr}\left({\left({\mathit{C}}_1{\mathbf{\Sigma }}_0\right)}^2\right)={\left[\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)\right]}^{-2}\mathrm{tr}\left({\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)}^2\right).$$

Since

$$\begin{array}{cc}\hfill \mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)& =\mathrm{tr}\left(\mathit{A}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{K}\right)\hfill \\ \hfill & =\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1/2}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1/2}\right)\hfill \\ \hfill & \ge {\lambda }_{min}\left(\mathit{K}\right)\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}\right),\hfill \end{array}$$

and it follows from the assumption on $\mathit{W}$ and Corollary 1,

$$\begin{array}{cc}\hfill {\lambda }_{min}\left(\mathit{K}\right)& =p^{-1}{\lambda }_{min}\left({\mathit{GWG}}^T\right)\hfill \\ \hfill & \ge {\lambda }_{min}\left(\mathit{W}\right){\lambda }_{min}\left(p^{-1}{\mathit{GG}}^T\right)\hfill \\ \hfill & \ge \delta {\lambda }_{min}\left(p^{-1}{\mathit{GG}}^T\right)\hfill \\ \hfill & \to \delta b_{-}\left(\tau \right)>0 \mathrm{a}.\mathrm{s}.,\hfill \end{array}$$

$$\begin{array}{cc}\hfill \mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}\right)& =\mathrm{tr}\left({({\mathit{I}}_{n-q}+\gamma {\mathit{A}}^T\mathit{K}\mathit{A})}^{-1}\right)\hfill \\ \hfill & =\sum _{i=1}^{n-q}{\displaystyle \frac{1}{1+{\lambda }_i\left(\gamma {\mathit{A}}^T\mathit{KA}\right)}}\hfill \\ \hfill & \ge {\displaystyle \frac{n-q}{1+\gamma {\lambda }_{max}\left({\mathit{A}}^T\mathit{KA}\right)}}={\mathcal{O}}_p\left(n\right),\hfill \end{array}$$

we know that $\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right){\asymp }_{p}n$. On the other hand,

$$\mathrm{tr}\left({\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)}^2\right)=\mathrm{tr}\left({\left({\mathbf{\Sigma }}_0^{1/2}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0^{1/2}\right)}^2\right)$$

and since ${\mathit{I}}_p\ge \mathit{W}$, it follows that

$$\begin{array}{cc}\hfill {\mathbf{\Sigma }}_0^{1/2}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0^{1/2}& \le {\mathbf{\Sigma }}_0^{1/2}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T{p}^{-1}{\mathit{GG}}^T\mathit{A}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0^{1/2}\hfill \end{array}$$

According to Corollary 1

$$\mathrm{tr}\left({\left({\mathbf{\Sigma }}_0^{1/2}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0^{1/2}\right)}^2\right)\le \mathrm{tr}\left({\left({\mathbf{\Sigma }}_0^{1/2}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T{p}^{-1}{\mathit{GG}}^T\mathit{A}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0^{1/2}\right)}^2\right)={\mathcal{O}}_p\left(n\right),$$

which implies that $\mathrm{tr}\left({\left({\mathit{C}}_1{\mathbf{\Sigma }}_0\right)}^2\right)={\mathcal{O}}_p\left(n^{-1}\right)$.

For the second term, it is clear that

$$\mathrm{tr}\left({\left({\mathit{C}}_2{\mathbf{\Sigma }}_0\right)}^2\right)={(n-q)}^{-2}\mathrm{tr}\left({\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)}^2\right)\le {(n-q)}^{-1}{\lambda }_{max}^2\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right).$$

Since

$$\begin{array}{cc}\hfill {\lambda }_{max}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)& \le {\lambda }_{max}\left({\mathbf{\Sigma }}_{\gamma }^{-1}\right){\lambda }_{max}\left({\mathbf{\Sigma }}_0\right)\hfill \\ \hfill & ={\left[{\lambda }_{min}\left({\mathbf{\Sigma }}_{\gamma }\right)\right]}^{-1}{\lambda }_{max}({\mathit{I}}_{n-q}+{\gamma }_0{\mathit{A}}^T\mathit{KA})\hfill \\ \hfill & ={\displaystyle \frac{1+{\gamma }_0{\lambda }_{max}\left({\mathit{A}}^T\mathit{KA}\right)}{1+\gamma {\lambda }_{max}\left({\mathit{A}}^T\mathit{KA}\right)}}\hfill \\ \hfill & \le {\displaystyle \frac{{\gamma }_0}{\gamma }}\vee 1,\hfill \end{array}$$

we can know that $\mathrm{tr}\left({\left({\mathit{C}}_2{\mathbf{\Sigma }}_0\right)}^2\right)={\mathcal{O}}_p\left(n^{-1}\right)$.

Similarly for the third term, we have

$$\begin{array}{cc}\hfill \mathrm{tr}\left({\mathit{C}}_1{\mathbf{\Sigma }}_0{\mathit{C}}_2{\mathbf{\Sigma }}_{\mathbf{0}}\right)& ={\left[(n-q)\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)\right]}^{-1}\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_{\mathbf{0}}\right)\hfill \\ \hfill & \le {\lambda }_{max}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right){\left[(n-q)\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)\right]}^{-1}\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)\hfill \\ \hfill & \le {\lambda }_{max}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right){\left[(n-q)\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)\right]}^{-1}\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T{p}^{-1}{\mathit{GG}}^T\mathit{A}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)\hfill \\ \hfill & ={\mathcal{O}}_p(n^{-2}·n)={\mathcal{O}}_p\left(n^{-1}\right).\hfill \end{array}$$

Therefore, $\mathrm{Var}[\Delta |\mathit{G}]={\mathcal{O}}_p\left(n^{-1}\right)$ and by Chebyshev’s inequality, for any $t>0$,

$$\mathbb{P}\left(\left|\Delta -\mathbb{E}[\Delta |\mathit{G}]\right|>t|\mathit{G}\right)\le {\displaystyle \frac{\mathrm{Var}[\Delta |\mathit{G}]}{t^2}}\stackrel{p}{\to }0, \mathrm{as} n\to \infty .$$

It then follows from the Dominated Convergence Theorem that

$$\mathbb{P}\left(\right|\Delta -\mathbb{E}[\Delta |\mathit{G}]|>t)\to 0,\forall t>0,$$

which implies that $\Delta -\mathbb{E}[\Delta |\mathit{G}]=o_p\left(1\right)$.

Next, let us focus on $\mathbb{E}[\Delta |\mathit{G}]$. It is easy to see that

$$\begin{array}{cc}\hfill \mathbb{E}[\Delta |\mathit{G}]& =\mathbb{E}\left[{\mathit{y}}^T\mathit{A}({\mathit{C}}_1-{\mathit{C}}_2){\mathit{A}}^T\mathit{y}|\mathit{G}\right]\hfill \\ \hfill & ={\sigma }_{ϵ}^2\mathrm{tr}\left(({\mathit{C}}_1-{\mathit{C}}_2){\mathbf{\Sigma }}_{\mathbf{0}}\right)\hfill \\ \hfill & ={\sigma }_{ϵ}^2\left[{\displaystyle \frac{\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)}{\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)}}-{\displaystyle \frac{\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)}{n-q}}\right].\hfill \end{array}$$

(A2)

Since

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)}{\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)}}& \le {\displaystyle \frac{{\lambda }_{max}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}\right)}{\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)}}\hfill \\ \hfill & ={\lambda }_{max}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)\le {\displaystyle \frac{{\gamma }_0}{\gamma }}\vee 1,\hfill \end{array}$$

it follows from Bounded Convergence Theorem that

$$\mathbb{E}\left[{\displaystyle \frac{\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)}{\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)}}\right]\to \mathbb{E}\left[\underset{n\to \infty }{lim}{\displaystyle \frac{\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)}{\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)}}\right],\mathrm{as} n\to \infty .$$

Moreover, note that

$$\begin{array}{c}\hfill \mathbb{E}\left[\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)\right]=\mathbb{E}\left[\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}\right)\right]+{\gamma }_0\mathbb{E}\left[\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}\right)\right],\end{array}$$

and according to Theorem 2, the ESD of ${\displaystyle \frac{p}{n}}{\mathit{A}}^T\mathit{KA}$ converges in distribution almost surely to a nonrandom distribution F. Let ${\lambda }_1,\dots ,{\lambda }_{n-q}$ be the eigenvalues of $(p/n){\mathit{A}}^T\mathit{KA}$, then

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}\right)}{n-q}}& ={\displaystyle \frac{1}{n-q}}\sum _{i=1}^{n-q}{\displaystyle \frac{(n/p){\lambda }_i}{{(1+(n/p)\gamma {\lambda }_i)}^2}}\to \int {\displaystyle \frac{\tau x}{{(1+\tau \gamma x)}^2}}\mathrm{d}F\left(x\right) \mathrm{a}.\mathrm{s}.\hfill \\ \hfill {\displaystyle \frac{\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)}{n-q}}& ={\displaystyle \frac{1}{n-q}}\sum _{i=1}^{n-q}{\displaystyle \frac{(n/p){\lambda }_i}{1+(n/p)\gamma {\lambda }_i}}\to \int {\displaystyle \frac{\tau x}{1+\tau \gamma x}}\mathrm{d}F\left(x\right) \mathrm{a}.\mathrm{s}.\hfill \\ \hfill {\displaystyle \frac{\mathrm{tr}\left(\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}\right){)}^2\right)}{n-q}}& ={\displaystyle \frac{1}{n-q}}\sum _{i=1}^{n-q}{\displaystyle \frac{{(n/p)}^2{\lambda }_i^2}{{(1+\gamma (n/p){\lambda }_i)}^2}}\to \int {\displaystyle \frac{{\tau }^2{x}^2}{{(1+\tau \gamma x)}^2}}\mathrm{d}F\left(x\right) \mathrm{a}.\mathrm{s}..\hfill \end{array}$$

For notation simplicity, we define

$$\begin{array}{cc}\hfill {\varphi }_1& =\int {\displaystyle \frac{\tau x}{{(1+\tau \gamma x)}^2}}\mathrm{d}F\left(x\right)\hfill \\ \hfill {\varphi }_2& =\int {\displaystyle \frac{{\tau }^2{x}^2}{{(1+\tau \gamma x)}^2}}\mathrm{d}F\left(x\right).\hfill \end{array}$$

Similarly, since ${(n-q)}^{-1}\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)\le {\lambda }_{max}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)\le {\gamma }_0/\gamma \vee 1$, it follows from Bounded Convergence Theorem that

$$\mathbb{E}\left[{\displaystyle \frac{\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)}{n-q}}\right]\to \mathbb{E}\left[\underset{n\to \infty }{lim}{\displaystyle \frac{\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)}{n-q}}\right],\mathrm{as} n\to \infty .$$

Moreover, note that

$$\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)=\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}\right)+{\gamma }_0\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}\right),$$

and by Theorem 2,

$$\begin{array}{c}\hfill {\displaystyle \frac{\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}\right)}{n-q}}={\displaystyle \frac{1}{n-q}}\sum _{i=1}^{n-q}{\displaystyle \frac{1}{1+(n/p)\gamma {\lambda }_i}}\to \int {\displaystyle \frac{1}{1+\tau \gamma x}}\mathrm{d}F\left(x\right) \mathrm{a}.\mathrm{s}..\end{array}$$

Let

$$\begin{array}{cc}\hfill {\mathit{\psi }}_1& =\int {\displaystyle \frac{1}{1+\tau \gamma x}}\mathrm{d}F\left(x\right)\hfill \\ \hfill {\mathit{\psi }}_2& =\int {\displaystyle \frac{\tau x}{1+\tau \gamma x}}\mathrm{d}F\left(x\right).\hfill \end{array}$$

Then we have

$$\mathbb{E}[\Delta |\mathit{G}]={\sigma }_{ϵ}^2\left({\displaystyle \frac{{\varphi }_1}{{\mathit{\psi }}_2}}+{\gamma }_0{\displaystyle \frac{{\varphi }_2}{{\mathit{\psi }}_2}}-{\mathit{\psi }}_1-{\gamma }_0{\mathit{\psi }}_2\right)={\sigma }_{ϵ}^2\left({\displaystyle \frac{{\varphi }_1}{{\mathit{\psi }}_2}}-{\mathit{\psi }}_1\right)\left(1+{\gamma }_0{\displaystyle \frac{{\varphi }_2/{\mathit{\psi }}_2-{\mathit{\psi }}_2}{{\varphi }_1/{\mathit{\psi }}_2-{\mathit{\psi }}_1}}\right)$$

Using Fubini Theorem and some tedious algebra, it follows that

$$\mathbb{E}\left[\Delta |\mathit{G}\right]={\sigma }_{ϵ}^2\left({\displaystyle \frac{{\gamma }_0}{\gamma }}-1\right)\left({\mathit{\psi }}_1-{\displaystyle \frac{{\varphi }_1}{{\mathit{\psi }}_2}}\right).$$

Note that since $f\left(x\right)={(1+\tau x)}^{-1}$ is non-increasing and $g\left(x\right)={(1+\tau x)}^{-1}\tau x$ is non-decreasing, we have for any $x,y\in \mathbb{R}$

$$\left(f\right(x)-f(y\left)\right)\left(g\right(x)-g(y\left)\right)\le 0,$$

and hence

$$\begin{array}{cc}\hfill 0& \ge \int \int (f(x)-f(y))(g(x)-g(y))\mathrm{d}F(x)\mathrm{d}F(y)\hfill \\ \hfill & =2\int f(x)g(x)\mathrm{d}F(x)-2\int f(x)\mathrm{d}F(x)\int g(x)\mathrm{d}F(x),\hfill \end{array}$$

which implies that

$$\int {\displaystyle \frac{1}{1+\tau x}}\mathrm{d}F\left(x\right)\int {\displaystyle \frac{\tau x}{1+\tau x}}\mathrm{d}F\left(x\right)\ge \int {\displaystyle \frac{\tau x}{{(1+\tau x)}^2}}\mathrm{d}F\left(x\right),$$

that is, ${\mathit{\psi }}_1{\mathit{\psi }}_2\ge {\varphi }_1$. Therefore, $\Delta \stackrel{p}{\to }{\sigma }_{ϵ}^2\left({\displaystyle \frac{{\gamma }_0}{\gamma }}-1\right)\left({\mathit{\psi }}_1-{\displaystyle \frac{{\varphi }_1}{{\mathit{\psi }}_2}}\right)$, which is a constant limit, and the limit is $>0$, $=0$, and $<0$ when $\gamma <{\gamma }_0$, $\gamma ={\gamma }_0$, and $\gamma >{\gamma }_0$, respectively. This proves the desired result as $\widehat{\gamma }$ is the solution to $\Delta =0$, and hence ${\widehat{\gamma }}_n\to {\gamma }_0$.

Next, we prove the second part of this theorem. Let

$$\begin{array}{cc}\hfill {\widehat{\sigma }}_{ϵ}^2& ={\displaystyle \frac{1}{n-q}}{\mathit{y}}^T{\mathit{P}}_{{\widehat{\gamma }}_n}\mathit{y}\hfill \\ \hfill & =\mathbb{E}\left[{\displaystyle \frac{1}{n-q}}{\mathit{y}}^T{\mathit{P}}_{{\gamma }_0}\mathit{y}\right]+\left({\displaystyle \frac{1}{n-q}}{\mathit{y}}^T{\mathit{P}}_{{\widehat{\gamma }}_n}\mathit{y}-{\displaystyle \frac{1}{n-q}}{\mathit{y}}^T{\mathit{P}}_{{\gamma }_0}\mathit{y}\right)+\left({\displaystyle \frac{1}{n-q}}{\mathit{y}}^T{\mathit{P}}_{{\gamma }_0}\mathit{y}-\mathbb{E}\left[{\displaystyle \frac{1}{n-q}}{\mathit{y}}^T{\mathit{P}}_{{\gamma }_0}\mathit{y}\right]\right).\hfill \end{array}$$

First note that ${\mathit{X}}^T{\mathit{P}}_{{\gamma }_0}\mathit{X}={\mathit{X}}^T{\mathit{V}}_{{\gamma }_0}^{-1}\mathit{X}-{\mathit{X}}^T{\mathit{V}}_{{\gamma }_0}^{-1}\mathit{X}{\left({\mathit{X}}^T{\mathit{V}}_{{\gamma }_0}^{-1}\mathit{X}\right)}^{-1}{\mathit{X}}^T{\mathit{V}}_{{\gamma }_0}^{-1}\mathit{X}=\mathbf{0}$, so we have

$$\begin{array}{cc}\hfill \mathbb{E}\left[{\displaystyle \frac{1}{n-q}}{\mathit{y}}^T{\mathit{P}}_{{\gamma }_0}\mathit{y}\right]& ={\displaystyle \frac{1}{n-q}}\left[\mathrm{tr}\left({\mathit{P}}_{{\gamma }_0}{\sigma }_{ϵ}^2{\mathit{V}}_{{\gamma }_0}\right)+{\mathit{\beta }}^T{\mathit{X}}^T{\mathit{P}}_{{\gamma }_0}\mathit{X}\mathit{\beta }\right]\hfill \\ \hfill & ={\displaystyle \frac{1}{n-q}}\left[{\sigma }_{ϵ}^2\mathrm{tr}\left({\mathit{I}}_n-{\mathit{V}}_{{\gamma }_0}^{-1}\mathit{X}{\left({\mathit{X}}^T{\mathit{V}}_{{\gamma }_0}\mathit{X}\right)}^{-1}{\mathit{X}}^T\right)\right]\hfill \\ \hfill & ={\displaystyle \frac{1}{n-q}}(n-q){\sigma }_{ϵ}^2={\sigma }_{ϵ}^2.\hfill \end{array}$$

Next, since ${\widehat{\gamma }}_n\stackrel{p}{\to }{\gamma }_0$, by continuous mapping theorem, we have

$$∥{\displaystyle \frac{1}{n-q}}{\mathit{P}}_{{\gamma }_n}-{\displaystyle \frac{1}{n-q}}{\mathit{P}}_{{\gamma }_0}∥\le {\displaystyle \frac{1}{n-q}}·n\underset{1\le i\le n}{max}({\mathit{P}}_{{\widehat{\gamma }}_n,ii}-{\mathit{P}}_{{\gamma }_0,ii})=o_p\left(1\right),$$

which implies that ${\displaystyle \frac{1}{n-q}}{\mathit{y}}^T{\mathit{P}}_{{\widehat{\gamma }}_n}\mathit{y}-{\displaystyle \frac{1}{n-q}}{\mathit{y}}^T{\mathit{P}}_{{\gamma }_0}\mathit{y}=o_p\left(1\right)$. Finally, since $\mathit{y}={\sigma }_{ϵ}{\mathit{V}}_{{\gamma }_0}^{1/2}\mathit{z}$ where $\mathit{z}\sim {\mathcal{N}}_n(\mathbf{0},{\mathit{I}}_n)$, by the famous Hanson Wright inequality, for any $t>0$,

$$\begin{array}{c}\hspace{1em}\mathbb{P}\left(\left|{\displaystyle \frac{1}{n-q}}{\mathit{y}}^T{\mathit{P}}_{{\gamma }_0}\mathit{y}-\mathbb{E}\left[{\displaystyle \frac{1}{n-q}}{\mathit{y}}^T{\mathit{P}}_{{\gamma }_0}\mathit{y}\right]\right|>t\right)\hfill \\ =\mathbb{P}\left(\left|{\mathit{z}}^T{\mathit{V}}_{{\gamma }_0}^{1/2}{\mathit{P}}_{{\gamma }_0}{\mathit{V}}_{{\gamma }_0}^{1/2}\mathit{z}-\mathbb{E}\left[{\mathit{z}}^T{\mathit{V}}_{{\gamma }_0}^{1/2}{\mathit{P}}_{{\gamma }_0}{\mathit{V}}_{{\gamma }_0}^{1/2}\mathit{z}\right]\right|>(n-q)t/{\sigma }_{ϵ}^2\right)\hfill \\ \lesssim exp\left\{-cmin\left({\displaystyle \frac{{(n-q)}^2{t}^2}{{\sigma }_{ϵ}^4{∥{\mathit{V}}_{{\gamma }_0}^{1/2}{\mathit{P}}_{{\gamma }_0}{\mathit{V}}_{{\gamma }_0}^{1/2}∥}_F^2}},{\displaystyle \frac{(n-q)t}{{\sigma }_{ϵ}^2∥{\mathit{V}}_{{\gamma }_0}^{1/2}{\mathit{P}}_{{\gamma }_0}{\mathit{V}}_{{\gamma }_0}^{1/2}∥}}\right)\right\}.\hfill \end{array}$$

Note that

$$\begin{array}{cc}\hfill ∥{\mathit{V}}_{{\gamma }_0}^{1/2}{\mathit{P}}_{{\gamma }_0}{\mathit{V}}_{{\gamma }_0}^{1/2}∥& \le ∥{\mathit{I}}_n-{\mathit{V}}_{{\gamma }_0}^{-1/2}\mathit{X}{\left({\mathit{X}}^T{\mathit{V}}_{{\gamma }_0}^{-1}\mathit{X}\right)}^{-1}{\mathit{X}}^T{\mathit{V}}_{{\gamma }_0}^{-1/2}∥\le 1,\hfill \\ \hfill {∥{\mathit{V}}_{{\gamma }_0}^{1/2}{\mathit{P}}_{{\gamma }_0}{\mathit{V}}_{{\gamma }_0}^{1/2}∥}_F^2& \le n∥{\mathit{V}}_{{\gamma }_0}^{1/2}{\mathit{P}}_{{\gamma }_0}{\mathit{V}}_{{\gamma }_0}^{1/2}∥\le n,\hfill \end{array}$$

so we obtain

$$\mathbb{P}\left(\left|{\displaystyle \frac{1}{n-q}}{\mathit{y}}^T{\mathit{P}}_{{\gamma }_0}\mathit{y}-\mathbb{E}\left[{\displaystyle \frac{1}{n-q}}{\mathit{y}}^T{\mathit{P}}_{{\gamma }_0}\mathit{y}\right]\right|>t\right)\lesssim exp\left\{-\mathcal{O}\left(n\right)\right\}\to 0,$$

which implies that ${\widehat{\sigma }}_{ϵ}^2={\sigma }_{ϵ}^2+o_p\left(1\right)$. □

Appendix A.3. Proof of Corollary 2

Proof. 

For simplicity, let $\mathit{A}=(\mathit{G}-\overline{\mathit{g}}\otimes {\mathbf{1}}_n){\mathit{W}}^{1/2}$ and $\mathit{B}=\tilde{G}{\mathit{W}}^{1/2}$. Then $\tilde{\mathit{K}}=p^{-1}{\mathit{BB}}^T$. Let ${\mathit{K}}^{\prime }=p^{-1}{\mathit{AA}}^T$. Now note that

$$\begin{array}{cc}\hfill {∥\mathit{A}∥}_F^2& =\mathrm{tr}\left({\mathit{AA}}^T\right)\hfill \\ \hfill & =\mathrm{tr}\left((\mathit{G}-\overline{\mathit{g}}\otimes {\mathbf{1}}_n)\mathit{W}{(\mathit{G}-\overline{\mathit{g}}\otimes {\mathbf{1}}_n)}^T\right)\hfill \\ \hfill & =\mathrm{tr}\left({\mathit{GWG}}^T\right)-2\mathrm{tr}\left(\mathit{GW}{(\overline{\mathit{g}}\otimes {\mathbf{1}}_n)}^T\right)+\mathrm{tr}\left((\overline{\mathit{g}}\otimes {\mathbf{1}}_n)\mathit{W}{(\overline{\mathit{g}}\otimes {\mathbf{1}}_n)}^T\right).\hfill \end{array}$$

Since ${\mathit{I}}_p\ge \mathit{W}$, we have $p^{-1}{\mathit{GG}}^T\ge p^{-1}{\mathit{GWG}}^T$ and

$$\begin{array}{cc}\hfill p^{-1}\mathrm{tr}\left(\mathit{GWG}6T\right)& \le p^{-1}\mathrm{tr}\left({\mathit{GG}}^T\right)={\mathcal{O}}_p\left(n\right).\hfill \\ \hfill p^{-1}\mathrm{tr}\left(\mathit{GW}{(\overline{g}\otimes {\mathbf{1}}_n)}^T\right)& =p^{-1}\mathrm{tr}\left(\mathit{GW}{\left(\left({\displaystyle \frac{1}{n}}{\mathbf{1}}_n^T\mathit{G}\right)\otimes {\mathbf{1}}_n\right)}^T\right)\hfill \\ \hfill & =p^{-1}\mathrm{tr}\left(\left({\displaystyle \frac{1}{n}}{\mathit{GWG}}^T{\mathbf{1}}_n\right)\otimes {\mathbf{1}}_n^T\right)\hfill \\ \hfill & =n^{-1}{\mathbf{1}}_n^T{p}^{-1}{\mathit{GWG}}^T{\mathbf{1}}_n\hfill \\ \hfill & \le {\lambda }_{max}\left(p^{-1}{\mathit{GWG}}^T\right)\hfill \\ \hfill & \le {\lambda }_{max}\left(p^{-1}{\mathit{GG}}^T\right)={\mathcal{O}}_p\left(1\right).\hfill \\ \hfill p^{-1}\mathrm{tr}\left((\overline{\mathit{g}}\otimes {\mathbf{1}}_n)\mathit{W}{(\overline{\mathit{g}}\otimes {\mathbf{1}}_n)}^T\right)& =p^{-1}\mathrm{tr}\left[\left(\left({\displaystyle \frac{1}{n}}{\mathbf{1}}_n^T\mathit{G}\right)\otimes {\mathbf{1}}_n\right)\mathit{W}{\left(\left({\displaystyle \frac{1}{n}}{\mathbf{1}}_n^T\mathit{G}\right)\otimes {\mathbf{1}}_n\right)}^T\right]\hfill \\ \hfill & =p^{-1}\mathrm{tr}\left[\left({\displaystyle \frac{1}{n^2}}{\mathbf{1}}_n^T{\mathit{GWG}}^T{\mathbf{1}}_n]\right)\otimes \left({\mathbf{1}}_n{\mathbf{1}}_n^T\right)\right]\hfill \\ \hfill & =n^{-1}{\mathbf{1}}_n^T{p}^{-1}{\mathit{GWG}}^T{\mathbf{1}}_n\hfill \\ \hfill & \le {\lambda }_{max}\left(p^{-1}{\mathit{GWG}}^T\right)={\mathcal{O}}_p\left(1\right).\hfill \end{array}$$

Combining all of these yields $p^{-1}{∥\mathit{A}∥}_F^2={\mathcal{O}}_p\left(n\right)$. On the other hand,

$$\begin{array}{cc}\hfill {∥\mathit{B}∥}_F^2& =\mathrm{tr}\left({\mathit{BB}}^T\right)=\mathrm{tr}\left(\tilde{\mathit{G}}\mathit{W}{\tilde{\mathit{G}}}^T\right)\hfill \\ \hfill & =\mathrm{tr}\left((\mathit{G}-\overline{\mathit{g}}\otimes {\mathbf{1}}_n){\mathit{D}}_s^{-1}\mathit{W}{\mathit{D}}_s^{-1}{(\mathit{G}-\overline{\mathit{g}}\otimes {\mathbf{1}}_n)}^T\right)\hfill \\ \hfill & \le {\lambda }_{max}\left({\mathit{D}}_s^{-1}\mathit{W}{\mathit{D}}_s^{-1}\right){∥\mathit{G}-\overline{\mathit{g}}\otimes {\mathbf{1}}_n∥}_F^2\hfill \\ \hfill & \le {\displaystyle \frac{{max}_{1\le i\le p}{w}_i}{{min}_{1\le j\le p}{s}_j^2}}{∥\mathit{G}-\overline{\mathit{g}}\otimes {\mathbf{1}}_n∥}_F^2.\hfill \end{array}$$

By Lemma 2.6 in Jiang et al. [11],

$$\underset{1\le j\le p}{max}\left|s_j^2-1\right|\to 0\mathrm{a}.\mathrm{s}.,$$

which implies that ${\left({min}_{1\le j\le p}{s}_j^2\right)}^{-1}={\mathcal{O}}_p\left(1\right)$, and hence ${∥\mathit{B}∥}_F^2={\mathcal{O}}_p\left(n\right)$. Finally, since

$$\begin{array}{cc}\hfill {∥\mathit{A}-\mathit{B}∥}_F^2& =\mathrm{tr}\left((\mathit{A}-\mathit{B}){(\mathit{A}-\mathit{B})}^T\right)\hfill \\ \hfill & =\mathrm{tr}\left((\mathit{G}-\overline{\mathit{g}}\otimes {\mathbf{1}}_n)({\mathit{I}}_p-{\mathit{D}}_s^{-1})\mathit{W}({\mathit{I}}_p-{\mathit{D}}_s^{-1}){(\mathit{G}-\overline{\mathit{g}}\otimes {\mathbf{1}}_n)}^T\right)\hfill \\ \hfill & \le {\lambda }_{max}\left(({\mathit{I}}_p-{\mathit{D}}_s^{-1})\mathit{W}({\mathit{I}}_p-{\mathit{D}}_s^{-1})\right){∥\mathit{G}-\overline{\mathit{g}}\otimes {\mathbf{1}}_n∥}_F^2,\hfill \end{array}$$

and by Corollary 2.3 in Jiang et al. [11],

$$\begin{array}{cc}\hfill {\lambda }_{max}\left(({\mathit{I}}_p-{\mathit{D}}_s^{-1})\mathit{W}({\mathit{I}}_p-{\mathit{D}}_s^{-1})\right)& \le (\underset{1\le i\le p}{max}{w}_i){\lambda }_{max}\left({({\mathit{I}}_p-{\mathit{D}}_s^{-1})}^2\right)\hfill \\ \hfill & \le {\lambda }_{max}\left({({\mathit{I}}_p-{\mathit{D}}_s^{-1})}^2\right)\hfill \\ \hfill & =o_p\left(1\right)\hfill \end{array}$$

Therefore, we can bound the Levy’s distance between $F^{{\mathit{K}}^{\prime }}$ and $F^{\tilde{\mathit{K}}}$ by Corollary A.42 in Bai and Silverstein [19]:

$$\begin{array}{cc}\hfill L^4(F^{{\mathit{K}}^{\prime }},F^{\tilde{\mathit{K}}})& \le 2n^{-2}{p}^{-2}\left({∥\mathit{A}∥}_F^2+{∥\mathit{B}∥}_F^2\right){∥\mathit{A}-\mathit{B}∥}_F^2\hfill \\ \hfill & =n^{-2}\left({\mathcal{O}}_p\left(n\right)+{\mathcal{O}}_p\left(n\right)\right)·o_p\left(n\right)\hfill \\ \hfill & =o_p\left(1\right).\hfill \end{array}$$

Hence, the ESD of $\tilde{\mathit{K}}$ converges a.s. in distribution to the ESD of $\mathit{K}$. On the other hand,

$$\begin{array}{cc}\hfill ∥F^{{\mathit{K}}^{\prime }}-F^{{\mathit{GWG}}^T}∥& \le n^{-1}\mathrm{rank}(A-{\mathit{GW}}^{1/2})\hfill \\ \hfill & =n^{-1}\mathrm{rank}\left((\overline{g}\otimes {\mathbf{1}}_n){\mathit{W}}^{1/2}\right)\hfill \\ \hfill & \le n^{-1}\to 0,\mathrm{as} n\to \infty .\hfill \end{array}$$

Thus, the ESD of $\tilde{\mathit{K}}$ converges a.s. in distribution to the ESD of $p^{-1}{\mathit{GWG}}^T$, and the desired results in the corollary follows Theorem 5. □

Appendix A.4. Proof of Theorem 6

Proof. 

We follow the same framework as in the proof of Theorem 5. Let

$$\tilde{\mathit{M}}=f^{\prime }\left(0\right){\displaystyle \frac{{\mathit{GG}}^T}{p}}+v_p{\mathit{I}}_n.$$

Based on Theorem A.43 in Bai and Silverstein [19], we have

$$∥F_n^{\mathit{M}}-F_n^{\tilde{\mathit{M}}}∥\le {\displaystyle \frac{1}{n}}\mathrm{rank}(\mathit{M}-\tilde{\mathit{M}})={\displaystyle \frac{1}{n}}\to 0,\mathrm{as} n\to \infty .$$

The matrix $\tilde{\mathit{M}}$ will play a vital part in the remainder of the proof as it is easy to see that the LSD of $\tilde{\mathit{M}}$ converges in distribution a.s. to some nonrandom distribution function by Theorem 2. On the other hand, since the elements in $\mathit{G}$ are i.i.d. with $\mathbb{E}\left[G_{ij}\right]=0$ and $\mathbb{E}\left[G_{ij}^2\right]=1$, it is easy to see that the elements in ${\mathit{A}}^T\mathit{G}$ are still i.i.d. with a mean of 0 and unit variance. Moreover, since

$${\mathit{A}}^T\tilde{\mathit{M}}\mathit{A}=f^{\prime }\left(0\right){\displaystyle \frac{{\mathit{A}}^T{\mathit{GG}}^T\mathit{A}}{p}}+v_p{\mathit{I}}_{n-q},$$

we know that the LSD of ${\mathit{A}}^T\tilde{\mathit{M}}\mathit{A}$ also converges in distribution a.s. to some nonrandom distribution function, and we denote such distribution by F.

It can be seen from the proof of Theorem 5 that one major part of showing the result is to show that $\mathrm{tr}\left({\left({\mathit{C}}_1{\mathbf{\Sigma }}_0\right)}^2\right)={\mathcal{O}}_p\left(n^{-1}\right)$, $\mathrm{tr}\left({\left({\mathit{C}}_2{\mathbf{\Sigma }}_0\right)}^2\right)={\mathcal{O}}_p\left(n^{-1}\right)$ and $\mathrm{tr}\left({\mathit{C}}_1{\mathbf{\Sigma }}_0{\mathit{C}}_2{\mathbf{\Sigma }}_0\right)={\mathcal{O}}_p\left(n^{-1}\right)$. The proof of $\mathrm{tr}\left({\left({\mathit{C}}_2{\mathbf{\Sigma }}_0\right)}^2\right)={\mathcal{O}}_p\left(1\right)$ is exactly the same arguments as in the proof of Theorem 5, so we focus on the other two quantities.

As a consequence of Theorem A.45 in Bai and Silverstein [19] and Theorem 3, we have

$$L(F_{n-q}^{{\mathit{A}}^T\mathit{KA}},F_{n-q}^{{\mathit{A}}^T\mathit{MA}})\le ∥\mathit{M}-\mathit{K}∥=o_p\left(1\right).$$

Moreover, it follows from Theorem A.43 in Bai and Silverstein [19] that

$$∥F_{n-q}^{{\mathit{A}}^T\mathit{MA}}-F_{n-q}^{{\mathit{A}}^T\tilde{\mathit{M}}\mathit{A}}∥\le {\displaystyle \frac{1}{n-q}}\mathrm{rank}\left({\mathit{A}}^T(\mathit{M}-\tilde{\mathit{M}})\mathit{A}\right)\le {\displaystyle \frac{1}{n-q}},$$

which implies that

$$L(F_{n-q}^{{\mathit{A}}^T\mathit{KA}},F_{n-q}^{{\mathit{A}}^T\tilde{\mathit{M}}\mathit{A}})\le L(F_{n-q}^{{\mathit{A}}^T\mathit{KA}},F_{n-q}^{{\mathit{A}}^T\mathit{MA}})+∥F_{n-q}^{{\mathit{A}}^T\mathit{MA}}-F_{n-q}^{{\mathit{A}}^T\tilde{\mathit{M}}\mathit{A}}∥=o_p\left(1\right).$$

Therefore,

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{n-q}}\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)& ={\displaystyle \frac{1}{n-q}}\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}\right)={\displaystyle \frac{1}{n-q}}\sum _{i=1}^{n-q}{\displaystyle \frac{{\lambda }_i\left({\mathit{A}}^T\mathit{KA}\right)}{1+\gamma {\lambda }_i\left({\mathit{A}}^T\mathit{KA}\right)}}\hfill \\ \hfill & =\int {\displaystyle \frac{x}{1+\gamma x}}\mathrm{d}{F}_{n-q}^{{\mathit{A}}^T\mathit{KA}}\left(x\right)\hfill \\ \hfill & =\int {\displaystyle \frac{x}{1+\gamma x}}\mathrm{d}\left(F_{n-q}^{{\mathit{A}}^T\mathit{KA}}\left(x\right)-F_{n-q}^{{\mathit{A}}^T\tilde{\mathit{M}}\mathit{A}}\left(x\right)\right)+\int {\displaystyle \frac{x}{1+\gamma x}}\mathrm{d}{F}_{n-q}^{{\mathit{A}}^T\tilde{\mathit{A}}\mathit{A}}\left(x\right)\hfill \\ \hfill & \to 0+\int {\displaystyle \frac{x}{1+\gamma x}}\mathrm{d}F\left(x\right)\mathrm{a}.\mathrm{s}.,\hfill \end{array}$$

(A3)

which implies that $\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right){\asymp }_{p}n$. Similarly, note that

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{n-q}}\mathrm{tr}\left({\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)}^2\right)\hfill \\ \hfill =& {\displaystyle \frac{1}{n-q}}\sum _{i=1}^{n-q}{\displaystyle \frac{{(1+{\gamma }_0{\lambda }_i\left({\mathit{A}}^T\mathit{KA}\right))}^2{\lambda }_i^2\left({\mathit{A}}^T\mathit{KA}\right)}{{(1+{\lambda }_i\left({\mathit{A}}^T\mathit{KA}\right))}^4}}\hfill \\ \hfill =& \int {\displaystyle \frac{{(1+{\gamma }_{0}x)}^2{x}^2}{{(1+\gamma x)}^4}}\mathrm{d}{F}_{n-q}^{{\mathit{A}}^T\mathit{KA}}\left(x\right)\hfill \\ \hfill =& \int {\displaystyle \frac{{(1+{\gamma }_{0}x)}^2{x}^2}{{(1+\gamma x)}^4}}\mathrm{d}\left(F_{n-q}^{{\mathit{A}}^T\mathit{KA}}\left(x\right)-F_{n-q}^{{\mathit{A}}^T\tilde{\mathit{M}}\mathit{A}}\left(x\right)\right)+\int {\displaystyle \frac{{(1+{\gamma }_{0}x)}^2{x}^2}{{(1+\gamma x)}^4}}\mathrm{d}{F}_{n-q}^{{\mathit{A}}^T\tilde{\mathit{M}}\mathit{A}}\left(x\right)\hfill \\ \hfill \to & 0+\int {\displaystyle \frac{{(1+{\gamma }_{0}x)}^2{x}^2}{{(1+\gamma x)}^4}}\mathrm{d}F\left(x\right)\mathrm{a}.\mathrm{s}.,\hfill \end{array}$$

which implies that $\mathrm{tr}\left({\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)}^2\right)={\mathcal{O}}_p\left(n\right)$ and hence

$$\mathrm{tr}\left({\left({\mathit{C}}_1{\mathbf{\Sigma }}_0\right)}^2\right)={\left[\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)\right]}^{-2}\mathrm{tr}\left({\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)}^2\right)={\mathcal{O}}_p\left(n^{-1}\right).$$

For $\mathrm{tr}\left({\mathit{C}}_1{\mathbf{\Sigma }}_0{\mathit{C}}_2{\mathbf{\Sigma }}_0\right)$, note that

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{n-q}}\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)\hfill \\ \hfill =& {\displaystyle \frac{1}{n-q}}\sum _{i=1}^{n-q}{\displaystyle \frac{(1+{\gamma }_0{\lambda }_i\left({\mathit{A}}^T\mathit{KA}\right)){\lambda }_i\left({\mathit{A}}^T\mathit{KA}\right)}{{(1+\gamma {\lambda }_i\left({\mathit{A}}^T\mathit{KA}\right))}^2}}\hfill \\ \hfill =& \int {\displaystyle \frac{(1+{\gamma }_{0}x)x}{{(1+\gamma x)}^2}}\mathrm{d}{F}_{n-q}^{{\mathit{A}}^T\mathit{KA}}\left(x\right)\hfill \\ \hfill =& \int {\displaystyle \frac{(1+{\gamma }_{0}x)x}{{(1+\gamma x)}^2}}\mathrm{d}\left(F_{n-q}^{{\mathit{A}}^T\mathit{KA}}\left(x\right)-F_{n-q}^{{\mathit{A}}^T\tilde{\mathit{M}}\mathit{A}}\left(x\right)\right)+\int {\displaystyle \frac{(1+{\gamma }_{0}x)}{{(1+\gamma x)}^2}}\mathrm{d}{F}_{n-q}^{{\mathit{A}}^T\tilde{\mathit{M}}\mathit{A}}\left(x\right)\hfill \\ \hfill \to & 0+\int {\displaystyle \frac{(1+{\gamma }_{0}x)x}{{(1+\gamma x)}^2}}\mathrm{d}F\left(x\right)\mathrm{a}.\mathrm{s}.,\hfill \end{array}$$

(A4)

which implies that $\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)={\mathcal{O}}_p\left(n\right)$, and hence

$$\begin{array}{cc}\hfill \mathrm{tr}\left({\mathit{C}}_1{\mathbf{\Sigma }}_0{\mathit{C}}_2{\mathbf{\Sigma }}_0\right)& ={\left[(n-q)\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)\right]}^{-1}\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)\hfill \\ \hfill & \le {\lambda }_{max}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right){\left[(n-q)\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)\right]}^{-1}\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)\hfill \\ \hfill & ={\mathcal{O}}_p(n^{-2}·n)={\mathcal{O}}_p\left(n^{-1}\right).\hfill \end{array}$$

Therefore, $\mathrm{Var}[\Delta |\mathit{G}]={\mathcal{O}}_p\left(n^{-1}\right)$ and as in the proof of Theorem 5, it follows from Chebyshev’s inequality and Dominated Convergence Theorem that $\Delta -\mathbb{E}[\Delta |\mathit{G}]=o_p\left(1\right)$.

Similar to the proof of Theorem 5, we now focus on $\mathbb{E}[\Delta |\mathit{G}]$. Recall from Equation (A2) that

$$\begin{array}{cc}\hfill \mathbb{E}[\Delta |\mathit{G}]& ={\sigma }_{ϵ}^2\left[{\displaystyle \frac{\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)}{\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)}}-{\displaystyle \frac{\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)}{n-q}}\right]\hfill \\ \hfill & ={\sigma }_{ϵ}^2\left[{\displaystyle \frac{\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}{\mathit{A}}^T\mathit{KA}{\mathbf{\Sigma }}_{\gamma }^{-1}{\mathbf{\Sigma }}_0\right)}{\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)}}-{\displaystyle \frac{\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}\right)+{\gamma }_0\mathrm{tr}\left({\mathit{P}}_{\gamma }\mathit{K}\right)}{n-q}}\right].\hfill \end{array}$$

Note that

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{n-q}}\mathrm{tr}\left({\mathbf{\Sigma }}_{\gamma }^{-1}\right)& ={\displaystyle \frac{1}{n-q}}\sum _{i=1}^{n-q}{\displaystyle \frac{1}{1+\gamma {\lambda }_i\left({\mathit{A}}^T\mathit{KA}\right)}}=\int {\displaystyle \frac{1}{1+\gamma x}}\mathrm{d}{F}_{n-q}^{{\mathit{A}}^T\mathit{KA}}\left(x\right)\hfill \\ \hfill & =\int {\displaystyle \frac{1}{1+\gamma x}}\mathrm{d}\left(F_{n-q}^{{\mathit{A}}^T\mathit{KA}}\left(x\right)-F_{n-q}^{{\mathit{A}}^T\tilde{\mathit{M}}\mathit{A}}\left(x\right)\right)+\int {\displaystyle \frac{1}{1+\gamma x}}\mathrm{d}{F}_{n-q}^{{\mathit{A}}^T\tilde{\mathit{M}}\mathit{A}}\left(x\right)\hfill \\ \hfill & \to 0+\int {\displaystyle \frac{1}{1+\gamma x}}\mathrm{d}F\left(x\right).\hfill \end{array}$$

Combined with Equations (A3) and (A4), it is easy to see that $\mathbb{E}[\Delta |\mathcal{G}]$ converges to a constant limit. The remaining part of the proof follows the same statements as in the proof of Theorem 6, so it is omitted. □

Appendix A.5. Proof of Theorem 7

Proof. 

Let $\mathit{M}$ and $v_p$ be as defined in Equation (10). Now let

$$\tilde{\mathit{M}}=-2f^{\prime }\left(\tau \right){\displaystyle \frac{{\mathit{GG}}^T}{p}}+v_p{\mathit{I}}_n.$$

By Theorem A.43 in Bai and Silverstein [19] and the triangle inequality for matrix rank, we have

$$\begin{array}{cc}\hfill ∥F_n^{\mathit{M}}-F_n^{\tilde{\mathit{M}}}∥& \le {\displaystyle \frac{1}{n}}\mathrm{rank}\left(\mathit{M}-\tilde{\mathit{M}}\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{n}}\mathrm{rank}(f\left(\tau \right){\mathbf{1}}_n{\mathbf{1}}_n^T+f^{\prime }\left(\tau \right)\left[{\mathbf{1}}_n{\mathit{\psi }}^T+\mathit{\psi }{\mathbf{1}}_n^T\right]+\hfill \\ \hfill & \left.{\displaystyle \frac{f^{″}\left(\tau \right)}{2}}\left[{\mathbf{1}}_n{(\mathit{\psi }\circ \mathit{\psi })}^T+(\mathit{\psi }\circ \mathit{\psi }){\mathbf{1}}_n^T+2\mathit{\psi }{\mathit{\psi }}^T+4{\displaystyle \frac{\mathrm{tr}\left({\mathbf{\Sigma }}_p^2\right)}{p^2}}{\mathbf{1}}_n{\mathbf{1}}_n^T\right]\right)\hfill \\ \hfill & \le {\displaystyle \frac{7}{n}}\to 0,\mathrm{as} n\to \infty .\hfill \end{array}$$

On the other hand, as a consequence of Theorem A.45 in Bai and Silverstein [19] and Theorem 4,

$$L(F_{n-q}^{{\mathit{A}}^T\mathit{KA}},F_{n-q}^{{\mathit{A}}^T\mathit{MA}})\le ∥{\mathit{A}}^T(\mathit{K}-\mathit{M})\mathit{A}∥\le ∥\mathit{K}-\mathit{M}∥=o_p\left(1\right).$$

Moreover, it follows from Theorem A.43 in Bai and Silverstein [19] that

$$∥F_{n-q}^{{\mathit{A}}^T\mathit{MA}}-F_{n-q}^{{\mathit{A}}^T\tilde{\mathit{M}}\mathit{A}}∥\le {\displaystyle \frac{1}{n-q}}\mathrm{rank}\left({\mathit{A}}^T(\mathit{M}-\tilde{\mathit{M}})\mathit{A}\right)\le {\displaystyle \frac{1}{n-q}}\mathrm{rank}(\mathit{M}-\tilde{\mathit{M}})\le {\displaystyle \frac{7}{n-q}},$$

which implies that

$$L(F_{n-q}^{{\mathit{A}}^T\mathit{KA}},F_{n-q}^{{\mathit{A}}^T\tilde{\mathit{M}}\mathit{A}})\le L(F_{n-q}^{{\mathit{A}}^T\mathit{KA}},F_{n-q}^{{\mathit{A}}^T\mathit{MA}})+∥F_{n-q}^{{\mathit{A}}^T\mathit{MA}}-F_{n-q}^{{\mathit{A}}^T\tilde{\mathit{M}}\mathit{A}}∥=o_p\left(1\right).$$

The remaining of the proof is the same as the proof of Theorem 3. □