A New Class of Probability Distributions via Half-Elliptical Functions
Abstract
1. Introduction
2. The Bi-Elliptic Distribution
2.1. Definition
Normalization Condition
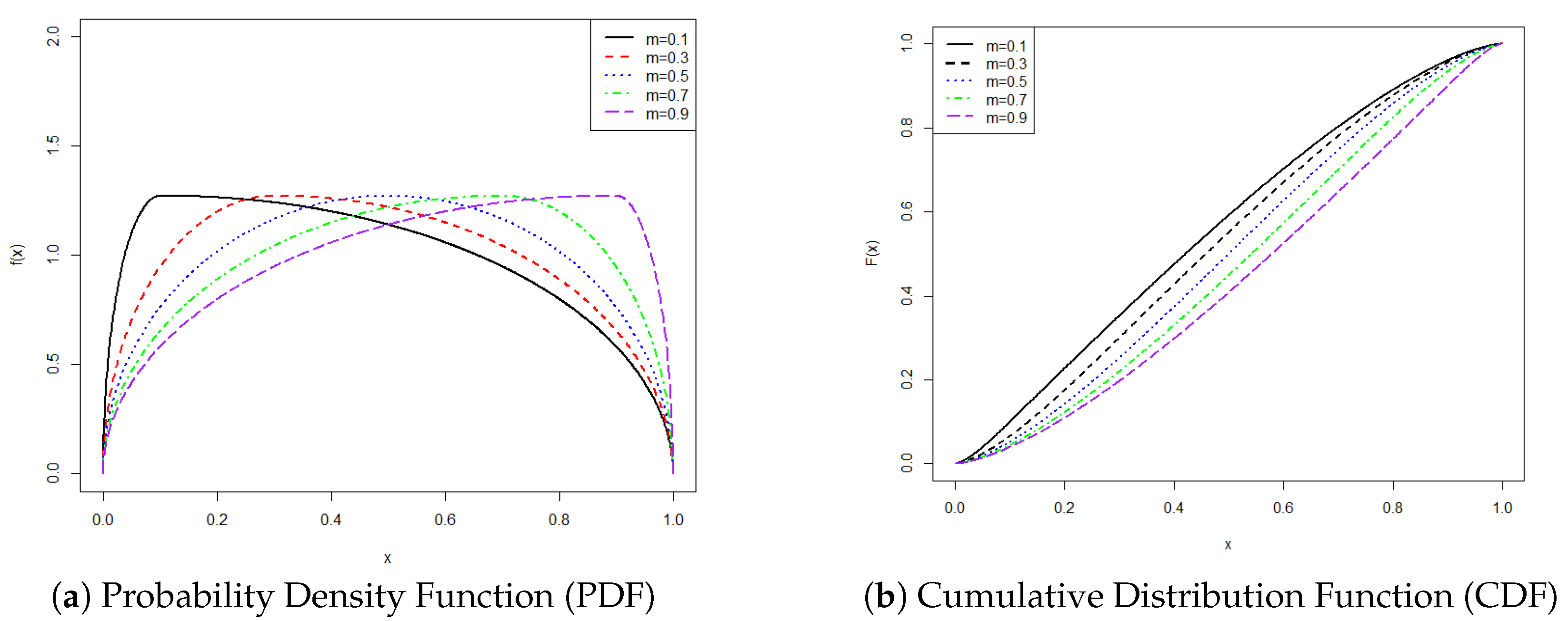
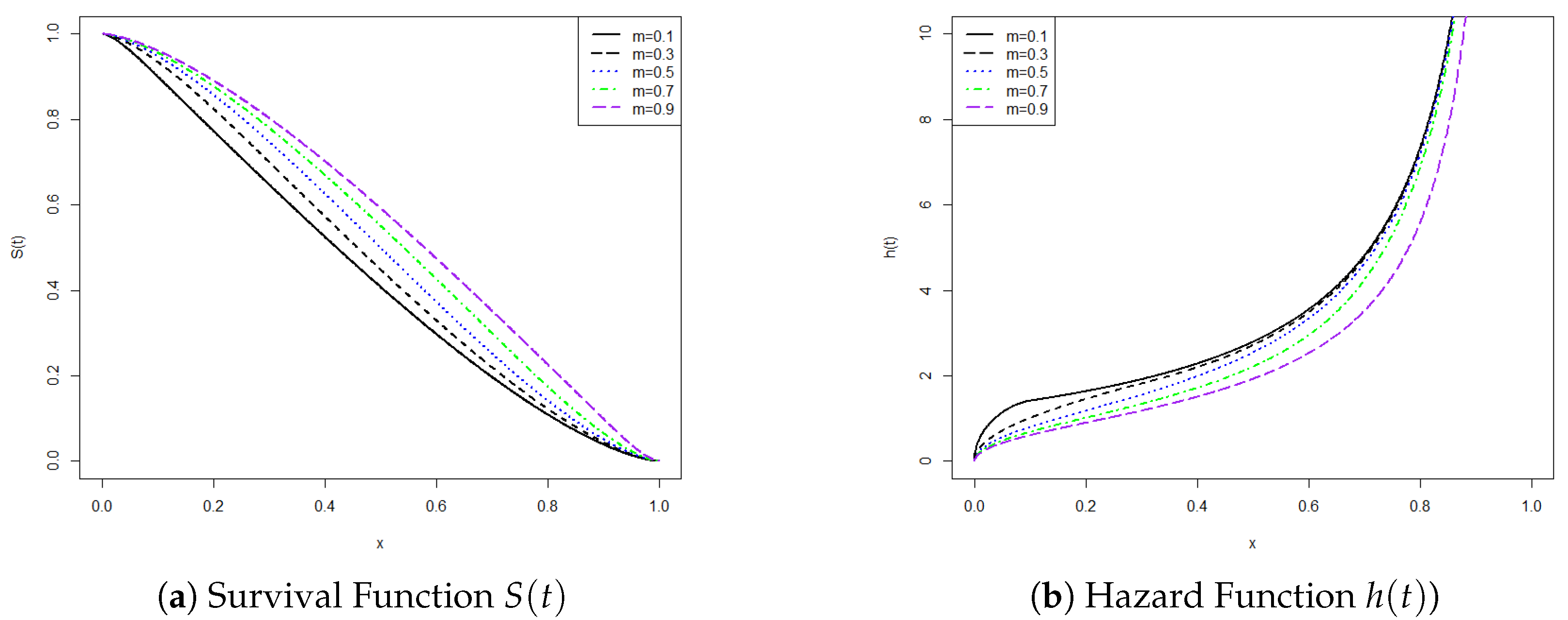
2.2. Properties
- For : let , so , .
- For : let , so , .
- is the cumulative distribution function (CDF) of the bi-elliptic distribution;
- is the probability density function (PDF) of the bi-elliptic distribution;
- denotes the position of the ordered statistic.
- For :
- For :
3. Parameter Estimation
3.1. Maximum Likelihood Estimation
3.2. One-Parameter Maximum Likelihood Estimation
3.3. Three-Parameter Maximum Likelihood Estimation
3.4. Numerical Implementation and Computational Considerations
3.4.1. One-Parameter MLE for m
3.4.2. Three-Parameter MLE for a, b, and m
3.4.3. Comparison with Alternative Methods
4. Monte Carlo Simulations
- Generate uniform random numbers from a uniform distribution on [0,1].
- Compute quantiles via numerical inversion: For each , solve numerically to find , where is the bi-elliptic CDF. We used the R function uniroot() in R package: stat for implementation.
- Output samples: Collect all values to form the random sample .
4.1. One-Parameter MLE
4.2. Three-Parameter MLE
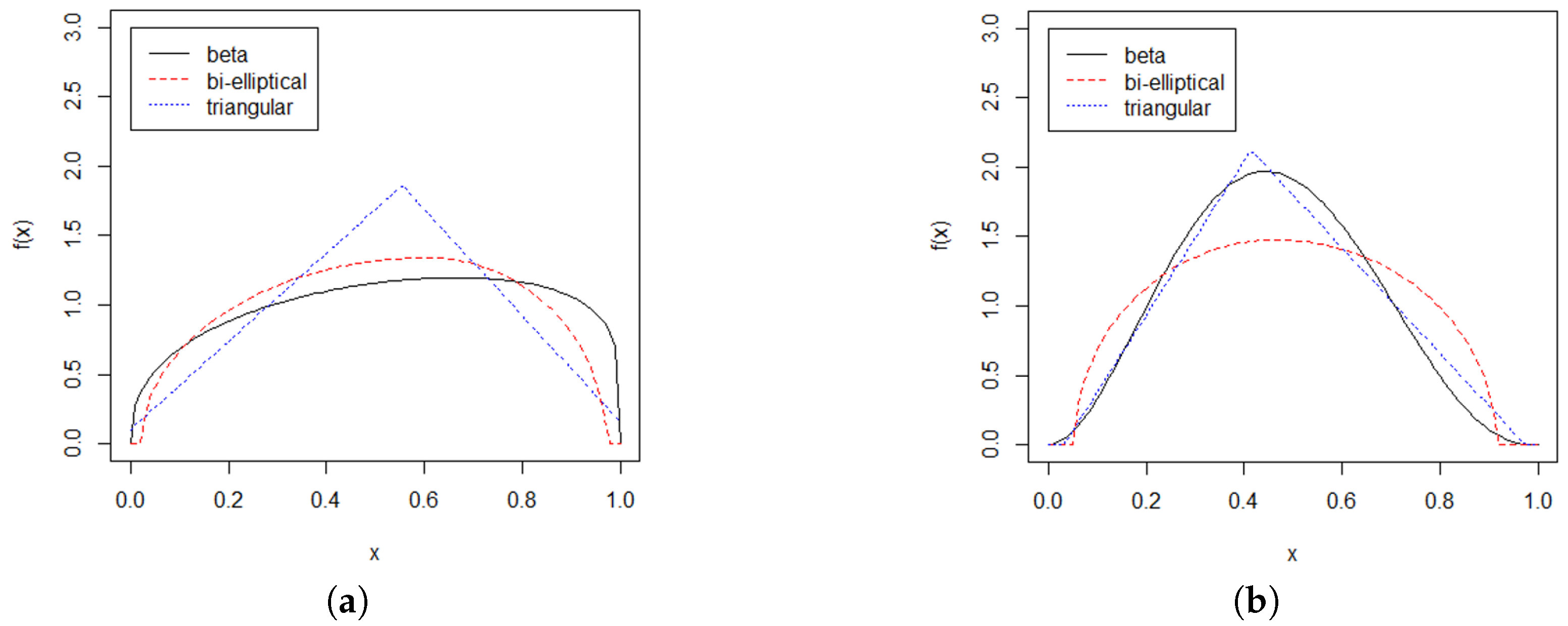
5. Comparing the Bi-Elliptic Distribution and the Triangular Distribution as a Proxy for the Beta Distribution
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Properties Such as MGF, Moments, etc.
Appendix A.1. Moment Generating Function (MGF)
Appendix A.1.1. Left Arc Integral (a ≤ x ≤ m)
Appendix A.1.2. Right Arc Integral (m ≤ x ≤ b)
Appendix A.1.3. Final MGF Expression
Appendix A.2. First Four Moments
Appendix A.2.1. First Moment (Mean)
Appendix A.2.2. Second Moment
Appendix A.2.3. Third Moment
Appendix A.2.4. Fourth Moment
Appendix A.2.5. Variance
Appendix A.3. The Rényi Entropy
- Step 1: Split the Integral into Left and Right Arcs
- Step 2: Left Arc Substitution ()
- 1.
- Substitute , giving , .
- 2.
- Limits change from to .
- 3.
- Integral becomes:
- Step 3: Right Arc Substitution ()
- 1.
- Substitute , giving , .
- 2.
- Limits change from to .
- 3.
- Integral becomes:
- Step 4: Combine Both ArcsHere, cancels the dependency on m.Evaluate :
- -
- Substitute , :
- -
- Using the Beta function :
- Step 5:Substitute the Beta function result:
- Step 6: Final ResultHence, the Rényi entropy of order ,for the bi-elliptic distribution isFurther simplification gives:
References
- Kotz, S.; van Dorp, J.R. Beyond Beta: Other Continuous Families of Distributions with Bounded Support and Applications; World Scientific: Singapore, 2004. [Google Scholar]
- García, C.B.; García Pérez, J.; van Dorp, J.R. Modeling heavy-tailed, skewed and peaked uncertainty phenomena with bounded support. Stat. Methods Appl. 2011, 20, 463–486. [Google Scholar] [CrossRef]
- Condino, F.; Domma, F. A new distribution function with bounded support: The reflected generalized Topp-Leone power series distribution. Metron 2017, 75, 51–68. [Google Scholar] [CrossRef]
- Mazucheli, J.; Menezes, A.F.; Dey, S. Unit-Gompertz distribution with applications. Statistica 2019, 79, 25–43. [Google Scholar]
- Ghitany, M.E.; Mazucheli, J.; Menezes, A.F.B.; Alqallaf, F. The unit-inverse Gaussian distribution: A new alternative to two-parameter distributions on the unit interval. Commun. Stat. Theory Methods 2018, 48, 3423–3438. [Google Scholar] [CrossRef]
- Bakouch, H.S.; Nik, A.S.; Asgharzadeh, A.; Salinas, H.S. A flexible probability model for proportion data: Unit-half-normal distribution. Commun. Stat. Case Stud. Data Anal. Appl. 2021, 7, 271–288. [Google Scholar] [CrossRef]
- Gemeay, A.M.; Sapkota, P.L.; Tashkandy, Y.A.; Bark, M.E.; Balogun, O.S.; Hussam, E. New bounded probability model: Properties, estimation, and applications. Heliyon 2024, 10, e38965. [Google Scholar] [CrossRef] [PubMed]
- Goel, N.S.; Strebel, D.E. Simple beta distribution representation of leaf orientation in vegetation canopies. Agron. J. 1984, 76, 800–802. [Google Scholar] [CrossRef]
- McDonald, J.B.; Xu, Y.J. A generalization of the beta distribution with applications. J. Econom. 1995, 66, 133–152. [Google Scholar] [CrossRef]
- Gupta, A.K.; Nadarajah, S. Handbook of Beta Distribution and Its Applications; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Johnson, D. The triangular distribution as a proxy for the beta distribution in risk analysis. J. R. Stat. Soc. Ser. D 1997, 46, 387–398. [Google Scholar] [CrossRef]
- Dorp, J.; Kotz, S. Generalized trapezoidal distributions. Metrika 2003, 58, 85–97. [Google Scholar] [CrossRef]
- Dorp, J.; Kotz, S. A novel extension of the triangular distribution and its parameter estimation. J. R. Stat. Soc. Ser. D 2002, 51, 63–79. [Google Scholar]
- Karlis, D.; Xekalaki, E. The Polygonal Distribution. In Advances in Mathematical and Statistical Modeling in Honor of Enrique Castillo; Arnold, B.C., Balakrishnan, N., Minués, M., Sarabia, J.M., Eds.; Birkhäuser: Boston, MA, USA, 2008; pp. 21–33. [Google Scholar]
- Vander Wielen, M.; Vander Wielen, R. The general segmented distribution. Commun. Stat. Theory Methods 2015, 44, 1994–2009. [Google Scholar] [CrossRef]
- Mazucheli, J.; Menezes, A.F.B.; Dey, S. The unit-Birnbaum-Saunders distribution with applications. Chil. J. Stat. 2018, 9, 47–57. [Google Scholar]
- Coad, A. The Growth of Firms: A Survey of Theories and Empirical Evidence; Edward Elgar Publishing Ltd.: Cheltenham, UK, 2009. [Google Scholar]
- Mulligan, D.W. Improved Modeling of Three-Point Estimates for Decision Making: Going Beyond the Triangle; Naval Postgraduate School: Monterey, CA, USA, 2016. [Google Scholar]
- Fletcher, S.G.; Ponnambalam, K. Stochastic control of reservoir systems using indicator functions: New enhancements. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Brent, R.P. An algorithm with guaranteed convergence for finding a zero of a function. Comput. J. 1971, 14, 422–425. [Google Scholar] [CrossRef]
- Lange, K. MM Optimization Algorithms; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2016. [Google Scholar]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Burnman, K.P.; Anderson, D.R. Model Selection and Multimodel Inference, A Practical Information-Theoretic Approach; Springer: New York, NY, USA, 2002. [Google Scholar]
| Measure | Definition | Estimate |
|---|---|---|
| Bias | ||
| Empirical Standard Error (Empirical SE) | ||
| Mean Square Error (MSE) | ||
| Root Mean Square Error (RMSE) |
| Size | Bias | Empirical SE | MSE | RMSE | |
|---|---|---|---|---|---|
| m = 0.1 | 200 | 0.0159 | 0.0792 | 0.0065 | 0.0808 |
| 400 | 0.0088 | 0.0563 | 0.0032 | 0.0569 | |
| 600 | 0.0061 | 0.0514 | 0.0027 | 0.0517 | |
| 800 | 0.0044 | 0.0479 | 0.0023 | 0.0481 | |
| 1000 | −0.0037 | 0.0451 | 0.0020 | 0.0453 | |
| m = 0.3 | 200 | 0.0072 | 0.1105 | 0.0123 | 0.1107 |
| 400 | 0.0045 | 0.0785 | 0.0062 | 0.0786 | |
| 600 | 0.0032 | 0.0632 | 0.0040 | 0.0633 | |
| 800 | −0.0021 | 0.0561 | 0.0031 | 0.0561 | |
| 1000 | 0.0025 | 0.0540 | 0.0029 | 0.0540 | |
| m = 0.5 | 200 | 0.0013 | 0.1179 | 0.0139 | 0.1179 |
| 400 | −0.0012 | 0.0838 | 0.0070 | 0.0838 | |
| 600 | 0.0009 | 0.0686 | 0.0047 | 0.0686 | |
| 800 | 0.0010 | 0.0607 | 0.0037 | 0.0607 | |
| 1000 | 0.0007 | 0.0547 | 0.0030 | 0.0547 | |
| m = 0.7 | 200 | −0.0065 | 0.1097 | 0.0121 | 0.1099 |
| 400 | −0.0022 | 0.0761 | 0.0058 | 0.0761 | |
| 600 | 0.0009 | 0.0620 | 0.0038 | 0.0620 | |
| 800 | −0.0022 | 0.0544 | 0.0030 | 0.0544 | |
| 1000 | −0.0017 | 0.0487 | 0.0024 | 0.0487 | |
| m = 0.9 | 200 | −0.0168 | 0.0771 | 0.0062 | 0.0789 |
| 400 | 0.0078 | 0.0529 | 0.0029 | 0.0534 | |
| 600 | −0.0044 | 0.0425 | 0.0018 | 0.0427 | |
| 800 | 0.0031 | 0.0371 | 0.0014 | 0.0372 | |
| 1000 | −0.0026 | 0.0327 | 0.0011 | 0.0328 |
| Size | Bias | Empirical SE | MSE | RMSE | |
|---|---|---|---|---|---|
| a = −1 | 200 | 0.0416 | 0.0601 | 0.0041 | 0.0641 |
| 400 | 0.0268 | 0.0375 | 0.0016 | 0.0405 | |
| 600 | 0.0192 | 0.0288 | 0.0009 | 0.0304 | |
| 800 | 0.0148 | 0.0238 | 0.0006 | 0.0246 | |
| 1000 | 0.0127 | 0.0184 | 0.0004 | 0.0196 | |
| b = 5 | 200 | −0.0540 | 0.0807 | 0.0072 | 0.0851 |
| 400 | −0.0343 | 0.0543 | 0.0032 | 0.0563 | |
| 600 | −0.0216 | 0.0373 | 0.0014 | 0.0378 | |
| 800 | −0.0172 | 0.0331 | 0.0011 | 0.0327 | |
| 1000 | −0.0165 | 0.0289 | 0.0009 | 0.0292 | |
| m = 0.3 | 200 | 0.0425 | 0.6818 | 0.3573 | 0.5978 |
| 400 | −0.0378 | 0.4645 | 0.1669 | 0.4085 | |
| 600 | −0.0383 | 0.3841 | 0.1145 | 0.3384 | |
| 800 | −0.0318 | 0.3139 | 0.0765 | 0.2766 | |
| 1000 | −0.0279 | 0.2783 | 0.0601 | 0.2452 |
| 1 | 1.2 | 1.4 | 1.6 | 1.8 | 2 | 2.5 | 3 | 3.5 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 10.066 | 1.918 | −6.733 | −14.623 | −22.296 | −29.908 | −45.229 | −61.163 | −74.815 | ||
| 23.765 | 13.193 | 0.262 | −11.879 | −23.828 | −35.026 | −57.999 | −79.103 | −96.519 | ||
| % | 99% | 99% | 92% | 68% | 39% | 20% | 4% | 0.70% | 0.50% | |
| r | 99% | 97% | 87% | 65% | 41% | 23% | 5% | 2% | 0.90% | |
| 6.173 | 3.081 | −2.514 | −10.034 | −16.564 | −23.794 | −39.446 | −54.045 | −67.704 | ||
| 17.767 | 14.166 | 7.386 | −3.13 | −12.592 | −22.43 | −44.675 | −64.882 | −82.487 | ||
| % | 95% | 96% | 99% | 91% | 77% | 61% | 22% | 8% | 4% | |
| r | 94% | 97% | 96% | 87% | 73% | 58% | 24% | 9% | 4% | |
| −1.700 | −1.610 | −3.815 | −8.597 | −14.277 | −19.959 | −34.647 | −48.833 | −62.024 | ||
| 4.162 | 7.042 | 4.775 | −1.359 | −8.858 | −16.679 | −36.352 | −54.951 | −71.696 | ||
| % | 84% | 96% | 97% | 94% | 85% | 72% | 38% | 18% | 10% | |
| r | 81% | 93% | 93% | 90% | 81% | 70% | 40% | 21% | 12% | |
| −8.647 | −7.736 | −8.192 | −10.410 | −14.568 | −19.127 | −31.892 | −44.586 | −57.418 | ||
| −6.283 | −2.150 | −1.422 | −4.286 | −9.734 | −15.477 | −32.175 | −48.420 | −64.392 | ||
| % | 66% | 88% | 93% | 91% | 86% | 78% | 49% | 28% | 16% | |
| r | 62% | 82% | 88% | 86% | 80% | 73% | 49% | 30% | 19% | |
| −17.017 | −14.320 | −13.379 | −14.247 | −16.075 | −20.384 | −30.409 | −42.249 | −53.422 | ||
| −18.339 | −11.950 | −8.839 | −9.589 | −11.858 | −17.318 | −30.354 | −44.83 | −58.678 | ||
| % | 40% | 70% | 82% | 85% | 82% | 74% | 50% | 33% | 21% | |
| r | 42% | 67% | 78% | 79% | 77% | 70% | 50% | 36% | 24% | |
| −24.240 | −21.475 | −19.367 | −18.221 | −20.012 | −22.113 | −31.092 | −41.352 | −51.936 | ||
| −27.151 | −21.733 | −16.687 | −14.860 | −17.067 | −19.831 | −30.899 | −43.639 | −56.88 | ||
| % | 24% | 52% | 71% | 77% | 72% | 68% | 53% | 35% | 21% | |
| r | 28% | 51% | 67% | 73% | 69% | 65% | 52% | 37% | 25% | |
| −61.550 | −53.756 | −47.594 | −44.105 | −41.357 | −40.748 | −42.803 | −47.288 | −53.401 | ||
| −76.637 | −65.648 | −55.050 | −48.96 | −45.003 | −43.972 | −45.472 | −50.903 | −58.258 | ||
| % | 6% | 7% | 14% | 22% | 26% | 31% | 30% | 25% | 21% | |
| r | 7% | 9% | 17% | 25% | 31% | 32% | 34% | 29% | 24% | |
| −75.059 | −68.325 | −60.512 | −55.512 | −53.495 | −50.528 | −50.604 | −53.617 | −57.843 | ||
| −88.337 | −84.029 | −72.241 | −64.083 | −60.338 | −56.246 | −55.619 | −58.229 | −63.477 | ||
| % | 1.50% | 4% | 7% | 13% | 14% | 20% | 22% | 22% | 20% | |
| r | 1.50% | 6% | 10% | 15% | 17% | 22% | 25% | 25% | 22% | |
| −89.653 | −82.796 | −72.130 | −67.252 | −63.540 | −60.938 | −59.210 | −60.364 | −62.992 | ||
| −114.394 | −101.53 | −88.022 | −78.783 | −72.639 | −68.977 | −65.661 | −66.351 | −69.603 | ||
| % | 0.20% | 6% | 5% | 8% | 10% | 12% | 17% | 17% | 15% | |
| r | 0.70% | 7% | 6% | 10% | 12% | 16% | 19% | 20% | 18% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, L.; Nguyen, N.; Erslan, P. A New Class of Probability Distributions via Half-Elliptical Functions. Mathematics 2025, 13, 1811. https://doi.org/10.3390/math13111811
Zheng L, Nguyen N, Erslan P. A New Class of Probability Distributions via Half-Elliptical Functions. Mathematics. 2025; 13(11):1811. https://doi.org/10.3390/math13111811
Chicago/Turabian StyleZheng, Lukun, Ngoc Nguyen, and Peyton Erslan. 2025. "A New Class of Probability Distributions via Half-Elliptical Functions" Mathematics 13, no. 11: 1811. https://doi.org/10.3390/math13111811
APA StyleZheng, L., Nguyen, N., & Erslan, P. (2025). A New Class of Probability Distributions via Half-Elliptical Functions. Mathematics, 13(11), 1811. https://doi.org/10.3390/math13111811






