Cooperative Behavior of Prosumers in Integrated Energy Systems

Abstract

The technical complexity of organizing energy systems’ operation has recently been compounded by the complexity of reconciling the interests of individual entities involved in interactions. This study proposes a possible solution to the problem of modeling their relationships within a large system. Our solution takes into account multiple levels of interactions, imperfect information, and conflicting interests. We present a mathematical statement of the problem of optimal interactions between the centralized system and prosumers in the integrated energy system (IES) with due consideration of the layered architecture of the IES. The paper also contributes a model for arranging the interactions between centralized and distributed energy sources for cases when IES prosumers form coalitions. The implementation of this model is based on multi-agent techniques and cooperative game theory tools. In order to arrive at a rational arrangement of the interactions of prosumers in the IES, the model implements different approaches to the allocation of the coalition’s total payoff (the Shapley value, Modiclus, PreNucleolus solution concepts). Furthermore, we propose a criterion for deciding on the “best” imputation. We contribute a multi-agent system that implements the proposed model and use a test IES setup to validate the model by simulations. The results of the simulations ensure optimal interactions between the entities involved in the energy supply process within the IES and driven by their own interests. The results also elucidate the conditions that make it feasible for prosumers to form coalitions.

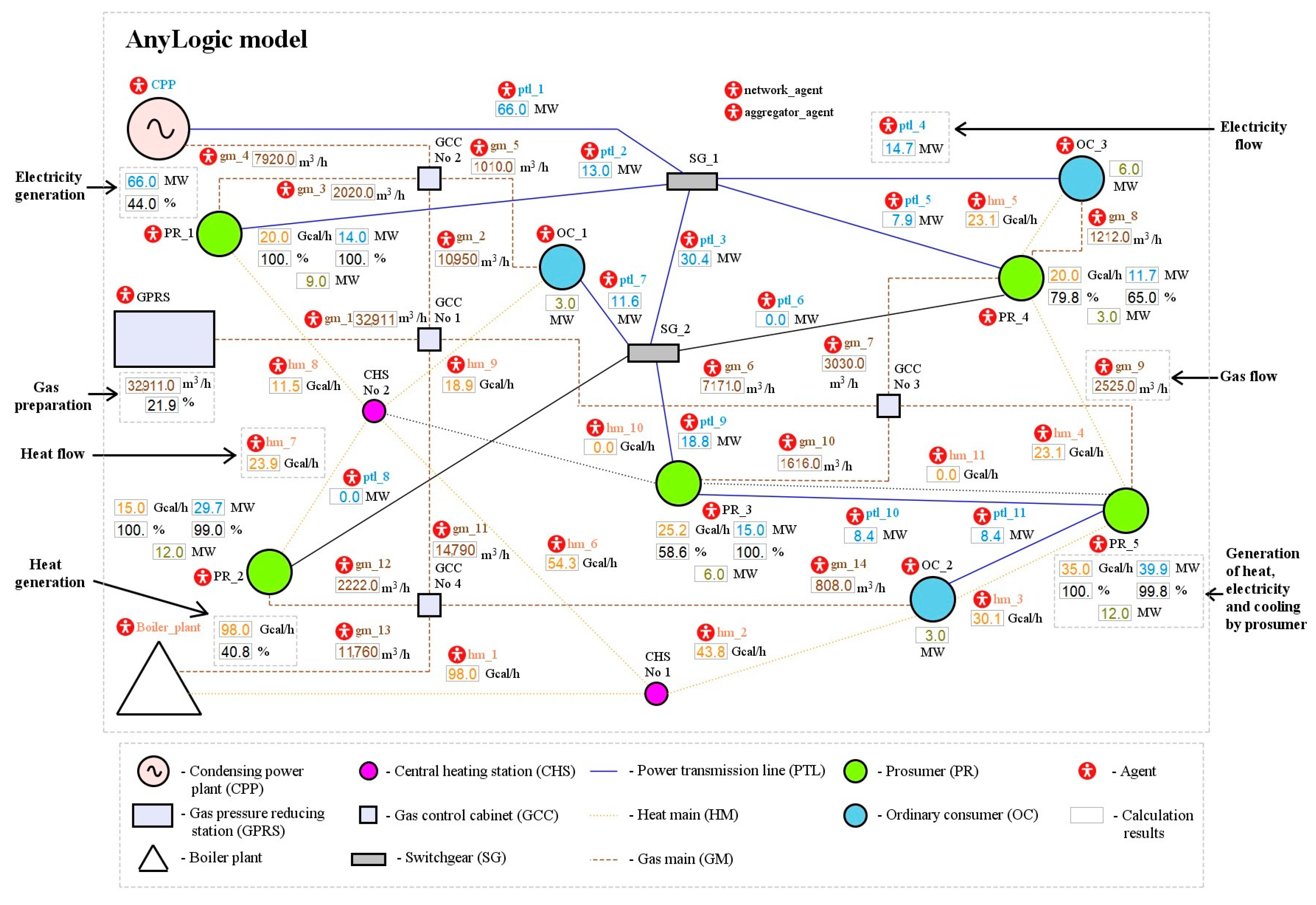
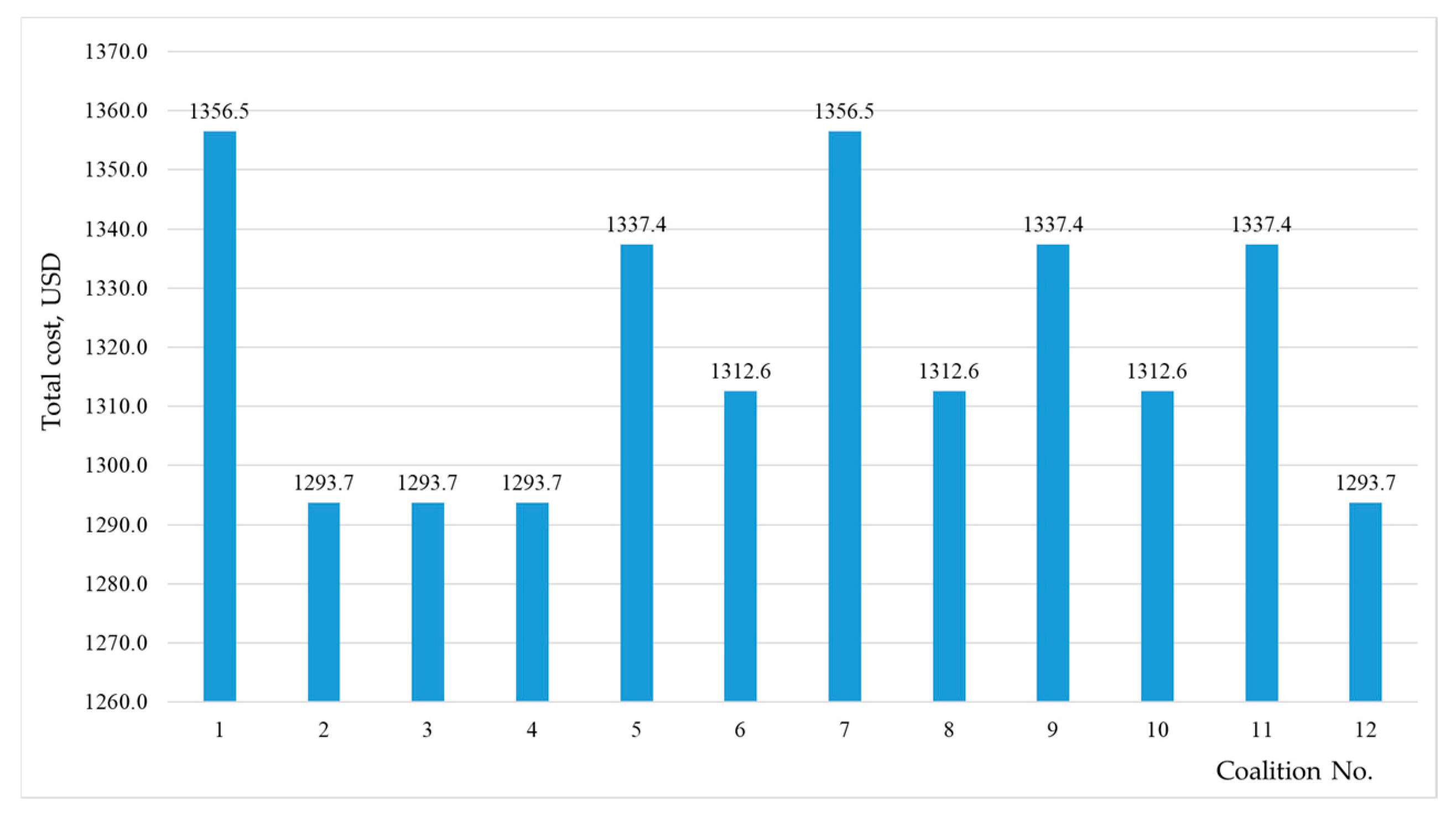
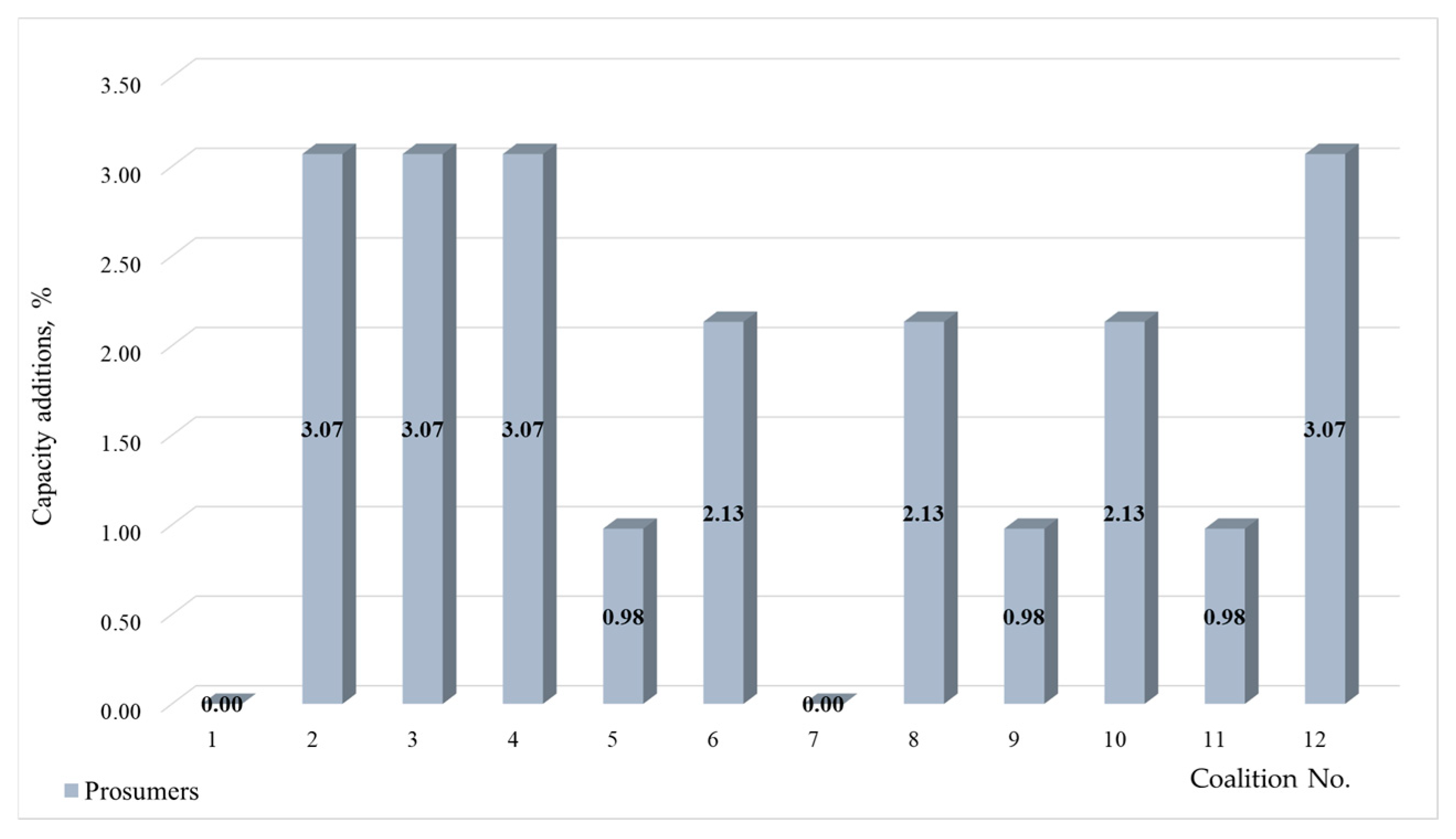
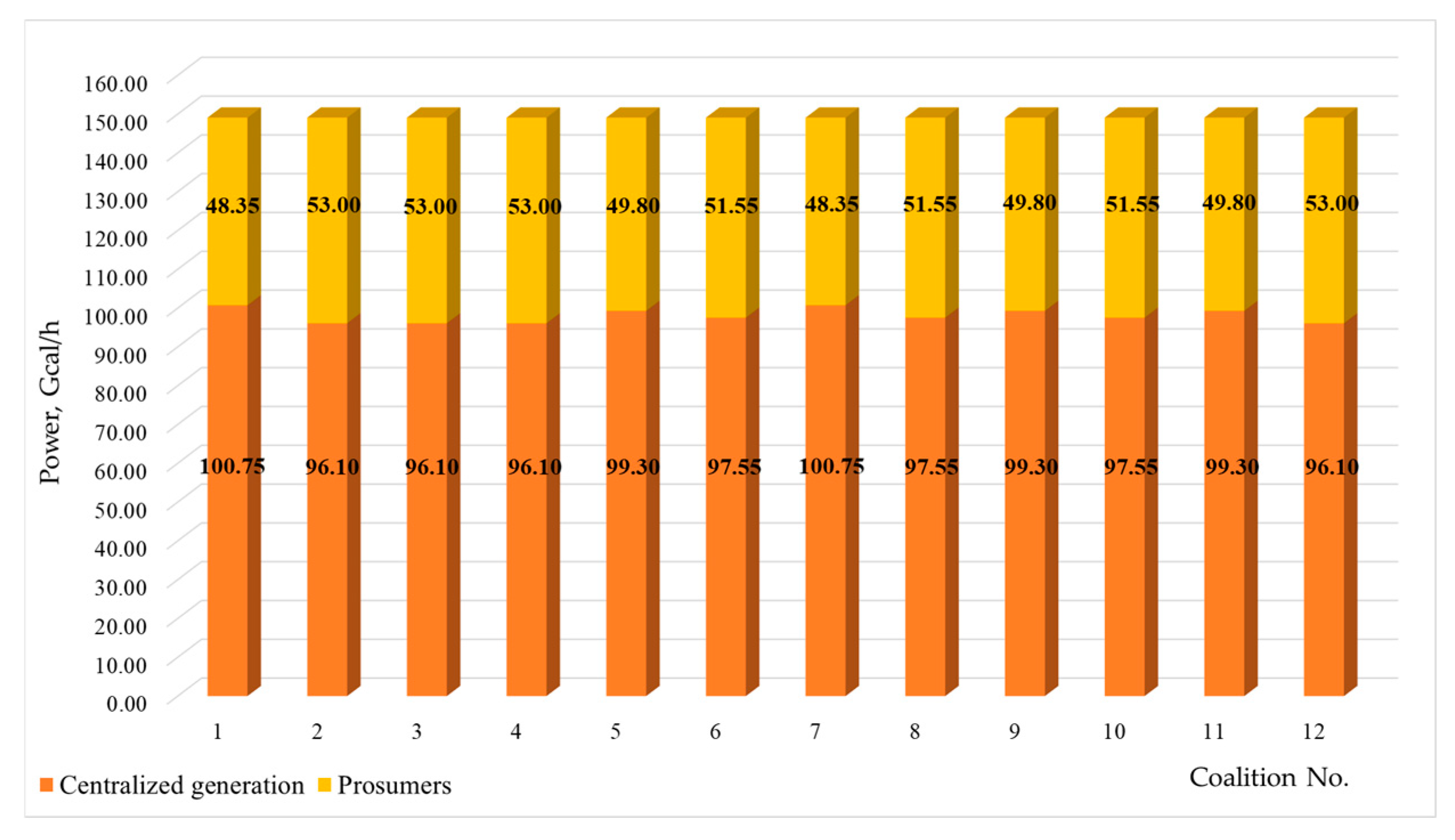
1. Introduction

Recent energy trends clearly gravitate towards energy transition, or the transformation of energy systems under the banner of the three Ds: decarbonization, digitalization, and decentralization [1]. Decentralization of energy systems, backed by modern technology (highly efficient energy sources of the latest generations, energy-saving automatic control systems, highly sensitive state-of-the-art devices, and sensors for tracking system parameters, etc.), will allow for meeting the needs of different levels of consumers, including prosumers, who will be able to choose the most efficient and cost-effective energy sources for themselves. This, in turn, will ensure better quality energy supply, which takes into account the interests of all entities involved in the energy system. In this regard, the expansion of centralized energy supply in developed countries is accompanied by the increasingly established trend of large-scale development of distributed energy generation systems [2,3], which allows prosumers to become involved in their energy supply, including by supplying energy back to the system. Consequently, competition between centralized and decentralized energy supply, on the one hand, and between large-scale and distributed power generation, on the other hand, becomes much tighter. This calls for the use of new approaches to forming energy systems and managing centralized and distributed energy sources so as to find the optimal balance between them.

The development of new technologies and the adoption of innovative energy equipment has a significant impact on the operation of energy infrastructures, including power supply, heating, cooling, and gas supply systems. These systems are becoming all the more intertwined, both at the technological and organizational levels. Conversion of one type of energy into another under normal operation, and emergencies in power, heating, cooling, and gas supply systems broadens their capabilities, enhances reliability and flexibility of control, and ensures a high level of comfort in residential, public, and industrial buildings, the efficiency of energy supply systems, and the mitigation of negative environmental impacts.

Energy supply is structured as a holistic system, which has made convex optimization models the staple tool for its modeling and optimization. This is due to a number of reasons: convex optimization models find the global optimum, have efficient computational algorithms developed for them, and produce solutions which are easy to interpret in economic terms [4]. In most cases, the problem is stated as a problem of maximizing the total payoff of all players, subject to constraints that include balancing constraints for each node in the system, generation constraints for energy sources, and capacity constraints for network sections.

New modeling methods that rely on game theory approaches undergo rapid development progress to address the increasing complexity of interactions in modern power supply systems, including conflicting interests and imperfect information about the state of the entire system available to each participant [5,6]. Both non-cooperative game theory and cooperative game theory can be used to that end. This paper presents one such complex system of interactions within an integrated energy system (IES).

The first problem is to model the interactions between the centralized part of the system and the consumers that run their own generation facilities. In particular, it is possible to state such a problem in terms of a Stackelberg game [7,8] by assigning the roles of the leader and follower to the centralized system (CS) and consumers, or to use an even more advanced model with multiple leaders [9]. Nevertheless, it is not possible to formulate the Stackelberg model [10] in its standard form due to imperfect information. For example, the CS may not have complete and detailed information about the distributed generation of prosumers. One conceivable way out is to search for equilibrium iteratively so that the decision-maker at each step has enough information to choose a strategy of their behavior.

The second problem that we cover in this study is how to model interactions between prosumers capable of forming coalitions [11]. To this end, we leverage the tools of cooperative game theory [12]. Having a shared payoff (in the case of consumers, it may be a reduction in energy costs) implies its distribution among the players. The solution must have a number of properties to attract consumers to join the coalition [13]. Furthermore, the CS may also be interested in a coalition.

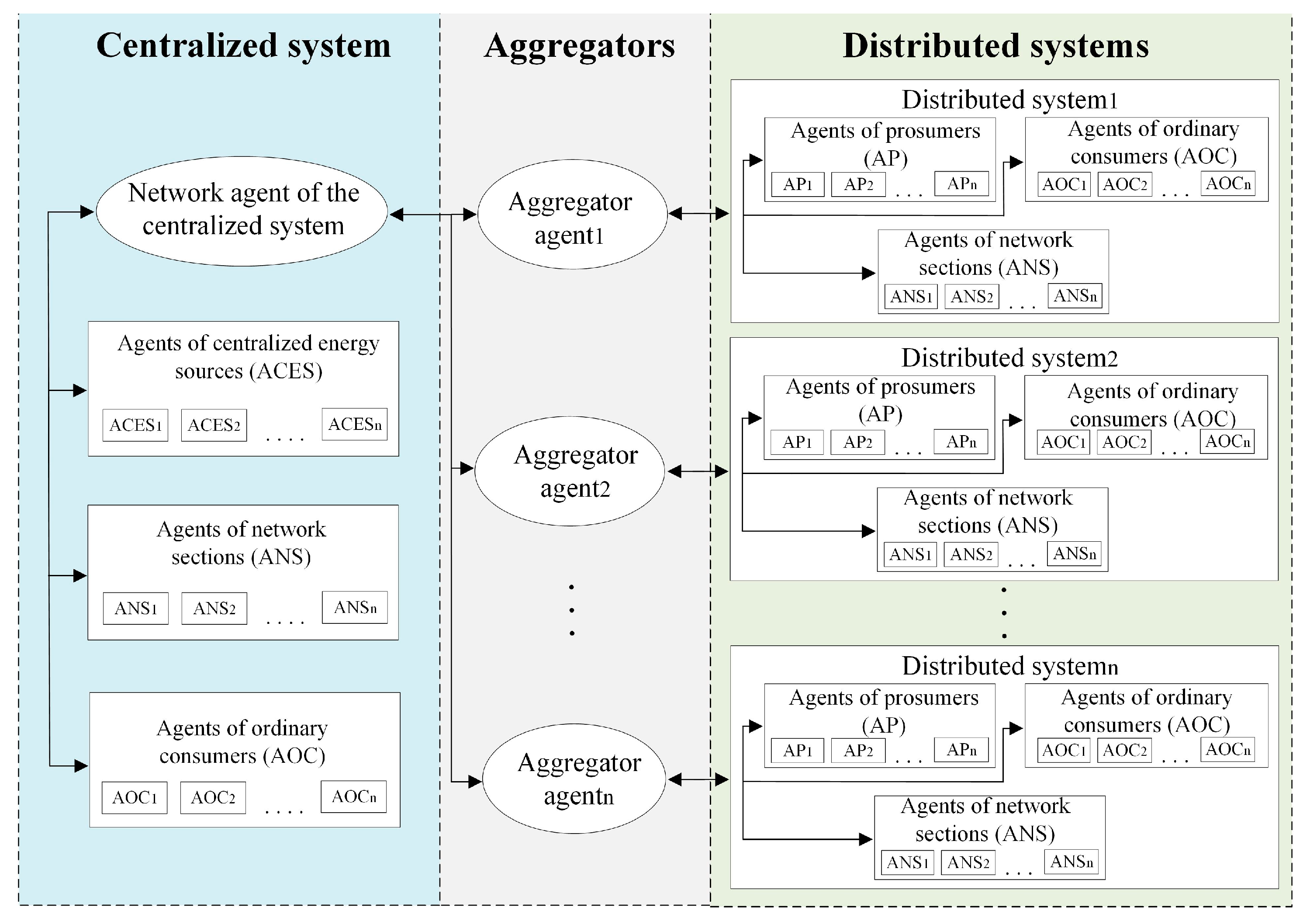
We choose the multi-agent approach to formalize complex interaction within energy systems, which include a number of entities driven by their own goals and interests as part of the energy supply process. The multi-agent approach is a branch of artificial intelligence that uses systems consisting of many interacting agents to solve complex problems. The approach has been successfully applied by researchers around the world to study engineering systems and search for solutions in systems with a large number of individual entities acting on their own [14,15]. It enables proper and detailed studies of the mechanisms of interaction and coordination of individual entities in the IES [16].

The conventional methods search for the best solution to a problem following a well-defined algorithm, all resources are pre-specified and remain fixed in the course of solving the problem. Moreover, the dimensionality of the problem is limited to avoid slowing down the solution process. Multi-agent techniques seek to obtain a solution that results from interactions between multiple independent purpose-driven agents [17,18]. To that end, they rely on a distributed approach by breaking down a complex problem into a set of problems of smaller dimensionality. This study also relies on the above technique to solve the problem stated above. Due to the fact that agents in the system are constantly exchanging data and monitoring the states of facilities of the IES, it is possible to respond quickly to various changes in the system and come up with decisions based on the actual state of affairs. This provides ample opportunities to exercise the necessary control and decision-making under imperfect information.

In this paper, we propose a model that implements the interaction between centralized and distributed energy sources when prosumers form coalitions within a layered IES. This study is a continuation of the authors’ research reported in [19]. It is important to consider the CS as a public planner, guided by maximizing the public welfare, whereas prosumers pursue their own interests, maximizing their own payoffs. The equilibrium under this setting should correspond to the Nash equilibrium in the Stackelberg game. The presence of constraints and imperfect information makes it impossible to compute the equilibrium analytically, which is why we rely on multi-agent modeling to find the equilibrium solution. The key contribution of this study is that it considers the possibility of consumers forming a coalition and finds a general equilibrium informed by such a possibility. A major novelty here is not only the calculation of the total payoff per se, but also the very model we propose for the efficient allocation of the coalition’s payoff. Its basic principles are to choose the allocation that is most fair in terms of contributions of players to the coalition and most stable in terms of their incentives to leave the coalition. We consider the C-core, Shapley value, PreNucleolus, Modiclus, and SM-core solution concepts. We test the model on IES structures that makes coalitions of different numbers of consumers possible. We argue that different solution concepts work best under different conditions.

The article is organized as follows. Section 2 provides a brief overview of the related body of published research. We review research contributions that use game theory tools to model interactions: non-cooperative games to describe the relationship between CS and prosumers with their own generation, and cooperative games to describe opportunities to form coalitions between consumers. The review also covers research on multi-agent modeling. Section 3 deals with the mathematical statement of the problem. It is organized into two parts. The first part describes the interaction between a centralized energy supply system and consumers (Section 3.1). The subsection defines the objective functions of all players and constraints. It also states the convex optimization problems that each player involved in the interaction is to solve. Section 3.2 outlines the basic principles for solving the multilevel problem stated in the previous subsection. Section 3.3 deals specifically with the interaction between consumers, which is construed as a cooperative game. This is where the principles of forming a coalition are defined, and the types of imputations of the coalition’s payoff are chosen. We propose a model for selecting the best imputation. Next, the model is tested. Section 4 outlines the basic principles of modeling the investigated problem in a multi-agent system. 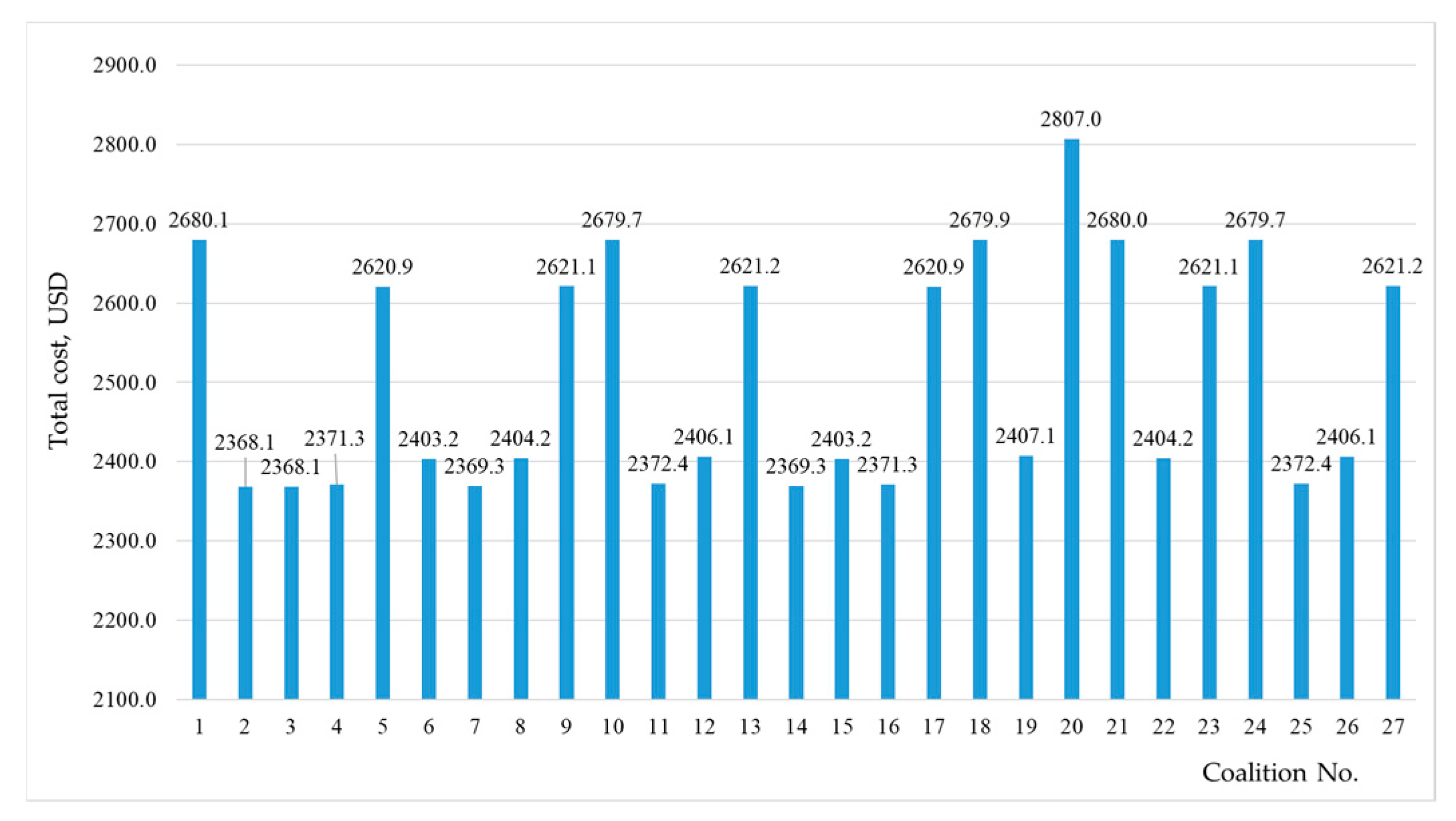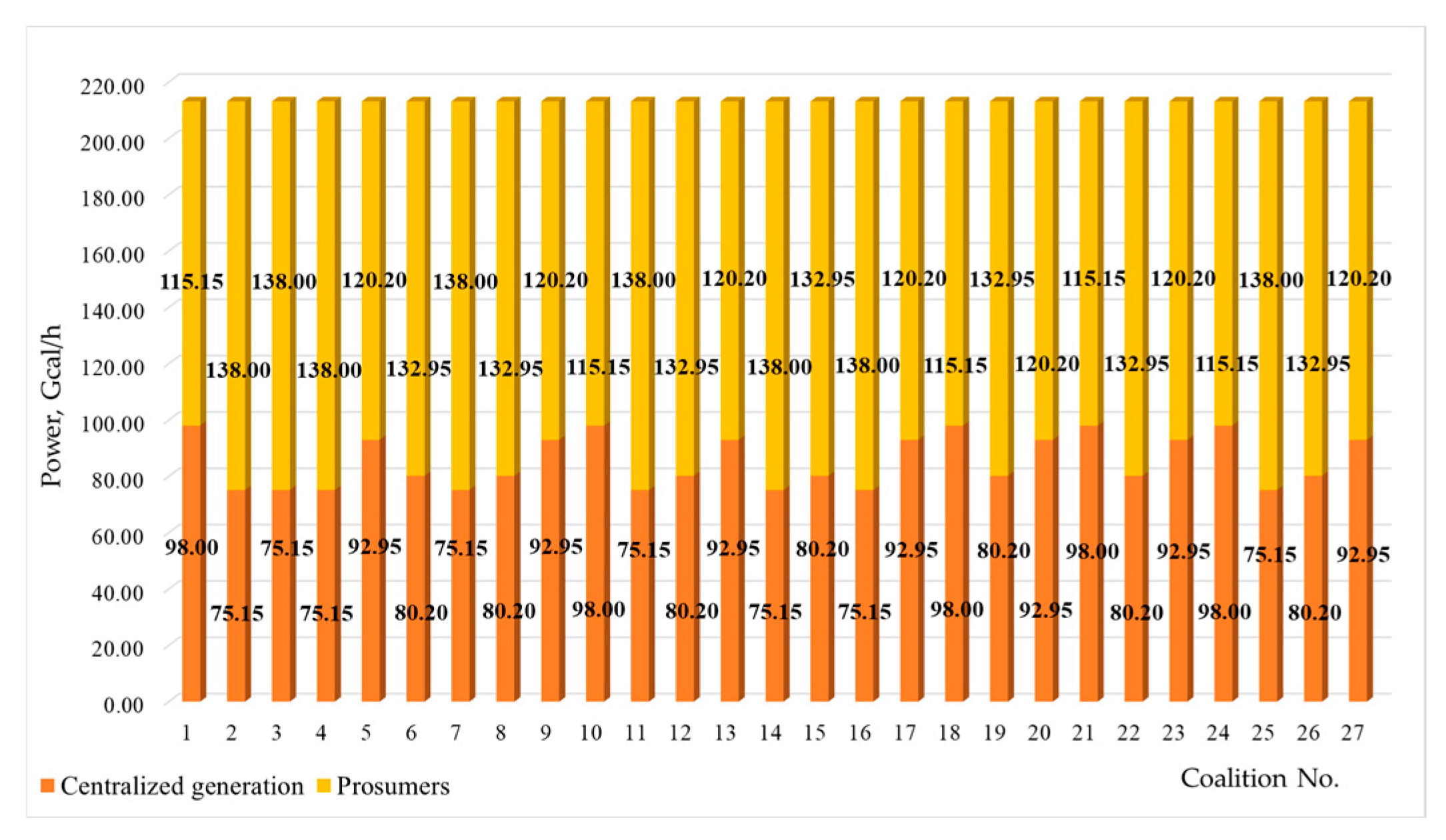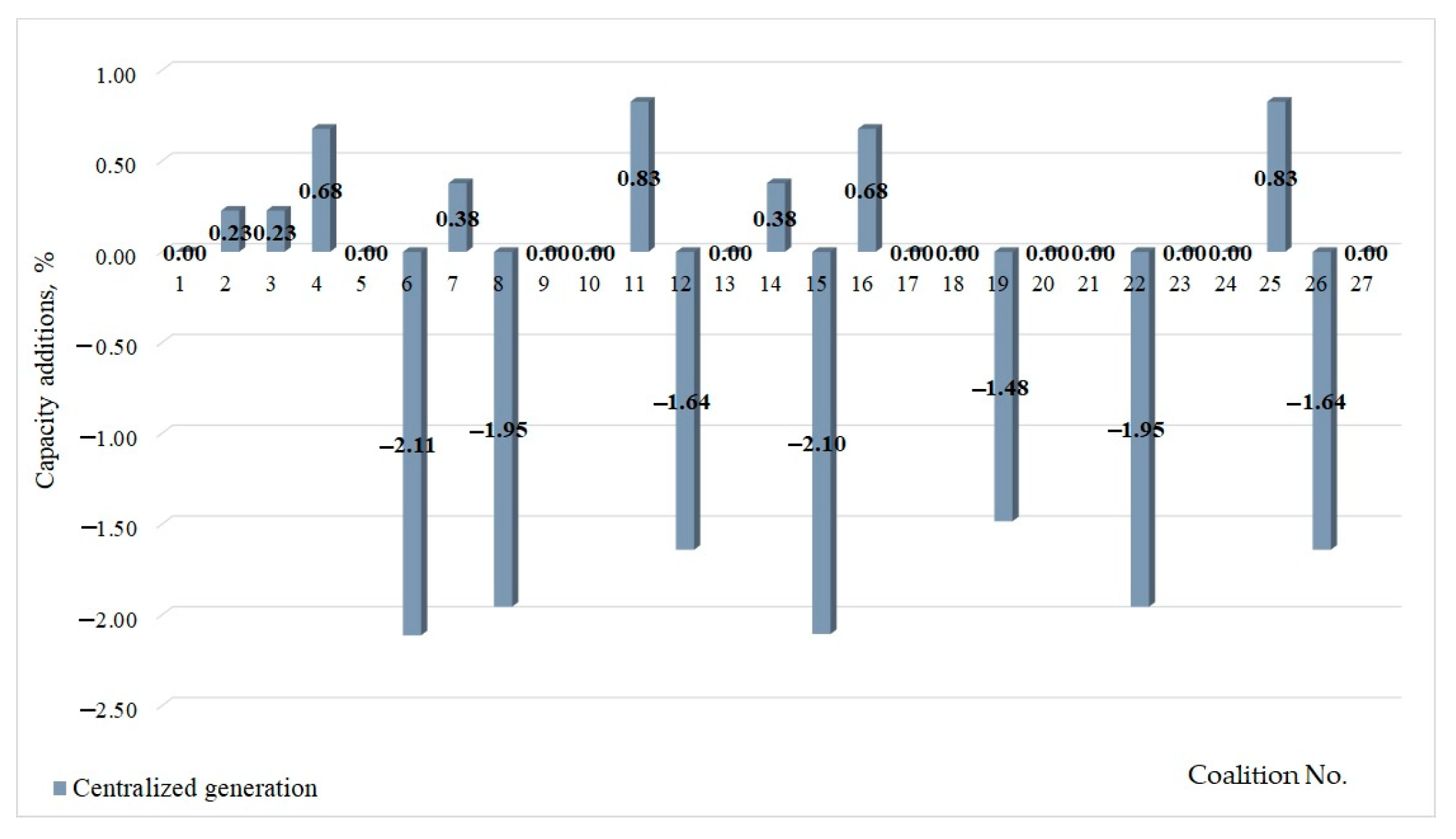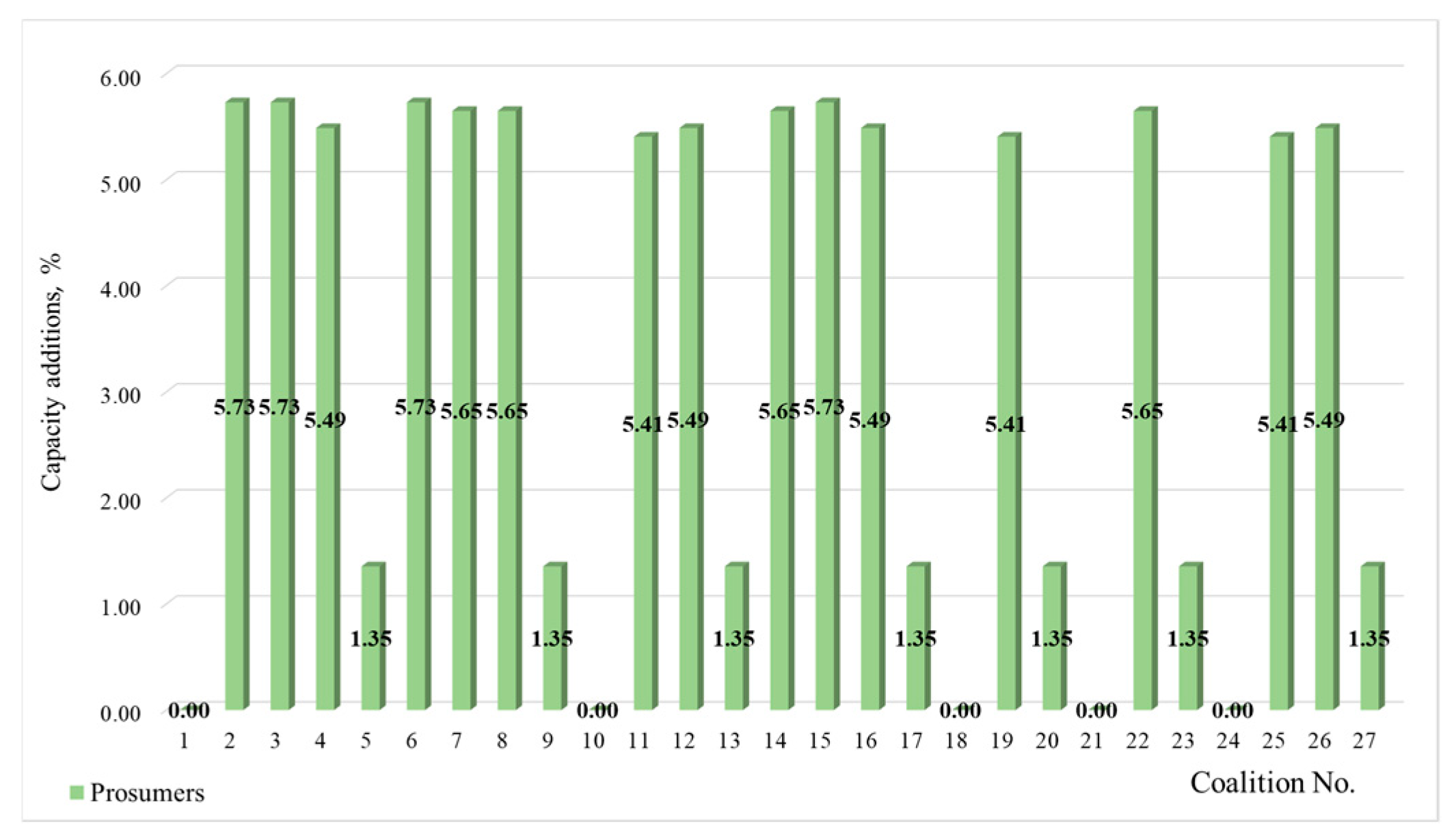Section 5 provides examples of energy system modeling. It shows the efficacy of forming a coalition among consumers and its consequences. We test different solution concepts as well as the principles of selecting the best one.

2. Literature Review

The complexity of modeling interactions between individual entities of energy systems is due to their conflicting interests that manifest themselves as maximization of their own gains. On the other hand, energy supply is a critical technology, and in this sense, large CSs strive for the efficient organization of the industry and therefore the maximization of public welfare. Such a perspective on the problem of interactions between CSs and consumers was reported in Refs. [11,20,21], including the effect of the possible cooperation of consumers. Ref. [21], in addition to the above, studied the case when a coalition of consumers could be beneficial to CSs. In that case, the CS was willing to incentivize consumers to cooperate.

The issues of interaction and cooperation between consumers within a distributed system have become the subject of a lively discussion after the publication of Ref. [22], which considered the case of cooperation that led to disconnection from the centralized power supply. The efficient organization of the industry should also take into account such possible effects. The study prioritized the application of cooperative game theory concepts that are capable of revealing the stability and efficiency of cooperation as well as the market power of the players [12]. Furthermore, these approaches take into account the gains from forming a coalition as compared to non-cooperative behavior [23]. The outcome of the cooperation is determined by the cooperative game solution chosen by the planner. The published research on forming coalitions of consumers within distributed systems most often reports the use of the Shapley value and related imputations [24] and, to a lesser extent, the Nucleolus [25]. The other concepts are not considered.

We rely on the multi-agent approach to model the joint behavior of different entities in the energy supply process in the IES. This approach enables the modelling of the behavior of active subsystems in the IES and taking into account multiple decision-makers in such systems when searching for trade-off solutions to organize the energy supply process. The multi-agent approach has proven its efficacy in solving various problems in the energy industry [26,27]. For example, Ref. [28] contributed a multi-agent system model for optimal control of microgrids with RES. Electricity loads are served by distributed energy sources in microgrids that run on energy resources of different types, and it is also possible to supply electricity from the centralized power supply system, serving loads of different categories. Ref. [29] reported a real-time autonomous energy management strategy for multi-energy systems. The proposed control strategy made intelligent agents optimize energy sales and their conversions to minimize daily costs. Ref. [30] used multi-agent deep reinforcement learning to control a microgrid in a mixed cooperative and competitive environment. Agents monitor wholesale energy prices, fluctuations in energy demand, and renewable energy performance in order to manage the hybrid energy storage system to minimize the cost of energy consumed and maximize the use of renewables.

Based on the literature review, we can conclude that the scope of the majority of studies of IESs is mostly limited to individual systems or their local interactions, most often considering small-scale energy systems with a limited amount of generating and network equipment. As for coalition interactions within distributed energy supply systems, the published research mainly covers the imputations derived from the Shapley value, which does not always deliver the most efficient payoff allocation.

We have opted for a multi-agent approach to take into account the complex nature of the behavior of energy system entities, which includes both public planner type behavior and the pursuit of only one’s own goals. Multi-agent interaction allows for the implementation of direct and feedback communication between IES entities, which enables each agent to use information about the other agents and adjust their decisions based on the received data. Furthermore, we have embedded an additional unit into the overall system to evaluate the performance of coalitions of prosumers and calculate their payoffs. Our model offers a tool for determining the imputation of a coalition’s payoff, such that it encourages individual consumers to join it.

3. Mathematical Problem Statement

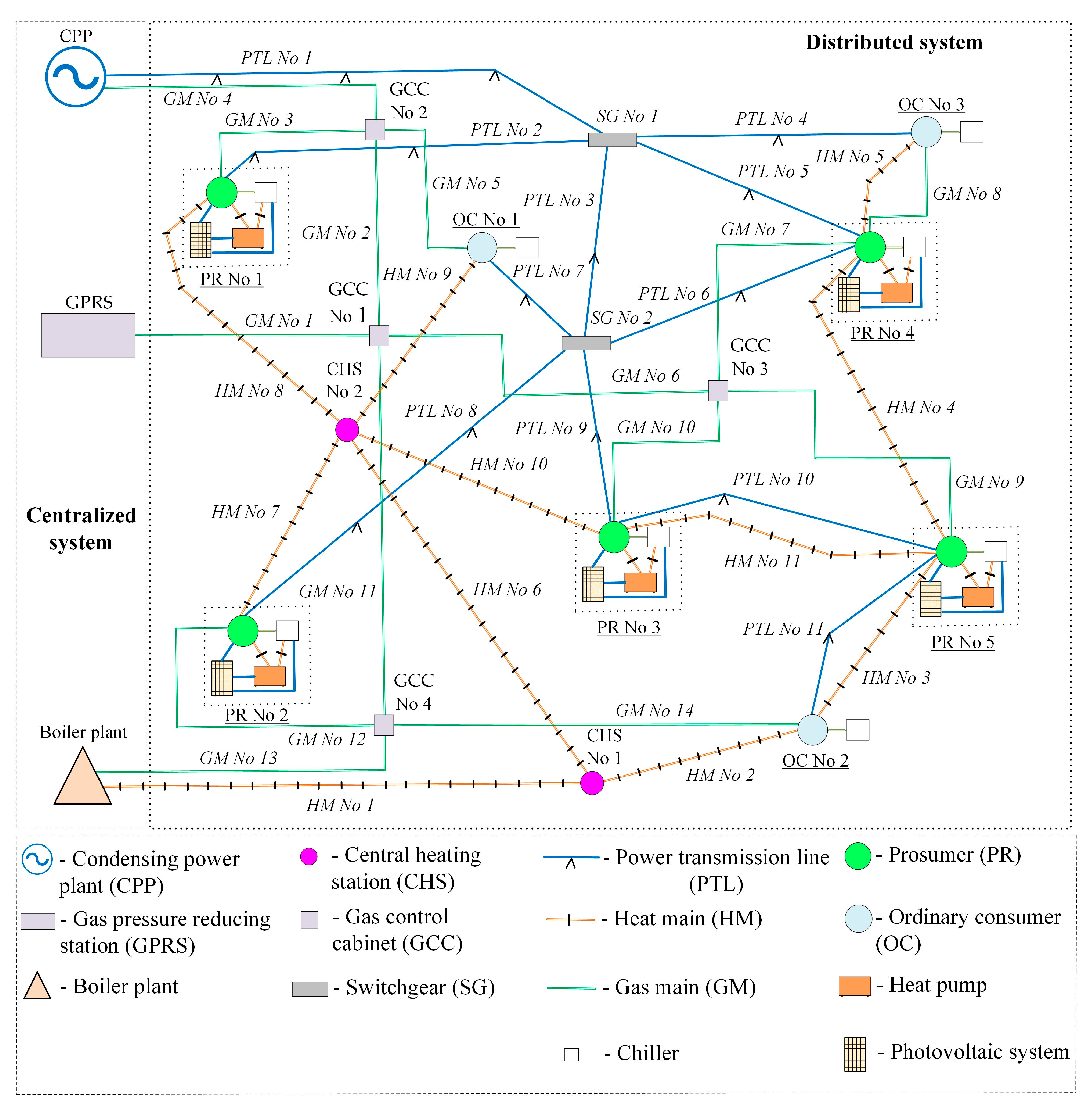
The object of the study is IES, which integrates electricity, heating, cooling, and gas supply systems that share an information environment backed by intelligent technology. The IES is divided into the following levels:

-

a centralized energy system with major energy sources and transmission systems,

-

distributed energy systems having distributed energy sources and distribution networks, and

-

energy consumption systems with consumers, including those with their own energy sources.

The paper considers the creation of an energy–technological meta-system that integrates electricity, heating, cooling, and gas systems. The systems inhabit a shared information environment backed by intelligent technology, which is a promising way of designing new generation energy systems [31].

Modeling prosumers as part of the IES warrants a thorough analysis because they have a significant impact on energy systems when adjusting their load profiles, and have independent energy sources, which complicates the control and management of the overall energy systems. Proper interaction between prosumers and the CS is not yet well established and calls for novel approaches and innovative models.

In this paper, the general model of interaction within IES is represented by several models that implement the operation of systems of different levels. These models are then embedded in the overall multi-agent system as behavioral strategies of agents of different sizes and levels. This subsection presents two models: (1) a mathematical statement of the problem that describes decision-making at the levels of the CS, prosumers, and coalitions of prosumers, and (2) a model of interaction within coalitions that allows us to determine the incentives for coalition formation and the allocation of the coalition’s payoff.

3.1. Mathematical Statement of the Problem of Interaction Between the CS and Consumers

The mathematical statement of the problem of finding the results of interactions between the CS and prosumers consists of maximizing the public welfare function on the part of the CS and maximizing the income (or minimizing the cost) by prosumers. The CS acts as a public planner, and prosumers make use of their own sources of distributed generation, including renewables. The problem is solved so as to minimize the cost of energy supply to consumers along optimal routes, subject to technological constraints. The given quantities are:

• electrical $e$, heat $h$, and gas $g$ networks; $GT=\left\{e,h,g\right\}$, consisting of the set of sections $J\supseteq \bigcup _{j\in GT}{J}_j$ and their transmission capacity, where $J_e\supseteq \bigcup _{k\in SD}{J}_{k,e}$ are the sections of the electrical network including power transmission lines (PTL) in the centralized $J_{cs,e}$ and distributed $J_{d,e}$ network $SD=\left\{cs,d\right\}$; $J_h\supseteq \bigcup _{k\in SD}{J}_{k,h}$ are the sections of the heat network, including heat mains (HM) in the centralized $J_{cs,h}$ and distributed $J_{d,h}$ networks; and $J_g\supseteq \bigcup _{k\in SD}{J}_{k,g}$ are the sections of the gas network including gas mains (GM) in the centralized $J_{cs,g}$ and distributed $J_{d,g}$ networks;
• energy sources $I\supseteq \bigcup _{k\in SD}\bigcup _{j\in GT}{I}_{k,j}$, including sources of electricity $I_{k,e}$, heating $I_{k,h}$, cooling $I_{k,c}$, and natural gas $I_{k,g}$;
• energy sources have constraints imposed on the amount of electricity ${\overline{Q}}_{k,e}^i$, heating ${\overline{Q}}_{k,h}^i$, cooling ${\overline{Q}}_{k,c}^i$, and natural gas production ${\overline{Q}}_{k,g}^i$, $i\in I,k\in SD$, respectively;
• energy consumers $\mathfrak{D}\supseteq {\mathfrak{D}}_{cr}\cup {\mathfrak{D}}_{pr}$, which are made up of a set of ordinary consumers ${\mathfrak{D}}_{cr}\supseteq \bigcup _{j\in GT}{\mathfrak{D}}_{cr,j}$, comprising electricity ${\mathfrak{D}}_{cr,e}$, heating ${\mathfrak{D}}_{cr,h}$, cooling ${\mathfrak{D}}_{cr,c}$, and gas ${\mathfrak{D}}_{cr,g}$ consumers, and a set of prosumers ${\mathfrak{D}}_{pr}\supseteq \bigcup _{j\in GT}{\mathfrak{D}}_{pr,j}$ comprising electricity ${\mathfrak{D}}_{pr,e}$, heating ${\mathfrak{D}}_{pr,h}$, cooling ${\mathfrak{D}}_{pr,c}$, and gas ${\mathfrak{D}}_{pr,g}$ prosumers and having their own distributed generation facilities. Demand for energy is specified in several ways: linear dependencies of consumption on price or some predetermined consumption volumes $Q_{pr,j}$, $Q_{cr,j}$, $j\in GT$.

3.1.1. Modeling Generation Facilities of the CS

The cost functions of centralized generation facilities and distributed generation facilities run by prosumers have a similar functional form. ${TC}_{k,j}^i\left(Q\right), j\in GT, k\in SD, i\in I$ is a cost function with non-decreasing marginal costs $M{C}_{k,j}^i\left(Q\right)$: for ${TC}_{k,j}^i\left(0\right)=0$, it is increasing $M{C}_{k,j}^i\left(Q\right)\ge 0$, and convex ${\left(M{C}_{k,j}^i\left(Q\right)\right)}^{\prime }\ge 0$, $M{C}_{k,j}^i\left(Q\right)\to \mathrm{\infty }$ given $Q\to \mathrm{\infty }$. Generation capacity constraints:

$$\underset{\_}{Q_{k,j}^i}{\le Q}_{k,j}^i\le \overline{Q_{k,j}^i},j\in GT,k\in SD,i\in I.$$

(1)

The energy supply function for the CS depends on each generation facility, its costs ${TC}_{cs,j}^i\left(Q\right)$, and it is a monotonically increasing function of ${SP}_{cs,j}^i\left(p^0\right)$. The producer shapes its supply function by maximizing the profit:

$${SP}_{cs,j}^i\left(p_j^0\right)=Argma{x}_Q\left(p_j^0\cdot Q-T{C}_j\left(Q\right)\right), j\in GT, i\in I.$$

(2)

Problem (1) is a convex optimization problem. Optimal generation is determined by the equation of the first order conditions of the problem (1), (2)

$${MC}_{cs,j}^i\left(Q\right)=p_j^0, if Q\in \left[\underset{\_}{Q_{k,j}^i},\overline{Q_{k,j}^i}\right], j\in GT,i\in I.$$

(3)

3.1.2. Modeling of Actions of Energy Consumers That Have No Generation of Their Own

The system has a network structure; the nodes of the system contain ordinary consumers and prosumers with demand functions $Q_{tr,j}^n\left(p_j^n\right)$, where $n\in [1,N]$ are the nodes of the system, and $p_j^n$ is the energy prices at the nodes of the system, $j\in GT$, $tr\in \{cr,pr\}$, $cr\in {\mathfrak{D}}_{cr}, pr\in {\mathfrak{D}}_{pr}$. Demand functions are decreasing functions with the following properties: $Q_{tr,j}^n\left(p_j^n\right)\to 0$ given $p_j^n\to 0$.

To build the model, we estimate the consumers’ payoff (consumer’s utility), which is formed on the basis of the inverse demand function $p_{tr}^n\left(Q\right)={Q_{tr,j}^n}^{-1}\left(Q\right).$ The utility function is as follows:

$$U_{tr,j}^n\left(Q\right)={\int }^Q{p}_{tr,j}^n\left(\theta \right)d\theta +\gamma , j\in GT, tr\in \left\{cr,pr\right\}, n\in [1,N].$$

In the above case, the utility function has properties common to the utility functions used in microeconomics: its differentiable $U_{tr,j}^n\left(0\right)=0$, increasing $M{U}_{tr,j}^n={\left(U_{tr,j}^n\left(Q\right)\right)}^{\prime }\ge 0$, concave ${\left({MU}_{tr,j}^n\left(Q\right)\right)}^{\prime }\le 0$, $M{U}_{tr,j}^n\left(Q\right)\to \mathrm{\infty }$ given $Q\to \mathrm{\infty }$, where $MU\left(\cdot \right)$ is the marginal utility function. Utility functions can be of established conventional forms, e.g., quadratic, or $U\left(Q\right)=a+b\cdot Q-c\cdot Q^2$—such a function yields a linear demand function. We can use the logarithmic relationship with the generated demand function as an inversely proportional function, etc. Our example is limited to the quadratic case or a fixed value of demand $Q$.

The payoff of the consumer who does not have its own generation sources:

$$v_{tr}^n\left(Q_{tr}^n\right)=\sum _{j\in GT}\left(U_{tr,j}^n\left(Q_{tr,j}^n\right)-p_j^n\cdot Q_{tr,j}^n\right)$$

(4)

In the case of the ordinary consumer $cr$, the consumption equals the demand known to the CS $Q_{cr,j}^n=Q_{cr,j}^n$. The main objective of the consumer is to maximize its own payoff given the energy prices at the node where the consumer is located. This will determine its demand:

$${\breve{Q}}_{tr}^n=\mathit{Argmax}{v}_{tr}^n\left(Q_{tr}^n\right),$$

(5)

$$\underset{\_}{Q_{tr,j}^n}\le Q_{tr,j}^n\le \overline{Q_{tr,j}^n}, j\in GT, n\in \left[1,N\right],tr\in \left\{cr,pr\right\}.$$

(6)

Problems (5) and (6) are convex optimization problems. The optimal consumption is determined by the equation of the first order conditions (4) and (5):

$$M{U}_{tr,j}^n\left(Q_{tr,j}^n\right)=p_j^n, j\in GT,n\in \left[1,N\right], tr\in \left\{cr,pr\right\}.$$

(7)

3.1.3. Modeling Prosumer Actions

The behavioral strategy of the individual prosumer pr is determined by the utility of energy consumption $Q_{pr,j}^n+q_{pr,j}$, $j\in GT$, $n\in \left[1,N\right],$ $pr\in {\mathfrak{D}}_{pr}$, where $q_{pr,j}$ is the amount of generation of energy of the type j at its own generation equipment, and $Q_{pr,j}^n$ is the demand for the energy supplied by the CS.

Marginal costs of sources located at prosumer nodes are assumed to have a single level ${TC}_{pr,j}\left(q\right)=c_{pr,j}^f+c_{pr,j}\cdot q$, where $c_{pr,j}^f$ are fixed costs. Prosumer’s payoff function

$$v_{pr}^n\left(p,Q\right)=\sum _{j\in GT}\left(U_{pr,j}^n\left(Q_{pr,j}^n+q_{pr,j}\right)-p_j^n\cdot Q_{pr,j}^n-{TC}_{pr,j}\left(q_{pr,j}\right)\right), n\in \left[1,N\right],pr\in {\mathfrak{D}}_{pr}$$

(8)

The behavioral strategy will be determined from the modified problems (5) and (6), where $v_{tr}^n\left(Q_{tr}^n\right)$ are determined by (8) with known prices $p_j^n$ offered by the CS and an additional constraint on its own generation:

$$q_{pr,j}<\overline{q_{pr,j}}, j\in GT, \forall pr\in {\mathfrak{D}}_{pr}.$$

(9)

3.1.4. Modeling the Actions of a Coalition of Prosumers and Ordinary Consumers

Consider a subsystem with distributed generation where there are the set consumers $T$. Each consumer $i\in T$ (ordinary consumer $cr\in T$ or prosumer $pr\in T$) within a distributed subsystem can act by:

• pursuing their own interests $\left\{i\right\}\in T$, obtaining the payoff (4) in the case of the ordinary consumer $cr$ or (8) in the case of the prosumer $pr$ and forming its strategy in line with the problems (5), (6) or (5), (6), (9), respectively;
• joining a coalition with other participants $S_k\subseteq T$. Coalitions can be of different sizes $S=\left(S_1,\dots ,S_K\right)\subseteq T$, where $S_K{\cap S}_{\mathrm{l}}=\mathrm{\varnothing }$ given $\mathrm{k}\ne l$,${\bigcup }_{\forall k}{S}_k=T$. In a coalition, consumers can exchange energy within a distributed subsystem.

The payoff of the coalition is formed based on individual players’ payoff functions.

$$v_{S_k}^n\left(p,Q\right)=\sum _{j\in GT}\left(\sum _{cr,pr\in S_k}\left(U_{cr,j}^n\left(Q_{cr,j}^n\right)+U_{pr,j}^n\left(Q_{pr,j}^n+q_{pr,j}\right)\right)-p_j^n\cdot Q_{S_k,j}^n-\sum _{pr\in S_k}{TC}_{pr,j}\left(q_{pr,j}\right)\right),$$

(10)

where $Q_{S_k,j}^n$ is the amount of energy that the coalition buys from the CS at the price $p_j^n$ at the node $n\in \left[1,N\right]$. The power balance for the coalition is as follows:

$$Q_{S_k,j}^n={\sum }_{tr\in S_k}{Q}_{tr,j}^n.$$

(11)

The coalition solves the problems (5), (6), (9), and (11), with the joint payoff function (10). Each player solves an additional problem, which is to ensure that by joining the coalition $S_k$, it gains more than if it were to act on its own. This problem is modeled with the use of cooperative game theory [12,32] and will be discussed in Section 3.

3.1.5. Transportation System Modeling

The IES transportation system consists of the following two parts: (1) a set of network sections of the centralized part of the energy system; (2) a set of network sections of the decentralized part of the power system. The model determines its availability solely by the network configuration, i.e., (dis)connectedness of certain nodes, and transmission losses. Transportation losses are modeled as the iceberg transport costs: part of the energy is lost during transportation, i.e., more energy must be produced than consumed. Real-world energy systems have non-linear transportation losses. Our model simplifies this aspect, which is carried out in order to arrive at a problem statement that lends itself to convex optimization methods. We denote this coefficient of losses by $\tau \ge 1$. When formalizing the model, we assume that generation facilities of a certain type of energy $j\in GT$ are located at a single node (node 0), and consumers with demand $Q_{tr,j}^n\left(p^n\right),n\in [1,N]$ are located at several nodes.

If the amount of energy Q is to be delivered to some node n, then the generation node 0 must produce $\tau Q$. The amount is $Q_j^{0n},j\in GT$, where the part of power grid $0n\in J$ of energy will be transferred to node n from the generation node 0 as long as the following property holds for the ratio of prices at the production and consumption nodes:

$${\displaystyle \frac{p_j^n}{p_j^0}}\ge {\tau }_j^n, j\in GT, n\in [1,N].$$

(12)

The cost of transferring energy of type j from node 0 to node n is described by the function ${TR}_j^n\left(Q_j^{0n},{\tau }_j^n\right),j\in GT$, where $Q_j^{0n}$ is the amount of energy transferred. The path $0n$ may include intermediate sections of the transportation system $ml$, where m and l are nodes of the network $m,l\in [0,N]$. Each section has constraints on energy transfer:

$$\underset{\_}{Q_j^{ml}}\le Q_j^{ml}\le \overline{Q_j^{ml}}, j\in GT, m,l\in \left[0,N\right], ml\in I.$$

(13)

The energy transportation system cost function is an increasing, convex, and differentiable function. The main objective of the transportation system is to minimize the cost of energy transfer subject to the constraint (12) and transmission capacity (13). It is also a convex optimization problem whose solution satisfies the conditions:

$$p_j^n>{\tau }_j^n\cdot p_j^0 \mathrm{and} {Q_j^{0n}=Q}_{tr,j}^n, j\in GT, 0n\in J.$$

(14)

or

$$p^n={\tau }_j^n\cdot p^{0 } \mathrm{a}\mathrm{n}\mathrm{d} {Q_j^{0n}\ge Q}_{tr,j}^n, j\in GT, 0n\in J.$$

(15)

3.1.6. The Main Objective of the CS Is to Maximize Public Welfare

Since energy supply to consumers is a critical technology, the CS of energy supply is regulated by the government and solves a public planner’s problem: the problem of maximizing public welfare while balancing supply and demand at the nodes of the system. Its solution will determine the prices at energy generation nodes and prices at the purchase nodes. The welfare function $W$ shows the difference between the total utility of consumption and the total cost of energy production, storage, and delivery, taking into account the capacity of the transmission lines.

The problem that the CS solves is the maximizing of public welfare $W\left(p,Q\right)$:

$$W\left(p,Q\right)=\sum _{j\in GT}\left(\sum _{n\in N}\left(\sum _{tr}{U}_{tr,j}^n\left(Q_{tr,j}^n\right)-p_j^n\cdot Q_{tr,j}^n\right)+\sum _{i\in I}\left(p_j^0\cdot Q_j^i-T{C}_j^i\left(Q_j^i\right)\right)-\sum _{n\in N}\sum _{0n\in J}T{R}_j^n\left(Q_j^{0n},{\tau }_j^n\right)\right)\to \underset{\mathit{Q},{\mathit{p}}^0,{\mathit{p}}^{\mathit{n}}}{\mathit{max},}$$

(16)

Given the energy balance and transportation losses (demand equals supply),

$$\sum _{n\in N}\sum _{tr}{\left({\tau }_j^n\right)}^{-1}\cdot Q_{tr,j}^n-\sum _{i\in I}{Q}_j^i =0, j\in GT.$$

(17)

where $Q_j^i$ is the amount of energy produced at the generation facility $i\in I$, and $Q_{tr,j}^n$ is the demand at node n. This takes into account the energy balance in the transportation system:

$$\sum _{i\in I}{Q}_j^i -\sum _{n\in N}{Q}_j^{0n}=0, j\in GT.$$

(18)

Furthermore, it can be shown that $\sum _I\sum _N{p}_j^n\cdot Q_{tr,j}^n=\sum _I{p_j^0\cdot Q}_j^i$ by utilizing (12) and (18).

In addition to the balance Equations (16) and (17), we take into account the constraints on the generation of different types of energy (1), constraints on demand (6), constraints on flows over the transportation system (12), (13), and conditions for converting one type of energy to another:

$$Q_l=Q_m{\delta }_{lm}^k, l,m\in GT, k\in I, {\delta }_{lm}^k\ge 0,$$

(19)

where ${\delta }_{lm}^n$ is the coefficient of conversion of one type of energy into another, which depends on the type of the power generation system used for energy conversion. The efficiency of the conversion is evaluated as part of solving the problem.

The problems (16)–(19), (1), (6), (12), and (13) are convex optimization problems and their solutions correspond to the market equilibrium given by relations (3), (7), (14), (15). The type of equilibrium follows from the general welfare theorem for a market under perfect competition [33] and its derivation is based on the use of Lagrange’s theorem for convex optimization problems [34].

The network we consider in the example is organized in a more complex way. The balance equations for all types of energy are specified for each node in the system and the prices at the nodes are determined on the basis of Lagrange multipliers on equality constraints of type (17) specified for each node [34].

The solution determines generation (sales) and purchase volumes, as well as nodal prices, taking into account transportation losses and transmission and generation constraints. The problem is solved by the CS agent, given the known demand on the part of consumers. The resulting prices are price signals to consumers, in that they determine their subsequent steps in generating demand and connecting their own sources.

3.2. Interactions Between the CS and Prosumers

When we deal with a system that includes prosumers, the problem statement changes so as to accommodate the behavioral strategies of individual consumers (8) or coalitions of consumers (10) driven by the goal of maximizing their payoffs. In this case, the payoff is the consumer’s surplus and profits generated by their own energy production.

This is a bilevel hierarchical setting. At the upper level, the prosumers maximize their payoff, and at the lower level, the CS solves the problem of maximizing public welfare given the actions of the upper-level player. Ordinary consumers who do not enter coalitions are not strategic players; their demand is predetermined by the payoff (demand) function (4) and is known to the CS, and their payoff is accounted for in the public welfare function, which is maximized by the CS.

Given perfect information, the solution to a bilevel Stackelberg game [35] would be to find a Nash equilibrium. We consider a case of imperfect information: the CS cannot have detailed information about distributed energy generation as well as the specifics of interactions within a coalition. Therefore, we use an iterative approach to solve real-world problems and the approach implements the best response model. Game dynamics models are a well-established alternative to static problems with perfect information. At each step, a player (the CS, a prosumer, or coalition of consumers) maximizes its own payoff under the assumption that the other players do not change their strategies from the previous step.

Referring to game timing, the CS, guided by the initial information on energy consumption, solves problems (16)–(19), (1), (6), (12), and (13), sets nodal energy prices per unit on the basis of dual variables of balance constraints, and announces the price information to the consumers located at the corresponding nodes. The consumers then respond to the provided price information by changing their energy demand to maximize their payoff, solving problems (5) and (6) with functions (8) and constraints (9), in the case of no coalition, and with functions (10) and constraints (9) and (11) in the case where they do form a coalition. In all cases, the solution is the best response to the actions of the other entities. The stopping criterion is the crossing of a certain threshold of fluctuations in demand and nodal prices between consecutive iterations.

It should be noted that the uniqueness of the Nash equilibrium is not essential to solving the problem of finding an equilibrium. We argue that the energy system can adopt one alternative set of optimized outcomes: energy price and consumption that can maximize the gains of the energy system, consisting of the CS and consumers, while satisfying the respective constraints.

3.3. Mathematical Statement of the Problem of Interactions Within a Coalition of Consumers

The second key part of the described system is the model of interactions within a coalition of consumers and the choices we make with respect to its configuration, payoffs, and imputation. This section provides a concise overview of concepts from cooperative game theory that we used to describe the principles of consumer interactions within a coalition.

The goal is for each participant to gain more by joining the coalition $S_k$ than if it were to act on its own. $(T,S,\eta )$ is a coalition game in its characteristic form [21,36] with coalitions $S_k$, which are partitions of the grand coalition T, and have the characteristic function of payoffs $\eta$ based on the absolute values of consumers’ payoffs (4), (8), or (10). Let us define coalition members $i\in S_k$, $k=\overline{1,K}$, where $K$ is the number of coalitions; then, the characteristic function of the game payoff is $(T,S,\eta )$:

$$\eta \left(S_k\right)={\displaystyle \frac{{v_S}_k-{\sum }_{i\in S_k}{v}_{tr,i}}{v_T-{\sum }_{i\in T}{v}_{tr,i}}}, tr\in \left(cr,pr\right), k=\overline{1,K}.$$

(20)

The payoff of a coalition is normalized relative to the sum of the payoffs of the members available to it, without joining the coalition, and the payoff of the grand coalition. Thus, $\eta \left(S_k\right)\in \left[\mathrm{0,1}\right].$ Below we provide the definitions needed to formalize the solutions of a cooperative game.

Definition 1 

[12]. The set of feasible payoff vectors in the game $(T,S,\eta )$, as the set:

$$X\left(T,\eta \right)=\left\{x\in R^T:{\sum }_{i\in T}{x}_i\le \eta \left(T\right)\right\}$$

Definition 2 

[12]. The set of Pareto-efficient payoffs in the game $(T,S,\eta )$ is the set:

$$X^0\left(T,\eta \right)=\left\{x\in R^T: {\sum }_{i\in T}{x}_i=\eta \left(T\right)\right\}$$

Definition 3 

[12]. The set of imputations in the game $(T,S,\eta )$ is the set of payoffs satisfying the property of individual rationality:

$$I\left(T,\eta \right)=\left\{x\in R^T:x_i\ge \eta \left(\left\{i\right\}\right),i\in S_k,k=\overline{1,K}.\right\}$$

Definition 4 

[12]. The core of a game $(T,S,\eta )$, denoted as $C\left(T,\eta \right)$, is defined by:

$$C\left(T,\eta \right)=\left\{x\in X\left(T,\eta \right): {\sum }_{i\in S_k}{x}_i\ge \eta \left(S_k\right) for S_k\subseteq T, k=\overline{1,K}\right\}$$

The non-emptiness of the core confirms the players’ interest in forming a coalition. At the same time, there is the problem of choosing a specific solution belonging to the C-core, and in the case that it is empty, the problem of choosing a solution among the set of feasible solutions. There are several solution concepts in cooperative game theory [12,32,36,37]. Each of the solutions is defined differently depending on how one construes efficiency, rationality, and fairness in the allocation of the total payoff.

3.3.1. Definitions of Possible Solutions to a Cooperative Game

This study uses the following solution concepts: the PreNucleolus, Modiclus, and Shapley value. The following definitions are needed to formalize point-valued solutions (imputations).

Definition 5 

[12]. A dual game to the game $(T,S,\eta )$ is the game $(T,S,{\eta }^{\ast })$, defined by:

$${\eta }^{\ast }\left(S_k\right)=\eta \left(T\right)-\eta \left(T\backslash S_k\right) for every S_k\subseteq T.$$

Definition 6 

[12]. The excess of the cooperative game $(T,S,\eta )$ of any coalition $S_k\subseteq T$ for any ${x\in X}^0\left(T,\eta \right)$, is:

$$e\left(x,\eta , S_k\right)=\eta \left(S_k\right)-{\sum }_{i\in S_k}{x}_i.$$

(21)

It is a measure of the dissatisfaction of the coalition $S_k$ members with the payoff $\eta \left(S_k\right)$.

Definition 7 

[12]. The excess of the dual game $(T,S,{\eta }^{\ast })$ of any coalition $S_k\subseteq T$ is $e\left(x,{\eta }^{\ast }, S_k\right)$. The excess of the dual game characterizes the veto power of the coalition.

Definition 8 

[12]. The excess of the sum for the game $(T,S,\eta )$ and its dual game $(T,S,{\eta }^{\ast })$ is defined as:

$$\overline{e}\left(x,\eta , S_k\right)={\displaystyle \frac{1}{2}}\left(e\left(x,\eta , S_k\right)+e\left(x,{\eta }^{\ast }, S_k\right)\right).$$

In what follows, we define the concepts of coalition payoff allocations considered in this paper: the PreNucleolus, Modiclus, and Shapley value.

Definition 9 

[12,38]. The PreNucleolus of the game $(T,S,\eta )$ is the set of payoffs $x\in X^0\left(T,\eta \right)$ such that:

$$\theta \left(e\left(y,\eta , S_k\right)\right){\ge }_{lex}\theta \left(e\left(x,\eta , S_k\right)\right), \forall y\in X^0\left(T,\eta \right).$$

where $\theta \left(z\right)=\left({\theta }^1\right(z),...,{\theta }^d(z\left)\right)$ be the vector in $R^d$, the Euclidean space of dimension d, whose components are the numbers ${\left(hi\right(x\left)\right)}_{i\in D}$ arranged in non-increasing order, that is,

$${\theta }^s\left(z\right)=\underset{S_k⊑T, \left|S_k\right|=s}{\mathit{max}}\underset{i\in S_k}{\mathit{min}}\left(h_i\left(z\right)\right), for all s=1,\dots ,d.$$

Let ≥lex denote the lexicographical ordering.

Definition 10 

[39]. The modified Nucleolus (Modiclus, or SM-core) of the game $(T,S,\eta )$ is the set of vectors $x\in X^0\left(T,\eta \right)$ such that:

$$\theta \left(\overline{e}\left(y,\eta , S_k\right)\right){\ge }_{lex}\theta \left(\overline{e}\left(x,\eta , S_k\right)\right), \forall y\in X^0\left(T,\eta \right).$$

Definition 11 

[40]. The Shapley value for the payoff allocation $\eta \left(T\right)$ of the game $(T,S,\eta )$ for $S_k\subseteq T$ is the vector whose entries are:

$${\phi }_i={\sum }_{ S_k\in T}{\displaystyle \frac{\left(k-1\right)!\left(t-k\right)!}{t!}}\left(\eta \left(S_k\right)-\eta \left(S_k\backslash \left\{i\right\}\right)\right), i\in T, k=\left|S_k\right|, t=\left|T\right|$$

where $\left|S_k\right|$ is the power of the coalition $S_k$.

3.3.2. Properties of Cooperative Games

In order to apply solution concepts for cooperative games such as the PreNucleolus and Modiclus, a cooperative game must exhibit certain properties. This paragraph lists the properties of cooperative games that guarantee the existence of the core, and it also states the theorems that underpin our choice of solution concepts for the investigated practical problem.

Definition 12 

[12]. A game $(T,S,\eta )$ is superadditive if $S_k, S_j\subseteq N, S_k\cap S_j=\varnothing$:

$$\eta \left(S_k\cup S_j\right)\le \eta \left(S_k\right)+\eta \left(S_j\right), k,j=\overline{1,K}.$$

Definition 13 

[41]. A game $(T,S,\eta )$ is balanced if there is a mapping $\delta :2^T\backslash \{\varnothing \}\to R_{+}$, ${\sum }_{S_k\in 2^T\backslash \{\varnothing \},k=\overline{1,K}}\delta \left(S_k\right)=1$ such that:

$$\sum _{S_k\in 2^T\backslash \{\varnothing \},k=\overline{1,K} }\delta \left(S_k\right)\eta \left(S_k\right)\le \eta \left(T\right).$$

(22)

Definition 14 

[12]. The game is convex if:

$$\eta \left(S_k\cup S_j\right)-\eta \left(S_k\cap S_j\right)\le \eta \left(S_k\right)+\eta \left(S_j\right), k,j=\overline{1,K}.$$

(23)

Convexity is a relaxed requirement for superadditivity.

The following theorems define properties of cooperative games in which there exists the core. This also includes the theorem stipulating that the PreNucleolus and Modiclus are point-valued.

Theorem 1 (The Bondareva–Shapley Theorem)

[36]. The core of the game $(T,S,\eta )$ is not empty if and only if the game is a balanced game.

The balance is, in general, quite difficult to check for, which warrants construction of sufficient conditions for non-emptiness of the core to define classes of games for which the C-core is guaranteed to be non-empty. Here, we will rely on the property of convex games, which was formulated in [12]:

Property 

[12]. A convex game is totally balanced.

It follows that if the game is convex, then the core is non-empty. Let us state the theorems on point-valued PreNucleolus and Modiclus solutions.

The existence and uniqueness of the PreNucleolus follows from Schmeidler’s theorem, although he considered the set of individually rational vectors $I\left(T,\eta \right)$.

Theorem 2 

[38]. The PreNucleolus consists of a unique point.

A similar theorem holds true for the Modiclus.

Theorem 3 

[39]. The Modiclus consists of a unique point.

Thus, after a cooperative game is formed, we can evaluate its properties and determine whether a coalition will be formed and whether the cooperative game is solvable. To that end, several properties need to be checked. In our modeling, we start with the easier task of checking for the convexity condition of a cooperative game. If it is satisfied, then we can compute solutions to the cooperative game (allocations). If the game is not convex, then we proceed to check for the balance of the game, which guarantees the existence of the core, and hence the possibility of computing the above point-valued solutions: the PreNucleolus, Modiclus, and Shapley value. In the examples considered below, the games prove non-convex, but at the same time are monotonous.

3.3.3. Criteria for Selecting the Best Solution to a Cooperative Game

In order to select a single solution, i.e., a payoff allocation between players, we need to introduce selection criteria. It is impossible to arrive at a solution that is both fair in the sense of each player’s contributions and stable in the sense of providing no incentive to split off while accounting for players’ veto power. Ref. [42] discussed several criteria that can be used to determine the “quality” of the obtained solution. We have developed the following system of criteria to choose a solution from the set:

Satisfaction index: The first “solution quality” criterion is based on the definition of the excess (20). Excess shows the benefits for players acting as part of a coalition, compared to their independent operation, and represents the amount of cost savings (payoff) that the coalition $S_k$ can realize by cooperating in accordance with imputation $x$. The larger the value $e\left(x,\eta ,S_k\right)$, the greater the amount of cost savings for the coalition S players. Moreover, the larger the payoff available to each player, the higher the satisfaction of the members that are parties to the imputation $x$.

$$w_1=1-\underset{S_k}{\mathit{min}}e\left(x,\eta , S_k\right)\to min.$$

(24)

It can be seen that the PreNucleolus and Nucleolus solutions will be the best for this criterion. Moreover, the best imputation with respect to the criterion $w_1$ will have the minimum value of this coefficient.

Fairness index: This criterion shows the deviation of the resulting imputation $x$ from the allocation of the payoff when players are paid equal shares. Moreover, the best imputation with respect to the criterion $w_1$ will have the minimum value of this coefficient:

$$w_2=\underset{i\in T}{\mathit{max}}{x}_i-\underset{i\in T}{\mathit{min}}{x}_i\to min,$$

(25)

Attractiveness index: This criterion shows the ratio of the sum of the losses of the player who left the coalition to what the coalition itself loses. The more a player loses, the more attractive it is for the player to join/not to leave a coalition. It is designated as $w_3$. The smaller the value $w_3$, the more attractive joining the coalition is for the player i.

$$w_3=\underset{i\in T}{\mathit{max}}\left\{1+{\displaystyle \frac{1-{\eta }_{T\backslash \left\{i\right\}}}{x_i}}\right\}\to min.$$

(26)

Aggregate criterion for selecting the best solution. Based on the above indices $w$, we calculate the aggregate index of the “quality” of the obtained solution.

$$\omega =w_1\cdot w_2\cdot w_3.$$

(27)

We assume that the smaller the $\omega$ value, the better the proposed allocation of the coalition’s payoff.

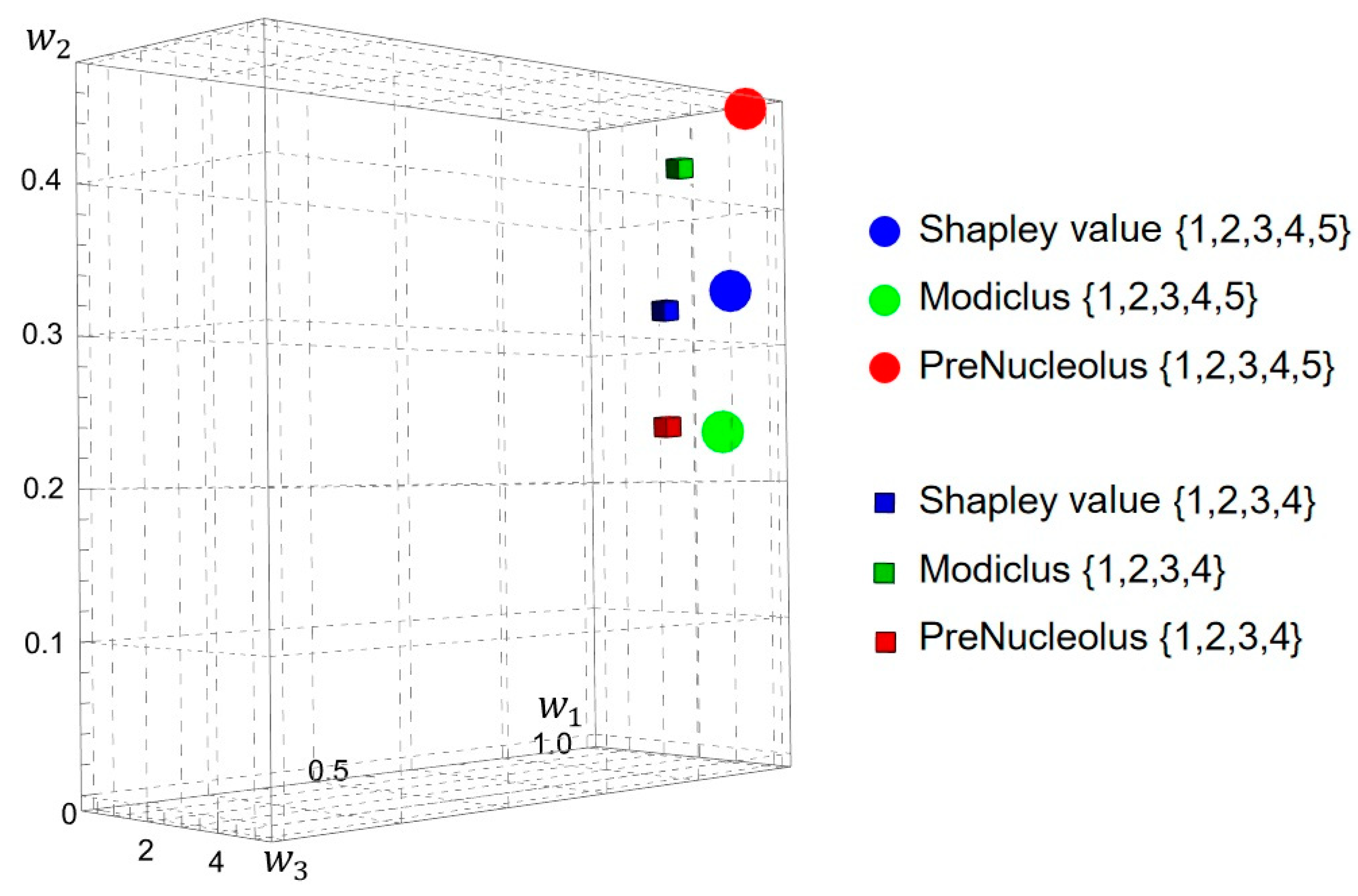
The considered solutions (allocations), such as the PreNucleolus, Modiclus, and Shapley value, are guaranteed to yield rational solutions only for the class of convex games. However, technical limitations of power systems can lead to non-convex cooperative games. In such a case, the contribution of individual players in a sub-coalition may be greater than in the grand coalition. Thus, it may be warranted to develop algorithms that avoid the formation of non-convex cooperative games, including through the identification of cooperation bottlenecks and the introduction of mechanisms that eliminate them.

4. Agent-Based Modeling of Interaction Between the CS and Consumers

We have designed the architecture of a multi-agent system (MAS) to leverage the multi-agent approach to the above-stated problems. The architecture is made up of three main levels of agent interaction (see Figure 1): the CS; aggregators; and distributed systems. Each level is represented by its own set of agents, which correspond to the energy facilities of that level and capture their behavior and characteristics. All agents can be divided into two main groups: agents that represent IES facilities and agents that control and coordinate IES facilities. The first group of agents includes agents of centralized energy sources (ACES); agents of network sections (ANS); agents of ordinary consumers (AOC); and agents of prosumers (AP). The second group of agents includes the network agent of the CS, and aggregator agents whose functions are control and coordination. These agents do not act strategically, so we do not describe them in detail here.

The task of organizing the interactions between the centralized part of the power system and prosumers when they form coalitions in the IES is solved on the basis of an original multi-agent system. A description of the agents’ algorithms was detailed elsewhere in [27,43]. In what follows, we provide a concise statement of the step-by-step algorithm of actions of the CS, prosumer, and ordinary consumer agents, as well as those of possible coalitions of consumers.

Step 1

Begin. Initialize variables, model coefficients, and the algorithm’s stopping parameter $\epsilon$. Determine the iteration number $t=t+1$.

Step 2

Actions of the CS agent: the CS solves the public welfare maximization problems (16)–(19), (1), (6), (12), and (13) as informed by predicted demand volumes (received from consumers). Result: planned volumes of energy generation ${\left(Q_j^i\right)}^t$, volumes of energy consumption ${\left(Q_{tr,j}^n\right)}^t$, volumes of energy transmission through the transportation system ${\left(Q_j^{0n}\right)}^t$, nodal prices of generation ${\left(p_j^0\right)}^t$, and consumption ${\left(p_j^n\right)}^t,j\in GT,i\in I,tr\in \left[cr,pr\right],n\in [1,N]$.

Step 3

Comparison of prices ${\left(p_j^n\right)}^t$ and ${\left(p_j^n\right)}^{t+1}$. If the prices differ by $\epsilon$ (the stopping parameter specified in advance), then go to Step 8.

Step 4

Otherwise:

Actions of consumer agents: receive a signal about nodal energy prices ${\left(p_j^n\right)}^t,j\in GT$ from the CS.

Step 5

Demand optimization by consumer agents for two cases:

• as individual actions of consumers, taking into account their own energy generation, available to them without forming coalitions, as the solution to problems (5)–(6), (8), (9);
• as actions of consumers forming a coalition when distributed generation is interconnected. Solution to problem (5), and (6), (9), (10), and (11).
• Consider all technically possible coalitions. Choose the most efficient one with the highest payoff $v$.
• Calculate possible payoff allocations among coalition members:
  • represent the game in its reduced form (20);
  • If the game is convex (23) then go to Step 5d(iv)
  • Else

    (a)

    If the game is balanced (22), then go to Step 5d(iv),

    (b)

    Else go to Step 5d(v);

  • Calculate payoff allocations for the PreNucleolus, Modiclus, Shapley value. Go to Step 5e;
  • Calculate payoff divisions for the PreNucleolus, Modiclus, Shapley value. Go to Step 5f;
• For each division, find the vector of the “quality” of the solution in accordance with (24)–(26) and calculate the aggregate vector (27), characterizing the properties of the solution of the game. Choose the best one.
• Consumer agents choose the most profitable option for loading their sources or consuming energy from the CS from a. and b., i.e., optimizing individual consumption or consumption as part of interactions within a coalition.

Step 6

The obtained results are sent by consumer agents to the next level (see Figure 1). The level of aggregator agents searches for a solution for interconnected consumer networks, subject to the constraints of the CS (13).

Step 7

Aggregator agents send the obtained results to the next level, i.e., the demand for energy from the CS, taking into account the capacity of the transportation network.

Step 8

Go to Step 1.

Step 9

End.

5. Example

5.1. System Description

Figure 2 shows the test architecture of the investigated IES. The system includes electricity, heating, gas, and cooling (chiller units with no pipeline networks) systems. In terms of its structure, the IES is divided into centralized and distributed systems.

The CS uses a condensing power plant (CPP) to generate electricity. The CPP is connected to the distributed system via power transmission line (PTL) No. 1. The distributed system is connected to switchgear (SG) No. 1. The boiler plant is used to generate heat. The boiler plant is connected to the distributed system via heat mains (HM) No. 1, which are in turn connected to central heating station (CHS) No. 1. A gas pressure reducing station (GPRS) regulates the gas flow to desired parameters and distributes it throughout the system. The GPRS is connected to the distributed system via gas main (GM) No. 1, which is in turn connected to gas control cabinet (GCC) No.1. The CS also includes GM No. 4 and GM No. 13, which are used to supply gas to the CPP and boiler plant. The distribution system includes five prosumers that have their own sources of electricity (photovoltaic systems) and heat sources (heat pumps), cold sources (chillers). The system also includes three ordinary consumers that do not have their own energy sources. Electricity is transmitted to consumers in the distributed system over 10 transmission lines, heat is delivered over 10 HMs, and gas for consumers’ auxiliary needs is delivered over 11 GMs. Network sections are dynamically distributed between centralized and decentralized systems depending on the coalition of prosumers under consideration. The calculations made for prosumers assume the possibility of converting electricity into thermal energy by heat pumps.

5.2. Special Considerations in Cost Calculations

The proposed test IES layout (see Figure 2) served as the basis for the 27 cases of different coalitions with prosumer interactions, which took into account their interests and capabilities of energy generation and conversion. The number of coalitions is limited by topological features of the structure and engineering constraints, since not all connections between consumers can be provided; e.g., a direct electrical connection between Prosumer 1 and Prosumer 5 is not possible, but it can be achieved by involving several intermediate nodes (SW 1, SW 2, Prosumer 3). These constraints hold for both the electrical system and heating system. Furthermore, we assumed that only one coalition is formed in the distributed network, whereas more complex cases where multiple coalitions may form on a set of consumers were not considered in this paper. These are the rules proposed by the aggregators.

Table 1. List of coalitions for prosumer interactions.

No	Coalition-Forming Scenario	Description
1	$\eta \left(\left\{i\right\}\right),i\in \left[\mathrm{1,5}\right]$	No cooperation. No prosumers interact with each other (Coalition 1).
2	$\eta \left(\mathrm{1,2},\mathrm{3,4},5\right)$	Grand coalition. All prosumers interact with each other (Coalition 2).
3	$\eta \left(\mathrm{1,2},\mathrm{3,5}\right),\eta \left(\left\{4\right\}\right)$	Partial cooperation. Prosumer 4 is not in the coalition (Coalition 6).
4	$\eta \left(\mathrm{2,3},5\right), \eta \left(\left\{1\right\}\right),\eta \left(\left\{5\right\}\right)$	Partial cooperation. Prosumers 2, 3, and 4 join the coalition. Prosumer 1 is not in the coalition. Prosumer 5 is not in the coalition (Coalition 14).
5	$\eta \left(\mathrm{2,4}\right),\eta \left(\left\{1\right\}\right),\eta \left(\left\{3\right\}\right),\eta \left(\left\{5\right\}\right)$	Partial cooperation. Prosumers 2 and 4 join the coalition. Prosumer 1 is not in the coalition. Prosumer 3 is not in the coalition. Prosumer 5 is not in the coalition (Coalition 23).

summarizes some of the coalitions formed in line with the constraints stated above. The full list of coalitions for four and five prosumers is provided in Appendix A.

5.3. Calculations for Different Cases of the Generation Capacity Available to Prosumers and the CS

5.3.1. Calculation for the Case of Five Prosumers

We relied on the test structure of the system presented in Figure 2 to assess the performance of the model and investigate the interaction of prosumers in the IES. We evaluated optimal power supply routes for all 27 possible coalition-forming scenarios. The calculation was performed simultaneously for electrical, heating, cooling, and gas supply systems and aimed at reducing the total cost for prosumers when they cooperate in the IES. The input data for the simulation are given in Appendix B.

Figure 3 shows an example model, and the results obtained for the first simulation setup with full cooperation. Each entity of the structure is represented by its agent; agents in the model are highlighted in red. The agents, while interacting with each other, performed the search for the most economically advantageous solution based on the capabilities and interests of consumers (5)–(6), (9), (10), (11), and the CS (16)–(19), (1), (6), (12), (13), subject to technical constraints.

A batch of calculations was performed in the AnyLogic program environment based on the above simulations.

Table 2. Total cost of power supply to five prosumers.

Simulation Setup	Prosumer 1, USD	Prosumer 2, USD	Prosumer 3, USD	Prosumer 4, USD	Prosumer 5, USD	Total Cost, USD
$\eta \left(\left\{i\right\}\right), i\in \left[\mathrm{1,5}\right]$	586.3	765.2	362.2	385.8	580.6	2680.1
$\eta \left(\mathrm{1,2},\mathrm{3,4},5\right)\equiv \eta \left(T\right)$	2368.1
Shapley value	557.2	707.5	192.5	354.5	556.3	2368.1
Modiclus	550.4	688.8	226.5	345.2	557.2	2368.1
PreNucleolus	564.5	710.6	165.6	362.4	565.0	2368.1

presents the total cost of supplying energy to prosumers for the cases of full cooperation and no cooperation, as well as the results of distributing the payoff of full cooperation (fair cost sharing) among prosumers as induced by different solution concepts:

Checking for the convexity (23) and balance (22) of the game proved the game to be non-convex and balanced. The PreNucleolus, Shapley value, and Modiclus point-valued solutions were calculated.

The total cost (compared to the simulation setup with no cooperation) changed as follows: for Prosumer 1, the costs decreased by 4.96%; for Prosumer 2, the costs decreased by 7.54%; and for Prosumers 3, 4, and 5, the costs decreased by 46.86%, 8.09%, and 4.18%, respectively. The case of Prosumer 1 shows that cooperation and the use of its own, cheaper energy sources notably decreased its total energy supply from USD 362.23 to USD 165.63, which was also due to the sale of its generated energy to other consumers. In general, there is a reduction in the total cost of energy supply to prosumers, while the CS serves a lesser percentage of prosumer’s loads, and prosumers substitute its energy with cheaper energy from their own sources generated within the coalition. The total cost of energy supply to prosumers when they form any of the 27 coalitions are shown in Appendix C. Figure 4a,b shows the total electricity and heat generation by centralized and distributed energy sources for the seven coalitions. Appendix C provides the data for 27 coalitions. The difference in total electricity generation for different coalitions is due to the presence of nodes of heat-to-electricity conversion by heat pumps.

5.3.2. Calculation for Four Prosumers

The second simulation setup for the above test structure (Figure 2) differs in the number of prosumers that can join the coalition (there are four of them) as well as in the ratio of available energy sources at the distributed and centralized systems. In this case, the prosumers can produce significantly less energy at their sources. Similarly to the previous case, 12 coalition options are formed, including complete cooperation $v\left(\mathrm{1,2},\mathrm{3,4}\right)\equiv v\left(T\right)$. Appendix D shows the total cost of energy supply to prosumers for a selection of coalitions they may form, as well as total power generation by centralized and distributed energy sources for the electricity and heating system.

The simulations yielded fair cost allocation among prosumers involved in cooperation. The reduced payoff matrix (reduced game) for several coalitions is shown in

Table 3. Reduced payoff matrix and payoff allocation for the coalitional game of four prosumers.

Simulation Setup	Prosumer 1	Prosumer 2	Prosumer 3	Prosumer 4	Sum
$\eta \left(\left\{i\right\}\right), i\in \left[\mathrm{1,4}\right]$	0.00	0.00	0.00	0.00	0.00
$\eta \left(\mathrm{1,2},\mathrm{3,4}\right)\equiv \eta \left(T\right)$	1.00				1.00
$\eta \left(\mathrm{2,3},4\right)$,$\eta \left(\left\{1\right\}\right)$	0.00	0.86			0.86
$\eta \left(\mathrm{1,3},4\right)$,$\eta \left(\left\{2\right\}\right)$	$\eta \left(\mathrm{1,3},4\right)$ = 0.69, $\eta \left(\left\{2\right\}\right)$ = 0.00				0.69
$\eta \left(\mathrm{1,2},4\right)$,$\eta \left(\left\{3\right\}\right)$	$\eta \left(\mathrm{1,2},4\right)$ = 0.30, $\eta \left(\left\{3\right\}\right)$ = 0.00				0.30
$\eta \left(\mathrm{1,2},3\right)$,$\eta \left(\left\{4\right\}\right)$	0.69			0.00	0.69
$\eta \left(\mathrm{1,2}\right)$,$\eta \left(\left\{3\right\}\right),\eta \left(\left\{4\right\}\right)$	0.00		0.00	0.00	0.00
$\eta \left(\mathrm{1,3}\right)$$, \eta \left(\left\{2\right\}\right),\eta \left(\left\{4\right\}\right)$	$\eta \left(\mathrm{1,3}\right)$ = 0.47, $\eta \left(\left\{2\right\}\right)$ = 0.0, $\eta \left(\left\{4\right\}\right)$ = 0.0				0.47
$\eta \left(\mathrm{1,4}\right)$,$\eta \left(\left\{2\right\}\right),\eta \left(\left\{3\right\}\right)$	$\eta \left(\mathrm{1,4}\right)$ = 0.20, $\eta \left(\left\{2\right\}\right)$ = 0.0, $\eta \left(\left\{3\right\}\right)$ = 0.0				0.20
$\eta \left(\mathrm{2,3}\right)$$, \eta \left(\left\{1\right\}\right),\eta \left(\left\{4\right\}\right)$	0.00	0.59		0.00	0.59
$\eta \left(\mathrm{2,4}\right)$$, \eta \left(\left\{1\right\}\right),\eta \left(\left\{3\right\}\right)$	$\eta \left(\mathrm{2,4}\right)$ = 0.25, $\eta \left(\left\{1\right\}\right)$ = 0.0, $\eta \left(\left\{3\right\}\right)$ = 0.0				0.25
$\eta \left(\mathrm{3,4}\right)$,$\eta \left(\left\{1\right\}\right),\eta \left(\left\{2\right\}\right)$	0.00	0.00	0.54		0.54
Shapley value	0.116	0.201	0.456	0.226	1.00
Modiclus	0.117	0.236	0.354	0.293	1.00
PreNucleolus	0.070	0.170	0.540	0.220	1.00

. Players who do not join the coalition have a zero payoff: $v\left(\left\{i\right\}\right)=0,i\notin S_k$. The properties of this game are similar to those of the five-player game: the game proved non-convex but balanced. Table 3 lists the resulting payoff allocations according to different solution concepts: the Shapley value, Modiclus, and PreNucleolus.

5.4. Choosing the “Best” Solution (Allocation of the Total Payoff) for the Coalition Game

As noted earlier, the solution concepts investigated in this study yield different results. What is important is how much each player’s contribution will be taken into account and how stable the resulting coalition will be. Figure 5 plots the size of the payoff increase, relative to the case of no cooperation, for the two members 2 and 3 of a coalition of five players.

In order to assess the quality of the obtained imputations, Section 3.3.3 proposes a set of properties to test the solutions (24)–(27).

Table 4. Characteristics of the solutions to the coalition game as obtained for different solution concepts.

Property	Shapley Value	Modiclus	PreNucleolus
Game for a coalition of five players
$w_1$	0.976	1	0.93
$w_2$	0.341	0.237	0.47
$w_3$	4.48	3.97	5.43
ω	1.49	0.94	2.37
Game for a coalition of four players
$w_1$	0.98	1	0.95
$w_2$	0.33	0.44	0.24
$w_3$	2.7	2.87	3.06
ω	0.87	1.26	0.7

shows the properties $w_1,w_2,w_3$ and the generalized property $\omega$, characterizing the Shapley value, Modiclus and PreNucleolus solutions obtained for the two considered cases. Figure 6 shows the generalized property $\omega$: it is assumed that the smaller the value of $\omega$, the better the imputation. We see that in the first case, where a coalition of five players and distributed generation account for a large share of the overall energy system, the Modiclus (indicated in bright green in the figure) is considered the “best” in the sense of allocation fairness and, to some extent, stability. The PreNucleolus allocation (shown in light red) proved best in the case of a four-player coalition and limited distributed generation capacity.

6. Discussion and Conclusions

Transformation of energy systems strengthens the interaction between different types of energy supply systems and forms IESs. It also creates new opportunities for energy consumers, including those with their own energy sources installed. These changes in energy systems raise the pressing issue of organizing interaction between different entities involved in the energy supply processes, especially those with generation facilities (centralized and decentralized energy sources). To solve the above problem, one is advised to properly consider its inherently unique features: the hierarchical principle underlying the IES architecture; multiple decision-makers with conflicting interests acting in the IES; imperfect information available to all participants of the interaction; possible coalitions of prosumers.

It is common to model the relationship between the CS and prosumers by a general statement of the public welfare maximization problem. In general, when cost functions of energy sources are convex and utility functions of consumers are concave, this problem is a convex optimization problem and has a solution. This takes into account the network structure of the location of generation facilities and consumers by imposing constraints on flows and supply and demand balances at the nodes of the system. Prices are determined by the Lagrange multiplier method and are essentially price signals for market participants: this implies that at generation nodes they will be equal to marginal costs, while at consumption nodes they are adjusted by adding transport costs (losses, network constraints) to them.

The problem becomes, at once, more difficult if consumers have their own goals and form behavioral strategies based on maximizing their own payoff. In this case, one could solve the problem by finding the equilibrium in the Stackelberg model. Energy sector studies consider possible ways of finding such equilibria in the form of a mathematical program with equilibrium constraints (MPEC, EPEC [9,10]), where the equilibrium constraints are first-order conditions for the problem of finding the maximum payoff of individual players. These are complex problem statements: the problems are non-convex and difficult to solve. In this study, we avoid this complexity by solving the problem with agent-based modeling tools, while simplifying the requirements for the knowledge of the system available to the players. The above means that there is no requirement for all participants involved in the interaction to have perfect information. Agents exchange signals and the problem is solved iteratively by applying the best response dynamics procedure in its discrete form; i.e., we use a distributed approach to solving the problem by breaking down a complex problem statement into a set of problems of smaller dimensionality.

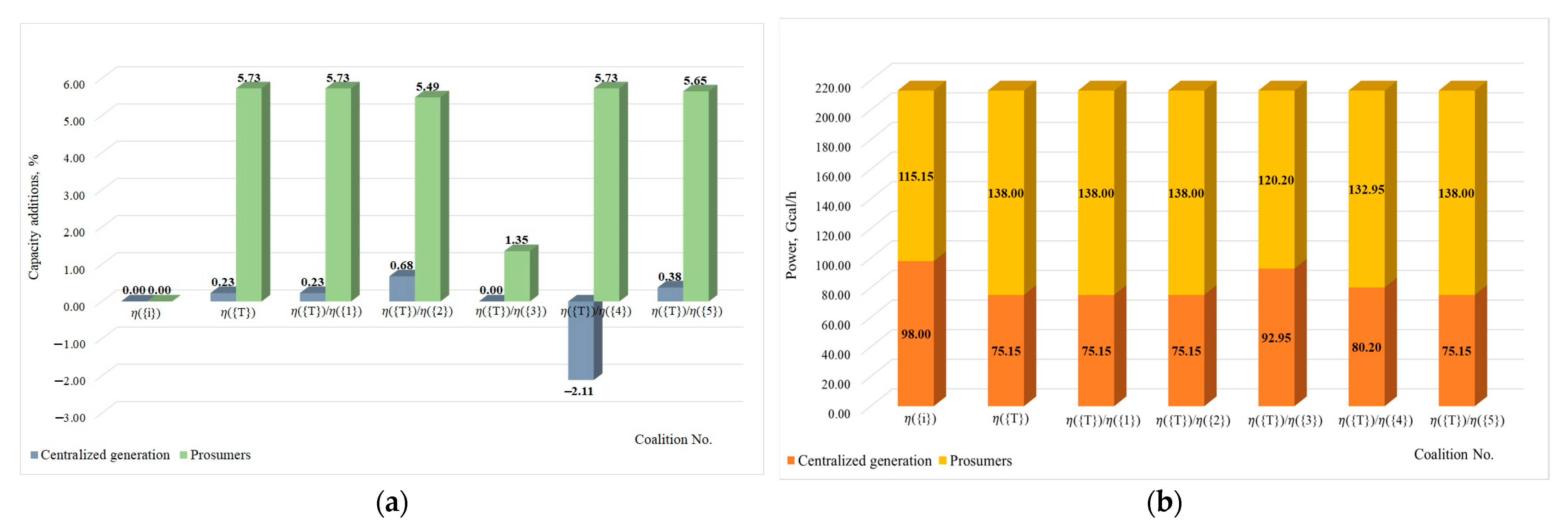
This approach allows for further consideration of coalitional interactions among consumers. This study models consumer cooperation, subject to technical constraints, and considers a set of possible coalitions from which consumers choose the most advantageous one. The outcome is the redistribution of power generation between the centralized and distributed system in the most efficient way.

Another critical element of our system is the built-in module for allocating the payoff of a coalition of consumers. This study considered a wider range of cooperative game solution concepts for coalitions within energy systems than reported elsewhere in the literature. The paper proposed a model for choosing an efficient allocation of the coalition’s payoff according to several criteria that determine how attractive a coalition will be for the players compared to operating on their own.

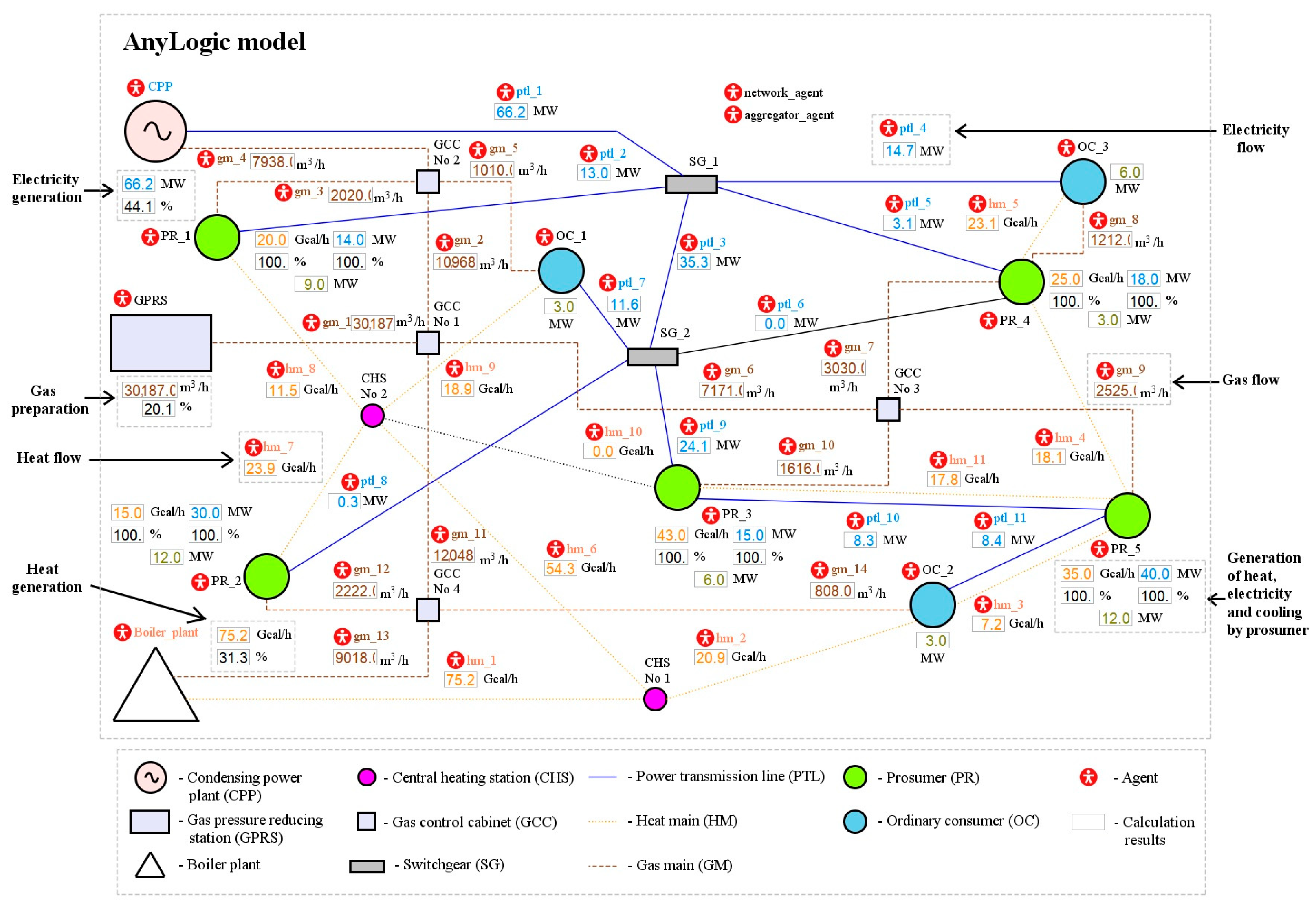
The paper detailed an original multi-agent system that implements the proposed model. The model was tested on a provisional structure of the IES by running multiple simulations. The findings of the simulations demonstrated that it was possible to ensure optimal interaction between the entities of the energy supply process in the IES. This was informed by their interests, which drove such entities to form coalitions of prosumers.

Admittedly, we resort to a number of simplifications in order to solve the investigated problem. Among other things, we assume that we are dealing with quadratic or linear costs for generating sources and convex or linear utility functions of consumers, which yield convex optimization problems with well-established solutions [34]. However, real-world energy systems often exhibit non-convexities (economies of scale, startup costs, start-up and shutdown costs for generating sources, non-linear transportation losses, etc.). This issue can be addressed by applying linearization methods when building the model, as well as by employing metaheuristics [44].

There are many open issues that warrant further development of our approach: 1. The conditions for finding a stable equilibrium should be elaborated further when solving the problem with the best response dynamics procedure as part of the agent-based model. Additional verification of the criteria for reaching equilibrium should be introduced. 2. This study considered a simplified version of coalitions, where it is possible to join only one coalition without considering the possibility of forming several ones on the same set of consumers. 3. It is possible to expand the number of criteria to assess the quality of the allocation of consumers’ payoffs that result from forming a coalition. 4. We need to investigate the setups where a coalition may be beneficial to the energy system as a whole, i.e., yield extra profits to those who do not join the coalition but are part of the system. 5. There are computational issues that will have to be faced when scaling up the system. In the case of large coalitions, the time to compute all outcomes of the cooperative game and determine the equilibrium grows exponentially. In such cases, a possible solution may be to use specialized algorithms that reduce the number of computations. 6. It also makes sense to explore the possibilities of manipulation behaviors by participants, which often arise due to imperfect information. The above list is by no means exhaustive.