On Rayleigh Quotient Iteration for the Dual Quaternion Hermitian Eigenvalue Problem

Abstract

The application of eigenvalue theory to dual quaternion Hermitian matrices holds significance in the realm of multi-agent formation control. In this paper, we study the use of Rayleigh quotient iteration (RQI) for solving the right eigenpairs of dual quaternion Hermitian matrices. Combined with dual representation, the RQI algorithm can effectively compute the eigenvalue along with the associated eigenvector of the dual quaternion Hermitian matrices. Furthermore, by utilizing the minimal residual property of the Rayleigh quotient, a convergence analysis of the Rayleigh quotient iteration is derived. Numerical examples are provided to illustrate the high accuracy and low CPU time cost of the proposed Rayleigh quotient iteration compared with the power method for solving the dual quaternion Hermitian eigenvalue problem.

1. Introduction

This paper concerns the dual quaternion Hermitian right eigenvalue problem

$$\widehat{A}\widehat{\mathbf{x}}=\widehat{\mathbf{x}}\widehat{\lambda },$$

(1)

where $\widehat{A}\in {\mathbb{DQ}}^{n\times n}$ is the objective dual quaternion Hermitian matrix and $\widehat{\lambda }\in \mathbb{DQ}$ and $\widehat{\mathbf{x}}\in {\mathbb{DQ}}^n$ constitute the right eigenpair of $\widehat{A}$.

Dual quaternion numbers and matrices have been widely applied to rigid body motion [1,2,3], hand-eye calibration problems [4,5], simultaneous localization and mapping (SLAM) problems [6,7], and kinematic modeling and control [8]. Qi et al. [9] first introduced a total order and an absolute value function for dual numbers. In addition, they also defined the magnitude of a dual quaternion and extended the norm to dual quaternion vectors. In [10], Qi and Luo investigated the right and left eigenvalues of square dual quaternion matrices. If a right eigenvalue corresponds to a dual number, it is also a left eigenvalue. In such cases, this dual number is referred to as an eigenvalue of the dual quaternion matrix. The researchers demonstrated that the right eigenvalues of a dual quaternion Hermitian matrix are themselves dual numbers, making them valid eigenvalues. Furthermore, it was established that an n-by-n dual quaternion Hermitian matrix possesses precisely n eigenvalues. The unitary decomposition for a dual quaternion Hermitian matrix and singular value decomposition for a general dual quaternion matrix were also proposed. According to the singular value decomposition for a general dual quaternion matrix, Ling et al. [11] defined the rank and appreciable rank of dual quaternion matrices, and some properties were studied. In [8], the significance of the eigenvalue theory of dual quaternion Hermitian matrices in multi-agent formation control was demonstrated.

In [12], Cui and Qi first proposed a power method for efficiently computing the dominant eigenvalue of a dual quaternion Hermitian matrix and reformulated the simultaneous localization and mapping (SLAM) problem as a rank-one dual quaternion completion problem, leveraging the findings from the eigenvalue analysis. So far, the methods for numerically computing the eigenvalues of a dual quaternion Hermitian matrix are still rarely explored.

It is well known that the power method [13] can compute the eigenvalue with the largest magnitude of a matrix. When computing eigenvalues of a Hermitian matrix near a specific target, the most commonly effective methods involve shifted inverse iteration [14] and the Rayleigh quotient iteration (RQI) [15,16]. In particular, RQI uses a shift based on the Rayleigh quotient of the current approximate eigenvector. As a result, RQI exhibits a nonstationary iteration process with a local cubic convergence rate [17,18,19,20,21]. Since RQI has a faster convergence rate, we develop the Rayleigh quotient iteration to compute the eigenpairs of a dual quaternion Hermitian matrix in this paper.

In this paper, we study the problem of solving the right eigenvalues for dual quaternion Hermitian matrices. The main contributions of this paper include the following: Firstly, we propose a Rayleigh quotient iteration (RQI) method for computing the eigenvalue and the associated eigenvector of the dual quaternion Hermitian matrix. Furthermore, by utilizing the minimal residual property of the Rayleigh quotient, a convergence analysis of the Rayleigh quotient iteration is derived. Secondly, we demonstrate the superior accuracy and efficiency of the proposed RQI method for solving the dual quaternion Hermitian eigenvalue problem; e.g., the residual errors are several orders of magnitudes smaller than the power method. Thirdly, we develop the dual representation of the dual quaternion matrix. Specifically, we establish an isomorphic mapping between the dual quaternion matrix and the dual matrix. This dual representation plays a crucial role in solving dual quaternion linear systems. The proposed dual representation also lays a foundation for the development of post-renewal structure-preserving algorithms.

The rest of this paper is organized as follows. In Section 2, we introduce some notations used throughout this paper and review some basic properties of dual quaternion matrices. In Section 3, we derive a dual representation of the dual quaternion matrix. In Section 4, we develop the Rayleigh quotient iteration (RQI) for computing the eigenpairs of dual quaternion Hermitian matrices and provide a convergence analysis. In Section 5, we present numerical experiments on dual quaternion Hermitian eigenvalue problems to illustrate the effectiveness of the proposed method compared with the power method. In Section 6, we summarize the paper.

2. Dual Quaternions and Dual Quaternion Matrices

In this section, some notations and basic definitions are introduced, which will be used in the rest of the paper.

2.1. Dual Numbers, Quaternions and Dual Quaternions

The dual number was introduced by Clifford in 1873 [22]. Denote the set of dual numbers as

$$\mathbb{D}=\left\{q=q_{\mathrm{st}}+q_{\mathcal{I}}ϵ|q_{\mathrm{st}},q_{\mathcal{I}}\in \mathbb{R}\right\},$$

where $ϵ$ is the infinitesimal unit, satisfying ${ϵ}^2=0$. We call $q_{\mathrm{st}}$ the real part or the standard part of q, and $q_{\mathcal{I}}$ the dual part or the infinitesimal part of q. The infinitesimal unit $ϵ$ is commutative in multiplication with real numbers, complex numbers and quaternions. Dual numbers form a commutative algebra of dimension two over the real number field. When $q_{\mathrm{st}}\ne 0$, we say that q is appreciable; otherwise, it is deemed infinitesimal.

The infinitesimal unit $ϵ$ in dual numbers is an algebraic construct representing an infinitesimally small quantity. In fact, $ϵ$ is a formal symbol representing an infinitesimal change. It is not a real number but a mathematical tool that allows us to capture the idea of an infinitely small quantity. In geometry, the infinitesimal element $ϵ$ can be seen as representing an infinitesimal displacement or rotation. This makes dual numbers useful for modeling small transformations in kinematics. The dual quaternion comprises two parts that can describe the rigid-body transformation of one coordinate frame with respect to another, where the standard part and dual part are quaternions representing the rotation and translation, respectively [1,2].

In [9], a total order for dual numbers was introduced. Given two dual numbers $p=p_{\mathrm{st}}+p_{\mathcal{I}}ϵ,q=q_{\mathrm{st}}+q_{\mathcal{I}}ϵ\in \mathbb{D}$, we have $p<q$, if either $p_{\mathrm{st}}<q_{\mathrm{st}}$ or $p_{\mathrm{st}}=q_{\mathrm{st}}$ and $p_{\mathcal{I}}<q_{\mathcal{I}}$. If $p_{\mathrm{st}}=q_{\mathrm{st}}$ and $p_{\mathcal{I}}=q_{\mathcal{I}}$, then $p=q$. Specifically, we call p positive, nonnegative, nonpositive, or negative when it satisfies the conditions $p>0,p\ge 0,p\le 0$ or $p<0$, respectively.

The zero element in $\mathbb{D}$ is $0_D=0+0ϵ$ and the unit element is $1_D=1+0ϵ$. For two dual numbers $p=p_{\mathrm{st}}+p_{\mathcal{I}}ϵ,q=q_{\mathrm{st}}+q_{\mathcal{I}}ϵ\in \mathbb{D}$, addition and multiplication are defined as follows:

$$\begin{array}{cc}\hfill & p+q=p_{\mathrm{st}}+q_{\mathrm{st}}+(p_{\mathcal{I}}+q_{\mathcal{I}})ϵ,\hfill \\ \hfill & pq=p_{\mathrm{st}}{q}_{\mathrm{st}}+(p_{\mathrm{st}}{q}_{\mathcal{I}}+p_{\mathcal{I}}{q}_{\mathrm{st}})ϵ.\hfill \end{array}$$

And the division of p and q is unambiguous if $q_{\mathrm{st}}\ne 0$ is appreciable and takes the form [23]

$${\displaystyle \frac{p_{\mathrm{st}}+p_{\mathcal{I}}ϵ}{q_{\mathrm{st}}+q_{\mathcal{I}}ϵ}}={\displaystyle \frac{p_{\mathrm{st}}}{q_{\mathrm{st}}}}+\left({\displaystyle \frac{p_{\mathcal{I}}}{q_{\mathrm{st}}}}-{\displaystyle \frac{p_{\mathrm{st}}{q}_{\mathcal{I}}}{q_{\mathrm{st}}^2}}\right)ϵ,q_{\mathrm{st}}\ne 0.$$

For an appreciable dual number $q=q_{\mathrm{st}}+q_{\mathcal{I}}ϵ$, it is invertible and

$$q^{-1}=q_{\mathrm{st}}^{-1}-q_{\mathrm{st}}^{-1}{q}_{\mathcal{I}}{q}_{\mathrm{st}}^{-1}ϵ,$$

as indicated by the equation $q{q}^{-1}=q^{-1}q=1$. If q is infinitesimal, then q is not invertible. For two dual numbers $p=p_{\mathrm{st}}+p_{\mathcal{I}}ϵ,q=q_{\mathrm{st}}+q_{\mathcal{I}}ϵ\in \mathbb{D}$, we have

$${\displaystyle \frac{p_{\mathrm{st}}+p_{\mathcal{I}}ϵ}{q_{\mathrm{st}}+q_{\mathcal{I}}ϵ}}={\displaystyle \frac{p_{\mathrm{st}}}{q_{\mathrm{st}}}}+\left({\displaystyle \frac{p_{\mathcal{I}}}{q_{\mathrm{st}}}}-{\displaystyle \frac{p_{\mathrm{st}}{q}_{\mathcal{I}}}{q_{\mathrm{st}}^2}}\right)ϵ=(p_{\mathrm{st}}+p_{\mathcal{I}}ϵ)q^{-1},q_{\mathrm{st}}\ne 0.$$

One can observe that the division of dual numbers is the inverse operation of the multiplication of dual numbers.

For a nonnegative and appreciable dual number q, the square root of q is also a nonnegative dual number. If q is positive and appreciable, then

$$\sqrt{q}=\sqrt{q_{\mathrm{st}}}+{\displaystyle \frac{q_{\mathcal{I}}}{2\sqrt{q_{\mathrm{st}}}}}ϵ.$$

The absolute value of $p=p_{\mathrm{st}}+p_{\mathcal{I}}ϵ\in \mathbb{D}$ is defined as

$$\left|p\right|=\left\{\begin{array}{cc}\left|p_{\mathrm{st}}\right|+sgn\left(p_{\mathrm{st}}\right)p_{\mathcal{I}}ϵ,\hfill & \mathrm{if}{p}_{\mathrm{st}}\ne 0,\hfill \\ \left|p_{\mathcal{I}}\right|ϵ,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

where “$sgn(·)$” is given by

$$sgn\left(a\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}a>0,\hfill \\ 0,\hfill & \mathrm{if}a=0,\hfill \\ -1,\hfill & \mathrm{if}a<0,\hfill \end{array}\right.\forall a\in \mathbb{R}.$$

For more details on dual numbers, see [9] and the references therein.

Denote the set of quaternions as

$$\mathbb{Q}=\left\{\tilde{q}=q_1+q_2\mathbf{i}+q_3\mathbf{j}+q_4\mathbf{k}|q_1,q_2,q_3,q_4\in \mathbb{R}\right\},$$

where $\mathbf{i},\mathbf{j},\mathbf{k}$ are three imaginary units of quaternions, satisfying

$$\begin{array}{cc}\hfill & {\mathbf{i}}^2={\mathbf{j}}^2={\mathbf{k}}^2=\mathbf{ijk}=-1,\hfill \\ \hfill & \mathbf{ij}=-\mathbf{ji}=\mathbf{k},\mathbf{jk}=-\mathbf{kj}=\mathbf{i},\mathbf{ki}=-\mathbf{ik}=\mathbf{j}.\hfill \end{array}$$

The real part of $\tilde{q}$ is $\mathrm{Re}\left(\tilde{q}\right)=q_1$. The imaginary part of $\tilde{q}$ is $\mathrm{Im}\left(\tilde{q}\right)=q_2\mathbf{i}+q_3\mathbf{j}+q_4\mathbf{k}$. A quaternion is called imaginary when its real part is equal to zero. The multiplication of quaternions adheres to the distributive law but is noncommutative.

The zero element in $\mathbb{Q}$ is $\tilde{0}=0+0\mathbf{i}+0\mathbf{j}+0\mathbf{k}$ and the unit element is $\tilde{1}=1+0\mathbf{i}+0\mathbf{j}+0\mathbf{k}$. For any $\tilde{q}=q_1+q_2\mathbf{i}+q_3\mathbf{j}+q_4\mathbf{k}\in \mathbb{Q}$, the conjugate of a quaternion is defined as

$${\tilde{q}}^{*}=q_1-q_2\mathbf{i}-q_3\mathbf{j}-q_4\mathbf{k}.$$

The magnitude of $\tilde{q}$ is $|\tilde{q}|=\sqrt{{\tilde{q}}^{*}\tilde{q}}=\sqrt{q_1^2+q_2^2+q_3^2+q_4^2}$, and it follows that the inverse of a nonzero quaternion $\tilde{q}$ is given by ${\tilde{q}}^{-1}={\tilde{q}}^{*}/{\left|\tilde{q}\right|}^2$.

Denote the set of dual quaternions as

$$\mathbb{DQ}=\left\{\widehat{q}={\tilde{q}}_{\mathrm{st}}+{\tilde{q}}_{\mathcal{I}}ϵ|{\tilde{q}}_{\mathrm{st}},{\tilde{q}}_{\mathcal{I}}\in \mathbb{Q}\right\}.$$

Similarly, we call ${\tilde{q}}_{\mathrm{st}},{\tilde{q}}_{\mathcal{I}}$ the standard part and the dual part of $\widehat{q}$, respectively. If ${\tilde{q}}_{\mathrm{st}}\ne 0$, then $\widehat{q}$ is appreciable; otherwise, $\widehat{q}$ is infinitesimal. Let $\widehat{p}={\tilde{p}}_{\mathrm{st}}+{\tilde{p}}_{\mathcal{I}}ϵ,\widehat{q}={\tilde{q}}_{\mathrm{st}}+{\tilde{q}}_{\mathcal{I}}ϵ\in \mathbb{DQ}$, then the addition of $\widehat{p}$ and $\widehat{q}$ is

$$\widehat{p}+\widehat{q}={\tilde{p}}_{\mathrm{st}}+{\tilde{q}}_{\mathrm{st}}+({\tilde{p}}_{\mathcal{I}}+{\tilde{q}}_{\mathcal{I}})ϵ$$

and the product of $\widehat{p}$ and $\widehat{q}$ is

$$\widehat{p}\widehat{q}={\tilde{p}}_{\mathrm{st}}{\tilde{q}}_{\mathrm{st}}+({\tilde{p}}_{\mathrm{st}}{\tilde{q}}_{\mathcal{I}}+{\tilde{p}}_{\mathcal{I}}{\tilde{q}}_{\mathrm{st}})ϵ.$$

The zero element in $\mathbb{DQ}$ is $\widehat{0}=\tilde{0}+\tilde{0}ϵ$ and the unit element is $\widehat{1}=\tilde{1}+\tilde{0}ϵ$. In general, $\widehat{p}\widehat{q}\ne \widehat{q}\widehat{p}$. The conjugate of $\widehat{p}={\tilde{p}}_{\mathrm{st}}+{\tilde{p}}_{\mathcal{I}}ϵ$ is ${\widehat{p}}^{*}={\tilde{p}}_{\mathrm{st}}^{*}+{\tilde{p}}_{\mathcal{I}}^{*}ϵ$. A dual quaternion $\widehat{q}={\tilde{q}}_{\mathrm{st}}+{\tilde{q}}_{\mathcal{I}}ϵ$ is invertible if and only if $\widehat{q}$ is appreciable. In this case, we have

$${\widehat{q}}^{-1}={\tilde{q}}_{\mathrm{st}}^{-1}-{\tilde{q}}_{\mathrm{st}}^{-1}{\tilde{q}}_{\mathcal{I}}{\tilde{q}}_{\mathrm{st}}^{-1}ϵ.$$

The magnitude of $\widehat{q}$ is defined as

$$\left|\widehat{q}\right|=\left\{\begin{array}{cc}\left|{\tilde{q}}_{\mathrm{st}}\right|+{\displaystyle \frac{{\tilde{q}}_{\mathrm{st}}{\tilde{q}}_{\mathcal{I}}^{*}+{\tilde{q}}_{\mathcal{I}}{\tilde{q}}_{\mathrm{st}}^{*}}{2\left|{\tilde{q}}_{\mathrm{st}}\right|}}ϵ,\hfill & \mathrm{if}{\tilde{q}}_{\mathrm{st}}\ne 0,\hfill \\ \left|{\tilde{q}}_{\mathcal{I}}\right|ϵ,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

which is a dual number. A dual quaternion $\widehat{q}={\tilde{q}}_{\mathrm{st}}+{\tilde{q}}_{\mathcal{I}}ϵ$ is called a unit dual quaternion if

$$\left|{\tilde{q}}_{\mathrm{st}}\right|=1\mathrm{and}{\tilde{q}}_{\mathrm{st}}{\tilde{q}}_{\mathcal{I}}^{*}+{\tilde{q}}_{\mathcal{I}}{\tilde{q}}_{\mathrm{st}}^{*}=0.$$

Further, for any dual quaternion number $\widehat{q}={\tilde{q}}_{\mathrm{st}}+{\tilde{q}}_{\mathcal{I}}ϵ\in \mathbb{DQ}$ and dual number $a=a_{\mathrm{st}}+a_{\mathcal{I}}ϵ\in \mathbb{D}$, there is

$${\displaystyle \frac{\widehat{q}}{a}}={\displaystyle \frac{{\tilde{q}}_{\mathrm{st}}+{\tilde{q}}_{\mathcal{I}}ϵ}{a_{\mathrm{st}}+a_{\mathcal{I}}ϵ}}={\displaystyle \frac{{\tilde{q}}_{\mathrm{st}}}{a_{\mathrm{st}}}}+\left({\displaystyle \frac{{\tilde{q}}_{\mathcal{I}}}{a_{\mathrm{st}}}}-{\displaystyle \frac{{\tilde{q}}_{\mathrm{st}}}{a_{\mathrm{st}}}}{\displaystyle \frac{a_{\mathcal{I}}}{a_{\mathrm{st}}}}\right)ϵ,a_{\mathrm{st}}\ne 0.$$

2.2. Dual Quaternion Matrices

Denote the set of dual quaternion matrices as

$${\mathbb{DQ}}^{m\times n}=\left\{\widehat{A}={\tilde{A}}_{\mathrm{st}}+{\tilde{A}}_{\mathcal{I}}ϵ|{\tilde{A}}_{\mathrm{st}},{\tilde{A}}_{\mathcal{I}}\in {\mathbb{Q}}^{m\times n}\right\}.$$

Again, we call ${\tilde{A}}_{\mathrm{st}},{\tilde{A}}_{\mathcal{I}}$ the standard part and the dual part of $\widehat{A}$, respectively. The conjugate transpose of $\widehat{A}$ is ${\widehat{A}}^{*}={\tilde{A}}_{\mathrm{st}}^{*}+{\tilde{A}}_{\mathcal{I}}^{*}ϵ$.

The zero matrix in ${\mathbb{DQ}}^{m\times n}$ is $\widehat{\mathbf{O}}=\tilde{\mathbf{O}}+\tilde{\mathbf{O}}ϵ$ and the identity matrix is $\widehat{\mathbf{I}}=\tilde{\mathbf{I}}+\tilde{\mathbf{O}}ϵ$. We say that a square dual quaternion matrix $\widehat{A}\in {\mathbb{DQ}}^{n\times n}$ is normal if ${\widehat{A}}^{*}\widehat{A}=\widehat{A}{\widehat{A}}^{*}$; Hermitian if ${\widehat{A}}^{*}=\widehat{A}$; unitary if ${\widehat{A}}^{*}\widehat{A}=I$, where I is the identity matrix; and invertible (nonsingular) if there exists a matrix $\widehat{B}\in {\mathbb{DQ}}^{n\times n}$ such that $\widehat{A}\widehat{B}=\widehat{B}\widehat{A}=I$. In this case, we denote ${\widehat{A}}^{-1}=\widehat{B}$. We have ${\left(\widehat{A}\widehat{B}\right)}^{-1}={\widehat{B}}^{-1}{\widehat{A}}^{-1}$ if $\widehat{A}$ and $\widehat{B}$ are invertible, and ${\left({\widehat{A}}^{*}\right)}^{-1}={\left({\widehat{A}}^{-1}\right)}^{*}$ if $\widehat{A}$ is invertible.

Given a dual quaternion Hermitian matrix $\widehat{A}\in {\mathbb{DQ}}^{n\times n}$, for any $\widehat{\mathbf{x}}\in {\mathbb{DQ}}^n$, the following equality holds:

$${\left({\widehat{\mathbf{x}}}^{*}\widehat{A}\widehat{\mathbf{x}}\right)}^{*}={\widehat{\mathbf{x}}}^{*}\widehat{A}\widehat{\mathbf{x}}.$$

This implies that ${\widehat{\mathbf{x}}}^{*}\widehat{A}\widehat{\mathbf{x}}$ is a dual number. A dual quaternion Hermitian matrix $\widehat{A}\in {\mathbb{DQ}}^{n\times n}$ is called positive semidefinite if for any $\widehat{\mathbf{x}}\in {\mathbb{DQ}}^n,{\widehat{\mathbf{x}}}^{*}\widehat{A}\widehat{\mathbf{x}}\ge \widehat{0}$; $\widehat{A}$ is called positive definite if for any $\widehat{\mathbf{x}}\in {\mathbb{DQ}}^n$ with $\widehat{\mathbf{x}}$ being appreciable, we have ${\widehat{\mathbf{x}}}^{*}\widehat{A}\widehat{\mathbf{x}}>\widehat{0}$ and is appreciable. A square quaternion matrix $\widehat{A}\in {\mathbb{DQ}}^{n\times n}$ is unitary if and only if its column (row) vectors constitute an orthogonal basis of ${\mathbb{DQ}}^n$.

The 2-norm of a dual quaternion vector $\widehat{\mathbf{x}}={({\widehat{x}}_1,\cdots ,{\widehat{x}}_n)}^{\top }\in {\mathbb{DQ}}^{n\times 1}$ is

$${\parallel \widehat{\mathbf{x}}\parallel }_2=\left\{\begin{array}{cc}\sqrt{{\sum }_{i=1}^n{\left|{\widehat{x}}_i\right|}^2},\hfill & \mathrm{if}{\tilde{\mathbf{x}}}_{\mathrm{st}}\ne \tilde{\mathbf{0}},\hfill \\ \sqrt{{\sum }_{i=1}^n{\left|{\tilde{x}}_{i,\mathcal{I}}\right|}^2}ϵ,\hfill & \mathrm{if}{\tilde{\mathbf{x}}}_{\mathrm{st}}=\tilde{\mathbf{0}}\mathrm{and}\widehat{\mathbf{x}}={\tilde{\mathbf{x}}}_{\mathcal{I}}ϵ.\hfill \end{array}\right.$$

For two given dual quaternion vectors $\widehat{\mathbf{x}}={\left({\widehat{x}}_1,{\widehat{x}}_2,\dots ,{\widehat{x}}_n\right)}^{\top },\widehat{\mathbf{y}}={\left({\widehat{y}}_1,{\widehat{y}}_2,\dots ,{\widehat{y}}_n\right)}^{\top }\in {\mathbb{DQ}}^n$, the dual quaternion-valued inner product $\langle \widehat{\mathbf{x}},\widehat{\mathbf{y}}\rangle$ is defined as

$$\langle \widehat{\mathbf{x}},\widehat{\mathbf{y}}\rangle ={\widehat{\mathbf{y}}}^{*}\widehat{\mathbf{x}}=\sum _{i=1}^n{\widehat{y}}_i^{*}{\widehat{x}}_i.$$

It is easy to see that $\langle \widehat{\mathbf{x}}\widehat{a}+\widehat{\mathbf{z}}\widehat{b},\widehat{\mathbf{y}}\rangle =\langle \widehat{\mathbf{x}},\widehat{\mathbf{y}}\rangle \widehat{a}+\langle \widehat{\mathbf{z}},\widehat{\mathbf{y}}\rangle \widehat{b}$ and $\langle \widehat{\mathbf{x}},\widehat{\mathbf{y}}\rangle ={\langle \widehat{\mathbf{y}},\widehat{\mathbf{x}}\rangle }^{*}$ for any $\widehat{\mathbf{x}},\widehat{\mathbf{y}},\widehat{\mathbf{z}}\in {\mathbb{DQ}}^n$ and $\widehat{a},\widehat{b}\in \mathbb{DQ}$. We say that $\widehat{\mathbf{x}}$ and $\widehat{\mathbf{y}}$ are orthogonal to each other if $\langle \widehat{\mathbf{x}},\widehat{\mathbf{y}}\rangle =0$, denoted by $\widehat{\mathbf{x}}\perp \widehat{\mathbf{y}}$. And for any $\widehat{\mathbf{x}}\in {\mathbb{DQ}}^n$, $\langle \widehat{\mathbf{x}},\widehat{\mathbf{x}}\rangle$ is a nonnegative dual number, and if $\widehat{\mathbf{x}}$ is appreciable, $\langle \widehat{\mathbf{x}},\widehat{\mathbf{x}}\rangle$ is a positive dual number [9].

Lemma 1. 

Given an appreciable dual quaternion vector $\widehat{\mathbf{x}}\in {\mathbb{DQ}}^n$, the norm ${\parallel ·\parallel }_2$ is induced by the inner product, i.e., ${\parallel \widehat{\mathbf{x}}\parallel }_2=\sqrt{\langle \widehat{\mathbf{x}},\widehat{\mathbf{x}}\rangle }$.

Proof. 

Write $\widehat{\mathbf{x}}={\tilde{\mathbf{x}}}_{\mathrm{st}}+{\tilde{\mathbf{x}}}_{\mathcal{I}}ϵ={({\widehat{x}}_1,\cdots ,{\widehat{x}}_n)}^{\top }\in {\mathbb{DQ}}^n$. The dual quaternion-valued inner product $\langle \widehat{\mathbf{x}},\widehat{\mathbf{x}}\rangle$ is defined by

$$\langle \widehat{\mathbf{x}},\widehat{\mathbf{x}}\rangle ={\widehat{\mathbf{x}}}^{*}\widehat{\mathbf{x}}=\sum _{i=1}^n{\widehat{x}}_i^{*}{\widehat{x}}_i,$$

and the 2-norm of $\widehat{\mathbf{x}}$ is defined by

$${\parallel \widehat{\mathbf{x}}\parallel }_2=\sqrt{\sum _{i=1}^n{\left|{\widehat{x}}_i\right|}^2},\mathrm{if}{\tilde{\mathbf{x}}}_{\mathrm{st}}\ne \tilde{\mathbf{0}}.$$

Let ${\widehat{x}}_i={\tilde{x}}_{i,\mathrm{st}}+{\tilde{x}}_{i,\mathcal{I}}ϵ\in \mathbb{DQ}$, $\forall i=1,2,\cdots ,n$. Then, it is easily verified that

$${\widehat{x}}_i^{*}{\widehat{x}}_i=({\tilde{x}}_{i,\mathrm{st}}^{*}+{\tilde{x}}_{i,\mathcal{I}}^{*}ϵ)({\tilde{x}}_{i,\mathrm{st}}+{\tilde{x}}_{i,\mathcal{I}}ϵ)={\tilde{x}}_{i,\mathrm{st}}^{*}{\tilde{x}}_{i,\mathrm{st}}+({\tilde{x}}_{i,\mathrm{st}}^{*}{\tilde{x}}_{i,\mathcal{I}}+{\tilde{x}}_{i,\mathcal{I}}^{*}{\tilde{x}}_{i,\mathrm{st}})ϵ,$$

and

$${\left|{\widehat{x}}_i\right|}^2={\left(\left|{\tilde{x}}_{i,\mathrm{st}}\right|+{\displaystyle \frac{{\tilde{x}}_{i,\mathrm{st}}{\tilde{x}}_{i,\mathcal{I}}^{*}+{\tilde{x}}_{i,\mathcal{I}}{\tilde{x}}_{i,\mathrm{st}}^{*}}{2\left|{\tilde{x}}_{i,\mathrm{st}}\right|}}ϵ\right)}^2={\left|{\tilde{x}}_{i,\mathrm{st}}\right|}^2+({\tilde{x}}_{i,\mathrm{st}}^{*}{\tilde{x}}_{i,\mathcal{I}}+{\tilde{x}}_{i,\mathcal{I}}^{*}{\tilde{x}}_{i,\mathrm{st}})ϵ={\widehat{x}}_i^{*}{\widehat{x}}_i.$$

which implies that ${\widehat{x}}_i^{*}{\widehat{x}}_i={\left|{\widehat{x}}_i\right|}^2$. This completes the proof.    □

Lemma 2. 

Given two dual quaternion vectors $\mathbf{x},\mathbf{y}\in {\mathbb{DQ}}^n$, the following properties hold:

(1) 

${\parallel \widehat{\mathbf{x}}\parallel }_2={\parallel {\widehat{\mathbf{x}}}^{*}\parallel }_2$;

(2) 

${\parallel \widehat{\mathbf{x}}+\widehat{\mathbf{y}}\parallel }_2^2=\parallel \widehat{\mathbf{x}}{\parallel }_2^2+{\parallel \widehat{\mathbf{y}}\parallel }_2^2+\langle \widehat{\mathbf{x}},\widehat{\mathbf{y}}\rangle +\langle \widehat{\mathbf{y}},\widehat{\mathbf{x}}\rangle$

Proof. 

The property (1) is obvious and is omitted here. If

$$\widehat{\mathbf{x}}={({\widehat{x}}_1,\cdots ,{\widehat{x}}_n)}^{\top },\widehat{\mathbf{y}}={({\widehat{y}}_1,\cdots ,{\widehat{y}}_n)}^{\top }\in {\mathbb{DQ}}^{n\times 1},$$

where ${\widehat{x}}_i={\tilde{x}}_{i,\mathrm{st}}+{\tilde{x}}_{i,\mathcal{I}}ϵ$, ${\widehat{y}}_i={\tilde{y}}_{i,\mathrm{st}}+{\tilde{y}}_{i,\mathcal{I}}ϵ\in \mathbb{DQ}$, then we have

$$\begin{array}{cc}\hfill {|{\widehat{x}}_i+{\widehat{y}}_i|}^2& ={\left(\left|{\tilde{x}}_{i,\mathrm{st}}+{\tilde{y}}_{i,\mathrm{st}}\right|+{\displaystyle \frac{({\tilde{x}}_{i,\mathrm{st}}+{\tilde{y}}_{i,\mathrm{st}})({\tilde{x}}_{i,\mathcal{I}}^{*}+{\tilde{y}}_{i,\mathcal{I}}^{*})+({\tilde{x}}_{i,\mathcal{I}}+{\tilde{y}}_{i,\mathcal{I}})({\tilde{x}}_{i,\mathrm{st}}^{*}+{\tilde{y}}_{i,\mathrm{st}}^{*})}{2\left|{\tilde{x}}_{i,\mathrm{st}}+{\tilde{y}}_{i,\mathrm{st}}\right|}}ϵ\right)}^2\hfill \\ \hfill & ={|{\tilde{x}}_{i,\mathrm{st}}+{\tilde{y}}_{i,\mathrm{st}}|}^2+(({\tilde{x}}_{i,\mathrm{st}}+{\tilde{y}}_{i,\mathrm{st}})({\tilde{x}}_{i,\mathcal{I}}^{*}+{\tilde{y}}_{i,\mathcal{I}}^{*})+({\tilde{x}}_{i,\mathcal{I}}+{\tilde{y}}_{i,\mathcal{I}})({\tilde{x}}_{i,\mathrm{st}}^{*}+{\tilde{y}}_{i,\mathrm{st}}^{*}))ϵ\hfill \\ \hfill & =({\tilde{x}}_{i,\mathrm{st}}^{*}+{\tilde{y}}_{i,\mathrm{st}}^{*})({\tilde{x}}_{i,\mathrm{st}}+{\tilde{y}}_{i,\mathrm{st}})+(({\tilde{x}}_{i,\mathrm{st}}+{\tilde{y}}_{i,\mathrm{st}})({\tilde{x}}_{i,\mathcal{I}}^{*}+{\tilde{y}}_{i,\mathcal{I}}^{*})+({\tilde{x}}_{i,\mathcal{I}}+{\tilde{y}}_{i,\mathcal{I}})({\tilde{x}}_{i,\mathrm{st}}^{*}+{\tilde{y}}_{i,\mathrm{st}}^{*}))ϵ\hfill \\ \hfill & ={\left|{\tilde{x}}_{i,\mathrm{st}}\right|}^2+{\left|{\tilde{y}}_{i,\mathrm{st}}\right|}^2+{\tilde{y}}_{i,\mathrm{st}}^{*}{\tilde{x}}_{i,\mathrm{st}}+{\tilde{x}}_{i,\mathrm{st}}^{*}{\tilde{y}}_{i,\mathrm{st}}+(({\tilde{x}}_{i,\mathrm{st}}+{\tilde{y}}_{i,\mathrm{st}})({\tilde{x}}_{i,\mathcal{I}}^{*}+{\tilde{y}}_{i,\mathcal{I}}^{*})+({\tilde{x}}_{i,\mathcal{I}}\hfill \\ \hfill & +{\tilde{y}}_{i,\mathcal{I}}\left)({\tilde{x}}_{i,\mathrm{st}}^{*}+{\tilde{y}}_{i,\mathrm{st}}^{*})\right)ϵ\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & |{\widehat{x}}_i{|}^2={\left|{\tilde{x}}_{i,\mathrm{st}}\right|}^2+({\tilde{x}}_{i,\mathrm{st}}^{*}{\tilde{x}}_{i,\mathcal{I}}+{\tilde{x}}_{i,\mathcal{I}}^{*}{\tilde{x}}_{i,\mathrm{st}})ϵ,\hfill \\ \hfill & |{\widehat{y}}_i{|}^2={\left|{\tilde{y}}_{i,\mathrm{st}}\right|}^2+({\tilde{y}}_{i,\mathrm{st}}^{*}{\tilde{y}}_{i,\mathcal{I}}+{\tilde{y}}_{i,\mathcal{I}}^{*}{\tilde{y}}_{i,\mathrm{st}})ϵ,\hfill \\ \hfill & {\widehat{y}}_i^{*}{\widehat{x}}_i={\tilde{y}}_{i,\mathrm{st}}^{*}{\tilde{x}}_{i,\mathrm{st}}+({\tilde{y}}_{i,\mathrm{st}}^{*}{\tilde{x}}_{i,\mathcal{I}}+{\tilde{y}}_{i,\mathcal{I}}^{*}{\tilde{x}}_{i,\mathrm{st}})ϵ,\hfill \\ \hfill & {\widehat{x}}_i^{*}{\widehat{y}}_i={\tilde{x}}_{i,\mathrm{st}}^{*}{\tilde{y}}_{i,\mathrm{st}}+({\tilde{x}}_{i,\mathrm{st}}^{*}{\tilde{y}}_{i,\mathcal{I}}+{\tilde{x}}_{i,\mathcal{I}}^{*}{\tilde{y}}_{i,\mathrm{st}})ϵ.\hfill \end{array}$$

It is easily verified that

$$|{\widehat{x}}_i+{\widehat{y}}_i{|}^2=|{\widehat{x}}_i{|}^2+{\left|{\widehat{y}}_i\right|}^2+{\widehat{y}}_i^{*}{\widehat{x}}_i+{\widehat{x}}_i^{*}{\widehat{y}}_i.$$

This completes the proof.    □

To measure the error in computations, we use norms defined over the real numbers, specifically the $2^R$-norm and $F^R$-norm. These norms were first defined in [12]. We review their definitions here. The $2^R$-norm of a dual quaternion vector $\widehat{\mathbf{x}}\in {\mathbb{DQ}}^{n\times 1}$ is defined as

$${\parallel \widehat{\mathbf{x}}\parallel }_{2^R}=\sqrt{{∥{\tilde{\mathbf{x}}}_{\mathrm{st}}∥}_2^2+{∥{\tilde{\mathbf{x}}}_{\mathcal{I}}∥}_2^2},$$

and the $F^R$-norm of a dual quaternion matrix $\widehat{A}\in {\mathbb{DQ}}^{m\times n}$ is defined as

$${\parallel \widehat{A}\parallel }_{F^R}=\sqrt{{\parallel {\tilde{A}}_{\mathrm{st}}\parallel }_F^2+{\parallel {\tilde{A}}_{\mathcal{I}}\parallel }_F^2}.$$

The $2^R$-norm and $F^R$-norm defined here do not strictly satisfy the norm definition because they do not meet the scaling condition of norms. We use them this way only for computational convenience.

For a given dual quaternion matrix $\widehat{A}\in {\mathbb{DQ}}^{n\times n}$. If there are $\widehat{\lambda }\in \mathbb{DQ}$, $\widehat{\mathbf{x}}\in {\mathbb{DQ}}^{n\times 1}$, where $\widehat{\mathbf{x}}$ is appreciable, such that

$$\widehat{A}\widehat{\mathbf{x}}=\widehat{\lambda }\widehat{\mathbf{x}},$$

then we say that $\widehat{\lambda }$ is a left eigenvalue of A, with $\widehat{\mathbf{x}}$ as an associated left eigenvector. If

$$\widehat{A}\widehat{\mathbf{x}}=\widehat{\mathbf{x}}\widehat{\lambda },$$

then we say that $\widehat{\lambda }$ is a right eigenvalue of A, with $\widehat{\mathbf{x}}$ as an associated right eigenvector. Based on Theorem 4.2 in [10], a dual quaternion Hermitian matrix $\widehat{A}\in {\mathbb{DQ}}^{n\times n}$ has exactly n eigenvalues (with associated n eigenvectors), which are dual numbers.

3. Dual Representation of the Dual Quaternion Matrix

In this section, we put forward a dual matrix isomorphic representation form of dual quaternion matrices.

Theorem 1. 

For any dual quaternion matrix $\widehat{A}={\tilde{A}}_{\mathrm{st}}+{\tilde{A}}_{\mathcal{I}}ϵ\in {\mathbb{DQ}}^{m\times n}$, where ${\tilde{A}}_{\mathrm{st}}=A_1+A_2\mathbf{i}+A_3\mathbf{j}+A_4\mathbf{k},{\tilde{A}}_{\mathcal{I}}={\overline{A}}_1+{\overline{A}}_2\mathbf{i}+{\overline{A}}_3\mathbf{j}+{\overline{A}}_4\mathbf{k}\in {\mathbb{Q}}^{m\times n}$ and $A_i,{\overline{A}}_i\in {\mathbb{R}}^{m\times n},i=1,2,3,4$. Define the map

$$\begin{array}{cc}\hfill \sigma :& {\mathbb{DQ}}^{m\times n}\to {\mathbb{D}}^{4m\times 4n},\hfill \\ \hfill & \widehat{A}\mapsto {\widehat{A}}^{\sigma }=\left[\begin{array}{cccc}{A}_1+{\overline{A}}_1ϵ& A_3+{\overline{A}}_3ϵ& A_2+{\overline{A}}_2ϵ& A_4+{\overline{A}}_4ϵ\\ -A_3-{\overline{A}}_3ϵ& A_1+{\overline{A}}_1ϵ& A_4+{\overline{A}}_4ϵ& -A_2-{\overline{A}}_2ϵ\\ -A_2-{\overline{A}}_2ϵ& -A_4-{\overline{A}}_4ϵ& A_1+{\overline{A}}_1ϵ& A_3+{\overline{A}}_3ϵ\\ -A_4-{\overline{A}}_4ϵ& A_2+{\overline{A}}_2ϵ& -A_3-{\overline{A}}_3ϵ& A_1+{\overline{A}}_1ϵ\end{array}\right].\hfill \end{array}$$

(2)

The map σ is an isomorphic mapping from ${\mathbb{DQ}}^{m\times n}$ to ${\mathbb{D}}^{4m\times 4n}$.

Proof. 

It is easy to know that $\sigma$ is a one-to-one mapping from ${\mathbb{DQ}}^{m\times n}$ to ${\mathbb{D}}^{4m\times 4n}$. Then, for any dual quaternion matrix $\widehat{C}={\tilde{C}}_{\mathrm{st}}+{\tilde{C}}_{\mathcal{I}ϵ}\in {\mathbb{DQ}}^{n\times s}$, where ${\tilde{C}}_{\mathrm{st}}=C_1+C_2\mathbf{i}+C_3\mathbf{j}+C_4\mathbf{k},{\tilde{C}}_{\mathcal{I}}={\overline{C}}_1+{\overline{C}}_2\mathbf{i}+{\overline{C}}_3\mathbf{j}+{\overline{C}}_4\mathbf{k}\in {\mathbb{Q}}^{n\times s}$, we have

$$\widehat{A}\widehat{C}=({\tilde{A}}_{\mathrm{st}}+{\tilde{A}}_{\mathcal{I}}ϵ)({\tilde{C}}_{\mathrm{st}}+{\tilde{C}}_{\mathcal{I}}ϵ)={\tilde{A}}_{\mathrm{st}}{\tilde{C}}_{\mathrm{st}}+({\tilde{A}}_{\mathrm{st}}{\tilde{C}}_{\mathcal{I}}+{\tilde{A}}_{\mathcal{I}}{\tilde{C}}_{\mathrm{st}})ϵ.$$

(3)

On the one hand, consider the standard part of the equality (3), we have

$$\begin{array}{cc}\hfill {\tilde{A}}_{\mathrm{st}}{\tilde{C}}_{\mathrm{st}}& =(A_1+A_2\mathbf{i}+A_3\mathbf{j}+A_4\mathbf{k})(C_1+C_2\mathbf{i}+C_3\mathbf{j}+C_4\mathbf{k})\hfill \\ \hfill & =A_1{C}_1-A_2{C}_2-A_3{C}_3-A_4{C}_4+(A_1{C}_2+A_2{C}_1+A_3{C}_4-A_4{C}_3)\mathbf{i}\hfill \\ \hfill & +(A_1{C}_3-A_2{C}_4+A_3{C}_1+A_4{C}_2)\mathbf{j}+(A_1{C}_4+A_2{C}_3-A_3{C}_2+A_4{C}_1)\mathbf{k},\hfill \end{array}$$

and consider the dual part of the equality (3); we obtain

$$\begin{array}{cc}\hfill {\tilde{A}}_{\mathrm{st}}{\tilde{C}}_{\mathcal{I}}+{\tilde{A}}_{\mathcal{I}}{\tilde{C}}_{\mathrm{st}}& =(A_1+A_2\mathbf{i}+A_3\mathbf{j}+A_4\mathbf{k})({\overline{C}}_1+{\overline{C}}_2\mathbf{i}+{\overline{C}}_3\mathbf{j}+{\overline{C}}_4\mathbf{k})\hfill \\ \hfill & +({\overline{A}}_1+{\overline{A}}_2\mathbf{i}+{\overline{A}}_3\mathbf{j}+{\overline{A}}_4\mathbf{k})(C_1+C_2\mathbf{i}+C_3\mathbf{j}+C_4\mathbf{k})\hfill \\ \hfill & =A_1{\overline{C}}_1-A_2{\overline{C}}_2-A_3{\overline{C}}_3-A_4{\overline{C}}_4+(A_1{\overline{C}}_2+A_2{\overline{C}}_1+A_3{\overline{C}}_4-A_4{\overline{C}}_3)\mathbf{i}\hfill \\ \hfill & +(A_1{\overline{C}}_3-A_2{\overline{C}}_4+A_3{\overline{C}}_1+A_4{\overline{C}}_2)\mathbf{j}+(A_1{\overline{C}}_4+A_2{\overline{C}}_3-A_3{\overline{C}}_2+A_4{\overline{C}}_1)\mathbf{k}\hfill \\ \hfill & +{\overline{A}}_1{C}_1-{\overline{A}}_2{C}_2-{\overline{A}}_3{C}_3-{\overline{A}}_4{C}_4+({\overline{A}}_1{C}_2+{\overline{A}}_2{C}_1+{\overline{A}}_3{C}_4-{\overline{A}}_4{C}_3)\mathbf{i}\hfill \\ \hfill & +({\overline{A}}_1{C}_3-{\overline{A}}_2{C}_4+{\overline{A}}_3{C}_1+{\overline{A}}_4{C}_2)\mathbf{j}+({\overline{A}}_1{C}_4+{\overline{A}}_2{C}_3-{\overline{A}}_3{C}_2+{\overline{A}}_4{C}_1)\mathbf{k}\hfill \\ \hfill & =A_1{\overline{C}}_1-A_2{\overline{C}}_2-A_3{\overline{C}}_3-A_4{\overline{C}}_4+{\overline{A}}_1{C}_1-{\overline{A}}_2{C}_2-{\overline{A}}_3{C}_3-{\overline{A}}_4{C}_4\hfill \\ \hfill & +(A_1{\overline{C}}_2+A_2{\overline{C}}_1+A_3{\overline{C}}_4-A_4{\overline{C}}_3+{\overline{A}}_1{C}_2+{\overline{A}}_2{C}_1+{\overline{A}}_3{C}_4-{\overline{A}}_4{C}_3)\mathbf{i}\hfill \\ \hfill & +(A_1{\overline{C}}_3-A_2{\overline{C}}_4+A_3{\overline{C}}_1+A_4{\overline{C}}_2+{\overline{A}}_1{C}_3-{\overline{A}}_2{C}_4+{\overline{A}}_3{C}_1+{\overline{A}}_4{C}_2)\mathbf{j}\hfill \\ \hfill & +(A_1{\overline{C}}_4+A_2{\overline{C}}_3-A_3{\overline{C}}_2+A_4{\overline{C}}_1+{\overline{A}}_1{C}_4+{\overline{A}}_2{C}_3-{\overline{A}}_3{C}_2+{\overline{A}}_4{C}_1)\mathbf{k},\hfill \end{array}$$

which implies that ${\left(\widehat{A}\widehat{C}\right)}_{[1,1]}^{\sigma }=A_1{C}_1-A_2{C}_2-A_3{C}_3-A_4{C}_4+(A_1{\overline{C}}_1-A_2{\overline{C}}_2-A_3{\overline{C}}_3-A_4{\overline{C}}_4+{\overline{A}}_1{C}_1-{\overline{A}}_2{C}_2-{\overline{A}}_3{C}_3-{\overline{A}}_4{C}_4)ϵ$, where the symbols ${\left({\widehat{A}}^{\sigma }\right)}_{[i,j]},i,j=1,2,3,4$ denote the block matrix at the position of row i and column j of ${\widehat{A}}^{\sigma }$. On the other hand, it is evident that

$${\widehat{C}}^{\sigma }=\left[\begin{array}{cccc}{C}_1+{\overline{C}}_1ϵ& C_3+{\overline{C}}_3ϵ& C_2+{\overline{C}}_2ϵ& C_4+{\overline{C}}_4ϵ\\ -C_3-{\overline{C}}_3ϵ& C_1+{\overline{C}}_1ϵ& C_4+{\overline{C}}_4ϵ& -C_2-{\overline{C}}_2ϵ\\ -C_2-{\overline{C}}_2ϵ& -C_4-{\overline{C}}_4ϵ& C_1+{\overline{C}}_1ϵ& C_3+{\overline{C}}_3ϵ\\ -C_4-{\overline{C}}_4ϵ& C_2+{\overline{C}}_2ϵ& -C_3-{\overline{C}}_3ϵ& C_1+{\overline{C}}_1ϵ\end{array}\right]\in {\mathbb{D}}^{4n\times 4s},$$

(4)

from the Formulas (2) and (4), we obtain ${\left({\widehat{A}}^{\sigma }{\widehat{C}}^{\sigma }\right)}_{[1,1]}=A_1{C}_1-A_2{C}_2-A_3{C}_3-A_4{C}_4+(A_1{\overline{C}}_1+{\overline{A}}_1{C}_1-A_2{\overline{C}}_2-{\overline{A}}_2{C}_2-A_3{\overline{C}}_3-{\overline{A}}_3{C}_3-A_4{\overline{C}}_4-{\overline{A}}_4{C}_4)ϵ$; then, ${\left(\widehat{A}\widehat{C}\right)}_{[1,1]}^{\sigma }={\left({\widehat{A}}^{\sigma }{\widehat{C}}^{\sigma }\right)}_{[1,1]}$. Similarly, we can prove ${\left(\widehat{A}\widehat{C}\right)}_{[i,j]}^{\sigma }={\left({\widehat{A}}^{\sigma }{\widehat{C}}^{\sigma }\right)}_{[i,j]},i,j=1,2,3,4$, and thus

$${\left(\widehat{A}\widehat{C}\right)}^{\sigma }={\widehat{A}}^{\sigma }{\widehat{C}}^{\sigma }.$$

Additionally, it is obvious that ${(\widehat{A}+\widehat{B})}^{\sigma }={\widehat{A}}^{\sigma }+{\widehat{B}}^{\sigma }$ holds for any dual quaternion matrix $\widehat{B}={\tilde{B}}_{\mathrm{st}}+{\tilde{B}}_{\mathcal{I}}\in {\mathbb{DQ}}^{m\times n}$. Therefore, we can conclude that $\sigma$ is an isomorphic mapping from ${\mathbb{DQ}}^{m\times n}$ to ${\mathbb{D}}^{4m\times 4n}$.    □

For matrix representations of a dual quaternion matrix, one may also refer to [24]. IBelow, we list some of the properties of ${\widehat{A}}^{\sigma }$ as follows.

Lemma 3. 

Let $\widehat{A},\widehat{B}\in {\mathbb{DQ}}^{m\times n}$, $\widehat{C}\in {\mathbb{DQ}}^{n\times s}$ and $a\in \mathbb{D}$. Then, the following properties hold.

(1) 

$\widehat{A}=\widehat{B}⟺{\widehat{A}}^{\sigma }={\widehat{B}}^{\sigma }$.

(2) 

${(\widehat{A}+\widehat{B})}^{\sigma }={\widehat{A}}^{\sigma }+{\widehat{B}}^{\sigma }$, ${\left(a\widehat{A}\right)}^{\sigma }=a{\widehat{A}}^{\sigma }$.

(3) 

${\left(\widehat{A}\widehat{C}\right)}^{\sigma }={\widehat{A}}^{\sigma }{\widehat{C}}^{\sigma }$.

Let ${\widehat{A}}_c^{\sigma }$ denote the first column block of $A^{\sigma }$; that is,

$${\widehat{A}}_c^{\sigma }=\left[\begin{array}{c}{A}_1+{\overline{A}}_1ϵ\\ -A_3-{\overline{A}}_3ϵ\\ -A_2-{\overline{A}}_2ϵ\\ -A_4-{\overline{A}}_4ϵ\end{array}\right]\in {\mathbb{D}}^{4m\times n}.$$

(5)

From this notation and Lemma 3, we have the following results.

Lemma 4. 

Let $\widehat{A},\widehat{B}\in {\mathbb{DQ}}^{m\times n}$, $\widehat{C}\in {\mathbb{DQ}}^{n\times s}$ and $a\in \mathbb{D}$. Then, the following properties hold.

(1) 

${(\widehat{A}+\widehat{B})}_c^{\sigma }={\widehat{A}}_c^{\sigma }+{\widehat{B}}_c^{\sigma }$.

(2) 

${\left(a\widehat{A}\right)}_c^{\sigma }=a{\widehat{A}}_c^{\sigma }$.

(3) 

${\left(\widehat{A}\widehat{C}\right)}_c^{\sigma }={\widehat{A}}^{\sigma }{\widehat{C}}_c^{\sigma }$.

Proof. 

We only prove the property (3). This property can be obtained from the proof of Theorem 1.    □

From Lemma 4, we know that ${\widehat{A}}_c^{\sigma }$ retains all the key information of ${\widehat{A}}^{\sigma }$. Based on this, we designed a structure-preserving algorithm for solving the dual quaternion linear system. The algorithms based on the real or complex structure-preserving strategy can be also found in [25,26].

4. Rayleigh Quotient Iteration for Computing the Appreciable Eigenvalue of a Dual Quaternion Hermitian Matrix

In this section, we study the Rayleigh quotient iteration (RQI) for computing the eigenvalue with the associated eigenvector of a dual quaternion Hermitian matrix. First of all, we review an important proposition in [10].

Proposition 1 

([10]). Suppose that $\widehat{\lambda }\in \mathbb{DQ}$ is a right eigenvalue of $\widehat{A}\in {\mathbb{DQ}}^{n\times n}$, with associated right eigenvector $\widehat{\mathbf{x}}\in {\mathbb{DQ}}^{n\times 1}$. Then,

$$\widehat{\lambda }={\displaystyle \frac{{\widehat{\mathbf{x}}}^{*}\widehat{A}\widehat{\mathbf{x}}}{{\widehat{\mathbf{x}}}^{*}\widehat{\mathbf{x}}}}.$$

Assume that the unit dual quaternion vector ${\widehat{\mathbf{u}}}_k$ is a reasonable approximation to $\widehat{\mathbf{x}}$; then, ${\theta }_k={\widehat{\mathbf{u}}}_k^{*}\widehat{A}{\widehat{\mathbf{u}}}_k$ is a good approximation to $\widehat{\lambda }$ too.

Theorem 2 

(Unitary Decomposition [10]). Suppose that $\widehat{A}={\tilde{A}}_{st}+{\tilde{A}}_{\mathcal{I}}ϵ\in {\mathbb{DQ}}^{n\times n}$ is a Hermitian matrix. Then, there are unitary matrix $\widehat{U}\in {\mathbb{DQ}}^{n\times n}$ and a diagonal matrix $\Sigma \in {\mathbb{D}}^{n\times n}$ such that $\Sigma ={\widehat{U}}^{*}\widehat{A}\widehat{U}$, where

$$\Sigma =diag\left({\lambda }_{1,\mathrm{st}}+{\lambda }_{1,{\mathcal{I}}_1}ϵ,\cdots ,{\lambda }_{1,\mathrm{st}}+{\lambda }_{1,{\mathcal{I}}_{k_1}}ϵ,{\lambda }_{2,\mathrm{st}}+{\lambda }_{2,{\mathcal{I}}_1}ϵ,\cdots ,{\lambda }_{r,\mathrm{st}}+{\lambda }_{r,{\mathcal{I}}_{k_r}}ϵ\right),$$

with the diagonal entries of Σ being n eigenvalues of $\widehat{A}$,

$$\widehat{A}{\widehat{\mathbf{u}}}_{i,j}={\widehat{\mathbf{u}}}_{i,j}\left({\lambda }_{i,\mathrm{st}}+{\lambda }_{i,{\mathcal{I}}_j}ϵ\right),$$

for $j=1,\cdots ,k_i$ and $i=1,\cdots ,r$, $\widehat{U}=\left({\widehat{\mathbf{u}}}_{1,1},\cdots ,{\widehat{\mathbf{u}}}_{1,k_1},\cdots ,{\widehat{\mathbf{u}}}_{r,k_r}\right)$, ${\lambda }_{1,\mathrm{st}}>{\lambda }_{2,\mathrm{st}}>\cdots >{\lambda }_{r,\mathrm{st}}$ are real numbers, ${\lambda }_{i,\mathrm{st}}$ is a $k_i$-multiple right eigenvalue of ${\tilde{A}}_{\mathrm{st}}$, ${\lambda }_{i,{\mathcal{I}}_1}\ge {\lambda }_{i,{\mathcal{I}}_2}\ge \cdots \ge {\lambda }_{i,{\mathcal{I}}_{k_i}}$ are also real numbers. Counting possible multiplicities ${\lambda }_{i,{\mathcal{I}}_j}$, the form Σ is unique.

Below, we define the Rayleigh quotient for Hermitian matrices and study its fundamental properties.

Definition 1. 

If $\widehat{A}\in {\mathbb{DQ}}^{n\times n}$ is a dual quaternion Hermitian matrix, then the Rayleigh Quotient $\widehat{\theta }$ is defined as

$$\theta (\widehat{A},\widehat{\mathbf{x}})={\displaystyle \frac{{\widehat{\mathbf{v}}}^{*}\widehat{A}\widehat{\mathbf{v}}}{{\widehat{\mathbf{v}}}^{*}\widehat{\mathbf{v}}}},\forall \mathbf{x}\in {\mathbb{DQ}}^n\setminus \left\{\mathbf{0}\right\}.$$

Proposition 2. 

$\theta (\widehat{A},\widehat{\mathbf{v}})=\theta (\widehat{A},\widehat{\mathbf{v}}\widehat{k})$, where $\widehat{\mathbf{v}}$ is an appreciable dual quaternion vector and $\widehat{k}$ is an appreciable dual quaternion.

Proof. 

$$\theta (\widehat{A},\widehat{\mathbf{v}}\widehat{k})={\displaystyle \frac{{\left(\widehat{\mathbf{v}}\widehat{k}\right)}^{*}\widehat{A}\left(\widehat{\mathbf{v}}\widehat{k}\right)}{{\left(\widehat{\mathbf{v}}\widehat{k}\right)}^{*}\left(\widehat{\mathbf{v}}\widehat{k}\right)}}={\displaystyle \frac{{\widehat{k}}^{*}{\widehat{\mathbf{v}}}^{*}\widehat{A}\widehat{\mathbf{v}}\widehat{k}}{{\widehat{k}}^{*}{\widehat{\mathbf{v}}}^{*}\widehat{\mathbf{v}}\widehat{k}}}={\displaystyle \frac{{\widehat{k}}^{*}\widehat{k}{\widehat{\mathbf{x}}}^{*}\widehat{A}\widehat{\mathbf{v}}}{{\widehat{k}}^{*}\widehat{k}{\widehat{\mathbf{v}}}^{*}\widehat{\mathbf{v}}}}={\displaystyle \frac{{\widehat{\mathbf{v}}}^{*}\widehat{A}\widehat{\mathbf{v}}}{{\widehat{\mathbf{v}}}^{*}\widehat{\mathbf{v}}}}=\theta (\widehat{A},\widehat{\mathbf{v}}).$$

   □

Then, for a nonzero vector $\widehat{\mathbf{v}}\in {\mathbb{DQ}}^n$, we can write it in coordinates with respect to an orthogonal basis ${\left\{{\widehat{\mathbf{u}}}_j\right\}}_{j=1,\dots ,n}$ as

$$\widehat{\mathbf{v}}=\sum _{j=1}^n{\widehat{\mathbf{u}}}_j{\widehat{x}}_j,{\widehat{x}}_j\in \mathbb{DQ}.$$

Proposition 3. 

If $\widehat{A}\in {\mathbb{DQ}}^{n\times n}$ is a dual quaternion Hermitian matrix, where $\widehat{A}$ is Hermitian, then the Rayleigh quotient equals

$$\theta (\widehat{A},\widehat{\mathbf{v}})={\displaystyle \frac{{\sum }_j{\lambda }_j{\widehat{x}}_j^{*}{\widehat{x}}_j}{{\sum }_j{\widehat{x}}_j^{*}{\widehat{x}}_j}},$$

where the dual numbers ${\lambda }_j$ are the right eigenvalues of the dual quaternion Hermitian matrix $\widehat{A}$.

Proof. 

According to Theorem 2, there exists a unitary matrix $U=\left({\widehat{\mathbf{u}}}_1,{\widehat{\mathbf{u}}}_2,\cdots ,{\widehat{\mathbf{u}}}_n\right)$ such that

$$\widehat{A}\widehat{U}=\widehat{U}\mathrm{diag}\left({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n\right),$$

where ${\widehat{\mathbf{u}}}_1,{\widehat{\mathbf{u}}}_2,\cdots ,{\widehat{\mathbf{u}}}_n$ constitute an orthogonal basis of ${\mathbb{DQ}}^n$. Since ${\widehat{\mathbf{u}}}_i^{*}{\widehat{\mathbf{u}}}_j={\delta }_{ij}$, we have

$${\widehat{\mathbf{v}}}^{*}\widehat{\mathbf{v}}=\left(\sum _i{\widehat{x}}_i^{*}{\widehat{\mathbf{u}}}_i^{*}\right)\left(\sum _j{\widehat{\mathbf{u}}}_j{\widehat{x}}_j\right)=\sum _{i,j}{\widehat{x}}_i^{*}{\widehat{\mathbf{u}}}_i^{*}{\widehat{\mathbf{u}}}_j{\widehat{x}}_j=\sum _j{\widehat{x}}_j^{*}{\widehat{x}}_j.$$

Analogously, since $\widehat{A}{\widehat{\mathbf{u}}}_j={\widehat{\mathbf{u}}}_j{\lambda }_j$, then we have

$${\widehat{\mathbf{v}}}^{*}\widehat{A}\widehat{\mathbf{v}}=\left(\sum _i{\widehat{x}}_i^{*}{\widehat{\mathbf{u}}}_i^{*}\right)\left(\sum _j{\widehat{\mathbf{u}}}_j{\lambda }_j{\widehat{x}}_j\right)=\sum _j{\widehat{x}}_i^{*}{\lambda }_j{\widehat{x}}_j=\sum _j{\lambda }_j{\widehat{x}}_i^{*}{\widehat{x}}_j.$$

This completes the proof.    □

Proposition 4. 

Let $\widehat{A}\in {\mathbb{DQ}}^{n\times n}$ be a dual quaternion Hermitian matrix. If ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n$ are eigenvalues of A with ${\lambda }_1\le {\lambda }_2\le \cdots {\lambda }_n$, then

$${\lambda }_1\le \theta (\widehat{A},\widehat{\mathbf{v}})\le {\lambda }_n,$$

where $\mathbf{v}$ is an appreciable dual quaternion vector.

Proof. 

According to Proposition 3, it holds that

$${\lambda }_1\left(\sum _j{\widehat{x}}_j^{*}{\widehat{x}}_j\right)\le \sum _j{\lambda }_j{\widehat{x}}_j^{*}{\widehat{x}}_j\le {\lambda }_n\left(\sum _j{\widehat{x}}_j^{*}{\widehat{x}}_j\right),$$

then

$${\lambda }_1\le {\displaystyle \frac{{\sum }_j{\lambda }_j{\widehat{x}}_j^{*}{\widehat{x}}_j}{{\sum }_j{\widehat{x}}_j^{*}{\widehat{x}}_j}}\le {\lambda }_n.$$

This is complete the proof.    □

For more general properties of the Rayleigh quotient of dual quaternion matrices, please refer to [27].

When seeking an eigenvalue and its eigenvector near a prescribed target, we typically employ the efficient Rayleigh quotient iteration (RQI) method, which is essentially a shift-and-invert power method with dynamic shifts. The iteration format of the Rayleigh quotient iteration method is as follows

$${\widehat{\theta }}_k={\widehat{\mathbf{u}}}_k^{*}\widehat{A}{\widehat{\mathbf{u}}}_k,(\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{w}}}_{k+1}={\widehat{\mathbf{u}}}_k,{\widehat{\mathbf{u}}}_{k+1}={\displaystyle \frac{{\widehat{\mathbf{w}}}_{k+1}}{\parallel {\widehat{\mathbf{w}}}_{k+1}{\parallel }_2}},$$

where ${\widehat{\mathbf{u}}}_k$ is the currently available approximate eigenvector with $\parallel {\widehat{\mathbf{u}}}_k{\parallel }_2=1$, and ${\widehat{\theta }}_k$ is the corresponding Rayleigh quotient. This process is repeated until convergent or the maximal iteration number is reached.

4.1. A Structure-Preserving Method for Solving the Linear System $(\widehat{A}-\widehat{\theta }I)\widehat{\mathbf{w}}=\widehat{\mathbf{u}}$

The key step of the Rayleigh quotient iteration is to effectively solve the shifted dual quaternion linear system $(\widehat{A}-\widehat{\theta }I)\widehat{\mathbf{w}}=\widehat{\mathbf{u}}$. From Lemma 4, we have the following equation

$$\begin{array}{cc}\hfill (\widehat{A}-\widehat{\theta }I)\widehat{\mathbf{w}}=\widehat{\mathbf{u}}& ⟺{\left[(\widehat{A}-\widehat{\theta }I)\widehat{\mathbf{w}}\right]}_c^{\sigma }={\widehat{\mathbf{u}}}_c^{\sigma }\hfill \\ \hfill & ⟺{(\widehat{A}-\widehat{\theta }I)}^{\sigma }{\widehat{\mathbf{w}}}_c^{\sigma }={\widehat{\mathbf{u}}}_c^{\sigma }.\hfill \end{array}$$

(6)

The Equation (6) is derived by the dual representation and the structure-preserving strategy. In this context, we equivalently transform the linear system over dual quaternions into a linear system over dual numbers.

To solve ${(\widehat{A}-\widehat{\theta }I)}^{\sigma }{\widehat{\mathbf{w}}}_c^{\sigma }={\widehat{\mathbf{u}}}_c^{\sigma }$, let ${(\widehat{A}-\widehat{\theta }I)}^{\sigma }={\tilde{A}}_{\mathrm{st}}+{\tilde{A}}_{\mathcal{I}}ϵ$, ${\widehat{\mathbf{w}}}_c^{\sigma }={\tilde{\mathbf{w}}}_{\mathrm{st}}+{\tilde{\mathbf{w}}}_{\mathcal{I}}ϵ$ and ${\widehat{\mathbf{u}}}_c^{\sigma }={\tilde{\mathbf{u}}}_{\mathrm{st}}+{\tilde{\mathbf{u}}}_{\mathcal{I}}ϵ$, where ${\tilde{A}}_{\mathrm{st}},{\tilde{A}}_{\mathcal{I}}\in {\mathbb{R}}^{4n\times 4n},{\tilde{\mathbf{w}}}_{\mathrm{st}},{\tilde{\mathbf{w}}}_{\mathcal{I}},{\tilde{\mathbf{u}}}_{\mathrm{st}},{\tilde{\mathbf{u}}}_{\mathcal{I}}\in {\mathbb{R}}^{4n\times 1}$, then we have

$$\begin{array}{cc}\hfill {(\widehat{A}-\widehat{\theta }I)}^{\sigma }{\widehat{\mathbf{w}}}_c^{\sigma }={\widehat{\mathbf{u}}}_c^{\sigma }& ⟺({\tilde{A}}_{\mathrm{st}}+{\tilde{A}}_{\mathcal{I}}ϵ)({\tilde{\mathbf{w}}}_{\mathrm{st}}+{\tilde{\mathbf{w}}}_{\mathcal{I}}ϵ)={\tilde{\mathbf{u}}}_{\mathrm{st}}+{\tilde{\mathbf{u}}}_{\mathcal{I}}ϵ\hfill \\ \hfill & ⟺{\tilde{A}}_{\mathrm{st}}{\tilde{\mathbf{w}}}_{\mathrm{st}}+{\tilde{A}}_{\mathrm{st}}{\tilde{\mathbf{w}}}_{\mathcal{I}}ϵ+{\tilde{A}}_{\mathcal{I}}{\mathbf{x}}_{\mathrm{st}}ϵ={\tilde{\mathbf{u}}}_{\mathrm{st}}+{\tilde{\mathbf{u}}}_{\mathcal{I}}ϵ\hfill \\ \hfill & ⟺{\tilde{A}}_{\mathrm{st}}{\tilde{\mathbf{w}}}_{\mathrm{st}}+({\tilde{A}}_{\mathrm{st}}{\tilde{\mathbf{w}}}_{\mathcal{I}}+{\tilde{A}}_{\mathcal{I}}{\tilde{\mathbf{w}}}_{\mathrm{st}})ϵ={\tilde{\mathbf{u}}}_{\mathrm{st}}+{\tilde{\mathbf{u}}}_{\mathcal{I}}ϵ.\hfill \end{array}$$

(7)

Considering the standard and dual parts of Equation (7), one can split it into the following two matrix equations

$$\left\{\begin{array}{c}{\tilde{A}}_{\mathrm{st}}{\tilde{\mathbf{w}}}_{\mathrm{st}}={\tilde{\mathbf{u}}}_{\mathrm{st}},\hfill \\ {\tilde{A}}_{\mathrm{st}}{\tilde{\mathbf{w}}}_{\mathcal{I}}+{\tilde{A}}_{\mathcal{I}}{\tilde{\mathbf{w}}}_{\mathrm{st}}={\tilde{\mathbf{u}}}_{\mathcal{I}},\hfill \end{array}\right.$$

which can be equivalently written as

$$\left[\begin{array}{cc}{\tilde{A}}_{\mathrm{st}}& {\tilde{A}}_{\mathcal{I}}\\ \mathbf{O}& {\tilde{A}}_{\mathrm{st}}\end{array}\right]\left[\begin{array}{c}{\tilde{\mathbf{w}}}_{\mathcal{I}}\\ {\tilde{\mathbf{w}}}_{\mathrm{st}}\end{array}\right]=\left[\begin{array}{c}{\tilde{\mathbf{u}}}_{\mathcal{I}}\\ {\tilde{\mathbf{u}}}_{\mathrm{st}}\end{array}\right].$$

(8)

This is a linear system problem over the field of real numbers. QR decomposition reduces it to solving

$$R\left[\begin{array}{c}{\tilde{\mathbf{w}}}_{\mathcal{I}}\\ {\tilde{\mathbf{w}}}_{\mathrm{st}}\end{array}\right]=Q^{\top }\left[\begin{array}{c}{\tilde{\mathbf{u}}}_{\mathcal{I}}\\ {\tilde{\mathbf{u}}}_{\mathrm{st}}\end{array}\right],$$

where $\left[\begin{array}{cc}{\tilde{A}}_{\mathrm{st}}& {\tilde{A}}_{\mathcal{I}}\\ \mathbf{O}& {\tilde{A}}_{\mathrm{st}}\end{array}\right]=QR$, Q is a unitary matrix and R is an upper triangular matrix. The above linear system can then be solved by back substitution.

In addition, if the linear system (8) is not consistent, then one can solve the following least squares problem

$$\underset{\tilde{\mathbf{w}}}{min}{∥\left[\begin{array}{cc}{\tilde{A}}_{\mathrm{st}}& {\tilde{A}}_{\mathcal{I}}\\ \mathbf{O}& {\tilde{A}}_{\mathrm{st}}\end{array}\right]\left[\begin{array}{c}{\tilde{\mathbf{w}}}_{\mathcal{I}}\\ {\tilde{\mathbf{w}}}_{\mathrm{st}}\end{array}\right]-\left[\begin{array}{c}{\tilde{\mathbf{u}}}_{\mathcal{I}}\\ {\tilde{\mathbf{u}}}_{\mathrm{st}}\end{array}\right]∥}_2.$$

Using the singular value decomposition, the least squares problem can be solved as follows. First of all, substitute $\left[\begin{array}{cc}{\tilde{A}}_{\mathrm{st}}& {\tilde{A}}_{\mathcal{I}}\\ \mathbf{O}& {\tilde{A}}_{\mathrm{st}}\end{array}\right]=U\Sigma V^{\top }$ into the system

$$U\Sigma V^{\top }\left[\begin{array}{c}{\tilde{\mathbf{w}}}_{\mathcal{I}}\\ {\tilde{\mathbf{w}}}_{\mathrm{st}}\end{array}\right]=\left[\begin{array}{c}{\tilde{\mathbf{u}}}_{\mathcal{I}}\\ {\tilde{\mathbf{u}}}_{\mathrm{st}}\end{array}\right],$$

and then multiply both sides by $U^{\top }$, we have

$$\Sigma V^{\top }\left[\begin{array}{c}{\tilde{\mathbf{w}}}_{\mathcal{I}}\\ {\tilde{\mathbf{w}}}_{\mathrm{st}}\end{array}\right]=U^{\top }\left[\begin{array}{c}{\tilde{\mathbf{u}}}_{\mathcal{I}}\\ {\tilde{\mathbf{u}}}_{\mathrm{st}}\end{array}\right].$$

Let $\mathbf{c}=U^{\top }\left[\begin{array}{c}{\tilde{\mathbf{u}}}_{\mathcal{I}}\\ {\tilde{\mathbf{u}}}_{\mathrm{st}}\end{array}\right]$, giving

$$\Sigma \mathbf{y}=\mathbf{c},$$

where $\mathbf{y}=V^{\top }\left[\begin{array}{c}{\tilde{\mathbf{w}}}_{\mathcal{I}}\\ {\tilde{\mathbf{w}}}_{\mathrm{st}}\end{array}\right]$. Since $\Sigma$ contains zero singular values, only the first $r=rank\left(\left[\begin{array}{cc}{\tilde{A}}_{\mathrm{st}}& {\tilde{A}}_{\mathcal{I}}\\ \mathbf{O}& {\tilde{A}}_{\mathrm{st}}\end{array}\right]\right)$ rows of $\Sigma$ are non-zero. Split the system into

$${\Sigma }_r{\mathbf{y}}_r={\mathbf{c}}_r,$$

where ${\Sigma }_r$ is the $r\times r$ submatrix of $\Sigma$ with non-zero singular values, ${\mathbf{y}}_r$ contains the first r components of $\mathbf{y}$ and ${\mathbf{c}}_r$ contains the first r components of $\mathbf{c}$. Solve for ${\mathbf{y}}_r$, it follows that

$${\mathbf{y}}_r={\Sigma }_r^{-1}{\mathbf{c}}_r.$$

Since $\mathbf{y}=V^{\top }\left[\begin{array}{c}{\tilde{\mathbf{w}}}_{\mathcal{I}}\\ {\tilde{\mathbf{w}}}_{\mathrm{st}}\end{array}\right]$, the solution is

$$\left[\begin{array}{c}{\tilde{\mathbf{w}}}_{\mathcal{I}}\\ {\tilde{\mathbf{w}}}_{\mathrm{st}}\end{array}\right]=V\mathbf{y}=V\left[\begin{array}{c}{\mathbf{y}}_r\\ \mathbf{0}\end{array}\right].$$

Therefore, the least squares solution is

$$\left[\begin{array}{c}{\tilde{\mathbf{w}}}_{\mathcal{I}}\\ {\tilde{\mathbf{w}}}_{\mathrm{st}}\end{array}\right]=V_r{\Sigma }_r^{-1}{U}_r^{\top }\left[\begin{array}{c}{\tilde{\mathbf{u}}}_{\mathcal{I}}\\ {\tilde{\mathbf{u}}}_{\mathrm{st}}\end{array}\right].$$

The proposed Rayleigh quotient iteration (RQI) for solving Problem (1) is summarized in Algorithm 1.

Algorithm 1 The Rayleigh quotient iteration (RQI)

Input: Given a normalized initial guess ${\widehat{\mathbf{u}}}_0\in {\mathbb{DQ}}^{n\times 1}$ with $\parallel {\widehat{\mathbf{u}}}_0{\parallel }_2=1$, the maximal iteration number $k_{max}$ and the stopping tolerance $\epsilon$. Output: Eigenvalue ${\widehat{\theta }}_k$ and eigenvector ${\widehat{\mathbf{u}}}_{k+1}$. 1: for  $k=0,1,2,\dots ,k_{max}$ do 2:    Compute the Rayleigh quotient ${\widehat{\theta }}_k={\widehat{\mathbf{u}}}_k^{*}\widehat{A}{\widehat{\mathbf{u}}}_k$. 3:    If $\widehat{A}-{\widehat{\theta }}_{k}I$ is singular, then solve $(\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{u}}}_{k+1}=\widehat{\mathbf{0}}$ for unit vector ${\widehat{\mathbf{u}}}_{k+1}$ and stop. Otherwise, solve equation $(\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{w}}}_{k+1}={\widehat{\mathbf{u}}}_k$ for ${\widehat{\mathbf{w}}}_{k+1}$. 4:    Normalize ${\widehat{\mathbf{u}}}_{k+1}={\widehat{\mathbf{w}}}_{k+1}/{\parallel {\widehat{\mathbf{w}}}_{k+1}\parallel }_2$. 5:    If ${\parallel \widehat{A}{\widehat{\mathbf{u}}}_{k+1}-{\widehat{\mathbf{u}}}_{k+1}{\widehat{\theta }}_k\parallel }_{2^R}⩽\epsilon$, then stop. 6: end for

Remark 1. 

To accelerate convergence, we run the power method several times to obtain an appropriate initial iteration vector.

Remark 2. 

To reduce the time and storage costs associated with frequent matrix decomposition in Algorithm 1, we may use some iterative methods to roughly solve the shifted linear system in Step 3, resulting in the so-called inexact Rayleigh quotient iteration.

4.2. Convergence Analysis

Similar to the Rayleigh quotient iteration for the real matrices, we show the eigenpair sequences $({\widehat{\theta }}_k,{\widehat{\mathbf{u}}}_k)$ converges to a fixed eigenvalue with an associated eigenvector. For purposes of analysis, it is convenient to combine lines 3 and 4 of Algorithm 1 into

$$(\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{u}}}_{k+1}={\widehat{\mathbf{u}}}_k{\tau }_k,$$

where ${\tau }_k$ is an appreciable positive dual number that ensures that $\parallel {\widehat{\mathbf{u}}}_{k+1}{\parallel }_2=1$.

First of all, we introduce the minimal residual property of the Rayleigh quotient.

Lemma 5. 

Given a dual quaternion Hermitian matrix $\widehat{A}$, for any unit dual quaternion vector $\widehat{\mathbf{x}}$ satisfying ${\parallel \widehat{\mathbf{x}}\parallel }_2=1$, the Rayleigh quotient $\theta ={\widehat{\mathbf{x}}}^{*}\widehat{A}\widehat{\mathbf{x}}$ satisfies

$${\parallel (\widehat{A}-\theta I)\widehat{\mathbf{x}}\parallel }_2\le {\parallel (\widehat{A}-\lambda I)\widehat{\mathbf{x}}\parallel }_2$$

for any dual number λ.

Proof. 

$$\begin{array}{cc}\hfill {\parallel (\widehat{A}-\lambda I)\mathbf{x}\parallel }_2^2& ={\left((\widehat{A}-\lambda I)\widehat{\mathbf{x}}\right)}^{*}\left((\widehat{A}-\lambda I)\widehat{\mathbf{x}}\right)\hfill \\ \hfill & =({\widehat{\mathbf{x}}}^{*}\widehat{A}-\lambda {\widehat{\mathbf{x}}}^{*})(\widehat{A}\widehat{\mathbf{x}}-\lambda \widehat{\mathbf{x}})\hfill \\ \hfill & ={\widehat{\mathbf{x}}}^{*}\widehat{A}\widehat{A}\widehat{\mathbf{x}}-2\lambda {\widehat{\mathbf{x}}}^{*}\widehat{A}\widehat{\mathbf{x}}+{\lambda }^2\hfill \\ \hfill & ={(\lambda -{\widehat{\mathbf{x}}}^{*}\widehat{A}\widehat{\mathbf{x}})}^2.\hfill \end{array}$$

(9)

Equality (9) is obtained by Lemma 1. Therefore, the Rayleigh quotient $\theta ={\widehat{\mathbf{x}}}^{*}\widehat{A}\widehat{\mathbf{x}}$ minimizes the residual norm ${\parallel (A-\lambda I)\widehat{\mathbf{x}}\parallel }_2$, proving the minimal residual property of the Rayleigh quotient.    □

Theorem 3. 

Suppose $\widehat{A}$ is a dual quaternion Hermitian matrix, and let ${\widehat{\mathbf{r}}}_k=(\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{u}}}_k$ be the residual at the kth step of the Rayleigh quotient iteration; then, the sequence $\left\{{∥{\widehat{\mathbf{r}}}_k∥}_2,k=0,1,\cdots \right\}$ is monotonically decreasing for any initial vector ${\widehat{\mathbf{u}}}_0$.

Proof. 

$$\begin{array}{cc}\hfill {∥{\widehat{\mathbf{r}}}_{k+1}∥}_2& ={\parallel (\widehat{A}-{\widehat{\theta }}_{k+1}I){\widehat{\mathbf{u}}}_{k+1}\parallel }_2\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \leqq {\parallel (\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{u}}}_{k+1}\parallel }_2\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & =\left|{\widehat{\mathbf{u}}}_k^{*}(\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{u}}}_{k+1}\right|\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & \leqq {\parallel {\widehat{\mathbf{u}}}_k^{*}(\widehat{A}-{\widehat{\theta }}_{k}I)\parallel }_2{\parallel {\widehat{\mathbf{u}}}_{k+1}\parallel }_2\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & ={\parallel {\widehat{\mathbf{u}}}_k^{*}(\widehat{A}-{\widehat{\theta }}_{k}I)\parallel }_2\hfill \\ \hfill & ={\parallel (\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{u}}}_k\parallel }_2\hfill \\ \hfill & ={\parallel {\widehat{\mathbf{r}}}_k\parallel }_2.\hfill \end{array}$$

Inequality (10) holds by Lemma 5. From lines 3 and 4 of Algorithm 1, we have

$$\left\{\begin{array}{c}(\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{w}}}_{k+1}={\widehat{\mathbf{u}}}_k\hfill \\ {\widehat{\mathbf{u}}}_{k+1}={\widehat{\mathbf{w}}}_{k+1}/{\parallel {\widehat{\mathbf{w}}}_{k+1}\parallel }_2\hfill \end{array}\right.⟹(\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{u}}}_{k+1}={\displaystyle \frac{{\widehat{\mathbf{u}}}_k}{\parallel {\widehat{\mathbf{w}}}_{k+1}{\parallel }_2}}$$

(13)

Taking the 2-norm on both sides of (13), we obtain

$${∥(\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{u}}}_{k+1}∥}_2=\left|{\widehat{\mathbf{u}}}_k^{*}(\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{u}}}_{k+1}\right|,$$

then (11) holds. Inequality (12) holds due to the Cauchy–Schwarz inequality (Proposition 5.5 in [10]). Equality for

$${∥{\widehat{\mathbf{r}}}_{k+1}∥}_2\le {∥{\widehat{\mathbf{r}}}_k∥}_2$$

is achieved when ${\widehat{\theta }}_{k+1}={\widehat{\theta }}_k$ and ${\widehat{\mathbf{u}}}_{k+1}^{*}$ is parallel to ${\widehat{\mathbf{u}}}_k^{*}(\widehat{A}-{\widehat{\theta }}_{k}I)$.    □

Theorem 4. 

Given a dual quaternion Hermitian matrix $\widehat{A}\in {\mathbb{DQ}}^{n\times n}$, let the RQI (Algorithm 1) be applied to a dual quaternion Hermitian matrix $\widehat{A}$ with a proper starting vector ${\widehat{\mathbf{u}}}_0$. When k goes to infinity, $({\widehat{\theta }}_k,{\widehat{\mathbf{u}}}_k)$ converges to an eigenpair $(\lambda ,\widehat{\mathbf{x}})$ of $\widehat{A}$.

Proof. 

By Theorem 3, the monotone sequence $\left\{{∥{\widehat{\mathbf{r}}}_k∥}_2\right\}$ has a lower bound of 0. Let

$$\underset{k\to \infty }{lim}{∥{\widehat{\mathbf{r}}}_k∥}_2=\underset{k\to \infty }{lim}{\parallel (\widehat{A}-\widehat{{\theta }_k}){\widehat{\mathbf{u}}}_k\parallel }_2\to \tau \ge 0.$$

(14)

Since ${\parallel {\mathbf{u}}_k\parallel }_2=1$, the sequence ${\left\{{\mathbf{u}}_k\right\}}_{k=0}^{\infty }$ forms a compact subset of ${\mathbb{DQ}}^n$, which implies that ${\left\{{\mathbf{u}}_k\right\}}_{k=0}^{\infty }$ must have at least one accumulation point. Additionally, the sequence ${\left\{{\widehat{\theta }}_k\right\}}_{k=0}^{\infty }$ is confined to the numerical range of $\widehat{A}$, a closed and bounded region in the space of dual numbers. Therefore, the sequence ${\left\{{\widehat{\theta }}_k\right\}}_{k=0}^{\infty }$ also has limit points. We discuss the following two cases separately based on the limit of the residual.

Case 1: $\tau =0$. By definition, if $(\widehat{\theta },\widehat{\mathbf{u}})$ is an accumulation point of the sequence ${\{{\widehat{\theta }}_k,{\widehat{\mathbf{u}}}_k\}}_{k=0}^{\infty }$, then there exists a subsequence $({\widehat{\theta }}_i,{\widehat{\mathbf{u}}}_i)$ indexed by some set $\mathcal{M}$ that converges to $(\widehat{\theta },\widehat{\mathbf{u}})$. When i goes to infinity in $\mathcal{M}$, we have

$$\widehat{\theta }\left(\widehat{\mathbf{u}}\right)=\underset{i\in \mathcal{M}}{lim}\widehat{\theta }\left({\widehat{\mathbf{u}}}_i\right)=\widehat{\theta }$$

and taking the limit of this subsequence results in

$${\parallel (\widehat{A}-\widehat{\theta }I)\widehat{\mathbf{u}}\parallel }_2=\underset{i\in \mathcal{M}}{lim}{\parallel (\widehat{A}-{\widehat{\theta }}_{i}I){\widehat{\mathbf{u}}}_i\parallel }_2=\tau =0.$$

Thus, $(\widehat{\theta },\widehat{\mathbf{u}})$ must be an eigenpair of A.

Case 2: $\tau >0$. Note that

$$\begin{array}{cc}\hfill {\parallel {\widehat{\mathbf{r}}}_{k+1}\parallel }_2^2& ={\parallel (\widehat{A}-{\widehat{\theta }}_{k+1}I){\widehat{\mathbf{u}}}_{k+1}\parallel }_2^2\hfill \\ \hfill & ={\parallel \widehat{A}{\widehat{\mathbf{u}}}_{k+1}-{\widehat{\theta }}_{k+1}{\widehat{\mathbf{u}}}_{k+1}-{\widehat{\theta }}_k{\widehat{\mathbf{u}}}_{k+1}+{\widehat{\theta }}_k{\widehat{\mathbf{u}}}_{k+1}\parallel }_2^2\hfill \\ \hfill & ={\parallel (\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{u}}}_{k+1}+({\widehat{\theta }}_k-{\widehat{\theta }}_{k+1}){\widehat{\mathbf{u}}}_{k+1}\parallel }_2^2\hfill \end{array}$$

$$\begin{array}{cc}\hfill & ={\parallel (\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{u}}}_{k+1}\parallel }_2^2+{|{\widehat{\theta }}_k-{\widehat{\theta }}_{k+1}|}^2+2|{\widehat{\theta }}_k-{\widehat{\theta }}_{k+1}|{\widehat{\mathbf{u}}}_{k+1}^{*}(\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{u}}}_{k+1}\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & ={\parallel (\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{u}}}_{k+1}\parallel }_2^2-{|{\widehat{\theta }}_k-{\widehat{\theta }}_{k+1}|}^2\hfill \end{array}$$

$$\begin{array}{cc}\hfill & ={\left|{\widehat{\mathbf{u}}}_k^{*}(\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{u}}}_{k+1}\right|}^2-{|{\widehat{\theta }}_k-{\widehat{\theta }}_{k+1}|}^2\hfill \\ \hfill & ={\parallel (\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{u}}}_k\parallel }_2^2·{\kappa }_k^2-{|{\widehat{\theta }}_k-{\widehat{\theta }}_{k+1}|}^2\hfill \\ \hfill & =\parallel {\widehat{\mathbf{r}}}_k{\parallel }_2^2·{\kappa }_k^2-{|{\widehat{\theta }}_k-{\widehat{\theta }}_{k+1}|}^2,\hfill \end{array}$$

(16)

Equality (15) is obtained by Lemma 2. Let

$$\langle {\widehat{\mathbf{u}}}_{k+1},(\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{u}}}_k\rangle =\parallel {\widehat{\mathbf{u}}}_{k+1}{\parallel }_2\parallel (\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{u}}}_k{\parallel }_2·{\kappa }_k={\parallel (\widehat{A}-{\widehat{\theta }}_{k}I){\widehat{\mathbf{u}}}_k\parallel }_2·{\kappa }_k$$

in (16). By the Cauchy–Schwarz inequality, we know that ${\kappa }_k^2\le 1$.

Since

$$\underset{k\to \infty }{lim}{∥{\widehat{\mathbf{r}}}_k∥}_2=\tau$$

and the monotonic residual property must hold in the limit, we have

$$\underset{k\to \infty }{lim}|{\widehat{\theta }}_k-{\widehat{\theta }}_{k+1}|=0.$$

Moreover, the sequence ${\left\{{\widehat{\theta }}_k\right\}}_{k=0}^{\infty }$ has limit points, and there can only be one of them. Thus,

$${\widehat{\theta }}_k\to \theta ,\mathrm{as}k\to \infty .$$

As $k\to \infty$,

$${\kappa }_k^2=\left({∥{\mathbf{r}}_{k+1}∥}_2^2+{\left|{\widehat{\theta }}_k-{\widehat{\theta }}_{k+1}\right|}^2\right)/{∥{\widehat{\mathbf{r}}}_k∥}_2^2\to 1,$$

so we have

$${\tau }_k=\left|{\widehat{\mathbf{u}}}_k^{*}\left(\widehat{A}-{\widehat{\theta }}_{k}I\right){\widehat{\mathbf{u}}}_{k+1}\right|={∥{\widehat{\mathbf{r}}}_k∥}_2·{\kappa }_k\to \tau .$$

(17)

Now,

$$\begin{array}{cc}\hfill {\tau }_k^2& ={\widehat{\mathbf{u}}}_{k+1}^{*}{\left(\widehat{A}-{\widehat{\theta }}_{k}I\right)}^{*}\left(\widehat{A}-{\widehat{\theta }}_{k}I\right){\widehat{\mathbf{u}}}_{k+1}\hfill \\ \hfill & \leqq {∥{\widehat{\mathbf{u}}}_{k+1}^{*}∥}_2{∥{\left(\widehat{A}-{\widehat{\theta }}_{k}I\right)}^{*}\left(\widehat{A}-{\widehat{\theta }}_{k}I\right){\widehat{\mathbf{u}}}_{k+1}∥}_2,\hfill \\ \hfill & ={∥{\left(\widehat{A}-{\widehat{\theta }}_{k}I\right)}^{*}{\widehat{\mathbf{u}}}_k{\tau }_k∥}_2,\mathrm{since}\left(\widehat{A}-{\widehat{\theta }}_{k}I\right){\widehat{\mathbf{u}}}_{k+1}={\widehat{\mathbf{u}}}_k{\tau }_k,\hfill \\ \hfill & ={∥{\widehat{\mathbf{r}}}_k∥}_2·{\tau }_k.\hfill \end{array}$$

Combining (14) and (17), equality in the Cauchy–Schwarz inequality must hold in the limit, as $k\to \infty$. Let $\mathcal{N}$ be a subsequence of $\{0,1,2,\cdots \}$ such that

$$\underset{k\in \mathcal{N}}{lim}{\widehat{\mathbf{u}}}_k=\widehat{\mathbf{u}}.$$

Since ${\parallel (\widehat{A}-\widehat{\theta }I)\widehat{\mathbf{u}}\parallel }_2=\tau$, it follows that ${(\widehat{A}-\widehat{\theta }I)}^{*}(\widehat{A}-\widehat{\theta }I)\widehat{\mathbf{u}}=\widehat{\mathbf{u}}{\tau }^2$ holds for each limit point. By using the same subsequence again, we obtain

$$\widehat{\theta }=\underset{k\in \mathcal{N}}{lim}\widehat{\theta }\left({\widehat{\mathbf{u}}}_k\right)=\widehat{\theta }\left(\widehat{\mathbf{u}}\right).$$

This shows that each limit point $\widehat{\mathbf{u}}$ of ${\left\{{\mathbf{u}}_k\right\}}_{k=0}^{\infty }$ is a singular vector of $\widehat{A}-\widehat{\theta }I$ associated with singular value $\tau$. Additionally, since $\widehat{A}-\widehat{\theta }I$ is Hermitian, we have

$$\tau =|{\lambda }_i-\widehat{\theta }|,$$

where ${\lambda }_i$ is one of the eigenvalues of $\widehat{A}$. This completes the proof.    □

4.3. Computing All Appreciable Eigenvalues of a Dual Quaternion Hermitian Matrix

Clearly, Algorithm 1 can only compute an appreciable eigenvalue and its corresponding eigenvector at a time. For the remaining irreducible eigenvalues of a dual quaternion Hermitian matrix, we can use the well-known deflation technique to gradually compute all appreciable eigenvalues. Specifically, by Theorem 2, a Hermitian matrix $\widehat{A}\in {\mathbb{DQ}}^{n\times n}$ can be equivalently represented in the following form

$$\widehat{A}=\widehat{U}\Sigma {\widehat{U}}^{*}=\sum _{i=1}^n{\lambda }_i{\widehat{\mathbf{u}}}_i{\widehat{\mathbf{u}}}_i^{*},$$

(18)

in which $\widehat{U}=\left[{\widehat{\mathbf{u}}}_1,\dots ,{\widehat{\mathbf{u}}}_n\right]\in {\mathbb{DQ}}^{n\times n}$ is a unitary matrix, $\Sigma =diag\left({\lambda }_1,\dots ,{\lambda }_n\right)\in {\mathbb{D}}^{n\times n}$ is a diagonal dual matrix, and the elements ${\lambda }_i,i=1,\dots ,n$ are ordered in descending order. Let

$${\widehat{A}}_k=\widehat{A}-\sum _{i=1}^{k-1}{\lambda }_i{\widehat{\mathbf{u}}}_i{\widehat{\mathbf{u}}}_i^{*}.$$

(19)

It follows that ${\lambda }_k$ and ${\widehat{\mathbf{u}}}_k$ constitute an eigenpair of ${\widehat{A}}_k$. We compute an appreciable eigenvalue of ${\widehat{A}}_k$ by applying the Rayleigh quotient iteration and repeat this process through Formula (19) until $k=n$, which allows us to obtain all appreciable eigenvalues. A concise summary of this procedure can be found in Algorithm 2.

Algorithm 2 Computing all appreciable eigenvalues

Input: Given a dual quaternion Hermitian matrix $\widehat{A}\in {\mathbb{DQ}}^{n\times n}$, the tolerance $\gamma$. Output: Eigenvalues ${\left\{{\lambda }_i\right\}}_{i=1}^k$ and eigenvectors ${\left\{{\widehat{\mathbf{u}}}_i\right\}}_{i=1}^k$. 1: Set ${\widehat{A}}_1=\widehat{A}$. 2: for  $k=1,2,\dots ,$ do 3:    Compute ${\lambda }_k,{\widehat{\mathbf{u}}}_k$ as the eigenpair of ${\widehat{A}}_k$ by Algorithm 1. 4:    Update ${\widehat{A}}_{k+1}={\widehat{A}}_k-{\lambda }_k{\widehat{\mathbf{u}}}_k{\widehat{\mathbf{u}}}_k^{*}$. 5:    If ${\parallel {\tilde{A}}_{k+1,\mathrm{st}}\parallel }_F⩽\gamma$, then stop. 6: end for

The complexity of Algorithm 1, the Rayleigh Quotient Iteration (RQI), depends on the matrix size n and the number of iterations $k_{max}$. Each iteration of the RQI involves a matrix-vector multiplication with a complexity of $O\left(n^2\right)$ and solving a linear system with a complexity of $O\left(n^3\right)$. Assuming $k_{max}$ iterations are required to converge, then Algorithm 1 has complexity $O\left(k_{max}{n}^3\right)$. Update ${\widehat{A}}_{k+1}={\widehat{A}}_k-{\lambda }_k{\widehat{\mathbf{u}}}_k{\widehat{\mathbf{u}}}_k^{*}$, this involves computing the outer product ${\widehat{\mathbf{u}}}_k{\widehat{\mathbf{u}}}_k^{*}$ with a complexity of $O\left(n^2\right)$ and subtracting it from ${\widehat{A}}_k$ with a complexity of $O\left(n^2\right)$. Thus, this step costs $O\left(n^2\right)$. Computing the Frobenius norm involves accessing every element of the matrix, which costs $O\left(n^2\right)$. Therefore, for m iterations, the overall complexity of Algorithm 2 is $O\left(m·k_{max}{n}^3\right)$.

Finally, we give the convergence theorem for Algorithm 2.

Theorem 5. 

Given a dual quaternion Hermitian matrix $A\in {\mathbb{DQ}}^{n\times n}$, Algorithm can return all appreciable eigenvalues and their corresponding eigenvectors of A.

Proof. 

The theorem can be derived from the combination of Equation (18) and Theorem 4. □

5. Numerical Experiments

In this section, some numerical examples are used to illustrate that Algorithm 2 is feasible and effective to solve the dual quaternion Hermitian eigenvalue problem (1). All the tests are performed under Windows 11 and MATLAB version 23.2.0.2365128 (R2023b) with an AMD Ryzen 7 5800H with Radeon Graphics CPU at 3.20 GHz and 16 GB of memory.

Example 1. 

Consider Problem (1) with a random dual quaternion Hermitian matrix $\widehat{A}={\tilde{A}}_{\mathrm{st}}+{\tilde{A}}_{\mathcal{I}}ϵ\in {\mathbb{DQ}}^{6\times 6}$, where the standard part of $\widehat{A}$ is ${\tilde{A}}_{\mathrm{st}}=A_{\mathrm{st},1}+A_{\mathrm{st},2}\mathbf{i}+A_{\mathrm{st},3}\mathbf{j}+A_{\mathrm{st},4}\mathbf{k}\in {\mathbb{Q}}^{6\times 6}$, and $A_{\mathrm{st},1},A_{\mathrm{st},2},A_{\mathrm{st},3}$ and $A_{\mathrm{st},4}$ are equal to

$$\left[\begin{array}{cccccc}0.6634& 0.1840& -0.0967& -0.0590& 0.1392& -0.0366\\ 0.1840& 0.6872& 0.7003& 0.2440& -0.0937& 0.2263\\ -0.0967& 0.7003& 0.8900& 0.3074& -0.1671& 0.1731\\ -0.0590& 0.2440& 0.3074& 0.1619& -0.0953& 0.0129\\ 0.1392& -0.0937& -0.1671& -0.0953& 0.0738& -0.0184\\ -0.0366& 0.2263& 0.1731& 0.0129& -0.0184& 0.46621\end{array}\right],\left[\begin{array}{cccccc}0& -0.3887& -0.4726& -0.0169& -0.0043& -0.3205\\ 0.3887& 0& -0.3203& -0.0722& 0.0841& 0.2418\\ 0.4726& 0.3203& 0& 0.0054& 0.0602& 0.4245\\ 0.0169& 0.0722& -0.0054& 0& -0.0046& 0.2474\\ 0.0043& -0.0841& -0.0602& 0.0046& 0& -0.1842\\ 0.3205& -0.2418& -0.4245& -0.2474& 0.1842& 0\end{array}\right],$$

$$\left[\begin{array}{cccccc}0& 0.5196& 0.5832& 0.3211& -0.1718& 0.0341\\ -0.5196& 0& 0.1365& 0.1215& -0.1603& 0.2871\\ -0.5832& -0.1365& 0& -0.0072& -0.1006& 0.4132\\ -0.3211& -0.1215& 0.0072& 0& -0.0521& 0.0369\\ 0.1718& 0.1603& 0.1006& 0.0521& 0& 0.0034\\ -0.0341& -0.2871& -0.4132& -0.0369& -0.0034& 0\end{array}\right],\left[\begin{array}{cccccc}0& -0.0324& 0.1329& 0.0221& 0.0059& -0.4517\\ 0.0324& 0& 0.0037& 0.1781& -0.0956& -0.3582\\ -0.1329& -0.0037& 0& 0.2225& -0.1549& -0.1844\\ -0.0221& -0.1781& -0.2225& 0& -0.0116& -0.1129\\ -0.0059& 0.0956& 0.1549& 0.0116& 0& -0.0112\\ 0.4517& 0.3582& 0.1844& 0.1129& 0.0112& 0\end{array}\right],$$

respectively. The dual part of $\widehat{A}$ is ${\tilde{A}}_{\mathcal{I}}=A_{\mathcal{I},1}+A_{\mathcal{I},2}\mathbf{i}+A_{\mathcal{I},3}\mathbf{j}+A_{\mathcal{I},4}\mathbf{k}\in {\mathbb{Q}}^{6\times 6}$, and $A_{\mathcal{I},1},A_{\mathcal{I},2},A_{\mathcal{I},3}$ and $A_{\mathcal{I},4}$ are equal to

$$\left[\begin{array}{cccccc}-0.8130& -0.0039& 0.2942& -0.1255& -0.1397& -0.0313\\ -0.0039& -0.3840& -0.2356& 0.1480& 0.8592& 0.4817\\ 0.2942& -0.2356& -0.0863& 0.4712& 1.0305& 0.2197\\ -0.1255& 0.1480& 0.4712& 0.2016& 0.3178& 0.6339\\ -0.1397& 0.8592& 1.0305& 0.3178& -0.3965& -0.3540\\ -0.0313& 0.4817& 0.2197& 0.6339& -0.3540& 0.2849\end{array}\right],\left[\begin{array}{cccccc}0& 0.0689& 0.4862& -0.4231& -0.3142& 0.1983\\ -0.0689& 0& 0.0069& -0.0679& -0.5687& -0.2706\\ -0.4862& -0.0069& 0& 0.2682& -0.4452& 0.1949\\ 0.4231& 0.0679& -0.2682& 0& -0.0837& 0.2557\\ 0.3142& 0.5687& 0.4452& 0.0837& 0& 0.5107\\ -0.1983& 0.2706& -0.1949& -0.2557& -0.5107& 0\end{array}\right],$$

$$\left[\begin{array}{cccccc}0& -0.7266& -0.2631& -0.0285& 0.8539& 0.5629\\ 0.7266& 0& -0.2641& 0.2712& -0.0399& 0.4132\\ 0.2631& 0.2641& 0& 0.4700& -0.4774& 0.0773\\ 0.0285& -0.2712& -0.4700& 0& -0.0426& 0.1856\\ -0.8539& 0.0399& 0.4774& 0.0426& 0& 0.6367\\ -0.5629& -0.4132& -0.0773& -0.1856& -0.6367& 0\end{array}\right],\left[\begin{array}{cccccc}0& 0.0525& 0.1599& -0.1970& 0.5612& 0.1146\\ -0.0525& 0& 0.7538& -0.2008& 0.2974& 0.4295\\ -0.1599& -0.7538& 0& -0.2703& 0.1851& 0.2496\\ 0.1970& 0.2008& 0.2703& 0& -0.2590& 0.0729\\ -0.5612& -0.2974& -0.1851& 0.2590& 0& -0.3074\\ -0.1146& -0.4295& -0.2496& -0.0729& 0.3074& 0\end{array}\right],$$

respectively.

In this experiment, we apply the Rayleigh quotient iteration (Algorithm 2) to compute all appreciable eigenvalues of $\widehat{A}$ with an initial unit dual quaternion vector

$$\widehat{\mathbf{q}}=\left[\begin{array}{c}-0.5514-1.3693\mathbf{i}-0.6843\mathbf{j}-0.5685\mathbf{k}\\ 0.2849+0.6141\mathbf{i}+2.7228\mathbf{j}+0.9304\mathbf{k}\\ -1.2502+0.1685\mathbf{i}-0.9310\mathbf{j}+0.4428\mathbf{k}\\ -0.4044-1.0874\mathbf{i}+0.1983\mathbf{j}+1.3718\mathbf{k}\\ -2.4265-0.4707\mathbf{i}-0.1511\mathbf{j}-0.4807\mathbf{k}\\ 0.8045+0.0331\mathbf{i}+0.8616\mathbf{j}+0.4602\mathbf{k}\end{array}\right]+\left[\begin{array}{c}1.2034-0.3999\mathbf{i}+1.5179\mathbf{j}+0.7439\mathbf{k}\\ 0.4025-1.5399\mathbf{i}+1.1467\mathbf{j}-0.5636\mathbf{k}\\ 1.2182-0.8999\mathbf{i}-0.1223\mathbf{j}+0.8272\mathbf{k}\\ -0.0179-0.3404\mathbf{i}-0.2029\mathbf{j}+1.3261\mathbf{k}\\ -0.9534+0.6708\mathbf{i}+0.2699\mathbf{j}+0.8289\mathbf{k}\\ -0.2012+0.0505\mathbf{i}+0.5192\mathbf{j}+0.1988\mathbf{k}\end{array}\right]ϵ.$$

This is a toy example to show the validity and reliability of our algorithm. We use the residual ${\parallel \widehat{A}{\widehat{\mathbf{v}}}_k-{\widehat{\mathbf{v}}}_k{\lambda }_k\parallel }_{2^R}\le 1\times {10}^{-10}$ as the stopping criterion. The RQI algorithm successively obtained the following six eigenvalues of the matrix $\widehat{A}$, and they are all dual numbers.

$$\begin{array}{cccc}\hfill & 58.248-14.5130ϵ,\hfill & \hfill 35.691+4.1262ϵ,& 21.769+8.1369ϵ,\hfill \\ \hfill & 11.176-5.9870ϵ,\hfill & \hfill 6.8844-2.0823ϵ,& 2.9425-1.1933ϵ.\hfill \end{array}$$

Meanwhile, the RQI algorithm obtains the residuals $\parallel \widehat{A}{\widehat{\mathbf{v}}}_i-{\widehat{\mathbf{v}}}_i{\lambda }_i{\parallel }_{2^R}$ for the above six eigenvalues, which are

$$\begin{array}{cc}\hfill & 2.842131593144027\times {10}^{-14},1.343608096502566\times {10}^{-13},\hfill \\ \hfill & 3.838679017102772\times {10}^{-14},4.374160421892654\times {10}^{-15},\hfill \\ \hfill & 3.549987504723655\times {10}^{-15},7.637401286299216\times {10}^{-15},\hfill \end{array}$$

respectively. Throughout the process, the RQI algorithm iterates a total of 19 steps and takes $0.0384$ s. In addition, we compare it with the power method (PM) [12], and the results are shown in

Table 1. The average numerical results of the RQI and PM methods for computing all eigenvalues of the dual quaternion matrix A.

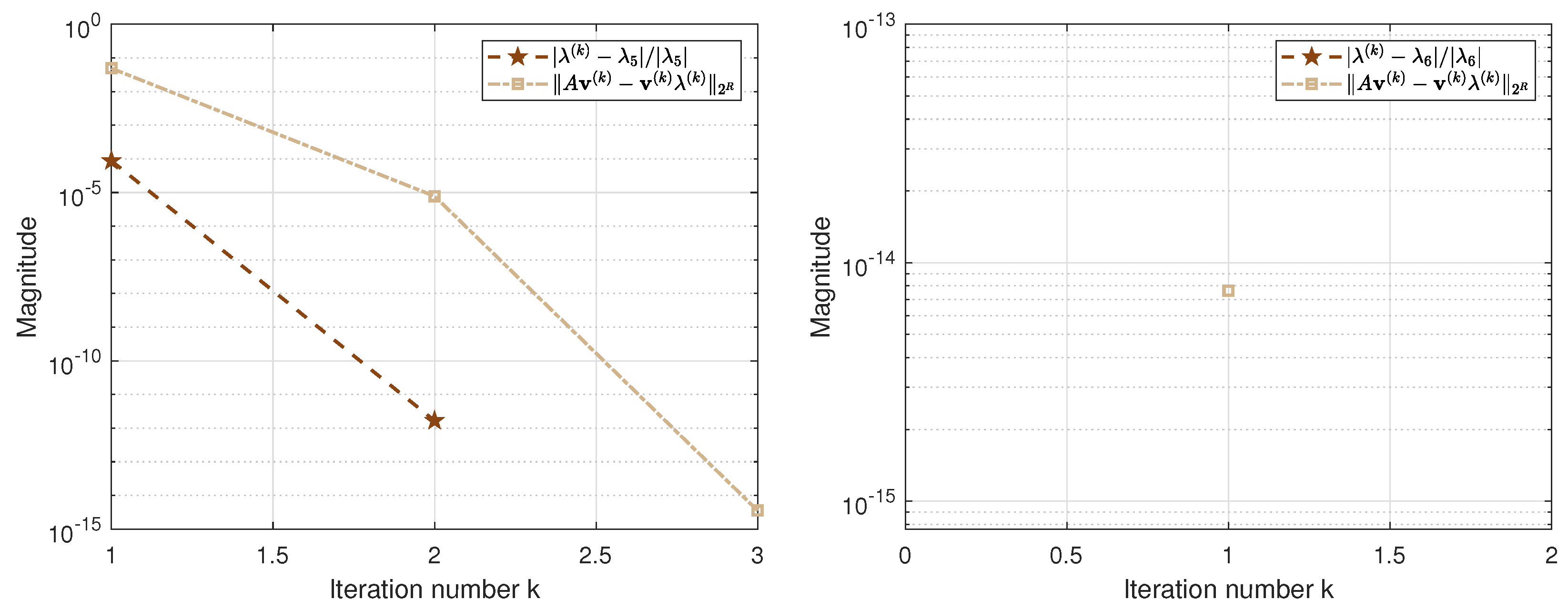
Method	Residual ${\parallel \widehat{\mathit{A}}\widehat{\mathit{v}}-\widehat{\mathit{v}}\mathit{\lambda }\parallel }_{2^{\mathit{R}}}$	Relative Error $|\widehat{\mathit{\lambda }}-{\mathit{\lambda }}_{\mathit{i}}|/|\mathit{\lambda }|$	IT	CPU (s)
RQI	6.425678537436753$\times {10}^{-14}$	7.6342876438642964$\times {10}^{-14}$	3	0.0064
PM	3.163485367353436$\times {10}^{-12}$	1.7456863573577357$\times {10}^{-13}$	41	0.0288

. The convergence curves of the Rayleigh quotient iteration are given in Figure 1. When computing the eigenvalues of the dense dual quaternion Hermitian matrix $\widehat{A}$, the efficiency of RQI surpasses that of PM in terms of iteration steps and CPU running time. Example 1 shows that Algorithm 1 is feasible and effective to solve Problem (1).

Example 2. 

Consider Problem (1) with the random Laplacian matrices. For a given graph $G=(V,E)$, which contains n vertices and m edges, the Laplacian matrix of graph G is defined as follows

$$L=D-\widehat{A},$$

where D is a diagonal real matrix, with diagonal entries signifying the degrees of the respective vertices, and $\widehat{A}=\left({\widehat{a}}_{ij}\right)$ is given as

$${\widehat{a}}_{ij}=\left\{\begin{array}{cc}{\widehat{\mathbf{q}}}_i^{*}{\widehat{\mathbf{q}}}_j,\hfill & \mathit{if}(i,j)\in E,\hfill \\ \widehat{0},\hfill & \mathit{otherwise},\hfill \end{array}\right.$$

where $\widehat{\mathbf{q}}=\left({\widehat{q}}_i\right)\in {\mathbb{DQ}}^{n\times 1}$ with ${\parallel \widehat{\mathbf{q}}\parallel }_2=1$. The Laplacian matrix has extensive practical applications [8,12,28]. Typically, in the field of multi-agent formation control, ${\widehat{q}}_i$ represents the configuration of the ith rigid body, while $a_{ij}$ represents the relative configuration between the ith rigid body and the jth rigid body, and matrix A denotes the adjacency matrix of relative configurations.

To ensure that all eigenvalues are appreciable, we introduce a small perturbation to the Laplacian matrix. Let $\check{L}=L+\alpha I_n$, where $\alpha$ is a nonzero real number. Then, $\lambda$ is an eigenvalue of L if and only if $\lambda +\alpha$ is an eigenvalue of $\check{L}$. We then define the residual

$$\parallel \widehat{L}{\widehat{\mathbf{v}}}_k-{\widehat{\mathbf{v}}}_k{\lambda }_k{\parallel }_{2^R}$$

of Problem (1) and the relative error

$${\displaystyle \frac{|{\lambda }_k-{\lambda }_i|}{|{\lambda }_i|}}$$

of the approximation to the desired eigenvalues during the iteration. The two indices are used to check whether the implemented methods converge to the desired eigenvalue with the associated eigenvector.

Then, we further consider the Laplacian matrix of circles with $10,20,50,100$ points. The residual of an eigenpair $({\lambda }_k,{\widehat{\mathbf{v}}}_k)$ is measured by $\parallel \widehat{L}{\widehat{\mathbf{v}}}_k-{\widehat{\mathbf{v}}}_k{\lambda }_k{\parallel }_{2^R}$. We either use the residual ${\parallel \widehat{L}{\widehat{\mathbf{v}}}_k-{\widehat{\mathbf{v}}}_k{\lambda }_k\parallel }_{2^R}\le 1\times {10}^{-10}$ or the number of iteration step has reached the upper limit of 15,000 as the stopping criterion.

Table 2. Numerical results of RQI and PM methods for computing the largest eigenpair of the random Laplacian matrices, where $\mathrm{RSE}:=\parallel \widehat{L}\widehat{\mathbf{v}}-\widehat{\mathbf{v}}{\lambda \parallel }_{2^R}$.

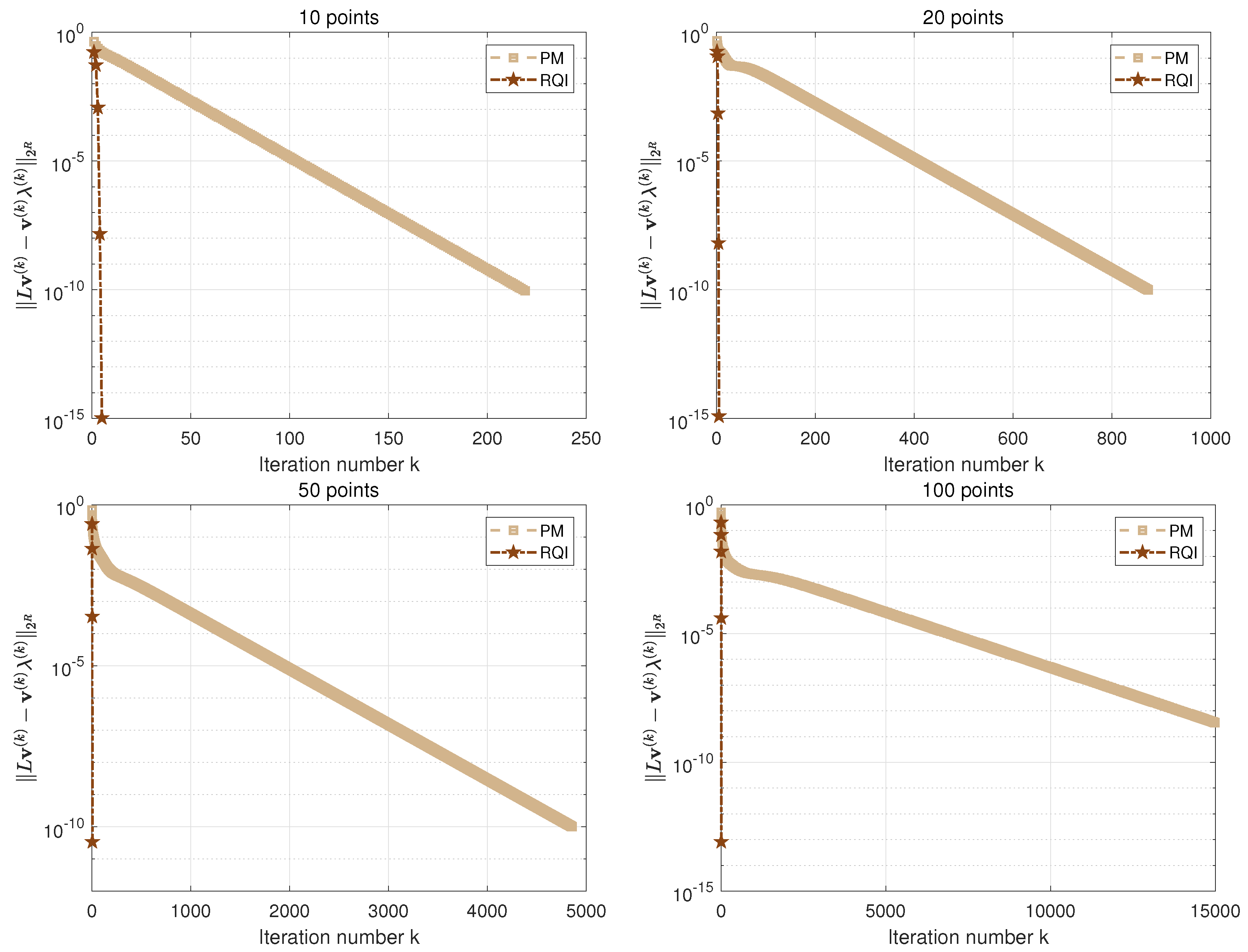
Method	n	10	20	50	100	200	400
	IT	5	5	4	4	5	5
RQI	CPU (s)	0.0103	0.0159	0.0148	0.0783	0.1734	1.1012
	RSE	1.0436$\times {10}^{-15}$	1.2212$\times {10}^{-15}$	3.3790$\times {10}^{-11}$	8.2080$\times {10}^{-14}$	1.1310$\times {10}^{-13}$	6.3420$\times {10}^{-14}$
	IT	219	873	4856	—	—	—
PM	CPU (s)	0.1347	0.5200	2.9406	—	—	—
	RSE	9.0942$\times {10}^{-11}$	9.8542$\times {10}^{-11}$	9.9711$\times {10}^{-11}$	—	—	—

and

Table 3. Numerical results of RQI and PM methods for computing the second smallest eigenpair of the random Laplacian matrices, where $\mathrm{RSE}:=\parallel \widehat{L}\widehat{\mathbf{v}}-\widehat{\mathbf{v}}{\lambda \parallel }_{2^R}$.

Method	n	10	20	50	100	200	400
	IT	5	3	7	5	5	6
RQI	CPU (s)	0.0113	0.0849	0.0288	0.0963	0.2547	2.7683
	RSE	6.7524$\times {10}^{-13}$	5.9735$\times {10}^{-12}$	3.3790$\times {10}^{-11}$	7.7547$\times {10}^{-12}$	3.5472$\times {10}^{-12}$	8.7542$\times {10}^{-14}$
	IT	533	1055	4666	—	—	—
PM	CPU (s)	0.1634	0.9198	3.0257	—	—	—
	RSE	1.7548$\times {10}^{-11}$	9.9296$\times {10}^{-11}$	9.9883$\times {10}^{-11}$	—	—	—

list the number of iterations, the CPU time, and the residuals for the Rayleigh quotient iteration and power method [12]. The symbol “—” means that the iteration step k has reached the upper limit of 15,000, but it did not derive a solution.

As indicated by the data presented in Table 2 and Table 3 and illustrated in Figure 2, the Rayleigh quotient iteration demonstrates superior efficiency compared to the power method. It achieves rapid convergence in just a few iterations when calculating eigenvalues for Laplacian matrices of various sizes. This efficiency leads to shorter computation times and enhanced accuracy. These findings underscore the suitability of the Rayleigh quotient iteration method for computing eigenvalues in large-scale dual quaternion Hermitian matrices.

6. Conclusions

In this paper, we have investigated the problem of solving right eigenvalues for dual quaternion Hermitian matrices. Firstly, we have presented the dual representation of dual quaternion matrices, which plays an important role in solving the dual quaternion linear systems. Secondly, leveraging this dual representation, we have proposed the Rayleigh quotient iteration for computing the eigenvalue with the associated eigenvector of dual quaternion Hermitian matrices. Thirdly, by utilizing minimal residual property of the Rayleigh quotient, we have derived a convergence analysis for the Rayleigh quotient iteration. Finally, we have provided numerical examples to illustrate the efficiency of the Rayleigh quotient iteration for solving the dual quaternion Hermitian eigenvalue problem.