Evaluating the Discrete Generalized Rayleigh Distribution: Statistical Inferences and Applications to Real Data Analysis

Abstract

Various discrete lifetime distributions have been observed in real data analysis. Numerous discrete models have been derived from a continuous distribution using the survival discretization method, owing to its simplicity and appealing formulation. This study focuses on the discrete analog of the newly generalized Rayleigh distribution. Both classical and Bayesian statistical inferences are performed to evaluate the efficacy of the new discrete model, particularly in terms of relative bias, mean square error, and coverage probability. Additionally, the study explores different important submodels and limiting behavior for the new discrete distribution. Various statistical functions have been examined, including moments, stress–strength, mean residual lifetime, mean past time, and order statistics. Finally, two real data examples are employed to evaluate the new discrete model. Simulations and numerical analyses play a pivotal role in facilitating statistical estimation and data modeling. The study concludes that the discrete generalized Rayleigh distribution presents a notably appealing alternative to other competing discrete distributions.

1. Introduction

As each day passes, the volume of data in our world increases exponentially, necessitating the development of new statistical distributions to better characterize the features of many phenomena and experiments. While a great deal of lifetime data appear to be continuous, they are originally discrete. This discrepancy ensures the need for more appropriate methods to generate discrete distributions that more accurately represent the data in the experiment. Discrete distributions are frequently employed in statistical modeling for several reasons.

Discrete distributions are used to model data that can only take on a finite or countably infinite number of values, such as counts, proportions, and binary outcomes, for example, the number of customers in a store, the number of heads in a coin flip, or the number of defective items in a production line. Discrete distributions are often easy to understand and interpret as they model data that take on a limited number of values. The probability mass function (pmf) or probability generating function (pgf) of a discrete distribution is a simple function that provides the probability of each possible outcome. Also, many discrete distributions have closed-form expressions for their pmf or pgf, which makes it easy to work with them mathematically. This allows for efficient computation of probabilities and moments without the need for integration. Furthermore, discrete distributions can be used to model a wide variety of real-world phenomena, such as the distribution of species in an ecosystem, the distribution of genetic variations in a population, or the distribution of traffic on a road network.

Recently, many discrete distributions have been considered, particularly in medicine, engineering, reliability, survival analysis, and more. For more descriptions and applications of discrete distributions, refer to [1,2,3,4,5,6,7,8,9]. Hence, many authors have conducted much work to originate and develop discrete models from different aspects.

The characterization of continuous random variables can be performed either by their probability density function, cumulative distribution function, moments, moment-generating function, hazard rate functions, or others. Different discretization methods appeared in the literature to create an appropriate discrete distribution based on the underlying continuous model.

By deriving discrete analogs or counterparts of well-known continuous distributions, statisticians can better tailor their models to the specific nature of the data. Usually, creating a discrete analog from a continuous distribution is based on the principle of preserving one or more characteristic properties of the continuous one. Consequently, different ways to discretize a continuous distribution appear in the literature depending on the property the researcher intends to preserve; for example, Lai [10] used the survival and the hazard rate preservation methods to create discrete distributions from different continuous ones. Haj Ahmad and Almetwally [11] used the survival, hazard rate, and probability distribution function preservation methods to discretize the generalized Pareto distribution.

The benefit of using the survival discretization method is that it can maintain the statistical properties of the original distribution, including median and percentiles, in addition to the overall shape of the distribution. A drawback of this method is that it can be computationally intensive and may require numerical methods for complex distributions.

For the hazard preservation method, the main benefit is that it preserves the hazard function of the continuous distribution. This is important in applications like reliability analysis where the failure rate is a key parameter. On the other hand, mathematical complexity can be viewed using this method, especially for continuous distributions with nonlinear hazard functions. This complexity can increase computational time and resource requirements. Another drawback of the hazard preservation method is that it only preserves the hazard function, but other characteristics of the distribution (like mean, variance, or skewness) may not be as accurately retained. For more details about other discretization methods and their properties, one may refer to [12,13] who provided a review of several discretization methods.

From the previous research work, it is evident that the results look appealing and motivational to continue creating new discrete distributions to model new data.

In the present study, we obtain a discrete analog of the continuous new generalized Rayleigh distribution (NGRD) using the survival discretization method that depends on the survival function. See for example [6,7], in which the survival discretization approach was used to obtain the discrete normal and discrete Rayleigh distributions, respectively. Using the same approach, more discrete distributions have been introduced and studied; see for example [14,15,16,17,18,19,20,21,22,23].

Still, there is an enduring need to create and develop more discrete models and to generate new ones because of modeling and fitting real data, which appear and spread constantly in human life. The efficiency in discretization methods refers to the ability of a method to produce accurate and useful discretized versions of continuous data with minimal loss of information. Also, discrete distributions derived from continuous ones can inherit their flexibility and adaptability. This allows statisticians to model a wider range of data characteristics, such as skewness or kurtosis, which might be difficult with standard discrete distributions. In statistical methodology, continuous distributions may have characteristics that are missing in the discrete space; hence, creating discrete analogs can fill these gaps, providing new tools for data analysis.

The suggested discrete model with three parameters offers an immense degree of fitness to skewed, symmetric, monotone, and inverse J-shape types of data. Therefore, some statistical functions and properties are achieved, in addition to observing the submodels and limiting behavior of the proposed discrete distribution. Examining statistical inference is crucial; therefore, point and interval estimation for the unknown parameters using the maximum likelihood estimator and the Bayesian method is performed.

Simulation analysis via numerical techniques such as Monte Carlo simulation is employed to evaluate the estimators using the maximum likelihood and the Bayesian estimation methods to compare the performance of these two methods. The efficiency is assessed using the relative bias, the mean squared error, and the coverage probability of the confidence intervals. Two real datasets are analyzed to emphasize the empirical validation of the new model, where several goodness-of-fit measures are employed. The first example is related to the industrial field, where several strikes that occurred in coal mining in the UK were recorded over four weeks. Modeling and predicting the number of strikes will save human lives and money. The second example is related to the number of fires that occurred in Greece’s forests in the year 1998 during the summer months. The main purposes of this study are, first, to introduce new discrete analogs of the continuous NGRD and evaluate some of its important statistical functions, second, to perform the inferential statistics related to the new distributions’ parameters and compare the results, and, third, to assess the efficiency of the new discrete distribution by modeling real data examples and comparing the goodness-of-fit measures with other discrete distributions that were studied earlier in the literature.

The originality of this work emanates from the basis of exploring the creation of a new discrete analog from less commonly used continuous distributions and investigating their properties, potential applications, and how they compare to existing distributions. Also, it focuses on specific application areas, such as the industrial, engineering, and reliability fields. To our knowledge, no previous work has studied the discrete new generalized Rayleigh distribution and employed it to model real-life data examples from different scientific fields.

The authors’ contributions to this study can be summarized as follows:

• Development of a New Discrete Model: Creation of a discrete analog of the continuous new generalized Rayleigh distribution (NGRD) using the survival discretization method.
• Statistical Functions and Properties: Achievement of various statistical functions and properties of the proposed discrete distribution, including observing its submodels and limiting behavior.
• Statistical Inference Examination: Conducting point and interval estimation for the unknown parameters using both the maximum likelihood estimator (MLE) and the Bayesian method.
• Simulation Analysis for Estimator Evaluation: Implementation of numerical techniques such as Monte Carlo simulation to evaluate the estimators derived from MLE and Bayesian estimation methods through relative bias, mean squared error, and coverage probability of confidence intervals
• Empirical Validation via Real Data Analysis: Analyzing two real datasets to validate the new model empirically, including modeling industrial and environmental phenomena.
• Comparison with other Distributions: Comparing the goodness of fit of the new model with other discrete distributions previously studied in the literature.

The remaining parts of this work are organized as follows: Section 2 describes the new generalized Rayleigh distribution. The discretization methods are presented in Section 3, along with some statistical functions. In Section 4, the maximum likelihood and the Bayesian inference are presented. In Section 5, simulation analysis and the tabulated results are carried out. Some real data examples are provided in Section 6. Finally, conclusions are remarked on in Section 7.

2. Model Description

The Rayleigh distribution (RD) is a continuous distribution that has much practical importance; hence, many of its statistical characteristics, inference, and reliability analysis have been studied by several authors, and numerous extended forms of the Rayleigh distribution have been proposed. For example, Ref. [24] applied the inverse Rayleigh to the failure times data. Ref. [25] introduced the transmuted Rayleigh and used it to model the amount of nicotine in the blood. In [26], the authors studied the beta-generalized Rayleigh distribution and its application. Ref. [27] obtained the transmuted inverse Rayleigh distribution to lifetime data. Ref. [28] obtained a new modified Rayleigh distribution named the Kumaraswamy generalized Rayleigh distribution with application to real data. For more information, refer to [29,30,31]. In this work, we are interested in studying a new form of the Rayleigh distribution called a new generalized Rayleigh distribution (NGR), which was first introduced by Shen et al. [32]. It has three parameters and it was shown that the NGR is suitable for modeling large data values rather than small data values. However, as a continuous distribution, it is restricted from describing discrete data forms. Discretizing the NGR distribution is our goal; therefore, it yields a subsequent distribution that accommodates the countable data while retaining the influential tail modeling characteristics of the NGR. In this study, we carry out a discrete version of the NGR and use it to model real data.

The probability density function (pdf) and the survival function (S) of the continuous NGR are provided respectively as:

$$f\left(x;\alpha ,\beta ,\theta \right)=\frac{2\alpha \beta \theta \left(\alpha -1\right)x{e}^{-\theta x^2}{(1-e^{-\theta x^2})}^{\beta -1}}{{\left[\alpha -{\left(1-e^{-\theta x^2}\right)}^{\beta }\right]}^2},x>0,$$

(1)

and

$$S\left(x;\alpha ,\beta ,\theta \right)=\frac{\alpha [1-{\left(1-e^{-\theta x^2}\right)}^{\beta }]}{\alpha -{\left(1-e^{-\theta x^2}\right)}^{\beta }},$$

(2)

in which the parameters $\alpha >1,\beta >0,\theta >0$.

The hazard rate function is

$$h\left(x;\alpha ,\beta ,\theta \right)=\frac{2\beta \theta \left(\alpha -1\right)x{e}^{-\theta x^2}{(1-e^{-\theta x^2})}^{\beta -1}}{\left[1-{\left(1-e^{-\theta x^2}\right)}^{\beta }\right]{\left[\alpha -{\left(1-e^{-\theta x^2}\right)}^{\beta }\right]}^2}.$$

(3)

To identify submodels or special distributions that arise from this general form, we can consider different values or limits of parameters $\alpha$, $\beta$, and $\theta$. Here are some special cases:

• Standard Rayleigh Distribution: When $\theta =1$ and $\beta =1$, the term $(1-e^{-x^2})$ simplifies to the CDF of the standard Rayleigh distribution. This is observed if the parameter $\alpha$ also approaches infinity, which simplifies the formula to $1-e^{-x^2}$, the CDF of the standard Rayleigh distribution.
• Exponential Distribution: If $\beta$ approaches infinity, the term $\Lambda$ = ${(1-e^{-\theta x^2})}^{\beta }$ can approach an exponential-like behavior for small values of x, depending on how $\theta$ is defined.
• Modified Rayleigh Distribution: For specific fixed values of $\alpha$ and $\beta$, you can obtain various forms of modified Rayleigh distributions, where the behavior is measured by the degree of skewness and kurtosis determined by these parameters.
• Weibull-like Distribution: By interchanging between $\theta$ and $\beta$, especially when $\beta$ is not equal to 1, the distribution can possess Weibull-like properties.

By discretizing the continuous range of x, discrete versions of this distribution can be derived, which may be useful for certain types of count data or integer-valued measurements.

Since our goal in this work is to define a new discrete NGR distribution, we generate a discrete analog based on the survival discretization method, which is denoted by DNGR. The pmf and cumulative distribution function (CDF) are obtained. Furthermore, the moments, stress–strength function, the mean residual, and mean past lifetimes, order statistics, and L-moments are obtained. All these statistical functions are used for studying the features of the DNGR.

3. The Discrete New Generalized Rayleigh Distribution

Roy and Gupta [3,4] defined the probability mass function (pmf) for a discrete distribution using the survival function and it was expressed as follows:

$$P\left(X=k\right)=S\left(k\right)-S\left(k+1\right),k=0,1,2,\dots$$

(4)

where $S\left(x\right)$ is the survival function provided by Equation (2); hence, the pmf of the discrete analog of NGR distribution, namely DNGR, is written as

$$P\left(X=k\right)=\frac{\alpha [1-\Lambda \left(k;\theta ,\beta \right)]}{\alpha -\Lambda \left(k;\theta ,\beta \right)}-\frac{\alpha \left[1-\Lambda \left(k+1;\theta ,\beta \right)\right]}{\alpha -\Lambda \left(k+1;\theta ,\beta \right)},$$

(5)

where $\Lambda \left(k;\theta ,\beta \right)={\left(1-e^{-\theta k^2}\right)}^{\beta }$.

The CDF of the DNGR distribution can be written as

$$P\left(X<k\right)=F\left(k+1\right)=1-\frac{\alpha \left[1-\Lambda \left(k+1;\theta ,\beta \right)\right]}{\alpha -\Lambda \left(k+1;\theta ,\beta \right)}.$$

(6)

The quantile function with given values of parameters as $\alpha ,\beta$, and $\theta$ of the DNGR distribution is provided by

$$x_i=\sqrt{\frac{-1}{\theta }ln\left[1-{\left(\frac{\alpha q}{\alpha +q-1}\right)}^{1/\beta }\right]}-1;q=[0,1],i=1,\dots ,n.$$

(7)

The hazard rate function (HRF) of the DNGR distribution is provided by

$$h_{\mathrm{DNGR}1}\left(k\right)=\frac{\left[1-\Lambda \left(k;\theta ,\beta \right)\right]\left[\alpha -\Lambda \left(k+1;\theta ,\beta \right)\right]}{\left[\alpha -\Lambda \left(k;\theta ,\beta \right)\right]\left[1-\Lambda \left(k+1;\theta ,\beta \right)\right]}-1.$$

(8)

We also observe that the reversed hazard rate function for the DNGR of this distribution is provided by

$$r_{DNGR}\left(k;\alpha ,\beta ,\theta \right)=\frac{f\left(k;\alpha ,\beta ,\theta \right)}{F\left(k+1;\alpha ,\beta ,\theta \right)},$$

(9)

$$\begin{array}{c}\hfill r_{DNGR}\left(k;\alpha ,\beta ,\theta \right)=\left[\frac{\alpha \left[1-\Lambda \left(k;\theta ,\beta \right)\right]}{\alpha -\Lambda \left(k;\theta ,\beta \right)}-\frac{\alpha \left[1-\Lambda \left(k+1;\theta ,\beta \right)\right]}{\alpha -\Lambda \left(k+1;\theta ,\beta \right)}\right]\\ \hfill \times \left[\frac{\alpha -\Lambda \left(k+1;\theta ,\beta \right)}{\left(\alpha -\Lambda \left(k+1;\theta ,\beta \right)\right)-\alpha \left[1-\Lambda \left(k+1;\theta ,\beta \right)\right]}\right]\end{array}$$

(10)

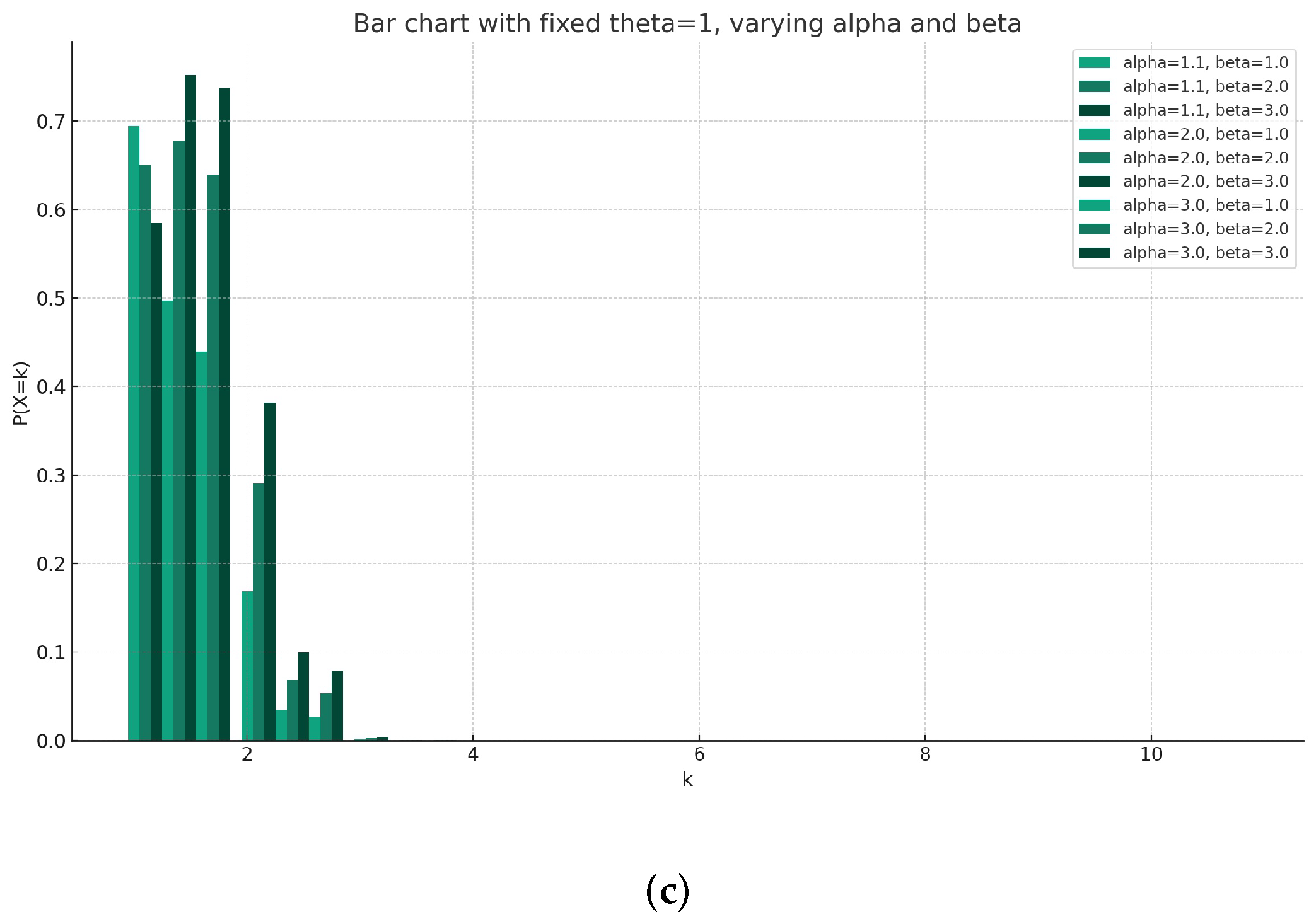
In Figure 1, the bar charts represent each parameter $\alpha ,\theta ,\mathrm{and}\beta$ that has a specific role in the behavior of the pmf, and their effects are observable when we fix one and vary the others. An explanation of the effect of each parameter based on the plots is as follows:

1.

Effect of $\alpha$ when $\theta$ and $\beta$ are changeable:

When $\alpha$ is fixed, the variations in $\theta$ and $\beta$ create different trends in the probability values. Higher values of $\theta$ tend to stretch the curve horizontally, meaning, for a given $\alpha$, as $\theta$ increases, the decrease in probability values with increasing k is less steep. Higher values of $\beta$ tend to amplify the curve vertically, making the probability have fewer values for higher k values. The reaction between $\theta$ and $\beta$ at a fixed $\alpha$ demonstrates that $\theta$ affects the spread of the distribution, while $\beta$ affects the sharpness of the probability decrease.

2.

Effect of $\theta$ when $\alpha$ and $\beta$ are changeable:

With $\theta$ fixed, the changes in $\alpha$ and $\beta$ show distinct patterns. An increase in $\alpha$ generally results in higher probability values across all k. This is because a higher $\alpha$ relative to $\Lambda$(k; $\theta$,$\beta$) increases the numerator and decreases the denominator of the function $P(X=k)$, resulting in a larger overall value. The effect of $\beta$ at a fixed $\theta$ is similar to its effect when $\alpha$ is fixed; it controls the sharpness of the decrease in probability values. Higher $\beta$ values cause a quicker decline in probability as k increases.

3.

Fixing $\beta$ and varying $\alpha$ and $\theta$, we can see that

As $\alpha$ increases, for a fixed $\beta$, the overall probability values increase, similar to when $\theta$ is fixed. The role of $\theta$ here is nuanced; for lower values of k, the impact of changing $\theta$ is minimal, but, as k increases, higher $\theta$ values preserve higher probabilities, indicating a wider spread in the distribution. From the above explanations, it is clear that $\alpha$ primarily scales the probability values, $\beta$ determines the rate at which the probability values decline as k increases (sharpness of the distribution), and $\theta$ controls the spread or dispersion of the distribution across k values. The combination of these three parameters can thus shape the function’s distribution in various ways, and each has a distinctive role in the form of the probability curve.

In Figure 2, the plots represent the HRF of the DNGR distribution for various combinations of parameters $\alpha ,\theta ,\mathrm{and}\beta$. Each subplot corresponds to a different set of these parameters. The values of k range from 1 to 10. The curves are increasing for different values of the parameters; we can realize the effect of increasing the parameter $\theta$ while keeping other parameters fixed by going steeply to the left. For the effect of $\beta$, assuming other parameters are fixed, it can be figured by increasing in a slower mode when k takes small values. Finally, the effect of increasing the values of $\alpha$ while fixing the remaining parameters is going to the left more steeply.

The limiting behavior of DNGR for different choices in parameter values at the boundary points includes

${\lim }_{k\to \infty }p\left(k\right)=0$, ${\lim }_{k\to 0}p\left(k\right)=0$,

${\lim }_{\alpha \to 1}p\left(k\right)=0$, ${\lim }_{\alpha \to \infty }p\left(k\right)=\Lambda \left(k+1;\theta ,\beta \right)-\Lambda \left(k;\theta ,\beta \right)$,

${\lim }_{\theta \to 0}p\left(k\right)=0,$${\lim }_{\theta \to \infty }p\left(k\right)=0$,

${\lim }_{\beta \to 0}p\left(k\right)=0,$ and ${\lim }_{\beta \to \infty }p\left(k\right)=0$.

From the above limiting behavior of the DNGR, some submodels and special cases can be derived, such as

• Discrete standard Rayleigh Distribution: When $\theta =1$ and $\beta =1$, and $\alpha$ approaches infinity, the pmf simplifies to $(1-e^{-{(x+1)}^2})-(1-e^{-x^2})$, which represents the pmf of the discrete Rayleigh distribution created from applying the survival discretization method.
• Discrete Exponential-like Distribution: For large values of $\beta$ and specific values of $\theta$, the DNGR distribution might possess characteristics similar to an exponential distribution for smaller values of k, where the exponential decay behavior is more evident, since the term $\Lambda$ = ${(1-e^{-\theta k^2})}^{\beta }$ has a decaying form and can be considered as exponential-like function.
• Discrete Uniform Distribution: If the parameters $\alpha$, $\beta$, and $\theta$ are chosen such that the pmf becomes constant for all k within a certain range, the DNGR distribution could approximate a discrete uniform distribution.
• Geometric-like Distribution: By adjusting $\theta$ and $\beta$, you might be able to create a distribution that behaves like the geometric distribution, especially if the probability of larger k values decays like the geometric series.

These possible submodels and special cases demonstrate the versatility and adaptability of the DNGR distribution. The ability to derive such a variety of distributions from a single distribution highlights the potential utility of the DNGR distribution in modeling a wide range of discrete data scenarios. Each submodel or special case would be suited to different types of data and could provide unique insights depending on the context of the analysis.

3.1. Moments

Assume a non-negative random variable $k\sim DNGR\left(\alpha ,\beta ,\theta \right)$. The $s^{th}$ moment, say ${\psi }_s^{\prime }$, can be expressed as follows

$${\psi }_s^{\prime }=\sum _{k=0}^{\infty }{k}^{s}f\left(k;\alpha ,\beta ,\theta \right),$$

and then

$${\psi }_s^{\prime }=\sum _{k=0}^{\infty }{k}^s\left[\frac{\alpha \left[1-\Lambda \left(k;\theta ,\beta \right)\right]}{\alpha -\Lambda \left(k;\theta ,\beta \right)}-\frac{\alpha \left[1-\Lambda \left(k+1;\theta ,\beta \right)\right]}{\alpha -\Lambda \left(k+1;\theta ,\beta \right)}\right].$$

(11)

It is impossible to write an exact form of the $s^{th}$ moment; hence, R programming with version (4.3.0) is helpful, and the moment is evaluated numerically. Equation (11) is convergent for $\alpha >1,\beta >0$, and $\theta >0$.

Table 1. Summary of descriptive statistics for the DNGR distribution.

$\mathit{\theta }$	$\mathit{\alpha }$	$\mathit{\beta }$	Minimum	Mean	Variance	Maximum	SK	Kt
0.8	1.05	0.3	0	1.5140	0.4643	3	−0.0700	1.2956
	1.05	1.2	0	1.9760	0.3338	4	−0.0563	1.3066
	1.05	2.5	0	2.1890	0.3176	4	−0.0479	1.3039
	1.05	3	1	2.2420	0.3137	4	−0.0461	1.3030
	2.2	0.3	0	0.6480	0.4305	3	0.1245	1.1141
	2.2	1.2	0	1.2470	0.3664	3	0.0229	1.2125
	2.2	2.5	0	1.5330	0.3252	3	0.0203	1.2296
	2.2	3	0	1.6020	0.3179	3	0.0212	1.2320
	3	0.3	0	0.5810	0.4098	3	0.1629	1.1205
	3	1.2	0	1.1880	0.3570	3	0.0373	1.2097
	3	2.5	0	1.4770	0.3178	3	0.0320	1.2281
	3	3	0	1.5450	0.3163	3	0.0325	1.2307
1.5	1.05	0.3	0	1.0800	0.2799	3	−0.0699	1.2957
	1.05	1.2	0	1.4600	0.2827	3	−0.0564	1.3066
	1.05	2.5	0	1.6570	0.2396	3	−0.0481	1.3039
	1.05	3	0	1.7020	0.2214	3	−0.0461	1.3031
	2.2	0.3	0	0.4520	0.2860	2	0.1244	1.1142
	2.2	1.2	0	0.9210	0.2190	2	0.0229	1.2125
	2.2	2.5	0	1.1120	0.1616	2	0.0203	1.2295
	2.2	3	0	1.1510	0.1624	2	0.0213	1.2321
	3	0.3	0	0.4010	0.2725	2	0.1629	1.1205
	3	1.2	0	0.8800	0.2258	2	0.0374	1.2096
	3	2.5	0	1.0830	0.1503	2	0.0321	1.2280
	3	3	0	1.1210	0.1485	2	0.0325	1.2306
3	1.05	0.3	0	0.8230	0.1598	2	−0.0700	1.2956
	1.05	1.2	0	0.9890	0.0689	2	−0.0563	1.3067
	1.05	2.5	0	1.0460	0.0680	2	−0.0480	1.3040
	1.05	3	0	1.0610	0.0734	2	−0.0459	1.3031
	2.2	0.3	0	0.2800	0.2038	2	0.1245	1.1143
	2.2	1.2	0	0.6820	0.2231	2	0.0229	1.2123
	2.2	2.5	0	0.8840	0.1127	2	0.0203	1.2296
	2.2	3	0	0.9200	0.0857	2	0.0210	1.2320
	3	0.3	0	0.2420	0.1856	2	0.1628	1.1204
	3	1.2	0	0.6360	0.2357	2	0.0374	1.2097
	3	2.5	0	0.8590	0.1292	2	0.0321	1.2280
	3	3	0	0.9020	0.0985	2	0.0325	1.2307

explores some functions like the minimum, mean, variance, maximum, skewness (SK), and kurtosis (Kt) for different values of $\alpha ,\beta$, and $\theta$. In addition, the DNGR distribution is appropriate for modeling both over- and under-dispersed data since, in this model, the variance can be smaller than the mean, which is the case with some standard classical discrete distributions, in addition to the positive and negative skewness values, which show that this distribution can be skewed to the right or left. Also, a very small skew value that tends to zero indicates a symmetry possible curve for the pmf. A higher kurtosis means more of the variation is due to infrequent extreme deviations as opposed to frequent modestly sized deviations. By varying $\theta$, $\alpha$, and $\beta$, one can realize the distribution changes. For instance, with $\theta$ = 0.8 and $\alpha$ = 0.5, $\beta$ changing from 0.84 to 2.73 drastically increases the kurtosis, indicating a heavier tail.

3.2. Stress–Strength Analysis

The stress–strength (reliability) analysis is an important tool in mechanical design. The idea relies on the probability of failure that is obtained from the probability of $r$ exceeding $r^{*}$. Assume that both $r$ and $r^{*}$ are in the positive domain. The expected reliability ($R^{*}$) can be calculated by

$$R^{*}=P\left[K_r\le K_{r^{*}}\right]=\sum _{k=0}^{\infty }{f}_{K_r}\left(k\right)R_{K_{r^{*}}}\left(k\right),$$

(12)

in which $K_r\sim DNGR\left({\alpha }_1,{\beta }_1,{\theta }_1\right)$ and $K_{r^{*}}\sim DNGR\left({\alpha }_2,{\beta }_2,{\theta }_2\right)$, and then $R^{*}$ can be expressed as follows

$$R^{*}=\sum _{k=0}^{\infty }\left[\frac{{\alpha }_1\left[1-{\Lambda }_1\left(k;{\theta }_1,{\beta }_1\right)\right]}{{\alpha }_1-{\Lambda }_1\left(k;{\theta }_1,{\beta }_1\right)}-\frac{{\alpha }_1\left[1-{\Lambda }_1\left(k+1;{\theta }_1,{\beta }_1\right)\right]}{{\alpha }_1-{\Lambda }_1\left(k+1;{\theta }_1,{\beta }_1\right)}\right]\left[\frac{{\alpha }_2\left[1-{\Lambda }_2\left(k;{\theta }_2,{\beta }_2\right)\right]}{{\alpha }_2-{\Lambda }_2\left(k;{\theta }_2,{\beta }_2\right)}\right],$$

where ${\Lambda }_1\left(k;{\theta }_1,{\beta }_1\right)={\left(1-e^{-{\theta }_1{k}^2}\right)}^{{\beta }_1}$ and ${\Lambda }_2\left(k;{\theta }_2,{\beta }_2\right)={\left(1-e^{-{\theta }_2{k}^2}\right)}^{{\beta }_2}$.

We cannot obtain a closed form for the above equation; consequently, simulation analysis is utilized to obtain a numerical solution. In Section 6, numerical analysis is performed to obtain the value of the stress–strength function under two real data applications.

3.3. The Mean Residual and the Mean Past Lifetimes

In reliability and survival analysis, many lifetime measures have been discussed in the literature. They were defined to study the aging behavior of the experimental units. One of these measures is the mean residual lifetime (MRL), which is a helpful tool in determining burn-in and maintenance policies. For discrete distributions, the MRL is defined as follows:

$$\zeta \left(i\right)=E\left(k-i\left|\phantom{k-ik\ge i}\right.k\ge i\right)=\frac{1}{S\left(i\right)}\sum _{j=i+1}^{l}S\left(j\right);i\in \mathbb{N},$$

(13)

where $0<l<\infty .$

If the random variable k follows the DNGR distribution with parameters $\alpha ,\beta$, and $\theta$, which is denoted by $k\sim DNGR\left(\alpha ,\beta ,\theta \right)$, then the MRL is expressed as

$$\zeta \left(i\right)=\frac{\alpha -\Lambda \left(i;\theta ,\beta \right)}{\alpha \left[1-\Lambda \left(i;\theta ,\beta \right)\right]}\sum _{j=i+1}^l\frac{\alpha \left[1-\Lambda \left(j;\theta ,\beta \right)\right]}{\alpha -\Lambda \left(j;\theta ,\beta \right)}.$$

(14)

The mean past lifetime (MPL) is another important measure in reliability analysis. The MPL measures the time elapsed after the failure of $K$ units given that the system has failed sometime earlier to i. In the discrete case, the MPL is defined as follows

$${\zeta }^{*}\left(i\right)=E\left(i-k|k<i\right)=\frac{1}{F\left(i-1\right)}\sum _{m=1}^{i}F\left(m-1\right);i\in \mathbb{N}-\left\{0\right\},$$

(15)

where ${\zeta }^{*}\left(0\right)=0$; see [33].

Then,

$${\zeta }^{*}\left(i\right)={\left[1-\frac{\alpha -\Lambda \left(i;\theta ,\beta \right)}{\alpha \left[1-\Lambda \left(i;\theta ,\beta \right)\right]}\right]}^{-1}\sum _{m=1}^i\left[1-\frac{\alpha \left[1-\Lambda \left(m-1;\theta ,\beta \right)\right]}{\alpha -\Lambda \left(m-1;\theta ,\beta \right)}\right].$$

(16)

3.4. Order Statistics

Let $K_1,K_2,\dots ,K_n$ be a random sample with the DNGR distribution and $K_{1:n},K_{2:n},\dots ,K_{n:n}$ denote the corresponding order statistics. Then, the CDF of $i^{th}$ order statistics at the value k can be written as follows

$$F_{i:n}\left(k;\alpha ,\beta ,\theta \right)=\sum _{i=1}^n\left(\begin{array}{c}n\\ m\end{array}\right){\left[F_i\left(k;\alpha ,\beta ,\theta \right)\right]}^m{\left[1-F_i\left(k;\alpha ,\beta ,\theta \right)\right]}^{n-m}.$$

(17)

By using the negative binomial theorem, then

$$F_{i:n}\left(k;\alpha ,\beta ,\theta \right)=\sum _{i=1}^n\sum _{j=1}^{n-m}\left(\begin{array}{c}n\\ m\end{array}\right){\left(\begin{array}{c}n-m\\ j\end{array}\right)\left(-1\right)}^j{\left[F_i\left(k;\alpha ,\beta ,\theta \right)\right]}^{m+j}.$$

(18)

Therefore,

$$F_{i:n}\left(k;\alpha ,\beta ,\theta \right)=\sum _{i=1}^n\sum _{j=1}^{n-m}\left(\begin{array}{c}n\\ m\end{array}\right){\left(\begin{array}{c}n-m\\ j\end{array}\right)\left(-1\right)}^j{\left[1-\frac{\alpha \left[1-\Lambda \left(k;\theta ,\beta \right)\right]}{\alpha -\Lambda \left(k;\theta ,\beta \right)}\right]}^{m+j}.$$

(19)

Consequently, the pmf of the $i^{th}$ order statistic under the DNGR can be derived and expressed as follows

$$f_{i:n}\left(k;\alpha ,\beta ,\theta \right)=\sum _{i=1}^n\sum _{j=1}^{n-m}\left(\begin{array}{c}n\\ m\end{array}\right){\left(\begin{array}{c}n-m\\ j\end{array}\right)\left(-1\right)}^j{\left[\frac{\alpha \left[1-\Lambda \left(k;\theta ,\beta \right)\right]}{\alpha -\Lambda \left(k;\theta ,\beta \right)}-\frac{\alpha \left[1-\Lambda \left(k+1;\theta ,\beta \right)\right]}{\alpha -\Lambda \left(k+1;\theta ,\beta \right)}\right]}^{m+j}.$$

So, the ${\upsilon }^{th}$ moments of $k_{i:n}$ can be written as follows

$$E\left(K_{i:n}^{\nu }\right)=\sum _{k=0}^{\infty }\sum _{i=1}^n\sum _{j=1}^{n-m}\left(\begin{array}{c}n\\ m\end{array}\right){\left(\begin{array}{c}n-m\\ j\end{array}\right)\left(-1\right)}^j{k}^{\nu }{\left[\frac{\alpha \left[1-\Lambda \left(k;\theta ,\beta \right)\right]}{\alpha -\Lambda \left(k;\theta ,\beta \right)}-\frac{\alpha \left[1-\Lambda \left(k+1;\theta ,\beta \right)\right]}{\alpha -\Lambda \left(k+1;\theta ,\beta \right)}\right]}^{m+j}.$$

4. Estimation

Two estimation methods are considered in this work: frequentist maximum likelihood estimation (MLE) and the Bayesian estimation method. Simulation analysis and numerical techniques are performed in Section 5 to assess the performance of these estimation methods.

4.1. Maximum Likelihood Estimation

In this section, we use the maximum likelihood estimation MLE method to estimate the unknown parameters of the DNGR distributions. To evaluate the required estimators, numerical techniques are used, such as the well-known Newton–Raphson technique.

Let $x_1,\dots ,x_n$ be a random sample following the DNGR, and then, from pmf in Equation (5), the log-likelihood function is written as

$$\begin{array}{c}\hfill \mathsf{\ell }\left(\alpha ,\beta ,\theta \right)=\sum _{k=1}^n\log \left(\alpha \left(\alpha -1\right)\right)+\log \left(\Lambda \left(x_{k+1};\theta ,\beta \right)-\Lambda \left(x_k;\theta ,\beta \right)\right)\\ \hfill -\log \left(\alpha -\Lambda \left(x_k;\theta ,\beta \right)\right)-\log \left(\alpha -\Lambda \left(x_{k+1};\theta ,\beta \right)\right)\end{array}$$

(20)

The MLEs for $\alpha ,\beta$, and $\theta$ are obtained by finding the partial derivatives of $\mathsf{\ell }\left(\alpha ,\beta ,\theta \right)$ for $\alpha ,\beta$, and $\theta$, then equating the three equations to zero and solving numerically.

$$\frac{\mathsf{\partial }\mathsf{\ell }\left(\alpha ,\beta ,\theta \right)}{\mathsf{\partial }\alpha }=\sum _{k=1}^n\frac{2\alpha -1}{\alpha \left(\alpha -1\right)}-\frac{1}{\alpha -\Lambda \left(x_k;\theta ,\beta \right)}-\frac{1}{\alpha -\Lambda \left(x_{k+1};\theta ,\beta \right)}=0,$$

(21)

$$\frac{\mathsf{\partial }\mathsf{\ell }\left(\alpha ,\beta ,\theta \right)}{\mathsf{\partial }\beta }=\sum _{k=1}^n\frac{{\Lambda }_{\beta }\left(x_{k+1};\theta ,\beta \right)-{\Lambda }_{\beta }\left(x_k;\theta ,\beta \right)}{\Lambda \left(x_{k+1};\theta ,\beta \right)-\Lambda \left(x_k;\theta ,\beta \right)}+\frac{{\Lambda }_{\beta }\left(x_k;\theta ,\beta \right)}{\alpha -\Lambda \left(x_k;\theta ,\beta \right)}+\frac{{\Lambda }_{\beta }\left(x_{k+1};\theta ,\beta \right)}{\alpha -\Lambda \left(x_{k+1};\theta ,\beta \right)}=0$$

(22)

and

$$\frac{\mathsf{\partial }\mathsf{\ell }\left(\alpha ,\beta ,\theta \right)}{\mathsf{\partial }\theta }=\sum _{k=1}^n\frac{{\Lambda }_{\theta }\left(x_{k+1};\theta ,\beta \right)-{\Lambda }_{\theta }\left(x_k;\theta ,\beta \right)}{\Lambda \left(x_{k+1};\theta ,\beta \right)-\Lambda \left(x_k;\theta ,\beta \right)}+\frac{{\Lambda }_{\theta }\left(x_k;\theta ,\beta \right)}{\alpha -\Lambda \left(x_k;\theta ,\beta \right)}+\frac{{\Lambda }_{\theta }\left(x_{k+1};\theta ,\beta \right)}{\alpha -\Lambda \left(x_{k+1};\theta ,\beta \right)}=0.$$

(23)

Such that ${\Lambda }_{\beta }\left(x_k;\theta ,\beta \right)=\frac{\mathsf{\partial }\Lambda \left(x_k;\theta ,\beta \right)}{\mathsf{\partial }\beta }=\Lambda \left(x_k;\theta ,\beta \right)\log (1-e^{-\theta {x_k}^2})$ and ${\Lambda }_{\theta }\left(x_k;\theta ,\beta \right)=\frac{\mathsf{\partial }\Lambda \left(x_k;\theta ,\beta \right)}{\mathsf{\partial }\theta }=\beta {x_k}^2{e}^{-\theta {x_k}^2}\Lambda \left(x_k;\theta ,\beta -1\right)$. To solve the system of nonlinear Equations (21)–(23), only numerical methods are helpful. Many numerical techniques were used in the literature; here, we use the Newton–Raphson method, and all results are illustrated in Section 5.

4.2. Bayesian Inference

The Bayesian estimation method is used in this section to estimate the unknown parameters of the DNGR. The basic assumption of the Bayesian method is that the model parameters are considered random variables that follow a distribution known as the prior distribution. Since prior information is usually only available, we must specify a suitable prior option. We choose the gamma conjugate prior distribution for the parameters $\alpha ,\beta$, and $\theta$. It is defined by assuming gamma distributions for $\alpha ,\beta$, and $\theta$.

Therefore, the prior distributions for $\alpha ,\beta$, and $\theta$ can be written as

$${\pi }_1\left(\alpha \right)=\frac{{b_1}^{a_1}}{\Gamma \left(a_1\right)}{\alpha }^{a_1-1}{e}^{-b_1\alpha },$$

$${\pi }_2\left(\beta \right)=\frac{{b_2}^{a_2}}{\Gamma \left(a_2\right)}{\beta }^{a_2-1}{e}^{-b_2\beta }$$

and

$${\pi }_3\left(\theta \right)=\frac{{b_3}^{a_3}}{\Gamma \left(a_3\right)}{\theta }^{a_3-1}{e}^{-b_3\theta }$$

where $a_1,a_2,a_3,b_1,b_2$, and $b_3$ are nonnegative hyper parameters of the assumed distributions.

Hence, the joint prior for $\alpha ,\beta$, and $\theta$ is

$$\pi (\alpha ,\beta ,\theta )\propto {\alpha }^{a_1-1}{{\beta }^{a_2-1}{\theta }^{a_3-1}e}^{-{(b}_1\alpha +b_2\beta +b_3\theta )}.$$

(24)

The joint posterior of $\alpha ,\beta$, and $\theta$ given the data is defined as

$${\pi }^{*}\left(\alpha ,\beta ,\theta \mid x\right)=\frac{1}{k}L(\underline{x}\mid \alpha ,\beta ,\theta )\pi (\alpha ,\beta ,\theta ),$$

(25)

where $L(\underline{x}\mid \alpha ,\beta ,\theta )$ is the likelihood function of the DNGRD and $K=\int \int \int L(\underline{x}\mid \alpha ,\beta ,\theta )\pi (\alpha ,\beta ,\theta )d\alpha d\beta d\theta$.

The DNGRD parameters are estimated using a symmetric squared error (SE) loss function. A simulation study is used to investigate the performance of the estimators using the aforementioned loss function. As criteria for the superiority of the estimation methods, the bias, the mean square error (MSE), the average length (AL) of the confidence intervals, and the coverage probability (CP) are computed.

Under the SE loss function, Bayes estimation for the parameters $\alpha$, $\beta$, and $\theta$ is defined as the mean or expected value regarding the joint posterior, provided as

$${\widehat{\alpha }}_{SE}=\frac{1}{k}\int \int \int \alpha L(\underline{x}\mid \alpha ,\beta ,\theta )\pi (\alpha ,\beta ,\theta )d\alpha d\theta$$

(26)

$${\widehat{\beta }}_{SE}=\frac{1}{k}\int \int \int \beta L(\underline{x}\mid \alpha ,\beta ,\theta )\pi (\alpha ,\beta ,\theta )d\alpha d\theta$$

(27)

$${\widehat{\theta }}_{SE}=\frac{1}{k}\int \int \int \theta L(\underline{x}\mid \alpha ,\beta ,\theta )\pi (\alpha ,\beta ,\theta )d\alpha d\theta$$

(28)

To evaluate the expected values and triple integration in Equations (26)–(28), numerical methods are required. We choose to use the Markov chain Monte Carlo (MCMC) technique via the Gibbs sampling method and by developing appropriate R code. The joint posterior density is

$${\pi }^{*}(\alpha ,\beta ,\theta \mid \underline{x})=\frac{1}{K}\prod _{i=1}^n\left[\frac{[1-\Lambda \left(i;\theta ,\beta \right)]}{\alpha -\Lambda \left(i;\theta ,\beta \right)}-\frac{\left[1-\Lambda \left(i+1;\theta ,\beta \right)\right]}{\alpha -\Lambda \left(i+1;\theta ,\beta \right)}\right]{\alpha }^{a_1}{{\beta }^{a_2-1}{\theta }^{a_3-1}e}^{-{(b}_1\alpha +b_2\beta +b_3\theta )}$$

(29)

Bayes estimation for parameters $\alpha$, $\beta ,$ and $\theta$ under SE loss function is performed respectively using Equations (26)–(28) and the posterior density Equation (29).

The estimators are numerically evaluated simulations using R codes under the SE loss function, and their results are summarized and presented in

Table 2. MLE and Bayes for parameters of DNGR distribution: $\alpha =1.5$.

$\mathit{\alpha }=1.5$				MLE					Bayesian
$\mathit{\theta }$	$\mathit{\beta }$	n		RB	MSE	Lower	Upper	CP	RB	MSE	Lower	Upper
0.8	0.5	30	$\alpha$	0.3587	1.5243	0.2760	4.8362	96.4%	−0.0637	0.1796	1.1698	1.6971
			$\theta$	0.1163	0.3028	0.3278	1.4583	94.8%	−0.0900	0.1096	0.5657	0.8743
			$\beta$	2.8414	1.6217	0.3864	3.4549	97.4%	0.2762	0.1846	0.4248	0.8864
		70	$\alpha$	0.1490	1.4933	0.3716	4.8186	96.2%	−0.1036	0.2005	1.1424	1.5800
			$\theta$	0.0150	0.1898	0.4403	1.1837	94.0%	−0.0572	0.0651	0.6586	0.8455
			$\beta$	1.4425	1.5862	0.8267	3.6157	96.0%	0.3645	0.2151	0.4609	0.9003
		100	$\alpha$	0.2670	1.2867	0.4987	4.2996	96.6%	−0.0749	0.1473	1.2081	1.5686
			$\theta$	0.0141	0.1323	0.5527	1.0698	94.8%	−0.0573	0.0556	0.6889	0.8096
			$\beta$	0.9287	1.0745	0.9939	3.2935	96.2%	0.2963	0.1636	0.5165	0.7786
		200	$\alpha$	0.2572	1.0381	0.5976	4.0743	93.4%	−0.0433	0.0803	1.3303	1.5184
			$\theta$	−0.0401	0.1044	0.5730	0.9629	95.0%	−0.0446	0.0400	0.7257	0.7991
			$\beta$	0.8044	0.9101	1.4005	3.6436	93.2%	0.1773	0.0955	0.5222	0.6549
0.8	2	30	$\alpha$	−0.2630	0.4948	0.5194	1.6917	96.4%	−0.0723	0.1817	1.1206	1.6439
			$\theta$	0.1964	0.2533	0.5674	1.3469	95.0%	−0.1627	0.1504	0.5360	0.8156
			$\beta$	0.1821	0.6169	1.3875	3.3410	95.4%	0.0193	0.1575	1.7350	2.3384
		70	$\alpha$	−0.2876	0.4697	0.7042	1.4329	98.2%	−0.0650	0.1782	1.1407	1.6102
			$\theta$	0.1781	0.2057	0.6514	1.2336	95.4%	−0.1452	0.1284	0.5898	0.8055
			$\beta$	0.1783	0.6075	1.3907	3.2658	97.6%	0.0268	0.1401	1.8049	2.2871
		100	$\alpha$	−0.2344	0.4531	0.8432	1.4810	99.8%	−0.0867	0.1618	1.1862	1.5461
			$\theta$	0.1899	0.1968	0.7066	1.1973	95.4%	−0.1317	0.1115	0.6174	0.7637
			$\beta$	0.1585	0.5414	1.4561	3.1780	96.6%	0.0243	0.0945	1.8941	2.2078
		200	$\alpha$	−0.2144	0.3822	0.8523	1.4703	99.6%	−0.0418	0.0796	1.3468	1.5366
			$\theta$	0.1631	0.1540	0.7699	1.0910	94.8%	−0.1128	0.0931	0.6638	0.7529
			$\beta$	0.1403	0.5402	1.3709	3.0190	98.4%	0.0133	0.0482	1.9454	2.0992
1.3	0.5	30	$\alpha$	−0.0161	1.8375	0.1289	5.0806	95.2%	−0.0893	0.2022	1.1191	1.6715
			$\theta$	0.2417	0.5574	0.7108	2.5176	97.0%	−0.0770	0.1671	0.9649	1.5162
			$\beta$	2.9986	1.9656	0.1495	4.4932	95.4%	0.2996	0.1973	0.4097	0.8957
		70	$\alpha$	−0.0127	1.8093	0.2549	4.9173	96.0%	−0.1216	0.2207	1.1361	1.5891
			$\theta$	0.2073	0.4650	0.8261	2.3130	96.8%	−0.0716	0.1243	1.0573	1.3653
			$\beta$	1.0203	1.8424	0.2329	4.2970	96.0%	0.4009	0.2295	0.4769	0.9082
		100	$\alpha$	−0.0157	1.2760	0.2963	3.5147	95.8%	−0.0973	0.1743	1.1848	1.5360
			$\theta$	0.1764	0.4309	0.8514	2.2450	97.2%	−0.0625	0.1035	1.0952	1.3359
			$\beta$	0.9256	0.9678	0.5612	3.8173	96.2%	0.3340	0.1821	0.5292	0.8175
		200	$\alpha$	−0.0142	0.9294	0.3171	3.0604	96.4%	−0.0507	0.0912	1.3314	1.5228
			$\theta$	0.0813	0.3153	0.8228	1.9886	98.0%	−0.0378	0.0594	1.1915	1.3146
			$\beta$	0.5671	0.6315	0.6249	3.0816	99.2%	0.1931	0.1029	0.5286	0.6659
	2	30	$\alpha$	−0.3113	0.6551	0.1315	1.9347	99.4%	−0.1012	0.2185	1.0986	1.6487
			$\theta$	0.1534	0.3004	1.0585	1.9403	93.6%	−0.1306	0.2070	0.9252	1.3786
			$\beta$	0.1334	0.7466	0.8986	3.6349	98.4%	0.0235	0.1570	1.7458	2.3302
		70	$\alpha$	−0.3117	0.6555	0.1310	1.9338	99.4%	−0.1027	0.2185	1.0986	1.6487
			$\theta$	0.1526	0.2934	1.0744	1.9225	93.8%	−0.1263	0.2067	0.9265	1.3857
			$\beta$	0.1323	0.7438	0.9007	3.6028	98.4%	0.0216	0.1529	1.7548	2.3035
		100	$\alpha$	−0.3207	0.4811	1.0057	1.0321	93.8%	−0.0914	0.2108	1.1902	1.4334
			$\theta$	0.1929	0.2756	1.3192	1.7823	100.0%	−0.1151	0.1656	1.0148	1.2705
			$\beta$	0.0887	0.1776	1.9162	2.1927	100.0%	0.0154	0.0757	1.9316	2.1534
		200	$\alpha$	−0.3188	0.4782	1.0096	1.0341	93.3%	−0.0538	0.0946	1.3235	1.5159
			$\theta$	0.1594	0.2403	1.3682	1.7462	94.7%	−0.0763	0.1043	1.1427	1.2673
			$\beta$	0.0809	0.1683	1.9258	2.1821	95.9%	0.0140	0.0496	1.9582	2.1127

and

Table 3. MLE and Bayes for parameters of DNGR distribution: $\alpha =3$.

$\mathit{\alpha }=3$				MLE					Bayesian
$\mathit{\theta }$	$\mathit{\beta }$			RB	MSE	Lower	Upper	CP	RB	MSE	Lower	Upper
1.3	0.5	30	$\alpha$	0.1917	2.0185	0.2210	7.3712	96.2%	−0.0038	0.1558	2.6689	3.2541
			$\theta$	0.5325	1.0676	0.3977	3.5868	93.2%	−0.0696	0.1621	0.9486	1.4541
			$\beta$	9.3388	5.0389	1.4536	8.8852	96.4%	0.4023	0.2277	0.5010	0.8988
		70	$\alpha$	0.3736	1.8015	1.3537	6.8878	92.6%	−0.0071	0.1313	2.7384	3.2252
			$\theta$	0.3598	0.6399	0.9110	2.6245	95.2%	−0.0784	0.1300	1.0446	1.3579
			$\beta$	9.7520	5.4079	0.7873	9.9648	96.4%	0.5596	0.2929	0.6081	0.9368
		100	$\alpha$	0.3083	2.0838	0.2612	7.5884	95.4%	−0.0040	0.0897	2.8073	3.1475
			$\theta$	0.3510	0.5847	1.0390	2.4735	96.2%	−0.0627	0.1003	1.1033	1.3265
			$\beta$	9.7169	5.4798	0.3857	10.3312	93.6%	0.4114	0.2145	0.5799	0.8143
		200	$\alpha$	0.8118	3.5689	0.3173	10.5536	95.8%	−0.0021	0.0452	2.9092	3.0800
			$\theta$	0.3223	0.4785	1.2655	2.1725	95.8%	−0.0367	0.0585	1.1795	1.3146
			$\beta$	9.6584	5.0771	2.2548	8.4036	96.0%	0.2381	0.1241	0.5548	0.6959
	0.9	30	$\alpha$	−0.1503	1.6360	0.5364	5.6349	95.6%	−0.0038	0.1618	2.6992	3.3379
			$\theta$	0.3752	0.8357	0.4565	3.1191	97.8%	−0.1104	0.1934	0.9110	1.3977
			$\beta$	6.1647	6.2502	0.8019	5.0945	97.0%	0.1488	0.1888	0.7805	1.3184
		70	$\alpha$	−0.1584	1.0898	0.6006	4.4492	97.6%	−0.0134	0.1395	2.7034	3.2184
			$\theta$	0.1830	0.4443	0.8017	2.2740	93.0%	−0.1119	0.1694	0.9717	1.2952
			$\beta$	5.3507	5.0649	2.6369	4.7944	97.8%	0.1222	0.1722	0.8992	1.2938
		100	$\alpha$	0.1317	2.0370	0.6525	4.3156	94.2%	−0.0031	0.0883	2.8246	3.1589
			$\theta$	0.2120	0.4331	0.9200	2.2311	92.0%	−0.0901	0.1313	1.0629	1.2857
			$\beta$	6.4228	6.0394	3.2486	4.1124	96.4%	0.1633	0.1653	0.8964	1.1761
		200	$\alpha$	0.1701	1.6929	0.3436	3.6772	94.2%	−0.0031	0.0461	2.8961	3.0742
			$\theta$	0.1568	0.2695	1.1578	1.8498	95.0%	−0.0485	0.0704	1.1800	1.3009
			$\beta$	6.7695	6.3441	3.5224	3.8463	97.2%	0.0836	0.0848	0.9010	1.0514
2	0.5	30	$\alpha$	−0.1881	0.6957	1.6375	3.2338	95.6%	−0.0047	0.1551	2.6721	3.2679
			$\theta$	−0.0411	0.5058	0.9386	2.8969	90.0%	−0.0553	0.1959	1.5765	2.2175
			$\beta$	4.5180	2.5199	0.5683	4.9497	96.8%	0.2992	0.1983	0.3997	0.9025
		70	$\alpha$	−0.2116	0.8253	1.3305	3.3996	100.0%	−0.0067	0.1355	2.6983	3.2384
			$\theta$	−0.0649	0.6639	0.5929	3.1475	97.2%	−0.0726	0.1869	1.6464	2.0764
			$\beta$	4.1615	2.3945	0.2558	4.9057	100.0%	0.4675	0.2563	0.5129	0.9282
		100	$\alpha$	−0.2105	0.8825	1.1588	3.5784	100.0%	−0.0039	0.0929	2.8218	3.1785
			$\theta$	−0.0837	0.6576	0.5849	3.0803	100.0%	−0.0565	0.1382	1.7356	2.0397
			$\beta$	3.8575	2.2378	0.2023	4.6552	100.0%	0.3167	0.1723	0.5349	0.7985
		200	$\alpha$	−0.0747	0.3607	2.2214	3.3303	92.6%	−0.0021	0.0450	2.9162	3.0799
			$\theta$	−0.2174	0.5774	0.8199	2.3105	95.2%	−0.0275	0.0695	1.8580	2.0248
			$\beta$	3.0823	1.7603	0.3725	3.7098	95.4%	0.1803	0.0975	0.5084	0.6579
	1.1	30	$\alpha$	−0.4095	1.4678	0.1957	3.3470	99.6%	−0.0073	0.1620	2.6815	3.2895
			$\theta$	−0.0105	0.6870	0.6319	3.3262	100.0%	−0.0911	0.2397	1.5140	2.1195
			$\beta$	2.5931	3.5294	0.1257	8.0306	99.6%	0.1034	0.1881	0.9228	1.5108
		70	$\alpha$	−0.3289	1.1819	0.7368	3.2901	100.0%	−0.0127	0.1424	2.6825	3.1929
			$\theta$	−0.1004	0.6782	0.5283	3.0700	100.0%	−0.0941	0.2211	1.5755	1.9901
			$\beta$	2.3766	2.7979	1.7584	5.6701	97.8%	0.1644	0.2140	1.0552	1.4943
		100	$\alpha$	−0.2776	0.9788	1.1578	3.1769	92.8%	−0.0075	0.0892	2.8212	3.1590
			$\theta$	−0.1742	0.6667	0.5362	2.7671	93.0%	−0.0655	0.1549	1.7024	2.0002
			$\beta$	2.3582	2.7976	1.6383	5.7497	98.2%	0.1111	0.1451	1.0470	1.3534
		200	$\alpha$	−0.2445	0.8234	1.5320	3.0013	93.8%	−0.0041	0.0453	2.8966	3.0706
			$\theta$	−0.2436	0.5653	0.9504	2.0750	97.4%	−0.0367	0.0844	1.8520	2.0008
			$\beta$	2.2435	2.5427	2.3663	4.7694	96.6%	0.0569	0.0753	1.0850	1.2456

.

5. Simulation Analysis

In this section, Monte Carlo simulations are performed to assess the effectiveness of the suggested estimators for the parameters $\alpha ,\theta$, and $\beta$ that were established in Section 4.1. We will sum up by providing the simulation scenario. The findings of the simulation are then offered for debate.

5.1. Simulation Scenario

In this subsection, several Monte Carlo simulation studies are carried out to assess the effectiveness of the acquired maximum likelihood estimates and Bayesian estimation of $\alpha ,\theta$, and $\beta$. Now, we suggest the following steps to gather a sample from the DNGR model:

• Set $\alpha ,\theta$, and $\beta$ to their actual values as shown:
  In Table 2: $\alpha =1.5,\theta =0.8,\beta =0.5$, $\alpha =1.5,\theta =0.8,\beta =2$, $\alpha =1.5,\theta =1.3,\beta =0.5$, $\alpha =1.5,\theta =1.3,\beta =2$.
  In Table 3: $\alpha =3,\theta =1.3,\beta =0.5$, $\alpha =3,\theta =1.3,\beta =0.9$, $\alpha =3,\theta =2,\beta =0.5$, $\alpha =3,\theta =2,\beta =1.1$.
• Specific values for n (total test units) should be determined as 30, 70, 100, 200.
• Generate a uniform random variable within the range of 0 to 1. Utilize the quantile function described in Equation (7) to produce a random sample from the DNGR $(\alpha ,\theta ,\beta )$ distribution. Afterwards, round the quantity of samples to the nearest whole number.
• Compute the MLEs and $100(1-\gamma )$% via ‘maxLik’ package in R program with version number (4.3.0), with Fisher information matrix (Hessian matrix).
• Use ‘coda’ package in R program with version number (4.3.0), to obtain the Bayes’ inferences by running the MCMC sampler 12,000 times and 2000 is burn-in.
• Repeat the above steps 5000 times.
• The relative bias (RB), mean squared error (MSE), average lower, average upper, and coverage probability (CP) of the parameter are specifically determined for each group (n, or actual value of the parameter). For more details about comparing interval estimates, we discuss using the CP requirement in our evaluations. R 4.2.2 programming language is used to carry out all numerical analyses. In Table 2 and Table 3, respectively, all numerical findings for $\alpha ,\beta$, and $\theta$ are obtained and presented.

5.2. Simulation Conclusion

The performance of the suggested point and interval estimate algorithms is the main topic of this subsection. We can infer the following facts from Table 2 and Table 3:

• The acquired estimates of the unknown parameters $\alpha ,\theta$, and $\beta$ generally perform well in terms of lowest MSE, RB, and difference between upper and lower values with CP.
• The MSE, RB, and CI of $\alpha ,\theta$, and $\beta$ tend to decline as n rises. This result supports the associated estimates’ consistency property of DNGR distribution when the necessary sample size is raised.
• As the true value of $\beta$ increases, for each setting, the MSE, RB, and CL measures of unknown parameters $\alpha$ and $\beta$ decrease, while they increase regarding unknown parameter $\theta$.
• The MSE, RB, and CL measures of all unknown parameters $\alpha ,\theta$, and $\beta$ increase for each set as the true value of $\theta$ grows.
• For CI of Bayesian, the credible interval decreases when the sample size increases.
• Almost always, and regardless of sample size, Bayesian estimation based on the SE loss function yields the minimal RB and MSE values.

6. Real Data Examples

This section presents the analysis of two applications using different real datasets. The main goals of this section are

• Examine the usefulness and applicability of the proposed model to real phenomena;
• Show the applicability of the inferential results to a real practical situation;
• Evaluate whether the proposed model is a better choice than the other seven models.

Data I: The first dataset includes the number of strikes that occurred in the UK coal mining industry over four consecutive week periods between 1948 and 1959. It was derived from Kendall [34]. An empirical model was used to analyze this example by Ridout and Besbeas [35] and is presented in

Table 4. Data I: The number of strikes and their frequency that occurred in the UK coal mining industry.

data	0	1	2	3	4 or more
Freq	46	76	24	9	1

.

Data II: The number of fires that occurred in Greece between 1 July and 31 August, 1998. We only take into account fires in forest districts. These data have a sample size of 124. The minimum value is 0, the first quartile is 2, the median value is 4, the mean value is 5.065, the third quartile’s maximum value is 8, and the variance value is 18.256. The data are as follows: 2, 4, 4, 3, 3, 1, 2, 4, 3, 1, 1, 0, 5, 5, 0, 3, 1, 1, 0, 1, 0, 2, 0, 1, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 4, 2, 2, 1, 2, 1, 2, 0, 2, 2, 1, 0, 3, 2, 1, 2, 2, 7, 3, 5, 2, 5, 4, 5, 6, 5, 4, 3, 8, 4, 3, 8, 4, 4, 3, 10, 5, 4, 5, 12, 3, 8, 12, 10, 11, 6, 1, 8, 9, 12, 9, 4, 8, 12, 11, 8, 6, 4, 7, 9, 15, 12, 15, 15, 12, 9, 16, 7, 11, 9, 11, 6, 5, 20, 9, 8, 8, 5, 7, 10, 6, 6, 5, 5, 15, 6, 8, 5, 6. These data were discussed by [36].

Based on the first and second datasets, the DNGRD probability model is contrasted and compared with the other seven competing models to show the reliability and superiority of the proposed model, including Poisson, binomial, geometric, discrete Burr (DB) by [37], discrete Marshall–Olkin Lomax (DMOL) by [38], new discrete Lindley (NDL) by [39], and discrete odd perks exponential (DOPE) by [40] distributions. To specify the best model, several criteria are used, namely: Akaike $(AIC=2p-2\widehat{l})$, where p is the length of the model parameter and $\widehat{l}$ is log-likelihood value, consistent Akaike $(CAIC=-2\widehat{l}+\frac{2np}{n-p-1})$, Bayesian $(BIC=-2\widehat{l}+pln\left(n\right))$, and Hannan–Quinn $(HQIC=-2\widehat{l}+pln(ln\left(n\right))$ information criteria. Along with these, the $X^2-square$ statistic and its p-value are taken into account. If a probability model distribution has the highest p-value and the lowest values for all other metrics, it is obvious that it will provide the best fit for a particular collection of data. The maximum likelihood estimates (with their standard errors (St.Es)), as well as the fitted model selection criteria, are shown in

Table 5. MLE estimates and different measures of fit for Data I.

		Estimators	SE	AIC	CAIC	BIC	HQIC	${\mathit{X}}^2$	p-Value
DNGR	$\alpha$	33.0996	13.6357	382.7571	382.9150	391.9067	386.4733	3.6721	0.4522
	$\theta$	0.3343	0.0434
	$\beta$	0.9276	0.1425
DOPE	$\alpha$	39.3584	3.5957	387.5354	387.6933	396.6850	391.2516	5.2373	0.2638
	$\theta$	0.2757	0.0264
	$\beta$	3.1307	0.5099
Binomial	$\theta$	0.9937	0.1315	386.1302	386.1562	389.1801	387.3689	10.1078	0.0387
Poision	$\theta$	0.9936	0.0798	386.1302	386.1562	389.1801	387.3689	9.8986	0.0422
DB	$\alpha$	4.6524	0.6986	388.4190	388.4974	394.5187	390.8964	5.4076	0.2480
	$\beta$	0.5940	0.0448
DMOL	$\alpha$	21.1960	7.5845	386.4288	386.5867	395.5784	390.1450	3.9771	0.4091
	$\theta$	1.8892	0.3088
	$\beta$	0.0028	0.0009
Geometric	$\theta$	0.5017	0.0284	433.1343	433.1603	436.1842	434.3731	50.7984	0.0000
NDL	$\theta$	0.5017	0.0284	433.1343	433.1603	436.1842	434.3731	50.7984	0.0000

and

Table 6. MLE estimates and different measures for Data II.

		Estimators	SE	AIC	CAIC	BIC	HQIC	${\mathit{X}}^2$	p-Value
DNGRD	$\alpha$	12.5091	2.5308	668.4150	668.6150	676.8759	671.8520	22.8025	0.2986
	$\theta$	0.0122	0.0027
	$\beta$	0.4495	0.1299
DOPE	$\alpha$	44.2111	9.3605	685.1374	685.3374	693.5983	688.5744	32.6330	0.0370
	$\theta$	0.0134	0.0017
	$\beta$	0.7291	0.0844
Binomial	$\theta$	0.9608	0.2622	821.7835	821.8163	824.6038	822.9292	12776.3387	0.0000
Poision	$\theta$	5.0645	0.2021	821.7835	821.8163	824.6038	822.9292	26469.5465	0.0000
DB	$\alpha$	2.5385	0.4910	748.2257	748.3249	753.8663	750.5170	91.3536	0.0000
	$\beta$	0.7611	0.0425
DMOL	$\alpha$	4.6349	1.8610	674.2602	674.4602	682.7210	677.6972	25.0095	0.2011
	$\theta$	13.0180	3.2683
	$\beta$	0.0031	0.0018
Geometric	$\theta$	0.1649	0.0135	675.3352	675.3679	678.1554	676.4808	27.5152	0.1214
NDL	$\theta$	0.1649	0.0135	675.3352	675.3679	678.1554	676.4808	27.5152	0.1214

using the R programming language and the ’bbmle’ package in R program with version number (4.3.0), that was recommended.

To compare the performance and efficiency of the DNGR distribution with other distributions listed in Table 5, using measures of goodness of fit and p-values, we can proceed as follows:

1-DNGR versus DOPE:

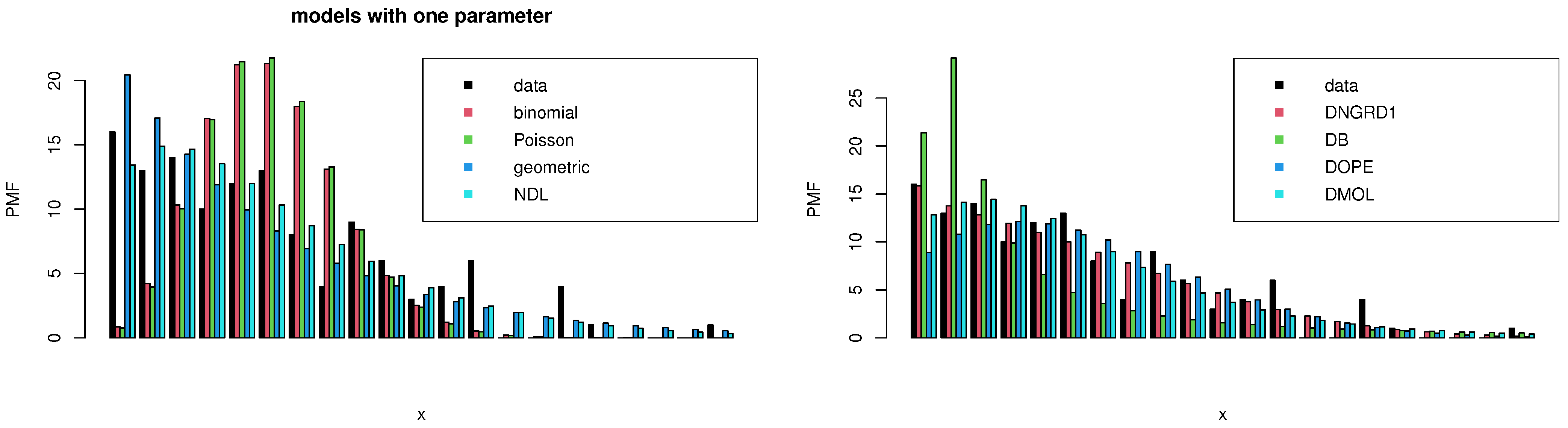
DNGR shows a better fit with a lower $AIC$, $CAIC$, $BIC$, and $HQIC$. The chi-squared value is lower for DNGR, indicating a better fit. DNGR has a higher p-value, suggesting a better fit to the data than DOPE.

2-DNGR versus Binomial/Poisson:

DNGR has a higher p-value than both binomial and Poisson distributions, indicating a more suitable model for the data. The information criteria (AIC, CAIC, HQIC) for DNGR are lower compared to binomial and Poisson, suggesting a better fit than binomial and Poisson.

3-DNGR versus DMOL:

DNGR and DMOL have comparable p-values, but DNGR shows better performance in terms of information criteria.

4-DNGR versus DB:

DNGR has a higher p-value than DB, indicating that DNGR shows slightly better performance in terms of information criteria.

5-DNGR versus Geometric/NDL:

DNGR outperforms both geometric and NDL distributions in terms of p-value, indicating a significantly better fit. DNGR has lower information criteria values, further suggesting its superiority in model fitting. Overall, DNGR appears to offer a more efficient and suitable fit for Data I compared to the other listed distributions.

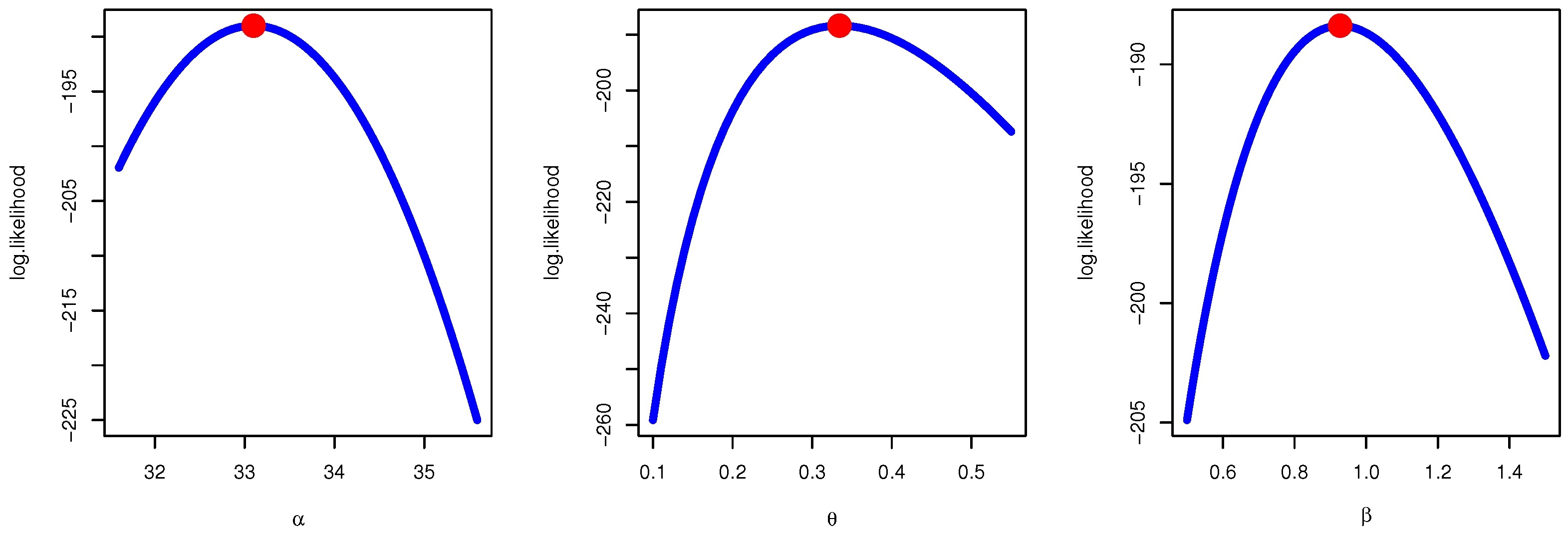
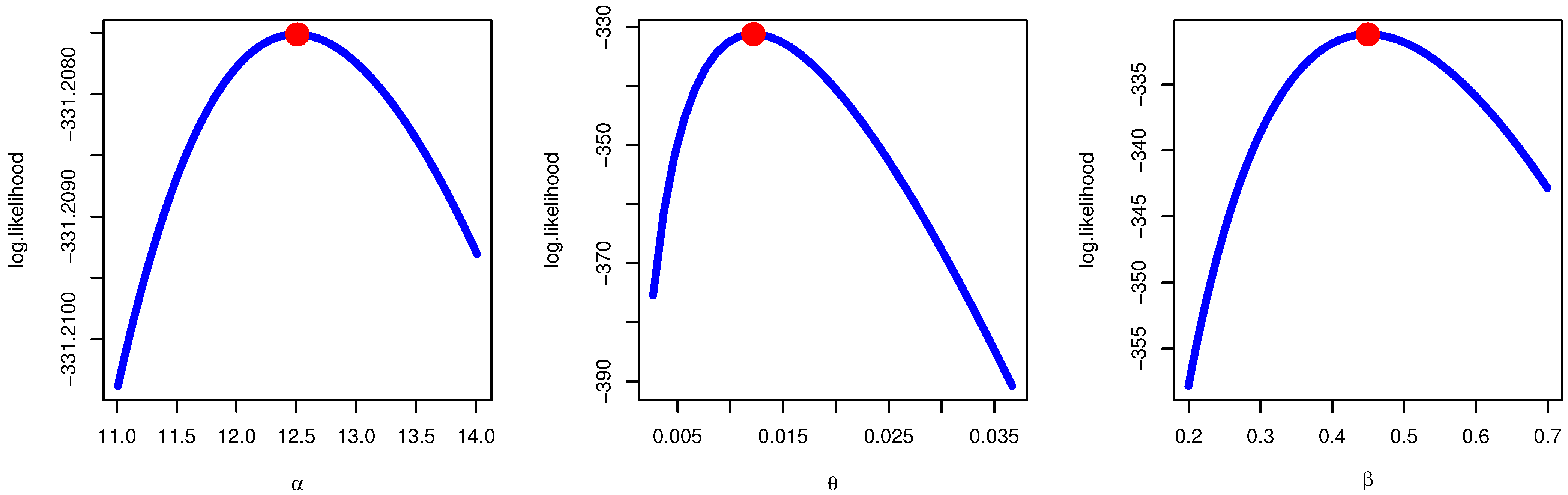
Figure 3, Figure 4 and Figure 5 confirm these results for Data I (the black point refer to data; the pink point refer to DNGR distribution). Additionally, it is evident from Data II in Table 6 that the DNGR distribution is the best distribution among all the examined models in terms of the P-value, whereas Figure 6, Figure 7 and Figure 8 confirm these results for Data II. Figure 3 confirms the results of MLE fitting and demonstrates the existence, uniqueness, and maximum point of likelihood value of the likelihood estimates for Data I. 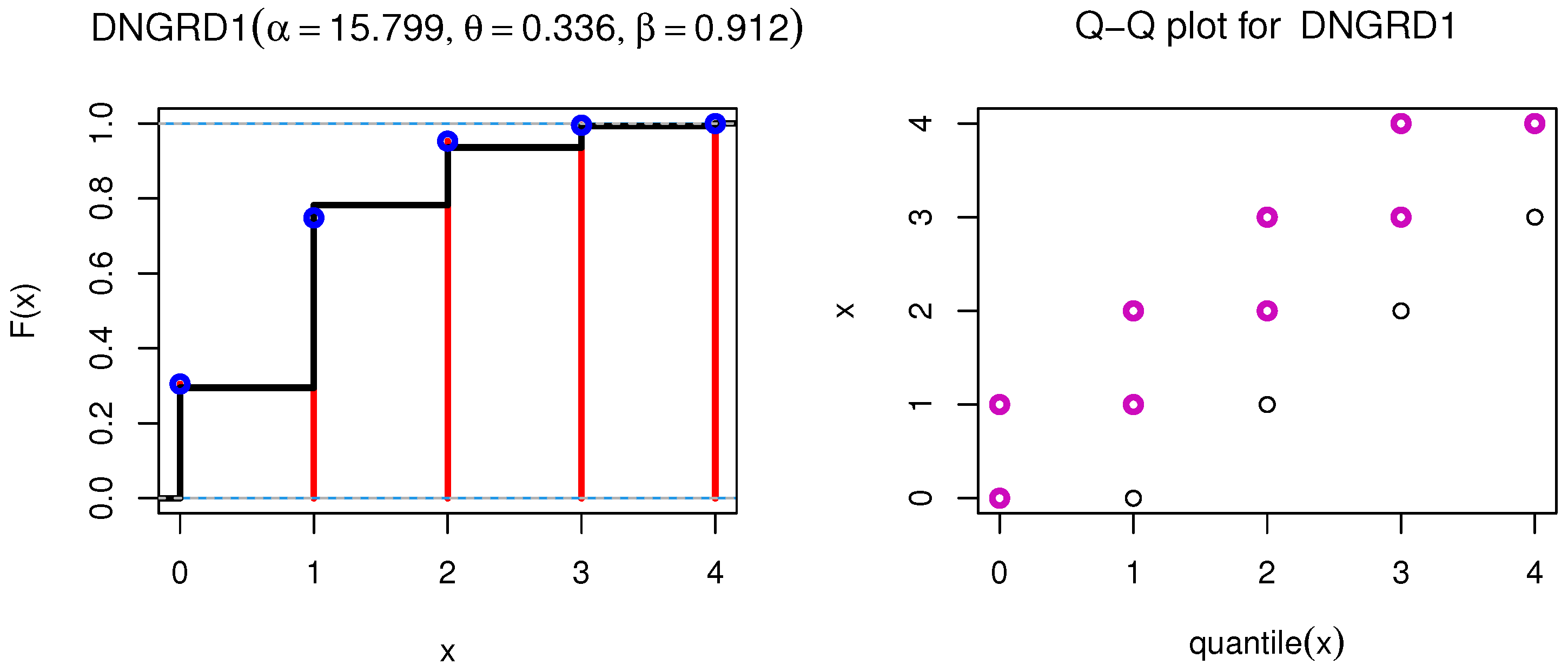Figure 4 regarding associated empirical CDF and estimated CDF plot illustrates the connection between observed cumulative probability and observation through a visual plot and also Q–Q plot for Data I. Figure 5 highlights estimated frequency by using PMF for each comparative model for Data I.

Table 7. Survival and hazard rate functions for DNGR distribution with different values of Data I.

x	$\mathit{S}\left(\mathit{x};33.0994,0.3343,0.9275\right)$	$\mathit{h}\left(\mathit{x};33.0994,0.3343,0.9275\right)$
0	0.6952	0.4383
1	0.2518	1.7607
2	0.0472	4.3343
3	0.0045	9.3889
4	0.0002	19.2691

indicates survival and hazard rate functions for DNGR distribution with different values of Data I, noting that the survival value decreased when the values of Data I increased, while the hazard rate value increased when the values x of Data I increased.

Figure 6 confirms the results of MLE fitting and demonstrates the existence, uniqueness, and maximum point of likelihood value of the likelihood estimates for Data II. Figure 7 regarding associated empirical CDF and estimated CDF plot illustrates the connection between observed cumulative probability and observation through a visual plot and Q–Q plot for Data II. Figure 8 highlights estimated frequency by using PMF for each comparative model for Data II.

Table 8. Survival and hazard rate functions for DNGR distribution with different values of Data II.

x	$\mathit{S}\left(\mathit{x};12.5091,0.0122,0.4495\right)$	$\mathit{h}\left(\mathit{x};12.5091,0.0122,0.4495\right)$
0	0.8721	0.1466
2	0.6577	0.1572
4	0.4725	0.1879
5	0.3919	0.2059
8	0.2023	0.2686
20	0.0023	0.6490

indicates survival and hazard rate functions for DNGR distribution with different values of Data II, noting that the survival values decreased when the values of Data II increased, while the hazard rate value increased when the values x of Data II increased.

7. Conclusions

In this study, the authors successfully developed a novel discrete analog from the continuous generalized Rayleigh distribution denoted by DNGR through the application of the survival discretization method. Several key attributes of the DNGR model were studied, such as its unimodal probability mass function, which exhibits varying degrees of symmetry and skewness based on parameter selection. Comprehensive statistical measures for DNGR were derived, including moments, stress–strength function, moment-generating function, and mean residual and mean past lifetimes. The potential submodels and special cases derived from the DNGR demonstrate the versatility and adaptability of the DNGR distribution, which can be suitable for modeling different types of data and could provide unique insights depending on the context of the analysis. Furthermore, the practical applicability of the work was enhanced by conducting detailed simulation analyses and presenting the results in tabular form. Point and interval estimation using both the maximum likelihood and the Bayesian methods were obtained, supplementing these with simulation analyses executed using R code. This was complemented by a numerical analysis aimed at evaluating the estimation methods for DNGR’s unknown parameters and assessing the efficiency of these methods. A significant aspect of their contribution is the application of the DNGR model to real-world data. Two real data examples were selected, one from the industrial sector concerning UK coal mining strikes and another focusing on environmental issues related to fires in Greece. Their analysis revealed that the DNGR model outperformed seven competitive discrete distributions in various goodness-of-fit measures, demonstrating its superior ability to model the given datasets effectively. This finding was further illustrated through detailed tables and figures showcasing the properties and efficiency of the new model. As a pathway for future work, the authors suggest exploring alternative discretization methods to assess their performance and applicability to a broader range of real-life data scenarios.