Wearable Sensors for Athletic Performance: A Comparison of Discrete and Continuous Feature-Extraction Methods for Prediction Models
Abstract
1. Introduction
- Feature-extraction efficacy: How do discrete and continuous feature-extraction methods compare when modeling athletic performance metrics, such as the peak power output in the CMJ?
- Model robustness: How robust are different model types, based on discrete or continuous features, or combinations of both, to variations in data distribution and sample size?
- Generalizability: How consistent are the findings between studies where different sensors, placements, and/or data-collection protocols are used?
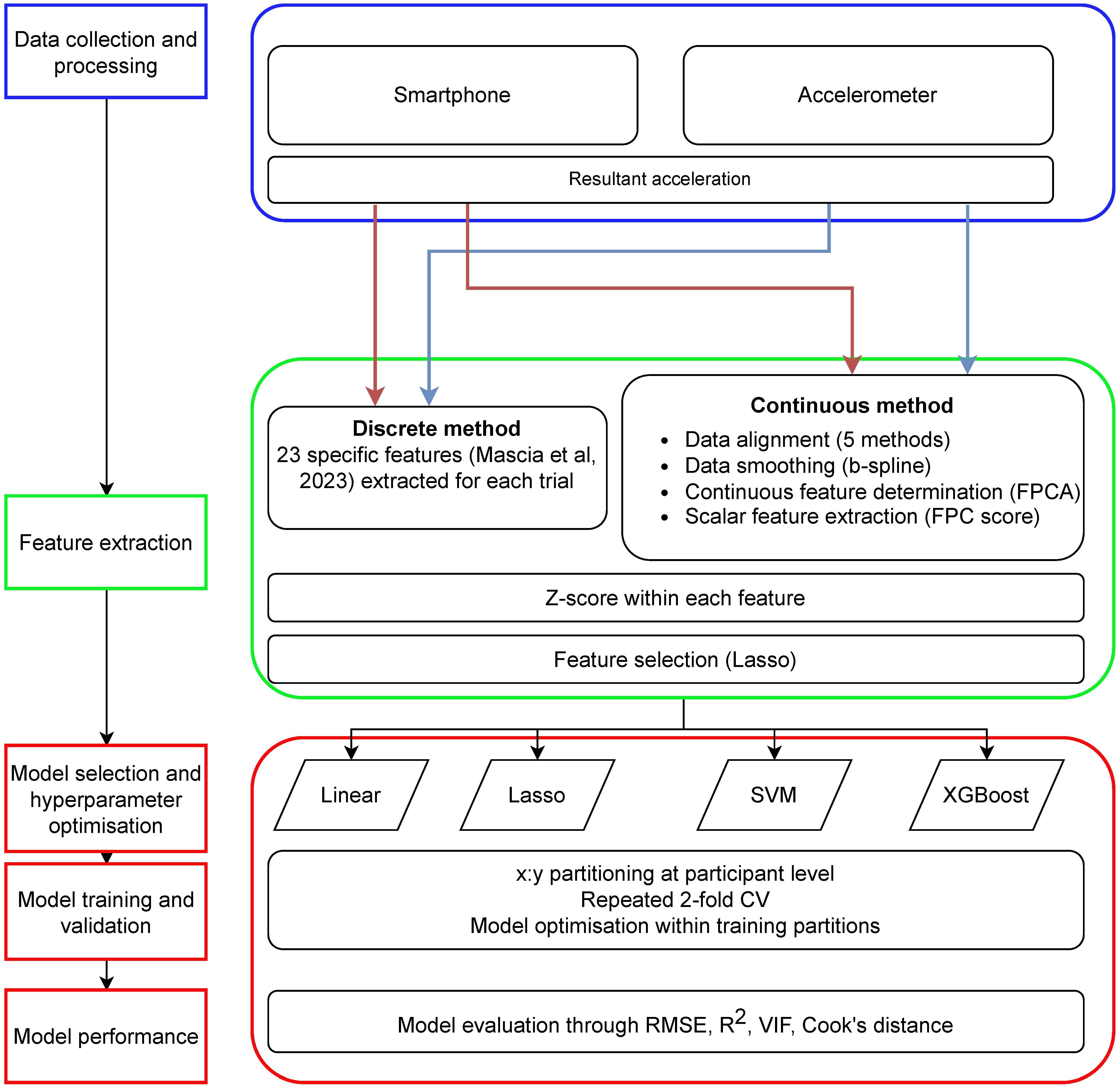
2. Methods
2.1. Data Collections
2.2. Discrete Feature Extraction
2.3. Continuous Feature Extraction
2.4. Feature Selection
2.5. Dataset Truncation
2.6. Models
- a linear model allowing for extensive inference of the model fit, including explained variance, shrinkage, and other statistics that can support our investigation;
- Lasso linear regression using L1 regularization to handle potentially large numbers of predictors and curb overfitting [31];
- a support vector machine (SVM), a non-parametric model to serve as an alternative to the linear parametric models above [32]; and
2.7. Evaluation
2.8. Full Modeling Procedure
3. Results
3.1. Continuous Feature-Extraction: Alignment Evaluation
3.2. Feature Characteristics
3.3. Linear Model Inference
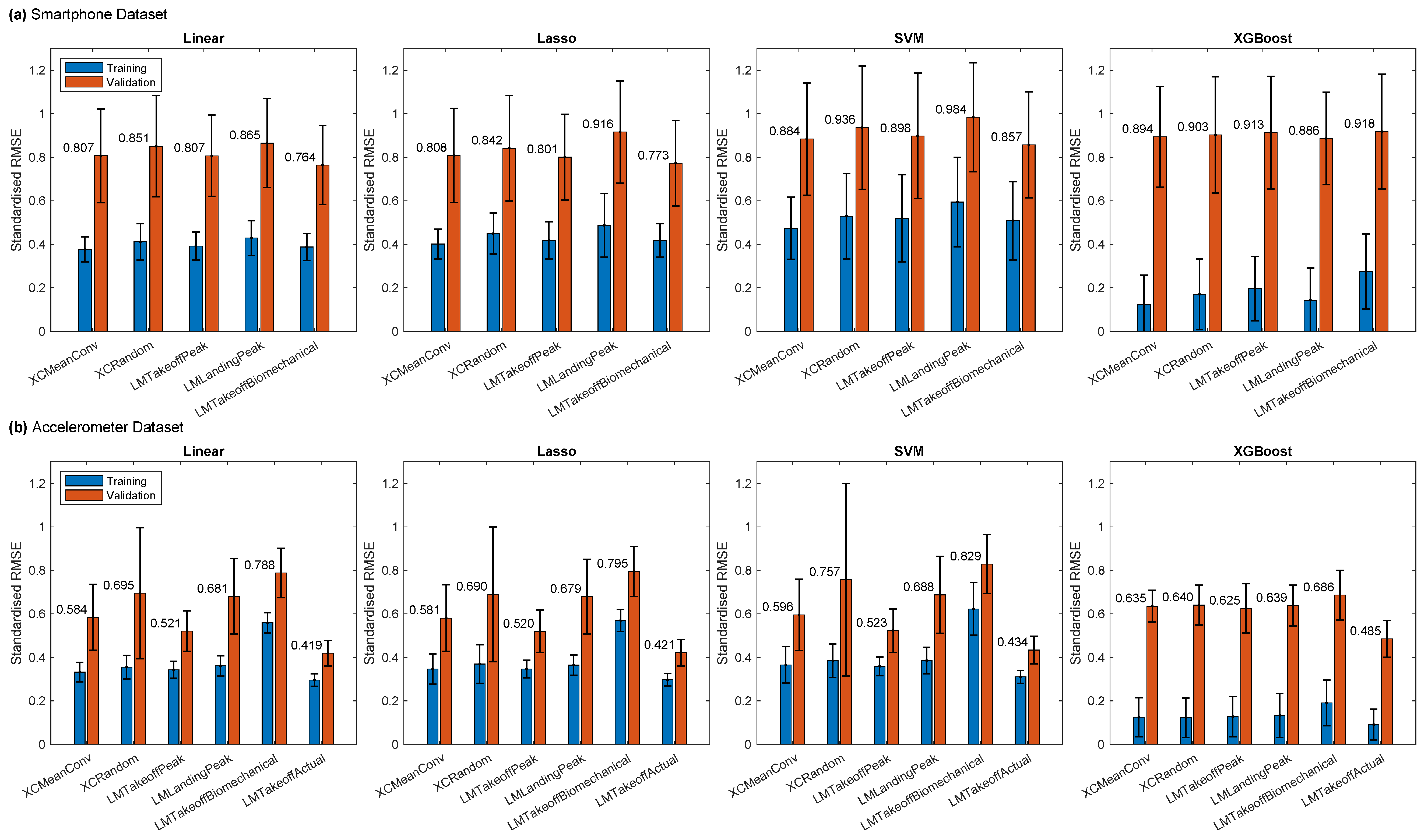
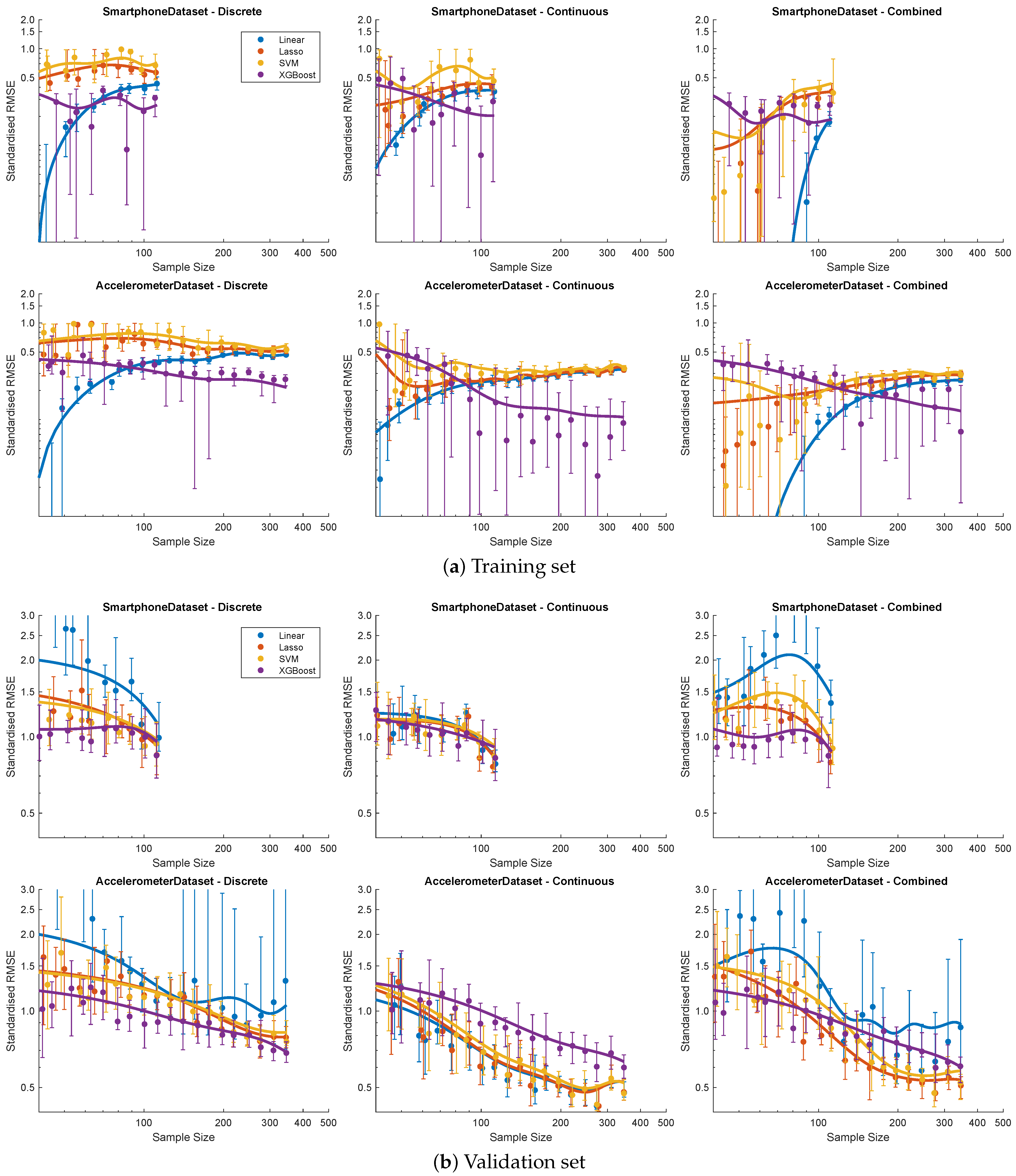
3.4. Model Performance
3.5. Sample Size Truncation
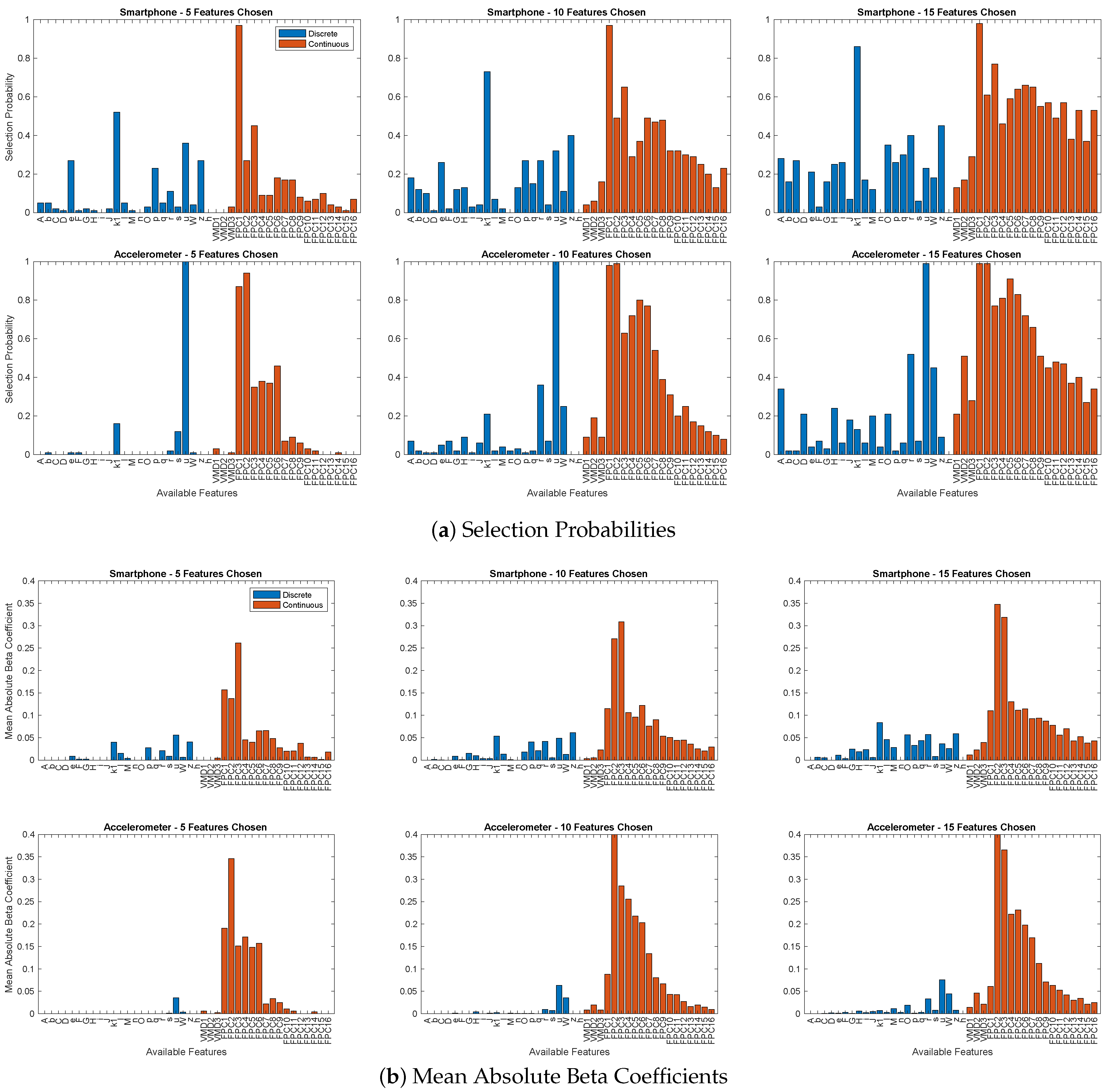
3.6. Feature-Selection Preference
4. Discussion
4.1. Research Question 1: Feature-Extraction Efficacy
4.2. Research Question 2: Model Robustness
4.3. Research Question 3: Generalizability
4.4. Acceleration Signal Type
4.5. Alignment Methods
4.6. Limitations and Future Directions
4.7. Practical Implications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CMJ | Countermovement Jump |
| CV | Cross-validation |
| FPC | Functional Principal Component |
| FPCA | Functional Principal Component Analysis |
| GCV | Generalized Cross-Validation |
| IMU | Inertial Measurement Unit |
| Lasso | Least Absolute Shrinkage and Selection Operator |
| LIME | Local Interpretable Model-agnostic Explanations |
| ML | Machine Learning |
| RMSE | Root Mean Squared Error |
| SD | Standard Deviation |
| SHAP | SHapley Additive exPlanations |
| SNR | Signal-to-Noise Ratio |
| SVM | Support Vector Machine |
| VGRF | Vertical Ground Reaction Force |
| VIF | Variance Inflation Factor |
| VMD | Variational Mode Decomposition |
| XGBoost | eXtreme Gradient Boosting |
Appendix A. Methods
Appendix A.1. Discrete Features
| ID | Feature | Units | Description |
|---|---|---|---|
| A | Unweighting phase duration | s | |
| b | Minimum acceleration | m/s² | |
| C | Time from minimum to maximum acceleration | s | |
| D | Main positive impulse time | s | Time duration of positive acceleration from to the last positive sample prior |
| e | Maximum acceleration | m/s² | |
| F | Time from acceleration positive peak to takeoff | s | |
| G | Ground contact duration | s | |
| H | Time from minimum acceleration to the end of braking phase | s | |
| I | Maximum positive slope of acceleration | m/s³ | |
| k1 | Acceleration at the end of the braking phase | m/s² | |
| J | Time from negative peak velocity to the end of braking phase | s | |
| l | Negative peak power | W/kg | |
| M | Positive power duration | s | Self-explanatory |
| n | Positive peak power | W/kg | |
| O | Time distance between positive peak power and takeoff | s | |
| p | Mean slope between acceleration peaks | au | |
| q | Shape factor | au | Ratio between the area under the curve from to the last positive sample prior (lasting D) and the one of a rectangle of sides D and e |
| r | Impulse ratio | au | |
| s | Minimum negative velocity | m/s | |
| u | Mean concentric power | W/kg | Average value of |
| W | Power peaks delta time | s | |
| z | Mean eccentric power | W/kg | Average value of |
| High central frequency | Hz | Highest VMD central frequency, associated with wobbling tissues and noise | |
| Middle central frequency | Hz | Middle VMD central frequency, associated with wobbling tissues | |
| Low central frequency | Hz | Lowest VMD central frequency, associated with the jump proper | |
| h | Jump height | m | Height computed via TOV from |
Appendix A.2. Signal Alignment
Appendix A.3. Functional Smoothing
Appendix B. Extended Results
Appendix B.1. Alignment Evaluation


Appendix B.2. Feature Distributions
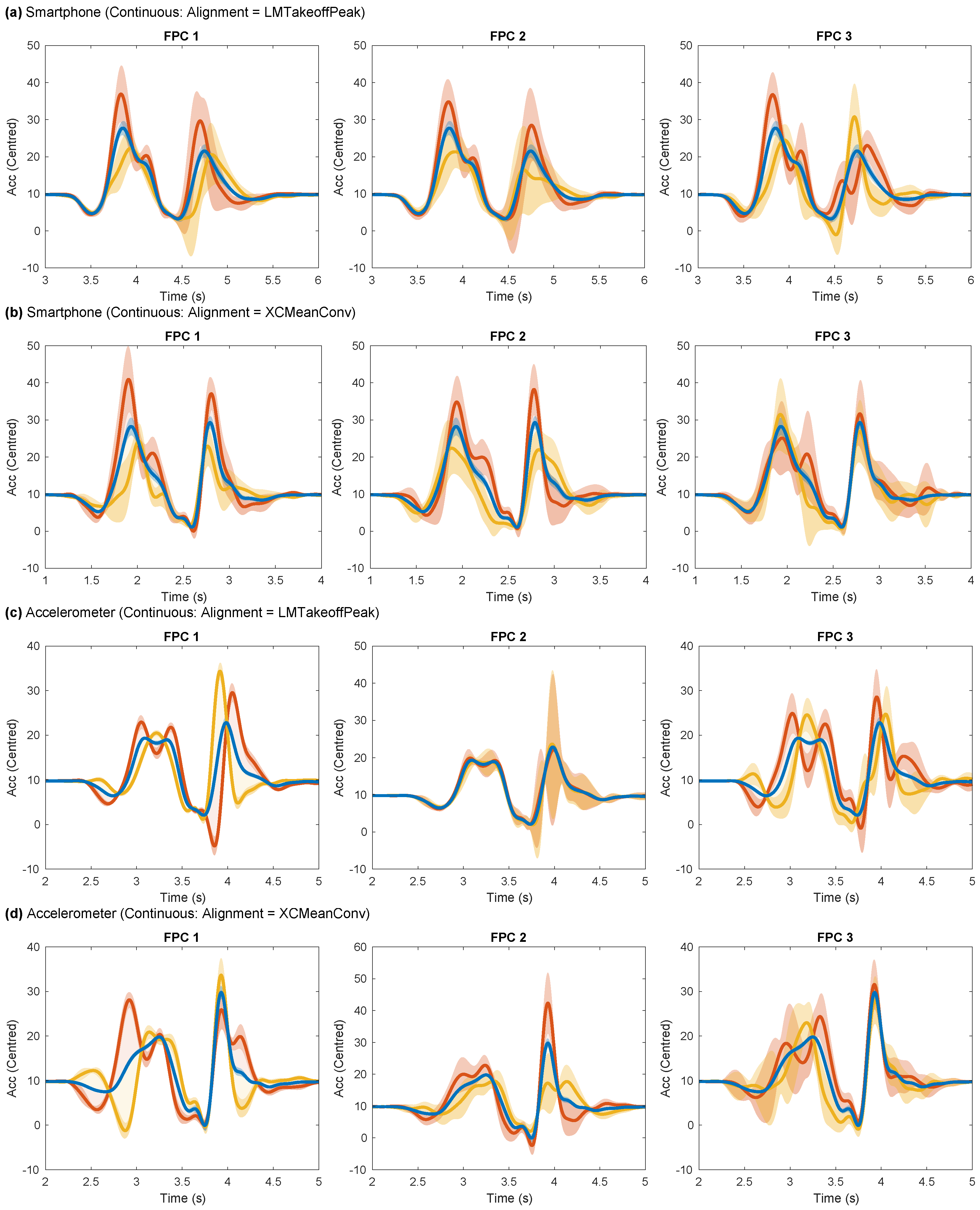
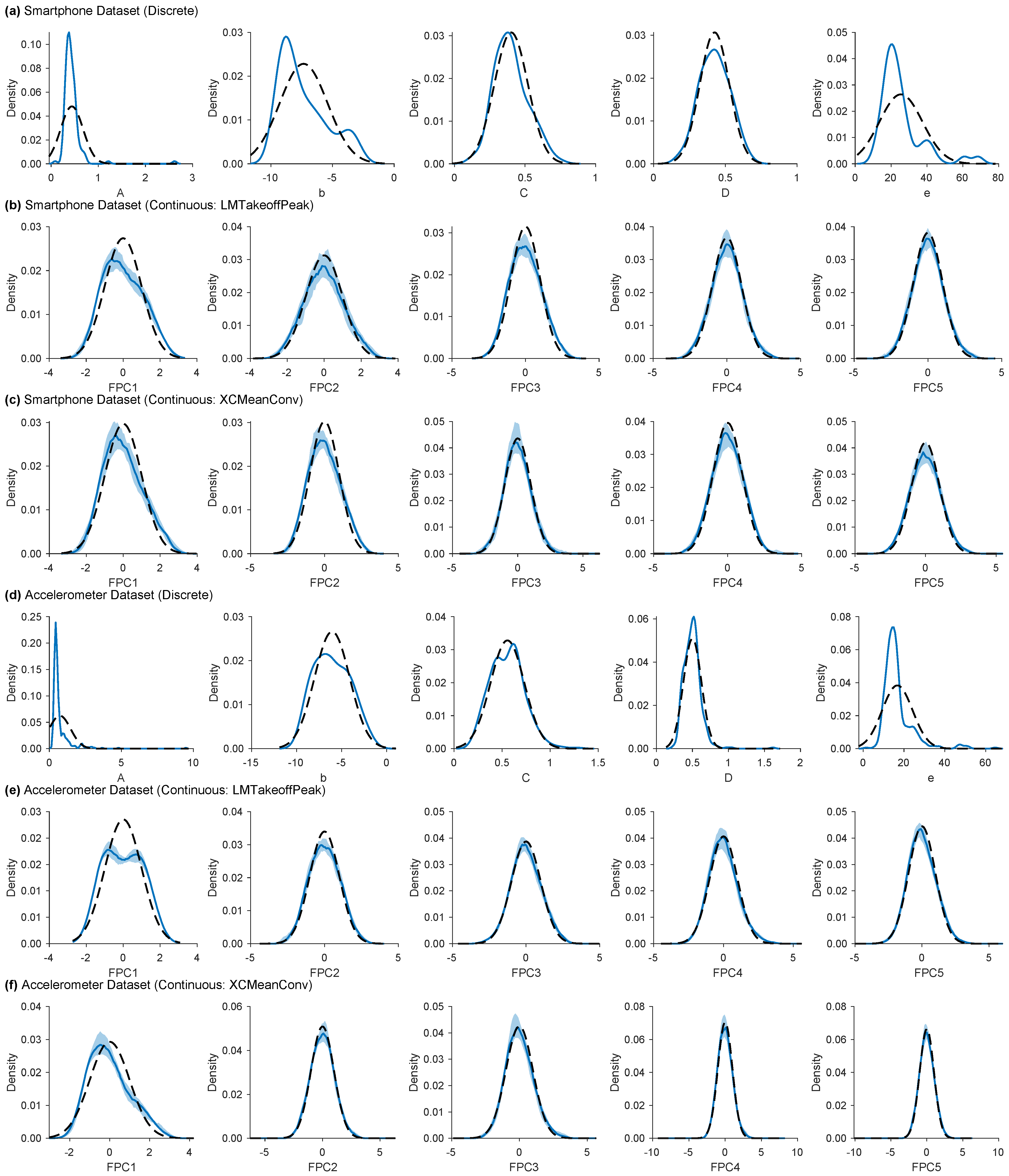
Appendix B.3. Linear Model Beta Coefficients

References
- Seshadri, D.R.; Drummond, C.; Craker, J.; Rowbottom, J.R.; Voos, J.E. Wearable Devices for Sports: New Integrated Technologies Allow Coaches, Physicians, and Trainers to Better Understand the Physical Demands of Athletes in Real time. IEEE Pulse 2017, 8, 38–43. [Google Scholar] [CrossRef]
- Adesida, Y.; Papi, E.; McGregor, A.H. Exploring the Role of Wearable Technology in Sport Kinematics and Kinetics: A Systematic Review. Sensors 2019, 19, 1597. [Google Scholar] [CrossRef]
- Preatoni, E.; Bergamini, E.; Fantozzi, S.; Giraud, L.I.; Orejel Bustos, A.S.; Vannozzi, G.; Camomilla, V. The Use of Wearable Sensors for Preventing, Assessing, and Informing Recovery from Sport-Related Musculoskeletal Injuries: A Systematic Scoping Review. Sensors 2022, 22, 3225. [Google Scholar] [CrossRef]
- Cust, E.E.; Sweeting, A.J.; Ball, K.; Robertson, S. Machine and deep learning for sport-specific movement recognition: A systematic review of model development and performance. J. Sport. Sci. 2019, 37, 568–600. [Google Scholar] [CrossRef]
- Chambers, R.; Gabbett, T.J.; Cole, M.H.; Beard, A. The Use of Wearable Microsensors to Quantify Sport-Specific Movements. Sport. Med. 2015, 45, 1065–1081. [Google Scholar] [CrossRef] [PubMed]
- Ancillao, A.; Tedesco, S.; Barton, J.; O’Flynn, B. Indirect Measurement of Ground Reaction Forces and Moments by Means of Wearable Inertial Sensors: A Systematic Review. Sensors 2018, 18, 2564. [Google Scholar] [CrossRef] [PubMed]
- Johnson, W.; Mian, A.; Robinson, M.A.; Verheul, J.; Lloyd, D.G.; Alderson, J.A. Multidimensional ground reaction forces and moments from wearable sensor accelerations via deep learning. arXiv 2019, arXiv:1903.07221v3. [Google Scholar]
- Hughes, G.T.; Camomilla, V.; Vanwanseele, B.; Harrison, A.J.; Fong, D.T.; Bradshaw, E.J. Novel technology in sports biomechanics: Some words of caution. Sport. Biomech. 2024, 23, 393–401. [Google Scholar] [CrossRef] [PubMed]
- Dorschky, E.; Camomilla, V.; Davis, J.; Federolf, P.; Reenalda, J.; Koelewijn, A.D. Perspective on “in the wild” movement analysis using machine learning. Hum. Mov. Sci. 2023, 87, 103042. [Google Scholar] [CrossRef]
- Dowling, J.J.; Vamos, L. Identification of Kinetic and Temporal Factors Related to Vertical Jump Performance. J. Appl. Biomech. 1993, 9, 95–110. [Google Scholar] [CrossRef]
- Oddsson, L. What Factors Determine Vertical Jumping Height? In Biomechanics in Sports V; Tsarouchas, L., Ed.; Hellenic Sports Research Institute: Athens, Greece, 1989; pp. 393–401. [Google Scholar]
- Donoghue, O.A.; Harrison, A.J.; Coffey, N.; Hayes, K. Functional Data Analysis of Running Kinematics in Chronic Achilles Tendon Injury. Med. Sci. Sport. Exerc. 2008, 40, 1323–1335. [Google Scholar] [CrossRef] [PubMed]
- Ryan, W.; Harrison, A.J.; Hayes, K. Functional data analysis of knee joint kinematics in the vertical jump. Sport. Biomech. 2006, 5, 121–138. [Google Scholar] [CrossRef] [PubMed]
- Warmenhoven, J.; Cobley, S.; Draper, C.; Harrison, A.J.; Bargary, N.; Smith, R. Considerations for the use of functional principal components analysis in sports biomechanics: Examples from on-water rowing. Sport. Biomech. 2017, 18, 317–341. [Google Scholar] [CrossRef]
- Richter, C.; O’Connor, N.E.; Marshall, B.; Moran, K. Analysis of Characterizing Phases on Waveforms: An Application to Vertical Jumps. J. Appl. Biomech. 2014, 30, 316–321. [Google Scholar] [CrossRef] [PubMed]
- Halilaj, E.; Rajagopal, A.; Fiterau, M.; Hicks, J.L.; Hastie, T.J.; Delp, S.L. Machine learning in human movement biomechanics: Best practices, common pitfalls, and new opportunities. J. Biomech. 2018, 81, 1–11. [Google Scholar] [CrossRef]
- Rantalainen, T.; Finni, T.; Walker, S. Jump height from inertial recordings: A tutorial for a sports scientist. Scand. J. Med. Sci. Sport. 2020, 30, 38–45. [Google Scholar] [CrossRef] [PubMed]
- Claudino, J.G.; Cronin, J.; Mezêncio, B.; McMaster, D.T.; McGuigan, M.; Tricoli, V.; Amadio, A.C.; Serrão, J.C. The countermovement jump to monitor neuromuscular status: A meta-analysis. J. Sci. Med. Sport 2017, 20, 397–402. [Google Scholar] [CrossRef] [PubMed]
- McMahon, J.J.; Suchomel, T.J.; Lake, J.P.; Comfort, P. Understanding the Key Phases of the Countermovement Jump Force-Time Curve. Strength Cond. J. 2018, 40, 96–106. [Google Scholar] [CrossRef]
- Mascia, G.; De Lazzari, B.; Camomilla, V. Machine learning aided jump height estimate democratization through smartphone measures. Front. Sport. Act. Living 2023, 5, 1112739. [Google Scholar] [CrossRef]
- White, M.G.E.; Bezodis, N.E.; Neville, J.; Summers, H.; Rees, P. Determining jumping performance from a single body-worn accelerometer using machine learning. PLoS ONE 2022, 17, e0263846. [Google Scholar] [CrossRef]
- Jones, T.; Smith, A.; Macnaughton, L.S.; French, D.N. Strength and Conditioning and Concurrent Training Practices in Elite Rugby Union. J. Strength Cond. Res. 2016, 30, 3354–3366. [Google Scholar] [CrossRef] [PubMed]
- Cormack, S.J.; Newton, R.U.; McGuigan, M.R. Neuromuscular and Endocrine Responses of Elite Players to an Australian Rules Football Match. Int. J. Sport. Physiol. Perform. 2008, 3, 359–374. [Google Scholar] [CrossRef] [PubMed]
- Cronin, J.; Hansen, K.T. Strength and power predictors of sports speed. J. Strength Cond. Res. 2005, 19, 349–357. [Google Scholar] [CrossRef]
- Owen, N.J.; Watkins, J.; Kilduff, L.P.; Bevan, H.R.; Bennett, M.A. Development of a Criterion Method to Determine Peak Mechanical Power Output in a Countermovement Jump. J. Strength Cond. Res. 2014, 28, 1552–1558. [Google Scholar] [CrossRef] [PubMed]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Ramsay, J.O.; Silverman, B.W. Functional Data Analysis, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2005. [Google Scholar]
- White, M.G.E.; Neville, J.; Rees, P.; Summers, H.; Bezodis, N. The effects of curve registration on linear models of jump performance and classification based on vertical ground reaction forces. J. Biomech. 2022, 140, 111167. [Google Scholar] [CrossRef] [PubMed]
- White, M.G.E. Generalisable FPCA-Based Models for Predicting Peak Power in Vertical Jumping Using Accelerometer Data. Ph.D. Thesis, Swansea University, Swansea, UK, 2021. [Google Scholar]
- Kutner, M.H.; Nachtsheim, C.J.; Neter, J.; Li, W. Applied Linear Statistical Models, 5th ed.; McGraw-Hill/Irwin: Boston, MA, USA, 2005. [Google Scholar]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Nielsen, D. Tree Boosting with XGBoost-Why Does XGBoost Win “Every” Machine Learning Competition? Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2016. [Google Scholar]
- Shao, J. Linear Model Selection by Cross-validation. J. Am. Stat. Assoc. 1993, 88, 486–494. [Google Scholar] [CrossRef]
- Cawley, G.C.; Talbot, N.L.C. On Over-fitting in Model Selection and Subsequent Selection Bias in Performance Evaluation. J. Mach. Learn. Res. 2010, 11, 2079–2107. [Google Scholar]
- Vabalas, A.; Gowen, E.; Poliakoff, E.; Casson, A.J. Machine learning algorithm validation with a limited sample size. PLoS ONE 2019, 14, e0224365. [Google Scholar] [CrossRef] [PubMed]
- Harrison, A.; Ryan, W.; Hayes, K. Functional data analysis of joint coordination in the development of vertical jump performance. Sport. Biomech. 2007, 6, 199–214. [Google Scholar] [CrossRef] [PubMed]
- Moudy, S.; Richter, C.; Strike, S. Landmark registering waveform data improves the ability to predict performance measures. J. Biomech. 2018, 78, 109–117. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Lundberg, S.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. arXiv 2016, arXiv:1602.04938. [Google Scholar]
- Kumar, I.E.; Venkatasubramanian, S.; Scheidegger, C.; Friedler, S. Problems with Shapley-value-based explanations as feature importance measures. In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020; Volume 119, pp. 5491–5500. [Google Scholar]
- Slack, D.; Hilgard, S.; Jia, E.; Singh, S.; Lakkaraju, H. Fooling LIME and SHAP: Adversarial Attacks on Post hoc Explanation Methods. In Proceedings of the AAAI/ACM Conference on AI, Ethics, and Society, New York, NY, USA, 7–9 February 2020; pp. 180–186. [Google Scholar] [CrossRef]
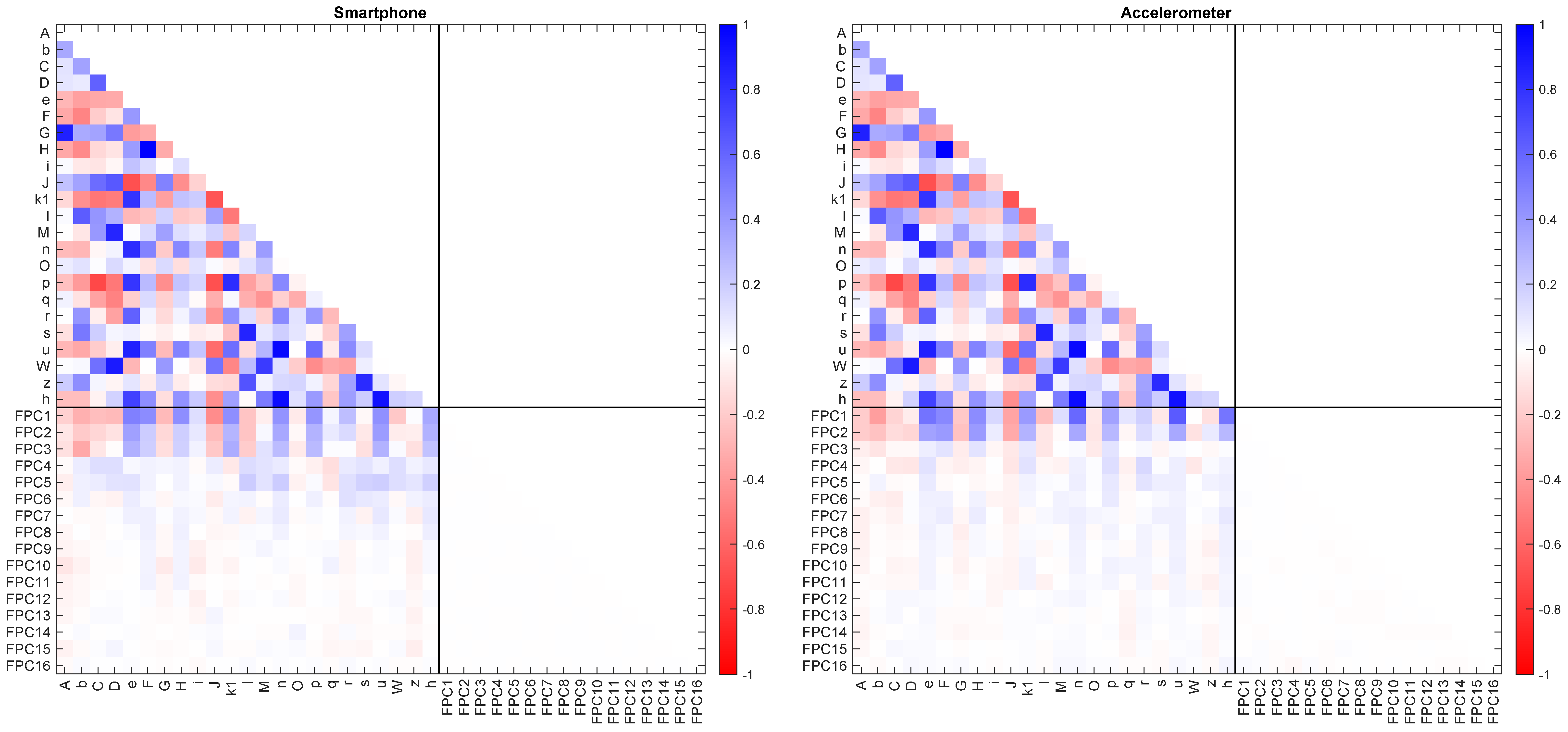

| Smartphone | Accelerometer | |
|---|---|---|
| Participants | 22 males, 10 females | 48 males, 25 females * |
| Age (mean ± SD) | 26.5 ± 4.1 years | 21.6 ± 3.3 years |
| Height (mean ± SD) | 1.74 ± 0.08 m | 1.75 ± 0.10 m |
| Mass (mean ± SD) | 70.0 ± 10.9 kg | 71.2 ± 15.1 kg |
| Device | Redmi 9T phone | Trigno sensor |
| Manufacturer | Xiaomi Technology, Beijing, China | Delsys Inc., Natick, MA, USA |
| Sampling Frequency | 128 Hz | 250 Hz |
| Onboard Sensors | Accelerometer: ±8 g; | Accelerometer ±9 g |
| Gyroscope: ±360 deg/s | ||
| Placement | Handheld at sternum level | Taped to lower back (L4) |
| Reference force platform | Bertec | 9260AA |
| Manufacturer | AMTI, Watertown, MA, USA | Kistler, Winterthur, Switzerland |
| Sampling Frequency | 1000 Hz | 1000 Hz |
| Valid jumps included | 119 | 347 |
| Peak Power (W/kg) † | 40.7 ± 8.9 | 45.1 ± 7.6 |
| Signal for Analysis | Resultant Acceleration | Resultant Acceleration |
| Dataset | Encoding | Standardized Training RMSE * | F-Statistic † | Explained Variance, | Shrinkage ‡ | Proportion Outliers | Proportion Highly Correlated |
|---|---|---|---|---|---|---|---|
| Smartphone | Discrete | 0.430 ± 0.062 | 8.34 ± 3.04 | 0.808 ± 0.055 | 0.108 ± 0.033 | 0.042 ± 0.018 | 0.827 ± 0.032 |
| Continuous | 0.392 ± 0.065 | 15.8 ± 6.3 | 0.840 ± 0.053 | 0.061 ± 0.021 | 0.054 ± 0.018 | 0.000 ± 0.000 | |
| Accelerometer | Discrete | 0.469 ± 0.041 | 24.3 ± 5.9 | 0.777 ± 0.039 | 0.034 ± 0.007 | 0.014 ± 0.015 | 0.831 ± 0.059 |
| Continuous | 0.343 ± 0.039 | 75.8 ± 18.3 | 0.880 ± 0.029 | 0.012 ± 0.003 | 0.052 ± 0.012 | 0.000 ± 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
White, M.; De Lazzari, B.; Bezodis, N.; Camomilla, V. Wearable Sensors for Athletic Performance: A Comparison of Discrete and Continuous Feature-Extraction Methods for Prediction Models. Mathematics 2024, 12, 1853. https://doi.org/10.3390/math12121853
White M, De Lazzari B, Bezodis N, Camomilla V. Wearable Sensors for Athletic Performance: A Comparison of Discrete and Continuous Feature-Extraction Methods for Prediction Models. Mathematics. 2024; 12(12):1853. https://doi.org/10.3390/math12121853
Chicago/Turabian StyleWhite, Mark, Beatrice De Lazzari, Neil Bezodis, and Valentina Camomilla. 2024. "Wearable Sensors for Athletic Performance: A Comparison of Discrete and Continuous Feature-Extraction Methods for Prediction Models" Mathematics 12, no. 12: 1853. https://doi.org/10.3390/math12121853
APA StyleWhite, M., De Lazzari, B., Bezodis, N., & Camomilla, V. (2024). Wearable Sensors for Athletic Performance: A Comparison of Discrete and Continuous Feature-Extraction Methods for Prediction Models. Mathematics, 12(12), 1853. https://doi.org/10.3390/math12121853






