On Optimal Embeddings in 3-Ary n-Cubes

Abstract

The efficiency of a graph embedding problem when simulating one interconnection network in another interconnection network is characterized by the influential parameter of wirelength. Obtaining the minimum wirelength in an embedding problem determines the quality of that embedding. In this paper, we obtained the convex edge partition of 3-Ary n-Cubes and the minimized wirelength of the embeddings of both 3-Ary n-Cubes and circulant networks.

1. Introduction

In a multiprocessor computing system, the connection pattern is determined by the interconnection network; thus, it is a crucial component in the performance of efficient communication in a multiprocessor computing system. From a topological perspective, these complexed interconnection networks can be modeled as simple graphs. As microprocessor technology develops to the nanoscale, the implementation of 100 billion transistors in a chip multi-processor (CMP) has become a reality. In the design of high-performance CMPs, the efficiency of communication between cores is dependent on processor allocation, data storage and communication between processors, which has also become a massive concern [1] for a quality network. It has become popular to use network-on-chip (NoC) technology to develop very large-scale integration (VLSI) systems in multi-processor chips, because of its primary advantages, including low power utilization, high integration, low cost and dense volume. Due to the area constraints on processors, the overall wirelength of NoC has arisen as the most pressing issue concerning its effective communication; thus, the topology structure must meet a few specific requirements. It is one of the most important factors that must be considered for an NoC when determining the cost of the network architectures [2,3].

Using architecture with a complex structure will worsen the issues of the connectivity of processors and wiring costs. Thus, using a convenient network in parallel over the highly connected network under certain circumstances will be made possible using the embedding feature by scrutinising the NoC performance in the communication of chip multi-processors and other VLSI systems. In the field of interconnection networks, the embedding problem plays a significant role in the simulation of architectures and in using the modified parallel algorithms of one network in another network [4]. Embeddings and their applications have been extensively studied in many research works, some of which include the embedding of cycles into hypercubes [5], complete trees into hypercubes [6], cycles and wheels into trees [4], paths into star graphs [7], hypercubes into grids [8], and cycles into recursive circulants [9], and the fault-tolerant Hamilton embedding of alternating group graphs [10], meshes into crossed cubes [11] and meshes into twisted cubes [12].

We have solved the problem of embedding a circulant network into a 3-Ary n-Cube and vice versa by obtaining the minimum wirelength, and have proved that the 3-Ary n-Cube can be embedded into a circulant network with dilation 1. In addition, we have calculated the time complexity of embedding a circulant network into a 3-Ary n-Cube and vice versa. Owing to their greater routing capabilities and fault tolerance, circulant networks, which are generalizations of double-loop networks, have been used to design computer and communication networks [13,14]. These networks have many interesting topological properties suited to parallel computing, such as vertex transitivity, small diameter, and regularity, and are applied in modeling quantum spin networks [15,16]. The 3-Ary n-Cube is a k-Ary n-Cube with $k=3$. It was first employed in the construction of multicomputers such as Ipsc/2 and Ipsc/860, after which it was used in J-Machine, Cray T3D, and T3E [17]. In [18,19,20,21], various k-Ary n-Cube topological characteristics have been discussed. Due to some advantageous topological properties of 3-Ary n-Cube that are suitable for interconnection networks, such as regularity, symmetric nature, pancyclicity, reduced communication lapsed time and ease of implementation [21,22,23], it has been used as the most common interconnection network in multiprocessor computing systems. Thus, it has been used in the design of parallel computers such as Cray XT5 and Blue Gene/L supercomputers [24] and has also been used for constructing networks in the CamCube [25] and NovaCube data centers [26]. 3-Ary n-Cubes have attracted a lot of research attention [27,28,29]. Paths, cycles with faulty nodes and links have been embedded as guest graphs in 3-Ary n-Cubes [30,31] and 3-Ary n-Cubes have been embedded as guest graphs in paths, cycles and grids [32,33].

In this paper, we have obtained the convex edge cuts of 3-Ary n-Cubes, embedded circulant networks into 3-Ary n-Cubes and found the optimal wirelength of embedding circulant networks into 3-Ary n-Cubes and vice versa. The following are the paper’s main contributions:

(1)

We have given the results and proven that the minimum wirelength of the circulant network, $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$ into the 3-Ary n-Cube, $H_n$, and the 3-Ary n-Cube, $H_n$ into the circulant network, $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$ are $\mathcal{WL}\left(G\left(3^n;\pm \left\{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\right\}\right),H_n\right)=\frac{n{3}^n}{2}\left(3^n-3^{n-1}-2\right)$ and $\mathcal{WL}(H_n,G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)=n{3}^n$, respectively.

(2)

We have proved that the dilation of an embedding h of 3-Ary n-Cube, $H_n$, into the circulant network, $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$ is 1.

(3)

The time complexity of obtaining the minimum wirelength of the circulant network, $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$, into the 3-Ary n-Cube, $H_n$, and the 3-Ary n-Cube, $H_n$, into the circulant network, $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$, is $O\left(3^n\right)$ and $O\left(n{3}^n\right)$, respectively. The remaining part of the paper is structured as follows: Section 2 gives the preliminary works and concepts needed for the results obtained in the paper, Section 3 gives an overview of the 3-Ary n-Cube network, $H_n$, Section 4 gives the minimum wirelength of the circulant network, $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$, into the 3-Ary n-Cube, $H_n$, Section 5 gives the minimum wirelength of the 3-Ary n-Cube, $H_n$, into the circulant network, $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$, Section 6 gives the time complexity of the main results obtained and Section 7 gives the concluding remarks of the paper.

2. Fundamentals

In this section, the fundamental concepts and definitions required for the main results of the paper are discussed.

Definition 1

([34]). From a graph, the selection of a certain subset of vertices such that the cardinality of edges in the subgraph having endpoints from the selected vertices is maximum among all other subgraphs, inducing the same number of vertices, is called the optimal subgraph (or set).

Definition 2

([35]). For any $r,s\in V\left(H_{\mathcal{V},\mathcal{E}}\right)$, then a subgraph $H_{\mathcal{V},\mathcal{E}}$ of graph $G_{\mathcal{V},\mathcal{E}}$ is the convex of all shortest paths, and $\mathcal{P}(r,s)$ belongs to $H_{\mathcal{V},\mathcal{E}}$.

Definition 3

([36]). Consider the finite and simple graphs $G_{\mathcal{V},\mathcal{E}}$ and $H_{\mathcal{V},\mathcal{E}}$. Embedding the h of $G_{\mathcal{V},\mathcal{E}}$ into $H_{\mathcal{V},\mathcal{E}}$ is defined as follows:

1.

h is a 1-1 function from $\mathcal{V}\left(G_{\mathcal{V},\mathcal{E}}\right)\to \mathcal{V}\left(H_{\mathcal{V},\mathcal{E}}\right)$;

2.

${\mathcal{P}}_h$ is a 1-1 function from $\mathcal{E}\left(G_{\mathcal{V},\mathcal{E}}\right)$ to $\{{\mathcal{P}}_h(r,s):{\mathcal{P}}_h(r,s)$ is a path in $H_{\mathcal{V},\mathcal{E}}$ connecting the end vertices $h\left(r\right)$ and $h\left(s\right)$ for $(r,s)\in \mathcal{E}\left(G_{\mathcal{V},\mathcal{E}}\right)\}$.

Definition 4

([36]). For every edge, $e_{r,s}\in \mathcal{E}\left(G_{\mathcal{V},\mathcal{E}}\right)$, the cardinality of edges in ${\mathcal{P}}_h(r,s)$ in $H_{\mathcal{V},\mathcal{E}}$ is called the dilation of $e_{r,s}$. The maximal dilation along all of the $G_{\mathcal{V},\mathcal{E}}$, edges is the embedding’s h dilation. The dilation of $G_{\mathcal{V},\mathcal{E}}$ into $H_{\mathcal{V},\mathcal{E}}$ is represented as $\mathcal{D}(G_{\mathcal{V},\mathcal{E}},H_{\mathcal{V},\mathcal{E}})$, which is the lowest dilation of the overall embedding.

Definition 5

([36]). The cardinality of edges $e=e_{r,s}$ of $G_{\mathcal{V},\mathcal{E}}$ such that e belongs to the path $\mathcal{P}(r,s)$ connecting vertices $h\left(r\right)$ and $h\left(s\right)$ in $H_{\mathcal{V},\mathcal{E}}$ is denoted by ${\mathcal{EC}}_h\left(e\right)$. ${\mathcal{EC}}_h(G_{\mathcal{V},\mathcal{E}},H_{\mathcal{V},\mathcal{E}})=max\left\{{\mathcal{EC}}_h\left(e\right)\right|e\in \mathcal{E}\left(H_{\mathcal{V},\mathcal{E}}\right)\}$. Then, $\mathcal{EC}(G_{\mathcal{V},\mathcal{E}},H_{\mathcal{V},\mathcal{E}})=min\left\{{\mathcal{EC}}_h(G_{\mathcal{V},\mathcal{E}},H_{\mathcal{V},\mathcal{E}})\right|h$ is an embedding from $G_{\mathcal{V},\mathcal{E}}$ into $H_{\mathcal{V},\mathcal{E}}\}$, which defines the least edge congestion of $G_{\mathcal{V},\mathcal{E}}$ into $H_{\mathcal{V},\mathcal{E}}$.

Definition 6

([8]). ${\mathcal{WL}}_h(G_{\mathcal{V},\mathcal{E}},H_{\mathcal{V},\mathcal{E}})={\sum }_{(r,s)\in \mathcal{E}\left(G_{\mathcal{V},\mathcal{E}}\right)}{d}_{H_{\mathcal{V},\mathcal{E}}}(h\left(u\right),h\left(v\right))={\sum }_{e\in \mathcal{E}\left(H_{\mathcal{V},\mathcal{E}}\right)}\mathcal{EC}\left(e\right)$ is the wirelength of an embedding h of $G_{\mathcal{V},\mathcal{E}}$ into $H_{\mathcal{V},\mathcal{E}}$. $d_{H_{\mathcal{V},\mathcal{E}}}(h\left(r\right).h\left(s\right))$—length of the path, ${\mathcal{P}}_h(r,s)$, in $H_{\mathcal{V},\mathcal{E}}$. $\mathcal{E}{C}_h\left(e\right)$—congestion in an edge e in $H_{\mathcal{V},\mathcal{E}}$. Then, the minimum wirelength of $G_{\mathcal{V},\mathcal{E}}$ into $H_{\mathcal{V},\mathcal{E}}$ is $\mathcal{WL}(G_{\mathcal{V},\mathcal{E}},H_{\mathcal{V},\mathcal{E}})=min\{{\mathcal{WL}}_h(G_{\mathcal{V},\mathcal{E}},H_{\mathcal{V},\mathcal{E}})$, and h is an embedding from $G_{\mathcal{V},\mathcal{E}}$ to $H_{\mathcal{V},\mathcal{E}}\}$.

Remark 1.

$\mathcal{EC}\left(R\right)={\sum }_{e\in R}\mathcal{EC}\left(e\right)$, R is a collection of edges in $H_{\mathcal{V},\mathcal{E}}$.

Lemma 1

([8]). Let $G_{\mathcal{V},\mathcal{E}}$ and $H_{\mathcal{V},\mathcal{E}}$ be any graph and h be an embedding of $G_{\mathcal{V},\mathcal{E}}$ into $H_{\mathcal{V},\mathcal{E}}$. Let R be an edgecut of $H_{\mathcal{V},\mathcal{E}}$ such that the graph remains in two components, $H_{\mathcal{V},\mathcal{E}}^1$ and $H_{\mathcal{V},\mathcal{E}}^2$, after removing the edges of R, and let $G_{\mathcal{V},\mathcal{E}}^1=h^{-1}\left(H_{\mathcal{V},\mathcal{E}}^1\right)$ and $G_{\mathcal{V},\mathcal{E}}^2=h^{-1}\left(H_{\mathcal{V},\mathcal{E}}^2\right)$. Furthermore, R meets the following requirements.

1.

$\forall e=e_{(r,s)}\in G_{\mathcal{V},\mathcal{E}}^i,i=1,2,{\mathcal{P}}_h(h\left(u\right),h\left(v\right))$ has no edges in R.

2.

$\forall e=e_{(r,s)}$ in G with $r\in G_{\mathcal{V},\mathcal{E}}^1$ and $s\in G_{\mathcal{V},\mathcal{E}}^2$, $P_h(h\left(r\right),h\left(s\right))$ has exactly one edge in R.

3.

$G_{\mathcal{V},\mathcal{E}}^1$ and $G_{\mathcal{V},\mathcal{E}}^2$ are optimal subgraphs.

Then,

$$\mathcal{EC}\left(R\right)=\sum _{r\in V\left(G_{\mathcal{V},\mathcal{E}}^1\right)}de{g}_{G_{\mathcal{V},\mathcal{E}}}\left(r\right)-2|\mathcal{E}\left(G_{\mathcal{V},\mathcal{E}}^1\right)|=\sum _{r\in V\left(G_{\mathcal{V},\mathcal{E}}^2\right)}de{g}_{G_{\mathcal{V},\mathcal{E}}}\left(r\right)-2\left|\mathcal{E}\left(G_{\mathcal{V},\mathcal{E}}^2\right)\right|$$

and ${\mathcal{EC}}_h\left(R\right)$ is the minimum.

Corollary 1.

If $G_{\mathcal{V},\mathcal{E}}$ is a regular graph such that edges induced by $V\left(G_{\mathcal{V},\mathcal{E}}^1\right)$ are an optimal set satisfying the Lemma 1, then edges induced by $V\left(G_{\mathcal{V},\mathcal{E}}^2\right)$ are also an optimal set.

Lemma 2

($s$-Partition Lemma [37]). Let $h:G_{\mathcal{V},\mathcal{E}}\to H_{\mathcal{V},\mathcal{E}}$ be an embedding function. Let $\left[s\mathcal{E}\left(H_{\mathcal{V},\mathcal{E}}\right)\right]$ represent a subset of edges of $H_{\mathcal{V},\mathcal{E}}$, where each $e=e_{r,s}$ in $H_{\mathcal{V},\mathcal{E}}$ is repeated exactly s times. Assuming that each $R_j$ is an edge cut of $H_{\mathcal{V},\mathcal{E}}$ that satisfies the Congestion Lemma, let $R_1,R_2,\dots ,R_l$ be a partition of $\left[s\mathcal{E}\left(H_{\mathcal{V},\mathcal{E}}\right)\right]$. Then,

$$\mathcal{W}{L}_h(G_{\mathcal{V},\mathcal{E}},H_{\mathcal{V},\mathcal{E}})=\frac{1}{s}\sum _{j=1}^l\mathcal{EC}\left(R_j\right).$$

Definition 7

([35]). The circulant network $G(n;\pm J)$, $J\subseteq \{1,2,\dots ,i\},1\le i\le \lfloor \frac{n}{2}\rfloor$, with undirected edges, is defined as a graph with a vertex set, $\mathcal{V}=\{0,1,\dots ,n-1\}$ such that two vertices l and k have an edge if $\mathcal{E}=\left\{\right(l,k):|k-l|\equiv j(modn),j\in J\}$.

Lemma 3

([38]). A collection of m successive vertices from the $G(n;\pm 1)$, $1\le m\le n$, induces an optimal subgraph of $G(n;\pm J)$, where $J=\{1,2,\dots ,i\},1\le i<\lfloor \frac{n}{2}\rfloor ,n\ge 3$.

Theorem 1

([38]). The cardinality of edges induced in an optimal subgraph on m vertices of $G(n;\pm J)$, $J=\{1,2,\dots ,i\},1\le i<\lfloor \frac{n}{2}\rfloor ,1\le m\le n,n\ge 3$ is provided by

$$\xi =\left\{\begin{array}{cc}m(m-1)/2;\hfill & m\le i+1\hfill \\ ki-i(i+1)/2;\hfill & i+1<m\le n-i\hfill \\ \frac{1}{2}\{{(n-m)}^2+(4i+1)k-(2j+1)n\};\hfill & n-i<k\le n.\hfill \end{array}\right.$$

Definition 8

([39]). In a set with integer entries of n-tuples, the lexicographic order is defined as $(u_1,\dots ,u_n)>(v_1,\dots ,v_n)$ if ∃ an integer i, $1\le i\le n$, $\ni u_j=v_j$ for $u_i>v_i$ and $1\le j<i$.

Theorem 2

([40]). If the lexicographic ordering vertices of the cartesian product $G\times G$ are optimum, then any $n\ge 3$ is optimal for $G^n$.

Corollary 2.

The lexicographic ordering is the optimal ordering for obtaining the maximum subgraph in $H_n$, $n\ge 2$.

Definition 9

([27]). 3-Ary n-Cube, $H_n(n\ge 1)$, is a graph on $3^n$ vertices, in which each of the vertices of the form $r=(r_{n-1},r_{n-2},\dots ,r_0)$, such that $0\le r_l\le 2$ for $0\le l\le n-1$. Two vertices $r=(r_{n-1},r_{n-2},\dots ,r_0)$ and $s=(s_{n-1},s_{n-2},\dots ,s_0)$ are adjacent if ∃ m, $0\le m\le n-1$, ∋ $r_m=s_m\pm 1$$\left(mod3\right)$ and $r_m=s_m$, for every $l\in \{0,1,\dots ,m-1,m+1,\dots ,n-1\}$.

Lemma 4

([41]). If G is a 3-Ary n-Cube, $H_n$, $n\ge 2$; then, $I_G\left(m\right)=(m_1+0)3^{m_1}+(m_2+1)3^{m_2}+(m_3+2)3^{m_3}+\dots +(m_r+(r-1))3^{m_r}$, $m_i=0,1,2,\dots ,n$, $1\le i\le r$; where $I_G\left(m\right)$ is the maximum cardinality of edges induced for m vertices, where $m=3^{m_1}+3^{m_2}+3^{m_3}+\dots +3^{m_r}$ and $m_1\ge m_2\ge m_3\ge \dots \ge m_r$.

3. Structure of ${\mathit{H}}_{\mathit{n}},\mathit{n}\mathbf{\ge }\mathbf{1}$

This section gives an overview on the recursive structure of 3-Ary n-Cube, $H_n$, and explains the role of the convex edge partition in obtaining a convex subgraph when an edge partition is given. The recursive structure of 3-Ary n-Cube, $H_n$, is as follows:

(i)

$H_1$ is a three-cycle, and $H_2$ is a $3\times 3$-torus. We view this as three copies of $H_1$ placed one below the other with horizontal binding edges and vertical binding edges, as shown in Figure 1. $H_3$ comprises three copies of $H_2$ placed linearly with corresponding horizontal and vertical binding edges, as shown in Figure 1.

(ii)

$H_n,n\ge 4$ has a structure described as follows:

(a)

When n is even, $H_n$ comprises three copies of $H_{n-1}$ placed linearly.

(b)

When n is odd, $H_n$ comprises three copies of $H_{n-1}$ placed one below the other.

(c)

All the horizontal and vertical binding edges are defined recursively as in (i).

(d)

When n is odd, even if all three copies of $H_{n-1}$ are placed linearly, the graph obtained is isomorphic to that generated as in (b).

(iii)

The vertex set of $H_n$ can be partitioned into $3^{n-2}$ sets of vertices, each inducing a subgraph isomorphic to $H_2$.

(iv)

$H_n$ comprises $3^k$ copies of $H_{n-k}$ subgraphs recursively, where $1\le k\le n-1$.

(v)

There are three copies of $H_{n-1}$: $H_{n-1,0}$, $H_{n-1,1}$ and $H_{n-1,2}$. There are three set of binding edges ($H_{n-1,0}$, $H_{n-1,1}$) joining the corresponding vertices from $H_{n-1,0}$ to $H_{n-1,1}$, ($H_{n-1,0}$, $H_{n-1,2}$) joining the corresponding vertices from $H_{n-1,0}$ to $H_{n-1,2}$ and ($H_{n-1,1}$, $H_{n-1,2}$) joining the corresponding vertices from $H_{n-1,1}$ to $H_{n-1,2}$.

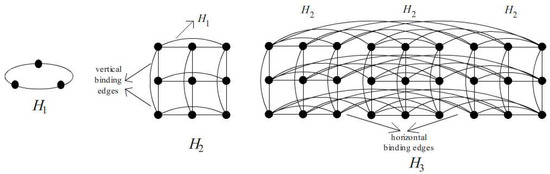
Figure 1. Structure of $H_1,H_2$ and $H_3$.

Notation:

(i)

$(H_{n-i,j}^h,H_{n-i,(j+1)mod3}^h)$ denote the edges connecting $H_{n-i,j}$ and $H_{n-i,(j+1)mod3}$ copies in $H_n$ lying one below the other.

(ii)

$(H_{n-i,j}^h,H_{n-i,(j+2)mod3}^h)$ denote the edges connecting $H_{n-i,j}$ and $H_{n-i,(j+2)mod3}$ copies in $H_n$ lying one below the other.

(iii)

$(H_{n-k,l}^v,H_{n-k,(l+1)mod3}^v)$ denote the edges connecting $H_{n-i,j}$ and $H_{n-i,(j+1)mod3}$ copies in $H_n$ lying linearlly.

(iv)

$(H_{n-k,l}^v,H_{n-k,(l+2)mod3}^v)$ denote the edges connecting $H_{n-i,j}$ and $H_{n-i,(j+2)mod3}$ copies in $H_n$ lying linearlly.

Convex edge partition of ${\mathit{H}}_{\mathit{n}}$:

In each $H_n$, there are three copies of $H_{n-1}$ joined recursively by horizontal and vertical binding edges, as shown in Figure 1. The edge set of $H_n$ is partitioned in the sense it must disconnect the graph into two convex subgraphs of $H_n$. For $n\ge 2$, the horizontal edge cuts are defined as $S_i^j\to \{(H_{n-i,j}^h,H_{n-i,(j+1)mod3}^h),(H_{n-i,j}^h,H_{n-i,(j+2)mod3}^h)\}$, where $1\le i\le \lfloor \frac{n}{2}\rfloor$ and $0\le j\le 2$. The vertical edge cuts are defined as $T_k^l\to \{(H_{n-k,l}^v,H_{n-k,(l+1)mod3}^v),(H_{n-k,l}^v,H_{n-k,(l+2)mod3}^v)\}$, where $1\le k\le \lceil \frac{n}{2}\rceil$ and $0\le l\le 2$. By removing the horizontal and vertical binding edges of $H_{n-1}$ in $H_n$ recursively, the network $H_n$ can be disconnected into components, since these edges are the binding edges of $H_{n-1}$ in $H_n$. One component of each of the $3n$ edge cuts is isomorphic to $H_{n-1}$, whereas $H_{n-1}$ is the previous dimension of $H_n$ and also the subgraph of $H_n$. Thus, every shortest path between any two points remains in it, and so it is a convex subgraph. Since $H_n$ is a $2n$-regular graph, if there exist two components such that one component of it is a convex subgraph, then the other component is also a convex subgraph. Thus, the edge cuts $S_i^j$ and $T_k^l$ of $H_n$ are convex edge cuts.

4. Wirelength of Embedding Circulant Network into 3-Ary n-Cube

This section comprises the results on the minimum wirelength for embedding the circulant network, $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$, into the 3-Ary n-Cube, $H_n$.

Lemma 5.

The edge cuts $S_i^j=\{(H_{n-i,j}^h,H_{n-i,(j+1)mod3}^h),(H_{n-i,j}^h,H_{n-i,(j+2)mod3}^h)\}$ for $1\le i\le \lfloor \frac{n}{2}\rfloor$ and $0\le j\le 2$ induce an optimal subgraph in $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$.

Proof. 

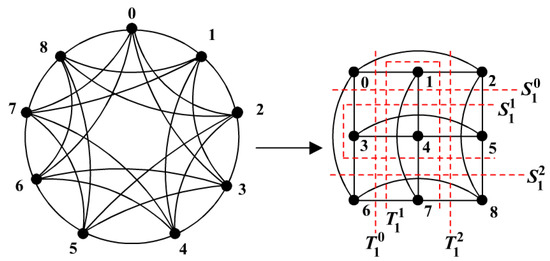
Label the vertices of $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$ in clockwise direction as $0,1,2\dots ,3^n-1$ and $H_n$, considering lexicographic ordering. Let the edges of $H_n$ be partitioned by the edge cuts $S_i^j$, for $1\le i\le \lfloor \frac{n}{2}\rfloor$, $0\le j\le 2$. See Figure 2. Each edge cut $S_i^j$ disjoins $H_n$ into two components such that one of its components is a copy of $H_{n-1}$ and the number of edges induced by each edge cut $S_i^j$ of r vertices in the inverse image is $r(r-1)/2$ by Theorem 1, which induces an optimal subgraph in $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$. Thus, the edge cuts $S_i^j$ for $1\le i\le \lfloor \frac{n}{2}\rfloor$, $0\le j\le 2$ induce an optimal subgraph in $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$.    □

Figure 2. Embedding $G(9;\pm \{1,2,3\left\}\right)$ into $H_2$.

Lemma 6.

The edge cuts $T_k^l=\{(H_{n-k,l}^v,H_{n-k,(l+1)mod3}^v),(H_{n-k,l}^v,H_{n-k,(l+2)mod3}^v)\}$, for $1\le k\le \lceil \frac{n}{2}\rceil$ and $0\le l\le 2$ induce an optimal subgraph in $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$.

Proof. 

The vertices of $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$ are labeled in clockwise direction as $0,1,2\dots ,3^n-1$ and $H_n$, considering lexicographic ordering. Let the edges of $H_n$ be partitioned by the edge cuts $T_k^l$, for $1\le k\le \lceil \frac{n}{2}\rceil$, $0\le l\le 2$. See Figure 2. Each edge cut $T_k^l$ disjoins $H_n$ into two components such that one of its components is a copy of $H_{n-1}$ and the number of edges induced by each edge cut $T_k^l$ of r vertices in the inverse image is $r(r-1)/2$ by Theorem  1, which induces an optimal subgraph in $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$. Thus, the edge cuts $T_k^l$, for $1\le k\le \lceil \frac{n}{2}\rceil$, $0\le l\le 2$ induce an optimal subgraph in $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$.    □

Theorem 3.

The wirelength of an embedding h of $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$ into $H_n$ is the minimum.

Proof. 

Consider $S_i^j$, $1\le i\le \lfloor \frac{n}{2}\rfloor$, $0\le j\le 2$ be the horizontal edge cut of $H_n$ and $T_k^l$, $1\le k\le \lceil \frac{n}{2}\rceil$, $0\le l\le 2$ be the vertical edge cut of $H_n$. By Lemmas 5 and 6, each edge cut $S_i^j$ and $T_k^l$ induces the maximum subgraph in $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$, respectively. For convenience, let $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$ and $H_n$ be denoted as G and H, respectively. The removal of $S_i^j$ leads the graph $H_n$ into disconnected components $H_{ij}$ and $H_{i{j}^{{}^{\prime }}}$ such that the inverse images in $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$ are $G_{ij}=h^{-1}\left(H_{ij}\right)$ and $G_{i{j}^{{}^{\prime }}}=h^{-1}\left(H_{i{j}^{{}^{\prime }}}\right)$, which are optimal sets in $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$. Thus, the edge cuts $S_i^j$ satisfy the congestion lemma. Therefore, $\mathcal{EC}\left(S_i^j\right)$ is the minimum. Similarly, the edge cut $T_k^l$ leads the graph $H_n$ into disconnected components $H_{kl}$ and $H_{k{l}^{{}^{\prime }}}$ such that the inverse images in $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$ are $G_{kl}=h^{-1}\left(H_{kl}\right)$ and $G_{k{l}^{{}^{\prime }}}=h^{-1}\left(H_{k{l}^{{}^{\prime }}}\right)$, which are optimal sets in $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$. Therefore $\mathcal{EC}\left(T_k^l\right)$ is the minimum. See Figure 2. Consequently, the Partition Lemma indicates that wirelength, $\mathcal{WL}\left(G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right),H_n\right)$, is the minimum, which is optimal.    □

Remark 2.

$E\left[Y_a^b\right]$—Edges induced by vertices in the components of the set partitioned by the edge cut $Y_a^b$.

Algorithm 1 Embedding of the circulant network $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$ into the 3-Ary n-Cube, $H_n$.

Let $h:H_n\leftarrow G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$; $h\left(v_0\right)=v_0,\forall v_0$∈$\mathcal{V}\left(G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)\right)$; Label the vertices of $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$ in clockwise order; Label the vertices of $H_n$ in lexicographic ordering;      Let $S_i^j\subset \mathcal{V}\left(H_n\right)$ and $T_k^l\subset \mathcal{V}\left(H_n\right)$ with maximum $E\left[S_i^j\right]$ and $E\left[T_k^l\right]$ in $E(G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$; for $1\le i\le \lfloor \frac{n}{2}\rfloor$, $1\le k\le \lceil \frac{n}{2}\rceil$, $0\le j,l\le 2$ do       for all $(v_0,x)\in$$\mathcal{E}\left(H_n\right)$ with $x\in S_i^j,T_k^l$, where $S_i^j$ and $T_k^l$ are edge cuts;          if $S_i^j$ and $T_k^l$ are convex sets in $H_n$ and every $E\left[S_i^j\right]$ and $E\left[T_k^l\right]$ are maximum in $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$ then;          h is an optimal embedding;     else          h is not an optimal embedding;          end if       end for $h:H_n\leftarrow G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$ induces minimum wirelength; end for return h

Theorem 4.

The minimum wirelength of $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$ in $H_n$ is given by

$$\mathcal{WL}\left(G\left(3^n;\pm \left\{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\right\}\right),H_n\right)=\frac{n{3}^n}{2}\left(3^n-3^{n-1}-2\right).$$

Proof. 

By Lemmas 1 and 2,

$$\begin{array}{cc}\hfill & \mathcal{WL}\left(G\left(3^n;\pm \left\{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\right\}\right),H_n\right)\hfill \\ \hfill & =\frac{1}{2}\left(\sum _{i=1}^{\lfloor \frac{n}{2}\rfloor }\sum _{j=1}^2\mathcal{EC}\left(S_i^j\right)+\sum _{k=1}^{\lceil \frac{n}{2}\rceil }\sum _{l=1}^2\mathcal{EC}\left(T_k^l\right)\right)\hfill \\ \hfill & =\frac{1}{2}\left(\sum _{i=1}^{\lfloor \frac{n}{2}\rfloor }\sum _{j=1}^2\left(r|V\left(G_{ij}\right)|-2|E(G_{ij}\right)|+\sum _{k=1}^{\lceil \frac{n}{2}\rceil }\sum _{l=1}^2\left(r|V\left(G_{kl}\right)|-2|E(G_{kl}\right)\right)\hfill \\ \hfill & =\frac{1}{2}\left(3\left((3^n-3)\left(3^{n-1}\right)-3^{n-1}(3^{n-1}-1)\right)\left(⌊\frac{n}{2}⌋+⌈\frac{n}{2}⌉\right)\right)\hfill \\ \hfill & =\frac{1}{2}\left(3^n\left(3^n-3^{n-1}-2\right)\left(⌊\frac{n}{2}⌋+⌈\frac{n}{2}⌉\right)\right)\hfill \\ \hfill & =\frac{n{3}^n}{2}\left(3^n-3^{n-1}-2\right)\hfill \end{array}$$

   □

5. Wirelength of Embedding 3-Ary n-Cube into Circulant Network

In this section, we obtain the dilation of embedding the 3-Ary n-Cube, $H_n$, into the circulant network, $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$, as 1. Furthermore, we give the minimum wirelength of it.

Remark 3.

Let the adjacent vertices u and v of $H_n$ be represented by the labels r and s, respectively, where $r>s$. For every edge $(u,v)$ in $H_n$, $r-s\in \{1,2,3^{k-1},2\left(3^{k-1}\right)\},2\le k\le n$ and $n\ge 2$.

Dilation Algorithm:

Input: 3-Ary n-Cube, $H_n$, and the circulant network $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$, $n\ge 2$.

Algorithm: Consider the vertices of $H_n$ and $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$ with regard to Lexicographic ordering and $0,1,2\dots ,3^n-1$ in the clockwise direction, respectively. Let h be an embedding of $H_n$ into $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$ defined by $h\left(u\right)=u$, and assume ${\mathcal{P}}_h(u,v)$ as the shortest route between $h\left(u\right)$ and $h\left(v\right)$ in $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$, for each vertex $u\in \mathcal{V}\left(H_n\right)$ and for every edge $(u,v)\in \mathcal{E}\left(H_n\right)$. See Figure 3.

Output: An embedding h of $H_n$ into $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$ with dilation 1.

Proof of Correctness. 

Let 3-Ary n-Cube, $H_n$, and the circulant network $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$ be G and H, respectively. For every edge $e=(u,v)$ in G, $r-s\in \{1,2,3^{k-1},2\left(3^{k-1}\right)\},2\le k\le n$ and $n\ge 2$, we have the following cases:

$$r-s=\left\{\begin{array}{cc}1\hfill & ;(f\left(r\right),f\left(s\right))\in \mathcal{E}\left(G(3^n;\pm \left\{1\right\})\right)\hfill \\ 2\hfill & ;(f\left(r\right),f\left(s\right))\in \mathcal{E}\left(G(3^n;\pm \left\{2\right\})\right)\hfill \\ 3^{k-1},2\left(3^{k-1}\right)\hfill & ;(f\left(r\right),f\left(s\right))\in \mathcal{E}\left(G(3^n;\pm \left\{3^{k-1}\right\})\right),2\le k<n,n>2\hfill \\ 3^{n-1},2\left(3^{n-1}\right)\hfill & ;(f\left(r\right),f\left(s\right))\in \mathcal{E}\left(G(3^n;\pm \left\{3^{n-1}\right\})\right).\hfill \end{array}\right.$$

Thus, for every edge $(u,v)$ in $H_n$, there exists a ${\mathcal{P}}_h(u,v)=1$ in $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$. Hence, the dilation of embedding h of $H_n$ into $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$ is 1. The result of the dilation algorithm, which yields the minimum wirelength, is the following theorem:    □

Algorithm 2 Embedding of 3-Ary n-Cube, $H_n$, into the circulant network, $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$.

Let $h:G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)\leftarrow H_n$; $h\left(v_0\right)=v_0,\forall v_0$∈$\mathcal{V}\left(H_n\right)$; Label the vertices of $H_n$ in lexicographic ordering; $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$ should be labelled in clockwise direction; For $(a,b)\in E\left(H_n\right)$, $dil(a,b)=|{\mathcal{P}}_h(h\left(a\right),h\left(b\right))|$, where ${\mathcal{P}}_h(h\left(a\right),h\left(b\right))$ is a shortest path between $h\left(a\right)$ and $h\left(b\right)$ in $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$ then;       h induces minimum dilation;     else       h does not induces minimum dilation;    for $e=1$ to $n{3}^n$ do       $dil(a,b)$ for all $(a,b)\in$$\mathcal{E}\left(H_n\right)$;      end for $\mathcal{WL}(H_n,G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right))={\sum }_{(a,b)\in \mathcal{E}\left(H_n\right)}dil(a,b)$; $h:G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)\leftarrow H_n$ induces minimum wirelength; return h

Theorem 5.

The minimum wirelength of $H_n$ in $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$ is given by

$$\mathcal{WL}(H_n,G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)=n{3}^n.$$

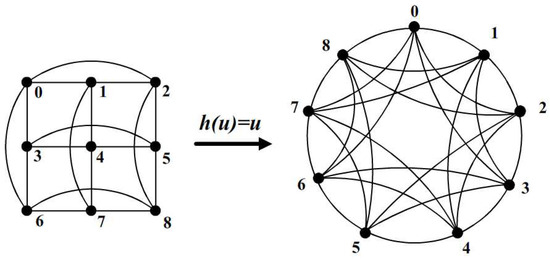
Figure 3. Embedding $H_2$ into $G(9;\pm \{1,2,3\left\}\right)$.

6. Asymptotic Notation of Optimal Wirelength

The total amount of time an algorithm needs to run from start to finish is its runtime complexity. A function of the instance attributes is how many steps an algorithm requires to complete a particular task. An algorithm’s precise step count can be extremely challenging to determine [42]. However, by following the edge isopermetric problem and convex edge partition techniques, and the congestion and partition lemmas, the number of steps involved in the wirelength algorithm is computed directly, which reduces the difficulty in calculating the time complexity of the embedding algorithm. The time required to attain the ideal wirelength of the circulant network in the 3-Ary n-Cube and vice versa using embedding algorithms A and B, respectively, is described in this section.

Time complexity Algorithm 1: Input: $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$—circulant network and $H_n$-3-Ary n-Cube.

Algorithm: Embedding Algorithm 1.

Output: The time taken to run Embedding Algorithm 1.

Method of Proof: Let the number of vertices be $x=3^n$. We spend x time units for assigning the labels of $x=3^n$ vertices. By Algorithm 1, we have $3n$ edge cuts. Thus, we need $3n$ units of time for obtaining the edge cuts and a further $3n$ units of time are needed to calculate the edge congestion on each edge cut. Finally, we need one unit of time for calculating wirelength. Thus, the total time taken is

$$\begin{array}{cc}\hfill & =x+3n+3n+1\hfill \\ \hfill & =x+6n+1\hfill \\ \hfill & \le x+x+x\hfill \\ \hfill & \le 3x\hfill \end{array}$$

As a result, it takes $O\left(x\right)$ time to obtain the optimal wirelength for embedding h of $G\left(3^n;\pm \{1,2,\dots ,⌊\frac{3^n}{2}⌋-1\}\right)$ into $H_n$.

Time complexity Algorithm 2:

Input: $H_n$—3-Ary n-Cube and $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$—circulant network.

Algorithm: Embedding Algorithm 2.

Output: Embedding Algorithm 2 run time.

Method of Proof: Let the number of vertices be $x=3^n$. We spend x time units for assigning the labels of $x=3^n$ vertices. By Algorithm 2, we have $n{3}^n$ edges. Thus, we need $n{3}^n$ units of time for obtaining the dilation of each edge. Finally, we need one unit of time for calculating wirelength. Thus, the total time taken is

$$\begin{array}{cc}\hfill & =x+n{3}^n+1\hfill \\ \hfill & =x+nx+1\hfill \\ \hfill & \le nx+nx+nx\hfill \\ \hfill & \le 3nx\hfill \end{array}$$

Consequently, it takes $O\left(nx\right)$ time of embedding h to obtain the optimum wirelength of $H_n$ in $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$.

7. Conclusions

This paper deals with the results regarding the minimum wirelength of embedding and time complexity for inputting the same circulant network into the 3-Ary n-Cube and vice versa. Furthermore, we have given the results of the dilation of an embedding h of $H_n$ into $G\left(3^n;\pm \{1,2,\dots ,3^{n-1}\}\right)$, found to be 1, and 3-Ary n-Cube network’s convex edge partition. It is interesting to note that 3-Ary n-Cube satisfies both the convex edge partition and edge isoperimetric problem, which are the necessary conditions for the network to play the role of both host and guest network in embedding problems. From the literature, it can be seen that few networks have been explored to date for use in embedding problems as both host and guest networks using convex edge partition and the edge isoperimetric problem, respectively. Finding such networks will be a good research focus in the future.