Microelongated Thermo-Elastodiffusive Waves of Excited Semiconductor Material under Laser Pulses Impact

Abstract

The current study focuses on one-dimensional (1D) deformation in an excited microelongated semiconductor medium impacted by optoelectronics with exponential laser-pulsed heat. Diffusion effect is considered in a photothermal problem of a semiconducting media. Microelongated optoelectronics and a broad variety of concepts have been introduced. Appropriate solutions to a set of microelongated photothermal diffusion differential equations have been found. The homogeneous (thermal and mechanical) and isotropic characteristics of the medium are thought to be in the $x$-direction, including coupled diffusion equations. The linear photo-thermoelasticity (PTE) theory of semiconductors is used to describe thermo-elastodiffusive waves. As a case study, the developed theoretical framework may be used to explore the microelongation-photo-thermoelastic problem in a semiconductor medium caused by the laser pulse. The analytical linear solutions for the main quantities during thermoelastic (TD) and electronic (ED) deformation are obtained using Laplace transforms for dimensionless quantities. To obtain exact expressions of the important physical variables according to certain boundary surface conditions, numerical approximations solutions of the fundamental relevant relations are performed in the Laplace inverse time domain. To describe the wave propagation of the physical fields graphically, the computational results for silicon (Si) semiconductor material are derived using several cases of thermal memory and microelongation factors.

1. Introduction

A substance known as a semiconductor material has electrical conductivity attributes that fall in between those of a conductor and those of non-conductor or insulator materials. This suggests that semiconductors may change their behavior from conducting to insulating depending on the external environment. As the temperature increases, a semiconductor’s internal resistance gradually decreases, enabling a current to pass through it. The most well-known, pure semiconductor is silicon, whereas gallium arsenide is a compound semiconductor element. In recent years, the scientific world has been more interested in semiconductor gain processes on ultrafast time scales. To investigate how semiconductor laser amplifiers react to ultrashort (picosecond or shorter time scales) light pulses in this region, some experimental approaches have been carried out. Empirical testing has shown the complexity of gain, measured along the timeframe in the order of picoseconds. The idea that this kind of gain response is caused by unusual behavior of the carrier ensemble on short time scales; notably, the conduction of dynamic carrier heating is supported by mathematical calculations [1]. The process of electronic deformation (ED) occurs when the electrons go to the surface after being tremendously excited. On the other hand, the increase in temperature causes the inner particles to vibrate and collide, allowing thermoelastic deformation (TE) to emerge. In this situation, semiconductor materials may be studied as elastic materials. These materials may be studied using the so-called photo-thermoelasticity theory during ED and TE deformation processes [2]. In light of these deformations, it is necessary to take into account the microinertia process of the material’s microelements (ED and TD). The behavior of semiconductor materials with changing internal structures is insufficiently explained by classical theories [3]. In contemporary science, the surface deformation of a material is now dominated by laser heating. An extremely adaptable tool for altering the surfaces of materials is the laser. When the laser’s intensity is extremely high, it interacts with the surface of the material and causes absorption there.

Attempts to predict the behavior of materials with internal structures using just the classical theory have shown to be inadequate. Eringen and Suhubi [4,5] have suggested a nonlinear theory for microelastic solids. Eringen [6,7,8] devised the linear theory of micropolar elasticity, which accounts for the fact that material particles in solids may undergo both macro- and micro-rotations. Axial stretch was considered in Eringen’s [9] model of a micropolar elastic solid. The micropolar hypothesis was expanded by many writers to include thermal effects [10,11,12,13]. Both the idea of temperature rate-dependent thermoelasticity and the theory of Lord and Shulman [14] are significant examples of generalized thermoelasticity. In a study of the thermodynamics of thermoelastic substances, Muller [15] proposed an entropy production inequality, which restricts a specific class of constitutive equations. A generalization of this inequality was introduced by Green and Laws [16]. Green and Lindsay [17] established an alternate representation of these constitutive equations. All the equations of the coupled theory are modified by these two constants, which were created independently and explicitly and act as relaxation times [12]. Nevertheless, Shaw and Othman [18] investigated specific issues in the thermoelasticity theory by means of a conformable fractional differential equation. Rayleigh and Reflection wave propagation in a nonlocal rotating isotropic piezo-thermoelastic material with fractional derivatives was investigated by Lata et al. [19,20,21,22,23].

Around the beginning of the twentieth century, studies into semiconductor properties were beginning to be conducted. Due to scientific and industrial advances, semiconductors had extensive applications in the 20th century, being incorporated into anything from solar cells that produce renewable energy to electrical circuits in medical equipment. Maruszewski [24,25] introduced new theoretical models that take into account the interplay of the elastic, thermal, and charge carrier fields in elastic semiconductors. The thermal diffusivity of semiconductors during heat and mass transport processes has recently been studied based on the overlap between thermal, elastic, and plasma waves [26,27]. The photothermal (PT) technique is used in contemporary research on delicate photoacoustic processes in semiconductor materials [28]. Both TE and ED deformation are required by the PT process, which analyses semiconductors’ physical characteristics. The effects of a laser beam, electromagnetic radiation, and acoustic waves on a semiconductor material were investigated [29]. The photo-thermoelasticity theory was used by several authors to study a variety of topics about elastic semiconductor materials [30,31,32]. The absorbed optical energy on the free surface of homogeneous and non-homogeneous semiconductor materials was examined when thermal conductivity varied during PT transport activities [33,34,35,36,37]. Khamis et al. [38] studied the semiconductor medium under the impact of thermal piezoelectricity in the context of photo-thermal excitation. Mahdy et al. [39,40] used the time-fractional heat order and Thomson effects under the impact of pulse heat flux to investigate the magneto-photothermal semiconductor medium during variable thermal conductivity. In all of the aforementioned studies, the interaction between electrons and holes was ignored while they were examining semiconductors using PT theory. However, the effect of microelongation under the effect of laser pulses has been ignored when there was no heat source. The excited electrons with holes were found to be dispersed toward the semiconductor’s surface and move about, creating an electron cloud known as carrier density and hole charge in studies on the characteristics of semiconductors (plasma).

The main objective of this work is to examine the effects of electron diffusion in the presence of microelongation parameters. The homogeneous, isotropic, microelongated semiconductor medium is used to analyze the propagation of elasto-thermodiffusive waves during photo-generated excitation. In this paper, we use the photo-thermoelasticity theory to the study of laser-induced thermo-elastodiffusive waves in a semiconductor medium. A new model for one-dimensional deformation processes is developed using the microelongated semiconductor in accordance with the microinertia of medium. A completely new mathematical photo-thermoelasticity model is developed, including elongation in 1D deformation and dimensionless quantities. Under the appropriate conditions, Laplace transforms for the partial differential governing equation are applied analytically. Mathematically, the reverse of the Laplace transform is numerically utilized to provide the complete solutions of the main variables in this problem. Finally, by presenting the results of the physical field quantities graphically, analytical verification can be provided. The impacts of microelongation and laser pulses factor are studied, as well as the thermal memory of silicon medium. Graphical representations of the numerical findings have been made and are discussed.

2. Governing Equation

The Cartesian coordinate is utilized in 1D deformation at reference temperature $T_0$, in which case all field variables are independent of the $y$ and $z$ coordinates. In the linear theory of photo-thermoelasticity of microelongated semiconductors, the governing field equations in 1D for temperature distribution $T(x,t)$, the microelongational function $\phi (x,t)$, displacement $u(x,t)$, $H(x,t)$ and electron diffusion field (carrier density) $N(x,t)$ depend on the time $t$ and the $x$-axis in accordance with the semiconductor’s electric neutrality. The constitutive equations for microelongated semiconductor photo-thermoelastic media are presented in the general form of tensors [2]:

$$\begin{array}{l}{\sigma }_i{}_I=({\lambda }_o\phi +\lambda u_r{,}_r){\delta }_i{}_I+2\mu u_{I,}{}_i-{\delta }_i{}_I{\delta }_{h}H-\widehat{\gamma }(1+v_o\frac{\partial }{\partial t})T{\delta }_i{}_I-((3\lambda +2\mu )d_{n}N){\delta }_i{}_I,\\ m_i=a_0{\phi }_{,i},\\ s-\sigma ={\lambda }_o{u}_i{,}_i-{\beta }_1(1+{\tau }_{\theta }\frac{\partial }{\partial t})T+-((3\lambda +2\mu )d_{n}N){\delta }_2{}_i-{\delta }_2{}_i{\delta }_{h}H+{\lambda }_1\phi .\end{array}\},$$

(1)

When the body forces electro-magnetic pressure and heat sources are absent, according to the microelongated photo-thermoelastic theory, the main equations may be found in 1D [9].

$$\rho \frac{{\partial }^{2}u}{\partial t^2}=(2\mu +\lambda )\frac{{\partial }^{2}u}{\partial x^2}-\gamma (1+{\tau }_{\theta }\frac{\partial }{\partial t})\frac{\partial T}{\partial x}+{\lambda }_o\frac{\partial \phi }{\partial x}-{\delta }_n\frac{\partial N}{\partial x}-{\delta }_h\frac{\partial H}{\partial x},$$

(2)

$$\begin{array}{l}K(1+{\tau }_{\theta }\frac{\partial }{\partial t})\frac{{\partial }^{2}T}{\partial x^2}+m_{nq}\frac{{\partial }^{2}N}{\partial x^2}+m_{hq}\frac{{\partial }^{2}H}{\partial x^2}- \rho (a_1^n\frac{\partial N}{\partial t}+a_1^h\frac{\partial H}{\partial t})- \\ (1+{\tau }_q\frac{\partial }{\partial t})\left[\rho C_e\frac{\partial T}{\partial t}+\rho T_0{\alpha }_n\frac{\partial N}{\partial t}+\rho T_0{\alpha }_h\frac{\partial H}{\partial t}+ T_0\gamma \frac{\partial }{\partial x}\frac{\partial u}{\partial t}\right]-\\ \left[\frac{\rho a_1^n}{t^n}N+\frac{\rho a_1^h}{t^h}H\right]={\widehat{\gamma }}_1{T}_o\frac{\partial \phi }{\partial t}\end{array}\},$$

(3)

$$\begin{array}{l}{m}_{qn}\frac{{\partial }^{2}T}{\partial x^2}+D_n\rho \frac{{\partial }^{2}N}{\partial x^2}-\rho (1-a_2^n T_0{\alpha }_n+t^n\frac{\partial }{\partial t})\frac{\partial N}{\partial t}\\ -a_2^n\left[\rho C_e\frac{\partial T}{\partial t}+\rho T_0{\alpha }_h\frac{\partial H}{\partial t}+ T_0\gamma \frac{\partial }{\partial x}\frac{\partial u}{\partial t}\right] =-\frac{\rho }{t_1^n}(1+t^n\frac{\partial }{\partial t})N\end{array}\},$$

(4)

$$\begin{array}{l}{m}_{qh}\frac{{\partial }^{2}T}{\partial x^2}+D_h\rho \frac{{\partial }^{2}H}{\partial x^2}-\rho (1-a_2^h T_0{\alpha }_h+t^h\frac{\partial }{\partial t})\frac{\partial H}{\partial t}-\\ a_2^h\left[\rho C_e\frac{\partial T}{\partial t}+\rho T_0{\alpha }_n\frac{\partial N}{\partial t}+ T_0\gamma \frac{\partial }{\partial t}\frac{\partial u}{\partial x}\right] =-\frac{\rho }{t_1^h}(1+t^h\frac{\partial }{\partial t})H\end{array}\},$$

(5)

$${\alpha }_o\frac{{\partial }^2\phi }{\partial x^2}-{\lambda }_1\phi -{\lambda }_o\frac{\partial u}{\partial x}+{\gamma }_1\left(1+{\tau }_{\theta }\frac{\partial }{\partial t}\right)T=\frac{1}{2}j\rho \frac{{\partial }^2\phi }{\partial t^2},$$

(6)

where ${\delta }_h$ is the elastic-diffusive parameter of holes, $k$ expresses the diffusivity, $D_h$ is the coefficients of diffusion for the holes, ${\gamma }_1=(3\lambda +2\mu ){\alpha }_{\vartheta }$, ${\alpha }_{\vartheta }$ is the microelongational thermal expansions coefficient, $t^h$ is the thermal memories of holes, and ${\alpha }_h$ is the thermos-diffusive constants of the holes. The other notations correspond as: $a_1^n=\frac{a_{Qn}}{a_Q}$, $a_1^h=\frac{a_{Qh}}{a_Q}$, $a_2^n=\frac{a_{Qn}}{a_n}$ and $a_2^h=\frac{a_{Qh}}{a_h}$.

For the effects of the electron and hole carrier field in 1D, the microelongated constitutive equation is as follows [41]:

$${\sigma }_{xx}=(2\mu +\lambda )\frac{\partial u}{\partial x}-(\gamma (1+{\tau }_{\theta }\frac{\partial }{\partial t})T+{\delta }_{n}N)-{\delta }_{h}H+{\lambda }_1\phi =\sigma .$$

(7)

The main equations shown in [36,37,38,39,40] may be simplified further by transforming them using the dimensionless values listed below:

$$\begin{array}{l}(x^{\prime },u^{\prime })=\frac{{\omega }^{*}(x,u)}{C_T}, (t^{\prime },{\tau }_q^{\prime },{\tau }_{\theta }^{\prime },t^{n^{\prime }},t^{h^{\prime }},t_1^{n^{\prime }},t_1^{h^{\prime }})={\omega }^{*}(t, {\tau }_q,{\tau }_{\theta },t^n,t^h,t_1^n,t_1^h),C_L^2=\frac{\mu }{\rho }, \\ {\beta }^2=\frac{C_T^2}{C_L^2}, k=\frac{K}{\rho C_e}, {{\sigma }^{\prime }}_{ij}=\frac{{\sigma }_{ij}}{2\mu +\lambda }, N^{\prime }=\frac{{\delta }_n(N)}{2\mu +\lambda }, C_T^2=\frac{2\mu +\lambda }{\rho }, \overline{\phi }=\frac{\rho C_T^2}{T_o\widehat{\gamma }}\phi , \\ {\omega }^{*}=\frac{C_e(\lambda +2\mu )}{K}, ({\overline{\delta }}_n,{\overline{\delta }}_h)=\frac{({\delta }_n{n}_0,{\delta }_h{h}_0)}{\gamma T_0}, T^{\prime }=\frac{\gamma T}{2\mu +\lambda },H^{\prime }=\frac{{\delta }_n(H)}{2\mu +\lambda } .\end{array}\}.$$

(8)

When Equation (8) is used in combination with Equations (2)–(7), the dashes are omitted for convenience, resulting in:

$$\left\{\frac{{\partial }^2}{\partial x^2}-\frac{{\partial }^2}{\partial t^2}\right\}u-(1+{\tau }_{\theta }\frac{\partial }{\partial t})\frac{\partial T}{\partial x}-\frac{\partial N}{\partial x}+a_1\frac{\partial \phi }{\partial x}-{\alpha }_{21}\frac{\partial H}{\partial x}=0,$$

(9)

$$\begin{array}{l}\left((1+{\tau }_{\theta }\frac{\partial }{\partial t})\frac{{\partial }^2}{\partial x^2} -(1+{\tau }_q\frac{\partial }{\partial t})\frac{\partial }{\partial t}\right)T+\left({\alpha }_1\frac{{\partial }^2}{\partial x^2}-{\alpha }_2(1+{\tau }_q\frac{\partial }{\partial t})-{\alpha }_3\frac{\partial }{\partial t}-{\alpha }_4\right)N+\\ \left({\alpha }_5\frac{{\partial }^2}{\partial x^2}-(1+{\tau }_{\alpha }\frac{\partial }{\partial t}){\alpha }_6-{\alpha }_7\right)H-{\epsilon }_1(1+{\tau }_q\frac{\partial }{\partial t})\frac{\partial }{\partial t}\left(\frac{\partial u}{\partial x}\right)-\zeta \frac{\partial \phi }{\partial t}=0\end{array}\},$$

(10)

$$\begin{array}{r}\left\{\frac{{\partial }^2}{\partial x^2}-{\alpha }_8\frac{\partial }{\partial t}\right\}T+\left\{{\alpha }_9\frac{{\partial }^2}{\partial x^2}-({\alpha }_{10}+t^n\frac{\partial }{\partial t}){\alpha }_{11}+(1+t^n\frac{\partial }{\partial t})\frac{{\alpha }_{11}}{t^n}\right\}N- \\ {\alpha }_{12}\frac{\partial H}{\partial t}-{\alpha }_{13} \frac{\partial }{\partial x}\frac{\partial u}{\partial t} =0\end{array}\} ,$$

(11)

$$\begin{array}{r}\left\{\frac{{\partial }^2}{\partial x^2}-{\alpha }_{18}\frac{\partial }{\partial t}\right\}T+\left\{{\alpha }_{14}\frac{{\partial }^2}{\partial x^2}-({\alpha }_{15}+t^h\frac{\partial }{\partial t}){\alpha }_{16}\frac{\partial }{\partial t}+(1+t^h\frac{\partial }{\partial t}){\alpha }_{17}\right\}H- \\ {\alpha }_{19}\frac{\partial N}{\partial t}-{\alpha }_{20}\frac{\partial }{\partial t}\frac{\partial u}{\partial x}=0\end{array}\} ,$$

(12)

$$(\frac{{\partial }^2}{\partial x^2}-C_3-C_4\frac{{\partial }^2}{\partial t^2})\phi -C_5\frac{\partial u}{\partial x}+C_6(1+{\tau }_{\theta }\frac{\partial }{\partial t})T=0$$

(13)

$${\sigma }_{xx}=\left(\frac{\partial u}{\partial x}-( (1+{\tau }_{\theta }\frac{\partial }{\partial t})T +N)\right)+a_1\phi -H=\mathsf{\sigma }.$$

(14)

where

$$\begin{array}{l}{\alpha }_1=\frac{m_{nq}{\alpha }_t}{d_n K} ,{\alpha }_2=\frac{T_0{\alpha }_n}{C_e}, {\alpha }_3=\frac{a_1^n}{C_e},{\alpha }_4=\frac{a_1^n\gamma }{C_e{\tau }^n(2\mu +\lambda )},{\alpha }_5=\frac{\gamma m_{hq} h_0}{(2\mu +\lambda )K},{\alpha }_6=\frac{T_0 {\alpha }_h K h_0}{C_e},\\ {\alpha }_7=\frac{a_1^h\gamma {\omega }^{\ast }}{t^{h}K},{\alpha }_8=\frac{a_2^{n}K}{m_{qn}},{\alpha }_9=\frac{D_n\rho {\alpha }_t}{m_{qn} d_n},{\alpha }_{10}=1-a_2^n{T}_0{\alpha }_n,{\alpha }_{11}=\frac{{\alpha }_{t}K}{m_{qn} d_n{C}_e},{\alpha }_{12}=\frac{a_2^n\gamma h_0{\alpha }_h{\omega }^{\ast }}{m_{qn}},\\ {\alpha }_{13}=\frac{a_2^n{\gamma }^2{T}_0{\omega }^{\ast }}{\rho m_{qn}},{\alpha }_{14}=\frac{D_n{h}_0\gamma }{C_T^2 m_{qh}},{\alpha }_{15}=1-a_2^h{T}_0{\alpha }_n,{\alpha }_{16}=\frac{\gamma h_0{\omega }^{\ast }}{m_{qh}},{\alpha }_{17}=\frac{\gamma h_0{\omega }^{\ast }}{m_{qh}{\tau }_1^h},{\alpha }_{18}=a_2^h\frac{K}{m_{qh}},\\ {\alpha }_{19}=\frac{a_2^h\gamma T_0{\alpha }_n(2\mu +\lambda ){\omega }^{\ast }}{m_{qh}{\delta }_n},{\alpha }_{20}=\frac{a_2^h{\gamma }^2{T}_0 {\omega }^{\ast }}{m_{qh}\rho },{\alpha }_{21}=\frac{{\delta }_h}{(2\mu +\lambda )},{\epsilon }_1=\frac{T_0{\gamma }^2{\omega }^{\ast }}{\rho K},a_1=\frac{{\lambda }_o}{\rho c_T^2},\zeta =\frac{{\widehat{\gamma }}_1\widehat{\gamma }{T}_o}{K\rho },\\ C_3=\frac{{\lambda }_1{\omega }^{*}{}^2}{{\alpha }_0{C}_T^2}, C_4=\frac{\rho j{\omega }^{*}{}^4}{{\alpha }_0{C}_2^2},\hspace{1em}{C}_5=\frac{{\lambda }_o{\omega }^{*}{}^2}{{\alpha }_0{C}_T^2},\hspace{1em}{C}_6=\frac{{\widehat{\gamma }}_1\rho {\omega }^{*}{}^2{T}_o}{\widehat{\gamma }{\alpha }_0}.\end{array}$$

The following initial conditions, which may be expressed as follows, should be taken into account for this problem:

$$\begin{array}{l}{u(x, t)|}_{t=0}= {\frac{\partial u(x, t)}{\partial t}|}_{t=0}=0, {T(x,t)|}_{t=0}={\frac{\partial T(x, t)}{\partial t}|}_{t=0}=0, {N(x,t)|}_{t=0}={\frac{\partial N(x, t)}{\partial t}|}_{t=0}=0, \\ {\phi (x,t)|}_{t=0}={\frac{\partial \phi (x, t)}{\partial t}|}_{t=0}=0, {H(x,t)|}_{t=0}={\frac{\partial H(x, t)}{\partial t}|}_{t=0}=0\end{array}$$

(15)

3. Analytical Solution Procedure

The partial differential equations are transformed into ordinary differential equations in the time–space domain using the above conditions provided (ODE). These methods, with Equation (15), may be used to build function $\mathsf{\Delta }(x, t)$ according to the Laplace transform:

$$L(\mathsf{\Delta }(x, t))=\overline{\mathsf{\Delta }}(x, s)={\displaystyle \underset{0}{\overset{\infty }{\int }}\mathsf{\Delta }(x, t)\exp (-st)} dt.$$

(16)

The following equations may be derived from the Laplace transform Equation (16):

$$\left(D^2-s^2\right)\overline{u}-q_{14}D\overline{T}-D\overline{N}-a_{1}D\overline{\phi }-{\alpha }_{21}\overline{H}=0,$$

(17)

$$\left(q_1 D^2-q_2\right)\overline{T}+\left({\alpha }_1{D}^2-q_3\right)\overline{N}+\left({\alpha }_5{D}^2-q_4\right)\overline{H}-q_{5}D\overline{u}-s\zeta \overline{\phi }=0,$$

(18)

$$\left(D^2-q_7\right)\overline{T}+\left({\alpha }_9{D}^2-q_6\right)\overline{N} -q_8\overline{H}-q_{9}D\overline{u} =0,$$

(19)

$$\left(D^2-q_{10}\right)\overline{T}+\left({\alpha }_{14}{D}^2-q_{11}\right)\overline{H}-q_{12}\overline{N}-q_{13}D\overline{u}=0,$$

(20)

$$(D^2-C_7)\phi -C_{5}Du+C_{8}T=0,$$

(21)

$$\overline{\sigma }=D\overline{u}-(1+s{\tau }_{\theta })\left(\overline{T} +\overline{N}\right)+a_1\overline{\phi }-\overline{H}.$$

(22)

where

$$\begin{array}{l}D=\frac{d}{dx},q_1=(1+{\tau }_{\theta }s),q_2=(1+{\tau }_{q}s) s,q_3=\left({\alpha }_2(1+{\tau }_{q}s)+{\alpha }_{3}s+{\alpha }_4\right),q_4=(1+{\tau }_{q}s){\alpha }_6+{\alpha }_7\\ q_5=(1+{\tau }_q s){\epsilon }_1 s,q_6=({\alpha }_{10}+t^{n}s){\alpha }_{11}-(1+t^{n}s)\frac{{\alpha }_{11}}{t^n},q_7={\alpha }_8 s,q_8={\alpha }_{12}s,C_7=C_3+C_4{s}^2,\\ q_9={\alpha }_{13} s,q_{10}={\alpha }_{18}s,q_{11}=({\alpha }_{15}+t^{h}s){\alpha }_{16}s-(1+t^{h}s){\alpha }_{17},q_{12}={\alpha }_{19}s,q_{13}={\alpha }_{20}s,C_8=C_6{q}_1.\end{array}$$

The following differential equation may be obtained by using the process of elimination between quantities $\overline{T}, \overline{u}, \overline{H},\overline{N}$ and $\overline{\phi }$ in the preceding equation:

$$\left(D^{10}-{\eta }_1{D}^8+{\eta }_2{D}^6-{\eta }_3{D}^4+{\eta }_4{D}^2+{\eta }_5\right)\left\{\overline{\phi },\overline{T},\overline{N},\overline{H}, \overline{u}\right\}=0$$

(23)

where

$$\begin{array}{l}{\eta }_1=\frac{-1}{{\alpha }_1}\left\{\beta {\alpha }_9{q}_1-s^2{\alpha }_1+{\alpha }_1{q}_1{q}_{14}+{\alpha }_9{q}_5{q}_{14}-\beta {\alpha }_1-{\alpha }_1{q}_7+{\alpha }_9{q}_2-q_3-q_5\right\},\\ {\eta }_2=\frac{1}{{\alpha }_1}\left\{\begin{array}{l}-\beta s^2{\alpha }_9{q}_1+\beta s^2{\alpha }_1-\beta {\alpha }_1{q}_9{q}_{14}-\beta {\alpha }_9{q}_5{q}_{14}+s^2{\alpha }_1{q}_7-s^2{\alpha }_9{q}_2+\beta {\alpha }_1{q}_7-\beta {\alpha }_9{q}_2-\\ \beta q_1{q}_6+\beta q_1{q}_9+s^2{q}_3-q_3{q}_9{q}_{14}-q_5{q}_6{q}_{14}+\beta q_3+\beta q_5-q_2{q}_6+q_2{q}_9+q_3{q}_7+q_5{q}_7\end{array}\right\},\\ {\eta }_3=\frac{-1}{{\alpha }_1}\left\{\begin{array}{l}-\beta s^2{\alpha }_1{q}_7+\beta s^2{\alpha }_9{q}_2+\beta s^2{q}_1{q}_6-\beta s^2{q}_3+\beta q_3{q}_9{q}_{14}+\beta q_5{q}_6{q}_{14}+\\ s^2{q}_2{q}_6-s^2{q}_3{q}_7+\beta q_2{q}_6-\beta q_2{q}_9-\beta q_3{q}_7-\beta q_5{q}_7\end{array}\right\},\\ {\eta }_4=\frac{-1}{{\alpha }_1}\left\{\begin{array}{l}-\beta s^2{\alpha }_1{q}_7+\beta s^2{\alpha }_9{q}_2+\beta s^2{q}_1{q}_6-q_3{q}_9{q}_{14}-q_5{q}_6{q}_{14}+\beta q_3+\beta q_5+\\ -\beta s^2{\alpha }_9{q}_1+\beta s^2{\alpha }_1-\beta {\alpha }_1{q}_9{q}_{14}-\beta {\alpha }_9{q}_5{q}_{14}+s^2{\alpha }_1{q}_7\end{array}\right\},\\ {\eta }_5=\frac{1}{{\alpha }_1}\left\{-\beta s^2{q}_2{q}_6+\beta s^2{q}_3{q}_7\right\}.\end{array}$$

The differential equation’s characteristic equation is shown below:

$$\left(D^2-r_1^2\right)\left(D^2-r_2^2\right) \left(D^2-r_3^2\right)\left(D^2-r_4^2\right)\left(D^2-r_5^2\right)\left\{\overline{\phi },\overline{T},\overline{N},\overline{H}, \overline{u}\right\}=0$$

(24)

where $r_i(i=1, 2, 3, 4, 5)$ refers the roots of the above equation when $x\to \infty$.

The generalized linear solution of Equation (18) for the temperature is shown in the illustration below:

$$\overline{T}(x, s)={\displaystyle \sum _{i=1}^5{\mathsf{\Lambda }}_i}(s) e^{-k_{i}x}.$$

(25)

From the other perspective, linear solutions of the other important physical quantities may be represented mathematically:

$$\overline{N}(x, s)={\displaystyle \sum _{i=1}^5{\mathsf{\Lambda }}_i^{\prime }}(s) e^{-r_{i}x}={\displaystyle \sum _{i=1}^5{H}_{1i}{\mathsf{\Lambda }}_i(s)} e^{-r_{i}x},$$

(26)

$$\overline{u}(x,s)={\displaystyle \sum _{i=1}^5{\mathsf{\Lambda }}_i^{″}}(s) {\mathrm{e}}^{-r_{i}x}={\displaystyle \sum _{i=1}^5{H}_{2i} {\mathsf{\Lambda }}_i}(s) {\mathrm{e}}^{-r_{i}x},$$

(27)

$$\overline{\phi } (x,s)={\displaystyle \sum _{i=1}^5{\mathsf{\Lambda }}_i^{‴}}(s) {\mathrm{e}}^{-r_{i}x}={\displaystyle \sum _{i=1}^5{H}_{3i} {\mathsf{\Lambda }}_i}(s) {\mathrm{e}}^{-r_{i}x},$$

(28)

$$\overline{H} (x,s)={\displaystyle \sum _{i=1}^5{\mathsf{\Lambda }}_i^{″″}} \exp (-r_{i}x)={\displaystyle \sum _{i=1}^5{H}_{4i} {\mathsf{\Lambda }}_i} \exp (-r_{i}x),$$

(29)

$$\overline{\sigma } (x,s)={\displaystyle \sum _{i=1}^5{\mathsf{\Lambda }}_i^{″″\prime }} \exp (-r_{i}x)={\displaystyle \sum _{i=1}^5{H}_{5i} {\mathsf{\Lambda }}_i} \exp (-r_{i}x).$$

(30)

where ${\mathsf{\Lambda }}_i, {\mathsf{\Lambda }}_i^{\prime }, {\mathsf{\Lambda }}_i^{″}, {\mathsf{\Lambda }}_i^{‴}$, ${\mathsf{\Lambda }}_i^{″″}$ and ${\mathsf{\Lambda }}_i^{″″\prime }$ are unknown parameters that depend on $S$.

$$\begin{array}{l}{H}_{1i}=\frac{-(m_i{}^4+(-s^2+q_9{q}_{14}-q_7)m_i{}^2+s^2{q}_7)}{(m_i{}^4{\alpha }_9+(-s^2{\alpha }_9-q_6+q_9)m_i{}^2+s^2{q}_6)m_i{}^2-{\alpha }_1},\\ H_{2i}=\frac{m_i(({\alpha }_9{q}_{14}-1)m_i{}^2-q_6{q}_{14}+q_7)}{(m_i{}^4{\alpha }_9+(-s^2{\alpha }_9-q_6+q_9)m_i{}^2+s^2{q}_6)},\\ H_{3i}=\frac{-\beta }{m_i{}^2-\beta },H_{5i}={\alpha }_5\left(m_i H_{2i}-(( 1+s{\tau }_{\theta })+H_{1i})\right).\end{array}$$

4. Applications

In this section of the article, we evaluate parameters ${\mathsf{\Lambda }}_i$. A very little amount of heat escapes into the surrounding region as a result of pulsed laser stimulation, since temperature changes occur quickly or at least within a short period. As a consequence, pulsed laser excitation is advantageous for studies of absorption. It is also established that a range of physical reactions, some of which need energy, may take place when a laser beam impacts a solid microelongated semiconductor surface. A portion of the energy from the laser light is transformed into heat when it strikes a material. This kind of heat creation sends heat waves across the medium, which has certain impacts (e.g., photothermal effects) [41,42,43].

(I)

When $x=0$, the pulsing heat flow boundary condition may be represented by the thermally gradient temperature in the following ways:

$${\frac{\partial T\left(x,t\right)}{\partial x}|}_{x=0}=-q_0\frac{{{\displaystyle t^2{e}^{-\frac{t}{{{\displaystyle t}}_p}}}}^{}}{16t_p^2}.$$

(31)

When it is applied to a thermal condition load at time of pulse heat flux $t_p$ with constant $q_0$ and pulse parameter $p$, the Laplace transforms provide:

$${{\displaystyle \sum _{i=1}^5{k}_i{\mathsf{\Lambda }}_i}(s) e^{-k_{i}x}|}_{x=o}=\frac{q_0{t}_p}{8{(1+p{t}_p)}^3}.$$

(32)

Figure 1 illustrates the pattern that includes the temporal period of a laser pulse (exponential laser-pulsed heat):

(II)

The load force $\Im$ may be expressed as follows when the Laplace transform is used, and it is regarded as a mechanical condition at the boundary $x=0$:

$$\overline{\sigma }(0,s)=\overline{\Im }\Rightarrow {\displaystyle \sum _{i=1}^5{H}_{4i} {\mathsf{\Lambda }}_i}(s)=\Im .$$

(33)

(III)

The carriers are capable of obtaining the following value on the sample’s surface, $x=0$, as they disperse, where they have a chance of undergoing recombination. Consequently, the following equation might be used to express the carrier density boundary condition. In this, the plasma condition under the Laplace transform is derived using the carrier density diffusive and is shown as follows:

$$\overline{N}(0, s)=\frac{ƛn_0}{D_e}\overline{R}(s)\Rightarrow {\displaystyle \sum _{i=1}^5{H}_{1i}{\mathsf{\Lambda }}_i(s)} =\frac{ƛn_0}{\tilde{s}{D}_e}.$$

(34)

(IV)

One may choose the microelongation condition as an elongation free on the surface $x=0$:

$$\overline{\phi }=0\Rightarrow {\displaystyle \sum _{i=1}^5{H}_{3i} {\mathsf{\Lambda }}_i}(s) =0.$$

(35)

(V)

On the other hand, the equilibrium concentration situation for the hole charge carrier field at the boundary condition may be obtained in this instance by using the Laplace transform:

$$\overline{H}(0,s)=h_0\Rightarrow {\displaystyle \sum _{i=1}^5{H}_{4i} {\mathsf{\Lambda }}_i} =h_0.$$

(36)

where $R(s)$ is to the Heaviside unit step function and $ƛ$ is an arbitrary parameter.

5. Inversion of the Laplace Transforms

One must invert the transforms in the physical domain to obtain the results. The complete 1D solutions for the fundamental dimensionless physical fields in the time domain may be determined by using the Laplace transform’s inverse. The Riemann-sum approximation technique and a numerical approach are used to invert the Laplace transformations. As a result, a rapid Fourier transform-based numerical inversion of the Laplace transform (NILT) approach is used [44]. For any function $\overline{\mathsf{\Phi }}(x, s)$, it can be reversed as:

$$\mathsf{\Phi }(x, t^{\prime })=L^{-1}\{\overline{\mathsf{\Phi }}(x, s)\}=\frac{1}{2\pi i}{\displaystyle {\int }_{n-i\infty }^{n+i\infty }{\mathrm{e}}^{s{t}^{\prime }} }\overline{\mathsf{\Phi }}(x, s)ds.$$

(37)

where $s=n+i\mathrm{M}$($n, \mathrm{M}\in R$). In $\left[0, 2t^{\prime }\right]$, the Fourier series is used to expand function $\mathsf{\Phi }(x, t^{\prime })$ as:

$$\mathsf{\Phi }(x, t^{\prime })=\frac{e^{n{t}^{\prime }}}{t^{\prime }}\left[\frac{1}{2}\overline{\mathsf{\Phi }}(x, n)+Re{\displaystyle \sum _{k=1}^N\overline{\mathsf{\Phi }}(x,n+\frac{ik\pi }{t^{\prime }}){(-1)}^n}\right].$$

(38)

where $i=\sqrt{-1}$ is the imaginary unit and $Re$ is the real part. For convergence, $N$ is chosen freely when $n{t}^{\prime }$ $\approx 4.7$ [44].

6. Validation

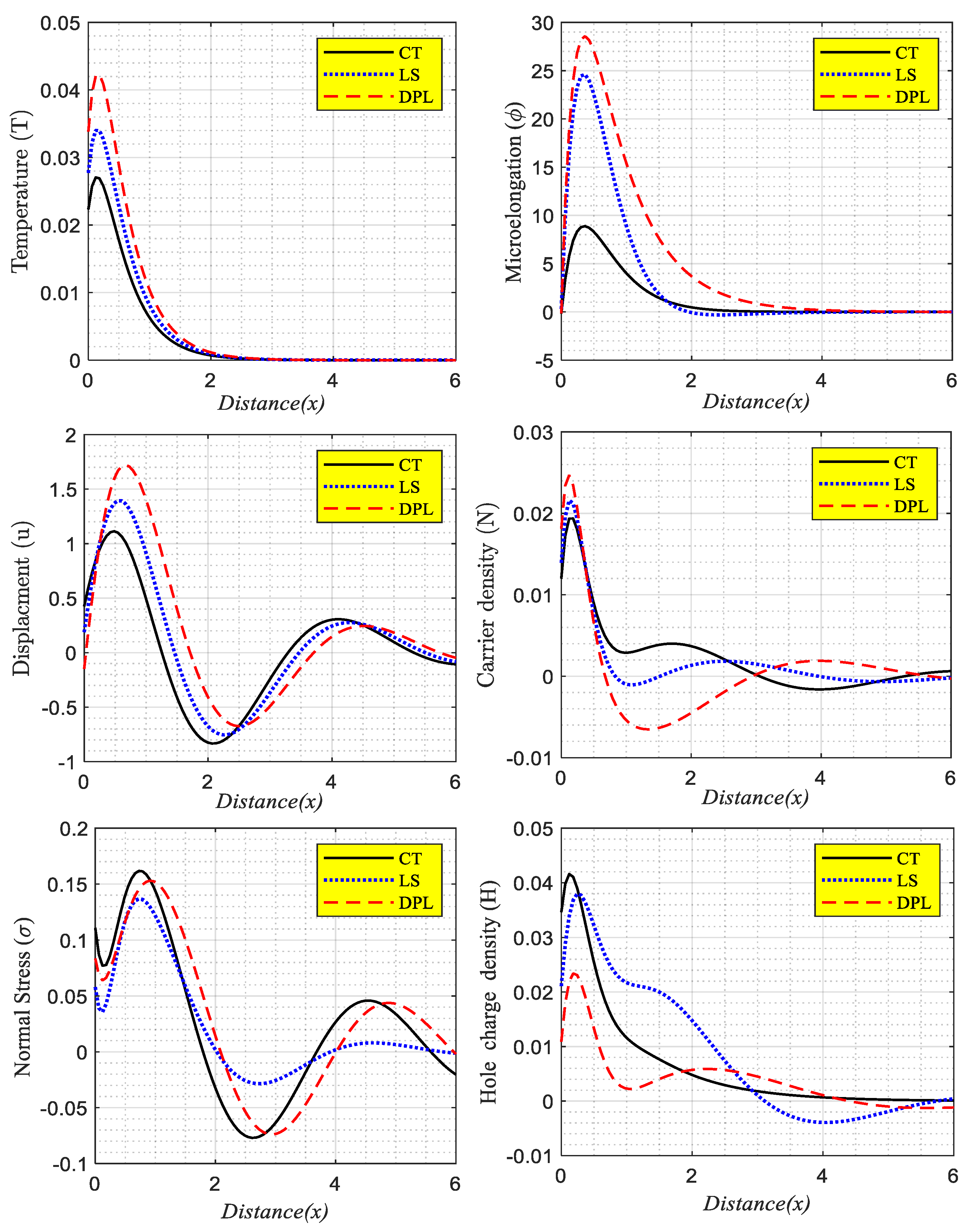
6.1. The Microelongated Thermoelasticity Models

However, the governing Equations (2)–(6) are simplified to the generalized microelongated thermoelasticity theory when the electrons charge field (carrier density) and the holes charge field are omitted (i.e., $N=0$ and $H=0$). The four equations may be rewritten as follows in 1D as [7,8]:

$$K(1+{\tau }_{\theta }\frac{\partial }{\partial t})\frac{{\partial }^{2}T}{\partial x^2}- (1+{\tau }_q\frac{\partial }{\partial t})\left[\rho C_e\frac{\partial T}{\partial t}+ T_0\gamma \frac{\partial }{\partial x}\frac{\partial u}{\partial t}\right]={\widehat{\gamma }}_1{T}_o\frac{\partial \phi }{\partial t},$$

(39)

$$\rho \frac{{\partial }^{2}u}{\partial t^2}=(2\mu +\lambda )\frac{{\partial }^{2}u}{\partial x^2}-\gamma (1+{\tau }_{\theta }\frac{\partial }{\partial t})\frac{\partial T}{\partial x}+{\lambda }_o\frac{\partial \phi }{\partial x},$$

(40)

$${\alpha }_o\frac{{\partial }^2\phi }{\partial x^2}-{\lambda }_1\phi -{\lambda }_o\frac{\partial u}{\partial x}+\gamma \left(1+{\tau }_{\theta }\frac{\partial }{\partial t}\right)T=\frac{1}{2}j\rho \frac{{\partial }^2\phi }{\partial t^2},$$

(41)

$$(2\mu +\lambda )\frac{\partial u}{\partial x}-\gamma (1+{\tau }_{\theta }\frac{\partial }{\partial t})T+{\lambda }_1\phi =\sigma .$$

(42)

The dual-phase lag (DPL) when $0\le {\tau }_{\theta }<{\tau }_q$ is obtained. The Lord and Șhulman (LS) model can be observed when ${\tau }_{\theta }=0$ and $0<{\tau }_q$. Finally, the coupled thermos-elasticity (CT) model is introduced when ${\tau }_{\theta }={\tau }_q=0.0$.

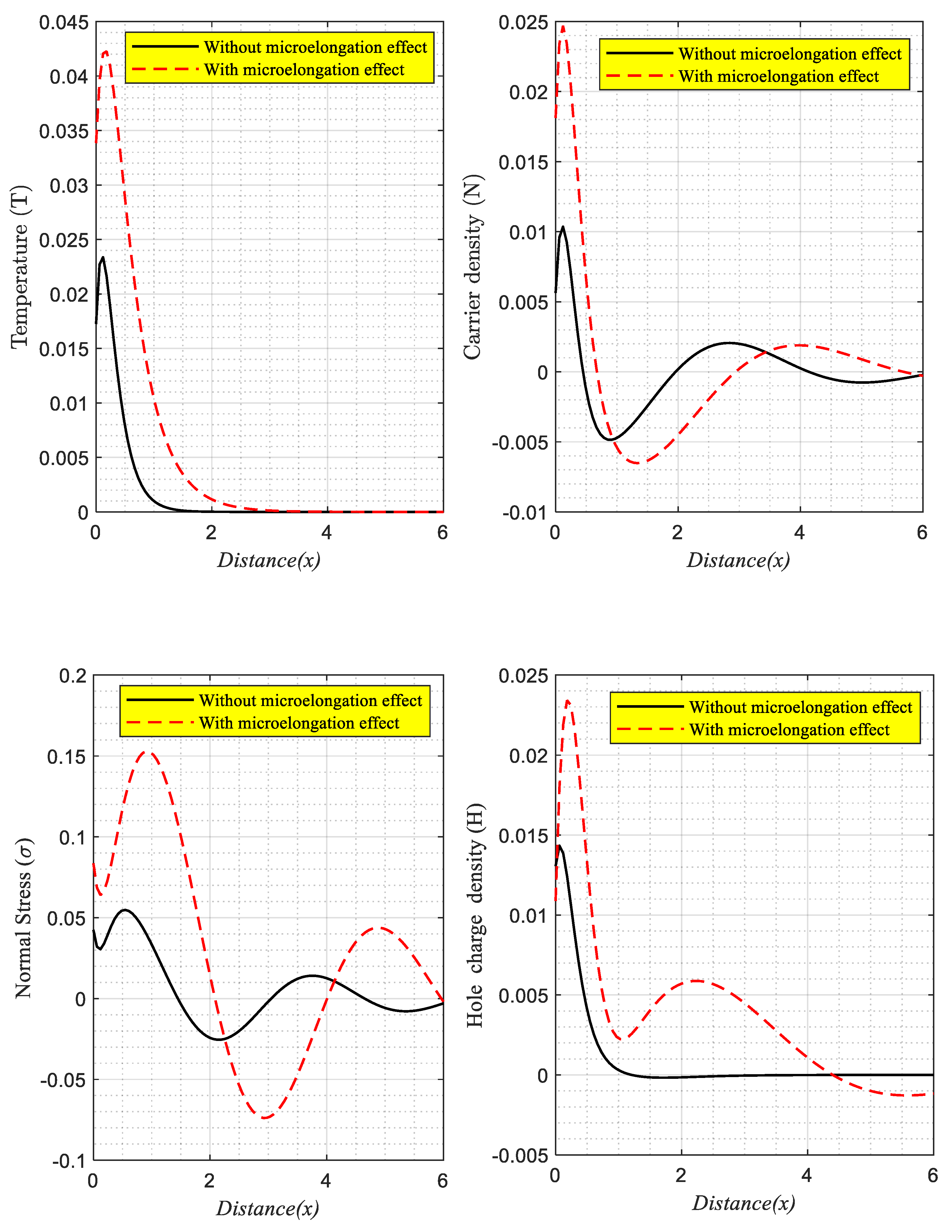
6.2. The Influence of Microelongation Parameters

When the microelongation parameters are ignored (${\alpha }_o={\lambda }_o={\lambda }_1=0$), the set of equations describes the case of the generalized photo-thermoelasticity theory when one is taking into consideration the interaction between the elastic, thermal, and electronic waves, and holes [45,46,47].

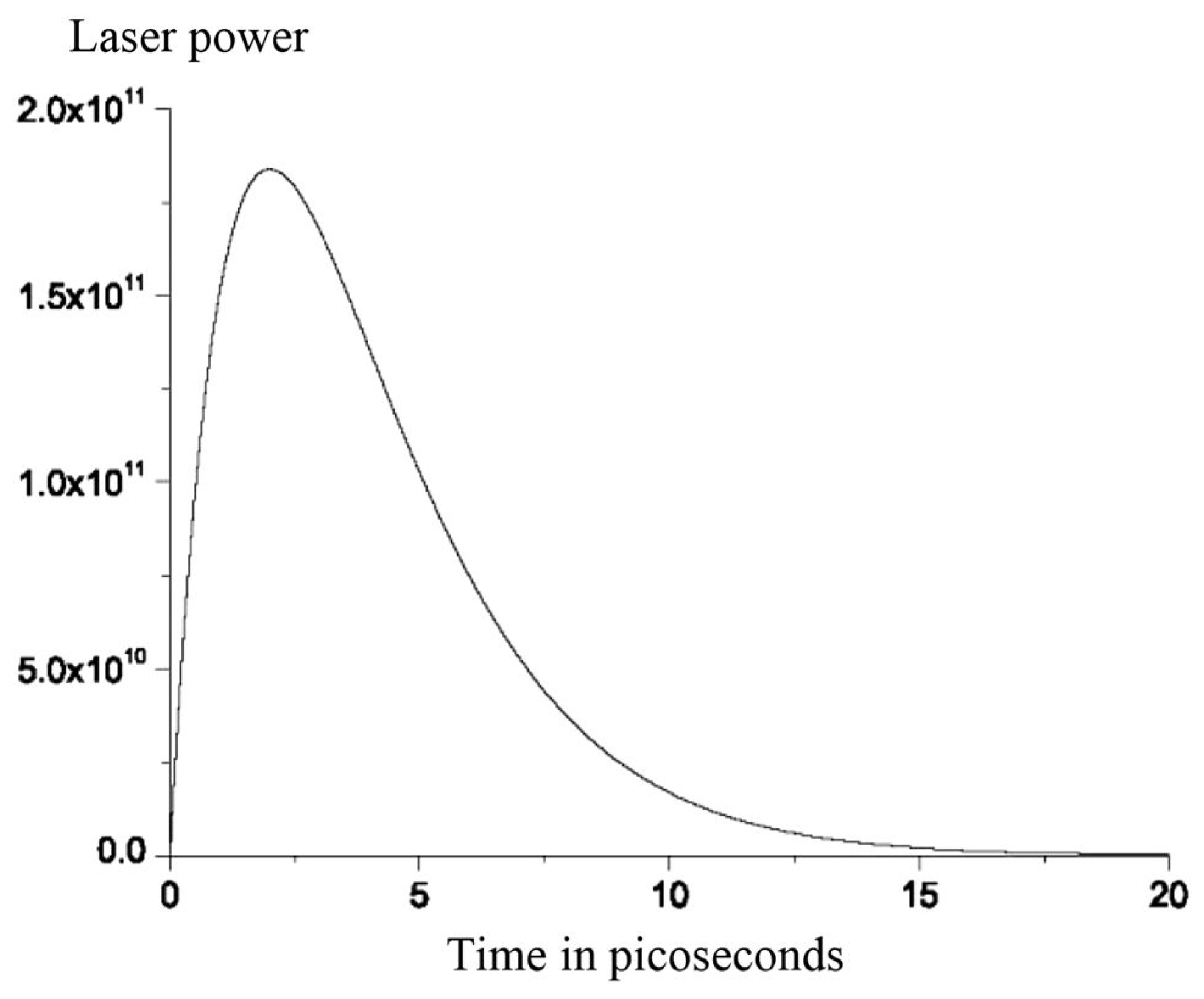
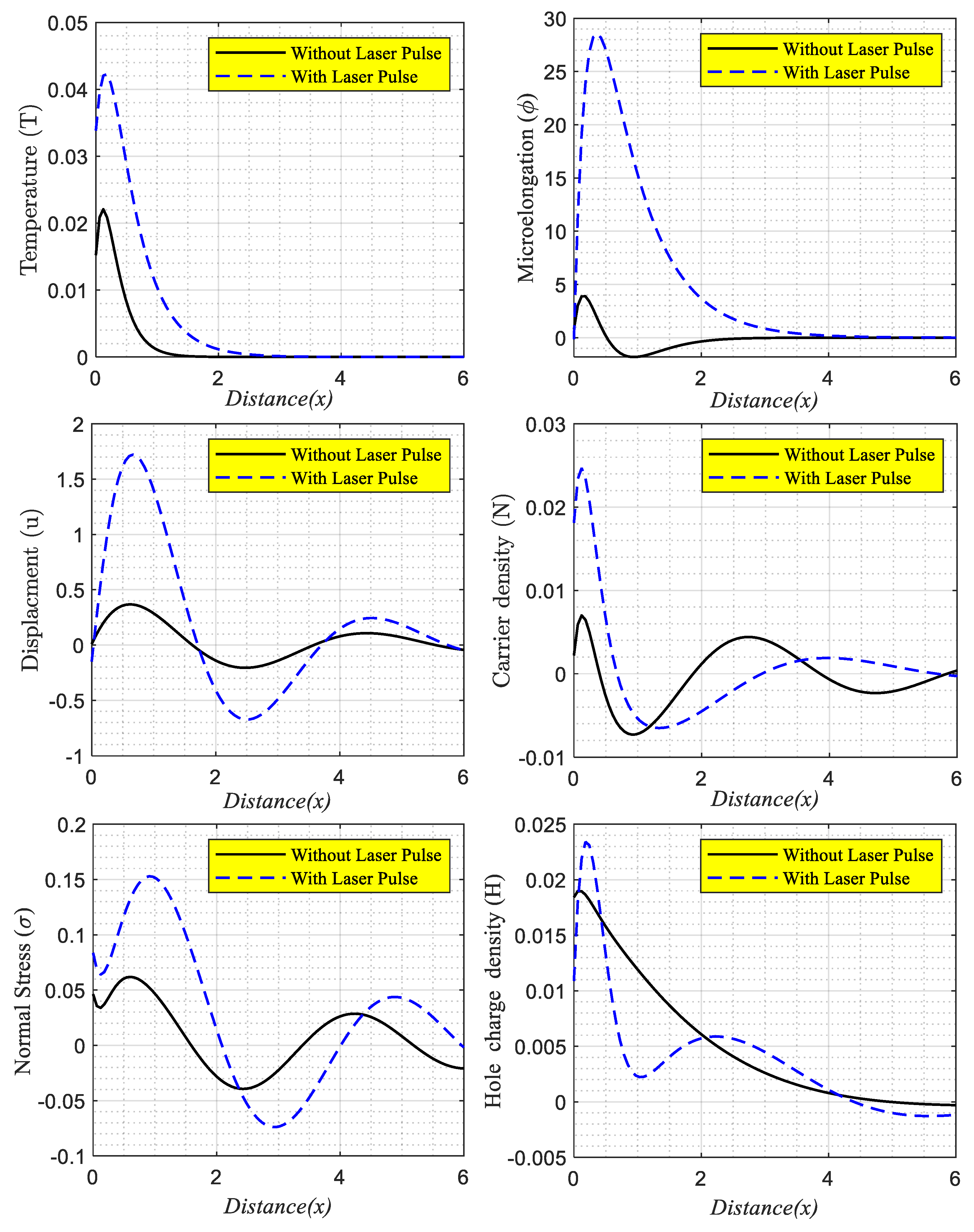
6.3. The Laser Pulses Impact

The effect of the exponential laser-pulsed heat is shown by the preceding basic boundary condition (I). When the power intensity of the effect of the laser pulses is disregarded, the model under examination transforms into a model of the photo-thermoelasticity theory with a holes effect under the impact of microelongation parameters [45].

7. Numerical Results and Discussion

The authors validated the accuracy of the theoretical and analytical conclusions that were obtained and compared them to previous achievements. The numerical simulations of wave propagation in the significant physical fields are discussed in this section. The elastic wave (displacement), plasma wave (electron diffusion), mechanical wave (stress), holes charge, and thermal wave that are created for a short time may all be graphically represented. Utilizing the input parameters in the SI unit of the microelongated semiconductor silicon (Si) material, the Matlab (2022a) software of the authors’ computer is used to graph the distribution of the main wave distributions. The following physical constants for Si are listed in

Table 1. The SI units of the physical constants for Si medium.

Unit	Symbol	Value
${\mathrm{N}/\mathrm{m}}^2$	$\lambda$ $\mu$	$6.4\times {10}^{10}$ $6.5\times {10}^{10}$
${\mathrm{kg}/\mathrm{m}}^3$	$\rho$	$2330$
$\mathrm{K}$	$T_0$	$800$
$\sec \left(\mathrm{s}\right)$	$\tau$	$5\times {10}^{-5}$
${\mathrm{K}}^{-1}$	${\alpha }_t$	$4.14\times {10}^{-6}$
${\mathrm{Wm}}^{-1}{\mathrm{K}}^{-1}$	$K$	$150$
$\mathrm{J}/(\mathrm{kg} \mathrm{K})$	$C_e$	$695$
$\mathrm{m}/\mathrm{s}$	$\tilde{s}$	$2$
${\mathrm{vk}}^{-1}$	$m_{qn}$	$1.4\times {10}^{-5}$
	$m_{nq}$	$1.4\times {10}^{-5}$
	$m_{qh}$	$-0.004\times {10}^{-6}$
	$m_{hq}$	$-0.004\times {10}^{-6}$
$\mathrm{J}\cdot {\mathrm{m}}^{-2}$	$p$	${10}^{11}$
${\mathrm{m}}^2{\mathrm{s}}^{-1}$	$D_n$	$0.35\times {10}^{-2}$
${\mathrm{m}}^2{\mathrm{s}}^{-1}$	$D_h$	$0.125\times {10}^{-2}$
${\mathrm{m}}^2/\mathrm{s}$	${\alpha }_n$	$1\times {10}^{-2}$
${\mathrm{m}}^2/\mathrm{s}$	${\alpha }_h$	$5\times {10}^{-3}$
$\mathrm{ps}$	$t_p$	$4$
Constants	$q_0$ $\Im$	3 2
$\mathrm{J}\cdot {\mathrm{m}}^{-2}$	$p$	${10}^{11}$
${\mathrm{m}}^2$	$j$	$0.2\times {10}^{-19}$
${\mathrm{Nm}}^{-2}$	${\lambda }_0$	$0.5\times {10}^{10}$
${\mathrm{Nm}}^{-2}$	${\lambda }_1$	$0.5\times {10}^{10}$
${\mathrm{Nm}}^{-2}$	$k$	${10}^{10}$
${\mathrm{K}}^{-1}$	${\alpha }_{\vartheta }$	$0.017\times {10}^{-3}$
${\mathrm{Nm}}^{-2}$	${\alpha }_0$	$0.779\times {10}^{-9}$

[46,47]:

7.1. The Photo-Thermoelasticity Models

According to models based on the theory of microelongated photo-thermoelasticity, Figure 2 (first category) depicts the change in the distribution of the main physical variables under the impact of various relaxation times with increasing distance in the microelongated semiconductor medium. In this group, real-dimensional numerical computations are performed in a relatively small amount of time, $t=0.001$, while being influenced by laser pulses. As observed in the figure, the dual phase lag (DPL when $0\le {\tau }_{\theta }<{\tau }_q$) model is represented by the dashed line, while the dotted.

Line represents the Lord and Shulman (LS when ${\tau }_{\theta }=0$, $0<{\tau }_q=0.0002$) model, and the solid line represents the theory of coupled thermoelasticity (CT, when ${\tau }_{\theta }={\tau }_q=0.0$). The first subfigure depicts the thermal (heat) wave’s distribution, which is represented by the temperature distribution, where the distribution begins at the surface’s positive value and satisfies the boundary condition [48,49]. The numerical study showed that the structure’s maximum temperature consistently occurs close to the front of the heat wave and gradually decreases as the depth in the medium increases. The thermal wave distribution rises at the surface to achieve its maximum value as a direct consequence of the laser pulses’ influence, then progressively decreases, taking the form of an exponential function. Further, under the surface, where the impact of the laser pulses is reduced, the distribution ultimately converges with the zero line to achieve the equilibrium state. These findings are consistent with what has been shown in actual experiments [50,51]. Microelongation wave propagation (the second subfigure), which begins at the surface from zero and increases in the closed initial range as a result of the action of laser pulses, may be used to characterize the microelongation scalar function. It then progressively diminishes with exponential behavior. The microelongation wave converges to the zero line far from the semiconductor surface because of the weak laser pulse effect until it reaches the equilibrium condition within the medium. The displacement distribution with increasing distance is used to indicate the shift in the elastic wave in the third subfigure. Due to the thermal impact of the laser pulses, the distribution begins at the surface nearing the zero value and progressively increases in the beginning to reach the highest value towards the edge. The distribution then alternately lowers and grows until it reaches its minimum value, just before it reaches an equilibrium state within the microelongated semiconductor medium. The increased collisions between the inner particles as a direct consequence of the heating action of the laser pulses cause this apparent perturbation in the elastic wave distribution. The fourth and sixth subfigures show the dispersion of plasma waves, which are represented by electron and hole diffusive activity with increasing distance (carrier density and hole charge density). In two cases, these distributions begin with positive values at the surface and satisfy the boundary surface conditions throughout the processes of recombination and replacement between them. When the temperature rise caused by the influence of laser pulses causes the diffusivity of electrons and holes to increase on the surface, they do so until they reach their maximum value. Moving further from the surface causes the distribution to progressively decrease until it achieves equilibrium in accordance with the zero line within the microelongated semiconductor medium, which is compatible with the experimental information and takes the shape of an exponential function [45,46]. On the other hand, the fifth subfigure depicts how the mechanical wave changes as the distance increases using normal stress distribution. The distribution starts out as a result of mechanical stress, which was applied at the surface from the positive value, satisfying the boundary condition and causing the distribution to smoothly decelerate in the initial range close to the edge. When the distribution reaches equilibrium within the semiconductor medium, it climbs gradually to achieve its maximum value before adopting a curve in the shape of wave distribution. The mechanical load and thermal impact of the laser pulses are both responsible for this apparent behavior in mechanical wave distribution. This results from the generation of mechanical forces and the operation of ultrafast lattice deformation.

7.2. The Laser Pulses Effect

The principal fields in this phenomenon vary depending on the different values of the laser pulses based on the power intensity (the pulse parameter $p$) versus a horizontal distance $x$, as shown in Figure 3 (second category). The numerical simulation is carried out during thermoelastic and electronic deformations over short moments, $t=0.001$, under the influence of microelongation parameters, according to the DPL model. Two instances fall within this category: the first one is the disappearance of the laser pulse’s influence (without the laser pulses effect), and the second one is the case of the laser pulses’ effects (with the laser pulses effect). We investigated the impact of laser pulses on this model of equations, since it is evident that the thermal effect of laser pulses modifies the behavior of wave propagation in an obvious manner. From this, it is evident that the microelongated photothermal mechanical model, which accounts for all of these phenomena, can describe the ultrafast photothermal response to the laser pulse effect across the semiconductor medium.

7.3. The Effect of Elongation Parameters

The third category (Figure 4) illustrates the variations in the main fields in this occurrence based on the different values of the microelongation parameters evaluated against the horizontal distance. The DPL model states that a numerical simulation is run during the brief electronic holes diffusion induced by laser pulses. Two instances fall within this category, the first of which is the loss of the microelongation parameters (without microelongation parameters when ${\alpha }_o={\lambda }_o={\lambda }_1=0$), and the second one is obtained when microelongation parameters are present. On the other hand, the behavior of wave propagation varies across all distributions. It is observed that the main field distribution behavior is greatly influenced by the microelongation parameters.

8. Conclusions

In this study, we have presented the effects of mechanical loading, thermal memory, and extended photo-thermoelasticity on the properties of an n-type microelongated silicon semiconductor when it is subjected to laser pulses. The relationship between thermo-elastic, microelongation, mechanical, and plasma waves is investigated when the material is photoexcited during an elasto-thermodiffusive process. The novel model is examined in the context of the microelongation effect during electronic holes diffusion. The difference between photo-thermoelasticity theories is taken into consideration based on thermal relaxation times. Thermal memory has a considerable influence on all of the main physical distribution wave propagations. However, all wave propagations are significantly influenced by the intensity of the laser pulses, as well as microelongation. A photo-thermoelastic model was employed to forecast these variables, since the laser source had limitations in terms of its diameter and lifetime. An increasingly potent technique for assessing a material’s influence on its microstructure as a microelongated semiconductor is the generation of elastic waves as a consequence of brief thermal heating. The fact that these waves travel at rates of just a few kilometers per second is due to the extensive usage of semiconductors in the manufacturing of electronics and medical equipment. On the other hand, the direct possibility of creation, detection, and control being employed in the solar cell, as well as the energy of these waves being concentrated close to the top region of the device’s surface, make this sort of issue vital to research.