Abstract
This paper is devoted to studying the influence of the structure of a complex system on its integral risk. When solving risk management problems, it often becomes necessary to take into account structural effects, which most often include risk transfer and failure propagation. This study discusses the influence of the position of the elements of a protected system inside a fixed structure of the “star” type on its integral risk. The authors demonstrate that the problem of the optimal placement of elements in such a structure from the point of view of minimizing the risk cannot be precisely solved by analytical methods and propose an algorithm for solving it with bounded errors. For the case of equal expected damages in case of a successful attack of a system element, the authors calculate upper estimates for the relative error of solving the placement problem using the proposed algorithm and also propose a methodology for rapid risk assessment for systems with a “star” type structure. Finally, for the particular case when the risks of elements are in a certain ratio, the authors have found an exact solution to the problem of the optimal placement of elements.
Keywords:
complex systems; complex networks; risk; network structure; risk management; risk minimization algorithms; problem of optimal placement of elements MSC:
91B05
1. Introduction
Many complex real-world systems, such as power grids, the Internet, transport networks, and networks of complex information systems, exhibit properties due to their structure when random or deliberate attacks occur. To describe these properties, researchers often use risk management models based on complex networks. In this case, it is possible to focus both on the structure of the system as a whole and on quantitative assessments of risks and/or expected losses in the event of an adverse event of uncertainty. It should also be noted that these phenomena can be considered both in statics and dynamics. Table 1 presents the classification of structural properties and lists the models and methods used in their study.

Table 1.
Models and methods for investigating properties arising from the structure of a complex system, manifested in random or deliberate attacks.
When considering the intrinsic properties of a network in statics, the subject of study is the change in its properties when removing vertices or edges. Various topological or statistical metrics are used to describe the properties. Among the former, indicators of centrality [1,2,3], efficiency [4,5,6], and clustering coefficient [7,8,9] are most often used. Among the latter, self-organized criticality is often involved [10,11,12].
In the dynamic approach, one usually studies the phenomena of convergence of the node trajectories (synchronization [13,14,15], consensus [16,17,18]), as well as instruments for controlling it (pinning control [19,20,21]).
In the case of studying complex networks that reflect real objects, the need arises for a quantitative assessment of the damage resulting from the realization of an adverse event of uncertainty. When considering a network in statics, these include vulnerability and reliability [21,22,23]. Reliability measures the extent to which a network is able to withstand such an event without degrading its performance. Vulnerability, in turn, is defined as the ability of the network to function continuously in the event of random failures or deliberate attacks.
Considering a network in dynamics involves studying a scenario where a disruption in the functioning of one node leads to a decrease in reliability and an increase in the vulnerability of related nodes, the sequential failure of several nodes can cause a cascading failure [24,25,26].
A related class of problems are resource allocation problems for risk management. As a rule, their formulations are variations of the classical Nash bargaining problem [27]. The basic concepts of its solution were shaped by Nash himself [28], and later a monotonic solution was obtained based on an alternative system of axioms [29]. These solutions with various modifications are still used for risk management today (see, for example, [30,31]).
A similar axiomatic approach can be applied to risk analysis in a dynamic system. In this case, as a rule, the problem in one way or another is reduced to a static one. For example, [32] solves the problem of managing economic risks for a finite set of enterprises under various scenarios. Another study solves the problem of risk management in a complex system with a given mutual influence of elements by analyzing converging multi-stage cognitive games [33]. Nevertheless, such studies as the above are extremely rare. It appears that the reason for this is the complexity of the synthesis of solution algorithms that ensure monotonicity, i.e., guaranteeing that the allocation of a resource to reduce the risk of one element will not lead to an increase in the risk value for another element due to the influence of the structure.
This paper is part of a research devoted to the study of the influence of the position of the elements in a protected system of a given structure on the integral risk of the system. The purpose of the research is to find methods for solving the problem of optimal resource allocation in order to minimize the integral risk of systems with elements that mutually affect each other. The basic model for describing such an influence is a complex network with a perimeter.
The exact solution of such a problem in general cannot be obtained by computationally simple methods. Therefore, we focused on finding ways to solve it, providing some predetermined accuracy and ease of implementation. At the same time, it is important that the proposed methods are based on rules and assessments. Only in this case, one can numerically assess the quality of a particular solution. For this reason, we do not consider several approaches, e.g., stochastic methods.
To formulate the basic principles for constructing solutions to the problem of resource allocation minimizing risk in systems with elements that mutually affect each other, it is necessary to have an idea of how the eigen risks of the elements of the system should relate to each other depending on the distance from the perimeter. To obtain such an idea, we consider the problem of the optimal placement of elements with known eigen risks inside a certain predefined structure. This problem becomes more difficult with the increasing complexity of the structure’s topology. Therefore, it is reasonable to first examine its solution for the simplest topology (chain structure), then move on to a more complex version (“star”), then to a tree structure, and, finally, to an arbitrary one.
In our previous work, simple chain structures were investigated [34]. Here, we discuss more complex structures of the “star” type with a single-vertex perimeter. The main result of this work is an algorithm for solving the problem of the pseudo-optimal placement of elements of a protected system in the attack structure of the “star with m rays” type with elements of equal “cost” (in other words, the values of the expected damage for all elements of the system are assumed equal).
The structure of the material presented in this work is as follows: In Section 2, we introduce the necessary definitions and formulate a general statement of the problem. Section 3 contains a discussion concerning several possible heuristic approaches to its solution in the particular case of equality of damages and counterexamples to them. In Section 4, we propose a number of restrictions that are reasonable from a practical standpoint, making it possible to obtain an approximate optimal solution for the case of elements with equal damages. We construct the upper estimates of the error of the solution in Section 5. In Section 6, a methodology for rapid risk assessment of systems with a “star” type structure is proposed. Finally, in Section 7, we give an exact solution for the case when the expected damages of the elements are different, but their risks are connected by a given ratio.
2. General Problem Statement
Suppose that a protected system includes n elements (objects, so far of arbitrary nature) . Let us also assume that two numbers are assigned to each element:
is the eigen probability of a successful attack on the ith element;
is the damage that will be inflicted if the ith element is successfully attacked.
Definition 1.
The eigen risk of the ith element is defined as the quantity
Let us set the attack structure Wm = ⟨G(V, E), T⟩, T ⊆ V, where G(V, E) is a graph with a set of vertices V and a set of edges E, and T is a subset of V called the perimeter. In this paper, we will consider structures with a perimeter that includes exactly one vertex.
Definition 2.
A structure of the type of “star with m rays” will be defined as a structure Wm = ⟨G(V, E), T⟩, such that
Here, is the number of vertices in the bth ray, which is a simple chain starting at the vertex vb1. For all such vertices, the perimeter v0 is an adjacent vertex. In general, lb is not bounded. Figure 1 shows a star structure with four rays of length 3 each.
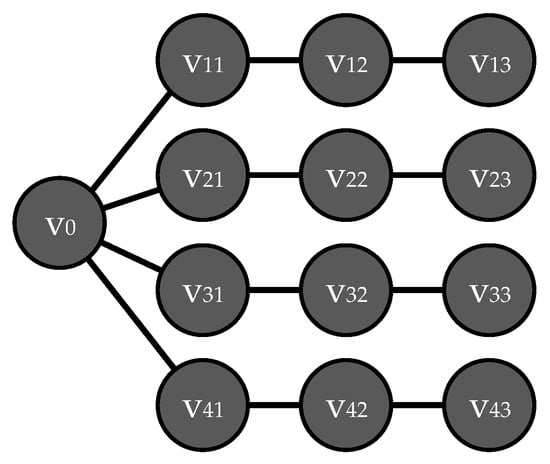
Figure 1.
A “star” type structure with 4 rays of length 3.
Definition 3.
If for the attack structure Wm = ⟨G(V, E), T⟩ there is a one-to-one mapping M: V → S, then we will call it a mapping of the attack structure Wm to the set S.
Definition 4.
The one-to-one mapping M−1: S → V, the inverse of the previously defined mapping M: V → S, will be called a placement of the elements of S in the attack structure Wm.
Note that the criterion for the existence of such a mapping will be the equality between the number of vertices in the graph G(V, E) and the number of elements of the protected system. If the number of vertices is infinite, then the set S must be countable.
Definition 5.
The local risk of an element of the protected system mapped to the vertex vbl of the attack structure of the type “star with m rays” is defined as the value
where ⟨v0, vbl⟩ is a simple path connecting the perimeter vertex v0 to the vertex vbl.
The local risk of an element mapped to vertex v0 is equal to its eigen risk. Note that in the considered case, a simple path always exists and is unique.
Definition 6.
The integral risk of a system with the set S of protected elements, mapped to the attack structure of the “star with m rays” type Wm using a one-to-one mapping M−1: S → V, is defined as the value
Suppose that the protected system includes a set of elements S = {s1, s2, …, sn}, with their corresponding eigen probabilities of a successful attack and damages . Suppose also that the expected attack has a structure of the “star with m rays” type Wm = ⟨G(V, E), T⟩, where Then, the problem of minimizing the integral risk of the protected system is to find such a placement M−1 of the elements of S in the Wm structure that
For the special case m = 1, the general solution is given in [34]. However, even for m = 2, it is not possible to find a criterion for the ordering of vertices that minimizes the integral risk. Therefore, in what follows, we will formulate a number of assumptions that allow us to solve this problem for real systems with acceptable accuracy. However, first, let us consider several heuristic approaches to finding an algorithm for solving problem (7).
3. Heuristic Algorithms for Solving the Problem of Minimizing Integral Risk
Let us assume that the expected damage during a successful attack on each of the elements is estimated equally, that is, Then, problem (7) takes the form
Based on general considerations, it seems that the optimal placement of elements is such that the higher the probability of a successful attack, the further away from the perimeter the element should be situated. This is congruent with the result obtained earlier in [34] for a simple chain structure. Recall it:
Definition 7.
The nodesare not strictly ordered in ascending (descending) order of local risk and write () if, given the attack structure W1 (in the sense of Definition 2) for any placements such that there holds the inequality ().
Statement 1.
Let. Then, ∀ i < n
In the considered particular case of equality of damages, this statement means that the eigen probabilities of a successful attack by placed elements should increase (more precisely, not decrease) with distance from the perimeter.
Let us formulate the following:
Statement 2.
For each placementthat minimizes integral risk, the following holds: if for arbitrarythere are verticesin the Wm structure, then .
If this statement was proved correct, it would become possible to simplify the problem by considering, separately, the subsets of vertices located at a fixed distance from the perimeter. Unfortunately, this statement is incorrect. Let us consider a fairly simple counterexample for a two-ray attack structure.
Let the protected system include a set of elements with the following eigen probabilities of a successful attack: , , , . Let us define a structure W2 with .
Counterexample 1. First, let us construct a placement that simultaneously satisfies the conditions from Statements 1 and 2 (Figure 2a). We obtain
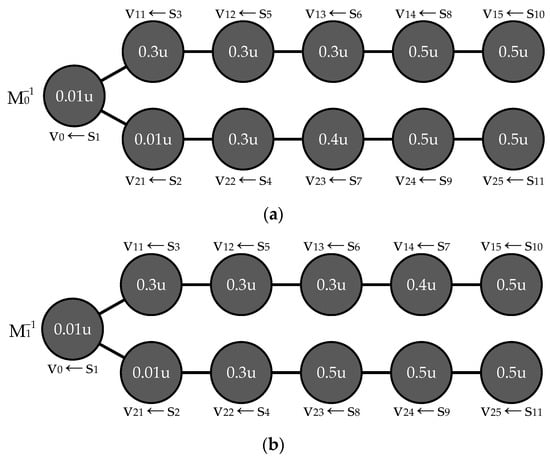
Figure 2.
An example of a placement satisfying the conditions of both Statements 1 and 2 (a), and a placement satisfying the condition of Statement 1 but not Statement 2 and at the same time providing a lower value of integral risk (b).
Now, let us construct a placement which differs from in that while (Figure 2b). We obtain
The resulting placement (Figure 2b) satisfies the condition of Statement 1 but not the condition of Statement 2. Since it provides a lower value of integral risk, Statement 2 is false.
Note that the probabilities of a successful attack of the elements mapped to the vertices v11 and v21 differ greatly (in the example above, by thirty times). Thus, the integral risk in one of the rays turns out to be much less than in the other, which causes the effect illustrated by the counterexample. Hence, the idea naturally arises to construct the placement iteratively, gradually moving away from the center, so that the intermediate risk values on the rays are approximately equal. For the given system, this will be the mapping (Figure 3).
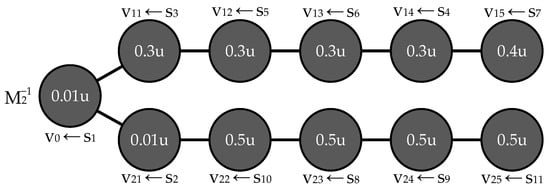
Figure 3.
An example of a placement that equalizes the intermediate values of the integral risk obtained while moving away from the perimeter.
The resulting integral risk is
which is even less than for the map . However, this mapping is also not a solution to problem (2), since there is the following:
Counterexample 2. Let us construct a placement (Figure 4), which differs from in that , whereas .
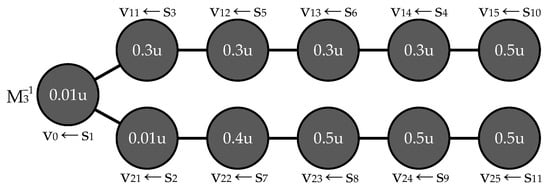
Figure 4.
Example of a placement that is a solution to problem (2).
The resulting integral risk is
Thus, the proposed heuristic also does not provide a solution to the problem.
In conclusion, let us attempt to construct a criterion for placing elements in a subset of vertices located at a distance j from the perimeter, that is, . We arbitrarily choose two vertices and from this set. Let us check under what conditions the following inequality will be satisfied for the mapping that minimizes integral risk:
For notation convenience, let us denote , . For the remaining vertices, instead of , we will write , and instead of , . Let us also introduce a notation for the integral risk of a subset of the attack structure, which is a simple chain and includes vertices
Let us calculate the difference in the values Δ of integral risk for the cases when the elements are mapped to the vertices with eigen probabilities of a successful attack, respectively, equal and (case 1), and vice versa (case 2). Recall that .
If , then the integral risk will be less than for the placement from case 1. Otherwise, it is the same as in case 2. Due to the fact that , and , this inequality holds if, and only if,
The resulting relation tells us that the optimal placement of elements in the subset of vertices depends both on the placement of elements in vertices which are located closer to the perimeter and further away relative to the considered ones. Thus, the iterative construction of optimal placement is impossible, and it seems that the exact solution of problems (7) and (8), even in the particular case of equality of expected damages, is possible only by an exhaustive search of placements.
Since the number of possible permutations of elements is expressed in terms of a factorial, an exhaustive search is practically impossible even for systems with a relatively small number of elements. Therefore, in what follows, we will look for a possibility to approximately solve problem (8) by a computationally simple algorithm with some error estimated from above.
4. Approximate Solution to the Problem of the Optimal Placement of Elements
As in the previous section, let us consider a special case of equality of the values of the expected damage, that is, solve problem (8). From the standpoint of practice, the expression
can be interpreted as a value characterizing the security of the system as a whole. It is quite reasonable to assume that the more protected elements the system includes, the more attractive it is for an attacker. Therefore, the better protected each element individually is, the more elements there are in the system.
For the system containing a single element, the expression (18) will be exactly equal to the probability that it will be successfully attacked. Thus, the value of this expression does not exceed one. Let us extend this restriction to all the systems under consideration and introduce the concept of the marginal eigen risk.
Definition 8.
The marginal eigen risk of an element of the protected system with the attack structureis defined as the quantity
It is easy to verify that if , then
whereas for = ∞ ∀b ∈ {1, …, m}, m ≤ ∞, this expression is equal to one.
Now, let us consider how integral risk behaves with the gradual complication of the attack structure and the protected system. In the simplest case, when the system consists of a single element its placement in the attack structure is unique, and the integral risk of the system under given constraints does not exceed .
If there are n elements in the protected system, and the attack structure includes m = n − 1 rays, including one edge each, then the upper estimate of the integral risk introduced by the element is equal to , and the contribution of the elements mapped to the vertices will be no more than Note that the first expression tends to zero as n → ∞, and the second to u. Further, for convenience, let us say that the ray has length k if the path from the perimeter vertex to its hanging vertex includes k edges.
Finally, consider a variant of the attack structure with rays. In the case of even n, one of the rays will have length 1, while the others will have length 2. For odd n, all rays will have length 2. The upper estimate of the integral risk introduced by the elements mapped to the vertices will be no more than . This value also tends to zero as .
This leads to two important conclusions. First, the more rays the attack structure has, the less influence on the integral risk of the system is exerted by the elements mapped to the vertices with . Second, for , the increase in risk on the set of vertices does not exceed ten percent of the maximum possible value. Specific values for small m and l are given in Table 2.

Table 2.
Upper estimates for the risk increment in a structure with m rays on subsets of vertices that are away from the perimeter by 1–3 edges, as well as the corresponding upper estimates for the integral risk values; rounding is to the fourth digit with excess.
Note that for the perimeter vertex, as well as the vertices , located at a distance of 1 from it, the solution of the problem of the optimal placement of elements of the protected system is trivial due to the need to fulfill the criterion of the ordering of elements proved in [34]. Namely, in the particular case under consideration, an element with a minimum eigen risk (minimum probability of a successful attack) should be mapped to the perimeter, whereas to the vertices , m elements from the remaining ones with the lowest eigen risk, starting from the number b corresponding to the longest ray.
Thus, the most interesting practical standpoint is the solution of the problem of the optimal placement of elements of the protected system in a subset of the vertices of the attack structure, which are separated from the perimeter by two edges, that is, . Note also that the quantity for fixed values (that is, corresponding to subsets and so on) monotonically decreases with the growth of m. At the same time, the first derivative of the expression has a root ; therefore, the upper estimate for the risk increment reaches maximum if the attack structure has four rays. This fact allows us to further limit ourselves to considering such structures as the “least favorable” in the sense of finding the optimal placement of elements to minimize the integral risk. The values of deviation from the optimal solution will be maximal precisely for .
For an approximate solution to problem (8), we propose to use the following algorithm:
- Select the element with the lowest eigen risk and map it to the vertex-perimeter .
- From the remaining ones, select m elements with the lowest eigen risks and map them to the vertices so that the lengths of the rays corresponding to these vertices depend inversely on the eigen risk of the element mapped to the vertex.
- For each of the subsets of vertices successively select elements with the lowest eigen risks from the remaining ones and place them at the vertices of the corresponding subset in an arbitrary way.
In the next section, we will construct upper estimates of the error of solving problem (8) by using this algorithm.
5. Upper Estimates of Errors in Solving the Problem of the Optimal Placement of Elements
To obtain estimates of the error in solving the problem of the optimal placement of elements in the attack structure of the “star with m rays” type, we will conduct a numerical experiment consisting of the following: Let us successively generate attack structures with the number of rays m from 2 to 11, each of which has a length lb ≥ 3. The number of rays is limited because of the computing power available to us for the experiment.
Let us introduce the following restrictions:
Next, let us generate integral risk expressions for all placements obtained by permutations of elements mapped into subsets and then (separately) . Then, let us consider all possible absolute values of the difference of these expressions and, for each of them, search for a global maximum. Dividing the resulting value by the minimum of the integral risk from these two expressions subtracted from each other, we obtain the relative difference between them. The maximum of relative differences will give us a numerical estimate of the error in solving the problem of the optimal placement of elements of the protected system in the attack structure.
The results of the experiment are summarized in Table 3. They indicate that the value of the relative error varies within small limits. In this case, the increase in the relative error of solving problem (8) on the vertices located at a distance of two edges from the perimeter is 6.07% in the least favorable case.

Table 3.
Numerical estimates for the relative error of solving the problem of the optimal placement of elements in subsets of the vertices of the attack structure; rounding is to the fourth digit with excess (* is an unreliable value due to overflow).
Note that the relative error increments for structures with an even number of rays are always greater than those for structures with an odd number of rays that is greater by one. This effect is explained in the following way: Suppose that there is an optimal placement . Then, inside each subset for a fixed l, criterion (17) is fulfilled. Since this is a pairwise comparison criterion, we can order and number the elements mapped to the subset under consideration with numbers from 1 to (some may not exist).
In order to construct a mapping with the maximum possible deviation (increment) of the integral risk obtained by permutations of elements inside the subset , it suffices to map elements into it in reverse order. At the same time, for odd k, the element with the number will remain in its place, while the number of pairwise permutations will be the same for (k − 1) elements. Due to the previously introduced restriction on the maximum value of the eigen risk, the contribution of each of these pairwise permutations will decrease with an increase in the value of k.
It should be noted that on the sets , the value of the relative error drops sharply, and one can talk about the boundedness of the sum of errors. Recall that earlier in Table 2, the values of the absolute maximum increase in risk for subsets of vertices were given under the given limits of the marginal eigen risk. Since the risk cannot be zero, the upper estimate of the risk increase always exceeds the upper estimate of the relative error. The former, in turn, is calculated as , and the infinite sum of such terms converges: . The last column of Table 3 shows the sums of such series that majorize relative errors. Starting from m = 3, the total relative error in the non-optimal placement of elements of the protected system in vertices separated from the perimeter by three or more edges does not exceed two percent and decreases with an increase in the number of rays in the attack structure.
Note also that in all cases, the maximum relative error is achieved when both elements with a very small eigen risk (the probability of a successful attack on such elements in the experiment will be equal to the machine epsilon) and elements with a marginal eigen risk are simultaneously present in the system. In this regard, another series of experiments were conducted where the spread of eigen risks was limited.
Definition 9.
The residual eigen risk for the protected system, which includes a set of elements, is defined as the quantity
Let us require the residual eigen risk to be , , , . The results of numerical experiments are shown in Table 4.

Table 4.
Numerical estimates of the relative error of solving the problem of the optimal placement of elements in subsets of vertices of the attack structure at a given threshold of residual risk; rounding is to the fourth digit with excess.
Under the restriction , the error values differ little from the case when . However, if the spread of eigen risks is small, then the value of the relative error is noticeably reduced. For example, if , then with any placement of the elements of the protected system at the vertices , the integral risk will exceed the minimum by less than 5%.
6. Methodology for Rapid Risk Assessment of Complex Systems with a “Star” Type Structure
Let us consider the question of assessing the risks of a certain complex system that includes a set S of protected elements placed in the attack structure of the type of “star with m rays” Wm. Assume that the defender does not know both the eigen probabilities of a successful attack on each of the protected elements and the values of damage inflicted by an attacker in the event of a successful attack on any element. At the same time, let us assume that they know the values and , , whereas
Then, for m = 1, the estimate for the integral risk of this system will have the following form:
where u is some estimate of the “average” damage. Note that these sums will be finite even for a system with a countable set of protected elements, provided that .
Now, suppose that the attack structure has two rays with approximately the same lengths and , that is, . Then, the value of the integral risk of such a system can be estimated from below and from above in terms of and , respectively. Let us first write down the expression for the estimate from below:
The value will be zero for odd n and 1 for even. In the first case, we will get two rays of the same length, and in the second, their lengths will differ by one. For the upper estimate, the expression will be the same up to the replacement of by .
Now, let us write down an expression for the lower estimate of the integral risk of a system with a structure that includes an arbitrary finite number of rays m:
Let us estimate how much the estimate changes when the number of rays increases to (m + 1). To achieve this, let us write down an expression for the lower estimate of the integral risk for such a structure:
It is rather difficult to algebraically estimate the value , so let us investigate visually what happens when moving from a “star with m rays” to a “star with (m + 1) rays” (Figure 5). Recall that integral risk is the sum of the local risks of elements of the protected system. The specific values of the local risks depend on the position of the elements in the structure, but when constructing the upper and lower estimates, the values of the eigen risks are the same for all elements.
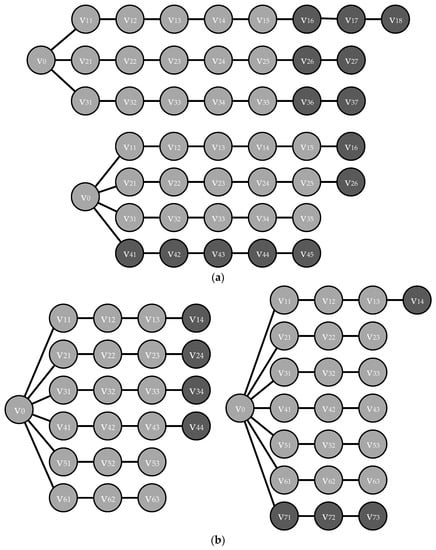
Figure 5.
“Star” type structures (a) with 3 and 4 rays; (b) with 6 and 7 rays.
The values of local risks will be higher, the lower the value of the second index of the vertex. At the same time, the vertices with the same second indices will have the same values of the local risks. When a new (m + 1)th ray is added, vertices appear in the structure. Vertices with indices from to will be present both in a structure with m rays and in a new one with an additional ray added. In the structure with m rays, the remaining vertices will have second indices larger than , while of them will have the same indices in both structures (and, accordingly, the same local risks).
These arguments lead us to the fact that the upper and lower estimates of the integral risk monotonically increase with the increase in the number of rays in the structure. Noticing that
we discover that the quantity for also monotonically increases with the growth of m. When , the equality of the upper and lower estimates is achieved.
7. Solving the Problem for Elements with Different Damage Values
Earlier, we considered a particular case when the damage from a successful attack on elements is estimated the same, that is, Let us assume that the damages are different. At the same time, let us require that the following relation be fulfilled:
It is easy to make sure that for each one-ray structure of the form this relation ensures the equality of integral risks for any set of corresponding one-to-one mappings , where T is some set of indices. Let us show that for such elements there exists an exact solution to problem (7).
First, let us note that any structure of the “star with m rays” type can be divided into m structures of the type as follows: Let be defined as in Definition 2. Then, let us define , , …, , while
whereas for the remaining
Then, , , and . For a given mapping , due to it being one-to-one, one can find such a partition of the set of protected elements that
and the quantity can be written as
Now, let us show that when the relation (17) is fulfilled for any placement such that , the integral risk will reach a minimum. For convenience, let us renumber the protected elements so that Then, and
Now, consider another placement , resulting from by permutation of two elements: and any other , that is, . Without loss of generality, we assume that is in the structure .
Let us write down the value of the integral risk for placement :
Note that due to relation (17),
Since , then , which means that the placement is the solution of problem (7).
8. Discussion
In this study, we propose an algorithm for solving the problem of the pseudo-optimal placement of elements of a protected system in the structure of an attack of the “star with m rays” type in the particular case of equal damages during a successful attack on an element. While the optimal placement problem can generally be solved only by exhaustive search, the proposed algorithm allows solving it in linear time with some estimated error depending on the number of rays in the attack structure.
To construct upper estimates of the solution errors, we experimentally calculated them for small structures, consisting of 2 to 11 rays of a length of 4 to 6 elements. The parameters of the structures were limited by the computing power available to us on the one hand and the precision of the machine representation of floating-point numbers on the other. At the same time, even such a small experiment clearly visualizes the intuitive idea that the relative error generally decreases with an increase in the number of rays in the structure. Thus, to obtain the upper estimates, it is sufficient to consider the values obtained for the minimum non-degenerate “star” of two rays. Additionally, we clarified the upper estimates for the error of solving the problem with a bounded limiting eigen risk for different levels of residual risk in a particular case (with equal damages).
Furthermore, we proposed a method of rapid risk assessment of systems with the considered attack structure in a situation where the defender does not know neither the values of the eigen probabilities of a successful attack of elements nor the values of the expected damages of them. At the same time, the defender presumably knows the values of the residual and marginal risks, and they are also able to imagine some average value of damage. We investigated the behavior of the difference between the upper and lower integral risk estimates and found that it increases with the number of rays in the structure of the system. Note that the relative error of the algorithm of the sub-optimal placement of elements proposed above decreases with an increase in the number of rays in the “star”. Thus, the more difficult the system’s risk is to evaluate, the better the algorithm works.
Finally, we proposed an exact solution to the problem of the optimal placement of elements with various damages but with a restriction on the ratio of their eigen risks (29). Namely, the ratio of the probability that an element will not be successfully attacked to the value of its eigen risk must be equal for all elements of the system. Meaningfully, this condition reflects the natural requirement that the higher the expected damage to an element, the better it should be protected. The fulfillment of this condition makes the elements neutral to their location inside the ray, i.e., their rearrangement does not affect the integral risk of a subsystem consisting of this ray alone.
The solution to the problem is to put an element with the lowest eigen probability of its successful attack into the vertex-perimeter, which is common to all rays. This solution is not intuitive because this element will also have the maximum value of the expected damage among all elements. However, this solution provides the minimum integral risk for the system. The given example illustrates that the eigen probability of a successful attack of an element (and, accordingly, the security of the element) is more important than the expected damage when it comes to the perimeter.
9. Conclusions
The obtained results can be used in risk management in complex networks. The conducted numerical experiments allow a reasonable conclusion to be drawn that one should focus primarily on reducing the vulnerability of the perimeter, as well as nodes directly accessible from it. The nodes located farther away do not have a significant impact on the level of risk of the system as a whole. The algorithm proposed in this paper allows for solving the problem of minimizing integral risk with any predetermined accuracy for systems having a “star” type structure with a single-vertex perimeter. In the future, we plan to generalize the proposed algorithm for application to systems with a tree-like structure and, in prospect, an arbitrary topology.
The results obtained so far do not suggest a wide application in practice. They can be used, for instance, to manage risks in small computer networks, but such problems usually arise when protecting large networks with complex topologies. Nevertheless, the obtained results are the foundation for the transition to the study of more complex structures. We plan to thoroughly discuss the practical aspects in subsequent papers devoted to risk management in complex networks of arbitrary topology.
Author Contributions
Conceptualization, A.K.; investigation, A.S.; methodology, A.K.; supervision, A.K.; writing—original draft, A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rodrigues, F.A. Network centrality: An introduction. In A Mathematical Modeling Approach from Nonlinear Dynamics to Complex Systems; Macau, E.E.N., Ed.; Springer: Cham, Switzerland, 2019; pp. 177–196. [Google Scholar] [CrossRef]
- Saxena, A.; Iyengar, S. Centrality Measures in Complex Networks: A Survey. arXiv 2020, arXiv:2011.07190. [Google Scholar]
- Kanyou, C.; Kouokam, E.; Emvudu, Y. Structural network analysis: Correlation between centrality measures. In Proceedings of the CARI 2022, Yaoundé, Dschang, Cameroon, 22 September–3 October 2022. [Google Scholar]
- Boguñá, M.; Krioukov, D.; Claffy, K.C. Navigability of complex networks. Nat. Phys. 2009, 5, 74–80. [Google Scholar] [CrossRef]
- Pu, C.L.; Cui, W. Vulnerability of complex networks under path-based attacks. Physica A 2015, 419, 622–629. [Google Scholar] [CrossRef]
- Chen, B.; Cao, L. An optimized algorithm for calculating the average path length of complex network. In Proceedings of the 2017 10th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 9–10 December 2017; IEEE Computer Society: Washington, DC, USA, 2017; Volume 1, pp. 334–337. [Google Scholar] [CrossRef]
- Serrano, M.Á.; Boguñá, M. Clustering in complex networks. I. General formalism. Phys. Rev. E 2006, 74, e056114. [Google Scholar] [CrossRef] [PubMed]
- Saramäki, J.; Kivelä, M.; Onnela, J.P.; Kaski, K.; Kertesz, J. Generalizations of the clustering coefficient to weighted complex networks. Phys. Rev. E 2007, 75, e027105. [Google Scholar] [CrossRef] [PubMed]
- Clemente, G.P.; Grassi, R. Directed clustering in weighted networks: A new perspective. Chaos Solitons Fractals 2018, 107, 26–38. [Google Scholar] [CrossRef]
- Cajueiro, D.O.; Andrade, R.F. Controlling self-organized criticality in complex networks. Eur. Phys. J. B 2010, 77, 291–296. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, H.; Lin, W.; Lai, Y.C.; Wang, X. Growth, collapse and self-organized criticality in complex networks. Sci. Rep. 2016, 6, e24445. [Google Scholar] [CrossRef]
- Hoffmann, H.; Payton, D.W. Optimization by self-organized criticality. Sci. Rep. 2018, 8, 2358. [Google Scholar] [CrossRef]
- Wang, P.; Wen, G.; Yu, X.; Yu, W.; Wan, Y. Synchronization of resilient complex networks under attacks. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 1116–1127. [Google Scholar] [CrossRef]
- Tang, Y.; Qian, F.; Gao, H.; Kurths, J. Synchronization in complex networks and its application—A survey of recent advances and challenges. Annu. Rev. Control 2014, 38, 184–198. [Google Scholar] [CrossRef]
- Zhao, L.H.; Wen, S.; Li, C.; Shi, K.; Huang, T. A recent survey on control for synchronization and passivity of complex networks. IEEE Trans. Netw. Sci. Eng. 2022, 9, 4235–4254. [Google Scholar] [CrossRef]
- Kocarev, L. (Ed.) Consensus and Synchronization in Complex Networks; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ma, L.; Wang, Z.; Han, Q.L.; Liu, Y. 2017. Consensus control of stochastic multi-agent systems: A survey. Sci. China Inf. Sci. 2017, 60, e120201. [Google Scholar] [CrossRef]
- Bodkhe, U.; Mehta, D.; Tanwar, S.; Bhattacharya, P.; Singh, P.K.; Hong, W.C. A survey on decentralized consensus mechanisms for cyber physical systems. IEEE Access 2020, 8, 54371–54401. [Google Scholar] [CrossRef]
- Xing, W.; Shi, P.; Agarwal, R.K.; Zhao, Y. A survey on global pinning synchronization of complex networks. J. Franklin Inst. 2019, 356, 3590–3611. [Google Scholar] [CrossRef]
- Suarez, O.J.; Vega, C.J.; Elvira-Ceja, S.; Sanchez, E.N.; Rodriguez, D.I. Sliding-mode pinning control of complex networks. Kybernetika 2018, 54, 1011–1032. [Google Scholar] [CrossRef]
- Freitas, S.; Yang, D.; Kumar, S.; Tong, H.; Chau, D.H. Graph vulnerability and robustness: A survey. IEEE Trans Knowl Data Eng 2022, e1–e20. [Google Scholar] [CrossRef]
- Criado, R.; Romance, M. Structural vulnerability and robustness in complex networks: Different approaches and relationships between them. In Handbook of Optimization in Complex Networks; Thai, M.T., Pardalos, P.M., Eds.; Springer: New York, NY, USA, 2012; pp. 3–36. [Google Scholar] [CrossRef]
- Wang, C.; Xia, Y. Robustness of complex networks considering attack cost. IEEE Access 2020, 8, e172398–e172404. [Google Scholar] [CrossRef]
- Jalili, M.; Perc, M. Information cascades in complex networks. J. Complex Netw. 2017, 5, 665–693. [Google Scholar] [CrossRef]
- Nowzari, C.; Preciado, V.M.; Pappas, G.J. Analysis and control of epidemics: A survey of spreading processes on complex networks. IEEE Control Syst. Mag. 2016, 36, 26–46. [Google Scholar] [CrossRef]
- Wang, S.; Liu, J. Designing comprehensively robust networks against intentional attacks and cascading failures. Inf. Sci. 2019, 478, 125–140. [Google Scholar] [CrossRef]
- Nash, Z. The bargaining problem. Econometrica 1950, 18, 155–162. [Google Scholar] [CrossRef]
- Nash, Z. Two-person cooperative games. Econometrica 1953, 21, 128–140. [Google Scholar] [CrossRef]
- Kalai, E.; Smorodinsky, M. Other solutions to Nash’s bargaining problem. Econometrica 1975, 43, 513–518. [Google Scholar] [CrossRef]
- Degefu, D.M.; He, W.; Yuan, L. Monotonic bargaining solution for allocating critically scarce transboundary water. Water Resour. Manag. 2017, 31, 2627–2644. [Google Scholar] [CrossRef]
- Kalashnikov, A.O.; Anikina, E.V. Management of risks for complex system based on a generalized arbitration scheme. In Proceedings of the 14th International Conference Management of Large-Scale System Development (MLSD), Moscow, Russia, 27–29 September 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Chen, C.; Iyengar, G.; Moallemi, C.C. An axiomatic approach to systemic risk. Manag. Sci. 2013, 59, 1373–1388. [Google Scholar] [CrossRef]
- Kalashnikov, A.O.; Anikina, E.V. Management of information risks for complex system using the “cognitive game” mechanism. Vopr. Kiberbezop. [Cybersecur. Issues] 2020, 4, 2–10. [Google Scholar] [CrossRef]
- Shiroky, A.; Kalashnikov, A. Mathematical problems of managing the risks of complex systems under targeted attacks with known structures. Mathematics 2021, 9, e2468. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).