Abstract
This paper presents two new fault models for networked systems. These fault models are more realistic and generalized for networked systems in the sense that they can represent the effects of fault at the node and network levels. At the network layer, the uncertain effects of the network lines are modeled using a Markov chain with complex transition probabilities simultaneously with the stochastic behavior of the network using a Bernoulli process. A new output feedback-based controller, which is two-mode dependent and considers network uncertainties and output measurements for gain calculation, is presented. Using the tools of robust control and stochastic stability, linear matrix inequality-based sufficient conditions are derived. The proposed controller successfully maintains the system’s performance by tolerating the effects of simultaneous sensor and actuator faults, ensuring the stability of networked loops. Simulation results verify the applicability of the presented fault-tolerant control against multiple simultaneous faults.
Keywords:
fault modeling; networked systems; fault-tolerant control; stochastic stability; Markovian jump system MSC:
97M50
1. Introduction
We encounter Networked Control Systems (NCSs) in several applications, for instance, in the automobile and manufacturing industries, airplanes, and tele-health monitoring. In these applications, NCSs offer many benefits such as cost reduction, easy installation, reduced maintenance, and maximum efficiency with reliability. Along with these benefits, NCSs include many challenging issues due to limited bandwidth and the utilization of shared resources by NCS components. These issues include network-induced random time delays due to queuing, processing, transmission, and propagation time at different nodes and links. The packets may also suffer from uncertain data packet dropouts due to network traffic. These uncertainties can significantly degrade the performance of systems if not addressed adequately. To address these issues, researchers have focused their efforts on this in the last few years [1,2,3,4].
To model these network-induced uncertainties, researchers have used the Markov chain and Bernoulli process [2,3,4,5]. The Markov chain, used in the most of the literature, requires complete knowledge of Transition Probabilities (TPs). In practical applications, these are costly and very hard to obtain, in some cases, even impossible. It is, therefore, very important to consider partly known TPs in the Markov chain. This is why stability criteria are proposed for Markovian jump systems (MJSs) with partially known TPs in [6,7], and results with less conservative outcomes are presented in [8,9,10]. The conditions for the stability and stabilization of NCSs with partially known TPs are presented in [11]. Markov-based modeling of time-delay with partly known TPs is important when all the data packets reach the destination. In practical applications, data packets may drop out due to the network traffic in the shared network links. It is worthwhile to mention that in the literature, researchers only addressed either the time-delay or the packet drop out in networked systems. The inadequate modeling of network uncertainties during the controller design process makes the controller strategies very limited in practical engineering. We address both the network’s main impurities simultaneously.
In addition to the communication network impurities, faults may occur in sensors, actuators, and/or process components [12,13,14,15,16,17,18], making the control of networked systems more challenging. These faults can degrade performance, lead to instability, and even cause fatalities [18]. In networked systems, the effects of faults may propagate from one node to other nodes. These propagated effects of faults increase the severity of local node faults [19]. To the authors’ knowledge, in the literature on networked systems, the propagated effects of faults at the network level, along with network’s main uncertainties, must still be addressed. For this purpose, we proposed two new fault models that are more generalized for networked systems. These fault models mathematically represent the magnitude of node-level and network-level faults simultaneously with their propagated effects and the network’s main impurities. Immediate maintenance and repair are not always available, so fault tolerance has received great attention both in academia and practice [20,21]. Motivated by these challenges, researchers have reported Fault-Tolerant Control (FTC) strategies for sensor or actuator faults [17,18,22,23]. In the aforementioned literature, researchers have addressed a single fault or a single type of fault at a time; that is, either multiple sensor faults or multiple actuator faults with either time-delay or packet loss. Assuming the occurrence of a single fault or single type of multiple faults at a time makes the diagnostic and tolerance algorithm very limited in use. In practice, actuator and sensor faults may develop simultaneously due to poor networked environments. To the best of our knowledge, very few researchers have addressed the issue of multiple types of simultaneous fault tolerance in networked systems. Excellent work is done in [20] on double-fault, investigating the guaranteed cost FTC in networked systems using the piecewise delay method. The authors modeled the system with a constant time-delay, which is a conservative approach from a practical point of view. Secondly, the state feedback control requires the information of all states of the system, which are, in practice, very difficult to obtain.
Driven by the mentioned challenges in the literature survey, an FTC is proposed for the tolerance of faults at the node and network levels, along with network-induced uncertain effects. Contributions in the article can be summarized as follows: (1) We propose two new fault models for networked systems that cover the effects and magnitude of faults at the node and network levels, simultaneously with propagated faulty effects and the network’s major impurities. (2) To adequately model the major network-induced time delay, we use the Markov chain with partially known TPs, simultaneously with the packet dropouts using the Bernoulli process. In the literature, time-delay with partial TPs and packet loss is not addressed with simultaneous multiple types of faults. (3) A two-mode dependent controller is proposed, which considers network-induced effects along with sensor measurements for a gain calculation to address multiple types of simultaneous generalized faults. (4) In comparison with work in the literature, simultaneous sensor and actuator faults are addressed for networked systems, using an LMI with the help of the proposed two-mode dependent output feedback controller.
The subsequent sections of the script are organized as follows. Section 2 is dedicated to problem formulation, first presenting the fault models for networked systems, and then modeling uncertain network-induced imperfections. Section 3 is dedicated to presenting the proposed FTC design for NCSs based on the Markov jump system and Bernoulli process. Lastly, Section 4 presents the simulated study of the proposed FTC discussed for the DC motor to ensure its effectiveness and the applicability of the system.
Notation: The occurrence probabilities are defined as . The notation denotes wherever we show quadratic forms . All the used symbols are defined in the respective sections, and I represents an identity matrix. We provided a key table (Table 1) for symbols and notation at the end of the manuscript for better understanding.

Table 1.
Notation used throughout the manuscript.
2. Problem Formulation
Consider a networked environment, as shown in Figure 1, where six nodes are connected in a network. There is one faulty node that affects the neighboring connected nodes as the faulty effects propagate via network links. Each node of the network is a complete process, i.e., a plant with sensors and actuators. This process can be controlled over networks, as demonstrated in Figure 2. The controller controls the plant from a remote location in the presence of faults and disturbances via a communication network. Plant dynamics are given as described in Equation (1).
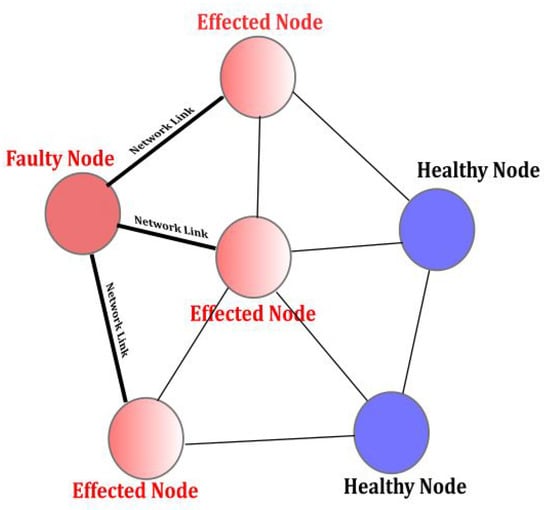
Figure 1.
Control over communication network.
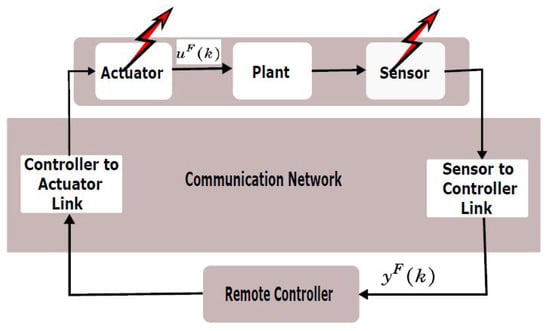
Figure 2.
Control over communication network.
Here, the state vector is , the control input is , and the external disturbance is , which belong to , where is the space of finite-energy discrete-time signals. The output is , where the constant matrices A, B, H, and C are of compatible dimensions. Additionally, the output matrix has a full-row rank.
2.1. Proposed Fault Models for Networked Systems
The fault models used in the existing research are either the constant faults model, probabilistic fault model, or generalized fault model. Only in the generalized fault model is time-delay considered for networked systems [20]. In a practical networked environment, packet dropout can not be ignored. Additionally, the propagated effects of fault from the neighboring connected node are also required to be incorporated into the fault models. To incorporate the faulty effects into the fault models at the node and network levels, we proposed two fault models for sensors and actuators in a networked environment. The sensor fault model is presented as:
where
is the faults matrix such that . The l given in subscript indicates the status of each individual sensor as
The range of l is from 1 to m. The network-induced uncertainties are and ; these are the random variables for data packets dropout and random time-delays, respectively.
where every , , up to , is a binary random variable. is the time-delay in the sensor-to-controller network links. The function represents the faulty effects that propagate from the neighboring connected nodes.
Similarly, the proposed actuator fault model is given as:
where
is the faults matrix for the actuator such that . The l given in subscript indicates the status of each individual actuator as
The range of l is from 1 to m. The network-induced uncertainties are and ; these are the random variables for data packets dropout and random time-delays, respectively.
where every , , up to , is a binary random variable and is the time-delay in the controller-to-actuator network links. The function represents the faulty effects that propagate from the neighboring connected nodes.
Remark 1.
The overall network-induced uncertainties , are considered here, instead of the separate induction of uncertainties from sensor-to-controller links and controller-to-actuator links. Similarly, for the calculation of the controller’s gain, the propagated effects are neglected to avoid computational complexity.
2.2. Network-Induced Uncertainties Modeling
The lump delay and the packet loss are mathematically modeled as below.
2.2.1. Time-Delay Modeling
The exchange of measurement and control data between the plant and the controller occurred via a shared communication network, as shown in Figure 2. The data packets may experience random time-delays or even drop while traversing through the network. We consider random variation in in the range
The time-delays are modeled with a Markov chain with a partially known Transition Probabilities Matrix (TPM) . There are N number of delay states, i.e, , where corresponds to , corresponds to , and so on. Let denote the partially known TPM of the Markov chain, given as:
where for all and . For example, if , the partial known TPM is given as below.
where the ? in the matrix are the unknown time-delay states’ transition probabilities, and the remaining entries are known TPs. Let , represent the column indices that are used for the unknown and known values in the row of the above matrix, respectively. Here, for all . The known entries, , of TPM can be rewritten as:
where .
The represents the known TP with the index in the row of the TPM. The restriction of complete knowledge of TPs for practical applications is often difficult to satisfy. Furthermore, the TP matrix covers the two different cases: completely known and completely unknown TPs in the Markov chain.
2.2.2. Packet Dropout Modeling
To adequately model the network-induced uncertainties, we model the packet dropout along with time-delay while using complex TPs. We model the packet dropouts with a binary random vector , where denotes the packet dropouts in the communication link. implies that the packet is successfully delivered via the link, and denotes that the packet has dropped out, where i ranges from 1 to m. The following probabilities are assumed for :
where E is the expected value and is the probability of packet propagation in the channels. implies that the packet has a maximum chance of successful propagation, while the other case means that the packet is lost. The missing parameter is described via the Bernoulli process.
Remark 2.
Time-delay tk is taken into account for the case where , which means the controller can only use the delayed version of the output if the data packet is successfully transmitted and propagated over the network link. We assume zero time-delays for the case of , which means that the packet has dropped out. It is very important to note that in most of the literature, the time-delay is only addressed if complex transition probabilities are used. In practical engineering, the packet dropout cannot be ignored in the network links, as the components of NCSs utilize shared communication channels, which may result in packet loss. This packet dropout leads to performance degradation.
2.3. Output Feedback-Based Controller Design
The remotely located controller was chosen to be the output feedback and is based, static, and two-mode-dependent, as given below.
is the gain of the controller.
Remark 3.
The control law u(k) given in Equation (7) clearly demonstrates that it depends on the sensor’s measured output, network-induced time-delay, packet dropout, and the fault matrix Ψ. The controller’s gain K tolerates the effects of fault.
The augmented vector for states is . Substituting 2, 6, and 16 in 1, the model of the closed-loop system with sensor and actuator faults, communication delays, and packet dropouts is obtained as:
The above derived system in Equation (17) is a close-loop stochastic system with multiple types of faults that are sensor and actuator faults, one data packet dropout mode , and one time-delay mode , where the probabilities of transitions are described using the Markov chain with partially known TPs and the stochastic parameter using the Bernoulli process. In the above Equation (17),
I is the identity matrix of completable dimensions.
3. Fault-Tolerant Control for Networked System
Definition 1.
The stochastic Markovian jump system given in Equation (17) is stable with any initial condition , , if the following inequality is fulfilled.
here, is the solution of the augmented state equation given in Equation (17) at time k under the initial conditions , , .
Theorem 1.
For a closed-loop system, as in (17), there exists an output-based feedback control of the form given in Equation (16), if there exist matrices , , , , satisfying
where
According to the definition, , it is derived, so that
Proof.
For proof, we chose the Lyapunov candidate as
then,
It can be verified that , which implies . This inequality ensures the stochastic stability for the close-loop Equation (9). We defined the main augmented states vector as and wrote Equation (10) as
We conducted pre- and post-multiplication of to and defining , , and then used the Schur complement. Next, network-induced uncertain impurities were introduced to , which resulted in the following inequality that is given in the theorem.
The controller gain is derived from the definition , and it is derived that
Lemma 1.
There exist nonsingular matrices for the output matrix with rank p such that . For this, there exist full-rank matrices that satisfy the condition given below as
where . The U is calculated using the SVD of matrix. , where σ are the singular nonzero values of .
Corollary 1.
Let , , , and be the known scalars. Then, the system given in (17) is a fault-tolerant, stochastically stable system if there exist , , , , , , and such that the LMI hold, and the desired FTC can be achieved by .
Proof.
If there exist matrices , , and satisfying the equation given in Lemma 1 and there exist nonsingular matrices that satisfy , then, consequently, it is equivalent to:
The post-multiplication of , ( to orthogonal matrix ) results in:
It can be readily derived that
and . The controller equation is . The desired gain is equal to:
□
□
4. Simulation Results
A numerical example is given below with simulation results to validate the applicability of the proposed FTC design.
A DC motor system is shown in Figure 3 in a networked environment, where the state-space representation for the DC motor system is given below. The state variable is the armature winding current and is the motor rotational speed. The inputs are armature winding input voltage and load torque , where the physical parameters are in Table 2. The signal chosen for external disturbance is .
by using the physical parameters of Table 2 and the application of the zero-order hold method of discretization on the inputs with a sampling period of , the discrete-time system with the initial conditions is described as:
to demonstrate the simultaneous sensors and actuator faults in the networked environment, we considered the following sensor and actuator faults.
the value denotes that the sensor and actuator are 30 percent faulty, meaning they are working at 70 percent. Probabilities of the stochastic variable for data packet dropouts are given in Figure 4 with the probability . is the maximum time-delay in the network links that are shown in the same Figure 4. The transition probability matrix for the time-delays using the Markov chain is given as
where the “” in the matrix are unknown transition probabilities. The Markov evolution of control mode is shown in Figure 5.
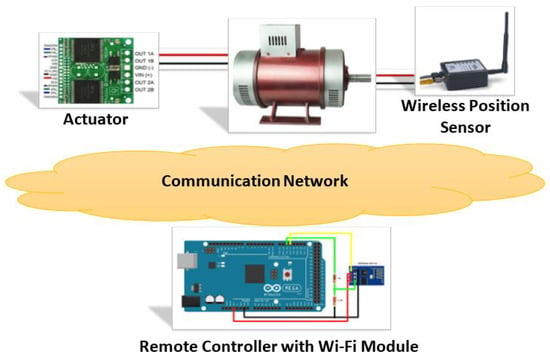
Figure 3.
Networked DC motor control system.

Table 2.
Numerical values for the state space equation of DC motor.
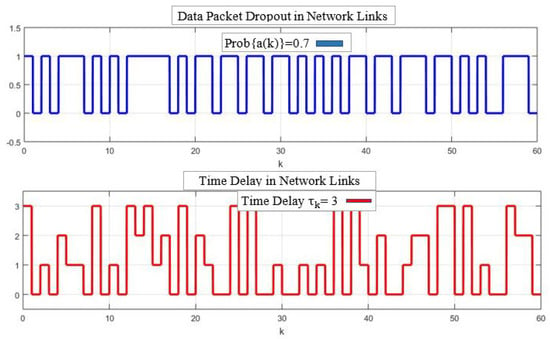
Figure 4.
Network-induced stochastic faults with and time-delay .
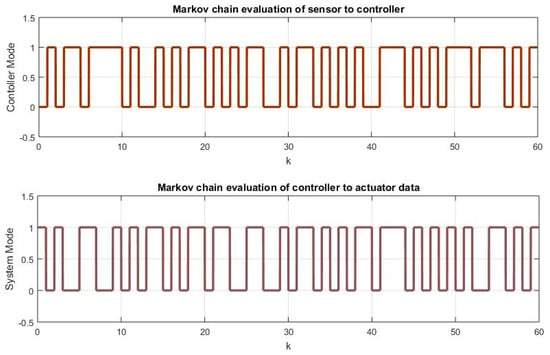
Figure 5.
Evolution of Markov chain.
This 30 percent sensor fault is applied at , as shown in Figure 6. The proposed FTC technique successfully tolerates its effects and stabilizes the states. The 70 percent actuator fault is applied at simultaneously with the sensor fault. The states are still stable, even in the presence of simultaneous sensor and actuator faults. To show the applicability of the proposed FTC, we increased the magnitude of sensor and actuator faults up to 70 percent. The proposed FTC tolerates the simultaneous effects of 70 faults, as shown in Figure 7.
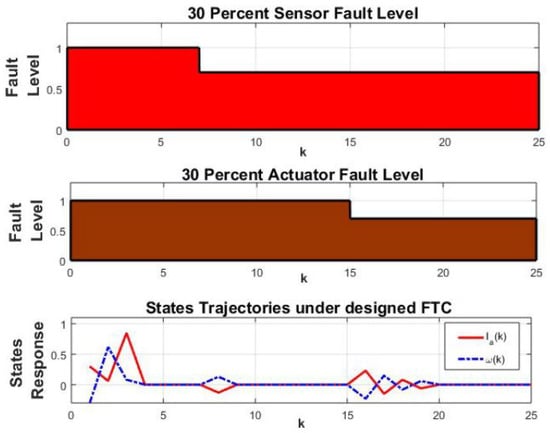
Figure 6.
Tolerance of 30 percent sensor and actuator simultaneous faults.
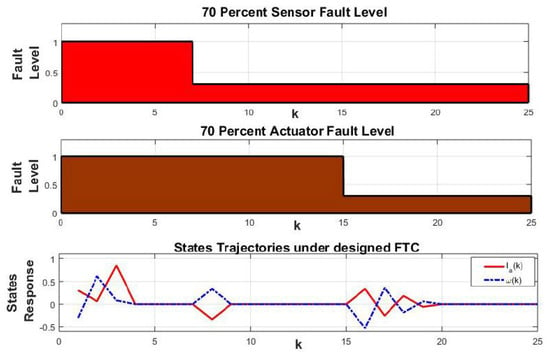
Figure 7.
Case 2: Multiple (sensor and actuator) types of simultaneous faults. Fault level is 70 percent.
Comparative Analysis: To compare the results of the proposed FTC with conventional controllers, we simulated the aforementioned data as they were, with a conventional controller. The results are given in Figure 8, which demonstrates that the conventional controller is unable to tolerate the effects of faults and cannot stabilize the states of the DC motor in the presence of faults in a networked environment. Gain matrices are given for the case when we consider 70 percent simultaneous sensor and actuator faults under the proposed FTC in a networked environment.
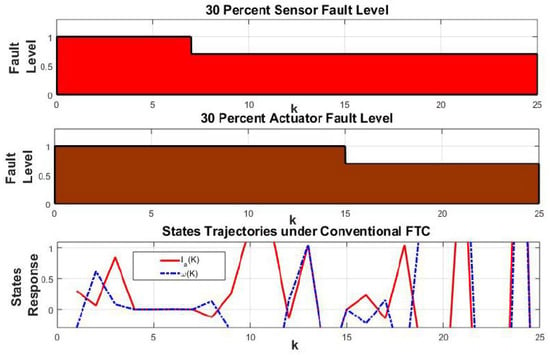
Figure 8.
State response of the networked DC motor system under normal FTC.
5. Conclusions
This research proposed two new fault models for sensors and actuators in a networked environment, along with a new FT-NCS scheme. The proposed fault models adequately address the faulty effects at the node and network levels. In these fault models, network-induced time-delay and packet dropouts are modeled simultaneously using the Markov chain with complex TPs and Bernoulli process, respectively. The FT-NCS scheme is an output feedback-based strategy where the controller depends on the networked affected output of the system. The proposed scheme successfully tolerates the effects of simultaneous sensor and actuator faults. A numerical example together with simulation results verifies the performance and stochastic stability of the networked systems. Designing a dynamic controller gain can further improve the tolerance capability of the proposed FTC design for practical applications.
Author Contributions
Conceptualization, M.A.A.; Methodology, A.M. (Atif Mahmood); Software, A.S.K.; Formal analysis, A.M. (Atif Mahmood) and A.Q.K.; Resources, N.U., A.M. (Alsharef Mohammad) and A.N.; Writing—original draft, A.M. (Atif Mahmood); Writing—review & editing, A.M. (Atif Mahmood). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Deanship for Research and Innovation, Ministry of Education in Saudi Arabia through the project number: IFP22UQU4290235DSR217.
Data Availability Statement
Not applicable.
Acknowledgments
The authors extend their appreciation to the Deanship for Research and Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number: IFP22UQU4290235DSR217.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NCS | Networked Control System |
| FTC | Fault-Tolerant Control |
| TP | Transition Probabilities |
References
- Kang, W.; Cheng, J.; Wang, B.; Park, J.; Fardoun, H.M. Event-triggered reliable control for Markovian jump systems subject to nonuniform sampled data. J. Frankl. Inst. 2017, 354, 5877–5894. [Google Scholar] [CrossRef]
- Zhang, T.; Gao, J.; Li, J. Event-triggered Hinf filtering for discrete-time Markov jump delayed neural networks with quantizations. Syst. Sci. Control. Eng. 2018, 6, 74–84. [Google Scholar] [CrossRef]
- Qu, H.; Wei, N.; Li, M.; Li, Y. Observer-based guaranteed cost control for networked control systems with packet dropout and nonlinear disturbance. Trans. Inst. Meas. Control 2020, 30, 3039–3053. [Google Scholar] [CrossRef]
- Bahreini, M.; Farsangi, M.M.; Lee, K.Y. Output feedback stabilization of networked brushless dc motor with random delay via Markovian jump systems. IFAC-Pap. Line 2015, 30, 55–60. [Google Scholar] [CrossRef]
- Xu, Z.; Ni, H.; Reza Karimi, H.; Zhang, D. A Markovian jump system approach to consensus of heterogeneous multiagent systems with partially unknown and uncertain attack strategies. Int. J. Robust Nonlinear Control 2020, 30, 3039–3053. [Google Scholar] [CrossRef]
- Li, Y.; Yu, Z.; Liu, Y.; Ren, J. Stochastic Stabilization for Discrete-Time Markovian Jump Systems With Time-Varying Delay and Two Markov Chains Under Partly Known Transition Probabilities. IEEE Access 2021, 9, 26937–26947. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, W. Stability and stabilization analysis of Markovian jump systems with generally bounded transition probabilities. IEEE Access 2020, 13, 8416–8434. [Google Scholar]
- Sun, H.-J.; Zhangp, Y.; Wu, A.-G. Stochastic stability analysis of Markovian jump linear systems with incomplete transition descriptions. IEEE Access 2018, 12, 1974–1982. [Google Scholar] [CrossRef]
- Zhang, Y.; He, Y.; Wu, M.; Zhang, J. Stabilization for Markovian jump systems with partial information on transition probability based on free-connection weighting matrices. IEEE Access 2011, 47, 79–84. [Google Scholar] [CrossRef]
- Qiu, L.; Shi, Y.; Xu, B.; Yao, F. Robust stochastic stability and delayed-state-feedback stabilisation of uncertain Markovian jump linear systems with random time delays. IET Control Theory Appl. 2015, 9, 1878–1886. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, C.; Fei, M.-R.; Tian, Y.-C. Output feedback control of networked systems with a stochastic communication protocol. J. Frankl. Inst. 2017, 9, 3838–3853. [Google Scholar] [CrossRef]
- Tan, C.; Li, L.; Zhang, H. Stabilization of networked control systems with both network-induced delay and packet dropout. Automatica 2015, 59, 194–199. [Google Scholar] [CrossRef]
- Nazir, M.; Khan, A.Q.; Mustafa, G.; Abid, M. Robust fault detection for wind turbines using reference model-based approach. J. King Saud Univ.-Eng. Sci. 2017, 29, 244–252. [Google Scholar] [CrossRef]
- Bahreini, M.; Zarei, J. Robust finite-time fault-tolerant control for networked control systems with random delays: A Markovian jump system approach. Nonlinear Anal. Hybrid Syst. 2020, 36, 100873. [Google Scholar] [CrossRef]
- Khan, A.S.; Khan, A.Q.; Iqbal, N.; Sarwar, M.; Mahmood, A.; Shoaib, M.A. Distributed fault detection and isolation in second order networked systems in a cyber–physical environment. ISA Trans. 2020, 103, 131–142. [Google Scholar] [CrossRef]
- Mahmood, A.; Khan, A.Q.; Mustafa, G.; Ullah, N.; Abid, M.; Khan, A.S. Remote Fault-Tolerant Control for Industrial Smart Surveillance System. Math. Probl. Eng. 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Shen, M.; Yan, S.; Zhang, G. A new approach to event-triggered static output feedback control of networked control systems. ISA Trans. 2016, 65, 468–474. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Ma, G.; Pagilla, P.R.; Ge, S.S. Dynamic output feedback asynchronous control of networked Markovian jump systems. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 2705–2715. [Google Scholar] [CrossRef]
- Ye, Z.; Zhang, D.; Cheng, J.; Wu, Z.-G. Event-Triggering and Quantized Sliding Mode Control of UMV Systems Under DoS Attack. IEEE Trans. Veh. Technol. 2022, 71, 8199–8211. [Google Scholar] [CrossRef]
- Mohsen, B.; Jafar, Z. Robust fault-tolerant control for networked control systems subject to random delays via static-output feedback. ISA Trans. 2019, 153–162. [Google Scholar]
- Bahreini, M.; Zarei, J.; Razavi-Far, R.; Saif, M. Robust fault-tolerant control of uncertain networked control systems subject to random delays and data packet dropouts. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; Volume 9, pp. 2459–2464. [Google Scholar]
- Zhu, Q.; Lu, K.; Zhu, Y. Guaranteed Cost Fault-Tolerant Control of Double-Fault Networked Control Systems: 304 Piecewise Delay Method. IEEE Trans. Syst. Man Cybern. Syst. 2019, 2019. [Google Scholar] [CrossRef]
- Zhu, Q.; Lu, K.; Zhu, Y. Observer-based feedback control of networked control systems with delays and packet dropouts, Automatica. J. Dyn. Syst. Meas. Control 2016, 59, 194–199. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).