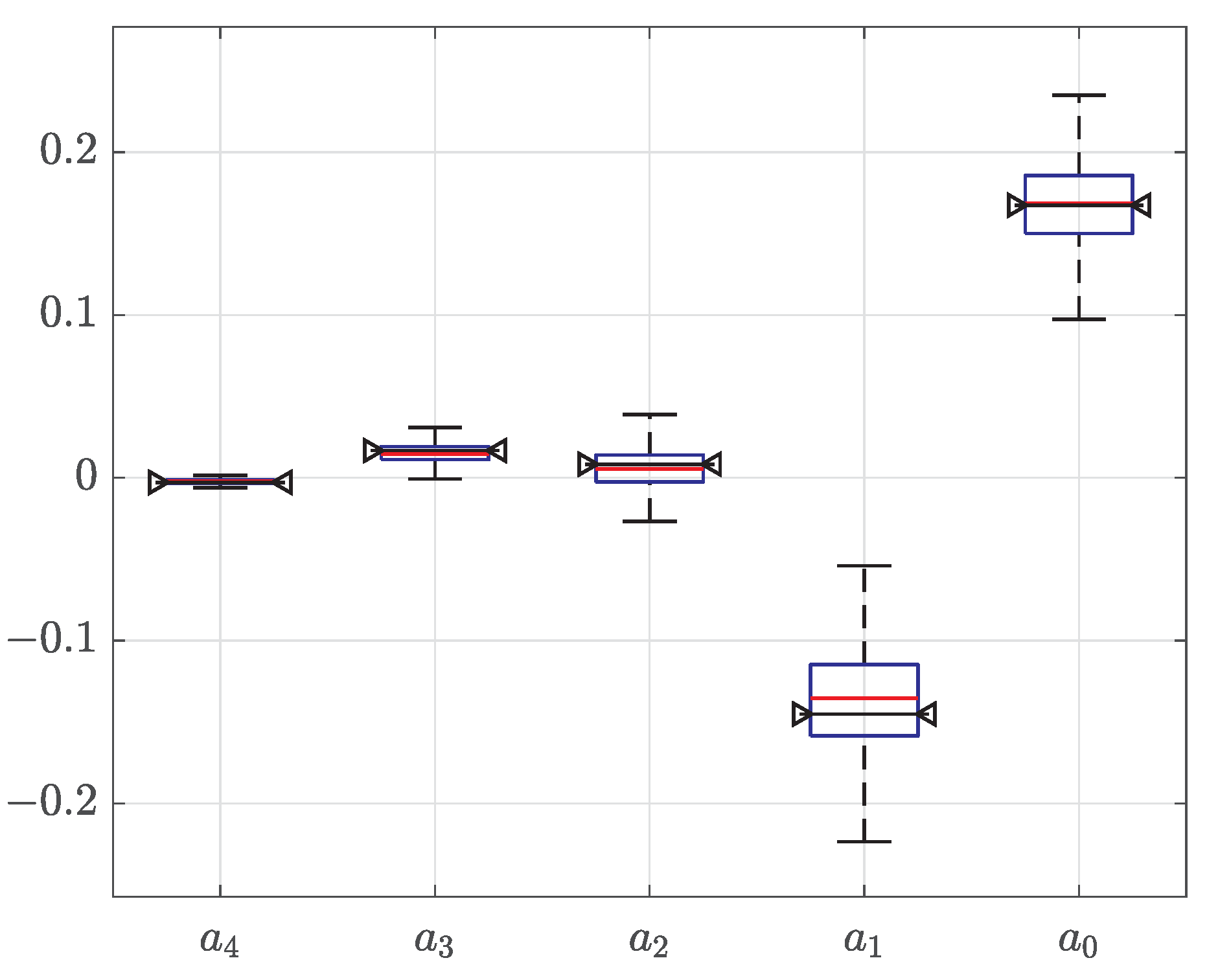Polynomial Distributions and Transformations

Abstract

Polynomials are common algebraic structures, which are often used to approximate functions, such as probability distributions. This paper proposes to directly define polynomial distributions in order to describe stochastic properties of systems rather than to assume polynomials for only approximating known or empirically estimated distributions. Polynomial distributions offer great modeling flexibility and mathematical tractability. However, unlike canonical distributions, polynomial functions may have non-negative values in the intervals of support for some parameter values; their parameter numbers are usually much larger than for canonical distributions, and the interval of support must be finite. Hence, polynomial distributions are defined here assuming three forms of a polynomial function. Transformations and approximations of distributions and histograms by polynomial distributions are also considered. The key properties of the polynomial distributions are derived in closed form. A piecewise polynomial distribution construction is devised to ensure that it is non-negative over the support interval. A goodness-of-fit measure is proposed to determine the best order of the approximating polynomial. Numerical examples include the estimation of parameters of the polynomial distributions and generating polynomially distributed samples.

1. Introduction

Approximating functions is motivated by reducing the computational complexity and achieving the analytical tractability of mathematical models. This also includes the problems of finding low-complexity and low-dimensional mathematical models for continuous or discrete-time observations, such as time-series data, and empirically determined features, such as histograms. This paper is concerned with the latter problem, i.e., how to effectively model the probability distributions of observation data. In particular, it is proposed to define polynomial probability distributions rather than to assume polynomial approximations of probability distributions. This is a major departure from the reasoning found in the existing literature.

Polynomial distributions provide superior flexibility over other canonical distributions, albeit at a cost of a larger number of parameters, and the support interval is constrained to a finite range of values. The main advantages of polynomial distributions are that they can yield parameterized closed-form expressions and enable the modeling of complex multi-modal and time-evolving probability distributions. These distributions are encountered, for example, when describing causal interactions and state transitions in dynamic systems. This may lead to the development of novel probabilistic mathematical frameworks. The disadvantage is that, in the case of a general polynomial function, it may be difficult to ensure that the polynomial is non-negative over the whole intended interval of support. The non-negativity can be guaranteed, for example, by assuming squared polynomials.

The Weierstrass theorem [1] is the fundamental result in the approximation theory of functions. It states that every continuous function can be uniformly approximated with an arbitrary precision over any finite interval by a polynomial of a sufficient order. The uniform approximation can be expressed as a sequence of algebraic polynomials uniformly converging over a given interval to the function of interest. The approximation accuracy can be evaluated by different metrics including $l_p$-norms, minimax norm, and others. The best approximating function from a set or a sequence of functions and its properties can be determined by the Jackson theorem. The Stone–Weierstrass theorem generalizes the function approximation to cases of multivariate functions and functions in multiple dimensions [2].

Runge’s phenomenon arises when the approximating polynomials contain a set of predefined points, which can prevent uniform convergence from being possible [3]. The equidistant approximating points can be optimized using the Lebesgue constant as a measure of the approximation accuracy [4,5].

Polynomials can be used to approximate known probability distributions as well as distributions estimated as histograms [6,7]. Reference [8] is one of the earlier works that assume the approximation of probability distributions by a polynomial. The fitting of multivariate polynomials to multivariate cumulative distributions and their partial derivatives is studied in [9], whereas multivariate polynomial interpolation is studied in [10]. The conditions for the coefficients of a polynomial to be a sum of two squared polynomials are determined in [11].

The problem of fitting a polynomial into a finite number of data samples has been investigated in the classic reference [12]. The polynomial curve fitting methods are often available in various software packages [13]. Modeling times series data by piecewise polynomials is considered in [14,15]. The least-squares polynomial approximation of random data samples with standard and induced densities is compared in [16]. A new method for polynomial interpolation of data points within a plane is proposed in [17]. Interestingly, the recent survey [18] on approximating probability distributions does not mention polynomial approximation as one of the available methods.

The polynomial expansion of chaos for the reliability analysis of systems is proposed in [19]. A polynomial kernel for feature learning from data is considered in [20]. The Stone–Weierstrass theorem is assumed in [21] to design a neural network that can approximate an arbitrary measurable function. The method for function approximation by a polynomial using a neural network is investigated in [22].

Polynomials can be sparse, i.e., only some of their coefficients—including the coefficient determining the order—are non-zero. The polynomials with special properties are named; for example, there are Lagrange, Legendre, Diskson, Chebyshev, and Bernstein polynomials [23,24]. Special polynomials, such as Hermite and Lagrangian polynomials, can form the basis for function decomposition. There is a close link between approximating periodic continuous functions and trigonometric polynomials in the Fourier analysis [25]. A procedure for orthogonal polynomial decomposition of multivariate distributions was devised in [26] in order to compute the output of a multidimensional system with the stochastic input.

Reference [23] is a comprehensive textbook on the theory of polynomials covering fundamental theorems, special polynomials, polynomial algebra, finding and approximating polynomial roots, finding polynomial factors, solving polynomial equations, and defining polynomial inequalities and properties of polynomial approximations. The other textbook [24] includes additional topics, such as critical points of polynomials, the compositions of polynomial functions, theorems and conjectures about polynomials, and defining extremal properties of polynomials. Although the textbook [27] focuses on solving differential equations by polynomial approximations, it also provides a necessary background on polynomials including their definitions and properties. Differential equations are solved by Jacobi polynomial approximation in [28].

The properties of minima and maxima of polynomials were studied in [29]. An algorithm for finding the global minimum of a general multivariate polynomial was developed in [30]. The number of local minima of a multivariate polynomial is bounded in [31]. Sturm series are assumed in [32] to find the maxima of a polynomial.

In this paper, polynomial distributions are introduced in Section 2 including transformations of the polynomial distributions, fitting a histogram with a polynomial distribution, constructing a piecewise polynomial distribution, and defining the basic properties of a random polynomial function. In Section 3, selected properties of the polynomial distributions are derived. The estimation problems involving polynomial distributions and determining the polynomial order are considered in Section 4. Numerical examples are presented in Section 5 including constructing a piecewise polynomial, generating polynomially distributed random samples, estimating parameters of polynomial distributions by the method of moments and by fitting the observations, and approximating distributions by Lagrange interpolation. Section 5 ends with a summary of key findings. The paper is concluded in Section 6. In addition, the key expressions for polynomial functions in Form I, II, and III are summarized in Appendix A, Appendix B and Appendix C, respectively.

The following notations are used in the paper: X denotes a random variable whereas x denotes a specific value of this random variable; ${(·)}^T$ is matrix transpose; ${(·)}^{-1}$ is matrix inverse; the operators, $E\left[·\right]$ and $var\left[·\right]$, denote expectation and variance, respectively; $(·)!$ denotes factorial, $\stackrel{!}{=}$ is used to find a value satisfying the indicated equality, and $〈·,·〉$ denotes the dot-product of two vectors.

2. Defining Polynomial Distributions

Given a continuous and finite interval, $(l,u)$, $-\infty <l<u<+\infty$, the probability density function (PDF), $p\left(x\right)$, of a random variable, X, with the support, $(l,u)$, must satisfy the following two conditions,

$$\begin{array}{cc}\hfill p\left(x\right)& \ge 0,\forall x\in (l,u)\hfill \\ \hfill {\int }_l^{u}p\left(x\right)& dx=1.\hfill \end{array}$$

(1)

Assume that the PDF, $p\left(x\right)$, can be linearly expanded as

$$p\left(x\right)=a_0+\sum _{i=1}^n{a}_i{b}_i\left(x\right)$$

(2)

into the n-dimensional basis of generally non-linear functions, $b_i\left(x\right)$. These functions can also be parameterized as $b_i\left(x\right)\equiv b(x;{\theta }_i)$. Provided that the functions, $b_i\left(x\right)$, are themselves PDFs, i.e., they satisfy the conditions (1), then the PDF (2) is referred to as mixture distribution, and ${\sum }_{i=0}^n{a}_i=1$.

In this paper, the functions, $b_i\left(x\right)=x^i$, are assumed, so that, the expression (2) represents an ordinary univariate polynomial of degree, n. The coefficients, $a_i$, can be a function of another common variable, e.g., $a_i\left(y\right)$, $i=0,1,\dots ,n$; this multivariate polynomial is referred to as algebraic function. The multivariate polynomial having the same degree of a non-zero term is referred to as being homogeneous (formerly a quantic polynomial).

The following three representations of real-valued polynomial functions are considered in this paper.

Definition 1.

$$\begin{array}{ccc}\mathrm{Form}\mathrm{I}:& \hspace{1em}{p}_n\left(x\right)=\sum _{i=0}^n{a}_i{x}^i,& \hspace{1em} a_i\in \mathcal{R},a_n\ne 0\hfill \end{array}$$

(3a)

$$\begin{array}{ccc}\mathrm{Form}\mathrm{II}:& \hspace{1em}{p}_n\left(x\right)=a_n\prod _{i=1}^n(x-r_i),& r_i\in ,a_n\ne 0\hfill \end{array}$$

(3b)

$$\begin{array}{ccc}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{Form}\mathrm{III}:& \hspace{1em}{p}_n\left(x\right)=\sum _{i=1}^n\frac{a_i}{x-r_i},& \hspace{1em} a_i\ne 0,r_i\ne r_j\forall i\ne j\hfill \end{array}$$

(3c)

Form I is a canonical polynomial function. Form II indicates that every n-degree polynomial has exactly n, generally complex-valued, roots $r_i$ [33]. The number of real-valued roots can be determined by Sturm’s theorem. Form III is a rational polynomial function. The basic properties of the polynomial Forms I, II, and III are summarized in Appendix A, Appendix B and Appendix C, respectively, including roots, indefinite and definite integrals, derivatives, general statistical moments, and characteristic or moment-generating functions. Note that every polynomial function, $p_n\left(x\right)$, of any order, n, diverges when its argument, x, becomes unbounded. In addition, Forms I and II are equivalent as shown in Appendix B, and, for complex-conjugate roots, $(x-r_i)(x-r_i^{*})={(x-Re\left(r_i\right))}^2+Im{\left(r_i\right)}^2>0$. Form I defined by (3a) can also be computed recursively as

$$\begin{array}{cc}\hfill p_n\left(x\right)& =(...(((a_{n}x+a_{n-1})x+a_{n-2})x+a_{n-3})...)x+a_0\hfill \\ \hfill & =x{p}_{n-1}\left(x\right)+a.\hfill \end{array}$$

(4)

A Form I or II polynomial, $p_n\left(x\right)$, of degree n and all of its derivatives, $p_n^{\left(k\right)}\left(x\right)=\frac{d^k}{d{x}^k}{p}_n\left(x\right)$, $k\le n$, is continuous and strictly bounded over a finite interval, $x\in (l,u)$. However, the polynomial forms in Definition 1 represent a PDF, if and only if, they satisfy both conditions (1). This can be achieved by using linear and non-linear transformations, which are defined in the following lemma.

Lemma 1.

A polynomial, $p_n\left(x\right)$, can become a PDF by using either of the following transformations.

(a)

There exist finite real constants, A and B, such that the linearly transformed polynomial, $A{p}_n\left(x\right)+B$, satisfies PDF conditions (1).

(b)

There exists a real positive constant, $A>0$, such that the polynomial, $A|p_n\left(x\right)|$, or, $A{\left(p_n\left(x\right)\right)}_{+}$, satisfies PDF conditions (1) where $|·|$ denotes absolute value, and ${(·)}_{+}$ changes the negative values of its argument to zero.

(c)

There exists a low-degree polynomial, $q_k\left(x\right)$, such that the polynomial, $q_k\left(p_n\left(x\right)\right)$, satisfies PDF conditions (1); for instance, $q_1\left(x\right)=Ax+B$ [cf. (a)], or, $q_2\left(x\right)=A{x}^2$, $A>0$.

Proof. 

(a)

Let, $b={min}_{x\in (l,u)}{p}_n\left(x\right)$, so that, $p_n\left(x\right)-b\ge 0$. Then, $A^{-1}={\int }_l^u{p}_n\left(x\right)-bdx$, and, $B=-Ab$.

(b)

For any, x, the functions, $|p_n\left(x\right)|\ge 0$, and, ${\left(p_n\left(x\right)\right)}_{+}\ge 0$. Then, $A^{-1}={\int }_l^u\left|p_n\left(x\right)\right|dx$, or, $A^{-1}={\int }_l^u{\left(p_n\left(x\right)\right)}_{+}dx$, respectively.

(c)

The linear transformation, $q_1\left(x\right)$, was considered in (a). The transformation, $p_n^2\left(x\right)\ge 0$, and, $A^{-1}={\int }_l^u{p}_n^2\left(x\right)dx$.

□

The polynomial PDFs defined in Lemma 1 can be further constrained by the required number of local minima, maxima, and roots within the interval of support, $(l,u)$. There can also be additional constraints on smoothness expressed in terms of the minimum required polynomial order.

By Bolzano’s theorem, a continuous function having opposite sign values in an interval also has a root between these values. Consequently, a polynomial, $p_n\left(x\right)$, of order n have at least one maximum or minimum between every two adjacent roots, and there can be a maximum or minimum located at the roots themselves [29]. Moreover, provided that the polynomial is considered over a finite interval, the boundary points of the support interval should be treated as additional roots, i.e., the boundary points can create local maximum or minimum as well as allow additional extrema to exist before the first nearest root. In the case of Form II polynomials, the condition of the first derivative to be zero can be equivalently expressed as

$$\frac{d}{dx}{p}_n\left(x\right)\stackrel{!}{=}0\iff \frac{d}{dx}log{p}_n\left(x\right)=\frac{{\dot{p}}_n\left(x\right)}{p_n\left(x\right)}=\sum _{i=1}^n\frac{1}{x-r_i}\stackrel{!}{=}0.$$

(5)

However, this approach still requires finding the roots of (5) for every sub-interval, $(r_i,r_{i+1})$, $i=0,1,\dots ,n$, where $r_0\equiv l$ and $r_{n+1}\equiv u$. It may be much easier to find the local extrema by considering the recursion,

$$p_n\left(x\right)=\int p_{n-1}\left(x\right)dx=\sum _{i=0}^{n-1}\frac{a_i}{i+1}{x}^{i+1}+c$$

(6)

provided that the roots of the polynomial, $p_{n-1}\left(x\right)=a_{n-1}{\prod }_{i=1}^{n-1}(x-r_i)$, are known, and, $c=a_0$, denotes the constant of integration. These roots can be known by design, i.e., the locations of minima and maxima are selected a priori in a given interval of support. More importantly, in the case of a polynomial PDF, the local maxima represent the modes of such a distribution.

The Form I polynomial PDF can be generalized as

$$p_n\left(x\right)=\sum _{i=0}^n{a}_i{g}^i\left(x\right),x\in (l,u)$$

(7)

where $g\left(x\right)$ is a mathematical expression (i.e., not a transformation). For instance, it is possible to assume polynomials with fractional rather than integer powers of the independent variable [34].

For $g\left(x\right)=e^{j{\omega }_{0}x}$, $j=\sqrt{-1}$, ${\omega }_0=2\pi /(u-l)>0$, the PDF (7) becomes the truncated exponential Fourier series, i.e.,

$$p_n\left(x\right)=\sum _{i=0}^n{a}_i{e}^{j{\omega }_{0}ix},a_i=\frac{1}{u-l}{\int }_l^u{p}_n\left(x\right)e^{-j{\omega }_{0}ix}dx.$$

(8)

The corresponding k-th general moments are then computed as

$${\int }_l^u{x}^k{p}_n\left(x\right)dx=\sum _{i=0}^n{a}_i{\int }_l^u{x}^k{e}^{j{\omega }_{0}ix}dx=\sum _{i=0}^n{a}_i{(-1)}^k{W}^{\left(k\right)}(j{\omega }_{0}i)$$

(9)

where $W(j\omega )={\int }_l^u{e}^{j\omega x}dx$ is the Fourier transform of a rectangular window located over the interval, $(l,u)$.

For $g\left(x\right)=e^x$, PDF (7) becomes,

$$p_n\left(x\right)=\sum _{i=0}^n{a}_i{e}^{ix},x\in (l,u)$$

(10)

which can be readily integrated, although general statistical moments can only be expressed as special functions.

Consider now the general case of PDF (7), for $n=2$. Thus, given $p_2\left(x\right)$ and $g\left(x\right)$, and positive integers $i_1$ and $i_2$, the task is to find the coefficients $a_0$, $a_1$ and $a_2$ of the PDF decomposition,

$$p_2\left(x\right)=a_2{g}^{i_2}\left(x\right)+a_1{g}^{i_1}\left(x\right)+a_0,x\in (l,u).$$

(11)

Multiplying both sides of (11) by $g^{-i}\left(x\right)\dot{g}\left(x\right)$ and integrating, we obtain,

$${\int }_l^u{p}_2\left(x\right)g^{-i}\left(x\right)\dot{g}\left(x\right)dx=a_2{\int }_l^u{g}^{i_2}\left(x\right)g^{-i}\left(x\right)\dot{g}\left(x\right)dx+a_1{\int }_l^u{g}^{i_1}\left(x\right)g^{-i}\left(x\right)\dot{g}\left(x\right)dx+a_0{\int }_l^{g\left(u\right)}{g}^{-i}\left(x\right)\dot{g}\left(x\right)dx.$$

(12)

Assuming a substitution, $y=g\left(x\right)$, Equation (12) can be rewritten as

$${\int }_{g\left(l\right)}^{g\left(u\right)}{p}_2\left(g^{-1}\left(y\right)\right)y^{-i}dy=a_2{\int }_{g\left(l\right)}^{g\left(u\right)}{y}^{i_2-i}dy+a_1{\int }_{g\left(l\right)}^{g\left(u\right)}{y}^{i_1-i}dy+a_0{\int }_{g\left(l\right)}^{g\left(u\right)}{y}^{-i}dy.$$

(13)

Provided that, $g\left(u\right)=-g\left(l\right)=v$, and $i_1>0$ is an odd-integer, and $i_2>0$ is an even-integer, then, for $i=i_1$ and $i=i_2$, respectively,

$$\begin{array}{cc}\hfill {\int }_{-v}^v{p}_2\left(g^{-1}\left(y\right)\right)y^{-i_1}dy& =a_2\underset{=0}{\underbrace{{\int }_{-v}^v{y}^{i_2-i_1}dy}}+2a_{1}v+a_0\underset{=0}{\underbrace{{\int }_{-v}^v{y}^{-i_1}dy}}\hfill \\ \hfill {\int }_{-v}^v{p}_2\left(g^{-1}\left(y\right)\right)y^{-i_2}dy& =2a_{2}v+a_1\underset{=0}{\underbrace{{\int }_{-v}^v{y}^{i_1-i_2}dy}}+a_0{\int }_{-v}^v{y}^{-i_2}dy\hfill \end{array}$$

(14)

and, therefore,

$$\begin{array}{cc}\hfill a_1& =\frac{1}{2v}\underset{-v}{\overset{v}{\int }}{p}_2\left(g^{-1}\left(y\right)\right)y^{-i_1}dy\hfill \\ \hfill a_2& =\frac{1}{2v}\underset{-v}{\overset{v}{\int }}\left(p_2\left(g^{-1}\left(y\right)\right)-a_0\right)y^{-i_2}dy.\hfill \end{array}$$

(15)

The offset, $a_0$, must be computed from some other constraint, for example, as the minimum value to guarantee a non-negativity of $p_2\left(x\right)$. Note that the function, $g\left(x\right)$, in (11) must be chosen, so the integrals (15) converge.

2.1. Probability Density Transformations

In general, if $g\left(x\right)$ is an invertible transformation of a random variable, X, having the PDF, $p\left(x\right)$, the PDF, $q\left(x\right)$, of random output variable, $g\left(x\right)$, is, [35]

$$q\left(x\right)=\frac{p\left(g^{-1}\left(x\right)\right)}{|\dot{g}\left(g^{-1}\left(x\right)\right)}=p\left(g^{-1}\left(x\right)\right)\left|{\dot{g}}^{-1}\left(x\right)\right|$$

(16)

where $\dot{g}\left(x\right)=\frac{d}{dx}g\left(x\right)$. Assuming $p\left(x\right)$ is a Form I polynomial PDF, $p_n\left(x\right)$, the transformed PDF is also a Form I polynomial, i.e.,

$$q_n\left(x\right)=\left|{\dot{g}}^{-1}\left(x\right)\right|\sum _{i=1}^n{a}_i{g}^{-i}\left(x\right)=\sum _{i=1}^n{a}_i{\left(\frac{\sqrt[i]{|{\dot{g}}^{-1}\left(x\right)|}}{g\left(x\right)}\right)}^i$$

(17)

in the variable, $\sqrt[i]{|{\dot{g}}^{-1}\left(x\right)|}{g}^{-1}\left(x\right)$.

Assuming a linear transformation, $g_1\left(x\right)=b_{1}x+b_0$, the PDF (17) is also a polynomial PDF of the same order, i.e.,

$$q_n\left(x\right)=\sum _{i=1}^n\frac{a_i}{|b_1|b_1^i}{(x-b_0)}^i.$$

(18)

However, the linear transformation changes the support, $(l,u)$ of $p_n\left(x\right)$, to $(b_{1}l+b_0,b_{1}u+b_0)$, if $b_1>0$, and $(b_{1}u+b_0,b_{1}l+b_0)$, if $b_1<0$.

Another example of a non-linear transformation with memory that preserves polynomial form of the resulting distribution is an integrator. In particular, let, $g^{-1}\left(x\right)={\int }_{-\infty }^{x}f\left(u\right)du\equiv F\left(x\right)$, i.e., $g\left(x\right)=F^{-1}\left(x\right)$, such that, $f\left(u\right)\ge 0$, for $\forall u$. Then, substituting into (16), the transformed PDF can be written as

$$q_m\left(x\right)=b_{1}f\left(x\right)p_n\left(b_{1}F\left(x\right)+b_0\right)$$

(19)

where $b_1\ne 0$ and $b_0$ are arbitrary real constants. Provided that $f\left(x\right)$ is a polynomial of order, k, $F\left(x\right)$ is a polynomial of order, $(k+1)$ (cf. Appendix A) and, thus, $m=n(k+1)k$. The family of PDFs with a form similar to (19) are considered in [36], which could be investigated also for our case of the polynomial distributions.

Consider now a general case of a polynomial nonlinear transformation, $g_k\left(x\right)$, and denote as $x_i$, $i=1,2,\dots ,N\left(y\right)$, all the roots of, $g_k\left(x\right)=y$. Then, the PDF (16) is rewritten as

$$q_m\left(y\right)=\sum _{j=1}^{N\left(y\right)}\frac{p_n\left(x_j\left(y\right)\right)}{|\dot{g_k}\left(x_j\left(y\right)\right)|}$$

(20)

i.e., it is a sum of ratios of polynomials, i.e., $q_m\left(y\right)$ is a polynomial of a certain order, m.

Linear and non-linear transformations of a random variable can be used to change the interval of support of its probability distribution. The following Lemma 2 assumes linear transformations to convert the interval of support, $(l,u)$, into $(-1,+1)$ and vice versa. Lemma 3 proposes two transformations on how to convert the interval of support, $(-1,+1)$, to semi-finite or infinite intervals of support, respectively.

Lemma 2.

The interval of support, $(l,u)$, of a PDF, $p\left(x\right)$, is changed to the interval, $(-1,+1)$, by a linear transformation, $\frac{2}{u-l}x-\frac{u+l}{u-l}$, which transforms the PDF, $p\left(x\right)$, to the PDF, $\frac{u-l}{2}p\left(\frac{(u-l)x-(u+l)}{2}\right)$. Furthermore, the linear transformation, $\frac{(u-l)}{2}x+\frac{u+l}{2}$, transforms the PDF, $p\left(x\right)$, with support, $(-1,+1)$, into the PDF, $\frac{2}{u-l}p\left(\frac{2x-(u+l)}{u-l}\right)$, with the interval of support, $(l,u)$.

Proof. 

The linear transformation, $Ax+B$, transforms any PDF, $p\left(x\right)$, into the PDF, ${\left|A\right|}^{-1}p\left(\frac{x-B}{A}\right)$, [35]. □

Lemma 3.

The PDF, $p\left(x\right)$, defined over the finite interval of support, $(-1,+1)$, can be transformed into the PDF, ${(x^2+x+1/4)}^{-1}p\left(\frac{2x-1}{2x+1}\right)$, with semi-infinite support, $(0,+\infty )$, using the non-linear transformation, $\frac{1}{2}\left(\frac{1+x}{1-x}\right)$. Similarly, the non-linear transformation, $\mathrm{atanh}\left(x\right)$, can be assumed to extend the support to all real numbers, for a PDF, $p\left(x\right)$, defined over the support interval, $(-1,+1)$. The transformed PDF becomes ${\cosh }^{-2}\left(x\right)p\left(\tanh \left(x\right)\right)$.

Proof. 

The functions, $g\left(x\right)=\frac{1}{2}\left(\frac{1+x}{1-x}\right)$, and, $g\left(x\right)=\mathrm{atanh}\left(x\right)$, are increasing, i.e., invertible in the interval, $(-1,+1)$. Then, in (20), $N\left(y\right)=1$, the inverse transforms, $\frac{2x-1}{2x+1}$, and, $\tanh \left(x\right)$, and their derivatives, ${(x^2+x+1/4)}^{-1}$, and, ${\cosh }^{-2}\left(x\right)$, respectively. □

Furthermore, there are scenarios when deterministic values, $x\in (l,u)$, are transformed by a polynomial function, $p_n\left(x\right)$, having the random coefficients, $a_i$. The output value of such a transformation,

$$y=p_n\left(x\right)=\sum _{i=0}^n{a}_i{x}^i$$

(21)

is a random variable. Provided that $a_i$ are independent and distributed as $f_{a_i}\left(a_i\right)$, and conditioned on x, the random variable Y is a sum of independent random variables, so its PDF is given by a multi-fold convolution,

$$f_{y|x}\left(y\right|x)=\left(\prod _{i=0}^n\left|x^{-i}\right|\right)f_{a_0}\left(y\right)⊛f_{a_1}(y/x)⊛\cdots ⊛f_{a_n}(y/x^n)$$

(22)

since, $a_i{x}^i$, are distributed as $|x^{-i}|f_{a_i}(y/x^i)$. Furthermore, the conditional mean and variance of Y, respectively, are,

$$E\left[Y|X\right]=\sum _{i=0}^{n}E\left[a_i\right]x^i,\mathrm{and},var\left[Y|X\right]=\sum _{i=0}^{n}var\left[a_i\right]x^{2i}.$$

(23)

Provided that $a_i$ have equal means, then for any n and $x\in (-1,+1)$, $E\left[Y|X\right]>0$, if $E\left[a_i\right]>0$, and $E\left[Y|X\right]<0$, if $E\left[a_i\right]<0$. Note also that, if $a_i$ have equal variances, then the variance of Y is minimized for $x=0$, and, it is equal to, $var\left[Y|X=0\right]=var\left[a_0\right]$.

The bounds for the number of real roots of random but sparse polynomials were provided in [37]. A numerical method for efficiently finding the zeros of complex-valued polynomials of very large orders was developed in [38]. Another method for a rapid root finding of polynomials is presented in [39].

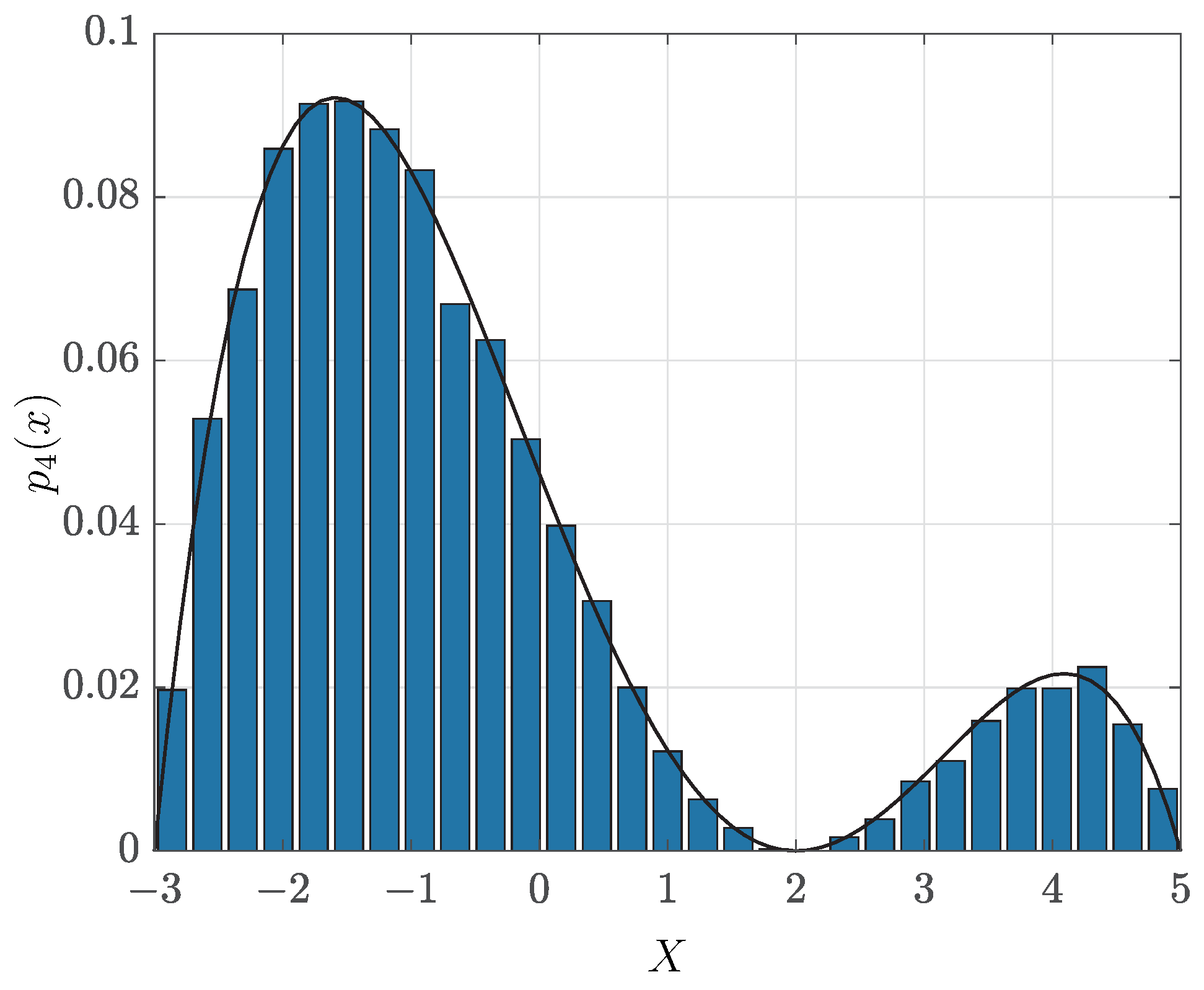
2.2. Polynomial PDF Fit of a Histogram

Approximating a continuous function by a polynomial over a finite interval is formalized by the well-known Weierstrass theorem [1]. Runge’s phenomenon occurs when the approximating function must contain predefined points [3]. The polynomial approximation represents the problems of existence as well as the uniqueness of such a polynomial, and also the problem of how to find it. These problems are crucially dependent on the choice of metric for the goodness of approximation.

Hence, consider the problem of approximating a PDF having the finite support by a polynomial PDF. For instance, the empirical histogram can be fitted by a polynomial function, or a known PDF can be approximated by a polynomial in order to achieve mathematical tractability. However, in neither of these cases, the resulting polynomial is guaranteed to satisfy conditions (1), since the polynomial coefficients are normally chosen to obtain the best fit.

The polynomial PDF can be obtained by assuming a polynomial function, which is non-negative over a given interval for any values of its coefficients. One example of such a polynomial is, $p_n^2\left(x\right)$, which has degree, $2n$. The true PDF, $q\left(x\right)$, can be then approximated as

$$q\left(x\right)\approx p_n^2\left(x\right),\mathrm{or},\sqrt{q\left(x\right)}\approx p_n\left(x\right).$$

(24)

The latter strategy by first transforming $q\left(x\right)$ with a square root is numerically more stable. Other invertible transformations of $q\left(x\right)$ can also be assumed, provided that they yield the non-negative polynomial, $p_n\left(x\right)$, since scaling $p_n\left(x\right)$ to have a unit area usually does not affect the approximation error significantly.

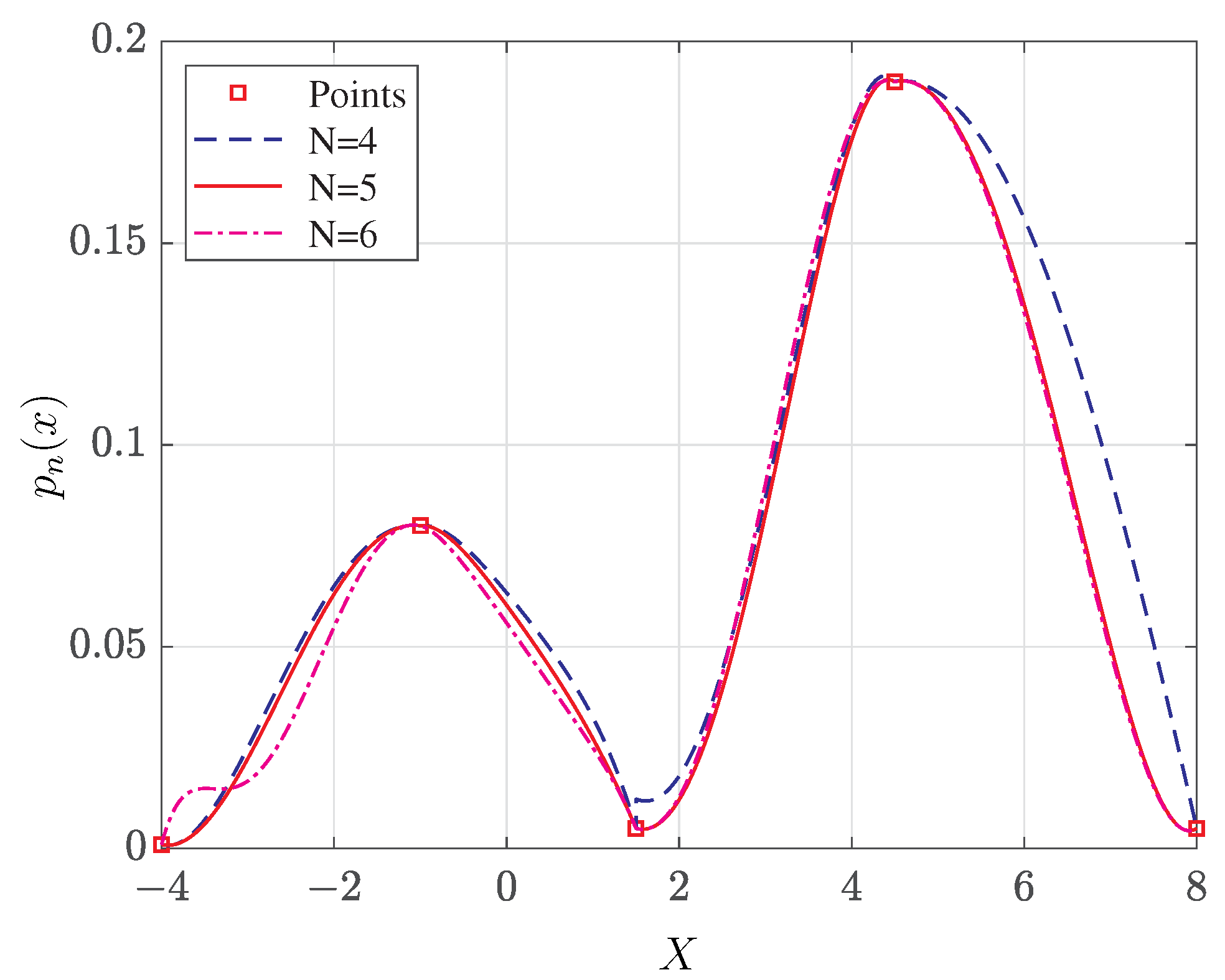
For instance, the data points, $(x_i,\sqrt{y_i})$, $l\le x_i\le u$, $i=1,2,\dots ,M$, can be interpolated by Lagrange polynomials [5],

$$L_i\left(x\right)=\prod _{\genfrac{}{}{0pt}{}{j=1}{i\ne j}}^M\frac{x-x_i}{x_i-x_j}.$$

(25)

Then, the true PDF, $p\left(x\right)$, is approximated as

$$p\left(x\right)\approx {\left(\sum _{i=1}^M\sqrt{y_i}{L}_i\left(x\right)\right)}^2\equiv q_{2(M-1)}\left(x\right)$$

(26)

which is a polynomial of order, $2(M-1)$. In order to normalize the approximation (26), let,

$$c_{ij}=\prod _{\genfrac{}{}{0pt}{}{j_1=1}{j_1\ne i}}^M\prod _{\genfrac{}{}{0pt}{}{j_2=1}{j_2\ne j}}^M(x_i-x_{j_1})(x_j-x_{j_2})$$

(27)

and,

$$\begin{array}{cc}\hfill s_{ij}={\int }_l^u{L}_i\left(x\right)L_j\left(x\right)dx& =c_{ij}^{-1}{\int }_l^u\prod _{\genfrac{}{}{0pt}{}{j_1=1}{j_1\ne i}}^M\prod _{\genfrac{}{}{0pt}{}{j_2=1}{j_2\ne j}}^M(x-x_{j_1})(x-x_{j_2})dx\hfill \\ & =c_{ij}^{-1}\sum _{k=0}^{2(M-1)}{a}_k{\int }_l^u{x}^{k}dx=c_{ij}^{-1}\sum _{k=0}^{2(M-1)}\frac{a_k}{k+1}(u^{k+1}-l^{k+1}).\hfill \end{array}$$

(28)

Then, the area is calculated as

$${\int }_l^u{q}_{2(M-1)}\left(x\right)dx=\sum _{i=1}^M\sum _{j=1}^M\sqrt{y_i{y}_j}{s}_{ij}.$$

(29)

The Lagrange polynomials satisfy, $q_{2(M-1)}\left(x_i\right)=y_i$, so they are subject to Runge’s phenomenon [3]. In particular, the approximation error can be estimated as [3],

$$p\left(x\right)-q_{2(M-1)}\left(x\right)=\frac{p^{(M+1)}\left(\tilde{x}\right)}{(M+1)!}\prod _{i=1}^M(x-x_i)$$

(30)

where $l\le \tilde{x}\le u$. Provided that $|p^{(M+1)}\left(x\right)|<\infty$, for $\forall M$, and, $\forall x\in (l,u)$, $q_{2(M-1)}\left(x\right)$ converges uniformly to $p\left(x\right)$, i.e., ${sup}_x|p\left(x\right)-q_{2(M-1)}\left(x\right)|=0$, as $M\to \infty$. The PDF, $p\left(x\right)$, is often only known as a sequence of sample points, $(x_i,y_i)$, so the derivatives, $p^{(M+1)}\left(x\right)$, cannot be determined. However, the approximation can be improved by using Chebyshev or extended Chebyshev points instead of equally spaced points [4].

The most common method for fitting a polynomial to a histogram is a linear regression [40]. Denote the vectors, $\mathit{y}=\left[y_i\right]$, $i=1,2,\dots ,M$, and, $\mathit{a}=\left[a_j\right]$, $j=0,1,\dots ,n$, and the matrix, $\mathit{X}=\left[x_i^j\right]$. The constrained least squares (LS) problem is then formulated as

$$\underset{\mathit{a}}{min}{∥\mathit{y}-\mathit{X}\mathit{a}∥}^2,\text{s.t.}{\mathit{w}}^T\mathit{a}=1$$

(31)

where the weights, $w_i=\frac{1}{i+1}(u^{i+1}-l^{i+1})$, assuming the support interval, $(l,u)$. The first derivative of the corresponding Lagrangian is set equal to zero, and the estimated coefficients, $\widehat{\mathit{a}}$, of the fitting polynomial, $p_n\left(x\right)$, are computed as [41],

$$\begin{array}{cc}\hfill \frac{d}{d\mathit{a}}\mathcal{L}\left(\lambda \right)& =2{\mathit{X}}^T\mathit{X}\mathit{a}-2{\mathit{X}}^T\mathit{y}+\lambda {\mathit{w}}^T\stackrel{!}{=}\mathbf{0}\hfill \\ \hfill \Rightarrow \widehat{\mathit{a}}& ={\left({\mathit{X}}^T\mathit{X}\right)}^{-1}\left({\mathit{X}}^T\mathit{y}+\frac{\lambda }{2}{\mathit{w}}^T\right).\hfill \end{array}$$

(32)

In order to approximate a known continuous distribution, $f\left(x\right)$, over a finite interval, $(l,u)$, representing the full or truncated support of that distribution, the constrained least-squares (32) can be again used assuming the distribution samples, $f(l+{\Delta }_{x}i)$, $i=0,1,\dots$.

If $p_n\left(x\right)$ is the best polynomial fit of a histogram, or of a sampled known PDF, then it must be evaluated whether it is non-negative over the whole support of interest, $(l,u)$, for example, due to Runge’s phenomenon as discussed in Section 2.2. This can be readily and reliably tested by numerically computing the integral, $I_1=Im\left({\int }_l^u\sqrt{p_n\left(x\right)}dx\right)$, or, $I_2={\int }_l^u{p}_n\left(x\right)-\left|p_n\left(x\right)\right|dx$. If $p_n\left(x\right)$ contains negative values within the interval, $(l,u)$, then $I_1\ne 0$, and $I_2<0$, respectively. It is also possible to assume a logarithm instead of the square root in the definition of the integral, $I_1$.

In this case, the polynomial fitted to a histogram contains negative values, a constant, $d>0$, can be added to the observed data points, i.e., $y_i\mapsto \frac{y_i+d/{\Delta }_x}{1+Md}$, where ${\Delta }_x=x_{i+1}-x_i$, and the scaling ensures that, ${\Delta }_x{\sum }_{i=1}^M{y}_i=1$. Correspondingly, the fitted polynomial is also shifted and scaled as $p_n\left(x\right)\mapsto \frac{p_n\left(x\right)+d/{\Delta }_x}{1+dM}$, so ${\int }_l^u{p}_n\left(x\right)dx=1$.

Furthermore, the roots of a polynomial, $p_n\left(x\right)$, can be constrained in order to guarantee that it is non-negative over a finite interval, $(l,u)$. This is formulated in the following theorem.

Theorem 1.

A Form II real-valued polynomial, $p_n\left(x\right)$, of order n with $a_n>0$ and the roots, $r_1\le r_2\le \dots \le r_n$, is non-negative over the interval, $(l,u)$, provided that all its roots satisfy at least one of the following conditions:

(a)

a root has even multiplicity;

(b)

a root has a complex conjugate pair;

(c)

a (real-valued) root is smaller than l;

(d)

a real-valued root has odd multiplicity and is larger than u; the number of such roots must be even.

Proof. 

Form II polynomial is a product of linear functions, $(x-r_i)$. Cases (a), (b), and (c) are trivial. Case (d) is a combinatorial problem. The roots with odd multiplicity cannot be smaller than u. Even if these roots are all larger than u, then their number must be even in order for their negative parts to cancel out for all values smaller than u. □

Corollary 1.

A Form II real-valued polynomial, $p_n\left(x\right)$, of order n with $a_n>0$ and the roots, $r_1\le r_2\le \dots \le r_n$, has negative values in the interval, $(l,u)$, provided that there is an odd-number of real-valued roots with odd multiplicities that are greater than l, or, there is an even number of real-valued roots with odd multiplicities, and at least one root is located between l and u.

Theorem 1 can also be used for Form I polynomials, provided that they are converted to Form II as indicated in Appendix B. Even though the roots cannot be obtained analytically for polynomials of order $n>4$ (Abel-–Ruffini’s theorem), it may be sometimes possible to consider a product, ${\prod }_j{p}_{n_j}\left(x\right)$, of polynomials of orders, $n_j\le 4$, for $\forall j$.

2.3. Piecewise Polynomial PDF

In some applications, a piecewise polynomial curve fitting can be assumed. In particular, the following construction is proposed to fit a set of $(M+1)$ points, $(x_i,y_i)$, $i=1,\dots ,(M+1)$, $x_i<x_{i+1}$, and $y_i\ge 0$, representing local extrema of a histogram, or of a known PDF. The construction yields a piecewise polynomial PDF, $p_n\left(x\right)$, of the same order n, over the interval, $(l,u)$, with $l=x_1$ and $u=x_{M+1}$, such that, exactly, $p_n\left(x_i\right)=y_i$. The data points, $(x_i,y_i)$, are referred to as control points of the piecewise polynomial $p_n$. It should be noted that univariate piecewise polynomial functions are generally referred to as splines, and their control points as knots.

The following construction defines a piecewise polynomial PDF by sample points representing an alternating sequence of local maxima and minima. The points between the subsequent extrema are then interpolated by increasing or decreasing polynomial segments with a defined continuity order between these segments. As long as the minima are non-negative, all segments are non-negative. However, the resulting curve must be normalized, so that it has a unit area, i.e., it is a PDF.

Definition 2.

Let $p_n\left(x\right)$ be piecewise continuous, and composed of M non-overlapping polynomial segments, $q_{\left(i\right)n}\left(x\right)$, i.e.,

$$p_n\left(x\right)=A\sum _{i=1}^M{w}_i{q}_{\left(i\right)n}\left(x\right).$$

(33)

The segments, $q_{\left(i\right)n}\left(x\right)$, are increasing, i.e., $q_{\left(i\right)n}^{\prime }\left(x\right)>0$, over their support intervals, $(x_i,x_{i+1})$. The points, $x_i$, define the local minima and maxima, such that, if $y_i$ is a local minimum, then $y_{i+1}$ is a local maximum and vice versa. The weights, $w_i=+1$, if $y_i$ is a local minimum, and $w_i=-1$, if $y_i$ is a local maximum. The constant, $A>0$, is chosen, so that, $p_n\left(x\right)$, integrates to unity over its interval of support, $(x_1,x_{M+1})$. In addition, a continuity (smoothness) of order C requires that the first C derivatives,

$$\underset{ϵ\to 0^{+}}{lim}{p}_n^{\left(k\right)}(x+ϵ)=\underset{ϵ\to 0^{+}}{lim}{p}_n^{\left(k\right)}(x-ϵ),\forall x\in (x_1,x_{M+1}),and,\forall k=0,1,\dots ,C$$

(34)

which needs to be true at all points of the local minima and maxima, i.e.,

$$\underset{ϵ\to 0^{+}}{lim}{q}_{\left(i\right)n}^{\left(k\right)}(x_{i+1}-ϵ)=\underset{ϵ\to 0^{+}}{lim}{q}_{(i+1)n}^{\left(k\right)}(x_{i+1}+ϵ),i=1,\dots ,M-1.$$

(35)

In order to construct the desired segment polynomials, $q_{\left(i\right)n}\left(x\right)$, consider two increasing polynomials, $u_n\left(x\right)={\sum }_{i=0}^n{a}_i{x}^i$, and, $v_n\left(x\right)={\sum }_{i=0}^m{b}_i{x}^i$, such that, for some $x_0$, the derivatives,

$$\begin{array}{cc}\hfill u_n^{\left(k\right)}\left(x_0\right)& =-v_n^{\left(k\right)}\left(x_0\right),k=0,1,\dots ,C\hfill \\ \hfill \sum _{i=k}^n{a}_i{x}_0^{i-k}& =-\sum _{i=k}^m{b}_i{x}_0^{i-k}\hfill \end{array}$$

(36)

or, in matrix notation,

$$\underset{{\mathit{X}}_C\left(x_0\right)}{\underbrace{\left[\begin{array}{ccccc}{x}_0^n& x_0^{n-1}& \cdots & x_0& 1\\ x_0^{n-1}& x_0^{n-2}& \cdots & 1& 0\\ & \ddots & & \ddots & \\ x_0^{n-C}& \cdots & 1& 0& 0\end{array}\right]}}·\underset{\mathit{a}}{\underbrace{\left[\begin{array}{c}{a}_n\\ a_{n-1}\\ ⋮\\ a_0\end{array}\right]}}=-\left[\begin{array}{ccccc}{x}_0^m& x_0^{m-1}& \cdots & x_0& 1\\ x_0^{m-1}& x_0^{m-2}& \cdots & 1& 0\\ & \ddots & & \ddots & \\ x_0^{m-C}& \cdots & 1& 0& 0\end{array}\right]·\underset{\mathit{b}}{\underbrace{\left[\begin{array}{c}{b}_m\\ b_{m-1}\\ ⋮\\ b_0\end{array}\right]}}.$$

(37)

For $m=n$, Equation (37) can be rewritten as

$${\mathit{X}}_C\left(x_0\right)(\mathit{a}+\mathit{b})=\mathbf{0}$$

(38)

so the coefficients $\mathit{a}$ and $\mathit{b}$ are in the null space of ${\mathit{X}}_C\left(x_0\right)$.

Provided that ${\mathit{a}}_{\left(i\right)}$ denotes the coefficients of $q_{\left(i\right)n}\left(x\right)={\sum }_{i=0}^n{a}_i{x}^i$, it is required that,

$$\begin{array}{cc}\hfill {\mathit{X}}_C\left(x_2\right)({\mathit{a}}_{\left(1\right)}+{\mathit{a}}_{\left(2\right)})& =\mathbf{0}\hfill \\ \hfill {\mathit{X}}_C\left(x_3\right)({\mathit{a}}_{\left(2\right)}+{\mathit{a}}_{\left(3\right)})& =\mathbf{0}\hfill \\ \hfill ⋮& \\ \hfill {\mathit{X}}_C\left(x_M\right)({\mathit{a}}_{(M-1)}+{\mathit{a}}_{\left(M\right)})& =\mathbf{0}.\hfill \end{array}$$

(39)

Note that the matrices, ${\mathit{X}}_C\left(x_i\right)$, are computed assuming the control points, $x_i$.

Given the first vector of coefficients, ${\mathit{a}}_{\left(1\right)}$, the other coefficient vectors, ${\mathit{a}}_{\left(i\right)}$, $i=2,3,\dots ,M-1$, can be computed iteratively using the underdetermined sets of Equation (39). The numerical feasibility of this problem requires that the order, $n\gg C$.

The vector, ${\mathit{a}}_{\left(1\right)}$, must be selected, so that $q_{\left(1\right)n}\left(x_1\right)=y_1$, and, $q_{\left(1\right)n}\left(x_{M+1}\right)=y_{M+1}$, and $q_{\left(1\right)n}\left(x\right)>0$ is C-continuous for $x\in (x_1,x_2)$. Let sample $q_{\left(1\right)n}\left(x\right)$ at K equidistant points between $x_1$ and $x_2$. The coefficients ${\mathit{a}}_{\left(1\right)}$ are then the solution of the quadratic program,

$$\begin{array}{c}min〈{\mathit{a}}_{\left(1\right)},{\mathit{a}}_{\left(1\right)}〉\\ s.t.〈{\mathit{X}}_0\left(x_1\right),{\mathit{a}}_{\left(1\right)}〉=y_1,〈{\mathit{X}}_0\left(x_2\right),{\mathit{a}}_{\left(1\right)}〉=y_2\\ 〈w_1{\mathit{X}}_0{\Delta }_1,{\mathit{a}}_{\left(1\right)}〉>0\end{array}$$

(40)

where ${\mathit{X}}_0\left(x\right)=[x^n,x^{n-1},\dots ,x,1]$, and ${\Delta }_1=(x_2-x_1)/(K-1)$ is the equidistant sampling step. The last condition in (40) enforces $q_{\left(1\right)n}\left(x\right)$ to be approximately increasing between the points $x_1$ and $x_2$. The other coefficients, ${\mathit{a}}_{\left(i\right)}$, $i>1$, are computed similarly to the program (40), but with an additional constraint due to (39). The extended quadratic program to compute these coefficients is defined as

$$\begin{array}{c}min〈{\mathit{a}}_{\left(i\right)},{\mathit{a}}_{\left(i\right)}〉\\ s.t.〈{\mathit{X}}_0\left(x_i\right),{\mathit{a}}_{\left(i\right)}〉=y_i,〈{\mathit{X}}_0\left(x_{i+1}\right),{\mathit{a}}_{\left(i\right)}〉=y_{i+1}\\ 〈w_i{\mathit{X}}_0{\Delta }_i,{\mathit{a}}_{\left(i\right)}〉>0\\ {\mathit{X}}_C\left(x_i\right)({\mathit{a}}_{(i-1)}+{\mathit{a}}_{\left(i\right)})=\mathbf{0}\end{array}$$

(41)

where ${\Delta }_i=(x_{i+1}-x_i)/(K-1)$, and $i=2,3,\dots ,M$.

More importantly, quadratic programs (40) and (41) require that the constraints are sufficiently underdetermined, i.e., $n\gg C$, otherwise, the solution may be difficult to find, or even may not exist. Moreover, the solution is less numerically stable for a linear program than for a quadratic program and, therefore, the quadratic programs should be considered.

3. Derived Characteristics of a Polynomial Distribution

The cumulative distribution function (CDF) can be readily obtained for Form I polynomial PDF as shown in Appendix A, i.e.,

$$\begin{array}{cc}\hfill P_n\left(x\right)& ={\int }_l^x{p}_n\left(v\right)dv=\sum _{i=0}^n\frac{a_i}{i+1}(x^{i+1}-l^{i+1}),x\in (l,u)\hfill \\ \hfill & =x\sum _{i=0}^n\frac{a_i}{i+1}{x}^i-l\sum _{i=0}^n\frac{a_i}{i+1}{l}^i=x{\tilde{p}}_n\left(x\right)-l{\tilde{p}}_n\left(l\right).\hfill \end{array}$$

(42)

Note also that, for symmetric support interval, when $u=-l$, $P_n\left(u\right)={\sum }_{i=0}^n\frac{a_i}{i+1}(u^{i+1}-{(-u)}^{i+1})$, so the normalization of PDF to unity is only affected by even-index coefficients, $a_i$.

In the case of a Form II polynomial PDF, it is best to convert it to Form I first as shown in Appendix B.

The median ($q=1/2$), and more generally, the quantile, $X_q$, of a polynomial distribution is defined as

$$P_n\left(X_q\right)=X_q{\tilde{p}}_n\left(X_q\right)-l{\tilde{p}}_n\left(l\right)\stackrel{!}{=}q,0<q<1.$$

(43)

Denoting, $P_0\left(q\right)=l{\tilde{p}}_n\left(l\right)+q$, the quantile is the unique root of the polynomial, $x{\tilde{p}}_n\left(x\right)-P_0\left(q\right)=a\left(q\right)(x-X_q)$.

The expressions for general moments and characteristic or moment-generating functions are derived in Appendix A, Appendix B and Appendix C, respectively.

The Kullback–Leibler (KL) divergence or relative entropy between two polynomial distributions, $p_n\left(x\right)={\sum }_{i=0}^n{a}_i{x}^i=a_n{\prod }_{i=1}^n(x-r_i)$, and, $q_m\left(x\right)=b_m{\prod }_{j=1}^m(x-s_j)$, is defined as

$$\begin{array}{cc}\hfill \mathrm{KL}(p_n\parallel q_m)& ={\int }_l^u{p}_n\left(x\right)log\frac{p_n\left(x\right)}{q_m\left(x\right)}dx={\int }_l^u\sum _{i=0}^n{a}_i{x}^{i}log\frac{a_n{\prod }_{l=1}^n(x-r_l)}{b_m{\prod }_{j=1}^m(x-s_j)}dx\hfill \\ \hfill & =\sum _{i=0}^n{a}_i{\int }_l^u{x}^i\left(log\frac{a_n}{b_m}+\sum _{l=1}^{n}log(x-r_l)-\sum _{j=1}^{m}log(x-s_j)\right)dx\hfill \\ \hfill & =\sum _{i=0}^n{a}_i\left(\frac{u^{i+1}-l^{i+1}}{i+1}log\frac{a_n}{b_m}+\sum _{l=1}^n{\int }_l^u{x}^{i}log(x-r_l)dx-\sum _{j=1}^m{\int }_l^u{x}^{i}log(x-s_j)dx\right).\hfill \end{array}$$

(44)

The inner integral, ${\int }_l^u{x}^{i}log(x-r_l)dx$, can be expressed in terms of the hypergeometric, ${}_2{F}_1$, functions with the help of, for example, Mathematica software.

Differential entropy of a polynomial distribution, $p_n\left(x\right)$, is defined as

$$\begin{array}{cc}\hfill H\left(p_n\right)& =-{\int }_l^u{p}_n\left(x\right)log{p}_n\left(x\right)dx=-{\int }_l^u\sum _{i=0}^n{a}_i{x}^{i}log{a}_n\prod _{i=1}^n(x-r_i)dx\hfill \\ \hfill & =\sum _{i=0}^n{a}_i\left(\frac{log{a}_n}{i+1}(u^{i+1}-l^{i+1})+\sum _{l=1}^n{\int }_l^u{x}^{i}log(x-r_l)dx\right).\hfill \end{array}$$

(45)

Finally, the sum, $Z=X+Y$, of two independent random variables, X, and, Y, having the polynomial distributions, $p_n\left(x\right)$, and, $q_m\left(y\right)$, respectively, with the same interval of support, $(l,u)$, also has the polynomial distribution, $f_m\left(z\right)$, given by the convolution,

$$\begin{array}{cc}\hfill f_m\left(z\right)& ={\int }_l^u{p}_n\left(x\right)q_m(z-x)dx={\int }_l^u\sum _{i=0}^n{a}_i{x}^i\sum _{j=0}^m{b}_j{(z-x)}^{j}dx\hfill \\ & =\sum _{i=0}^n\sum _{j=0}^m{a}_i{b}_j{\int }_l^u{x}^i{(z-x)}^{j}dx=\sum _{i=0}^n\sum _{j=0}^m{a}_i{b}_j\sum _{k=0}^j\left(\genfrac{}{}{0pt}{}{j}{k}\right)z^{j-k}{\int }_l^u{x}^{i+k}dx\hfill \\ & =\sum _{i=0}^n\sum _{j=0}^m{a}_i{b}_j\sum _{k=0}^j\left(\genfrac{}{}{0pt}{}{j}{k}\right)z^{j-k}\frac{1}{i+k+1}\left(u^{i+k+1}-l^{i+k+1}\right)\hfill \\ & =\sum _{i=0}^n\sum _{j=0}^m\sum _{k=0}^j\left(\genfrac{}{}{0pt}{}{j}{k}\right)\frac{a_i{b}_j}{i+k+1}\left(u^{i+k+1}-l^{i+k+1}\right)z^{j-k}.\hfill \end{array}$$

(46)

4. Estimation Problems Involving Polynomial Distributions

The parameter estimation of the polynomial distributions is subject to the following equality and inequality constraints, respectively,

$$\begin{array}{cc}\hfill {\mathit{a}}^T{\mathit{X}}_0-1& =0\hfill \\ \hfill -{\mathit{a}}^T{\mathit{X}}_k& \le 0,k=1,2,\dots ,K\hfill \end{array}$$

(47)

where the column vectors, ${\mathit{X}}_0=[(u^{i+1}-l^{i+1})/(i+1)]$, and, ${\mathit{X}}_k=\left[{(l+(k-1)(u-l)/(K-1))}^i\right]$, $i=0,1,\dots ,n$. The equality constraint guarantees that the estimated polynomial integrates to unity. The second constraint requires that the estimated polynomial is non-negative at K equidistant points within the interval of support, $(l,u)$. The value of K must be determined empirically.

Consider the problem of estimating the coefficients, $\mathit{a}$, of a polynomial PDF, $p_n(x;\mathit{a})$. For M independent measurements, $x_m$, the likelihood function is,

$$L(\mathit{x};\mathit{a})=\prod _{m=1}^M{p}_n(x_m;\mathit{a})=\prod _{m=1}^M\sum _{i=0}^n{a}_i{x}_m^i=\prod _{m=1}^M{\mathit{a}}^T{\mathit{x}}_m$$

(48)

where the column vector, ${\mathit{x}}_m=\left[x_m^i\right]$, $i=0,1,\dots ,n$. The Karush–-Kuhn-–Tucker (KKT) function representing the constrained maximum (log-) likelihood (ML) estimation is [42],

$$\mathcal{K}(\mathit{a};\mathit{x};\left\{{\mu }_k\right\})=logL(\mathit{x};\mathit{a})+{\mu }_0({\mathit{a}}^T{\mathit{X}}_0-1)+\sum _{k=1}^K{\mu }_k{\mathit{a}}^T{\mathit{X}}_k$$

(49)

where ${\mu }_k\le 0$, and, ${\mu }_k{\mathit{a}}^T{\mathit{X}}_k=0$, for $\forall k\ge 1$. The first vector-derivative of $\mathcal{K}$ by $\mathit{a}$ [41] must be equal to zero, i.e.,

$$\frac{\partial }{\partial \mathit{a}}\mathcal{K}(\mathit{a};\mathit{x};\left\{{\mu }_k\right\})\stackrel{!}{=}\mathbf{0}\iff \frac{\partial }{\partial \mathit{a}}\sum _{m=1}^{M}log\left({\mathit{a}}^T{\mathit{x}}_m\right)=\sum _{m=1}^M\frac{{\mathit{x}}_m^T}{{\mathit{a}}^T{\mathit{x}}_m}=-\sum _{k=0}^K{\mu }_k{\mathit{X}}_k^T.$$

(50)

Expression (50) together with constraint (47) represent the set of $(n+K+2)$ non-linear equations with the same number of unknowns, which must be solved numerically.

The cosine theorem can be assumed instead of logarithm in maximizing (49) and (50), since,

$$\underset{\mathit{a}}{argmax}\prod _{m=1}^M{\mathit{a}}^T{\mathit{x}}_m=\underset{\mathit{a}}{argmax}\prod _{m=1}^M\frac{{\mathit{a}}^T}{∥\mathit{a}∥}\frac{{\mathit{x}}_m}{∥{\mathit{x}}_m∥}=\underset{\mathit{a}}{argmax}\prod _{m=1}^{M}cos{\varphi }_m$$

(51)

where ${\varphi }_m$ is the angle between the vectors $\mathit{a}$ and ${\mathit{x}}_m$. The unconstrained maximization of (51) can be performed using the geometric-arithmetic mean inequality [43]. Specifically, the likelihood (51) is maximized when the coefficient vector, $\mathit{a}$, is aligned with all the observations, ${\mathit{x}}_m$. It can be approximated by assuming that the distances between the normalized vectors, ${\mathit{a}}^T/∥\mathit{a}∥$, and, ${\mathit{x}}_m/∥{\mathit{x}}_m∥$, are constant, for $\forall m$. Then, the estimate is the centroid of observations, i.e., $\widehat{\mathit{a}}=\frac{1}{M}{\sum }_{m=1}^M{\mathit{x}}_m/∥{\mathit{x}}_m∥$.

The estimator complexity can be greatly reduced if constraint (47) is ignored. In this case, the estimated coefficients, $\widehat{\mathit{a}}$, may not satisfy the PDF conditions (1). Assuming that the estimate, $\widehat{\mathit{a}}$, is not too far from the true vector, $\mathit{a}$, the first estimate can be improved by the subsequent estimator,

$$\widehat{\widehat{\mathit{a}}}=\underset{\mathit{a}}{argmin}∥\mathit{a}-\widehat{\mathit{a}}∥s.t.\mathrm{constraints}\left(47\right).$$

(52)

The estimator (52) minimizes the distance between the first estimate, $\widehat{\mathit{a}}$, and the subsequent estimate, $\widehat{\widehat{\mathit{a}}}$, under constraint (47). More importantly, the corresponding set of equations to solve (52) is now linear.

In the sequel, we drop the inequality constraints in (47) since closed-form expressions can be obtained with the equality constraint. For $M=2$, or, equivalently, only two out of M measurements are considered at a time, the ML estimator can be constrained as in (31), i.e.,

$${\widehat{\mathit{a}}}_{12}=\underset{\mathit{a}}{argmax}{\mathit{a}}^T{\mathit{X}}_{12}\mathit{a},\text{s.t.}{\mathit{w}}^T\mathit{a}=1$$

(53)

where ${\mathit{x}}_i=\left[x_i^j\right]$, $j=0,1,\dots ,n$, and ${\mathit{X}}_{12}={\mathit{x}}_1{\mathit{x}}_2^T$ is a $(n+1)\times (n+1)$ square matrix. The first derivative of the corresponding Lagrangian must be equal to zero, i.e., [41]

$$\begin{array}{cc}\hfill & \frac{\partial }{\partial \mathit{a}}\left({\mathit{a}}^T{\mathit{X}}_{12}\mathit{a}+\lambda ({\mathit{w}}^T\mathit{a}-1)\right)\stackrel{!}{=}\mathbf{0}\hfill \\ \hfill & \Rightarrow \mathit{a}=-\frac{\lambda }{2}{\mathit{X}}_{12}^{-1}\mathit{w},\lambda =\frac{-2}{{\mathit{w}}^T{\mathit{X}}_{12}^{-1}\mathit{w}}.\hfill \end{array}$$

(54)

Consequently, the ML estimate is,

$${\widehat{\mathit{a}}}_{12}=\frac{{\mathit{X}}_{12}^{-1}\mathit{w}}{{\mathit{w}}^T{\mathit{X}}_{12}^{-1}\mathit{w}}$$

(55)

and its likelihood is equal to, ${\left({\mathit{w}}^T{\mathit{X}}_{12}^{-1}\mathit{w}\right)}^{-1}$. Finally, the observation pairs, $({\mathit{x}}_1,{\mathit{x}}_2)$, $({\mathit{x}}_3,{\mathit{x}}_4)$, …, are independent, so the final ML estimate is,

$$\widehat{\mathit{a}}=\frac{2}{M}\sum _{i=1}^{M/2}\frac{{\mathit{X}}_{2i-1,2i}^{-1}\mathit{w}}{{\mathit{w}}^T{\mathit{X}}_{2i-1,2i}^{-1}\mathit{w}}.$$

(56)

The Cramer–Rao bound has been defined to lower-bound the covariance matrix of the estimation error, $\widehat{\mathit{a}}-\mathit{a}$, of any unbiased estimator, i.e.,

$$cov\left[\widehat{\mathit{a}}-\mathit{a}\right]\stackrel{E\left[\widehat{\mathit{a}}\right]=\mathit{a}}{=}var\left[\widehat{\mathit{a}}\right]\ge {\mathit{J}}^{-1}\left(\mathit{a}\right)$$

(57)

where $\mathit{J}\left(\mathit{a}\right)$ is the Fisher information matrix. In order to calculate the elements of this matrix, it is better to assume Form II of the polynomial distribution, $p_n(x;\mathit{r})=a_n{\prod }_{i=1}^n(x-r_i)$, and the problem of estimating the parameters, $\mathit{r}$, i.e.,

$$\begin{array}{cc}\hfill {\left[\mathit{J}\right]}_{ij}& =E\left[\left(\frac{\partial }{\partial r_i}log{p}_n(x;\mathit{r})\right)\left(\frac{\partial }{\partial r_j}log{p}_n(x;\mathit{r})\right)\right]\hfill \\ \hfill & =E\left[\left(\frac{\partial }{\partial r_i}log(x-r_i)\right)\left(\frac{\partial }{\partial r_j}log(x-r_j)\right)\right]\hfill \\ \hfill & =E\left[\frac{1}{(x-r_i)}\frac{1}{(x-r_j)}\right]={\int }_l^u{a}_n\prod _{\begin{array}{c}k=1\\ k\ne i,j\end{array}}^n(x-r_k)dx.\hfill \end{array}$$

(58)

The last integral in (58) can be computed by converting the Form II polynomial into Form I.

The coefficients, $\mathit{a}$, can also be estimated by the method of moments [7,44]. In particular, the k-th general moment of a polynomial distribution, $p_n\left(x\right)$, is, (cf. Appendix A)

$${\mathcal{M}}_k={\int }_l^u{x}^k\sum _{i=0}^n{a}_i{x}^{i}dx=\sum _{i=0}^n\frac{a_i}{i+k+1}\left(u^{i+k+1}-l^{i+k+1}\right).$$

(59)

Observing a vector of the first K general moments, $\mathit{M}=\left[{\mathcal{M}}_k\right]$, $k=1,2,\dots ,K$, and pre-computing the matrix, $\mathit{B}=\left[{(i+k+1)}^{-1}(u^{i+k+1}-l^{i+k+1})\right]$, $i=0,1,\dots ,n$, and ignoring non-negativity constraint in (47), the estimation can be again defined as the constrained or unconstrained least-square regression, i.e.,

$$\widehat{\mathit{a}}=\underset{\mathit{a}}{argmin}∥\mathit{M}-\mathit{B}\mathit{a}∥,\text{s.t.}{\mathit{w}}^T\mathit{a}=1$$

(60)

which can be efficiently solved as in (32).

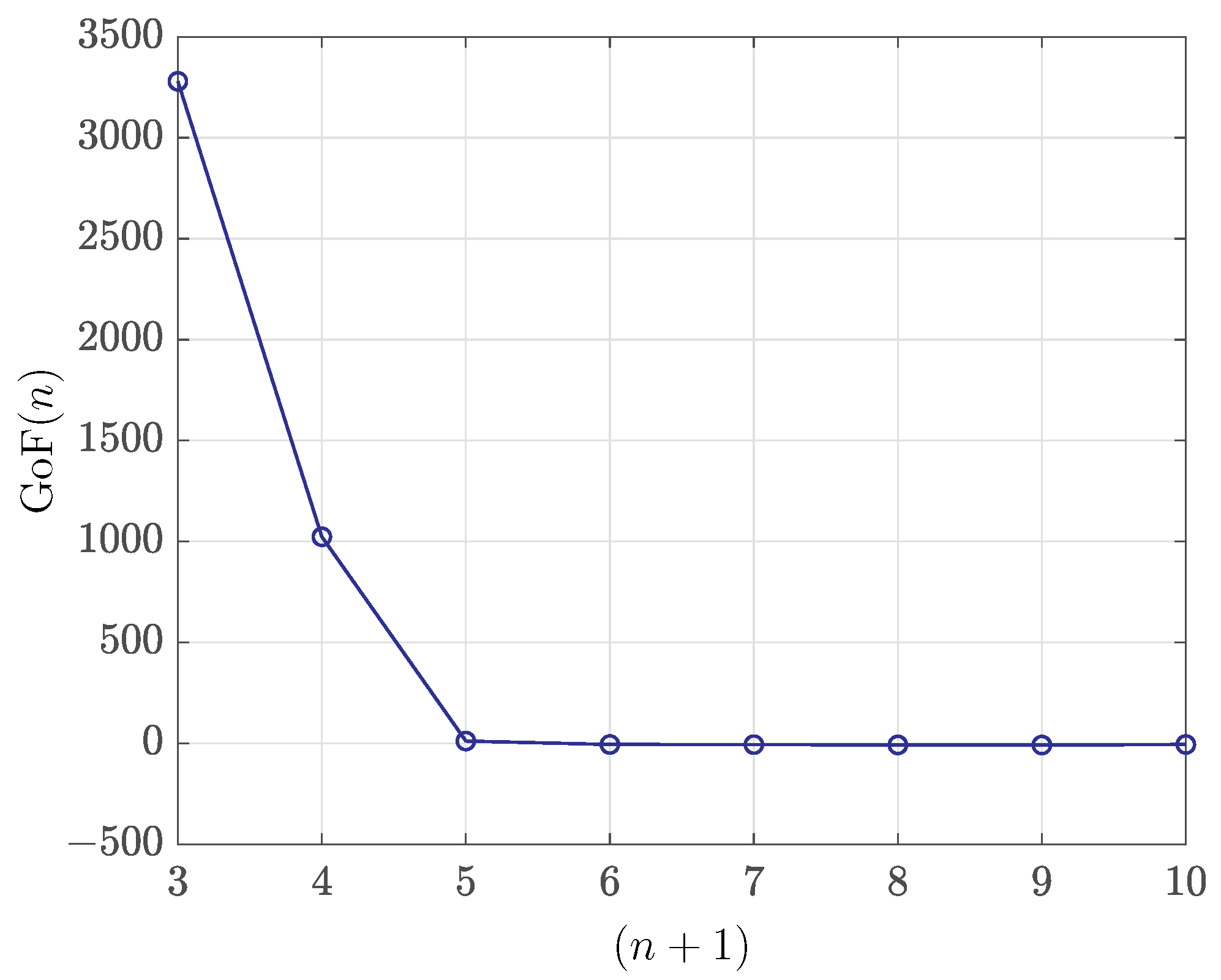
Other Estimation Problems

In addition to estimating the coefficients, $a_i$, of the polynomial distribution, $p_n\left(x\right)$, an important task is to also decide the polynomial order, n. The usual strategy is to estimate a sequence of PDFs, $p_n\left(x\right)$, with increasing orders, $n=n_{min},n_{min}+1,\dots$, and then choose the one minimizing the Akaike information criterion (AIC),

$$\mathrm{AIC}\left(n\right)=2(n+1)-2L(\mathit{x};\mathit{a})$$

(61)

which penalizes the model complexity, $\propto (n+1)$, while maximizing the likelihood L defined in (48).

However, the AIC cannot be used with non-parametric and other likelihood-free estimation methods. In the case of the polynomial distributions, the empirical moments can be readily computed from the observed random samples as well as estimated using the inferred distribution parameters. In particular, denote ${\mathit{M}}_{\mathrm{emp}}\left(\mathit{x}\right)$, the vector of the first K empirical moments. Let, ${\mathit{M}}_{\mathrm{est}}\left(\widehat{\mathit{a}}\right)$ be the vector of the first K moments computed assuming the estimated coefficients of the polynomial distribution, $p_n\left(x\right)$. Similarly to the AIC definition (61), we propose that the goodness of fit (GoF) of a polynomial distribution to observed data can be estimated as

$$\mathrm{GoF}\left(n\right)={∥{\mathit{M}}_{\mathrm{emp}}\left(\mathit{x}\right)-{\mathit{M}}_{\mathrm{est}}\left(\widehat{\mathit{a}}\right)∥}_2^2-n-1.$$

(62)

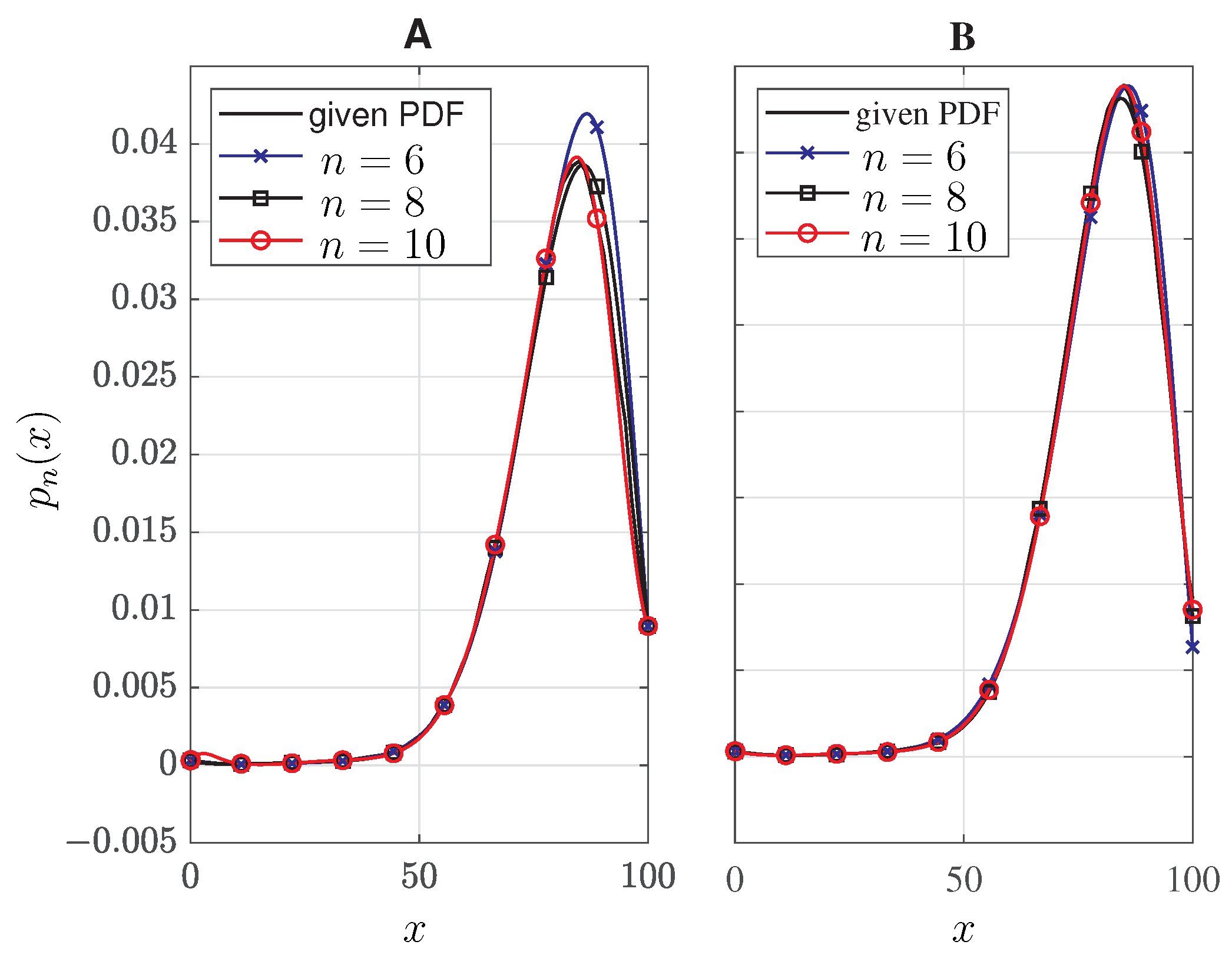
Thus, the squared Euclidean distance between the two-moment vectors is penalized by the number of model coefficients, i.e., $(n+1)$. In our numerical examples, we observed that n should be chosen as the smallest polynomial order causing a sudden significant drop in the value of $\mathrm{GoF}$.

Furthermore, Bayesian estimation methods for estimating the coefficients, $\mathit{a}$, require adopting a prior, $p\left(\mathit{a}\right)$. Since the coefficients are likely to be mutually correlated, defining the prior distribution may be challenging, unless a Gaussian prior can be assumed. On the other hand, consider a general probabilistic model with observations X and a parameter, $\theta$, which is described by the likelihood, $p\left(x\right|\theta )$, and the prior, $p\left(\theta \right)$. If the likelihood and the prior are both polynomially distributed, then the corresponding posterior, $p\left(\theta \right|x)\propto p(x\left|\theta \right)p\left(\theta \right)$, is also polynomially distributed.

Finally, polynomial distributions can also be considered in variational Bayesian inference to approximate the posterior, $p\left(\theta \right|\mathit{x})$, and lower-bound the evidence, $p\left(\mathit{x}\right)$. The parameters of the polynomial distribution can also be inferred without computing the likelihood by assuming the approximate Bayesian computations.

5. Numerical Examples

This section briefly explores the numerical properties of the polynomial distributions by means of several examples, since the practical approximations of functions is a rather extensive subject [45]. The examples are presented in Section 5.1, Section 5.2, Section 5.3 and Section 5.4, including constructing a piecewise polynomial PDF, generating samples of a polynomially distributed random variable, estimating the parameters of a polynomial PDF from observed random samples, and approximating a given PDF by a polynomial PDF.

5.1. Constructing Piecewise Polynomial PDF

The first example in Figure 1 demonstrates the construction of a piecewise polynomial PDF as described in Section 2.3. Given the continuity order $C=2$, the given set of 5 control points can be connected by 4 increasing or decreasing polynomial functions of order $n=5$ or $n=6$. For polynomial orders smaller than 5 or larger than about 8, it was observed that Runge’s phenomenon starts to appear, which indicates that the polynomial order cannot be chosen completely arbitrarily.

5.2. Generating Random Samples Using Polynomial PDF

Consider now the methods how to generate polynomially distributed random samples. Similar to most other distributions, polynomial distributions cannot be easily inverted. It is then challenging to use the inverse method for generating random variables. On the other hand, the CDF of a polynomially distributed random variable is another polynomial as shown in Appendix A. A CDF discretization can be used as a general strategy for implementing the inverse method of generating random samples from the distribution with a known CDF. In particular, consider approximating the CDF by a piecewise linear function between the samples, $(x_i,F\left(x_i\right))$, $i=1,2,\dots$. The inverse value, $X=F^{-1}\left(U\right)$, where $U\in (0,1)$ is a uniformly distributed random variable, is then approximated by a piecewise linear function as

$$x=x_i+\frac{(x_{i+1}-x_i)(u-F\left(x_i\right))}{F(x_{i+1}-F\left(x_i\right))}.$$

(63)

Moreover, polynomial distributions can also be assumed to obtain a proposal distribution for the rejection and importance of sampling methods. Assuming the latter, denote the expected value, $\theta =E_q\left[g\left(x\right)\right]$, assuming a random observation, X, from a complex distribution, $q\left(x\right)$. The mean can be computed by assuming instead the distribution, $p\left(x\right)$, as

$$\theta ={\int }_l^{u}g\left(x\right)\frac{q\left(x\right)}{p\left(x\right)}p\left(x\right)dx=E_p\left[g\left(x\right)\frac{q\left(x\right)}{p\left(x\right)}\right].$$

(64)

The corresponding difference in variances is,

$${var}_q\left[g\left(x\right)\right]-{var}_p\left[g\left(x\right)\frac{q\left(x\right)}{p\left(x\right)}\right]={\int }_l^u{g}^2\left(x\right)\left(1-\frac{q\left(x\right)}{p\left(x\right)}\right)q\left(x\right)dx.$$

(65)

Consequently, the better $p\left(x\right)$ approximates $g\left(x\right)q\left(x\right)$, the larger the variance reduction by sampling from $p\left(x\right)$ instead of $q\left(x\right)$. It is easy to show that, if $p\left(x\right)=g\left(x\right)q\left(x\right)/\theta$, then ${var}_p\left[g\left(x\right)\frac{q\left(x\right)}{p\left(x\right)}\right]=0$. Consequently and importantly, it is likely that the flexibility of the polynomial PDF, $p_n\left(x\right)$, allows approximating $g\left(x\right)q\left(x\right)$ with much better accuracy than any other canonical distribution.

Figure 2 assumes the piecewise polynomial distribution, $p_5\left(x\right)$, designed in the example in Figure 1 in order to generate samples from the target distribution, $q\left(x\right)$. The distribution, $q\left(x\right)$, is chosen to be a mixture of two truncated skewed-Gaussian distributions [46,47]. In particular, the rejection sampling method requires that, $q\left(x\right)\le A{p}_5\left(x\right)$, for some $A>0$ and $\forall x$. Note that the third and the fifth (counting from left) control points were moved slightly above zero in Figure 2 (and already also in Figure 1) in order to satisfy the required inequality.

In the sequel, the examples assume the polynomial PDF,

$$p_4\left(x\right)=\frac{75}{896}\left(-\frac{x^4}{30}+\frac{x^3}{5}+\frac{x^2}{10}-\frac{26x}{15}+2\right),x\in (-3,5).$$

(66)

The random samples from this distribution were generated by discretizing the support interval, $(-3,5)$, into 30 equally sized bins. The distribution and the empirical histogram for ${10}^4$ generated samples are shown in Figure 3.

5.3. Estimating Parameters of Polynomial PDF

Estimating the coefficients of the polynomial PDF must be constrained in order to satisfy the PDF conditions (1). The numerical experiments revealed that ML methods described in Section 4 are generally less suitable for estimating longer vectors of parameters. The ML methods require a relatively large number of observations, which quickly leads to the accumulation of numerical errors. On the other hand, non-parametric methods, such as the method of moments and the LS fitting appear to be much more robust, and they work well, even if the number of observations is relatively small.

Figure 4 shows the absolute error between the PDF (66) and the PDF, ${\widehat{p}}_4\left(x\right)$, estimated using the method of moments with 500 data samples. It can be observed that at least the first $K=5$ moments are required to achieve a good estimation accuracy.

Figure 5 shows the distributions of the estimated coefficients for the PDF (66) using a constrained LS fit of the histogram with 10 bins and 50 data samples. The little triangles at the sides of the boxes in Figure 5 indicate the true values of the coefficients. Interestingly, the smallest accuracy in terms of the largest variance occurs for the lower-order coefficients, $a_1$, and, $a_0$. If the polynomial order, n, is not known a priori, it can be determined by plotting the $\mathrm{GoF}$ measure (62) as shown in Figure 6. It can be observed that the value of $\mathrm{GoF}$ drops sharply when n is increased to 4, and then it remains nearly constant even if n is increased further.

5.4. Approximating PDF by Polynomial PDF

Even if the closed-form expression of a given PDF is available, the expression may be too complex to use in mathematical derivations [46,47]. In this case, a polynomial approximation of the PDF can be assumed. The approximation of a given PDF by a polynomial PDF is studied in Figure 7. In particular, Figure 7 compares the ordinary (unconstrained) LS fit (panel A), and the constrained LS fit (panel B) in order to satisfy the PDF constraints (1). It can be observed that assuming the constraints suppresses Runge’s phenomenon. However, in all cases considered, the polynomial PDF struggles to approximate the peak value of the given PDF, even when the polynomial order is increased.

Finally, the approximation of a given PDF by Lagrange polynomials defined in Section 2.2 is investigated in Figure 8. Recall that Lagrange approximation is an interpolating polynomial function having the order given by the number of sampling points. Specifically, the left panel (A) in Figure 8 assumes equidistant sampling points, whereas the right panel (B) in Figure 8 shows the approximations with Chebyshev sampling points [4]. It can be observed that the latter case is clearly more accurate including the peak of the given PDF. More importantly, for the PDF example in Figure 8, the polynomial PDF approximation consisting of Lagrange polynomials is much easier to compute than performing the constrained LS curve fitting or using other statistical estimation methods, such as the method of moments.

5.5. Summary of Observations

In general, the ML estimation of a vector of parameters of a polynomial distribution becomes numerically problematic when the polynomial orders are larger than only about 2 (and because numerical errors quickly accumulate with the number of observations). On the other hand, non-parametric and likelihood-free methods appear to be much more robust and numerically stable. For instance, the method of moments and the constrained LS fit can estimate the parameters of polynomial distributions efficiently, even if the number of observations is relatively small.

It is always useful to inspect the estimated polynomial coefficient values since some of those values can be near zero. The corresponding coefficients can then be rounded to zero, i.e., removed. Provided that these coefficients are the ones with the largest indices, the order of the estimated polynomial is reduced.

If the likelihood is not computed, the AIC cannot be used to determine the best polynomial order. In this paper, we propose defining the goodness of the polynomial fit as the squared Euclidean distance between the empirical and estimated general moments, which are penalized by the number of parameters to be estimated.

The Lagrange interpolation yields a polynomial function of the same order as the number of distribution samples. This method is usually less accurate when the samples are equidistant. Better accuracy can be achieved with Chebyshev or extended Chebyshev samples. Consequently, the bins of a histogram should be optimized rather than assumed with equal sizes in order to improve the interpolation accuracy.

In some cases, Runge’s phenomenon can be avoided or mitigated by extending the given finite support interval with zero samples since oscillations of the approximating function tend to concentrate near the approximation interval boundaries.

6. Conclusions

Polynomials are often used for approximating univariate and multivariate functions, including probability distributions in order to enable mathematical tractability and simulation efficiency. This paper defined polynomial distributions, which can also be used to approximate other canonical and empirically estimated distributions over a finite interval of support. Polynomial distributions can be considered as more flexible alternatives to commonly used canonical distributions. More importantly, in this paper, many key properties, as well as limitations of the polynomial distributions, were derived and presented as closed-form expressions.

There is a need for defining a family of distributions, such as polynomial distributions that can be used more universally for solving problems in probability, statistics, and data analysis. The polynomial distributions considered in this paper are univariate and continuous; the extension to multivariate and discrete polynomial distributions may be the subject of future work. Polynomials could be generalized as weighted linear sums of non-linear functions in the same variables. A number of research problems remain open. For example, given a polynomial, it would be useful to algebraically identify all sub-intervals where it is non-negative. Or, given a polynomial order and an interval of support, the task is to find all polynomials that represent a PDF. This problem can be further constrained by the desired number of modes, the smoothness and/or sparsity conditions, and assuming other statistical and algebraic properties of the polynomial distributions. Moreover, the problem of determining the minimum polynomial degree or sparsity to satisfy the given constraints was not fully considered in this paper. It would be very useful to investigate how to interpret polynomial distributions, especially as they may arise naturally when observing some stochastic phenomena.