An Analysis of the New Reliability Model Based on Bathtub-Shaped Failure Rate Distribution with Application to Failure Data
Abstract
:1. Introduction
2. NHPP–NPF Model Description
2.1. NHPP-NPF Model Formation
2.2. Model Characteristics
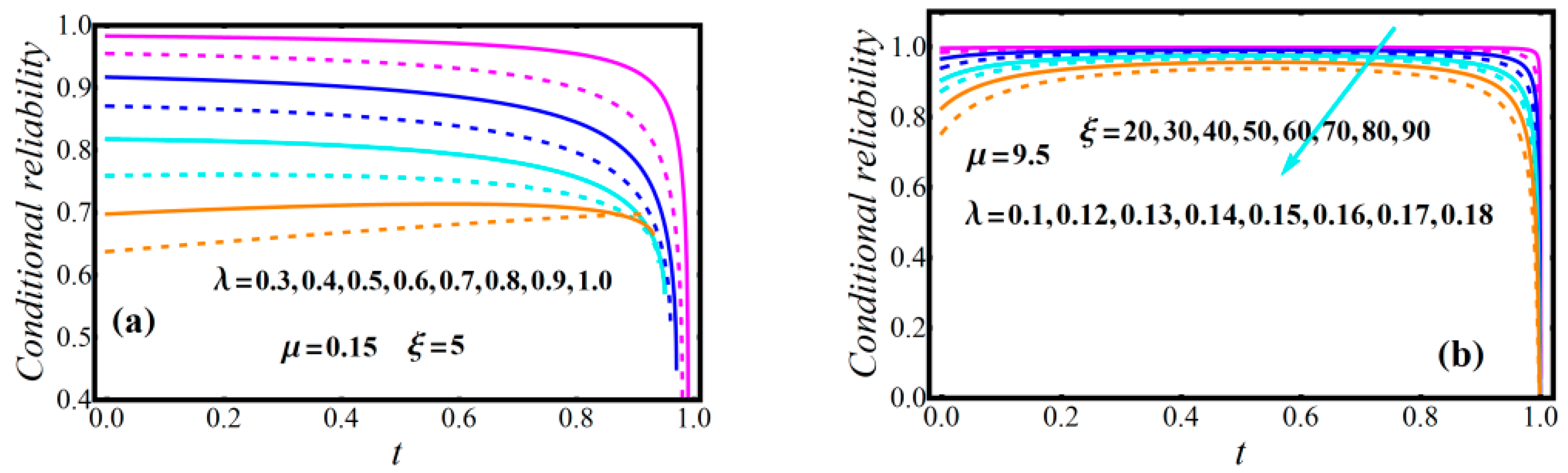
2.3. Diagrams of Model Attributes
3. Estimation Techniques
NLSE, NWLSE and MLE Techniques
4. Performance Evaluation
4.1. Failure Datasets
4.2. Model Performance Measures
- Under all approaches of estimation, the parameter estimates for the suggested model are estimated.
- Mean square error (MSE), the coefficient of determination (R2), predicted relative variation (PRV), and bias are calculated for effective model selection.
- The MVF of the suggested models is examined by comparing the estimation techniques.
- By examining the performance of the suggested model, research information on the ideal model is provided.
5. Results and Discussion
5.1. Evaluation of the Estimation Techniques
- The NHPP–NPF framework supports values that represent a more accurate model for the majority of the evaluation criteria in most situations when utilizing all three approaches.
- The outcomes of the many evaluation criteria varied, which suggests that it is necessary to research multiple criteria when comparing them.
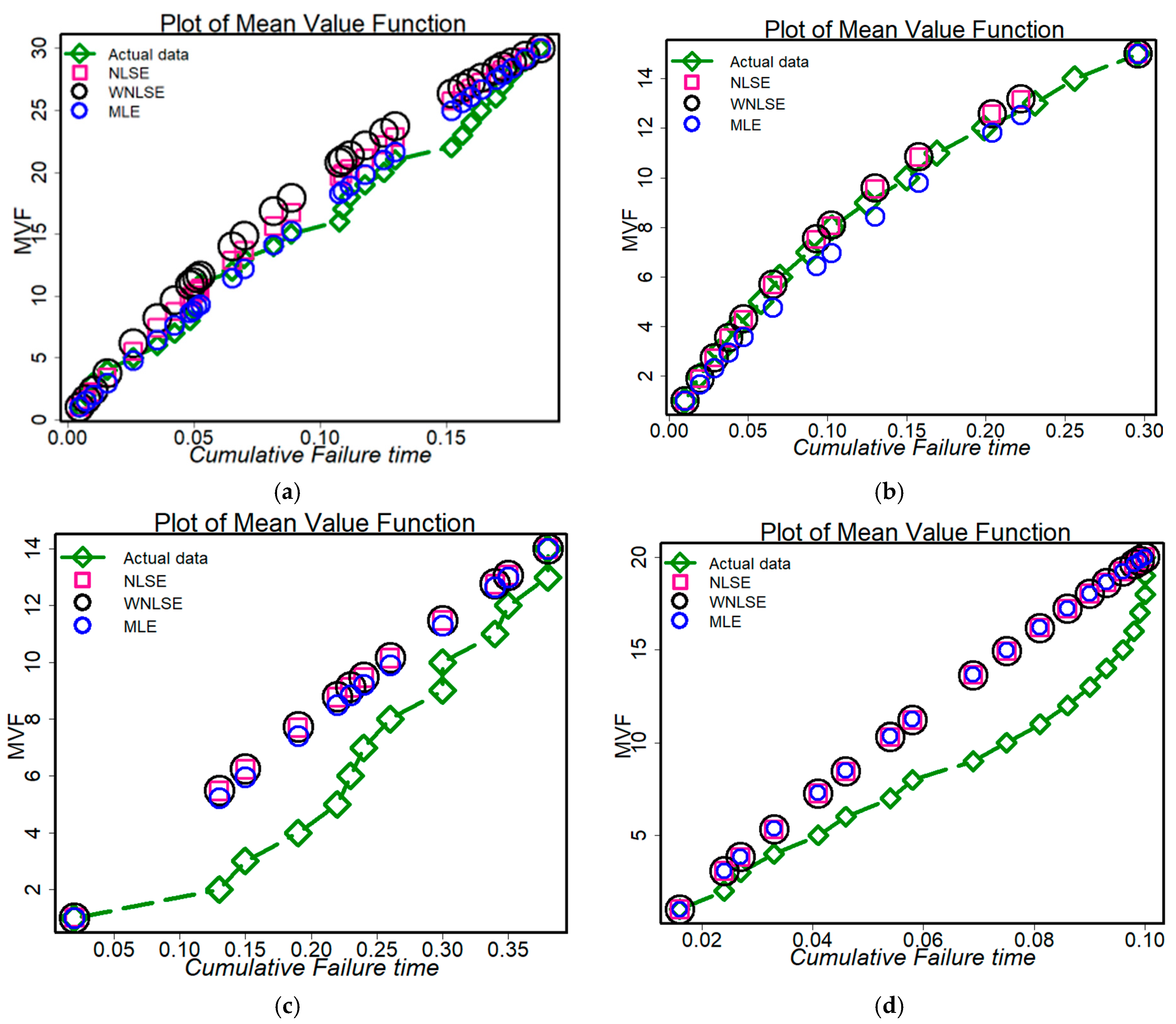
- The actual and fitted curves of software failures using the MLE, NLSE, and WNLSE approaches are shown in Figure 7a–e. These graphs show that our novel model, when applied to the MLE or WNLSE approaches, ensured that all datasets under consideration were well-fitted. In particular, when employing the WNLSE, NLSE, and MLE approaches, the suggested model was better suited for simulating the failure datasets. The suggested model, however, did not perform well when using the NLSE approach for DSI instead of the MLE and WNLSE methods.
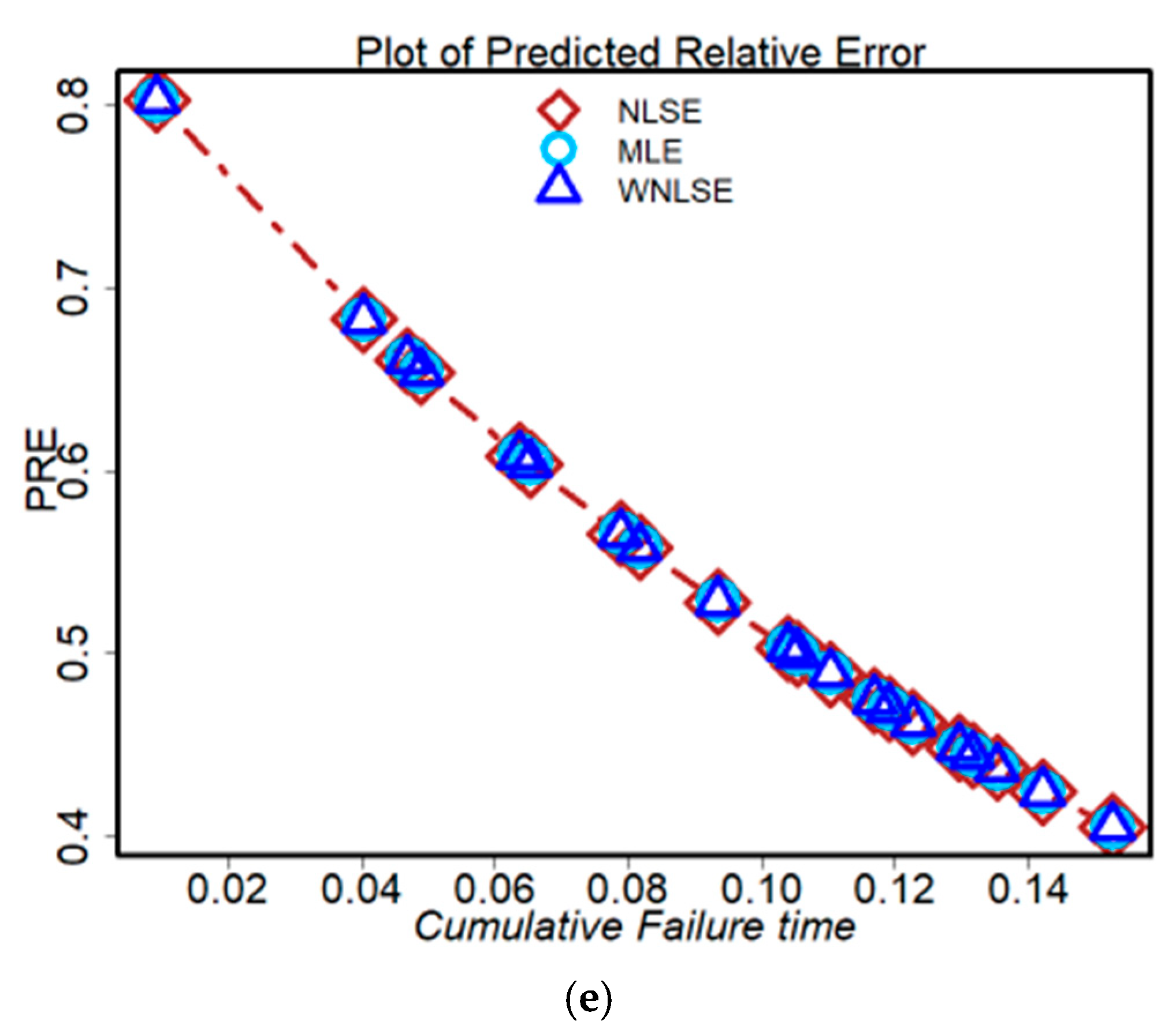
- Figure 8a–e shows the PRE outcomes for our NHPP–NPF model. The similarities among the three approaches may be seen in their early significant estimation error (deviation from zero) and later steadily moving toward observation. This was expected because there were initially few data that could be used to determine the parameters of the models; as time passed and more data became available, the models’ accuracy increased and their PRE decreased until it was zero.
5.2. Performance Evaluation of the SRGMs on Certain Real Datasets
- The MSE values for all investigated models were fairly similar; suggesting that all investigated models could accurately describe the five selected systems with just little variations in performance. The NHPP–NPF model ranked first for all datasets.
- The for all examined models was close to 1. As a result, all examined models are appropriate for modeling the software projects under consideration. The NHPP–NPF model positioned second for DSI, while it ranked first for DS2 to DS5.
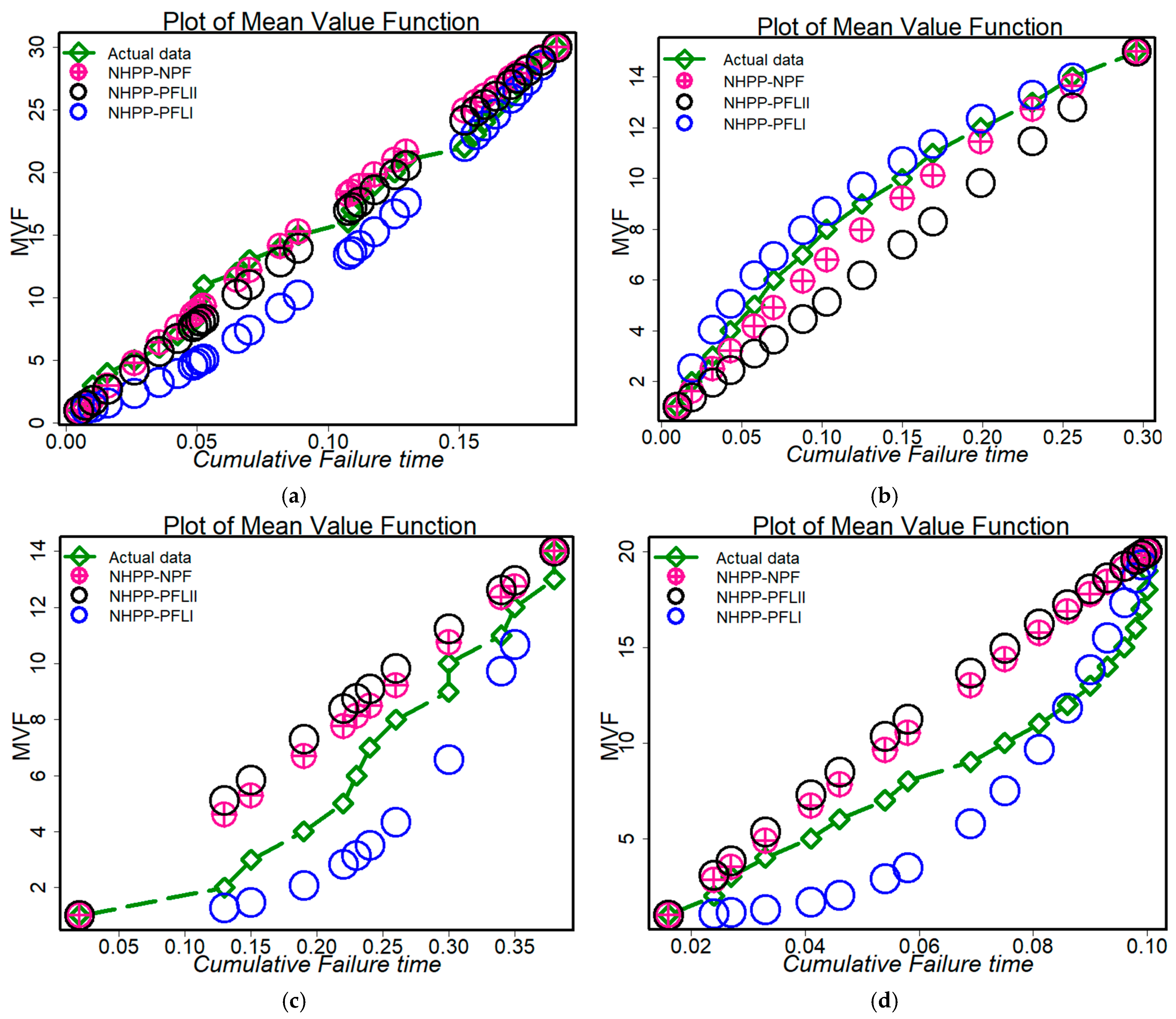
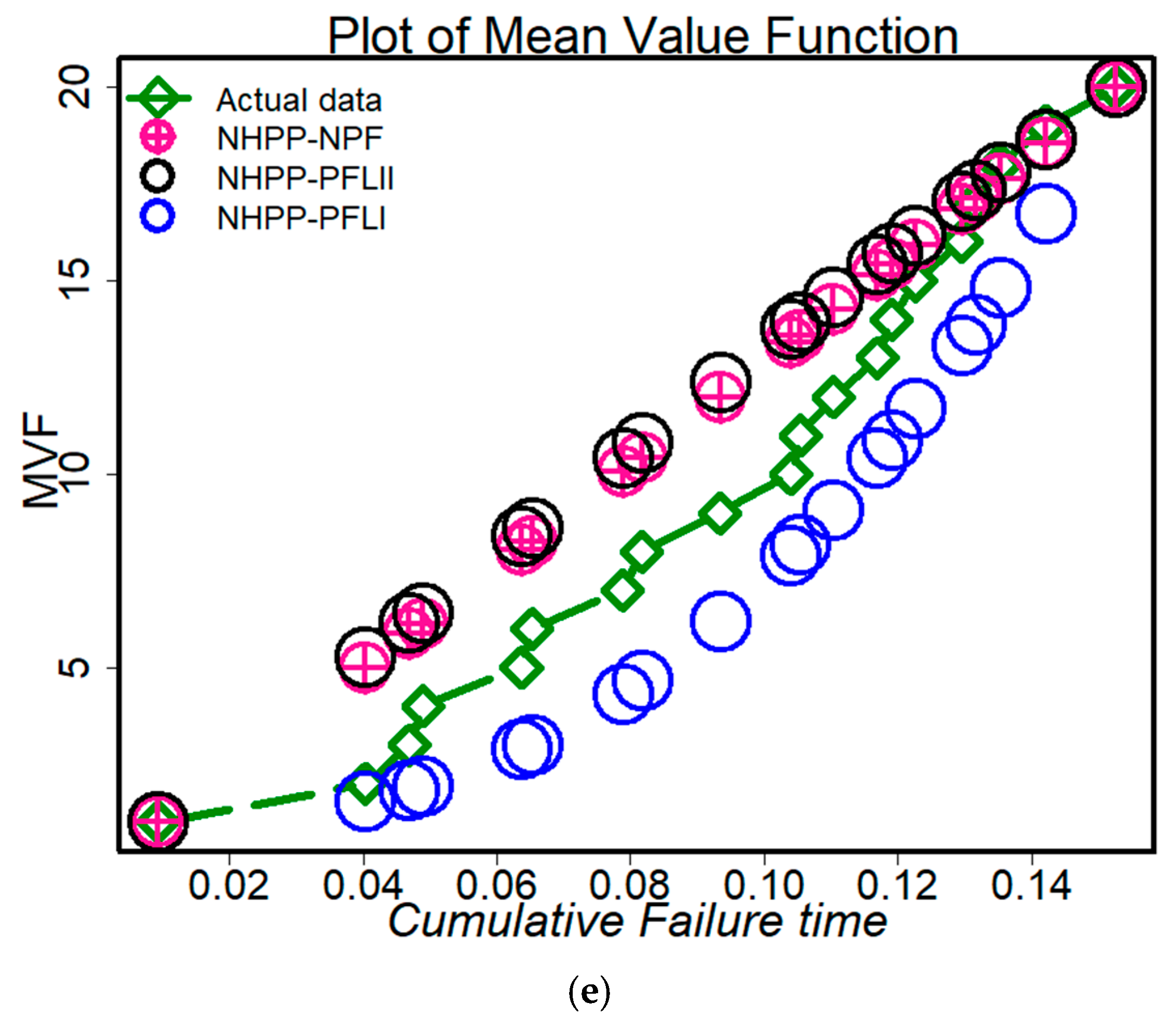
- Figure 9a–e shows the actual and predicted results depending on the four models under consideration. The figures demonstrate how well-fitted each of the chosen models was in analyzing the failure data. Specifically, the suggested model was among the best candidates for modeling the chosen datasets.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gokhale, S.S.; Lyu, M.R.; Trivedi, K.S. Software reliability analysis incorporating fault detection and debugging activities. In Proceedings of the Ninth International Symposium on Software Reliability Engineering (Cat. No. 98TB100257), IEEE, Paddeborn, Germany, 4–7 November 1998; pp. 202–211. [Google Scholar]
- Xie, M. Software Reliability Modelling; World Scientific: Singapore, 1991; Volume 1. [Google Scholar]
- Dalal, S.R.; Mallows, C.L. Some graphical aids for deciding when to stop testing software. IEEE J. Sel. Areas Commun. 1990, 8, 169–175. [Google Scholar] [CrossRef]
- Zeephongsekul, P.; Xia, G.; Kumar, S. Software-reliability growth model: Primary-failures generate secondary-faults under imperfect debugging. IEEE Trans. Reliab. 1994, 43, 408–413. [Google Scholar] [CrossRef]
- Jones, W.D. Reliability models for very large software systems in industry. In Proceedings of the 1991 International Symposium on Software Reliability Engineering, IEEE Computer Society, Austin, TX, USA, 17–18 May 1991; pp. 35–36. [Google Scholar]
- Pham, H. Software Reliability; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Kapur, P.K.; Kumar, S.; Garg, R.B. Contributions to Hardware and Software Reliability; World Scientific: Singapore, 1999; Volume 3. [Google Scholar]
- Gokhale, S.S. Architecture-based software reliability analysis: Overview and limitations. IEEE Trans. Dependable Secur. Comput. 2007, 4, 32–40. [Google Scholar] [CrossRef]
- Wang, W.L.; Hemminger, T.L.; Tang, M.H. A moving average non-homogeneous Poisson process reliability growth model to account for software with repair and system structures. IEEE Trans. Reliab. 2007, 56, 411–421. [Google Scholar] [CrossRef]
- Kapur, P.K.; Xie, M.; Garg, R.B.; Jha, A.K. A discrete software reliability growth model with testing effort. In Proceedings of the 1994 1st International Conference on Software Testing, Reliability and Quality Assurance (STRQA’94), IEEE, New Delhi, India, 21–22 December 1994; pp. 16–20. [Google Scholar]
- Kapur, P.K.; Younes, S.; Agarwala, S. A general discrete software reliability growth model. Int. J. Model. Simul. 1998, 18, 60–65. [Google Scholar] [CrossRef]
- Schneidewind, N.F. Analysis of error processes in computer software. In Proceedings of the International Conference on Reliable Software, Los Angeles, CA, USA, 21–23 April 1975; pp. 337–346. [Google Scholar]
- Xie, M.; Zhao, M. On some reliability growth models with simple graphical interpretations. Microelectron. Reliab. 1993, 33, 149–167. [Google Scholar] [CrossRef]
- Song, K.Y.; Chang, I.H.; Pham, H. A software reliability model with a Weibull fault detection rate function subject to operating environments. Appl. Sci. 2017, 7, 983. [Google Scholar] [CrossRef]
- Kim, H.-C.; Sebuk-gu, S.-e.; Chungcheongnam-do, C.-s. Assessing software reliability based on NHPP using SPC. Int. J. Softw. Eng. Its Appl. 2013, 7, 61–70. [Google Scholar]
- Park, S.K. A Comparative Study on the Attributes of NHPP Software Reliability Model Based on Exponential Family and Non-Exponential Family Distribution. J. Theor. Appl. Inf. Technol. 2021, 99, 5735–5747. [Google Scholar]
- Xu, J.; Yao, S. Software reliability growth model with partial differential equation for various debugging processes. Math. Probl. Eng. 2016, 2016, 2476584. [Google Scholar] [CrossRef]
- Al-Mutairi, N.N.; Al-Turk, L.I.; Al-Rajhi, S.A. A New Reliability Model Based on Lindley Distribution with Application to Failure Data. Math. Probl. Eng. 2020, 2020, 4915812. [Google Scholar] [CrossRef]
- Dohi, X.X.T. On the role of Weibull-type distributions in NHPP-based software reliability modeling. Int. J. Perform. Eng. 2013, 9, 123. [Google Scholar]
- Pham, H. Distribution Function and its Applications in Software Reliability. Int. J. Perform. Eng. 2019, 15, 1306. [Google Scholar] [CrossRef]
- Kim, H.-C. A Study on Comparative Evaluation of Software Reliability Model According to Learning Effect of Exponential-exponential Distribution. Int. J. Eng. Res. Technol. 2020, 3043–3047. [Google Scholar] [CrossRef]
- Hui, Z.; Liu, X. Research on software reliability growth model based on Gaussian new distribution. Procedia Comput. Sci. 2020, 166, 73–77. [Google Scholar] [CrossRef]
- Tae-Jin, Y. A Study on the Reliability Performance Analysis of Finite Failure NHPP Software Reliability Model Based on Weibull Life Distribution. Int. J. Eng. Res. Technol. 2019, 12, 1890–1896. [Google Scholar]
- Yang, T.J. A Comparative study on the Cost and Release Time of Software Development Model Based on Lindley-Type Distribution. Int. J. Eng. Res. Technol. 2020, 13, 2185–2190. [Google Scholar] [CrossRef]
- Kim, H.C.; Moon, S.C. A Study on the Reliability Performance Evaluation of Software Reliability Model Using Modified Intensity Function. J. Inf. Technol. Appl. Manag. 2018, 25, 109–116. [Google Scholar]
- Kim, H.C.; Shin, H.C. The Comparative Study of NHPP Software Reliability Model Based on Exponential and Inverse Exponential Distribution. J. Korea Inst. Inf. Electron. Commun. Technol. 2016, 9, 133–140. [Google Scholar] [CrossRef]
- Li, S.; Dohi, T.; Hiroyuki, O. Burr-type NHPP-based software reliability models and their applications with two type of fault count data. J. Syst. Softw. 2022, 191, 111367. [Google Scholar] [CrossRef]
- Dallas, A. 1. lntroduction Let X be a random variable with distribution function. Ann. Inst. Stat. Math. 1976, 28, 491–497. [Google Scholar] [CrossRef]
- Meniconi, M.; Barry, D.M. The power function distribution: A useful and simple distribution to assess electrical component reliability. Microelectron. Reliab. 1996, 36, 1207–1212. [Google Scholar] [CrossRef]
- Tavangar, M. Power function distribution characterized by dual generalized order statistics. J. Iran. Stat. Soc. 2011, 10, 13–27. [Google Scholar]
- Chang, S.K. Characterizations of the power function distribution by the independence of record values. J. Chungcheong Math. Soc. 2007, 20, 139–146. [Google Scholar]
- Cordeiro, G.M.; dos Santos Brito, R. The beta power distribution. Braz. J. Probab. Stat. 2012, 26, 88–112. [Google Scholar]
- Tahir, M.H.; Alizadeh, M.; Mansoor, M.; Cordeiro, G.M.; Zubair, M. The Weibull-power function distribution with applications. Hacet. J. Math. Stat. 2016, 45, 245–265. [Google Scholar] [CrossRef]
- Jabeen, R.; Zaka, A. Estimation of parameters of the continuous uniform distribution: Different classical methods. J. Stat. Manag. Syst. 2020, 23, 529–547. [Google Scholar] [CrossRef]
- Butt, N.S.; ul Haq, M.A.; Usman, R.M.; Fattah, A.A. Transmuted power function distribution. Gazi Univ. J. Sci. 2016, 29, 177–185. [Google Scholar]
- Iqbal, M.Z.; Arshad, M.Z.; Özel, G.; Balogun, O.S. A better approach to discuss medical science and engineering data with a modified Lehmann Type II model. F1000 Res. 2021, 10, 823. [Google Scholar] [CrossRef]
- Yamada, S.; Ohba, M.; Osaki, S. S-shaped reliability growth modeling for software error detection. IEEE Trans. Reliab. 1983, 32, 475–484. [Google Scholar] [CrossRef]
- Chiu, K.C.; Huang, Y.S.; Lee, T.Z. A study of software reliability growth from the perspective of learning effects. Reliab. Eng. Syst. Saf. 2008, 93, 1410–1421. [Google Scholar] [CrossRef]
- Ishii, T.; Dohi, T.; Okamura, H. Software reliability prediction based on least squares estimation. Qual. Technol. Quant. Manag. 2012, 9, 243–264. [Google Scholar] [CrossRef]
- Sindhu, T.N.; Atangana, A. Reliability analysis incorporating exponentiated inverse Weibull distribution and inverse power law. Qual. Reliab. Eng. Int. 2021, 37, 2399–2422. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, H.W.; Cui, G.; Yang, X.Z. Software reliability growth model with change-point and environmental function. J. Syst. Softw. 2006, 79, 1578–1587. [Google Scholar] [CrossRef]
- Pillai, K.; Nair, V.S. A model for software development effort and cost estimation. IEEE Trans. Softw. Eng. 1997, 23, 485–497. [Google Scholar] [CrossRef]
- Hayakawa, Y.; Telfar, G. Mixed poisson-type processes with application in software reliability. Math. Comput. Model. 2000, 31, 151–156. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Xu, M. Parameter estimation of Jelinski-Moranda model based on weighted nonlinear least squares and heteroscedasticity. arXiv arXiv preprint. 2015, arXiv:1503.00094. [Google Scholar]
- Li, Q.; Pham, H. NHPP software reliability model considering the uncertainty of operating environments with imperfect debugging and testing coverage. Appl. Math. Model. 2017, 51, 68–85. [Google Scholar] [CrossRef]
- Wood, A. Predicting software reliability. Computer 1996, 29, 69–77. [Google Scholar] [CrossRef]
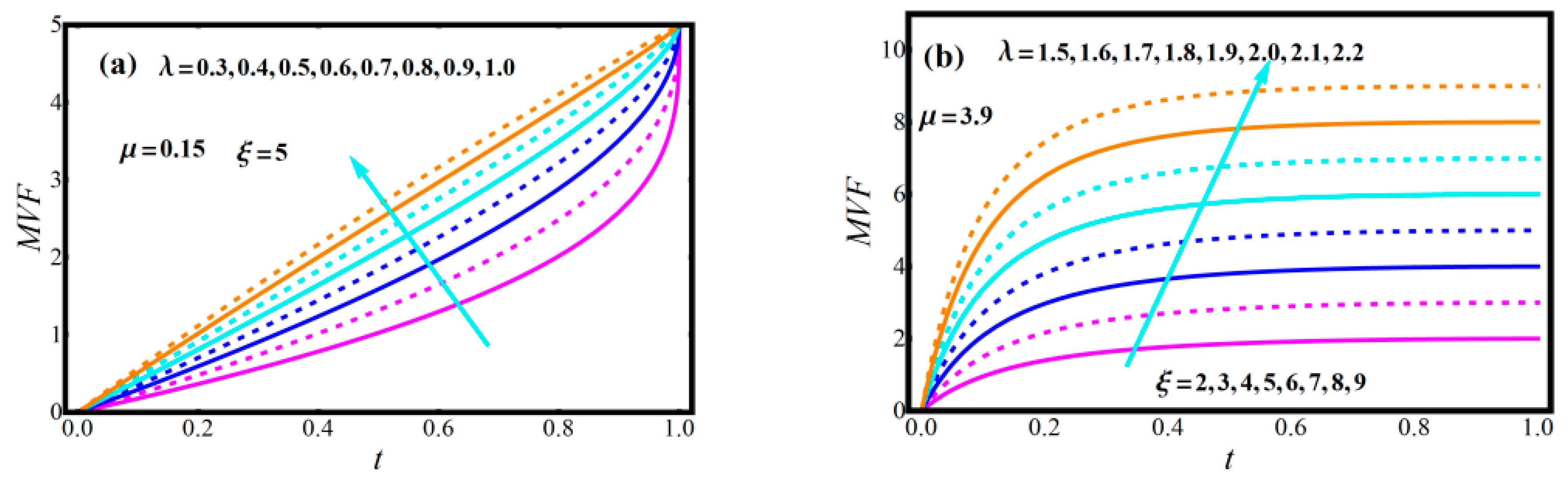


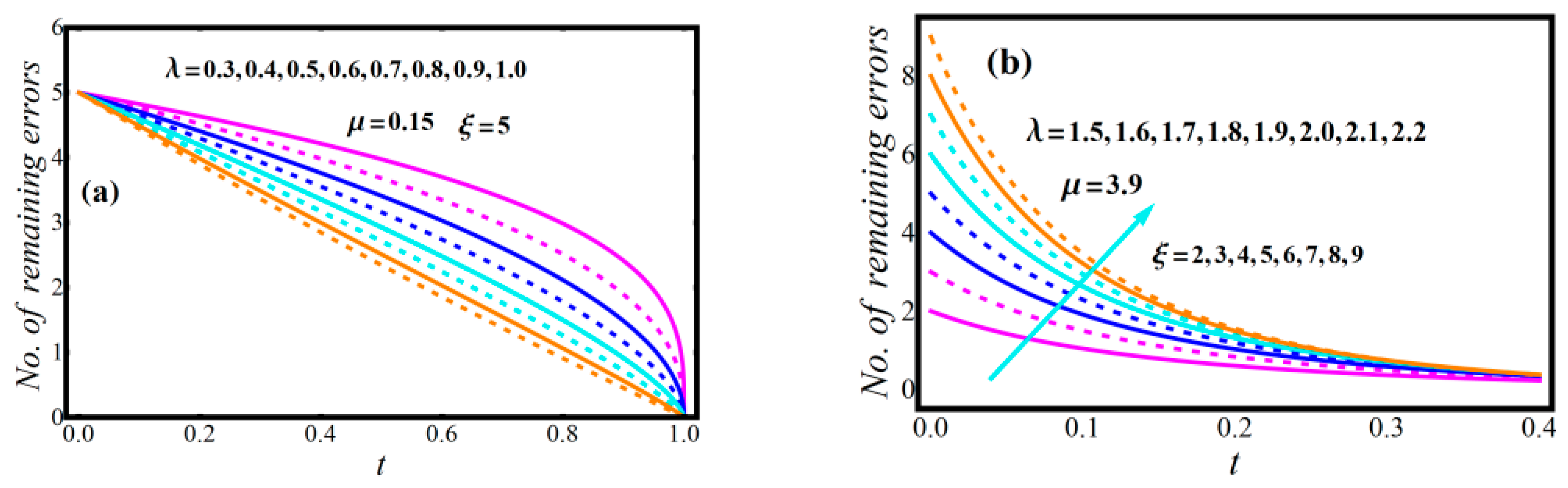
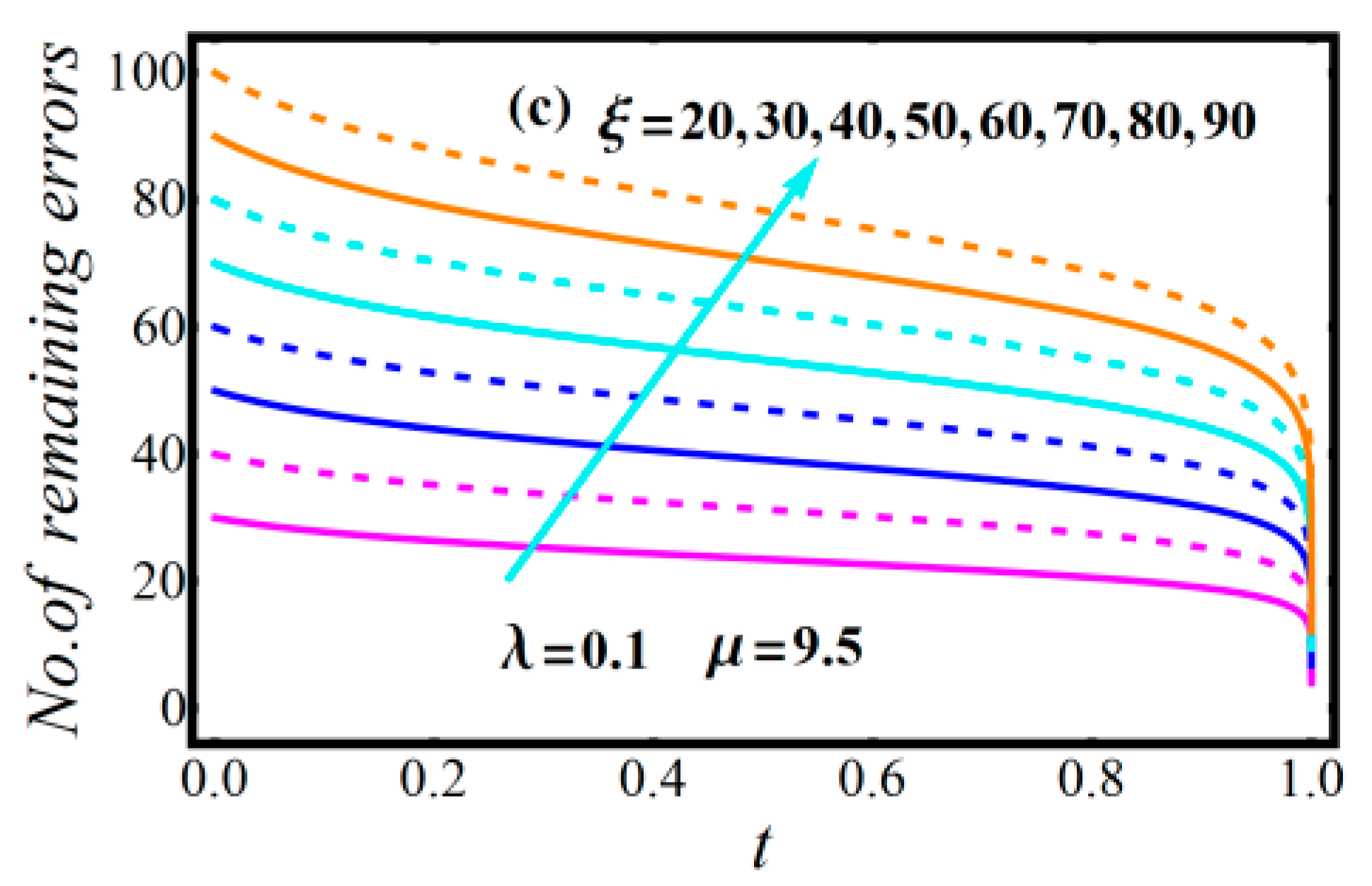
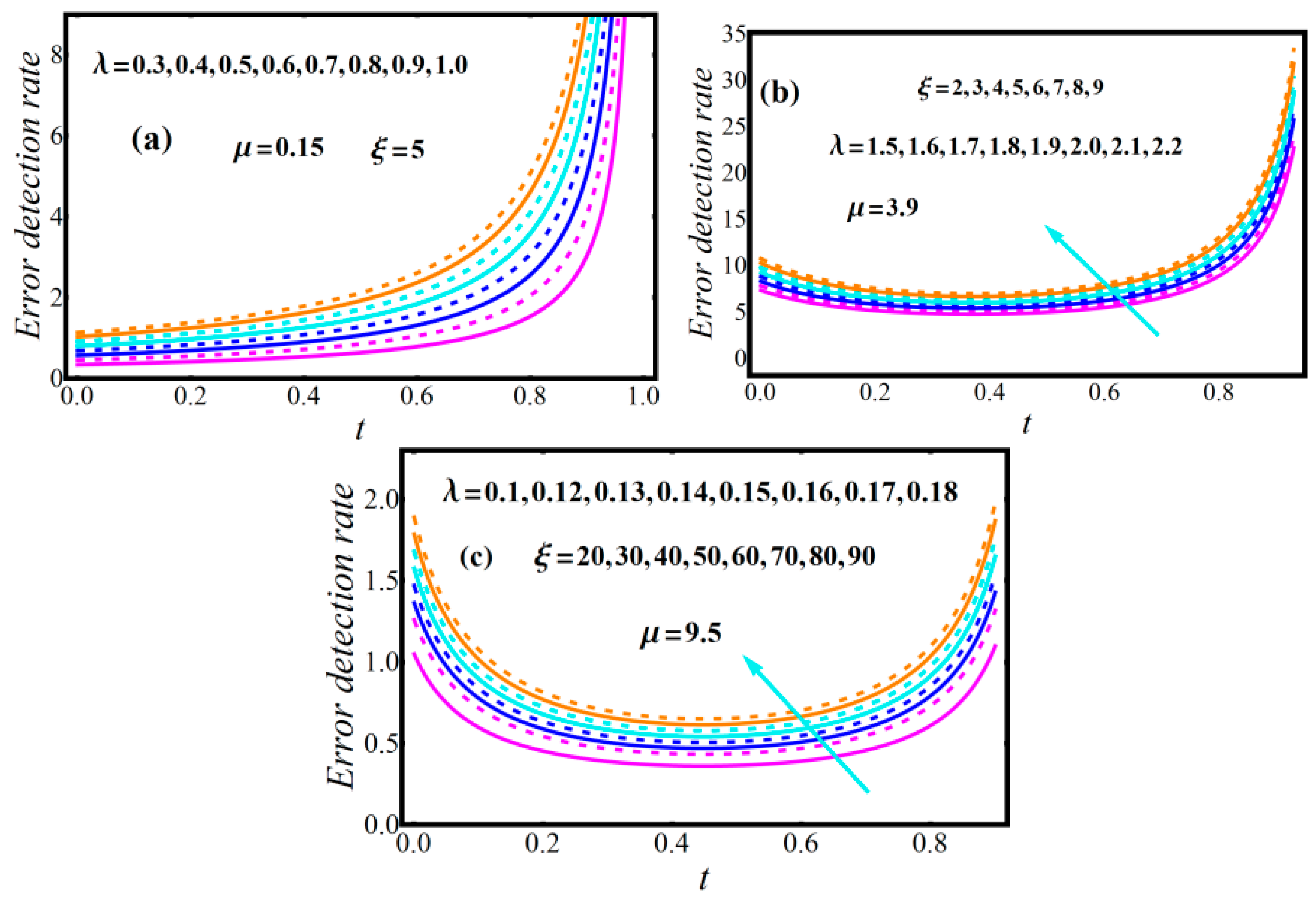



| Dataset | Method of Estimation | Evaluation Criteria | ||||||
|---|---|---|---|---|---|---|---|---|
| MSE | 𝑅-Squared | PRV | Bias | |||||
| DS1 | MLE | 4.5742 | 1.9311 | 0.1297 | 0.0258 | 0.9160 | 0.2957 | 0.1429 |
| NLSE | 2.7767 | 1.1877 | 1.8450 | 0.0132 | 0.5723 | 0.6538 | 0.3134 | |
| WNLSE | 2.7548 | 1.7996 | 1.7997 | 0.0012 | 0.9959 | 0.0602 | 0.0301 | |
| DS2 | MLE | 2.1665 | 2.5853 | 0.2602 | 0.0142 | 0.9373 | 0.2048 | 0.0963 |
| NLSE | 1.7548 | 2.1456 | 1.5465 | 0.0024 | 0.9895 | 0.0849 | 0.0401 | |
| WNLSE | 1.7646 | 2.1458 | 1.5960 | 0.0012 | 0.9947 | 0.0597 | 0.0281 | |
| DS3 | MLE | 1.8977 | 0.7488 | 0.4875 | 0.0008 | 0.9820 | 0.0522 | 0.0250 |
| NLSE | 1.8344 | 0.6999 | 0.9199 | 0.0003 | 0.9945 | 0.0279 | −0.0132 | |
| WNLSE | 1.7910 | 0.7340 | 0.8923 | 0.0004 | 0.9922 | 0.0486 | −0.0161 | |
| DS4 | MLE | 1.7814 | 1.6657 | 1.1161 | 0.0002 | 0.9941 | 0.0223 | 0.0107 |
| NLSE | 1.7999 | 1.6999 | 1.1001 | 2.9 × 10−10 | 1.0000 | 3.1 × 10−5 | 1.4 × 10−5 | |
| WNLSE | 1.8001 | 1.6998 | 1.1000 | 3.4 × 10−10 | 1.0000 | 3.4 × 10−5 | 1.6 × 10−5 | |
| DS5 | MLE | 4.4177 | 1.2913 | 0.4699 | 0.0037 | 0.9642 | 0.1126 | 0.0545 |
| NLSE | 3.7680 | 1.1952 | 1.0991 | 0.0001 | 0.9988 | 0.0202 | 0.0097 | |
| WNLSE | 3.7548 | 1.1752 | 1.0659 | 0.0015 | 0.9858 | 0.0695 | 0.0334 | |
| Criteria | Dataset | PFLII | PFLI | NHPP–NPF |
|---|---|---|---|---|
| DS1 | 0.0414 | 0.0938 | 0.0258 | |
| MSE | DS2 | 0.7098 | 0.0494 | 0.0132 |
| DS3 | 0.0445 | 0.2279 | 0.0008 | |
| DS4 | 0.0342 | 0.0071 | 0.0002 | |
| DS5 | 0.0774 | 0.0334 | 0.0037 | |
| 𝑅-squared | DS1 | 0.9296 | 0.8135 | 0.9160 |
| DS2 | 0.6323 | 0.9355 | 0.9373 | |
| DS3 | 0.8618 | 0.5218 | 0.9820 | |
| DS4 | 0.8766 | 0.9873 | 0.9941 | |
| DS5 | 0.8209 | 0.9372 | 0.9642 | |
| PRV | DS1 | 0.3570 | 0.5284 | 0.2957 |
| DS2 | 1.3944 | 0.3821 | 0.2048 | |
| DS3 | 0.3820 | 0.8151 | 0.0522 | |
| DS4 | 0.3398 | 0.1423 | 0.0223 | |
| DS5 | 0.5135 | 0.3068 | 0.1126 | |
| Bias | DS1 | 0.1679 | −0.2465 | 0.1429 |
| DS2 | 0.6323 | −0.1765 | 0.0963 | |
| DS3 | 0.1802 | −0.3749 | 0.0250 | |
| DS4 | 0.1622 | −0.0654 | 0.0107 | |
| DS5 | 0.2456 | −0.1400 | 0.0545 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sindhu, T.N.; Anwar, S.; Hassan, M.K.H.; Lone, S.A.; Abushal, T.A.; Shafiq, A. An Analysis of the New Reliability Model Based on Bathtub-Shaped Failure Rate Distribution with Application to Failure Data. Mathematics 2023, 11, 842. https://doi.org/10.3390/math11040842
Sindhu TN, Anwar S, Hassan MKH, Lone SA, Abushal TA, Shafiq A. An Analysis of the New Reliability Model Based on Bathtub-Shaped Failure Rate Distribution with Application to Failure Data. Mathematics. 2023; 11(4):842. https://doi.org/10.3390/math11040842
Chicago/Turabian StyleSindhu, Tabassum Naz, Sadia Anwar, Marwa K. H. Hassan, Showkat Ahmad Lone, Tahani A. Abushal, and Anum Shafiq. 2023. "An Analysis of the New Reliability Model Based on Bathtub-Shaped Failure Rate Distribution with Application to Failure Data" Mathematics 11, no. 4: 842. https://doi.org/10.3390/math11040842
APA StyleSindhu, T. N., Anwar, S., Hassan, M. K. H., Lone, S. A., Abushal, T. A., & Shafiq, A. (2023). An Analysis of the New Reliability Model Based on Bathtub-Shaped Failure Rate Distribution with Application to Failure Data. Mathematics, 11(4), 842. https://doi.org/10.3390/math11040842







