On the Exact Evaluation of Integrals of Wavelets

Abstract

Wavelet expansions are a powerful tool for constructing adaptive approximations. For this reason, they find applications in a variety of fields, from signal processing to approximation theory. Wavelets are usually derived from refinable functions, which are the solution of a recursive functional equation called the refinement equation. The analytical expression of refinable functions is known in only a few cases, so if we need to evaluate refinable functions we can make use only of the refinement equation. This is also true for the evaluation of their derivatives and integrals. In this paper, we detail a procedure for computing integrals of wavelet products exactly, up to machine precision. The efficient and accurate evaluation of these integrals is particularly required for the computation of the connection coefficients in the wavelet Galerkin method. We show the effectiveness of the procedure by evaluating the integrals of pseudo-splines.

1. Introduction

A refinable function is defined recursively through a functional equation usually called refinement or scaling equation. In its general form, the refinement equation can be written as [1,2]

$$\mathsf{\Phi }\left(x\right)=\sum _{\alpha \in \mathcal{Z}}{a}_{\alpha }\mathsf{\Phi }(Mx-\alpha ),x\in {\mathbb{R}}^s,$$

(1)

where the compactly supported real sequence $\mathbf{a}=\{a_{\alpha },\alpha \in \mathcal{Z}\}$, $\mathcal{Z}\subset {\mathbb{Z}}^s$, is the refinement mask associated with $\mathsf{\Phi }$ and $M\in {\mathbb{N}}^{s\times s}$ with ${lim}_{k\to \infty }{M}^{-k}=0$ being the dilation matrix. It is known that if

$$\sum _{\alpha \in \mathcal{Z}}{a}_{\alpha }=\left|det\left(M\right)\right|,$$

(2)

then there exists a unique distribution solution to the refinement equation such that $\widehat{\mathsf{\Phi }}\left(0\right)=1$, where $\widehat{\mathsf{\Phi }}$ denotes the Fourier transform of the function $\mathsf{\Phi }$ [1,3].

Refinable functions are the building blocks for the construction of wavelets. In fact, a wavelet $W\left(x\right)$ can be derived by a refinable function as

$$W\left(x\right)=\sum _{\alpha \in {\mathbb{Z}}^s}{d}_{\alpha }\mathsf{\Phi }(Mx-\alpha ),x\in {\mathbb{R}}^s,$$

(3)

where $\mathbf{d}=\{d_{\alpha },\alpha \in {\mathbb{Z}}^s\}$ is the wavelet mask, which can be designed in order to obtain W satisfying prescribed properties [2,4,5,6,7].

Refinable functions and wavelets find applications in several fields. In signal and image processing, they are a well-established tool for constructing filter banks for denoising, compression, feature extractions, to name a few applications [5,6]. In geometric modeling, refinable functions give rise to efficient algorithms for constructing surfaces of arbitrary topology, with applications in industrial design, computer graphics, 3D animation [8,9]. In approximation theory, the refinement functions are used to create nested sequences of approximation spaces that can be used to construct adaptive approximations of operators for the solution of differential problems [10,11,12,13,14].

The analytic expression of refinable functions and associated wavelets is available in only a very few cases. However, they can be evaluated exactly, up to machine precision, at the M-adic points $M^{-k}{\mathbb{Z}}^s$, $k\in {\mathbb{Z}}_{+}$, using recursively Equations (1) and (3), provided that the values on the integers $\mathsf{\Phi }\left(\alpha \right)$, $\alpha \in \mathcal{Z}$, are given. It is well known that the values on the integers of a refinable function and its derivatives can be obtained by solving an eigenvalue/eigenvector problem for a matrix whose entries depend only on the mask [5,15]. The aim of this paper is to describe in detail how to construct this matrix and how to obtain the values of the refinable function and its derivatives from the eigenvectors. Interestingly, the integrals of the product of refinable functions can also be evaluated exactly, up to machine precision, by solving an eigenvalue/eigenvector problem that depends only on the mask [15]. We will show how to construct the eigenvalue problem for these integrals and give some examples. Since a wavelet is a linear combination of the translates of a refinable function (see (3)), integrals of product of wavelets can be easily derived from integrals of refinable functions. We want to emphasize that the exact evaluation of integrals of refinable functions and wavelets is especially important when using adaptive wavelet methods for the solution of differential problems, for instance, for the evaluation of the connection coefficients in the wavelet Galerkin method.

The paper is organized as follows. In Section 2, we recall some basic facts about refinable functions and subdivision schemes. A subdivision scheme is a recursive algorithm constructed from the refinement mask, whose properties are closely related to the properties of the associated refinable function. In this section, we also show how to construct the eigenvalue/eigenvector problem for the exact evaluation of the values of a refinable function and of its derivatives on the integers. The core of the paper is Section 3 where we detail the procedure for the exact evaluation of integrals of products of refinable functions and of their derivatives. As an illustrative example, in Section 4, this procedure is applied to evaluate integrals of pseudo-splines. Finally, in Section 5, we discuss results and conclusions.

2. Materials and Methods

2.1. Refinable Functions and Subdivision Schemes

For the sake of simplicity, we consider the case of dyadic and isotropic dilation factor, i.e., $M=2E$, where E is the identity matrix. Let us denote by ${\mathsf{\Phi }}_{\mathbf{a}}$ the refinable function associated with the mask $\mathbf{a}$. ${\mathsf{\Phi }}_{\mathbf{a}}$ satisfies the refinement equation

$${\mathsf{\Phi }}_{\mathbf{a}}\left(x\right)=\sum _{\alpha \in \mathcal{Z}}{a}_{\alpha }{\mathsf{\Phi }}_{\mathbf{a}}(2x-\alpha ),x\in {\mathbb{R}}^s,$$

(4)

where the refinement mask $\mathbf{a}=\{a_{\alpha },\alpha \in \mathcal{Z}\}$ is a compactly supported real sequence. For details, we refer the reader to the monographs [4,5,6].

The existence of a unique ${\mathsf{\Phi }}_{\mathbf{a}}$ solution to (4), as well as its properties, depend on the properties of the mask $\mathbf{a}$. We recall that a necessary condition for the existence of a unique solution to the refinement Equation (4) with ${\widehat{\mathsf{\Phi }}}_{\mathbf{a}}\left(0\right)=1$ is that the mask $\mathbf{a}$ fulfills the basic sum rules [3]

$$\sum _{\beta \in {\mathbb{Z}}^s}{a}_{\alpha -2\beta }=1,\alpha \in {\mathbb{Z}}^s.$$

(5)

Moreover, if $\mathbf{a}$ is compactly supported, ${\mathsf{\Phi }}_{\mathbf{a}}$ is compactly supported, too, with $supp\left({\mathsf{\Phi }}_{\mathbf{a}}\right)\subseteq ⟨\mathcal{Z}⟩$, where $⟨·⟩$ denotes the convex hull of its argument. In the following, we will assume that ${\mathsf{\Phi }}_{\mathbf{a}}$ is a compactly supported and continuous refinable function.

The existence of a unique ${\mathsf{\Phi }}_{\mathbf{a}}$ with ${\widehat{\mathsf{\Phi }}}_{\mathbf{a}}\left(0\right)=1$ can be related to the convergence of the associated subdivision scheme, which is defined through the refinement mask $\mathbf{a}$ as follows [3,9].

Let $S_{\mathbf{a}}$ be the subdivision operator acting on a sequence $\mathsf{\Lambda }={\left\{{\lambda }_{\alpha }\right\}}_{\alpha \in {\mathbb{Z}}^s}\in {\ell }^{\infty }\left({\mathbb{Z}}^s\right)$ as

$${\left(S_{\mathbf{a}}\mathsf{\Lambda }\right)}_{\alpha }=\sum _{\beta \in {\mathbb{Z}}^s}{a}_{\alpha -2\beta }{\lambda }_{\beta },\alpha \in {\mathbb{Z}}^s.$$

(6)

The subdivision scheme ${\mathcal{S}}_{\mathbf{a}}$ is the recursive application of the subdivision operator starting from an initial sequence ${\mathsf{\Lambda }}^0\in {\ell }^{\infty }\left({\mathbb{Z}}^s\right)$, i.e.,

$${\mathcal{S}}_{\mathbf{a}}:\left\{\begin{array}{c}{\mathsf{\Lambda }}^0=\mathsf{\Lambda }\in {\ell }^{\infty }\left({\mathbb{Z}}^s\right),\hfill \\ \\ \hfill {\mathsf{\Lambda }}^{k+1}:={S_{\mathbf{a}}\mathsf{\Lambda }}^k,k\ge 0.\hfill \end{array}\right.$$

(7)

The subdivision scheme is convergent if for any bounded sequence $\mathsf{\Lambda }\in {\ell }^{\infty }\left({\mathbb{Z}}^s\right)$ there exists a uniformly continuous limit function $f_{\mathsf{\Lambda }}$ satisfying

$$\underset{k\to \infty }{lim}\underset{\alpha \in {\mathbb{Z}}^s}{sup}|{\lambda }_{\alpha }^k-f_{\mathsf{\Lambda }}\left(2^{-k}\alpha \right)|=0,$$

(8)

with $f_{\mathsf{\Lambda }}\ne 0$ for at least a starting sequence. If the subdivision scheme is convergent, there exists a unique refinable function solution to (4) that coincides with the limit function obtained when using the $\delta$ sequence as starting sequence, i.e., 

$${\mathsf{\Phi }}_{\mathbf{a}}=\underset{k\to \infty }{lim}{\delta }^k,$$

(9)

where ${\delta }^k:={S_{\mathbf{a}}\delta }^{k-1}$, $k\ge 1$, with ${\delta }^0=\delta$.

On the other hand, if ${\mathsf{\Phi }}_{\mathbf{a}}$ is ${\ell }^{\infty }$-stable, i.e., the stability estimate

$$C\underset{\alpha \in {\mathbb{Z}}^s}{sup}\left|{\lambda }_{\alpha }\right|\le \underset{x\in {\mathbb{R}}^s}{sup}\left|\sum _{\alpha \in {\mathbb{Z}}^s}{\lambda }_{\alpha }{\mathsf{\Phi }}_{\mathbf{a}}(x-\alpha )\right|$$

(10)

holds for some positive constant C independent of $\mathsf{\Lambda }$, then the subdivision scheme ${\mathcal{S}}_{\mathbf{a}}$ is convergent [3].

Assuming that ${\mathsf{\Phi }}_{\mathbf{a}}\in C^d\left({\mathbb{R}}^s\right)$, by differentiating (4), we obtain the refinement equation for the partial derivatives $D^{\nu }\mathsf{\Phi }\left(x\right)=\frac{{\partial }^{{\nu }_1}}{\partial x_1^{{\nu }_1}}\cdots \frac{{\partial }^{{\nu }_s}}{\partial x_s^{{\nu }_s}}\mathsf{\Phi }(x_1,\dots ,x_s)$, $\nu =({\nu }_1,\dots ,{\nu }_s)\in {\mathbb{Z}}_{+}^s$, i.e.,

$$D^{\nu }{\mathsf{\Phi }}_{\mathbf{a}}\left(x\right)=2^{\left|\nu \right|}\sum _{\alpha \in \mathcal{Z}}{a}_{\alpha }{D}^{\nu }{\mathsf{\Phi }}_{\mathbf{a}}(2x-\alpha ),x\in {\mathbb{R}}^s.$$

(11)

where

$$\left|\nu \right|={\nu }_1+\dots +{\nu }_s\le d.$$

(12)

Derivatives of Univariate Refinable Functions

In the univariate case ($s=1$), the sum rules (5) imply that the mask symbol, i.e., the z-transform

$$a\left(z\right)=\sum _{\alpha \in \mathcal{Z}}{a}_{\alpha }{z}^{\alpha },z\in \mathbb{C},$$

(13)

can be factorized as $a\left(z\right)=2^{-1}(1+z)b\left(z\right)$, where the difference symbol

$$b\left(z\right)=\sum _{\alpha \in \mathcal{Z}}{b}_{\alpha }{z}^{\alpha }$$

(14)

is a Laurent polynomial such that $b\left(1\right)=2$. It can be shown [3,9] that if ${\mathsf{\Phi }}_{\mathbf{a}}\in C^1\left(\mathbb{R}\right)$ is ${\ell }^{\infty }$-stable, then the subdivision scheme ${\mathcal{S}}_{\mathbf{b}}$ associated with the difference mask $\mathbf{b}=\{b_{\alpha },\alpha \in \mathcal{Z}\}$ is convergent and the first derivative of ${\mathsf{\Phi }}_{\mathbf{a}}$ can be easily evaluated by the backward finite difference of ${\mathsf{\Phi }}_{\mathbf{b}}$, i.e.,

$$D^1{\mathsf{\Phi }}_{\mathbf{a}}\left(x\right)={\mathsf{\Phi }}_{\mathbf{b}}\left(x\right)-{\mathsf{\Phi }}_{\mathbf{b}}(x-1),x\in \mathbb{R}.$$

(15)

More generally, if ${\mathsf{\Phi }}_{\mathbf{a}}\in C^d\left(\mathbb{R}\right)$ is ${\ell }^{\infty }$-stable, the symbol can be factorized as $a\left(z\right)=2^{-d}{(1+z)}^{d}b\left(z\right)$, $d\ge 1$, and ${\mathcal{S}}_{\mathbf{b}}$ is convergent [3], then the higher derivatives of ${\mathsf{\Phi }}_{\mathbf{a}}$ can be easily evaluated as

$$D^{\nu }{\mathsf{\Phi }}_{\mathbf{a}}\left(x\right)={\nabla }^{\nu }{\mathsf{\Phi }}_{\mathbf{b}}\left(x\right),x\in \mathbb{R},1\le \nu \le d,$$

(16)

where the backward finite difference operator is defined recursively as

$${\nabla }^{\nu }f\left(x\right)=\nabla \left({\nabla }^{\nu -1}\right)f\left(x\right),\nabla f\left(x\right)=f\left(x\right)-f(x-1).$$

(17)

2.2. The Eigenvalue/Eigenvector Problem for Refinable Functions

When the mask $\mathbf{a}$ is compactly supported on $\mathcal{Z}\subset {\mathbb{Z}}^s$, the refinable Equation (4) evaluated on the integers $\alpha \in {\mathbb{Z}}^s$, gives rise to the following eigenvalue/eigenvector problem

$${\mathsf{\Phi }}_{\mathbf{a}}\left(\alpha \right)=\sum _{\beta \in \mathcal{F}}{a}_{2\alpha -\beta }{\mathsf{\Phi }}_{\mathbf{a}}\left(\beta \right),\alpha \in \mathcal{F},$$

(18)

where $\mathcal{F}\subset {\mathbb{Z}}^s$ denotes the set of integers where ${\mathsf{\Phi }}_{\mathbf{a}}\left(\alpha \right)\ne 0$ [5,15]. Analogously, the partial derivatives of ${\mathsf{\Phi }}_{\mathbf{a}}$ satisfy the eigenvalue/eigenvector problem

$$2^{-\left|\nu \right|}{D}^{\nu }{\mathsf{\Phi }}_{\mathbf{a}}\left(\alpha \right)=\sum _{\beta \in \mathcal{F}}{a}_{2\alpha -\beta }{D}^{\nu }{\mathsf{\Phi }}_{\mathbf{a}}\left(\beta \right),\alpha \in \mathcal{F}.$$

(19)

Defining the sequence $V^{\nu }=(V_{\alpha }^{\nu }=D^{\nu }{\mathsf{\Phi }}_{\mathbf{a}}\left(\alpha \right),\alpha \in \mathcal{F})$, the eigenvalue/eigenvector problems (18) and (19) can be written as

$$2^{-\left|\nu \right|}{V}^{\nu }=A{V}^{\nu },0\le \left|\nu \right|\le d,$$

(20)

where the matrix A has entries $A_{\alpha ,\beta }=a_{2\alpha -\beta }$.

The eigenvalues can be simple or not, depending on the value of $\nu$ and on the properties of the mask $\mathbf{a}$. For instance, when $\left|\nu \right|=0$, the eigenvalue 1 is simple. Moreover, if the subdivision scheme ${\mathcal{S}}_{\mathbf{a}}$ is convergent, then the eigenvector $V^0=\left\{{\mathsf{\Phi }}_{\mathbf{a}}\left(\alpha \right)\right\}$ is the unique sequence satisfying [15]

$$\sum _{\alpha \in \mathcal{F}}{V}_{\alpha }^0=1.$$

(21)

In the univariate case ($s=1$) also the eigenvalues $2^{-\ell }$, $1\le \ell \le d$, are simple. In this case, the convergence of the subdivision scheme ${\mathcal{S}}_{\mathbf{a}}$ ensures that the sequence $V^{\ell }=(D^{\ell }{\mathsf{\Phi }}_{\mathbf{a}}\left(\alpha \right),\alpha \in \mathcal{F}\subset \mathbb{Z})$ is the unique sequence satisfying (20) such that

$$\sum _{\alpha \in \mathcal{F}}{\alpha }^p{V}_{\alpha }^{\ell }={(-1)}^p\ell !{\delta }_{p\ell },0\le p\le \ell .$$

(22)

In the multivariate case ($s>1$), the eigenvalues $2^{-\left|\nu \right|}$, $1\le \left|\nu \right|\le d$, may not be simple so that the corresponding eigenvectors are not unique. If $\mathsf{\Phi }\in C^d\left({\mathbb{R}}^s\right)$ satisfies the stability estimate (10), then $V^{\nu }$ is the unique sequence that satisfies both the eigenvalue/eigenvector problem (20) and the conditions

$$\sum _{\alpha \in \mathcal{F}}{\alpha }^{\mu }{V}_{\alpha }^{\nu }={(-1)}^{\mu }\nu !{\delta }_{\mu \nu },\left|\mu \right|\le \left|\nu \right|\le d.$$

(23)

The Eigenvalue/Eigenvector Problem for Bivariate Refinable Functions ($s=2$)

Assuming the mask $\mathbf{a}=\{a_{({\alpha }_1,{\alpha }_2)},({\alpha }_1,{\alpha }_2)\in \mathcal{Z}\}$ is compactly supported in $\mathcal{Z}\subset {\mathbb{Z}}^2$, the eigenvalue/eigenvector problem becomes

$$2^{-\left(\right|{\nu }_1|+|{\nu }_2\left|\right)}{V}^{({\nu }_1,{\nu }_2)}=A{V}^{({\nu }_1,{\nu }_2)},0\le {\nu }_1+{\nu }_2\le d,$$

(24)

where

$$A=(a_{(2{\alpha }_1-{\beta }_1,2{\alpha }_2-{\beta }_2)},({\alpha }_1,{\alpha }_2)\in \mathcal{Z},({\beta }_1,{\beta }_2)\in \mathcal{Z}).$$

(25)

If ${\mathsf{\Phi }}_{\mathbf{a}}\in C^d\left({\mathbb{R}}^2\right)$ satisfies the stability condition (10), the unique solution of Equation (24) satisfying the conditions

$$\sum _{({\alpha }_1,{\alpha }_2)\in \mathcal{Z}}{\alpha }_1^{{\mu }_1}{\alpha }_2^{{\mu }_2}{V}_{({\alpha }_1,{\alpha }_2)}^{({\nu }_1,{\nu }_2)}={(-1)}^{{\mu }_1}{(-1)}^{{\mu }_2}{\nu }_1!{\nu }_2!{\delta }_{{\mu }_1{\nu }_1}{\delta }_{{\mu }_2{\nu }_2},{\mu }_1+{\mu }_2\le {\nu }_1+{\nu }_2\le d,$$

(26)

is $V^{({\nu }_1,{\nu }_2)}=\left(V_{({\alpha }_1,{\alpha }_2)}^{({\nu }_1,{\nu }_2)}=\frac{{\partial }^{{\nu }_1}}{\partial x_1}\frac{{\partial }^{{\nu }_2}}{\partial x_2}{\mathsf{\Phi }}_{\mathbf{a}}({\alpha }_1,{\alpha }_2),({\alpha }_1,{\alpha }_2)\in \mathcal{F}\subset {\mathbb{R}}^2\right)$.

3. Exact Evaluation of Integrals of Refinable Functions

In this section, we are interested in the exact evaluation of integrals of type

$${\int }_{\mathcal{I}}{D}^{{\nu }_1}{\mathsf{\Phi }}_{\mathbf{a}}(2^{j}x-\alpha )D^{{\nu }_2}{\mathsf{\Phi }}_{\mathbf{a}}(2^{j}x-\beta )dx,\alpha ,\beta \in {\mathbb{Z}}^s,j\in \mathbb{Z},$$

(27)

where $\mathcal{I}\subseteq {\mathbb{R}}^s$ and ${\nu }_1,{\nu }_2\in {\mathbb{Z}}^s$, $0\le |{\nu }_1|,|{\nu }_2|\le d$, with $D^0{\mathsf{\Phi }}_{\mathbf{a}}={\mathsf{\Phi }}_{\mathbf{a}}$. We assume ${\mathsf{\Phi }}_{\mathbf{a}}\in C^d\left({\mathbb{R}}^s\right)$ satisfies the stability condition (10) and $\mathbf{a}$ is a compactly supported mask. When $\mathcal{I}={[0,1]}^s$, the above integrals can be written as

$${\int }_{{\mathbb{R}}^s}\chi \left(x\right)D^{{\nu }_1}{\mathsf{\Phi }}_{\mathbf{a}}(2^{j}x-\alpha )D^{{\nu }_2}{\mathsf{\Phi }}_{\mathbf{a}}(2^{j}x-\beta )dx,\alpha ,\beta \in {\mathbb{Z}}^s,j\in \mathbb{Z},$$

(28)

where $\chi \left(x\right)$ is the characteristic function of the interval ${[0,1]}^s$. Since $\chi$ is also a refinable function, at the end, we have to evaluate the integrals of products of integer translates and dilates of refinable functions and their derivatives over the whole ${\mathbb{R}}^s$. We first consider the case $j=0$.

Let us define the function

$${\mathsf{\Psi }}_{\mathbf{a}}(x_1,x_2)={\int }_{{\mathbb{R}}^s}\chi \left(y\right){\mathsf{\Phi }}_{\mathbf{a}}(y-x_1){\mathsf{\Phi }}_{\mathbf{a}}(y-x_2)dy,x_1,x_2\in {\mathbb{R}}^s.$$

(29)

We note that the values ${\mathsf{\Psi }}_{\mathbf{a}}({\alpha }_1,{\alpha }_2)$, ${\alpha }_1,{\alpha }_2\in {\mathbb{Z}}^s$, i.e., the values of ${\mathsf{\Psi }}_{\mathbf{a}}$ on the integers, coincide with the integrals (28) for $|{\nu }_1|+|{\nu }_2|=0$ and $j=0$. It turns out that ${\mathsf{\Psi }}_{\mathbf{a}}$ is a $2s$-variate refinable function with refinement mask [15]

$$\mathbf{h}=\left\{h_{{\alpha }_1,{\alpha }_2}\right\},h_{{\alpha }_1,{\alpha }_2}=\frac{1}{2^s}\sum _{\beta \in \mathcal{E}}{c}_{\beta }{a}_{\beta -{\alpha }_1}{a}_{\beta -{\alpha }_2},{\alpha }_1,{\alpha }_2\in {\mathbb{Z}}^s,$$

(30)

where $\mathcal{E}=\{\alpha ={\alpha }_1\cdots {\alpha }_s,0\le {\alpha }_i\le 1,1\le i\le s\}$ and

$$\mathbf{c}=\{c_{\alpha }=1,\alpha \in \mathcal{E}\}$$

(31)

is the mask of the characteristic function. Since the mask $\mathbf{a}$ is compactly supported, the mask $\mathbf{h}$ is compactly supported too, and so is ${\mathsf{\Psi }}_{\mathbf{a}}$. Thus, the integrals for $j=0$ can be evaluated by solving the eigenvalue/eigenvector problem (24) for the mask $\mathbf{h}$. If ${\mathsf{\Phi }}_{\mathbf{a}}$ is a stable refinable function, the solution to the eigenvector problem is unique [15].

For the integrals involving derivatives of refinable functions, we notice that

$$D_{x_1}^{{\nu }_1}{D}_{x_2}^{{\nu }_2}{\mathsf{\Psi }}_{\mathbf{a}}(x_1,x_2)={\int }_{{\mathbb{R}}^s}\chi \left(y\right)D_{x_1}^{{\nu }_1}{\mathsf{\Phi }}_{\mathbf{a}}(y-x_1)D_{x_2}^{{\nu }_2}{\mathsf{\Phi }}_{\mathbf{a}}(y-x_2)dy,$$

(32)

so that the integrals are the entries of the eigenvector corresponding to the eigenvalue $2^{-\left(\right|{\nu }_1|+|{\nu }_2\left|\right)}$. Unfortunately, for $|{\nu }_1|+|{\nu }_2|>0$, the uniqueness of the eigenvector is not guaranteed nor can it be retrieved by imposing conditions (23).

Provided that the symbol

$$a\left(z\right)=\sum _{\alpha }{a}_{\alpha }{z}^{\alpha },z\in {\mathbb{C}}^s,$$

(33)

can be factorized as

$$a\left(z\right)=2^{-|{\nu }_1|}{(1+z)}^{{\nu }_1}{b}_1\left(z\right)=2^{-|{\nu }_2|}{(1+z)}^{{\nu }_2}{b}_2\left(z\right),$$

(34)

an easy way to evaluate the integrals (32) is to substitute the derivatives $D_{x_1}^{{\nu }_1}{\mathsf{\Phi }}_{\mathbf{a}}(y-x_1)$, $D_{x_2}^{{\nu }_2}{\mathsf{\Phi }}_{\mathbf{a}}(y-x_2)$ by the finite difference Formula (16). If the difference symbols

$$b_1\left(z\right)=\sum _{\alpha }{b}_{1,\alpha }{z}^{\alpha },b_2\left(z\right)=\sum _{\alpha }{b}_{2,\alpha }{z}^{\alpha },$$

(35)

are associated with a convergent subdivision scheme, Equation (16) gives

$$D_x^{{\nu }_1}{\mathsf{\Phi }}_{\mathbf{a}}\left(x\right)={\mathsf{\Delta }}_x^{{\nu }_1}{\mathsf{\Phi }}_{{\mathbf{b}}_1}\left(x\right),D_x^{{\nu }_2}{\mathsf{\Phi }}_{\mathbf{a}}\left(x\right)={\mathsf{\Delta }}_x^{{\nu }_2}{\mathsf{\Phi }}_{{\mathbf{b}}_2}\left(x\right),x\in \mathbb{R},$$

(36)

where ${\mathsf{\Phi }}_{{\mathbf{b}}_1}$ and ${\mathsf{\Phi }}_{{\mathbf{b}}_2}$ are the refinable functions associated with the difference masks

$${\mathbf{b}}_1=\left\{b_{1,\alpha }\right\},{\mathbf{b}}_2=\left\{b_{2,\alpha }\right\},$$

(37)

respectively. Since

$${\mathsf{\Psi }}_{{\mathbf{b}}_1,{\mathbf{b}}_2}(x_1,x_2)={\int }_{{\mathbb{R}}^s}\chi \left(y\right){\mathsf{\Phi }}_{{\mathbf{b}}_1}(y-x_1){\mathsf{\Phi }}_{{\mathbf{b}}_2}(y-x_2)dy,$$

(38)

is a refinable function, the values on the integers ${\mathsf{\Psi }}_{{\mathbf{b}}_1,{\mathbf{b}}_2}(\alpha ,\beta )$, $\alpha ,\beta \in {\mathbb{Z}}^s$, can be obtained by solving the eigenvalue/eigenvector problem (24) with mask

$$\tilde{\mathbf{h}}=\left\{{\tilde{h}}_{{\alpha }_1,{\alpha }_2}\right\},{\tilde{h}}_{{\alpha }_1,{\alpha }_2}=\frac{1}{2}\sum _{\beta \in \mathcal{E}}{c}_{\beta }{b}_{1,\beta -{\alpha }_1}{b}_{2,\beta -{\alpha }_2}.$$

(39)

In conclusion,

$$D_{x_1}^{{\nu }_1}{D}_{x_2}^{{\nu }_2}{\mathsf{\Psi }}_{\mathbf{a}}(\alpha ,\beta )={\mathsf{\Delta }}_{x_1}^{{\nu }_1}{\mathsf{\Delta }}_{x_2}^{{\nu }_2}{\mathsf{\Psi }}_{{\mathbf{b}}_1,{\mathbf{b}}_2}(\alpha ,\beta ).$$

(40)

When $j>0$, we can use the change of the integration variable $2^{j}x\to x$ and the refinement equation for $\chi$ into the integrals (28) to obtain

$$2^{-js}\sum _{{\gamma }_1\in \mathcal{E}}{c}_{{\gamma }_1}{\int }_{{\mathbb{R}}^s}\chi (2^{-j+1}x-{\gamma }_1)D^{{\nu }_1}{\mathsf{\Phi }}_{\mathbf{a}}(x-\alpha )D^{{\nu }_2}{\mathsf{\Phi }}_{\mathbf{a}}(x-\beta )dx,$$

(41)

where $c_{{\gamma }_1}$ are the coefficients of the mask associated with $\chi$ (see (31)). Using repeatedly the refinement equation for $\chi$ in the above equation, we obtain

$$\begin{array}{c}{\displaystyle {\int }_{{\mathbb{R}}^s}\chi \left(x\right)D^{{\nu }_1}{\mathsf{\Phi }}_{\mathbf{a}}(2^{j}x-\alpha )D^{{\nu }_2}{\mathsf{\Phi }}_{\mathbf{a}}(2^{j}x-\beta )dx,=}\hfill \\ \\ \hfill {\displaystyle 2^{-js}\sum _{{\gamma }_1\in \mathcal{E}}\cdots \sum _{{\gamma }_j\in \mathcal{E}}{c}_{{\gamma }_1}\cdots c_{{\gamma }_j}{\int }_{{\mathbb{R}}^s}\chi \left(x\right)D^{{\nu }_1}{\mathsf{\Phi }}_{\mathbf{a}}(x-(\alpha -\tilde{\gamma }))D^{{\nu }_2}{\mathsf{\Phi }}_{\mathbf{a}}(x-(\beta -\tilde{\gamma }))dx,}\hfill \end{array}$$

(42)

where ${\displaystyle \tilde{\gamma }=\sum _{\ell =1}^j{2}^{j-\ell }{\gamma }_{\ell }}$. Thus, the integrals (28) can be expressed as a sum of integrals with $j=0$.

3.1. Integrals of Univariate Refinable Functions on Finite Intervals

In this section, we focus on the evaluation of the integrals

$$I_{k,l,j}({\mathsf{\Phi }}_{\mathbf{a}};\mathcal{I})={\int }_{\mathcal{I}}{\mathsf{\Phi }}_{\mathbf{a}}(2^{j}x-k){\mathsf{\Phi }}_{\mathbf{a}}(2^{j}x-l)dx,k,l,\in \mathbb{Z},j\in {\mathbb{Z}}_{+},$$

(43)

where $\mathcal{I}\subset \mathbb{R}$ is a finite interval with dyadic rational length and ${\mathsf{\Phi }}_{\mathbf{a}}$ is a stable univariate refinable function associated with the compactly supported mask

$$\mathbf{a}=\{a_0,\dots ,a_{n+1}\}.$$

(44)

Without loss of generality, we can assume $\mathcal{I}=[0,1]$.

If $supp\left({\mathsf{\Phi }}_{\mathbf{a}}(2^{j}x-k)\right)\subseteq [0,1]$ or $supp\left({\mathsf{\Phi }}_{\mathbf{a}}(2^{j}x-l)\right)\subseteq [0,1]$, by the change of integration variable $2^{j}x-k\to x$, it is easy to show that $I_{k,l,j}({\mathsf{\Phi }}_{\mathbf{a}};\mathcal{I})=2^{-j}{I}_{0,l-k,0}({\mathsf{\Phi }}_{\mathbf{a}};\mathbb{R})$. Thus, except for the multiplicative factor $2^{-j}$, the integrals are the values on the integers of the function

$${\mathsf{\Psi }}_{0,\mathbf{a}}\left(x\right)={\int }_{\mathbb{R}}{\mathsf{\Phi }}_{\mathbf{a}}\left(y\right){\mathsf{\Phi }}_{\mathbf{a}}(y-x)dy,x\in \mathbb{R}.$$

(45)

It is well known [5,15] that ${\mathsf{\Psi }}_{\mathbf{a}}$ is a refinable function with mask

$$\mathbf{h}=\{h_{\alpha },-n-1\le \alpha \le n+1\},h_{\alpha }=\frac{1}{2}\sum _{\beta =0}^{n+1}{a}_{\beta }{a}_{\beta -\alpha },-n-1\le \alpha \le n+1,$$

(46)

so that its values on the integers are the entries of the unique eigenvector $V=(V_{\alpha },-n\le \alpha \le n)$ corresponding to the eigenvalue 1 of the matrix $H=\left(h_{2\alpha -\beta }\right)$ and such that ${\sum }_{\alpha }{V}_{\alpha }=1$.

If both $supp\left({\mathsf{\Phi }}_{\mathbf{a}}(2^{j}x-k)\right)$ and $supp\left({\mathsf{\Phi }}_{\mathbf{a}}(2^{j}x-l)\right)$ are not contained in $[0,1]$, we can write the integral as

$$I_{k,l,j}({\mathsf{\Phi }}_{\mathbf{a}};[0,1])={\int }_{\mathbb{R}}{\chi }_{[0,1]}\left(x\right){\mathsf{\Phi }}_{\mathbf{a}}(2^{j}x-k){\mathsf{\Phi }}_{\mathbf{a}}(2^{j}x-l)dx,k,l\in \mathbb{Z},$$

(47)

where ${\chi }_{[0,1]}\left(x\right)$ is the characteristic function of the interval $[0,1]$.

Using (42) we obtain

$$I_{k,l,j}({\mathsf{\Phi }}_{\mathbf{a}};[0,1])=2^{-j}\sum _{{\gamma }_1=0}^1\cdots \sum _{{\gamma }_j=0}^1{c}_{{\gamma }_1}\cdots c_{{\gamma }_j}{I}_{k-\tilde{\gamma },l-\tilde{\gamma },0}({\mathsf{\Phi }}_{\mathbf{a}};[0,1]),$$

(48)

where $\tilde{\gamma }={\sum }_{\ell =1}^j{2}^{j-\ell }{\gamma }_{\ell }$ and $\mathbf{c}=\{c_{\alpha },0\le \alpha \le 1\}=\{1,1\}$ is the refinement mask of ${\chi }_{[0,1]}$. Thus, it is sufficient to evaluate the integrals

$$I_{k,l}({\mathsf{\Phi }}_{\mathbf{a}};[0,1])={\int }_{\mathcal{I}}{\mathsf{\Phi }}_{\mathbf{a}}(x-k){\mathsf{\Phi }}_{\mathbf{a}}(x-l)dx={\int }_{\mathbb{R}}{\chi }_{[0,1]}\left(x\right){\mathsf{\Phi }}_{\mathbf{a}}(x-k){\mathsf{\Phi }}_{\mathbf{a}}(x-l)dx,$$

(49)

which are non-zero only when $-n\le k,l\le 0$.

From Section 3, we know that we can evaluate the integrals (49) by solving the eigenvector problem

$$V^{\left(0\right)}=G{V}^{\left(0\right)},$$

(50)

where $G=\left(g_{2\alpha -\beta }\right)$ with

$$g_{{\alpha }_1,{\alpha }_2}=\frac{1}{2}\left(a_{-{\alpha }_1}{a}_{-{\alpha }_2}+a_{1-{\alpha }_1}{a}_{1-{\alpha }_2}\right),-n-1\le {\alpha }_1,{\alpha }_2\le 1.$$

(51)

3.2. Integrals of Derivatives of Univariate Refinable Funcions

For integrals involving the first derivative $D_x{\mathsf{\Phi }}_{\mathbf{a}}$, i.e.,

$$I_{k,l}(D_x{\mathsf{\Phi }}_{\mathbf{a}};[0,1])={\int }_{\mathcal{I}}{D}_x{\mathsf{\Phi }}_{\mathbf{a}}(x-k)D_x{\mathsf{\Phi }}_{\mathbf{a}}(x-l)dx,k,l,\in \mathbb{Z},$$

(52)

we notice that they are the values on the integers of the partial derivative $\frac{\partial }{\partial x_1}\frac{\partial }{\partial x_2}{\mathsf{\Psi }}_{\mathbf{a}}(x_1,x_2)$ (see (29)).

Assuming $a\left(z\right)=(1+z)b\left(z\right)/2$ and substituting the differentiation formula (15) in Equation (52), we obtain

$$I_{k,l}(D_x{\mathsf{\Phi }}_{\mathbf{a}};[0,1])={\mathsf{\Delta }}_{x_1}{\mathsf{\Delta }}_{x_2}{\mathsf{\Psi }}_{\mathbf{b}}(k,l)=\sum _{{\alpha }_1,{\alpha }_2=0}^1{(-1)}^{{\alpha }_1+{\alpha }_2}{I}_{k-{\alpha }_1,l-{\alpha }_2}({\mathsf{\Phi }}_{\mathbf{b}};[0,1]),$$

(53)

where ${\mathsf{\Psi }}_{\mathbf{b}}$ is the bivariate refinable function associated with the mask

$${\tilde{g}}_{{\alpha }_1,{\alpha }_2}=\frac{1}{2}\left(b_{-{\alpha }_1}{b}_{-{\alpha }_2}+b_{1-{\alpha }_1}{b}_{1-{\alpha }_2}\right),-n-1\le {\alpha }_1,{\alpha }_2\le 1,$$

(54)

and ${\mathsf{\Phi }}_{\mathbf{b}}$ is the univariate refinable function associated with the difference mask $\mathbf{b}=\{b_{\alpha },0\le \alpha \le n\}$. At the end, the integrals (52) can be evaluated by solving the eigenvalue/eigenvector problem (24) for ${\mathsf{\Psi }}_{\mathbf{b}}$ and taking the backward finite difference of the unique eigenvector corresponding to the eigenvalue 1.

Analogously, the integrals

$${\int }_{\mathcal{I}}{\mathsf{\Phi }}_{\mathbf{a}}(x-k)D_x{\mathsf{\Phi }}_{\mathbf{a}}(x-l)dx,k,l,\in \mathbb{Z},$$

(55)

can be evaluated by solving the eigenvalue/eigenvector problem (24) with mask

$${\widehat{g}}_{{\alpha }_1,{\alpha }_2}=\frac{1}{2}\left(a_{-{\alpha }_1}{b}_{-{\alpha }_2}+a_{1-{\alpha }_1}{b}_{1-{\alpha }_2}\right),-n-1\le {\alpha }_1,{\alpha }_2\le 1,$$

(56)

and taking the backward finite difference ${\mathsf{\Delta }}_{x_2}$ of the unique eigenvector corresponding to the eigenvalue 1.

4. Examples

As an example, we evaluate the integrals of the translates of the pseudo-splines, a family of compactly supported refinable functions which contains some well-known refinable functions as special cases. The pseudo-splines of type I were introduced in [16]. Their symbol is defined as

$$|a_{(m,n)}^I{\left(z\right)|}^2=2{\left(\frac{1+z}{2}\right)}^{2m}\sum _{j=0}^n\left(\genfrac{}{}{0pt}{}{m+n}{j}\right){(-1)}^j{\left(\frac{1-z}{2}\right)}^{2j}{\left(\frac{1+z}{2}\right)}^{2(n-j)}.$$

(57)

It depends on the two integer parameters $m,n\ge 0$ with $n\le m-1$. The pseudo-splines of type I are compactly supported on $[0,m+n]$ and belong to $C^{m-1}\left(\mathbb{R}\right)$. When $n=0$, the symbol $a_{(m,0)}^I\left(z\right)$ coincides with the symbol associated with the cardinal B-splines, while $a_{(m,m-1)}^I\left(z\right)$ coincides with the symbol of the Daubechies family [4]. The cardinal B-spline ${\mathsf{\Phi }}_{(m,0)}^I\left(x\right)$ is a piecewise polynomial of degree $m-1$ with breakpoints on the integers. It is non-negative in its support $[0,m]$, it is centrally symmetric and it is refinable with mask [17]

$${\mathbf{a}}_{(m,0)}^I=\{a_{(m,0),\alpha }^I,0\le \alpha \le m\},a_{(m,0),\alpha }^I=\frac{1}{2^{m-1}}\left(\genfrac{}{}{0pt}{}{m}{\alpha }\right).$$

(58)

The pseudo-spline ${\mathsf{\Phi }}_{(m,m-1)}^I\left(x\right)$ is the Daubechies refinable function of order m and is orthogonal and nonsymmetric. The mask coefficients do not have an explicit expression except for $m=2,3$. Their values computed up to order $m=10$ can be found in [4].

In [18], the authors considered the pseudo-splines of type II, which are the autocorrelation of the pseudo-splines of type I. Their symbol is

$$a_{(m,n)}^{II}\left(z\right)={\left|a_{(m,n)}^I\left(z\right)\right|}^2.$$

(59)

The pseudo-splines of type II are symmetric, compactly supported on $[0,2(m+n\left)\right]$ and belong to $C^{2(m-1)}\left(\mathbb{R}\right)$. When $n=0$, the symbol $a_{(m,0)}^{II}\left(z\right)$ coincides with the symbol associated with the cardinal B-splines of degree $2m-1$, while $a_{(m,m-1)}^{II}\left(z\right)$ coincides with the symbol of the symmetric interpolatory schemes introduced in [19]. The latter are associated with the interpolatory symmetric refinable functions ${\mathsf{\Phi }}_{(m,m-1)}^{II}\left(x\right)$, which are compactly supported on $[0,2(m+n\left)\right]$. We recall that interpolatory means that ${\mathsf{\Phi }}_{(m,m-1)}^{II}\left(\alpha \right)=0$ for all integers $\alpha \in [0,2(m+n\left)\right]$ except for $\alpha =m+n$ when its value is 1. In particular, the symbol

$$a_{(2,1)}^{II}\left(z\right)=-\frac{1}{16}+\frac{9z^2}{16}+z^3+\frac{9z^4}{16}-\frac{z^6}{16}$$

(60)

corresponds to the mask of the four-point scheme

$${\mathbf{a}}_{(2,1)}^{II}=\left\{-\frac{1}{16},0,\frac{9}{16},1,\frac{9}{16},0,-\frac{1}{16}\right\}.$$

(61)

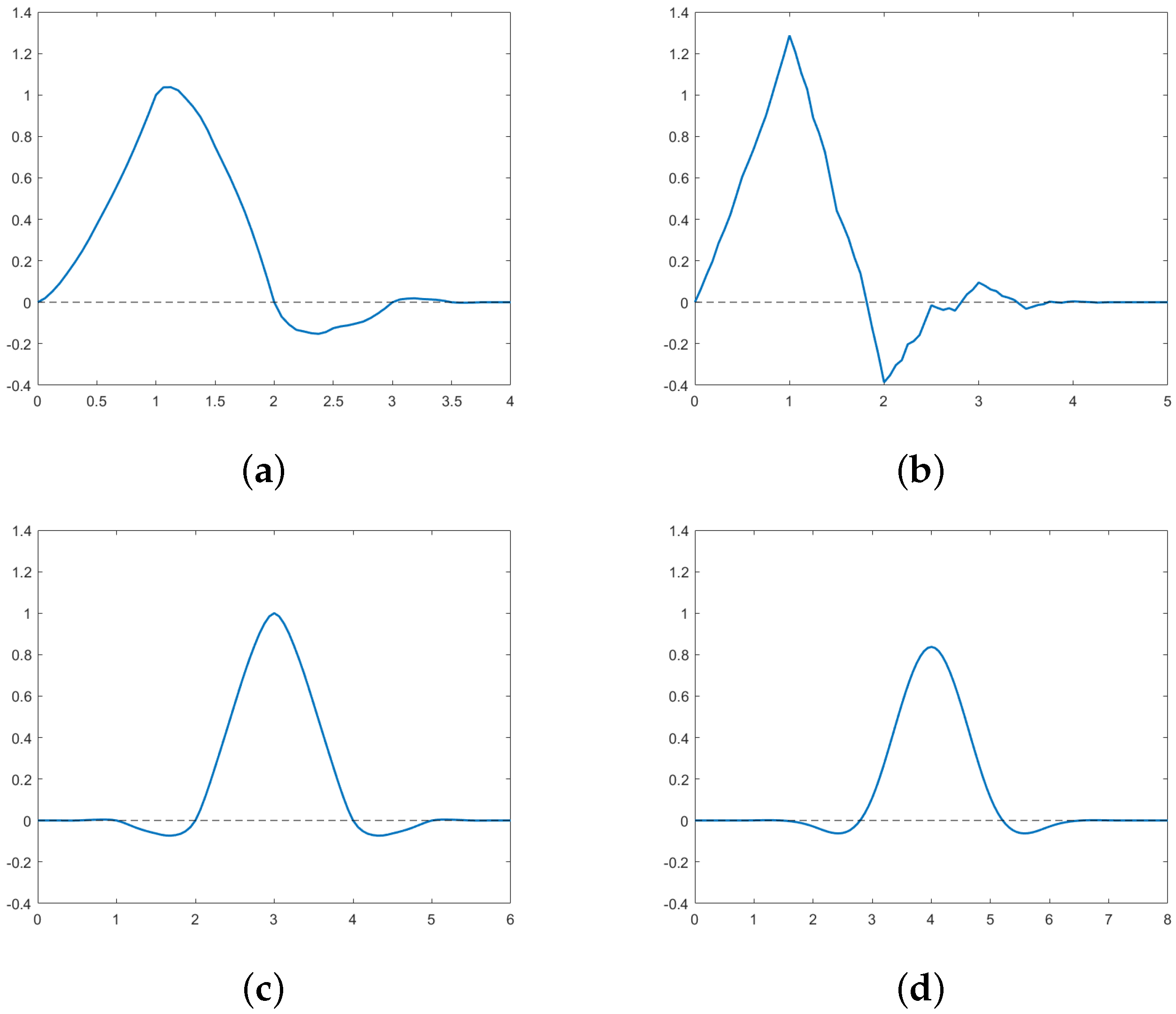
In the pseudo-spline family, only the cardinal B-splines have a known analytic form [20] and therefore, in order to evaluate integrals of products of refinable functions for $n>0$, the procedure described in the previous section must be evoked. Here, we evaluate the integrals of the pseudo-splines ${\mathsf{\Phi }}_{(3,n)}^I$ for $n=1,2$ and ${\mathsf{\Phi }}_{(m,1)}^{II}$ for $m=2,3$. Starting from the values on the integers, we can use recursively the refinement equation to evaluate the pseudo-splines at the dyadic points $2^{-j}\mathbb{Z}$ (see Figure 1 where $j=4$).

Figure 1. (a) The pseudo-spline of type I ${\mathsf{\Phi }}_{(3,1)}^I$. (b) The orthogonal pseudo-spline ${\mathsf{\Phi }}_{(3,2)}^I$. (c) The interpolatory pseudo-spline ${\mathsf{\Phi }}_{(2,1)}^{II}$. (d) The pseudo-spline of type II ${\mathsf{\Phi }}_{(3,1)}^{II}$.

In Table 1 and Table 2, the values of the integrals $I_{k,l}({\mathsf{\Phi }}_{(3,1)}^I;[0,1])$, $-3\le k,l\le 0$, and $I_{k,l}({\mathsf{\Phi }}_{(3,2)}^I;[0,1])$, $-4\le k,l\le 0$, evaluated up to machine precision, are listed.

Table 1. The values of the integrals $I_{k,l}({\mathsf{\Phi }}_{(3,1)}^I;[0,1])$ evaluated up to machine precision.

$\mathit{k}\setminus \mathit{l}$	−3	−2	−1	0
−3	$9.405347704967639·{10}^{-5}$	$-7.429899242365393·{10}^{-4}$	$5.965724179228820·{10}^{-3}$	$6.355932203389832·{10}^{-4}$
−2	$-7.429899242365290·{10}^{-4}$	$1.194479158530555·{10}^{-2}$	$-7.761299435028242·{10}^{-2}$	$-3.477928350126270·{10}^{-2}$
−1	$5.965724179228801·{10}^{-3}$	$-7.761299435028246·{10}^{-2}$	$5.682811971152597·{10}^{-1}$	$1.878898825796037·{10}^{-1}$
0	$6.355932203389766·{10}^{-4}$	$-3.477928350126270·{10}^{-2}$	$1.878898825796037·{10}^{-1}$	$2.569680934156055·{10}^{-1}$

Table 2. The values of the integrals $I_{k,l}({\mathsf{\Phi }}_{(3,2)}^I;[0,1])$ evaluated up to machine precision.

$\mathit{k}\setminus \mathit{l}$	−4	−3	−2
−4	$1.477911329137502·{10}^{-6}$	$3.249351710498510·{10}^{-5}$	$-1.343887189602012·{10}^{-4}$
−3	$3.249351710498180·{10}^{-5}$	$1.338460917999608·{10}^{-3}$	$-5.684787772731729·{10}^{-3}$
−2	$-1.343887189602028·{10}^{-4}$	$-5.684787772731725·{10}^{-3}$	$3.106353271270828·{10}^{-2}$
−1	$4.413282832766463·{10}^{-4}$	$1.892752442573810·{10}^{-2}$	$-1.176759414601629·{10}^{-1}$
0	$-2.496131194086296·{10}^{-19}$	$-4.413282832766528·{10}^{-4}$	$-1.879313570677787·{10}^{-2}$
$\mathit{k}\setminus \mathit{l}$	−1	0
−4	$4.413282832766551·{10}^{-4}$	$2.468424057727266·{10}^{-20}$
−3	$1.892752442573811·{10}^{-2}$	$-4.413282832766530·{10}^{-4}$
−2	$-1.176759414601628·{10}^{-1}$	$-1.879313570677789·{10}^{-2}$
−1	$4.709487303525829·{10}^{-1}$	$1.233282357157897·{10}^{-1}$
0	$1.233282357157897·{10}^{-1}$	$4.966477981053796·{10}^{-1}$

In Table 3 and Table 4, the values of the integrals $I_{k,l}(D_x{\mathsf{\Phi }}_{(3,1)}^I;[0,1])$, $-3\le k,l\le 0$, and $I_{k,l}(D_x{\mathsf{\Phi }}_{(3,2)}^I;[0,1])$, $-4\le k,l\le 0$, evaluated up to machine precision, are listed.

Table 3. The values of the integrals $I_{k,l}(D_x{\mathsf{\Phi }}_{(3,1)}^I;[0,1])$ evaluated up to machine precision.

$\mathit{k}\setminus \mathit{l}$	−3	−2	−1	0
−3	$5.411255411255435·{10}^{-3}$	$-2.218614718614711·{10}^{-2}$	$2.813852813852805·{10}^{-2}$	$-1.136363636363638·{10}^{-2}$
−2	$-2.218614718614718·{10}^{-2}$	$1.677489177489169·{10}^{-1}$	$-2.689393939393933·{10}^{-1}$	$1.233766233766235·{10}^{-1}$
−1	$2.813852813852817·{10}^{-2}$	$-2.689393939393933·{10}^{-1}$	$1.453463203463204·{10}^0$	$-1.212662337662338·{10}^0$
0	$-1.136363636363642·{10}^{-2}$	$1.233766233766235·{10}^{-1}$	$-1.212662337662338·{10}^0$	$1.100649350649351·{10}^0$

Table 4. The values of the integrals $I_{k,l}(D_x{\mathsf{\Phi }}_{(3,2)}^I;[0,1])$ evaluated up to machine precision.

$\mathit{k}\setminus \mathit{l}$	−4	−3	−2
−4	1.983592433357107$·{10}^{-4}$	1.530794761546635$·{10}^{-3}$	$-4.779464493845230·{10}^{-3}$
−3	1.530794761546657$·{10}^{-3}$	4.602360988387802$·{10}^{-2}$	$-1.282995712968333·{10}^{-1}$
−2	$-4.779464493845280·{10}^{-3}$	$-1.282995712968330·{10}^{-1}$	4.673646354266377$·{10}^{-1}$
−1	8.407453346105716$·{10}^{-3}$	2.034383342832282$·{10}^{-1}$	$-1.011817206037050·{10}^0$
0	$-5.357142857142803·{10}^{-3}$	$-1.226931676318198·{10}^{-1}$	6.775316064010912$·{10}^{-1}$
$\mathit{k}\setminus \mathit{l}$	−1	0
−4	$8.407453346105731·{10}^{-3}$	$-5.357142857142848·{10}^{-3}$
−3	$2.034383342832284·{10}^{-1}$	$-1.226931676318198·{10}^{-1}$
−2	$-1.011817206037050·{10}^0$	$6.775316064010909·{10}^{-1}$
−1	$3.051861626311564·{10}^0$	$-2.251890207903847·{10}^0$
0	$-2.251890207903848·{10}^0$	$1.702408911991719·{10}^0$

In Table 5 and Table 6, the values of the integrals $I_{k,l}({\mathsf{\Phi }}_{(2,1)}^{II};[0,1])$, $-5\le k\le 0$, $-5\le l\le -3$, and $I_{k,l}({\mathsf{\Phi }}_{(3,1)}^{II};[0,1])$, $-7\le k\le 0$, $-7\le l\le -4$, evaluated up to machine precision, are listed. Since the pseudo-splines are centrally symmetric, the integrals for $-3\le l\le 0$ can be obtained by the symmetry properties

$$\begin{array}{c}\hfill I_{k,l}({\mathsf{\Phi }}_{(m,n)}^{II};[0,1])=I_{-l-2(m+n)+1,-k-2(m+n)+1}({\mathsf{\Phi }}_{(m,n)}^{II};[0,1]),\hfill \\ \\ \hfill I_{k,l}({\mathsf{\Phi }}_{(m,n)}^{II};[0,1])=I_{l,k}({\mathsf{\Phi }}_{(m,n)}^{II};[0,1]).\hfill \end{array}$$

Table 5. The values of the integrals $I_{k,l}({\mathsf{\Phi }}_{(2,1)}^{II};[0,1])$ evaluated up to machine precision.

$\mathit{k}\setminus \mathit{l}$	−5	−4	−3
−5	$5.116257874460724·{10}^{-6}$	$-8.276163812145549·{10}^{-5}$	$1.223026662915586·{10}^{-3}$
−4	$-8.276163812145549·{10}^{-6}$	$2.614407773849806·{10}^{-3}$	$-2.921345302778139·{10}^{-2}$
−3	$1.223026662915586·{10}^{-3}$	$-2.921345302778139·{10}^{-2}$	$3.978644961832378·{10}^{-1}$
−2	$2.816182665282207·{10}^{-4}$	$-2.134545530552364·{10}^{-2}$	$1.956342116650678·{10}^{-1}$
−1	$-3.796236980093334·{10}^{-5}$	$2.231891234044411·{10}^{-3}$	$-2.134545530552362·{10}^{-2}$
0	$-1.482905070348861·{10}^{-7}$	$-3.796236980093487·{10}^{-5}$	$2.816182665282243·{10}^{-4}$

Table 6. The values of the integrals $I_{k,l}({\mathsf{\Phi }}_{(3,1)}^{II};[0,1])$ evaluated up to machine precision.

$\mathit{k}\setminus \mathit{l}$	−7	−6	−5	−4
−7	$2.471301925974684·{10}^{-8}$	$-1.395875479686866·{10}^{-6}$	$4.454752965851973·{10}^{-6}$	$4.892398758858539·{10}^{-5}$
−6	$-1.395875479686949·{10}^{-6}$	$9.722157641353062·{10}^{-5}$	$-2.139339860762161·{10}^{-4}$	$-4.332435082294774·{10}^{-3}$
−5	$4.454752965854710·{10}^{-6}$	$-2.139339860762127·{10}^{-4}$	$2.589299713488763·{10}^{-3}$	$-7.870711960958931·{10}^{-3}$
−4	$4.892398758858467·{10}^{-5}$	$-4.332435082294773·{10}^{-3}$	$-7.870711960958921·{10}^{-3}$	$3.377964641315861·{10}^{-1}$
−3	$7.773866800986866·{10}^{-6}$	$-9.339605823889749·{10}^{-4}$	$-2.195108918141705·{10}^{-2}$	$2.288901274136763·{10}^{-1}$
−2	$-1.969121331976882·{10}^{-6}$	$2.459688163128797·{10}^{-4}$	$6.354809670166827·{10}^{-4}$	$-2.195108918141705·{10}^{-2}$
−1	$5.801489206488096·{10}^{-8}$	$-1.198584434179334·{10}^{-5}$	$2.459688163128797·{10}^{-4}$	$-9.339605823889730·{10}^{-4}$
0	$3.191528292077578·{10}^{-11}$	$5.801489206488360·{10}^{-8}$	$-1.969121331976856·{10}^{-6}$	$7.773866800990127·{10}^{-6}$

In Table 7 and Table 8, the values of the integrals $I_{k,l}(D_x{\mathsf{\Phi }}_{(2,1)}^{II};[0,1])$, $-5\le k\le 0$, $-5\le l\le -3$, and $I_{k,l}(D_x{\mathsf{\Phi }}_{(3,1)}^{II};[0,1])$, $-7\le k\le 0$, $-7\le l\le -4$, evaluated up to machine precision, are shown. Also in this case, the integrals for $-3\le l\le 0$ can be obtained by symmetry.

Table 7. The values of the integrals $I_{k,l}(D_x{\mathsf{\Phi }}_{(2,1)}^{II};[0,1])$ evaluated up to machine precision.

$\mathit{k}\setminus \mathit{l}$	−5	−4	−3
−5	$2.777777777777467·{10}^{-4}$	$-2.222222222222164·{10}^{-3}$	$3.611111111111101·{10}^{-3}$
−4	$-2.222222222222133·{10}^{-3}$	$3.527777777777726·{10}^{-2}$	$-4.666666666666633·{10}^{-2}$
−3	$3.611111111111009·{10}^{-3}$	$-4.666666666666641·{10}^{-2}$	$1.075555555555556·{10}^0$
−2	$-1.666666666666628·{10}^{-3}$	$-3.611111111110925·{10}^{-3}$	$-1.027222222222223·{10}^0$
−1	$5.080672813160866·{10}^{-18}$	$1.722222222222225·{10}^{-2}$	$-3.611111111111147·{10}^{-3}$
0	$4.525501419255835·{10}^{-20}$	$-8.844442985958084·{10}^{-19}$	$-1.666666666666667·{10}^{-3}$

Table 8. The values of the integrals $I_{k,l}(D_x{\mathsf{\Phi }}_{(3,1)}^{II};[0,1])$ evaluated up to machine precision.

$\mathit{k}\setminus \mathit{l}$	−7	−6	−5	−4
−7	$1.800273644710908·{10}^{-6}$	$-5.290448342381944·{10}^{-5}$	$3.470271682158227·{10}^{-4}$	$1.567105861812087·{10}^{-4}$
−6	$-5.290448342381998·{10}^{-5}$	$1.906204102861672·{10}^{-3}$	$-1.189757439834966·{10}^{-2}$	$-1.360635067201347·{10}^{-2}$
−5	$3.470271682158154·{10}^{-4}$	$-1.189757439834967·{10}^{-2}$	$7.808373767258711·{10}^{-2}$	$4.118636082849043·{10}^{-2}$
−4	$1.567105861812070·{10}^{-4}$	$-1.360635067201344·{10}^{-2}$	$4.118636082849041·{10}^{-2}$	$6.014774534800320·{10}^{-1}$
−3	$-5.191351035369562·{10}^{-4}$	$2.610202916007258·{10}^{-2}$	$-1.347429248319731·{10}^{-1}$	$-5.200541434472525·{10}^{-1}$
−2	$6.933751699985054·{10}^{-5}$	$-2.460284570668251·{10}^{-3}$	$2.941432061469777·{10}^{-2}$	$-1.347429248319734·{10}^{-1}$
−1	$-2.829703823829584·{10}^{-6}$	$1.171056534476690·{10}^{-5}$	$-2.460284570668251·{10}^{-3}$	$2.610202916007260·{10}^{-2}$
0	$-6.254256978012706·{10}^{-9}$	$-2.829703823829591·{10}^{-6}$	$6.933751699984900·{10}^{-5}$	$-5.191351035369660·{10}^{-4}$

We notice that all the computations were performed in Matlab (version 2022b). The eigenvalue/eigenvector problem was solved with the function eig.

5. Conclusions

Except for the seminal paper by Dahmen and Micchelli [15], the literature is scarce in terms of papers dealing with methods for the exact evaluation of the connection coefficients involving refinable functions and wavelets. In [21], a similar reasoning is used to evaluate the connection coefficients of a wavelet Galerkin method but the evaluation of integrals involving derivatives of wavelets is a little cumbersome since the authors do not take advantage of the differentiation rule (40). In [22], the authors describe a method derived from [23] for the exact evaluation of the integrals (27). The drawback of the proposed method is that it gives rise to a linear system for which the existence and uniqueness of the solution are not guaranteed. Moreover, nothing is said about integrals involving boundary functions. On the other hand, since refinable functions can only be calculated on the dyadic points, for evaluating the integrals with quadrature rules, the Newton–Cotes formula should be employed, having the dyadic points as nodes. However, to obtain an accurate approximation, these formulas require a large number of nodes which would produce a loss of accuracy in the values of the refinable functions as they are calculated through the recursive use of Equation (4).

Instead, our approach, which follows directly from [15], allows to evaluate the integrals of both refinable functions and their derivatives by solving an eigenvalue/eigenvector problem that involves only the refinement masks. The conditions (23), which guarantee the existence and uniqueness of the solution, can be easily imposed while, in the case of integrals of derivatives, the use of the differentiation rule (40) avoids the difficulty of imposing further conditions.

The examples in Section 4 show the effectiveness of the method in evaluating integrals of refinable functions whose explicit expressions is not known.

As a final remark, we note that the same procedure can be used to evaluate integrals of multivariate refinable functions and wavelets with any dilation matrix M, while a generalization to integrals involving multiwavelets can be found in [24].