Effect of Weight Thresholding on the Robustness of Real-World Complex Networks to Central Node Attacks
Abstract
1. Introduction
2. Methods
2.1. Real-World Networks
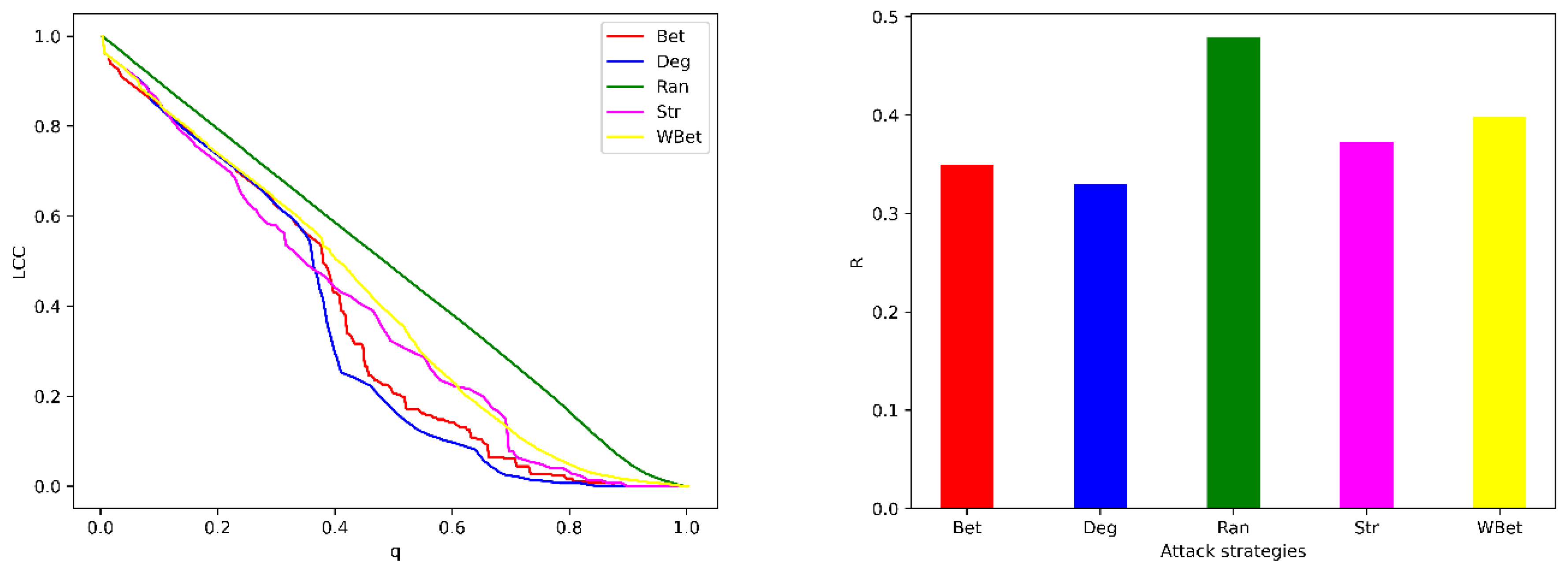
2.2. Attack Strategies
- Degree (Deg): The degree of a node is a simple local centrality measure defined as the number of links connected to it. The degree of node i is given by
- Strength (Str): A node’s strength is the sum of the weights of links connected to that node. It is a weighted version of the degree centrality [6].
- Betweenness (Bet): Betweenness of a node is the number of shortest paths (between all the pairs of nodes) passing through it [3,4,5]. This binary metric defines the shortest path between two nodes as the minimum number of links needed to travel from one node to another. Mathematically, betweenness of node i is:
- Weighted betweenness (WBet): Weighted betweenness of a node is defined as the number of weighted shortest paths passing through that node [7].
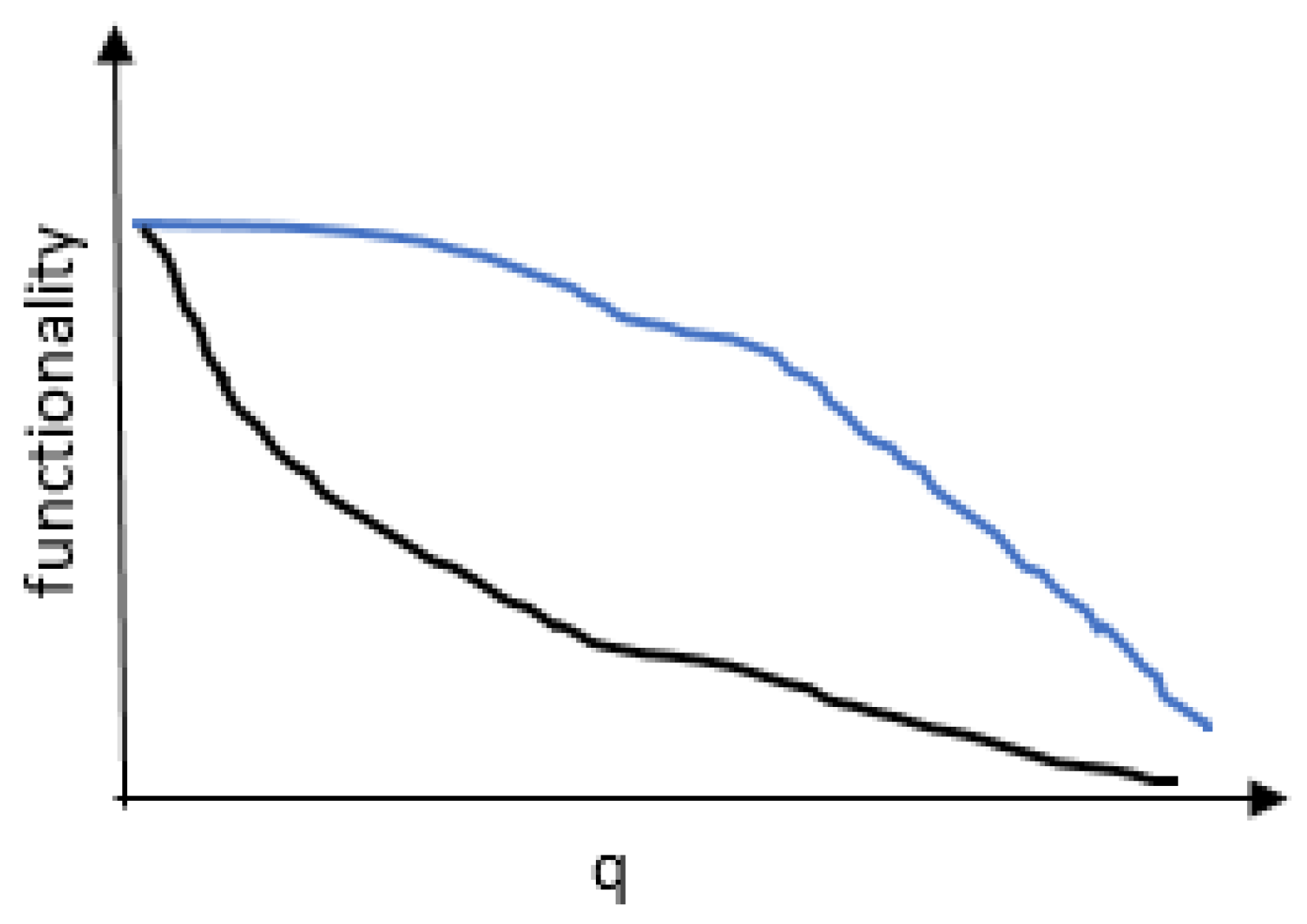
2.3. Network Robustness Indicator
2.4. Weight Thresholding
| Algorithm 1: Methodology of WT analysis. | |
| Procedure Weight Thresholding (G, N, L) | |
| 1: | WT = {0.0, 0.05, 0.1, …………., 0.85, 0.9} |
| 2: | for each WT |
| 3: | for i = 1 to m |
| 4: | link_set = {links in the increasing order of their weight} |
| 5: | weak_linkset = {WT fraction of weak links from link_set} |
| 6: | G′ = G − weak_linkset |
| 7: | Initial attack (G′, N, L′) |
| 8: | Recalculated attack (G′, N, L′) |
| Procedure Initial attack (G′, N, L′) | |
| 1: | Find Initial LCC |
| 2: | for i = 1 to n |
| 3: | node_set = { nodes of G′ in the decreasing order of centrality measure } |
| 4: | while (LCC ! = 1) |
| 5: | Remove a node x from the G′ (in the order of node_set) |
| 6: | Find LCC of new network |
| 7: | node_set = node_set − x |
| Procedure Recalculated attack (G′, N, L′) | |
| 1: | Find Initial LCC |
| 2: | for i = 1 to n |
| 3: | while (LCC ! = 1) |
| 4: | Calculate centrality meaures |
| 5: | node_set = { nodes of G′ in the decreasing order of centrality measure } |
| 6: | Remove a node x from the G′ (in the order of node_set) |
| 7: | Find LCC of new network |
| 8: | node_set = node_set − x |
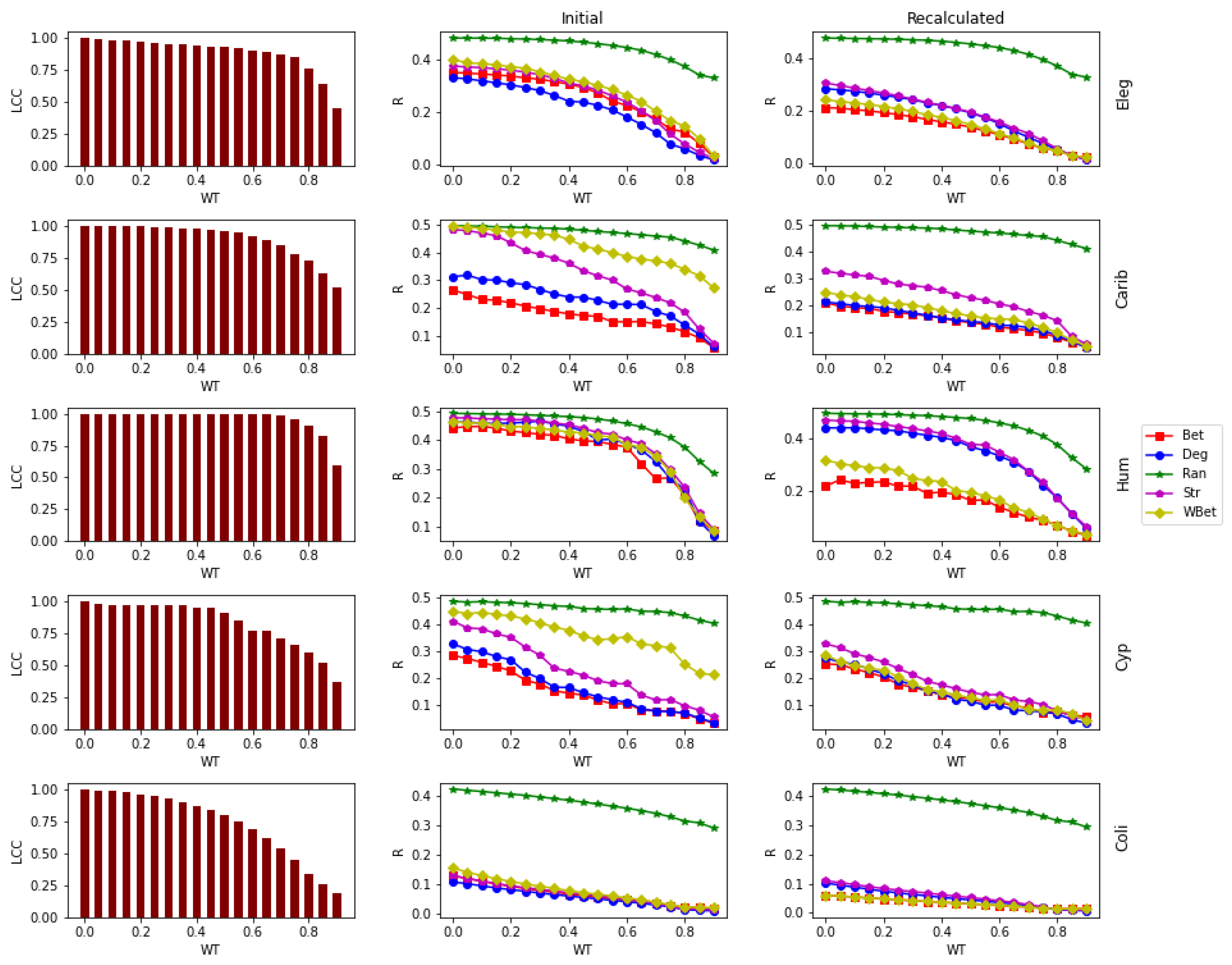
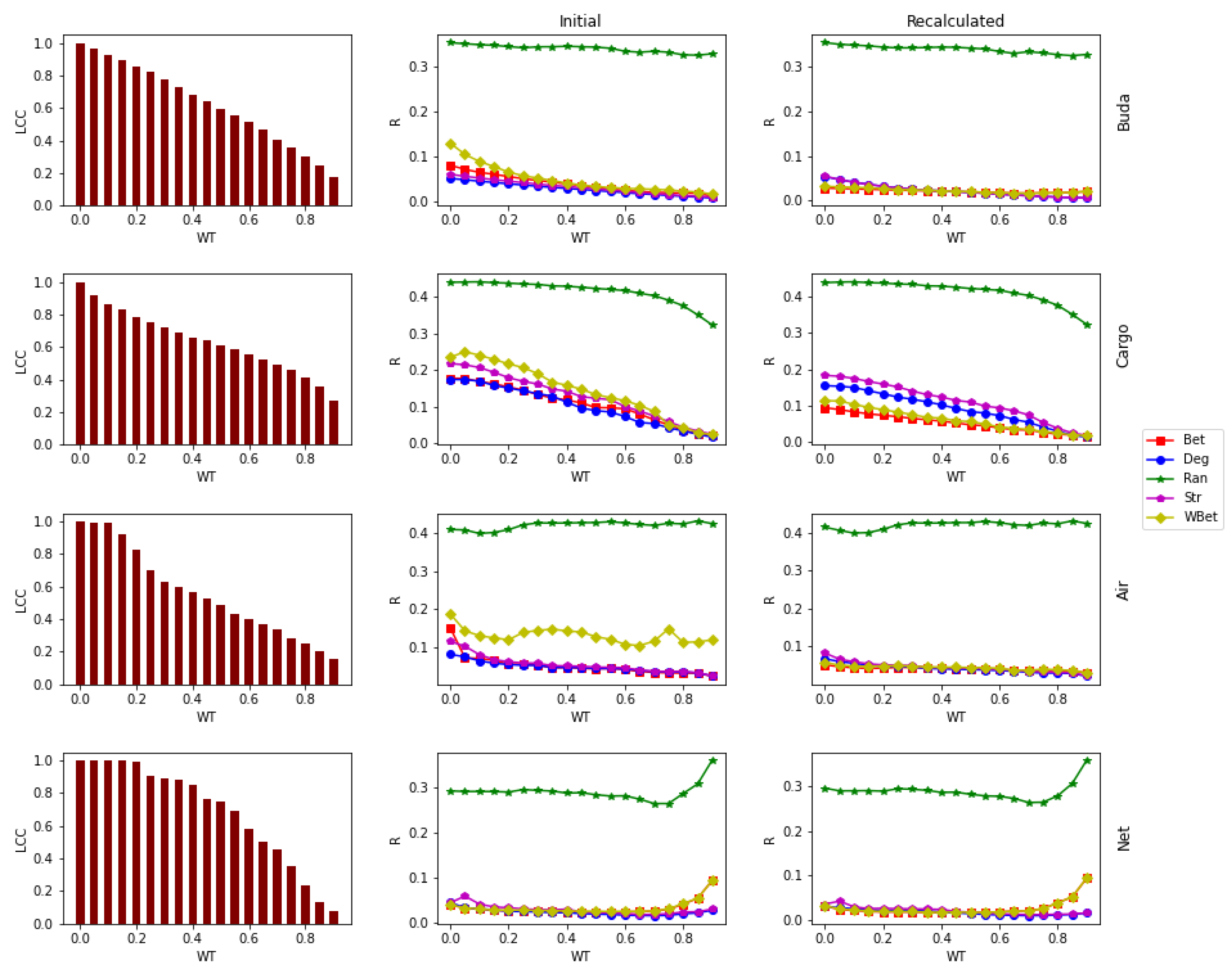
3. Results and Discussion
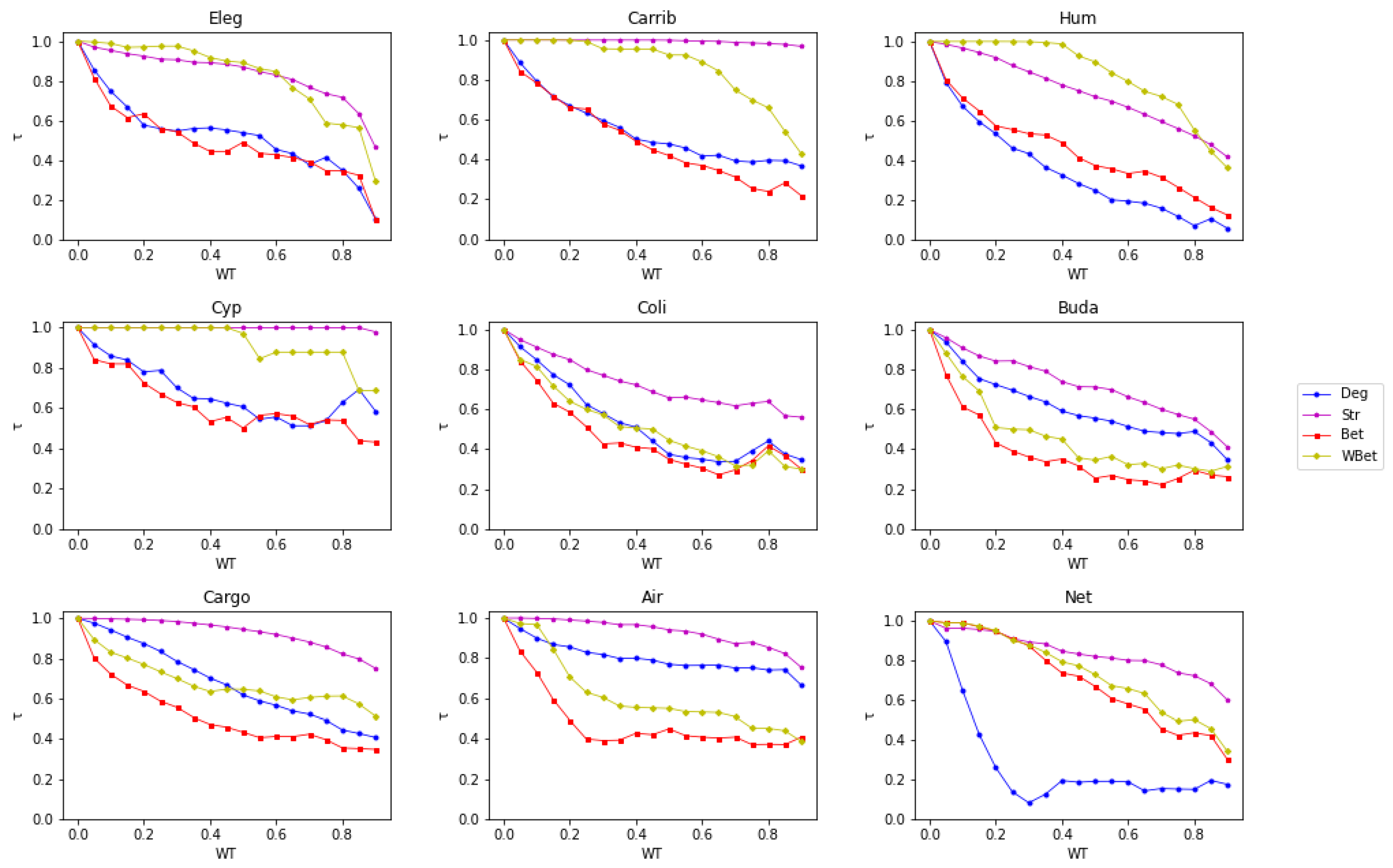
Analyzing Node Centrality Ranking under WT by Kendall’s Tau Coefficient
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Albert, R.; Jeong, H.; Barabasi, A.-L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef] [PubMed]
- Albert, R.; Barabasi, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Holme, P.; Kim, B.J.; Yoon, C.N.; Han, S.K. Attack vulnerability of complex networks. Phys. Rev. E 2002, 65, 056109. [Google Scholar] [CrossRef]
- Bellingeri, M.; Cassi, D.; Vincenzi, S. Efficiency of attack strategies on complex model and real-world networks. Phys. A Stat. Mech. Its Appl. 2014, 414, 174–180. [Google Scholar] [CrossRef]
- Iyer, S.; Killingback, T.; Sundaram, B.; Wang, Z. Attack robustness and centrality of complex networks. PLoS ONE 2013, 8, e59613. [Google Scholar] [CrossRef] [PubMed]
- Bellingeri, M.; Cassi, D. Robustness of weighted networks. Phys. A Stat. Mech. Its Appl. 2018, 489, 47–55. [Google Scholar] [CrossRef]
- Nguyen, Q.; Nguyen, N.K.K.; Cassi, D.; Bellingeri, M. New betweenness centrality node attack strategies for real-world complex weighted networks. Complexity 2021, 2021, 1677445. [Google Scholar] [CrossRef]
- Allesina, S.; Pascual, M. Googling food webs: Can an eigenvector measure species’ importance for coextinctions? PLoS Comput. Biol. 2009, 5, e1000494. [Google Scholar] [CrossRef]
- Lekha, D.S.; Balakrishnan, K. Central attacks in complex networks: A revisit with new fallback strategy. Phys. A Stat. Mech. Its Appl. 2020, 549, 124347. [Google Scholar] [CrossRef]
- Divya, P.B.; Lekha, D.S.; Johnson, T.; Balakrishnan, K. Vulnerability of link-weighted complex networks in central attacks and fallback strategy. Phys. A Stat. Mech. Its Appl. 2021, 590, 126667. [Google Scholar]
- Nie, T.; Guo, Z.; Zhao, K.; Lu, Z.-M. New attack strategies for complex networks. Phys. A Stat. Mech. Its Appl. 2015, 424, 248–253. [Google Scholar] [CrossRef]
- Nie, T.; Guo, Z.; Zhao, K.; Lu, Z.-M. The dynamic correlation between degree and betweenness of complex network under attack. Phys. A Stat. Mech. Its Appl. 2016, 457, 129–137. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, X.-K.; Li, P.; Zhang, K.; Small, M. Node importance for dynamical process on networks: A multiscale characterization. Chaos 2011, 21, 016107. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Wang, L.; Sun, S.; Xia, C. Identification of influential spreaders based on classified neighbors in realworld complex networks. Appl. Math. Comput. 2018, 320, 512–523. [Google Scholar] [CrossRef]
- Bellingeri, M.; Bevacqua, D.; Scotognella, F.; Cassi, D. The heterogeneity in link weights may decrease the robustness of real-world complex weighted networks. Sci. Rep. 2019, 9, 10692. [Google Scholar] [CrossRef]
- Crucitti, P.; Latora, V.; Marchiori, M.; Rapisarda, A. Efficiency of scale-free networks: Error and attack tolerance. Phys. A Stat. Mech. Its Appl. 2003, 320, 622–642. [Google Scholar] [CrossRef]
- Bellingeri, M.; Bevacqua, D.; Scotognella, F.A.; Alfieri, R.; Cassi, D. A comparative analysis of link removal strategies in real complex weighted networks. Sci. Rep. 2020, 10, 3911. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Li, S.; Ma, H. Effect of edge removal on topological and functional robustness of complex networks. Phys. A Stat. Mech. Its Appl. 2009, 388, 2243–2253. [Google Scholar] [CrossRef][Green Version]
- Granovetter, M.S. The strength of weak ties. Am. J. Sociol. 1973, 78, 1360–1380. [Google Scholar] [CrossRef]
- Pajevic, S.; Plenz, D. The organization of strong links in complex networks. Nat. Phys. 2012, 8, 429–436. [Google Scholar] [CrossRef]
- Garas, A.; Argyrakis, P.; Havlin, S. The structural role of weak and strong links in a financial market network. Eur. Phys. J. B 2008, 63, 265–271. [Google Scholar] [CrossRef]
- Yan, X.; Jeub, L.G.S.; Flammini, A.; Radicchi, F.; Fortunato, S. Weight thresholding on complex networks. Phys. Rev. E 2018, 98, 042304. [Google Scholar] [CrossRef]
- Csermely, P. Weak Links: The Universal Key to the Stability of Networks and Complex Systems; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Radicchi, F.; Ramasco, J.J.; Fortunato, S. Information filtering in complex weighted networks. Phys. Rev. E 2011, 83, 046101. [Google Scholar] [CrossRef] [PubMed]
- Bartoldson, B.; Morcos, A.; Barbu, A.; Erlebacher, G. The generalization-stability tradeoff in neural network pruning. Adv. Neural Inf. Process. Syst. 2020, 33, 20852–20864. [Google Scholar]
- Freund, A.J.; Giabbanelli, P.J. An experimental study on the scalability of recent node centrality metrics in sparse complex networks. Front. Big Data 2022, 5, 797584. [Google Scholar] [CrossRef]
- Srinivasan, S.; Das, S.; Bhowmick, S. Application of Graph Sparsification in Developing Parallel Algorithms for Updating Connected Components. In Proceedings of the IEEE International Parallel and Distributed Processing Symposium Workshops, Chicago, IL, USA, 23–27 May 2016. [Google Scholar]
- Namaki, A.; Shirazi, A.H.; Raei, R.; Jafari, G. Network analysis of a financial market based on genuine correlation and threshold method. Phys. A Stat. Mech. Its Appl. 2011, 390, 3835–3841. [Google Scholar] [CrossRef]
- Lynall, M.-E.; Bassett, D.S.; Kerwin, R.; McKenna, P.J.; Kitzbichler, M.; Muller, U.; Bullmore, E. Functional connectivity and brain networks in schizophrenia. J. Neurosci. 2010, 30, 9477–9487. [Google Scholar] [CrossRef] [PubMed]
- Allesina, S.; Bodini, A.; Bondavalli, C. Secondary extinctions in ecological networks: Bottlenecks unveiled. Ecol. Model. 2006, 194, 150–161. [Google Scholar] [CrossRef]
- Garrison, K.A.; Scheinost, D.; Finn, E.S.; Shen, X.; Constable, R.T. The (in) stability of functional brain network measures across thresholds. Neuroimage 2015, 118, 651–661. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Eytan, M.; David, H. Enhancing network robustness via shielding. IEEE/ACM Trans. Netw. 2017, 25, 2209–2222. [Google Scholar] [CrossRef]
- Liu, M.; Qi, X.; Pan, H. Optimizing communication network geodiversity for disaster resilience through shielding approach. Reliab. Eng. Syst. Saf. 2022, 228, 108800. [Google Scholar] [CrossRef]
- Xiao, S.; Xiao, G. On imperfect node protection in complex communication networks. J. Phys. A Math. Theor. 2011, 44, 055101. [Google Scholar] [CrossRef]
- Colizza, V.; Pastor-Satorras, R.; Vespignani, A. Reaction-diffusion processes and metapopulation models in heterogeneous. Nat. Phys. 2007, 3, 276–282. [Google Scholar] [CrossRef]
- Newman, M.E.J. Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. 2006, 74, 036104. [Google Scholar] [CrossRef] [PubMed]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Latora, V.; Nicosia, V.; Russo, G. Complex Networks: Principles, Methods and Applications; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Allard, A.; Serrano, M.A.; Garcia-Perez, G.; Boguna, M. The geometric nature of weights in real complex networks. Nat. Commun. 2017, 8, 14103. [Google Scholar] [CrossRef]
- Serrano, A.M.; Boguna, M.; Sagues, F. Uncovering the hidden geometry behind metabolic networks. Mol. BioSyst. 2012, 8, 843–850. [Google Scholar] [CrossRef]
- Avena-Koenigsberger, A.; Goni, J.; Betzel, R.F.; Heuvel, M.P.V.D.; Griffa, A.; Hagmann, P.; Thiran, J.-P.; Sporns, O. Using Pareto optimality to explore the topology and dynamics of the human connectome. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2014, 369, 20130530. [Google Scholar] [CrossRef]
- Hagmann, P.; Cammoun, L.; Gigandet, X.; Meuli, R.; Honey, C.J.; Wedeen, V.J.; Sporns, O. Mapping the structural core of human cerebral cortex. PLoS Biol. 2008, 6, 1479–1493. [Google Scholar] [CrossRef]
- Bellingeri, M.; Bodini, A. Food web’s backbones and energy delivery in ecosystems. Oikos 2016, 125, 586–594. [Google Scholar] [CrossRef]
- Opitz, S. Trophic Interactions in Caribbean Coral Reefs; International Center for Living Aquatic Resources Management (ICLARM): Penang, Malaysia, 1996. [Google Scholar]
- Heymans, J.J.; Ulanowicz, R.E.; Bondavalli, C. Network analysis of the South Florida Everglades graminoid marshes and comparison with nearby cypress ecosystems. Ecol. Model. 2002, 149, 5–23. [Google Scholar] [CrossRef]
- Bellingeri, M.; Vincenzi, S. Robustness of empirical food webs with varying consumer’s sensitivities to loss of resources. J. Theor. Biol. 2013, 333, 18–26. [Google Scholar] [CrossRef] [PubMed]
- Szalkai, B.; Kerepesi, C.; Varga, B.; Grolmusz, V. The Budapest Reference Connectome Server v2.0. Neurosci. Lett. 2015, 595, 60–62. [Google Scholar] [CrossRef] [PubMed]
- Cohen, R.; Erez, K.; Ben-Avraham, D.; Havlin, S. Breakdown of the internet under intentional attack. Phys. Rev. Lett. 2001, 86, 3682–3685. [Google Scholar] [CrossRef]
- Brandes, U. A faster algorithm for betweenness centrality. J. Math. Sociol. 2004, 25, 163–177. [Google Scholar] [CrossRef]
- Jordán, F. Keystone Species and Food Webs. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2009, 364, 1733–1741. [Google Scholar] [CrossRef]
- Nguyen, Q.; Pham, H.-D.; Cassi, D.; Bellingeri, M. Conditional attack strategy for real-world complex networks. Phys. A Stat. Mech. Its Appl. 2019, 530, 121561. [Google Scholar] [CrossRef]
- Kendall, M.G. The treatment of ties in ranking problems. Biometrika 1945, 33, 239–251. [Google Scholar] [CrossRef] [PubMed]
| Networks | Key | Ref. | Type | Node | Link | Weight | N | L | <k> | <w> | LCC |
|---|---|---|---|---|---|---|---|---|---|---|---|
| C. elegans | Eleg | [37,38] | Biological | Neurons | Neurons connection | Number of Connections | 297 | 2344 | 15.8 | 3.761 | 297 |
| Cargoship | Cargo | [39] | Transport | Ports | Route | Shipping journeys | 834 | 4348 | 10.4 | 97.709 | 821 |
| US airport | Air | [35] | Transport | Airports | Route | Passengers | 500 | 2979 | 11.9 | 152,320.2 | 500 |
| E. coli | Coli | [39,40] | Biological | Metabolites | Common reaction | Number of Common reactions | 1100 | 3636 | 6.61 | 1.364 | 1100 |
| Netscience | Net | [36] | Social | authors | Coauthorship | Number of Common papers | 1461 | 2741 | 3.75 | 0.434 | 379 |
| Human12a | Hum | [41,42] | Biological | Brain regions | Connection between regions | Connection density | 501 | 6038 | 24.1 | 0.01 | 501 |
| Caribbean | Carib | [43,44] | Ecological Food web | Species | Trophic relation | Amount of biomass | 249 | 3503 | 28.13 | 0.067 | 249 |
| CypDry | Cyp | [45,46] | Ecological Food web | Species | Trophic relation | Amount of biomass | 66 | 503 | 15.24 | 0.358 | 65 |
| Budapest | Buda | [47] | Biological | Brain regions | Neural connection | Amount of track flow | 480 | 1000 | 4.167 | 5.024 | 467 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
John, J.M.; Bellingeri, M.; Lekha, D.S.; Cassi, D.; Alfieri, R. Effect of Weight Thresholding on the Robustness of Real-World Complex Networks to Central Node Attacks. Mathematics 2023, 11, 3482. https://doi.org/10.3390/math11163482
John JM, Bellingeri M, Lekha DS, Cassi D, Alfieri R. Effect of Weight Thresholding on the Robustness of Real-World Complex Networks to Central Node Attacks. Mathematics. 2023; 11(16):3482. https://doi.org/10.3390/math11163482
Chicago/Turabian StyleJohn, Jisha Mariyam, Michele Bellingeri, Divya Sindhu Lekha, Davide Cassi, and Roberto Alfieri. 2023. "Effect of Weight Thresholding on the Robustness of Real-World Complex Networks to Central Node Attacks" Mathematics 11, no. 16: 3482. https://doi.org/10.3390/math11163482
APA StyleJohn, J. M., Bellingeri, M., Lekha, D. S., Cassi, D., & Alfieri, R. (2023). Effect of Weight Thresholding on the Robustness of Real-World Complex Networks to Central Node Attacks. Mathematics, 11(16), 3482. https://doi.org/10.3390/math11163482








