Abstract
This paper investigates the problem of stochastically cooperative output regulation of heterogeneous multi-agent systems (MASs) subject to hidden Markov jumps using observer-based distributed control. In order to address a more realistic situation than prior studies, this paper focuses on the following issues: (1) asynchronous phenomena in the system mode’s transmission to the controller; (2) the impact of system mode switching on network topology; and (3) the emergence of coupled terms between the mode-dependent Lyapunov matrix and the control gain in control design conditions. Specifically, to reduce the complexity arising from the asynchronous controller-side mode, the leader–state observer is developed so that the solution pair of regulator equations can be integrated into the observer. Furthermore, a linear decoupling method is proposed to handle the emergence of the aforementioned coupled terms; this provides sufficient LMI conditions to achieve stochastically cooperative output regulation for heterogeneous MASs. Finally, the validity of the proposed method is shown through two illustrative examples.
Keywords:
heterogeneous multi-agent systems; cooperative output regulation problem; hidden Markov jumps; asynchronous distributed control; time-varying network topology MSC:
93A16
1. Introduction
Multi-agent systems (MASs) refer to complex systems composed of multiple autonomous agents that interact with each other and their environment, they have been used in various research fields, including robotics [1,2], automated vehicles [3,4], unmanned autonomous vehicles [5,6,7,8], and urban networks [9,10]. Recently, with the advent of these systems, effective techniques for cooperating MASs with different structures and parameters (referred to as heterogeneous MASs) have been swiftly developed for various purposes, including leader following and formation.
Over the past few years, the cooperative output regulation problem has also been regarded as one of the most fundamental consensus problems for MASs. In this problem, one essential requirement is to develop a control strategy that ensures stable and efficient cooperation between agents while achieving the desired overall performance. Additionally, the control strategy should be able to achieve appropriate behaviors with MASs by explicitly considering the interconnections and interactions between multiple agents. Following this, various methods have been proposed to deal with the cooperative output regulation problem of heterogeneous MASs on the premise of a fixed network topology and system parameters (see [11,12,13,14,15] and references therein). However, the network topology and system parameters can randomly change due to obstacles posed by network sizes, functional connectivity disturbances, limited communication ranges, and random packet losses.
As a mathematical model for handling the aforementioned random changes, Markov jump multi-agent systems have been widely utilized in many control problems, such as the leader–following consensus control [16,17], scaled consensus control [18], the formation control [19], and the cooperative output regulation [20,21,22,23]. The above studies mainly focused on control problems for MASs with deterministic dynamics (with no sudden changes), and the Markov process was only used to model sudden changes in the network topology, or vice versa. However, little effort has been devoted to research on realistic cases in which rapid changes in the system modes of MASs affect the network topology. A more serious problem is that due to network issues, such as packet dropout and data transmission delay, the controller modes cannot be designed in accurate synchronization with the system or network topology modes. Thus, it is necessary to carefully consider the impact of this asynchronous problem when designing a controller that operates in such an environment. According to this need, [24] used a hidden Markov model (HMM) to deal with the problem of the leader–following consensus for MASs with asynchronous control modes. However, in [24], random changes in the network topology are modeled as a Markov process, but the system parameters of MASs are assumed to be deterministic. Hence, to overcome these weaknesses, more progress needs to be made toward addressing the impact of changes in both system parameters and network topology while achieving the HMM-based cooperative output regulation for continuous-time heterogeneous MASs.
Based on the above discussion, the main goal of this paper is to address the problem of stochastically cooperative output regulation for continuous-time heterogeneous MASs with hidden Markov jumps in the system mode and network topology. First, a mode-dependent leader–state observer is designed to transmit an estimated leader–state to each follower agent. After that, an asynchronous mode-dependent distributed controller is designed so that it can ensure the stochastically cooperative output regulation of MASs. To be specific, the main contributions of this paper can be summarized as follows.
- This paper makes a first attempt to reflect the influence of the asynchronous mode between heterogeneous MASs and observer-based distributed controllers while achieving stochastically cooperative output regulation subject to Markov jumps. Different from [22,23,25,26], the realistic case where rapid changes in the system modes of MASs affect the network topology is considered in the control design processes.
- This paper proposes a method to design a continuous-time leader–state observer capable of estimating the leader–state value for each agent under abrupt changes in both systems and network topology. Also, it introduces an alternative mechanism by integrating system-mode-dependent solutions of regulator equations into the output of the leader–state observer to reduce the complexity arising from the asynchronous controller-side mode.
- In the control design process, the asynchronous mode-dependent control gain is coupled with the system-mode-dependent Lyapunov matrix, which makes it difficult to directly use the well-known variable replacement technique [27]. For this reason, this paper suggests a suitable linear decoupling method that is capable of handling the aforementioned coupling problem.
The rest of the paper is organized as follows. Section 2 presents a class of heterogeneous MASs with hidden Markov jumps under our consideration. Next, Section 3 presents methods for designing a mode-dependent leader–state observer and asynchronous mode-dependent distributed controllers for MASs. In Section 4, two illustrative examples are provided to demonstrate the validity of the proposed method. Finally, the concluding remarks are given in Section 5.
Notations: denotes the eigenvalue set of matrix A. In symmetric block matrices, is used as an ellipsis for terms induced by symmetry. stands for a block-diagonal matrix; denotes the scalars or vectors, ; denotes any square matrix ; ⊗ denotes the Kronecker product; denotes the n-dimension identity matrix; denotes the Euclidean norm of vector x; denotes the maximum eigenvalue of matrix A; denotes matrix A; denotes the real part of ; denotes the set ; denote the mathematical expectation; “T” and “” represent matrix transposition and inverse, respectively. The triplet notation denotes a probability space, where , and Pr represent the sample space, the algebra of events, and the probability measure defined on , respectively.
2. Preliminaries and Problem Statement
2.1. Heterogeneous Multi-Agent System Description
Let us consider the following continuous-time Markov jump dynamics of the ith follower and the leader (or exogenous system), defined on a complete probability space :
where , , and denote the state, the control input, and the output of the ith follower, respectively; and are the state and the output of the leader, respectively; is the set of agents; denotes the time-varying switching system mode with denoting the set of systems modes; and N is the number of follower agents. In (1), , , , , , and are known system matrices with appropriate dimensions; and and are controllable and detectable, respectively. In addition, the process is characterized by a continuous-time homogeneous Markov process with the following transition probabilities (TPs):
where is the little-o notation defined as ; and indicates the transition rate (TR) from mode g to mode h at time and satisfies that , and for .
Remark 1.
Different from other studies [22,23,25,26,28], this paper deals with the case where changes in system parameters (affected by the life span of system components, the increase in heat of motors, wear and tear, etc.) directly lead to signal loss or degradation in the transmission quality between agents, inducing changes in the network topology. In addition, external influences could also impact the system parameters and communication network of agents at the same time. Therefore, in this paper, the network topology mode is set to be the same as the system mode .
To be specific, Figure 1 shows a block diagram of the cooperative output regulation of multi-agent systems under our consideration, which contains four main parts: the multi-agent system (), network analyzer, leader–state observer, and distributed controller (). Functionally, the network analyzer finds the current network topology mode using data transmitted over a wireless local area network (black dash line), and the mode information is transmitted to the observer directly and to the distributed controller over a wireless wide area network (blue dash line). As in [23,29], the leader–state observer provides the estimated leader–state for the ith agent to overcome the difficulty that some followers cannot receive information directly from the leader. Next, based on , , and , the controller generates the control input and transmits it to the ith agent so that the output approaches as time increases. In a real environment, since the transmission of the network topology mode can be affected by various network issues from a wireless wide area network, such as network-induced delay, packet dropout, network congestion, and interference, this paper employs another asynchronous observation mode, . In other words, this paper considers a hidden Markov model (HMM) concept with and when designing the distributed controller, where the asynchronism between the two is described as the following conditional probability: , which satisfies and for and .
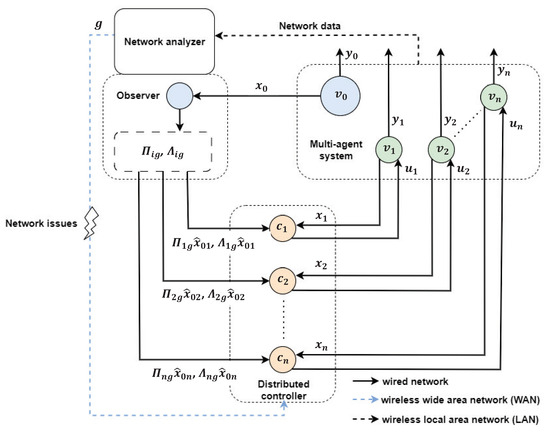
Figure 1.
Block diagram of the cooperative output regulation of multi-agent systems.
Remark 2.
If the network topology mode observed in the network analyzer is not affected by network issues in the transmission process, there will be no asynchronous phenomenon between and , i.e., and . To cover this special case, the conditional probability matrix can be set to the identity matrix .
Assumption A1.
For , .
Assumption A2.
For , there are pairs of solutions for the following regulator equations:
where and .
Remark 3.
Assumption 1 is made only for convenience and loses no generality. In fact, if the linear output regulation problem is solvable by any controller under Assumption 1, it is also solvable by the same controller even if Assumption 1 is violated. More explanations can be found in [30]. Assumption 2 provides the well-known regulator equations [23,31] whose solutions impose a necessary condition for the control design process. Furthermore, the feasibility of Assumption 2 is guaranteed according to Remark 4.
Remark 4
([30]). For , the solution pair of Assumption 2 exists if and only if all eigenvalues satisfy
2.2. Communication Topology
As mentioned in Remark 1 and Figure 1, the network topology of (1) with is represented as a mode-dependent weighted and directed graph (digraph) formed by N follower agents. Here, denotes the node set; denotes the edge set with the ordered pair that has information flow leaving from agent to agent at time t; and denotes the adjacency matrix with if and only if , and otherwise. In addition, the neighbor set and degree of are defined as and , respectively, and the Laplacian matrix of is given by , where . Furthermore, a directed path leaving from node to node is a sequence of ordered edges [24]. In particular, the multi-agent system under our consideration consists of N follower agents and one leader with a spanning tree from the leader to each agent in the network topology. Thus, to represent such a system, this paper considers an extended graph with , , and , where denotes the leader adjacency matrix with if and only if the leader transmits information to , and otherwise. That is, the union of graphs is given by , and its node set is equal to .
Remark 5.
By considering the bidirectional information link between agents, this paper ensures that all agents have the opportunity to communicate with each other, depending on the network topology modes.
The following definitions and lemma will be adopted in this paper.
Definition 1
([32,33]). Let us consider a Markov jump linear system with state . For any initial conditions, , , and , if the state satisfies
then the Markov jump linear system is stochastically stable.
Definition 2
([20,23,34]). The heterogeneous MAS system (1) is said to achieve the stochastically cooperative output regulation if it holds that
- System (1) is stochastically stable when ,
- For any initial conditions, and ,where represents the error between the output of the ith agent and the output of the leader.
Lemma 1
([35]). For any matrix , and matrices X and Y of compatible dimensions, the following inequality holds:
3. Main Results
As in [29], this paper first designs a mode-dependent leader–state observer that provides an estimated leader–state for each agent. Following that, this paper designs a distributed controller that achieves cooperative output regulation for heterogeneous multi-agent systems (1).
3.1. Leader–State Observer Design
As depicted in Figure 1, the leader–state observer directly receives g and from the network analyzer and the leader. Thus, the mode-dependent observer for the ith agent can be established as follows: for ,
where is the estimated leader–state for the ith agent; and is the observer gain. Thus, based on the ith observation error state , it is obtained that
That is, the resultant error system is represented as follows:
where .
The following theorem provides the stabilization condition for system (10), formulated in terms of LMIs.
Theorem 1.
Suppose there exists and such that the following conditions hold: for ,
Then, system (10) is stochastically stable under the Markov network topology, and the observer gain is obtained by .
Proof.
Let us choose a mode-dependent Lyapunov function of the following form:
where . Then, the weak infinitesimal operator acting on provides
Thus, by (13), it can be seen that holds if
where . That is, (14) implies that there exists a small scalar , such that , and by a generalization of Dynkin’s formula, it is obtained that
which results in
Hence, based on Definition 1, system (10) can be said to be stochastically stable. Moreover, defining , condition (14) can be converted into
which becomes (11). □
Remark 6.
It is worth noting that not all follower agents can obtain the leader–state values directly under the switching network topology, but only the one who is connected to the leader. For distributed control purposes, the mode-dependent leader–state observer is designed for each agent, such that the estimated states can track the leader–state values by intermittent communication. Indeed, following Theorem 1, system (10) is stochastically stable, which leads to .
Remark 7.
As shown in Figure 1, is multiplied by each component in the solution pair of regulator equations as the output of the leader–state observer and then sent to the controller to reduce the complexity arising from the asynchronous controller-side mode.
3.2. Distributed Controller Design
Let us define . Then, the error system of the ith agent is given as follows:
Furthermore, for (17), the following distributed control law is considered:
where denotes the asynchronous mode-dependent controller gain with .
Thus, based on Assumption 2, the closed-loop system with (17) and (18) is described as follows:
The following theorem presents the LMI-based cooperative output regulation conditions of (19).
Theorem 2.
For any scalars , , and , suppose that there exist , , , and , such that the following conditions hold for , :
where
Then, system (1) achieves the cooperative output regulation, where the controller gain is constructed by .
Proof.
Let us consider the following mode-dependent Lyapunov function:
where . Then, applying the weak infinitesimal operator to leads to
Also, by Lemma 1, it is obtained that
where , and
Thus, the condition implies
where . Furthermore, using a generalization of Dynkin’s formula, it is obtained that
Thus, it is valid that
Also, Theorem 1 ensures , where scalar stands for a finite constant. Accordingly, by considering a sufficiently small scalar , such that , it follows from (25) that
which guarantees that the system (19) is stochastically stable according to Definition 1. As a result, since condition (26) leads to
Hence, based on Definition 2, it can be seen that condition guarantees the stochastically cooperative output regulation of system (1). Meanwhile, condition can be converted into
where , and . Furthermore, by the Schur complement, condition (21) ensures for . Thus, based on (21), condition (28) holds if it is satisfied that
Also, applying the Schur complement to (29) yields
where
Accordingly, by Lemma 1, condition (30) holds if
which is converted by the Schur complement as follows:
Indeed, performing the congruent transformation to (20) by
we can obtain
where , and
That is, since (33) is equivalent to (32) by the Schur complement, it can be seen that (20) and (21) imply (28), i.e, . □
Remark 8.
In the synchronous case (), the bilinear problems (the third and fifth terms on the right-hand side) of condition (29) could be addressed using the conventional variable replacement technique by denoting , and then applying the Schur complement method to derive the final LMI conditions. However, because of the difference between the system and controller modes in the asynchronous case (), it is impossible to use the aforementioned approach. Hence, additional numerical processes and equivalent LMI conditions are introduced here to handle the coupling problems in condition (29).
Remark 9.
The most recent studies concentrated on addressing the cooperative output regulation problem of heterogeneous Markov jump MASs, where both system and controller modes operate synchronously [23,34], or on deterministic system parameters with a switching network topology [20,21]. Meanwhile, the proposed control strategy in this work can, overall, cover these two problems. Furthermore, we make a first attempt to reflect the influence of the asynchronous mode between the continuous-time heterogeneous MASs and observer-based distributed controllers on achieving stochastically cooperative output regulation subject to Markov jumps. Thus, it is hard to draw a direct comparison since the lack of comparable results developed in a similar framework to this study.
4. Illustrative Examples
To show the validity of the proposed method, this paper provides two examples.
Example 1.
Let us consider the following heterogeneous multi-agent system with and , adopted in [23]:
In addition, the used network topology is depicted in Figure 2 (each agent is a numbered circle), which can be characterized as follows:
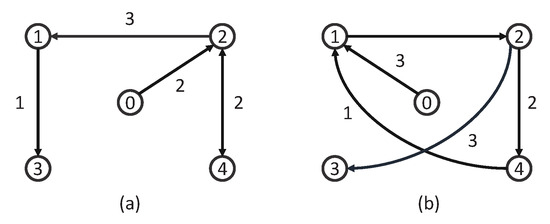
Figure 2.
Network topology: (a) for , and (b) for .
Also, based on Assumption 2, Furthermore, to handle two synchronous and asynchronous cases between the system and controller modes, we consider the following transition rate and conditional probability :
Thereupon, for , , and , Theorems 1 and 2 provide the following leader–state observer gain and controller gain :
Case 1 (Synchronous case):
Case 2 (Asynchronous case):
The details of the hardware used in this experiment are provided in Table 1 and the experiment is conducted using MATLAB for both cases. Based on the central limit theorem, the expected computation times are nearly 0.0363 s for the synchronous case and 0.0394 s for the asynchronous case (after 10,000 trials). Although there is a slight difference, the computation times to derive the final results are approximately similar for both cases overall.

Table 1.
System specifications.
Let us consider the following initial conditions: , , , , and . As shown in Figure 3, suppose that the hidden mode (also called the system mode) and the observed mode (also called the control mode) are generated according to (36)–(38). Then, based on (39), Figure 4 shows the leader–state estimation error , where . That is, from Figure 4, it can be seen that steadily approaches as time increases, which reveals that the observer (8) with (39) can accurately estimate the leader–state despite abrupt changes in the system mode (related to the network topology mode). Next, based on (40), Figure 5a shows the leader and agent outputs for the synchronous case, which demonstrates the cooperative output regulations to ensure that all agent outputs (see the solid lines) follow the leader’s output (see the green-dotted line). Furthermore, Figure 6a shows the output error , clearly illustrating how the agent output approaches the leader’s output from the given initial conditions. Meanwhile, based on (41), Figure 5b shows the leader and agent outputs for the asynchronous case, which illustrates that all agent outputs follow the leader’s output as time increases, despite the emergence of Markov switching and the asynchronous phenomenon. Figure 6b shows that the output error steadily converges to zero as time increases; hence, it validates the results presented in Figure 5b. Eventually, from Figure 5a,b, it can be seen that the proposed method can be successfully used to achieve the cooperative output regulation for heterogeneous multi-agent systems, with hidden Markov jumps containing both synchronous and asynchronous cases.
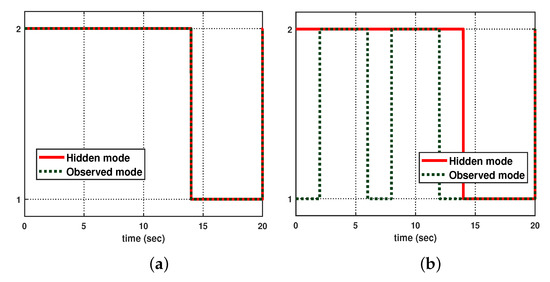
Figure 3.
Mode evolution: (a) synchronous case, and (b) asynchronous case.
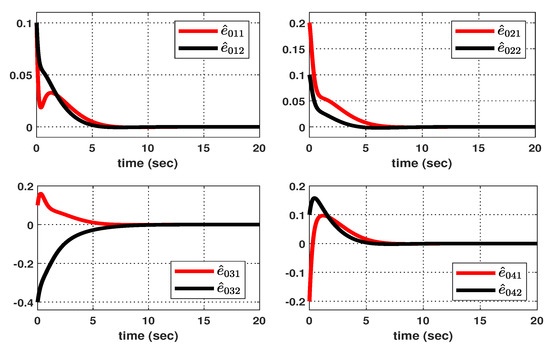
Figure 4.
Estimation error .
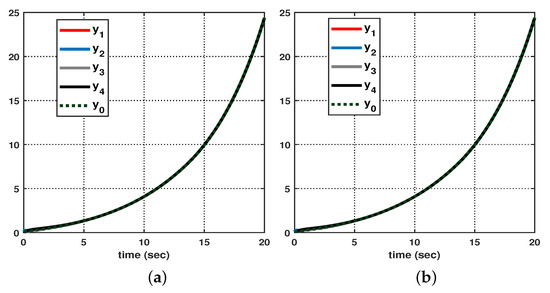
Figure 5.
Output of leader and agents: (a) synchronous case, and (b) asynchronous case.
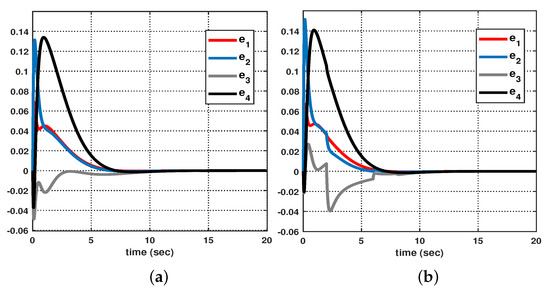
Figure 6.
Output error between leader and agents: (a) synchronous case, and (b) asynchronous case.
Example 2
(Practical application). Consider the following double integrator dynamics driven by different types of actuators, adopted in [36], for , and :
where the system state consists of the position , the velocity , and the actuator state ; denotes the speed of the actuator; and are gains; and represents the influence of velocity on the actuator. Specifically, the value of is changed according to the Markov process of system mode , which is affected by the environment on the actuator, or internal factors, such as temperature, humidity, and lifespan.
If , the actuator is influenced by the velocity, otherwise, (refer to [36] for more details). In this paper, the system parameters are set to , , , , , , , , , and . Furthermore, to synchronize the position and velocity of agents, the leader is described according to [36] as follows:
In addition, the used network topology is depicted in Figure 7 (each agent is a numbered circle), which can be characterized as follows:
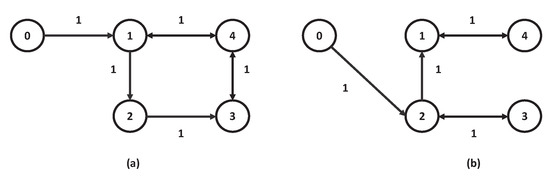
Figure 7.
Network topology: (a) for , and (b) for .
Also, based on Assumption 2, we can see that
Furthermore, to handle the two synchronous and asynchronous cases between the system and controller modes, we consider the following transition rate and conditional probability :
Thereupon, for , , and , Theorems 1 and 2 provide the following observer gain and controller gain :
Case 1 (Synchronous case):
Case 2 (Asynchronous case):
Let us consider the following initial conditions: , (), , , , and . And, as shown in Figure 8, suppose that the hidden mode (also called the system mode) and the observed mode (also called the control mode) are generated according to (44)–(46). Then, based on (47), Figure 9 shows the leader–state estimation error , where . That is, as shown in Figure 9, steadily approach as time increases, which reveals that the observer (8) with (47) can accurately estimate the leader–state regardless of the abrupt changes in the system (42). Subsequently, Figure 10a shows the leader and agent outputs for the synchronous case, which verifies that (48) achieves the cooperative output regulation of (42) since all the agent outputs (see the solid lines) follow the leader’s output (see the green-dotted line). Meanwhile, based on (49), Figure 10b shows the leader and agent outputs for the asynchronous case; this also illustrates that all agent outputs follow the leader’s output as time increases despite the emergence of the Markov switching and the asynchronous phenomenon. Eventually, from Figure 10a,b, it can be seen that the proposed method can be effectively used to realize the cooperative output regulation for (42) with hidden Markov jumps containing both synchronous and asynchronous cases.
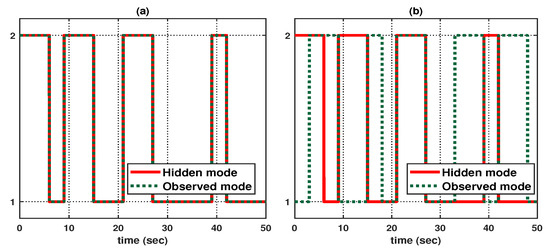
Figure 8.
Mode evolution: (a) synchronous case, and (b) asynchronous case.
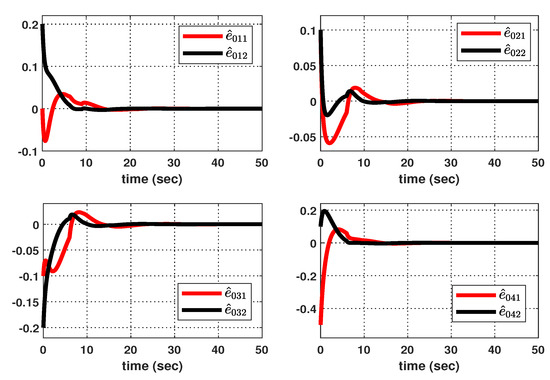
Figure 9.
Estimation error .
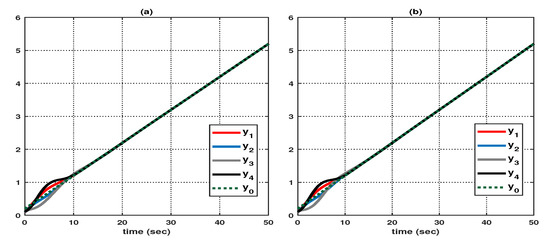
Figure 10.
Output of leader and agents: (a) synchronous case, and (b) asynchronous case.
5. Concluding Remarks
In this paper, we investigated the stochastic cooperative output regulation problem of heterogeneous multi-agent systems subject to hidden Markov jumps. In particular, when dealing with this problem, we also considered a time-varying network topology that changes according to the system operation mode. First, a leader–state observer was designed using a mode-dependent Lyapunov function to ensure that all agents can accurately estimate the leader–state. Then, an asynchronous mode-dependent distributed controller was designed to ensure the stochastic cooperative output regulation for heterogeneous multi-agent systems with hidden Markov jumps. In addition, recent studies [37,38,39] motivated us to extend the proposed strategy to cover more practical control problems, such as stochastic time delay, input saturation, and unknown system dynamics in the continuous-time (discrete-time) domain for a wider range of applications.
Author Contributions
Conceptualization, G.-B.H.; methodology, G.-B.H.; software, G.-B.H.; validation, S.-H.K.; formal analysis, G.-B.H. and S.-H.K.; writing—review & editing, G.-B.H. and S.-H.K.; supervision, S.-H.K.; funding acquisition, S.-H.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the 2023 Research Fund of the University of Ulsan under Grant 2023-0331.
Data Availability Statement
The authors confirm that the data supporting the findings of this study are available within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jiménez, A.C.; García-Díaz, V.; Bolaños, S. A decentralized framework for multi-agent robotic systems. Sensors 2018, 18, 417. [Google Scholar] [CrossRef] [PubMed]
- Dai, S.; Wu, Z.; Zhang, P.; Tan, M.; Yu, J. Distributed Formation Control for a Multi-Robotic Fish System with Model-Based Event-Triggered Communication Mechanism. IEEE Trans. Ind. Electron. 2023, 70, 11433–11442. [Google Scholar] [CrossRef]
- Huang, Z.; Chu, D.; Wu, C.; He, Y. Path planning and cooperative control for automated vehicle platoon using hybrid automata. IEEE Trans. Intell. Transp. Syst. 2018, 20, 959–974. [Google Scholar] [CrossRef]
- Xiao, S.; Ge, X.; Han, Q.L.; Zhang, Y. Dynamic event-triggered platooning control of automated vehicles under random communication topologies and various spacing policies. IEEE Trans. Cybern. 2021, 52, 11477–11490. [Google Scholar] [CrossRef]
- Cui, J.; Liu, Y.; Nallanathan, A. Multi-agent reinforcement learning-based resource allocation for UAV networks. IEEE Trans. Wirel. Commun. 2019, 19, 729–743. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, Z.; Xiao, M. UAVs’ formation keeping control based on Multi–Agent system consensus. IEEE Access 2020, 8, 49000–49012. [Google Scholar] [CrossRef]
- Yan, Z.; Han, L.; Li, X.; Dong, X.; Li, Q.; Ren, Z. Event-Triggered formation control for time-delayed discrete-Time multi-Agent system applied to multi-UAV formation flying. J. Frankl. Inst.-Eng. Appl. Math. 2023, 360, 3677–3699. [Google Scholar] [CrossRef]
- Chen, Y.J.; Chang, D.K.; Zhang, C. Autonomous tracking using a swarm of UAVs: A constrained multi-agent reinforcement learning approach. IEEE Trans. Veh. Technol. 2020, 69, 13702–13717. [Google Scholar] [CrossRef]
- Pham, V.H.; Sakurama, K.; Mou, S.; Ahn, H.S. Distributed Control for an Urban Traffic Network. IEEE Trans. Intell. Transp. Syst. 2022, 23, 22937–22953. [Google Scholar] [CrossRef]
- Qu, Z.; Pan, Z.; Chen, Y.; Wang, X.; Li, H. A distributed control method for urban networks using multi-agent reinforcement learning based on regional mixed strategy Nash-equilibrium. IEEE Access 2020, 8, 19750–19766. [Google Scholar] [CrossRef]
- Ma, Q.; Xu, S.; Lewis, F.L.; Zhang, B.; Zou, Y. Cooperative output regulation of singular heterogeneous multiagent systems. IEEE Trans. Cybern. 2015, 46, 1471–1475. [Google Scholar] [CrossRef]
- Li, Z.; Chen, M.Z.; Ding, Z. Distributed adaptive controllers for cooperative output regulation of heterogeneous agents over directed graphs. Automatica 2016, 68, 179–183. [Google Scholar] [CrossRef]
- Hu, W.; Liu, L. Cooperative output regulation of heterogeneous linear multi-agent systems by event-triggered control. IEEE Trans. Cybern. 2016, 47, 105–116. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Cai, Y.; Lu, Y. Distributed cooperative output regulation of heterogeneous linear multi-agent systems based on event-and self-triggered control with undirected topology. ISA Trans. 2020, 99, 191–198. [Google Scholar] [CrossRef] [PubMed]
- Yuan, C. Cooperative H∞ output regulation of heterogeneous parameter-dependent multi-agent systems. J. Frankl. Inst.-Eng. Appl. Math. 2017, 354, 7846–7870. [Google Scholar] [CrossRef]
- Wang, Y.; Xia, J.; Wang, Z.; Zhou, J.; Shen, H. Reliable consensus control for semi-Markov jump multi-agent systems: A leader-following strategy. J. Frankl. Inst.-Eng. Appl. Math. 2019, 356, 3612–3627. [Google Scholar] [CrossRef]
- Zhang, G.; Li, F.; Wang, J.; Shen, H. Mixed H∞ and passive consensus of Markov jump multi-agent systems under DoS attacks with general transition probabilities. J. Frankl. Inst.-Eng. Appl. Math. 2023, 360, 5375–5391. [Google Scholar] [CrossRef]
- Li, M.; Deng, F.; Ren, H. Scaled consensus of multi-agent systems with switching topologies and communication noises. Nonlinear Anal.-Hybrid Syst. 2020, 36, 100839. [Google Scholar] [CrossRef]
- Li, B.; Wen, G.; Peng, Z.; Wen, S.; Huang, T. Time-varying formation control of general linear multi-agent systems under Markovian switching topologies and communication noises. IEEE Trans. Circuits Syst. II-Express Briefs 2020, 68, 1303–1307. [Google Scholar] [CrossRef]
- Liu, Z.; Yan, W.; Li, H.; Zhang, S. Cooperative output regulation problem of discrete-time linear multi-agent systems with Markov switching topologies. J. Frankl. Inst.-Eng. Appl. Math. 2020, 357, 4795–4816. [Google Scholar] [CrossRef]
- Meng, M.; Liu, L.; Feng, G. Adaptive output regulation of heterogeneous multiagent systems under Markovian switching topologies. IEEE Trans. Cybern. 2017, 48, 2962–2971. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Li, T. Cooperative output feedback tracking control of stochastic linear heterogeneous multi-agent systems. IEEE Trans. Autom. Control 2021, 33, 7154–7180. [Google Scholar]
- Dong, S.; Chen, G.; Liu, M.; Wu, Z.G. Cooperative adaptive H∞ output regulation of continuous-time heterogeneous multi-agent Markov jump systems. IEEE Trans. Circuits Syst. II-Express Briefs 2021, 68, 3261–3265. [Google Scholar] [CrossRef]
- Nguyen, N.H.A.; Kim, S.H. Leader-following consensus for multi-agent systems with asynchronous control modes under nonhomogeneous Markovian jump network topology. IEEE Access 2020, 8, 203017–203027. [Google Scholar] [CrossRef]
- Ding, L.; Guo, G. Sampled-data leader-following consensus for nonlinear multi-agent systems with Markovian switching topologies and communication delay. J. Frankl. Inst.-Eng. Appl. Math. 2015, 352, 369–383. [Google Scholar] [CrossRef]
- Nguyen, N.H.A.; Kim, S.H. Asynchronous H∞ observer-based control synthesis of nonhomogeneous Markovian jump systems with generalized incomplete transition rates. Appl. Math. Comput. 2021, 411, 126532. [Google Scholar] [CrossRef]
- Dong, J.; Yang, G.H. Robust H2 control of continuous-time Markov jump linear systems. Automatica 2008, 44, 1431–1436. [Google Scholar] [CrossRef]
- Sakthivel, R.; Sakthivel, R.; Kaviarasan, B.; Alzahrani, F. Leader-following exponential consensus of input saturated stochastic multi-agent systems with Markov jump parameters. Neurocomputing 2018, 287, 84–92. [Google Scholar] [CrossRef]
- He, G.; Zhao, J. Cooperative output regulation of T-S fuzzy multi-agent systems under switching directed topologies and event-triggered communication. IEEE Trans. Fuzzy Syst. 2022, 30, 5249–5260. [Google Scholar] [CrossRef]
- Huang, J. Nonlinear Output Regulation: Theory and Applications; SIAM: Bangkok, Thailand, 2004. [Google Scholar]
- Yaghmaie, F.A.; Lewis, F.L.; Su, R. Output regulation of linear heterogeneous multi-agent systems via output and state feedback. Automatica 2016, 67, 157–164. [Google Scholar] [CrossRef]
- Arrifano, N.S.; Oliveira, V.A. Robust H∞ fuzzy control approach for a class of markovian jump nonlinear systems. IEEE Trans. Fuzzy Syst. 2006, 14, 738–754. [Google Scholar] [CrossRef]
- Nguyen, T.B.; Kim, S.H. Nonquadratic local stabilization of nonhomogeneous Markovian jump fuzzy systems with incomplete transition descriptions. Nonlinear Anal.-Hybrid Syst. 2021, 42, 101080. [Google Scholar] [CrossRef]
- He, S.; Ding, Z.; Liu, F. Output regulation of a class of continuous-time Markovian jumping systems. Signal Process. 2013, 93, 411–419. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, L.; De Souza, C.E. Robust control of a class of uncertain nonlinear systems. Syst. Control Lett. 1992, 19, 139–149. [Google Scholar] [CrossRef]
- Wieland, P.; Sepulchre, R.; Allgöwer, F. An internal model principle is necessary and sufficient for linear output synchronization. Automatica 2011, 47, 1068–1074. [Google Scholar] [CrossRef]
- Yan, S.; Gu, Z.; Park, J.H.; Xie, X. Distributed-delay-dependent stabilization for networked interval type-2 fuzzy systems with stochastic delay and actuator saturation. IEEE Trans. Syst. Man Cybern.-Syst. 2022, 53, 3165–3175. [Google Scholar] [CrossRef]
- Yan, S.; Gu, Z.; Park, J.H.; Xie, X. A delay-kernel-dependent approach to saturated control of linear systems with mixed delays. Automatica 2023, 152, 110984. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Y. Global exponential stability of discrete-time almost automorphic Caputo–Fabrizio BAM fuzzy neural networks via exponential Euler technique. Knowl.-Based Syst. 2022, 246, 108675. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).