Abstract
In accordance with the ideas of V.I. Vernadsky, the Earth’s biosphere can exist only because of the high degree of closure of the cyclic matter transformations carried out by all living organisms by using the energy from the Sun. In the course of its evolution, the Earth’s biosphere has undergone a number of cardinal transformations, but, at least for the last 20 million years, the gas composition of the atmosphere, and primarily the concentration of carbon dioxide, has remained practically unchanged. Nevertheless, the high degree of closure of material flows in the Earth’s biosphere seems paradoxical, since closure is not an adaptive feature of an individual undergoing natural selection for traits that give an advantage here and now (the Vernadsky–Darwin paradox). The stages in the formation of the closure of the Earth’s biosphere are considered in the context of four epochs that differ in the energy available to living organisms: (1) geochemical energy; (2) solar energy; (3) energy of oxidative phosphorylation; and (4) consumption of living flesh, predation. The paper considers possible options for resolving the VD paradox using as the example models of closed ecological systems (CES) with low species diversity. The fundamental inapplicability of ecological models with rigid metabolism for the description of CES is shown. Three mechanisms for resolving the VD paradox are proposed and the conditions for their implementation are assessed: (1) a stochastic mechanism: random selection of closing organisms (decomposers) with the corresponding stoichiometric ratios; (2) changing the consumption stoichiometry by switching catabolic pathways to different types of substances (proteins, fats, carbohydrates); and (3) changing the consumption stoichiometry by choosing food, depending on the state of internal nutrient pools. The present study leads to the conclusion that the Vernadsky–Darwin paradox can be resolved in nature by combining the mechanisms that simultaneously provide both a current competitive advantage and the ability to close trophic chains with a wide variation in the composition of material flows.
Keywords:
closure of the biosphere; the Vernadsky–Darwin paradox; models of closed ecological systems MSC:
37M05
1. Introduction
The biosphere, which occupies the topmost level of the biological hierarchy, is not a mere sum of the local ecological systems that constitute it. It has the property that differentiates it from virtually any ecosystem.
The key feature of the biosphere, which ensures its long-term existence, is the balance of material flows, which is termed “closure”. In thermodynamics, a closed system is a system that exchanges only energy with the environment. In addition to this requirement, ecological closure presupposes the existence of an internal cycle of transformations in matter carried out by living organisms.
In accordance with the ideas of V.I. Vernadsky, the Earth’s biosphere can exist only because of the high degree of closure of the cyclic matter transformations carried out by all living organisms by using the energy from the Sun. Everything that an organism produces, including itself, is consumed by other organisms, etc. Thus, a continuous cyclic network of metabolic chemical transformations is established in the biosphere, thanks to the functioning of which the same atoms of chemical elements are repeatedly used by living organisms. In essence, when we say “biosphere” we mean “closure”, and when we talk about closure, we are dealing with the biosphere.
Once again, we note that ecological closure does not mean physical impermeability—an ecosystem in which there is an intensive circulation of substances or even one of some limiting growth biogen (for example, phosphorus or nitrogen in a lake) can exchange matter with the environment. In this case we can speak of partial closure, and there are coefficients for estimating the degree of an ecosystem closure [1,2]. However, for the biosphere (and for us living in it) the proximity of the closure coefficients to unity is extremely important, and the potential danger of biospheric flows’ imbalance can be illustrated by the next simple assessment.
The Earth’s atmosphere contains ~700 Gt of carbon. The mass of terrestrial biomass in carbon units is ~500 Gt. The annual net primary photosynthesis production of terrestrial plants (that is, the amount of atmospheric carbon transferred to biomass) is ~60 Gt. If plant photosynthesis were the only process, then plants would reduce the concentration of CO2 in the atmosphere to 10% of the existing level in ~10 ÷ 15 years. This level corresponds to the compensation point of C3 plants, i.e., corresponds to the cessation of plant growth and then their death. Note that C3 plants account for 95% of all land plants.
This catastrophe does not occur due to the existence of reverse flow into the atmosphere as a result of the respiration of all heterotrophic organisms, and this flow, before the beginning of the industrial era, almost perfectly matches the flow from the atmosphere.
In the course of its evolution, the Earth’s biosphere has undergone a number of cardinal transformations, but, at least for the last 20 million years, the gas composition of the atmosphere, and primarily the concentration of carbon dioxide, has remained practically unchanged [3]. The maximum range of changes in carbon dioxide concentration during the last four ice ages, which occurred over the past 400 thousand years, was ~100 p.p.m. [4]. At the same time, the range of changes in global temperature reached 10 degrees.
It is important that after such serious disturbances, the biosphere–climate system (BCS, also known as the Earth System) does not leave the region of attraction of its dynamic attractor. This indicates the existence of a mechanism or mechanisms for the conservation of a relatively stable state of the biosphere over the past 20 million years.
However, the very existence of such a highly closed and stable state of the biosphere is paradoxical. Barlow and Volk [5] first drew attention to this paradox and called it the Vernadsky paradox. The authors formulated it in the form of questions: “The puzzle is this: How can an aggregate of open-system life forms evolve and persist for billions of years within a global system that is largely closed to matter influx and outflow?” and “How is it, then, that the inputs and outputs of a myriad open-system forms a life mesh in such a way that material closure as a boundary condition of the planet does not destroy the organized subsystems?”
Later, the important role of evolution in the biosphere closure formation was emphasized in [6] and the paradox acquired a double name. Understanding of the nature of the paradox was formulated as follows: At the population/community level, every system seeks to exponential propagation and multiplication (according to the Darwinian–Maltusian law). They are necessarily open systems. However, for all of them to survive, they must be included into higher systems with cycling (biotic turnover) which trends to be closed, and is therefore more stable (according to the biogeochemical principles of Vernadsky). Moreover, multiplication, natural selection, and evolution take place at the level of population/community. However, at the level of the higher systems with biotic turnover, there is no coordinated coherent inheritance, and the complicated cycle is not able to evolve as a single whole. It means that the biotic turnover differs from the organism as a single whole with its own inheritance.
If we take into account that the current highly closed state of the biosphere, with which it entered the industrial revolution, is the result of its evolutionary and ecological development, this paradox can be formulated as follows: “The closure of the biosphere is not an adaptive property of an individual (or population)”.
To highlight the key contradiction, a more compact formulation of this paradox was proposed: “The closure of the biosphere is not an adaptive property of an individual (or population)” [7].
Indeed, in the course of natural selection, the individual that captures more resources and leaves behind more viable offspring survives, i.e., in the course of natural selection, organisms win by the advantage that comes from winning here and now. The consequences of breaking the closure of the biosphere will be felt much later than the direct results of selection. Since the closure of the biosphere occurred against the background of natural selection, working in the “orthogonal”, if not in the opposite direction, it seems logical to expand the name of this paradox to the Vernadsky–Darwin paradox (VD paradox) [7].
The biosphere has been approaching the present state for ~3.8 billion years, undergoing serious changes. Judson [8] identifies four epochs in the development of the biosphere, which differ in the source of energy available to living beings: (1) geochemical energy; (2) solar energy; (3) energy of oxidative phosphorylation; and (4) consumption of living flesh, predation. We will briefly trace the history of the biosphere in the context of the formation of its closure, comparing the change in the degree of closure of the biosphere with energy epochs, and, at the same time, consider how organisms could ensure this closure, i.e., how the biosphere resolved or overcame the VD paradox.
The very first question is: When did the biosphere appear? Not as a place where living organisms exist, but as a system of interacting organisms, populations, and ecosystems? Most experts tend to believe that life on Earth arose under anaerobic conditions near hydrothermal vents that supply energy for chemoautotrophic synthesis [8,9,10,11]. The alternative hypothesis, which suggests the heterotrophic nature of the first organisms, encounters a number of objections, which are discussed in detail in [7]. It is important that, in any case, the heterotrophic hypothesis leads to the absence of the closure of the material flow and, consequently, to the absence of the biosphere as a system of interactions.
The hypothesis of the chemoautotrophic origin of life leads to a picture of separate isolated oases of life around hydrothermal vents. There was practically no interaction between them due to the limited resources available. The global closure of material flows was virtually at zero level, and the conditions corresponded to the VD paradox.
About 2.5 billion years ago, the emergence of cyanobacteria, capable of oxygen photosynthesis, took place, which led to the ‘Great Oxidation Event’, or GOE. The oxygen concentration increased from an initial fraction of 10−5 of the current level of atmospheric oxygen, reaching 0.1–1% of the current level by ~2 billion years ago. During the GOE, the primary biosphere arose, where the global change in the gas composition of the atmosphere affected all organisms in contact with the atmosphere, and instead of separate and practically non-interacting chemoautotrophic oases, a single, even though weakly connected, quasi-ecological system arose. If we compare it with the identification of four energy epochs of life on Earth proposed above, the appearance of the biosphere corresponds to the end of the second and the beginning of the third energy epochs—the transition to oxidative phosphorylation, when the oxygen and CO2 cycle arose.
After the GOE, the concentration of oxygen in the Earth’s atmosphere did not change for 1.5 billion years. This means that a precise balance has been achieved between the rate of photosynthesis and the mineralization of organic matter carried out by decomposers. Since the oxygen concentration in the atmosphere only slightly exceeded the Pasteur point and no increased sedimentation of organic matter occurred, it can be assumed that an increased oxygen concentration was created inside the microbial mats, which ensured the rapid mineralization of dead biomass and the return of nutrients to phototrophs [12,13]. It can be supposed that microbial communities were rather highly closed systems, while the biosphere, despite the extremely accurate overall balance of material flows, was a system with weak global connections—a loosely structured biosphere. At this stage, the question arises of possible mechanisms or ways to resolve the VP paradox at the level of the microbial mat.
The next energy stage in the development of the biosphere is the transition to the consumption of living flesh, predation. An intricately branched system of trophic relationships arises, and from that moment we can talk about the biosphere as a full-fledged system; the biosphere has passed into the “mature” biosphere stage. Obviously, in such a system, additional mechanisms may arise that contribute to the elimination of the VD paradox.
The resolution of the paradox is a good example of how a purely academic interest in the mechanisms of the Earth’s biosphere formation can be of vital practical importance against the backdrop of modern global changes. Indeed, knowledge of the biosphere formation mechanisms will make it possible to obtain estimates of its stability in modern conditions and can help in finding possible ways to prevent possible catastrophic consequences [14,15,16].
The resolution of this paradox is not only of academic interest. It also has important practical objectives: (1) to obtain an assessment of the stability of the biosphere in the context of global changes and to search for possible ways to prevent potential catastrophic consequences [11,12,13] and (2) to create closed ecological human life support systems (CELSS) for the projected Lunar and Martian settlements.
The second area of practical application of theoretical studies on the formation of biosphere closure is the creation of closed ecological life support systems (CELSS) for the discussed lunar and Martian bases. Of course, in this case, it is not practical to rely on evolution, but it will be possible to create a bioengineered CELSS by taking into account and using the identified mechanisms for ensuring the closure of material flows.
Thereby the purpose of this work is to find approaches to resolving the Vernadsky–Darwin paradox using good-fitting mathematical models that take into account the restrictions associated with the closure of material flows.
2. Materials and Methods
To search for ways to resolve the VD paradox, a tool is needed to adequately describe the biosphere, taking into account its specific property—the high degree of closure of the nutrient cycle. Mathematical models can become such a tool. However, the construction of a biosphere model faces two interrelated problems: (1) the high complexity of the biosphere; (2) lack of data on the dynamics of its variables.
A comprehensive mathematical model of the biosphere will be extremely difficult to analyze: the lack of data will not allow estimating the parameters of the model, and the relatively short duration of time series of observations for a small number of variables will not allow validation of the biospheric model.
The situation seems hopeless, but we should remember the advice of one of the founders of cybernetics, W.R. Ashby [17]: “…scientist must be very careful about what questions he asks. He must ask for what he really wants to know, and not what he thinks he wants. Thus the beginner/astrophysicists/will say simply that he wants to know what the star cluster/of 20,000 members/will do, i.e., he wants the trajectories of the components. If this knowledge, however, could be given to him, it would take the form of many volumes filled with numerical tables, and he would then realise that he did not really want all that. In fact, it usually happens that the significant question is something simple, such as “will the cluster contact to a ball, or will it spread out into a disc?”
Similarly, in this case, we do not need information about the dynamics of many animal and plant species of the Earth at all, but we need to understand the mechanisms of biosphere stability and, first of all, the mechanisms for ensuring high closure of flows in the biosphere. Since the biosphere existed for a long time in the form of isolated microbial mats representing communities with low species diversity, it makes sense to start the first attempt to resolve the VD paradox from such closed ecological systems (CES).
The following definition will be useful in our future work: “If a similarity can be established between two objects in at least one specific sense, then between these objects there are relations of the original and the model” [18].
According to this definition, the CES of microbial mats and the Earth’s biosphere are models of each other in terms of closure—the key property of the biosphere. Obviously, if any mechanism ensures the closure of flows in a system with few species, then it will also work in a system with a rich species composition. Moreover, the use of small-sized CES dramatically expands the experimental capability of research. These are experimental CES of various types [19,20], including life support systems (LSS) for space applications [21,22,23,24]. Folsom microcosms and micro-CES are almost direct experimental models of the microbial mat.
Experimental CES are a unique tool for studying the biosphere.
Firstly, experimental CES, by definition, are closed, i.e., reproduce the key property of the biosphere, which means that the reproduction of a stable cycle in the experiment and the explanation of this stability in a mathematical model will make it possible to gain further insight into the mechanisms of the closure of the material flows and the stability of the biosphere.
Secondly, CES are quite simple and observable, which makes it possible to monitor the state of the system closely and continuously, which is impossible to achieve with natural ecosystems. The ability to vary the experimental conditions and to create experimental perturbations during observations is unique: it is virtually impossible to do this in natural ecosystems.
Thirdly, the observability of laboratory CES makes it possible to create almost comprehensive mathematical models of these systems, to which well-established procedures for reducing complexity can be applied, and which can ultimately lead to the construction of a unified description of various types of CES, including, in the limit, the Earth’s biosphere.
However, in order to be able to generalize and use the data obtained on laboratory ecosystems for designing a CELSS and for describing (even though conceptually) the biosphere, it is necessary to use mathematical models with a good fit to natural ecological systems in general and laboratory CES in particular.
Traditional models of ecosystems are constructed by analogy with models of chemical kinetics. In these models, each species is in fact an autocatalyst that consumes strictly defined proportions of nutrients, similar to the stoichiometric coefficients of chemical reactions. We will call such models rigid metabolism models (RM models). As the number of species described by a model increases, the stability of RM models decreases [25]. However, real ecosystems tend to become more stable as their complexity increases [26]. There is a contradiction between the trends in changes in the stability of real ecosystems and their mathematical models based on the rigid metabolism model.
In addition, the well-known competitive exclusion principle (CEP) states that the number of species stably coexisting at the same trophic level cannot exceed the amount of resources available to them [27]. Later, the CEP was expanded, showing that several species can coexist on the same nutrient substrate if their number does not exceed the number of density dependent growth control factors (DDGCFs) in the system [28,29]. DDGCFs also include substances that inhibit or promote growth and predation [30].
In nature, however, there are situations in which the so-called “paradox of the plankton” is observed [31]. The essence of the paradox is that in some ecosystems, the number of species exceeds the number of revealed DDGCFs. This situation can be observed in both aquatic and terrestrial ecosystems [32].
Since there are quite a few attempts to resolve theoretically this paradox, then the question naturally arises about the applicability of the proposed approaches to resolving the VD paradox. However, as expected, the proposed approaches are aimed at ensuring the coexistence of species, and practically do not touch upon the issues of stoichiometric compliance, and completely ignore the closure of flows. There is an attempt to resolve the paradox through the search for configurations and parameters of mathematical models, in which the coexistence of species is possible in excess of the amount of resources consumed [33], but these models work in certain, and very artificial conditions. There is an attempt to explain the paradox of plankton by the fact that in the environment there are a large number of physically separated zones that differ in resource profile, within which the coexistence of species corresponds to the principle of competitive exclusion [34]. Such approaches to resolving the plankton paradox cannot help us.
Of interest are approaches in which species coexist not under stationary conditions, but under conditions of dynamic chaos [35]. The fact that this possibility has been demonstrated on a rather simple model of one trophic level, against which many claims can be made, is not so important. It is more important to understand to what extent the regime of dynamic chaos is realizable in nature. It turned out [36] that the chaotic component in the time series of population abundance occurs in 30% of cases and is most common among plankton and insects and least among birds and mammals.
A similar approach is demonstrated in [37], which considers the evolutionary aspects of resolving the plankton paradox within the framework of game theory, where the number of species fluctuates during extinction and emergence of new species, and the ability of species to consume resources may change over time. However, to ensure the coexistence of species in such a model, a high intensity of mutations and selection is required, which might exist in plankton, but cannot be extended to other organisms.
Without denying the possible contribution of stochastics to the formation of a high level of biosphere isolation, one has to admit that stochastics alone is not enough: mechanisms are needed that work constantly and everywhere, and not in 30% of cases on a selected set of organisms. At the same time, the proposed mechanisms should simultaneously either resolve or contribute to the resolution of the plankton paradox.
When formulating the requirements for mathematical models designed to resolve the VD paradox, one more thing should be singled out, which is of critical importance.
Previously, it has been shown that in models of CES with based on rigid metabolism, taking into account not only the limiting nutrient, but also other nutrients, a nontrivial steady state is often absent, which makes it impossible to use such models to describe CES [38]. This aspect seems to be very important for further work, since it directly concerns the tools used in this theoretical study.
We will now illustrate the nature of the restrictions that make it impossible to use models with fixed stoichiometric coefficients to describe closed ecosystems. We describe the CES in the most general form, without specifying the type of trophic functions:
where the rates of matter transformation per unit biomass are denoted as ; N—the number of metabolic species ensuring chemical matter transformations; Xi—biomasses of producers and consumers; Xm—biomasses of decomposers; Sk—concentrations or amounts of nutrients taking part in the cycling and taken into account in the CES description of a selected level of accuracy; and —an analog of stoichiometric coefficient in ecology.
As we are considering the ideal case of 100% closure, we postulate that everything produced by the i-th species (including its own biomass) is consumed by other organisms, i.e., . Note that steady state is the necessary condition for the closure of such a system. Therefore, when discussing the conditions for the presence of a steady state, we are actually discussing the feasibility of the complete closure of the system, which means the possibility of a long, even potentially infinite, existence of the system.
Since the purpose of this stage is to analyze the conditions for the closure of the system with respect to the matter, we will proceed to the consideration of the steady states of the CES. We thus simplify the form of writing the original system of differential equations:
where , and asterisks mark steady-state values of variables of the CES. Here, Vi are velocities of flows entering the transformation node (metabolic species) and flows outgoing from it, which have different stoichiometry.
The nature of the limitations of models with fixed stoichiometric coefficients can be illustrated by consideration of a biologically quite abstract, but mathematically concrete example of a CES consisting of two producers (X1, X2) and one consumer (Y) (1). There are flows of biomass, carbon dioxide, oxygen, and water in the system.
Consider the conditions for the existence of a steady state in a CES. We present each process carried out by a separate species as a column vector of normalized stoichiometric coefficients with a dimension equal to the number of chemical compounds (including the biomass of species) involved in the chemical transformations in the ecosystem. For example, the process carried out by the producer X1 is represented by a vector which components are stoichiometric coefficients of the form αi1.
As an illustration, consider the general form of such vectors for an ecosystem consisting of two producers (X1, X2) and one consumer (Y) (1). There are flows of biomass, carbon dioxide, oxygen, and water in the system. For simplicity, we assume that dead organic matter is decomposed very quickly due to the high activity of the microbiota, whose biomass can be neglected.
where O describes the dynamics of O2, C—CO2, and H—H2O.
For the steady-state case, system (1) will be written as a matrix equation:
where A is the matrix composed of column vectors of stoichiometric coefficients characterizing the processes carried out by the species included in the CES of stoichiometric coefficients of the system, and . For the considered model to have steady state, Equation (2) linear in Vi must have a solution. The system of linear homogeneous Equation (2) has a nonzero solution if and only if the rank of the matrix A is less than the number of variables.
To check the possibility of the appearance of hidden dependencies of stoichiometric coefficients, which can lead to a decrease in the rank of the matrix and, therefore, to the automatic elimination of the stated problem, and to reduce the degree of arbitrariness, we will carry out a calculation using a specific example with real stoichiometric coefficients and ratios of typical biochemical reactions.
In order not to make the illustration too intricate, we will assume that organisms include only three chemical elements—oxygen, carbon, and hydrogen. Hence, in this illustrative model, organisms will consist only of fats (palmitic acid—C16H32O2—will be used as a typical representative), lignin (cinnamic acid tetramer C10H11O2 will be used as an average representative), glucose—C6H12O6, and cellulose—(C6H10O5)n. These typical representatives were chosen to assess the potential level of closure of real CELSS [39].
The corresponding equations for the synthesis and, accordingly, the decomposition of these substances have the form:
C16H32O2: 16H2O + 16CO2 ↔ C16H32O2 + 23O2
C10H11O2: 22H2O + 40CO2 ↔ 4C10H11O2 + 47O2
C6H12O6: 6H2O + 6CO2 ↔ C6H12O6 + 6O2
C6H10O5: 5H2O + 6CO2 ↔ C6H10O5 + 6O2
In order to demonstrate the stoichiometric difference between the simulated organisms (the biochemical difference between the model organisms rather than the correspondence to the compositions of real organisms is important here), we arbitrarily assign the following compositions to them:
Then the elemental composition of all components of the model can be presented as a matrix of mass fractions for the three main nutrients and the selected composition of the biomass of model organisms:
Now we write down the stoichiometric coefficients for the processes considered in the model. Process V1 corresponds to photosynthesis of biomass of Producer 1:
To calculate the stoichiometric coefficients of this process, it is necessary to find a solution to the following vector equation:
with obvious additional conditions: ν1 + ν2 = 1 and ν3 + ν4 = 1.
The stoichiometric coefficients rounded to three decimal places are: ν1 = −0.746, ν2 = −0.254, ν3 = 0.385, and ν4 = 0.615. As is customary, the sign in front of the stoichiometric coefficient indicates the loss or production of a substance in the reaction. We place the found stoichiometric coefficients in the matrix of Equation (2):
Having carried out a similar procedure for all processes, we fill the matrix:
The system of linear homogeneous Equation (2) has a nonzero solution if and only if the rank of matrix A is less than the number of variables. The rank of this matrix is 4, which means that this system has no solution.
Verification of this conclusion in computational experiments for different variants of trophic functions (a simple product of the corresponding variables and the Mitscherlich formula) confirmed its correctness. Moreover, when selecting the parameters of the model, one can obtain a rather complex transition process, which, nevertheless, ends with the extinction of one or two species (Figure 1).
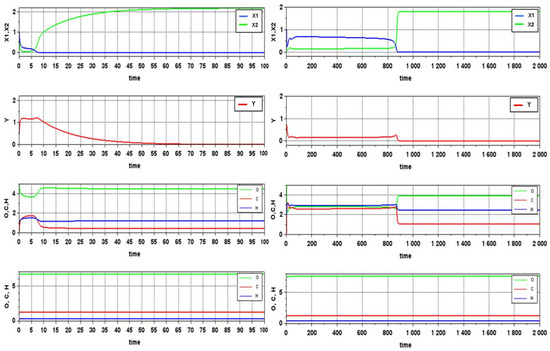
Figure 1.
Transition processes of the model at different values of the parameters. The lower graphs demonstrate the implementation of conservation laws for chemical elements. Note that such verification of the satisfiability of conservation laws was carried out for all cases in the course of computer simulations. To save space, such graphs are not shown again in the other figures.
This example illustrates the situation in which the stoichiometric ratios of elements in the organisms under consideration are chosen arbitrarily, i.e., it corresponds to the rough case that typically occurs in nature. Of course, the values of the parameters can be specifically selected to ensure the degeneracy of the matrix (which will be shown below for another model), but this non-rough case does not suit us for describing real systems.
The assessment of the presence or absence of a steady state is a non-strict mathematical proof—a situation is possible when a solution for Vi exists, but there is no suitable ratio of steady-state variables included in the expressions for Vi, for example, when they are negative. That is, the presence of a solution to this linear system does not guarantee the presence of a steady state for the model, but the absence of a solution to this system indicates the fatal absence of a steady state for the model.
Here we are faced with a very important question about our ability to distinguish between the true steady state of a real system and a very long transition process, when the rate of change of variables is less than the measurement accuracy. It seems that from a “practical” point of view, both for researchers and for the inhabitants of the ecosystem the sufficient duration of the transition process, which is orders of magnitude greater than the time of individual existence of an individual and the rate of mutational changes, is of fundamental importance. In addition, a 100% degree of closure is, most likely, an idealization that is not achievable in reality. In the future, to assess the feasibility of the CES, we will primarily rely on the duration of its existence.
There seem to be two possible ways to overcome the limitations of RM models in order to make it possible in principle to describe the exact steady state of the CES: (1) to increase the number of organisms, which formally corresponds to an increase in the number of variables in the system of the considered type, and (2) to switch to ecosystem models in which stoichiometric coefficients can change (models with flexible metabolism, FM models). Obviously, removing the limitation of RM models is a necessary, but perhaps not sufficient, condition for resolving the VD paradox. We will now take a look at how the two approaches discussed above can contribute to overcoming the VD paradox at different stages of the evolution of the biosphere.
3. Results
3.1. The Feasibility of Closing the Microbial Mat System by Organisms with Rigid Metabolism
We now consider the possibility (conditions) of resolving the VD paradox inside microbial mats. We will construct a model of such a system, taking into account the stoichiometric proportions of nutrients (for example, carbon, nitrogen, and phosphorus) in the biomass of autotrophic and heterotrophic bacteria.
Consider the general form of the proposed model (3). Let the biomass growth rate of autotroph X depend on the concentration of nutrients in the environment (Ai) and be described by a formula close to the Mitscherlich formula [40]. Taking into account the discussion of an adequate form of the formula describing the extinction of organisms [41], we introduce a quadratic dependence of the rate of extinction on the concentration of biomass. The dying biomass turns into several forms of detritus Dk corresponding to nutrients, which are then consumed by decomposers Yi. The proportion of nutrients for each species is given by the ratio ai/bi. The decomposer mineralizes detritus by first converting it into its own biomass and then lysing the biomass of dead heterotrophic bacteria. In addition, the laws of conservation of nutrients operate in the system (Ai).
To begin with, consider the case in which the microbial mat contains one autotrophic species and one heterotrophic species in the presence of two nutrients. Then the model contains one equation each for an autotroph and a heterotroph, and two equations each for detritus and mineralized nutrients:
Now we estimate the conditions for the existence of a steady state of the system. From Equations (2)–(4) of (4), we obtain:
This condition shows that a steady state exists in the system only when the ratios of nutrients in the biomass of the autotroph and decomposer match each other, i.e., if they are genetically identical organisms. It seems obvious that organisms that perform different functions cannot have an identical structure and, therefore, an identical elemental composition determined by genetics.
One possible way to resolve the Vernadsky–Darwin paradox at the level of the microbial mat in this model is to assume that the trophic level of decomposers consists of two species differing in stoichiometric composition.
We determine what conditions the stoichiometric composition of decomposers must satisfy in the case of two types of decomposers. In model (3), we have two equations describing the dynamics of decomposers, and we write it explicitly:
Having carried out simple calculations, we find that in the steady state the following relation must be fulfilled between the biomasses of decomposers:
For expression (7) to make sense, the expression in parentheses must be positive. This requirement is met if the ratios of the amounts of nutrients in the biomass of organisms satisfy the following conditions:
Inequality-type relationships are typical of nature. They expand the conditions for the existence (coexistence) of the cycle, and one can hope for the possibility of the existence of a steady state in the CES of a microbial mat with two decomposers.
A trial numerical integration of the system equations for different parameters confirmed the feasibility of a steady state in this model (Figure 2A). At the same time, combinations of parameters for which there is no steady state were more common than combinations corresponding to a steady state. However, even in the absence of a steady state in the system, interesting dynamics of the transition process is observed: while the variables describing the key nutrients in mineral and organic (detritus) forms undergo changes, the variables describing the biomass of organisms have large values and almost do not change. The system looks quite safe. However, when the transition process is over, the system rapidly breaks down (Figure 2B).
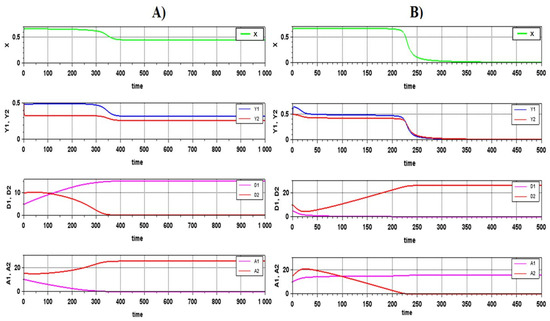
Figure 2.
Dynamics of variables of a microbial mat closed system: (A)—a mat with a stable steady state; (B)—rapid destruction of the system after the equilibrium of nutrients and detritus is established. Here and in all subsequent figures, the lower graphs represent visual control of the conformity to the laws of nutrient conservation.
To visualize the feasibility of the presence of the steady closed state in the system under conditions (7), we construct a parametric portrait of the model, that is, we estimate the regions of existence of a steady/quasi-steady state on the plane of the selected parameters. These parameters will be the specific growth rates of the autotrophic component (μX) and one of the heterotrophs (μ1) at different values of the stoichiometric composition of the other heterotroph.
Since the system is too complex for analytical study, we will use direct numerical integration of the system over a given time interval. We will assume that the system, after the integration time has elapsed, is in a steady state if the changes in the increments of the variables describing the concentrations of nutrients are less than 0.001 per step of numerical integration and the biomass of each organism is above 0.002. Obviously, with this approach, we cannot distinguish the long existence in a slow transition process from the presence of a true steady state, which is not entirely correct. However, this approach gives an idea of the range of parameter values corresponding to long-term existence, which makes it possible for the system to be modified through mutations and, as it were, start over. As noted above, from the point of view of an external observer (and what is very important, the inhabitants of the microbial mat), the true steady state and the quasi-steady state are practically indistinguishable.
The parametric portraits were calculated at a1X = 0.3; a11 = 0.2. The ranges of variations in specific growth rates were: μX = 0 ÷ 3; μ1 = 0 ÷ 10. The parametric portraits (Figure 3) show that the region of existence of a steady/quasi-steady state is not very wide, but, nevertheless, it can ensure the long-term existence of the system with noticeable variations in the stoichiometric composition of organisms resulting from the mutation process.
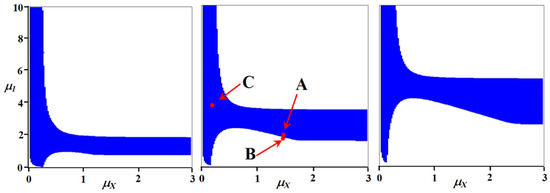
Figure 3.
Parametric portraits of the model in coordinates of the specific growth rate of an autotroph (μX) and one of the heterotrophs (μ1) at different values of the stoichiometric composition of the second heterotroph (in the order of the portraits): a12 = 0.35, 0.50, 0.80. The integration time was 5000 relative units. That is, the state of the system was assessed upon reaching this time. Coordinates of selected points for viewing system dynamics: (A) μX = 1.5, μ1 = 1.9: (B) μX = 1.5, μ1 = 1.8; (C) μX = 0.2, μ1 = 3.5.
To check the correctness of the calculation of the parametric portrait and reveal the possible features of the system behavior in different regions of the portrait, we calculated the dynamics at the points selected on the portrait (Figure 4). As expected, the regions of the “steady” state included both true steady states (point A) and states with a long transition period (point C), which corresponded to the chosen criterion in the chosen integration interval (5000 rel. time units). The change in the nature of the behavior of the system when crossing the boundary of the stable region occurs quite abruptly (point B), especially for values of μX > 1.
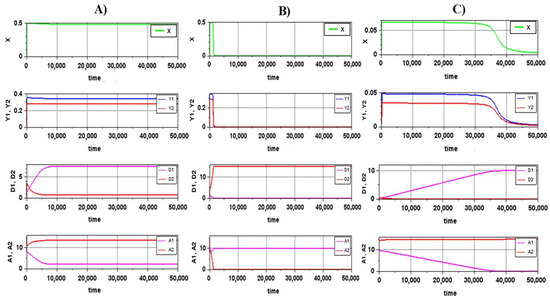
Figure 4.
Dynamics of the system corresponding to different points in the parametric portrait. The designations of the points are the same as the designations in Figure 3: (A) true steady state; (B) very fast destruction of the system when crossing the stability boundary; (C) a long transition period.
The study of a two-nutrient system could suggest that a similar method of ensuring the closure of the system by increasing the number of representatives of the trophic level of decomposers to the number of key nutrients would also work with a larger number of controlled nutrients. At the same time, it is unlikely that the number of decomposers can be greater than the number of nutrients, according to Gause’s competitive exclusion principle. It turned out that an increase in the number of decomposers to the number of key nutrients does not lead to a steady state in the CES.
Analysis of model (3) for the case with three nutrients and three decomposers showed that for the system to have steady state, the matrix of the form:
must be degenerate, i.e., have linearly dependent lines or columns, and this is virtually improbable for the independently formed values of stoichiometric coefficients. The parametric portraits of the three-nutrient system confirmed that assumption. The parametric portraits were calculated at a1X = 0.3; a2X = 0.3; a3X = 0.4; a11 = 0.1; a21 = 0.2; a31 = 0.7; a13 = 0.1; a23 = 0.7; and a33 = 0.2. The ranges in variations in specific growth rates were μX = 0÷3; μ1 = 0÷10.
As noted above, parametric portraits obtained by direct integration allow us to select areas corresponding to the existence of the system during a given period, but this existence can be a long (sometimes very long) and outwardly favorable for living organisms transition process, which ends with the destruction of the system. Figure 5 presents parametric portraits of the existence of a three-nutrient system for 5000 relative time units. In selected areas, the transitional mode can take time that is an order of magnitude longer than that used to build portraits. However, in the end, the systems come to destruction; not a single stable system was found after the transition process was completed.
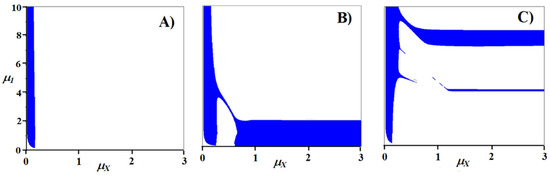
Figure 5.
Parametric portraits of the three-nutrient system with different stoichiometric relationships of the second decomposer: (A) a12 = 0.25, a22 = 0.1, a32 = 0.65; (B) a12 = 0.4, a22 = 0.1, a32 = 0.5; (C) a12 = 0.7, a22 = 0.1, a32 = 0.2.
However, if the stoichiometric ratios are selected in a special way so that they make matrix (8) degenerate, then a steady state can exist in the system in a very narrow region. Indeed, at stoichiometric ratios of the first decomposer equal to a11 = 0.1, a21 = 0.225, a31 = 0.675, the rank of matrix (9) becomes equal to 2, and there may be a steady state in the system (Figure 6A).
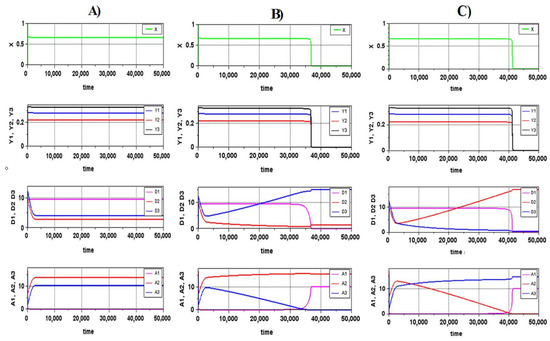
Figure 6.
Dynamics of the transition process in the three-nutrient system with a degenerate matrix (9) (non-rough case) for small deviations in the stoichiometric ratio from the singular point. The values of the variable parameter in the presence of a steady state a21 = 0.225 (A) and in the case of the extinction of the system a21 = 0.2253 (B), a21 = 0.2246 (C).
The integration of the system showed that all (except one) selected areas corresponded to a very long transition process ending in the death of the system. Only one region, indicated by an arrow in Figure 7, corresponds to the steady state. Actually, this region is a straight-line segment, but in the figure, it has a finite width because of the earlier-described method used to construct the parametric portrait, when we cannot distinguish between a long transient that looks like a steady state and a true steady state. However, from the “point of view” of living organisms, these cases are also indistinguishable until this transitional process approaches the stage of rapid catastrophic changes.
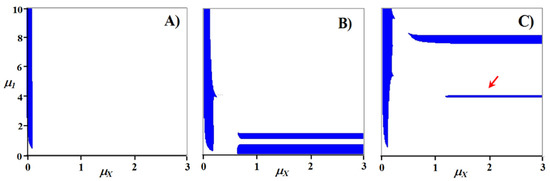
Figure 7.
The parametric portrait of the system for the non-rough case of stoichiometric ratios of the second decomposer (the values correspond to Figure 5): (A) a12 = 0.25, a22 = 0.1, a32 = 0.65; (B) a12 = 0.4, a22 = 0.1, a32 = 0.5; (C) a12 = 0.7, a22 = 0.1, a32 = 0.2. The red arrow denotes the regions of the parameters corresponding to the steady state.
Thus, theoretical analysis and computational experiments showed that the formation of closure in an ecological system with low species diversity (microbial mat), with all variables in a steady state, in the general case cannot be ensured by a mutation process that generates variants of decomposers with fixed stoichiometric coefficients. What can be achieved at the most is a long transition process with almost steady values of the biomass of organisms.
At the same time, the transition state of a system with low species diversity can be long enough for, say, mutants with a different stoichiometric ratio of nutrients to appear and for the system to pass into a new transition process. That is, to resolve the VD paradox within the framework of such a process, it is necessary to assume an almost continuous process of selection of mutants that provide acceptable stoichiometric ratios.
3.2. A Flexible Metabolism Model—“Catabolic Modifier”
Consider a microbial mat model based on the flexible metabolism notion and conceptually similar to the “Switching Paths” model [42]. According to this model, the stoichiometric coefficients of anabolism (plastic metabolism) are fixed and determined by genetics. At the same time, catabolism (energy metabolism) in the model is assumed to be variable—the body directs into energy metabolism those substances that are excessive and not needed for anabolism.
The demonstration model includes one autotroph and one heterotroph; the major detritus substances are proteins, fats, and carbohydrates; the mineral forms taken into account are carbon and nitrogen. The laws of conservation for carbon and nitrogen operate in the model. The model variables are —autotroph; —heterotroph (decomposer); —proteins (in detritus); —fats (in detritus); Ch—carbohydrates (in detritus); —carbon (mineralized, suitable for use as food for the autotroph); —nitrogen (the same as carbon); and a—average concentration of ATP as an indicator of vital functions in cells of the heterotroph.
where , Vx, KC, KN are Mitscherlich’s coefficients for the function of autotroph’s reproduction, taking into account two limiting substances;
—death rate, taking into account mineral starvation;
—the function of heterotroph’s reproduction. The formula takes into account that fats and carbohydrates are interchangeable, but proteins are not: λF, λCh, KP, KF, and KCh—coefficients of the function of heterotroph’s reproduction described below.
Functions describe nutrient consumption for energy metabolism. These functions are responsible for mineralization of proteins, fats, and carbohydrates of the dead autotroph by the heterotroph. These functions determine mortality—if it is not possible to maintain metabolism, the heterotroph begins to die off. Mortality of the heterotroph is described by the function:
In the model, βXP, βXF, βXCh, βYP, βYF, and βYCh are stoichiometric coefficients (fractions) of proteins, fats, and carbohydrates in the autotroph (X) and heterotroph (Y); γPC, γPN, γFC, γFN, γChC, and γChN are fractions of carbon and nitrogen in proteins, fats, and carbohydrates.
In this case, the following relations are satisfied:
The model assumes that the intensity of the use of proteins, fats, and carbohydrates in energy metabolism is determined by the parameters αP, αF, and αCh. Variations in these parameters change the final consumption stoichiometry
To assess the capabilities of this mechanism to ensure the closure of the material flows, simple principles for controlling the values of these coefficients are considered: (A) the coefficients are equal to each other and constant; (B) the organism sends to the energy metabolism mainly the substance whose concentration is the greatest; and (C) the substance whose utilization rate is the greatest is mainly directed to the energy metabolism.
The choice of one or another compound for catabolism was performed in the model using the SoftMax function known from neural network practice, which in this case served as a difference amplifier:
In the case of constant coefficients, the choice of a substance for catabolism is spontaneous—the substance whose quantity is the greatest is predominantly consumed in the reaction. In fact, we have the effect of an increase in the number of variables in the system of equations with the number of model equations remaining unchanged—degrees of freedom are added.
The form of parametric portraits of the model was found to be practically independent of the above methods of choosing the parameters ai. This independence is so complete that it makes no sense to show all the options. Figure 8 shows a parametric portrait of the model for the case of selection according to the rate of substance oxidation during catabolism. All parametric portraits are characterized by a wide region of stable existence of a steady state. The dynamics of the initial transition process is shown in Figure 9.
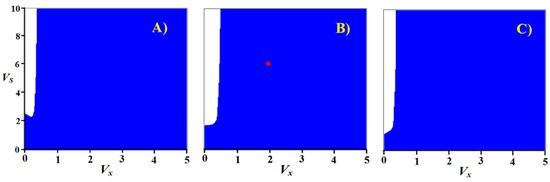
Figure 8.
Parametric portraits of the system for the case of selection according to the rate of substance oxidation during catabolism. Stoichiometric ratios: (A) βXP = 0.1, βYP = 0.1; (B) βXP = 0.1, βYP = 0.2; (C) βXP = 0.1, βYP = 0.4. Red dot on sub picture (B) represents the parameter values VX = 2 and VS = 3 which are chosen to illustrate typical dynamics of the system shown on Figure 9.
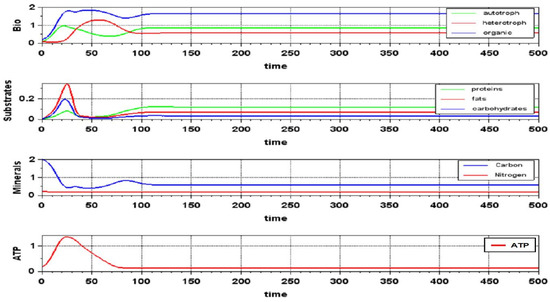
Figure 9.
The dynamics of the transition process in the “Switching Paths” model. The values of the model parameters correspond to a point on the parametric portrait in Figure 8B with the parameter values VX = 2 and VS = 3.
Analysis of the system shows that since the region of stable existence of closure in a system functioning according to the “Switching Paths” model is very extensive, the VD paradox is resolved quite simply here. It is enough for evolution to select organisms with a wide variation in the sets of substances that can be used in energy metabolism, and the possibility of such a switch provides a selective advantage here and now, which practically eliminates this paradox.
3.3. A flexible Metabolism Model—“Internal Regulatory Pool”
In small-sized systems, another variant of flexible metabolism is possible, which, in microbial mats, is implemented under the assumption that there are mineral salts with a predominant content of one of the nutrients, and the autotroph can selectively consume them. To the greatest extent, this type of flexible metabolism is associated with the appearance of predators, i.e., organisms that consume other organisms and are able to choose a victim. The appearance of predators corresponds to the onset of the fourth energy epoch in the development of life on Earth [8]—the consumption of living flesh—predation.
We will consider the corresponding model—“Internal regulatory pool” [38,42]. The model assumes that the consumed food is broken down in the body into monomers and accumulates in the corresponding internal pools, from where they are supplied for the synthesis of the organism biomass. Depending on the degree of filling of the pools, the organism selectively consumes food that predominantly contains a deficient nutrient. The minimal version of the model includes two producers (X1 and X2) and one consumer (Y) and two nutrients (for example, nitrogen and phosphorus or carbon and nitrogen, the content of which in the pools is indicated by the letters a and b with the corresponding indices, and in free form by the symbols A and B). The model has the following form:
where aim and bim denote capacity limits of the pools of the i-th organism; αi and βi are stoichiometric ratios of nutrients in the biomass of the i-th organism (αi + βi = 1); Pi() and F() are the rates of biomass synthesis from the nutrients contained in the pools; ki—constants of food uptake rate.
As can be seen from the parametric portraits (Figure 10), the region of existence of a stable steady state in the system is very large and is practically independent of the stoichiometric ratios of nutrients in the species included in the system.
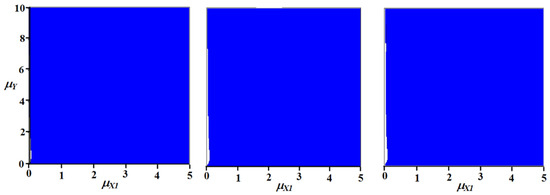
Figure 10.
A parametric portrait of a model with switching pools with different stoichiometric proportions of the biomass of one of the producers (α1 = 0.5, 0.7, 0.9).
It is important, however, that such a result is possible when the stoichiometric ratio of nutrients in the biomass of the consumer occupies an intermediate position relative to the ratios of nutrients in the biomass of the producers. For each nutrient, there must be a producer that has a greater portion of some nutrient than the consumer does.
4. Discussion
Unfortunately, it was not possible to find related publications in the literature, so it is not possible to compare obtained results with the approaches of other authors. The present study discusses three possible mechanisms for ensuring the closure/quasi-closure of material flows where several nutrients are taken into account:
- (1)
- The stochastic mechanism—random selection of closing organisms (decomposers) with the corresponding stoichiometric ratios;
- (2)
- Changing the consumption stoichiometry by switching catabolic pathways to different types of substances (proteins, fats, carbohydrates);
- (3)
- Changing the consumption stoichiometry by choosing food, depending on the state of internal nutrient pools.
The possibilities of these mechanisms in ensuring the closure of ecosystems were considered singly, each in isolation from others. At the same time, for example, the switching of catabolite pathways is characteristic of the vast majority of organisms. Therefore, it is natural to assume that in the process of evolutionary formation of the biosphere closure, all three mechanisms operate, complementing each other.
The further development of this direction is the verification and refinement of the proposed models on experimental models of low-species CES of small size. Of interest is the possibility of identifying the species diversity of heterotrophic bacteria in fossil bacterial mats in order to test the assumption about the required species diversity within an ancient bacterial CES. The proposed “Catabolic modifier” model can be, after the necessary modification, used to simulation the components (including a human beings) of the CES in the design of LSS for long-term space missions [43].
The current study leads to the conclusion that the Vernadsky–Darwin paradox can be resolved in nature by combining the mechanisms discussed in this work, which provide both the current competitive advantage and the ability to close trophic chains, with a wide variation in the composition of material flows.
5. Conclusions
- It is shown that models based on rigid metabolism (characterized by fixed values of stoichiometric coefficients of nutrient consumption) in general case do not have a non-trivial stationary state, and therefore cannot ensure the existence of a closed ecological system for an arbitrarily long time. However, the time of the transient process can be long enough to allow the appearance of mutants capable, in principle, of utilizing the dead ends of the organic matter and returning them back to the cycle.
- Models based on so-called flexible metabolism have a stable stationary state in a wide range of parameters, and therefore are capable of describing an arbitrarily long existence of a CES.
- Based on our research, we can conclude that the Vernadsky–Darwin paradox can be resolved in nature by combining the considered mechanisms that provide both the current competitive advantage and the ability to close trophic chains with a wide variation in the composition of substance flows.
Author Contributions
Conceptualization, S.B. and A.D.; methodology, A.D.; software, S.B.; formal analysis, S.B.; writing—original draft preparation, S.B.; writing—review and editing, A.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by RUSSIAN SCIENCE FOUNDATION, grant number 23-44-00059.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Finn, J.T. Measures of ecosystem structure and function derived from analysis of flows. J. Theor. Biol. 1976, 56, 363–380. [Google Scholar] [CrossRef]
- Bartsev, S.I. Naturally deducing estimate for the coefficient of CELSS closure. Adv. Space Res. 2003, 31, 75–1682. [Google Scholar] [CrossRef]
- Pearson, P.N.; Palmer, M.R. Atmospheric carbon dioxide concentrations over the past 60 million years. Nature 2000, 406, 695–699. [Google Scholar] [CrossRef]
- Mulvaney, R.; Abram, N.J.; Hindmarsh, R.C.A.; Arrowsmith, C.; Fleet, L.; Triest, J.; Sime, L.C.; Alemany, O.; Foord, S. Recent Antarctic Peninsula warming relative to Holocene climate and ice-shelf history. Nature 2012, 489, 141–144. [Google Scholar] [CrossRef]
- Barlow, C.; Volk, T. Open systems living in a closed biosphere: A new paradox for the Gaia debate. BioSystems 1990, 23, 371–384. [Google Scholar] [CrossRef]
- Pechurkin, N.S. The Biogeochemical Principles of Vernadsky as the Basis for a New Field of Science—Biospherics. J. Sib. Fed. Univ. Biol. 2008, 1, 189–193. [Google Scholar] [CrossRef]
- Bartsev, S.I.; Degermendzhi, A.G.; Sarangova, A.B. Closure of Earth’s Biosphere: Evolution and Current State. J. Sib. Fed. Univ. Biol. 2019, 12, 337–347. [Google Scholar] [CrossRef]
- Judson, O.P. The energy expansions of evolution. Nat. Ecol. Evol. 2017, 1, 9. [Google Scholar] [CrossRef]
- Lazcano, A.; Miller, S.L. The origin and early evolution of life: Prebiotic chemistry, the pre-RNA world, and time. Cell 1996, 85, 793–798. [Google Scholar] [CrossRef]
- Russell, M.J.; Hall, A.J. The onset and early evolution of life. In Evolution of Early Earth’s Atmosphere, Hydrosphere, and Biosphere—Constraints from Ore Deposits: Geological Society of America Memoir 198; Kesler, S.E., Ohmoto, H., Eds.; Geological Society of America: Boulder, CO, USA, 2006; pp. 1–32. [Google Scholar] [CrossRef]
- Amenabar, M.J.; Boyd, E.S. A review of the mechanisms of mineral-based metabolism in early Earth analog rock-hosted hydrothermal ecosystems. World J. Microbiol. Biotechnol. 2019, 35, 1–18. [Google Scholar] [CrossRef]
- Abed, R.M.M. Interaction between cyanobacteria and aerobic heterotrophic bacteria in the degradation of hydrocarbons. Int. Biodeterior. Biodegrad. 2010, 64, 58–64. [Google Scholar] [CrossRef]
- Morris, J.J.; Kirkegaard, R.; Szul, M.J.; Johnson, Z.I.; Zinser, E.R. Facilitation of robust growth of Prochlorococcus colonies and dilute liquid cultures by ‘helper’ heterotrophic bacteria. Appl. Environ. Microbiol. 2008, 74, 4530–4534. [Google Scholar] [CrossRef]
- Bartsev, S.I.; Degermendzhi, A.G.; Erokhin, D.V. Global Minimal Model of Long-Term Carbon Dynamics in the Biosphere. Dokl. Earth Sci. 2005, 401, 326–329. [Google Scholar]
- Bartsev, S.I.; Degermendzhi, A.G.; Erokhin, D.V. Principle of the worst scenario in the modelling past and future of biosphere dynamics. Ecol. Model. 2008, 216, 160–171. [Google Scholar] [CrossRef]
- Steffen, W.; Rockström, J.; Richardson, K.; Lenton, T.M.; Folke, C.; Liverman, D.; Summerhayes, C.P.; Barnosky, A.D.; Cornell, S.E.; Crucifix, M.; et al. Trajectories of the Earth System in the Anthropocene. Proc. Natl. Acad. Sci. USA 2018, 115, 8252–8259. [Google Scholar] [CrossRef]
- Ashby, W.R. An Introduction to Cybernatics; Chapman & Hall Ltd.: London, UK, 1957; 295p. [Google Scholar]
- Lerner, A.Y. The Beginnings of Cybernetics; Nauka: Moscow, Russia, 1967; 400p. (In Russian) [Google Scholar]
- Folsome, C.E.; Hanson, J.A. The emergence of materially closed system ecology. In Ecosystem Theory and Application; Polunin, N., Ed.; John Wiley & Sons: New York, NY, USA, 1986; pp. 269–299. [Google Scholar]
- Kovrov, B.G. Artificial microecosystems with a closed cycle of substances as a model of the biosphere. In Biophysics of Cell Populations and Supra-Organizational Systems; Nauka: Moscow, Russia, 1992; pp. 62–70. (In Russian) [Google Scholar]
- Gitelson, J.I.; Terskov, I.A.; Kovrov, B.G.; Sidko FYa Lisovsky, G.M.; Okladnikov, Y.N.; Belyanin, V.B.; Trubaehev, I.N. Life-support systems with autonomic control employing plant photosynthesis. Acta Astronaut. 1976, 3, 633–650. [Google Scholar] [CrossRef]
- Allen, J. Biosphere 2: The Human Experiment; Penguin Books, A Synergetic Press, Inc.: London, UK, 1991; 156p. [Google Scholar]
- Nelson, M.; Dempster, W.; Alvarez-Romo, N.; MacCallum, T. Atmospheric dynamics and bioregenerative technologies in a soil-based ecological life support system: Initial results from Biosphere 2. Adv. Space Res. 1994, 14, 417–426. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Yao, Z.; Fu, Y.; Feng, J. Review of research into bioregenerative life support system(s) which can support humans living in space. Life Sci. Space Res. 2021, 31, 113–120. [Google Scholar] [CrossRef]
- May, R.M. Stability in multi-species community models. Math. Biosci. 1971, 12, 59–79. [Google Scholar] [CrossRef]
- Ives, A.R.; Carpenter, S.R. Stability and Diversity of Ecosystems. Science 2007, 317, 58–62. [Google Scholar] [CrossRef]
- Gause, G.F. A mathematical approach to issues of struggle for existence. Zool. Zhurnal (J. Zool.) 1933, 12, 170–177. (In Russian) [Google Scholar]
- Degermendzhi, A.G.; Pechurkin, N.S.; Furyaeva, A.V. Analysis of commensal interactions of two microbial populations in continuous culture. Ekologiya (Ecology) 1978, 2, 91–94. (In Russian) [Google Scholar]
- Degermendzhi, A.G.; Pechurkin, N.S.; Tushkova, G.I.; Furyaeva, A.V. Mechanism of stable coexistence of diploid and haploid Sacharomyces cerevisiae yeasts in continuous culture. Izv. SO AN SSSR (Proc. SB USSR AS) Biol. Ser. 1979, 1, 62–68. (In Russian) [Google Scholar]
- Odum, E.P. Basic Ecology; CBS College Publishing: Philadelphia, PA, USA, 1983; 613p. [Google Scholar]
- Hutchinson, G.E. The paradox of the plankton. Am. Nat. 1961, 95, 137–145. [Google Scholar] [CrossRef]
- Levine, J.M.; HilleRisLambers, J. The importance of niches for the maintenance of species diversity. Nature 2009, 461, 254–257. [Google Scholar] [CrossRef] [PubMed]
- Record, N.R.; Pershing, A.J.; Maps, F. The paradox of the “paradox of the plankton”. ICES J. Mar. Sci. 2014, 71, 236–240. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; O’Malley, R.; Boss, E.; Karp-Boss, L. Phytoplankton biodiversity and the inverted paradox. ISME Commun. 2021, 1, 9. [Google Scholar] [CrossRef]
- Huisman, J.; Weissing, F. Biodiversity of plankton by species oscillations and chaos. Nature 1999, 402, 407–410. [Google Scholar] [CrossRef]
- Rogers, T.L.; Johnson, B.J.; Munch, S.B. Chaos is not rare in natural ecosystems. Nat. Ecol. Evol. 2022, 6, 1105–1111. [Google Scholar] [CrossRef]
- Huang, W.; de Araujo Campos, P.R.; de Oliveira, V.M.; Ferrreira, F.F. A resource-based game theoretical approach for the paradox of the plankton. PeerJ 2016, 4, e2329. [Google Scholar] [CrossRef]
- Bartsev, S.I. Stoichiometric constraints and complete closure of long-term life support systems. Adv. Space Res. 2004, 34, 1509–1516. [Google Scholar] [CrossRef] [PubMed]
- Volk, T.; Rummel, J.D. Mass Balances for a Biological Life Support System Simulation Model. Adv. Space Res. 1987, 7, 141–148. [Google Scholar] [CrossRef] [PubMed]
- Mitscherlich, E.A. Yield Laws; Akademie-Verlag: Berlin, Germany; FRG: Tokyo, Japan, 1956; 75p. (In German) [Google Scholar]
- Tyutyunov, Y.V.; Titova, L.I. From Lotka–Volterra to Arditi–Ginzburg: 90 Years of Evolving Trophic Functions. Biol. Bull. Rev. 2020, 10, 167–185. [Google Scholar] [CrossRef]
- Saltykov, M.Y.; Bartsev, S.I.; Lankin, Y.P. Stability of Closed Ecology Life Support Systems (CELSS) models as dependent upon the properties of metabolism of the described species. Adv. Space Res. 2012, 49, 223–229. [Google Scholar] [CrossRef]
- Antonenko, S.V.; Bartsev, S.I.; Degermendzhi, A.G. An Artificial Habitat for Colonizing the Solar System. Her. Russ. Acad. Sci. 2015, 85, 402–411. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).