Abstract
It is well known that the permanent magnet synchronous motor (PMSM) exhibits chaotic characteristics when its parameters fall within a certain range, which can lead to system instability. This article proposes an adaptive control strategy for achieving the fixed-time chaotic stabilization of PMSM, even in the presence of unknown parameters and perturbations. The developed controller is synthesized by combining a parametric adaptive mechanism with a fixed-time control technique. The stability analysis demonstrates that the system states under the developed controller can converge to small neighborhoods around the equilibrium point within a fixed time. Thanks to the adoption of the parametric adaptive mechanism, the developed controller is not only insensitive to unknown parameters but also robust against perturbations. Finally, simulated studies are conducted to verify and emphasize the effectiveness of the developed control strategy.
Keywords:
permanent magnet synchronous motor; chaotic stabilization; fixed-time control; adaptive control MSC:
34C28; 37D45; 93C40
1. Introduction
Permanent magnet synchronous motors (PMSMs) play a crucial role in various industrial applications. It is well-known that PMSMs can exhibit chaotic behavior when their parameters fall within a certain range, which may lead to system instability. Ensuring the safe operation of PMSMs requires the significant consideration of chaotic stabilization [1,2,3]. Chaotic systems exhibit irregular and unpredictable dynamic behavior, which is highly insensitive to initial conditions. To control or manipulate chaotic systems, two main approaches are commonly used. The first approach involves using feedback control techniques to regulate the system states from chaos to order. The second approach involves estimating the system states using filtering techniques and then utilizing these estimates for regulation. The chaotic stabilization of PMSMs falls under the first approach, where appropriate feedback control is added to achieve the desired behavior. Various methods have been extensively investigated for chaotic control, including adaptive control [4,5,6], backstepping control [7,8,9,10,11,12,13,14], sliding mode control [15,16,17,18,19,20,21,22], iterative learning control [23], and intelligent control [24,25,26,27,28,29,30,31,32,33,34,35].
Notably, most of the above controllers can only achieve asymptotic stabilization or, at best, exponential stabilization. In contrast, finite-time control can ensure that the system states stabilize to zero or small neighborhoods around zero within a bounded settling time. Finite-time control is mainly designed based on either the homogeneous system theory [36] or the finite-time Lyapunov stability theory [37]. Finite-time controllers have been utilized for the stabilization of chaotic systems in [38,39,40,41,42,43,44,45,46]. In [47], a finite-time adaptive control scheme was implemented for the chaotic stabilization of PMSM with uncertain parameters. Moreover, ref. [48] developed a terminal sliding mode controller for the finite-time synchronization of fractional-order PMSM.
However, finite-time control has the disadvantage of having the settling time heavily determined by the initial system states, which limits its practical application. Fortunately, fixed-time control can overcome this weakness, as its settling time is bounded and independent of the initial system states. Fixed-time control is primarily designed based on the bilimit homogeneous system theory [49] or the fixed-time Lyapunov stability theory [50,51]. Fixed-time controllers have been developed for the stabilization of chaotic systems in [52,53,54,55,56,57]. For instance, ref. [58] proposed a fixed-time adaptive control approach for the stabilization of the Lorenz system, while a similar controller was applied to the stabilization and synchronization of hyperchaotic Lü systems in [59]. However, these studies [58,59] did not consider perturbations, and the performance of the controllers in the presence of perturbations cannot be guaranteed.
Inspired by the aforementioned content, in this article, we propose an adaptive control strategy for achieving the fixed-time chaotic stabilization of PMSM in the presence of unknown parameters and perturbations. The developed controller is a combination of the parametric adaptive mechanism and fixed-time control technique. The major contributions of this work are two-fold.
- The developed controller is designed within the fixed-time control framework. Stability analysis demonstrates that the developed controller can ensure the system states stabilize within a fixed time to small neighborhoods around the equilibrium point.
- The parametric adaptive mechanism is incorporated into the developed controller to estimate the unknown parameters and perturbations, respectively. Unlike the controllers in [58,59], this design ensures that the developed controller is not only insensitive to unknown parameters but also robust against perturbations.
2. Preliminaries and Problem Description
2.1. Preliminaries
The following lemmas can support to obtain the main results.
Lemma 1
(Ref. [51]). Consider the nonlinear system:
where is a continuous function vector and stands for the set of real numbers. If there is a positive definite function , such that , where , , , , and , then system (1) is practically fixed-time stable and can stabilize to the following small neighborhood about zero:
where , in fixed time .
Lemma 2
(Ref. [60]). For , , , , , the following inequality is true:
Lemma 3
(Ref. [60]). For , , , and , the following inequalities are true:
2.2. Problem Description
Referring to [1,2], the PMSM system can be expressed as
where is the quadrature-axis current, is the direct-axis current, is the motor angular frequency, and and are the system parameters. When and , the PMSM system has the chaotic characteristics. The chaotic phenomena are illustrated in Figure 1 with the initial states set as , , and . Let . It is easy to find that the PMSM system has three equilibrium points , , and .
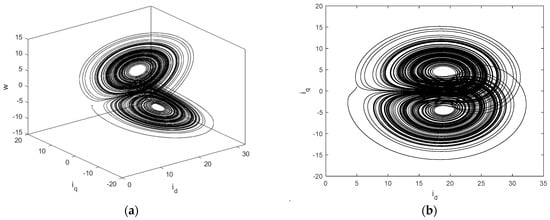
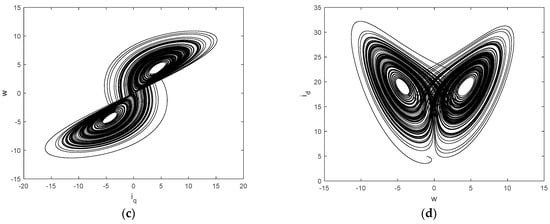
Figure 1.
Chaos of the PMSM system: (a) projection on the XYZ space; (b) projection on the XY plane; (c) projection on the YZ plane; (d) projection on the ZX plane.
The PMSM system in the presence of controls and perturbations can be described as
where , , and are the control inputs and , , and are the perturbations. The parameters and and the perturbations , , and are supposed to be unknown in the control design.
The objective is to develop an appropriate controller such that the system states can stabilize to the small neighborhoods about the specific equilibrium point in fixed time.
3. Main Results
The main results are provided in this section. First, the controller is developed for the chaotic stabilization about the equilibrium point . Then, the controllers for the chaotic stabilization about the equilibrium points and are designed in a similar way.
3.1. Chaotic Control about
Theorem 1.
For PMSM system (6), if the fixed-time adaptive controller is developed as
where , , , , , , , , , , , , and are the estimations of , , , , and , is defined as , and the parametric adaptive mechanism is provided as
where , , , , , , , , , and , then the system states can stabilize to the small neighborhoods about the equilibrium point in fixed time.
Proof.
The Lyapunov function is involved as
where , , , , and are the estimation errors of , , , , and . Evaluating the time differentiation of yields
Substituting the fixed-time adaptive controller (7) and the parametric adaptive mechanism (8) into (10), we have
It is not difficult to derive the following inequalities:
Substituting the above inequalities into (11), we have
where is defined as
Consider the item in the above inequality. Two cases are discussed in the sequel. For the case that , we have
For the case that , recalling Lemma 2, we have
where . Construct a compact set satisfying , where . Combining (19) and (20), we have the following inequality:
where is defined as
Likewise, the following inequalities can be easily derived:
Substituting the above inequalities into (17) and recalling Lemma 3, we have
where , , and are defined as
By Lemma 1, the closed-loop system is practically fixed-time stable and can stabilize to the following small neighborhood about zero:
where , in fixed time, . Recalling the definition of , it follows that all error variables , , , , , , , and can stabilize to the small neighborhoods about zero in fixed time. This completes the proof. □
3.2. Chaotic Control about and
Similarly, the controllers for the chaotic stabilization about the equilibrium points and are provided in Theorems 2 and 3, respectively.
Theorem 2.
For PMSM system (6), if the fixed-time adaptive controller is developed as
and the parametric adaptive mechanism is provided as
then the system states can stabilize to the small neighborhoods about the equilibrium point in fixed time.
Theorem 3.
For PMSM system (6), if the fixed-time adaptive controller is developed as
and the parametric adaptive mechanism is provided as
then the system states can stabilize to the small neighborhoods about the equilibrium point in fixed time.
Remark 1.
It is worth noting that perturbations were not considered in [58,59], and as a result, the performance of the controllers in those studies in the presence of perturbations cannot be guaranteed. In contrast, in this article, we have embedded the parametric adaptive mechanism (Equation (8)) to estimate the unknown parameters and perturbations. This design ensures that the developed controller is not only insensitive to unknown parameters, but also robust against perturbations.
Remark 2.
The dynamic behavior of chaotic systems, such as the PMSM system, is irregular, unpredictable, and highly insensitive to initial conditions. Due to this inherent nature, achieving complete stabilization of chaotic systems is impossible. In fact, the developed controller cannot stabilize the attractor itself but can only guide the system states to achieve the desired behavior.
4. Simulated Studies
Simulated studies are carried out to demonstrate the developed control strategy in this section. Without loss of generality, we take account of the chaotic stabilization about the equilibrium point . The following simulations are deployed though two scenarios. Scenario 1 is the performance comparisons and Scenario 2 is the fixed-time stability tests.
4.1. Performance Comparisons
In Scenario 1, the performance comparisons are made to show the advantages of the developed controller. In the simulations, the parameters are set as and , and the perturbations are given as , , and . The parameters and perturbations are supposed to be unknown in the control design. The initial system states are chosen as , , and .
Besides the developed controller (7), the existing linear feedback controller is also utilized for comparisons, which is presented as
where , , and .
In the simulations, the parameters of the developed controller (7) are made as , , , , , , , , , , , , , , , , , and . The initial values of the adaptive parameters are set as , , , , and . The parameters of the existing controller (36) are made as , , and .
The simulation results of Scenario 1 are given in Figure 2, Figure 3 and Figure 4. Specifically, Figure 2 shows the time history of the system states. It is desirable that both the developed and existing controllers can fulfill the chaotic stabilization successfully. Quantitatively, the steady-state state errors , , and under the developed controller are within the ranges of , , and , and under the existing controller are within the ranges of , , and . The existing controller can attain the much larger steady-state state errors than the developed controller. This implies that the stabilization performance of the developed controller is better than that of the existing controller in terms of higher control accuracy. The time history of the control inputs is presented in Figure 3. The control inputs under the existing controller even have a larger magnitude than those under the developed controller. This means that comparisons are quite fair or at least not partial to the developed controller. Figure 4 gives the time history of the adaptive parameters. These adaptive parameters are changing smoothly with time. Owing to the utilization of the parametric adaptive mechanism, the developed controller is not only insensitive to unknown parameters but also robust against perturbations. By contrast, the disturbance rejection property of the existing linear feedback controller is really poor.
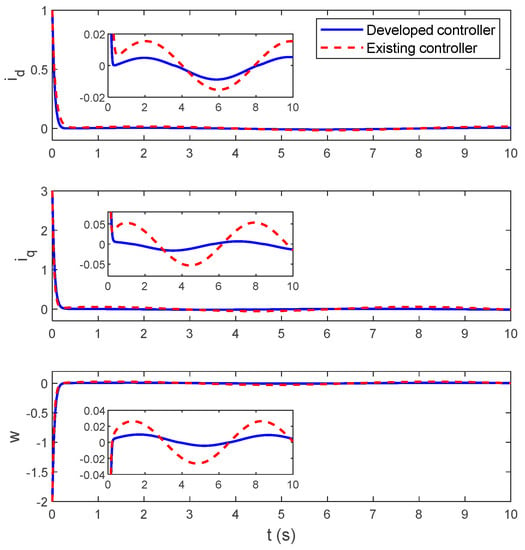
Figure 2.
System states (Scenario 1).
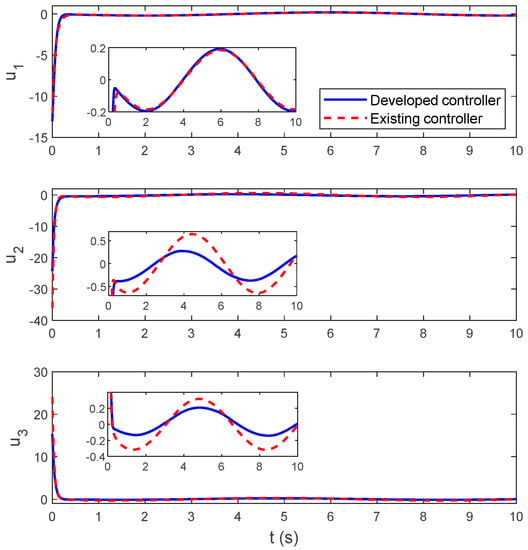
Figure 3.
Control inputs (Scenario 1).
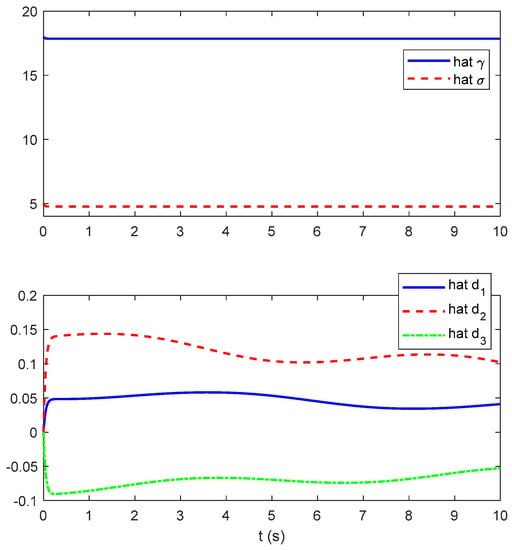
Figure 4.
Adaptive parameters (Scenario 1).
4.2. Fixed-Time Stability Tests
In Scenario 2, the tests with different initial system states are provided to examine the fixed-time stability capability of the developed controller. Three groups of initial system states are considered. In Group 1, the initial system states are chosen as , , and . In Group 2, the initial system states are chosen as , , and . In Group 3, the initial system states are chosen as , , and . In Group 4, the initial system states are chosen as , , and . The perturbations and parameters of the developed controller (7) are chosen in the same way as those in Scenario 1.
The simulation results of Scenario 2 are provided in Figure 5 and Figure 6. It is clearly seen that the developed controller can realize the chaotic stabilization within the similar settling time in the presence of different initial system states. This means that the settling time is bounded and particularly the upper bound is irrelevant to the initial system states. Therefore, it can be derived that the developed controller has the fixed-time stability capability.
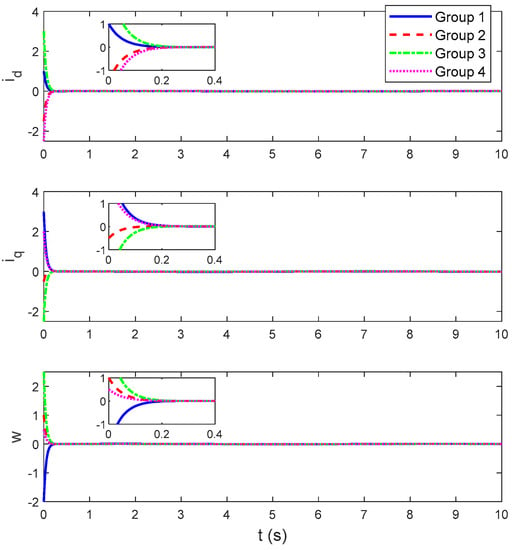
Figure 5.
System states (Scenario 2).
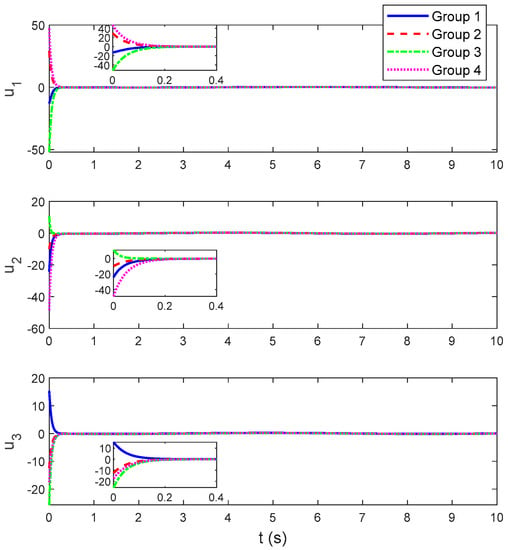
Figure 6.
Control inputs (Scenario 2).
5. Conclusions
This article addresses the fixed-time chaotic stabilization of PMSM subject to unknown parameters and perturbations by developing an adaptive control strategy. The developed controller is synthesized by combining it with the parametric adaptive mechanism under the fixed-time control framework. Stability analysis demonstrates that the system states under the developed controller can stabilize within fixed time to small neighborhoods around the equilibrium point. A distinctive advantage of the developed controller is its insensitivity to unknown parameters and robustness against perturbations. Finally, the developed control strategy is verified and highlighted through simulated studies.
Author Contributions
Conceptualization, Q.Y., H.J., S.B., J.L. and A.A.A.-B.; methodology, Q.Y., H.J., S.B., J.L. and A.A.A.-B.; software, Q.Y., H.J., S.B., J.L. and A.A.A.-B.; validation, Q.Y., H.J., S.B., J.L. and A.A.A.-B.; formal analysis, Q.Y., H.J., S.B., J.L. and A.A.A.-B.; writing—original draft, Q.Y., H.J., S.B., J.L. and A.A.A.-B.; writing—review & editing, Q.Y., H.J., S.B., J.L. and A.A.A.-B.; supervision, Q.Y. and H.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was funded by Institutional Fund Projects under grant no. (IFPIP: 600-611-1443). The authors gratefully acknowledge technical and financial support provided by the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jing, Z.; Park, J.B.; Joo, Y.H.; Zhang, B.; Chen, G. Bifurcations and chaos in a permanent-magnet synchronous motor. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 383–387. [Google Scholar]
- Jing, Z.; Yu, C.; Chen, G. Complex dynamics in a permanent-magnet synchronous motor model. Chaos Solitons Fractals 2004, 22, 831–848. [Google Scholar] [CrossRef]
- Zribi, M.; Oteafy, A.; Smaoui, N. Controlling chaos in the permanent magnet synchronous motor. Chaos Solitons Fractals 2009, 41, 1266–1276. [Google Scholar] [CrossRef]
- Chen, S.; Lü, J. Synchronization of an uncertain unified chaotic system via adaptive control. Chaos Solitons Fractals 2002, 14, 643–647. [Google Scholar] [CrossRef]
- Chen, S.; Lü, J. Parameters identification and synchronization of chaotic systems based upon adaptive control. Phys. Lett. A 2002, 299, 353–358. [Google Scholar] [CrossRef]
- Yau, H.-T.; Chen, C.-L. Chaos control of Lorenz systems using adaptive controller with input saturation. Chaos Solitons Fractals 2007, 34, 1567–1574. [Google Scholar] [CrossRef]
- Wang, C.; Ge, S.S. Adaptive synchronization of uncertain chaotic systems via backstepping design. Chaos Solitons Fractals 2001, 12, 1199–1206. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, S. Adaptive backstepping synchronization of uncertain chaotic system. Chaos Solitons Fractals 2004, 21, 643–649. [Google Scholar] [CrossRef]
- Bowong, S.; Kakmeni, F.M.M. Synchronization of uncertain chaotic systems via backstepping approach. Chaos Solitons Fractals 2004, 21, 999–1011. [Google Scholar] [CrossRef]
- Bowong, S. Adaptive synchronization of chaotic systems with unknown bounded uncertainties via backstepping approach. Nonlinear Dyn. 2007, 49, 59–70. [Google Scholar] [CrossRef]
- Peng, C.-C.; Chen, C.-L. Robust chaotic control of Lorenz system by backstepping design. Chaos Solitons Fractals 2008, 37, 598–608. [Google Scholar] [CrossRef]
- Yu, S.-H.; Hyun, C.-H.; Park, M. Control and synchronization of new hyperchaotic system using active backstepping design. Int. J. Fuzzy Log. Intell. Syst. 2011, 11, 77–83. [Google Scholar] [CrossRef]
- Yu, S.-H.; Hyun, C.-H.; Park, M. Backstepping control and synchronization for 4-D Lorenz-Stenflo chaotic system with single input. Int. J. Fuzzy Log. Intell. Syst. 2011, 11, 143–148. [Google Scholar] [CrossRef]
- Tu, J.; He, H.; Xiong, P. Adaptive backstepping synchronization between chaotic systems with unknown Lipschitz constant. Appl. Math. Comput. 2014, 236, 10–18. [Google Scholar] [CrossRef]
- Yau, H.-T. Design of adaptive sliding mode controller for chaos synchronization with uncertainties. Chaos Solitons Fractals 2004, 22, 341–347. [Google Scholar] [CrossRef]
- Yan, J.-J.; Yang, Y.-S.; Chiang, T.-Y.; Chen, C.-Y. Robust synchronization of unified chaotic systems via sliding mode control. Chaos Solitons Fractals 2007, 34, 947–954. [Google Scholar] [CrossRef]
- Li, W.-L.; Chang, K.-M. Robust synchronization of drive-response chaotic systems via adaptive sliding mode control. Chaos Solitons Fractals 2009, 39, 2086–2092. [Google Scholar] [CrossRef]
- Wang, B.; Wen, G. On the synchronization of uncertain master-slave chaotic systems with disturbance. Chaos Solitons Fractals 2009, 41, 145–151. [Google Scholar] [CrossRef]
- Feki, M. Sliding mode control and synchronization of chaotic systems with parametric uncertainties. Chaos Solitons Fractals 2009, 41, 1390–1400. [Google Scholar] [CrossRef]
- Zribi, M.; Smaoui, N.; Salim, H. Synchronization of the unified chaotic systems using a sliding mode controller. Chaos Solitons Fractals 2009, 42, 3197–3209. [Google Scholar] [CrossRef]
- Pourmahmood, M.; Khanmohammadi, S.; Alizadeh, G. Synchronization of two different uncertain chaotic systems with unknown parameters using a robust adaptive sliding mode controller. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 2853–2868. [Google Scholar] [CrossRef]
- Liu, H.; Yang, J. Sliding-mode synchronization control for uncertain fractional-order chaotic systems with time delay. Entropy 2015, 17, 4202–4214. [Google Scholar] [CrossRef]
- Cheng, C.-K.; Chao, P.C.-P. Trajectory tracking between Josephson junction and classical chaotic system via iterative learning control. Appl. Sci. 2018, 8, 1285. [Google Scholar] [CrossRef]
- Kim, J.-H.; Park, C.-W.; Kim, E.; Park, M. Fuzzy adaptive synchronization of uncertain chaotic systems. Phys. Lett. A 2005, 334, 295–305. [Google Scholar] [CrossRef]
- Liu, Y.-J.; Zheng, Y.-Q. Adaptive robust fuzzy control for a class of uncertain chaotic systems. Nonlinear Dyn. 2009, 57, 431–439. [Google Scholar] [CrossRef]
- Lin, D.; Wang, X. Self-organizing adaptive fuzzy neural control for the synchronization of uncertain chaotic systems with random-varying parameters. Neurocomputing 2011, 74, 2241–2249. [Google Scholar] [CrossRef]
- Lin, D.; Wang, X.; Yao, Y. Fuzzy neural adaptive tracking control of unknown chaotic systems with input saturation. Nonlinear Dyn. 2012, 67, 2889–2897. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Shahriari-Kahkeshi, M.; Alcaraz, R.; Wang, X.; Singh, V.P.; Pham, V.-T. Entropy analysis and neural network-based adaptive control of a non-equilibrium four-dimensional chaotic system with hidden attractors. Entropy 2019, 21, 156. [Google Scholar] [CrossRef]
- Le, T.-L.; Huynh, T.-T.; Nguyen, V.-Q.; Lin, C.-M.; Hong, S.-K. Chaotic synchronization using a self-evolving recurrent interval type-2 Petri cerebellar model articulation controller. Mathematics 2020, 8, 219. [Google Scholar] [CrossRef]
- Zhu, Z.-Y.; Zhao, Z.-S.; Zhang, J.; Wang, R.-K.; Li, Z. Adaptive fuzzy control design for synchronization of chaotic time-delay system. Inf. Sci. 2020, 535, 225–241. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Munoz-Pacheco, J.M.; Moroz, I.; Wei, Z.; Castillo, O. A new multi-stable fractional-order four-dimensional system with self-excited and hidden chaotic attractors: Dynamic analysis and adaptive synchronization using a novel fuzzy adaptive sliding mode control method. Appl. Soft Comput. 2020, 87, 105943. [Google Scholar] [CrossRef]
- Wang, S.-Y.; Lin, C.-M.; Li, C.-H. Design of adaptive TSK fuzzy self-organizing recurrent cerebellar model articulation controller for chaotic systems control. Mathematics 2021, 11, 1567. [Google Scholar] [CrossRef]
- Xiong, P.-Y.; Jahanshahi, H.; Alcaraz, R.; Chu, Y.-M.; Gómez-Aguilar, J.F.; Alsaadi, F.E. Spectral entropy analysis and synchronization of a multi-stable fractional-order chaotic system using a novel neural network-based chattering-free sliding mode technique. Chaos Solitons Fractals 2021, 144, 110576. [Google Scholar] [CrossRef]
- Yao, Q. Neural adaptive learning synchronization of second-order uncertain chaotic systems with prescribed performance guarantees. Chaos Solitons Fractals 2021, 152, 111434. [Google Scholar] [CrossRef]
- Zaqueros-Martinez, J.; Rodriguez-Gomez, G.; Tlelo-Cuautle, E.; Orihuela-Espina, F. Fuzzy synchronization of chaotic systems with hidden attractors. Entropy 2023, 25, 495. [Google Scholar] [CrossRef] [PubMed]
- Bhat, S.P.; Bernstein, D.S. Geometric homogeneity with applications to finite-time stability. Math. Control Signals Syst. 2005, 17, 101–127. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Li, S.; Tian, Y.-P. Finite time synchronization of chaotic systems. Chaos Solitons Fractals 2003, 15, 303–310. [Google Scholar] [CrossRef]
- Aghababa, M.P.; Khanmohammadi, S.; Alizadeh, G. Finite-time synchronization of two different chaotic with unknown parameters via sliding mode technique. Appl. Math. Model. 2011, 35, 3080–3091. [Google Scholar] [CrossRef]
- Aghababa, M.P.; Aghababa, H.P. Chaos suppression of rotational machine systems via finite-time control method. Nonlinear Dyn. 2012, 69, 1881–1888. [Google Scholar] [CrossRef]
- Aghababa, M.P.; Aghababa, H.P. A general nonlinear adaptive control scheme for finite-time synchronization of chaotic systems with uncertain parameters and nonlinear inputs. Nonlinear Dyn. 2012, 69, 1903–1914. [Google Scholar] [CrossRef]
- Wang, S.; Yousefpour, A.; Yusuf, A.; Jahanshahi, H.; Alcaraz, R.; He, S.; Munoz-Pacheco, J.M. Synchronization of a non-equilibrium four-dimensional chaotic system using a disturbance-observer-based adaptive terminal sliding mode control method. Entropy 2020, 22, 271. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.; Yousefpour, A.; Jahanshahi, H.; Kocamaz, U.E.; Moroz, I. Hopf bifurcation and synchronization of a five-dimensional self-exciting homopolar disc dynamo using a new fuzzy disturbance-observer-based terminal sliding mode control. J. Frankl. Inst. 2021, 358, 814–833. [Google Scholar] [CrossRef]
- Narayanan, G.; Ali, M.S.; Alam, M.I.; Rajchakit, G.; Boonsatit, N.; Kumar, P.; Hammachukiattikul, P. Adaptive fuzzy feedback controller design for finite-time Mittag-Leffler synchronization of fractional-order quaternion-valued reaction-diffusion fuzzy molecular modeling of delayed neural networks. IEEE Access 2021, 9, 130862–130883. [Google Scholar] [CrossRef]
- Wang, Y.-L.; Jahanshahi, H.; Bekiros, S.; Bezzina, F.; Chu, Y.-M.; Aly, A.A. Deep recurrent neural networks with finite-time terminal sliding mode control for a chaotic fractional-order financial system with market confidence. Chaos Solitons Fractals 2021, 146, 110881. [Google Scholar] [CrossRef]
- Alsaadi, F.E.; Jahanshahi, H.; Yao, Q.; Mou, J. Recurrent neural networkbased technique for synchronization of fractional-order systems subject to control input limitations and faults. Chaos Solitons Fractals 2023, 173, 113717. [Google Scholar] [CrossRef]
- Wang, J.; Chen, X.; Fu, J. Adaptive finite-time control of chaos in permanent magnet synchronous motor with uncertain parameters. Nonlinear Dyn. 2014, 78, 1321–1328. [Google Scholar] [CrossRef]
- Narayanan, G.; Ali, M.S.; Iqbal, M.M.; Kumar, P. Synchronization of fractional-order permanent magnet synchronous generator model based on terminal sliding mode control with switching surface. Math. Eng. Sci. Aerosp. 2021, 12, 655–667. [Google Scholar]
- Andrieu, V.; Praly, L.; Astolfi, A. Homogeneous approximation, recursive observer design, and output feedback. SIAM J. Control Optim. 2008, 47, 1814–1850. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control. 2012, 57, 2106–2110. [Google Scholar] [CrossRef]
- Jiang, B.; Hu, Q.; Friswell, M.I. Fixed-time attitude control for rigid spacecraft with actuator saturation and faults. IEEE Trans. Control Syst. Technol. 2016, 51, 332–340. [Google Scholar] [CrossRef]
- Ni, J.; Liu, L.; Liu, C.; Hu, X.; Li, S. Fast fixed-time nonsingular terminal sliding mode control and its application to chaos suppression in power system. IEEE Trans. Circuits Syst. II Exp. Briefs 2017, 64, 151–155. [Google Scholar] [CrossRef]
- Yao, Q. Synchronization of second-order chaotic systems with uncertainties and disturbances using fixed-time adaptive sliding mode control. Chaos Solitons Fractals 2021, 142, 110372. [Google Scholar] [CrossRef]
- Yao, Q.; Jahanshahi, H.; Batrancea, L.M.; Alotaibi, N.D.; Rus, M.-I. Fixed-time output-constrained synchronization of unknown chaotic financial systems using neural learning. Mathematics 2022, 10, 3682. [Google Scholar] [CrossRef]
- Alsaade, F.W.; Yao, Q.; Bekiros, S.; Al-zahrani, M.S.; Alzahrani, A.S.; Jahanshahi, H. Chaotic attitude synchronization and anti-synchronization of master-slave satellites using a robust fixed-time adaptive controller. Chaos Solitons Fractals 2022, 165, 112883. [Google Scholar] [CrossRef]
- Yao, Q.; Alsaade, F.W.; Al-zahrani, M.S.; Jahanshahi, H. Fixed-time neural control for output-constrained synchronization of second-order chaotic systems. Chaos Solitons Fractals 2023, 169, 113284. [Google Scholar] [CrossRef]
- Bekiros, S.; Yao, Q.; Mou, J.; Alkhateeb, A.F.; Jahanshahi, H. Adaptive fixed-time robust control for function projective synchronization of hyperchaotic economic systems with external perturbations. Chaos Solitons Fractals 2023, 172, 113609. [Google Scholar] [CrossRef]
- Wang, H.; Yue, H.; Liu, S.; Li, T. Adaptive fixed-time control for Lorenz systems. Nonlinear Dyn. 2020, 102, 2617–2625. [Google Scholar] [CrossRef]
- Wang, H.; Ai, Y. Adaptive fixed-time control and synchronization for hyperchaotic Lü systems. Appl. Math. Comput. 2022, 433, 127388. [Google Scholar] [CrossRef]
- Hardy, G.H.; Littlewood, J.E.; Pólya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).