1. Introduction
Diverse areas of optimization and numerical analysis present obstacles for the development of derivative-free approaches. Traditional iterative techniques rely on higher-order derivatives, or only first-order derivatives in the case of multi-point classes, to guide the search for optimal solutions. However, due to the lack of formal mathematical formulations, deriving derivatives in real-world situations may be computationally expensive, impractical, or even impossible. This restriction makes it difficult for standard methodologies to be applied to complicated systems and real-world issues. Such difficulties are addressed by derivative-free approaches, which only rely on function evaluations. A considerable problem still exists in constructing such algorithms with great efficiency, convergence, and robustness. Due to this, novel strategies must be created that can successfully handle optimization issues without the use of explicit derivatives. The one-point modified Traub–Steffensen [
1] approach is one among the most well-known derivative-free techniques for multiple roots, as indicated by
where
,
,
, and
n is the multiplicity of the root.
A system’s stability can also be examined using multiple roots. Multiple roots in a dynamical system correlate to several equilibrium points, and researching the stability of these points can aid in understanding how the system behaves under various circumstances. In numerous domains, including optimization, system analysis, and stability analysis, the utilization of multiple roots of nonlinear equations can yield useful information. We can better comprehend the problem and create more effective remedies by identifying multiple roots.
For numerous zeros of nonlinear functions, various authors recently devised optimal and non-optimal (in terms of the Kung–Traub hypothesis; see [
2]) non-derivative approaches [
3,
4,
5,
6,
7].
In order to attain a high order of convergence with a minimal amount of function evaluations, a high-efficiency non-derivative technique for the multiple-roots method is proposed. On the basis of these ideas, we create a two-step derivative-free approach that converges to the fourth order. The proposed method is optimal in terms of the Kung–Traub hypothesis [
2] since it only performs three function evaluations throughout each cycle.
We compare our new derivative method with existing methods of the same order, i.e., with a derivative [
8,
9,
10,
11,
12,
13] and without a derivative [
3,
4,
5]. In the numerical section, new methods and existing methods are applied to real-life problems, i.e., Planck law radiation, Van der Waals, Manning for isentropic supersonic flow, the blood rheology model and two academics problems. The van der Waals equation is an equation of state that attempts to explain how the behavior of real gas molecules, which have finite sizes and interact with one another, differs from that of an ideal gas. The spectrum distribution of energy emitted by a black body at a specific temperature is described by the Planck law equation, a fundamental equation in quantum mechanics. It is used to explain the black body radiation that is seen and how temperature affects it. The flow rate of a fluid through a channel is determined using the empirical Manning equation in open channel flow. In order to calculate the fluid flow rate, the channel’s shape, slope, and roughness are all taken into consideration. In isentropic supersonic flow, where the fluid is moving at a high velocity and the pressure waves it generates are moving at or above the speed of sound, this equation is specifically used. Models of blood rheology use mathematics to illustrate how blood moves through the circulatory system. These simulations take into account properties like viscosity, elasticity, and shear stress to comprehend the intricate dynamics of blood flow. Comparing the newly proposed method to the current iterative root-finding method, the convergence area is wider.
The outline of the paper is given as follows:
Section 2 of the paper delves into the development of this proposed scheme and provides three essential theorems, each specifically designed for
, and
. These theorems establish the foundation for the subsequent sections. In
Section 3, the main general theorem for the convergence order is unveiled, elucidating the scheme’s efficiency. Moreover,
Section 4 expounds on the authors’ numerical experiments, where they rigorously test the scheme’s efficacy on both real-life and academic problems. Finally,
Section 5 offers concluding remarks, summarizing the paper’s contributions and outlining potential future research directions.
2. Development of Scheme
Consider the following iterative approach for
,
where
and
are the unknown parameters with
.
In order to establish the validity of our result, we conducted rigorous testing by varying the value of n across multiple instances. Through extensive experimentation and analysis, we consistently observed the same outcome, thus providing compelling evidence for the generalizability and reliability of our findings across different values of n. We first examine the situation and demonstrate the validity of the following theorem.
Theorem 1. With of Φ, let’s assume that is a multiple solution. We presume is an analytic function in D vicinity of the zero α. So, the algorithm (2) has convergence order four, when , and . Proof. is used to indicate an error at the
k-th stage. As a result of Taylor’s expansion of
about
, we yield
where
for
,
,
and
.
Similarly, we have that
about
where
and
.
From the first step of (
2), we obtain
Expanding
around
, it yields
Using (
3) and (
6), we have
Inserting (
3), (
4), (
6) and (
7) in the last step of (
2), and after some calculations, yields
where
Now, fixing the coefficients of
and
to zero, we obtain
Now, by using (
8) in (
2), we have
□
Theorem 2. If Theorem 1 is adopted, then the algorithm (2) for has at least an order of four of convergence if and . Proof. Considering that
and
expanding
around
by Taylor series gives
where
for
.
Similarly, expanding
about
yields
where
Inserting (
9) and (
10) in (
2), yields
In a similar fashion, expanding
about
, we have
From (
9) and (
13), we have
By using (
9)–(
14) in the last step of (
2), we obtain
where
.
The equations can now be solved by setting the coefficients of
and
to zero. We have
The error Equation (
15) is given by
Hence, Theorem 2 is proved. □
Now, we state the theorem for .
Theorem 3. If Theorem 1 is adopted, then the algorithm (2) for has at least 4th order of convergence if and . Furthermore, the error equation for (2) is provided by where for .
4. Numerical Results
To resolve some nonlinear equations, we use the NM with
. The examples support the theoretical findings while also demonstrating the method’s viability and effectiveness. In the continuation, we use the formula (see [
14])
to compute the computational order of convergence. The new algorithm’s performance is compared to that of the nine existing methods:
- (i)
Li et al. [
9]
iteration function (LLC):
- (ii)
Li et al. [
10]
iteration function (LCN):
where
- (iii)
Sharma and Sharma [
11]
iteration function (SSM):
- (iv)
Iteration function from Zhou et al. [
13] (ZCS):
- (v)
Iteration function from Soleymani et al. [
12] (SBM):
where
- (vi)
Iteration function from Kansal et al. [
8] (KKB):
where
- (vii)
Iteration function from Sharma et al. [
3] (SKJ):
- (viii)
Iteration function from Behl et al. [
4] (BAM):
where
- (ix)
Iteration function from Kumar et al. [
5] (KKS):
The computations are made using multiple-precision arithmetic in
Mathematica [
15]. The multiplicities of the considered functions are demonstrated in
Table 1. In addition,
Table 2,
Table 3,
Table 4,
Table 5,
Table 6 and
Table 7 contain the following points:
- (1)
The multiplicity n of the relevant function.
- (2)
The number of iterations mentioned on the basis of stopping criteria .
- (3)
The first three estimated errors of the iterative methods are recorded.
- (4)
Utilize (
26) in order to compute the COC.
- (5)
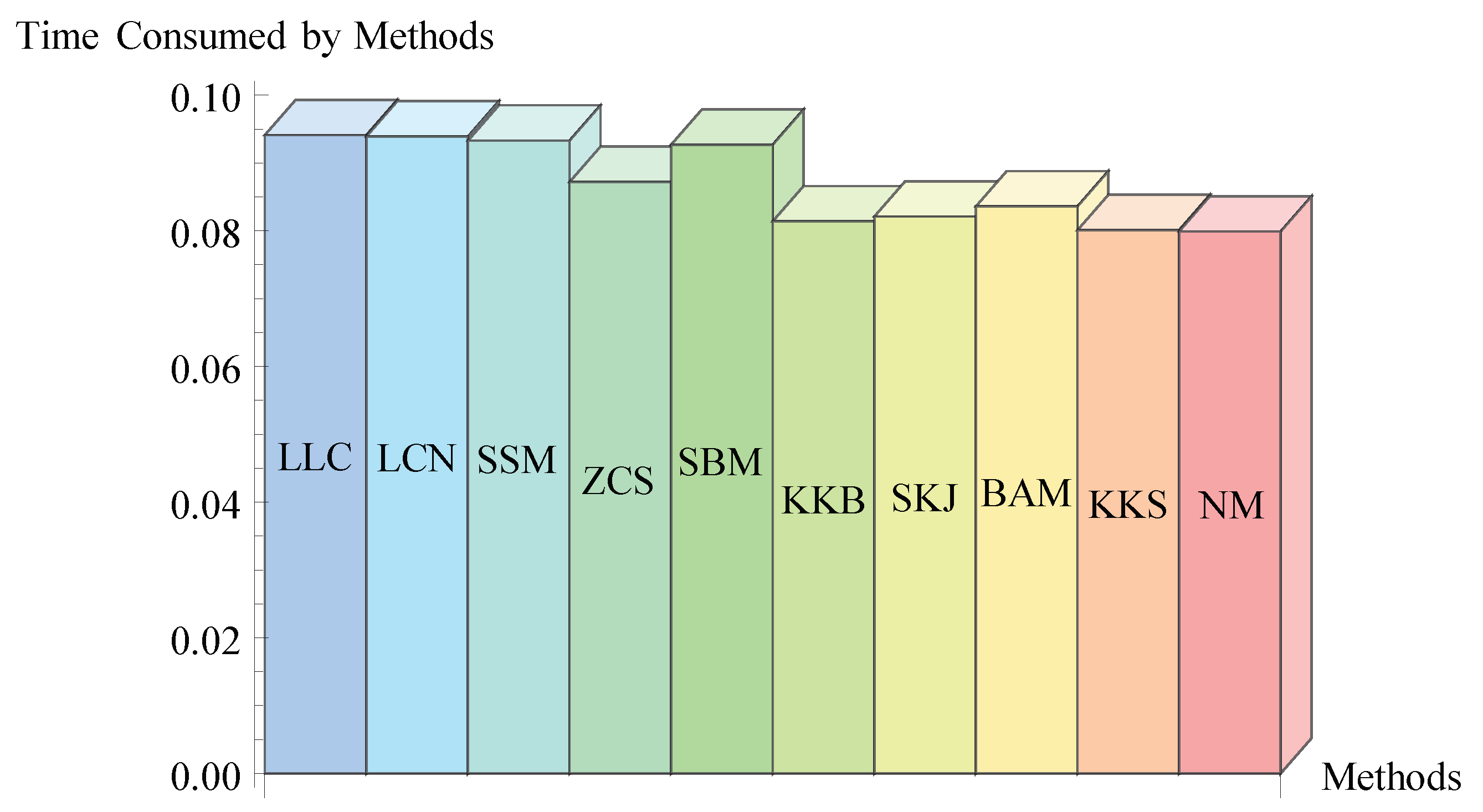
Figure 1.
Bar chart of problem .
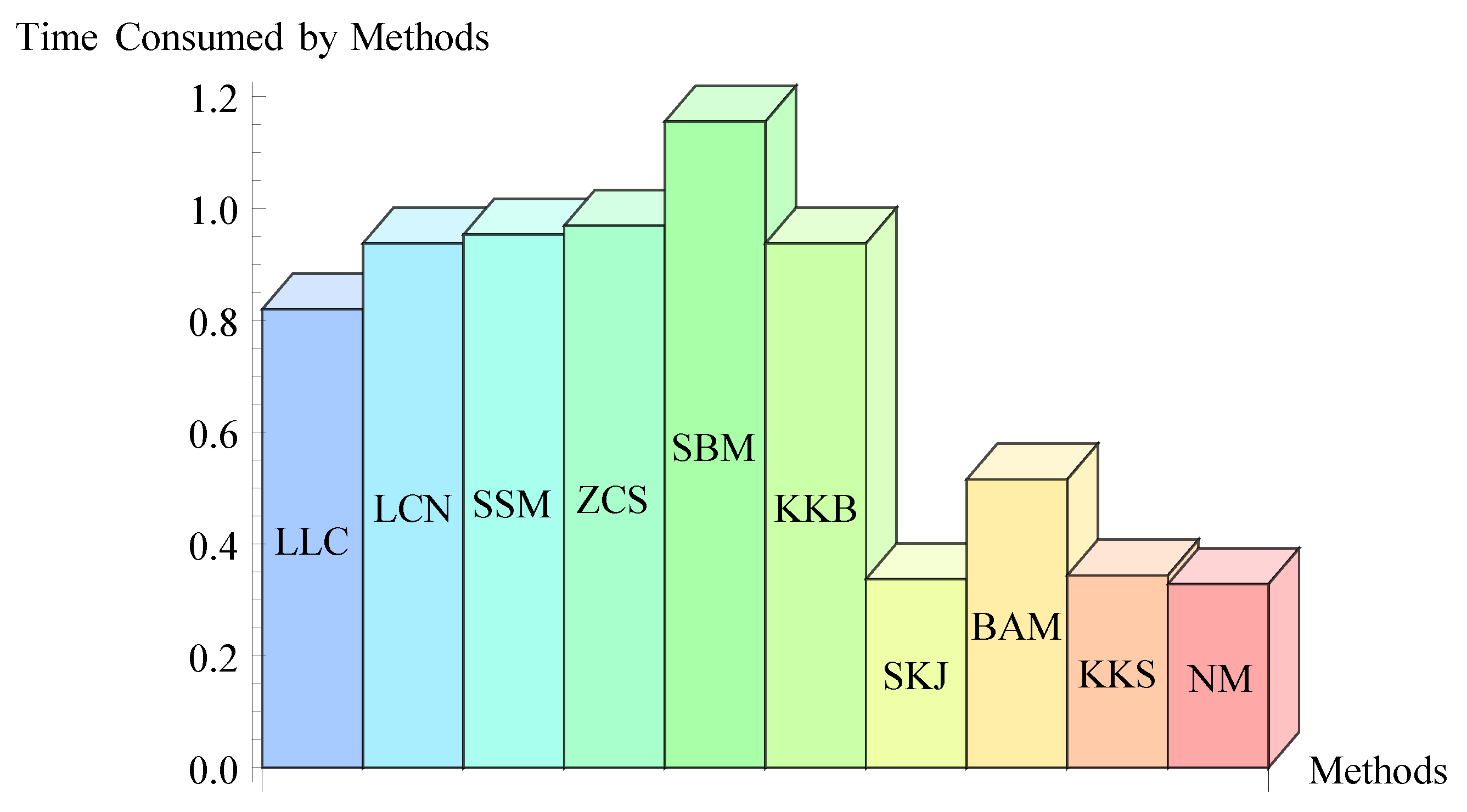
Figure 1.
Bar chart of problem .
Figure 2.
Bar chart of problem .
Figure 2.
Bar chart of problem .
Figure 3.
Bar chart of problem .
Figure 3.
Bar chart of problem .
Figure 4.
Bar chart of problem .
Figure 4.
Bar chart of problem .
Figure 5.
Bar chart of problem .
Figure 5.
Bar chart of problem .
Figure 6.
Bar chart of problem .
Figure 6.
Bar chart of problem .
Example 1. Van der Waals equation [
16]
: The Van der Waals equation is a non-differential equation that models the behavior of real gases, taking into account intermolecular forces and the finite size of gas molecules. Compared to the ideal gas law, it offers a more accurate explanation of gas behavior. The equation introduces correction terms for attractive forces and molecular volume. The Van der Waals equation finds applications in thermodynamics, chemical engineering, and material science, enabling the study of real gas behavior and phase transitions under various conditions: where we have the following:
R: universal gas constant;
V: volume;
P: pressure;
T: temperature.
To calculate the value of V, we can write (27) as There are values of n, P, R, T, and of a particular gas. In this way, the expression (28) has three solutions. So by using a specific set of values, we have It has the following three roots: , , and . The desired root is therefore . The approaches are evaluated using the initial estimate of . Table 2 presents the computed results. Example 2. Planck’s radiation law problem [
16]
: The mathematical equation for Planck’s law of radiation is given by where we have the following:
represents the spectral radiance or energy density per unit wavelength at a given wavelength λ and temperature T.
k and h stand for the Boltzmann and Planck constants, respectively.
c is the speed of light in vacuum.
λ is the wavelength of radiation.
T stand for temperature in Kelvin.
The equation expresses the spectral distribution of radiation emitted by a black body at a specific temperature T across different wavelengths λ. It shows how the radiance or intensity of the emitted radiation changes with both the temperature and wavelength.
The Planck law radiation problem focuses on the spectral distribution of radiation emitted by a blackbody at different temperatures. It describes the relationship between the intensity or energy density of radiation and the wavelength, providing insights into the behavior of electromagnetic radiation and its thermal properties in various physical systems.
It is clear that a maximum value for occurs when , implying that By choosing , we have We examined this case three times and produced the necessary nonlinear function It is clear from the above equation that it has a multiple root but it is not taken into account. Bardie [
16]
has more information. Hence, we choose as a multiple root with . Table 3 displays the numerical results. Example 3. The Manning equation is used to approximate the mean flow velocity in open channel flow (see [
17]
). The mathematical equation is as follows: Then, it shows the relationship between the Mach numbers and before and after the corner, and , γ is the specific heat ratio of the gas. The Manning equation is widely used in civil engineering and hydraulic applications for estimating flow velocities and designing open channel systems. It provides a practical approach to estimate flow characteristics in a variety of channel configurations.
We resolve the equation for in a unique case study when , and . As it is, we have where .
We took this case into consideration four times and discovered the necessary nonlinear function. The above function has zero at . Utilizing the original estimate , this zero is determined. Table 4 presents the numerical outcomes. Example 4. Blood rheology model: We take into account the research on the blood rheology model, which looks at the physical and flow properties of blood. The term Caisson fluid is used to describe blood, a non-Newtonian fluid. The Caisson fluid model predicts how fundamental fluids flow in tubes so that there is a velocity gradient from wall to wall and the fluid’s central core travels like a plug with little distortion. When analyzing the plug flow of Caisson fluids, the function is used as a nonlinear equation.
We use the non-linear equation to calculate the flow rate reduction for . This function has zero . To compute this zero, let us use the original estimate . Table 5 displays the computed findings. Example 5. Now, we consider the preceding standard complex root problem: This function has zero . Let us choose the initial approximation to compute this zero. Table 6 depicts the computed findings. Example 6. As a final consideration, we look at a non-differential function at , which is given by This function has zero . As a starting point, let us compute this zero using the approximation . The computed outcomes are shown in Table 7 of the report. To find the multiplicity of the above-chosen functions, adopt the following formula:
where
and
. We obtain the multiplicity by using this formula with our new approach, NM. In
Table 1, the calculated outcomes are displayed.
Table 1.
Multiplicity of considered functions.
Table 1.
Multiplicity of considered functions.
| Problems | Multiplicity |
|---|
| 2 |
| 3 |
| 4 |
| 3 |
| 5 |
| 4 |
Table 2.
Results of the methods for problem .
Table 2.
Results of the methods for problem .
| Methods | k | | | | COC | CPU |
|---|
| LLC | 6 | | | | 4.000 | 0.0941 |
| LCN | 6 | | | | 4.000 | 0.0939 |
| SSM | 6 | | | | 4.000 | 0.0933 |
| ZCM | 6 | | | | 4.000 | 0.0872 |
| SBM | 6 | | | | 4.000 | 0.0927 |
| KKB | 6 | | | | 4.000 | 0.0814 |
| SKJ | 6 | | | | 4.000 | 0.0821 |
| BAM | 6 | | | | 4.000 | 0.0836 |
| KKS | 5 | | | | 4.000 | 0.0801 |
| NM | 5 | | | | 4.000 | 0.0799 |
Table 3.
Results of the methods for problem .
Table 3.
Results of the methods for problem .
| Methods | k | | | | COC | CPU |
|---|
| LLC | 4 | | | | 4.000 | 0.8192 |
| LCN | 4 | | | | 4.000 | 0.9367 |
| SSM | 4 | | | | 4.000 | 0.9523 |
| ZCS | 4 | | | | 4.000 | 0.9681 |
| SBM | 4 | | | | 4.000 | 1.1543 |
| KKB | 4 | | | | 4.000 | 0.9367 |
| SKJ | 3 | | | 0 | 4.000 | 0.3371 |
| BAM | 3 | | | 0 | 4.000 | 0.5150 |
| KKS | 3 | | | 0 | 4.000 | 0.3435 |
| NM | 3 | | | 0 | 4.000 | 0.3281 |
Table 4.
Results of the methods for problem .
Table 4.
Results of the methods for problem .
| Methods | k | | | | COC | CPU |
|---|
| LLC | 4 | | | | 4.000 | 1.6220 |
| LCN | 4 | | | | 4.000 | 1.7322 |
| SSM | 4 | | | | 4.000 | 1.6847 |
| ZCS | 4 | | | | 4.000 | 1.7000 |
| SBM | 4 | | | | 4.000 | 1.9821 |
| KKB | 4 | | | | 4.000 | 1.7476 |
| SKJ | 4 | | | | 4.000 | 1.3955 |
| BAM | 4 | | | | 4.000 | 2.2621 |
| KKS | 4 | | | | 4.000 | 1.3401 |
| NM | 4 | | | | 4.000 | 1.3219 |
Table 5.
Results of the methods for problem .
Table 5.
Results of the methods for problem .
| Methods | k | | | | COC | CPU |
|---|
| LLC | - | - | - | - | - | - |
| LCN | - | - | - | - | - | - |
| SSM | 10 | | | | 4.000 | 0.0323 |
| ZCS | 6 | | | | 4.000 | 0.0622 |
| SBM | 5 | | | | 4.000 | 0.0454 |
| KKB | 261 | 666 | 396 | 162 | 4.000 | 0.5319 |
| SKJ | 5 | | | | 4.000 | 0.0187 |
| BAM | 5 | | | | 4.000 | 0.0310 |
| KKS | 5 | | | | 4.000 | 0.0183 |
| NM | 5 | | | | 4.000 | 0.0180 |
Table 6.
Results of the methods for problem .
Table 6.
Results of the methods for problem .
| Methods | k | | | | COC | CPU |
|---|
| LLC | 4 | | | | 4.000 | 1.4352 |
| LCN | 4 | | | | 4.000 | 2.1376 |
| SSM | 4 | | | | 4.000 | 2.1383 |
| ZCS | 4 | | | | 4.000 | 2.1845 |
| SBM | 4 | | | | 4.000 | 2.6374 |
| KKB | 4 | | | | 4.000 | 2.1690 |
| SKJ | 4 | | | | 4.000 | 0.4578 |
| BAM | 4 | | | | 4.000 | 0.6860 |
| KKS | 4 | | | | 4.000 | 0.4527 |
| NM | 4 | | | | 4.000 | 0.4498 |
Table 7.
Results of the methods for problem .
Table 7.
Results of the methods for problem .
| Methods | k | | | | COC | CPU |
|---|
| LLC | - | - | - | - | - | - |
| LCN | - | - | - | - | - | - |
| SSM | - | - | - | - | - | - |
| ZCS | - | - | - | - | - | - |
| SBM | 7 | | | | 4.000 | 0.5169 |
| KKB | - | - | - | - | - | - |
| SKJ | - | - | - | - | - | - |
| BAM | - | - | - | - | - | - |
| KKS | 10 | | | | 2.000 | 0.2663 |
| NM | 7 | | | | 4.000 | 0.1725 |
Remark 4. Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7 demonstrate that the suggested technique exhibits a constant convergence behavior and follows the conclusions made in Section 2 and Section 3. In all of the issues, it appears that the provided algorithm goes through k iterations, as few as or as many as the approaches under consideration. The estimated errors of the algorithm described are shown in Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7 to be comparable to those of other approaches. Our new approach is more consistent than other approaches and produces results that are reliable and reproducible. Our approach produces consistent results throughout the considered problem. Additionally, the results demonstrate the new method’s high efficiency when compared to the CPU time of approaches in the same domain that were also under consideration. Figure 1 through Figure 6, which demonstrate how efficiently the new algorithm outperforms the existing one, also indicate the time consumption. Similar numerical studies on a wide range of other problems also support this result. By reducing the amount of time needed to finish, our new method has a clear benefit over other methods. By using our method, researchers can benefit from improved productivity and expedited results, which ultimately improves their work flow. 5. Conclusions
This research study concludes by presenting the creation of an ideal derivative-free method for locating multiple roots. The method demonstrates a remarkable convergence rate of order four, as proven by a theorem. Moreover, the practical applications of this method extend to various real-life problems, including the Van der Waals equation, Planck’s radiation, the Manning problem, and the blood rheology model. The numerical results obtained from applying the proposed method surpass those of existing iterative methods. The improved accuracy and efficiency of the derivative-free approach make it a valuable tool for solving problems with multiple roots.
Overall, this research contributes to the field of numerical analysis by providing a robust and efficient method for finding multiple roots. Its applications in diverse scientific and engineering domains highlight its versatility and effectiveness. The promising results obtained pave the way for the further exploration and implementation of this method in various practical scenarios.