Chaos-Based Image Encryption: Review, Application, and Challenges
Abstract
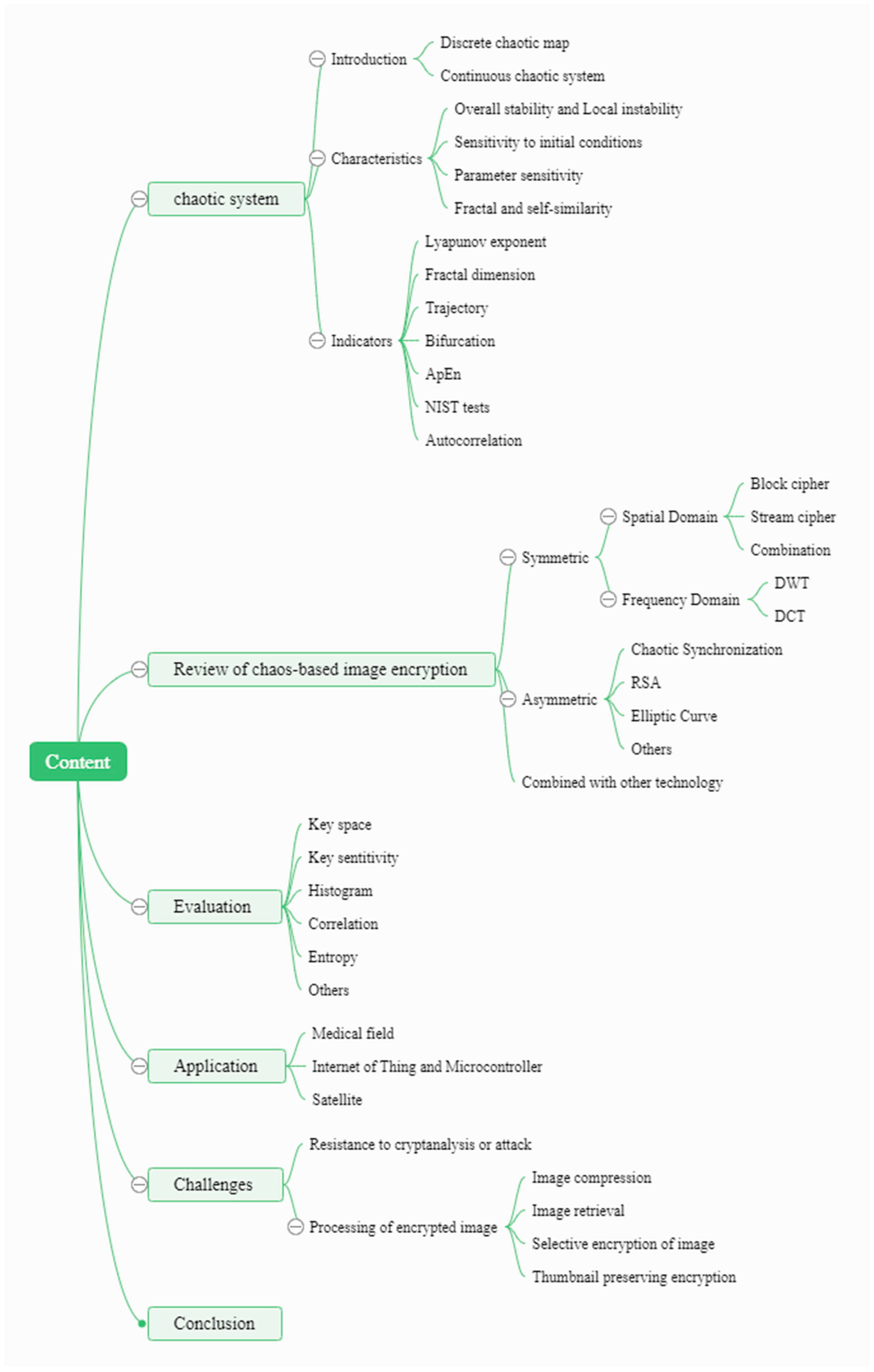
1. Introduction
1.1. A Brief Introduction to Chaos-Based Cryptography
1.2. A Brief Introduction to Image Encryption
1.3. A Brief Introduction to Chaos-Based Image Encryption
2. Chaotic Systems
2.1. A Brief Introduction to Chaotic Systems
2.2. Typical Characteristics and Indicators of the Chaotic System
2.2.1. Characteristics
- Overall stability and local instability
- Sensitivity to initial conditions
- Parameter Sensitivity
- Fractal and self-similarity
2.2.2. Indicators
- Lyapunov exponent (LE)
- Fractal dimension
- Trajectory
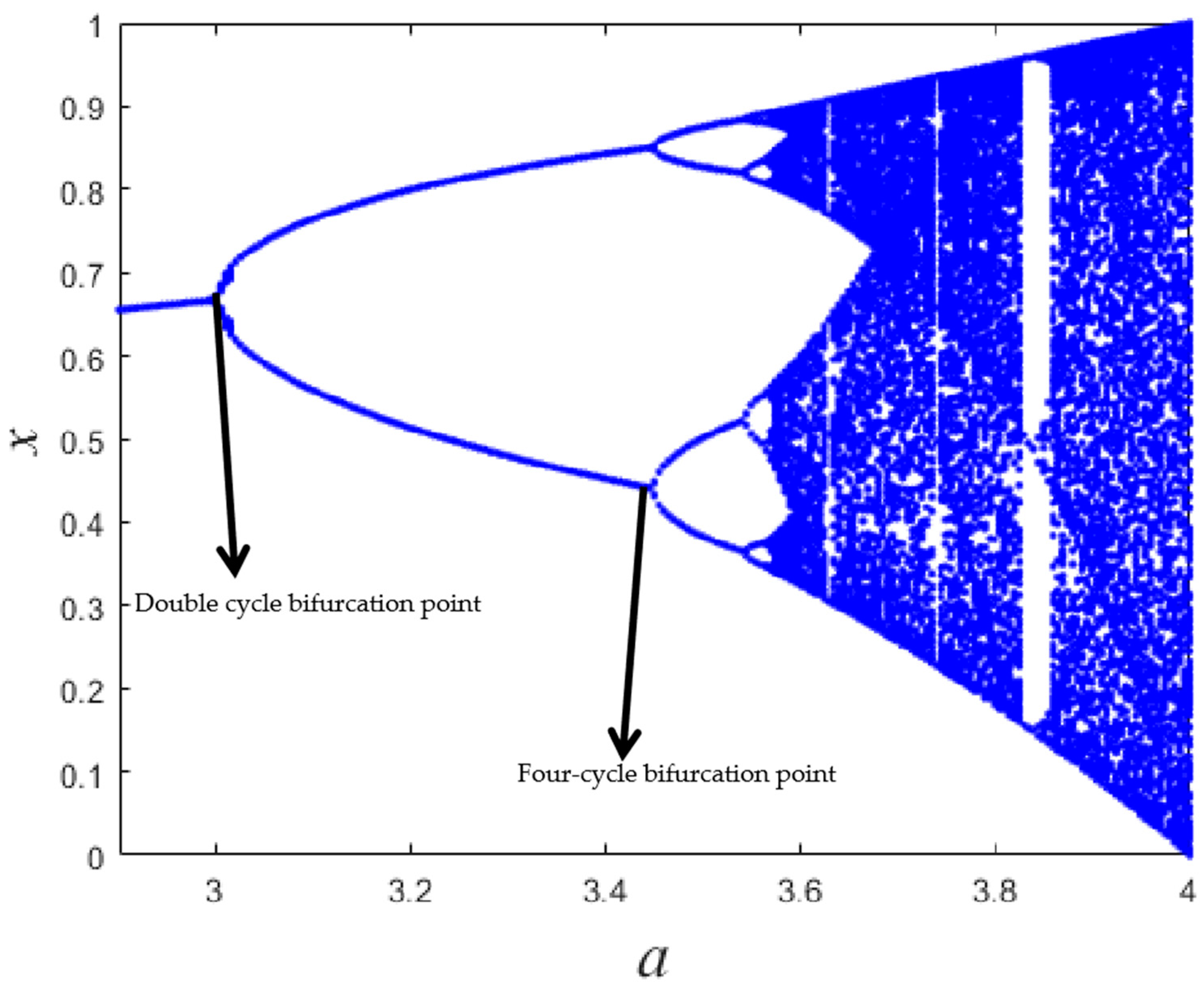
- Bifurcation
- Approximate entropy (ApEn)
- NIST Statistical Tests
- Autocorrelation
3. A Review of Chaos-Based Image Encryption
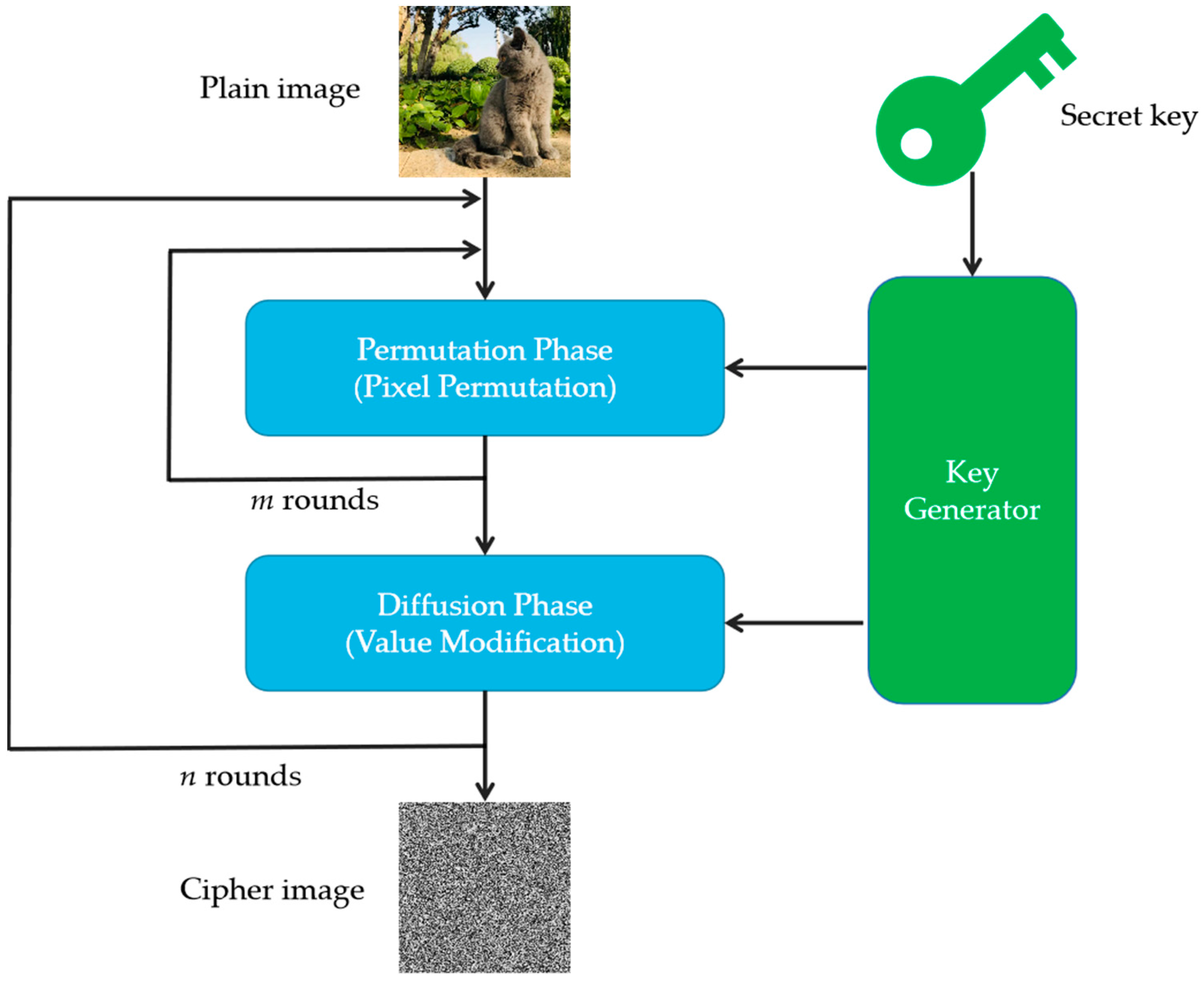
3.1. Chaos-Based Image Encryption Based on Symmetric Encryption
3.1.1. Chaotic Image Encryption Based on the Spatial Domain
Chaotic Image Encryption Based on the Block Cipher
- Algorithms when chaotic systems are employed as the PRNG
- Chaotic image-encryption algorithms with improved performance or chaotification
- Block-cipher-based image encryption with a coupling chaotic system
- Block-cipher-based image encryption with a hyperchaos system
- Algorithms when chaotic systems are combined with S-Boxes
- Chaotic image-encryption algorithms based on bitplane operation
- Color chaotic image-encryption algorithms based on the block cipher
Chaos-Based Image Encryption Based on Stream Cipher
- Stream-cipher-based image encryption with the classic chaotic system
- Stream-cipher-based image encryption with the coupled chaotic system
- Stream-cipher-based image encryption with the spatiotemporal chaotic system
Chaos-Based Image Encryption Based on Both Block and Stream Ciphers
3.1.2. Chaos-Based Image Encryption Based on the Frequency Domain
- Discrete Wavelet Transform (DWT)-based algorithms
- Discrete Cosine Transform (DCT)-based algorithms
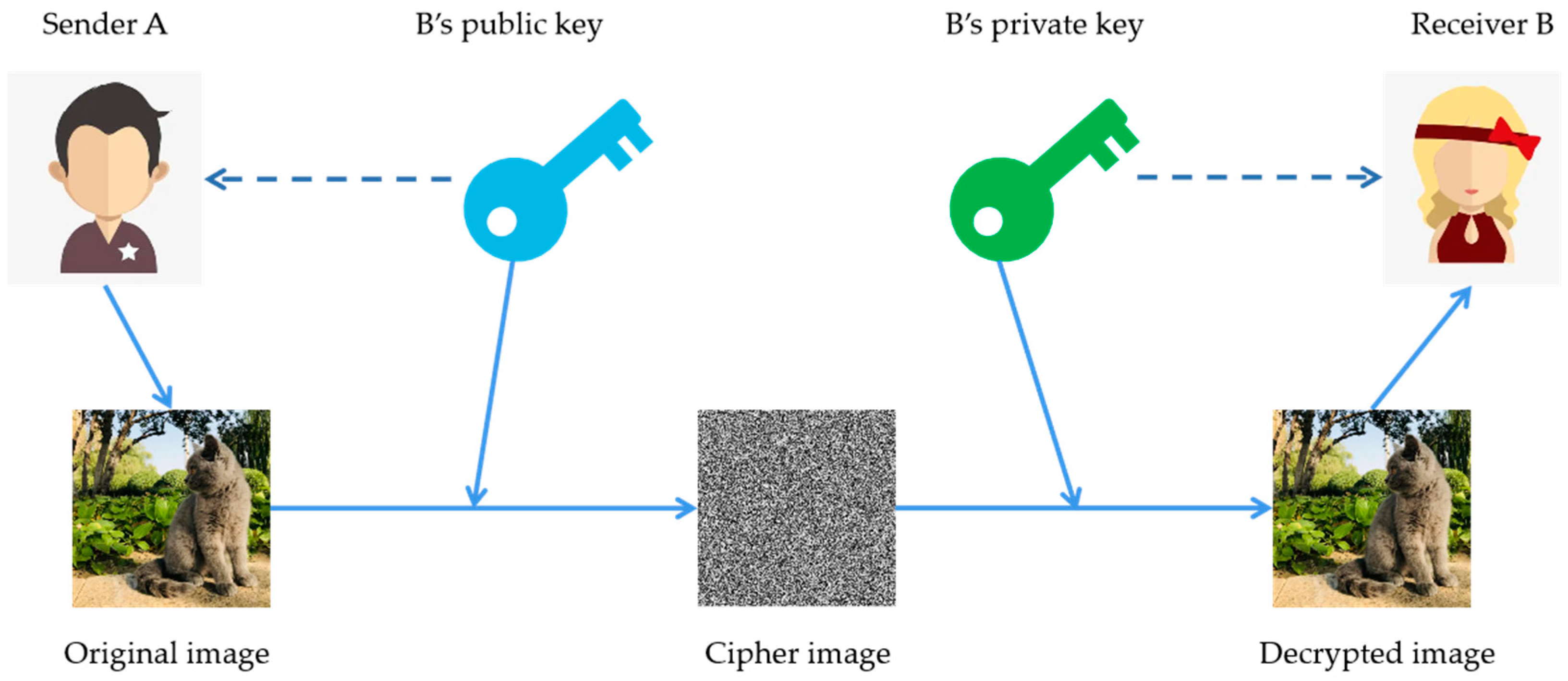
3.2. Chaos-Based Image Encryption Based on Asymmetric Encryption (Public Key Algorithm)
3.2.1. Chaotic-Synchronization-Based Asymmetric Image Encryption
3.2.2. RSA-Based Asymmetric Chaotic Image Encryption
3.2.3. Elliptic-Curve-Based Asymmetric Chaotic Image Encryption
3.2.4. Some Other Chaos-Based Asymmetric Chaotic Image-Encryption Methods
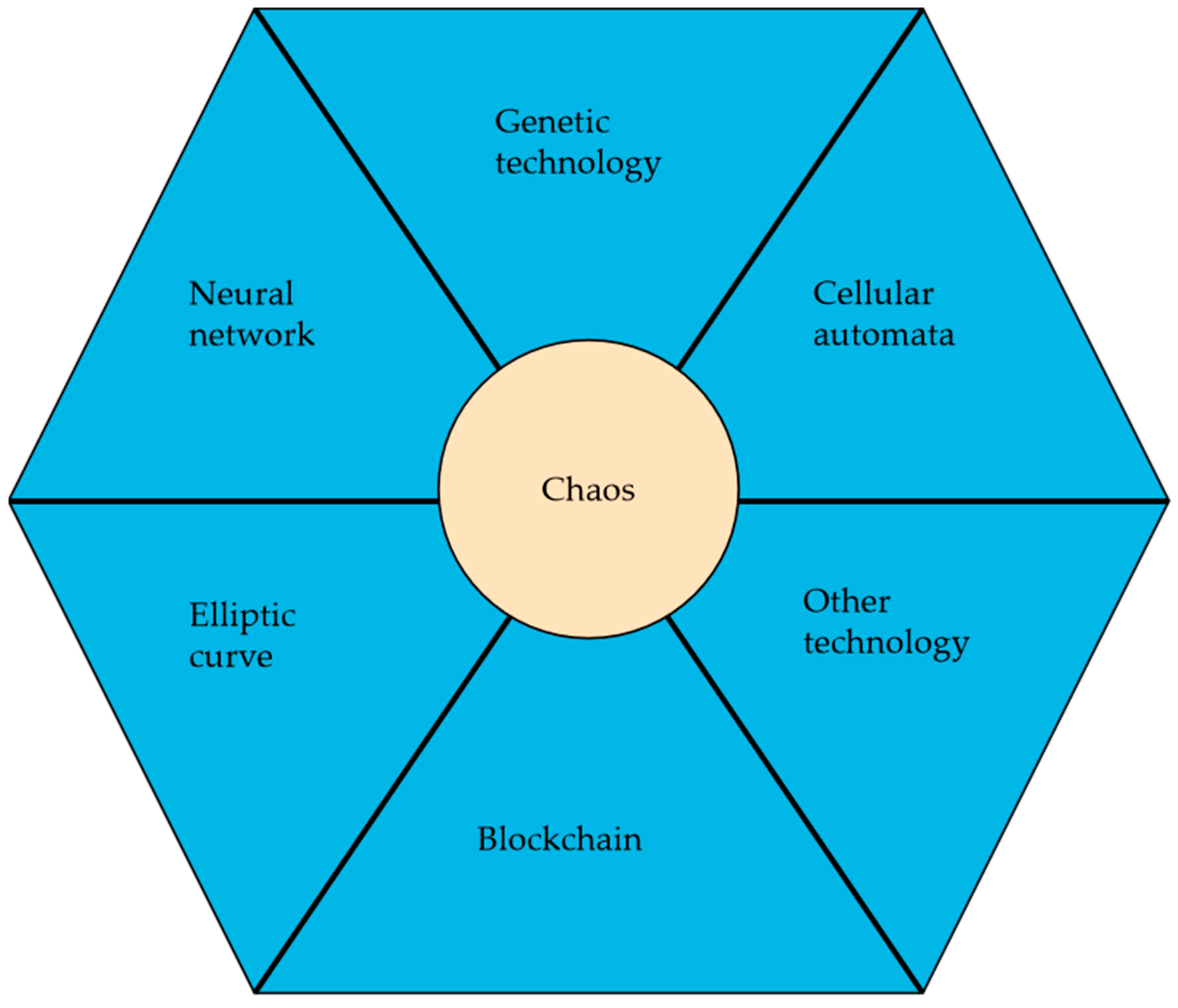
3.3. Chaos-Based Image Encryption with Other Technology
3.3.1. Chaos-Based Image Encryption with Neural Networks
3.3.2. Chaos-Based Image Encryption with Genetic Technology
3.3.3. Chaos-Based Image Encryption with Cellular Automata
3.3.4. Chaos-Based Image Encryption with Blockchain Technology
3.3.5. Chaos-Based Image Encryption with an Elliptic Curve
3.3.6. Chaos-Based Image Encryption with Some Other Technology
3.4. Review of the Chaos-Based Image-Encryption Algorithms with Outstanding Contributions
4. Security Evaluation of Image-Encryption Algorithms
- Key space
- Key sensitivity
- Histogram
- Correlation analysis
- Information entropy (Shannon entropy)
- Local information entropy
- Unified average changing intensity (UACI)
- Number of pixels change rate (NPCR)
- Resistance to different attacks
5. The Application Areas of Chaos-Based Image Encryption
5.1. Application of Chaos-Based Image Encryption in the Medical Field
5.2. Application of Chaos-Based Image Encryption in the Internet of Things (IoT) and Microcontroller Field
5.3. Application of Chaos-Based Image Encryption in the Satellite Field
6. The Challenges of Chaos-Based Image Encryption
6.1. Resistance to Cryptanalysis or Attack
6.2. Processing of an Encrypted Image
6.2.1. Image Compression
6.2.2. Image Retrieval
6.2.3. Selective Encryption of Images
6.2.4. Thumbnail-Preserving Encryption
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Li, T.-Y.; Yorke, J.A. Period three implies chaos. In The Theory of Chaotic Attractors; Springer: New York, NY, USA, 2004; pp. 77–84. [Google Scholar] [CrossRef]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Matthews, R. On the derivation of a “chaotic” encryption algorithm. Cryptologia 1989, 13, 29–42. [Google Scholar] [CrossRef]
- Sobhy, M.I.; Shehata, A.-E. Chaotic algorithms for data encryption. In Proceedings of the 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing, Proceedings (Cat. No. 01CH37221), Salt Lake City, UT, USA, 7–11 May 2001; pp. 997–1000. [Google Scholar]
- Zhang, X.; Chen, W. A new chaotic algorithm for image encryption. In Proceedings of the 2008 International Conference on Audio, Language and Image Processing, Shanghai, China, 7–9 July 2008; pp. 889–892. [Google Scholar]
- Tang, G.; Wang, S.; Lü, H.; Hu, G. Chaos-based cryptograph incorporated with S-box algebraic operation. Phys. Lett. A 2003, 318, 388–398. [Google Scholar] [CrossRef]
- Çavuşoğlu, Ü.; Kaçar, S.; Pehlivan, I.; Zengin, A. Secure image encryption algorithm design using a novel chaos based S-Box. Chaos Solitons Fractals 2017, 95, 92–101. [Google Scholar] [CrossRef]
- Liu, S.; Guo, C.; Sheridan, J.T. A review of optical image encryption techniques. Opt. Laser Technol. 2014, 57, 327–342. [Google Scholar] [CrossRef]
- Chang, H.K.-C.; Liu, J.-L. A linear quadtree compression scheme for image encryption. Signal Process. Image Commun. 1997, 10, 279–290. [Google Scholar] [CrossRef]
- Mira, C. Chaotic Dynamics: From the One-Dimensional Endomorphism to the Two-Dimensional Diffeomorphism; World Scientific: Singapore, 1987. [Google Scholar]
- Avrutin, V.; Gardini, L.; Sushko, I.; Tramontana, F. Continuous and Discontinuous Piecewise-Smooth One-Dimensional Maps: Invariant Sets and Bifurcation Structures; World Scientific: Singapore, 2019. [Google Scholar]
- Leonel Rocha, J.; Taha, A.-K. Allee’s effect bifurcation in generalized logistic maps. Int. J. Bifurc. Chaos 2019, 29, 1950039. [Google Scholar] [CrossRef]
- Amin, M.; Faragallah, O.S.; Abd El-Latif, A.A. A chaotic block cipher algorithm for image cryptosystems. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 3484–3497. [Google Scholar] [CrossRef]
- Liu, H.; Kadir, A. Asymmetric color image encryption scheme using 2D discrete-time map. Signal Process. 2015, 113, 104–112. [Google Scholar] [CrossRef]
- Chen, G.; Mao, Y.; Chui, C.K. A symmetric image encryption scheme based on 3D chaotic cat maps. Chaos Solitons Fractals 2004, 21, 749–761. [Google Scholar] [CrossRef]
- Chen, G.; Ueta, T. Yet another chaotic attractor. Int. J. Bifurc. Chaos 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Chow, S.-N.; Hale, J.K. Methods of Bifurcation Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 251. [Google Scholar]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; Booz-Allen and Hamilton Inc.: Mclean, VA, USA, 2001. [Google Scholar]
- Scharinger, J.; Pichler, F. Efficient image encryption based on chaotic maps. In Proceedings of the 20th workshop of the Austrian Association for Pattern Recognition (OAGM/AAPR) on Pattern Recognition 1996, Munich, Germany, 30 June 1996; pp. 159–170. [Google Scholar]
- Fridrich, J. Symmetric ciphers based on two-dimensional chaotic maps. Int. J. Bifurc. Chaos 1998, 8, 1259–1284. [Google Scholar] [CrossRef]
- Scharinger, J. Fast encryption of image data using chaotic Kolmogorov flows. J. Electron. Imaging 1998, 7, 318–325. [Google Scholar] [CrossRef]
- Li, C.; Luo, G.; Qin, K.; Li, C. An image encryption scheme based on chaotic tent map. Nonlinear Dyn. 2017, 87, 127–133. [Google Scholar] [CrossRef]
- Xiang, T.; Liao, X.; Tang, G.; Chen, Y.; Wong, K.-W. A novel block cryptosystem based on iterating a chaotic map. Phys. Lett. A 2006, 349, 109–115. [Google Scholar] [CrossRef]
- Miyamoto, M.; Tanaka, K.; Sugimura, T. Truncated Baker transformation and its extension to image encryption. In Proceedings of the Mathematics of Data/Image Coding, Compression, and Encryption II, Denver, CO, USA, 19–20 July 1999; pp. 13–25. [Google Scholar]
- Yen, J.-C.; Guo, J.-I. Efficient hierarchical chaotic image encryption algorithm and its VLSI realisation. IEE Proc.-Vis. Image Signal Process. 2000, 147, 167–175. [Google Scholar] [CrossRef]
- Fridrich, J. Image encryption based on chaotic maps. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics, Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; pp. 1105–1110. [Google Scholar]
- Salleh, M.; Ibrahim, S.; Isnin, I.F. Enhanced chaotic image encryption algorithm based on Baker’s map. In Proceedings of the 2003 International Symposium on Circuits and Systems, 2003. ISCAS’03, Bangkok, Thailand, 25–28 May 2003. [Google Scholar]
- Lian, S.; Sun, J.; Wang, Z. A block cipher based on a suitable use of the chaotic standard map. Chaos Solitons Fractals 2005, 26, 117–129. [Google Scholar] [CrossRef]
- Wong, K.-W.; Kwok, B.S.-H.; Law, W.-S. A fast image encryption scheme based on chaotic standard map. Phys. Lett. A 2008, 372, 2645–2652. [Google Scholar] [CrossRef]
- Guan, Z.-H.; Huang, F.; Guan, W. Chaos-based image encryption algorithm. Phys. Lett. A 2005, 346, 153–157. [Google Scholar] [CrossRef]
- Xiao, D.; Liao, X.; Wei, P. Analysis and improvement of a chaos-based image encryption algorithm. Chaos Solitons Fractals 2009, 40, 2191–2199. [Google Scholar] [CrossRef]
- Baptista, M. Cryptography with chaos. Phys. Lett. A 1998, 240, 50–54. [Google Scholar] [CrossRef]
- Pareek, N.K.; Patidar, V.; Sud, K.K. Image encryption using chaotic logistic map. Image Vis. Comput. 2006, 24, 926–934. [Google Scholar] [CrossRef]
- Wang, Y.; Wong, K.-W.; Liao, X.; Chen, G. A new chaos-based fast image encryption algorithm. Appl. Soft Comput. 2011, 11, 514–522. [Google Scholar] [CrossRef]
- Fouda, J.A.E.; Effa, J.Y.; Sabat, S.L.; Ali, M. A fast chaotic block cipher for image encryption. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 578–588. [Google Scholar] [CrossRef]
- Nepomuceno, E.G.; Nardo, L.G.; Arias-Garcia, J.; Butusov, D.N.; Tutueva, A. Image encryption based on the pseudo-orbits from 1D chaotic map. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 061101. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.; Chen, G.; Lian, S. A novel fast image encryption scheme based on 3D chaotic baker maps. Int. J. Bifurc. Chaos 2004, 14, 3613–3624. [Google Scholar] [CrossRef]
- Wang, Y.; Wong, K.-W.; Liao, X.; Xiang, T.; Chen, G. A chaos-based image encryption algorithm with variable control parameters. Chaos Solitons Fractals 2009, 41, 1773–1783. [Google Scholar] [CrossRef]
- Tong, X.; Cui, M. Image encryption scheme based on 3D baker with dynamical compound chaotic sequence cipher generator. Signal Process. 2009, 89, 480–491. [Google Scholar] [CrossRef]
- Huang, X. Image encryption algorithm using chaotic Chebyshev generator. Nonlinear Dyn. 2012, 67, 2411–2417. [Google Scholar] [CrossRef]
- Ye, G.; Wong, K.-W. An efficient chaotic image encryption algorithm based on a generalized Arnold map. Nonlinear Dyn. 2012, 69, 2079–2087. [Google Scholar] [CrossRef]
- Wang, X.; Liu, L.; Zhang, Y. A novel chaotic block image encryption algorithm based on dynamic random growth technique. Opt. Lasers Eng. 2015, 66, 10–18. [Google Scholar] [CrossRef]
- Chen, J.-X.; Zhu, Z.-L.; Fu, C.; Yu, H.; Zhang, L.-B. A fast chaos-based image encryption scheme with a dynamic state variables selection mechanism. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 846–860. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S. A new image encryption algorithm based on logistic chaotic map with varying parameter. SpringerPlus 2016, 5, 289. [Google Scholar] [CrossRef] [PubMed]
- Pak, C.; Huang, L. A new color image encryption using combination of the 1D chaotic map. Signal Process. 2017, 138, 129–137. [Google Scholar] [CrossRef]
- Nardo, L.G.; Nepomuceno, E.G.; Arias-Garcia, J.; Butusov, D.N. Image encryption using finite-precision error. Chaos Solitons Fractals 2019, 123, 69–78. [Google Scholar] [CrossRef]
- Santos, T.A.; Magalhães, E.P.; Basílio, N.P.; Nepomuceno, E.G.; Karimov, T.I.; Butusov, D.N. Improving Chaotic Image Encryption Using Maps with Small Lyapunov Exponents. In Proceedings of the 2020 Moscow Workshop on Electronic and Networking Technologies (MWENT), Moscow, Russia, 11–13 March 2020; pp. 1–4. [Google Scholar]
- Hua, Z.; Zhu, Z.; Yi, S.; Zhang, Z.; Huang, H. Cross-plane colour image encryption using a two-dimensional logistic tent modular map. Inf. Sci. 2021, 546, 1063–1083. [Google Scholar] [CrossRef]
- Behnia, S.; Akhshani, A.; Mahmodi, H.; Akhavan, A. A novel algorithm for image encryption based on mixture of chaotic maps. Chaos Solitons Fractals 2008, 35, 408–419. [Google Scholar] [CrossRef]
- Jafarizadeh, M.; Behnia, S. Hierarchy of chaotic maps with an invariant measure and their coupling. Phys. D Nonlinear Phenom. 2001, 159, 1–21. [Google Scholar] [CrossRef]
- Jafarizadeh, M.; Behnia, S.; Khorram, S.; Nagshara, H. Hierarchy of chaotic maps with an invariant measure. J. Stat. Phys. 2001, 104, 1013–1028. [Google Scholar] [CrossRef]
- Seyedzadeh, S.M.; Mirzakuchaki, S. A fast color image encryption algorithm based on coupled two-dimensional piecewise chaotic map. Signal Process. 2012, 92, 1202–1215. [Google Scholar] [CrossRef]
- Zhou, Y.; Bao, L.; Chen, C.P. A new 1D chaotic system for image encryption. Signal Process. 2014, 97, 172–182. [Google Scholar] [CrossRef]
- Alawida, M.; Samsudin, A.; Teh, J.S.; Alkhawaldeh, R.S. A new hybrid digital chaotic system with applications in image encryption. Signal Process. 2019, 160, 45–58. [Google Scholar] [CrossRef]
- Gao, T.; Chen, Z. A new image encryption algorithm based on hyper-chaos. Phys. Lett. A 2008, 372, 394–400. [Google Scholar] [CrossRef]
- Gao, T.; Chen, Z. Image encryption based on a new total shuffling algorithm. Chaos Solitons Fractals 2008, 38, 213–220. [Google Scholar] [CrossRef]
- Zhu, C. A novel image encryption scheme based on improved hyperchaotic sequences. Opt. Commun. 2012, 285, 29–37. [Google Scholar] [CrossRef]
- Zhu, H.; Zhao, C.; Zhang, X. A novel image encryption–compression scheme using hyper-chaos and Chinese remainder theorem. Signal Process. Image Commun. 2013, 28, 670–680. [Google Scholar] [CrossRef]
- Liu, W.; Sun, K.; Zhu, C. A fast image encryption algorithm based on chaotic map. Opt. Lasers Eng. 2016, 84, 26–36. [Google Scholar] [CrossRef]
- Yu, F.; Xu, S.; Xiao, X.; Yao, W.; Huang, Y.; Cai, S.; Yin, B.; Li, Y. Dynamics analysis, FPGA realization and image encryption application of a 5D memristive exponential hyperchaotic system. Integration 2023, 90, 58–70. [Google Scholar] [CrossRef]
- Zhang, L.; Liao, X.; Wang, X. An image encryption approach based on chaotic maps. Chaos Solitons Fractals 2005, 24, 759–765. [Google Scholar] [CrossRef]
- Jolfaei, A.; Mirghadri, A. Image encryption using chaos and block cipher. Comput. Inf. Sci. 2011, 4, 172. [Google Scholar] [CrossRef]
- Zhou, Q.; Wong, K.-W.; Liao, X.; Xiang, T.; Hu, Y. Parallel image encryption algorithm based on discretized chaotic map. Chaos Solitons Fractals 2008, 38, 1081–1092. [Google Scholar] [CrossRef]
- Gu, G.; Han, G. An enhanced chaos based image encryption algorithm. In Proceedings of the First International Conference on Innovative Computing, Information and Control-Volume I (ICICIC’06), Beijing, China, 30 August–1 September 2006; pp. 492–495. [Google Scholar]
- Zhu, Z.-L.; Zhang, W.; Wong, K.-W.; Yu, H. A chaos-based symmetric image encryption scheme using a bit-level permutation. Inf. Sci. 2011, 181, 1171–1186. [Google Scholar] [CrossRef]
- Li, X.; Xie, Z.; Wu, J.; Li, T. Image encryption based on dynamic filtering and bit cuboid operations. Complexity 2019, 2019, 7485621. [Google Scholar] [CrossRef]
- Xu, C.; Sun, J.; Wang, C. A novel image encryption algorithm based on bit-plane matrix rotation and hyper chaotic systems. Multimed. Tools Appl. 2020, 79, 5573–5593. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, B.; Wu, Z. Research on color image encryption algorithm based on bit-plane and Chen Chaotic System. Entropy 2022, 24, 186. [Google Scholar] [CrossRef] [PubMed]
- Song, W.; Fu, C.; Zheng, Y.; Tie, M.; Liu, J.; Chen, J. A parallel image encryption algorithm using intra bitplane scrambling. Math. Comput. Simul. 2023, 204, 71–88. [Google Scholar] [CrossRef]
- Patidar, V.; Pareek, N.; Sud, K. A new substitution–diffusion based image cipher using chaotic standard and logistic maps. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3056–3075. [Google Scholar] [CrossRef]
- Huang, C.-K.; Nien, H.-H. Multi chaotic systems based pixel shuffle for image encryption. Opt. Commun. 2009, 282, 2123–2127. [Google Scholar] [CrossRef]
- Kanso, A.; Ghebleh, M. A novel image encryption algorithm based on a 3D chaotic map. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2943–2959. [Google Scholar] [CrossRef]
- Ying, W.; DeLing, Z.; Lei, J.; Yaoguang, W. The spatial-domain encryption of digital images based on high-dimension chaotic system. In Proceedings of the IEEE Conference on Cybernetics and Intelligent Systems, Singapore, 1–3 December 2004; pp. 1172–1176. [Google Scholar]
- Gan, Z.-H.; Chai, X.-L.; Han, D.-J.; Chen, Y.-R. A chaotic image encryption algorithm based on 3-D bit-plane permutation. Neural Comput. Appl. 2019, 31, 7111–7130. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Y.; Liang, S.; Li, D. A new chaotic algorithm for image encryption. Chaos Solitons Fractals 2006, 29, 393–399. [Google Scholar] [CrossRef]
- Guo, J.-I. A new chaotic key-based design for image encryption and decryption. In Proceedings of the 2000 IEEE International Symposium on Circuits and Systems (ISCAS), Geneva, Switzerland, 28–31 May 2000; pp. 49–52. [Google Scholar]
- Li, S.; Zheng, X. Cryptanalysis of a chaotic image encryption method. In Proceedings of the 2002 IEEE International Symposium on Circuits and Systems (ISCAS), Phoenix-Scottsdale, AZ, USA, 26–29 May 2002. [Google Scholar]
- Kwok, H.; Tang, W.K. A fast image encryption system based on chaotic maps with finite precision representation. Chaos Solitons Fractals 2007, 32, 1518–1529. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X. Color image encryption based on one-time keys and robust chaotic maps. Comput. Math. Appl. 2010, 59, 3320–3327. [Google Scholar] [CrossRef]
- Mazloom, S.; Eftekhari-Moghadam, A.M. Color image encryption based on coupled nonlinear chaotic map. Chaos Solitons Fractals 2009, 42, 1745–1754. [Google Scholar] [CrossRef]
- Liu, S.; Sun, J.; Xu, Z. An Improved Image Encryption Algorithm based on Chaotic System. J. Comput. 2009, 4, 1091–1100. [Google Scholar] [CrossRef]
- Volos, C.K.; Kyprianidis, I.M.; Stouboulos, I.N. Image encryption process based on chaotic synchronization phenomena. Signal Process. 2013, 93, 1328–1340. [Google Scholar] [CrossRef]
- Kaneko, K.; Tsuda, I. Complex Systems: Chaos and Beyond: Chaos and Beyond: A Constructive Approach with Applications in Life Sciences; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Pisarchik, A.; Flores-Carmona, N.; Carpio-Valadez, M. Encryption and decryption of images with chaotic map lattices. Chaos Interdiscip. J. Nonlinear Sci. 2006, 16, 033118. [Google Scholar] [CrossRef] [PubMed]
- Rhouma, R.; Meherzi, S.; Belghith, S. OCML-based colour image encryption. Chaos Solitons Fractals 2009, 40, 309–318. [Google Scholar] [CrossRef]
- Xiang, T.; Wong, K.-W.; Liao, X. Selective image encryption using a spatiotemporal chaotic system. Chaos Interdiscip. J. Nonlinear Sci. 2007, 17, 023115. [Google Scholar] [CrossRef]
- Sun, F.; Liu, S.; Li, Z.; Lü, Z. A novel image encryption scheme based on spatial chaos map. Chaos Solitons Fractals 2008, 38, 631–640. [Google Scholar] [CrossRef]
- Zhang, Y.-Q.; Wang, X.-Y. A symmetric image encryption algorithm based on mixed linear–nonlinear coupled map lattice. Inf. Sci. 2014, 273, 329–351. [Google Scholar] [CrossRef]
- Zhang, Y.-Q.; Wang, X.-Y. A new image encryption algorithm based on non-adjacent coupled map lattices. Appl. Soft Comput. 2015, 26, 10–20. [Google Scholar] [CrossRef]
- Belkhouche, F.; Qidwai, U. Binary image encoding using 1D chaotic maps. In Proceedings of the Annual Technical Conference IEEE Region 5, New Orleans, LA, USA, 11 April 2003; pp. 39–43. [Google Scholar]
- Xiao, H.-P.; Zhang, G.-J. An image encryption scheme based on chaotic systems. In Proceedings of the 2006 International Conference on Machine Learning and Cybernetics, Dalian, China, 13–16 August 2006; pp. 2707–2711. [Google Scholar]
- Wang, X.; Wang, X.; Zhao, J.; Zhang, Z. Chaotic encryption algorithm based on alternant of stream cipher and block cipher. Nonlinear Dyn. 2011, 63, 587–597. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X. Color image encryption using spatial bit-level permutation and high-dimension chaotic system. Opt. Commun. 2011, 284, 3895–3903. [Google Scholar] [CrossRef]
- Xu, L.; Li, Z.; Li, J.; Hua, W. A novel bit-level image encryption algorithm based on chaotic maps. Opt. Lasers Eng. 2016, 78, 17–25. [Google Scholar] [CrossRef]
- Luo, Y.; Du, M.; Liu, J. A symmetrical image encryption scheme in wavelet and time domain. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 447–460. [Google Scholar] [CrossRef]
- Pang, C.-J. An image encryption algorithm based on discrete wavelet transform and two dimension cat mapping. In Proceedings of the 2009 International Conference on Networks Security, Wireless Communications and Trusted Computing, Wuhan, China, 25–26 April 2009; pp. 711–714. [Google Scholar]
- Al-Maadeed, S.; Al-Ali, A.; Abdalla, T. A new chaos-based image-encryption and compression algorithm. J. Electr. Comput. Eng. 2012, 2012, 15. [Google Scholar] [CrossRef]
- Wu, X.; Wang, D.; Kurths, J.; Kan, H. A novel lossless color image encryption scheme using 2D DWT and 6D hyperchaotic system. Inf. Sci. 2016, 349, 137–153. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, L.; Liu, T.; Chen, H.; Li, P.; Lin, C.; Liu, S. Color image encryption by using Arnold transform and color-blend operation in discrete cosine transform domains. Opt. Commun. 2011, 284, 123–128. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Jiang, D. A novel triple-image encryption and hiding algorithm based on chaos, compressive sensing and 3D DCT. Inf. Sci. 2021, 574, 505–527. [Google Scholar] [CrossRef]
- Cheng, C.-J.; Cheng, C.-B. An asymmetric image cryptosystem based on the adaptive synchronization of an uncertain unified chaotic system and a cellular neural network. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 2825–2837. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, X.; Zhong, X. Generalized chaos synchronization circuit simulation and asymmetric image encryption. IEEE Access 2019, 7, 37989–38008. [Google Scholar] [CrossRef]
- Çavuşoğlu, Ü.; Akgül, A.; Zengin, A.; Pehlivan, I. The design and implementation of hybrid RSA algorithm using a novel chaos based RNG. Chaos Solitons Fractals 2017, 104, 655–667. [Google Scholar] [CrossRef]
- Jiao, K.; Ye, G.; Dong, Y.; Huang, X.; He, J. Image encryption scheme based on a generalized Arnold map and RSA algorithm. Secur. Commun. Netw. 2020, 2020, 9721675. [Google Scholar] [CrossRef]
- Xu, Q.; Sun, K.; Zhu, C. A visually secure asymmetric image encryption scheme based on RSA algorithm and hyperchaotic map. Phys. Scr. 2020, 95, 035223. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, Z.; Xu, X.; Zhang, F.; Xu, J. Optical image encryption algorithm based on hyper-chaos and public-key cryptography. Opt. Laser Technol. 2020, 127, 106171. [Google Scholar] [CrossRef]
- Ye, G.; Jiao, K.; Huang, X. Quantum logistic image encryption algorithm based on SHA-3 and RSA. Nonlinear Dyn. 2021, 104, 2807–2827. [Google Scholar] [CrossRef]
- Ye, G.-D.; Wu, H.-S.; Huang, X.-L.; Tan, S.-Y. Asymmetric image encryption algorithm based on a new 3D-ILM chaotic map. Chin. Phys. B 2022, 32, 030504. [Google Scholar] [CrossRef]
- Niyat, A.Y.; Moattar, M.H.; Torshiz, M.N. Color image encryption based on hybrid hyper-chaotic system and cellular automata. Opt. Lasers Eng. 2017, 90, 225–237. [Google Scholar] [CrossRef]
- Luo, Y.; Ouyang, X.; Liu, J.; Cao, L. An image encryption method based on elliptic curve elgamal encryption and chaotic systems. IEEE Access 2019, 7, 38507–38522. [Google Scholar] [CrossRef]
- Laiphrakpam, D.S.; Khumanthem, M.S. A robust image encryption scheme based on chaotic system and elliptic curve over finite field. Multimed. Tools Appl. 2018, 77, 8629–8652. [Google Scholar] [CrossRef]
- Liu, H.; Kadir, A.; Li, Y. Asymmetric color pathological image encryption scheme based on complex hyper chaotic system. Optik 2016, 127, 5812–5819. [Google Scholar] [CrossRef]
- Sui, L.; Duan, K.; Liang, J.; Zhang, Z.; Meng, H. Asymmetric multiple-image encryption based on coupled logistic maps in fractional Fourier transform domain. Opt. Lasers Eng. 2014, 62, 139–152. [Google Scholar] [CrossRef]
- Sui, L.; Duan, K.; Liang, J.; Hei, X. Asymmetric double-image encryption based on cascaded discrete fractional random transform and logistic maps. Opt. Express 2014, 22, 10605–10621. [Google Scholar] [CrossRef]
- Shakiba, A. A randomized CPA-secure asymmetric-key chaotic color image encryption scheme based on the Chebyshev mappings and one-time pad. J. King Saud Univ.-Comput. Inf. Sci. 2021, 33, 562–571. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Q.-H.; Hu, Y. Asymmetric color image cryptosystem using detour cylindrical-diffraction and phase reservation & truncation. IEEE Access 2018, 6, 53976–53983. [Google Scholar]
- Zhang, Y.; Zhang, L.; Zhong, Z.; Yu, L.; Shan, M.; Zhao, Y. Hyperchaotic image encryption using phase-truncated fractional Fourier transform and DNA-level operation. Opt. Lasers Eng. 2021, 143, 106626. [Google Scholar] [CrossRef]
- Lian, S. A block cipher based on chaotic neural networks. Neurocomputing 2009, 72, 1296–1301. [Google Scholar] [CrossRef]
- Bigdeli, N.; Farid, Y.; Afshar, K. A novel image encryption/decryption scheme based on chaotic neural networks. Eng. Appl. Artif. Intell. 2012, 25, 753–765. [Google Scholar] [CrossRef]
- Wang, X.-Y.; Li, Z.-M. A color image encryption algorithm based on Hopfield chaotic neural network. Opt. Lasers Eng. 2019, 115, 107–118. [Google Scholar] [CrossRef]
- Ratnavelu, K.; Kalpana, M.; Balasubramaniam, P.; Wong, K.; Raveendran, P. Image encryption method based on chaotic fuzzy cellular neural networks. Signal Process. 2017, 140, 87–96. [Google Scholar] [CrossRef]
- Chen, L.; Yin, H.; Huang, T.; Yuan, L.; Zheng, S.; Yin, L. Chaos in fractional-order discrete neural networks with application to image encryption. Neural Netw. 2020, 125, 174–184. [Google Scholar] [CrossRef]
- Chen, L.-P.; Yin, H.; Yuan, L.-G.; Lopes, A.M.; Machado, J.T.; Wu, R.-C. A novel color image encryption algorithm based on a fractional-order discrete chaotic neural network and DNA sequence operations. Front. Inf. Technol. Electron. Eng. 2020, 21, 866–879. [Google Scholar] [CrossRef]
- Man, Z.; Li, J.; Di, X.; Sheng, Y.; Liu, Z. Double image encryption algorithm based on neural network and chaos. Chaos Solitons Fractals 2021, 152, 111318. [Google Scholar] [CrossRef]
- Bao, H.; Hua, Z.; Liu, W.; Bao, B. Discrete memristive neuron model and its interspike interval-encoded application in image encryption. Sci. China Technol. Sci. 2021, 64, 2281–2291. [Google Scholar] [CrossRef]
- Xu, Q.; Chen, X.; Chen, B.; Wu, H.; Li, Z.; Bao, H. Dynamical analysis of an improved FitzHugh-Nagumo neuron model with multiplier-free implementation. Nonlinear Dyn. 2023, 111, 8737–8749. [Google Scholar] [CrossRef]
- Sun, J.; Li, C.; Wang, Z.; Wang, Y. Dynamic analysis of HR-FN-HR neural network coupled by locally active hyperbolic memristors and encryption application based on Knuth-Durstenfeld algorithm. Appl. Math. Model. 2023, 121, 463–483. [Google Scholar] [CrossRef]
- Abdullah, A.H.; Enayatifar, R.; Lee, M. A hybrid genetic algorithm and chaotic function model for image encryption. AEU-Int. J. Electron. Commun. 2012, 66, 806–816. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Q.; Wei, X. A RGB image encryption algorithm based on DNA encoding and chaos map. Comput. Electr. Eng. 2012, 38, 1240–1248. [Google Scholar] [CrossRef]
- Zhang, Q.; Guo, L.; Wei, X. A novel image fusion encryption algorithm based on DNA sequence operation and hyper-chaotic system. Opt.-Int. J. Light Electron Opt. 2013, 124, 3596–3600. [Google Scholar] [CrossRef]
- Wang, X.-Y.; Zhang, Y.-Q.; Bao, X.-M. A novel chaotic image encryption scheme using DNA sequence operations. Opt. Lasers Eng. 2015, 73, 53–61. [Google Scholar] [CrossRef]
- Chai, X.; Chen, Y.; Broyde, L. A novel chaos-based image encryption algorithm using DNA sequence operations. Opt. Lasers Eng. 2017, 88, 197–213. [Google Scholar] [CrossRef]
- Chai, X.; Fu, X.; Gan, Z.; Lu, Y.; Chen, Y. A color image cryptosystem based on dynamic DNA encryption and chaos. Signal Process. 2019, 155, 44–62. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, L. A novel image encryption algorithm based on SPWLCM and DNA coding. Math. Comput. Simul. 2021, 190, 723–744. [Google Scholar] [CrossRef]
- Gao, X.; Sun, B.; Cao, Y.; Banerjee, S.; Mou, J. A color image encryption algorithm based on hyperchaotic map and DNA mutation. Chin. Phys. B 2022, 32, 030501. [Google Scholar] [CrossRef]
- Sen, S.; Shaw, C.; Chowdhuri, D.R.; Ganguly, N.; Chaudhuri, P.P. Cellular automata based cryptosystem (CAC). In Proceedings of the Information and Communications Security: 4th International Conference, ICICS, Singapore, 9–12 December 2002; pp. 303–314. [Google Scholar]
- Abdo, A.; Lian, S.; Ismail, I.A.; Amin, M.; Diab, H. A cryptosystem based on elementary cellular automata. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 136–147. [Google Scholar] [CrossRef]
- Wolfram, S. Random sequence generation by cellular automata. Adv. Appl. Math. 1986, 7, 123–169. [Google Scholar] [CrossRef]
- Wang, X.; Luan, D. A novel image encryption algorithm using chaos and reversible cellular automata. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 3075–3085. [Google Scholar] [CrossRef]
- Enayatifar, R.; Sadaei, H.J.; Abdullah, A.H.; Lee, M.; Isnin, I.F. A novel chaotic based image encryption using a hybrid model of deoxyribonucleic acid and cellular automata. Opt. Lasers Eng. 2015, 71, 33–41. [Google Scholar] [CrossRef]
- Wu, J.; Liao, X.; Yang, B. Color image encryption based on chaotic systems and elliptic curve ElGamal scheme. Signal Process. 2017, 141, 109–124. [Google Scholar] [CrossRef]
- Zheng, Z.; Xie, S.; Dai, H.-N.; Chen, X.; Wang, H. Blockchain challenges and opportunities: A survey. Int. J. Web Grid Serv. 2018, 14, 352–375. [Google Scholar] [CrossRef]
- Li, R. Fingerprint-related chaotic image encryption scheme based on blockchain framework. Multimed. Tools Appl. 2021, 80, 30583–30603. [Google Scholar] [CrossRef]
- Neela, K.; Kavitha, V. Blockchain based Chaotic Deep GAN Encryption scheme for securing medical images in a cloud environment. Appl. Intell. 2022, 53, 4733–4747. [Google Scholar] [CrossRef]
- Singh, C.E.J.; Sunitha, C.A. Chaotic and Paillier secure image data sharing based on blockchain and cloud security. Expert Syst. Appl. 2022, 198, 116874. [Google Scholar] [CrossRef]
- El-Latif, A.A.A.; Li, L.; Niu, X. A new image encryption scheme based on cyclic elliptic curve and chaotic system. Multimed. Tools Appl. 2014, 70, 1559–1584. [Google Scholar] [CrossRef]
- Abd El-Latif, A.A.; Niu, X. A hybrid chaotic system and cyclic elliptic curve for image encryption. AEU-Int. J. Electron. Commun. 2013, 67, 136–143. [Google Scholar] [CrossRef]
- Abdelfatah, R.I. Secure image transmission using chaotic-enhanced elliptic curve cryptography. IEEE Access 2019, 8, 3875–3890. [Google Scholar] [CrossRef]
- Sinha, A.; Singh, K. A technique for image encryption using digital signature. Opt. Commun. 2003, 218, 229–234. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, Q.; Xu, L.; Ahmad, M.A.; Liu, S. Double image encryption by using iterative random binary encoding in gyrator domains. Opt. Express 2010, 18, 12033–12043. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Chen, G. Controlling Chaos and Bifurcations in Engineering Systems; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Naveenkumar, S.; Panduranga, H. Chaos and hill cipher based image encryption for mammography images. In Proceedings of the 2015 International Conference on Innovations in Information, Embedded and Communication Systems (ICIIECS), Coimbatore, India, 19–20 March 2015; pp. 1–5. [Google Scholar]
- Mostafa, S.; Fahim, M.A.N.I.; Hossain, A.A. A new chaos based medical image encryption scheme. In Proceedings of the 2017 6th International Conference on Informatics, Electronics and Vision & 2017 7th International Symposium in Computational Medical and Health Technology (ICIEV-ISCMHT), Himeji, Japan, 1–3 September 2017; pp. 1–6. [Google Scholar]
- Belazi, A.; Talha, M.; Kharbech, S.; Xiang, W. Novel medical image encryption scheme based on chaos and DNA encoding. IEEE Access 2019, 7, 36667–36681. [Google Scholar] [CrossRef]
- Ibrahim, S.; Alhumyani, H.; Masud, M.; Alshamrani, S.S.; Cheikhrouhou, O.; Muhammad, G.; Hossain, M.S.; Abbas, A.M. Framework for efficient medical image encryption using dynamic S-boxes and chaotic maps. IEEE Access 2020, 8, 160433–160449. [Google Scholar] [CrossRef]
- Vaseghi, B.; Mobayen, S.; Hashemi, S.S.; Fekih, A. Fast reaching finite time synchronization approach for chaotic systems with application in medical image encryption. IEEE Access 2021, 9, 25911–25925. [Google Scholar] [CrossRef]
- Boutros, A.; Hesham, S.; Georgey, B. Hardware acceleration of novel chaos-based image encryption for IoT applications. In Proceedings of the 2017 29th International Conference on Microelectronics (ICM), Beirut, Lebanon, 10–13 December 2017; pp. 1–4. [Google Scholar]
- Nath, S.; Som, S.; Negi, M. Lca approach for image encryption based on chaos to secure multimedia data in iot. In Proceedings of the 2019 4th International Conference on Information Systems and Computer Networks (ISCON), Mathura, India, 21–22 November 2019; pp. 410–416. [Google Scholar]
- Jain, J.; Jain, A.; Srivastava, S.K.; Verma, C.; Raboaca, M.S.; Illés, Z. Improved Security of E-Healthcare Images Using Hybridized Robust Zero-Watermarking and Hyper-Chaotic System along with RSA. Mathematics 2022, 10, 1071. [Google Scholar] [CrossRef]
- Stanciu, M.; Datcu, O. Atmel AVR microcontroller implementation of a new enciphering algorithm based on a chaotic Generalized Hénon Map. In Proceedings of the 2012 9th International Conference on Communications (COMM), Bucharest, Romania, 21–23 June 2012; pp. 319–322. [Google Scholar]
- Murillo-Escobar, M.A.; Cruz-Hernández, C.; Abundiz-Pérez, F.; López-Gutiérrez, R.M. Implementation of an improved chaotic encryption algorithm for real-time embedded systems by using a 32-bit microcontroller. Microprocess. Microsyst. 2016, 45, 297–309. [Google Scholar] [CrossRef]
- Janakiraman, S.; Thenmozhi, K.; Rayappan, J.B.B.; Amirtharajan, R. Lightweight chaotic image encryption algorithm for real-time embedded system: Implementation and analysis on 32-bit microcontroller. Microprocess. Microsyst. 2018, 56, 1–12. [Google Scholar] [CrossRef]
- García-Guerrero, E.; Inzunza-González, E.; López-Bonilla, O.; Cárdenas-Valdez, J.; Tlelo-Cuautle, E. Randomness improvement of chaotic maps for image encryption in a wireless communication scheme using PIC-microcontroller via Zigbee channels. Chaos Solitons Fractals 2020, 133, 109646. [Google Scholar] [CrossRef]
- Usama, M.; Khan, M.K.; Alghathbar, K.; Lee, C. Chaos-based secure satellite imagery cryptosystem. Comput. Math. Appl. 2010, 60, 326–337. [Google Scholar] [CrossRef]
- Bentoutou, Y.; Bensikaddour, E.-H.; Taleb, N.; Bounoua, N. An improved image encryption algorithm for satellite applications. Adv. Space Res. 2020, 66, 176–192. [Google Scholar] [CrossRef]
- Vaseghi, B.; Hashemi, S.S.; Mobayen, S.; Fekih, A. Finite time chaos synchronization in time-delay channel and its application to satellite image encryption in OFDM communication systems. IEEE Access 2021, 9, 21332–21344. [Google Scholar] [CrossRef]
- Sobhy, M.I.; Shehata, A.-E. Methods of attacking chaotic encryption and countermeasures. In Proceedings of the 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing, Proceedings (Cat. No. 01CH37221), Salt Lake City, UT, USA, 7–11 May 2001; pp. 1001–1004. [Google Scholar]
- Alvarez, G.; Amigó, J.M.; Arroyo, D.; Li, S. Lessons learnt from the cryptanalysis of chaos-based ciphers. Chaos-Based Cryptogr. Theory Algorithms Appl. 2011, 42, 257–295. [Google Scholar]
- Rhouma, R.; Belghith, S. Cryptanalysis of a new image encryption algorithm based on hyper-chaos. Phys. Lett. A 2008, 372, 5973–5978. [Google Scholar] [CrossRef]
- Solak, E.; Cokal, C.; Yildiz, O.T.; Biyikoğlu, T. Cryptanalysis of Fridrich’s chaotic image encryption. Int. J. Bifurc. Chaos 2010, 20, 1405–1413. [Google Scholar] [CrossRef]
- Xie, E.Y.; Li, C.; Yu, S.; Lü, J. On the cryptanalysis of Fridrich’s chaotic image encryption scheme. Signal Process. 2017, 132, 150–154. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, D. Cryptanalysis of S-box-only chaotic image ciphers against chosen plaintext attack. Nonlinear Dyn. 2013, 72, 751–756. [Google Scholar] [CrossRef]
- Ye, G.; Pan, C.; Huang, X.; Zhao, Z.; He, J. A chaotic image encryption algorithm based on information entropy. Int. J. Bifurc. Chaos 2018, 28, 1850010. [Google Scholar] [CrossRef]
- Li, C.; Lin, D.; Feng, B.; Lü, J.; Hao, F. Cryptanalysis of a chaotic image encryption algorithm based on information entropy. IEEE Access 2018, 6, 75834–75842. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Z.; Chen, R. Cryptanalysis and improvement in a plaintext-related image encryption scheme based on hyper chaos. IEEE Access 2019, 7, 126450–126463. [Google Scholar] [CrossRef]
- Li, Z.; Peng, C.; Li, L.; Zhu, X. A novel plaintext-related image encryption scheme using hyper-chaotic system. Nonlinear Dyn. 2018, 94, 1319–1333. [Google Scholar] [CrossRef]
- Yuen, C.-H.; Wong, K.-W. A chaos-based joint image compression and encryption scheme using DCT and SHA-1. Appl. Soft Comput. 2011, 11, 5092–5098. [Google Scholar] [CrossRef]
- Brindha, M.; Gounden, N.A. A chaos based image encryption and lossless compression algorithm using hash table and Chinese Remainder Theorem. Appl. Soft Comput. 2016, 40, 379–390. [Google Scholar] [CrossRef]
- Chai, X.; Fu, X.; Gan, Z.; Zhang, Y.; Lu, Y.; Chen, Y. An efficient chaos-based image compression and encryption scheme using block compressive sensing and elementary cellular automata. Neural Comput. Appl. 2020, 32, 4961–4988. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, M.; Tong, X.; Wang, Z. A chaos-based image compression and encryption scheme using fractal coding and adaptive-thresholding sparsification. Phys. Scr. 2022, 97, 105201. [Google Scholar] [CrossRef]
- Candès, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Xiao, D.; Deng, M.; Zhu, X. A reversible image authentication scheme based on compressive sensing. Multimed. Tools Appl. 2015, 74, 7729–7752. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, J.; Chen, F.; Zhang, L.Y.; Wong, K.-W.; He, X.; Xiao, D. Embedding cryptographic features in compressive sensing. Neurocomputing 2016, 205, 472–480. [Google Scholar] [CrossRef]
- Yang, C.; Pan, P.; Ding, Q. Image encryption scheme based on mixed chaotic bernoulli measurement matrix block compressive sensing. Entropy 2022, 24, 273. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Yan, Y.; Lin, Y.; Li, Y. Image Security Retrieval Based on Chaotic Algorithm and Deep Learning. IEEE Access 2022, 10, 67210–67218. [Google Scholar] [CrossRef]
- Yue-Hei Ng, J.; Yang, F.; Davis, L.S. Exploiting local features from deep networks for image retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Boston, MA, USA, 7–12 June 2015; pp. 53–61. [Google Scholar]
- Gordo, A.; Almazán, J.; Revaud, J.; Larlus, D. Deep image retrieval: Learning global representations for image search. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; pp. 241–257. [Google Scholar]
- Song, W.; Fu, C.; Zheng, Y.; Cao, L.; Tie, M.; Sham, C.-W. Protection of image ROI using chaos-based encryption and DCNN-based object detection. Neural Comput. Appl. 2022, 34, 5743–5756. [Google Scholar] [CrossRef]
- Wang, J.; Liu, L.; Xu, M.; Li, X. A novel content-selected image encryption algorithm based on the LS chaotic model. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 8245–8259. [Google Scholar] [CrossRef]
- Shan, Y.; He, M.; Yu, Z.; Wu, H. Pixel level Image Encryption Based on Semantic Segmentation. In Proceedings of the 2018 International Conference on Control, Artificial Intelligence, Robotics & Optimization (ICCAIRO), Prague, Czech Republic, 19–21 May 2018; pp. 147–152. [Google Scholar]
- Hanbury, A. A survey of methods for image annotation. J. Vis. Lang. Comput. 2008, 19, 617–627. [Google Scholar] [CrossRef]
- Radenović, F.; Tolias, G.; Chum, O. Fine-tuning CNN image retrieval with no human annotation. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 1655–1668. [Google Scholar] [CrossRef]
- Yang, C.-H.; Weng, C.-Y.; Yang, Y.-Z. TPEIP: Thumbnail preserving encryption based on sum preserving for image privacy. J. Inf. Secur. Appl. 2022, 70, 103352. [Google Scholar] [CrossRef]
- Tajik, K.; Gunasekaran, A.; Dutta, R.; Ellis, B.; Bobba, R.B.; Rosulek, M.; Wright, C.V.; Feng, W.-C. Balancing Image Privacy and Usability with Thumbnail-Preserving Encryption. IACR Cryptol. Eprint Arch. 2019, 2019, 295. [Google Scholar]
- Zhang, Y.; Zhao, R.; Xiao, X.; Lan, R.; Liu, Z.; Zhang, X. HF-TPE: High-fidelity thumbnail-preserving encryption. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 947–961. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, R.; Zhang, Y.; Lan, R.; Chai, X. High-efficiency and visual-usability image encryption based on thumbnail preserving and chaotic system. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 2993–3010. [Google Scholar] [CrossRef]
- Zhu, Z.; Liu, L. Thumbnail-preserving encryption based on improved logistic system. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 10167–10179. [Google Scholar] [CrossRef]


| Year | Authors and Reference | Contribution | Label |
|---|---|---|---|
| 1998 | Jiri Fridrich [26] | A chaos-based image-encryption algorithm was proposed for the first time. | Symmetric Encryption |
| 1998 | Josef Scharinger [27] | They highlighted the PRNG role in image encryption. | Symmetric Encryption |
| 2004 | Guanrong Chen and Yaobin Mao [18] | They first extended Cat maps and images to 3D encryption at the same time. | Symmetric Encryption |
| 2005 | Linhua Zhang and Xiaofeng Liao [67] | They combined PLM with S-Box to apply image encryption. | Symmetric Encryption; S-Box |
| 2006 | K. Pareek Vinod [39] | They first proposed a chaotic color image-encryption algorithm. | Symmetric Encryption; Color image |
| 2006 | A. N. Pisarchik [90] | A spatiotemporal chaotic system was first applied to image encryption. | Symmetric Encryption; Spatiotemporal |
| 2007 | S. Kwok and Wallace K. S. Tang [84] | Chaotic image encryption based on a stream cipher was proposed for the first time. | Symmetric Encryption |
| 2008 | Tiegang Gao and Zengqiang Chen [61] | They first applied hyperchaotic systems to image-encryption algorithms | Symmetric Encryption; Hyperchaotic |
| 2019 | Lucas G. Nardo and Erivelton G [52] | The limited precision error was used as a source of randomness in a chaotic image-encryption algorithm. | Symmetric Encryption |
| 2011 | Zhi-liang ZhuWei Zhang [71] | A chaotic system was applied to image encryption at the bitplane level. | Symmetric Encryption; Bitplane |
| 2016 | Lu Xu and Zhi Li [100] | They combined PWLCM and BBD for image encryption. | Symmetric Encryption; Bitplane |
| 2008 | S. Behnia and A. Akhshani [55] | They used chaotic maps for image encryption after coupling for the first time. | Symmetric Encryption; Chaotification |
| 2015 | Xingyuan Wang and Lintao Liu [48] | The dynamic growth technique was introduced into a chaos-based image-encryption algorithm. | Symmetric Encryption; Chaotification |
| 2019 | Moatsum Alawida and Azman Samsudin [60] | TLTS and TSTS, formed using 1D chaotic systems as a seed map, were employed in image encryption. | Symmetric Encryption; Chaotification |
| 2020 | Zhongyun Hua and Zhihua Zhu [54] | They proposed LTMM-CIEA and used cross-planar arrangement and non-sequential diffusion. | Symmetric Encryption; Chaotification |
| 2013 | Chao-Jung Cheng and Chi-Bin Cheng [107] | They first applied asymmetric cryptography to chaotic image encryption. | Asymmetric Encryption |
| 2017 | Jiahui Wu and Xiaofeng Liao [115] | They first introduced an elliptic curve to a chaotic image-encryption algorithm. | Asymmetric Encryption |
| 2017 | Ünal. C and Akif. A [109] | They first introduced RSA into a chaotic image-encryption algorithm. | Asymmetric Encryption |
| 2019 | Ali Shakiba [121] | An asymmetric image-encryption algorithm based on Chebyshev polynomial. | Asymmetric Encryption |
| 2009 | Chun-jiang pang [102] | DWT-based frequency-domain chaotic image encryption was proposed for the first time. | Frequency Domain |
| 2011 | Zhengjun Liu and Lie Xu [105] | Chaotic color image encryption based on DCT. | Frequency Domain |
| 2012 | Abdul Hanan Abdullah [134] | It was the first time to combine chaotic system and gene technology for image encryption. | Genetic technology |
| 2012 | Lili Liu and Qiang Zhang [135] | A combination of DNA and chaotic systems for color image encryption. | Genetic technology |
| 2017 | Xiuli Chai [138] | They utilized a DNA matrix for image encryption while the chaotic system is for RCP and CCP. | Genetic technology |
| 2009 | Shiguo Lian [124] | Image encryption was carried out by combining neural networks with a chaotic system. | Neural networks |
| 2013 | Xingyuan Wang and Dapeng Luan [145] | Cellular automata were applied to a chaotic image-encryption scheme for the first time. | Cellular automata |
| 2021 | Ruiping Li [149] | The blockchain framework was used in chaotic image encryption. | Blockchain |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Liu, L. Chaos-Based Image Encryption: Review, Application, and Challenges. Mathematics 2023, 11, 2585. https://doi.org/10.3390/math11112585
Zhang B, Liu L. Chaos-Based Image Encryption: Review, Application, and Challenges. Mathematics. 2023; 11(11):2585. https://doi.org/10.3390/math11112585
Chicago/Turabian StyleZhang, Bowen, and Lingfeng Liu. 2023. "Chaos-Based Image Encryption: Review, Application, and Challenges" Mathematics 11, no. 11: 2585. https://doi.org/10.3390/math11112585
APA StyleZhang, B., & Liu, L. (2023). Chaos-Based Image Encryption: Review, Application, and Challenges. Mathematics, 11(11), 2585. https://doi.org/10.3390/math11112585






