An Efficient Metaheuristic Algorithm for Job Shop Scheduling in a Dynamic Environment
Abstract
1. Introduction
2. Problem Description
- All machines from a set of are available at time 0;
- A single operation can only be executed on one machine at a time;
- A single machine can only execute one operation at a time;
- The operation executed on machine can only be interrupted if a dynamic event occurs (machine breakdown, new job arrival or process time change);
- The next operation cannot be executed until the previous operation is completed;
- The processing times of the operation and the assigned machine are known in advance. During a single operation, the processing time may change due to a dynamic event that changes the original processing time of the operation;
- The original operation processing time is know;
- The setup times do not depend on the sequence of operation execution and the machine on which the operation is executed but are included in the operation processing time;
- The transfer time between machines is 0.
| Initial jobs ; | |
| New jobs ; | |
| Machines | |
| Set of routing constraints ; | |
| Set of new jobs’ routing constraints ; | |
| Process time of operation ; | |
| Process time of new job operation ; | |
| Completion time of job on machine ; | |
| Completion time of new job on machine ; | |
| Starting time of the operation ; | |
| Starting time of a new operation ; | |
| The start time of the rescheduled job order; | |
| The start time that the machine will be idled at the start of rescheduling a job order. |
3. Metaheuristic Method
3.1. Multi-Phase Particle Swarm Optimization
3.2. Improved Multi-Phase Particle Swarm Optimization
| Algorithm 1 The general pseudo-code of the IMPPSO |
| Step 0: Setting the parameters. The number of rows and columns of the cellular neighbor network, the neighbor type of the cellular neighbor network , the rewiring probability of the cellular neighbor network , the minimum/maximum depth of the cellular neighbor network , the nearest neighbors of the cellular neighbor network , the size of the swarm (Note that ), the dimension of the problem , the lower and upper boundary values for the problem (corresponding to the first row and the second row, respectively), the number of phases , the frequency change of the phase , the number of groups within each phase , the maximum sub-dimension length , the initial velocity change variable value , the final velocity change variable value , and the maximum number of iterations . Step 1 Initialize the variables. The phase change count , the last velocity change and the count of consecutive generations with no change in global best fitness . Step 2: Initialize the population. The velocity , position and their fitness , the global best position and its fitness . Step 3: Initialize the cellular neighbor network using the algorithm [30]. Step 4: Iterative population. for Step 4.1: Calculate the current velocity change variable. Step 4.2: Determine whether the reinitiate velocity condition is met and reinitiate the velocity when it is met. Step 4.3: Determine the current phase . Step 4.4: Update the particle. for Step 4.4.1: Determine the group for the current particle. Step 4.4.2: Obtain the nearest neighbor’s best position for the current particle. Step 4.4.3: Initialize the dimension set of the problem. Step 4.4.4: Determine the size of the select index of the sub-dimension for updating. Step 4.4.5: Update the sub-dimension. while Step 4.4.5.1: Select the sub-dimension for updating. Step 4.4.5.2: Cache the position of the current particle. Step 4.4.5.3: Set the coefficient’s value in each group within each phase. Step 4.4.5.4: Update the velocity of the current particle. Step 4.4.5.5: Update the temporary position. Step 4.4.5.6: Handle the constraints. Step 4.4.5.7: Evaluate the fitness of the temporary position. Step 4.4.5.8: Update the position of the current particle. Step 4.4.5.9: Delete the updated sub-dimensions. end end Step 4.5: Determine whether the global best position has changed. Step 4.6: Update the nearest neighbor’s best position. end |
3.2.1. Cellular Neighbor Network Introduction
3.2.2. Velocity Reinitialization
3.2.3. Sub-Dimension Selection
3.2.4. Constraint Handling
3.3. Encoding Example
4. Numerical Experiment
4.1. Benchmark Instances
4.2. Experimental Design
4.3. Parameter Settings
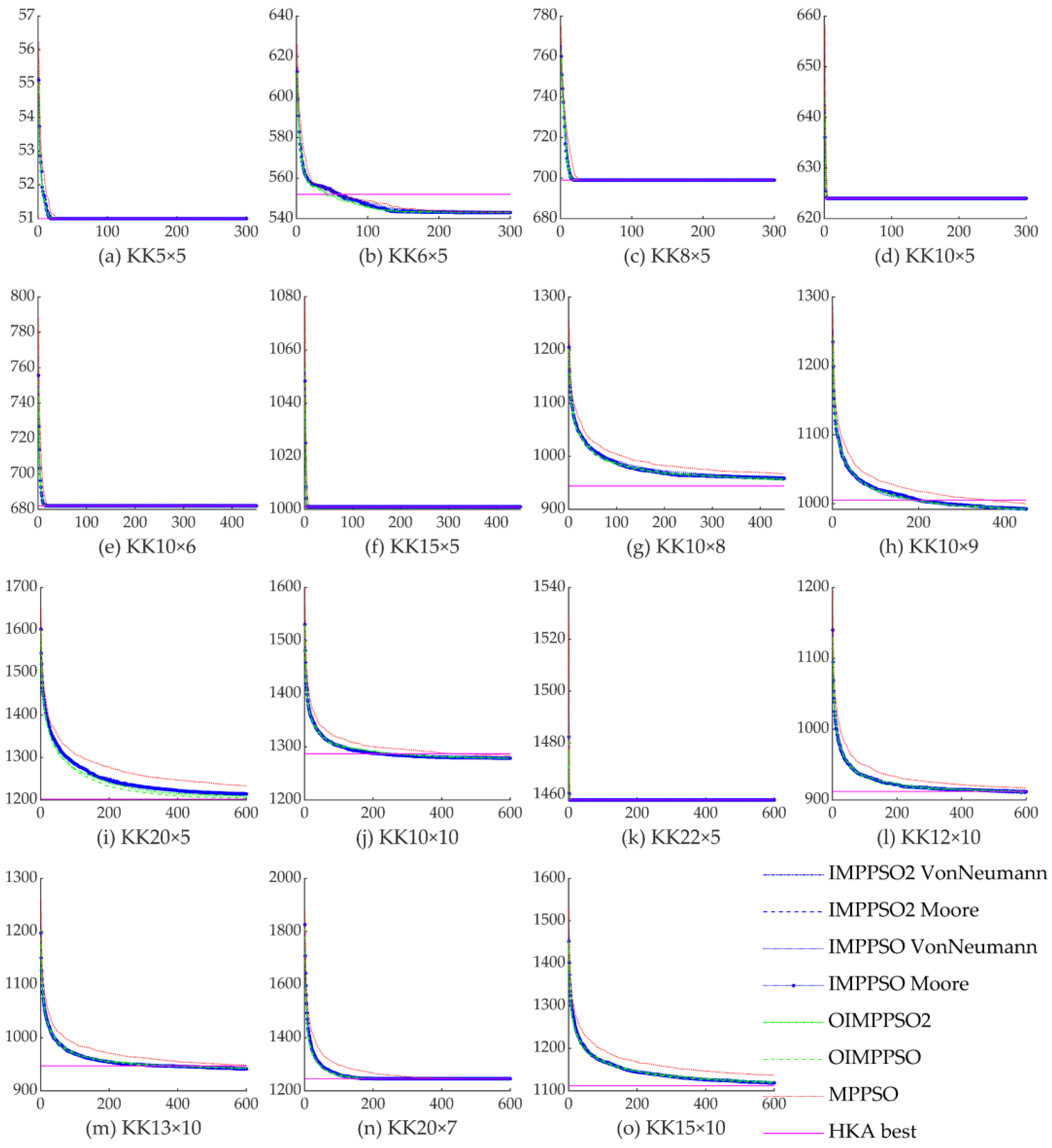
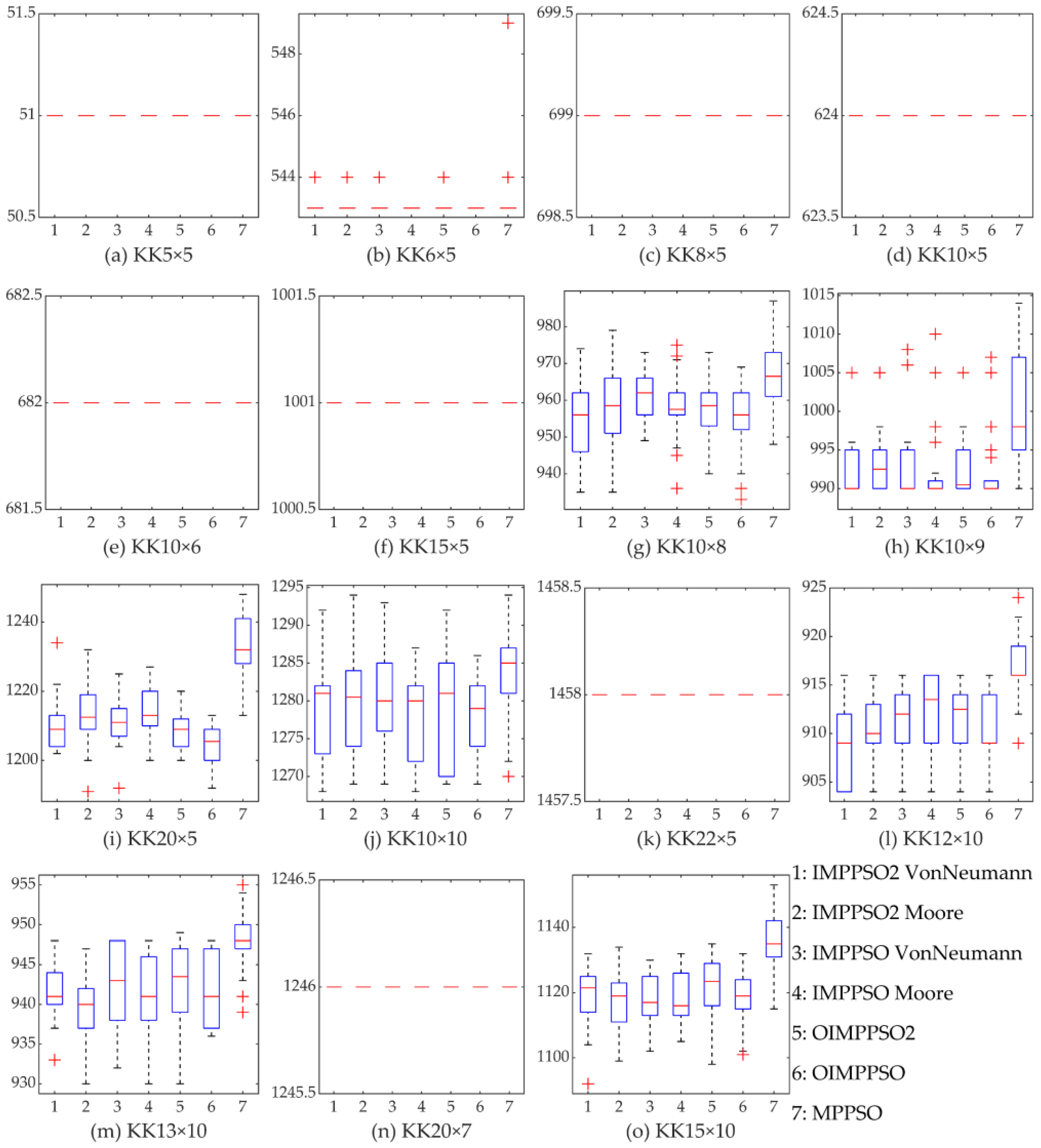
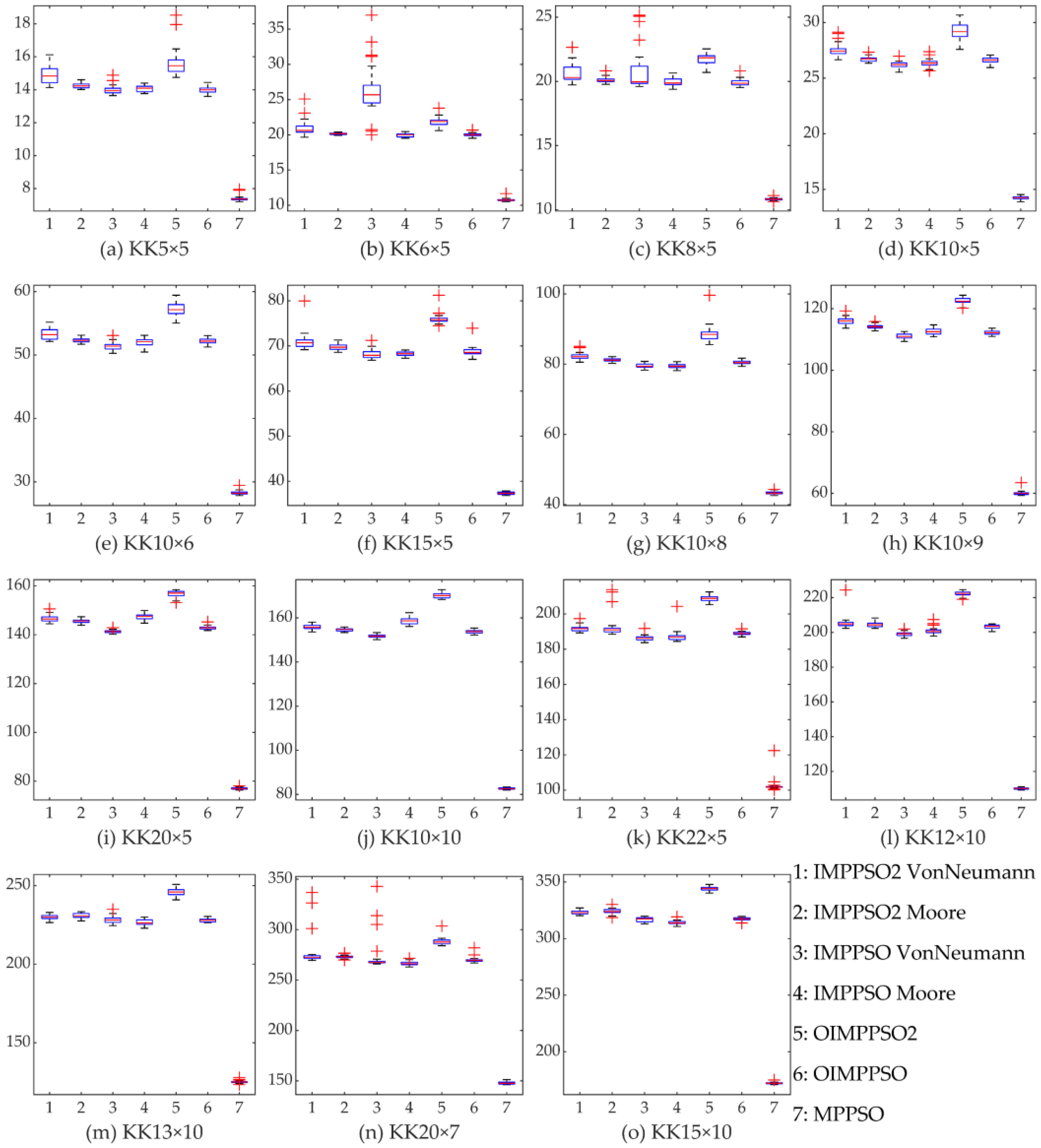
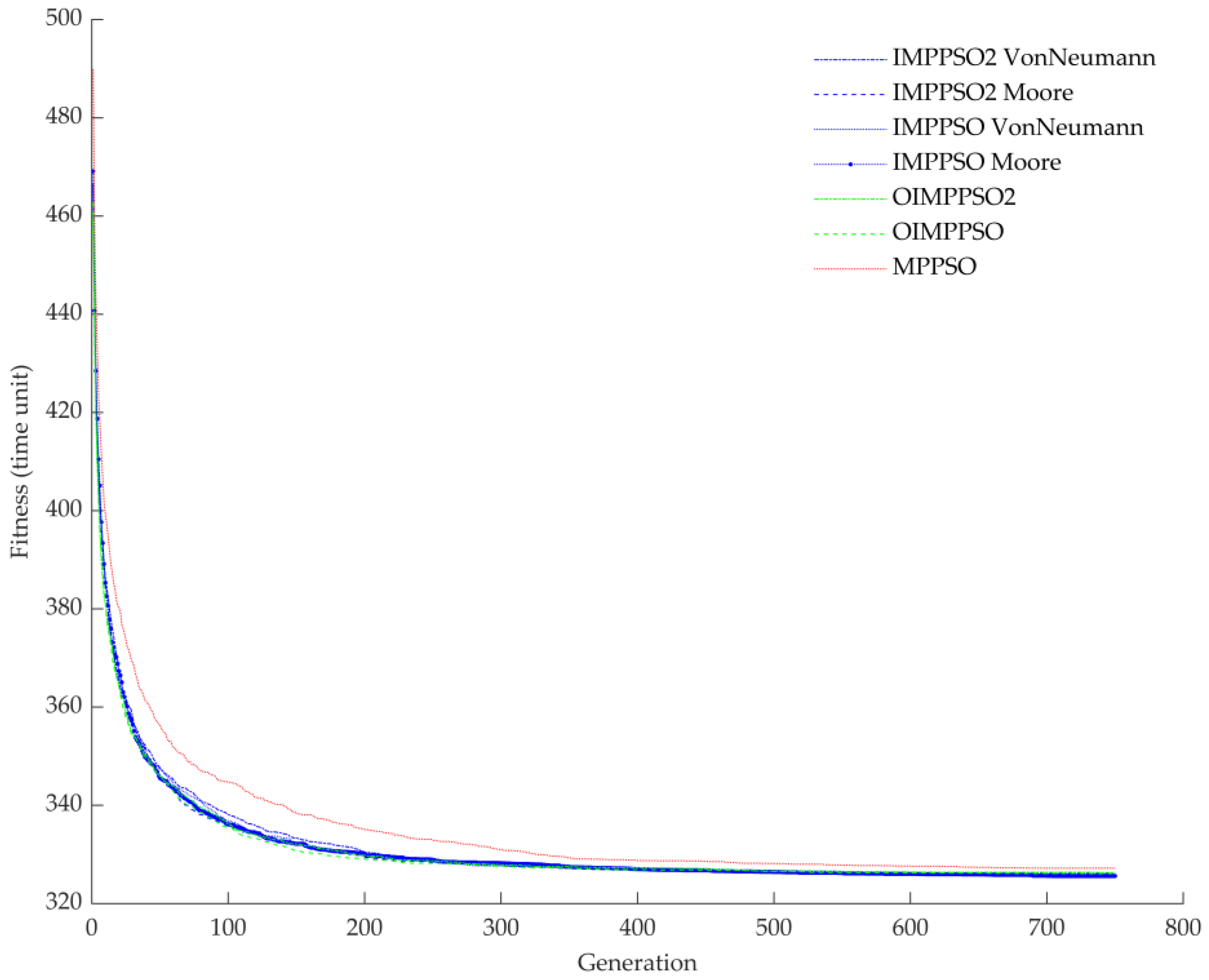
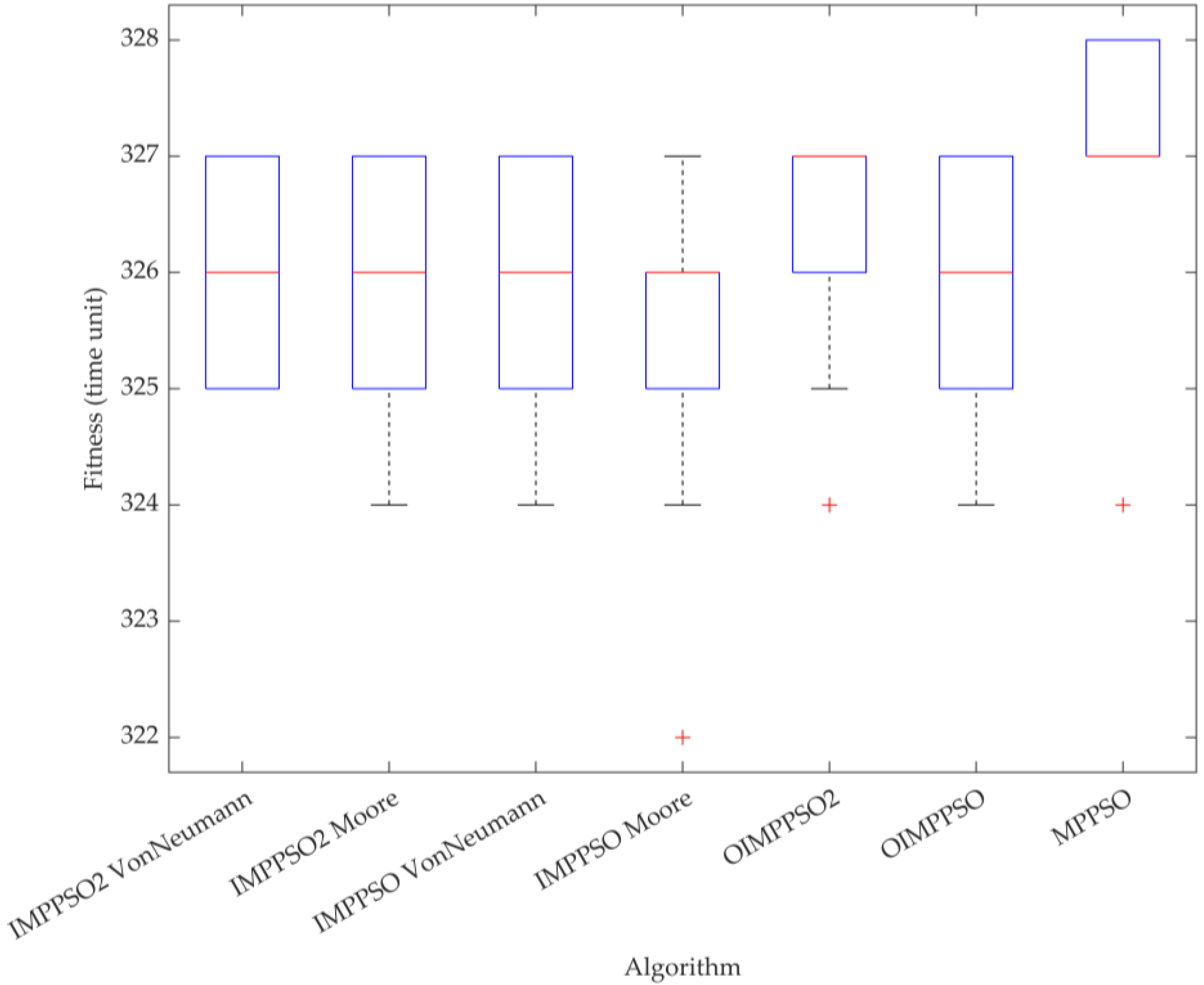
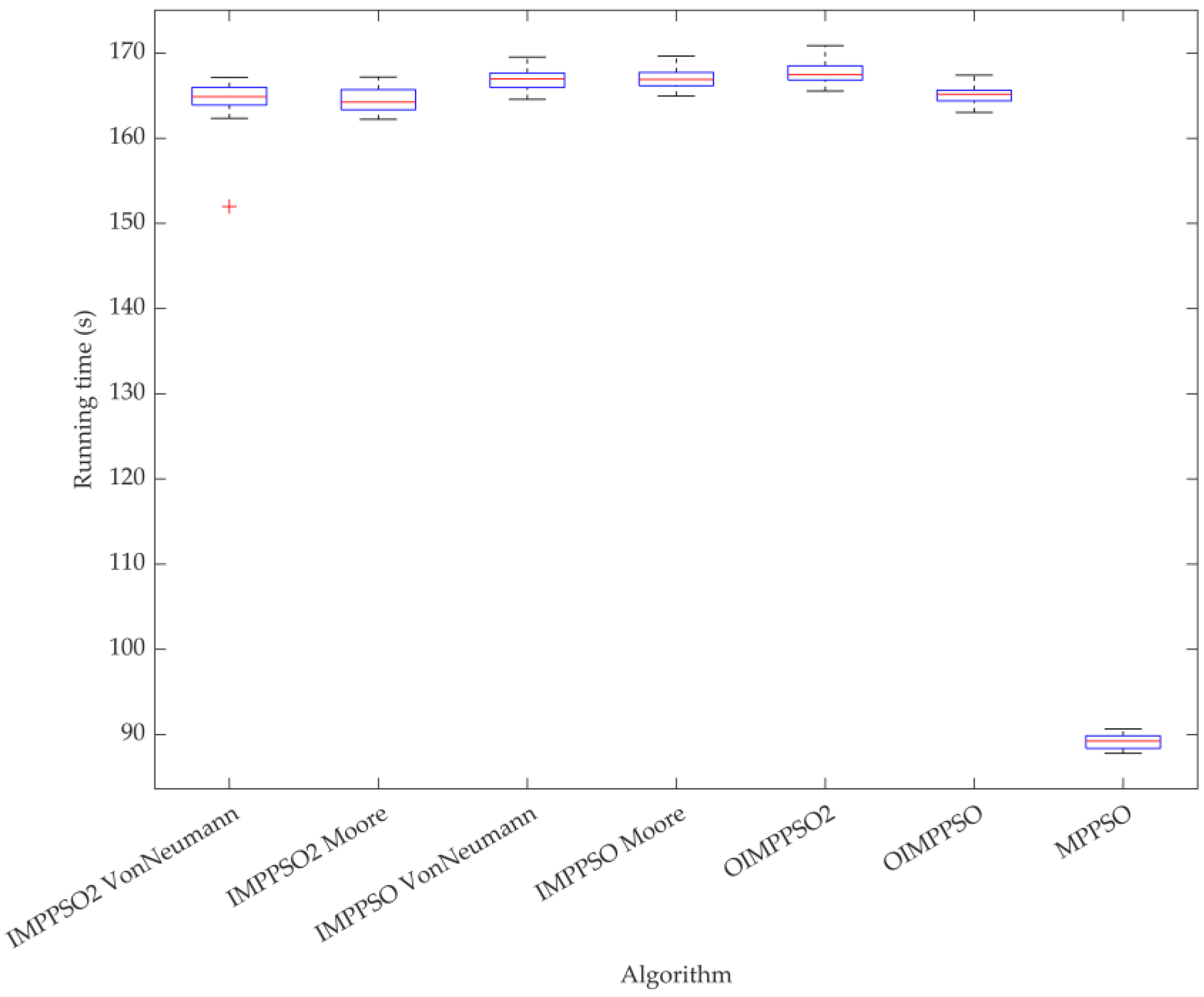
4.4. Experimental Result
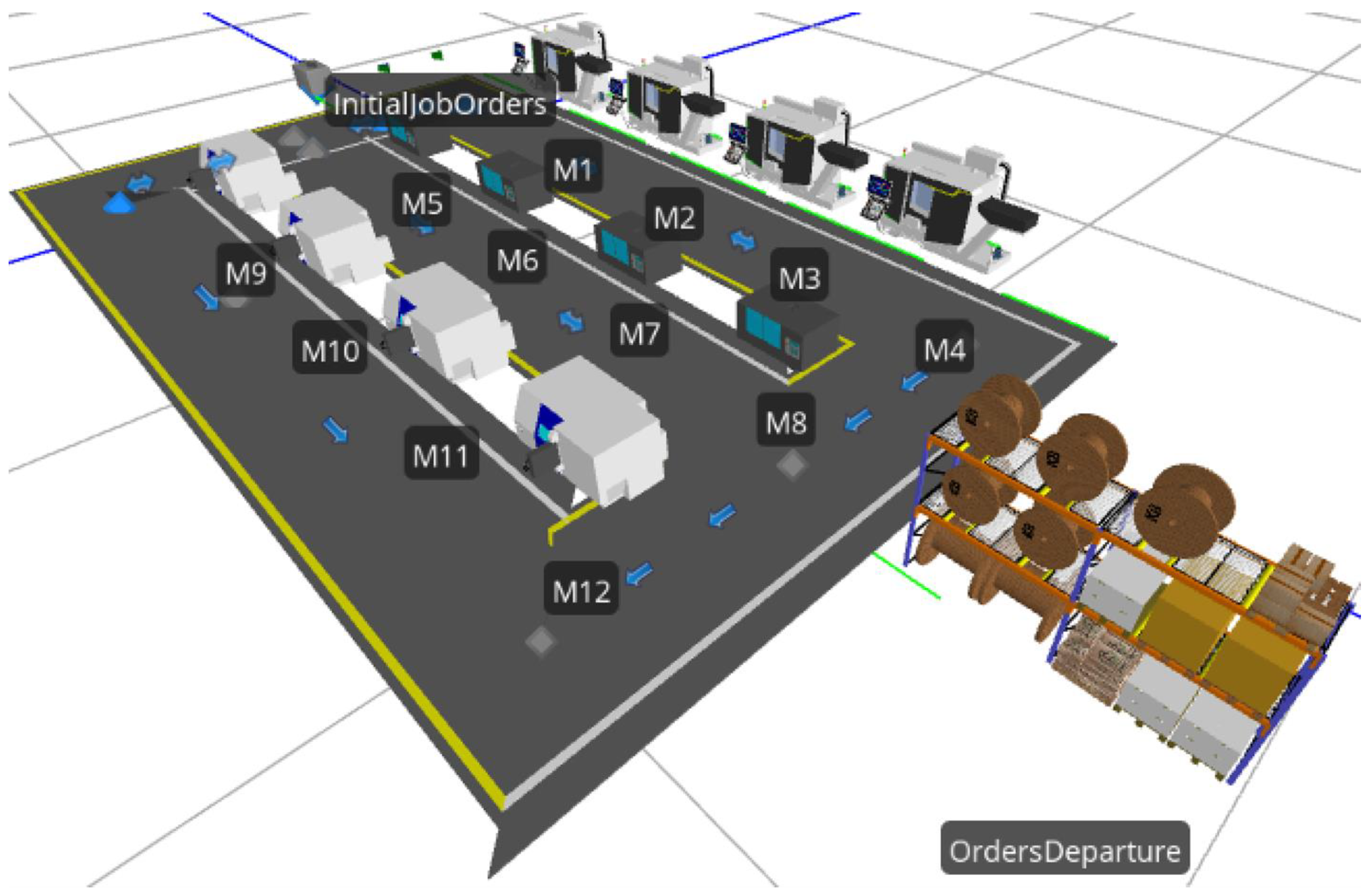
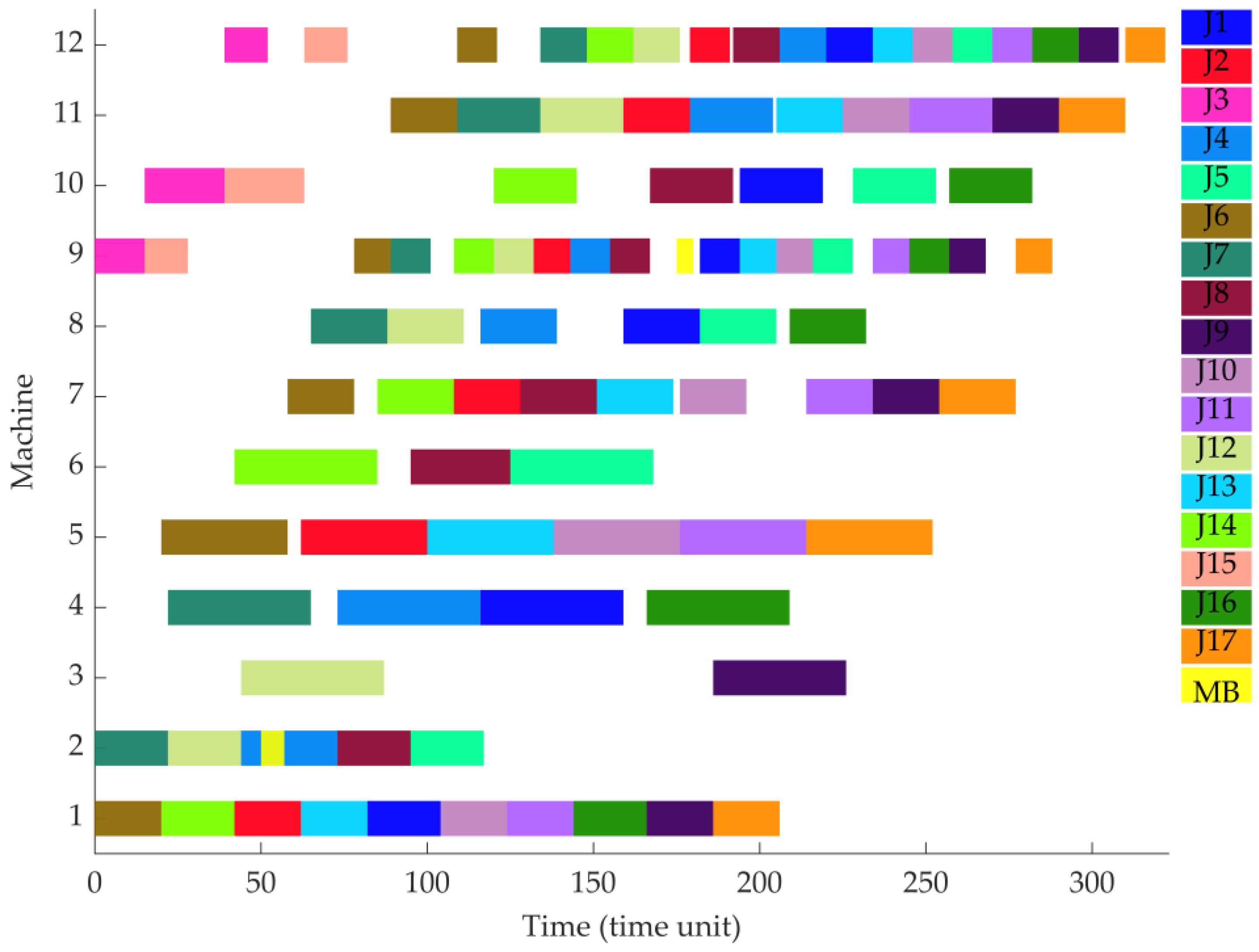
5. Case Study
5.1. Case Description
5.2. Algorithm Experiment
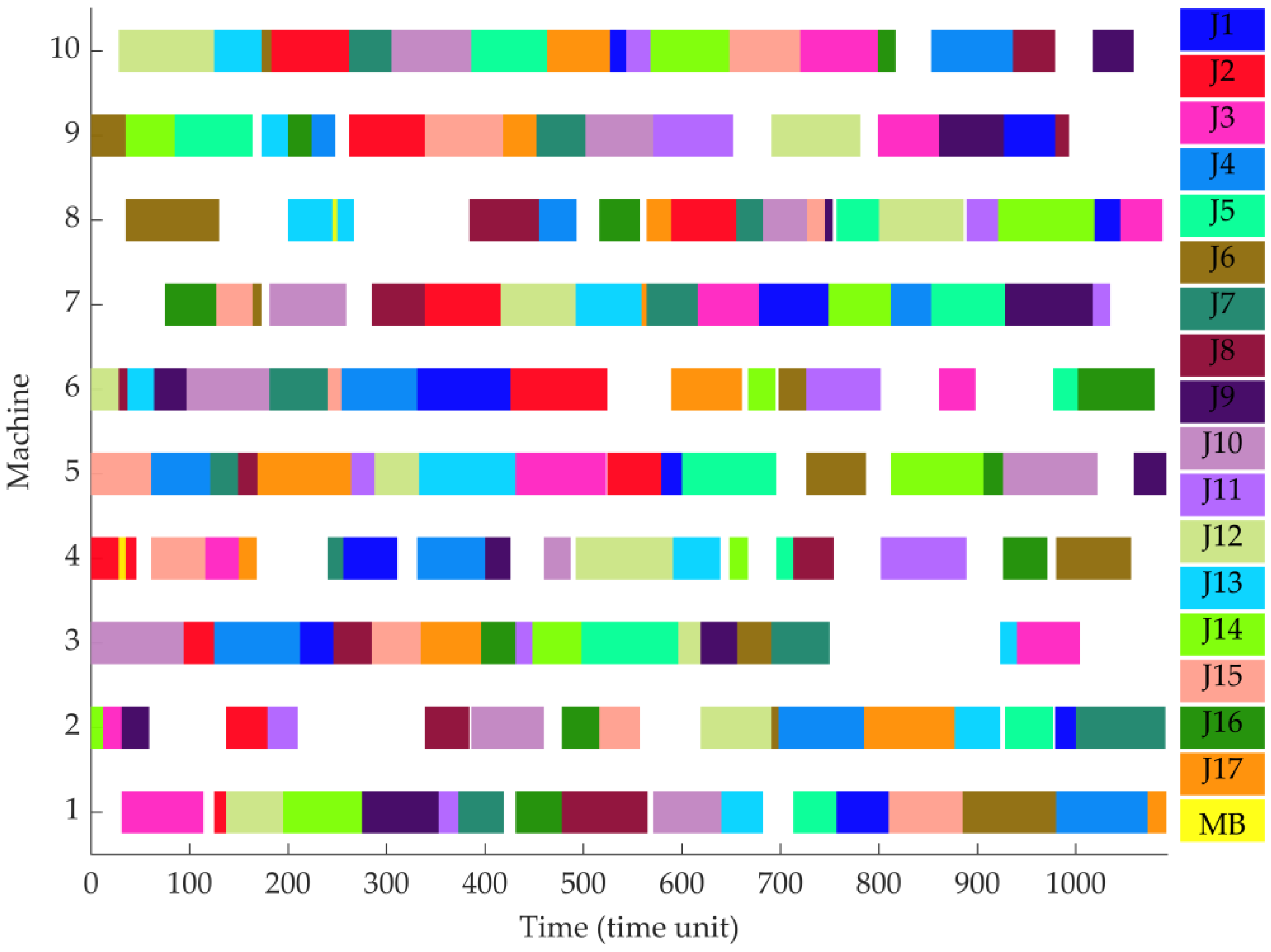
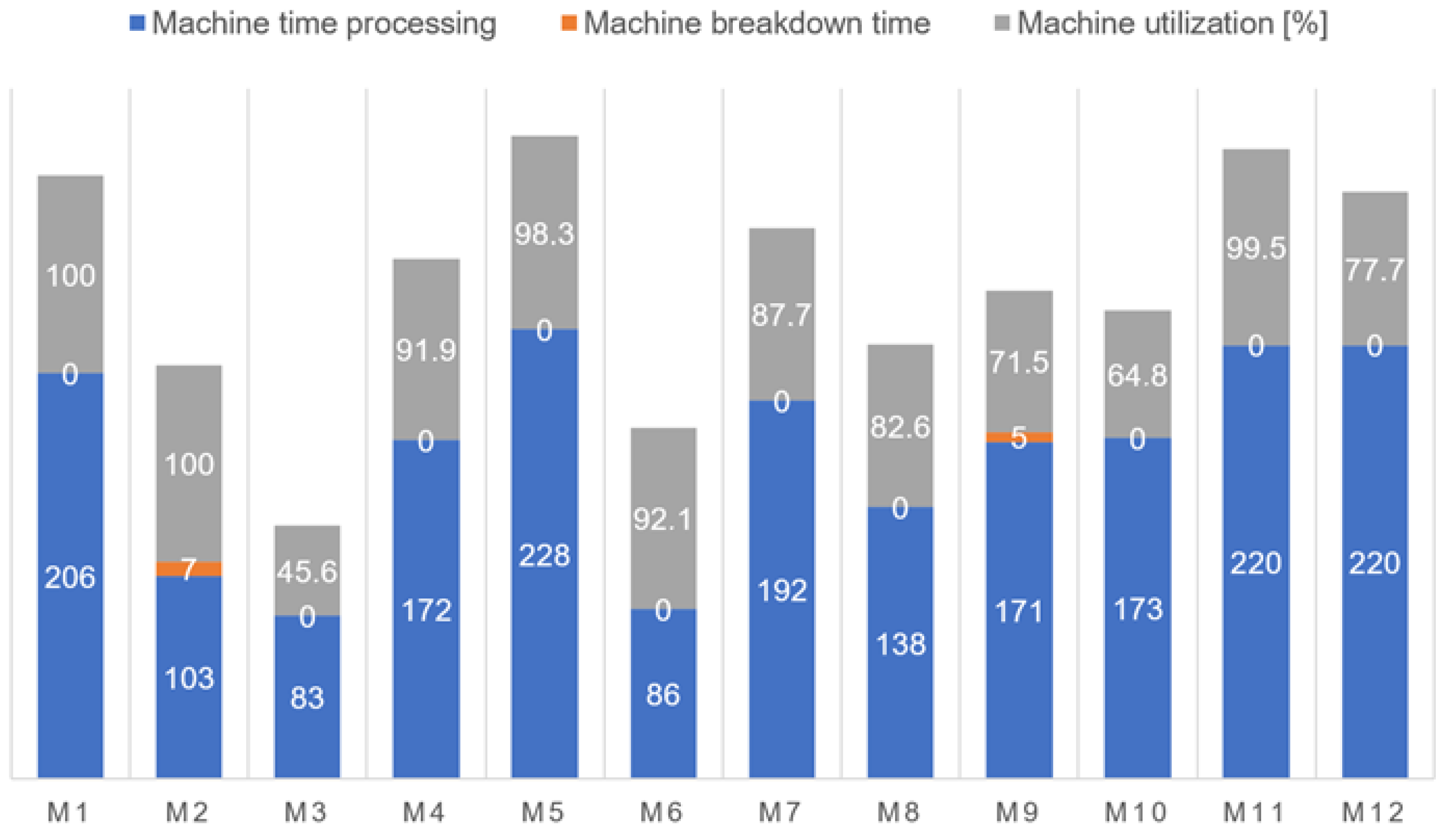
5.3. Simulation Modelling Result
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ramasesh, R. Dynamic Job Shop Scheduling: A Survey of Simulation Research. Omega 1990, 18, 43–57. [Google Scholar] [CrossRef]
- Hinderer, K.; Rieder, U.; Stieglitz, M. Introduction and Organization of the Book. In Dynamic Optimization; Universitext; Springer International Publishing: Cham, Switzerland, 2016; pp. 1–11. ISBN 978-3-319-48813-4. [Google Scholar]
- Park, J.; Mei, Y.; Nguyen, S.; Chen, G.; Zhang, M. An Investigation of Ensemble Combination Schemes for Genetic Programming Based Hyper-Heuristic Approaches to Dynamic Job Shop Scheduling. Appl. Soft Comput. 2018, 63, 72–86. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J.; Yang, S. An Improved Particle Swarm Optimization Algorithm for Dynamic Job Shop Scheduling Problems with Random Job Arrivals. Swarm Evol. Comput. 2019, 51, 100594. [Google Scholar] [CrossRef]
- Chryssolouris, G.; Subramaniam, V. Dynamic Scheduling of Manufacturing Job Shops Using Genetic Algorithms. J. Intell. Manuf. 2001, 12, 281–293. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, L.; Li, X. A Hybrid Genetic Algorithm and Tabu Search for a Multi-Objective Dynamic Job Shop Scheduling Problem. Int. J. Prod. Res. 2013, 51, 3516–3531. [Google Scholar] [CrossRef]
- Nguyen, S.; Zhang, M.; Johnston, M.; Tan, K.C. Automatic Design of Scheduling Policies for Dynamic Multi-Objective Job Shop Scheduling via Cooperative Coevolution Genetic Programming. IEEE Trans. Evol. Comput. 2014, 18, 193–208. [Google Scholar] [CrossRef]
- Aydin, M.E.; Öztemel, E. Dynamic Job-Shop Scheduling Using Reinforcement Learning Agents. Rob. Auton. Syst. 2000, 33, 169–178. [Google Scholar] [CrossRef]
- Shahrabi, J.; Adibi, M.A.; Mahootchi, M. A Reinforcement Learning Approach to Parameter Estimation in Dynamic Job Shop Scheduling. Comput. Ind. Eng. 2017, 110, 75–82. [Google Scholar] [CrossRef]
- Shen, X.-N.; Yao, X. Mathematical Modeling and Multi-Objective Evolutionary Algorithms Applied to Dynamic Flexible Job Shop Scheduling Problems. Inf. Sci. 2015, 298, 198–224. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Madenoğlu, F.S.; Hamzadayı, A. Greedy Randomized Adaptive Search for Dynamic Flexible Job-Shop Scheduling. J. Manuf. Syst. 2020, 56, 425–451. [Google Scholar] [CrossRef]
- Zhang, F.; Mei, Y.; Nguyen, S.; Zhang, M. Evolving Scheduling Heuristics via Genetic Programming With Feature Selection in Dynamic Flexible Job-Shop Scheduling. IEEE Trans. Cybern. 2021, 51, 1797–1811. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, J.-J.; Huang, Z. Automatic Design of Scheduling Policies for Dynamic Flexible Job Shop Scheduling via Surrogate-Assisted Cooperative Co-Evolution Genetic Programming. Int. J. Prod. Res. 2020, 58, 2561–2580. [Google Scholar] [CrossRef]
- Nie, L.; Gao, L.; Li, P.; Li, X. A GEP-Based Reactive Scheduling Policies Constructing Approach for Dynamic Flexible Job Shop Scheduling Problem with Job Release Dates. J. Intell. Manuf. 2013, 24, 763–774. [Google Scholar] [CrossRef]
- Zhang, M.; Tao, F.; Nee, A.Y.C. Digital Twin Enhanced Dynamic Job-Shop Scheduling. J. Manuf. Syst. 2021, 58, 146–156. [Google Scholar] [CrossRef]
- Kuck, M.; Ehm, J.; Hildebrandt, T.; Freitag, M.; Frazzon, E.M. Potential of Data-Driven Simulation-Based Optimization for Adaptive Scheduling and Control of Dynamic Manufacturing Systems. In Proceedings of the 2016 Winter Simulation Conference (WSC), Washington, DC, USA, 11–14 December 2016; pp. 2820–2831. [Google Scholar]
- Zhou, L.; Zhang, L.; Ren, L.; Wang, J. Real-Time Scheduling of Cloud Manufacturing Services Based on Dynamic Data-Driven Simulation. IEEE Trans. Ind. Inform. 2019, 15, 5042–5051. [Google Scholar] [CrossRef]
- Yang, W.; Takakuwa, S. Simulation-Based Dynamic Shop Floor Scheduling for a Flexible Manufacturing System in the Industry 4.0 Environment. In Proceedings of the 2017 Winter Simulation Conference (WSC), Las Vegas, NV, USA, 3–6 December 2017; pp. 3908–3916. [Google Scholar]
- Ojstersek, R.; Buchmeister, B. Simulation Based Resource Capacity Planning with Constraints. Int. J. Sim. Model. 2021, 20, 672–683. [Google Scholar] [CrossRef]
- Vinod, V.; Sridharan, R. Simulation-Based Metamodels for Scheduling a Dynamic Job Shop with Sequence-Dependent Setup Times. Int. J. Prod. Res. 2009, 47, 1425–1447. [Google Scholar] [CrossRef]
- Vinod, V.; Sridharan, R. Simulation Modeling and Analysis of Due-Date Assignment Methods and Scheduling Decision Rules in a Dynamic Job Shop Production System. Int. J. Prod. Econ. 2011, 129, 127–146. [Google Scholar] [CrossRef]
- Xiong, H.; Fan, H.; Jiang, G.; Li, G. A Simulation-Based Study of Dispatching Rules in a Dynamic Job Shop Scheduling Problem with Batch Release and Extended Technical Precedence Constraints. Eur. J. Oper. Res. 2017, 257, 13–24. [Google Scholar] [CrossRef]
- Zou, J.; Chang, Q.; Arinez, J.; Xiao, G.; Lei, Y. Dynamic Production System Diagnosis and Prognosis Using Model-Based Data-Driven Method. Expert Syst. Appl. 2017, 80, 200–209. [Google Scholar] [CrossRef]
- Jemmali, M.; Hidri, L.; Alourani, A. Two-stage Hybrid Flowshop Scheduling Problem With Independent Setup Times. Int. J. Sim. Model. 2022, 21, 5–16. [Google Scholar] [CrossRef]
- Kundakcı, N.; Kulak, O. Hybrid Genetic Algorithms for Minimizing Makespan in Dynamic Job Shop Scheduling Problem. Comput. Ind. Eng. 2016, 96, 31–51. [Google Scholar] [CrossRef]
- Heppner, F.; Grenander, U. A Stochastic Nonlinear Model for Coordinated Bird Flocks. In The Ubiquity of Chaos; Krasner, S., Ed.; AAAS Publications: Washington, DC, USA, 1990; pp. 233–238. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the Proceedings of ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Al-Kazemi, B.S.N. Multiphase Particle Swarm Optimization; Syracuse University: New York, NY, USA, 2002. [Google Scholar]
- Zhang, H. Research on Multi-Objective Swarm Intelligence Algorithms for Door-to-Door Railway Freight Transportation Routing Design; Beijing Jiaotong University: Beijing, China, 2019. [Google Scholar]
- Zhang, H.; Buchmeister, B.; Li, X.; Ojstersek, R. Advanced Metaheuristic Method for Decision-Making in a Dynamic Job Shop Scheduling Environment. Mathematics 2021, 9, 909. [Google Scholar] [CrossRef]
- Li, X.-Y.; Yang, L.; Li, J. Dynamic Route and Departure Time Choice Model Based on Self-Adaptive Reference Point and Reinforcement Learning. Phys. A Stat. Mech. Its Appl. 2018, 502, 77–92. [Google Scholar] [CrossRef]
- Wikipedia Von Neumann Neighborhood. Available online: https://en.wikipedia.org/wiki/Von_Neumann_neighborhood (accessed on 26 August 2020).
- Wikipedia Moore Neighborhood. Available online: https://en.wikipedia.org/wiki/Moore_neighborhood (accessed on 23 June 2022).
- Sha, D.Y.; Lin, H.-H. A Multi-Objective PSO for Job-Shop Scheduling Problems. Expert Syst. Appl. 2010, 37, 1065–1070. [Google Scholar] [CrossRef]
- Marinakis, Y.; Marinaki, M. A Hybrid Particle Swarm Optimization Algorithm for the Open Vehicle Routing Problem. In Swarm Intelligence, Proceedings of the 8th International Conference, ANTS 2012, Brussels, Belgium, 12–14 September 2012; Dorigo, M., Birattari, M., Blum, C., Christensen, A.L., Engelbrecht, A.P., Groß, R., Stützle, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 180–187. ISBN 978-3-642-32650-9. [Google Scholar]
- Ojstersek, R.; Lalic, D.; Buchmeister, B. A New Method for Mathematical and Simulation Modelling Interactivity: A Case Study in Flexible Job Shop Scheduling. Adv. Prod. Eng. Manag. 2019, 14, 435–448. [Google Scholar] [CrossRef]
- Guzman, E.; Andres, B.; Poler, R. A Decision-Making Tool for Algorithm Selection Based on a Fuzzy TOPSIS Approach to Solve Replenishment, Production and Distribution Planning Problem. Mathematics 2022, 10, 1544. [Google Scholar] [CrossRef]

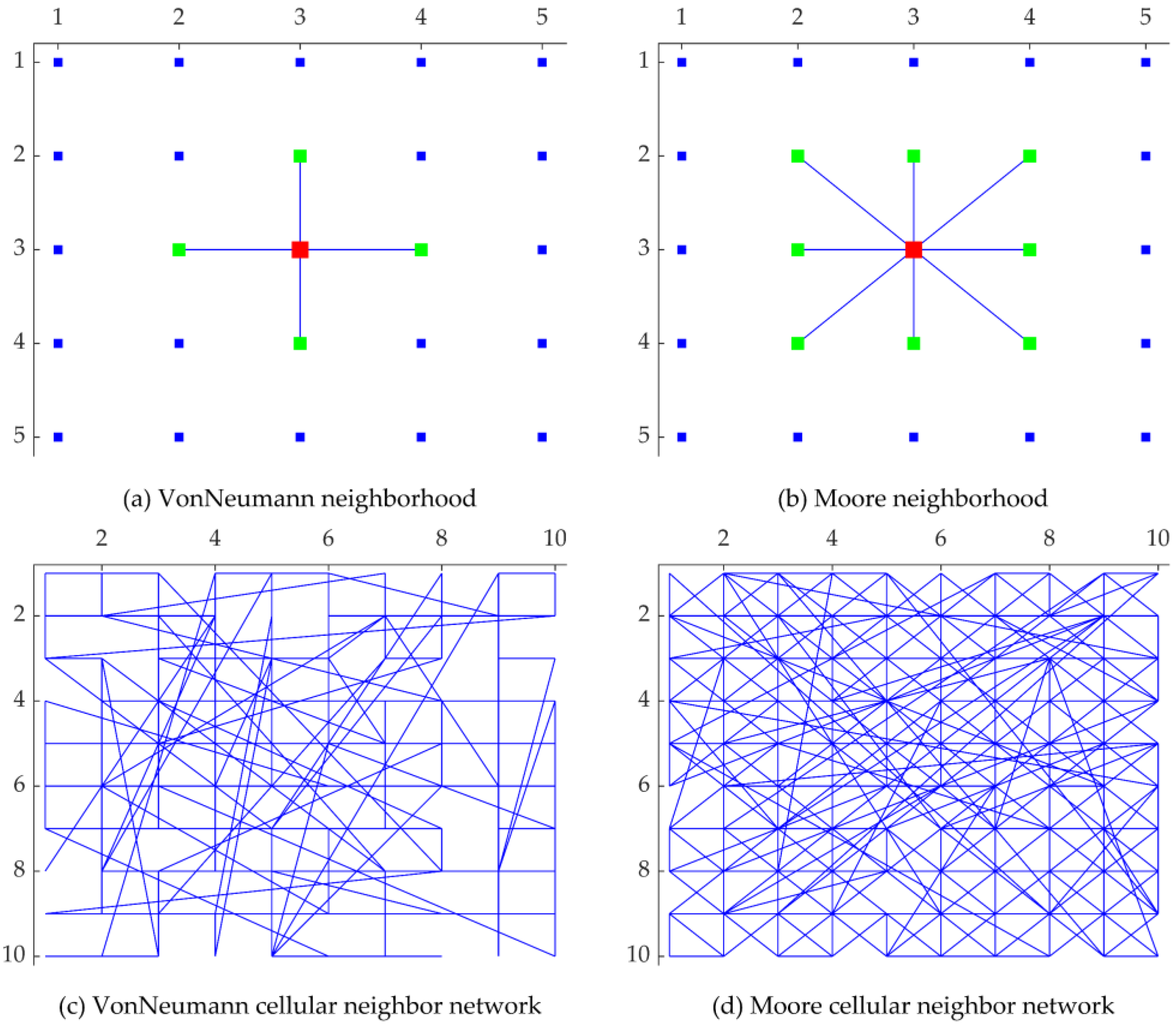


| No | Jobs | Occurrence Time | Machine No | Processing Times | Original Processing Time | Remarks |
|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 3 | 2 | ||
| 2 | 1 | 0 | 1 | 8 | ||
| 3 | 1 | 0 | 2 | 4 | 6 | Change in the process time |
| 4 | 2 | 0 | 2 | 6 | ||
| 5 | 2 | 0 | 3 | 5 | ||
| 6 | 2 | 0 | 1 | 4 | ||
| 7 | 3 | 0 | 1 | 7 | ||
| 8 | 3 | 0 | 3 | 8 | ||
| 9 | 3 | 0 | 2 | 4 | 5 | Change in the process time |
| 10 | 4 | 0 | 1 | 4 | ||
| 11 | 4 | 0 | 3 | 5 | ||
| 12 | 4 | 0 | 2 | 5 | ||
| 13 | 5 | 5 | 3 | 7 | New job arrival | |
| 14 | 5 | 5 | 1 | 3 | New job arrival | |
| 15 | 5 | 5 | 2 | 6 | New job arrival | |
| 16 | 0 | 12 | 2 | 3 | Machine breakdown |
| Size Type | No. | Name | Size n × m | Number of Operations | Number of Dynamic Operations | Total | GAM Best | HKA Best | Improvement Rate (%) |
|---|---|---|---|---|---|---|---|---|---|
| small | 1 | KK5 × 5 | 5 × 5 | 25 | 10 | 35 | 51 | 51 | 0 |
| 2 | KK6 × 5 | 6 × 5 | 30 | 15 | 45 | 557 | 552 | 0.90 | |
| 3 | KK8 × 5 | 8 × 5 | 40 | 5 | 45 | 699 | 699 | 0 | |
| 4 | KK10 × 5 | 10 × 5 | 50 | 5 | 55 | 624 | 624 | 0 | |
| medium | 5 | KK10 × 6 | 10 × 6 | 60 | 6 | 66 | 682 | 682 | 0 |
| 6 | KK15 × 5 | 15 × 5 | 75 | 5 | 80 | 1001 | 1001 | 0 | |
| 7 | KK10 × 8 | 10 × 8 | 80 | 8 | 88 | 1027 | 944 | 8.08 | |
| 8 | KK10 × 9 | 10 × 9 | 90 | 18 | 108 | 1049 | 1005 | 4.19 | |
| large | 9 | KK20 × 5 | 20 × 5 | 100 | 5 | 105 | 1361 | 1202 | 11.68 |
| 10 | KK10 × 10 | 10 × 10 | 100 | 10 | 110 | 1389 | 1287 | 7.34 | |
| 11 | KK22 × 5 | 22 × 5 | 110 | 15 | 125 | 1458 | 1458 | 0 | |
| 12 | KK12 × 10 | 12 × 10 | 120 | 10 | 130 | 1002 | 912 | 8.98 | |
| 13 | KK13 × 10 | 13 × 10 | 130 | 10 | 140 | 1016 | 947 | 6.79 | |
| 14 | KK20 × 7 | 20 × 7 | 140 | 14 | 154 | 1326 | 1246 | 6.03 | |
| 15 | KK15 × 10 | 15 × 10 | 150 | 20 | 170 | 1280 | 1112 | 13.13 |
| No | Name | Value | No | Name | Value | No | Name | Value | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 6 | 100 | 11 | 15 | ||||
| 2 | 10 | 7 | 2 | 12 | 5 | ||||
| 3 | 0.5 | 8 | 5 | 13 | 10 | ||||
| 4 | 5 | 9 | 2 | 14 | small | 300 | |||
| 5 | 6 | 10 | 10 | medium | 450 | ||||
| large | 600 | ||||||||
| Name | KK6 × 5 | KK10 × 8 | KK10 × 9 | KK20 × 5 | KK10 × 10 | KK12 × 10 | KK13 × 10 | KK15 × 10 | |
|---|---|---|---|---|---|---|---|---|---|
| IMPPSO2 VonNeumann | Min | 543 | 935 | 990 | 1202 | 1268 | 904 | 933 | 1092 |
| Max | 544 | 974 | 1005 | 1234 | 1292 | 916 | 948 | 1132 | |
| Mean | 543.03 | 955.10 | 993.43 | 1210.60 | 1278.73 | 909.30 | 941.47 | 1118.73 | |
| Std. | 0.18 | 10.17 | 5.58 | 7.33 | 6.31 | 4.27 | 4.04 | 8.71 | |
| SR | 100 | 16.67 | 100 | 6.67 | 93.33 | 76.67 | 93.33 | 23.33 | |
| IMPPSO2 Moore | Min | 543 | 935 | 990 | 1191 | 1269 | 904 | 930 | 1099 |
| Max | 544 | 979 | 1005 | 1232 | 1294 | 916 | 947 | 1134 | |
| Mean | 543.07 | 958 | 993.30 | 1212.93 | 1279.57 | 910.43 | 939.43 | 1117.87 | |
| Std. | 0.25 | 10.56 | 4.04 | 8.41 | 6.68 | 3.46 | 4.44 | 8.38 | |
| SR | 100 | 6.67 | 100 | 10 | 90 | 73.33 | 100 | 33.33 | |
| IMPPSO VonNeumann | Min | 543 | 949 | 990 | 1192 | 1269 | 904 | 932 | 1102 |
| Max | 544 | 973 | 1008 | 1225 | 1293 | 916 | 948 | 1130 | |
| Mean | 543.13 | 961.37 | 992.53 | 1210.90 | 1279.80 | 911.77 | 942.23 | 1117.53 | |
| Std. | 0.35 | 6.83 | 4.46 | 6.47 | 5.38 | 3.41 | 5.43 | 7.10 | |
| SR | 100 | 0 | 93.33 | 3.33 | 96.67 | 56.67 | 73.33 | 23.33 | |
| IMPPSO Moore | Min | 543 | 936 | 990 | 1200 | 1268 | 904 | 930 | 1105 |
| Max | 543 | 975 | 1010 | 1227 | 1287 | 916 | 948 | 1132 | |
| Mean | 543 | 958.47 | 992.33 | 1214.10 | 1278.53 | 911.70 | 941.23 | 1118.87 | |
| Std. | 0 | 8.10 | 4.90 | 6.43 | 5.64 | 4.26 | 5.12 | 7.40 | |
| SR | 100 | 3.33 | 96.67 | 3.33 | 100 | 43.33 | 83.33 | 16.67 | |
| OIMPPSO2 | Min | 543 | 940 | 990 | 1200 | 1269 | 904 | 930 | 1098 |
| Max | 544 | 973 | 1005 | 1220 | 1292 | 916 | 949 | 1135 | |
| Mean | 543.07 | 957.73 | 992.37 | 1208.97 | 1278.60 | 911.90 | 942.80 | 1121.43 | |
| Std. | 0.25 | 7.26 | 3.52 | 5.59 | 7.32 | 3.35 | 5.17 | 8.99 | |
| SR | 100 | 3.33 | 100 | 16.67 | 93.33 | 50 | 76.67 | 10 | |
| OIMPPSO | Min | 543 | 933 | 990 | 1192 | 1269 | 904 | 936 | 1101 |
| Max | 543 | 969 | 1007 | 1213 | 1286 | 916 | 948 | 1132 | |
| Mean | 543 | 955.37 | 991.77 | 1204.63 | 1278.23 | 910.80 | 941.97 | 1118.50 | |
| Std. | 0 | 8.94 | 4.27 | 5.86 | 5.20 | 3.46 | 4.34 | 7.47 | |
| SR | 100 | 10 | 96.67 | 36.67 | 100 | 66.67 | 90 | 16.67 | |
| MPPSO | Min | 543 | 948 | 990 | 1213 | 1270 | 909 | 939 | 1115 |
| Max | 549 | 987 | 1014 | 1248 | 1294 | 924 | 955 | 1153 | |
| Mean | 543.23 | 966.67 | 999.80 | 1233.33 | 1283.33 | 916.90 | 948.20 | 1136.20 | |
| Std. | 1.10 | 9.22 | 7.33 | 8.80 | 6.50 | 3.44 | 3.57 | 8.72 | |
| SR | 100 | 0 | 70 | 0 | 76.67 | 10 | 30 | 0 |
| M1 | ON 1 | 22 | 13 | 113 | 133 | 83 | 103 | 65 | 154 | 77 | 98 | 128 | 46 | 7 | 150 | 59 | 40 | 170 |
| ST 2 | 31 | 125 | 137 | 195 | 275 | 353 | 373 | 431 | 478 | 571 | 640 | 713 | 757 | 810 | 885 | 980 | 1073 | |
| FT 3 | 114 | 137 | 195 | 275 | 353 | 373 | 419 | 478 | 565 | 640 | 682 | 757 | 810 | 885 | 980 | 1073 | 1092 | |
| M2 | ON | 131 | 21 | 81 | 14 | 101 | 75 | 95 | 155 | 147 | 118 | 56 | 37 | 169 | 129 | 49 | 9 | 70 |
| ST | 0 | 12 | 31 | 137 | 179 | 339 | 386 | 478 | 516 | 619 | 691 | 698 | 785 | 877 | 928 | 979 | 1000 | |
| FT | 12 | 31 | 59 | 179 | 210 | 384 | 460 | 516 | 557 | 691 | 698 | 785 | 877 | 923 | 977 | 1000 | 1091 | |
| M3 | ON | 91 | 12 | 32 | 1 | 73 | 145 | 163 | 153 | 104 | 134 | 43 | 117 | 85 | 55 | 69 | 130 | 29 |
| ST | 0 | 94 | 125 | 212 | 246 | 285 | 335 | 396 | 431 | 448 | 498 | 596 | 619 | 656 | 691 | 923 | 940 | |
| FT | 94 | 125 | 212 | 246 | 285 | 335 | 396 | 431 | 448 | 498 | 596 | 619 | 656 | 691 | 750 | 940 | 1004 | |
| M4 | ON | 11 | 142 | 23 | 161 | 63 | 2 | 35 | 84 | 96 | 116 | 127 | 136 | 45 | 78 | 108 | 159 | 60 |
| ST | 0 | 61 | 116 | 150 | 240 | 256 | 331 | 400 | 460 | 492 | 591 | 648 | 696 | 713 | 802 | 926 | 980 | |
| FT | 46 | 116 | 150 | 168 | 256 | 311 | 400 | 426 | 487 | 591 | 639 | 667 | 713 | 754 | 889 | 971 | 1056 | |
| M5 | ON | 141 | 31 | 61 | 72 | 162 | 102 | 114 | 125 | 24 | 19 | 5 | 44 | 58 | 139 | 158 | 100 | 90 |
| ST | 0 | 61 | 121 | 149 | 169 | 264 | 288 | 333 | 431 | 524 | 579 | 600 | 726 | 812 | 906 | 926 | 1059 | |
| FT | 61 | 121 | 149 | 169 | 264 | 288 | 333 | 431 | 523 | 579 | 600 | 696 | 787 | 906 | 926 | 1022 | 1092 | |
| M6 | ON | 111 | 71 | 121 | 82 | 92 | 62 | 144 | 34 | 3 | 18 | 168 | 137 | 57 | 107 | 28 | 50 | 160 |
| ST | 0 | 28 | 37 | 64 | 97 | 181 | 240 | 254 | 331 | 426 | 589 | 667 | 698 | 726 | 861 | 977 | 1002 | |
| FT | 28 | 37 | 64 | 97 | 181 | 240 | 254 | 331 | 426 | 524 | 661 | 695 | 726 | 802 | 898 | 1002 | 1080 | |
| M7 | ON | 151 | 143 | 53 | 93 | 74 | 17 | 115 | 126 | 166 | 67 | 25 | 6 | 138 | 38 | 48 | 88 | 110 |
| ST | 75 | 127 | 164 | 181 | 285 | 339 | 416 | 492 | 559 | 564 | 616 | 678 | 749 | 812 | 853 | 928 | 1017 | |
| FT | 127 | 164 | 173 | 259 | 339 | 416 | 492 | 559 | 564 | 616 | 678 | 749 | 812 | 853 | 928 | 1017 | 1035 | |
| M8 | ON | 52 | 124 | 76 | 36 | 156 | 167 | 20 | 68 | 99 | 149 | 86 | 47 | 120 | 109 | 140 | 10 | 30 |
| ST | 35 | 200 | 384 | 455 | 516 | 564 | 589 | 655 | 682 | 727 | 745 | 757 | 800 | 889 | 921 | 1019 | 1045 | |
| FT | 130 | 267 | 455 | 493 | 557 | 589 | 655 | 682 | 727 | 745 | 753 | 800 | 886 | 921 | 1019 | 1045 | 1088 | |
| M9 | ON | 51 | 132 | 41 | 123 | 152 | 33 | 16 | 146 | 164 | 66 | 97 | 106 | 119 | 27 | 87 | 8 | 80 |
| ST | 0 | 35 | 85 | 173 | 200 | 224 | 262 | 339 | 418 | 452 | 502 | 571 | 691 | 799 | 861 | 927 | 979 | |
| FT | 35 | 85 | 164 | 200 | 224 | 248 | 339 | 418 | 452 | 502 | 571 | 652 | 781 | 861 | 927 | 979 | 993 | |
| M10 | ON | 112 | 122 | 54 | 15 | 64 | 94 | 42 | 165 | 4 | 105 | 135 | 148 | 26 | 157 | 39 | 79 | 89 |
| ST | 28 | 125 | 173 | 183 | 262 | 305 | 386 | 463 | 527 | 543 | 568 | 648 | 720 | 799 | 853 | 936 | 1017 | |
| FT | 125 | 173 | 183 | 262 | 305 | 386 | 463 | 527 | 543 | 568 | 648 | 720 | 799 | 817 | 936 | 979 | 1059 |
| Jobs | Occurrence Time | Machine Sequence | Processing Time [Time Unit] | Dynamic Event |
|---|---|---|---|---|
| J1 | 0 | M1, M4, M8, M9, M10, M12 | 139 | |
| J2 | 0 | M1, M5, M7, M9, M11, M12 | 121 | |
| J3 | 0 | M9, M10, M12 | 52 | Change in the process time to 50 |
| J4 | 0 | M2, M4, M8, M9, M11, M12 | 139 | |
| J5 | 0 | M2, M6, M8, M9, M10, M12 | 137 | |
| J6 | 0 | M1, M5, M7, M9, M11, M12 | 121 | |
| J7 | 0 | M2, M4, M8, M9, M11, M12 | 139 | |
| J8 | 0 | M2, M6, M7, M9, M10, M12 | 146 | Change in the process time to 149 |
| J9 | 0 | M1, M3, M7, M9, M11, M12 | 123 | |
| J10 | 0 | M1, M5, M7, M9, M11, M12 | 121 | |
| J11 | 0 | M1, M5, M7, M9, M11, M12 | 126 | |
| J12 | 0 | M2, M3, M8, M9, M11, M12 | 139 | |
| J13 | 0 | M1, M5, M7, M9, M11, M12 | 124 | |
| J14 | 0 | M1, M6, M7, M9, M10, M12 | 139 | |
| J15 | 0 | M9, M10, M12 | 50 | |
| J16 | 125 | M1, M4, M8, M9, M10, M12 | 139 | New job arrival |
| J17 | 155 | M1, M5, M7, M9, M11, M12 | 125 | New job arrival |
| 0 | 50 | M2 | 7 | Machine breakdown |
| 0 | 175 | M9 | 5 | Machine breakdown |
| Machine | Machine Time Processing [Time Unit] | Machine Utilization [%] | Operational Cost [EUR] |
|---|---|---|---|
| M1 | 206 | 100 | 1476 |
| M2 | 103 | 100 | 601 |
| M3 | 83 | 45.6 | 540 |
| M4 | 172 | 91.9 | 1519 |
| M5 | 228 | 98.3 | 1976 |
| M6 | 86 | 92.1 | 846 |
| M7 | 192 | 87.7 | 1152 |
| M8 | 138 | 82.6 | 1035 |
| M9 | 171 | 71.5 | 1083 |
| M10 | 173 | 64.8 | 1298 |
| M11 | 220 | 99.5 | 1907 |
| M12 | 220 | 77.7 | 1320 |
| Size Type | No | Name | GAM Best | HKA Best | IMPPSO Best | Improvement Rate for GAM (%) | Improvement Rate for HKA (%) |
|---|---|---|---|---|---|---|---|
| small | 1 | KK5 × 5 | 51 | 51 | 51 | 0 | 0 |
| 2 | KK6 × 5 | 557 | 552 | 543 | 2.51 | 1.63 | |
| 3 | KK8 × 5 | 699 | 699 | 699 | 0 | 0 | |
| 4 | KK10 × 5 | 624 | 624 | 624 | 0 | 0 | |
| medium | 5 | KK10 × 6 | 682 | 682 | 682 | 0 | 0 |
| 6 | KK15 × 5 | 1001 | 1001 | 1001 | 0 | 0 | |
| 7 | KK10 × 8 | 1027 | 944 | 933 | 9.15 | 1.17 | |
| 8 | KK10 × 9 | 1049 | 1005 | 990 | 5.62 | 1.49 | |
| large | 9 | KK20 × 5 | 1361 | 1202 | 1191 | 12.49 | 0.92 |
| 10 | KK10 × 10 | 1389 | 1287 | 1268 | 8.71 | 1.48 | |
| 11 | KK22 × 5 | 1458 | 1458 | 1458 | 0 | 0 | |
| 12 | KK12 × 10 | 1002 | 912 | 904 | 9.78 | 0.88 | |
| 13 | KK13 × 10 | 1016 | 947 | 930 | 8.46 | 1.80 | |
| 14 | KK20 × 7 | 1326 | 1246 | 1246 | 6.03 | 0 | |
| 15 | KK15 × 10 | 1280 | 1112 | 1092 | 14.69 | 1.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Buchmeister, B.; Li, X.; Ojstersek, R. An Efficient Metaheuristic Algorithm for Job Shop Scheduling in a Dynamic Environment. Mathematics 2023, 11, 2336. https://doi.org/10.3390/math11102336
Zhang H, Buchmeister B, Li X, Ojstersek R. An Efficient Metaheuristic Algorithm for Job Shop Scheduling in a Dynamic Environment. Mathematics. 2023; 11(10):2336. https://doi.org/10.3390/math11102336
Chicago/Turabian StyleZhang, Hankun, Borut Buchmeister, Xueyan Li, and Robert Ojstersek. 2023. "An Efficient Metaheuristic Algorithm for Job Shop Scheduling in a Dynamic Environment" Mathematics 11, no. 10: 2336. https://doi.org/10.3390/math11102336
APA StyleZhang, H., Buchmeister, B., Li, X., & Ojstersek, R. (2023). An Efficient Metaheuristic Algorithm for Job Shop Scheduling in a Dynamic Environment. Mathematics, 11(10), 2336. https://doi.org/10.3390/math11102336








