A Differential Relation of Metric Properties for Orientable Smooth Surfaces in ℝ³

Abstract

The Gauss–Bonnet formula finds applications in various fundamental fields. Global or local analysis on the basis of this formula is possible only in integral form since the Gauss–Bonnet formula depends on the choice of a simple region of an orientable smooth surface S. The objective of the present paper is to construct a differential relation of the metric properties concerned at a point on S. Pointwise analysis on S is possible through the differential relation, which is expected to provide new geometrical insights into existing studies where the Gauss–Bonnet formula is applied in integral form.

1. Introduction

Let S be an orientable smooth surface in ${\mathbb{R}}^3$ and R a region of S with boundary. Then the Gauss–Bonnet formula, which can be found in textbooks of classical differential geometry (e.g., [1,2]), states that:

$${\int \int }_{R}K+{\int }_{\partial R}{\kappa }_g=2\pi \chi \left(R\right),$$

(1)

where K is the Gaussian curvature over S, ${\kappa }_g$ is the geodesic curvature over the boundary $\partial R$ of R in S, and $\chi \left(R\right)$ is the Euler–Poincar$\acute{\mathrm{e}}$ characteristic of R. Common to various applications of the Gauss–Bonnet formula so far, any local or global analysis is viable only in integral form, since the relation between geometry and topology depends on the choice of R. For instance, the deflection angle of light by gravitational lensing has been calculated on the basis of the Gauss–Bonnet formula, and the setup for integral regions is indispensable for this calculation [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]. As a pioneering example of such an application, Gibbons and Werner considered two regions of a static, spherically symmetric spacetime [5]: one is bounded by two geodesics connecting the source and observer, and the other is a simply connected, asymptotically flat region. The integral of Gaussian curvature over the former is the key term for the calculation of the deflection angle. More precisely, the deflection angle of light can be calculated for asymptotically flat spacetimes, as follows:

$$\alpha =-{\int \int }_{S_o}\mathcal{K}d\sigma ,$$

(2)

where $\mathcal{K}$ is the Gaussian curvature over an optical surface and $d\sigma$ is its element. This formula can have different forms depending on physical situations (see, e.g., [4,9,12,13]), but the integral of $\mathcal{K}$ is essential in common.

Turning the point of view from a simple region of S to its single point p, five metric properties are concerned at p: the Gaussian curvature, the normal to S, the geodesic curvatures of intersecting curves at p, their speeds, and the angles of intersection between those curves. To the best of our knowledge, the differential relation between these five geometric objects has not been uncovered so far. If this differential relation is constructed, it will be employable for pointwise analysis on S. Further, as those five properties are associated in the Gauss–Bonnet formula, it could provide new geometrical insights into existing applications of the formula that inevitably relied on integral analysis. The objective of the present paper is thus to construct a differential relation between the above-described five geometric objects for a general extension of application of the Gauss–Bonnet formula to differential analysis.

2. Preliminaries and the Main Results

Let $\mathbf{r}:U\to S$ be a parametrization of S in an open set $U\subseteq {\mathbb{R}}^2$. We consider a rectangular domain $D\subset U$: $[u_c-\mathsf{\Delta }u/2,u_c+\mathsf{\Delta }u/2]\times [v_c-\mathsf{\Delta }v/2,v_c+\mathsf{\Delta }v/2]$, where $(u_c,v_c)$ is the coordinate of the center ${\sigma }_c$ of D. In addition, we use P to denote the image under $\mathbf{r}(u,v)$ of D. This image has four external angles and these are denoted by ${\theta }_i$, $i=1,2,3,4$, which are ordered in the positive orientation from the angle formed at the lower right vertex of P. In addition, the positively oriented boundary of P consists of four curves and these are denoted by $c_i$, $i=1,2,3,4$, which are ordered in the same orientation from the upper one. Apart from these curves, we use ${\gamma }_i$, $i=1,2,3,4$, to denote the subsets of $\mathbf{r}(u,v)$ corresponding to the sides of D. These are represented as follows:

$${\gamma }_1\left(u\right):=\mathbf{r}(u,v_c+\mathsf{\Delta }v/2),u\in [u_c-\mathsf{\Delta }u/2,u_c+\mathsf{\Delta }u/2];$$

(3)

$${\gamma }_2\left(v\right):=\mathbf{r}(u_c-\mathsf{\Delta }u/2,v),v\in [v_c-\mathsf{\Delta }v/2,v_c+\mathsf{\Delta }v/2];$$

(4)

$${\gamma }_3\left(u\right):=\mathbf{r}(u,v_c-\mathsf{\Delta }v/2),u\in [u_c-\mathsf{\Delta }u/2,u_c+\mathsf{\Delta }u/2];$$

(5)

$${\gamma }_4\left(v\right):=\mathbf{r}(u_c+\mathsf{\Delta }u/2,v),v\in [v_c-\mathsf{\Delta }v/2,v_c+\mathsf{\Delta }v/2].$$

(6)

The trajectories of the boundary paths $c_1$ and $c_2$ are overlapped with those of ${\gamma }_1\left(u\right)$ and ${\gamma }_2\left(v\right)$, respectively, but with opposite orientation. On the other hand, $c_3$ and $c_4$ are compatible with ${\gamma }_3\left(u\right)$ and ${\gamma }_4\left(v\right)$, respectively. Figure 1 illustrates the introduced notations on D and P.

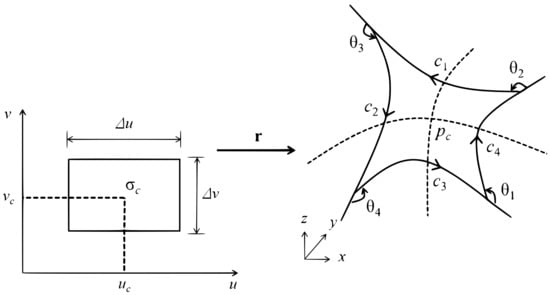
Figure 1. A rectangular region in the $uv$-plane and the image under $\mathbf{r}$ of the rectangle.

Remark 1.

It can be easily seen that P is a simple region of S and $\chi \left(P\right)=1$.

We present two definitions for the surface S and the parametrization $\mathbf{r}(u,v)$.

Definition 1.

We define two real-valued functions $F_a,F_b:{\mathbf{r}}^{-1}\left(S\right)\to \mathbb{R}$, as follows:

$$F_a(u,v):={\kappa }_g\left(\mathbf{r}(u,v=\mathit{const})\right)\left|{\mathbf{r}}^{\prime }(u,v=\mathit{const})\right|,(u,v)\in U;$$

(7)

$$F_b(u,v):={\kappa }_g\left(\mathbf{r}(u=\mathit{const},v)\right)\left|{\mathbf{r}}^{\prime }(u=\mathit{const},v)\right|,(u,v)\in U,$$

(8)

where ${\kappa }_g$ is the geodesic curvature of a coordinate curve on the map of $\mathbf{r}(u,v)$ and $|{\mathbf{r}}^{\prime }(u,v=\mathit{const})|$ and $|{\mathbf{r}}^{\prime }(u=\mathit{const},v)|$ are the speeds of the coordinate curves $v=\mathit{const}.$ and $u=\mathit{const}.$, respectively.

Remark 2.

Given that S is orientable and smooth, it can be easily seen that $F_a(u,v)$ and $F_b(u,v)$ are at least of class $C^1\left(U\right)$. First, these two functions are explicitly written as follows:

$$F_a(u,v)=\frac{⟨{\mathbf{r}}_{uu},\mathbf{n}\wedge {\mathbf{r}}_u⟩}{|{\mathbf{r}}_u{|}^2},$$

(9)

$$F_b(u,v)=\frac{⟨{\mathbf{r}}_{vv},\mathbf{n}\wedge {\mathbf{r}}_v⟩}{|{\mathbf{r}}_v{|}^2},$$

(10)

where the subscripts u, v, $uu$, and $vv$ denote the first- and second-order derivatives of $\mathbf{r}(u,v)$ with respect to u and v and $\mathbf{n}$ is the unit normal to S. The coordinates of $\mathbf{r}(u,v)$ are of class $C^{\omega }\left(U\right)$ since S is smooth. In addition, every 2-form on S is positive by the definition of an orientable surface in [2], so that $|{\mathbf{r}}_u|,|{\mathbf{r}}_v|\ne 0$ in U. These two facts yield that the first-order derivatives of $F_a(u,v)$ and $F_b(u,v)$ with respect to u and v are continuous in U.

Definition 2.

Two intersecting coordinate lines at some point $(u,v)\in U$ quadrisect a region centered at the point, and the images under $\mathbf{r}(u,v)$ of the coordinate lines form an oriented angle of intersection on each quadrant. These are measured by the positively turning displacements from ${\mathbf{r}}_u$ to ${\mathbf{r}}_v$, from ${\mathbf{r}}_v$ to $-{\mathbf{r}}_u$, from $-{\mathbf{r}}_u$ to $-{\mathbf{r}}_v$, and from $-{\mathbf{r}}_v$ to ${\mathbf{r}}_u$, where ${\mathbf{r}}_u$ and ${\mathbf{r}}_v$ are the tangent vectors to the coordinate curves $v=\mathit{const}.$ and $u=\mathit{const}.$, respectively. For such angles on each point of S, we define four intersection angle functions such that ${\varphi }_i:{\mathbf{r}}^{-1}\left(S\right)\to \mathbb{R}$, $i=1,2,3,4$, which are ordered in the positive orientation from the angle formed on the first quadrant. Figure 2 illustrates ${\varphi }_i$ at $p_c=\mathbf{r}\left({\sigma }_c\right)$.

Figure 2. The intersection angle formed by two intersecting coordinate curves on (a–d) each of the four quadrants.

Remark 3.

The four intersection angle functions are related to each other; ${\varphi }_1$ and ${\varphi }_2$ are vertically opposite to ${\varphi }_3$ and ${\varphi }_4$, respectively, and ${\varphi }_1$ and ${\varphi }_3$ are adjacent to ${\varphi }_2$ and ${\varphi }_4$, respectively. Therefore, three relations between ${\varphi }_i$ are established: ${\varphi }_1={\varphi }_3$, ${\varphi }_2={\varphi }_4$, and ${\varphi }_2=\pi -{\varphi }_1$. In order to reduce the notations ${\varphi }_i$, we substitute ${\varphi }_1$ with ϕ and then, the others are naturally expressed in terms of ϕ by those three relations: ${\varphi }_1={\varphi }_3=\varphi$ and ${\varphi }_2={\varphi }_4=\pi -\varphi$.

The definition of ${\varphi }_i$ seems redundant, but it helps the reader to systematically understand the process of expressing the sum of ${\theta }_i$ in differential form in the proof of Theorem 1. The following states our main results.

Theorem 1.

Let S be an orientable smooth surface in ${\mathbb{R}}^3$, and let $\mathbf{r}:U\to S$ be a parametrization of S in an open set $U\subseteq {\mathbb{R}}^2$. Then for each $(u,v)\in U$

$$K|\mathbf{N}|+\left(\frac{\partial F_b}{\partial u}-\frac{\partial F_a}{\partial v}\right)-\frac{{\partial }^2\varphi }{\partial u\partial v}=0,$$

(11)

where K is the Gaussian curvature over S, $\mathbf{N}$ is the normal to S, $F_a$ and $F_b$ are the products of the geodesic curvatures of the coordinate curves $v=\mathit{const}.$ and $u=\mathit{const}.$ and the speeds of those curves, respectively, and ϕ is the positively oriented angle of intersection from the coordinate curve $v=\mathit{const}.$ to $u=\mathit{const}.$ on S.

Corollary 1.

The Gaussian curvature, which is explicitly expressed from the differential relation of Theorem (1), is intrinsic for orientable smooth surfaces in ${\mathbb{R}}^3$.

3. Real Analyticity of $\mathbf{\varphi }$

We present a lemma that states the real analyticity of $\varphi$. For the proof of this lemma, we recall three propositions proven in [18].

Proposition 1

([18], Proposition 2.2.3). Let f be a real analytic function defined on an open set $U\subseteq {\mathbb{R}}^m$. Then f is continuous and has continuous, real analytic partial derivatives of all orders. Further, the indefinite integral of f with respect to any variable is real analytic.

Proposition 2

([18], Proposition 2.2.2). Let $U,V\subseteq {\mathbb{R}}^m$ be open. If $f:U\to \mathbb{R}$ and $g:V\to \mathbb{R}$ are real analytic, then $f+g$, $f·g$ are real analytic on $U\cap V$, and $f/g$ is real analytic on $U\cap V\cap \{x:g(x)\ne 0\}$.

Proposition 3

([18], Proposition 2.2.8). If $f_1,f_2,\dots ,f_m$ are real analytic in some neighborhood of the point $\alpha \in {\mathbb{R}}^k$ and g is real analytic in some neighborhood of the point $(f_1\left(\alpha \right),f_2\left(\alpha \right),\dots ,f_m\left(\alpha \right))\in {\mathbb{R}}^m$, then $g[f_1\left(x\right),f_2\left(x\right),\dots ,f_m\left(x\right)]$ is real analytic in a neighborhood of α.

Lemma 1.

The intersection angle function $\varphi (u,v)$ is real analytic in U.

Proof. 

As mentioned in Remark 2, $|{\mathbf{r}}_u|,|{\mathbf{r}}_v|\ne 0$ in U. Accordingly, when $\mathbf{r}(u,v)$ is given as $\left(f\right(u,v),g(u,v),h(u,v\left)\right)$, $\varphi (u,v)$ can be explicitly written by the formula of the angle between two nonzero vectors, as follows:

$$\varphi (u,v)=arccos\left(\frac{⟨{\mathbf{r}}_u,{\mathbf{r}}_v⟩}{|{\mathbf{r}}_u\left|\right|{\mathbf{r}}_v|}\right)=arccos\left(\frac{f_u{f}_v+g_u{g}_v+h_u{h}_v}{\sqrt{f_u^2+g_u^2+h_u^2}\sqrt{f_v^2+g_v^2+h_v^2}}\right),$$

(12)

where the subscripts u and v denote the first-order derivatives of $f(u,v)$, $g(u,v)$, and $h(u,v)$ with respect to u and v. We shall prove this lemma by showing that the composite arc cosine function in Equation (12) is real analytic in U, and this will proceed in a bottom-up way.

Since S is smooth, $f(u,v)$, $g(u,v)$, and $h(u,v)$ are real analytic in U. By Proposition 1, any derivatives of these functions with respect to u and v are thus real analytic, and further, by Proposition 2, any products of these derivatives and any sums of these products are also real analytic. The numerator of the input for $arccos\left(x\right)$ is thus real analytic in U. For the denominator, $\sqrt{f_u^2+g_u^2+h_u^2}$ and $\sqrt{f_v^2+g_v^2+h_v^2}$ are the compositions of $\sqrt{x}$ and $f_u^2+g_u^2+h_u^2$ and $\sqrt{x}$ and $f_v^2+g_v^2+h_v^2$, respectively. The inputs for $\sqrt{x}$ are real analytic in U for the same reason above. Further, these inputs cannot be equal to zero in U (as mentioned at the beginning of this proof). Taking into account that the elementary function $\sqrt{x}$, $x\in {\mathbb{R}}^{+}$, is real analytic in ${\mathbb{R}}_{*}^{+}$, by Proposition 3, $\sqrt{f_u^2+g_u^2+h_u^2}$ and $\sqrt{f_v^2+g_v^2+h_v^2}$ are real analytic in U. Further, by Proposition 2, so is the product of these two composite square root functions. When put together, the numerator and denominator, again by Proposition 2, the resultant rational function is real analytic in U. According to the Cauchy–Schwarz inequality, the rational function, which is the input for $arccos\left(x\right)$, can have an absolute value less than or equal to 1 in U. However, ${\mathbf{r}}_u$ and ${\mathbf{r}}_v$ are linearly independent by the definition of an orientable surface, so that the absolute value is always less than 1 in U. Taking into consideration that $arccos\left(x\right)$, $\left|x\right|\le 1$, is real analytic in $\left|x\right|<1$, by Proposition 3 this fact yields that the composite arc cosine function is real analytic in U. □

4. Proofs

The outline for the proof of Theorem 1 is as follows. At a build-up stage, the Gauss–Bonnet formula is applied to P to obtain a base equation. At the latter part, the base equation is discretized and then the differential relation is derived by taking the limit of the discretized equation as $(\mathsf{\Delta }u,\mathsf{\Delta }v)\to (0,0)$.

Proof of Theorem 1

The Gauss–Bonnet formula is rewritten for P:

$${\int \int }_{P}KdA+{\int }_{\partial P}{\kappa }_g\left(s\right)ds+\sum _{i=1}^4{\theta }_i=2\pi .$$

(13)

First, the integral of Gaussian curvature over P is given by the integral over D, as follows:

$${\int \int }_{P}KdA={\int \int }_{D}K|\mathbf{N}|dudv.$$

(14)

Second, the integrals of geodesic curvature along the positively oriented boundary paths of P are written. The geodesic curvature of an oriented regular curve contained in an oriented surface changes sign when the orientation of the curve is reversed [1]. Accordingly, the geodesic curvatures of $c_1$ and $c_2$ can be represented by those of ${\gamma }_1\left(u\right)$ and ${\gamma }_2\left(v\right)$ with opposite signs, respectively:

$${\kappa }_g\left(c_1\right)=-{\kappa }_g\left({\gamma }_1\left(u\right)\right),$$

(15)

$${\kappa }_g\left(c_2\right)=-{\kappa }_g\left({\gamma }_2\left(v\right)\right).$$

(16)

On the other hand, the geodesic curvatures of $c_3$ and $c_4$ are compatible with those of ${\gamma }_3\left(u\right)$ and ${\gamma }_4\left(v\right)$:

$${\kappa }_g\left(c_3\right)={\kappa }_g\left({\gamma }_3\left(u\right)\right),$$

(17)

$${\kappa }_g\left(c_4\right)={\kappa }_g\left({\gamma }_4\left(v\right)\right).$$

(18)

The integral of geodesic curvature along $c_i$ may be represented by that over ${\gamma }_i$, as follows:

$${\int }_{c_1}{\kappa }_g\left(s\right)ds=-{\int }_{u_c+\frac{\mathsf{\Delta }u}{2}}^{u_c-\frac{\mathsf{\Delta }u}{2}}-{\kappa }_g\left({\gamma }_1\left(u\right)\right)|{\gamma }_1^{\prime }\left(u\right)|du,$$

(19)

$${\int }_{c_2}{\kappa }_g\left(s\right)ds=-{\int }_{v_c+\frac{\mathsf{\Delta }v}{2}}^{v_c-\frac{\mathsf{\Delta }v}{2}}-{\kappa }_g\left({\gamma }_2\left(v\right)\right)|{\gamma }_2^{\prime }\left(v\right)|dv,$$

(20)

$${\int }_{c_3}{\kappa }_g\left(s\right)ds={\int }_{u_c-\frac{\mathsf{\Delta }u}{2}}^{u_c+\frac{\mathsf{\Delta }u}{2}}{\kappa }_g\left({\gamma }_3\left(u\right)\right)|{\gamma }_3^{\prime }\left(u\right)|du,$$

(21)

$${\int }_{c_4}{\kappa }_g\left(s\right)ds={\int }_{v_c-\frac{\mathsf{\Delta }v}{2}}^{v_c+\frac{\mathsf{\Delta }v}{2}}{\kappa }_g\left({\gamma }_4\left(v\right)\right)|{\gamma }_4^{\prime }\left(v\right)|dv.$$

(22)

By means of Definition 1, the integrands in the right sides of Equations (19)–(22) are substitutable with $F_a(u,v_c+\mathsf{\Delta }v/2)$, $F_b(u_c-\mathsf{\Delta }u/2,v)$, $F_a(u,v_c-\mathsf{\Delta }v/2)$, and $F_b(u_c+\mathsf{\Delta }u/2,v)$, respectively. Accordingly, the above four integrals are rewritten in terms of $F_a(u,v)$ and $F_b(u,v)$:

$${\int }_{c_1}{\kappa }_g\left(s\right)ds={\int }_{u_c+\frac{\mathsf{\Delta }u}{2}}^{u_c-\frac{\mathsf{\Delta }u}{2}}{F}_a\left(u,v_c+\frac{\mathsf{\Delta }v}{2}\right)du,$$

(23)

$${\int }_{c_2}{\kappa }_g\left(s\right)ds={\int }_{v_c+\frac{\mathsf{\Delta }v}{2}}^{v_c-\frac{\mathsf{\Delta }v}{2}}{F}_b\left(u_c-\frac{\mathsf{\Delta }u}{2},v\right)dv,$$

(24)

$${\int }_{c_3}{\kappa }_g\left(s\right)ds={\int }_{u_c-\frac{\mathsf{\Delta }u}{2}}^{u_c+\frac{\mathsf{\Delta }u}{2}}{F}_a\left(u,v_c-\frac{\mathsf{\Delta }v}{2}\right)du,$$

(25)

$${\int }_{c_4}{\kappa }_g\left(s\right)ds={\int }_{v_c-\frac{\mathsf{\Delta }v}{2}}^{v_c+\frac{\mathsf{\Delta }v}{2}}{F}_b\left(u_c+\frac{\mathsf{\Delta }u}{2},v\right)dv.$$

(26)

By adding up these integrals,

$$\sum _{i=1}^4{\int }_{c_i}{\kappa }_g\left(s\right)ds={\oint }_{\partial D}\left(F_{a}du+F_{b}dv\right).$$

(27)

Since the positively oriented boundary $\partial D$ of D is a simple closed, piecewise smooth curve, and as stated in Remark 2, $\partial F_b/\partial u$ and $\partial F_a/\partial v$ are continuous in U, Green’s theorem holds for the above integral. Accordingly, the integral along $\partial D$ may be transformed into that over D, as follows:

$${\oint }_{\partial D}\left(F_{a}du+F_{b}dv\right)={\int \int }_D\left(\frac{\partial F_b}{\partial u}-\frac{\partial F_a}{\partial v}\right)dudv.$$

(28)

Third, the sum of the external angles of P is expressed in differential form. Since the domain for P is a rectangle, those external angles are measured by the positively turning displacements from ${\mathbf{r}}_u$ to ${\mathbf{r}}_v$, from ${\mathbf{r}}_v$ to $-{\mathbf{r}}_u$, from $-{\mathbf{r}}_u$ to $-{\mathbf{r}}_v$, and from $-{\mathbf{r}}_v$ to ${\mathbf{r}}_u$ at the vertices of P, respectively. This implies that the external angles ${\theta }_i$ can be represented in terms of ${\varphi }_i(u,v)$. Further, by the two relations established in Remark 3, ${\theta }_i$ is consequently expressed in terms of $\varphi$:

$${\theta }_1={\varphi }_1\left(u_c+\frac{\mathsf{\Delta }u}{2},v_c-\frac{\mathsf{\Delta }v}{2}\right)=\varphi \left(u_c+\frac{\mathsf{\Delta }u}{2},v_c-\frac{\mathsf{\Delta }v}{2}\right),$$

(29)

$${\theta }_2={\varphi }_2\left(u_c+\frac{\mathsf{\Delta }u}{2},v_c+\frac{\mathsf{\Delta }v}{2}\right)=\pi -\varphi \left(u_c+\frac{\mathsf{\Delta }u}{2},v_c+\frac{\mathsf{\Delta }v}{2}\right),$$

(30)

$${\theta }_3={\varphi }_3\left(u_c-\frac{\mathsf{\Delta }u}{2},v_c+\frac{\mathsf{\Delta }v}{2}\right)=\varphi \left(u_c-\frac{\mathsf{\Delta }u}{2},v_c+\frac{\mathsf{\Delta }v}{2}\right),$$

(31)

$${\theta }_4={\varphi }_4\left(u_c-\frac{\mathsf{\Delta }u}{2},v_c-\frac{\mathsf{\Delta }v}{2}\right)=\pi -\varphi \left(u_c-\frac{\mathsf{\Delta }u}{2},v_c-\frac{\mathsf{\Delta }v}{2}\right).$$

(32)

Since $\varphi (u,v)$ is real analytic in U (as stated in Lemma 1), $\varphi \left(\sigma \right)$, where $\sigma \in D$ is some point in the neighborhood of ${\sigma }_c$, may be expanded at ${\sigma }_c$ as a convergent Taylor-series if $\sigma$ lies within the region of convergence centered at ${\sigma }_c$. At this stage, it may be assumed that D is small enough to satisfy that its vertices lie within the region of convergence. When the values of $\varphi (u,v)$ corresponding to the vertices of D are expanded as Taylor-series at ${\sigma }_c$, this assumption ensures their convergence. The four Taylor-series expansions are written as follows:

$$\begin{array}{c}\varphi \left(u_c+\frac{\mathsf{\Delta }u}{2},v_c-\frac{\mathsf{\Delta }v}{2}\right)=\varphi \left({\sigma }_c\right)+\frac{\partial \varphi }{\partial u}{|}_{{\sigma }_c}\left(\frac{\mathsf{\Delta }u}{2}\right)-\frac{\partial \varphi }{\partial v}{|}_{{\sigma }_c}\left(\frac{\mathsf{\Delta }v}{2}\right)\hfill \\ +\frac{1}{2}\left\{\frac{{\partial }^2\varphi }{\partial u^2}{|}_{{\sigma }_c}{\left(\frac{\mathsf{\Delta }u}{2}\right)}^2-2\frac{{\partial }^2\varphi }{\partial u\partial v}{|}_{{\sigma }_c}\left(\frac{\mathsf{\Delta }u}{2}\right)\left(\frac{\mathsf{\Delta }v}{2}\right)+\frac{{\partial }^2\varphi }{\partial v^2}{|}_{{\sigma }_c}{\left(\frac{\mathsf{\Delta }v}{2}\right)}^2\right\}\hfill \\ +\sum _{n=3}^{\infty }\left\{\frac{1}{n!}\sum _{k=0}^n\left(\frac{n!}{(n-k)!k!}\right)\frac{{\partial }^{\left(n\right)}\varphi }{\partial u^{(n-k)}\partial v^{\left(k\right)}}{|}_{{\sigma }_c}{\left(-1\right)}^k{\left(\frac{\mathsf{\Delta }u}{2}\right)}^{n-k}{\left(\frac{\mathsf{\Delta }v}{2}\right)}^k\right\},\hfill \end{array}$$

(33)

$$\begin{array}{c}\varphi \left(u_c+\frac{\mathsf{\Delta }u}{2},v_c+\frac{\mathsf{\Delta }v}{2}\right)=\varphi \left({\sigma }_c\right)+\frac{\partial \varphi }{\partial u}{|}_{{\sigma }_c}\left(\frac{\mathsf{\Delta }u}{2}\right)+\frac{\partial \varphi }{\partial v}{|}_{{\sigma }_c}\left(\frac{\mathsf{\Delta }v}{2}\right)\hfill \\ +\frac{1}{2}\left\{\frac{{\partial }^2\varphi }{\partial u^2}{|}_{{\sigma }_c}{\left(\frac{\mathsf{\Delta }u}{2}\right)}^2+2\frac{{\partial }^2\varphi }{\partial u\partial v}{|}_{{\sigma }_c}\left(\frac{\mathsf{\Delta }u}{2}\right)\left(\frac{\mathsf{\Delta }v}{2}\right)+\frac{{\partial }^2\varphi }{\partial v^2}{|}_{{\sigma }_c}{\left(\frac{\mathsf{\Delta }v}{2}\right)}^2\right\}\hfill \\ +\sum _{n=3}^{\infty }\left\{\frac{1}{n!}\sum _{k=0}^n\left(\frac{n!}{(n-k)!k!}\right)\frac{{\partial }^{\left(n\right)}\varphi }{\partial u^{(n-k)}\partial v^{\left(k\right)}}{|}_{{\sigma }_c}{\left(\frac{\mathsf{\Delta }u}{2}\right)}^{n-k}{\left(\frac{\mathsf{\Delta }v}{2}\right)}^k\right\},\hfill \end{array}$$

(34)

$$\begin{array}{c}\varphi \left(u_c-\frac{\mathsf{\Delta }u}{2},v_c+\frac{\mathsf{\Delta }v}{2}\right)=\varphi \left({\sigma }_c\right)-\frac{\partial \varphi }{\partial u}{|}_{{\sigma }_c}\left(\frac{\mathsf{\Delta }u}{2}\right)+\frac{\partial \varphi }{\partial v}{|}_{{\sigma }_c}\left(\frac{\mathsf{\Delta }v}{2}\right)\hfill \\ +\frac{1}{2}\left\{\frac{{\partial }^2\varphi }{\partial u^2}{|}_{{\sigma }_c}{\left(\frac{\mathsf{\Delta }u}{2}\right)}^2-2\frac{{\partial }^2\varphi }{\partial u\partial v}{|}_{{\sigma }_c}\left(\frac{\mathsf{\Delta }u}{2}\right)\left(\frac{\mathsf{\Delta }v}{2}\right)+\frac{{\partial }^2\varphi }{\partial v^2}{|}_{{\sigma }_c}{\left(\frac{\mathsf{\Delta }v}{2}\right)}^2\right\}\hfill \\ +\sum _{n=3}^{\infty }\left\{\frac{1}{n!}\sum _{k=0}^n\left(\frac{n!}{(n-k)!k!}\right)\frac{{\partial }^{\left(n\right)}\varphi }{\partial u^{(n-k)}\partial v^{\left(k\right)}}{|}_{{\sigma }_c}{\left(-1\right)}^{n-k}{\left(\frac{\mathsf{\Delta }u}{2}\right)}^{n-k}{\left(\frac{\mathsf{\Delta }v}{2}\right)}^k\right\},\hfill \end{array}$$

(35)

$$\begin{array}{c}\varphi \left(u_c-\frac{\mathsf{\Delta }u}{2},v_c-\frac{\mathsf{\Delta }v}{2}\right)=\varphi \left({\sigma }_c\right)-\frac{\partial \varphi }{\partial u}{|}_{{\sigma }_c}\left(\frac{\mathsf{\Delta }u}{2}\right)-\frac{\partial \varphi }{\partial v}{|}_{{\sigma }_c}\left(\frac{\mathsf{\Delta }v}{2}\right)\hfill \\ +\frac{1}{2}\left\{\frac{{\partial }^2\varphi }{\partial u^2}{|}_{{\sigma }_c}{\left(\frac{\mathsf{\Delta }u}{2}\right)}^2+2\frac{{\partial }^2\varphi }{\partial u\partial v}{|}_{{\sigma }_c}\left(\frac{\mathsf{\Delta }u}{2}\right)\left(\frac{\mathsf{\Delta }v}{2}\right)+\frac{{\partial }^2\varphi }{\partial v^2}{|}_{{\sigma }_c}{\left(\frac{\mathsf{\Delta }v}{2}\right)}^2\right\}\hfill \\ +\sum _{n=3}^{\infty }\left\{\frac{1}{n!}\sum _{k=0}^n\left(\frac{n!}{(n-k)!k!}\right)\frac{{\partial }^{\left(n\right)}\varphi }{\partial u^{(n-k)}\partial v^{\left(k\right)}}{|}_{{\sigma }_c}{\left(-1\right)}^n{\left(\frac{\mathsf{\Delta }u}{2}\right)}^{n-k}{\left(\frac{\mathsf{\Delta }v}{2}\right)}^k\right\}.\hfill \end{array}$$

(36)

By introducing these expanded series into Equations (29)–(32) and then adding up the resultant equations,

$$\sum _{i=1}^4{\theta }_i=2\pi -\frac{{\partial }^2\varphi }{\partial u\partial v}{|}_{{\sigma }_c}\mathsf{\Delta }u\mathsf{\Delta }v+\tilde{R},$$

(37)

where $\tilde{R}$ is the sum of the remainders:

$$\begin{array}{c}\multicolumn{1}{c}{\tilde{R}=\sum _{n=3}^{\infty }\left[\frac{1}{n!}\sum _{k=0}^n\left(\frac{n!}{(n-k)!k!}\right)\frac{{\partial }^{\left(n\right)}\varphi }{\partial u^{(n-k)}\partial v^{\left(k\right)}}{|}_{{\sigma }_c}\right\{{\left(-1\right)}^k+\left(-1\right)}\\ \multicolumn{1}{c}{+{\left(-1\right)}^{n-k}+{\left(-1\right)}^{n+1}\left\}{\left(\frac{\mathsf{\Delta }u}{2}\right)}^{n-k}{\left(\frac{\mathsf{\Delta }v}{2}\right)}^k\right].}\end{array}$$

(38)

The sum of Equations (14), (28) and (37) follows from the Gauss–Bonnet formula:

$${\int \int }_D\left\{K|\mathbf{N}|+\left(\frac{\partial F_b}{\partial u}-\frac{\partial F_a}{\partial v}\right)\right\}dudv-\frac{{\partial }^2\varphi }{\partial u\partial v}{|}_{{\sigma }_c}\mathsf{\Delta }u\mathsf{\Delta }v+\tilde{R}=0,$$

(39)

where $2\pi$ has been canceled out. Since S is orientable and smooth, the integrand of the double integral in Equation (39) is continuous in D. The mean value theorem for definite integrals thus holds for the integral term in Equation (39). Accordingly, there exists some point ${\sigma }^{*}$ in the open region of D, such that

$${\int \int }_D\left\{K|\mathbf{N}|+\left(\frac{\partial F_b}{\partial u}-\frac{\partial F_a}{\partial v}\right)\right\}dudv=\left\{K\left({\sigma }^{*}\right)|\mathbf{N}\left({\sigma }^{*}\right)|+\left(\frac{\partial F_b}{\partial u}{|}_{{\sigma }^{*}}-\frac{\partial F_a}{\partial v}{|}_{{\sigma }^{*}}\right)\right\}\mathsf{\Delta }u\mathsf{\Delta }v.$$

(40)

By introducing the right side of Equation (40) into Equation (39),

$$\left\{K\left({\sigma }^{*}\right)|\mathbf{N}\left({\sigma }^{*}\right)|+\left(\frac{\partial F_b}{\partial u}{|}_{{\sigma }^{*}}-\frac{\partial F_a}{\partial v}{|}_{{\sigma }^{*}}\right)\right\}\mathsf{\Delta }u\mathsf{\Delta }v-\frac{{\partial }^2\varphi }{\partial u\partial v}{|}_{{\sigma }_c}\mathsf{\Delta }u\mathsf{\Delta }v+\tilde{R}=0.$$

(41)

The above equation is then divided by $\mathsf{\Delta }u\mathsf{\Delta }v$:

$$\left\{K\left({\sigma }^{*}\right)|\mathbf{N}\left({\sigma }^{*}\right)|+\left(\frac{\partial F_b}{\partial u}{|}_{{\sigma }^{*}}-\frac{\partial F_a}{\partial v}{|}_{{\sigma }^{*}}\right)\right\}-\frac{{\partial }^2\varphi }{\partial u\partial v}{|}_{{\sigma }_c}+\frac{\tilde{R}}{\mathsf{\Delta }u\mathsf{\Delta }v}=0.$$

(42)

By taking the limit of this equation as $(\mathsf{\Delta }u,\mathsf{\Delta }v)\to (0,0)$,

$$\begin{array}{c}\multicolumn{1}{c}{\underset{(\mathsf{\Delta }u,\mathsf{\Delta }v)\to (0,0)}{lim}\left\{K\left({\sigma }^{*}\right)|\mathbf{N}\left({\sigma }^{*}\right)|+\left(\frac{\partial F_b}{\partial u}{|}_{{\sigma }^{*}}-\frac{\partial F_a}{\partial v}{|}_{{\sigma }^{*}}\right)\right\}-\frac{{\partial }^2\varphi }{\partial u\partial v}{|}_{{\sigma }_c}}\\ \multicolumn{1}{c}{+\underset{(\mathsf{\Delta }u,\mathsf{\Delta }v)\to (0,0)}{lim}\left(\frac{\tilde{R}}{\mathsf{\Delta }u\mathsf{\Delta }v}\right)=0.}\end{array}$$

(43)

Let $I(u,v)$ be the integrand of the double integral in Equation (39). Since $I(u,v)$ is continuous in D (as mentioned above), the extreme value theorem holds for $I(u,v)$. Accordingly, there exist ${\sigma }_m$ and ${\sigma }_M$ in D, such that

$$I\left({\sigma }_m\right)\le I\left(\sigma \right)\le I\left({\sigma }_M\right),\forall \sigma \in D.$$

(44)

By the way,

$$\underset{(\mathsf{\Delta }u,\mathsf{\Delta }v)\to (0,0)}{lim}I\left({\sigma }_m\right)=\underset{(\mathsf{\Delta }u,\mathsf{\Delta }v)\to (0,0)}{lim}I\left({\sigma }_M\right)=I\left({\sigma }_c\right).$$

(45)

Since $I\left({\sigma }_m\right)\le I\left({\sigma }^{*}\right)\le I\left({\sigma }_M\right)$, by the squeeze theorem

$$\underset{(\mathsf{\Delta }u,\mathsf{\Delta }v)\to (0,0)}{lim}I\left({\sigma }^{*}\right)=I\left({\sigma }_c\right).$$

(46)

Therefore, ${\sigma }^{*}$ tends to ${\sigma }_c$ as $(\mathsf{\Delta }u,\mathsf{\Delta }v)\to (0,0)$. On the other hand, the remainder term in Equation (42) is written as follows:

$$\begin{array}{c}\frac{\tilde{R}}{\mathsf{\Delta }u\mathsf{\Delta }v}=\sum _{n=3}^{\infty }\left[\frac{1}{n!}\sum _{k=0}^n\left(\frac{n!}{(n-k)!k!}\right)\frac{{\partial }^{\left(n\right)}\varphi }{\partial u^{(n-k)}\partial v^{\left(k\right)}}{|}_{{\sigma }_c}\right\{{\left(-1\right)}^k+\left(-1\right)\hfill \\ +{\left(-1\right)}^{n-k}+{\left(-1\right)}^{n+1}\left\}\left(\frac{1}{4}\right){\left(\frac{\mathsf{\Delta }u}{2}\right)}^{n-k-1}{\left(\frac{\mathsf{\Delta }v}{2}\right)}^{k-1}\right].\hfill \end{array}$$

(47)

In the above equation, the sum of the power terms of $(-1)$ in the braces vanishes for all k for odd n and for even k for even n. All terms multiplied by this sum thus vanish irrespective of $\mathsf{\Delta }u$ and $\mathsf{\Delta }v$. On the other hand, all terms for odd k for even n tend to zero as $(\mathsf{\Delta }u,\mathsf{\Delta }v)\to (0,0)$. Together, $\tilde{R}/\left(\mathsf{\Delta }u\mathsf{\Delta }v\right)$ vanishes as $(\mathsf{\Delta }u,\mathsf{\Delta }v)\to (0,0)$. Finally, the differential relation at ${\sigma }_c$ is obtained as follows:

$$K\left({\sigma }_c\right)|\mathbf{N}\left({\sigma }_c\right)|+\left(\frac{\partial F_b}{\partial u}{|}_{{\sigma }_c}-\frac{\partial F_a}{\partial v}{|}_{{\sigma }_c}\right)-\frac{{\partial }^2\varphi }{\partial u\partial v}{|}_{{\sigma }_c}=0.$$

(48)

Since the point ${\sigma }_c$ is arbitrary, the above relation holds for each $\sigma \in U$. This completes the proof. □

As a preliminary setup for the proof of Corollary 1, the coefficients of the first and second fundamental forms of $\mathbf{r}(u,v)$ are denoted as follows:

$$E=⟨{\mathbf{r}}_u,{\mathbf{r}}_u⟩,F=⟨{\mathbf{r}}_u,{\mathbf{r}}_v⟩,G=⟨{\mathbf{r}}_v,{\mathbf{r}}_v⟩,$$

(49)

$$L=⟨{\mathbf{r}}_{uu},\mathbf{n}⟩,M=⟨{\mathbf{r}}_{uv},\mathbf{n}⟩,N=⟨{\mathbf{r}}_{vv},\mathbf{n}⟩.$$

(50)

According to Gauss’ Theorema Egregium, the Gaussian curvature of an orientable smooth surface embedded in ${\mathbb{R}}^3$ is intrinsic. As is well known, this is proved by showing that the Gaussian curvature is represented in terms only of E,F,G, and their derivatives. The proof of Corollary 1 will proceed in a similar fashion.

Proof of Corollary 1.

First, the Gaussian curvature K is expressed as a functional from Equation (11),

$$K=\frac{\left(\frac{\partial F_a}{\partial v}-\frac{\partial F_b}{\partial u}\right)+\frac{{\partial }^2\varphi }{\partial u\partial v}}{|\mathbf{N}|}.$$

(51)

The two entities $\varphi$ and $|\mathbf{N}|$ in this equation are straightforwardly written in terms of E, F, and G:

$$\varphi =arccos\left(\frac{F}{\sqrt{EG}}\right),$$

(52)

$$|\mathbf{N}|=\sqrt{EG-F^2}.$$

(53)

To express $F_a$ as a whole in the desired form, each of the terms consisting of $F_a$ in Equation (9) is first rewritten:

$$\begin{array}{cc}\hfill \mathbf{n}\wedge {\mathbf{r}}_u& =\frac{{\mathbf{r}}_u\wedge {\mathbf{r}}_v}{|{\mathbf{r}}_u\wedge {\mathbf{r}}_v|}\wedge {\mathbf{r}}_u\hfill \\ \hfill & =\frac{1}{\sqrt{EG-F^2}}\left(⟨{\mathbf{r}}_u,{\mathbf{r}}_u⟩{\mathbf{r}}_v-⟨{\mathbf{r}}_v,{\mathbf{r}}_u⟩{\mathbf{r}}_u\right)\hfill \\ \hfill & =\frac{E{\mathbf{r}}_v-F{\mathbf{r}}_u}{\sqrt{EG-F^2}}\hfill \end{array}$$

(54)

and

$${\mathbf{r}}_{uu}={\mathsf{\Gamma }}_{uu}^u{\mathbf{r}}_u+{\mathsf{\Gamma }}_{uu}^v{\mathbf{r}}_v+L\mathbf{n},$$

(55)

where ${\mathsf{\Gamma }}_{ij}^k$ are the Christoffel symbols of S. Then

$$\begin{array}{cc}\hfill F_a& =\frac{⟨{\mathbf{r}}_{uu},\mathbf{n}\wedge {\mathbf{r}}_u⟩}{|{\mathbf{r}}_u{|}^2}\hfill \\ \hfill & =\frac{⟨{\mathsf{\Gamma }}_{uu}^u{\mathbf{r}}_u+{\mathsf{\Gamma }}_{uu}^v{\mathbf{r}}_v+L\mathbf{n},\frac{E{\mathbf{r}}_v-F{\mathbf{r}}_u}{\sqrt{EG-F^2}}⟩}{E}\hfill \\ \hfill & =\frac{1}{E\sqrt{EG-F^2}}\left({\mathsf{\Gamma }}_{uu}^u⟨{\mathbf{r}}_u,E{\mathbf{r}}_v-F{\mathbf{r}}_u⟩+{\mathsf{\Gamma }}_{uu}^v⟨{\mathbf{r}}_v,E{\mathbf{r}}_v-F{\mathbf{r}}_u⟩\right)\hfill \\ \hfill & =\frac{1}{E\sqrt{EG-F^2}}\left({\mathsf{\Gamma }}_{uu}^u(EF-FE)+{\mathsf{\Gamma }}_{uu}^v(EG-F^2)\right)\hfill \\ \hfill & =\frac{\sqrt{EG-F^2}}{E}{\mathsf{\Gamma }}_{uu}^v.\hfill \end{array}$$

(56)

We recall the expression of the Christoffel symbol ${\mathsf{\Gamma }}_{uu}^v$, as follows:

$${\mathsf{\Gamma }}_{uu}^v=-\frac{E(E_v-2F_u)+E_{u}F}{2(EG-F^2)}.$$

(57)

By introducing this expression into the above equation,

$$F_a=-\frac{E(E_v-2F_u)+E_{u}F}{2E\sqrt{EG-F^2}}.$$

(58)

Similarly,

$$F_b=\frac{G(G_u-2F_v)+G_{v}F}{2G\sqrt{EG-F^2}}.$$

(59)

In substituting the rewritten expressions of $\varphi$, $\left|\mathbf{N}\right|$, $F_a$, and $F_b$ into the explicit expression of K and then manipulating the derivatives contained therein, it involves only E, F, G, and their derivatives. This completes the proof. □

5. Concluding Remarks and Examples

In summary, for orientable smooth surfaces in ${\mathbb{R}}^3$ we constructed a differential relation between five metric properties: K, $\left|\mathbf{N}\right|$, $F_a$, $F_b$, and $\varphi$. The differential relation can be applied to those surfaces given by either orthogonal or non-orthogonal parameterizations since Theorem 1 has no loss of generality for parametrization. In representing the Gaussian curvature explicitly from the differential relation of Theorem 1, the resultant equation may be regarded as a specific form of the Brioschi formula. However, it is emphasized that the objective of this study is not to establish a new expression for the Gaussian curvature, but to facilitate a general extension of the application of the Gauss–Bonnet formula via a differential relation of the metric properties of S.

We present examples of the differential relation of Theorem 1 by means of two surfaces given by orthogonal and non-orthogonal parameterizations, respectively. For a systematic investigation, we hereafter denote the three budgets of Equation (11) by $I_K$, $I_{{\kappa }_g}$, and $I_{\varphi }$ in order, respectively.

Example 1.

Let $S_1$ be a unit sphere, and let ${\mathbf{r}}_1$ be a parametrization of $S_1$ such that ${\mathbf{r}}_1(u,v)=(sinucosv,sinusinv,cosu)$, $(u,v)\in (0,\pi )\times (0,2\pi )$. Taking into account that ${\mathbf{r}}_1(u,v)$ is orthogonal and the geodesic curvature of the great circle $v=\mathit{const}.$ over $S_1$ is equal to zero, the differential relation of Equation (11) is reduced to a particularly elementary form, as follows:

$$K|\mathbf{N}|+\frac{\partial F_b}{\partial u}=0.$$

(60)

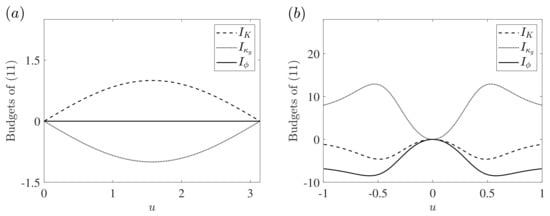
For a computer-aided investigation, we consider a subset of U as a test interval: $0<u<\pi$ at $v=\pi /6$. We computed $I_K$, $I_{{\kappa }_g}$, $I_{\varphi }$, and their sum for the considered interval. First, we confirmed that the root-mean-square (r.m.s.) value of the sum is zero. Figure 3a shows the variations of the three budgets as a function of u. The values of $I_{\varphi }$ are trivially zero since ${\mathbf{r}}_1$ is orthogonal. On the other hand, the values of $I_K$ counteract exactly those of $I_{{\kappa }_g}$.

Figure 3. Budgets of the differential Equation (11) as a function of u for two surfaces: (a) at $v=\pi /6$ for a unit sphere and (b) at $v=0$ for the monkey saddle.

Example 2.

Let $S_2$ be the $“$ monkey saddle” given by ${\mathbf{r}}_2(u,v)=(u,v,u^3-3v^{2}u)$, $(u,v)\in (-\infty ,\infty )\times (-\infty ,\infty )$. It is well known that $S_2$ is an orientable smooth surface. We computed $I_K$, $I_{{\kappa }_g}$, and $I_{\varphi }$ for a test interval: $-1\le u\le 1$ at $v=0$. For this case, the order of the r.m.s. value of the sum is identified as ${10}^{-14}$, and we attribute this error to the floating-point precision in our computation. As observed in Figure 3b, the sum of the three budgets agrees with the differential relation of Equation (11), but now with the non-trivial values of $I_{\varphi }$.