3D Flow of Hybrid Nanomaterial through a Circular Cylinder: Saddle and Nodal Point Aspects
Abstract
:1. Introduction
2. Problem Formulation
3. Numerical Procedure and Validation of Code
- Convert the BVP into IVP of the first order.
- Apply the shooting procedure to guess the missing boundary values.
- Apply the RKF-45 method to obtain the solution to IVP.
- Find the residuals for all the boundary conditions.
- If the residual error is greater than the error tolerance, adjust the initial guesses.
- If the residual error is less than error tolerance, numerical results are obtained.
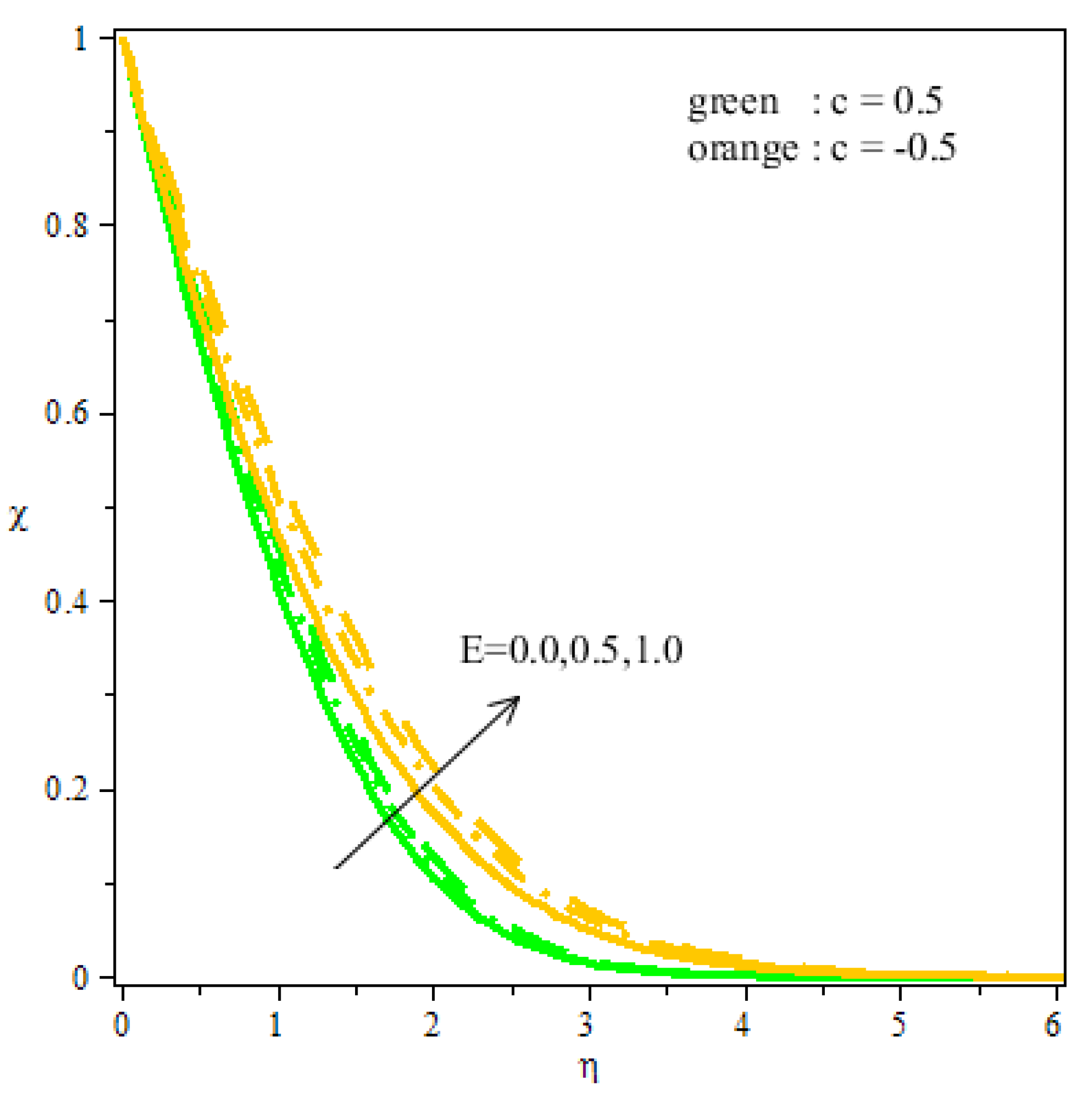
4. Results and Discussion
5. Final Remarks
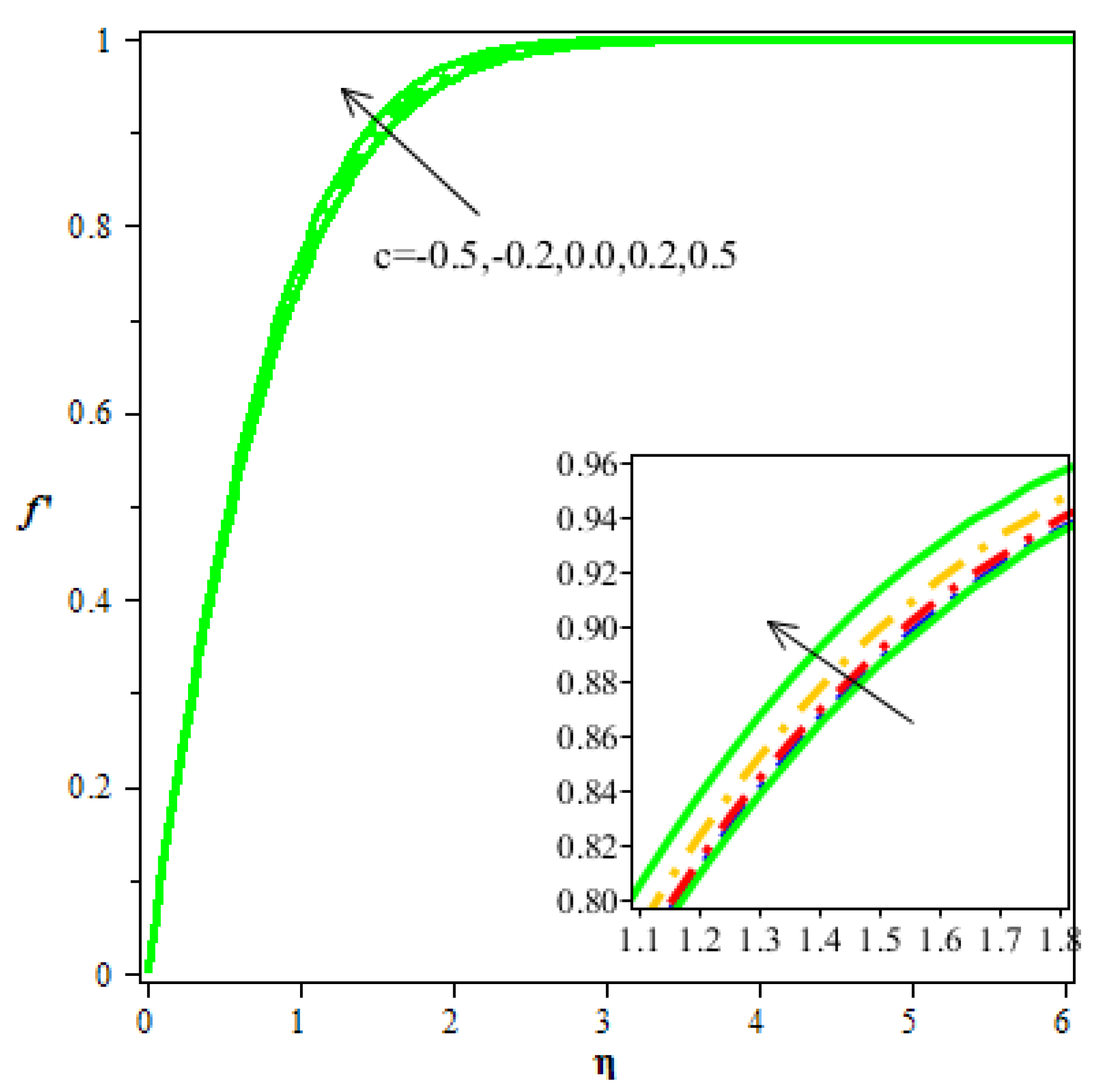
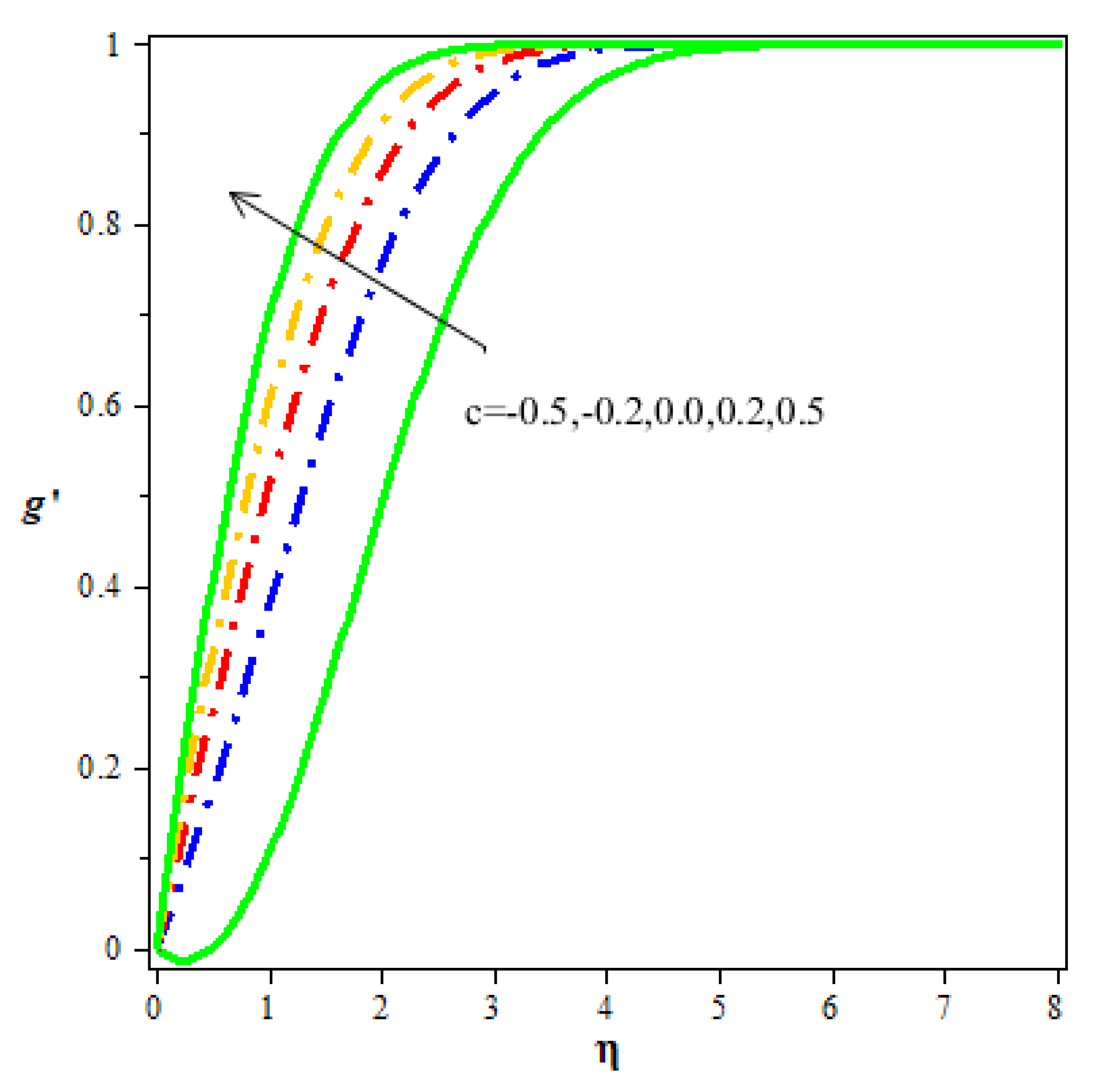
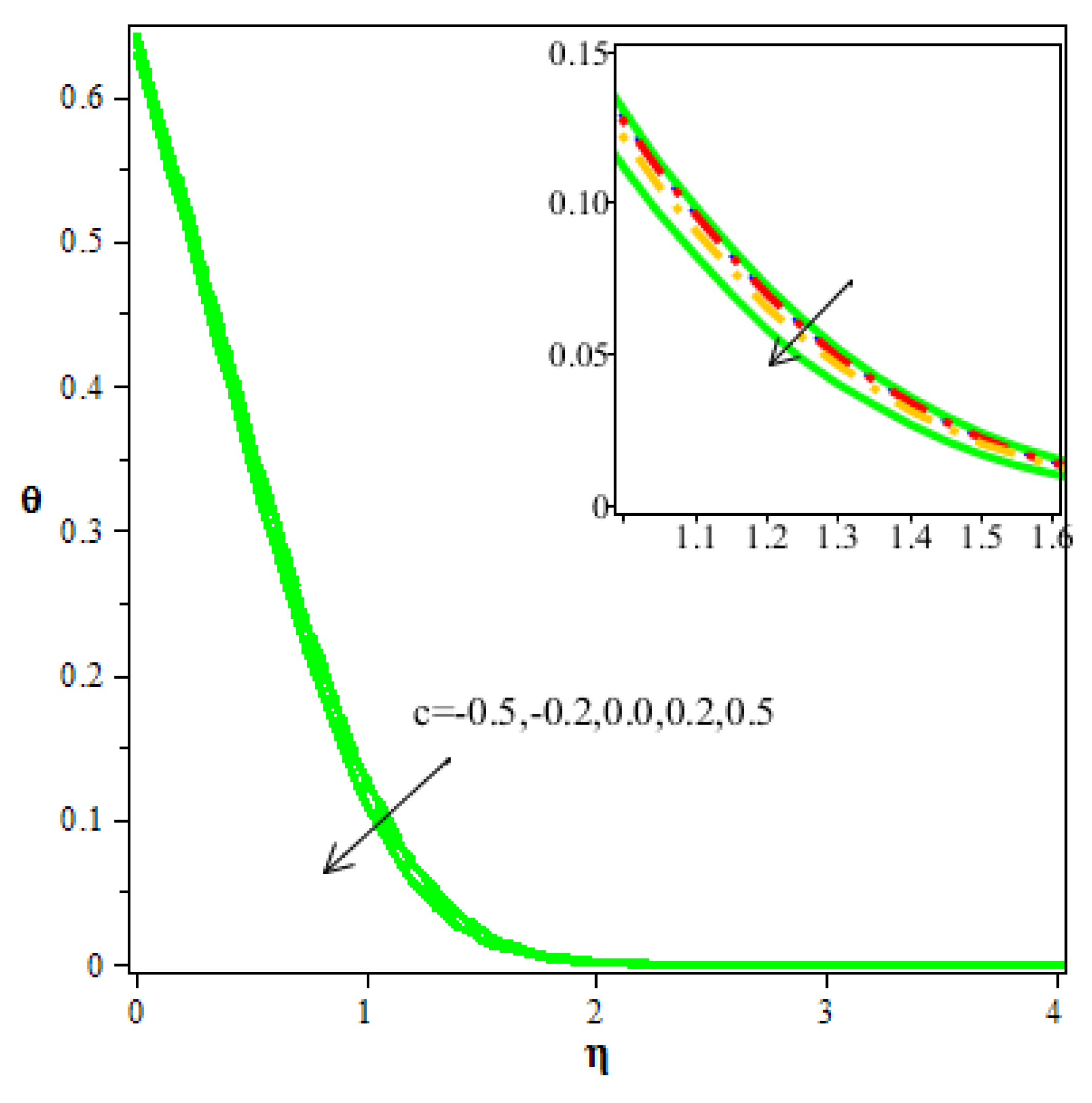
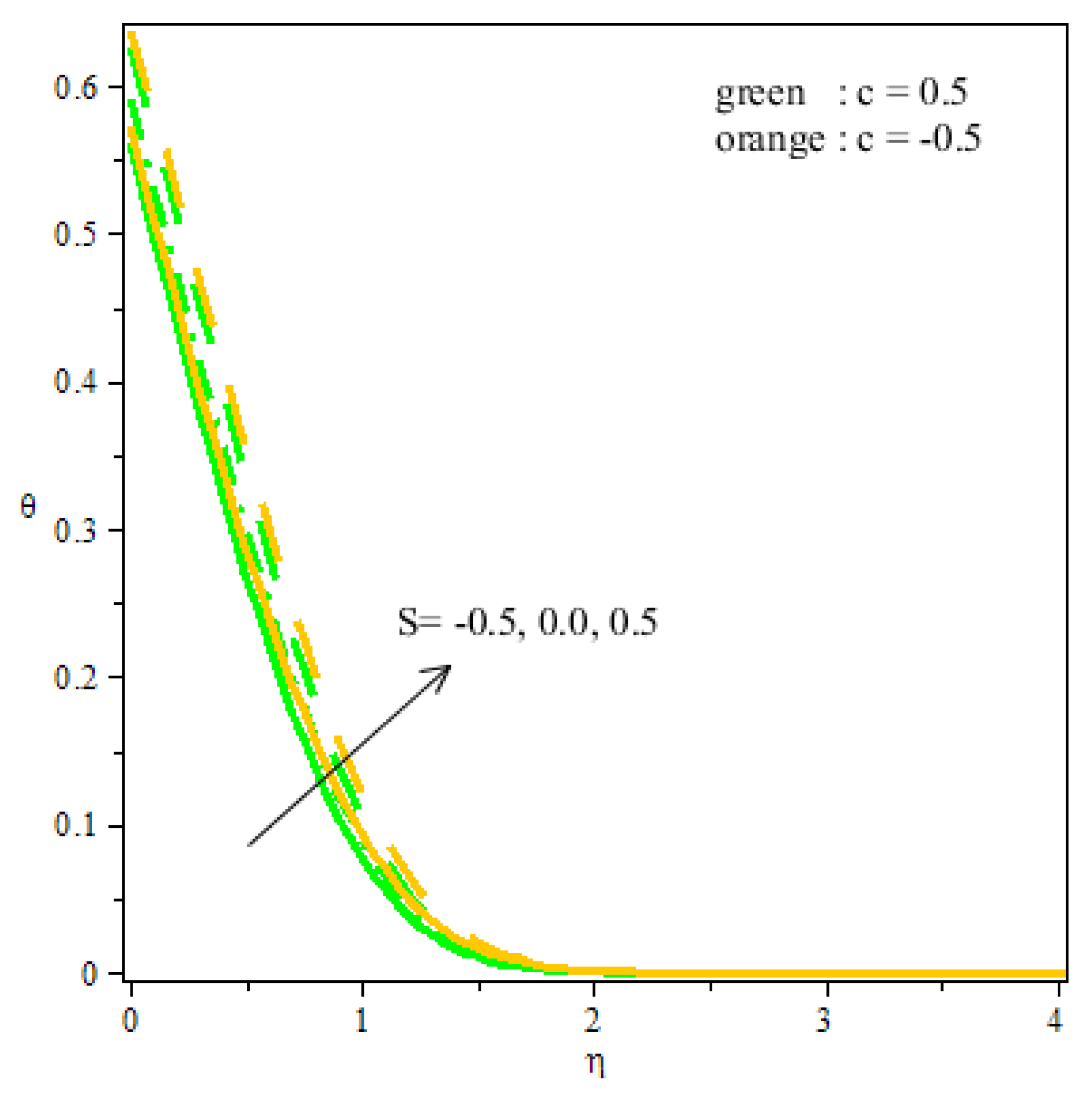
- A rise in the value of the streamline parameter upsurges the flow velocity and decreases the thermal distribution and concentration.
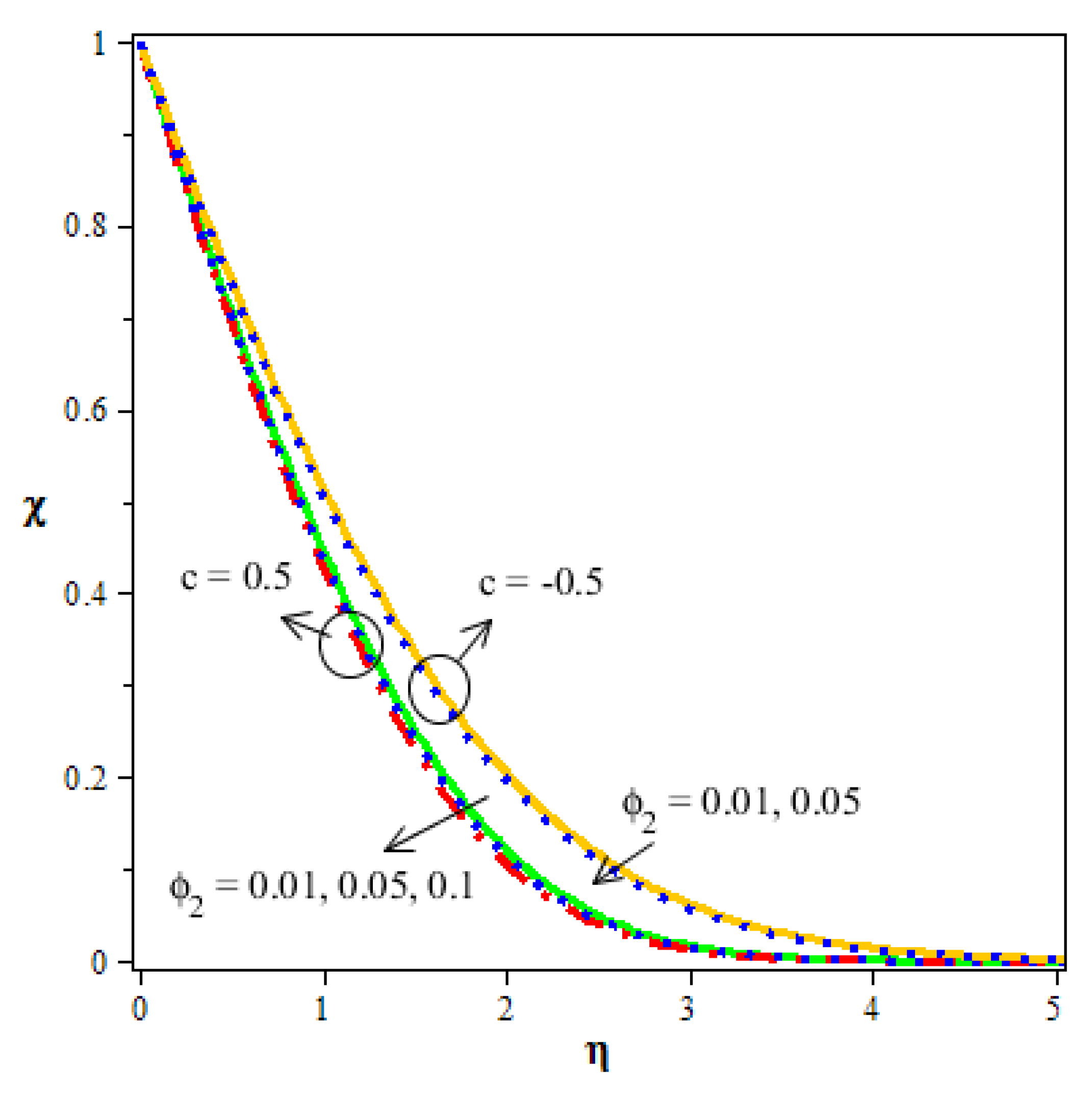
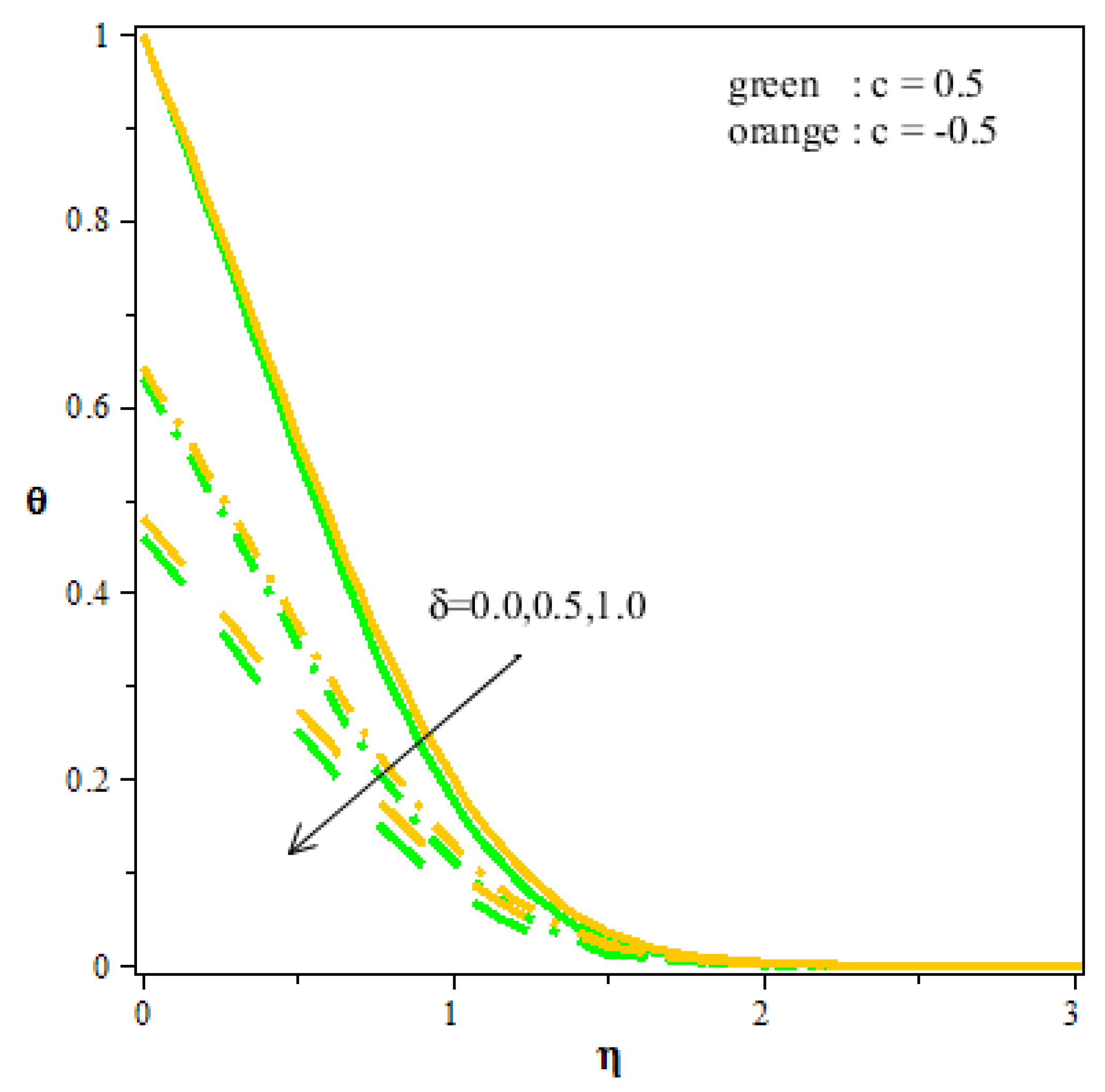
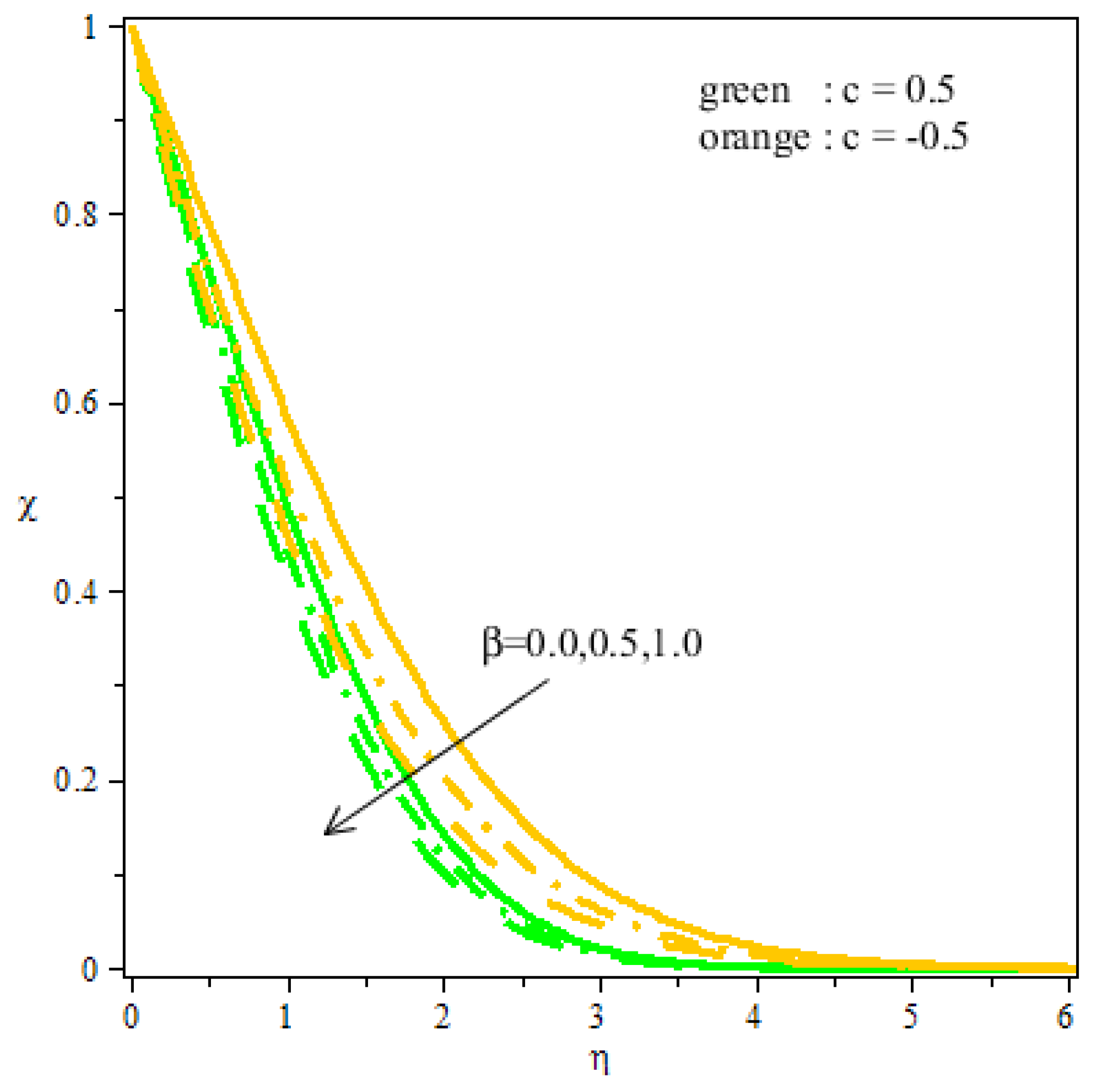
- Better thermal gradient and concentration are seen in the enhancement of volume fraction.
- Boundary layer thickness and concentration are decreased with increase in the Schmidt number.
- Thermal distribution and concentration are more in the saddle point than in the nodal point of a hybrid nanofluid.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Free stream dependent constants | |
| Gradient of streamline | |
| Concentration | |
| Wall concentration | |
| Ambient concentration | |
| Specific heat | |
| Skin friction along x and y direction | |
| Diffusivity | |
| E | Activation energy parameter |
| Activation energy | |
| Fluid | |
| Dimensionless velocity | |
| Dimensionless velocity | |
| Hybrid nanofluid | |
| Mass transfer | |
| Thermal conductivity | |
| Reaction rate | |
| Boltzmann constant | |
| Fitted rate constant | |
| Nusselt number | |
| Pr | Prandtl number |
| Surface heat flux | |
| Uniform heat source/sink coefficient | |
| Reynolds number | |
| Solid particle of | |
| Solid particle of | |
| Heat source/sink parameter | |
| Schmidt number | |
| Sherwood number | |
| Temperature | |
| Wall temperature | |
| Ambient temperature | |
| Free stream velocity | |
| Velocity components | |
| Coordinate axis | |
| Greek symbols | |
| Thermal diffusivity | |
| Dynamic viscosity | |
| Density | |
| Kinematic viscosity | |
| Heat capacitance | |
| Thermal slip | |
| Thermal slip parameter | |
| Temperature difference parameter | |
| Reaction rate | |
| Shear stresses surface in the x-direction | |
| Shear stresses surface in the y-direction | |
| The solid volume fraction of | |
| The solid volume fraction of | |
| Dimensionless temperature | |
| Dimensionless concentration | |
References
- Choi, S.U.S.; Eastman, J. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, San Francisco, CA, USA, 12–17 November 1995; Volume 66. [Google Scholar]
- Choi, S.U.S. Nanofluids: From Vision to Reality Through Research. J. Heat Transf. 2009, 131, 033106. [Google Scholar] [CrossRef]
- Koriko, O.K.; Shah, N.A.; Saleem, S.; Chung, J.D.; Omowaye, A.J.; Oreyeni, T. Exploration of bioconvection flow of MHD thixotropic nanofluid past a vertical surface coexisting with both nanoparticles and gyrotactic microorganisms. Sci. Rep. 2021, 11, 16627. [Google Scholar] [CrossRef] [PubMed]
- Rehman, F.U.; Nadeem, S.; Rehman, H.U.; Haq, R.U. Thermophysical analysis for three-dimensional MHD stagnation-point flow of nano-material influenced by an exponential stretching surface. Results Phys. 2018, 8, 316–323. [Google Scholar] [CrossRef]
- Fetecau, C.; Shah, N.A.; Vieru, D. General Solutions for Hydromagnetic Free Convection Flow over an Infinite Plate with Newtonian Heating, Mass Diffusion and Chemical Reaction. Commun. Theor. Phys. 2017, 68, 768. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Magnetic field influence on nanofluid thermal radiation in a cavity with tilted elliptic inner cylinder. J. Mol. Liq. 2017, 229, 137–147. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Abbasbandy, S.; Rashad, A.M.; Vajravelu, K. Radiation Effects on Mixed Convection over a Wedge Embedded in a Porous Medium Filled with a Nanofluid. Transp. Porous Media 2011, 91, 261–279. [Google Scholar] [CrossRef]
- Animasaun, I.L.; Shah, N.A.; Wakif, A.; Mahanthesh, B.; Sivaraj, R.; Koriko, O.K. Ratio of Momentum Diffusivity to Thermal Diffusivity: Introduction, Meta-Analysis, and Scrutinization, 1st ed.; Chapman and Hall/CRC: London, UK, 2022. [Google Scholar] [CrossRef]
- Saeed, M.; Kim, M.-H. Heat transfer enhancement using nanofluids (Al2O3-H2O) in mini-channel heatsinks. Int. J. Heat Mass Transf. 2018, 120, 671–682. [Google Scholar] [CrossRef]
- Sarkar, J.; Ghosh, P.; Adil, A. A review on hybrid nanofluids: Recent research, development and applications. Renew. Sustain. Energy Rev. 2015, 43, 164–177. [Google Scholar] [CrossRef]
- Asadi, A.; Alarifi, I.M.; Foong, L.K. An experimental study on characterization, stability and dynamic viscosity of CuO-TiO2/water hybrid nanofluid. J. Mol. Liq. 2020, 307, 112987. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Sherif, E.-S.M. Dual Solutions and Stability Analysis of a Hybrid Nanofluid over a Stretching/Shrinking Sheet Executing MHD Flow. Symmetry 2020, 12, 276. [Google Scholar] [CrossRef] [Green Version]
- Ramesh, G.K.; Shehzad, S.A.; Tlili, I. Hybrid nanomaterial flow and heat transport in a stretchable convergent/divergent channel: A Darcy-Forchheimer model. Appl. Math. Mech. 2020, 41, 699–710. [Google Scholar] [CrossRef]
- Ramesh, G.; Madhukesh, J. Activation energy process in hybrid CNTs and induced magnetic slip flow with heat source/sink. Chin. J. Phys. 2021, 73, 375–390. [Google Scholar] [CrossRef]
- Alghamdi, M. Significance of Arrhenius Activation Energy and Binary Chemical Reaction in Mixed Convection Flow of Nanofluid Due to a Rotating Disk. Coatings 2020, 10, 86. [Google Scholar] [CrossRef] [Green Version]
- Rekha, M.B.; Sarris, I.E.; Madhukesh, J.K.; Raghunatha, K.R.; Prasannakumara, B.C. Activation Energy Impact on Flow of AA7072-AA7075/Water-Based Hybrid Nanofluid through a Cone, Wedge and Plate. Micromachines 2022, 13, 302. [Google Scholar] [CrossRef] [PubMed]
- Ramesh, G. Analysis of active and passive control of nanoparticles in viscoelastic nanomaterial inspired by activation energy and chemical reaction. Phys. A Stat. Mech. Its Appl. 2020, 550, 123964. [Google Scholar] [CrossRef]
- Alsaadi, F.E.; Ullah, I.; Hayat, T.; Alsaadi, F.E. Entropy generation in nonlinear mixed convective flow of nanofluid in porous space influenced by Arrhenius activation energy and thermal radiation. J. Therm. Anal. 2019, 140, 799–809. [Google Scholar] [CrossRef]
- Asma, M.; Othman, W.; Muhammad, T. Numerical study for Darcy–Forchheimer flow of nanofluid due to a rotating disk with binary chemical reaction and Arrhenius activation energy. Mathematics 2019, 7, 921. [Google Scholar] [CrossRef] [Green Version]
- Ramzan, M.; Gul, H.; Zahri, M. Darcy-Forchheimer 3D Williamson nanofluid flow with generalized Fourier and Fick’s laws in a stratified medium. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 327–335. [Google Scholar]
- Jagan, K.; Sivasankaran, S.; Bhuvaneswari, M.; Rajan, S. Effect of Non-linear Radiation on 3D Unsteady MHD Nanoliquid Flow over a Stretching Surface with Double Stratification. Trends Math. 2019, 109–116. [Google Scholar] [CrossRef]
- Nayak, M.K.; Shaw, S.; Chamkha, A.J. 3D MHD Free Convective Stretched Flow of a Radiative Nanofluid Inspired by Variable Magnetic Field. Arab. J. Sci. Eng. 2019, 44, 1269–1282. [Google Scholar] [CrossRef]
- Irfan, M.; Khan, W.A.; Khan, M.; Gulzar, M.M. Influence of Arrhenius activation energy in chemically reactive radiative flow of 3D Carreau nanofluid with nonlinear mixed convection. J. Phys. Chem. Solids 2019, 125, 141–152. [Google Scholar] [CrossRef]
- A Alwawi, F.; Alkasasbeh, H.T.; Rashad, A.; Idris, R. Heat transfer analysis of ethylene glycol-based Casson nanofluid around a horizontal circular cylinder with MHD effect. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 2569–2580. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Nadeem, S.; Abbas, N. On both MHD and slip effect in micropolar hybrid nanofluid past a circular cylinder under stagnation point region. Can. J. Phys. 2019, 97, 392–399. [Google Scholar] [CrossRef]
- Tlili, I.; Waqas, H.; Almaneea, A.; Khan, S.U.; Imran, M. Activation Energy and Second Order Slip in Bioconvection of Oldroyd-B Nanofluid over a Stretching Cylinder: A Proposed Mathematical Model. Processes 2019, 7, 914. [Google Scholar] [CrossRef] [Green Version]
- Shah, N.A.; Wakif, A.; El-Zahar, E.R.; Thumma, T.; Yook, S.-J. Heat transfers thermodynamic activity of a second-grade ternary nanofluid flow over a vertical plate with Atangana-Baleanu time-fractional integral. Alex. Eng. J. 2022, 61, 10045–10053. [Google Scholar] [CrossRef]
- Rashid, U.; Baleanu, D.; Iqbal, A.; Abbas, M. Shape Effect of Nanosize Particles on Magnetohydrodynamic Nanofluid Flow and Heat Transfer over a Stretching Sheet with Entropy Generation. Entropy 2020, 22, 1171. [Google Scholar] [CrossRef]
- Manohar, G.R.; Venkatesh, P.; Gireesha, B.J.; Madhukesh, J.K.; Ramesh, G.K. Performance of water, ethylene glycol, engine oil conveying SWCNT-MWCNT nanoparticles over a cylindrical fin subject to magnetic field and heat generation. Int. J. Model. Simul. 2021, 1–10. [Google Scholar] [CrossRef]
- Mathews, J.H.; Fink, K.D. Numerical Methods Using MATLAB, 3rd ed.; Prentice Hall: Hoboken, NJ, USA, 1998. [Google Scholar]
- Ramesh, G.; Madhukesh, J.; Das, R.; Shah, N.A.; Yook, S.-J. Thermodynamic activity of a ternary nanofluid flow passing through a permeable slipped surface with heat source and sink. Waves Random Complex Media 2022, 1–21. [Google Scholar] [CrossRef]
- Gangadhar, K.; Nayak, R.E.; Rao, M.V.S.; Kannan, T. Nodal/Saddle Stagnation Point Slip Flow of an Aqueous Convectional Magnesium Oxide–Gold Hybrid Nanofluid with Viscous Dissipation. Arab. J. Sci. Eng. 2021, 46, 2701–2710. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Gupta, A. MHD flow and heat transfer at a general three-dimensional stagnation point. Int. J. Non-Linear Mech. 1998, 33, 125–134. [Google Scholar] [CrossRef]
- Dinarvand, S. Nodal/saddle stagnation-point boundary layer flow of CuO–Ag/water hybrid nanofluid: A novel hybridity model. Microsyst. Technol. 2019, 25, 2609–2623. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Nazar, R.; Pop, I. Flow and heat transfer at a general three-dimensional stagnation point in a nanofluid. Phys. B Condens. Matter 2010, 405, 4914–4918. [Google Scholar] [CrossRef]
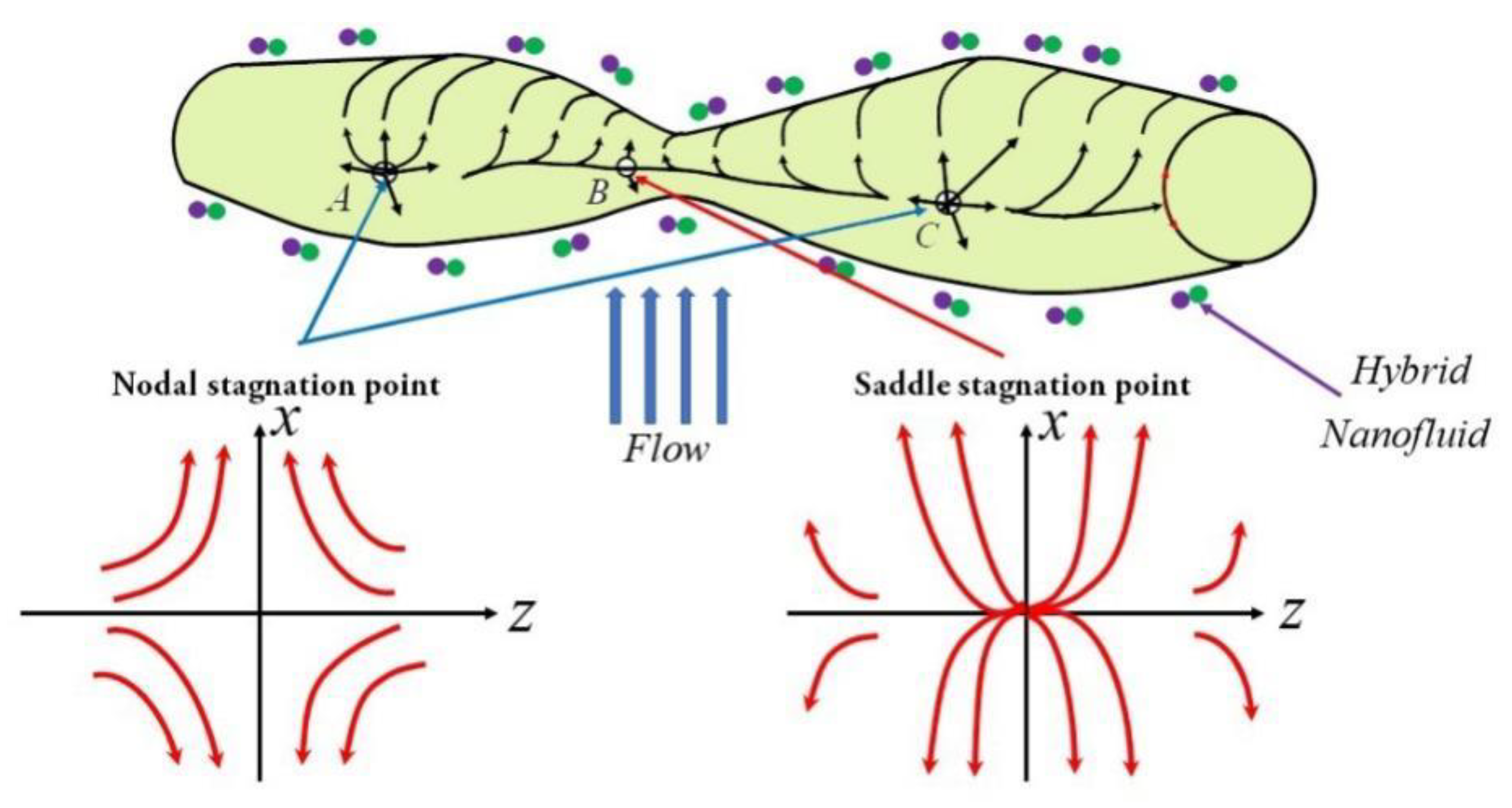

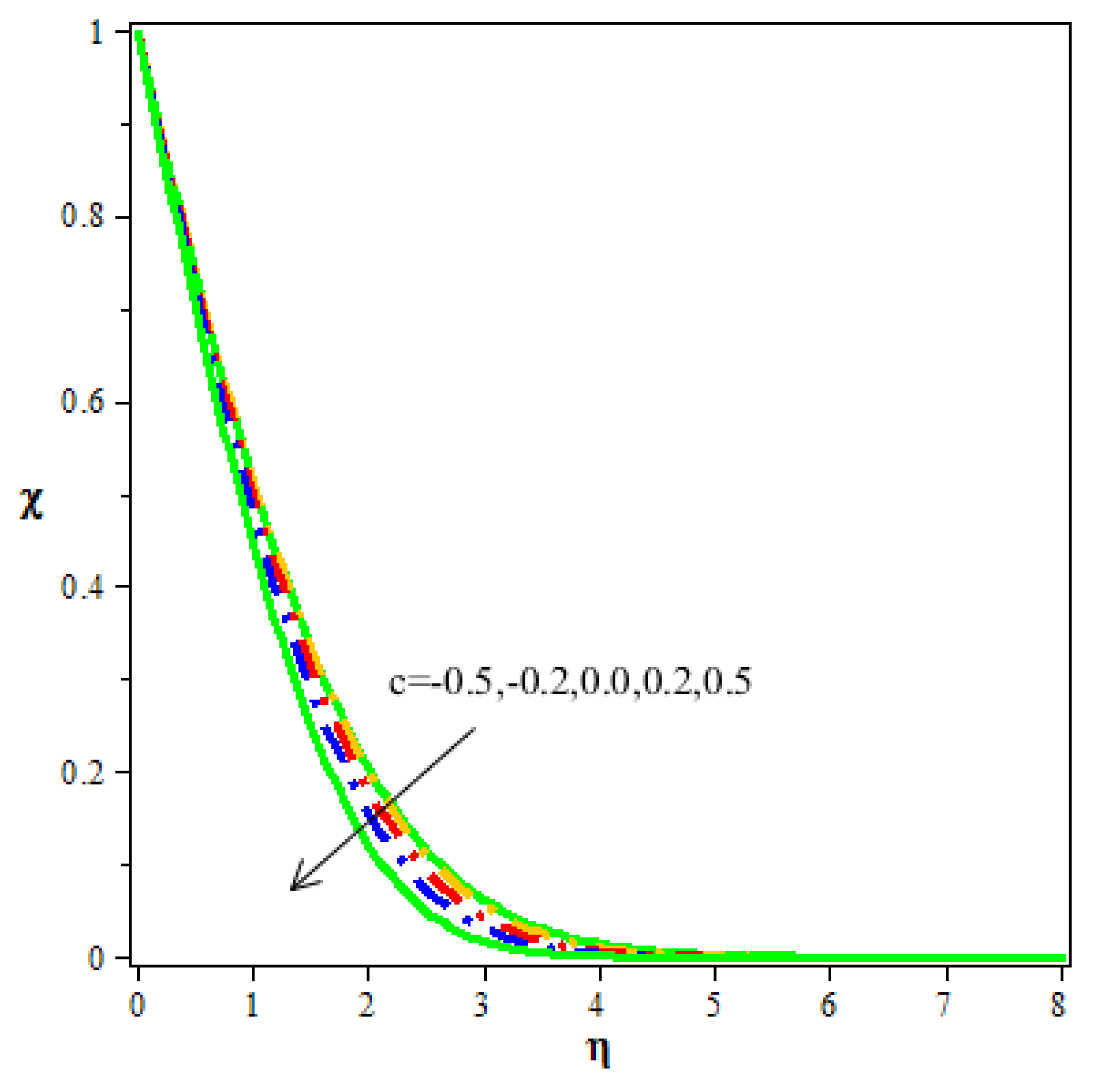
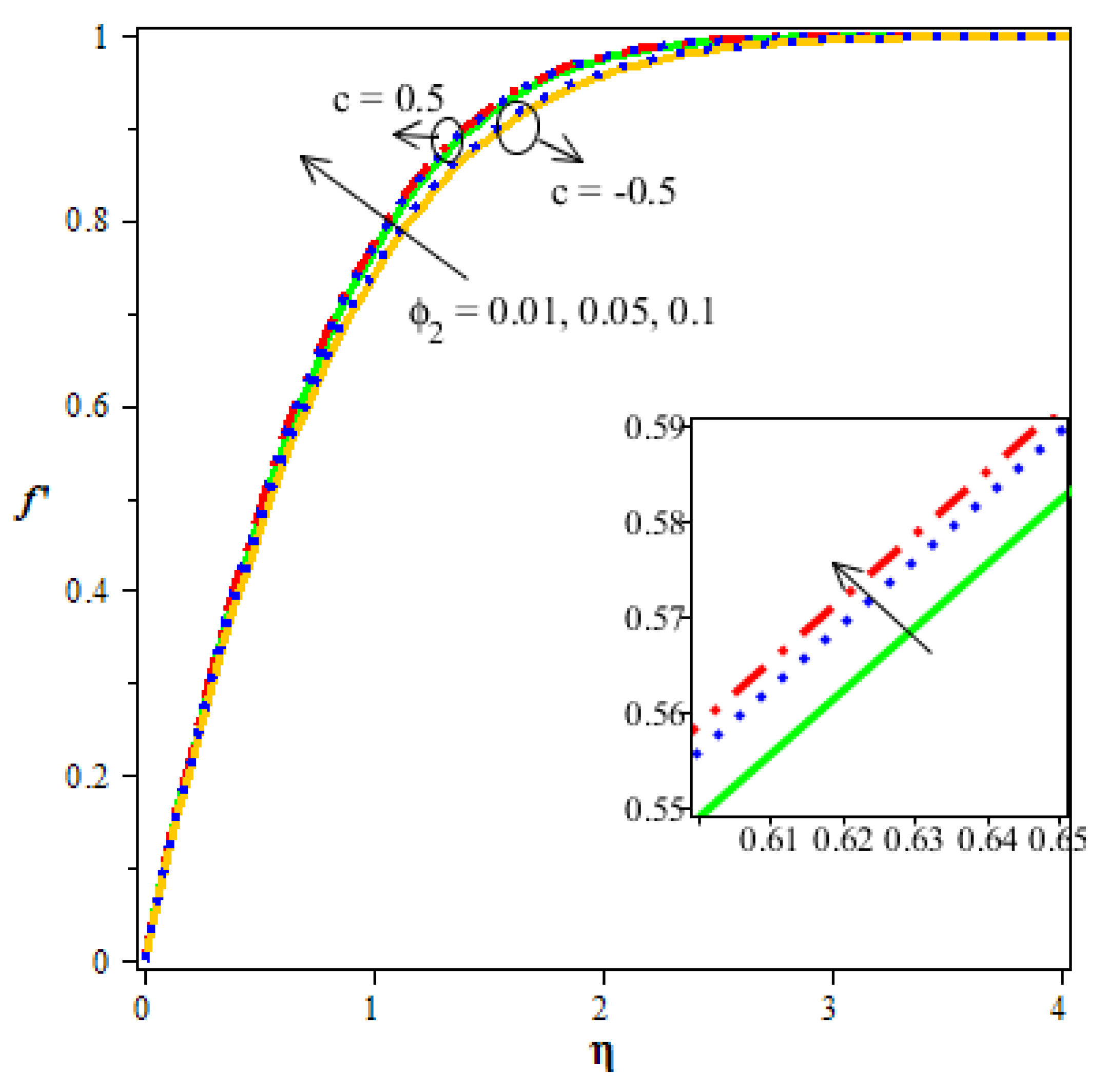
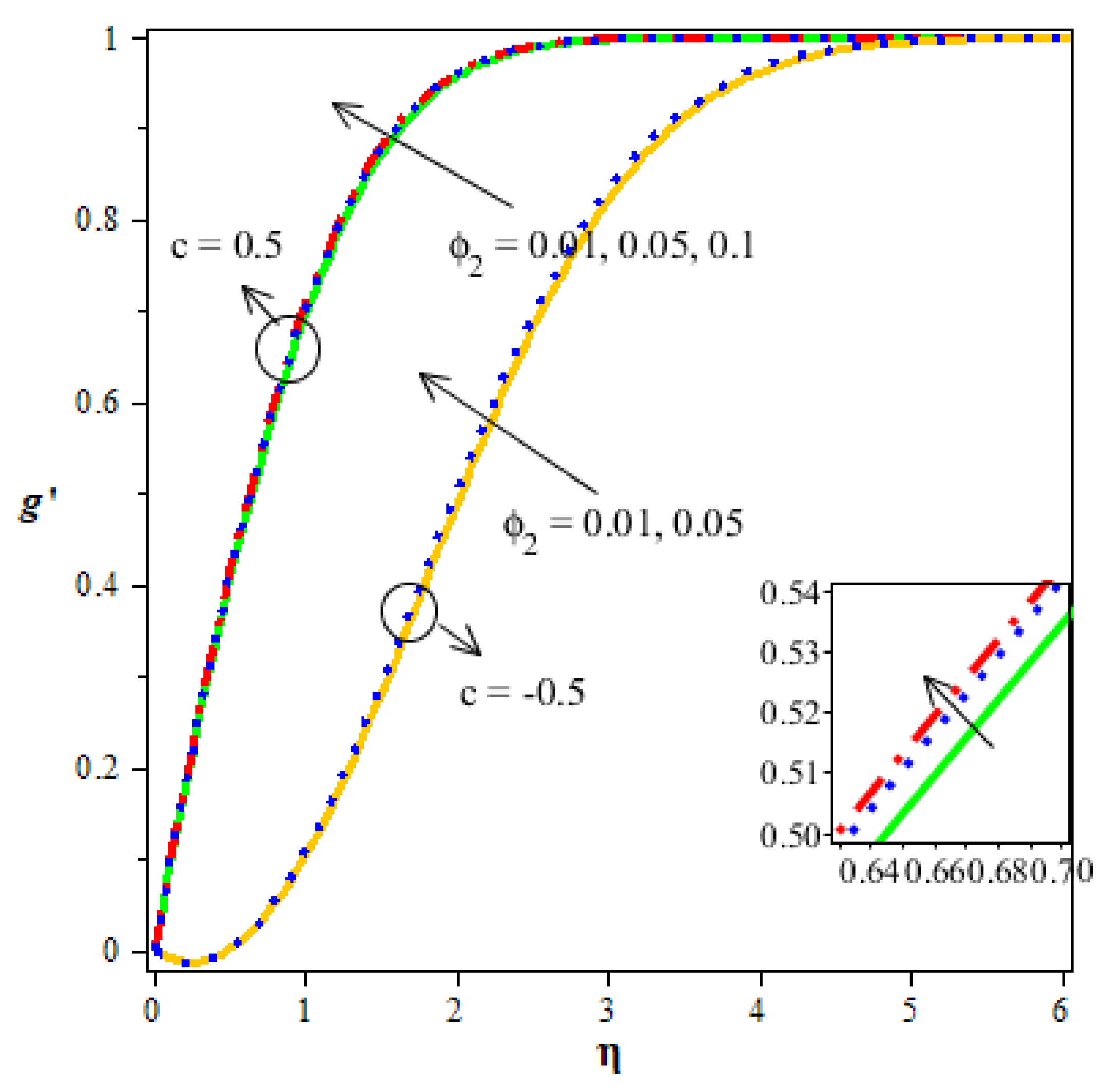
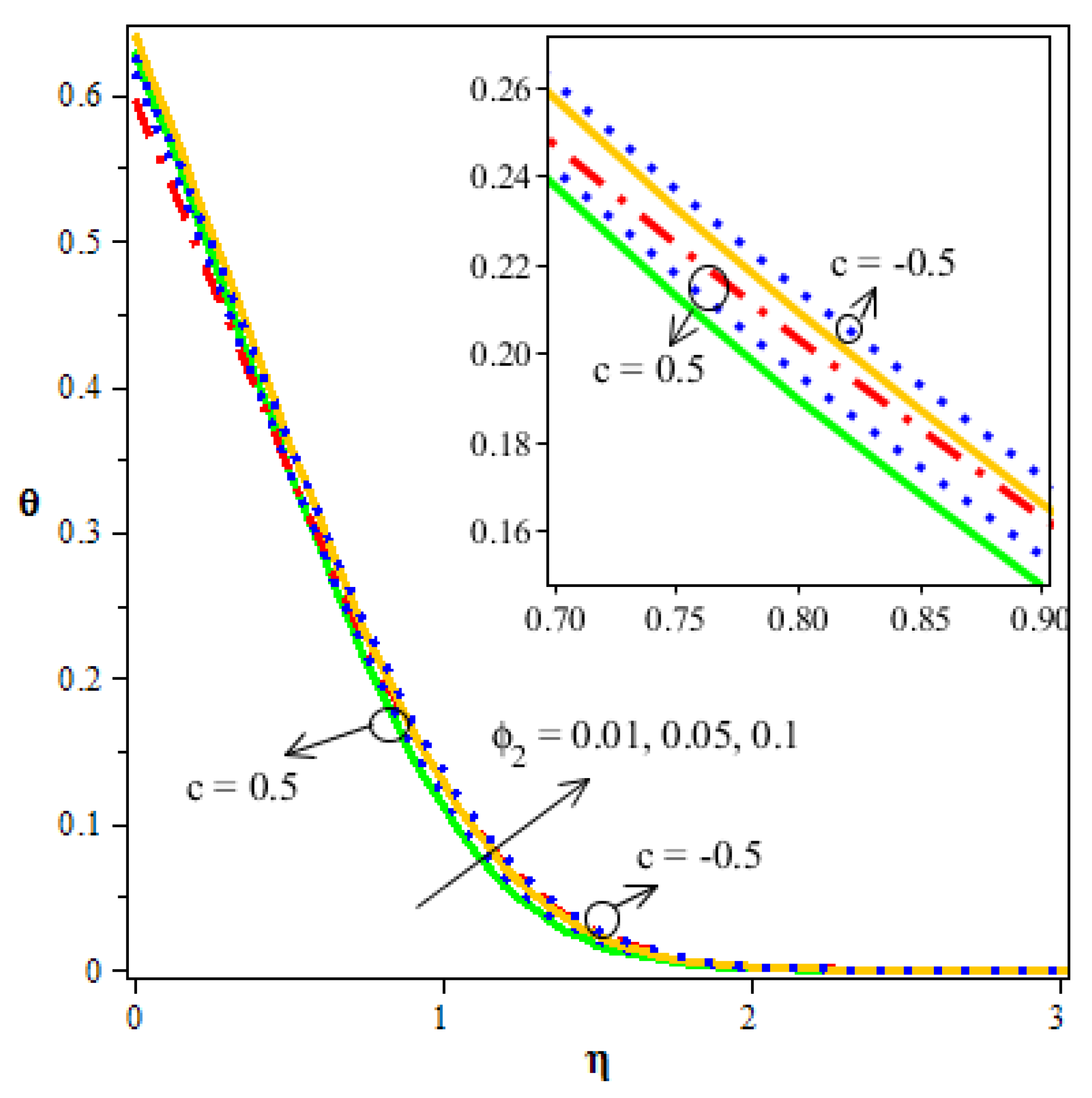

| Particles | |||
|---|---|---|---|
| 5180 | 670 | 9.7 | |
| 1800 | 717 | 5000 | |
| Water | 997.1 | 4179 | 0.613 |
| Gangadar et al. [33] | Bhattacharyya and Gupta [34] | Dinarvand [35] | Bachok et al. [36] | Present Study | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | ||||||||||
| −0.5 | 0.5 | −0.5 | 0.5 | −0.5 | 0.5 | −0.5 | 0.5 | −0.5 | 0.5 | |
| 1.2302 | 1.2669 | 1.2312 | 1.2679 | 1.2325 | 1.2681 | - | 1.2681 | 1.2308 | 1.2675 | |
| 0.0558 | 0.4991 | 0.0557 | 0.4993 | 0.0557 | 0.4993 | - | 0.4994 | 0.0555 | 0.4990 | |
| 1.1227 | 1.2938 | 1.1235 | 1.3302 | 1.1237 | 1.3301 | - | 1.3302 | 1.1231 | 1.2979 | |
| −0.5 | 1.127855 | −0.102224 | 0.523666 | 0.551725 |
| −0.2 | 1.123800 | 0.307432 | 0.521301 | 0.550452 |
| 0.0 | 1.130049 | 0.523008 | 0.524605 | 0.565968 |
| 0.2 | 1.140688 | 0.698789 | 0.530197 | 0.587699 |
| 0.5 | 1.161475 | 0.915078 | 0.540786 | 0.624976 |
| 0.01 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 1.161475 | 0.915078 | 0.540786 | 0.624976 |
| 0.02 | 1.173017 | 0.924171 | 0.527588 | 0.631374 | |||||
| 0.03 | 1.181275 | 0.930677 | 0.514390 | 0.637650 | |||||
| 0.01 | −0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 1.161475 | 0.915078 | 0.634573 | 0.627710 |
| 0.0 | 1.161475 | 0.915078 | 0.591876 | 0.626489 | |||||
| 0.5 | 1.161475 | 0.915078 | 0.540786 | 0.624976 | |||||
| 0.01 | 0.5 | 0.0 | 0.5 | 0.5 | 0.5 | 1.161475 | 0.915078 | 0.857072 | 0.613593 |
| 0.5 | 1.161475 | 0.915078 | 0.540786 | 0.624976 | |||||
| 1.0 | 1.161475 | 0.915078 | 0.395014 | 0.629594 | |||||
| 0.01 | 0.5 | 0.5 | 0.1 | 0.5 | 0.5 | 1.161475 | 0.915078 | 0.540786 | 0.315530 |
| 0.3 | 1.161475 | 0.915078 | 0.540786 | 0.505093 | |||||
| 0.5 | 1.161475 | 0.915078 | 0.540786 | 0.624976 | |||||
| 0.01 | 0.5 | 0.5 | 0.5 | 0.0 | 0.5 | 1.161475 | 0.915078 | 0.540786 | 0.521808 |
| 0.5 | 1.161475 | 0.915078 | 0.540786 | 0.624976 | |||||
| 1.0 | 1.161475 | 0.915078 | 0.540786 | 0.716755 | |||||
| 0.01 | 0.5 | 0.5 | 0.5 | 0.5 | 0.0 | 1.161475 | 0.915078 | 0.540786 | 0.703487 |
| 0.5 | 1.161475 | 0.915078 | 0.540786 | 0.624976 | |||||
| 1.0 | 1.161475 | 0.915078 | 0.540786 | 0.579943 |
| 0.01 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 1.127855 | −0.102224 | 0.523666 | 0.551725 |
| 0.02 | 1.139063 | −0.103240 | 0.511081 | 0.557363 | |||||
| 0.03 | 1.147081 | −0.103967 | 0.498476 | 0.563019 | |||||
| 0.01 | −0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 1.127855 | −0.102224 | 0.624321 | 0.554988 |
| 0.0 | 1.127855 | −0.102224 | Not Converging | ||||||
| 0.5 | 1.127855 | −0.102224 | 0.523666 | 0.551725 | |||||
| 0.01 | 0.5 | 0.0 | 0.5 | 0.5 | 0.5 | 1.127855 | −0.102224 | 0.814850 | 0.539718 |
| 0.5 | 1.127855 | −0.102224 | 0.523666 | 0.551725 | |||||
| 1.0 | 1.127855 | −0.102224 | 0.380486 | 0.511333 | |||||
| 0.01 | 0.5 | 0.5 | 0.1 | 0.5 | 0.5 | 1.127855 | −0.102224 | 0.523666 | 0.261420 |
| 0.3 | 1.127855 | −0.102224 | 0.523666 | 0.437491 | |||||
| 0.5 | 1.127855 | −0.102224 | 0.523666 | 0.551725 | |||||
| 0.01 | 0.5 | 0.5 | 0.5 | 0.0 | 0.5 | 1.127855 | −0.102224 | 0.523666 | 0.422603 |
| 0.5 | 1.127855 | −0.102224 | 0.523666 | 0.551725 | |||||
| 1.0 | 1.127855 | −0.102224 | 0.523666 | 0.659084 | |||||
| 0.01 | 0.5 | 0.5 | 0.5 | 0.5 | 0.0 | 1.127855 | −0.102224 | 0.523666 | 0.642921 |
| 0.5 | 1.127855 | −0.102224 | 0.523666 | 0.551725 | |||||
| 1.0 | 1.127855 | −0.102224 | 0.523666 | 0.497428 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madhukesh, J.K.; Ramesh, G.K.; Roopa, G.S.; Prasannakumara, B.C.; Shah, N.A.; Yook, S.-J. 3D Flow of Hybrid Nanomaterial through a Circular Cylinder: Saddle and Nodal Point Aspects. Mathematics 2022, 10, 1185. https://doi.org/10.3390/math10071185
Madhukesh JK, Ramesh GK, Roopa GS, Prasannakumara BC, Shah NA, Yook S-J. 3D Flow of Hybrid Nanomaterial through a Circular Cylinder: Saddle and Nodal Point Aspects. Mathematics. 2022; 10(7):1185. https://doi.org/10.3390/math10071185
Chicago/Turabian StyleMadhukesh, Javali K., Gosikere K. Ramesh, Govinakovi S. Roopa, Ballajja C. Prasannakumara, Nehad Ali Shah, and Se-Jin Yook. 2022. "3D Flow of Hybrid Nanomaterial through a Circular Cylinder: Saddle and Nodal Point Aspects" Mathematics 10, no. 7: 1185. https://doi.org/10.3390/math10071185
APA StyleMadhukesh, J. K., Ramesh, G. K., Roopa, G. S., Prasannakumara, B. C., Shah, N. A., & Yook, S.-J. (2022). 3D Flow of Hybrid Nanomaterial through a Circular Cylinder: Saddle and Nodal Point Aspects. Mathematics, 10(7), 1185. https://doi.org/10.3390/math10071185







