Simulation of Dissipative Hybrid Nanofluid (PEG-Water + ZrO2 + MgO) Flow by a Curved Shrinking Sheet with Thermal Radiation and Higher Order Chemical Reaction
Abstract
:1. Introduction
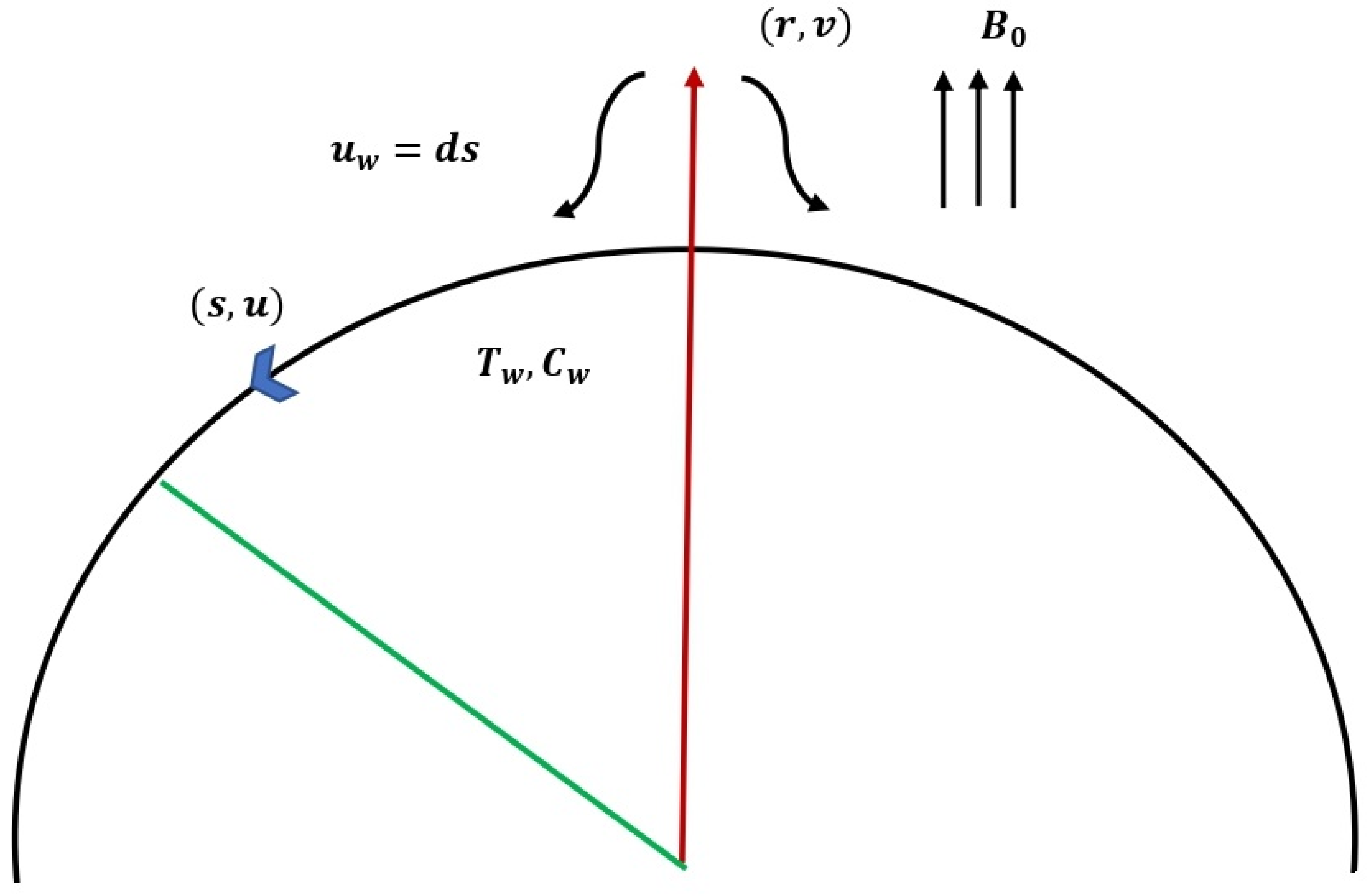
2. Problem Formulation
- Velocity of the sheet is denoted by where corresponds to shrinking;
- R is the radius of the circular nest in which the curved sheet is enclosed;
- The strength of the magnetic field, denoted by the symbol , is applied in the direction (see Figure 1), i.e., a magnetic field of uniform strength is applied transversely to the direction of the flow;
- and designate the ambient and surface concentrations while and designate the ambient and surface temperatures correspondingly;
- Higher order chemical reaction parameter is included in the diffusion equation to describe the mass transport phenomena. Thermal radiation and viscous dissipation parameters are included in the energy equation to describe the heat transport phenomena;
- Table 1 exhibits the values of thermo-physical properties of base fluid and nanomaterials involved in the hybrid nanofluid;
- Because it is so little in comparison to the external magnetic field, the induced magnetic field is ignored.
3. Numerical Procedure
4. Validation
5. Discussion of the Outcomes
5.1. Engineering Parameters of Interest
5.2. Statistical Analysis of Physical Parameters Using Correlation Coefficient
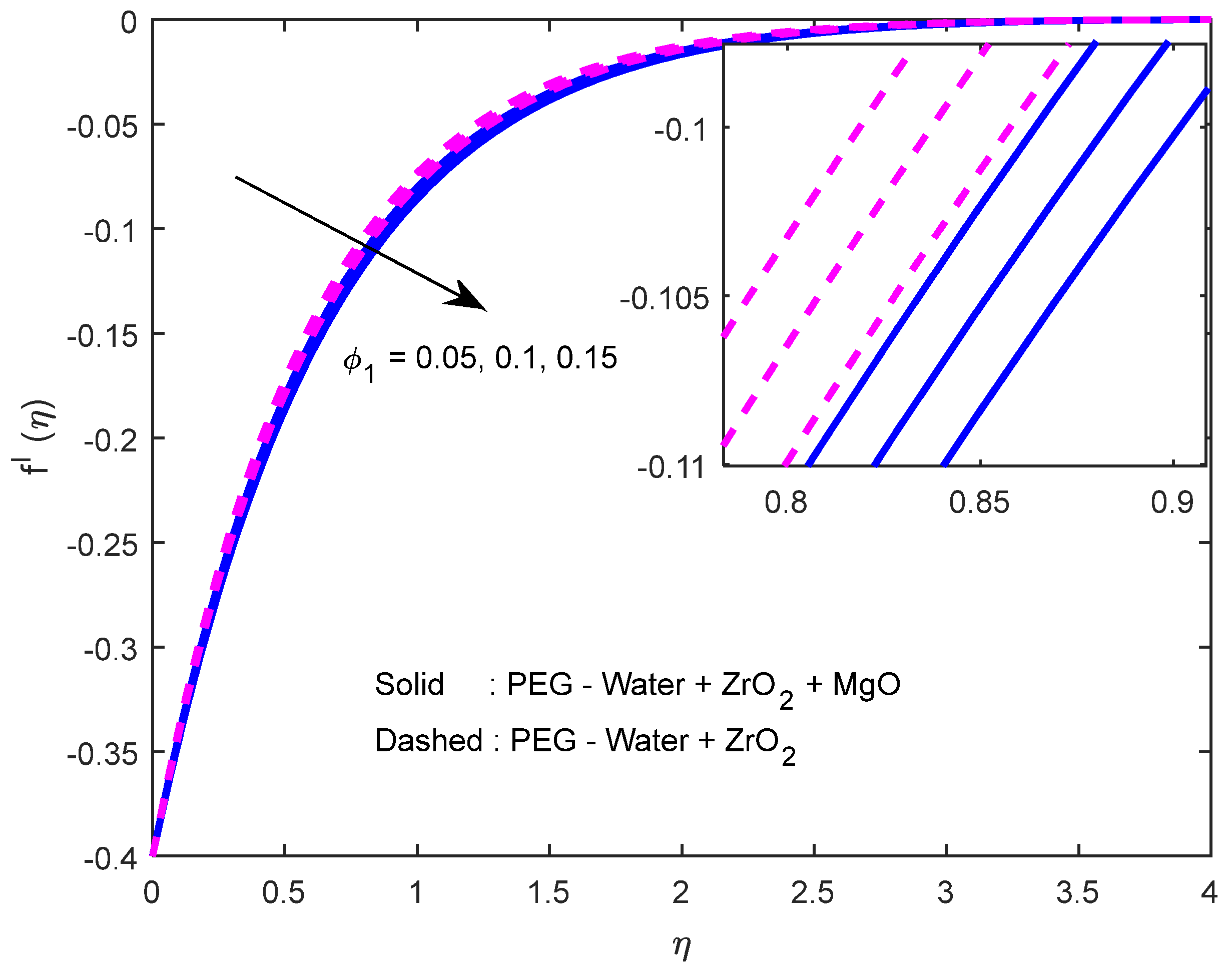
5.3. Regular Profiles including Velocity Profile
6. Conclusions
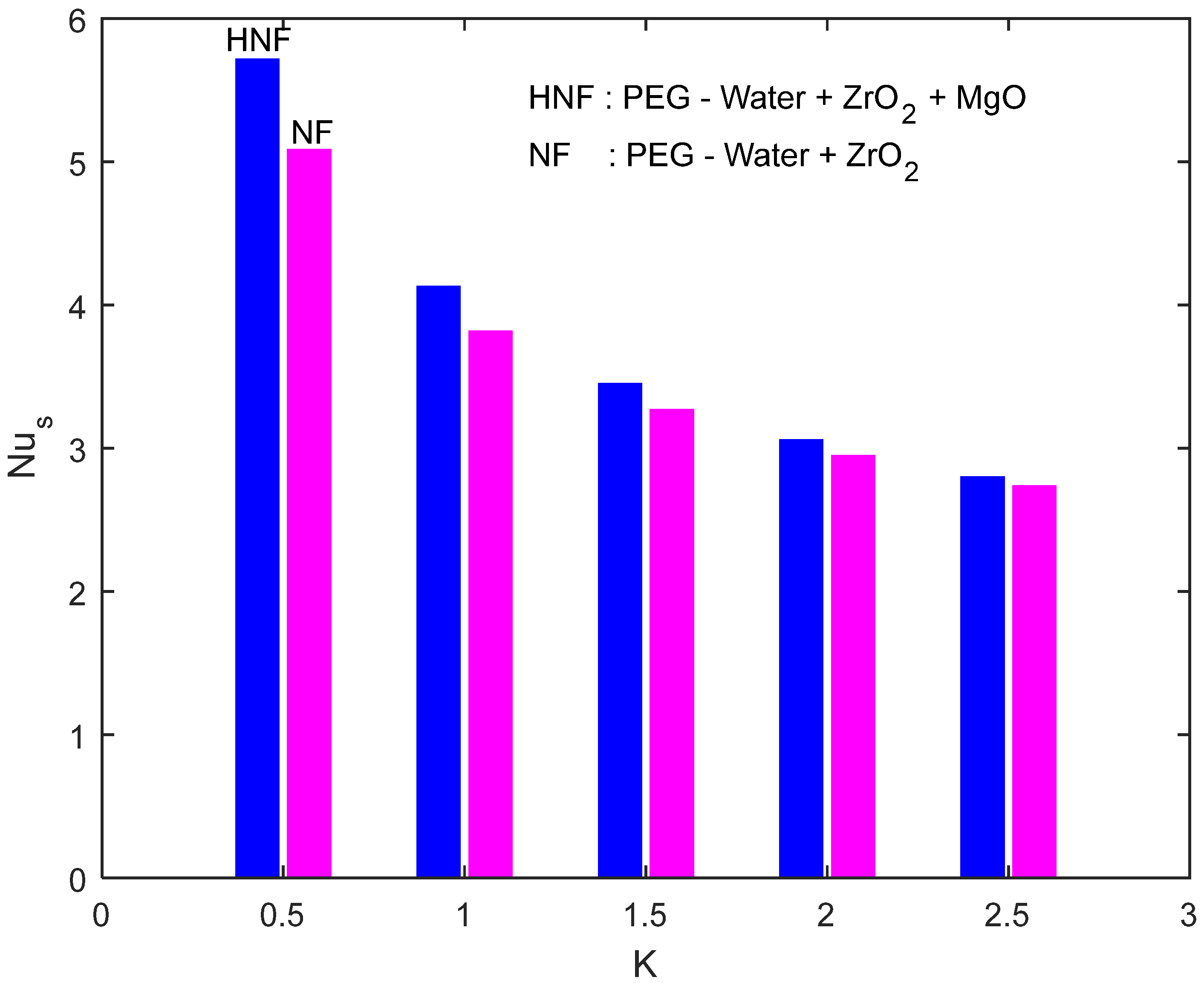
- It was noticed that, when radius of curvature parameter (K) takes input in the range , the skin friction coefficient decreases at a rate of 1.46633 (i.e., 146.633%) (in the case of hybrid nanofluid) and 1.11236 (i.e., 111.236%) (in the case of nanofluid) per unit value of curvature parameter;
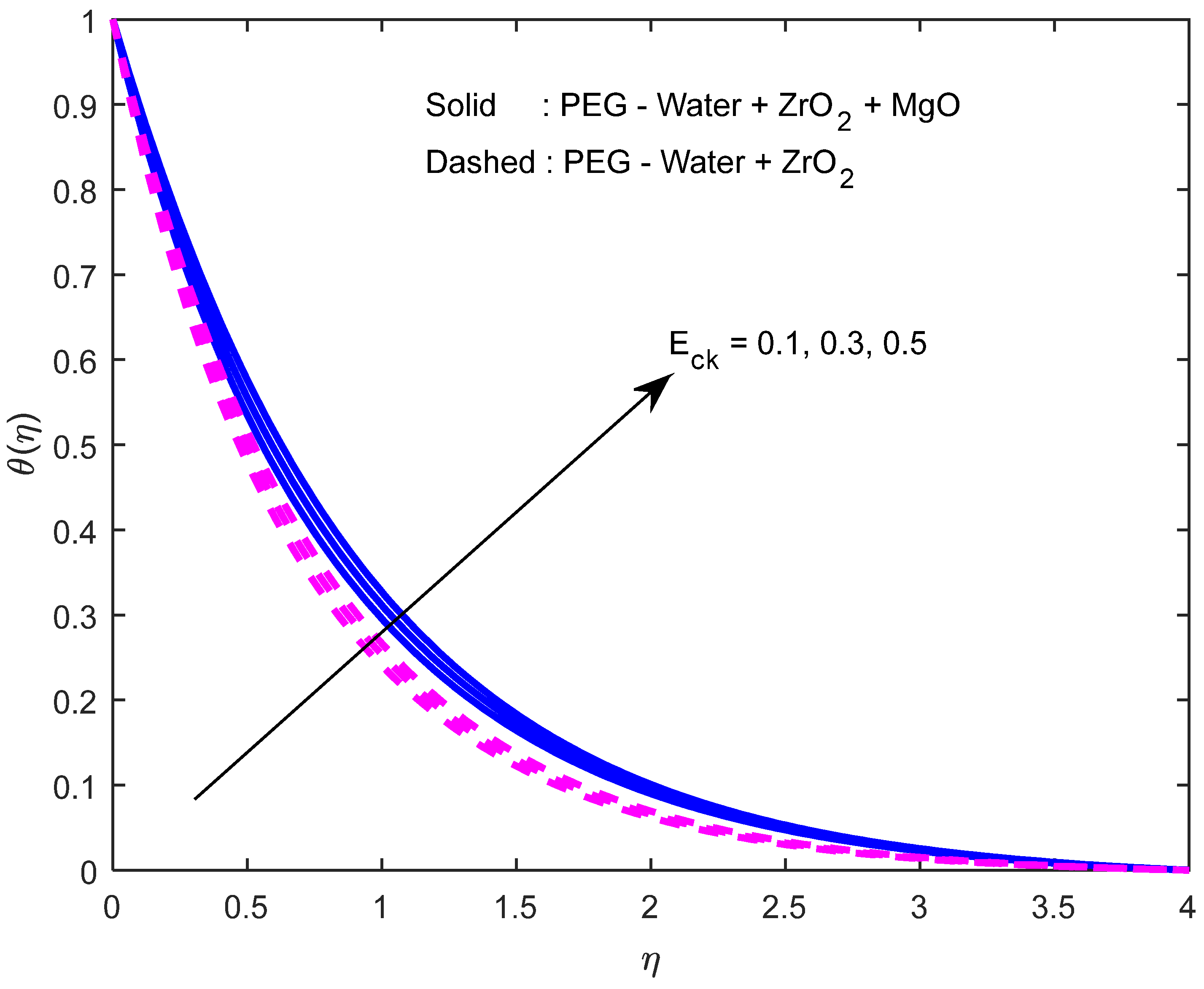
- It was detected that, when Eckert number increases, Nusselt number decreases. The decrement rates were observed as 1.41148 (i.e., 141.148%) (in the case of hybrid nanofluid) and 1.15337 (i.e., 115.337%) (in the case of nanofluid) when Eckert number takes input in the range ;
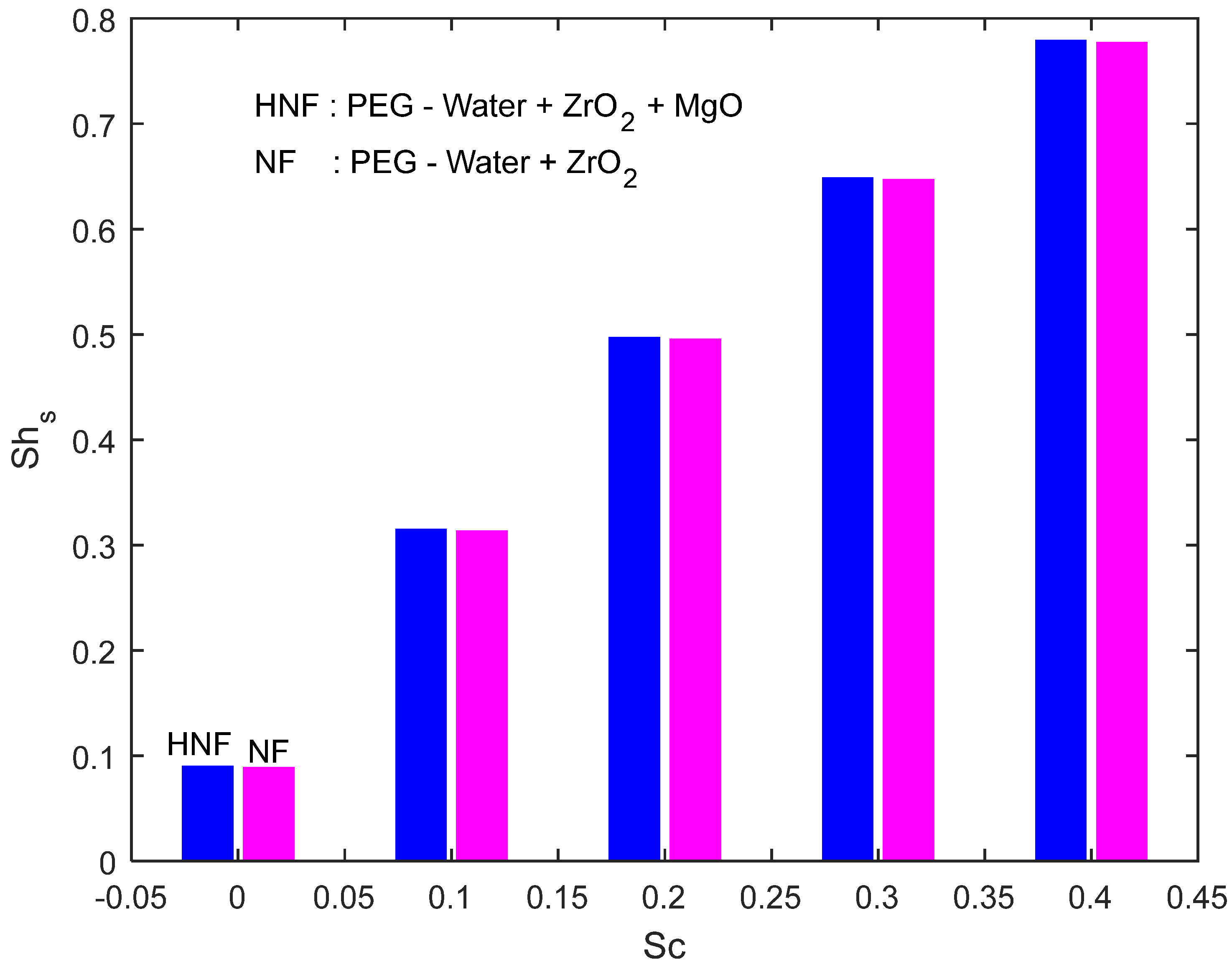
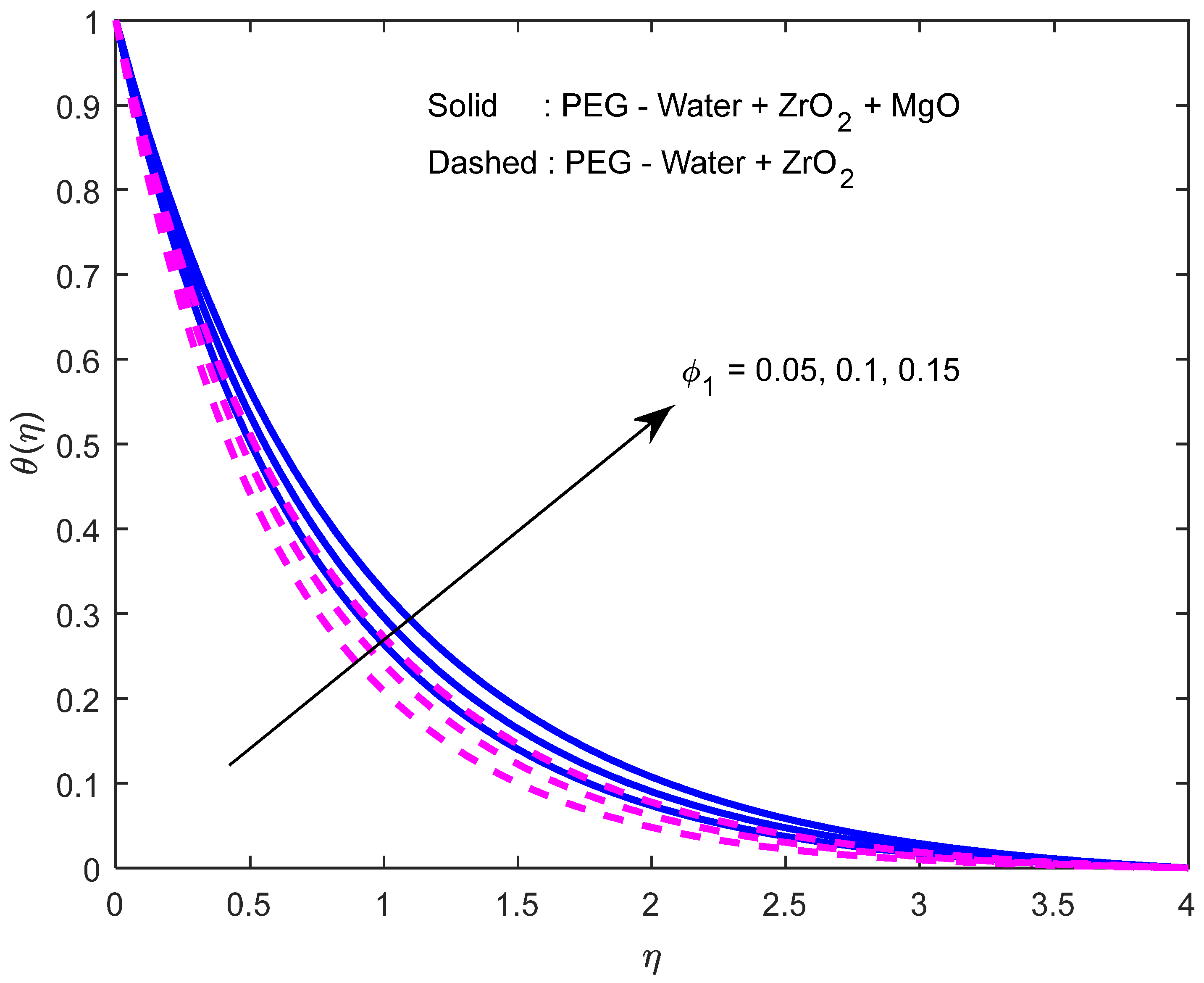
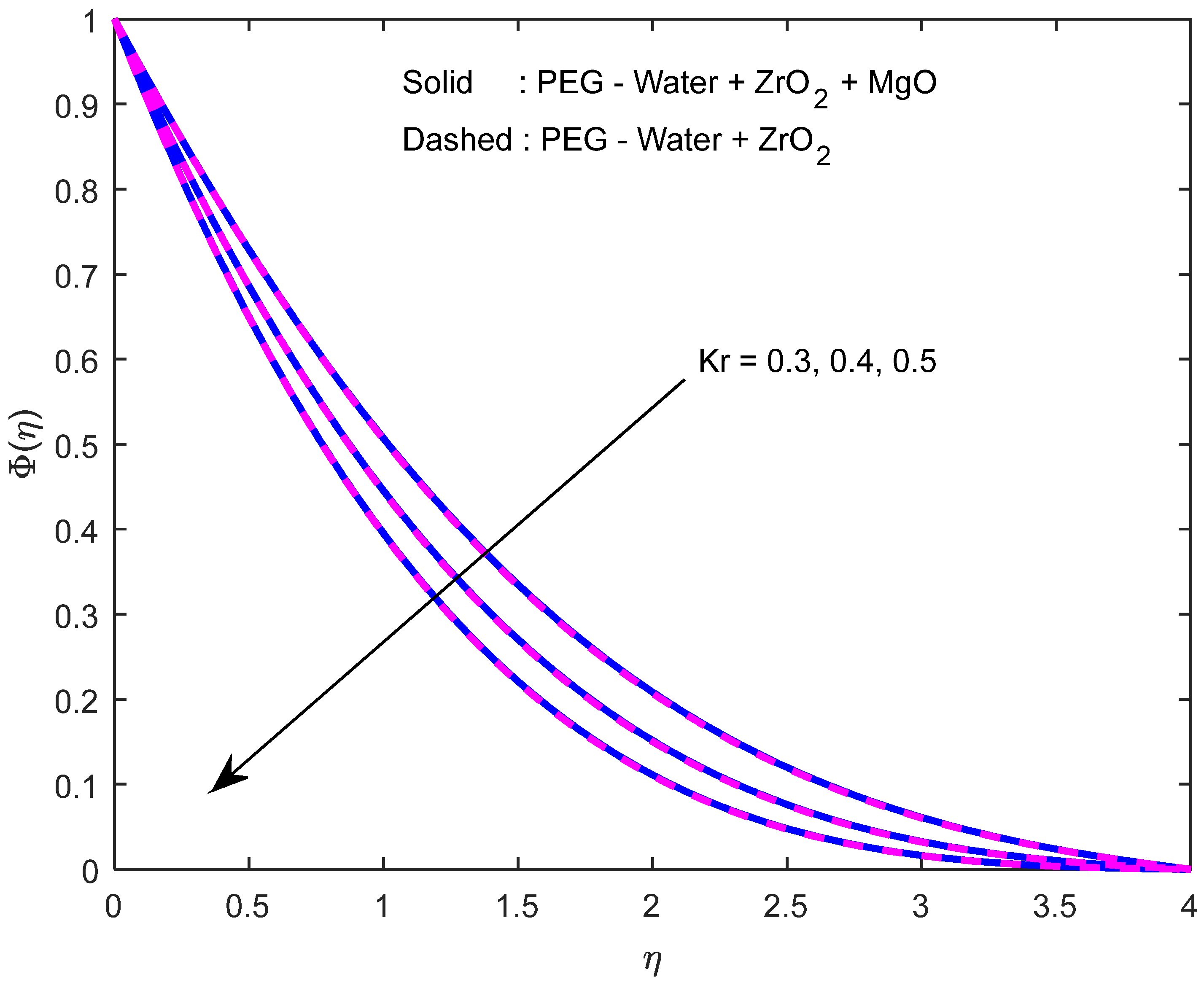
- It was revealed that increasing and speeds up mass transfer rate. When chemical reaction parameter takes input in the range , increment rates in mass transfer rate were 1.497214 (i.e., 149.7214%) (in the case of hybrid nanofluid) and 1.496621 (i.e., 149.6621%) (in the case of nanofluid) whereas increment rates in the same against were 1.711774 (i.e., 171.1774%) (in the case of hybrid nanofluid) and 1.710781 (i.e., 171.0781%) (in the case of nanofluid) with the range
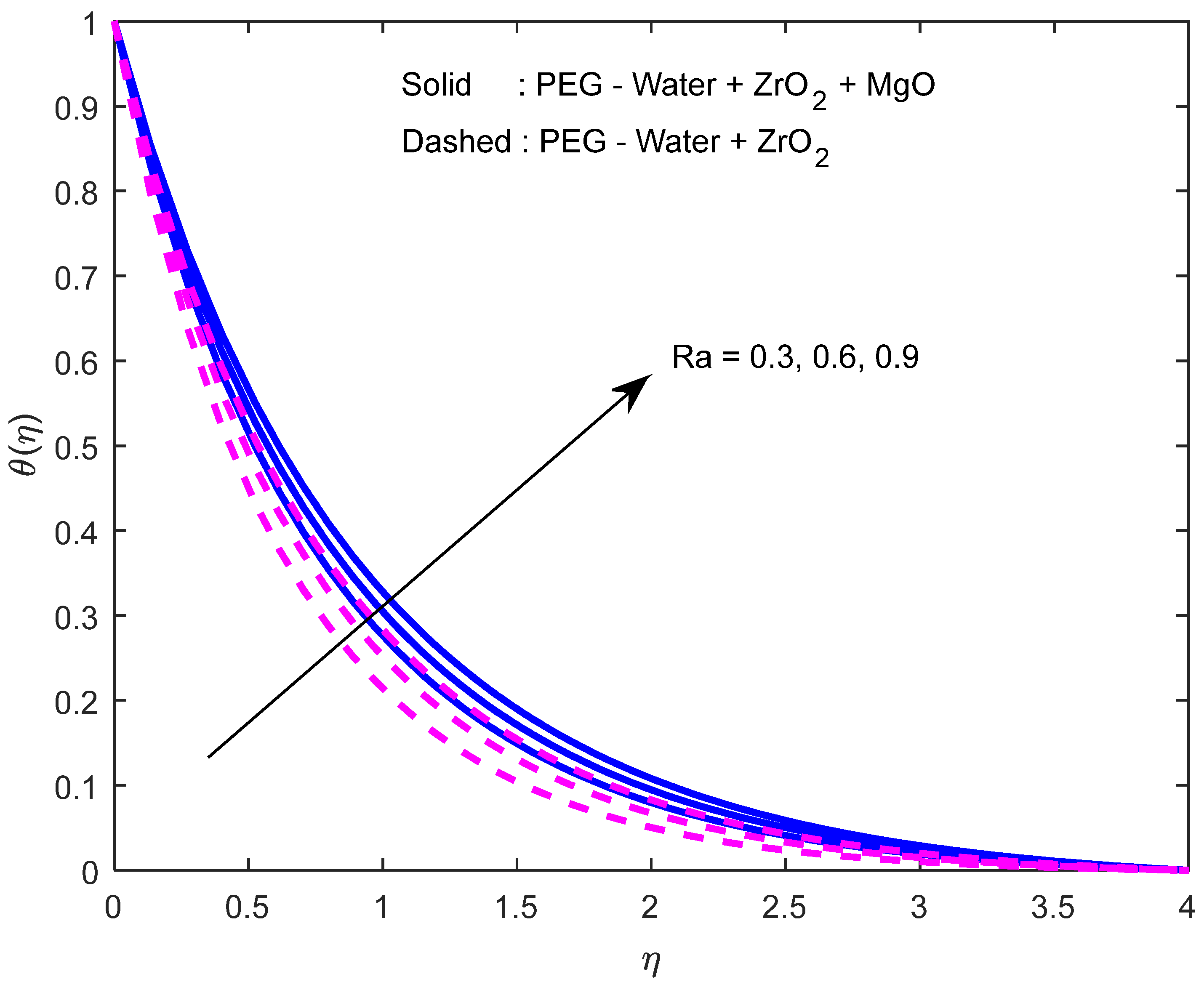
- Fluid temperature rises as thermal radiation rises.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Velocity components in directions | |
| Dimensional fluid pressure | |
| Dimensionless fluid pressure | |
| Dynamic viscosity | |
| Density | |
| Electrical conductivity | |
| Fluid temperature | |
| Thermal conductivity | |
| Stefan–Boltzmann constant | |
| Specific heat capacity | |
| Mean absorption coefficient | |
| Molecular diffusivity | |
| Dimensionless radius of curvature | |
| Rate of chemical reaction | |
| Permeability of the porous surface | |
| Fluid velocity | |
| Radiation parameter | |
| Fluid temperature | |
| Fluid concentration | |
| Prandtl number | |
| Magnetic field constraint | |
| Eckert number | |
| Dimensionless suction/injection parameter | |
| Order of chemical reaction | |
| Dimensional concentration | |
| Shrinking parameter | |
| Chemical reaction parameter | |
| Schmidt number | |
| Similarity variable | |
| Subscripts | |
| Fluid | |
| Mono nanofluid | |
| Hybrid nanofluid | |
| Nanomaterials (I, II) | |
References
- Ibrahim, F.S.; Hady, F.M. Mixed convection-radiation interaction in boundary-layer flow over horizontal surfaces. Astrophys. Space Sci. 1990, 168, 263–276. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Mishra, S.R.; Abbas, T.; Rashidi, M.M. A mathematical model of MHD nanofluid flow having gyrotactic microorganisms with thermal radiation and chemical reaction effects. Neural Comput. Appl. 2018, 30, 1237–1249. [Google Scholar] [CrossRef]
- Madaki, A.; Roslan, R.; Rusiman, M.; Raju, C.S.K. Analytical and numerical solutions of squeezing unsteady Cu and TiO2-nanofluid flow in the presence of thermal radiation and heat generation/absorption. Alex. Eng. J. 2018, 57, 1033–1040. [Google Scholar] [CrossRef]
- Koriko, O.K.; Animasaun, I.L.; Reddy, M.G.; Sandeep, N. Scrutinization of thermal stratification, nonlinear thermal radiation and quartic autocatalytic chemical reaction effects on the flow of three-dimensional Eyring-Powell alumina-water nanofluid. Multidiscip. Model. Mater. Struct. 2018, 14, 261–283. [Google Scholar] [CrossRef]
- Besthapu, P.; Haq, R.U.; Bandari, S.; Al-Mdallal, Q.M. Thermal radiation and slip effects on MHD stagnation point flow of non-Newtonian nanofluid over a convective stretching surface. Neural Comput. Appl. 2017, 31, 207–217. [Google Scholar] [CrossRef]
- Kotha, G.; Kukkamalla, K.; Ibrahim, S. Effect of thermal radiation on engine oil nanofluid flow over a permeable wedge under convective heating. Multidiscip. Model. Mater. Struct. 2019, 15, 187–205. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Waqas, M.; Seyyedi, S.M.; Hashemi-Tilehnoee, M.; Ganji, D.D. Numerical simulation for thermal radiation and porous medium characteristics in flow of CuO-H2O nanofluid. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 1–13. [Google Scholar] [CrossRef]
- Shit, G.C.; Mandal, S. Entropy Analysis on unsteady MHD flow of casson nanofluid over a stretching vertical plate with thermal radiation effect. Int. J. Appl. Comput. Math. 2019, 6, 2. [Google Scholar] [CrossRef]
- Raza, J. Thermal radiation and slip effects on magnetohydrodynamic (MHD) stagnation point flow of Casson fluid over a convective stretching sheet. Propuls. Power Res. 2019, 8, 138–146. [Google Scholar] [CrossRef]
- Pordanjani, A.H.; Aghakhani, S.; Karimipour, A.; Afrand, M.; Goodarzi, M. Investigation of free convection heat transfer and entropy generation of nanofluid flow inside a cavity affected by magnetic field and thermal radiation. J. Therm. Anal. 2019, 137, 997–1019. [Google Scholar] [CrossRef]
- Bilal, M. Micropolar flow of EMHD nanofluid with nonlinear thermal radiation and slip effects. Alex. Eng. J. 2020, 59, 965–976. [Google Scholar] [CrossRef]
- Kumar, B.; Srinivas, S. Unsteady hydromagnetic flow of Eyring-Powell Nanofluid over an inclined permeable stretching sheet with joule heating and thermal radiation. J. Appl. Comput. Mech. 2020, 6, 259–270. [Google Scholar]
- Aziz, A.; Shams, M. Entropy generation in MHD Maxwell nanofluid flow with variable thermal conductivity, thermal radiation, slip conditions, and heat source. AIP Adv. 2020, 10, 015038. [Google Scholar] [CrossRef] [Green Version]
- Reddy, P.S.; Sreedevi, P. Impact of chemical reaction and double stratification on heat and mass transfer characteristics of nanofluid flow over porous stretching sheet with thermal radiation. Int. J. Ambient Energy 2020, 43, 1626–1636. [Google Scholar] [CrossRef]
- Hosseinzadeh, K.; Roghani, S.; Mogharrebi, A.R.; Asadi, A.; Ganji, D.D. Optimization of hybrid nanoparticles with mixture fluid flow in an octagonal porous medium by effect of radiation and magnetic field. J. Therm. Anal. 2020, 143, 1413–1424. [Google Scholar] [CrossRef]
- Raju, S.S.K.; Babu, M.J.; Raju, C.S.K. Irreversibility Analysis in Hybrid Nanofluid Flow between Two Rotating Disks with Activation Energy and Cross-Diffusion Effects. Chin. J. Phys. 2021, 72, 499–529. [Google Scholar] [CrossRef]
- Revathi, G.; Sajja, V.S.; Babu, M.J.; Raju, C.S.K.; Shehzad, S.A.; Bapanayya, C. Entropy optimization in hybrid radiative nanofluid (CH3 OH+ SiO2 + Al2O3) flow by a curved stretching sheet with cross-diffusion effects. Appl. Nanosci. 2021, 1–15. [Google Scholar] [CrossRef]
- Alzahrani, H.A.H.; Alsaiari, A.; Madhukesh, J.K.; Kumar, R.N.; Prasanna, B.M. Effect of thermal radiation on heat transfer in plane wall jet flow of Casson nanofluid with suction subject to a slip boundary condition. Waves Random Complex Media 2022, 1–18. [Google Scholar] [CrossRef]
- Fetecau, C.; Shah, N.A.; Vieru, D. General solutions for hydromagnetic free convection flow over an infinite plate with Newtonian heating, mass diffusion and chemical reaction. Commun. Theor. Phys. 2017, 68, 768. [Google Scholar] [CrossRef]
- Famakinwa, O.A.; Koriko, O.K.; Adegbie, K.S.; Omowaye, A.J. Effects of viscous variation, thermal radiation, and Arrhenius reaction: The case of MHD nanofluid flow containing gyrotactic microorganisms over a convectively heated surface. Partial Differ. Equ. Appl. Math. 2022, 5, 100232. [Google Scholar] [CrossRef]
- Soundalgekar, V. Viscous dissipation effects on unsteady free convective flow past an infinite, vertical porous plate with constant suction. Int. J. Heat Mass Transf. 1972, 15, 1253–1261. [Google Scholar] [CrossRef]
- Jusoh, R.; Nazar, R.; Pop, I. Magnetohydrodynamic boundary layer flow and heat transfer of nanofluids past a bidirectional exponential permeable stretching/shrinking sheet with viscous dissipation effect. J. Heat Transf. 2018, 141, 012406. [Google Scholar] [CrossRef]
- Maleki, H.; Safaei, M.R.; Togun, H.; Dahari, M. Heat transfer and fluid flow of pseudo-plastic nanofluid over a moving permeable plate with viscous dissipation and heat absorption/generation. J. Therm. Anal. 2018, 135, 1643–1654. [Google Scholar] [CrossRef]
- Kumar, K.A.; Sugunamma, V.; Sandeep, N. Influence of viscous dissipation on MHD flow of micropolar fluid over a slendering stretching surface with modified heat flux model. J. Therm. Anal. 2019, 139, 3661–3674. [Google Scholar] [CrossRef]
- Afridi, M.; Qasim, M. Second law analysis of Blasius flow with nonlinear Rosseland thermal radiation in the presence of viscous dissipation. Propuls. Power Res. 2019, 8, 234–242. [Google Scholar] [CrossRef]
- Ibrahim, W.; Tulu, A. Magnetohydrodynamic (MHD) boundary layer flow past a wedge with heat transfer and viscous effects of nanofluid embedded in porous media. Math. Probl. Eng. 2019, 2019, 1–12. [Google Scholar] [CrossRef]
- Madhukesh, J.K.; Ramesh, G.K.; Roopa, G.S.; Prasannakumara, B.C.; Shah, N.A.; Yook, S.J. 3D Flow of Hybrid Nanomaterial through a Circular Cylinder: Saddle and Nodal Point Aspects. Mathematics 2022, 10, 1185. [Google Scholar] [CrossRef]
- Dero, S.; Rohni, A.M.; Saaban, A. Effects of the viscous dissipation and chemical reaction on Casson nanofluid flow over the permeable stretching/shrinking sheet. Heat Transf. 2020, 49, 1736–1755. [Google Scholar] [CrossRef]
- Mishra, A.K.; Pattnaik, P.K.; Mishra, S.R.; Senapati, N. Dissipative heat energy on Cu and Al2O3 ethylene–glycol-based nanofluid flow over a heated semi-infinite vertical plate. J. Therm. Anal. 2020, 145, 129–137. [Google Scholar] [CrossRef]
- Kumar, M.D.; Raju, C.S.K.; Sajjan, K.; El-Zahar, E.R.; Shah, N.A. Linear and quadratic convection on 3D flow with transpiration and hybrid nanoparticles. Int. Commun. Heat Mass Transfer 2022, 134, 105995. [Google Scholar] [CrossRef]
- Gayatri, M.; Reddy, K.J.; Babu, M.J. Slip flow of Carreau fluid over a slendering stretching sheet with viscous dissipation and Joule heating. SN Appl. Sci. 2020, 2, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Chiranjeevi, B.; Valsamy, P.; Vidyasagar, G. Radiation absorption on MHD free convective laminar flow over a moving vertical porous plate, viscous dissipation and chemical reaction with suction under the influence of transverses magnetic field. Mater. Today Proc. 2020, 42, 1559–1569. [Google Scholar] [CrossRef]
- Abbas, S.; Khan, M.I.; Kadry, S.; Khan, W.; Israr-Ur-Rehman, M.; Waqas, M. Fully developed entropy optimized second order velocity slip MHD nanofluid flow with activation energy. Comput. Methods Programs Biomed. 2020, 190, 105362. [Google Scholar] [CrossRef] [PubMed]
- Gopal, D.; Saleem, S.; Jagadha, S.; Ahmad, F.; Almatroud, A.O.; Kishan, N. Numerical analysis of higher order chemical reaction on electrically MHD nanofluid under influence of viscous dissipation. Alex. Eng. J. 2020, 60, 1861–1871. [Google Scholar] [CrossRef]
- Venkateswarlu, B.; Narayana, P.V.S. Cu-Al2O3/H2O hybrid nanofluid flow past a porous stretching sheet due to temperatue-dependent viscosity and viscous dissipation. Heat Transfer 2021, 50, 432–449. [Google Scholar] [CrossRef]
- Tassaddiq, A. Impact of Cattaneo-Christov heat flux model on MHD hybrid nano-micropolar fluid flow and heat transfer with viscous and joule dissipation effects. Sci. Rep. 2021, 11, 67. [Google Scholar] [CrossRef]
- Khan, M.I.; Hafeez, M.U.; Hayat, T.; Khan, M.I.; Alsaedi, A. Magneto rotating flow of hybrid nanofluid with entropy generation. Comput. Methods Programs Biomed. 2020, 183, 105093. [Google Scholar] [CrossRef]
- Ramesh, G.; Madhukesh, J.; Das, R.; Shah, N.A.; Yook, S.-J. Thermodynamic activity of a ternary nanofluid flow passing through a permeable slipped surface with heat source and sink. Waves Random Complex Media 2022, 1–21. [Google Scholar] [CrossRef]
- Shah, N.A.; Yook, S.-J.; Tosin, O. Analytic simulation of thermophoretic second grade fluid flow past a vertical surface with variable fluid characteristics and convective heating. Sci. Rep. 2022, 12, 5445. [Google Scholar] [CrossRef]
- Acharya, N.; Mabood, F. On the hydrothermal features of radiative Fe3O4–graphene hybrid nanofluid flow over a slippery bended surface with heat source/sink. J. Therm. Anal. 2020, 143, 1273–1289. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Stability analysis of MHD hybrid nanofluid flow over a stretching/shrinking sheet with quadratic velocity. Alex. Eng. J. 2020, 60, 915–926. [Google Scholar] [CrossRef]
- Gul, T.; Bilal, M.; Alghamdi, W.; Asjad, M.I.; Abdeljawad, T. Hybrid nanofluid flow within the conical gap between the cone and the surface of a rotating disk. Sci. Rep. 2021, 11, 1180. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Xu, Y.-P.; Qahiti, R.; Jafaryar, M.; Alazwari, M.A.; Abu-Hamdeh, N.H.; Issakhov, A.; Selim, M.M. Simulation of hybrid nanofluid flow within a microchannel heat sink considering porous media analyzing CPU stability. J. Pet. Sci. Eng. 2021, 208, 109734. [Google Scholar] [CrossRef]
- Gul, H.; Ramzan, M.; Nisar, K.S.; Mohamed, R.N.; Ghazwani, H.A.S. Performance-based comparison of Yamada–Ota and Hamilton–Crosser hybrid nanofluid flow models with magnetic dipole impact past a stretched surface. Sci. Rep. 2022, 12, 29. [Google Scholar] [CrossRef]
- Gumber, P.; Yaseen, M.; Rawat, S.K.; Kumar, M. Heat transfer in micropolar hybrid nanofluid flow past a vertical plate in the presence of thermal radiation and suction/injection effects. Partial Differ. Equ. Appl. Math. 2021, 5, 100240. [Google Scholar] [CrossRef]
- Abbas, Z.; Naveed, M.; Sajid, M. Hydromagnetic slip flow of nanofluid over a curved stretching surface with heat generation and thermal radiation. J. Mol. Liq. 2016, 215, 756–762. [Google Scholar] [CrossRef]
- Dawar, A.; Wakif, A.; Thumma, T.; Shah, N.A. Towards a new MHD non-homogeneous convective nanofluid flow model for simulating a rotating inclined thin layer of sodium alginate-based Iron oxide exposed to incident solar energy. Int. Commun. Heat Mass Transf. 2021, 130, 105800. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid Nanofluid Flow Past a Permeable Moving Thin Needle. Mathematics 2020, 8, 612. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Effect of thermal radiation on unsteady mixed convection flow and heat transfer over a porous stretching surface in porous medium. Int. J. Heat Mass Transf. 2009, 52, 3261–3265. [Google Scholar] [CrossRef]







| S.No. | Polyethylene Glycol–Water Mixture | |||
|---|---|---|---|---|
| 1 | 1110 | 5680 | 3560 | |
| 2 | 3354 | 502 | 955 | |
| 3 | 0.3712 | 1.7 | 45 | |
| 4 | - | - |
| Pr | Mukhopadhyay [49] | Present Study |
|---|---|---|
| 0.01 | 0.02944 | 0.029440 |
| 0.72 | 1.08855 | 1.088550 |
| 1.00 | 1.33334 | 1.333340 |
| 3.00 | 2.50972 | 2.509720 |
| 0.9941 | 0.003548 | 280.18 | 0.9946 | 0.004816 | 206.52 | |
| −0.9042 | 0.055026 | 16.43 | −0.9027 | 0.055844 | 16.16 | |
| −0.9999 | 0.000029 | 34479.31 | −0.9999 | 0.000029 | 34,479.31 | |
| −0.9580 | 0.012104 | 79.15 | −0.9587 | 0.011907 | 80.52 | |
| 0.9994 | 0.000177 | 5646.33 | 0.9994 | 0.000177 | 5646.33 | |
| 0.9998 | 0.000059 | 16,945.76 | 0.9998 | 0.000059 | 16,945.76 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veeram, G.; Poojitha, P.; Katta, H.; Hemalatha, S.; Babu, M.J.; Raju, C.S.K.; Shah, N.A.; Yook, S.-J. Simulation of Dissipative Hybrid Nanofluid (PEG-Water + ZrO2 + MgO) Flow by a Curved Shrinking Sheet with Thermal Radiation and Higher Order Chemical Reaction. Mathematics 2022, 10, 1706. https://doi.org/10.3390/math10101706
Veeram G, Poojitha P, Katta H, Hemalatha S, Babu MJ, Raju CSK, Shah NA, Yook S-J. Simulation of Dissipative Hybrid Nanofluid (PEG-Water + ZrO2 + MgO) Flow by a Curved Shrinking Sheet with Thermal Radiation and Higher Order Chemical Reaction. Mathematics. 2022; 10(10):1706. https://doi.org/10.3390/math10101706
Chicago/Turabian StyleVeeram, Gopinath, Pasam Poojitha, Harika Katta, Sanakkayala Hemalatha, Macherla Jayachandra Babu, Chakravarthula S. K. Raju, Nehad Ali Shah, and Se-Jin Yook. 2022. "Simulation of Dissipative Hybrid Nanofluid (PEG-Water + ZrO2 + MgO) Flow by a Curved Shrinking Sheet with Thermal Radiation and Higher Order Chemical Reaction" Mathematics 10, no. 10: 1706. https://doi.org/10.3390/math10101706
APA StyleVeeram, G., Poojitha, P., Katta, H., Hemalatha, S., Babu, M. J., Raju, C. S. K., Shah, N. A., & Yook, S.-J. (2022). Simulation of Dissipative Hybrid Nanofluid (PEG-Water + ZrO2 + MgO) Flow by a Curved Shrinking Sheet with Thermal Radiation and Higher Order Chemical Reaction. Mathematics, 10(10), 1706. https://doi.org/10.3390/math10101706








