Abnormality Detection and Failure Prediction Using Explainable Bayesian Deep Learning: Methodology and Case Study with Industrial Data
Abstract
:1. Introduction
1.1. Artificial Intelligence
- (i)
- Machine learning: This is based on deep learning and predictive analytics.
- (ii)
- Natural language processing: This is related to translation, classification, and information extraction.
- (iii)
- Speech: This is visualized as speech to text and text to speech.
- (iv)
- Expert systems: This corresponds to inference engine and knowledge base.
- (v)
- Planning, schedule, optimization: This is associated with reduction (transforming complex planning challenges into other forms such as the Boolean satisfiability problem), classical (completely deterministic planning with one initial state), probabilistic (planning under uncertainty and incomplete information), as well as temporal (planning by the incorporation of duration and concurrency of actions and events).
- (vi)
- Robotic: This considers reactive machine, limited memory, theory of mind, and self-aware.
- (vii)
- Vision: This is based on image recognition and computer/machine vision.
- (i)
- Failures of robustness: The system is subjected to unusual or unforeseen inputs, causing failures.
- (ii)
- Failures of specification: The system is attempting to do something that is subtly different from what the developer anticipated, which might result in surprising behaviors or consequences.
- (iii)
- Failures of assurance: In operational mode, the system cannot be fully supervised or regulated.
- (i)
- Transparency: An AI system mechanism should be understood.
- (ii)
- Reliability and safety: An AI system should work as intended and be safe to use.
- (iii)
- Privacy and security: AI systems should respect confidentiality and be protected.
- (iv)
- Fairness: AI systems should behave equally toward all human beings.
- (v)
- Inclusiveness: AI systems should inspire and promote human participation.
- (vi)
- Accountability: Responsibility measures must be available when the AI system malfunctions.
- (i)
- Justifying the model’s decision, detecting its problems, especially during the trial period of the AI model, strengthening reliability and safety.
- (ii)
- Complying with the regulations, transparency that leads to accountability, enhanced security, and data privacy.
- (iii)
- Helping to understand AI reasoning and decrease problems related to fairness in AI use.
- (iv)
- Assisting practitioners in verifying the required proprieties of the AI system from the developer.
- (v)
- Promoting interactivity and expanding human creativity by discovering new perspectives on the model or the data.
- (vi)
- Allowing resources to be more optimized, avoiding wastage.
- (vii)
- Fostering collaboration between experts, data scientists, users, and stakeholders.
1.2. Research Gaps and Opportunities
- (i)
- Lack of human involvement: Human engagement is crucial for assessing the generated explanation as the latter is meant for them. Furthermore, human–AI cooperation could contribute to the integration of human-related sciences and for the development of interactive AI, where experts and AI systems work hand in hand, providing more assurance in the AI system’s output.
- (ii)
- Explanation evaluation is practically absent: These measures are important for researchers and developers when evaluating explanation quality.
- (iii)
- Insufficiency in uncertainty management: Uncertainty quantification safeguards the system against adversarial examples where false explanations could be generated from unseen, new data. Moreover, it provides users with supplementary confidence in trusting AI methods prediction compared to point estimation statistical models. It is thus inconceivable for a working AI system to be devoid of this feature.
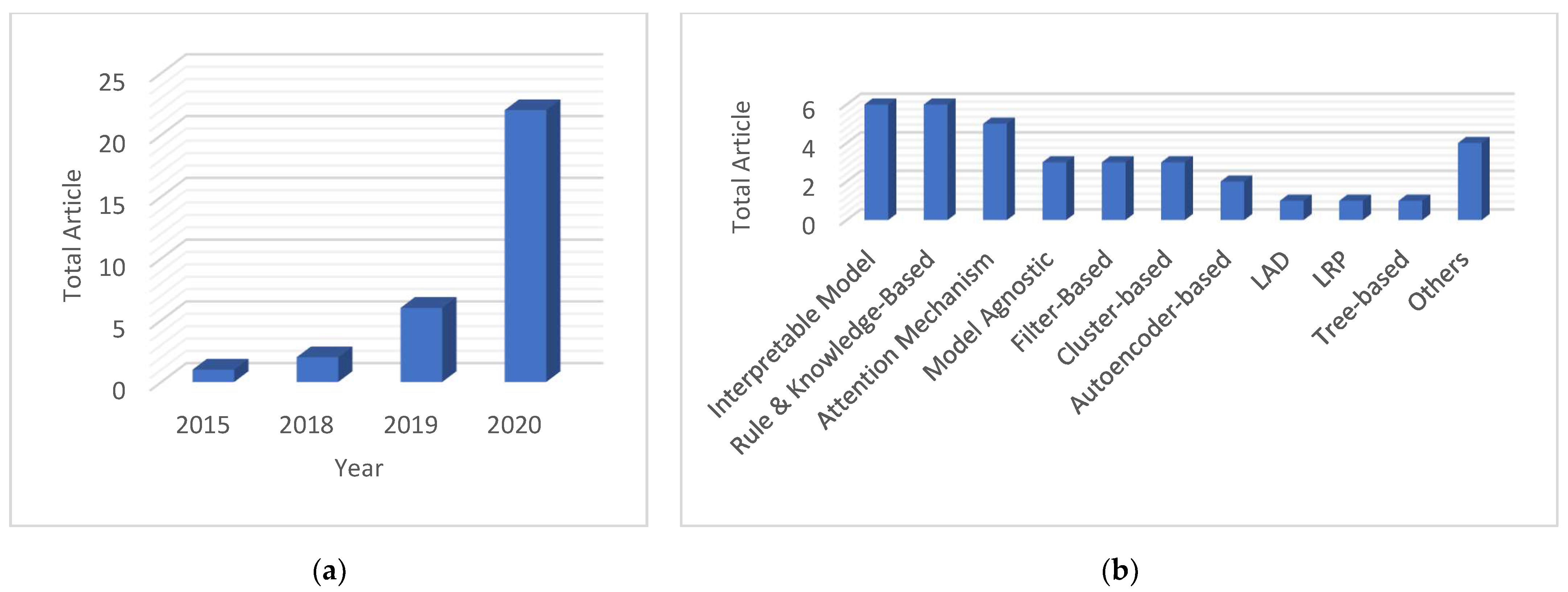
- (i)
- As shown in Figure 2b, model agnostic explainability, layer-wise relevance propagation, and logic analysis of data are less explored, but they possess great potential as they could be used with any black-box model without altering its performance.
- (ii)
- While Shapley additive explanations (SHAP) is an established method and employed in previous works, note that it was not used to improve PHM task’s performance.
- (iii)
- What are the important qualities of explanation issued from XAI methods, and how does one verify them?
- (iv)
- How does one distinguish between explanations of correct predictions and erroneous ones?
- (v)
- What are the other advantages of deep learning uncertainty quantification to promote its incorporation?
- (vi)
- As a flexible method, how can SHAP be exploited to enhance PHM performance?
- (i)
- To combine SHAP and deep learning uncertainty to constitute a wider explanation scope, where the first one explains the decision of the model, while the latter one describes its output confidence.
- (ii)
- To demonstrate the SHAP global explanation’s ability to improve prognostic task’s performance, which was absent from previous works.
- (iii)
- To conduct explanation evaluation, which is clearly deficient from previous PHM-XAI literature.
- (iv)
- To show the potential of deep learning uncertainty as an anomaly indicator for a real-world industrial dataset, which validates its capability.
- (v)
- To minimize deep learning uncertainties for enhancing anomaly detection and prognostic tasks.
- (i)
- To add model agnostic explainability to the collection of PHM-XAI articles, which is still lacking currently.
- (ii)
- To prove the local accuracy and consistency traits of the explanation. The former validates the efficiency property of Shapley values while the latter confirms the additivity and symmetry proprieties of these values.
1.3. Related Works
- (i)
- In the first phase, both knowledge-driven and data-driven fault recognition and root cause analysis, using data from failure mode/effect analysis and fault tree analysis, are employed simultaneously. The data streams and case-specific context data are used as inputs. Faults from the knowledge-driven methods or outliers from the data-driven methods are produced with an interpretation of the detected anomalies and stored inside a knowledge graph.
- (ii)
- In the second phase, the detected anomalies are shown in a dynamic dashboard complete that contains the raw data and interpretation of results, where the user modification is authorized. This is also stored in the knowledge graph.
- (iii)
- Then, in the third phase, the information in the knowledge graph, which are anomalies, the feedback, and all contextual meta-information, are used to improve the techniques of anomaly detection, fault recognition, and root cause analysis of both methods (knowledge-driven and data-driven). The reported accuracy is good for anomaly detection, better than other standalone data-driven methods, partly because of the XAI approach.
2. Methodology
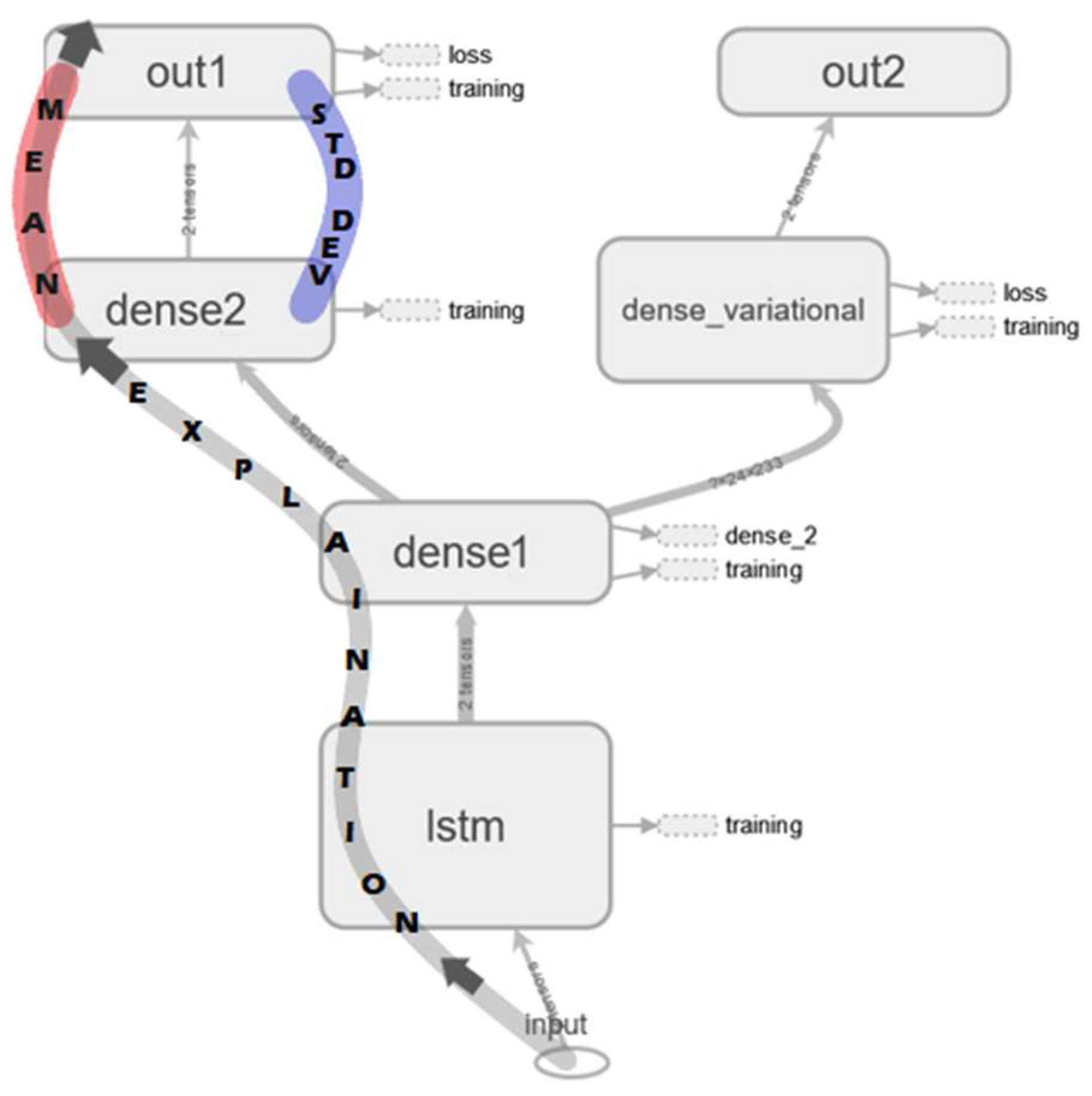
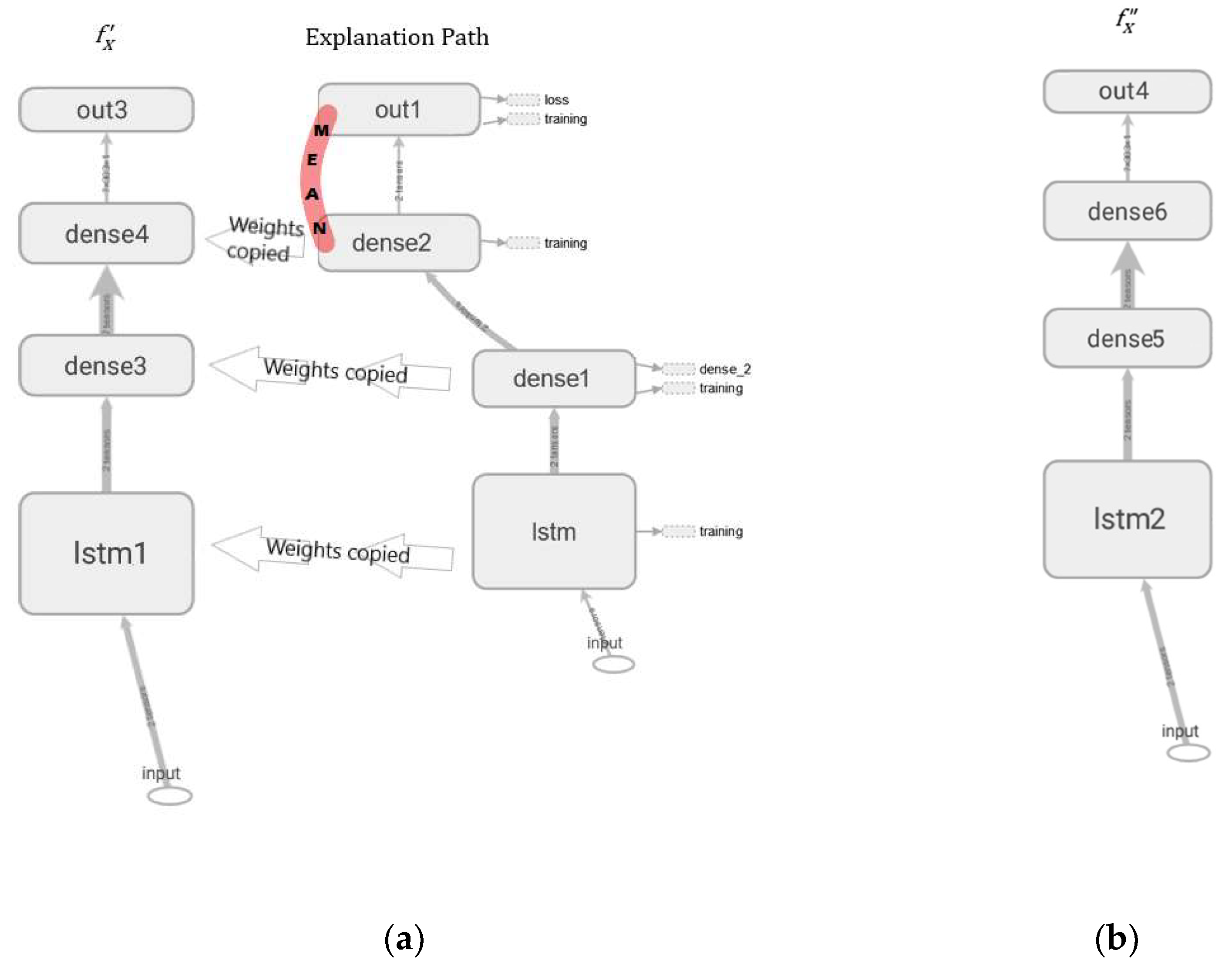
2.1. Multi Output Bayesian LSTM and Uncertainty Quantification Layers
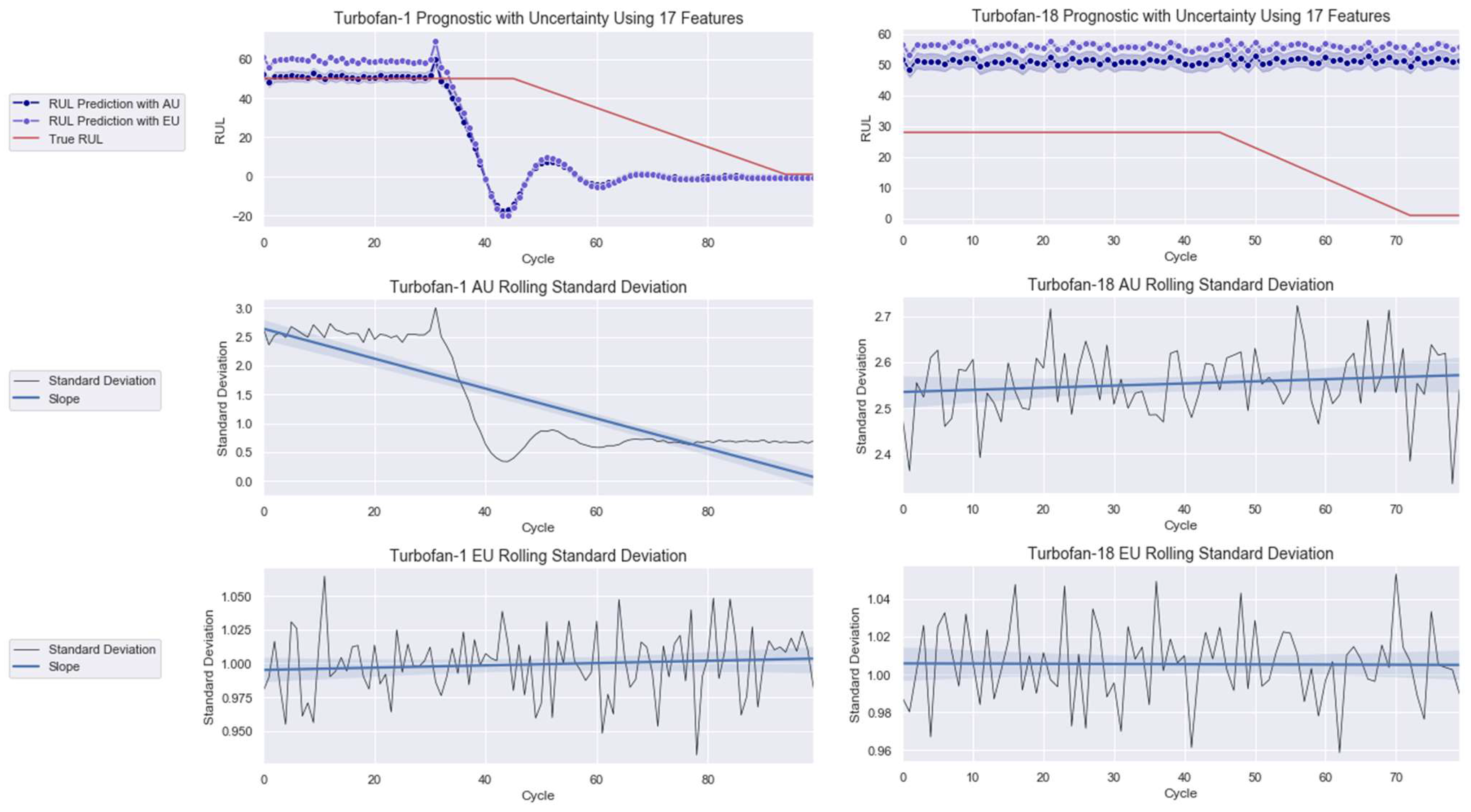
2.2. Minimization of Uncertainties, Anomaly Detection, and RUL Estimation
2.3. Model Performance Assesment and SHAP Explainability
2.4. Explanation Visualization
- (i)
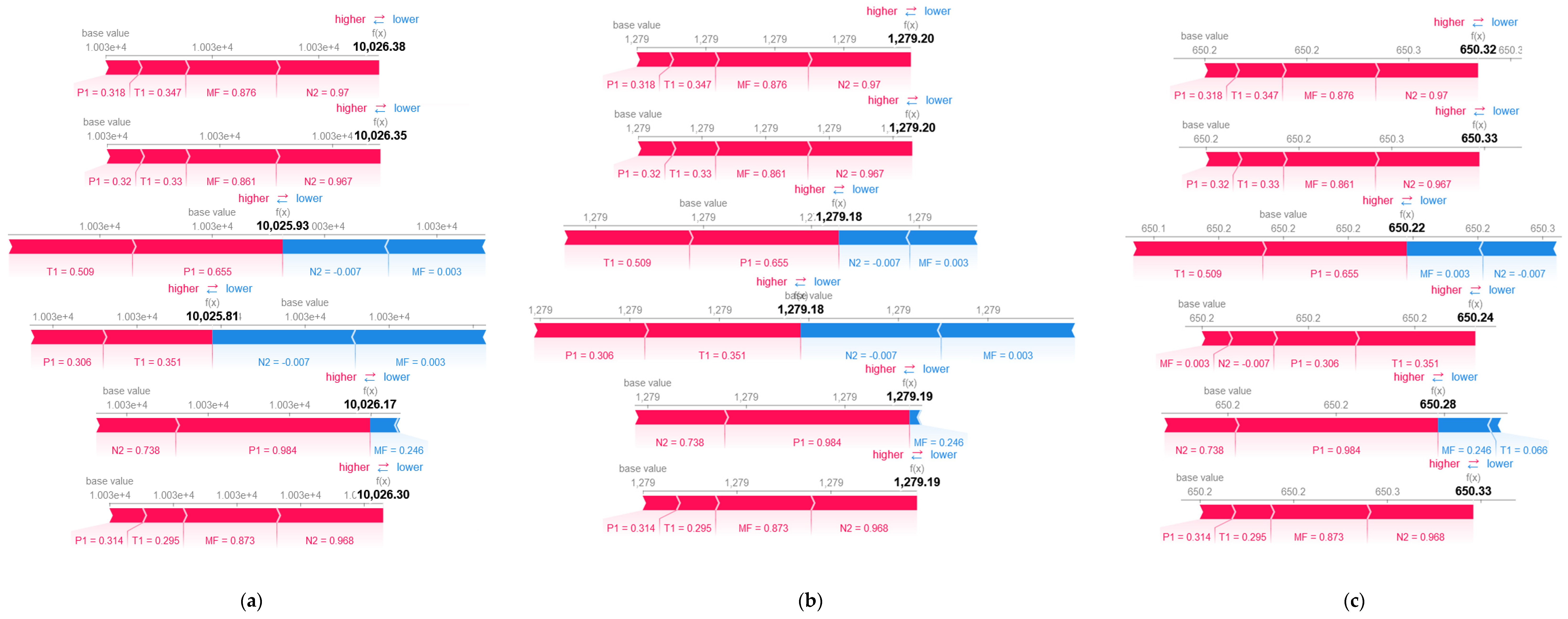
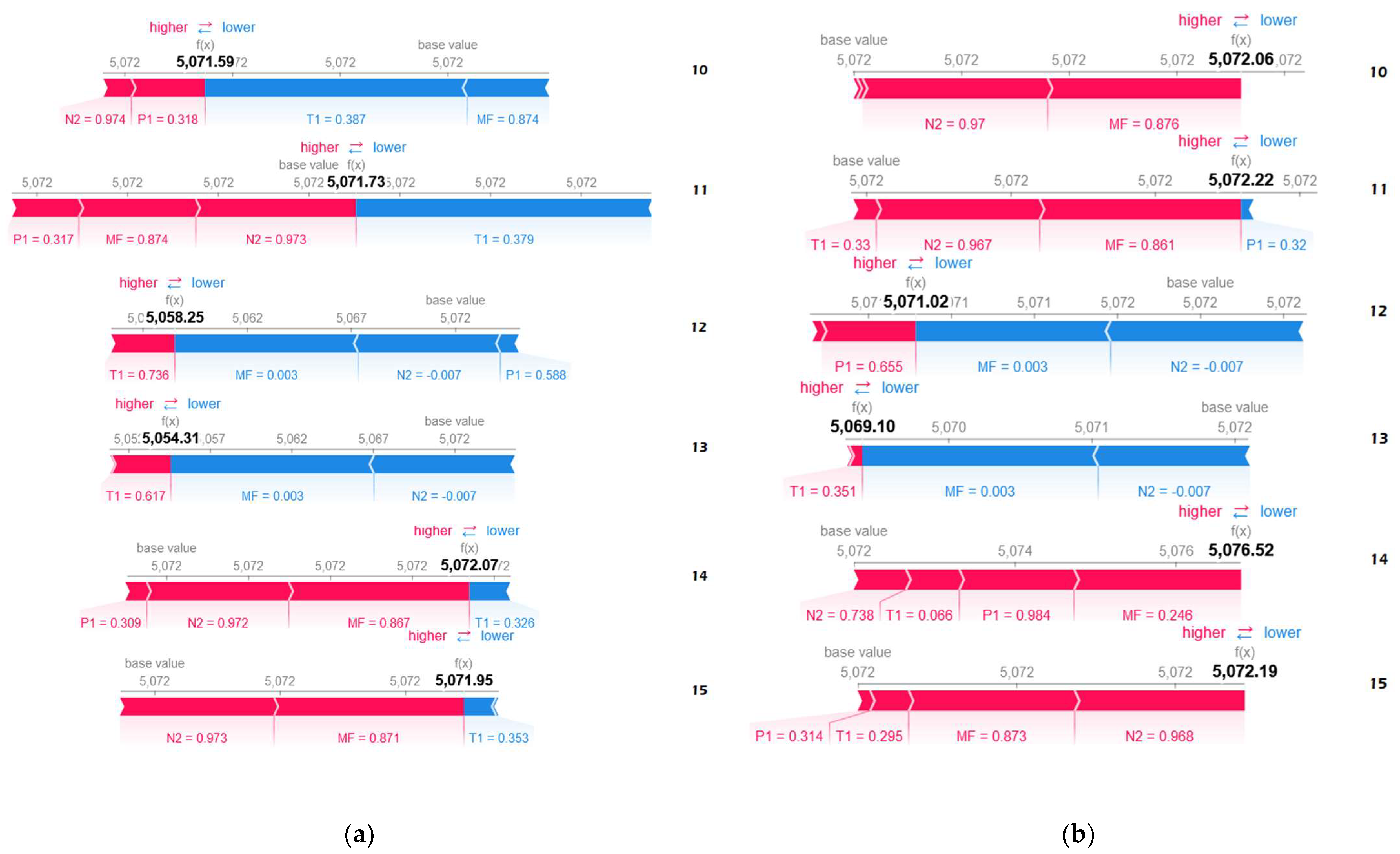
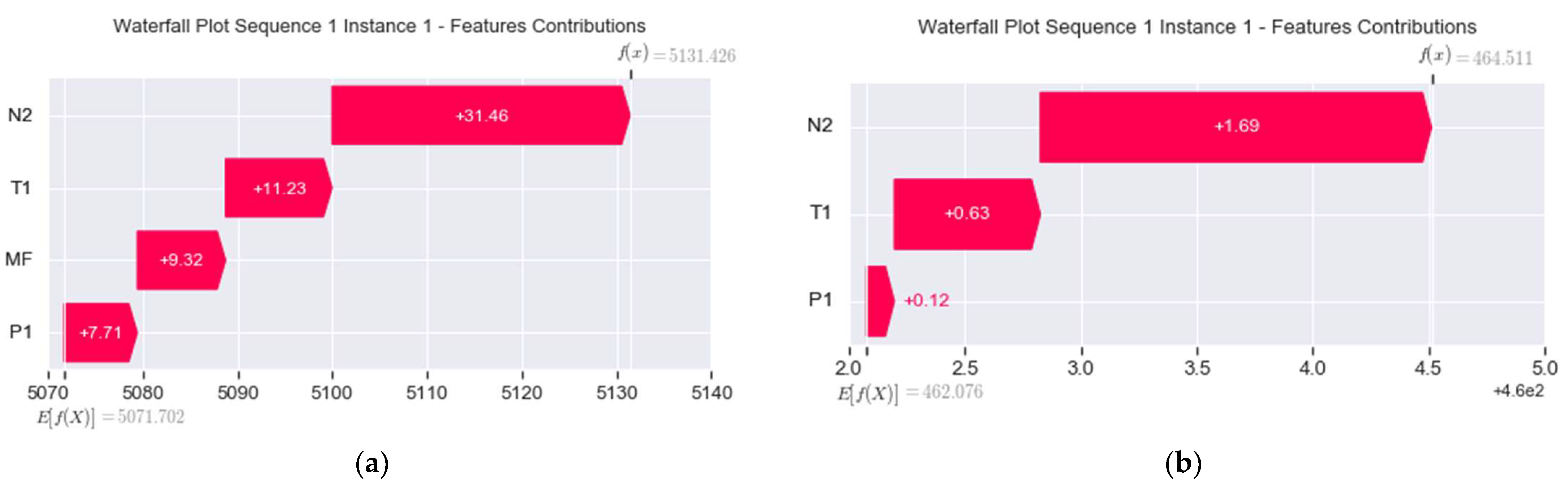
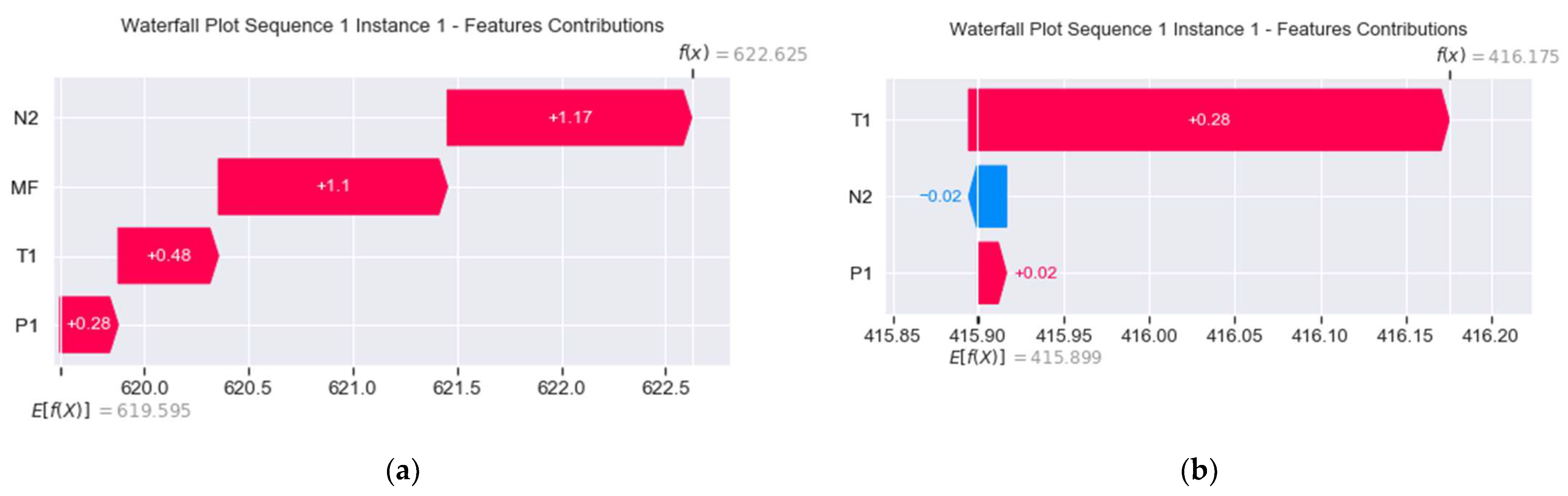
- Local: This is based on force and waterfall plots, which highlight the positive or negative forces of features influencing an instance’s output. On the one hand, the force plot shows successive colored bars, where each bar represents a feature contribution. The length of the colored bar represents its force amplitude or impact on the prediction, and the values associated with the features are the normalized values of the features. The red color means that the feature in question is pushing the prediction positively to increase the output value, , while the blue color means that the feature is dragging the prediction negatively to decrease the output. This plot was utilized for explaining anomalous instances. On the other hand, the waterfall plot arranges the feature contribution values in bar-like form according to their force amplitude, where the highest is in the top position, while the lowest is at the bottom spot, forming a waterfall-like pattern. Note that the color’s meaning is the same as before, that is, the direction of the force is clearly shown. This plot was used to verify the local accuracy and consistency properties of the explanation elaborated in the next subsection.
- (ii)
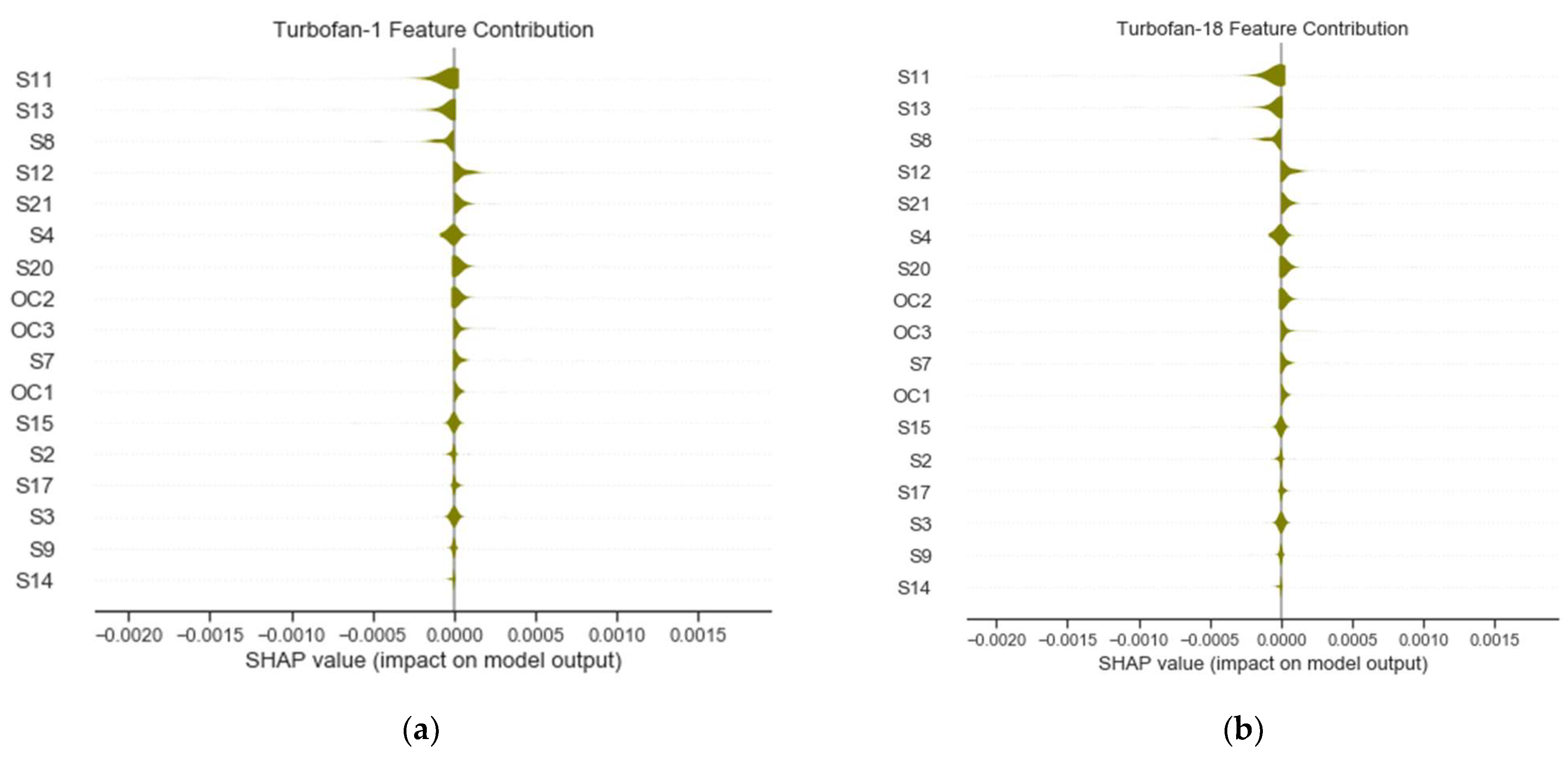
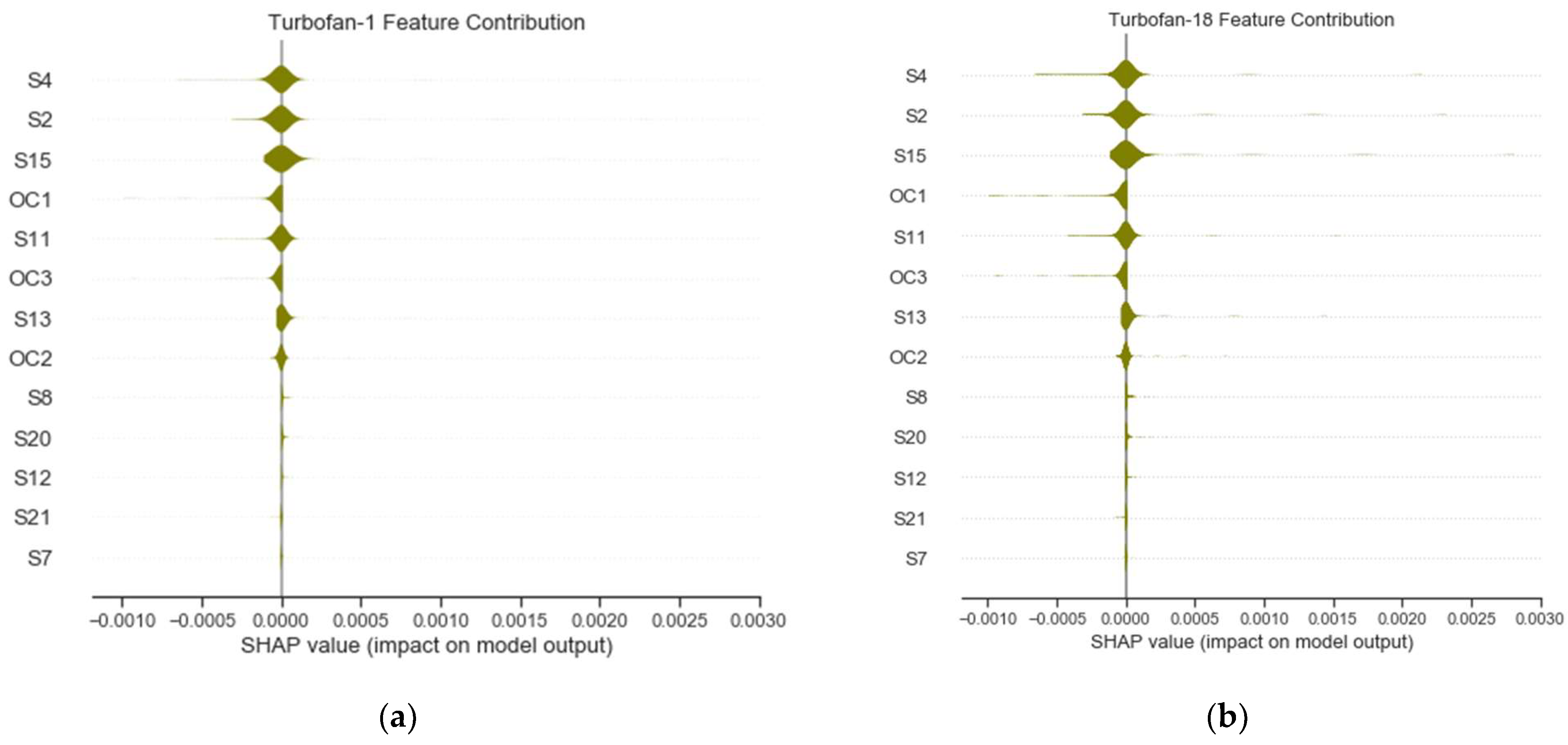
- Global: This is based on a summary plot, which highlights the most contributing features in a sequence. The plot arranges the features according to its contributing power and its forces’ directions. Here, the explanation was exploited to enhance the prognostic accuracy by employing only the most contributing features. The model was initially tested with all the features followed by only using 75% of the best of them. Therefore, the performances of the different settings were analyzed and compared with published results.
3. Results
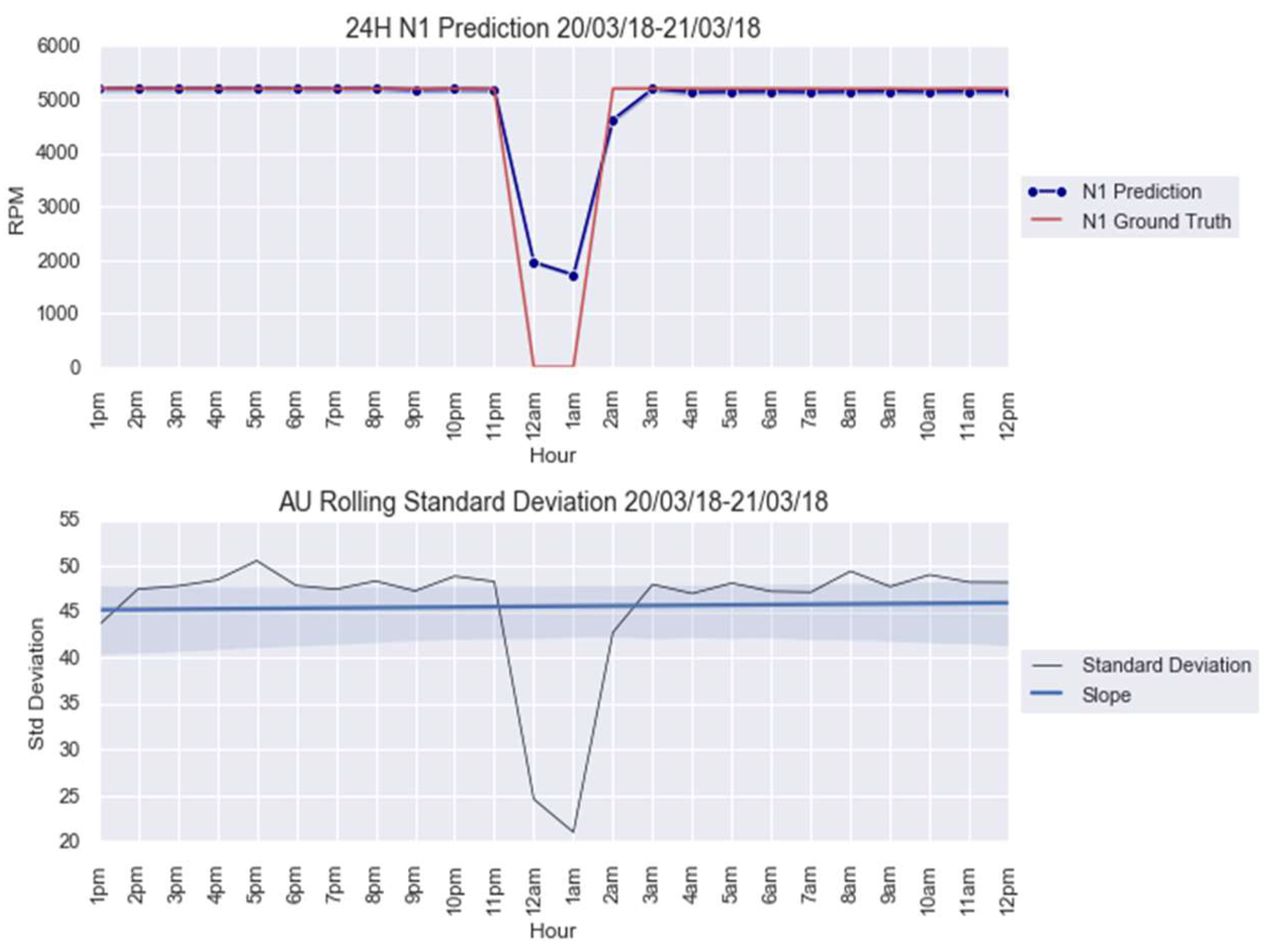
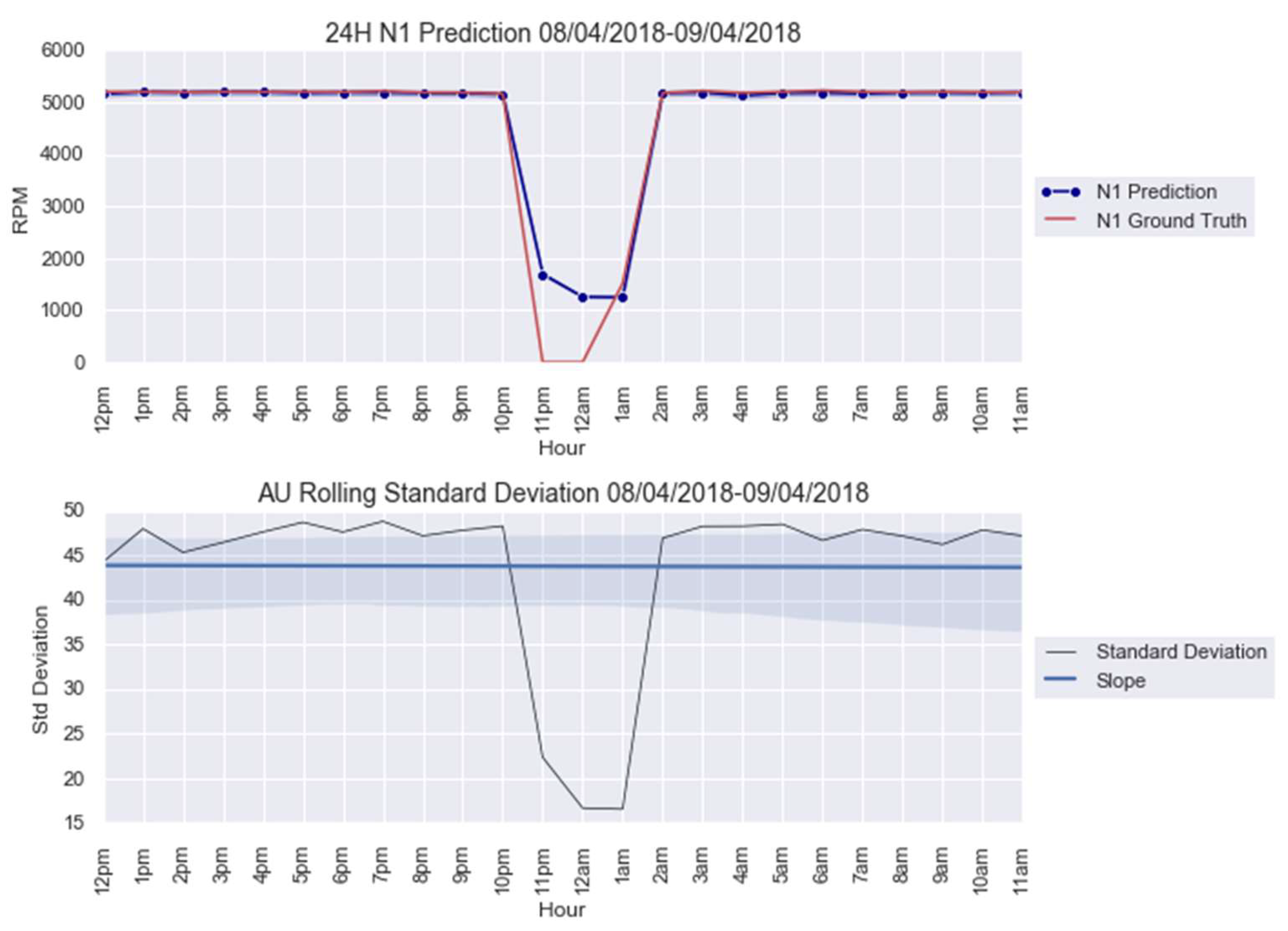
3.1. Case Study 1 from Industry: Real Gas Turbine Anomaly Detection
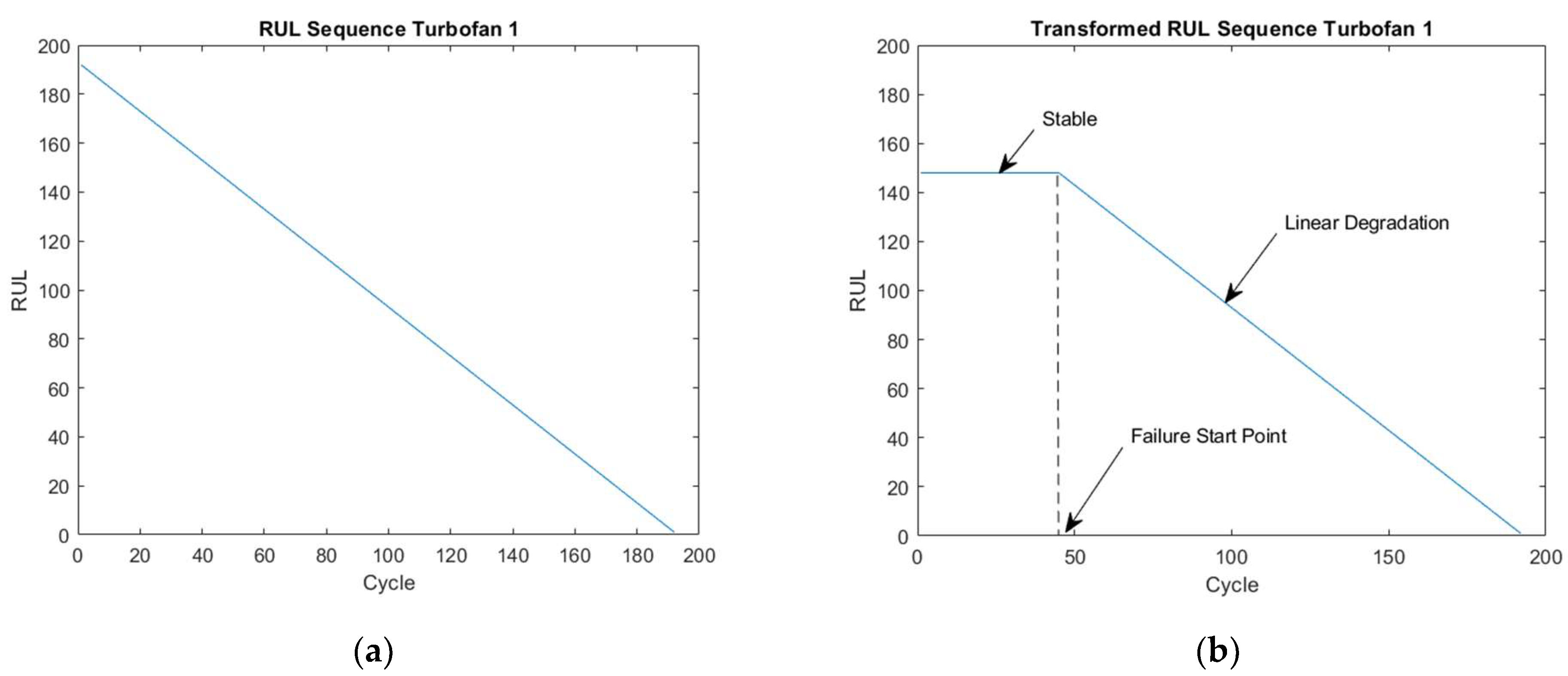
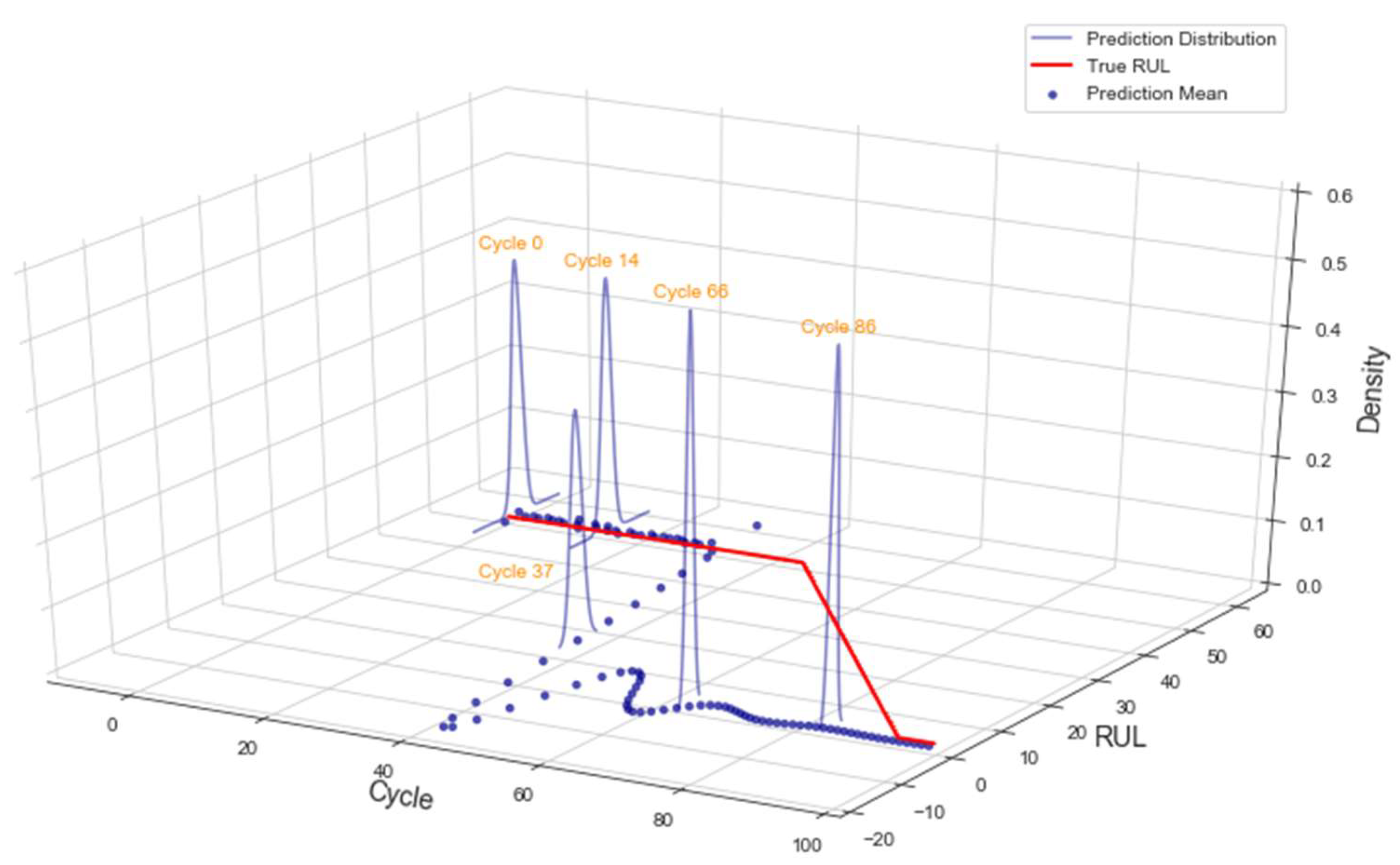
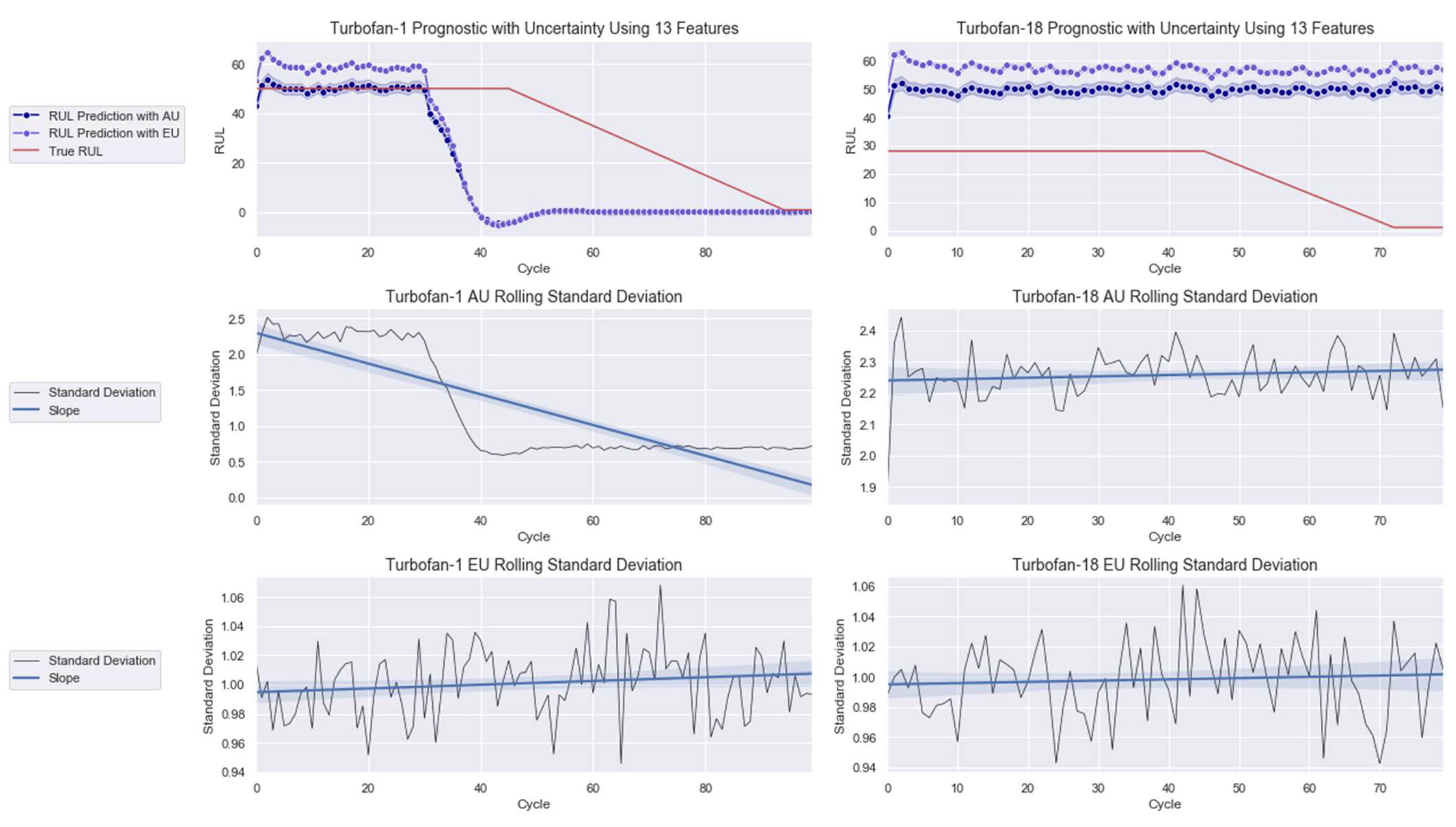
3.2. Case Study 2: Turbofan Engines Failure Prognostic
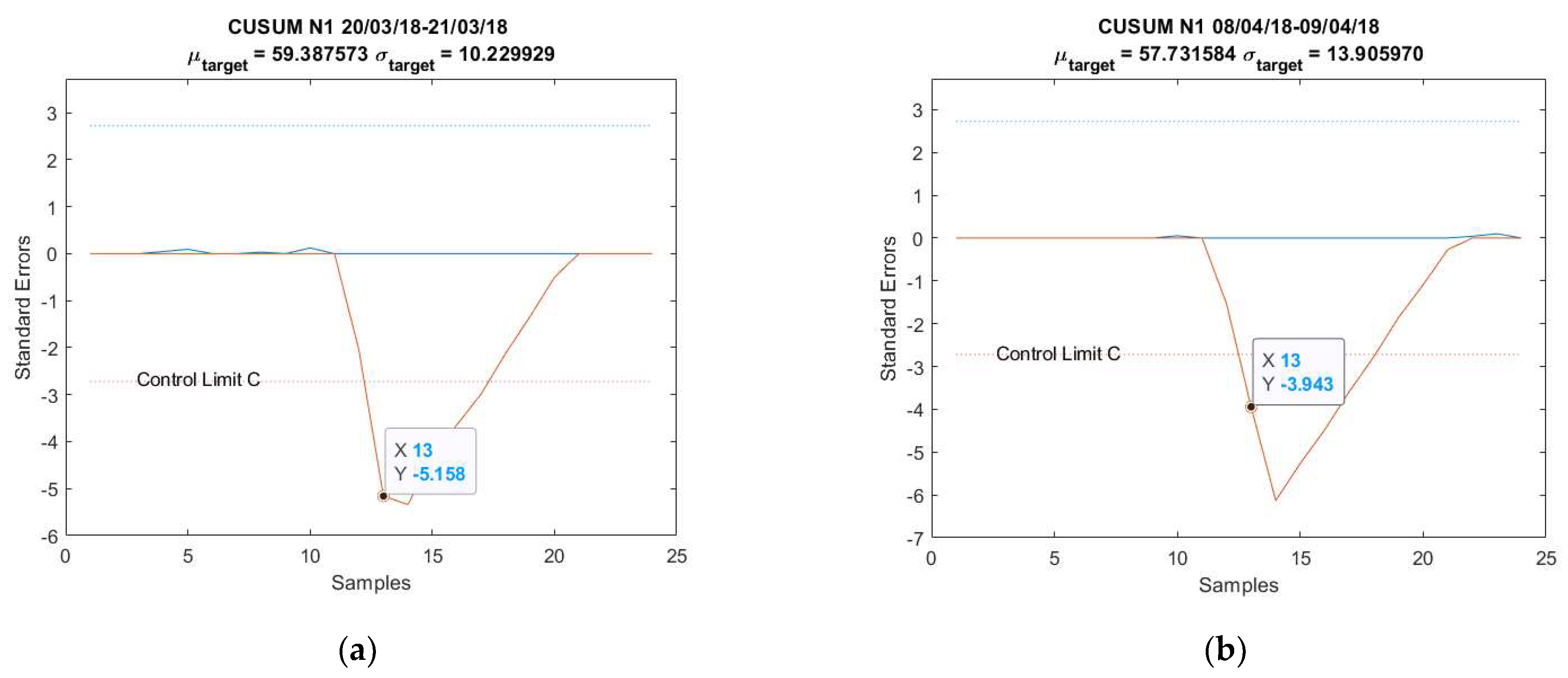
- = 31.46 + 11.23 + 9.32 + 7.71 = 59.72.
- = 5131.426 − 5071.702 = 59.724 ≈ 59.72.
- = 1.69 + 0.63 + 0.12 = 2.44.
- = 464.511 − 462.076 = 2.435 ≈ 2.44.
- = 1.17 + 1.1 + 0.48 + 0.28 = 3.03.
- = 622.625 − 619.595 = 3.03.
- = 0.28 − 0.02 + 0.02 = 0.28.
- = 416.175 − 415.899 = 0.276 ≈ 0.28.
- = 5131.426; = 464.511; − = 4666.915.
- = 622.625; = 416.175; − = 206.45.
- − > − .
- = 9.32; = 1.1, thus > .
4. Discussion
4.1. Anomaly Detection
4.2. Failure Prognostic
4.3. Safeguarding Security and Explanation Evaluation
4.4. Other Aspects
4.5. Impacts of the Current Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameters | Hidden Units | Fully Connected Layer Size | Mini Batch Size | Learning Rate |
|---|---|---|---|---|
| Space | 10 to 1000 | 10 to 500 | 26 to 130 | to |
| Sensor | Description | Unit |
|---|---|---|
| S1 | Total temperature fan inlet | 0R |
| S2 | Total temperature at low pressure compressor (LPC) outlet | 0R |
| S3 | Total temperature at high pressure compressor (HPC) outlet | 0R |
| S4 | Total temperature at low pressure turbine (LPT) outlet | 0R |
| S5 | Pressure at fan inlet | PSIA |
| S6 | Total pressure in bypass-duct | PSIA |
| S7 | Total pressure at HPC outlet | PSIA |
| S8 | Physical fan speed | RPM |
| S9 | Physical core speed | RPM |
| S10 | Engine pressure ratio (P50/P2) | N/A |
| S11 | Static pressure at HPC outlet | PSIA |
| S12 | Ratio of fuel flow to Ps30 | Pps/PSI |
| S13 | Corrected fan speed | RPM |
| S14 | Corrected core speed | RPM |
| S15 | Bypass ratio | N/A |
| S16 | Burner fuel-air ratio | N/A |
| S17 | Bleed enthalpy | N/A |
| S18 | Demanded fan speed | RPM |
| S19 | Demanded corrected fan speed | RPM |
| S20 | HPT coolant bleed | lbm/s |
| S21 | LPT coolant bleed | lbm/s |
Appendix B
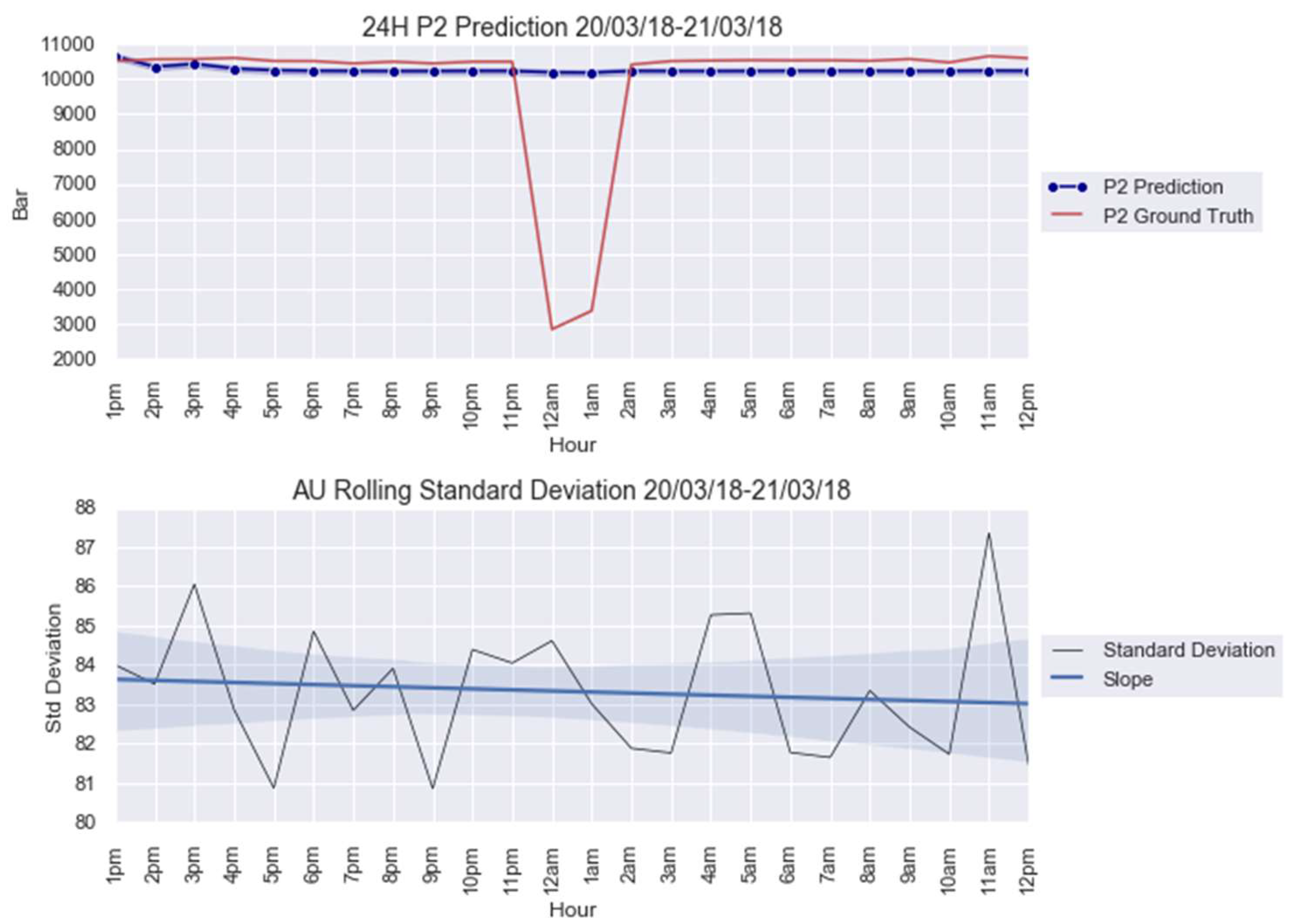
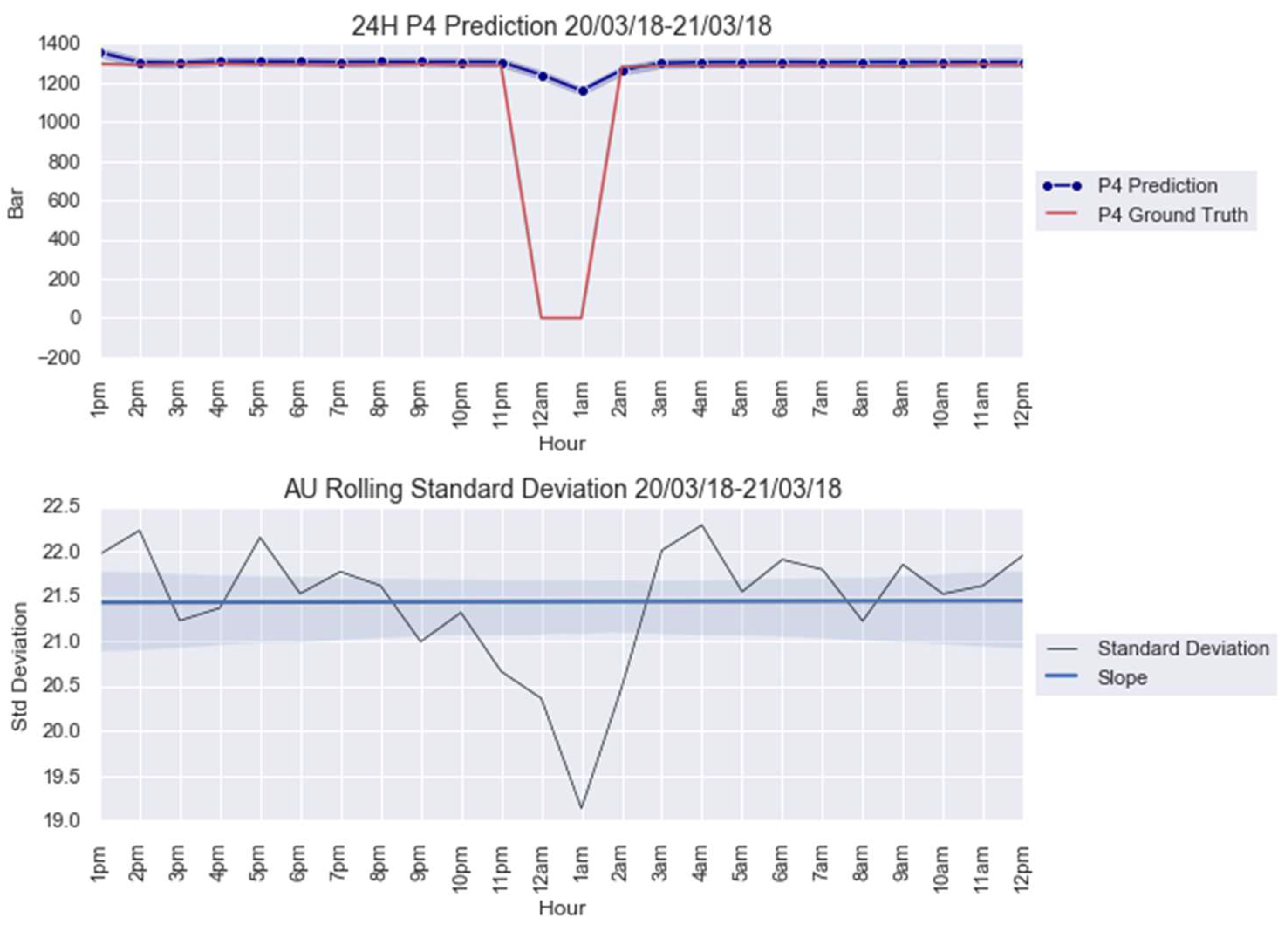
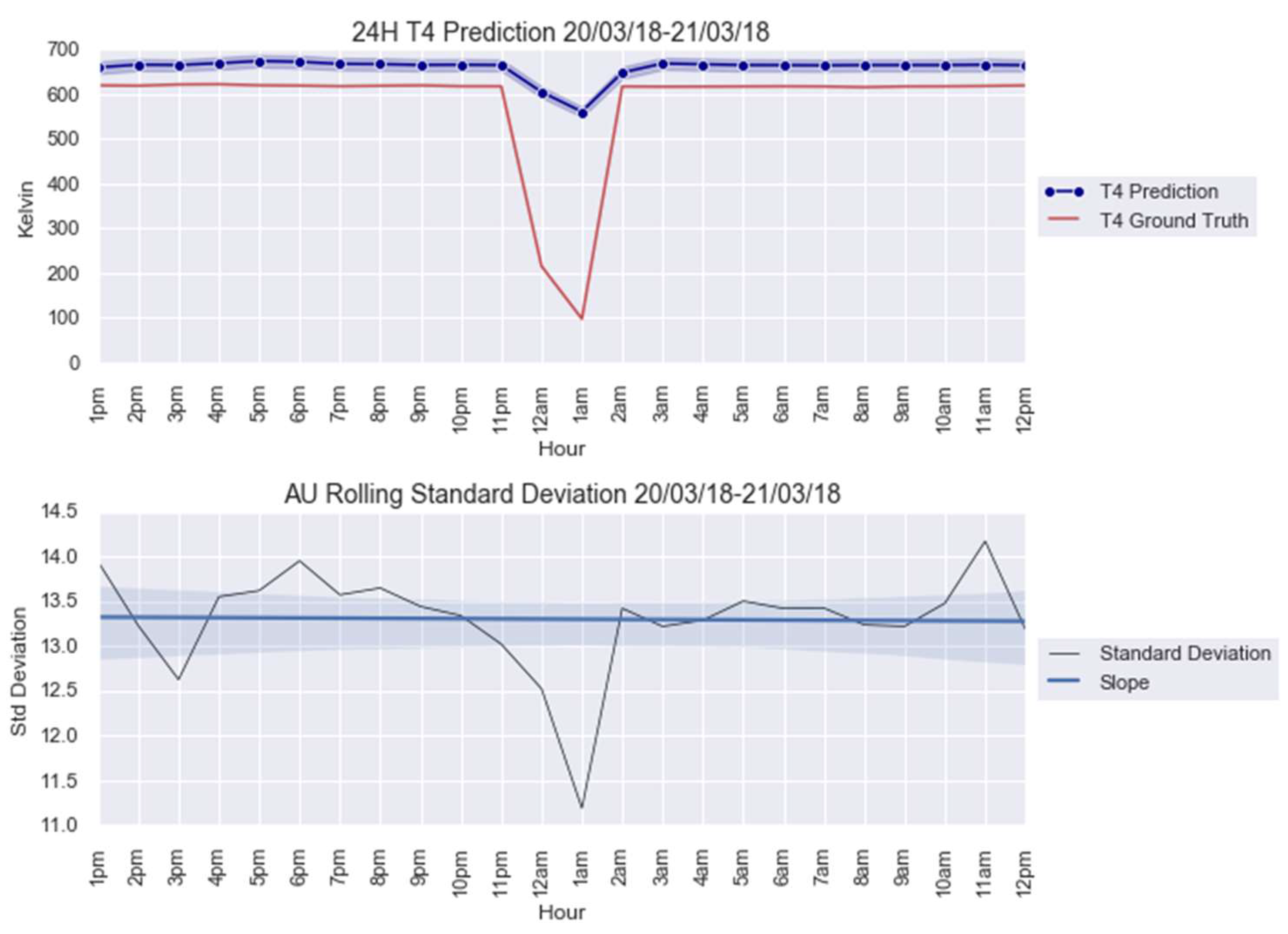
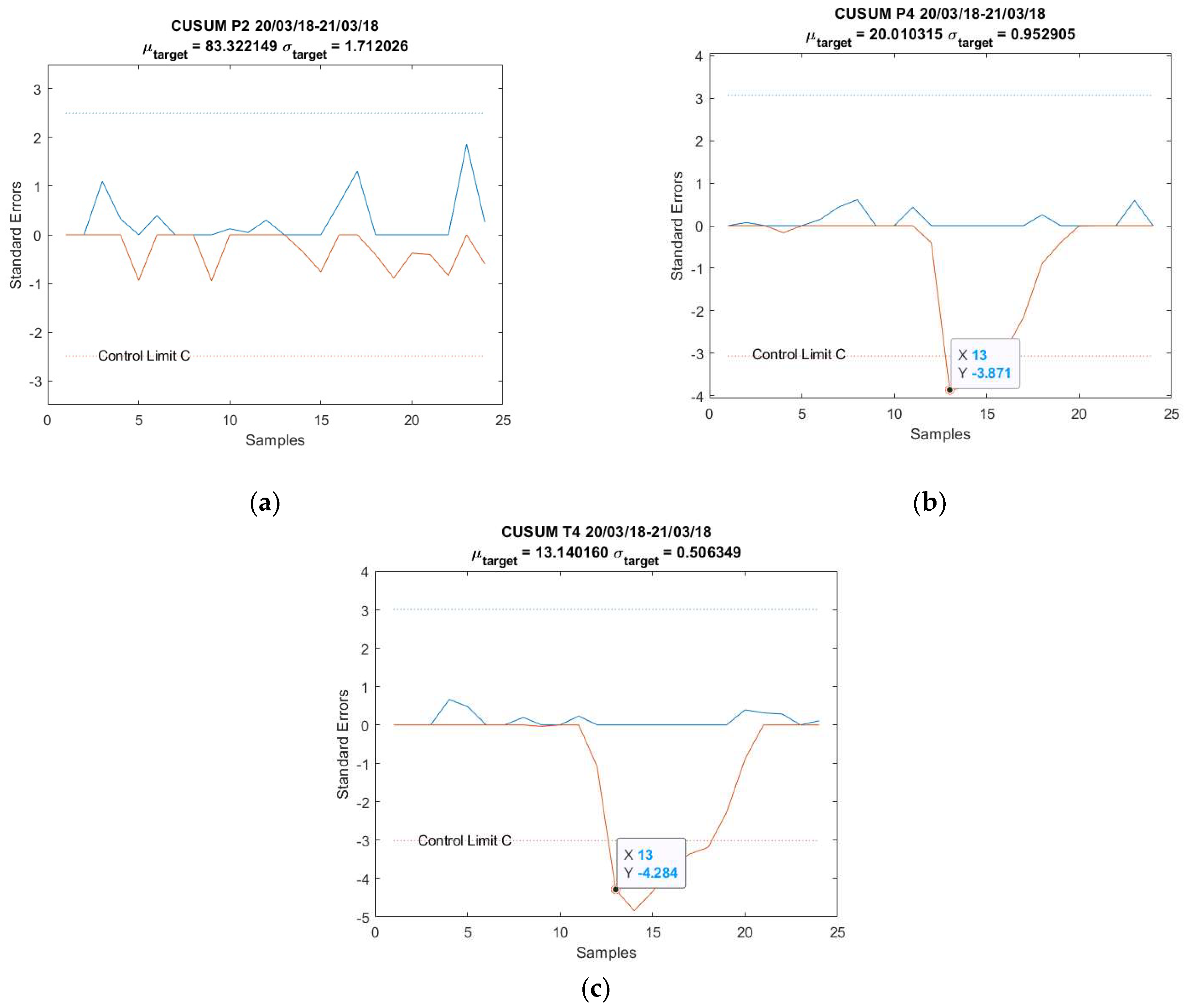

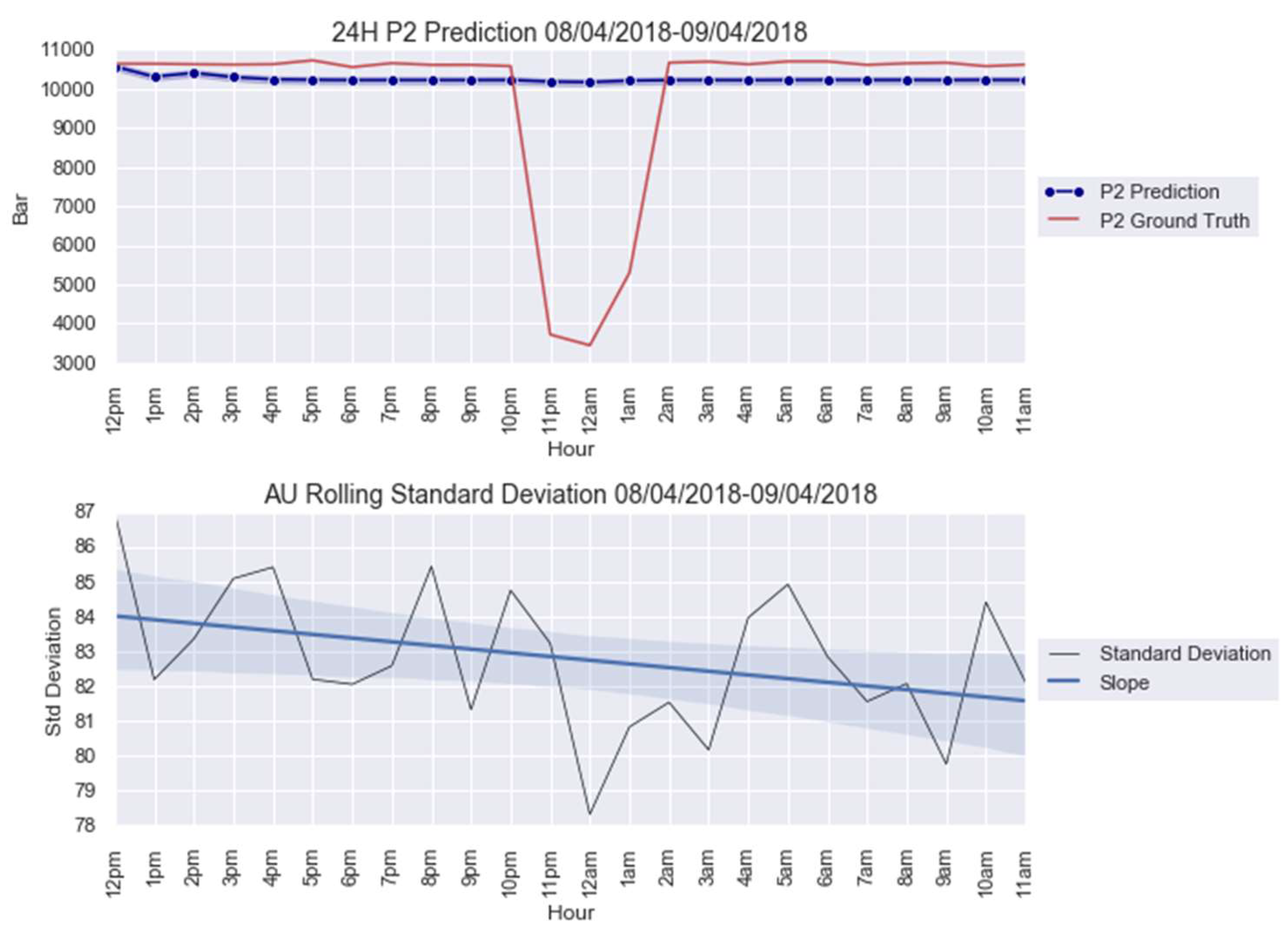
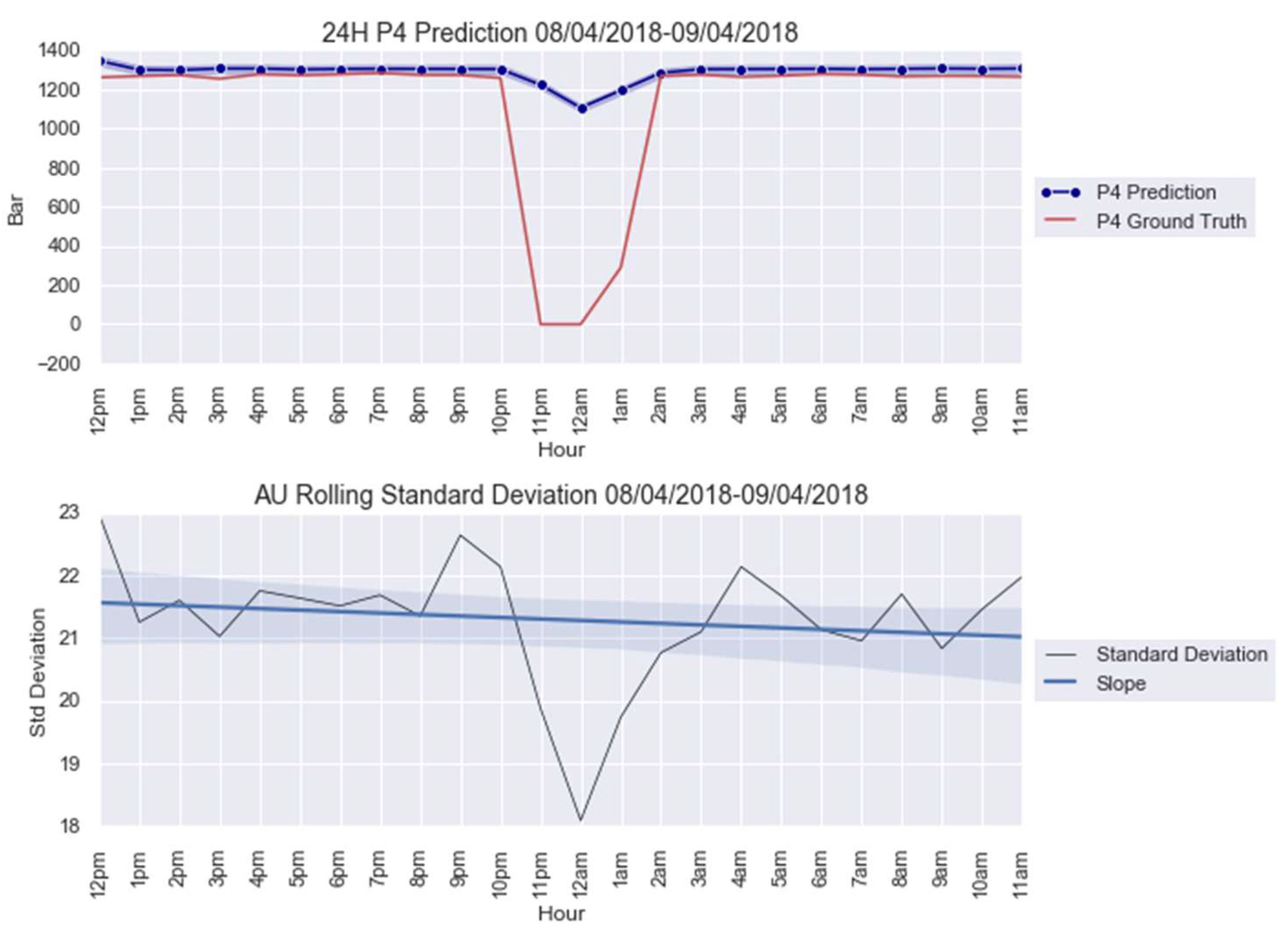
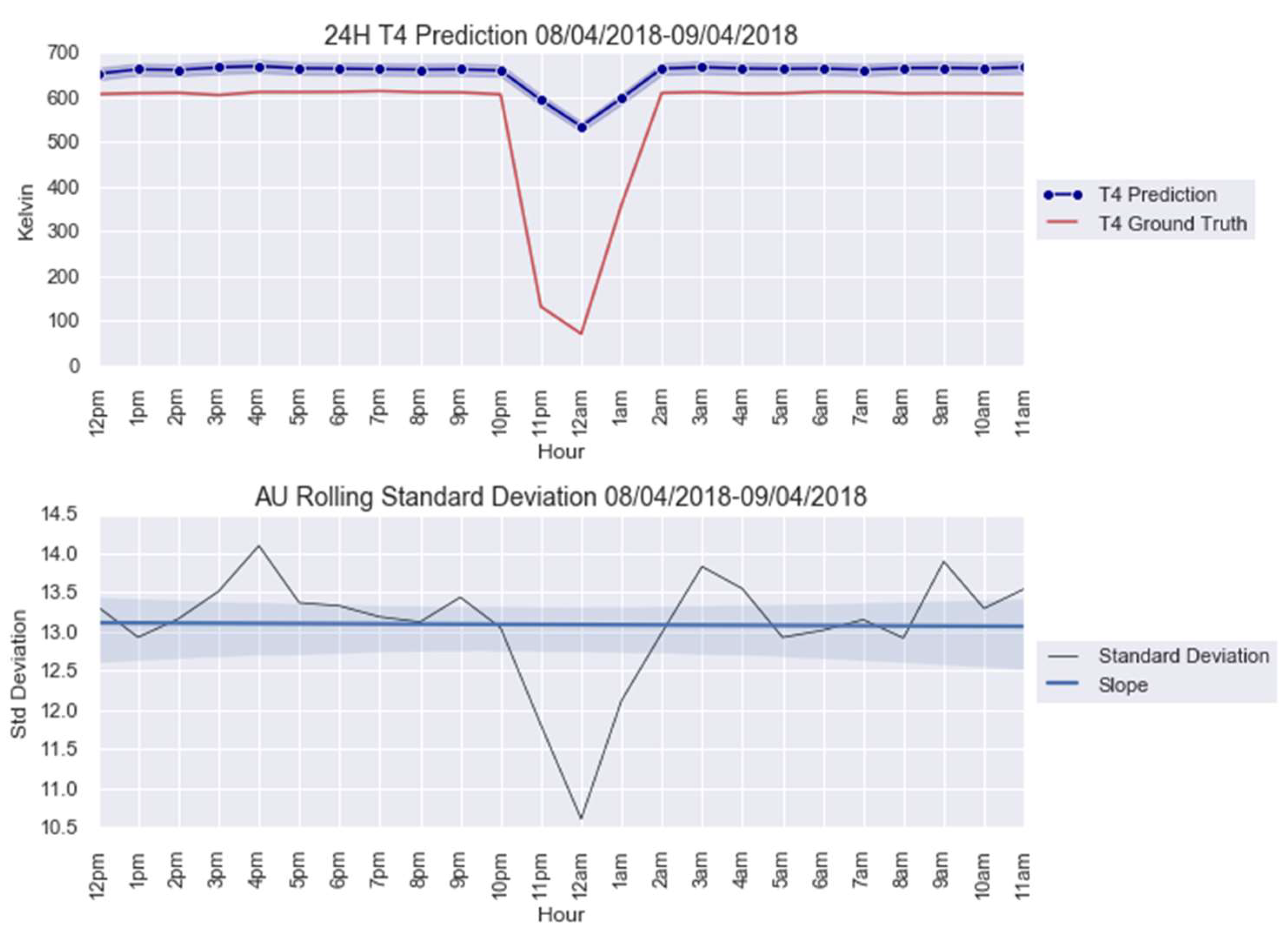
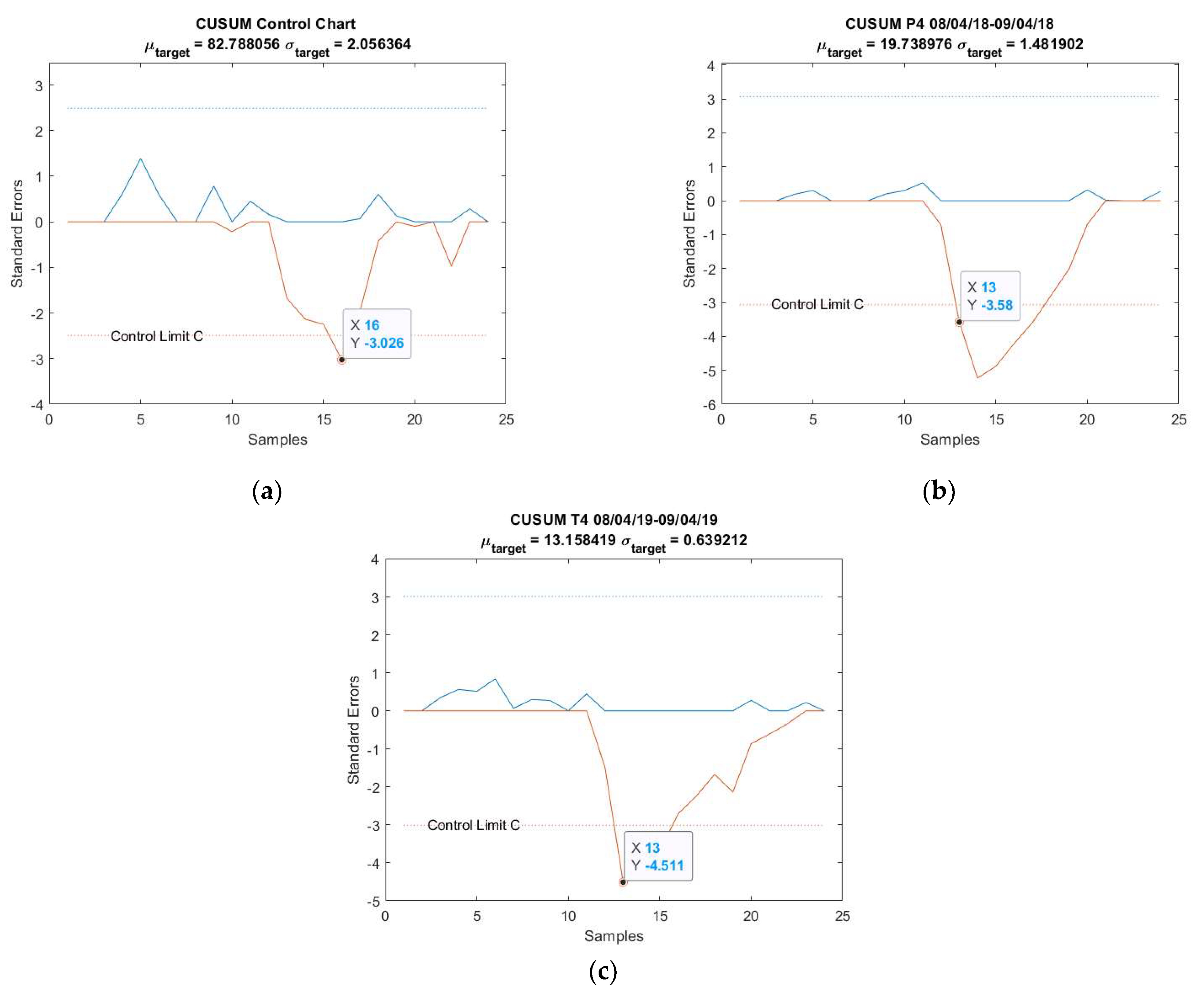
Appendix C
Appendix C.1. Bayes Theorem
Appendix C.2. Variational Inference
- (i)
- A probability, , is created over the weights and parameterized by as an approximation of given by
- (ii)
- From the above, a cost function, which seeks the minimum setting , can be developed fororwith being called the evidence lower bound. Hence, minimizing the cost function equals maximizing the evidence lower bound. As shown in [64], the cost function can be approximated as in (A10) using Monte Carlo sampled weights, , drawn from .
- (iii)
- Then, during backpropagation, every time a forward pass is performed, this cost function is evaluated with sampled weights. In turn, backward pass updates the weights. This iteration is conducted until the training is over. To perform backpropagation through distribution, the local reparameterization trick introduced in [65] for the variational autoencoder is employed.
References
- Monett, D.; Lewis, C.W. Getting Clarity by Defining Artificial Intelligence—A Survey; Studies in Applied Philosophy, Epistemology and Rational Ethics; Springer: Cham, Switzerland, 2018; pp. 212–214. [Google Scholar] [CrossRef]
- European Commision’s High Level Expert Group on Artificial Intelligence. A Definition of AI: Main Capabilities and Scientific Disciplines. Futurium: Your Voices, Our Future. Available online: ec.europa.eu/futurium/en/system/files/ged/ai_hleg_definition_of_ai_18_december_1.pdf (accessed on 22 December 2021).
- European Commission, Executive Agency for Small and Medium-Sized Enterprises. Artificial Intelligence: Critical Industrial Applications: Report on Current Policy Measures and Policy Opportunities. Available online: www.data.europa.eu/doi/10.2826/47005 (accessed on 22 December 2021).
- Deloitte. Scenarios and Potentials of AI’s Commercial Application in China. Intelligence Driven by Innovation—Deloitte Released China AI Industry Whitepaper. Available online: www2.deloitte.com/content/dam/Deloitte/cn/Documents/innovation/deloitte-cn-innovation-ai-whitepaper-en-191212.pdf (accessed on 22 December 2021).
- Anantrasirichai, N.; Bull, D. Artificial intelligence in the creative industries: A review. Artif. Intell. Rev. 2021, 55, 589–656. [Google Scholar] [CrossRef]
- Petit, N. Artificial Intelligence and automated law enforcement: A review paper. SSRN Electron. J. 2018. [Google Scholar] [CrossRef]
- Raimundo, R.; Rosário, A. The impact of artificial intelligence on Data System Security: A literature review. Sensors 2021, 21, 7029. [Google Scholar] [CrossRef] [PubMed]
- Bates, D.W.; Levine, D.; Syrowatka, A.; Kuznetsova, M.; Craig, K.J.; Rui, A.; Jackson, G.P.; Rhee, K. The potential of artificial intelligence to improve patient safety: A scoping review. NPJ Digit. Med. 2021, 4, 54. [Google Scholar] [CrossRef] [PubMed]
- Qiu, S.; Liu, Q.; Zhou, S.; Wu, C. Review of artificial intelligence adversarial attack and defense technologies. Appl. Sci. 2019, 9, 909. [Google Scholar] [CrossRef] [Green Version]
- Momade, M.H.; Durdyev, S.; Estrella, D.; Ismail, S. Systematic review of application of artificial intelligence tools in architectural, engineering and construction. Front. Eng. Built Environ. 2021, 1, 203–216. [Google Scholar] [CrossRef]
- Buczynski, W.; Cuzzolin, F.; Sahakian, B. A review of machine learning experiments in equity investment decision-making: Why most published research findings do not live up to their promise in real life. Int. J. Data Sci. Anal. 2021, 11, 221–242. [Google Scholar] [CrossRef]
- Jung, D.; Choi, Y. Systematic review of machine learning applications in mining: Exploration, exploitation, and reclamation. Minerals 2021, 11, 148. [Google Scholar] [CrossRef]
- Bustos, N.; Tello, M.; Droppelmann, G.; Garcia, N.; Feijoo, F.; Leiva, V. Machine learning techniques as an efficient alternative diagnostic tool for COVID-19 cases. Signa Vitae 2022, 18, 23–33. [Google Scholar]
- Mahdi, E.; Leiva, V.; Mara’Beh, S.; Martin-Barreiro, C. A new approach to predicting cryptocurrency returns based on the gold prices with support vector machines during the COVID-19 pandemic using sensor-related data. Sensors 2021, 21, 6319. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, Y.; Leiva, V.; Liu, S.; Ma, T. A new clustering algorithm based on a radar scanning strategy with applications to machine learning data. Expert Syst. Appl. 2022, 191, 116143. [Google Scholar] [CrossRef]
- Palacios, C.A.; Reyes-Suarez, J.A.; Bearzotti, L.A.; Leiva, V.; Marchant, C. Knowledge discovery for higher education student retention based on data mining: Machine learning algorithms and case study in Chile. Entropy 2021, 23, 485. [Google Scholar] [CrossRef] [PubMed]
- Deng, L. Achievements and Challenges of Deep Learning. Available online: www.microsoft.com/en-us/research/publication/achievements-and-challenges-of-deep-learning (accessed on 22 December 2021).
- Nazmus Saadat, M.; Shuaib, M. Advancements in deep learning theory and applications: Perspective in 2020 and beyond. Adv. Appl. Deep. Learn. 2020, 3. [Google Scholar] [CrossRef]
- Sejnowski, T.J. The unreasonable effectiveness of deep learning in artificial intelligence. Proc. Natl. Acad. Sci. USA 2020, 117, 30033–30038. [Google Scholar] [CrossRef] [Green Version]
- Dai, Z.; Liu, H.; Le, Q.V.; Tan, M. Coatnet: Marrying convolution and attention for all data sizes. arXiv 2021, arXiv:2106.04803. [Google Scholar]
- Rao, A.S.; Verweji, G. Sizing the Prize: What’s the Real Value of AI for Your Business and How Can You Capitalise? Available online: www.pwc.com/gx/en/news-room/docs/report-pwc-ai-analysis-sizing-the-prize.pdf (accessed on 10 January 2022).
- Arnold, Z.; Rahkovsky, I.; Huang, T. Tracking AI Investment: Initial Findings from the Private Markets; Center for Security and Emerging Technology: Washington, DC, USA, 2020. [Google Scholar] [CrossRef]
- PwC. Leveraging the Upcoming Disruptions from AI and IOT. Available online: www.pwc.com/gx/en/industries/tmt/publications/ai-and-iot.html (accessed on 22 December 2021).
- World Intellectual Property Organization. WIPO Technology Trends 2019—Artificial Intelligence. Available online: www.wipo.int/publications/en/details.jsp?id=4386 (accessed on 10 January 2022).
- Dernis, H.; Gkotsis, P.; Grassano, N.; Nakazato, S.; Squicciarini, M.; van Beuzekom, B.; Vezzani, A. World Corporate Top R&D Investors: Shaping the Future of Technologies and of AI; A Joint JRC and OECD Report. EUR 29831 EN. JRC Work. Pap.; Joint Research Centre: Ispra, Italy, 2019. [Google Scholar] [CrossRef]
- Arnold, Z.; Toner, H. AI Accidents: An Emerging Threat. Center for Security and Emerging Technology; Center for Security and Emerging Technology (CSET): Washington, DC, USA, 2021. [Google Scholar] [CrossRef]
- McGregor, S. Preventing repeated real world ai failures by cataloging incidents: The AI incident database. arXiv 2021, arXiv:2011.08512. [Google Scholar]
- Chagal-Feferkorn, K. AI Regulation in the World. A Quarterly Update. AI and Regulation. Available online: techlaw.uottawa.ca/sites/techlaw.uottawa.ca/files/ai-regulation-in-the-world_2020_q4_final.pdf (accessed on 22 December 2021).
- Gunning, D.; Vorm, E.; Wang, J.Y.; Turek, M. DARPA’s explainable AI program: A retrospective. Appl. AI Lett. 2021, 2, e61. [Google Scholar] [CrossRef]
- Streich, J.; Romero, J.; Gazolla, J.G.; Kainer, D.; Cliff, A.; Prates, E.T.; Brown, J.B.; Khoury, S.; Tuskan, G.A.; Garvin, M.; et al. Can exascale computing and explainable artificial intelligence applied to plant biology deliver on the United Nations sustainable development goals? Curr. Opin. Biotechnol. 2020, 61, 217–225. [Google Scholar] [CrossRef] [PubMed]
- Bussmann, N.; Giudici, P.; Marinelli, D.; Papenbrock, J. Explainable AI in fintech risk management. Front. Artif. Intell. 2020, 3, 26. [Google Scholar] [CrossRef]
- Tjoa, E.; Guan, C. A survey on explainable artificial intelligence: Toward medical XAI. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4793–4813. [Google Scholar] [CrossRef]
- Chen, K.; Hwu, T.; Kashyap, H.J.; Krichmar, J.L.; Stewart, K.; Xing, J.; Zou, X. Neurorobots as a means toward neuroethology and explainable AI. Front. Neurorob. 2020, 14, 570308. [Google Scholar] [CrossRef] [PubMed]
- Payrovnaziri, S.N.; Chen, Z.; Rengifo-Moreno, P.; Miller, T.; Bian, J.; Chen, J.H.; Liu, X.; He, Z. Explainable artificial intelligence models using real-world electronic health record data: A systematic scoping review. J. Am. Med. Inform. Assoc. 2020, 27, 1173–1185. [Google Scholar] [CrossRef] [PubMed]
- Barredo Arrieta, A.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; Garcia, S.; Gil-Lopez, S.; Molina, D.; Benjamins, R.; et al. Explainable artificial intelligence: Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef] [Green Version]
- Adadi, A.; Berrada, M. Peeking inside the black-box: A survey on explainable artificial intelligence. IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- Linardatos, P.; Papastefanopoulos, V.; Kotsiantis, S. Explainable AI: A review of machine learning interpretability methods. Entropy 2020, 23, 18. [Google Scholar] [CrossRef] [PubMed]
- Sheppard, J.W.; Kaufman, M.A.; Wilmering, T.J. IEEE standards for prognostics and health management. IEEE Aerosp. Electron. Syst. Mag. 2008, 24, 97–103. [Google Scholar]
- Thudumu, S.; Branch, P.; Jin, J.; Singh, J. A comprehensive survey of anomaly detection techniques for high dimensional big data. J. Big Data 2020, 7, 42. [Google Scholar] [CrossRef]
- Aykroyd, R.G.; Leiva, V.; Ruggeri, F. Recent developments of control charts, identification of big data sources and future trends of current research. Technol. Forecast. Soc. Change 2019, 144, 221–232. [Google Scholar] [CrossRef]
- Guo, J.; Li, Z.; Li, M. A review on prognostics methods for engineering systems. IEEE Trans. Reliab. 2020, 69, 1110–1129. [Google Scholar] [CrossRef]
- Gao, Z.; Liu, X. An overview on fault diagnosis, prognosis and resilient control for wind turbine systems. Processes 2021, 9, 300. [Google Scholar] [CrossRef]
- Nor, A.K.; Pedapati, S.R.; Muhammad, M. Reliability engineering applications in electronic, software, nuclear and Aerospace Industries: A 20 year review (2000–2020). Ain Shams Eng. J. 2021, 12, 3009–3019. [Google Scholar] [CrossRef]
- Nor, A.K.; Pedapati, S.R.; Muhammad, M.; Leiva, V. Overview of explainable artificial intelligence for prognostic and health management of industrial assets based on preferred reporting items for systematic reviews and meta-analyses. Sensors 2021, 21, 8020. [Google Scholar] [CrossRef] [PubMed]
- Ding, P.; Jia, M.; Wang, H. A dynamic structure-adaptive symbolic approach for slewing bearings’ life prediction under variable working conditions. Struct. Health Monit. 2020, 20, 273–302. [Google Scholar] [CrossRef]
- Kraus, M.; Feuerriegel, S. Forecasting remaining useful life: Interpretable deep learning approach via variational Bayesian inferences. Decis. Support Syst. 2019, 125, 113100. [Google Scholar] [CrossRef]
- Alfeo, A.L.; Cimino, M.G.C.A.; Manco, G.; Ritacco, E.; Vaglini, G. Using an autoencoder in the design of an anomaly detector for smart manufacturing. Pattern Recognit. Lett. 2020, 136, 272–278. [Google Scholar] [CrossRef]
- Steenwinckel, B.; De Paepe, D.; Vanden Hautte, S.; Heyvaert, P.; Bentefrit, M.; Moens, P.; Dimou, A.; Van Den Bossche, B.; De Turck, F.; Van Hoecke, S.; et al. Flags: A methodology for adaptive anomaly detection and root cause analysis on sensor data streams by fusing expert knowledge with machine learning. Future Gener. Comput. Syst. 2021, 116, 30–48. [Google Scholar] [CrossRef]
- Wang, J.; Bao, W.; Zheng, L.; Zhu, X.; Yu, P.S. An attention-augmented deep architecture for hard drive status monitoring in large-scale storage systems. ACM Trans. Storage 2019, 15, 21. [Google Scholar] [CrossRef]
- Sundar, S.; Rajagopal, M.C.; Zhao, H.; Kuntumalla, G.; Meng, Y.; Chang, H.C.; Shao, C.; Ferreira, P.; Miljkovic, N.; Sinha, S.; et al. Fouling modeling and prediction approach for heat exchangers using deep learning. Int. J. Heat Mass Transf. 2020, 159, 120112. [Google Scholar] [CrossRef]
- Le, D.D.; Pham, V.; Nguyen, H.N.; Dang, T. Visualization and explainable machine learning for efficient manufacturing and system operations. Smart Sustain. Manuf. Syst. 2019, 3, 20190029. [Google Scholar] [CrossRef]
- Epps, B.P.; Krivitzky, E.M. Singular value decomposition of noisy data: Noise Filtering. Exp. Fluids 2019, 60, 126. [Google Scholar] [CrossRef] [Green Version]
- Epps, B.P.; Krivitzky, E.M. Singular value decomposition of noisy data: Mode corruption. Exp. Fluids 2019, 60, 121. [Google Scholar] [CrossRef]
- Martinez-Cantin, R. BayesOpt: A Bayesian optimization library for nonlinear optimization, experimental design and bandits. J. Mach. Learn. Res. 2014, 15, 3735–3739. [Google Scholar]
- Mathwork. Detect Small Changes in Mean Using Cumulative Sum. Select Optimal Machine Learning Hyperparameters Using Bayesian Optimization—MATLAB. Available online: www.mathworks.com/help/stats/bayesopt.html (accessed on 22 December 2021).
- Song, Y.; Gao, S.; Li, Y.; Jia, L.; Li, Q.; Pang, F. Distributed attention-based temporal convolutional network for remaining useful life prediction. IEEE Internet Things J. 2021, 8, 9594–9602. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), New York, NY, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar]
- Molnar, C. Interpretable Machine Learning. A Guide for Making Black Box Models Explainable. Available online: https://christophm.github.io/interpretable-ml-book/ (accessed on 22 December 2021).
- Tahan, M.; Muhammad, M.; Abdul Karim, Z.A. A multi-nets ANN model for real-time performance-based automatic fault diagnosis of industrial gas turbine engines. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 2865–2876. [Google Scholar] [CrossRef]
- Saxena, A.; Goebel, K.; Simon, D.; Eklund, N. Damage propagation modeling for aircraft engine run-to-failure simulation. In Proceedings of the 2008 International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008; pp. 1–9. [Google Scholar]
- Ellefsen, A.L.; Ushakov, S.; Aesoy, V.; Zhang, H. Validation of data-driven labeling approaches using a novel deep network structure for remaining useful life predictions. IEEE Access 2019, 7, 71563–71575. [Google Scholar] [CrossRef]
- Ramasso, E.; Saxena, A. Performance benchmarking and analysis of prognostic methods for CMAPSS datasets. Int. J. Progn. Health Manag. 2020, 5, 1–15. [Google Scholar] [CrossRef]
- Graves, A. Practical variational inference for neural networks. In Advances in Neural Information Processing Systems, Proceedings of the 24th International Conference on Neural Information Processing Systems, Granada, Spain, 12–15 December 2011; Shawe-Taylor, J., Zemel, R., Bartlett, P., Pereira, F., Weinberger, K.Q., Eds.; Springer: Berlin, Germany, 2011; Volume 24, pp. 2348–2356. Available online: proceedings.neurips.cc/paper/2011/file/7eb3c8be3d411e8ebfab08eba5f49632-Paper.pdf (accessed on 22 December 2021).
- Blundell, C.; Cornebise, J.; Kavukcuoglu, K.; Wierstra, D. Weight uncertainty in neural networks. arXiv 2015, arXiv:1505.05424. [Google Scholar]
- Kingma, D.P.; Salimans, T.; Welling, M. Variational dropout and the local reparameterization trick. In Advances in Neural Information Processing Systems, Proceedings of the 29th Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; Cortes, C., Lawrence, N., Lee, D., Sugiyama, M., Garnett, R., Eds.; Springer: Berlin, Germany, 2015; Volume 28, pp. 2575–2583. Available online: papers.nips.cc/paper/2015/file/bc7316929fe1545bf0b98d114ee3ecb8-Paper.pdf (accessed on 22 December 2021).

| Notation | Input | Unit |
|---|---|---|
| Power turbine rotational speed | RPM | |
| Compressor inlet pressure | Bar | |
| Fuel mass flow rate | kg/s | |
| Compressor inlet temperature | K |
| Notation | Output | Unit |
|---|---|---|
| Gas generator rotational speed | RPM | |
| Compressor outlet pressure | Bar | |
| Gas generator turbine outlet pressure | Bar | |
| Gas generator turbine outlet temperature | K |
| Dataset | Date | Quantity (hour) |
|---|---|---|
| Training | 1 January 2018–23 October 2018 | 6672 |
| Testing | 26 November 2018–30 December 2018 | 816 |
| Validation | 23 October 2018–26 November 2018 | 816 |
| Anomaly 1 | 20–21 March 2018 | 24 |
| Anomaly 2 | 8–9 April 2018 | 24 |
| Unused Data | 385 | |
| Total | 8737 | |
| Model | Aleatoric Uncertainty | Epistemic Uncertainty |
|---|---|---|
| 20.40 | 27.11 | |
| 702.49 | 787.87 | |
| 11.10 | 92.15 | |
| 32.68 | 49.74 |
| Model | ||||
|---|---|---|---|---|
| 52.10 | 47.92 | 1.53 | 2.72 | |
| 87.35 | 82.70 | 1.87 | 2.49 | |
| 22.90 | 21.46 | 0.47 | 3.07 | |
| 14.20 | 13.27 | 0.30 | 3.05 |
| Dataset | Fault Mode | Operating Condition | Training Data | Testing Data |
|---|---|---|---|---|
| #1 | 1 | 2 | 100 | 100 |
| RMSE with Aleatoric Uncertainty | RMSE with Epistemic Uncertainty | Score with Aleatoric Uncertainty | Score with Epistemic Uncertainty |
|---|---|---|---|
| 17.94 | 18.41 | 1025.31 | 1231.10 |
| Combination | Contribution Order |
|---|---|
| 17 Features | S11, S13, S8, S12, S21, S4, S20, OC2, OC3, S7, OC1, S15, S2, S17, S9, S3, and S14 |
| RMSE with Aleatoric Uncertainty | RMSE with Epistemic Uncertainty | Score with Aleatoric Uncertainty | Score with Epistemic Uncertainty |
|---|---|---|---|
| 14.59 | 15.87 | 431.99 | 594.88 |
| Year | Methods | RMSE | Score |
|---|---|---|---|
| 2017 | variatioanal auto encoder + recurrent neural network | 14.80 | 419 |
| 2018 | convolutional neural network + feed forward neural network | 12.61 | 274 |
| 2019 | convolutional neural network + LSTM + feed forward neural network | 12.56 | 231 |
| 2021 | proposed method | 14.59 | 431 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nor, A.K.M.; Pedapati, S.R.; Muhammad, M.; Leiva, V. Abnormality Detection and Failure Prediction Using Explainable Bayesian Deep Learning: Methodology and Case Study with Industrial Data. Mathematics 2022, 10, 554. https://doi.org/10.3390/math10040554
Nor AKM, Pedapati SR, Muhammad M, Leiva V. Abnormality Detection and Failure Prediction Using Explainable Bayesian Deep Learning: Methodology and Case Study with Industrial Data. Mathematics. 2022; 10(4):554. https://doi.org/10.3390/math10040554
Chicago/Turabian StyleNor, Ahmad Kamal Mohd, Srinivasa Rao Pedapati, Masdi Muhammad, and Víctor Leiva. 2022. "Abnormality Detection and Failure Prediction Using Explainable Bayesian Deep Learning: Methodology and Case Study with Industrial Data" Mathematics 10, no. 4: 554. https://doi.org/10.3390/math10040554
APA StyleNor, A. K. M., Pedapati, S. R., Muhammad, M., & Leiva, V. (2022). Abnormality Detection and Failure Prediction Using Explainable Bayesian Deep Learning: Methodology and Case Study with Industrial Data. Mathematics, 10(4), 554. https://doi.org/10.3390/math10040554








