1. Introduction
Jacob Collier’s fascinating a cappella arrangement of “In The Bleak Midwinter” [
1] modulates from the key of E to the key of G half-sharp between the third and fourth verses. This is by design, and he explains this choice in his own metaphorical language [
2]. In response to the question “Why does music theory sound good to our ears?” on Wired.com Tech Support (on 26 May 2021), Jacob Collier answers “Music theory doesn’t really sound like anything. It sounds like parchment. Music sounds like stuff though, and the truth is no one knows. It’s a bit of a mystery.” [
3]. This work addresses precisely the question of how to geometrically model what music sounds like. We approach this question like a theoretical physicist would: the world consists of physical objects goverened by differential equations.
1.1. Background
Music is based on a temporal sequence of pitched sounds. Over time, theorists have analyzed patterns in musical works and described some classes of tones, sounds and sequences thereof as pitches, chords (harmonies) and melodies/chord progressions, respectively. The resulting theory is used in turn by composers to describe their musical inceptions and allow musicians to reproduce them. The theory of harmonies is also used by jazz musicians as a common basis for spontaneous musical creations.
There is a lot of research related to our differential-geometric approach to music perception. However, music psychology and music theory remain practically distinct as it was already noted by Carol Krumhansl in 1995 [
4]. She empirically develops in [
5] a tonal hierarchy in specific musical contexts such as scales and tonal music. Frieder Stolzenberg [
6] presents a formal model for harmony perception based on periodicity detection which is compatible with prior empirical results. Harrison and Pearce [
7] reanalyse and formalize consonance perception data from four previous major behavioral studies by way of a computer model written in R. Their conclusion is that simultaneous consonance derives in a large part from three phenomena: interference, periodicity/harmonicity, and cultural familiarity. This suggests that chord pleasantness is a multi-dimensional phenomenon, and experiment design in the study of pleasantness in chord perception is highly problematic. They extend their ideas to introduce a new model for the analysis and generation of voice leadings [
8]. Marjieh et al. [
9] provide a detailed analysis of the relationship between consonance and timbre. A speculative account on the evolutional aspect of consonance has been discussed in [
10] with the conclusion that understanding evolutionary aspects require elaborate cross-cultural and cross-species studies. Chan et al. [
11] combine the ideas of periodicity and roughness in the language of wave interferences in order to define stationary subharmonic tension (essentially the ratio of a generalization of roughness to different frequencies and periodicity) and use it to develop a new theory of transitional harmony, also known as tension and release. Tonal expectations have been analyzed from a sensoric and cognitive perspective in [
12]. Dmitri Tymoczko [
13,
14] provides a geometric model of musical chords. He also analyzed three different concepts of musical distance and observed that they are in practise related [
15]. Since our pitch perception is rather forgiving and imprecise, pitch perception corresponds to a probability distribution and therefore a smoothing should be applied to frequencies as in [
16], which gives a rigorous way of evaluating similarity of chords or more generally pitch collections using expectation tensors. Differential geometry has also been used in mathematical musicology by way of gauge theory with the aim of explaining tonal attraction [
17,
18]. Music was viewed as a dynamical system in order to study tonal relationships [
19] or musical performances [
20]. On the level of audio signals, [
21,
22] use Hopf bifurcation control to study sound changes in music. In [
23,
24], music theory for classical and jazz music is formalized by providing a mathematical model for tonality, voice leading and chord progressions, which is very different from the geometric and psychoacoustic approach presented in this paper but could help in further developing it. Recent work by Wall et al. [
25] analyzes voice leading and harmony in the context of musical expectancy which is precisely the motivation for our geometric model. Some very interesting vertical ideas on a scientific approach to music can be found in [
26], even though there are—strictly speaking—no new results in that specific article: the brain’s exceptional ability for soft computing and pattern recognition on incomplete or over-determined data is relevant for our model. Microtonal intervals have been discussed in the context of harmony by [
27,
28]. Several results from cognitive neuroscience studies in the context of music perception also need to be considered for a geometric model [
29,
30,
31,
32,
33]. A more conventional and more elaborate account on a scientific approach to music can be found in [
34]. William Sethares wrote a comprehensive analysis on musical sounds based on roughness [
35].
1.2. Aims
We hypothesize that there exists a simple underlying mathematical model and mechanism which is responsible for the harmonic and melodic development in music, in particular Western music. In order to study changes in sound and time, and since sound and time are best modelled as continuous spaces, we need differential geometry in order to study or construct musical trajectories on these spaces. Since the brain has not been understood well enough, there is currently no way of rigorously proving the correctness of a geometric model by deducing it from the way our brain processes music, even though there is a bit of work in this direction [
36,
37]. Instead, the goal of this research project is to validate the model by verifying its music theoretic implications. Our aim is to provide a framework from a differential geometer’s point of view in the spirit of [
14,
38] which is flexible enough to allow for various existing and forthcoming approaches to studying perceptive aspects of the space of notes and chords. In particular, this will remedy all the limitations of geometric models mentioned in [
5] (119ff.) by making the relations between notes and chords depend on the context and the order. A focal point for this study is the cadence, “a melodic or harmonic configuration that creates a sense of resolution” [
39] (pp. 105–106), which is an important basis for a lot of modern western music and has a long history in human evolution. It reduces tensions in chords, is related to falling fifths and minimizes voice leading distances. For us, it will serve as a guiding principle for the development of a differential-geometric model. While we hope that this model generalizes to other kinds of music because of its generalist approach, our focus will be on Western music. Note that there are many approaches to analyzing and developing music based on machine learning. For the time being, we will stay away from machine learning, even though we may later use techniques from parameter optimization or artifical neural networks to narrow down the model.
Despite numerous studies on music perception, there is a need for a holistic approach by way of a common computational framework in order to study and compare various psychoacoustic quantities such as tension, consonance and roughness in a given context. In the spirit of theoretical physics, we make use of mathematical models, abstractions and generalizations in order to create a geometric framework consistent with prevalent neuroscientific theories and results. We show how to rationalize, explain and predict psychoacoustic phenomena as well as disprove psychoacoustic theories using tools from differential geometry. We will not be able to reach as far as explaining Jacob Collier’s specific modulation to a half-key, but we will show why half-keys appear naturally from a psychoacoustic point of view. We will describe how this simple yet powerful differential-geometric model opens up new research directions.
1.3. Main Contribution
The problem with the abundance of competing approaches to dissonance and tension, apart from the great number of different terminologies, is that they are related but not the same, the neuronal processing behind the perception of music has not been understood and the music theory does not yet have a satisfactory explanation based on existing approaches to dissonance and tension. Our geometric model has been constructed in order for these approaches to be studied, compared, and combined. Despite numerous statistical evaluations of models for dissonance and tension, none of these models can be used directly to compose music or develop music further. The main contribution is therefore to present a new approach to music perception by combining the above approaches to music cognition and geometric modelling in a simple differential-geometric model which can be used together with suitable concepts of consonance and tension to deduce the laws of music theory, lends itself to further research and musical developments, as well as provide a flexible framework to relate the perception of music and music theory. This allows for systematically and quantitatively studying the perception of music and music theory with or without just intonation or various equally or not equally tempered systems and describing new approaches to composition and improvisation in the universal language of mathematics and with the tools provided by geometric analysis. It is general enough and modular so that some or all of the concrete sensoric functions presented here can be replaced with alternative ones. A possible outcome is, that we are able to use certain gradient vectors of psychoacoustic quality functions on the space of chords that explain which chord progressions sound good (at which speed and why) and thereby provide an effective tool for composers.
1.4. Implications
Therefore, the aim is not to provide yet another bottom-up approach, but to follow a top-down construction of a convenient model, which integrates roughness, consonance, tension with voice leading in order to be useful for analysing music, composing music and ultimately developing music further. In order to study time-dependent aspects of music, we need to be able to consider derivatives of psychoacoustic functions on a space of musical chords with a Riemannian structure. In particular, we want to associate musical expectation to tension on the space of chords. Even though many of the underlying ideas can be generalized, we restrict ourselves to Western music for reasons of accessibility and convenience with an octave spanning 12 semitones.
2. Foundations of Music Perception
In order to be able to construct a geometric framework which is consistent with the prevalent neuroscientific theories, let us first review and briefly discuss the most relevant results. Human evolution has optimized the ability of our sensory nervous system and our brain to process signals efficiently in order to quickly and easily produce the most useful interpretations and implications. Logarithmic perception of signals [
40] and pattern recognition [
41] are at the heart of this optimized mechanism and also provide the basis for music cognition. Signal detection theory provides a mathematical foundation for constructing psychometric functions as models for music perception [
42,
43,
44,
45]. Those readers who are not interested in the underlying mechanisms of music perception are welcome to continue with the mathematical part in
Section 3.
2.1. Neural Coding
Sensory organs such as eye, ears, skin, nose, and mouth collect various stimuli for transduction, i.e., the conversion into an action potential, which is then transmitted to the central nervous system [
46] and processed by the neuronal network in the brain as combination of spike trains [
47]. Both sensation and perception are based on a physiological process of recognizing patterns in the spike trains [
48].
2.2. Logarithmic Perception of Signals
By the Weber–Fechner law [
49] the perceived intensity
p of a signal is logarithmic to the stimulus intensity
S above a minimal threshold
:
Varshney and Sun [
40] gave a compelling argument, why this is due to an optimization process in biological evolution where the relative error in information-processing is minimized. Quantization in the brain due to limited resources forces a continuous input signal to be perceived logarithmically. The Weber–Fechner law applies to the perception of pressure, temperature, light, time, distance and—most importantly for us—to the frequency and amplitude of sound waves.
2.3. Phase Locking
Synchronization and phase locking is a mechanism in the brain for organizing data, recognizing patterns and soft computing. It has also been proposed and confirmed by Langner in the case of pitches [
50,
51]. Phase locking for multiple frequencies has been studied in [
52]. These pattern recognition capabilities can be explained by human evolution [
41]. In [
53] (pp. 193–213), it is argued how pattern recognition has improved over millions of years in order to allow for better predictions. It is even suggested that the current age of digitalization adds another layer of neurons to recognize new patterns. Pattern recognition is essential for living beings and humans in particular.
We immediately recognize shapes of objects and rhythmic repetitions of signals. Even if we do not see something clearly, because it is too far away, we can predict the shape within a context and thereby recognize the object. Pattern recognition in signals is based on phase-phase synchronizations. This applies for simultaneously emitted signals such as pictures and chords, but also for temporally adjacent patterns such as moving pictures and chord progressions. Signal predictions and expectations are based on a continuation of patterns. The more patterns diverge from the predicted patterns the more unexpected a signal is. Arguably, our brain prefers signals where patterns can be detected. Again, possible reasons for this can be found in evolution:
Patterns allow us to predict events, and correctly predicting events allows us to evade dangers or kill pray.
More abstractly, changes of patterns cause a rise of information, and we want to minimize the information we need to process,
According to [
54] processes of our working memory are accomplished by neural operations involving phase-phase synchronization. We can think of working memory as an echo of firing neurons in our brain. Temporally adjacent sounds yield synchronized firings, which not only allow us to detect a rhythm but enable us to detect pitches and relate pitches to each other in chord progressions and melodies.
Quantifying phase synchronizations had been addressed by [
55] which showed that phase-locking values provide better estimation of oscillatory synchronization than spectral coherence. There are other possible explanations for the relevance of simple ratios and periodicity as described in
Section 4.4 based on neural coding such as cross entropy and minimizing sensoric quantities in the context of estimating distances and other measures. At this point, phase-locking seems to be as good an explanation as any for all kinds of sensatoric phenomena and pattern recognition, even though it will eventually be necessary to confirm this or find better explanation for the signal expectation on the neuronal level. As the mechanism for expectation will be similar for different signals, a geometric model will help to reject explanations and find suitable ones based on psychoacoustic observations.
An example of a popular loss function is cross-entropy which is minimized for the training of artificial neural networks. Since we have a metric on each stratum we can study any height function from a differential geometric point of view. For example we can compute the differential or gradient of the dissonance function by way of which we can find the optimal direction in the space of chords to reduce dissonance as fast as possible.
Cross-entropy might be a good mathematical concept for the purpose of pattern recognition, where we match information received with the information already stored in the brain.
2.4. Audio Signals
A vibrating object causes surrounding air molecules to vibrate. As long as the kinetic energy is sustained it spreads as a wave by way of a chain reaction. This sound wave travels through the ear canal into the cochlea. Hair cells inside the cochlea convert the wave into an electrical signal, which then travels along the auditory nerve into the brain.
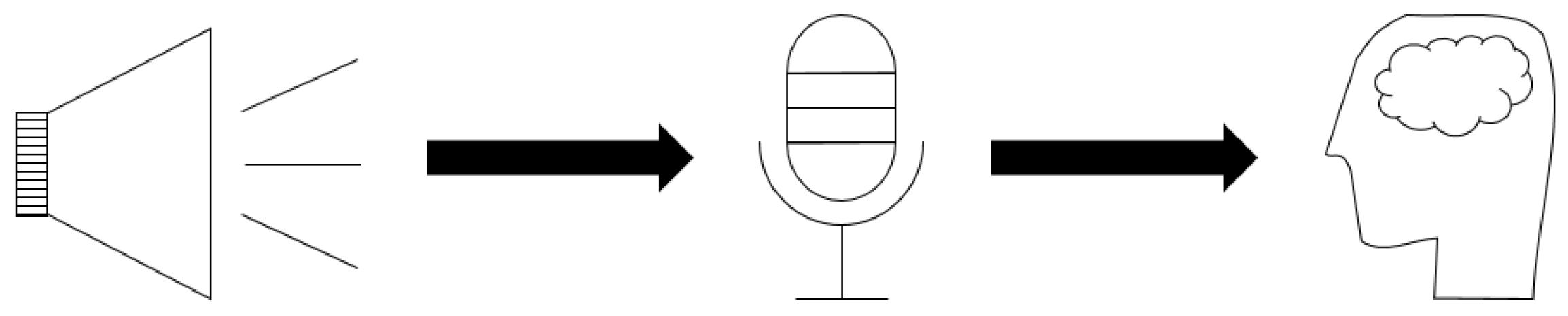
The audio signal goes through various stages of existence from the moment of creation to the perception in the brain. Due to a limited resolution of human perception frequency and amplitude is quantized, and the brain logarithmically perceives patterns thereof as certain sound features. These characteristics enable us to quickly recognize and describe instruments, voices and other sounds. We want to distinguish three major stages of an audio signal’s existence as shown in
Figure 1:
The produced sound, e.g., the vibrating molecules in the air as they are stimulated by a musical instrument or a loudspeaker.
The received sound, e.g., the vibrating microphone diaphragm or the hair cells in the cochlea, at which point the sound wave is converted into an electric signal, before it reaches the brain or different analog or digital recording devices.
The perceived sound, e.g., the interpretation by a person’s brain.
2.5. Spectrum
The shape of an object is an important factor in the way it can vibrate [
56]. It can be modeled by differential equations involving the geometry of the object. There are several such possibilities known as eigenmodes, each of which moves at a fixed frequency and amplitude as long as the energy is sustained. These eigenmodes are called partials, and the collection of all partials is known as the overtone spectrum of the audio signal. For example, the partials of an ideal vibrating string of length
L fixed at both its ends are
for
. In this case, the overtone spectrum is called the harmonic spectrum.
Pattern recognition and logarithmic signal perception seem instrumental for the qualitative analysis of sound and music: A musical instrument can play different notes, but our brain detects the same spectral pattern which enables us to identify the sound as coming from the same instrument. This sound quality is also known as timbre and the process of merging several frequencies tonal fusion. Analogous mechanisms apply to voice recognition. Depending on certain deviation patterns in the spectral pattern we can classify and compare different members of the same instrument family (saxophone, clarinet, flute, string, trombone, etc.). It is also exactly this spectral pattern which allows us to recognize the different tones that are played by various sources simultaneously and to determine which instruments are playing which notes, depending on how much training we have.
2.6. Pitch Detection
Upper partials cannot be easily singled out, only a fundamental frequency can usually be detected by humans. Sounds, where a fundamental frequency can be detected, are called pitched sounds. The process in our brain that detects the pitch is phase locking. The same mechanism is responsible for detecting a pitch in several octaves played together and for detecting a pitch in a tone with a missing fundamental, which seems compatible with autocorrelation [
57]. Several pitched tones can be played together to produce a chord, where each pitch can be detected.
Notice that different people might detect different fundamental frequencies depending on the context. This can be seen by considering the ascending Shepard’s scale [
58] constructed by a series of complex tones which is circular even though the pitch is perceived as only moving upward.
2.7. Interference
Simultaneously emitted Soundwaves interfere with each other. The interference between sine waves with slightly differing frequencies result in beatings which can be computed explicitly. Arbitrary sound waves such as those from pitched tones can be approximated by sums of sine waves. The various beatings between slightly different sine wave summands combine to a quality called roughness. Sethares [
35,
59] uses the Plomp–Levelt curves to provide a formula for measuring roughness and argues that this sound quality is behind tuning and scales. In particular, he suggests that some aspects of music theory can be transferred to compressed and stretched spectra, when played in compressed and stretched scales. This has been confirmed by recent results [
9].
It has been shown by Hinrichsen [
60] that the tuning of musical instruments such as pianos based on minimizing Shannon entropy of tone spectra is compatible with aural tuning and the Railsback curve. While the tuning of harmonic instruments approximating twelve-tone equal temperament using coinciding partials will work, tuning inharmonic instruments in the context of Western music is more challenging [
61].
Overtone singing is also an interesting aspects of interference. Possibly, overtones are sometimes not what you want to hear, maybe you want to stay away from them, because they are an unwanted artefact.
2.8. Just-Noticeable Difference and Critical Bandwidth
The probability for detecting a pitch change between two succeeding tones can be described rigorously using signal detection theory [
42,
45]. It is a collection of psychophysical methods based on statistics for analyzing and determining how signals and noise are perceived.
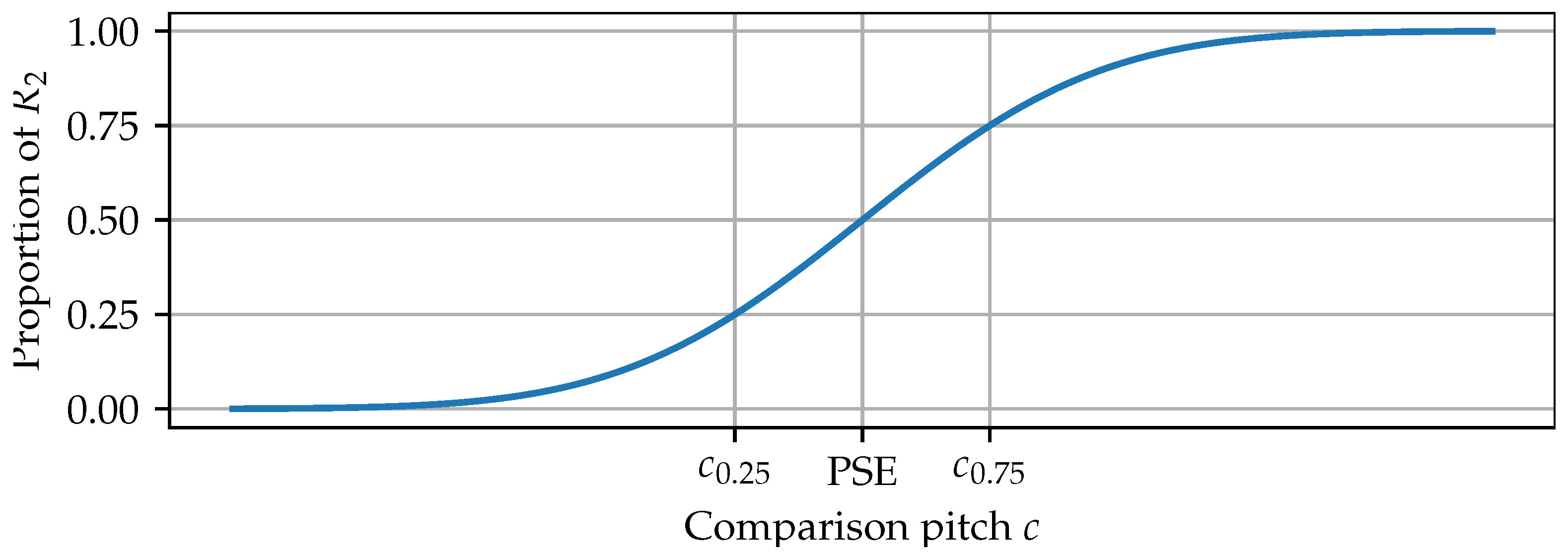
The just-noticeable difference (JND) also known as difference limen is often described as the minimal difference between two stimuli that can be noticed half of the time. Let us adapt the concise definition and method of computation from psychometric function analysis provided by [
62] to pitch changes. Suppose a subject is presented two succeeding tones as part of a pitch discrimination task. One of the tones is called the reference pitch
p, the other the comparison pitch
c. Responses
and
correspond to the choices
and
, respectively. There is no option
. A small set of tone pairs are repeated a number of times (15 to 20), and the subject has to choose one of the two responses. A psychometric function models the proportion of either
or
. For a fixed reference pitch
p the psychometric function for
should be a monotonically increasing function in the comparison pitch
c with values between 0 and 1, because for
c much bigger than
p the correct response
should be obvious. We will assume for simplicity that the shape of the curve fitted to the data follows a cumulative Gaussian as in
Figure 2, even though other functions such as sigmoid, Weibull, logistic or Gumbel are also a possibility [
63]. The point of subjective equality (PSE) is the comparison pitch at which the two responses in this discrimination task are equally likely, i.e., the median. Then, the JND is defined to be half its interquartile range, i.e.,
where
and
represent the comparison pitches, at which a change is detected with probability 0.25 and 0.75, respectively.
Notice that when two tones are played in succession the JND is bigger than when the two notes are played simultaneously. This is due to the interference discussed in
Section 2.7. Astonishingly, Section 7.2.2 of [
64] states that the JND for two succeeding tones with a pause (difference) is three times higher than the without a pause (modulation). Figure 7.2 in [
65] shows that the just-noticeable frequency modulation is approximately 3 Hz below 500 Hz and 0.7% of the frequency above 500 Hz. Clearly, the JND depends on the observer as well as other circumstances (noise) that might interfere with the perception of the signal.
The critical band is the frequency bandwidth within which the interference between two tones is perceived as beats or roughness, not as two separate tones. The JND is a lot smaller than the critical bandwidth. According to [
66] “a critical band is 100 Hz wide for center frequencies below 500 Hz, and 20% of the center frequency above 500 Hz”. A comparison between the critical band and the JND can be seen in Figure 7.2 of [
65] which in turn is based on Figure 12 in [
67].
In the context of periodicity, Stolzenburg [
6] uses the JND of 1% and 1.1% or, equivalently,
cent and
cent. In [
16], a standard deviation of 3 cent has been used due to experimentally obtained frequency difference limens of supposedly 3 cent [
68], even though the value of 1% in [
68] corresponds to about 18 cent as we have just seen. Still, the fact that they used the standard deviation of 3 cent for the Gaussian smoothing is an interesting aspect that we will revisit in
Section 4.4. It will be necessary to design experiments and perform further studies along the lines of [
69] to collect data for periodicity discrimination in the light of pitch and roughness correlations for tones within chords and between different chords, determine the best model and describe the dependency on noise [
43,
44,
70], which is beyond the scope of this work. Due to a lack of such a study, we will assume that cultural familiarity lets us associate slightly mistuned pitches with an ideal pitch and thereby detect and use the implied pitch for the perception of music.
2.9. Music Perception
Let us define music to be a temporal sequence of pitched sounds created by a formal system. Formal systems obey a set of rules for sound and rhythm, which are ultimately based on physics and mathematics respectively. Different cultures developed and are continuing to develop a variety of systems and scales besides the ones used in Western music [
71], for example Gamelan music [
35,
72], Arabic music [
73,
74], Turkish music [
75] and classical Indian music [
76]. In Western music, there are major subsystems such as classical and jazz music. Enculturation is an important factor in the listener’s musical expectation and perception [
77,
78], but we want to focus on a specific prevalent and in some way universal aspect of music, namely, pitch [
79,
80]. While the space of received sounds lends itself to a mathematical model, e.g., by using the frequencies and amplitudes computed by Fourier analysis, the spaces of produced and perceived sounds can be compared to it. Given a good microphone connected to some recording device and a good understanding of particle physics the space of produced sounds should be more or less the same as the space of received sounds. Our brain transforms sound waves of music by applying additional filters and perceiving pitch, timbre and loudness. There is also a short term memory effect in the brain, which we hypothesize to be responsible for the sense of resolution in certain chord progressions.
The perception of every person is different and can change via training or degradation. Sound and music are therefore very subjective and can be compared to food, in the sense that the chemical content of food corresponds to the Fourier decomposition of a sound, food can be analysed using chemistry just like we can analyse sound using Fourier analysis or harmony theory, different tastes can be analyzed using signal detection theory and can be described using various characteristics such as spiciness, sweetness, sourness, temperature, etc., just like sounds can be characterized as warm, loud, sweet, rough, etc., via a psychoacoustic analysis. In addition there is an after-taste to food, which might influence the characteristics of food-to-come, just like chord progressions need to be viewed within a musical context.
Chords are also called harmonies and play a key role in Western music. These can sound consonant or dissonant, and the change in this characteristic is an important aspect of musical pieces. Composers build up tension and resolve it subsequently by way of cadences. Notice that it clearly is not only a question of how consonant or dissonant chords sound in a chord progression: the precise way or direction of chord movement is important. It is this kind of aspect in music, that we want to illuminate by geometrically modeling the perception of chords. To this end, we revisit the geometric model of chords [
13] with a focus on music perception.
2.10. Mathematics and Music
While sound seems to be well-understood by physics and mathematical structures can be found at every point in music, neither one gives a deep understanding by providing a general principle of how music is perceived by humans. On the other hand, music itself is in reality a mathematical concept based on the brain’s perception of sound, put into action in a creative and aesthetically pleasing way: Any kind of scale has been developed mathematically to be compatible with some acoustic observations, rhythm is a time-dependent structure governed by elementary mathematics. Western music theory is a formal system consisting of an assortment of rules that have been deduced from various psychoacoustic preferences. An account of the major aspects surrounding mathematics and music can be found in [
81]. We want to emphasize the difference between two types of mathematical structures:
The first kind consists of superimposed formal systems in order to give music more structure and to make it more interesting. It starts with simple structures such as note lengths and bars to organize rhythm. Other examples include composition procedures such as the fugue characterized by imitation and counterpoint as well as various special techniques such as Kanon, Krebs, Umkehrung. Then, there is the twelve-tone technique invented by Arnold Schoenberg [
82]. For some of these structures we assume a twelve-tone equal temperament, which is itself a mathematical structure superimposed on pitched sounds, not accidentally but deliberately based on a second type of mathematical structure.
This second kind is more subtle, originally due to an evolutionary process and a preference for patterns but ultimately caused by psycho-physical mechanisms such as phase locking. It captures the structure inherent in music. It covers temporal structures such as rhythmic repetitions. Most Western instruments have approximately a harmonic overtone spectrum. Guided by the simultaneous or sequential perception of intervals and chords humans developed scales, instruments and music theory. Already Pythagoras discovered that simple rational relationships between fundamental frequencies correlate with pleasant sounding intervals. The twelve tones in an octave are also the result of simple rational relationships between frequencies, even though the two physical psychoacoustic qualities harmonicity/periodicity and roughness/interference have been shown to be fundamentally different [
9,
35]. Music theory is a formal system which captures more subtle perceptional aspects in Western music. It developed over centuries by the efforts of countless musicians and theorists, mainly however due to observed perceptive qualities of chord progressions.
Concise models of physical observations can be formulated in the universal language of mathematics, whose powerful tools allow us to deduce complex facts from simple ones. Therefore, the goal is to find a simple way of modeling sounds in the context of music perception, from which we can for example deduce good sounding chord progressions independent of functional harmony, create a music theory in other less common music systems as well as ultimately explain the established Western music theory of harmonies.
3. Riemannian Geometry of Chords
Tymoczko [
13] viewed the space of chords with
n notes as an orbifold [
83]. In [
84], the orbifold of chords had been generalized from a topological point of view, while we focus on the geometry. We argue that it is a Riemannian orbifold [
85] and show that the space of chords
with an arbitrary numbers of notes is a Whitney stratified space [
86] endowed with a metric given by the geodesic distance. The metric provides voice leading distance across different strata. Chord progressions can formally be viewed as sections of the (trivial)
-bundle over the real line. While our motivation is its use for Western music with its twelve-tone equal temperament, it can readily be adopted to other music. For simplicity, the geometric model represents the chords that can be played using a single instrument which can produce musical tones at any frequency (like a violin) but cannot duplicate notes (like a piano).
Pitches and frequencies can formally be identified with integers via
,
,
, etc. Therefore unit distance corresponds to a pitch distance of 100 Cent, which is compatible with the musician’s perception of distance between musical tones. The identification between frequency and pitch numbers is given by the function
where
corresponds to
. Chords can then be identified with integer tuples
. Instead, we will identify chords with tuples
for the following reasons:
There are usually minor pitch adjustments to make chords sound “better”.
The fundamental frequency can assume different values.
Quarter tones are entirely legitimate.
There are other tuning systems.
In particular, not even the piano is tuned using twelve-tone-equal temperament but their stretched tuning follows the Railsback curve [
60,
87].
We assume that instruments play pitches and that the perceived pitch is most relevant for our purpose. We do not include the overtone spectrum with all its amplitudes. When it becomes necessary it can easily be introduced.
Since chord notes are played simultaneously, the order of pitches in a chord is irrelevant. For example, the dominant seventh chord (0, 4, 7, 11) needs to be identified with (4, 0, 7, 11).
Lemma 1. Let be the finite symmetric group of all bijective functions .
- 1.
The permutationis a left action on . - 2.
The relationis an equivalence relation on .
Proof. Bijective functions of finite sets form a group.
We compute that
Therefore
acts on
from the left.
Clearly, the relation is reflexive since . If , we have for some . Since is a group we have . Therefore , and symmetry is satisfied. If and , then and for some . Therefore and so that the relation is transitive. □
Then the quotient by the symmetric group action is given by
, and its elements are written as
. This space
is known as the
n–the symmetric power of
and is an example of an orbifold [
83], a generalization of a manifold which is locally a quotient of a differentiable manifold by a finite group action. We can also identify notes with the same name but in different octaves before we consider the quotient by
. Then, we get the toroidal orbifold
considered by Tymoczko [
13,
14] in order to study efficient voice leading. From a mathematical point of view, this orbifold does not behave differently from
, but this model is not suitable for music perception. More importantly for us, Theorem 1 shows that it is a Riemannian orbifold [
85,
88,
89,
90] and a Riemannian orbit space [
91,
92,
93,
94].
Definition 1. A Riemannian orbifold is a metric space which is locally isometric to orbit spaces of isometric actions of finite groups on Riemannian manifolds. A Riemannian orbit space is the quotient of a Riemannian manifold by a proper and isometric Lie group action.
Proposition 1. Consider the metric on Euclidean space . Then, the symmetric group acts on by isometries.
Proof. Let
. Then, we obtain for any
by commutativity of the sum
□
This yields the following.
Theorem 1. The quotient space is a Riemannian orbifold and a Riemannian orbit space.
In order to study chord progressions it is necessary to consider chords of varying size. We need to construct a metric space of chords with an arbitrary number of tones that is useful for describing music. The metric should provide a sensible voice leading distance, in particular for chord progressions of the form or . Multiple same pitches as well as transitions between chords with a different number of tones can be dealt with by considering multiple same pitches in a chord only once, just like a piano plays chords. For example, is identified with .
Proposition 2. Consider the set of chordsThe relationfor all is an equivalence relation on . Proof. This is an immediate consequence of ≃ being an equivalence relation. □
This allows us to define the space of all chords.
Definition 2. Let the space of all chords and the space of chords with at most n pitches. Let . Let be the quotient map .
Remark 1. Notice that is the set of chords with exactly n different pitches.
Example 1. The space is the Euclidean plane as shown in Figure 3, where the points are identified with their mirror image when reflected across the diagonal, essentially equivalent to the lower (or the upper) triangle of the plane. consists of the singular points with respect to this reflection and is the boundary of . Lemma 2. The Stabilizer of the action of on is trivial for each .
Proof. The Stabilizer of action of on is given by . If then for some . Then, and therefore . Therefore is trivial for each . □
Proposition 3. is a Riemannian manifold of dimension n. The space of chords is the disjoint union of Proof. Due to Lemma 2 we have for . Therefore, is a canonical bijection, and inherits the Riemannian metric from . □
Remark 2. The family of chords is an example of a filtrationBy Proposition 3 the filtration of is an infinite-dimensional stratification, and are the strata of dimensions k. Remark 3. The Riemannian metric provides a norm for every . Furthermore, the Riemannian metric makes the orbifold into a metric space using the geodesic distance defined by Proposition 4. The distance on can be computed viawhere is an –metric on . Proof. In Euclidean space, the geodesic distance is given by the –metric. Let . Consider two representatives of p and q with und . Then, for which implies . Therefore is convex. Since is a fundamental domain for , the distance on is equal to the Euclidean distance in . Since the canonical projection is an isometric bijection, it follows that for we have . Since the closure of is also convex the same formula holds for all . □
Chord progressions in
with a small distance
correspond to efficient voice leading. The metric
on
clearly yields a metric on each stratum
. Finding a suitable distance on all of
is problematic. We can define the following functions
and
d and
and
, respectively:
Even if this is considered to be suitable for determining efficient voice leading, the following shows that this is not a metric on .
Proposition 5. The functions and d on and do not satisfy the triangle inequality.
Proof. Since we have
(see
Figure 4) this generalization does not satisfy the triangle inequality. The same holds for
. □
Since the aim is to do differential geometry on
the following result is important. See [
86] for a detailed treatment of stratified spaces from a geometric analysis point of view.
Theorem 2. For each , the filtration is a Whitney stratification of .
Proof. We show that Whitney’s condition B is satisfied. Consider the strata and for and embed them in some via a map . Let and be sequences of points in X and Y, respectively, both converging to the same point , such that the sequence of secant lines between and converges to a line in real projective space and the sequence of tangent planes to X at the points converges to a k–dimensional plane T of in the Grassmannian as i tends to infinity. The points uniquely lift to a sequence in . Let be the lift of Y to so that converges to . Choose the lift of Y such that . Then, uniquely lifts to a sequence of points in that converge to . Each tangent plane pulls back to the only plane in . The secant lines between and converge to a line in which is contained in . This implies that its push-forward is contained in . □
Since every stratum of is a metric space and a Riemannian manifold, and the notion of piecewise smooth paths makes sense in , we can define the geodesic distance on as follows.
Definition 3. We call a continuous path piecewise smooth, if there exists a partition of such that ρ restricted to is a smooth path in for some . Let be a piecewise smooth path, then we define if . The geodesic distance on is Theorem 3. The function d is a metric on . It can be computed via Proof. Clearly, . Since every stratum is a metric space and we have only a finite number of strata, we obtain for and . The concatenation of any piecewise smooth path from p to q and from q to r in is a piecewise smooth path from p to r, so that the triangle inequality holds. Therefore, the function d is a metric.
Let
be a sequence of piecewise smooth paths with
and
with a partition
of
such that
restricted to
is a smooth path in
for some
whose length converges to
. Since
is convex, this implies
Furthermore, we can assume that
because of this convexity. □
The metric on can be considered as a voice leading distance for music theory.
Example 2. Let us compute the distance between and . It can be computed by minimizing the concatenation of geodesic paths within and , and we obtainIn particular, we confirm together with and that the triangle inequality has not been violated as it was in Equation (
1).
See Figure 4. In summary, Theorems 1–3 show that is a well-behaved differential-geometric space:
This provides a rich structure for quantitative studies of psychoacoustic models with a voice leading distance on all of . The Riemannian metric allows us to study the shape of melodies and chord progressions by differentiating psychoacoustic functions and computing directional derivatives of paths in . This model is universal in the sense that it allows note and chord progressions in any musical system.
5. Music Perception
Time adds a layer of complexity to sound perception by way of considering paths and sequences in
. We will focus on musical expectation as well as on tension and release. Our ability to anticipate future events is another vital aspect of human evolution. Perceptual expectation has been studied in cognitive neuroscience [
69], and it is also a fundamental part of music perception [
25,
114,
115,
116,
117,
118]. Clearly, musical expectation depends on the listener, or, more precisely, on his brain and its musical training [
119]. It involves recognizing and predicting patterns both in sound and time set within a context. Among musicians this is also known as the concept of tension and release. Some aspects of its neuro-acoustic mechanism have been studied in the literature [
11,
120,
121]. While roughness plays a role in tuning, scales and the sound perception of chords, it is not audible in the psychoacoustic interaction between consecutive chords. We will demonstrate in this section why we should and how we can analyze a periodicity approach to tension and release using tools from differential geometry.
5.1. Tension and Release
Concepts related to the harmonic transitions are the circle of fifths, the Tonnetz model by Euler [
122,
123], the tonal pitch space by Lerdahl [
124], the tonal hierachy by Bharucha and Krumhansl [
5,
125], the gauge-theoretic approach to tonal attraction [
17,
18], and similar geometric structures describing harmonic relationships [
126,
127,
128]. Plus, the bass line clearly plays an important role in the perception of chord progressions [
129,
130]. There have been several studies about the relationship between these horizontal approaches and roughness, (vertical) harmonicity and as well as cultural familiarity [
100,
119,
121,
131,
132]. Both the models by Lehrdahl [
124] and by Bharucha and Krumhansl [
125] capture and describe distances for harmonic motions, and can both be viewed as a metric space in the mathematical sense [
133]. We will not view perceptive distances in harmonic transitions as a metric, because the order of tones or chords matters. Instead, we will show how to make the relations between notes and chords depend on the context and the order, and thereby remedy the limitations of geometric models mentioned in [
5] (119ff.). The intricate interplay between the voice leading distance presented in
Section 3 and harmonic transition is important, even though harmonies and harmony theory are often discussed without considering the individual note movement. The cognitive mechanisms are related and interfere with each other to create the sensation of transitional harmony. This is hinted at in [
127,
128].
Let us discuss the potential factors that affect transitional harmonicity. On the one hand we expect the basic principles behind harmonicity to play a role. We have not found much empirical evidence, but we hypothesize that the neuronal network mechanisms behind many sensations and particularly between horizontal and vertical harmony should be the same, and Tramo et al. [
36] (p. 96) also suggest that the vertical and the horizontal dimension of harmony is related. Therefore phase locking or an even more fundamental physiological principle will be behind transitional harmony. On the other hand we expect pattern recognition and the universal ability of detecting minima in sensoric input to be important. Minimization is implicitly used in defining the voice leading distance presented in
Section 3 given by the geodesic distance.
For our purpose there are two fundamentally different kinds of expectations:
If you listen to a piece of music, you can predict how it continues. You might be able to anticipate a few notes and chords depending on your training and background. Your anticipation will be based on tempo, meter, rhythm, melody, dynamics, form, chord progression which are time-dependent aspects of context. In the language of our geometric model: From a path in we want to anticipate its continuation. This will depend on its speed and its shape, including its direction, its curvature and other geometric aspects. You can compare a musical piece to a roller coaster ride, which you should construct or analyze using differential geometry. However, it will also depend on a second, time-independent kind of expectation.
Assume you are listening to a single chord, and you have to predict which chord could follow. You might wonder, which context this is in, and this might partially be responsible for your expectations. As before, it is based on your training and background. However, there are physical reasons for your anticipations as well. This certainly has to do with consonance of chords and voice leading, but also with the order in which two different chords are played. We can view this expectation either as a psychoacoustic evaluation of difference vectors on
or of ordered pairs of chords. We call this time-independent psychoacoustic quality for an ordered pair of chords the resolve. This time-independent quantity has been studied under different names in [
100,
134,
135,
136], but we would like to emphasize its dependence on its contextual reference by giving it this new name.
A progression of notes and chords with or without additional bass notes can be described as a sequence of points in , which can be viewed as a discretization of a path in parameterized by time. It can be approximated by a differentiable path. Either way, we can study differential geometric properties such as speed, momentum, acceleration, and angular speed in order to analyze and understand chord progressions better. Furthermore, we can consider differential geometric properties of the path after applying suitable height functions. We hypothesize that the time-independent expectation can be deduced from the resolve by way of differential geometry. If we are at a point , we can quantify the resolve as a height function on . In other words, the resolve is a function on .
Some interesting questions arise, which we do not attempt to answer here: Is the resolve the result of a priming with ordered pairs of chords based on cultural familiarity and training, or is it a multi-dimensional vector intrinsic to the starting chord or a local neighborhood of the starting chord, i.e., without the necessity of having ever heard the second chord? Is the training happening on the level of some basic neuronal mechanism for any chord progression or do we need all kinds of pairs of chords as training data? Do musicians and composers imagine the succeeding chord or do they sense the direction in which they have to move the notes?
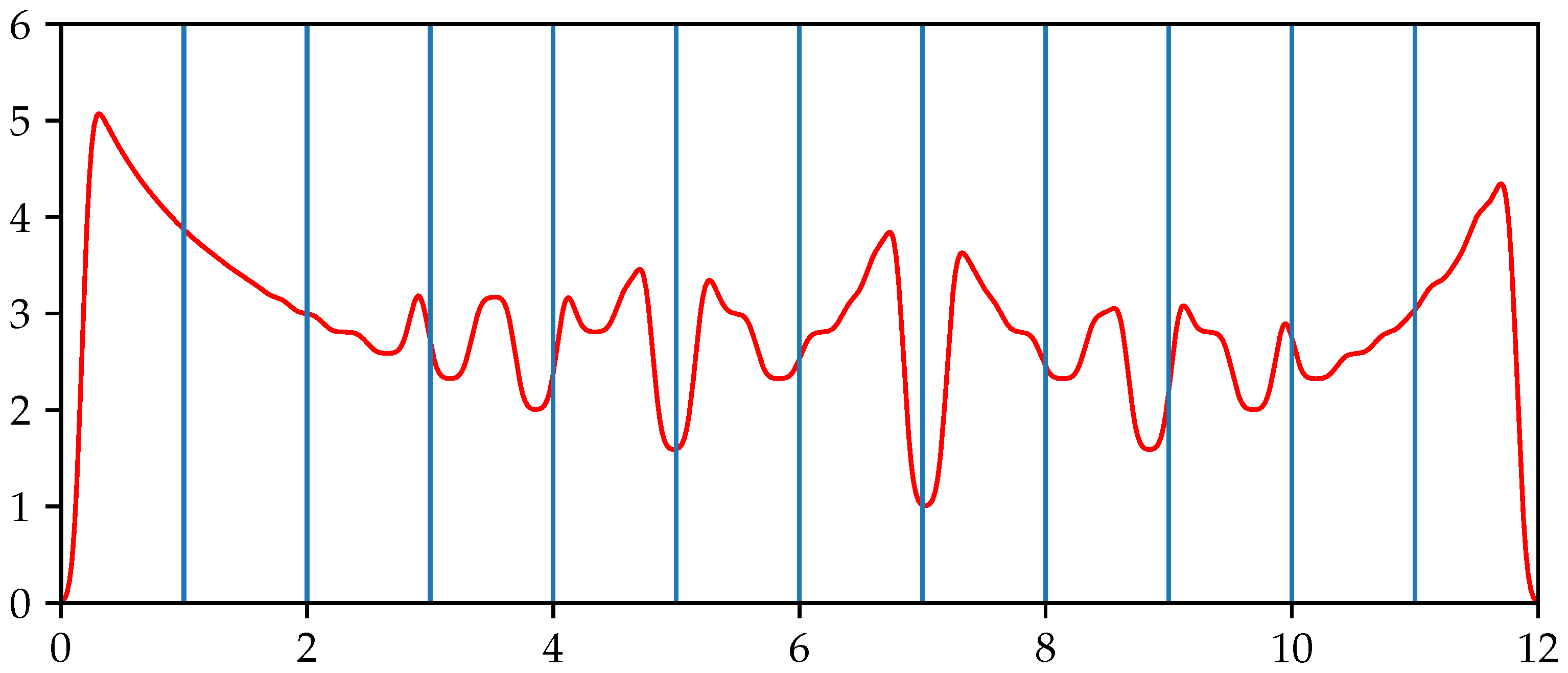
Research from [
11] attempts to quantify the resolve. They call it transitional harmony and compute it via
where
and
are the largest and smallest multiples of the chord tone periods that (nearly) coincide with the chord periodicity
which we introduced in
Section 4.5 and where the indices
s and
p correspond to the succeeding and nearest preceding chord, respectively. Even though the authors have found some strong correlations shown in Table 3 of [
11] supporting the validity of
, we question the definition due to its strong dependence on small pitch changes: music perception should not change a lot by small pitch variations, but it does in the definition given by Equation (
4). We hypothesize that the correlations found in Table 3 of [
11] are due to the correlation between harmonicity and roughness for instruments with harmonic spectra.
5.2. Two-Chord Progressions Starting with a Tritone
In order to motivate various approaches to the resolve we consider two-chord progressions of dyads within 12TET starting on a tritone where at least one note changes and each note does not move more than a semitone. Let us ignore the choice of octave in this section. There is a total of eight such chord movements.
The two parallel tritone movements considered on their own and out of context do not sound like they resolve anything, but adding the bass lines or yields the standard chord progression as and , respectively, where the tonalities are clearly very far away from each other. The first note in this notation always corresponds to the bass note. On the one hand this simple example confirms the well-known assumption that chords should always be viewed in a context, but on the other hand it represents the charm behind the technique of modulation in music. It is therefore nevertheless necessary to consider chord progressions without a given tonality or context. It just leaves chord progressions ambiguous, and probabilistic methods can be employed.
The strongest resolution from the perspective of periodicities or ratios should clearly the progression to the perfect fifth or . However, it does not sound like a good way of resolving the tritone. If we think of the notes as attracting or repelling magnets then both the notes should move in opposing directions in order to resolve the dissonance, which we will consider in the next paragraph. However, we can again add bass lines to make the first progression sound like the jazz resolution to the major seventh chord given by and the second progression like the resolution or partially represented by and , respectively.
The chord progression into a perfect fourth or also does not sound like a good way of resolving the tritone. Again, we can put them in a suitable context by adding bass lines. The first progression sounds like the jazz resolution to the major seventh chord partially given by and the second progression like the resolution or partially represented by and , respectively.
The best sounding dyad progression is the tritone
resolving into the major third
or the minor sixth
. Even though these progressions already sound like resolutions, it helps to view them in a context and a tonality in order to relate them to music theory. Possibly, our brain has already been primed for possible tonalities, and some tonalities are more probable than others. Clearly, the corresponding chord progressions are
partially represented by
and
. Notice that the tonality is already determined by the progression of dyads, the bass line only emphasizes the tonal center. An insightful work by Tom Sutcliffe [
137] picks up on the gap in the literature of failing to explain why voice leading in combination with root progressions is used in tonal pieces.
Let us describe a few possible approaches to transitional harmony between two chords, consider the differential geometry and revisit the above example.
5.3. Transitive Periodicity from the First to the Second Chord
Musical structures such as rhythmic patterns and periodicity cause phase locking [
138]. We therefore assume that the brain relates two chords
and
of a chord progression
through the working memory based on phase locking as described in
Section 2.3. On the one hand this seems compatible with the strong preference to descending fifths and ascending fourths over descending fourths and ascending fifths. On the other hand, if
and
only consist of one note each, a low periodicity of
with respect to
is desirable, because the neuronal firing is synchronized. This seems to be incompatible with voice leading at first, but as soon as you consider small chord movements with respect to voice leading, it is possible to move a short distance while being close with respect to phase synchronization. Therefore, we introduce a transitive periodicity analogously to the periodicity definition given in Equation (
3).
The transitive periodicity from
to
is the number of periods of
necessary to match up with a period multiple of
, where the periods for
and
are each due to phase locking. Formally, transitive periodicity from
to
is the periodicity of
relative to
, where
is the (set-theoretic) union of
and
:
Figure 10 shows
,
and the combined chord
.
This corresponds to computing
, but due to the JND from
Section 3 the smoothed periodicities are not the correct quantities to be used for computing transitive periodicity. We need to view
,
and
in the context of their related periodicities before smoothing. Due to technical difficulties we need to work with
rather than its quotient
. In analogy to
Section 4.5 we define
and for pitch tuples
Informally,
contains the
–tuples
with representatives
und
of
and
so that the periodicity of
relative to
is
p. In order to improve readability the first
n entries in the elements of
correspond to
. In order to incorporate approximations within a JND we define transitional periodicity
via
Just like in the case of periodicity in
Section 4.5 we can use the logarithmic transitive periodicity. In order to extend
p to
, it will be necessary to shift a chord
and
so that the lowest note of
is 0. For
let
and
. Then,
will be redefined as
.
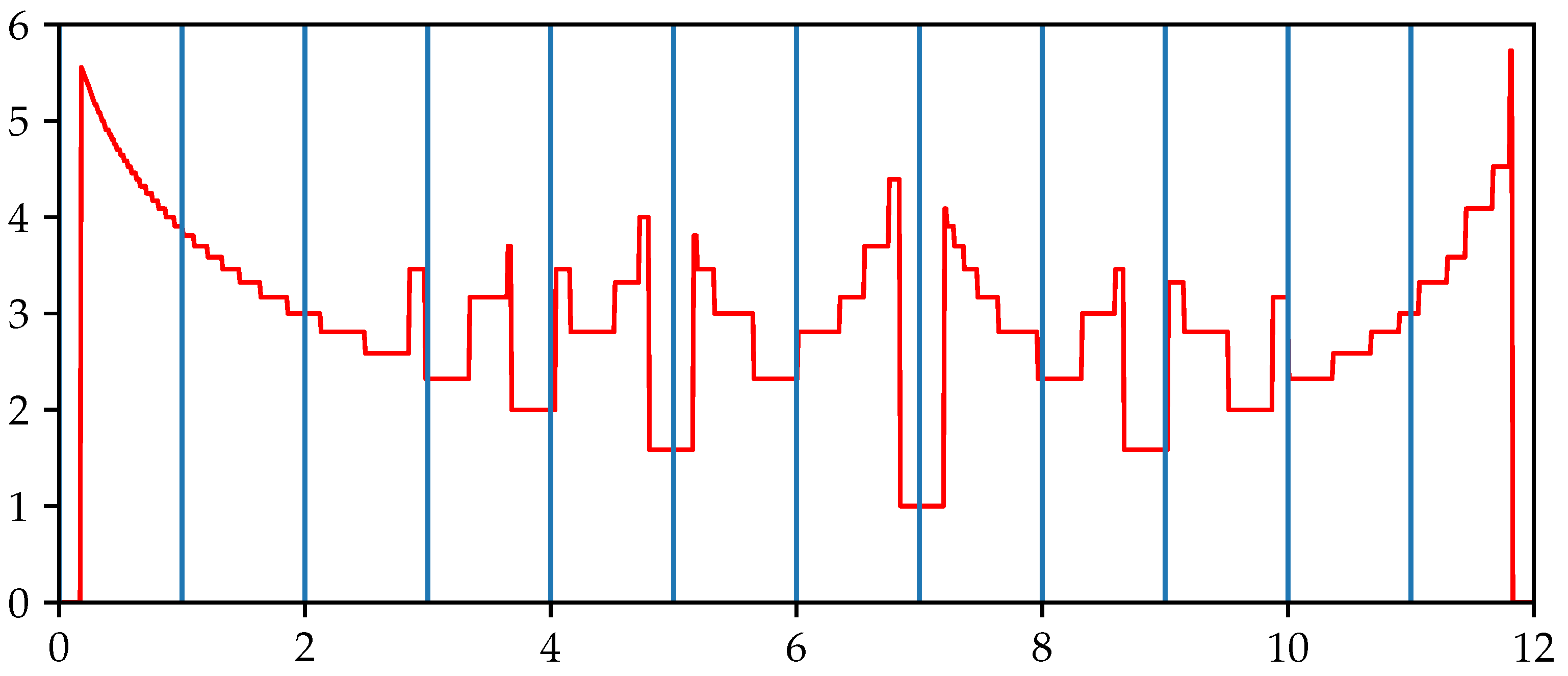
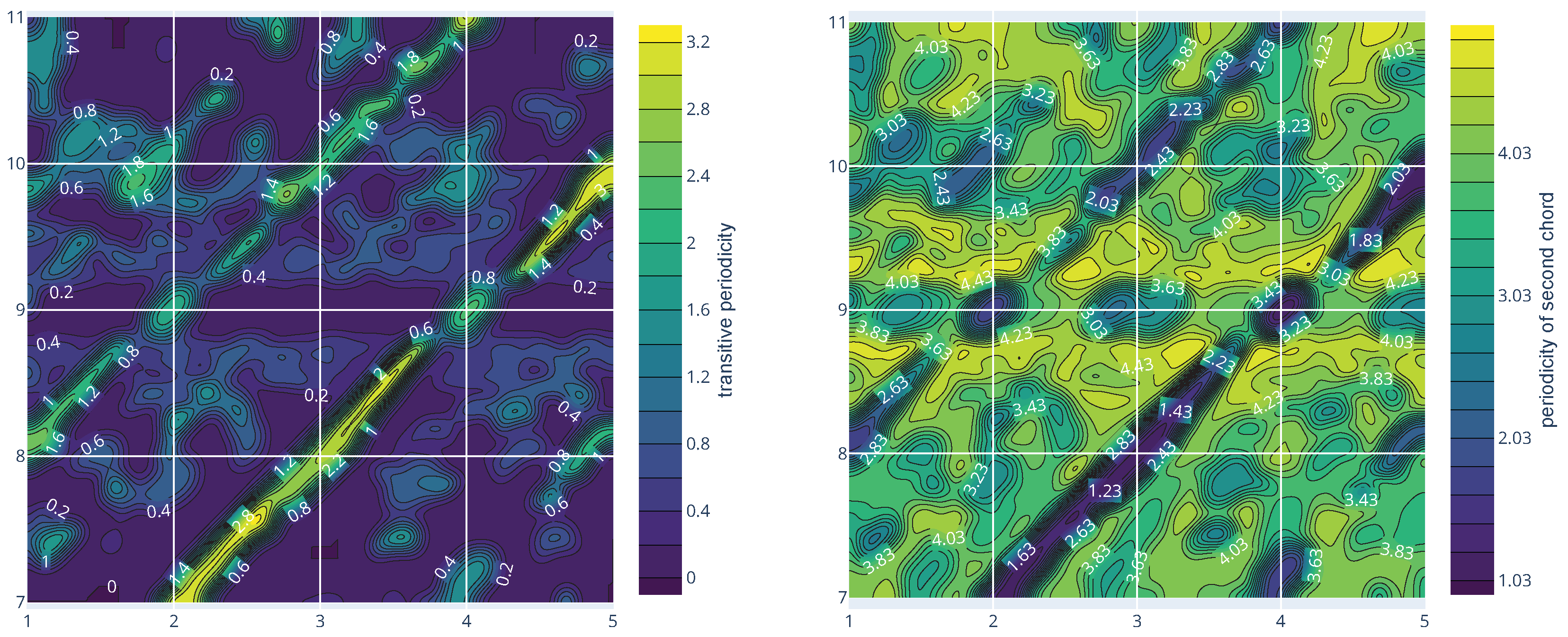
Let us revisit the example in
Section 5.2. The local neighborhood of the transitional periodicity
starting with the tritone
with the corresponding periodicities of
is shown in
Figure 11.
Notice that while the periodicities of the perfect fourth and fifth are smallest, the transitive periodicities resolving to the perfect fourth and fifth are bigger than the transitive periodicities resolving to other chords. Even if small transitive periodicities play a role in chord resolutions, they do not fully explain them. The algorithm for determining the transitive periodicity step function as in Equation (
3) is shown in Algorithm 2, where we define for
since we want
and
to be close with respect to voice leading. In the algorithm we need the projection to the last
n coordinates
.
We hypothesize that transitive periodicity will play a role in combination with the usual periodicity. A good chord resolution will have a low periodicity for the second chord as well as a low transitive periodicity .
The combined chord offers more possibilities for transitive quantities that can be studied in the context of music perception. For example, we can consider the periodicity
of
relative to
for the chord progression
.
| Algorithm 2 Determine transitive periodicity step function |
Require: ▹ = number of tones in Require: ▹ = chord with m tones Require: ▹ = maximal distance between the tones of and ▹ q = periodicity index ▹ Consider all chords with n notes close enough to whiledo ▹ While there are chords without periodicity for all do ▹ For all chords with relative periodicity q for all do ▹ For all new chords within JND ▹ Set periodicity to q ▹ Update new chords end for end for ▹ Increase periodicity index by 1 end while
|
5.4. Directional Derivative of Periodicity
Melodies and chord progressions not only have a sense of direction in , but the rate of change in psychoacoustic quantities with respect to these directions should play a role in music perception. Assuming that periodicity is a good measure for consonance, chord resolutions should decrease periodicity while traveling only a small distance with respect to voice leading. If this perceptive quality is truly local then the infinitesimal change in periodicity can be formulated using directional derivatives in chord space.
Due to the soft computing skills of our brain, periodicity on
can be considered to be continuously differentiable. Let
v be a tangent vector of
at a chord
. Let
be a continously differentiable path with
. Then, the directional derivative of the periodicity in the direction
at
is given by
The more negative
is, the stronger its resolution in the direction
v is perceived. It is not enough that the final chord is more consonant. For example, either resolution from a tritone to a perfect fifth in 12TET does not sound as good as the one to the minor sixth or the major third as we have discussed in
Section 5.2.
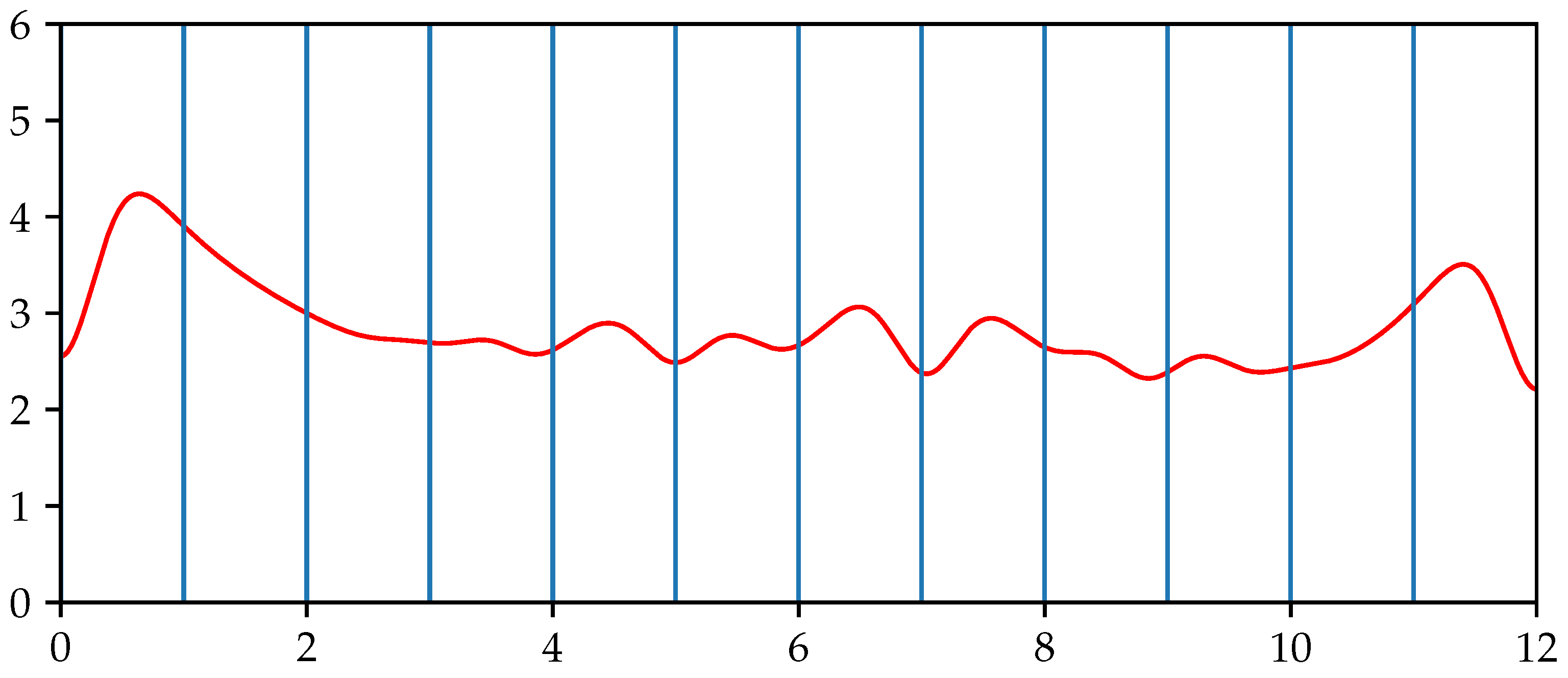
On the other hand, the parallel movement of chords does not change periodicity. This implies that
vanishes for
. Clearly, maximal infinitesimal change in periodicity (either negative or positive) is provided for
and
. If
Figure 8 is correct, however, then only a very small repelling movement will reduce periodicity which does not yield harmonic relationships of chords. The progressions
and
will increase periodicity. The progressions to the perfect fourth and fifth
and
will certainly decrease periodicity. Interestingly enough, the only feasible progressions
and
in 12TET do not reduce periodicity by much or at all. Still, they are the best resolutions available in 12TET.
While the directional derivative presents an interesting approach it needs to be viewed in combination with other aspects of transitional harmony as part of a Pareto optimal solution. Possibly, the periodicity function shown in
Figure 8 needs to be corrected as well. However, it shows that, in the case of the tritone, the chord progressions with the maximal effect on periodicity will move each note simultaneously inwards or outwards. Furthermore, it suggests that quarter tone movements will be the best chord resolution when considering periodicity only. This hypothesis is confirmed by the author’s perception.
6. Results and Discussion
Music is considered as something real and vital for humankind, but no attempt on a holistic model for music perception has yet been attempted. Clearly, humans do not perceive musical sounds as the complicated audio waves they are or as the way they are presented in music notation but as something simple and often beautiful. While music theory formalizes the music we perceive, music psychology carries out empirical studies about specific perceptive aspects. We envision that it should also be possible to deduce music theory from music psychology with the correct holistic model for music perception. Using psychoacoustic results and facts from music theory it should be possible to reverse engineer this model. With this in mind, we have introduced mathematical structures that allow for rigorous quantitative studies of music perception based on the mechanics described by physical or neuronal models. We laid an emphasis on a rigorous approach that is not more complicated than absolutely necessary and which can be extended when needed.
We revisit ideas by Tymoczko [
13,
14] to prove that the space of chords
is a metric space and a Whitney stratified space with a Riemannian structure. The geometry of
is not much more than Euclidean space itself. However, it allows us to apply calculus across different strata of
. Furthermore, the Riemannian metric on
allows us to consider the geodesic distance across different strata which yields a voice leading distance satisfying the triangle inequality. The geodesic approach is surprisingly simple and natural considering the common desire that distance functions satisfy certain conditions and in view of more elaborate attempts regarding voice leading distances [
127,
139,
140]. The space
only contains the objects for music production, but not any information about music perception.
Psychoacoustic quantities can be viewed, computed and analyzed as height functions on
. In particular, we have modified the periodicity approach to consonance by Stolzenburg [
6] in order to present a definition of periodicity for arbitrary chords. Roughness is another way of interpreting dissonance. Height functions themselves are static. Music is a dynamic process, so it might be necessary to consider the change in height function as a dynamical system in order to deduce properties of music. All of the psychoacoustic functions can be assumed to be differentiable which enables us to use tools from differential geometry to study them by considering gradient vectors and directional derivatives.
The height function for periodicity led to two possible approaches for transitive harmonicity. In particular, we showed how to use the differential structure of the periodicity graph on to study geometric properties of paths in and their respective lifts to the graph of psychoacoustic functions on . We implicitly assume that the geodesic distance agrees with the psychoacoustic reality. This needs to be verified empirically. Although we do not expect our two approaches for transitive harmonicity to be valid, we expect that other approaches to music perception can be analyzed using the differential geometric framework. Clearly, music works, because we look at a discrete subset of chords with certain properties. It will be interesting to see which tools are the correct ones for discretizing the differential-geometric model.
The differential-geometric structure invites studies that falsify or confirm psychoacoustic models for music. Ultimately, this approach can close the gap between music theory and music psychology. Even though the mechanisms discussed here stem from Western music, they are founded on more general physical and neuronal principles, which are in theory applicable to music from other cultures or sounds with inharmonic spectra. Furthermore, it will be interesting to study, generalize and extend the mathematical structures themselves and to incorporate statistical aspects of music perception in the model.