3.1. Curve Interpretation
Our objective is to establish a framework in which a given song, represented in three-dimensional space, can be analyzed using the “total curvature” approach. This approach enables us to evaluate the complexity of the song based on its geometric properties. By understanding and incorporating these concepts, composers and musicians can enhance the process of composition and performance. They can consider factors such as the number of laps, direction, and other related elements to determine the appropriate chord progressions and musical movements that align with the desired artistic expression. In the subsequent discussion, we will delve further into these aspects.
To facilitate our geometrical representation, we will focus on guitar chords consisting of triads, which are composed of three notes. In the case where a chord consists of more than three notes, we will consider only the first three notes, following the approach outlined in [
2].
To represent these triads in a geometric context, we will map them to points in the three-dimensional space . This space allows for the incorporation of the twelve possible pitches or tones in Western music theory. Each component of the point represents a note within the chord, and the combination of these three components defines the specific triad in our representation. By utilizing this mapping, we can explore and analyze the geometric properties of the triads within a three-dimensional framework.
By considering each chord as a vertex, the sequence of chords can be represented as an oriented curve. This curve connects the vertices in the order of their appearance in the song, providing a visual depiction of the chord progression.
It is important to note that multiple curves can pass through the given set of vertices, as there are various ways to connect them while preserving the sequence. However, our mathematical exploration aims to find consistent results regardless of the specific curve chosen. The analysis of the geometric properties and the application of mathematical tools will ensure that the chosen curve accurately represents the underlying musical structure and allows for meaningful comparisons and evaluations.
Notice that, with our geometrical approach, the sequence and define the same curve but in opposite directions.
To facilitate the conversion of a computer plot into a physical object, we initially developed a “working model” or technical model, as depicted in
Figure 3. In this model, we identified two key visual elements that we aimed to explore: (1) the curve representing the chord progression and (2) the coordinate system.
The wire in the model represents the edges defined by the vertices, forming a polygonal curve within three-dimensional space. This model served as a valuable tool from both a mathematical and design perspective. Mathematically, it provided a natural representation of a polygonal curve, which is one of the possible curve families that can pass through a given sequence of vertices. From a design standpoint, the physical aspect of interacting with the wire stimulated discussions regarding the use of different materials to convey distinct sensory experiences associated with the transitions between successive chords.
Overall, this working model played a crucial role in bridging mathematical concepts and design considerations, allowing us to further explore the geometric representation of the music and consider the tangible aspects of the chord progression.
This polygonal curve will be our geometrical approach to expressing music.
Figure 4, shows how a smooth curve (the derivative is continuous as well) can be transformed to a polygonal curve which preserves the total curvature properties. By these ideas, any simple curve that goes through these vertices can be selected, so we choose the closed polygonal curve.
The following proposition will define exactly the set of songs/curves we will deal with.
Assertion 1. To streamline our analysis, we specifically focused on the choruses of songs where the musical composition starts and ends with the same triad. This characteristic ensures that the chord progression forms a closed curve, simplifying our geometric representation.
In instances where the chords or vertices give rise to two-sided directional edges, we define the curvature as zero. This choice allows us to effectively handle cases where the curve transitions between chords without introducing curvature variations.
Lastly, if the same chord repeats in a successive manner, from the geometrical point of view there is no change in the chorus structure, so we will write this chord only once; as an example, see the sequence in Equation (1), which defines the chorus of “Across the Universe”. By imposing these simplifications, we aim to establish a clear and manageable framework for studying the geometric properties of choruses in music. This focused approach enables us to delve deeper into the analysis and interpretation of the musical structure within a three-dimensional context.
The special case of choruses of two chords is trivial and will not be discussed in our exploration.
Indeed, the characteristic of choruses in Western music often starting and ending with the same chord is quite prevalent. A preliminary examination of Beatles songs, as documented in [
1], reveals a considerable number of instances where this pattern is observed. Songs such as “Across the Universe”, “All Together Now”, “Ask Me Why”, “Baby in Black”, “Cry Baby Cry”, “Golden Slumbers”, “I’m So Tired”, “Julia”, and many others follow this structure.
Having developed our mathematical formulation, we are now prepared to showcase our construction and present the results, specifically focusing on the Beatles’ choruses. By applying the total curvature approach and exploring the geometric properties of the chord progressions, we aim to offer valuable insights into the complexity and structure of these iconic songs. This analysis provides a unique perspective that is accessible to both professional musicians and non-professional audiences with an interest in mathematics and music. Through this endeavor, we hope to enrich the understanding and appreciation of the Beatles’ music and contribute to the broader exploration of music through a mathematical lens.
The chorus of the Beatles’ song “Across the Universe” is defined by a sequence of three chords. In this particular case, the chord progression follows the sequence
which is a closed curve; see
Figure 5. This visualization emphasizes the simplicity of the chorus for the non-professional audience with the three-dimensional triangle (respective to the three different chords), while from the mathematical point of view, the curve wraps the triangle twice, which can be considered as an additional insight into the song structure. In our model, we decided to include this number of laps (wrapping).
The chorus of “Ask Me Why”, is obtained by
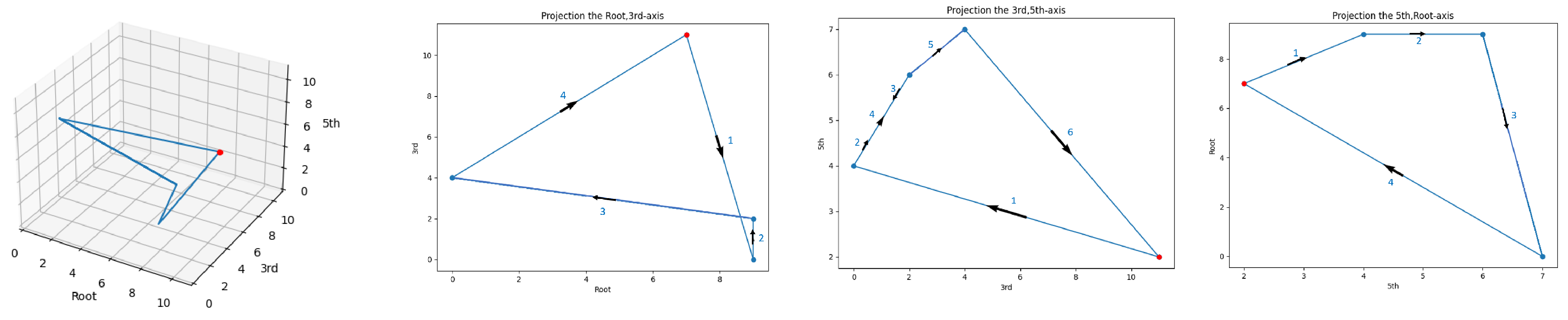
While the number of chords is similar to “Across the Universe”, it visualization is different. First, as seen in
Figure 6, while the three-dimensional curve is a simple curve, the projection of the root and third leads to a point where the curve intersects itself. In addition, in each of the projections, there are no laps. So the behavior of these two choruses that are represented by curves is different (by a proper measure).
Note that in three-dimensions, only the absolute value of the curvature is well defined, but since there is no curve direction (as clockwise or counterclockwise), the total curvature is meaningless. This leads us to project the three-dimensional curve onto the plane in three different ways by omitting one of the axes in each of the projections, where the total curvature or index is well defined. This projection onto three planes leads to three total curvatures, which will be the respective characterizations of the three-dimensional closed curve; i.e., each chorus has a respective vector of curvature which is obtained by the projections. As we already discussed, this calculation of total curvature or index for a close curve is determined by the index that holds the curve and not by local property, so we can choose the edges as straight lines, a polygonal curve, and the curvature will be obtained only in the vertices.
Remark 1. These projections show ‘the contribution’ of each note in the triad. If the plot is a thin domain (as an acute triangle), this hints that the respective notes are located ‘nearby’ and vice versa, as in some of the projections in the Beatles songs below.
Remark 2. Notice that curvature zero can be obtained in different cases, where the number of clockwise laps is equal to the number of counterclockwise laps. This complexity, for a chorus with more than three chords, led us to think of this case as an indicator function, i.e., if there exists such a ‘turn’ (curvature zero) or not.
3.2. Curvature as a Tool to Estimate Musical Complexity
Now, we are ready to apply our model.
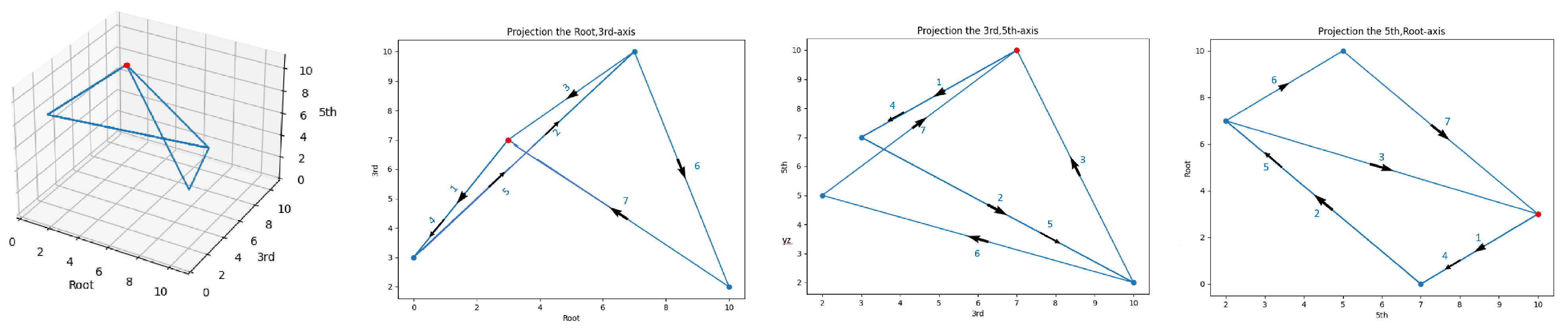
Figure 7 describes the process from the chorus of “Get Back” to the respective curves. In a similar way to “Across the Universe”, a
triangle is obtained. The
projection (green triangle) is a closed counterclockwise curve with a respective total curvature of
. The second projection leads to the red triangle, with a respective total curvature of
(closed clockwise curve). The third projection leads to the blue triangle, with a total curvature
. So, using our visualization, all choruses (geometric objects) which are defined by
in the same equivalent class, i.e., have the same total maneuver which leans on the total curvature vector of the curve.
Figure 8 represents the Beatles “Like Dreamers Do” chorus; as can be seen, despite the projections defining a non-convex domain, the
and
do not affect the total curvature (or index). In the
projection, a kind of knot, which leads to curvature zero, is obtained that can indicate a more complex move between chords compared to “Get Back” and may indicate the guiding hand of the composer trying to transmit. Finally, this chorus is defined by the total curvature vector
.
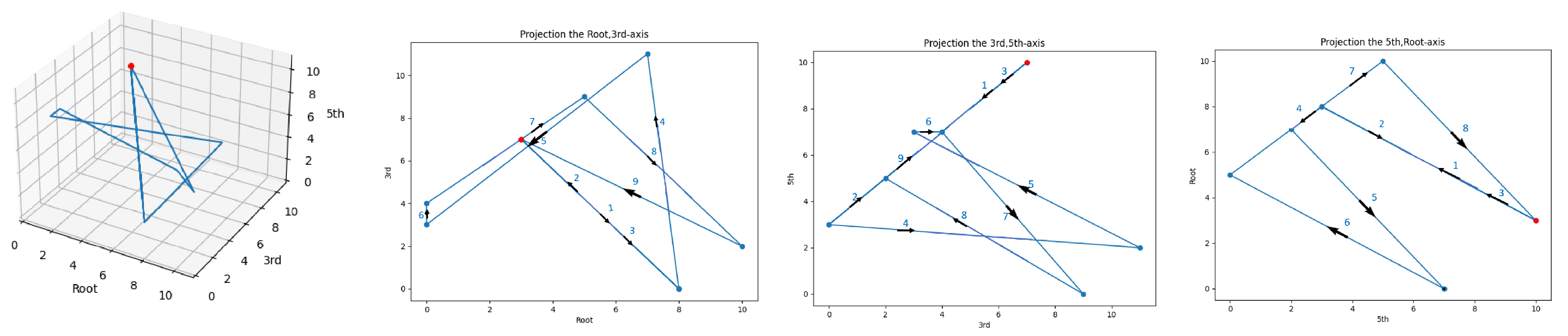
Figure 9 represents the Beatles “Hello, Goodbye” chorus. Notice that in the second and third projections, some of the chords are on the same edge, which are repetitions, and the numbering explains the direction of movement and gives the progression’s feel along the curve. Notice that in the
projection the curve is wrapped twice—two laps. In the first projection
, the total curvature is zero and leads to a knot, ‘feel’. The respective vector in this case is
.
Figure 10 leads to the vector
and can give a glance to the audience with no music theory background on how complex music can go with our geometrical representation, where a few laps (clockwise or counterclockwise) can give a “dizzy feel”, which may indicate that there exists at least one point in the projection, in which the curve defined its index (for more details, see Winding numbers in [
14]).
Remark 3. Since a major triad with root r is defined by and a minor triad by , if the chorus is not defined by a translation of a single chord, then the polygonal curve (where the number of chords ) cannot be embedded in the two-dimensional space; i.e., there exists a polygonal projection for each of the two-dimensional axes , and .
This exploration by a vector of curvature or index (by omitting ) can give us a new dimension for exploring songs; it does not give attention to the number of chords which define the song or the distance between them but examines the sequence of triads that constructs the chorus as a curve. The direction of progression along them leads to the respective behavior of the chorus, which is defined by laps, knots, and more, and all together can indicate the global structure which has been determined by the composer.
Indeed, the theoretical approach of exploring songs as geometric objects based on the progression of chords can establish connections between different songs that may not share the exact same chord progression but exhibit similar global progressions along their choruses. This highlights the importance of the overall pattern and movement of the curve rather than the specific chords themselves.
Furthermore, considering that a song can have multiple versions with different chord arrangements (such as live performances or recorded variations), the player or composer has the flexibility to choose the desired geometrical properties that best represent the intended musical motive. They can make decisions such as determining the number of geometrical loops present in the curve, whether the curve changes direction, and more. By manipulating the geometrical structure of the curve, the user can convey their artistic interpretation and enhance the musical experience for themselves and the audience.
This approach provides a creative and intuitive way for players and composers to engage with and shape the musical composition, allowing them to express their artistic vision through the chosen geometric properties of the curve. It opens up possibilities for exploration, interpretation, and customization, ultimately enriching the musical experience and offering new avenues for creativity.
One of the intriguing aspects of the method is its potential to sort choruses into equivalent classes based on their total curvature. By assigning a measure of complexity through the total curvature, choruses with similar geometric structures can be grouped together, regardless of the specific chord progressions or musical styles they belong to. This allows for a novel way of categorizing and comparing different songs, transcending traditional genre boundaries.
Furthermore, the geometric structure of a chorus can serve as a common ground to relate and connect various musical styles. Different musical styles may have distinct chord progressions and harmonic patterns, but their underlying geometric structures can reveal shared characteristics or similarities. This offers a fresh perspective on exploring and understanding the relationships between different musical genres and styles, potentially bridging the gap between diverse musical traditions.
By employing a geometrical framework, our method enables a unified approach to analyze and interpret choruses across musical styles, fostering a deeper understanding of the underlying structures that shape musical compositions. It opens up possibilities for cross-genre collaborations, creative inspiration, and the development of new musical ideas by drawing upon the geometric connections and relationships between different styles.
In
Appendix A additional exploration of Beatles choruses, where all explorations together give the reader an immediate chosen song comparison