Magnetic Field Influence of Photo-Mechanical-Thermal Waves for Optically Excited Microelongated Semiconductor

Abstract

A theoretical novel model is investigated that describes the dynamic effects of the microelongation processes of an exciting semiconductor medium. The influence of the magnetic field for the optically excited medium is taken into consideration according to the photothermal transport characteristics. The governing equations were derived during the electronic (ED) and thermoelastic (TED) deformation processes when the microelongation parameters of the semiconductor medium were taken into account. The interference between thermal-magnetic-microelongat-plasma-mechanical waves is investigated. The dimensionless expressions are utilized to solve the main equations according to the harmonic wave technique in two-dimensional (2D) deformation. The complete solutions of the expressions of the physical field were obtained when some conditions were taken on the outer semiconductor surface. The theoretical microelongated semiconductor model in this investigation was checked by comparing it with some previous studies. The numerical simulation for the main physical field distributions is graphically displayed when the silicon (Si) material is used. The impact of various factors such as the magnetic field, thermal memory effect, and microelongation on the wave propagations for main fields was discussed.

1. Introduction

Recently, the photothermal (PT) technique was established as an effective method to investigate the thermal and electronic properties of semiconductor materials. Semiconductors are materials that have recently been studied in depth because of their great importance in many modern industries such as sensors, solar cells, and advanced medical devices [1,2]. It is worth noting that most renewable energy production depends mainly on understanding the nature of semiconductors. Semiconductors are materials that are not sufficiently dielectric and also are not well-conductive. When the optical energy falling on the surface of a semiconductor material is absorbed, the electrons and the internal holes of the material are excited, and electronic deformation (ED) appears. The excited electrons move as a result of the thermal effect of light (optical energy) on the surface quickly, forming an electron cloud that can be described as convective density or plasma waves [3,4]. As a result of photo-excitation and the consequent thermal effect, a change occurs in the internal structure of the material in what is known as thermoelastic deformation (TED). According to that thermal excitation and transfer of electrons, mechanical (elastic) vibrations occur. Therefore, semiconductors are studied using the theory of thermoelasticity in addition to the photothermal theory. With the internal changes according to ED and TED, the microinertia transport of the microelements of the semiconductors should be taken into consideration [5].

With the development of the study of semiconductors depending on the rotational movements (micro-deformation) of the internal particles, the microelongation should be considered [6]. Several theories describing the micropolar theory of the internal particles of elastic bodies according to the microstructure were presented by Eringen [7,8]. As a special case of the theory of micromorphic, a new theory has been introduced, which is the microstretch thermoelasticity theory. Recently, the theory of microstretch thermoelasticity has been addressed by many researchers along with the study of many of its theoretical applications [9,10,11,12]. Lotfy and Othman et al. [13,14] used the effect of a magnetic field through a gravity field with initial stress to study the propagation of waves through an elastic body using the thermo-microstretch theory. Some scientists have used the theory of thermo-microstretch to study the governing equations of a hydromechanic viscoelastic porous medium [15,16]. Taking into account the effect of microelongation parameters, the effect of varying heat sources on a functionally graded microelongated elastic medium was studied [17,18]. Ailawalia et al. [19,20,21] studied the plane strain deformation according to the thermoelasticity theory when the microelongated elastic medium is considered under the impact of an internal heat source. On the other hand, Marin et al. [22,23,24,25,26,27] used the dipolar elastic bodies to develop the micropolar and microstretch theories according to the harmonic vibrations.

Gordon et al. [28] studied the long-transient effects due to the effects of red light absorption when using liquid samples that were exposed to a beam of laser rays. During the photoacoustic spectroscopy (PAS) of semiconductor material, the photothermal technique was used to understand the wave propagation properties of semiconductor materials [29]. In the context of photothermal excitation processes, many modern electrical engineering applications have emerged for the use of semiconductors in many industries [30,31,32]. Hobiny and Abbas [33] investigated the photothermal method to study the 2D deformation of thermoelastic interactions in semiconductors. Todorovic et al. [34,35] investigated the optically induced according to the ED mechanism in the context of the PAS technique for microcantilevers semiconducting. Lotfy et al. [36,37,38,39,40] studied the thermal effect of light and laser on semiconductors by studying the overlap in the governing equations between the theory of thermoelasticity and photothermal, and a new theory emerged, which is the photo-thermoelasticity theory. The effect of magnetic field with the Thomson effect was applied to investigate the photo-thermoelasticity theory according to the hyperbolic two-temperature theory when a polymer semiconductor material is used [41,42,43,44,45].

Most of the previous studies did not take into account the effect of the microelongation parameters on the optical properties when studying semiconductors in addition to the effect of the magnetic field. The present work presents a novel model describing the coupling between the thermoelastic theory and the photothermal theory when the microelongation parameters of semiconductors are taken into account. The influence of the magnetic field is also studied on the microelongated semiconductor according to the 2D deformation (TED and ED). The novel model can be named the photo-thermo-microelongated, which is described as dimensionless. During the optical excitation, the harmonic waves technique is utilized to obtain the analytical solutions of the main physical fields. The obtained results of the theoretical analysis are shown according to some numerical simulations graphically analyzed. The main impact of some parameters is discussed theoretically.

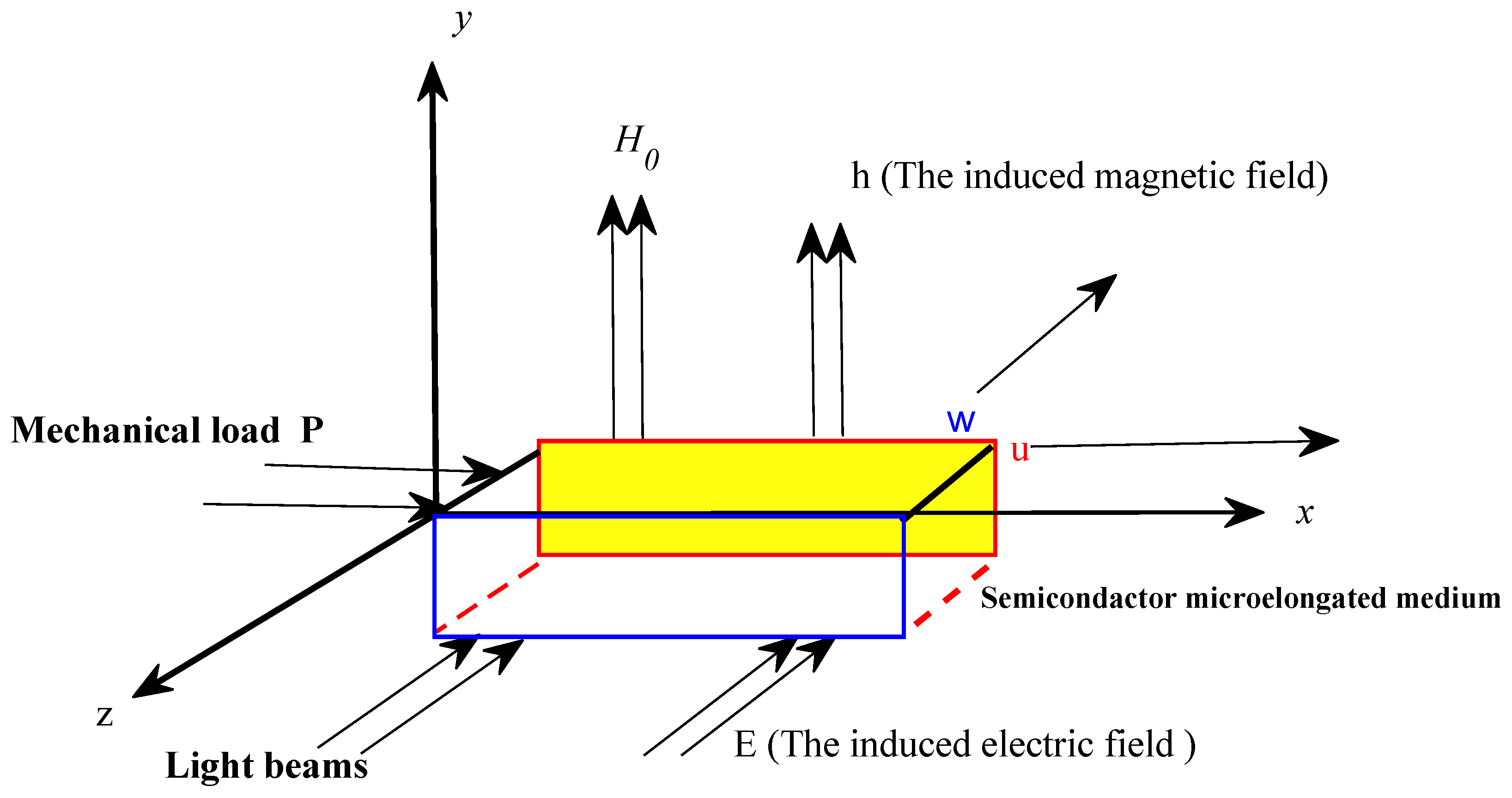
2. Mathematical Model and Main Equations

When the microelongated excited semiconductor medium is exposed to a uniform magnetic field according to the perfect conductivity permeated by an initial magnetic field, $\stackrel{\rightharpoonup }{H}=(0,H_0,0)$ is in the direction of $y$-axial, the induced magnetic field $\stackrel{\rightharpoonup }{h} = (0, h, 0)$ is obtained in the same direction. However, the current density $\stackrel{\rightharpoonup }{J}=(J_x,J_y,J_z)$ is obtained when the induced electric field $\stackrel{\rightharpoonup }{E} = (0, 0, E)$ is generated in the vertical direction. According to the slowly moving microelongated semiconductor medium with the velocity of particles $\frac{d\stackrel{\rightharpoonup }{u}}{dt}$, where $\stackrel{\rightharpoonup }{u}=(u, 0, w)=(u=u(x,z,t), 0, w=w(x,z,t)$ is the displacement vector in 2D, the strain relation in 2D is $e=\frac{\partial u}{\partial x}+\frac{\partial w}{\partial z}$ (cubical dilatation), the magnetic constant permeability is ${\tilde{\mu }}_0$ and the electric permittivity is ${\epsilon }_0$. The linearized electromagnetic Maxwell’s equations can be presented in the following form [41,44]:

$$\begin{array}{l}\stackrel{\rightharpoonup }{J}=curl \stackrel{\rightharpoonup }{h}-{\epsilon }_0\frac{\partial \stackrel{\rightharpoonup }{E}}{\partial t},\\ curl \overrightarrow{E}=-{\tilde{\mu }}_0\frac{\partial \stackrel{\rightharpoonup }{h}}{\partial t},\\ \stackrel{\rightharpoonup }{E}=-{\tilde{\mu }}_0(\frac{\partial \stackrel{\rightharpoonup }{u}}{\partial t}\times \stackrel{\rightharpoonup }{H}),\\ div \stackrel{\rightharpoonup }{h}=0, \stackrel{\rightharpoonup }{h}=H_0 (0, e, 0).\end{array}\}$$

(1)

From Equation (1) using the elimination method, yields:

$$\begin{array}{l}{E}_x = {\tilde{\mu }}_0 H_0 \frac{\partial w}{\partial t}, E_y = 0, E_z = -{\tilde{\mu }}_0 H_0 \frac{\partial u}{\partial t},\\ J_x = -(\frac{\partial h}{\partial z} + {\tilde{\mu }}_0 H_0 {\epsilon }_0 \frac{{\partial }^{2}w}{\partial t^2}), J_y = 0, J_z = \frac{\partial h}{\partial x} + {\tilde{\mu }}_0 H_0 {\epsilon }_0\frac{{\partial }^{2}u}{\partial t^2},\\ H_x = 0, H_z = 0, H_y = H_0 + h \left(x , y , z\right),\\ \stackrel{\rightharpoonup }{F}={\tilde{\mu }}_0(\stackrel{\rightharpoonup }{J} \times \stackrel{\rightharpoonup }{H})=(-{\tilde{\mu }}_0{H}_0\frac{\partial h}{\partial x}-{\epsilon }_0{\tilde{\mu }}_0^2{H}_0^2\frac{{\partial }^{2}u}{\partial t^2},0,-{\tilde{\mu }}_0{H}_0\frac{\partial h}{\partial z}-{\epsilon }_0{\tilde{\mu }}_0^2{H}_0^2\frac{{\partial }^{2}w}{\partial t^2}).\end{array}\}$$

(2)

where $\stackrel{\rightharpoonup }{F}={\tilde{\mu }}_0(\stackrel{\rightharpoonup }{J} \times \stackrel{\rightharpoonup }{H})$ is Lorentz’s electromagnetic force and the differentiation relative to the time is denoted by dot notation [46].

Using the Cartesian coordinates in 2D (see Figure 1, all main quantities depend on $(x,z,t)$), the other main quantities in this work are presented by: the carrier density $N(x, z, t)$ (plasma waves), the temperature $T(x, z, t)$ (thermal waves), and the scalar microelongational function $\phi (x, z, t)$. In this case, the main governing equations can be introduced according to the microelongated photo-thermoelasticity theory when the microelongated semiconductor medium is homogeneous, isotropic, and linear as follow:

(I)

The tensor form of the constitutive relations for the microelongated semiconductor photo-thermoelastic medium is [17,18,19,20,21]:

$$\begin{array}{l}{\sigma }_{ij}=({\lambda }_o\phi +\lambda u_r{,}_r){\delta }_{ij}+\mu (u_{i,j}+u_{j,k})-\hat{\gamma }(1+v_o\frac{\partial }{\partial t})T{\delta }_{ij}-((3\lambda +2\mu )d_{n}N){\delta }_{ij},\\ m_i=a_0{\phi }_{,i},\\ s-\sigma ={\lambda }_o{u}_i{,}_i-{\beta }_1(1+v_o\frac{\partial }{\partial t})T+-((3\lambda +2\mu )d_{n}N){\delta }_{2i}+{\lambda }_1\phi .\end{array}\}$$

(3)

(II)

The plasma waves equations that coupled with the thermal waves is [33]:

$$\dot{N}=D_E{N}_{,ii}- \frac{N}{\tau }+\kappa T$$

(4)

(III)

The motion equation under the effect of the electromagnetic field and the microelongation equation of the semiconductor medium in the context of the microelongation and microinertia processes are [44,45,46]:

$$(\lambda +\mu )u_{j,ij}+\mu u_{i,jj}+{\lambda }_o{\phi }_{,i}-\hat{\gamma }(1+v_o\frac{\partial }{\partial t})T_{,i}-{\delta }_n{N}_{,i}+\stackrel{\rightharpoonup }{F}=\rho {\ddot{u}}_i$$

(5)

$${\alpha }_o{\phi }_{,ii}-{\lambda }_1\phi -{\lambda }_o{u}_{j,j}+{\hat{\gamma }}_1(1+v_o\frac{\partial }{\partial t})T=\frac{1}{2}j\rho \ddot{\phi }$$

(6)

(IV)

The general form of the heat equation according to the interaction between the optical-thermal-elastic waves and the microinertia processes is [21,32,44]:

$$K{T}_{,ii}-\rho C_E(n_1+{\tau }_o\frac{\partial }{\partial t})\frac{\partial T}{\partial t}-\hat{\gamma }{T}_o(n_1+n_o{\tau }_o\frac{\partial }{\partial t})\frac{\partial u_{i,i}}{\partial t}+\frac{E_g}{\tau }N={\hat{\gamma }}_1{T}_o(n_1+{\tau }_o\frac{\partial }{\partial t})\phi$$

(7)

where $\kappa =\frac{\partial n_0}{\partial T}\frac{T}{\tau }$ according to the variation in the temperature case expresses the parameter of the coupling thermal activation, $n_0$ expresses the carrier charge concentration, and ${\hat{\gamma }}_1=(3\lambda +2\mu ){\alpha }_{t_2}$ is the microelongational thermal expansion, ${\alpha }_{t_2}$ is the coefficient of the microelongational linear thermal expansions. In the 2D deformations, Equations (4)–(7) in a general form can be rewritten as [46]:

$$\begin{array}{l}(\lambda +\mu )\left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}w}{\partial x\partial z}\right)+\mu \left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial z^2}\right)+ {\lambda }_o\frac{\partial \phi }{\partial x} \\ -\hat{\gamma }\left(1+v_o\frac{\partial }{\partial t}\right)\frac{\partial T}{\partial x}-{\delta }_n\frac{\partial N}{\partial x}-{\tilde{\mu }}_0{H}_0\frac{\partial h}{\partial x}-{\epsilon }_0{\tilde{\mu }}_0^2{H}_0^2\frac{{\partial }^{2}u}{\partial t^2}=\rho \left(\frac{{\partial }^{2}u}{\partial t^2}\right)\end{array}\}$$

(8)

$$\begin{array}{l}(\lambda +\mu )\left(\frac{{\partial }^{2}u}{\partial x\partial z}+\frac{{\partial }^{2}w}{\partial z^2}\right)+\mu \left(\frac{{\partial }^{2}w}{\partial x^2}+\frac{{\partial }^{2}w}{\partial z^2}\right)+ {\lambda }_o\frac{\partial \phi }{\partial z}\\ -\hat{\gamma }\left(1+v_o\frac{\partial }{\partial t}\right)\frac{\partial T}{\partial z}-{\delta }_n\frac{\partial N}{\partial z}-{\tilde{\mu }}_0{H}_0\frac{\partial h}{\partial z}-{\epsilon }_0{\tilde{\mu }}_0^2{H}_0^2\frac{{\partial }^{2}w}{\partial t^2}=\rho \left(\frac{{\partial }^{2}w}{\partial t^2}\right)\end{array}\}$$

(9)

$${\alpha }_o\left(\frac{{\partial }^2\phi }{\partial x^2}+\frac{{\partial }^2\phi }{\partial z^2}\right)-{\lambda }_1\phi -{\lambda }_{o}e+{\hat{\gamma }}_1\left(1+v_o\frac{\partial }{\partial t}\right)T=\frac{1}{2}j\rho \frac{{\partial }^2\phi }{\partial t^2}$$

(10)

$$\begin{array}{c}K\left(\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial z^2}\right)-\rho C_E\left(n_1+{\tau }_o\frac{\partial }{\partial t}\right)\frac{\partial T}{\partial t}-\hat{\gamma }{T}_o\left(n_1+n_o{\tau }_o\frac{\partial }{\partial t}\right)\frac{\partial e}{\partial t}+\frac{E_g}{\tau }N=\\ {\hat{\gamma }}_1{T}_o\left(n_1+{\tau }_o\frac{\partial }{\partial t}\right)\phi \end{array}\}$$

(11)

The types of the microelongated photo-thermoelasticity models depend on the value of the parameters $n_o , n_1$ (chosen constants) and thermal memory (coupled-dynamical model (CD), Green and Lindsay (GL) model, and Lord and Şhulman (LS) model) [42,43,44]. To put the main equations in a simplified form, the following dimensionless quantities can be presented as:

$$\begin{array}{l}\overline{N}=\frac{{\delta }_n}{2\mu +\lambda }N, ({\overline{x}}_i, {\overline{u}}_i)=\frac{1}{{\omega }^{*}{C}_T}(x_i, u_i), (\overline{t}, {\overline{\tau }}_o, {\overline{\nu }}_o)=\frac{(t, {\tau }_o,{\nu }_o)}{{\omega }^{*}},\\ C_T^2=\frac{2\mu +\lambda }{\rho }, \overline{T}=\frac{\hat{\gamma }T}{2\mu +\lambda }, {\overline{\sigma }}_{ij}=\frac{{\sigma }_{ij}}{2\mu +\lambda }, \overline{\phi }=\frac{\rho C_T^2}{T_o\hat{\gamma }}\phi , {\omega }^{*}=\frac{K_0}{\rho C_E{C}_T^2},\\ ({\Pi }^{\prime },{\psi }^{\prime })=\frac{(\Pi ,\psi )}{{\left(C_T{\omega }^{*}\right)}^2},C_L^2=\frac{\mu }{\rho } , h^{\prime }=\frac{h}{H_0}.\end{array}\}$$

(12)

According to the dimensionless Equation (12), the main equations can be represented as (dropping the superscripts):

$$({\nabla }^2-{\epsilon }_3-{\epsilon }_2\frac{\partial }{\partial t})N+{\epsilon }_{4}T=0$$

(13)

$$\begin{array}{l}\frac{{\partial }^{2}u}{\partial t^2}=\frac{(\lambda +\mu )}{\rho C_T^2}\frac{\partial e}{\partial x}+\frac{\mu }{\rho C_T^2}{\nabla }^{2}u+\frac{T_o\hat{\gamma }{\lambda }_o}{{(\rho C_T^2)}^2}\frac{\partial \phi }{\partial x}-(1+v_o\frac{\partial }{\partial t})\frac{\partial T}{\partial x}-\\ \frac{\partial N}{\partial x} -\frac{{\tilde{\mu }}_0{H}_0^2}{\rho {\omega }^{*}{C}_T}\frac{\partial h}{\partial x}-\frac{{\epsilon }_0{\tilde{\mu }}_0^2{H}_0^2}{\rho }\frac{{\partial }^{2}u}{\partial t^2}\end{array}\}$$

(14)

$$\begin{array}{l}\frac{{\partial }^{2}w}{\partial t^2}=\frac{(\lambda +\mu )}{\rho C_T^2}\frac{\partial e}{\partial z}+\frac{\mu }{\rho C_T^2}{\nabla }^{2}w+ \frac{T_o\hat{\gamma }{\lambda }_o}{{(\rho C_T^2)}^2}\frac{\partial \phi }{\partial z}-(1+v_o\frac{\partial }{\partial t})\frac{\partial T}{\partial z}-\\ \frac{\partial N}{\partial z}-\frac{{\tilde{\mu }}_0{H}_0^2}{\rho {\omega }^{*}{C}_T}\frac{\partial h}{\partial z}-\frac{{\epsilon }_0{\tilde{\mu }}_0^2{H}_0^2}{\rho }\frac{{\partial }^{2}w}{\partial t^2}\end{array}\}$$

(15)

$$({\nabla }^2-C_3-C_4\frac{{\partial }^2}{\partial t^2})\phi -C_{5}e+C_6(1+v_o\frac{\partial }{\partial t})T=0$$

(16)

$${\nabla }^{2}T-(n_1+{\tau }_o\frac{\partial }{\partial t})\frac{\partial T}{\partial t}-\epsilon (n_1+n_o{\tau }_o\frac{\partial }{\partial t})\frac{\partial e}{\partial t}+{\epsilon }_{5}N={\epsilon }_1\left(n_1+{\tau }_o\frac{\partial }{\partial t}\right)\phi$$

(17)

For more simplification, Helmholtz’s theory is used, which can be formulated as the displacement components in terms of the potential scalar function $\Pi (x,z,t)$ and vector space–time function $\mathsf{\Psi }(x,z,t)=(0,\psi ,0)$ as:

$$\overrightarrow{u}=grad \Pi +curl \mathsf{\Psi }, u= \frac{\partial \Pi }{\partial x} - \frac{\partial \psi }{\partial z}, w= \frac{\partial \Pi }{\partial \mathrm{z}} +\frac{\partial \psi }{\partial x}.$$

(18)

Using Equation (18) for the main Equations (14)–(17), yields:

$$(\alpha {\nabla }^2-{ℝ}_H\frac{{\partial }^2}{\partial t^2})\Pi +(1+v_o\frac{\partial }{\partial t})T+a_1\phi -N=0,$$

(19)

$$({\nabla }^2-{ℝ}_H{a}_3\frac{{\partial }^2}{\partial t^2})\psi =0,$$

(20)

$$({\nabla }^2-C_3-C_4\frac{{\partial }^2}{\partial t^2})\phi -C_5{\nabla }^2\Pi +C_6(1+v_o\frac{\partial }{\partial t})T=0$$

(21)

$$\left({\nabla }^2-(n_1\frac{\partial }{\partial t}+{\tau }_o\frac{{\partial }^2}{\partial t^2})\right)T-\epsilon (n_1\frac{\partial }{\partial t}+n_o{\tau }_o\frac{{\partial }^2}{\partial t^2}){\nabla }^2\Pi +{\epsilon }_{5}N-{\epsilon }_1\left(n_1+{\tau }_o\frac{\partial }{\partial t}\right)\phi =0$$

(22)

On the other hand, the constitutive Equation (3) in 2D deformation can be constructed as [28,30]:

$$\begin{array}{l}{\sigma }_{xx}=\frac{\partial u}{\partial x}+a_2 \frac{\partial w}{\partial z}-(1+v_o\frac{\partial }{\partial t}) T -N+a_1\phi ,\\ {\sigma }_{zz}=a_2\frac{\partial u}{\partial x}+ \frac{\partial w}{\partial z}-(1+v_o\frac{\partial }{\partial t}) T -N+a_1\phi ,\\ {\sigma }_{xz}=a_4 (\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}).\end{array}\}$$

(23)

where

$a_1=\frac{T_o\hat{\gamma }{\lambda }_o}{{(\rho C_T^2)}^2}, a_2=\frac{\lambda }{\rho C_T^2}, a_3=\frac{\rho C_T^2}{\mu }, \epsilon =\frac{{\hat{\gamma }}^2{\omega }^{*}{T}_o}{K_0\rho },{\epsilon }_1=\frac{{\hat{\gamma }}_1{\hat{\gamma }}^2{\omega }^{*}{T}_o}{K_0\rho (2\mu +\lambda )},{\epsilon }_2=\frac{{\omega }^{*}{C}_T^2}{D_E}$$, a_4=\frac{\mu }{\rho C_T^2}$, $C_4=\frac{\rho j{C}_T^2}{2{\alpha }_0},$${\epsilon }_3=\frac{{\omega }^{*2}{C}_T^2}{\tau D_E}, {\epsilon }_4=\frac{\kappa d_n{\omega }^{*2}\rho }{D_E{\alpha }_{t1}}, {\epsilon }_5=\frac{E_g\hat{\gamma }{\omega }^{*2}{C}_T^2}{\tau K_0{\delta }_n}, C_3=\frac{{\lambda }_1{C}_T^2{\omega }^{*2}}{{\alpha }_0},$

$C_5=\frac{{\lambda }_o\rho C_T^4{\omega }^{*2}}{{\alpha }_0{T}_0\hat{\gamma }},$$C_6=\frac{{\hat{\gamma }}_1\rho {\omega }^{*2}{T}_o}{\hat{\gamma }{\alpha }_0}$, ${ℝ}_H=1+{\epsilon }_0{\tilde{\mu }}_0^2{H}_0^2/\rho$, $\alpha =1+\frac{{\tilde{\mu }}_0{H}_0^2}{\rho {\omega }^{*}{C}_T}$.

The symbol ${\epsilon }_1$$,{\epsilon }_4$ and ${\epsilon }_5$ represent the coupling thermoelastic, coupling thermo-energy, and thermo-electric parameters, and ${ℝ}_H$ is the electromagnetic number that refers to the effect of the external magnetic field.

3. Harmonic Waves Analysis

The normal mode analysis depends on the harmonic wave technique utilized to obtain the complete solutions in 2D for the basic fields. The harmonic waves solutions can be formulated for a function $f(x, z, t)$ as [47,48,49]:

$$f(x, z, t)=\overline{f}(x)\exp (\omega t+ibz)$$

(24)

The function $\overline{f}(x)$ represents the amplitude of $f(x, y, t)$, $i=\sqrt{-1}$, $\mathsf{\omega }={\omega }_0+i \zeta$ is the complex time frequency and $b$ is the wave number in the direction of the z-axis. The normal mode technique Equation (24) is applied to Equations (13) and (19)–(22), which yields:

$$(D^2-{\alpha }_1)\overline{N}+{\epsilon }_4\overline{T}=0,$$

(25)

$$(\alpha D^2-A_1)\overline{\Pi }+A_2\overline{T}+a_1\overline{\phi }-\overline{N}=0,$$

(26)

$$(D^2-A_3)\overline{\psi }=0,$$

(27)

$$(D^2-A_4)\overline{\phi }-C_5(D^2-b^2)\overline{\Pi }+A_5\overline{T}=0,$$

(28)

$$(D^2-A_6)\overline{T}-A_7(D^2-b^2)\overline{\Pi }+{\epsilon }_5\overline{N}-A_8\overline{\phi }=0$$

(29)

$$\begin{array}{l}{\sigma }_{xx}=Du+ib{a}_2 w-A_{2}T -N+a_1\phi ,\\ {\sigma }_{zz}=a_{2}Du+ ibw-A_2 T -N+a_1\phi ,\\ {\sigma }_{xz}=a_4 (ibu+Dw).\end{array}\}$$

(30)

where

$$\begin{array}{l}{\alpha }_1=b^2+{\epsilon }_3+{\epsilon }_2\omega , A_1=\alpha b^2+{ℝ}_H{\omega }^2, A_2=1+{\nu }_o\omega , A_3=b^2+{ℝ}_H{a}_3{\omega }^2,\\ D=\frac{d}{d\mathrm{x}}, A_4=b^2+C_3+C_4{\omega }^2, A_5=C_6(1+{\nu }_o\omega ), \\ A_6=b^2+\omega (n_1+{\tau }_o\omega ),A_7=\epsilon (n_1\omega +n_o{\tau }_o{\omega }^2), A_8={\epsilon }_1(n_1+{\tau }_o\omega ) .\end{array}\}$$

(31)

Solving the system of Equations (25), (26), (28) and (29) using the elimination technique for the functions $\overline{\phi },\overline{N},\overline{T}$ and $\overline{\Pi }$, yields:

$$\left\{D^8-{ℂ}_1{D}^6+{ℂ}_2{D}^4-{ℂ}_3{D}^2+{ℂ}_4\right\}(\overline{\phi },\overline{N},\overline{T},\overline{\Pi })=0$$

(32)

where

${ℂ}_1=-\left(-A_2{A}_7+C_5{a}_1-A_1-A_4-A_6-{\alpha }_1\right){\alpha }^{-1}$,

${ℂ}_2=\left(\begin{array}{l}\left(A_2{A}_7-C_5{a}_1+A_1+A_4+A_6\right){\alpha }_1+\left(A_7-{\epsilon }_3\right){\epsilon }_4+\\ \left(b^2{A}_7+A_4{A}_7-A_8\right)A_2-b^2{C}_5{a}_1-A_5{A}_7{a}_1-A_6{C}_5{a}_1-A_1{A}_4+A_1{A}_6+A_4{A}_6\end{array}\right){\alpha }^{-1}$,

${ℂ}_3=\left(\begin{array}{l}-\left(\left(-A_2{A}_7+C_5{a}_1\right)b^2-A_2{A}_4{A}_7+A_5{A}_7{a}_1+A_6{C}_5{a}_1-A_1{A}_4-A_1{A}_6+A_2{A}_8-A_4{A}_6\right){\alpha }_1\\ \left(-C_5{a}_1+A_1+A_4\right){\epsilon }_4{\epsilon }_3+\left(-b^2{A}_7{a}_2-A_4{A}_7{a}_2+A_8\right){\epsilon }_4+(-A_2{A}_4{A}_7+A_5{A}_7{a}_1+\\ A_6{C}_5{a}_1)b^2-A_1{A}_4{A}_6+A_2{A}_4{A}_8-A_5{A}_8{a}_1\end{array}\right){\alpha }^{-1}$,

${ℂ}_4=\left(\begin{array}{l}\left(\left(b^2{C}_5{a}_1-A_1{A}_4\right){\epsilon }_3+b^2{A}_4{A}_7-A_4{A}_8\right){\epsilon }_4+\\ \left(\left(A_2{A}_4{A}_7-A_5{A}_7-A_6{C}_5{a}_1\right)b^2+A_1{A}_4{A}_6-A_2{A}_4{A}_8+A_5{A}_8{a}_1\right){\alpha }_1\end{array}\right){\alpha }^{-1}.$

The ordinary differential Equation (31) is decomposed (factorized) as:

$$\left(D^2-k_1^2\right)\left(D^2-k_2^2\right) \left(D^2-k_3^2\right)\left(D^2-k_4^2\right)\{ \overline{T}, \overline{N}, \overline{\Pi },\overline{\phi }\}(x)=0$$

(33)

The values of $k_n^2$$(n=1, 2, 3, 4)$ (roots) can be taken real and positive ($\mathrm{Re}(k_n)>0$).

The linear general solutions of Equation (32) for the main fields can be formulated in the following form:

$$\overline{T}(x)={\displaystyle \sum _{i=1}^4{\mathbb{Q}}_i} (b,\omega )e^{-k_{i}x}$$

(34)

$$\overline{\phi }(x)={\displaystyle \sum _{i=1}^4{{\mathbb{Q}}^{\prime }}_i} (b,\omega )e^{-k_{i}x}={\displaystyle \sum _{i=1}^4{h}_{1i}{\mathbb{Q}}_i} (b,\omega )e^{-k_{i}x}$$

(35)

$$\overline{\Pi }(x)={\displaystyle \sum _{i=1}^4{{\mathbb{Q}}^{″}}_i} (b,\omega )e^{-k_{i}x}={\displaystyle \sum _{i=1}^4{h}_{2i}{\mathbb{Q}}_i} (b,\omega )e^{-k_{i}x}$$

(36)

$$\overline{N}(x)={\displaystyle \sum _{i=1}^4{{\mathbb{Q}}^{‴}}_i} (b,\omega )e^{-k_{i}x}={\displaystyle \sum _{i=1}^4{h}_{3i}{\mathbb{Q}}_i(b,\omega )} e^{-k_{i}x}$$

(37)

where ${\mathbb{Q}}_i, {{\mathbb{Q}}^{\prime }}_i, {{\mathbb{Q}}^{″}}_i, {\mathbb{Q}}^{‴}$, $i=1, 2, 3, 4$ are parameters that should be determinate that depend on $b$ and $\omega$. The other coefficients of Equations (35)–(37) are:

$$\begin{array}{l}{h}_{1i}=\frac{\left(d_1{k}_i^4+d_2{k}_i^2+d_3\right)}{\left(k_i^6+d_4{k}_i^4+d_5{k}_i^2+d_6\right)},h_{3i}=-\frac{\left({\epsilon }_4\right)}{\left(k_i^2-{\alpha }_1\right)},h_{2i}=\frac{\left(A_2{k}_i^4+d_7{k}_i^2+d_8\right)}{\left(k_i^6+d_4{k}_i^4+d_5{k}_i^2+d_6\right)},\\ d_1=A_2{C}_5-A_5, d_2=-A_2{b}^2{C}_5-A_2{C}_5{\alpha }_1-C_5{a}_2{\epsilon }_4+A_1{A}_5+A_5{\alpha }_1,\\ d_3=b^2{A}_2{C}_5{\alpha }_1+b^2{C}_5{a}_2{\epsilon }_4-A_1{A}_5{\alpha }_1, d_4=C_5{a}_1-A_1-A_4-{\alpha }_1,\\ d_5=-b^2{C}_5{a}_1-C_5{a}_1{\alpha }_1+A_1{A}_4+A_1{\alpha }_1+A_4{\alpha }_1, d_6=b^2{\alpha }_1{a}_1{C}_5-A_1{A}_4{\alpha }_1,\\ d_7=-A_2{A}_4-A_2{\alpha }_1+A_5{a}_1-a_2{\epsilon }_4, d_8=A_2{A}_4{\alpha }_1+A_4{a}_2{\epsilon }_4-a_1{A}_5{\alpha }_1.\end{array}$$

On the other hand, Equation (27) can be decomposed as:

$$\left(D^2-k_5^2\right)\overline{\psi }(x)=0$$

(38)

where $k_5^2$ is the fifth roots (real and positive) of Equation (27) and takes the form:

$$k_5=\pm \sqrt{A_3}=\pm \omega \sqrt{a_3}$$

(39)

The solution of Equation (27) is:

$$\overline{\psi }(x)={\mathbb{Q}}_5(b,\omega ) \exp (-k_{5}x)$$

(40)

The displacement components (elastic waves) and the stress (mechanical waves) components can be rewritten in terms of ${\mathbb{Q}}_i$ according to Equations (18) and (23), respectively, when the normal mode analysis is applied as:

$$\overline{u}(x)=-{\displaystyle \sum _{i=1}^4{\mathbb{Q}}_i{h}_{2i}{k}_i{e}^{-k_{i}x}-ib{\mathbb{Q}}_5}{e}^{-k_{5}x}, \overline{w}(x)={\displaystyle \sum _{i=1}^{4}ib{h}_{2i}{\mathbb{Q}}_i{e}^{-k_{i}x}-k_5{\mathbb{Q}}_5{e}^{-k_{5}x}}$$

(41)

$$\begin{array}{l}{\overline{\sigma }}_{xx}={\displaystyle \sum _{n=1}^4{\mathbb{Q}}_n(h_{2i}(k_n^2-b^2{a}_2)-A_2-h_{3i}+a_1{h}_{1i})e^{-k_{n}x}-ib{k}_5(a_2-1){\mathbb{Q}}_5}{e}^{-k_{5}x},\\ {\overline{\sigma }}_{zz}={\displaystyle \sum _{n=1}^4{\mathbb{Q}}_n(h_{2i}(a_2{k}_n^2-b^2)-A_2-h_{3i}+a_1{h}_{1i})e^{-k_{n}x}-ib{k}_5(1-a_2){\mathbb{Q}}_5}{e}^{-k_{5}x},\\ {\overline{\sigma }}_{xz}={\displaystyle \sum _{n=1}^{4}ib{\mathbb{Q}}_n{k}_n(h_{2i}-1)e^{-k_{n}x}+(1+k_5^2){\mathbb{Q}}_5}{e}^{-k_{5}x}.\end{array}\}$$

(42)

4. Boundary Conditions

The unspecific parameters ${\mathbb{Q}}_n$ must be determined to obtain the complete solution. In this case, some conditions are applied on the outer microelongated semiconductor surface (at $x=0$) [50].

The mechanical loads with load pressure $p$ conditions under the influence of harmonic wave analysis can be taken at $x=0$:

$$\begin{array}{l}\begin{array}{l}{\sigma }_{xx}=-p,\\ {\overline{\sigma }}_{xx}=-\overline{p}\exp (\omega t+ibz). \end{array}\}\\ \begin{array}{l}{\sigma }_{xz}=0,\\ {\overline{\sigma }}_{xz}=0.\end{array}\}\end{array}\}$$

(43)

where $P(x, z, t)=\overline{p}(x)\exp (\omega t+ibz)$.

The thermal condition at $x=0$ is chosen in thermally isolated cases, which can be formulated as:

$$\begin{array}{l}\frac{\partial T}{\partial x}=0,\\ \frac{d\overline{T}}{dx}=0.\end{array}\}$$

(44)

The microelongation condition at the free surface can be chosen as an elongation-free case, which is obtained as:

$$\overline{\phi }=0$$

(45)

The carrier density condition can be chosen according to recombination processes to measure the electron concentration and velocity at $x=0$ as:

$$\frac{d\overline{N}}{dx}=-\frac{\tilde{s}{n}_0}{D_E}$$

(46)

Using Equations (43)–(46) and the values of $\overline{T},{\overline{\sigma }}_{xx}, {\overline{\sigma }}_{xz}, \overline{\phi }$ and $\overline{N}$, the following relations can be rewritten as:

$$\begin{array}{l}{\displaystyle \sum _{n=1}^4{\mathbb{Q}}_n(h_{2i}(k_n^2-b^2{a}_2)-A_2-h_{3i}+a_1{h}_{1i})-ib{k}_5(a_2-1){\mathbb{Q}}_5}=-\overline{p}\exp (\omega t+ibz),\\ {\displaystyle \sum _{n=1}^{4}ib{\mathbb{Q}}_n{k}_n(h_{2i}-1)+(1+k_5^2){\mathbb{Q}}_5}=0.\end{array}\}$$

(47)

$$\begin{array}{l} {\displaystyle \sum _{i=1}^4-k_i{\mathbb{Q}}_i} (b,\omega )=0, \\ {\displaystyle \sum _{i=1}^4{h}_{1i}{\mathbb{Q}}_i} (b,\omega )=0, \\ {\displaystyle \sum _{i=1}^4{h}_{3i}{k}_i{\mathbb{Q}}_i(b,\omega )}=\frac{\tilde{s}{n}_0}{D_E}\end{array}\}$$

(48)

Invoking the boundary conditions (47) and (48) at the surface $x=0$, we obtain a system of five equations. After applying the inverse of the matrix method, we have the values of the five constants ${\mathbb{Q}}_n$. In this case, the complete solutions are obtained when the parameters ${\mathbb{Q}}_n$ are determined.

5. Validation

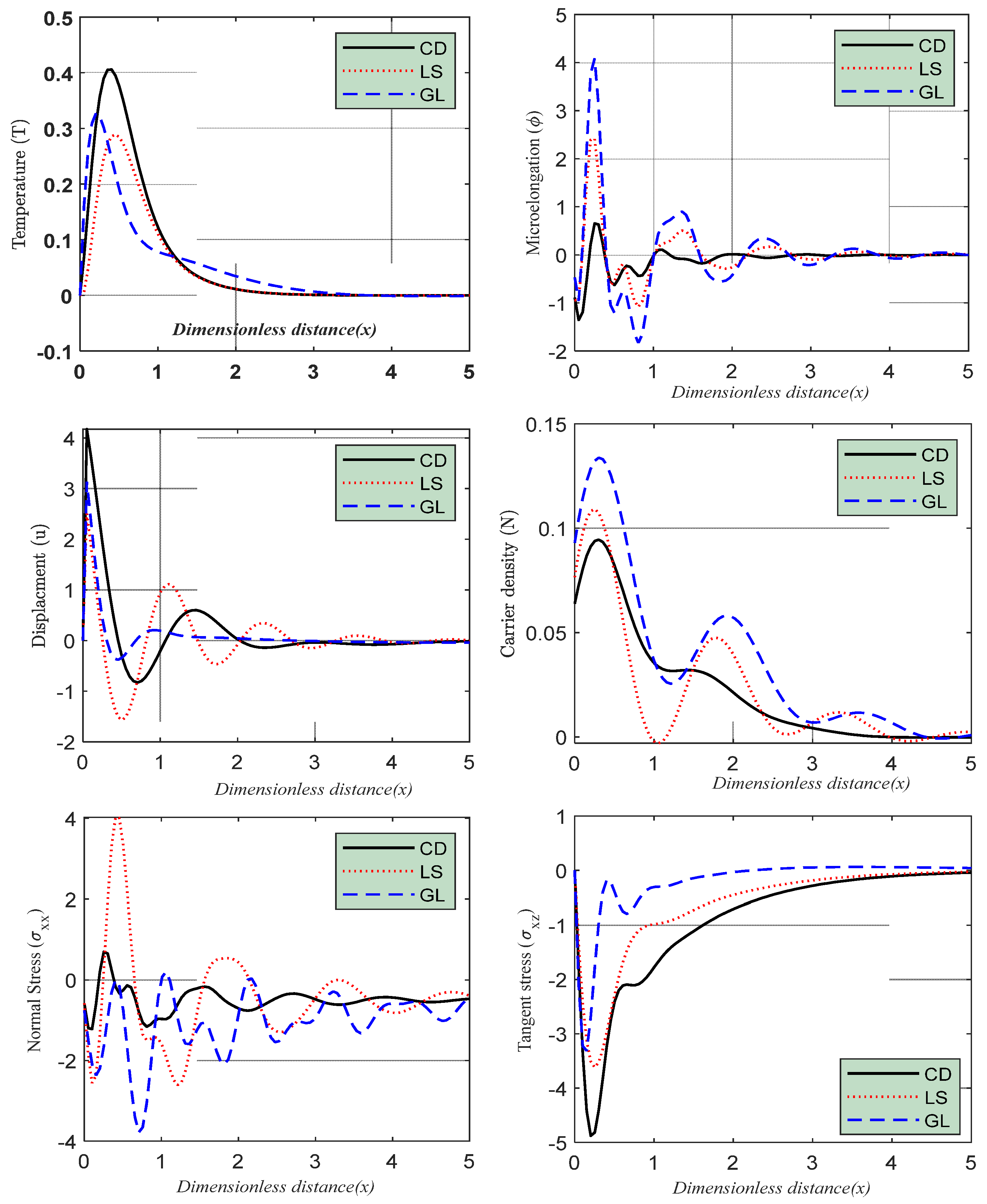
5.1. The Theory of Generalized Microelongation Thermoelasticity

When the carrier density $N(x, y, t)$ associated with the plasma wave is neglected (i.e., $N=0$), the microelongation magneto-thermoelasticity theory without the effect of optical energy is obtained. In this case, the governing Equations (2)–(5) are reduced to [19,20]:

$$\begin{array}{l}(\lambda +\mu )u_{j,ij}+\mu u_{i,jj}+{\lambda }_o{\phi }_{,i}-\hat{\gamma }(1+v_o\frac{\partial }{\partial t})T_{,i}+\stackrel{\rightharpoonup }{F}=\rho {\ddot{u}}_i,\\ {\alpha }_o{\phi }_{,ii}-{\lambda }_1\phi -{\lambda }_o{u}_{j,j}+{\hat{\gamma }}_1(1+v_o\frac{\partial }{\partial t})T=\frac{1}{2}j\rho \ddot{\phi },\\ K{T}_{,ii}-\rho C_E(n_1+{\tau }_o\frac{\partial }{\partial t})\dot{T}-\hat{\gamma }{T}_o(n_1+n_o{\tau }_o\frac{\partial }{\partial t}){\dot{u}}_{i,i}={\hat{\gamma }}_1{T}_o\dot{\phi }.\end{array}\}$$

(49)

5.2. The Generalized Photo-Thermoelasticity Theory

If the elongation parameters are neglected (${\alpha }_o={\lambda }_o={\lambda }_1=0$), the magneto-photo-thermoelasticity theory is appeared The system of Equations (2)–(5) are reduced to:

$$\begin{array}{l}\dot{N}=D_E{N}_{,ii}- \frac{N}{\tau }+\kappa T,\\ (\lambda +\mu )u_{j,ij}+\mu u_{i,jj}-\hat{\gamma }(1+v_o\frac{\partial }{\partial t})T_{,i}-{\delta }_n{N}_{,i}+\stackrel{\rightharpoonup }{F}=\rho {\ddot{u}}_i,\\ K{T}_{,ii}-\rho C_E(n_1+{\tau }_o\frac{\partial }{\partial t})\dot{T}-\hat{\gamma }{T}_o(n_1+n_o{\tau }_o\frac{\partial }{\partial t}){\dot{u}}_{i,i}+\frac{E_g}{\tau }N=0.\end{array}\}$$

(50)

This problem is studied according to [33,35].

5.3. Different Models of Microelongation Magneto-Photo-Thermoelasticity

The different models in this work can be obtained depending on the different values of the thermal memory (${\tau }_o, v_o$) and the constants $n_1$ and $n_o$ as follows [49]:

(i)

The CD model appears when $n_1=1 , n_o={\tau }_o=v_o=0$ [49].

(ii)

The LS model appears when $n_1=n_o=1, v_o=0, {\tau }_o>0$ [47].

(iii)

The GL model appears when $n_1=1, n_o=0, v_o\ge {\tau }_o>0$ [48].

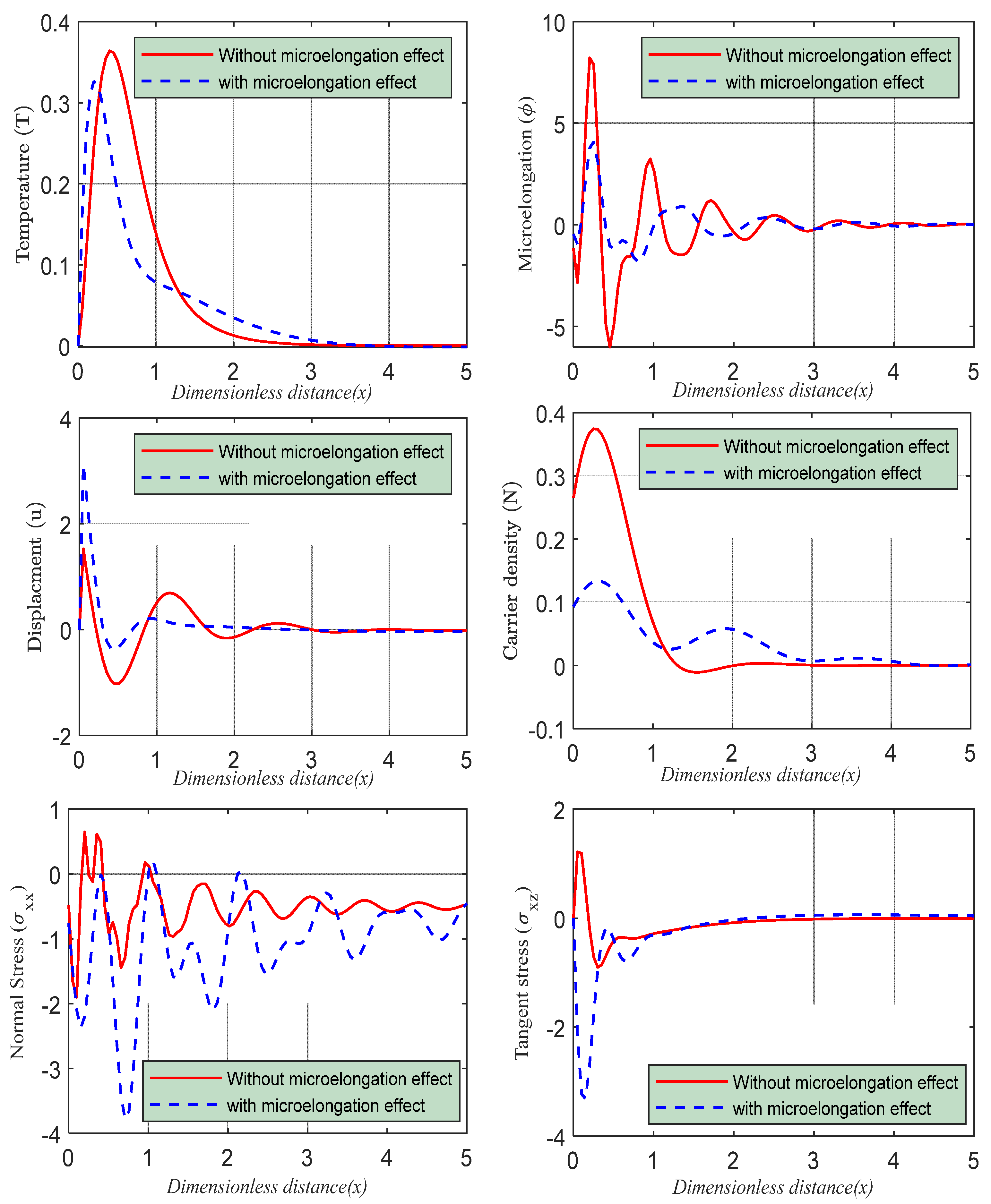
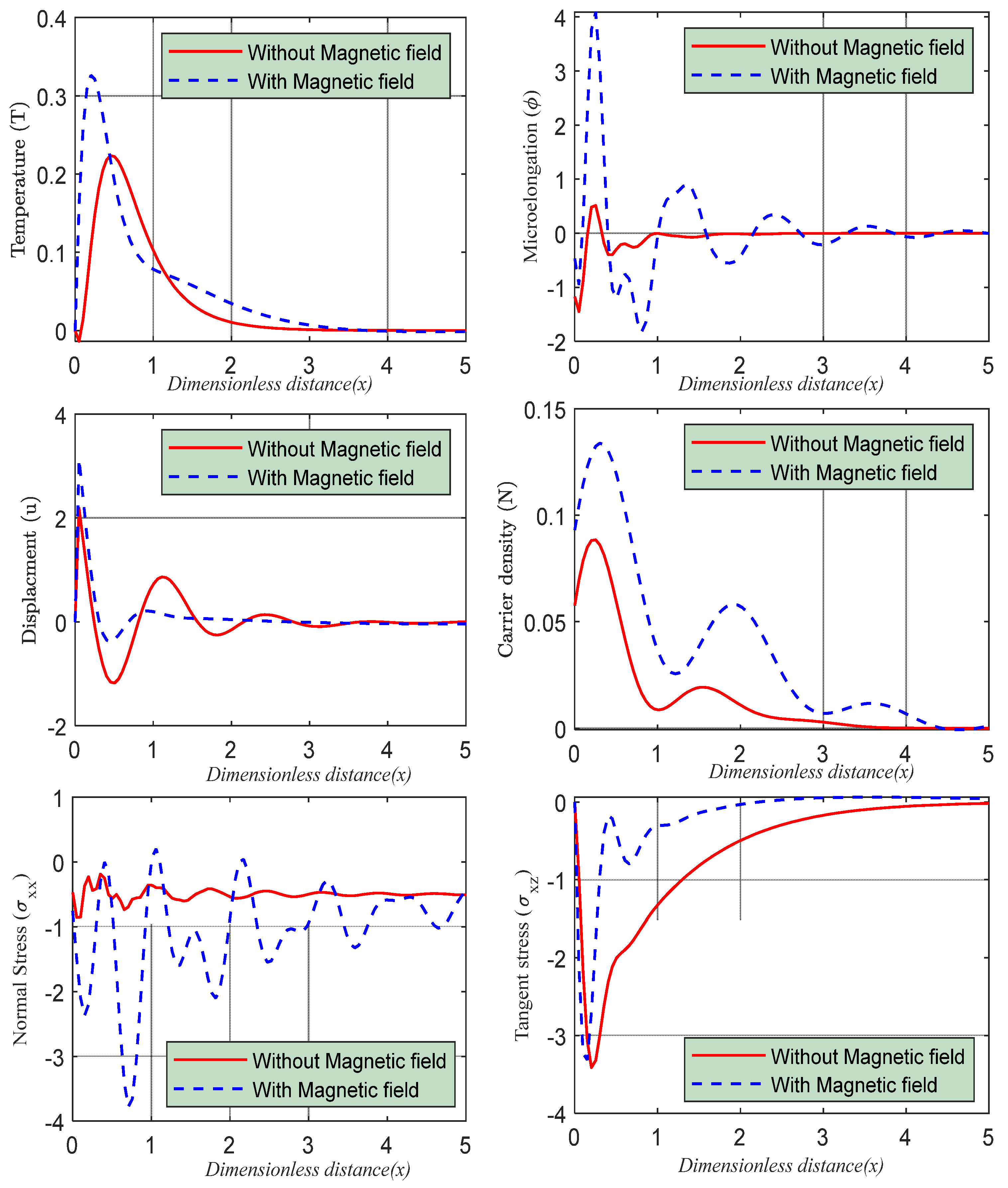
5.4. Influence of Electromagnetic Field

When the impact of a uniform magnetic field is ignored ($H_0=0$), then the induced magnetic field and induced electric field also is neglected. In this case, Lorentz’s electromagnetic force has vanished and the system of the system will describe the microelongation photo-thermoelasticity theory without a magnetic field.

6. Discussion and Numerical Outcomes

In this part, the propagation of waves of the main fields within the microelongated semiconductor medium is simulated. To perform this simulation numerically, the physical constants of the silicon (Si) material are used as an example of a semiconductor medium. With the help of a computer in Matlab, this numerical simulation was carried out.

Table 1. The physical input parameters of Si medium in SI units.

Unit	Symbol	Value	Unit	Symbol	Value
${\mathrm{Nm}}^{-2}$	$\lambda$ $\mu$	$6.4\times {10}^{10}$ $6.5\times {10}^{10}$	${\mathrm{m}}^3$	$d_n$	$-9\times {10}^{-31}$
$\mathrm{kg}·{\mathrm{m}}^{-3}$	$\rho$	$2330$	$\sec (\mathrm{s})$	${\tau }_0$	$0.00005$
$\mathrm{K}$	$T_0$	$800$	${\mathrm{m}}^2$	$j$	$0.2\times {10}^{-19}$
$\sec (\mathrm{s})$	$\tau$	$5\times {10}^{-5}$	$\mathrm{N}$	${\alpha }_0$	$0.779\times {10}^{-9}$
${\mathrm{K}}^{-1}$	${\alpha }_{t_1}$	$0.04\times {10}^{-3}$	$\mathrm{N}·{\mathrm{m}}^{-2}$	${\lambda }_0$	$0.5\times {10}^{10}$
${\mathrm{Wm}}^{-1}{\mathrm{K}}^{-1}$	$K_0$	$150$	$\mathrm{N}·{\mathrm{m}}^{-2}$	$k$	${10}^{10}$
$\mathrm{J}·{\mathrm{kg}}^{-1}·{\mathrm{K}}^{-1}$	$C_E$	$695$	$\mathrm{N}·{\mathrm{m}}^{-2}$	${\lambda }_1$	$0.5\times {10}^{10}$
${\mathrm{m}}^2·{\mathrm{s}}^{-1}$	$D_E$	$2.5\times {10}^{-3}$	${\mathrm{K}}^{-1}$	${\alpha }_{t_2}$	$0.017\times {10}^{-3}$
$\mathrm{m}·{\mathrm{s}}^{-1}$	$\tilde{s}$	$2$	${\mathrm{m}}^{-3}$	${\tilde{n}}_0$	${10}^{20}$
$\mathrm{H}·{\mathrm{m}}^{-1}$	${\tilde{\mu }}_0$	$4\pi \times {10}^{-7}$	$\sec (\mathrm{s})$	${\nu }_0$	$0.0005$
$\mathrm{F}·{\mathrm{m}}^{-1}$	${\epsilon }_0$	$8.85\times {10}^{-12}$	$\sec (\mathrm{s})$	$t$	$0.001$

displays the values of the physical constants entered for the silicon material and electromagnetic parameters [36,50,51,52]:

In this simulation, the transient waves are graphed when the following quantities are chosen in a dimensionless form such as $b=1$ and $\overline{P}=2$ at small time in the range $0\le x\le 5$ at $z=-1$ and $\mathsf{\omega }={\mathsf{\omega }}_0+\mathrm{i} \mathsf{\zeta }$ ($\mathsf{\zeta }=0.05$ and ${\mathsf{\omega }}_0=-2.5$).

Figure 2 shows the variation of the wave propagations for the main physical distributions according to the ED and TED with the axial horizontal distance $x$ under the effect of the magnetic field. The distributions of thermal wave (temperature), microelongation wave function, the elastic wave of displacement, and carrier intensity in the context of the plasma wave and the two mechanical waves ${\sigma }_{xx}$ and ${\sigma }_{xz}$ are studied according to the three different models CD, LS and GL during the photo-thermoelasticity theory. The three different models depend on the thermal memory values and the two parameters $n_0$ and $n_1$. All obtained evaluations are implemented for small non-dimensional time $t=0.001$. In a general view of Figure 2, all physical quantities under investigation satisfy the surface conditions of the microelongated semiconductor. Under the pressure force of the electromagnetic field and the thermal effect of light, the thermal wave and carrier density distribution begin from zero value and positive value, respectively, satisfying the boundary condition with the increase in the amplitude to reach the maximum point. The temperature distribution decreases with the wave behavior in the form of an exponential function until it reaches its lowest value with convergence with the zero line when the distance increases. On the other hand, the plasma wave in the second band decreases and increases as a wave behavior until it converges to the zero line. From the two subfigures, the behavior of the thermal wave and plasma wave agree with the experimental results given in [51]. The microelongation scalar function can be described by the microelongation wave propagation, which starts at the surface from the zero value and decreases in the closed first range due to the magnetic pressure force and increases then decreases periodically with the wave behavior. Far away from the semiconductor surface, the microelongation wave converges to a zero line due to the weakness of the magnetic field until reaches the state of equilibrium inside the medium. The elastic wave, which can be described by the displacement component $u$, starts at the surface and increases sharply due to the increase of particle vibrations according to the strength of magnetic field compression and thermal excitation to reach the peak value of maximum. But in the second range, the elastic wave decreases and increases periodically with wave behavior propagation with zero line convergence it until reaches the equilibrium state. The mechanical wave distribution is described by the normal stress component ${\sigma }_{xx}$ and tangent stress component ${\sigma }_{xz}$. The mechanical conditions are satisfied where ${\sigma }_{xx}$ and ${\sigma }_{xz}$ distributions start from the negative value and zero value, respectively, at the surface. The normal ${\sigma }_{xx}$ distribution decreases in the first range and increases in the second range; after that, it decreases and increases periodically with the wave behavior until it reaches the equilibrium state. On the other hand, the tangent ${\sigma }_{xz}$ distribution begins from zero point and decreases near the surface until it reaches the minimum value. In the second range, the tangent ${\sigma }_{xz}$ distribution increases gradually until it reaches the zero line (state of equilibrium) when the distance increases. The different values of the relaxation times affect the wave propagations of the physical fields. Wave propagation processes with different values for the photothermal elasticity models take on the same behavior in all subforms but differ in magnitude according to the values of the different relaxation times.

Figure 3 shows the comparisons of the main physical fields in the two different cases under the influence of a magnetic field at the same very small time. The first case is obtained when the microelongation parameters are neglected in the silicon material. On the other hand, the second case is studied when the microelongation parameters of the microelongated silicon material are taken into account. All computations are implemented in the context of the magneto-photo-thermoelasticity theory according to the GL model. From this figure, the wave propagations and their magnitudes depend on the microelongation parameters.

Figure 4 explains the behavior of the wave propagations with the distance in two cases. The first case describes the variation of the main physical fields under the effect of a magnetic field (with a magnetic field). By contrast, the second case describes the variation of the main physical fields in the absence of the magnetic field (without the magnetic field). The comparisons are implemented under the impact of the microelongation parameters according to the GL model for the same small non-dimensional time. The magnetic field has a great significant effect on all the wave propagations of all fields.

7. Conclusions

A novel model is applied to investigate the photo-thermoelasticity theory when the microelongated semiconductor material is used. The impact of the electromagnetic field during thermal-photo-excitation transport processes is taken into account. The governing equations describe the overlapping between the magneto-mechanical-thermal-plasma waves in 2D according to the TD and TED with the variation of thermal memory. The normal mode analysis is used to analyze the main equations according to the harmonic wave technique. The wave distributions vanish for the physical fields to reach the state of equilibrium. The wave propagation behavior depends on the thermal memory effect, which control the CD, LS, and GL models. Therefore, the thermal memory has a great significance on the wave propagation amplitude. The microelongation parameters affect the wave propagation distributions. On the other hand, the magnetic field causes more vibrations of particles, therefore affecting the behavior of the wave propagations during the re-deformation of the electronics. Microelongated materials have a wide use in such industries as sensors, medical devices, solar cells, and electric circuits.