A 2D Multi-Layer Model to Study the External Magnetic Field Generated by a Polymer Exchange Membrane Fuel Cell
Abstract
1. Introduction
1.1. Context of the Paper
1.2. Objective of the Paper
2. Mathematical Development of 2D Multi-Layer Model
2.1. Problem Description
2.1.1. Bipolar Plate of a PEMFC Stack
2.1.2. Normal and Faulty Conductive Segments
2.1.3. Modeling of Spatial Current Density Distribution in any Conductive Segments
2.2. List of Assumptions
- the end-effects are neglected (i.e., the magnetic variables are independent of z);
- the magnetic vector potential and current density have only one component along the z-axis, i.e., A = {0; 0; Az} and ;
- the skin depth effect is not considered;
- many industrial PEMFC stacks use graphite bipolar plates and non-magnetic stainless steels for rods and other mechanical parts [35]. Thus, the absolute magnetic permeability of all components used in bipolar plates of PEMFC stack are very close to the vacuum magnetic permeability .
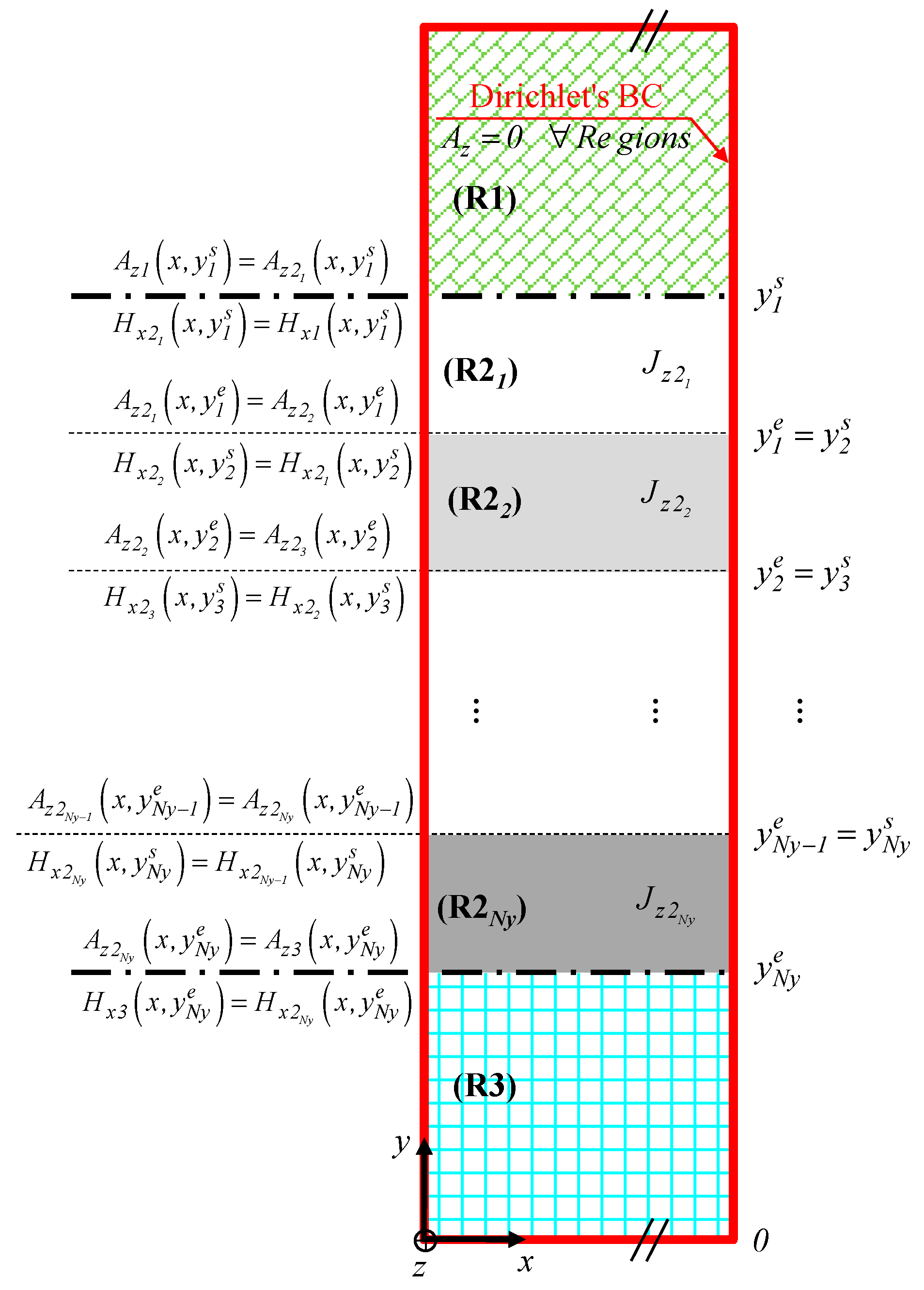
2.3. Problem Discretization in Regions
- Vacuum above the electrochemical active cell: Region 1 (R1) for with ;
- The electrochemical active cell: Region 2 (R2) for , which is divided in the y-axis into sub-regions i (R2i) for , with ;
- Vacuum below the electrochemical active cell: Region 3 (R3) for with .
2.4. Governing Partial Differential Equations (PDEs) in Cartesian Coordinates
2.5. Boundary Conditions (BCs)
2.6. General Solution of Magnetic Field in Each Region
3. Comparison of Analytical and Numerical Calculations
3.1. Problem Description
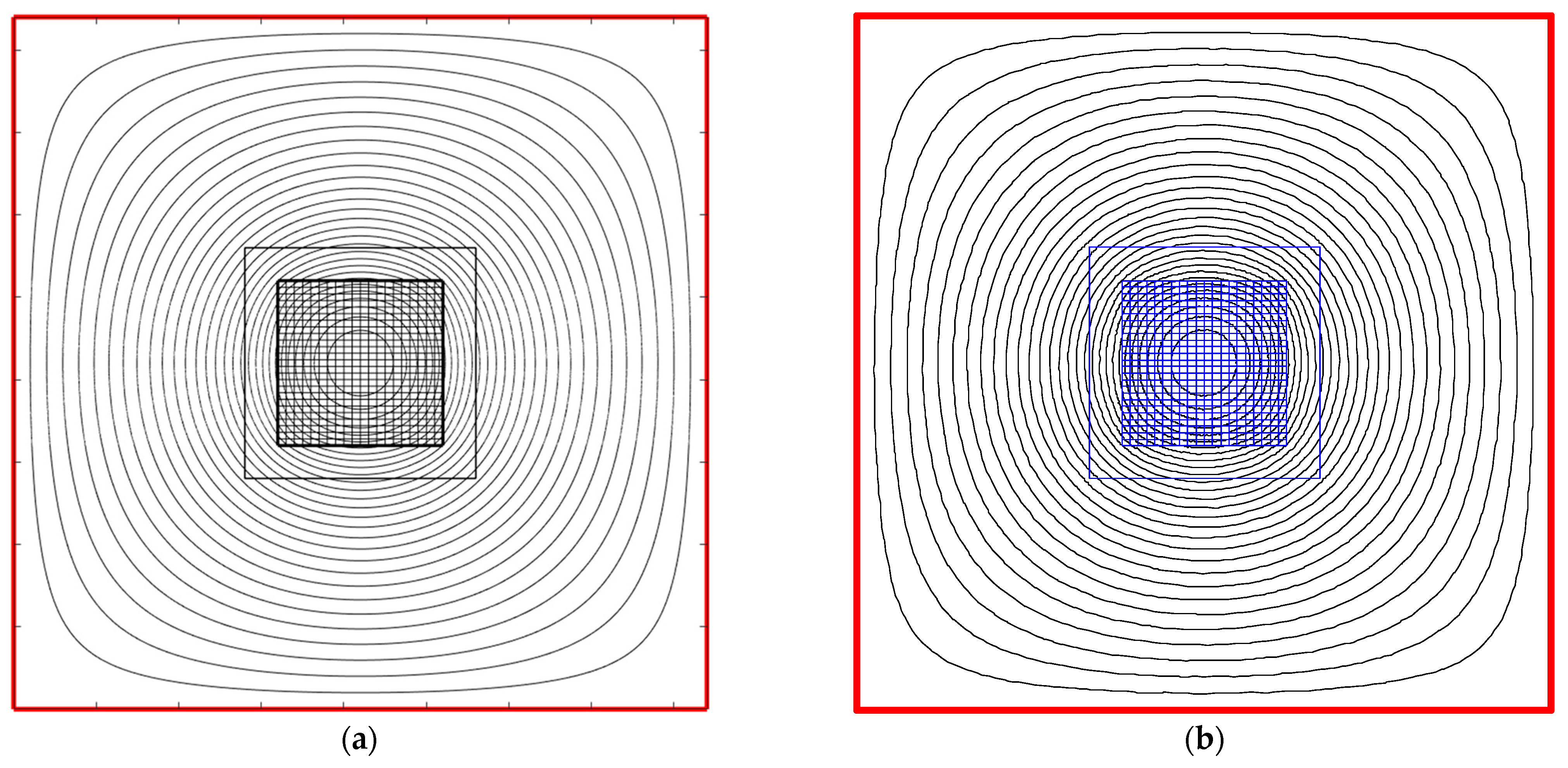
3.2. Analysis of Equipotential Lines
3.2.1. Healthy FC
3.2.2. FC Failure
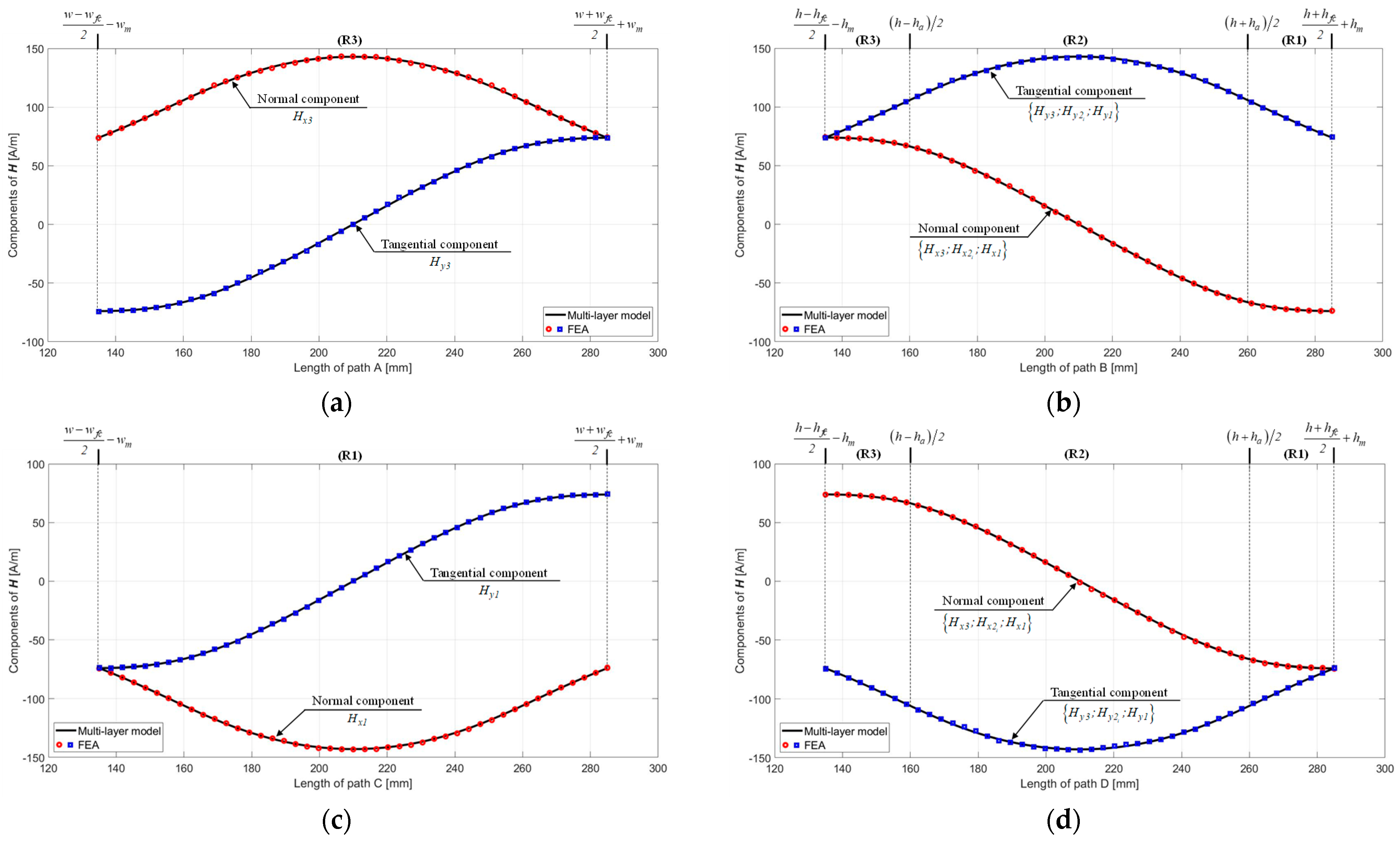
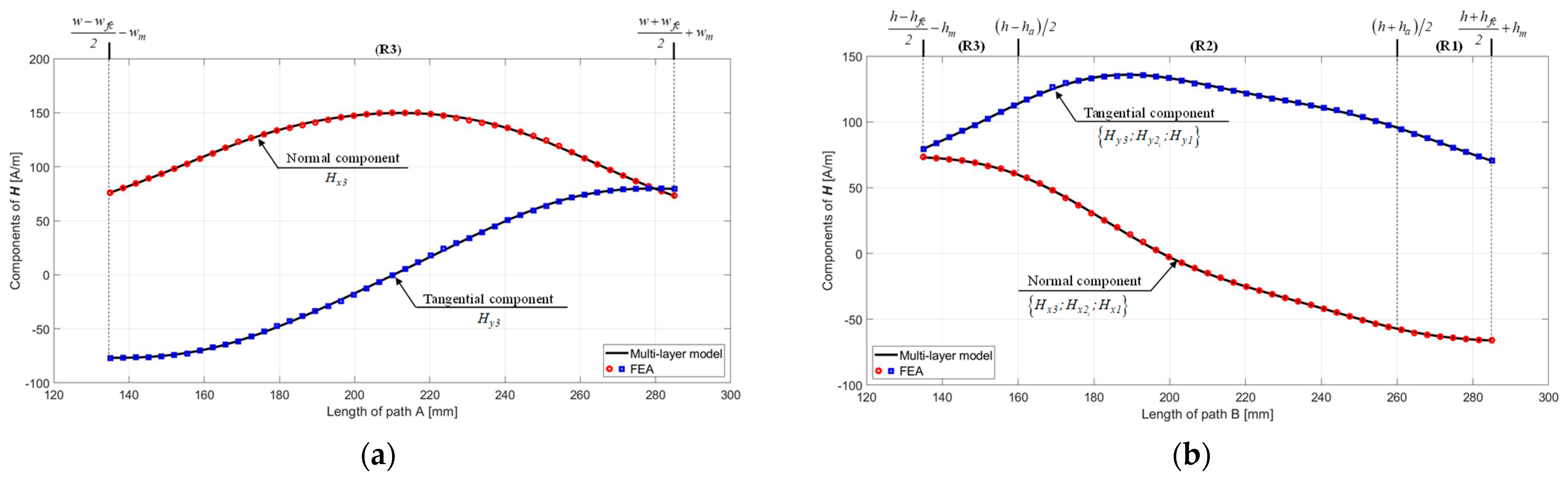
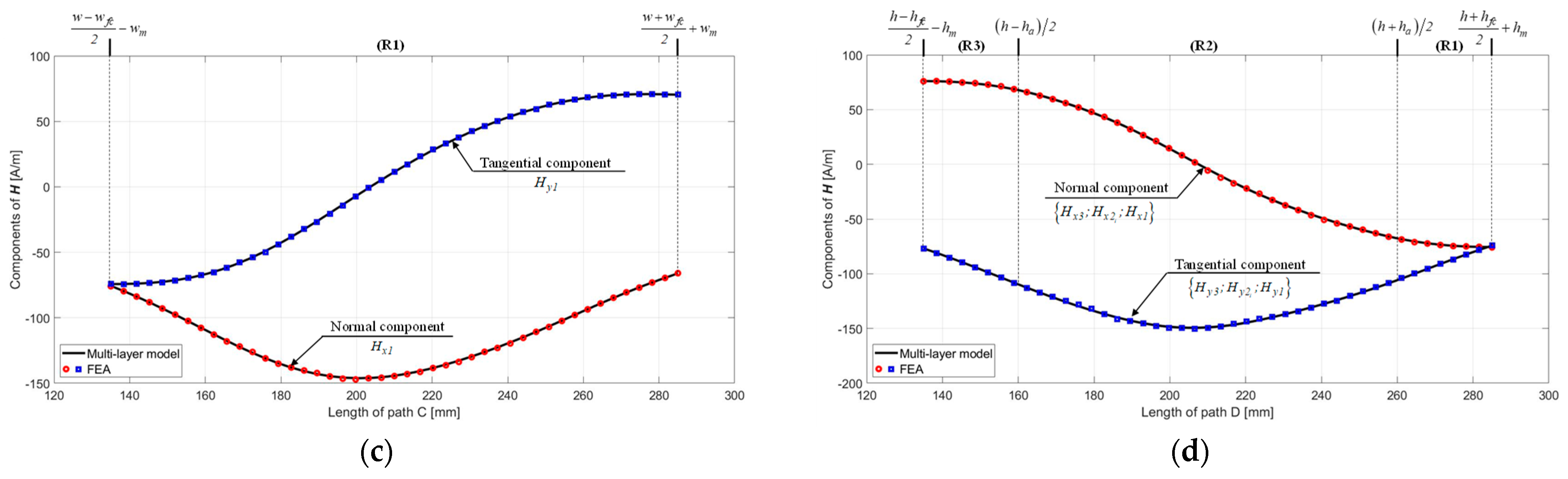
3.3. Analysis of Magnetic Field Distributions
3.3.1. Healthy FC
3.3.2. FC Failure
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dubas, F.; Espanet, C.; Miraoui, A. Design of a high-speed permanent magnet motor for the drive of a fuel cell air compressor. In Proceedings of the IEEE Vehicular Power and Propulsion Conference (VPPC), Chicago, IL, USA, 7–9 September 2005. [Google Scholar] [CrossRef]
- Hart, D.; Lehner, F.; Jones, S.; Lewis, J. The Fuel Cell Industry Review 2019. E4tech (an ERM Group Company). Available online: http://www.fuelcellindustryreview.com (accessed on 9 January 2020).
- Wilberforce, T.; Alaswad, A.; Palumbo, A.; Dassisti, M.; Olabi, A.G. Advances in stationary and portable fuel cell applications. Int. J. Hydrogen Energy 2016, 41, 16509–16522. [Google Scholar] [CrossRef]
- Gurz, M.; Baltacioglu, E.; Hames, Y.; Kaya, K. The meeting of hydrogen and automotive: A review. Int. J. Hydrogen Energy 2017, 42, 23334–23346. [Google Scholar] [CrossRef]
- Yue, M.; Jemei, S.; Gouriveau, R.; Zerhouni, N. Review on health-conscious energy management strategies for fuel cell hybrid electric vehicles: Degradation models and strategies. Int. J. Hydrogen Energy 2019, 44, 6844–6861. [Google Scholar] [CrossRef]
- Pahon, E.; Bouquain, D.; Hissel, D.; Rouet, A.; Vacquier, C. Performance analysis of proton exchange membrane fuel cell in automotive applications. J. Power Sources 2021, 510, 230385. [Google Scholar] [CrossRef]
- Abe, J.O.; Popoola, A.P.I.; Ajenifuja, E.; Popoola, O.M. Hydrogen energy, economy and storage: Review and recommendation. Int. J. Hydrogen Energy 2019, 44, 15072–15086. [Google Scholar] [CrossRef]
- Yue, M.; Lambert, H.; Pahon, E.; Roche, R.; Jemei, S.; Hissel, D. Hydrogen energy systems: A critical review of technologies, applications, trends and challenges. Renew. Sustain. Energy Rev. 2021, 146, 111180. [Google Scholar] [CrossRef]
- Inci, M.; Büyük, M.; Demir, M.H.; Ilbey, G. A review and research on fuel cell electric vehicles: Topologies, power electronic converters, energy management methods, technical challenges, marketing and future aspects. Renew. Sustain. Energy Rev. 2020, 137, 110648. [Google Scholar] [CrossRef]
- Lorenzo, C.; Bouquain, D.; Hibon, S.; Hissel, D. Synthesis of degradation mechanisms and of their impacts on degradation rates on proton-exchange membrane fuel cells and lithium-ion nickel–manganese–cobalt batteries in hybrid transport applications. Reliab. Eng. Syst. Saf. 2021, 212, 107369. [Google Scholar] [CrossRef]
- Aubry, J.; Steiner, N.Y.; Morando, S.; Zerhouni, N.; Hissel, D. Fuel cell diagnosis methods for embedded automotive applications. Energy Rep. 2022, 8, 6687–6706. [Google Scholar] [CrossRef]
- Hauer, K.-H.; Potthast, R.; Wüster, T.; Stolten, D. Magnetotomography—A new method for analysing fuel cell performance and quality. J. Power Sources 2005, 143, 67–74. [Google Scholar] [CrossRef]
- Buchholz, M.; Brebs, V. Dynamic modelling of a polymer electrolyte membrane fuel cell stack by nonlinear system identification. Fuel Cell. 2007, 7, 392–401. [Google Scholar] [CrossRef]
- Rubio, M.; Urquia, A.; Dormido, S. Diagnosis of performance degradation phenomena in PEM fuel cells. Int. J. Hydrogen Energy 2010, 35, 2586–2590. [Google Scholar] [CrossRef]
- Chevalier, S.; Trichet, D.; Auvity, B.; Olivier, J.; Josset, C.; Machmoum, M. Multiphysics DC and AC models of a PEMFC for the detection of degraded cell parameters. Int. J. Hydrogen Energy 2013, 38, 11609–11618. [Google Scholar] [CrossRef]
- Zheng, Z.; Petrone, R.; Péra, M.; Hissel, D.; Becherif, M.; Pianese, C.; Steiner, N.Y.; Sorrentino, M. A review on non-model based diagnosis methodologies for PEM fuel cell stacks and systems. Int. J. Hydrogen Energy 2013, 38, 8914–8926. [Google Scholar] [CrossRef]
- Geske, M.; Heuer, M.; Heideck, G.; Styczynski, Z.A. Current Density Distribution Mapping in PEM Fuel Cells as An Instrument for Operational Measurements. Energies 2010, 3, 770–783. [Google Scholar] [CrossRef]
- Pei, P.; Chen, H. Main factors affecting the lifetime of Proton Exchange Membrane fuel cells in vehicle applications: A review. Appl. Energy 2014, 125, 60–75. [Google Scholar] [CrossRef]
- Ghezzi, L.; Piva, D.; Di Rienzo, L. Current Density Reconstruction in Vacuum Arcs by Inverting Magnetic Field Data. IEEE Trans. Magn. 2012, 48, 2324–2333. [Google Scholar] [CrossRef]
- Begot, S.; Voisin, E.; Hiebel, P.; Artioukhine, E.; Kauffmann, J.M. D-optimal experimental design applied to a linear magnetostatic inverse problem. IEEE Trans. Magn. 2002, 38, 1065–1068. [Google Scholar] [CrossRef]
- Potthast, R.; Wannert, M. Uniqueness of Current Reconstructions for Magnetic Tomography in Multilayer Devices. SIAM J. Appl. Math. 2009, 70, 563–578. [Google Scholar] [CrossRef]
- Izumi, M.; Gotoh, Y.; Yamanaka, T. Verification of Measurement Method of Current Distribution in Polymer Electrolyte Fuel Cells. ECS Trans. 2009, 17, 401–409. [Google Scholar] [CrossRef]
- Lustfeld, H.; Reißel, M.; Schmidt, U.; Steffen, B. Reconstruction of Electric Currents in a Fuel Cell by Magnetic Field Measurements. J. Fuel Cell Sci. Technol. 2009, 6, 021012. [Google Scholar] [CrossRef]
- Nasu, T.; Matsushita, Y.; Okano, J.; Okajima, K. Study of Current Distribution in PEMFC Stack Using Magnetic Sensor Probe. J. Int. Counc. Electr. Eng. 2012, 2, 391–396. [Google Scholar] [CrossRef]
- Le Ny, M.; Chadebec, O.; Cauffet, G.; Dedulle, J.-M.; Bultel, Y.; Rosini, S.; Fourneron, Y.; Kuo-Peng, P. Current Distribution Identification in Fuel Cell Stacks From External Magnetic Field Measurements. IEEE Trans. Magn. 2013, 49, 1925–1928. [Google Scholar] [CrossRef]
- Le Ny, M.; Chadebec, O.; Cauffet, G.; Rosini, S.; Bultel, Y. PEMFC stack diagnosis based on external magnetic field measurements. J. Appl. Electrochem. 2015, 45, 667–677. [Google Scholar] [CrossRef]
- Nara, T.; Koike, M.; Ando, S.; Gotoh, Y.; Izumi, M. Estimation of localized current anomalies in polymer electrolyte fuel cells from magnetic flux density measurements. AIP Adv. 2016, 6, 056603. [Google Scholar] [CrossRef]
- Ifrek, L.; Cauffet, G.; Chadebec, O.; Bultel, Y.; Rouveyre, L.; Rosini, S. 2D and 3D fault basis for fuel cell diagnosis by external magnetic field measurements. Eur. Phys. J. Appl. Phys. 2017, 79, 20901. [Google Scholar] [CrossRef]
- Claycomb, J.R. Algorithms for the Magnetic Assessment of Proton Exchange Membrane (PEM) Fuel Cells. Res. Nondestruct. Eval. 2017, 29, 167–182. [Google Scholar] [CrossRef]
- Ifrek, L.; Chadebec, O.; Rosini, S.; Cauffet, G.; Bultel, Y.; Bannwarth, B. Fault Identification on a Fuel Cell by 3-D Current Density Reconstruction From External Magnetic Field Measurements. IEEE Trans. Magn. 2019, 55, 2512271. [Google Scholar] [CrossRef]
- Ifrek, L.; Rosini, S.; Cauffet, G.; Chadebec, O.; Rouveyre, L.; Bultel, Y. Fault detection for polymer electrolyte membrane fuel cell stack by external magnetic field. Electrochim. Acta 2019, 313, 141–150. [Google Scholar] [CrossRef]
- Katou, T.; Gotoh, Y.; Takahashi, N.; Izumi, M. Measurement Technique of Distribution of Power Generation Current Using Static Magnetic Field around Polymer Electrolyte Fuel Cell by 3D Inverse Problem FEM. Mater. Trans. 2012, 53, 279–284. [Google Scholar] [CrossRef]
- Yamanashi, R.; Gotoh, Y.; Izumi, M.; Nara, T. Evaluation of Generation Current inside Membrane Electrode Assembly in Polymer Electrolyte Fuel Cell Using Static Magnetic Field around Fuel Cell. ECS Trans. 2015, 65, 219–226. [Google Scholar] [CrossRef]
- Akimoto, Y.; Okajima, K.; Uchiyama, Y. Evaluation of Current Distribution in a PEMFC using a Magnetic Sensor Probe. Energy Procedia 2015, 75, 2015–2020. [Google Scholar] [CrossRef][Green Version]
- Plait, A.; Giurgea, S.; Hissel, D.; Espanet, C. New magnetic field analyzer device dedicated for polymer electrolyte fuel cells noninvasive diagnostic. Int. J. Hydrogen Energy 2020, 45, 14071–14082. [Google Scholar] [CrossRef]
- Plait, A.; Dubas, F. Experimental validation of a 2-D multi-layer model for fuel cell diagnosis using magneto-tomography. In Proceedings of the 23rd World Hydrogen Energy Conference (WHEC), Istanbul, Turkey, 26–30 June 2022. [Google Scholar]
- Lustfeld, H.; Reißel, M.; Steffen, B. Magnetotomography and Electric Currents in a Fuel Cell. Fuel Cells 2009, 9, 474–481. [Google Scholar] [CrossRef]
- Meeker, D.C. Finite Element Method Magnetics Ver. 4.2. Available online: http://www.femm.info (accessed on 10 October 2018).
- Stoll, R.L. The Analysis of Eddy Currents; Clarendon Press: Oxfort, UK, 1974. [Google Scholar]
- Dubas, F.; Boughrara, K. New Scientific Contribution on the 2-D Subdomain Technique in Cartesian Coordinates: Taking into Account of Iron Parts. Math. Comput. Appl. 2017, 22, 17. [Google Scholar] [CrossRef]







| Symbol | Quantity | Values |
|---|---|---|
| FC surface | 14 × 14 = 196 cm2 | |
| S = w × h | Infinite box surface | 42 × 42 = 1764 cm2 |
| Electrochemical active cell surface | 10 × 10 = 100 cm2 | |
| Number of conductive segments | 25 × 20 = 500 | |
| Conductive segment surface | 5 × 4 = 20 mm2 | |
| FC depth | 10 cm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plait, A.; Dubas, F. A 2D Multi-Layer Model to Study the External Magnetic Field Generated by a Polymer Exchange Membrane Fuel Cell. Mathematics 2022, 10, 3883. https://doi.org/10.3390/math10203883
Plait A, Dubas F. A 2D Multi-Layer Model to Study the External Magnetic Field Generated by a Polymer Exchange Membrane Fuel Cell. Mathematics. 2022; 10(20):3883. https://doi.org/10.3390/math10203883
Chicago/Turabian StylePlait, Antony, and Frédéric Dubas. 2022. "A 2D Multi-Layer Model to Study the External Magnetic Field Generated by a Polymer Exchange Membrane Fuel Cell" Mathematics 10, no. 20: 3883. https://doi.org/10.3390/math10203883
APA StylePlait, A., & Dubas, F. (2022). A 2D Multi-Layer Model to Study the External Magnetic Field Generated by a Polymer Exchange Membrane Fuel Cell. Mathematics, 10(20), 3883. https://doi.org/10.3390/math10203883









