Abstract
Due to their advantages, switched reluctance motors (SRMs) are interesting solutions for electric vehicle (EV) propulsion. However, they have the main drawback of high torque ripple. This paper develops a universal torque control (UTC) technique for SRM that can fulfill all vehicle requirements under a wide range of speeds. The developed UTC involves two different control techniques. It utilizes the direct instantaneous torque control (DITC) strategy in a low speed region, and the average torque control (ATC) strategy in high speeds. The selection of DITC and ATC is made based on their performance regarding torque ripple, torque/current ratio, and efficiency. Moreover, a novel transition control between the two control techniques is introduced. The results show the ability of the proposed UTC to achieve vehicle requirements while obtaining all the benefits of torque control over the possible range of speeds. The proposed UTC provides the best performance regarding minimum torque ripple, maximum torque/current ratio, and maximum efficiency over the whole speed range. The transition control achieves a smooth operation without any disturbances. The transition control helps to simplify the overall control algorithm, aiming to have a feasible and practical UTC without a complicated control structure.
Keywords:
switched reluctance motor; universal torque control; direct instantaneous torque control; average torque control; firing angles; optimization MSC:
70Q05; 37N35; 93-10; 13P25; 65K10
1. Introduction
Energy sources, pollution, and noise are currently the key issues facing many countries as a result of using enormous numbers of fuel-powered vehicles in transportation. Electric vehicles (EVs), on the other hand, can provide an alternative solution. They are considered the way for establishing a green transportation system [1,2]. For this purpose, many efforts have been made to solve the challenges facing EVs, such as saving energy and obtaining the highest performance at a reasonable cost. Various components of EVs can be optimized to enhance their performance. The most effective parts within the vehicle are the motors and their drive circuits. Generally, all types of electric motors can be used for EVs. Each motor type is associated with a set of benefits and drawbacks [3,4]. The switched reluctance motors (SRMs) can be considered a perfect choice because they have many features that are relevant to the requirements of EVs, such as, reasonable manufacturing cost, high fault resistance, high starting torque, normal operation in a high temperature environment, and they can provide high efficiency under high speed operation. Furthermore, SRMs do not contain permanent magnets nor conductors in the rotor structure, and thus, a robust and reliable operation exists. However, the SRMs encounter acoustic noise and considerable torque ripple [5,6,7]. These drawbacks make less utilization of SRMs in several industrial applications including the EVs. Therefore, they must be treated. Researchers have recently been focusing on solving these issues, and many strategies have been introduced. Some researchers proposed the optimization of SRM design by the modification of its geometrical dimensions [8,9,10,11]. These design modifications can minimize the acoustic noise and torque ripple only to a small extent [8,10].
On the other hand, other researchers succeeded in significantly reducing the SRM torque ripple and the associated acoustic noise by implementing innovative control techniques. Generally, the current chopping control (CCC) [12,13,14,15], instantaneous torque control (ITC) [16,17,18,19,20], and average torque control (ATC) [21,22,23,24,25] are the most popular control strategies. Despite the fact that these strategies can reduce torque ripple and improve system performance, they have disadvantages. For instant, the CCC can provide effective, uncomplicated, and low cost drive. İt causes some torque ripple because each phase current can only be controlled in the form of square waveforms [26]. Thus, only the excitation angles can be optimized for a given reference current [15]. Hence, this paper focuses on the ITC and ATC as they are the most promising torque control strategies that can provide a better overall performance [27].
The ITC strategies are able to provide the remarkable suppression of torque ripple since they control the torque instantaneously at each sample of the rotor position. The ITC strategies can be categorized into direct ITC (DITC) and indirect ITC (IITC) using the torque sharing function (TSF). In [17,18], the IITC is achieved based on an improved TSF. The proposed TSF can impose optimal profiling for the phase current to reach a minimized torque ripple with reduced copper losses. In [19], a modified firefly algorithm is used to optimize the PID parameters of the speed regulator to achieve a precise DITC with an improved speed-change response. In [20], a new DITC is implemented by replacing the commonly used hysteresis torque controller with a PWM controller. In this way, the switching frequency can be controlled. Additionally, the commutation region is divided into many sectors, and by modifying the duty cycle coefficients in these sectors, further torque ripple enhancement is obtained. In [16], an improved DITC is implemented by utilizing a real-time commutation methodology for both switching angles. The turn on angle (θon) is controlled basically to maximize the torque tracking ability of the hysteresis torque controller. At the same time, the turn off angle (θoff) is controlled in order to minimize the generated negative torque to an effective-less value. In [28], an improved DITC method is introduced. This method uses a torque sharing function (TSF) as well as it introduces an adaptive turn on angle control to suppress torque ripple and improve efficiency. However, it has a complex control structure.
In [21], the ATC strategy is investigated for EV applications. Then, an improved ATC is presented by optimizing both excitation angles, and the objective function is proposed to increase the performance of the SRM drive. In [22], the ATC is proposed involving both flux and current controllers. Unlike the conventional ATC, it controls the estimated average torque only over a complete electrical cycle. The new ATC can control the average torque through smaller intervals and thus can achieve less torque ripple. In [23], a sharing look-up table is used to equally divide the torque reference among motor phases, and thus, a reference value is set for each phase current, and by analytical accumulating each phase torque, the average torque can be estimated instantaneously. In [24], a multi-objective constrained optimization problem is created to implement an optimized ATC strategy. The objective function includes two terms: the efficiency and torque ripple. The control parameters are the switching angles, the constraints are set mainly to keep high torque/ampere ratio, and thus, further improvement is attained in order to meet the EVs’ requirements. In [29], after investigations, the ATC is selected over ITC for EV applications. The turn on and turn off angles are optimized to enhance driving efficiency and reduce torque ripple. Despite the simple structure of ATC, it has a high torque ripple at low speeds.
Unfortunately, the majority of the literature includes only a comparison between one basic torque control strategy and its modification or compares the same type of modified strategies. Nonetheless, very few have conducted a comparison between different types of techniques. Therefore, in the authors’ previous work [27], a comprehensive analysis and comparison between an improved DITC, IITC, and ATC are included regarding the requirements of EVs. The results showed the superiority of the proposed DITC since it produced lower torque ripples, highest efficiency, and the highest torque/ampere ratio at a low speed operation. Furthermore, the comparison also showed an advantage when using the ATC technique at high speeds. Above the rated speed of the SRM, a higher back-electromotive force is generated, and thus, the instantaneous torque can be only partially or poorly tracked. Therefore, the ATC method is proposed to be utilized at a high speed SRM operation. The study provides a pre-overview to implement a UTC strategy for the SRMs in EV application.
The literature shows the superior performance of ITC strategies (DITC and IITC) regarding the torque ripple reduction for low speed operation. It also gives the advantages of the ATC strategy in high speed regions as it gives a better torque/ampere ratio and hence better driving efficiency. For the best overall performance, the ITC and the ATC strategies have to be combined to implement a universal torque control (UTC) that provides the benefits of both strategies. Hence, it will be the best choice for several applications including EVs. In [25], the DITC is used below the rated speed of the SRM, while the ATC is utilized above the base speed. Furthermore, the excitation angles are optimized through a particle swarm algorithm to decrease the fuel consumption of the EVs (by attaining higher efficiency) and to guarantee a comfortable ride (by attaining lower torque ripple). However, the optimization of the excitation angles is only applied to the DITC at a low speed. No smooth transient is implemented between the DITC and the ATC. In [30], a unified controller is implemented by combining the DITC with the CCC method to attain torque ripple reduction in the low, medium, and high speed operation of the SRM. The unified controller also adopts a phase current demagnetization strategy to prevent negative torque production, and thus, a higher torque/ampere ratio can be attained.
The novelty of this article is the development of a novel UTC strategy that provides the best overall performance of SRM over the whole range of speeds while maintaining a feasible and practical control algorithm that fits several industrial applications including EVs. The proposed UTC uses DITC for low speed operation and ATC for high speeds to gather their benefits. The paper helps to overcome the problems and unfeasibility of developing such control. First, the paper uses modified DITC and ATC strategies to ensure a simple structure of the overall control algorithm. The modifications are made basically for performance improvement considering the ability of their integrations. Second, the proposed control guarantees maximum torque per ampere production via turn on angle optimization. It optimizes a turn off angle to improve efficiency and reduce torque ripples. Third, the novelty also includes a proposed smooth transition control (STC) from DITC to ATC and vice versa. The STC is guaranteed in motoring and generation modes of operation. Hence, this paper gives a novel UTC strategy that provides the best overall performance of SRM over the whole range of speeds, while maintaining a feasible and practical control algorithm.
The proposed method suits EV applications as it can fulfill the vehicle requirements that include minimum torque ripple for better drivability, maximum torque per ampere (MTPA) and/or maximum efficiency for longer millage per battery charge, wide speed operation, and high reliability to avoid breakdown on the road.
The rest of this article is outlined as follows: Section 3 describes the conventional structure of torque control strategies. The proposed UTC is given in Section 4. The STC is also included in this section. The results and discussions are presented in Section 5. Finally, Section 7 presents the conclusions.
2. Modeling of SRM
2.1. Machine Model
The SRM has highly nonlinear magnetic characteristics because of the salient structure of both stator and rotor poles. Hence, the flux-linkage λ(i,θ), inductance L(i,θ), and torque T(i,θ) are functions of both the current (i) and position (θ). The voltage equation of kth phase is given by Equation (1). It also illustrates how the flux is estimated from phase voltage. Equation (2) gives the electromagnetic torque of kth phase (Tk) and total electromagnetic torque (Te) with q-phases. Equation (3) shows the mechanical motion.
where R, J, B, ω, and TL are the phase resistance, inertia, frictional coefficient, rotor speed, and load torque.
The simulation of one phase of SRM is shown in Figure 1. The inputs are the rotor phase position (θph) and the phase voltage (Vph). The outputs are the phase current (iph) and phase torque (Tph). The finite element method (FEM) is employed to generate the magnetic characteristics of the studied SRM. The studied motor is 4 kW, 1500 r/min, 600 V, 8/6 poles, and 4 phases SRM. The calculated flux linkage and torque characteristics using FEM are shown in Figure 2a,b, respectively. This figure shows only part of the curves for simplification, while the complete flux and torque characteristics are calculated for current [0:0.5:30]A and position of [0:0.5:30]°. Due to the big size of FEM data, the interpolation and extrapolation within LUTs can ensure sufficient accuracy.
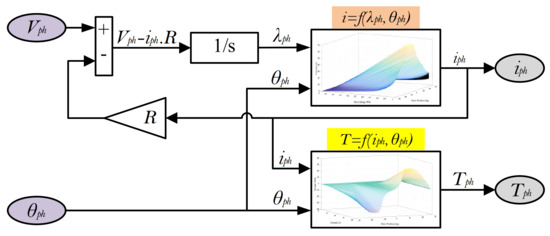
Figure 1.
Simulation of one phase of SRM.

Figure 2.
FEM-calculated characteristics: (a) flux linkage for [1:1:30]°; (b) torque for [1:1:30]A.
2.2. Performance Indices
The following indices are used for evaluations. The indices include average torque (Tav), mechanical output power (Pm), torque ripple (Trip), efficiency (η), switching frequency (fs) of power converter, average supply current (Iav), RMS supply current (IRMS), and copper losses (Pcu). The average and RMS values are calculated over one electrical cycle (τ).
where Tav is the average torque; ω is the motor speed; Tmax and Tmin are the maximum and minimum instantaneous values of output motor torque (Te) over one electrical cycle (τ); Vdc is the dc link voltage; Iav is the average supply current; is is instantaneous supply current; NT is the total number of switching of IGBTs over one electric cycle.
3. The Conventional ATC and DITC Techniques for SRMs
As concluded from the literature, the best performance is achieved by DITC for low speeds and is achieved by ATC for high speeds. Hence, they are chosen and adopted for this research.
3.1. The Conventional ATC Technique
Figure 3 shows the block diagram of conventional ATC [22,29]. Tref is the reference commanded torque; it is obtained from an outer loop speed controller. In Figure 3a, the average torque (Tav-est) is estimated online using a torque estimator. The torque error (ΔT) is processed through a PI torque controller that produces the reference current (iref). The mathematical representation of the PI controller is given generally in Equation (9). Its output (PIout) depends on the input error and the constant gains Kp and KI. In Figure 3a, the input error is ΔT and the output is iref. The closed loop direct current control is essential. The current controller is a hysteresis controller that outputs three voltage states from the power converter according to the current error ΔI and rotor position. If ΔI is greater than the current band, positive voltage is obtained. If ΔI is less than the current band, zero voltage is obtained. Finally, negative voltage is obtained if ΔI is less than the current band and the rotor position is after the turn off angle (θoff). The torque estimator depends on the machine model as given in Figure 1.


Figure 3.
Block diagram of ATC with (a) torque controller, and (b) torque to current conversion.
In Figure 3b, the reference torque (Tref) is converted directly to the reference current (iref) using the torque to current relationship as will be given later in Figure 7b. This helps to improve the dynamic performance [24]. In addition, the firing angles (θon and θoff) must be optimized for better performance. The optimization is given below.
Optimization of Firing Angles (θon and θoff) for ATC Technique
Due to the great effect of firing angles (θon and θoff) on SRM performance as they affect torque production, amount of torque ripple, efficiency, and the range of speed control [15,31], the firing angles (θon and θoff) are optimized based on a multi-objective problem to achieve the best overall performance. The multi-objective optimization includes the minimization of torque ripple (Trip), reduction of copper losses (Pcu), increasing torque/current ratio, and improvement of motor efficiency (η).
A single-objective optimization problem can be obtained from the multi-objective problem by a linear combination of torque ripple (Trip), copper losses (Pcu), and efficiency (η) as follows [27,29]:
where Fobj is the objective function; Trb, Pcub, and ηb are the base values for torque ripple, copper loss, and efficiency, respectively. wr, wcu, and wη are the weight factors for torque ripple, copper loss, and efficiency, respectively. The weight factors can be chosen according to the desired level of optimization. and are the minimum and the maximum limits of the θon, respectively.
For every operating point, defined by motor speed and loading torque, the firing angles (θon and θoff) are estimated to achieve Equation (10). The speed and torque are the inputs, and the firing angles (θon and θoff) are the outputs that fulfill Equation (10). The inputs, speed, and torque are changed in small steps, and the corresponding optimal firing angles are estimated.
3.2. The Conventional DITC Technique
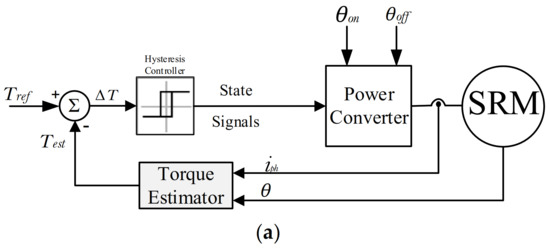

Figure 4.
The block diagram of DITC, (a) conventional DITC, (b) TSF-based DITC.
Tref is the reference commanded torque, it comes from an outer loop speed controller. In Figure 4a, the online torque estimator is essential to estimate the instantaneous motor torque (Test). The torque error (ΔT) is processed through a hysteresis torque controller that outputs the state signals. The current control is included within the torque controller. Limiting the torque means limiting the maximum current value.
In Figure 4b, a torque sharing function (TSF) is introduced with the DITC algorithm [28]. The TSF is used to distribute Tref between motor phases as described by Equation (13). The reference torque for each phase (Ta-ref, Tb-ref, Tc-ref, and Td-ref) is compared to its actual measured value (Ta, Tb, Tc, and Td). The torque errors (ΔTa, ΔTb, ΔTc, and ΔTd) are processed through a hysteresis torque controller that outputs the states. Sector judgment and voltage state table are employed to provide the proper control pulses. The sector judgment divides the control period into six sectors. The details are included in [28]. The voltage state table outputs the voltage state (Sp) (p could be phase a, b, c, or d) according to the torque error for each phase. For example, when ∆Ta > hysteresis band (∆T), Sa = 1; when ∆Ta < −∆T, Sa = 1; when phase is turned off, Sa = −1.
where θov is the overlap angle; θp depicts the rotor pitch angle.
Optimization of Firing Angles (θon and θoff) for DITC Technique
For DITC, the firing angles (θon and θoff) have to be optimized for better motor performance. The optimization is similar to that for ATC which is described by Equations (10)–(12). The difference is the structure of the control algorithm. Different weights can be chosen according to the required level of optimization.
4. The Proposed Universal Torque Control (UTC) of SRM for EVs
As each control technique provides a unique performance under a certain speed range, a combination of these techniques is the best solution in order to gain the benefits of each control technique. The best choice for the low speed range is the DITC. It provides a very low torque ripple, fast dynamic response, high efficiency, and the lowest RMS current. On the other hand, ATC is the best choice for high speeds. It provides high efficiency, a fast dynamic response, and the lowest RMS current. At high speeds, the vehicle inertial can filter the torque ripples [27].
A proposed universal control of SRM for EVs is given in Figure 5. It employs a DITC and ATC. The DITC is meant for low speeds and the ATC is meant for high speeds. The transition between the two techniques should be very smooth without transient or disturbances.
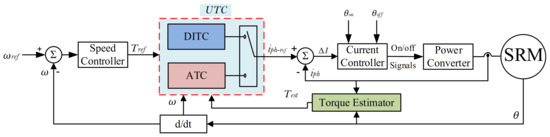
Figure 5.
The universal torque control (UTC) of SRM.
For developing such universal control (Figure 5), several problems arise. First, the conventional structures of ATC and DITC, shown in Figure 3 and Figure 4, are complicated to be combined in one control algorithm. The final UTC algorithm will be much more complicated. Second, the direct combination of conventional ATC and DITC seems to be infeasible. That is mainly because of the big differences between conventional ATC and conventional DITC regarding structure and operational principles. Third, these big differences could cause a non-smooth transition that could increase the noise and disturbance in a vehicle. The disturbance could be large enough to unstable the system operation. For these reasons, this paper improves the structure of conventional ATC and the structure of conventional DITC, in order to avoid the aforementioned issues, and aiming to have the best structure for the UTC strategy.
4.1. The Proposed DITC Technique
Figure 6a shows the block diagram of the modified DITC. The main difference is that it has a torque to current conversion as seen in Figure 6b. iref is obtained directly from Tref. In addition, the torque error (Tref − Test) is compensated after being multiplied by K1.

Figure 6.
The adopted DITC (a) block diagram; (b) the torque to current conversion.
The torque to current conversion is achieved by the analyses of torque characteristics (Figure 7). The best torque production is achieved over the period [θm, θm + θc] [33]. For each current magnitude, the average torque can be estimated. Then, a polynomial fitting can be simply applied, which is a very simple formulation as illustrated Figure 7b.

Figure 7.
Torque to current conversion: (a) torque curves over 15°; (b) current versus average torque.
4.2. The Proposed ATC Technique
Figure 8 shows the block diagram of the simplified ATC (SATC). The reference current (iref) is obtained directly from the outer loop speed controller. In such a system, there is no need to estimate the average torque online as the optimization of firing angles at each operating point can be completed to ensure the motor can produce the required torque. Hence, the closed loop torque control is no longer needed. As a result, the structure of the overall system is reduced, which means a less complicated control algorithm [27].

Figure 8.
Block diagram of SATC.
4.3. The Final Intergrated UTC
Figure 9 shows the proposed UTC. It uses the modified versions of DITC and the SATC in order to have a feasible integration. The outer loop speed controller feeds the reference commanded torque to DITC and SATC. A switching unit determines which control algorithm is employed accordingly with motor speed. The switching value of speed is chosen to be 2000 r/min. That means below 2000 r/min, the DITC is utilized, while for higher speeds the ATC is used.

Figure 9.
The proposed universal torque control (UTC) of SRM for EVs.
In order to have such an integration, a single torque to current conversion is needed. The firing angles are estimated online to improve the system performance. Furthermore, they are the keystone to have a smooth transition between the DITC and the ATC. The idea to guarantee a smooth transition is as follows.
Smooth Transition Control
The control will change from DITC to ATC after a certain speed (2000 r/min). At the changing instant, a smooth transition should occur. A smart solution without complications of the control algorithm could be the best. There is no need for cross-over control to transit from a state to another.
The UTC utilizes both the DITC and ATC. For each control strategy, the best performance is achieved with certain firing angles that achieve Equation (10). As the operation and structure of DITC is different from that of ATC, the solutions for the best firing angles that achieve Equation (10) for DITC and ATC will be large. Hence, the transition from one strategy (DITC) to the other (ATC), or vice versa, will lead to a large variation for the firing angles. This, in turn, gives rise to uncertainties and unpredicted performance for the system.
In this paper, the solution for a smooth transition is completed based on the solution of optimum excitation angles. A smooth transition from one technique to another can be guaranteed if small changes in the best firing angles can be achieved. Hence, this is the idea to achieve now.
Based on the observations, experience, and analysis of SRM behavior, the variations in the turn on angle (θon) with speed and loading torque are very large. The variations are also different from DITC to ATC. Hence, Equation (10) will not guarantee the best transition. For that reason, the authors propose the utilization of a single analytical formulation for the best turn on angle (θon) over the whole speed range for both the DITC and the ATC. The analytical solution for the turn on angle (θon) is given in detail in the previous authors’ work [31]. This solution is illustrated in Equation (14). This equation provides a simple analytical solution for the optimum turn on angles over the whole range of speeds.
where L(i,θ) is the phase inductance; VDC is the supply voltage; and ω is the rotor speed. θm is the angle at which rotor poles start to overlap with stator poles.
The control variables are ω and iref. Hence, the optimum θon depends mainly on the inductance L(i,θ) and its slope kb = dL(i,θ)/dθ. The inductance L(i,θ) = L(θ) is the only position dependent over the minimum inductance zone [−θm, θm]. This fact simplifies the solution and implementation of Equation (4). The inductance can be easily fitted against the position as in Equation (15). The constants a, b, and c are easily estimated from the inductance data.
For DITC, as it has an inherited capability for torque ripple reduction, its turn on angle can be optimized for MTPA using Equation (14). Its optimum turn off angle is estimated based on an optimization problem as in Equations (16)–(18). Greater importance is given to the efficiency due to the inherited capability of DITC for torque ripple reduction. Therefore, the weight factors are wη = 0.6, wr = 0.2, and wcu = 0.2.
For SATC, the turn on angle is optimized for MTPA using Equation (14) too. As SATC is employed for high speeds, torque ripples are not of great interest as they could be filtered by inertia. The efficiency becomes of the greatest value. Therefore, the firing angles are optimized for higher efficiency focusing. A higher efficiency weighting factor of wη = 0.6 is chosen, while the other weights are wr = 0.2 and wcu = 0.2.
The turn off angle is optimized based on the optimization problem that is described by Equations (16)–(19). Additional constraint is needed for SATC. It is given by Equation (19). This constraint guarantees the production of the commanded torque level within the obtained firing angles. Hence, the SATC has no need for a closed loop torque control.
Figure 10 shows the flowchart of the developed searching algorithm. At each operating point, the turn off angle (θoff) is changed in small steps. The simulation model is employed to calculate the torque ripple, copper loss, and efficiency at each step. At the end of the search, the minimum torque ripple, the minimum copper losses, and the maximum efficiency are defined as the base values (Trb, Pcub, and ηb). The turn off angle (θoff) is varied from θoff-min = 15° to θoff-max = 28° in steps of 0.2°, while the torque step is taken as 2 Nm.

Figure 10.
Flowchart of searching algorithm.
The optimized turn off angles for DITC and SATC are given in Figure 11. As noted, the turn off angles lie in a limited band.
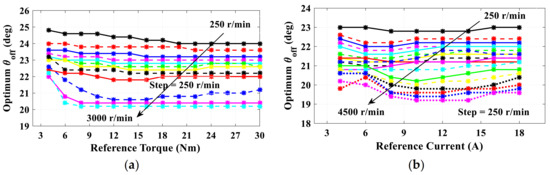
Figure 11.
The optimized θoff angles: (a) DITC, (b) ATC.
With firing angles’ optimization, a smooth transition is guaranteed. Both DITC and SATC utilize Equation (14) for the optimum turn on angle, which means a perfect transition over the turn on. The changing band of the turn off angle is very limited as seen in Figure 11. Hence, the transition from DITC to SATC will be very smooth too. As a result, no change will happen over the turn on angle. Furthermore, no big change will happen over the turn off angle. That means a guaranteed STC.
5. Simulation Results and Discussion
A series of simulation results are conducted to provide a detailed analysis for the control performance. Hence, it is a powerful tool to validate the performance of a proposed control. The simulation results include a dynamic performance evaluation under a sudden change of reference speed and load torque. They also include an investigation of control behavior under EV loading in acceleration and deceleration regions.
5.1. Sudden Change in Reference Speed and Load Torque
Figure 12 gives the results of sudden changes in reference motor speed and its loading torque. The changing profiles for reference speed are shown in Figure 12a. The reference speed (ωref) is changed from 1500 r/min to 2500 r/min at the time of 1.5 s. The transition from DITC to SATC and vice versa is illustrated by signal (Tsig). The positive value of Tsig means that UTC uses DITC, and the zero value of Tsig means that UTC uses SATC. The value of transition speed is 2000 r/min. Hence, the control starts with DITC until the speed of 2000 r/min, and then it changes to SATC for higher speeds than 2000 r/min. The loading torque profile is seen in Figure 12b, where a sudden change from 15 Nm to 12 Nm is observed at the time of 1.0 s.


Figure 12.
The simulation results under a sudden change in motor speed. (a) The motor speed; (b) the load torque; (c) the reference current; (d) the variation of the turn on angle; (e) the variation of the turn off angle; (f) the total electromagnetic torque; (g) the torque ripple; (h) the mechanical output power; (i) the switching frequency; (j) the efficiency.
Figure 12c shows the reference current. The transition from DITC to SATC is obvious. The reference current is compensated under DITC (0–1.63 s) to reduce the torque ripple. That is why it is a thick line. On the other side, the reference current has a smooth profile under SATC (1.63–2.5 s).
Figure 12d,e illustrate the variation of firing angles, turn on, and turn off angles, respectively. They are changing accordingly with motor speed and the current level to provide the best performance. The estimation of firing angles is obtained based on the optimization problems that are described by Equations (16)–(19). A smooth behavior for the firing angles at the instant of transition is observed that ensures a smooth transition.
Figure 12f gives the output torque profile of the motor. As seen, the DITC (0–1.63 s) provides a smooth torque profile. The SATC (1.63–2.5 s) has higher torque ripples. The value of torque ripples is seen in Figure 12g. The DITC shows the torque ripple value of about 20%. On the contrary, the torque ripple under SATC reaches 45%. At the instant of transition at time 1.5 s, the curve of the torque ripple shows a noticeable notch that can be absolutely ignored. Regularly, the ripples are estimated under steady state conditions (constant speed and level currents), and the notch appears because of the transition.
Figure 12h illustrates the output mechanical power. In both regions of control, the motor can provide its rated power (4 kW) even with 50% higher. The switching frequency is seen by Figure 12i. It is changing with speed but has a limited band. The maximum frequency is about 10.6 kHz.
The efficiency curve is seen in Figure 12j. As noted, the efficiency increases with the motor speed. At the transition instant, the efficiency is very clear to be increased as the SATC provides higher efficiencies than DITC. The DITC provides a very good efficiency of almost 96.5%. On the other hand, the SATC provides a higher efficiency (almost 97.5%).
5.2. Acceleration with Electric Vehicle Loading
Figure 13 illustrates the results with EV as a loading under acceleration (motoring action).

Figure 13.
The simulation results under EV acceleration. (a) the motor speed; (b) the load torque on the motor side; (c) the variation of the turn on angle; (d) the variation of the turn off angle; (e) the total electromagnetic torque; (f) the torque ripple; (g) the switching frequency; (h) the efficiency.
Figure 13a shows the motor speed. ωref is changing from 1000 to 2000 at the time of 0.6 s, then it changes from 2000 to 3000 at the time of 1.3 s. The transition is illustrated by Tsig. The motor starts under DITC and converts to SATC at the time of 1.3 s. Figure 13b gives the load torque profile. As the load torque represents an EV, it increases with speed.
Figure 13c,d show the variation of turn on and turn off angles, respectively. A smooth and adaptive variation is observed even at the instant of transition that reflects the smooth transition control. Figure 13e illustrates the output torque profile of the motor. A smooth transition is obvious over the torque curve. Lower ripples are observed under DITC compared to SATC. Figure 13f shows the values of the torque ripple. The ripple is about 23% under DITC and reaches 60% under SATC.
The switching frequency is seen by Figure 13g. It has a maximum value of about 10.6 kHz. The switching frequency decreases with speed as the motor employs single pulse control under high speeds. Figure 13h shows the efficiency curve. The efficiency is observed to be around 97.5% under high speeds.
As a conclusion, the proposed UTC provides lower torque ripples at low speeds by using the DITC in order to reduce the oscillations of the vehicle body and to provide better drivability. Furthermore, the proposed UTC provides better efficiency at high speeds by using SATC. The torque ripples at high speeds can be filtered by vehicle inertia. Hence, the proposed UTC is a superior choice for EVs and several industrial applications.
5.3. Acceleration and Deceleration with Electric Vehicle Loading
Figure 14 is the results for the acceleration and deceleration with EV loading. The speed profile is shown in Figure 14a. From 1.0 s to 1,2 s, the vehicle deaccelerates or brakes. Iref changes to negative at the beginning of the braking operation at 1.0 s as seen in Figure 14b. The negative Iref means that the motor is in forward generating mode. Hence, the firing angles are changed from motoring (increasing inductance) to generating (decreasing inductance) as illustrated by Figure 14c,d. The firing angles are changing smoothly in motoring and generating modes.

Figure 14.
The simulation results under starting with EV acceleration and deceleration. (a) The motor speed; (b) the reference current; (c) the variation of the turn on angle; (d) the variation of the turn off angle; (e) the average current; (f) the mechanical output power; (g) the total electromagnetic torque; (h) zoom on electromagnetic torque; (i) the torque ripple; (j) the switching frequency.
In the generating (braking) region, the motor returns the current back to the supply/battery; hence, the average current becomes negative as shown in Figure 14e. The mechanical power and torque become negative in the braking region as seen in Figure 14f,g, respectively.
Zooming on the torque profile in the braking zone is shown in Figure 14h. First, the motor brakes under DITC, then under SATC, as seen, and a very smooth transition under generating is observed too. The torque ripple is seen in Figure 14i: it spikes because the machine torque crosses zero while changing from positive (motoring) to negative (generating) and vice versa. The switching frequency still has a limited value as seen in Figure 14j.
Figure 15 shows one phase current and the phase inductance under the instant of braking. Before the time of 1.0 s, the machine is in motoring action. The current exists in the increasing inductance zone. Hence, it generates positive torque. On the other hand, after the instant of 1.0 s, the phase current exists in the decreasing inductance zone. Hence the generated torque is negative (braking torque). Note that the current is always positive as the SRM has a current that follows in one direction. The positive and negative torques are defined by the firing angles accordingly with the inductance profile. The generating current profile is seen to be a mirrored shape, with different amplitudes, to the motoring current profile.
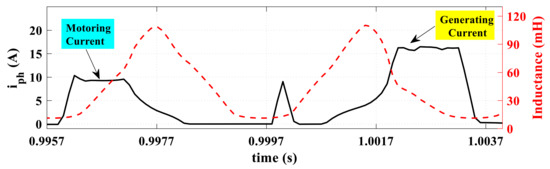
Figure 15.
The phase current in motoring and generating modes.
6. Comparative Analysis
In order to show the effectiveness of the proposed UTC, a comparative analysis is conducted over a wide speed range. The proposed UTC is compared to two control techniques. The first is the ATC in [29] (Figure 3). The firing angles (θon and θoff) of the ATC are optimized for the lowest torque ripple and the highest efficiency as in [29]. The optimization problem in Equations (16)–(19) is employed. The weights are set as wr = 0.4, and wη = 0.6. wcu is not included in [29]; hence, it is set to zero (wcu = 0).
The second technique for comparison is the DITC-based TSF in [28] (Figure 3b). In [28], the adaptive turn on angle control is introduced in [28] as seen in Figure 16. The conduction angle for TSF is constant: it is 15 for tested 8/6 SRM. Hence, the turn off angle is defined by θoff = θon + 15°.

Figure 16.
The simulation implementation of turn on and turn off angles of improved DITC of [28].
The comparative study is conducted under the dynamic loading condition, under the EV loading profile, and under the full load conditions as follows.
6.1. Under Dynamic Loading Conditions
Figure 17 shows the torque profiles, torque ripples, and efficiencies for the proposed UTC, ATC in [29], and DITC in [28]. The comparison is conducted for two speed levels: low speed of 1200 r/min, and high speed of 2400 r/min. This is mainly to illustrate the performance of the UTC in different control regions. The reference torque is changing between 10 Nm, 15 Nm, and 20 Nm.

Figure 17.
Comparative results under dynamic loading conditions. (a) Speed profile; (b) instantaneous torque of SATC in [29]; (c) instantaneous torque of DITC in [28]; (d) instantaneous torque of UTC; (e) torque ripple; (f) efficiency.
Figure 17a shows the speed curve. The speed is changed from 1200 r/min to 2400 r/min at a time of 0.4 s. Figure 17b,c show the instantaneous motor torque for ATC, DITC, and UTC, respectively. As noticed, the three control techniques can track properly their refence torque (Tref). The difference is the torque profile and amount of torque ripples.
Figure 17e shows the value of torque ripple. For low speed (0–0.4 s), the UTC shows the lowest torque ripple, followed by DITC, then SATC. For high speed (0.4–0.6 s), the UTC shows the lowest torque ripple followed by SATC. At high speeds, the DITC shows very high torque ripples.
Figure 17f gives the mean value of motor efficiency with a 60 Hz window. For low speed, the UTC shows the highest efficiency, followed by SATC, then DITC. For high speed, the UTC and SATC show the highest efficiencies. The DITC shows a lower efficiency.
6.2. Under EV Loading Profile
The steady state results under the EV load profile, for three control techniques, are shown in Figure 18. The average torque is seen in Figure 18a, and the UTC and SATC can track their reference torque. The DITC fails to provide the commanded reference torque at high speeds (after 2000 r/min). The torque ripples are given in Figure 18b. The UTC provides the lowest torque ripple over the entire speed range. The SATC shows low ripples at a high speed, while obtaining high ripples at low speeds. The DITC shows low ripples under a low speed only.

Figure 18.
The steady state characteristics under EV loading profile. (a) Average torque; (b) torque ripple; (c) efficiency; (d) torque/current ratio; (e) switching frequency.
Figure 18c shows the efficiency. The UTC and SATC show higher efficacies at high speeds compared to DITC. The average torque to RMS current ratio (Tav/IRMS), in Figure 18d, is a very important index for electric machines, and the higher the better. As observed, the UTC shows a high Tav/IRMS as the ATC. The DITC is the lowest. The switching frequency in Figure 18e lies in a limited band (<10 kHz) that fits well for experimental implementations without any constraints.
6.3. Under Full Load Conditions
The steady state results under the full load for three control techniques are shown in Figure 19. Figure 19a illustrates the full load average torque. The UTC and SATC can track their reference torque over the full speed range. The DITC fails tracking at high speeds (after 2000 r/min). Figure 19b gives the torque ripples. The UTC provides the lowest torque ripple over the entire speed range. The SATC shows high ripples at low speeds, and the DITC shows low ripples under low speed only. Figure 19c shows the efficiency. The UTC shows the highest efficiency over the full speed range.


Figure 19.
The steady state characteristics under full load conditions. (a) Average torque; (b) torque ripple; (c) efficiency; (d) torque/current ratio; (e) switching frequency.
6.4. Summary
Table 1 and Table 2 show the detailed conclusion for comparative study. Table 1 shows a summary of the control performance over speed ranges. As a conclusion, the UTC provides the best performance regarding average torque production, torque ripples, Tav/IRMS, and efficiency over the entire speed range. This is basically the contribution of this research; that is, to gather all the advantages in a single control method by combining two control strategies together. The proposed control method succeeded in gathering the advantages of the DITC for low speeds and the advantages of the ATC for high speeds. In addition, the proposed modification improved the performance of the proposed UTC to provide lower torque ripples and higher Tav/IRMS compared to the DITC at low speeds.

Table 1.
Summary of comparison results over speed ranges.

Table 2.
Summary of comparison results regarding control structure.
Table 2 discusses the control structure and its feasibility for real time implementations. It shows the superior performance of the proposed UTC as it has a moderate complexity of the control algorithm. Hence, it is a feasible control method with no constrains in experimental implementations. Furthermore, the proposed UTC has fast dynamics and does not require a TSF.
7. Conclusions
This paper presents the development of a UTC of SRM drives for EVs. The proposed UTC strategy is a combination of the DITC and SATC. The proposed technique utilizes a DITC for low speed operation and employs an SATC for high speeds. A very smart and smooth transition between the DITC and SATC is guaranteed within switching angles optimization. The results show the superior performance of the proposed UTC over the entire speed range. The proposed UTC can provide low torque ripples, even compared to conventional DITC, at low speeds. Furthermore, it shows the highest Tav/IRMS, even compared to the ATC. For high speeds, the proposed UTC shows a similar performance to the ATC that is the best for SRMs regarding efficiency and torque ripples. The torque ripples at high speeds can be filtered by vehicle inertia. The very low torque ripples at low speeds reduce the oscillations of the vehicle body and provide better drivability. The high efficiency at high speeds increases the milage per charge. Hence, the proposed UTC is a superior choice for EVs and several industrial applications. Moreover, the proposed UTC provides a simple structure, high dynamics, extended constant power range, and reduced torque ripples. This, in turn, makes the proposed UTC feasible for easy implementations with high reliability. Future works could include the experimental implementations of the proposed control considering measurement errors and time delays.
Author Contributions
Conceptualization, M.H.; Formal analysis, M.H. and F.A.-A.; Investigation, M.H. and M.N.I.; Methodology, M.H. and F.A.-A.; Project administration, L.S.; Software, M.H. and F.A.-A.; Validation, M.H. and F.A.-A.; Visualization, I.O. and M.N.I.; Writing—original draft, M.H. and M.N.I.; Writing—review and editing, M.H., M.N.I., and L.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lan, Y.; Benomar, Y.; Deepak, K.; Aksoz, A.; El Baghdadi, M.; Bostanci, E.; Hegazy, O. Switched Reluctance Motors and Drive Systems for Electric Vehicle Powertrains: State of the Art Analysis and Future Trends. Energies 2021, 14, 2079. [Google Scholar] [CrossRef]
- Yueying, Z.; Chuantian, Y.; Yuan, Y.; Weiyan, W.; Chengwen, Z. Design and optimisation of an In-wheel switched reluctance motor for electric vehicles. IET Intell. Transp. Syst. 2019, 13, 175–182. [Google Scholar] [CrossRef]
- Nam, K.H. AC Motor Control and Electrical Vehicle Applications; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Bostanci, E.; Moallem, M.; Parsapour, A.; Fahimi, B. Opportunities and Challenges of Switched Reluctance Motor Drives for Electric Propulsion: A Comparative Study. IEEE Trans. Transp. Electrif. 2017, 3, 58–75. [Google Scholar] [CrossRef]
- Zhu, J.; Cheng, K.W.E.; Xue, X. Design and Analysis of a New Enhanced Torque Hybrid Switched Reluctance Motor. IEEE Trans. Energy Convers. 2018, 33, 1965–1977. [Google Scholar] [CrossRef]
- Bramerdorfer, G.; Tapia, J.A.; Pyrhonen, J.J.; Cavagnino, A. Modern Electrical Machine Design Optimization: Techniques, Trends, and Best Practices. IEEE Trans. Ind. Electron. 2018, 65, 7672–7684. [Google Scholar] [CrossRef]
- Chen, H.; Yan, W.; Gu, J.J.; Sun, M. Multiobjective Optimization Design of a Switched Reluctance Motor for Low-Speed Electric Vehicles with a Taguchi-CSO Algorithm. IEEE/ASME Trans. Mechatron. 2018, 23, 1762–1774. [Google Scholar] [CrossRef]
- Mousavi-Aghdam, S.R.; Feyzi, M.R.; Bianchi, N.; Morandin, M. Design and Analysis of a Novel High-Torque Stator-Segmented SRM. IEEE Trans. Ind. Electron. 2016, 63, 1458–1466. [Google Scholar] [CrossRef]
- Ding, W.; Yang, S.; Hu, Y.; Li, S.; Wang, T.; Yin, Z. Design Consideration and Evaluation of a 12/8 High-Torque Modular-Stator Hybrid Excitation Switched Reluctance Machine for EV Applications. IEEE Trans. Ind. Electron. 2017, 64, 9221–9232. [Google Scholar] [CrossRef]
- Dmitrievskii, V.; Prakht, V.; Kazakbaev, V. Novel rotor design for high-speed flux reversal motor. Energy Rep. 2020, 6, 1544–1549. [Google Scholar] [CrossRef]
- Fang, G.; Pinarello Scalcon, F.; Xiao, D.; Vieira, R.; Grundling, H.; Emadi, A. Advanced Control of Switched Reluctance Motors (SRMs): A Review on Current Regulation, Torque Control and Vibration Suppression. IEEE Open J. Ind. Electron. Soc. 2021, 2, 280–301. [Google Scholar] [CrossRef]
- Al-Amyal, F.; Számel, L. Analytical Approach for the Turn-Off Angle in Switched Reluctance Motors. Lect. Notes Networks Syst. 2022, 217, 685–696. [Google Scholar] [CrossRef]
- Al-Amyal, F.; Hamouda, M.; Számel, L. Torque Quality Improvement of Switched Reluctance Motor Using Ant Colony Algorithm. Acta Polytech. Hung. 2021, 18, 129–150. [Google Scholar] [CrossRef]
- Shahabi, A.; Rashidi, A.; Afshoon, M.; Saghaıan Nejad, S.M. Commutation angles adjustment in SRM drives to reduce torque ripple below the motor base speed. Turkısh J. Electr. Eng. Comput. Sci. 2016, 24, 669–682. [Google Scholar] [CrossRef]
- Hamouda, M.; Számel, L. Optimum Control Parameters of Switched Reluctance Motor for Torque Production Improvement over the Entire Speed Range. Acta Polytech. Hung. 2019, 16, 3. [Google Scholar] [CrossRef]
- Al-Amyal, F.; Hamouda, M.; Számel, L. Performance improvement based on adaptive commutation strategy for switched reluctance motors using direct torque control. Alex. Eng. J. 2022, 61, 9219–9233. [Google Scholar] [CrossRef]
- Li, H.; Bilgin, B.; Emadi, A. An Improved Torque Sharing Function for Torque Ripple Reduction in Switched Reluctance Machines. IEEE Trans. Power Electron. 2019, 34, 1635–1644. [Google Scholar] [CrossRef]
- Li, C.; Zhang, C.; Liu, J.; Bian, D. A High-Performance Indirect Torque Control Strategy for Switched Reluctance Motor Drives. Math. Probl. Eng. 2021, 2021, 1–15. [Google Scholar] [CrossRef]
- Liu, J.; Wang, L.; Yi, L.; Zhu, G.; Yin, X. Optimization of SRM Direct Instantaneous Torque Control Strategy based on Improved Firefly Algorithm. In Proceedings of the 2019 3rd IEEE Conference on Energy Internet and Energy System Integration: Ubiquitous Energy Network Connecting Everything, EI2 2019, Changsha, China, 8–10 November 2019; pp. 364–368. [Google Scholar] [CrossRef]
- Wang, S.; Hu, Z.; Cui, X. Research on Novel Direct Instantaneous Torque Control Strategy for Switched Reluctance Motor. IEEE Access 2020, 8, 66910–66916. [Google Scholar] [CrossRef]
- Pillai, A.; Anuradha, S.; Gangadharan, K.V.; Umesht, P.; Bhaktha, S. Modeling and Analysis of Average Torque Control Strategy on Switched Reluctance Motor for E-mobility. In Proceedings of the CONECCT 2021 7th IEEE International Conference on Electronics, Computing and Communication Technologies, Bengaluru, India, 9–11 July 2021. [Google Scholar] [CrossRef]
- Fan, J.; Lee, Y. A Novel Average Torque Control of Switched Reluctance Motor Based on Flux-Current Locus Control. Can. J. Electr. Comput. Eng. 2020, 43, 273–281. [Google Scholar] [CrossRef]
- Usman Jamil, M.; Kongprawechnon, W.; Chayopitak, N. Average Torque Control of a Switched Reluctance Motor Drive for Light Electric Vehicle Applications. IFAC-PapersOnLine 2017, 50, 11535–11540. [Google Scholar] [CrossRef]
- Hamouda, M.; Abdel Menaem, A.; Rezk, H.; Ibrahim, M.N.; Számel, L. Numerical Estimation of Switched Reluctance Motor Excitation Parameters Based on a Simplified Structure Average Torque Control Strategy for Electric Vehicles. Mathematics 2020, 8, 1213. [Google Scholar] [CrossRef]
- Fang, G.; Bauman, J. Optimized switching angle-based torque control of switched reluctance machines for electric vehicles. In Proceedings of the 2020 IEEE Transportation Electrification Conference and Expo, ITEC 2020, Chicago, IL, USA, 22–26 June 2020; pp. 186–191. [Google Scholar] [CrossRef]
- Hamouda, M.; Szamel, L. Reduced Torque Ripple based on a Simplified Structure Average Torque Control of Switched Reluctance Motor for Electric Vehicles. In Proceedings of the 2018 International IEEE Conference and Workshop in Óbuda on Electrical and Power Engineering (CANDO-EPE), Budapest, Hungary, 20–21 November 2018; pp. 000109–000114. [Google Scholar] [CrossRef]
- Hamouda, M.; Menaem, A.A.; Rezk, H.; Ibrahim, M.N.; Számel, L. Comparative Evaluation for an Improved Direct Instantaneous Torque Control Strategy of Switched Reluctance Motor Drives for Electric Vehicles. Mathematics 2021, 9, 302. [Google Scholar] [CrossRef]
- Ren, P.; Zhu, J.; Jing, Z.; Guo, Z.; Xu, A. Improved DITC strategy of switched reluctance motor based on adaptive turn-on angle TSF. Energy Rep. 2022, 8, 1336–1343. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, H.; Yang, Z. Average torque control of switched reluctance machine drives for electric vehicles. IET Electr. Power Appl. 2015, 9, 459–468. [Google Scholar] [CrossRef]
- Husain, T.; Elrayyah, A.; Sozer, Y.; Husain, I. Unified control for switched reluctance motors for wide speed operation. IEEE Trans. Ind. Electron. 2019, 66, 3401–3411. [Google Scholar] [CrossRef]
- Hamouda, M.; Számel, L. A new technique for optimum excitation of switched reluctance motor drives over a wide speed range. Turkısh J. Electr. Eng. Comput. Sci. 2018, 26, 2753–2767. [Google Scholar] [CrossRef]
- Liu, L.; Zhao, M.; Yuan, X.; Ruan, Y. Direct instantaneous torque control system for switched reluctance motor in electric vehicles. J. Eng. 2019, 2019, 1847–1852. [Google Scholar] [CrossRef]
- Hamouda, M.; Menaem, A.A.; Rezk, H.; Ibrahim, M.N.; Számel, L. An improved indirect instantaneous torque control strategy of switched reluctance motor drives for light electric vehicles. Energy Rep. 2020, 6, 709–715. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).