Adaptive, Synchronous, and Mobile Online Education: Developing the ASYMPTOTE Learning Environment

Abstract

The COVID-19-induced distance education was perceived as highly challenging by teachers and students. A cross-national comparison of five European countries identified several challenges occurred during the distance learning period. On this basis, the article aims to develop a theoretical framework and design requirements for distance and online learning tools. As one example for online learning in mathematics education, the ASYMPTOTE system is introduced. It will be freely available by May 2022. ASYMPTOTE is aimed at the adaptive and synchronous delivery of online education by taking a mobile learning approach. Its core is the so-called digital classroom, which not only allows students to interact with each other or with the teacher but also enables teachers to monitor their students’ work progress in real time. With respect to the theoretical framework, this article analyses to what extent the ASYMPTOTE system meets the requirements of online learning. Overall, the digital classroom can be seen as a promising tool for teachers to carry out appropriate formative assessment and—partly—to maintain personal and content-related interaction at a distance. Moreover, we highlight the availability of this tool. Due to its mobile learning approach, almost all students will be able to participate in lessons conducted with ASYMPTOTE.

1. Introduction

During the first phase of the COVID-19 pandemic, teaching and learning changed massively. Instead of learning in a common place—the classroom—at a common time, the pandemic situation led to a spatial and temporal separation of students and teachers. This unforeseen and unprepared phase of distance education that occurred in spring 2020 is termed emergency remote teaching (ERT; [1]). The term ERT describes the temporary shift of instruction to distance and the rapid establishment of alternative ways to teach in order to maintain some form of school education. Teaching during ERT was mostly achieved by the means of digital media and the internet [2]. This reorganization of the teaching “shocked teachers at all levels and at the same time inspired them to find solutions to problems they have not encountered before” [3] (p. 456). As part of the urgent search for new teaching methods and the need to find creative solutions to the problems they faced [3], teachers all over the world aimed to develop a new form of continuity in education [4]: the implementation of online education as the “new normal” [5].

1.1. Purpose of the Article

This article presents the ASYMPTOTE project, one technical development that contributes to this “new normal” of online teaching. ASYMPTOTE stands for Adaptive Synchronous Mathematics Learning Paths for Online Teaching in Europe. The Erasmus+ project was started as a result of the COVID-19 pandemic. It is carried out by seven institutions from five European countries. This project aims to develop an adaptive, synchronous, and mobile system for online mathematics education in Europe.

In this article, we derive a theoretical framework for distance learning tools based on the experience of the ERT phase, since this was also the starting point for the ASYMPTOTE project. Subsequently, we broaden this view by a more general definition of the requirements for online learning tools. Then, the ASYMPTOTE system is presented as one example for an online learning environment in mathematics education, whose development has been started in the face of the COVID-19 pandemic. Besides the delivery of instruction during COVID-19-induced distance education, it also aims to support fully online instruction, such as online courses, and remote teaching activities or the partial supplementation of face-to-face classes with online activities, e.g., homework.

Lastly, we aim to investigate to what extent it meets the identified design requirements. In doing so, we formulate 10 statements expressing different aspects of the expected use of ASYMPTOTE for online teaching and learning.

These statements—the outcome of our self-report on our development of the ASYMPTOTE system—are not the output of an experimental evaluation of our tool but the result of a comparative analysis between the implemented features and the previous theoretical considerations and requirements. However, the statements can be seen as a starting point for a systematic evaluation of the ASYMPTOTE system by our project team and by other researchers in the field.

Overall, this article pursues the following five objectives:

• To identify the challenges encountered during COVID-19-induced distance learning through a cross-national comparison of five European countries;
• To develop a theoretical framework and design requirements for online learning environments in mathematics education that address the challenges of distance education;
• To present the ASYMPTOTE system as one example for the theory-driven development of an online learning environment;
• To self-report the extent to which the ASYMPTOTE system meets the identified challenges of distance learning and the theory-based design requirements; and
• To prepare the field for a future systematic empirical evaluation of the ASYMPTOTE system.

1.2. Structure of the Article

We firstly sketch how European teachers and students perceived school education in the ERT phase in spring 2020 (Section 2). This presentation is supported by national and transnational empirical studies involving distance education in Germany, Greece, Italy, Portugal, and Spain. This international comparison aims to provide insight into how teachers and learners dealt with ERT in central and southern Europe. Based on these country-specific perspectives, we derive five main issues for mathematics distance education that appeared in some form in all five states:

• Loss of personal interaction;
• Lack of adequate formative assessment;
• Deficit of curricular resources;
• Lack of technical equipment; and
• Lack of digital competencies.

On the basis of these issues encountered empirically, we built up a theoretical framework for distance learning tools in mathematics education. To explain the issues related to the unfamiliar setting and, in particular, to the perceived lack of personal contact, the Community of Inquiry (CoI) model is introduced (Section 3.1). Since the shift to the online setting clearly demands the adaptation of face-to-face instruction, we briefly refer to e-pedagogies (Section 3.2). To address the issue of the availability and handling of technologies, we follow a mobile learning approach (Section 3.3). Finally, to approach the problem of appropriate assessment, we discuss different approaches of how to present and evaluate tasks in a digital way, namely computer-based learning environments (CBLEs), learning paths, and learning trajectories. These approaches are progressed to the concept of the learning graph, which combines adaptive and self-regulated learning concepts (Section 3.4).

In Section 4.1, based on the theoretical considerations, requirements for the design of tools for mathematical distance learning are derived. Subsequently, the ASYMPTOTE system is presented as an example of digital tools that aim to address the problems of distance learning (Section 4.2). Finally, following the objective of the article, we will analyze to what extent the ASYMPTOTE system can meet the requirements of a digital tool for preparing, delivering, and organizing online classes.

1.3. Working Definition of Online and Distance Learning

Online learning is characterized by the access to learning experiences via the use of some technology [6] (p. 130). It is delivered through the internet in computer-mediated environments, which can provide flexible and interactive educational opportunities [6].

The term distance education describes teaching and learning in spatially separated educational settings [6]. It can be delivered online or via older forms of communication, such as correspondence-based courses that take place via the postal service [7,8]. Based on the technological delivery, distance education can be organized either synchronously or asynchronously [9,10]. While in the prior case the course is delivered live, i.e., the teaching and learning takes place at the same time, in asynchronous settings, the time of learning is flexible and individualized [10,11].

In this paper, we will use the term distance education to refer to the online teaching induced by the COVID-19 pandemic. In other words, we refer to the term distance learning as the starting point for the development of the ASYMPTOTE system, which is presented and analyzed below.

Distance education during the COVID-19 pandemic, also termed as emergency remote teaching, is a special case of online learning. More specifically, Hodges et al. [1] characterize ERT as follows:

“In contrast to experiences that are planned from the beginning and designed to be online, emergency remote teaching (ERT) is a temporary shift of instructional delivery to an alternate delivery mode due to crisis circumstances. It involves the use of fully remote teaching solutions for instruction or education that would otherwise be delivered face-to-face or as blended or hybrid courses and that will return to that format once the crisis or emergency has abated. The primary objective in these circumstances is not to re-create a robust educational ecosystem but rather to provide temporary access to instruction and instructional supports in a manner that is quick to set up and is reliably available during an emergency or crisis.”

2. State of the Art: Distance Education in Europe

Previous research had already shown before ERT that even the planned transition from face-to-face to remote teaching can lead to an ecoshock, i.e., the stressful and shocking reaction of learners to the new digital ecosystem [12]. It is not surprising, then, that the unplanned and unprepared movement to distance education during ERT in spring 2020 presented major challenges for both students and teachers.

As detailed in the Introduction, ASYMPTOTE is an Erasmus+ project carried out by seven institutions from five European countries (Germany, Greece, Italy, Portugal, and Spain). In what follows, without claiming completeness, we briefly outline the ERT phase across these five national European perspectives by referring to national and transnational empirical studies. Since similar distance education issues are found in the involved countries, the country-specific perspectives are merged afterwards to identify transnational European issues for COVID-19-induced distance education.

2.1. Distance Education in Germany

In Germany, all educational institutions from kindergarten to universities were closed in March 2020. Apart from regional differences, schools reopened after two months of school lockdown. Until the end of the school year 2020/2021, German federal states mostly followed a partial attendance model. The following school year started with regular in-person classes. However, due to the pandemic situation, a second national school lockdown was initiated from December 2020 until February 2021, and partly until June 2021.

National [13,14,15] and transnational studies [16,17] report a high proportion of asynchronous learning settings for Germany in spring 2020—the lessons were rarely held at a common time. Presumably due to this unfamiliar learning setting at home and at a flexible time, the average learning time in the first school closure dropped by half from 7.4 to 3.6 h per day [14]. Further, the asynchronous instruction went hand in hand with a decrease in student–teacher interaction [18] and student-to-student communication [17]. Not surprisingly, students and parents reported a perceived lack of personal contact with the teacher and the class [13,14,16].

From a socioeconomic perspective, lower-performing students and students from households with a lower social status reported greater problems concerning ERT than their classmates [14,15]. This finding can be viewed from both technical and pedagogical perspectives:

From a technical perspective, the availability of digital devices in spring 2020 was strongly linked to the household’s socioeconomic status: 18% of German low-income households did not have a computer or notebook and 46% did not have a tablet [15,19]. Thus, since students’ access to digital tools was strongly linked to their socioeconomic status, it clearly predetermined their chances of participating in distance education.

From a pedagogical point of view, in ERT, students had to take greater responsibility for structuring and organizing their learning progress, as both the teacher and classmates were not immediately available [16,20]. The teachers perceived formative assessment [18] and the diagnosis of learning progress and students’ adequate individual support [13,16] as major challenges.

2.2. Distance Education in Greece

Due to the COVID-19 pandemic, Greek health authorities ordered the closure of schools at a national level 3 times: namely, in March 2020, in November 2020, and lastly in March 2021. In these periods, traditional education was replaced with distance online synchronous and asynchronous teaching and learning processes.

To support schools, the Ministry of Education and Religious Affairs (MofERA) issued guidelines for distance education and provided a list of available resources. Moreover, Greece implemented educational broadcasting via state television, principally for primary-level students [21].

In studies on COVID-19-induced distance online education, teachers, in their majority, appeared willing to adopt online learning tools and practices during and after the pandemic [22,23]. They also indicated the need for training in order to enhance their pedagogical and learning design skills. Specifically, teachers stated that distance online learning required more effort compared to face-to-face education [23]. Due to the pandemic, teachers faced new problems—both personal (e.g., increased family needs) and work related (e.g., technological difficulties). These problems resulted in having limited available time for designing online learning material [23]. Another factor that played a major role in teachers’ difficulties during this time was the lack of technological capabilities concerning the applications used [22]. Furthermore, the teachers perceived the communication and the interaction with their students as challenging [23].

Additionally, teachers reported that the interest and participation of the students were not satisfying [22]. This statement is directly linked with students’ lack of adequate digital equipment and connectivity to the internet that the teachers observed [22,23]. Concerning internet connectivity, the Ministry of Education and Religious Affairs tried to mitigate the situation by providing access to the digital platforms and educational resources via mobile devices with zero data transfer charge for students [24]. However, students had no previous experience with the platforms used or with distance online learning applications in general [22], and combined with the lack of personal and technological support, their participation was unsubstantial [24]. It is important to note that students from households with lower income [23,24] and students with disabilities had extra obstacles to overcome during these times [25].

2.3. Distance Education in Italy

Italy was the first European country to be hit by the pandemic: on 20 February 2020, the first case of a person affected by COVID-19 was found in Italy. In early March 2020, schools and universities were closed. After a national lockdown until May 2020, slowly, the country and the educational system started re-opening.

In this scenario, the Ministry of Education coined the expression “School Never Stops” (“La Scuola non si ferma”, [26]) to continually provide students with online instruction. While the study of [27] reports the widely spread use of learning platforms, other authors state that teachers implemented a synchronous and individualized way of instruction: “about 88% of the teachers delivered synchronous video-lectures, 82% assigned homework to be realized mainly individually and 53% organized synchronous homework correction.” [28] (p. 10). However, synchronous team working, or collaborative asynchronous activities were rarely conducted [28].

In general, regardless of whether synchronous or asynchronous instruction modes were chosen, the distance education was perceived as challenging by teachers and students [27,29] due to teachers’ little or limited pre-experience on distance learning formats [29]. However, encouragingly, one-third of teachers also reported that they plan to continue using blended learning formats in the future [28]. In particular, the assessment of students’ new knowledge and the efficacy of the teachers’ actions were seen as major challenges [18].

In addition, we have to take into account that according to [30], about 27% of families reported not having suitable technology during the lockdown in Italy, and 30% of parents said that they did not have time to support their children with remote learning. Economic resources were allocated and distributed very quickly among schools to enhance distance education, and to provide technological tools to students with difficulties. However, it took a while to try to reach all students, and some of them were never reached [29]. Thus, it is not surprising that teachers reported a loss of contact with 6–10% of their students in the ERT phase [28].

2.4. Distance Education in Portugal

In Portugal, educational institutions were closed in mid-March 2020, i.e., teaching in Portugal moved from face-to-face teaching to remote teaching practices. Starting in September 2020, Portugal resumed its normal activity while the country underwent a second school lockdown from January until March 2021.

In the ERT phase, Portuguese teachers perceived a lack of guidance and supportive resources and tools for dealing with the distance learning situation [31]. Most of the schools decided to use synchronous sessions through the online platforms Google Meet and Classroom Teams free of charge [32]. To mitigate the effects of the interruption in teaching activities, the Ministry of Education provided guidelines for distance education and—in cooperation with the Portuguese television RTP—implemented the television program #EstudoEmCasa [33]. This television program was based on a project that started in the 1960s that aimed, at that time, to bring school to children from small villages in the interior of Portugal.

During ERT, Portuguese teachers stated that the increased workload, the need to chabge strategies and activities, and the issue of evaluation and feedback and time management were major difficulties [34]. Further, technical problems concerning the availability of appropriate tools and equipment and its handling were reported [31,34].

From the student’s perspective, the high autonomy during distance learning and the lack of digital competencies were seen as major restrictions of distance learning. Even more, with the availability of appropriate equipment and family-related conditions, two socio-economical aspects were reported as constraints by the students [34]. In line with this finding, the government invested in the technical equipment of students with less financial means [35]. Apart from this technical support of students with a lower social status, Cabrito [35] highlights that students and teachers acquired and developed skills to work with information and communication technologies, envisioning a new generation that is better prepared for a highly technological future. This expectation by teachers of more powerful ICT usage for teaching and learning was also reported in Germany and Spain [16].

2.5. Distance Education in Spain

In Spain, the COVID-19 pandemic meant that students had to stay at home and were taught by distance from March 2020 until the end of the school year. As the Spanish regions are fully competent in the organization of their school system, some regions implemented in-person and partial attendance models during the 2020/2021 academic year. In other regions, students from kindergarten to university level were educated using a face-to-face model accompanied by special measures, e.g., classes were divided into groups taught by different teachers. Teaching in the academic year 2021/22 was conceived as going “back to normality”.

In the phase of distance education, the frequency that synchronous tools were used was quite high compared, for instance, with Germany [16], including a comparably higher use of video conferences for mathematics teaching [36]. However, despite the frequent use of synchronous teaching in Spain, teachers reported problems regarding the communication with students [16]. Indeed, new challenges rose, such as the loss of control, the lack of discipline in lectures, and the lack of didactical-guided teaching [36]. Consequently, two out of three teachers declared the adaptation of their teaching to ERT as quite or very difficult [36]. The vast majority of Spanish teachers agreed that they felt overwhelmed (77%) and more stressed (68%) [37].

On the other hand, the availability of technical equipment for the students and teachers to be able to implement this novel method of teaching is quite reasonable and, more important, quite well spread among the different socio-economic levels: While, on average, 91% of students reported having a computer that they could use for school work, the user rate of 4 out of 5 students with a lower socioeconomic status is still quite high (OECD average: 78%) [38]. Yet, this favorable fact does not mean that there were no social gaps concerning home support—both technological or by parents: students from families with a higher income had increased access to internet-based devices and spent more time on learning activities during the pandemic [37]. Thus, as in other countries, the possibility of participating in distance education largely depended on social factors [39,40].

2.6. Distance Education in Europe: An Interim Conclusion

In the five European countries considered, teaching and learning in the ERT phase showed recurring issues caused by COVID-19-induced distance education. The brief overview reveals that in Germany, Greece, Italy, Portugal, and Spain, the following challenges of distance education occurred, which are summarized in

Table 1. Overview of the challenges regarding distance education that were encountered in Germany (GER), Greece (GRE), Portugal (POR), Italy (ITA), and Spain (ESP).

Challenge	GER	GRE	POR	ITA	ESP
Loss of personal interaction	x [13,14,16]	x [23]	x [32]	x [28]	x [16]
Lack of Adequate Formative Assessment	x [13,15,16,18]	x [23,24]	x [32,34]	x [18,27]	x [16]
Deficit of Curricular Resources	x [16]	x [21]	x [33,34]	x [26]	x [36]
Lack of Technical Equipment	x [14,15,19]	x [23,24]	x [34]	x [29,30]	x [37,38,39,40]
Lack of Digital Competences	x [13,14,16]	x [22,23]	x [31,33,34]	x [29]	x [37]

and briefly described in Section 2.6.1, Section 2.6.2, Section 2.6.3, Section 2.6.4 and Section 2.6.5:

2.6.1. Loss of Personal Interactions

Distance education required a rapid change in the instructional setting: The place of learning shifted from the common learning place “classroom” to the children’s rooms. Consequently, according to Johansen’s space-time matrix [11], the students did not learn in the same space, and in the case of asynchronous education, not even at the same time. Thus, it is not surprising that European students named the loss of familiar structures as one major difficulty during ERT. For Germany, a lack of student–teacher interaction [13,14,16,18] and communication among students [17] is reported. The studies of [16,23,28] confirm the lack of personal contact in Spain, Italy, and Greece.

In Spain, teachers also reported a loss of control and lack of discipline and the lack of didactical-guided teaching [36]. The latter issue, the rearrangement of their teaching strategies for distance education and the development of new teaching for online environments, was also reported as a challenge for teachers in Italy and Portugal [18,29,34]. Moreover, Portuguese and Greek teachers emphasized the increased workload compared to face-to-face teaching [23,34].

Undoubtedly, the changes in the environment caused by distance learning were even more massive when teaching and learning were conducted in an asynchronous mode, i.e., learning was organized at an individual location at a self-selected time. Thus, according to the space-time matrix [11], the students not only worked at different places but also at different times, which further increased the sense of social isolation reported by [16].

2.6.2. Lack of Adequate Formative Assessment

Due to the spatial separation, teachers in Germany, Spain, and Italy experienced difficulties in formative assessment [18] and the diagnosis of learning progress and students’ individual support [13,16]. Moreover, for Portugal, teachers reported that the evaluation and feedback of students’ working process were challenging [34].

This problem of adequate formative assessment was clearly related to the lack of student–teacher interaction reported in all five countries [13,15,16,18,23,34]. To monitor students’ work process, at least to some extent, at a distance, teachers in all five countries used learning platforms [16,24,27,32].

2.6.3. Deficit in Curricular Resources

Even if learning platforms were widely used for distance education, a lack of available digital tasks in the ERT phase can be assumed. On the one hand, the urgent development of digital education programs by the Italian, Portuguese, and Greek governments during the first school closure underpins this assumption. On the other hand, teachers reported the lack of supporting resources and tools for dealing with the distance learning situation in Portugal [31] or the self-creation of at least half of the used tasks in Spain [36].

To provide individual support to the students, it seemed important to provide tasks on students’ individual performance level—in particular, as the students experience larger autonomy and take responsibility for their learning in distance education [16,20,34]. Therefore, with respect to the potentials of digital tools [41,42], an adaptive allocation of tasks and a possibility for (self-)assessment could help to support students’ individual and autonomous work process at home and enable an appropriate form of differentiation in distance learning settings.

2.6.4. Lack of Technical Equipment

Lastly, it seems that the ERT phase most strongly affected the lower-performing students and students with a lower socioeconomic status. For all five countries, a strong linkage between the availability of technical devices and the household’s income was reported [19,23,24,30,34,37,38]. The importance of social factors for students’ learning progress in distance education [14,15,39,40] very likely resulted in an increase in the so-called digital divide—the influence of socioeconomic levels on accessing ICT [43,44]—even when the states provided financial and material support in response to this threat.

Further, lower-performing students and students with a lower socioeconomic status tended to receive less support from their parents and spent more time on learning activities during the ERT phase [14,15,29,37].

2.6.5. Lack of Digital Competences

Finally, participation in the digital world not only depended on the availability of technical equipment. Successful use of the tools also required that they were used appropriately. For all five states, however, studies reported a lack of digital competencies among teachers and students [13,16,22,23,29,31,34,37].

3. Theoretical Framework

In the previous section, we identified challenges in distance education through a cross-national comparison. In the following sections, we derive a theoretical framework that addresses these challenges. It is structured as follows:

• Section 3.1 and Section 3.2: To take into account the need of personal interaction at distance, we refer to the well-known Community of Inquiry model and to e-pedagogies;
• Section 3.3: To address the lack of technical equipment and of digital competencies, we follow a mobile learning approach; and
• Section 3.4: To deal with the lack of formative assessment during COVID-19 distance education, we discuss the concepts of learning trajectories and learning paths. Building on this, we introduce the idea of learning graphs.

3.1. Community of Inquiry

In a paper that is still relevant today, Jacquinot [45] suggests that distance can be managed, and absence can be eliminated in the specific field of distance education. In recent years, information and communication technologies (ICTs) have offered the possibility of addressing these two challenges simultaneously. On the one hand, they provide options to manage distance, at least in a spatial-temporal sense, with the use of synchronous and asynchronous means of communication, supported by the internet. On the other hand, ICTs provide social interactions between teachers and students and also between teachers themselves [46].

Through the use of multimedia technologies and the Internet, e-learning is a mode of teaching that aims to facilitate learning by facilitating digital access to resources and services, and synchronous and asynchronous interactions and cooperation [47].

Therefore, the absence/presence dichotomy is eliminated, at least from a technological point of view, particularly in the case of e-learning [11]. In addition to the mastery of these spatial-temporal aspects, one of the main and current challenges of e-learning is to create distance presence in order to facilitate learning [48,49,50,51,52]. To qualify and give substance to the concept of “presence” in e-learning, we consider the Community of Inquiry model in e-learning proposed by Garrison [50]. It considers certain types of social interaction, mainly of a collaborative nature, that give rise to a presence that encourages the emergence of a community of inquiry [50].

3.1.1. Definition of a Community and Learning Community

Before defining a community of inquiry, let us dwell on the term community. A community forms around a common objective. Specifically, a community is a social organization whose members, collectively, strive to achieve a goal [53,54,55]. It is, therefore, a co-construction that follows values, practices, rules of conversation, and rules of behavior [56,57]. The dominant logic of collaboration ensures that all members are on an equal level in terms of the position they occupy in the community, their participation in interactions, and the implementation of activities by accessing common resources [56,58].

A learning community is defined as a group of people who, as in the broader community, are involved in achieving a goal: solving problems through a collaborative process that constructs both individual and collective knowledge [46]. A learning community can also be virtual, and the technologies of the e-learning world contribute both to the construction of individual knowledge and to the interaction with others [46].

3.1.2. Definition of a Community of Inquiry

A community of inquiry is a learning community in which the problems to be solved are dealt with using the general principles of the scientific method, which fosters not only the construction of individual and collective knowledge but also the development of critical thinking [59].

Two conditions must be met to develop this kind of community [46]. The first condition provides that each member of the community must have motivation to maintain interactions with others, favoring collaboration, in order to undertake and/or carry out collective activities. The second condition rests on the socio-affective, emotional, and cognitive aspects implemented by the individual members of the community. In the school context, the teacher has the burden of supporting the students in order to stimulate their motivation and help them regulate their behavior in a collaborative logic manner. The educational possibilities offered by e-learning can also be used to promote the achievement of the constitution of the community of inquiry [46].

The first condition implies that learning occurs by collaborating with others. Collaboration means that when confronting peers, questions arise that stimulate the setting in motion of new ideas. Exchanges and negotiations, therefore, require the ability to clarify and structure one’s thinking, or to objectify and build one’s knowledge. Collaboration, therefore, makes it possible to critically examine the knowledge acquired [46]. The second position is that collaboration also promotes group learning. In fact, to solve a problem, the members of the community adopt the principles of the scientific method, define a strategy, test the results deriving from this process, and evaluate them [46].

3.1.3. The Community of Inquiry Model

Garrison’s Community of Inquiry (CoI) model [50], regarding e-learning, predicts that there are certain collaborative interactions that contribute to the generation of a distant presence that favors the development of such a community. The CoI framework consists of three overlapping key elements: social presence, cognitive presence, and teaching presence:

• Social presence refers to the “ability of the community of inquiry participants to project themselves socially and emotionally, in all aspects of their personality, through the communication media that they use” [48] (p. 94);
• Cognitive presence refers to “the degree to which the participants are able to construct and confirm meaning by using thought and dialogue in a learning community” [50] (p. 55);
• Teaching presence refers to the role played by the teachers in the “design, facilitation and management of the cognitive and social processes from an educational point of view” [50] (p. 55).
• The teacher plays the role of a mediator and facilitator in the establishment of a community of inquiry [50]. In fact, he/she is called on to create organizational and educational conditions so that a quality collaboration between learners can take place. Therefore, especially in an online learning environment, in which learners can easily be distracted, become passive, or feel isolated and disconnected from their peers and teacher, it is important to establish connections between those three presences in order to create and maintain an active, interactive, collaborative, and engaging online learning environment.

3.2. E-Pedagogy and Online Instruction

When it comes to teaching online, teachers usually lack pedagogy skills because they have never learnt online pedagogy [60]. Others find it hard to transition from traditional teaching to online classes and are “usually confused about application of didactical and methodological principles” [61], which became clearly visible during the COVID-19-induced distance education [13,16,22,23,29,31,34,37]. The lack of a theoretical framework that provides teachers with the guidelines needed in order to teach online led to the development of e-pedagogy or online pedagogy, a term that is used to describe “all issues that are related to the online education” [60], such as theoretical frameworks, instructional methods and practices, principles of teaching and learning, learning styles, course design, etc. Such a framework is proposed by Gilly Salmon and includes E-moderation, the Five-Stage Model [62], and E-tivities [63].

3.2.1. A Model for Online Pedagogy

Salmon proposes the Five-Stage Model, which is a pedagogical model for online teaching management that offers “essential support and development to learners at each stage as they build up expertise in learning online” [62] (p. 15). The Five-Stage Model divides online teaching into progressive stages that require different needs regarding technical support and moderation. Therefore, the Five-Stage Model outlines how to apply the CoI framework in order to develop a cognitive, social, and teaching presence with a series of steps [62]. To facilitate engagement with online activities, Salmon also proposed “E-tivities”, which is a model for designing online activities [63]. E-tivities are relevant for:

• At least two people that work or learn together, regardless of their location;
• People with special needs that can be assisted through technology; and
• Learning designers, academics, teachers, and trainers.

E-tivities can be implemented in online programs or blended learning, or mobile learning environments. They can be quickly and easily designed in advance, since they are reusable, scalable, and customizable.

In the same framework, Salmon proposes that online teachers act as e-moderators and their major role is to assist students in making meaning of their interactions [62]. E-moderators are expected to have the following five competences [62]:

• Understanding the online learning processes;
• Technical skills to use the software features;
• Online communication skills (non-verbal, verbal, and written);
• Content expertise to share with and support students’ personal learning; and
• Personal characteristics, such as empathy, creativity, confidence, and flexibility.

It is important to highlight that e-moderators do not need to have many years of experience or too many qualifications and they do not have to be experts in their field [62]. For example, the CoI framework that was presented previously guides online teachers in how to select content, how to set the learning climate, and how to support discourse to establish a quality educational experience through collaborative and constructivist approaches. However, in order to “align their teaching and design practices with the CoI framework” [64] (p. 18), online teachers have to be familiar with those frameworks that promote “collaborative interactive learning and teaching in online environments” [64] (p. 18). The development of e-pedagogy frameworks emerged from the need to support teachers when teaching online.

3.2.2. The Role of the Teacher in Online Pedagogy

Nowadays, the online teacher’s role is “to facilitate student learning” [60] (p. 66) and act as an observer of the students’ learning process. According to [65], a teacher, either teaching online or in a face-to-face environment, has a pedagogical, a social, and a managerial role. An online teacher, though, also has a technical role in addition to the previous ones. On the same note, Serdyukov [60] identified three types of online teachers: leaders, facilitators, and mediators. Leaders actively guide students’ learning while facilitators only respond to questions and provide support only when they are asked to do so. Mediators, on the other hand, are the preferable type in an online class, since they “are on a par with students, artfully engaging and interacting, but without direct management” [60] (p. 66). This notion is in line with [66], who emphasize flexibility, collaboration, the ability to learn from others, and the ability to share control with the participants as the main attributes an online teacher should have.

From these transformational roles that were described, it is obvious that teachers need to re-evaluate their beliefs and teaching practices about teaching in general, and online teaching in particular, and be flexible and open to learning. They need to take advantage of the affordances of the online environment. An effective online teacher offers students the opportunity to decide on their own about their learning while increasing their engagement, collaboration, inquiry, and involvement.

3.3. Mobile Learning

As already stated, online learning offers students many possibilities to make learning more effective, engaging, and adapted to their needs. Mobile learning, also m-learning, strengthens this approach as it “provides greater flexibility for students to be examined or interact at any time and in any place” [67] (p. 72). Here, m-learning is described as “the use of a wireless handheld device; a cell phone, personal digital assistant (PDA), mini-computer, or iPod to engage in some form of meaningful learning” [68] (p. 3) with which students have access to knowledge anytime and anywhere.

From being more technocentric, mobile learning definitions have recently shifted to being more learner-centered, focusing mostly on the mobility of both technology and learning. Although there is not a widely accepted definition of the term, Yamamoto [69] defines mobile learning not just as a means of supplying students with information that is accessible without barriers but also as a way of enlightenment that can be presented “without breaking apart from life” [69] (p. 16), either in real or virtual environments and with different mobile instruments. In each case, the student is always at the center of the learning process. Thus, it is obvious that mobile learning can be used in many different educational settings.

Especially for mathematics education, mobile technologies are a recent enrichment, and the COVID-19-pandemic created an emerging need for teaching mathematics online. According to Calder, Larkin, and Sinclair, “the potential for visual, interactive engagement with some learning experiences, coupled with the haptic and oral/aural affordances of the technology, change the nature of the Mathematical activity” [70] (p. 1). A good example of teaching mathematics with mobile learning in a learning setting that was based on the CoI framework and e-tivities is the study conducted by [71] on middle-school students’ building of mathematical knowledge using mobile devices outside the classroom. The results of this study showed that “learning through authentic activities involving the use of mobile phones can encourage and enrich K-12 students’ knowledge building in Mathematics” [71] (p. 101). However, since there is still a lack of a theoretical framework regarding the use of mobile technologies for mathematics learning [70], it is important to conduct more research on how to apply mobile learning in and out of the classroom. To address this need, the ASYMPTOTE pedagogical model has been created.

3.4. The Learning Graph Concept

In the following sections, the organization of online learning via digital learning platforms is addressed. Therefore, we first sketch the idea of computer-based learning environments. Secondly, we present the characteristics of individualized learning in online learning settings. Thirdly, considering the presentation of task sequences in online environments, the concepts of learning paths and learning trajectories are introduced. Based on these considerations, we present the concept of learning graphs as a pre-structured and simultaneously individualized online learning environment.

3.4.1. Computer-Based Learning Environments

The term computer-based learning environments (CBLEs) refers to open-ended student-centered learning environments that can adapt to the needs of individual students by systematically and dynamically providing platforms of key learning processes [72]. CBLE uses technology to engage students in problem solving, exploring, and manipulating concepts in order to assess and reflect on their knowledge [73]. The core idea is to organize interconnected learning themes, either in the form of a problem to be solved or in the form of a guiding objective. Therefore, CBLEs provide guided and pre-structured tasks [74] and foster students’ autonomous and self-regulated learning [75].

The discussion and collaboration between computer scientists and math educators’ communities around the design and implementation of CBLEs is not new. In the mid-1990s, Balacheff et al. [76,77] identified assessment, community interaction, experiential learning and design requirements, and technological changes as major issues for learning in computer environments. The same issues seem to still be highly relevant and are thus addressed in this article.

3.4.2. Individualized Online Learning

Individualized learning can be implemented using distance learning technologies in which, always considering the particular characteristics of each student, a follow-up of the acquisition of knowledge is provided. Students must be autonomous, both in acquiring knowledge and working with information [78]. According to Lebedev [79], it is important to consider the general characteristics of individualized learning: “the factors that lead to school failure (gaps in knowledge, defects in thinking, skills in educational work, reduced working capacity, etc.); the optimization of the educational process in relation to capable and gifted students; providing freedom to choose a number of elements of the learning process; formation of general educational skills; formation of adequate self-esteem of students“ (p. 1643).

3.4.3. Learning Paths and Learning Trajectories

In this article, two concepts for the design of online learning are considered: the learning path and learning trajectory. After consulting several existing works in the literature, a learning path is defined as sets of one or more learning activities that lead to a particular learning goal, with the aim of helping students to acquire knowledge and improve their skills [80,81,82,83]. Learning paths are defined as sets of one or more learning actions that lead to a particular learning goal.

A learning trajectory, according to Simon [84], is a teacher’s plan for a classroom activity, considering the learning goal, learning activities, and thinking and learning in which students might engage. In [84], the term hypothetical learning trajectory was used instead of learning trajectory to refer to the teacher’s prediction of how the students’ thinking/understanding will evolve in the context of the learning. In this work, we adopt the term learning trajectory.

The construction of an individual educational trajectory in online learning has a significant advantage in organizing learning since it is possible to choose the educational content that best matches the individual abilities and needs of the student [78].

Building on the two concepts, the learning path and learning trajectory, but transferring them to an online learning perspective, we conceptualize that:

• A learning path is defined as a sequence of learning activities selected by the student and adapted to the student’s individual needs;
• A learning trajectory is a pre-selection of learning activities by the teacher based on the didactical considerations of a student’s learning process, and focusing on its evaluation.

The learning activities, previously mentioned, aim to guide the users to accomplish their learning goals. For the construction of a learning path or a learning trajectory, the learning activities can take the form of courses, lessons, topics, or learning objects [85]:

• Course (or area), for example, the Linear Algebra course;
• Lesson (or general topic), for example, in the Linear Algebra course, the general topics are matrices, determinants, systems of linear equations, etc.;
• Topic (or concrete topic): for example, in the general topic matrices, the concrete topics are elementary operations on rows/columns of a matrix, elementary matrices and equivalence of matrices, row echelon form and reduced row echelon form, rank of a matrix, etc.; and
• Learning objects (or tasks) are the small units of learning, and are constructed regarding a certain learning objective.

In this article, we adopt the definition of the term task by [86]: a task is any practice, construction, problem solving, decision between different possibilities, experimentation, or inquiry that can incite teaching and learning. The term does not solely refer to something that the teacher requests the learners to do but also includes the learner’s individual choice.

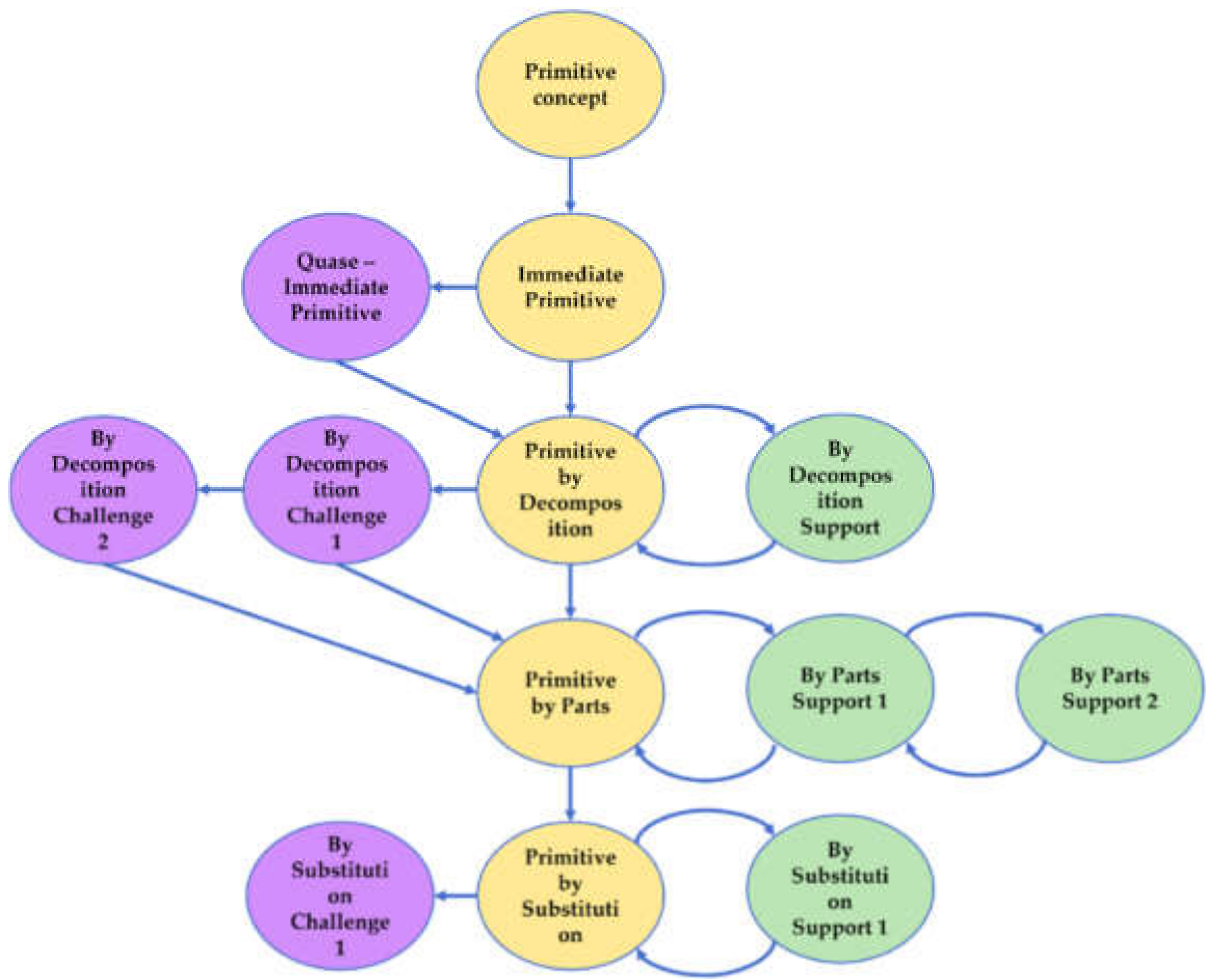
3.4.4. Learning Graphs

The educational knowledge graph has attracted much research attention in recent years. For example, in [87], the researchers integrate fragmented knowledge points into the course knowledge graph. In this way, both students and teachers can link fragmented knowledge, improving students’ knowledge and skills.

A lot of research about modeling learning processes that focuses on artificial intelligence (AI) in education exists. In [88], the authors present a survey of the key applications of data-driven AI techniques in education as a detailed bibliometric analysis of the domain. As an important part of artificial intelligence technology, the knowledge graph provides possibilities for smart education and promotes the innovation and development of smart education. In general, graph learning refers to machine learning on graphs. However, in the learning graphs described in this work, and that are developed in the ASYMPTOTE project (see Section 4.2), the use of AI techniques is not intended (training data for learning techniques, predictive analysis, clustering, among others). The idea is to use a micro-adaptive model (see [89], for example). Teachers will firstly define the main outcomes that students may achieve, also defining an ordering that hopes to increase in difficulty level or deep concepts. Then, teachers define support or advanced tasks, in order to adapt the trail previously created to the student’s response.

In this work, we use directed graphs as a significant and considerable structure for the efficient representation of learning paths and learning trajectories. A learning graph (LG) is defined as a directed graph, where each vertex represents a learning activity (or task), based on a learning trajectory as the intended and expected way of learning. However, the learning graph also includes further tasks to deepen students’ understanding of the mathematical topic (challenge tasks) or support tasks on a more basic level. The use of directed graphs is not a novelty in online learning systems (see, e.g., [90]).

In more detail, we call a learning graph a directed graph $G=\left(V,E\right)$, where the set of vertices $V$ consists of learning tasks, partitioned into main, support, and challenge tasks, and satisfying the following:

• Main tasks are mandatory, in the sense that all learning paths and all learning trajectories that can be defined in the learning graph include all these vertices;
• Support tasks and challenge tasks are vertices that can belong to a learning path but do not belong to any learning trajectory;
• Each support task or challenge task is related to one, and only one, main task, and the set of directed edges E has the following kinds of edges:
  • Vertices that are main tasks are total ordered, and there is a directed edge from the i-th to the (i + 1)-th vertex;
  • For each main task with a non-empty set of support tasks, these tasks, together with their main task, are total ordered, where the main task is the root, the first element of the ordered set. In this ordered set, there is a directed edge from the $i$-th to the (i + 1)-th vertex, and another edge in the opposite direction, from the (i + 1)-th to the i-th vertex;
  • For each main task with a non-empty set of challenge tasks, these tasks, together with their main task, are total ordered, where the main task is also the root, the first element of the ordered set. In this ordered set, there is a directed edge from the i-th to the (i + 1)-th vertex, and a directed edge from each challenge task to the main task that immediately follows the main task related to these challenge tasks, in the order defined in the subset of main tasks.

The learning graph defined above can be drawn as a “fish bone”, where the ordered main tasks appear in the middle vertical bone, the support tasks related to a main task as a right-side branch, and the challenge tasks related to a main task as a left-side branch. Figure 1 shows an example of a learning graph on the topics primitives and integrals.

In this context, given the learning graph, the learning trajectory is the sequence of main vertices, or one of their connected subsequences. This task sequence represents the intended workflow of the student. A prototypical example for a learning trajectory is shown in Figure 2a.

A learning path is the individual working process of the learner. An example for a learning path of a student is given in Figure 2b. In general, a learning path (ν₁, ν₂, …, ν_f) is any sequence of connected vertices starting in a main vertex ν₁ and ending in any vertex ν_f, which is accessible from ν₁. The vertices are connected by edges. However, we can omit the edges in this kind of graph since there are no multiple edges. Thus, considering Figure 2b, the individual learning path of a student can start with the first main task at the top of Figure 2b and end with one of the three tasks at the bottom of Figure 2b.

For the working process in the learning graph, the following conditions apply.

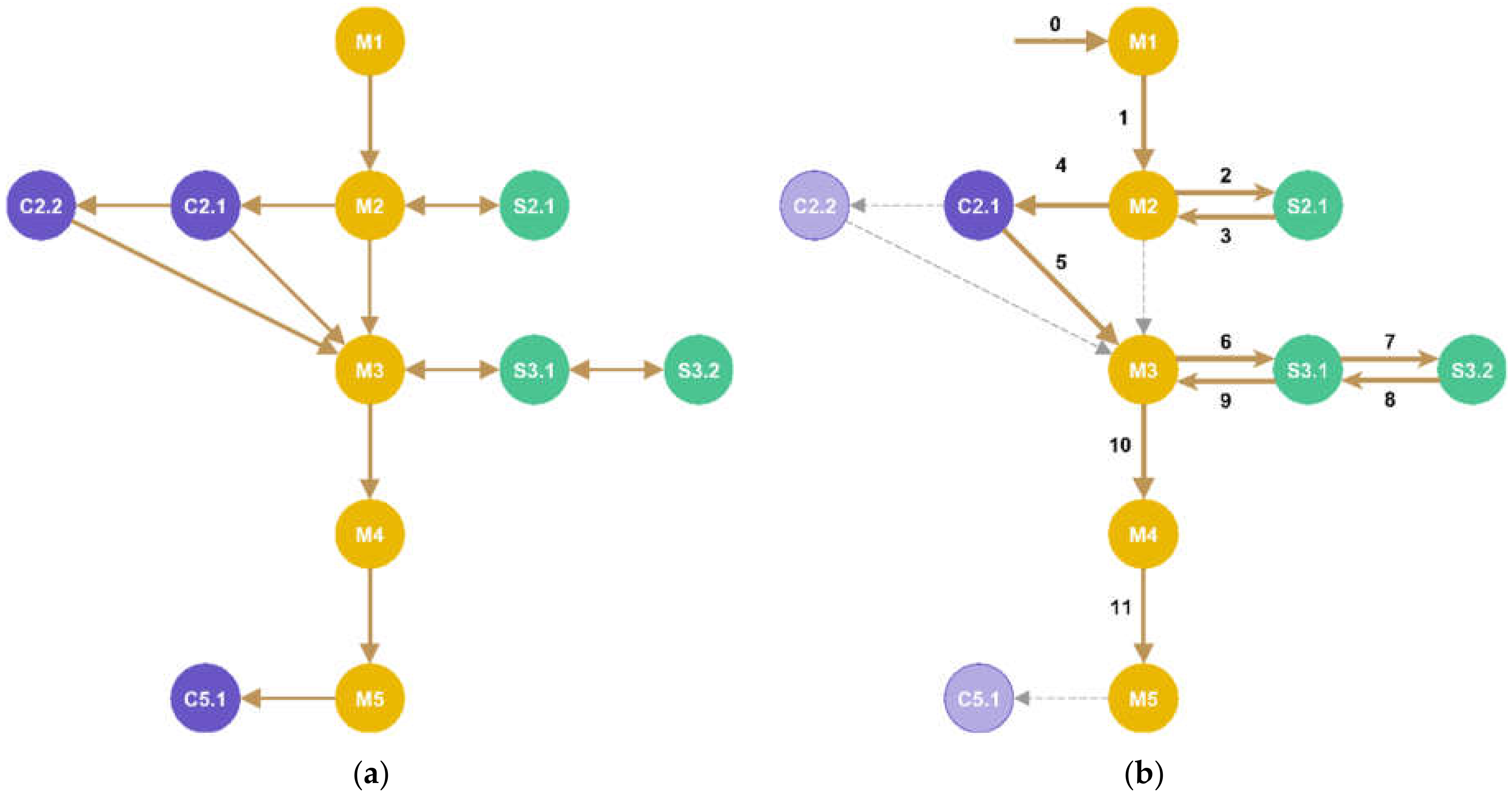
• Whenever a subsequence exists $\left(v_i,v_{i1},v_{i2}, \dots , v_{in}\right)$, where $v_i$ is a main task, and $v_{ij}$, $j=1, \dots , n$, are support tasks, it means that the support tasks $v_i$ to $v_{i\left\{n-1\right\}}$ were used (most likely $v_{i\left\{j+1\right\}}$ is accessed when a student cannot solve $v_{ij}$ yet);
• If the opposite direction of the subsequence above exists, namely $\left(v_{in}, \dots , v_{i2}, v_{i1}, v_i\right)$, it means that after processing the support task $v_{i\left\{j+1\right\}}$, the student is able to work on $v_{ij}$;
• For the other hand, if a subsequence exists $\left(v_i,v_{i1},v_{i2}, \dots , v_{in}\right)$, where $v_i$ is a main task, and $v_{ij}$, $j=1, \dots , n$, are challenge tasks, it means that the learner answered each task correctly and chose to proceed along the branch of challenge tasks;
• If an edge ($v_{ij}$, $v_{\left\{i+1\right\}}$) exists in the path, it means that, regardless of whether the learner answered the task correctly $v_{ij}$, he/she chose to proceed to the next main task, $v_{\left\{i+1\right\}}$;
• If $v_f$ is not a final vertex of the graph (the set of final vertices consists of the main and challenge tasks at the bottom), it means that the learner decided to finish his individual learning path before the end, e.g., for not having been successful, or simply by choice.

Figure 1 is an example of a learning graph in the general topic primitives and integrals. Vertices are tasks consisting of questions in the primitive concept, immediate primitive, quasi-immediate primitive, and primitive by decomposition, among others. As shown in Figure 2a, the main task built the intended learning trajectory. Figure 2b shows an example of a possible learning path of a student. In this way, using support and challenge tasks, interactive and complementary tasks are provided that allow students to meet unique interests and learning needs, study at various levels of complexity, and deepen their understanding.

In this sense, the way a learning graph is structured allows the learning trajectories to be defined, and satisfies the need for evaluation by the teacher, and to adapt such trajectories to develop individual learning paths. The creation of these learning paths is achieved by the user/student/learner progressing at their own pace, without leaving the principal focus of the teacher. Note that the learning trajectory defined previously by the teacher is always contained in each learning path developed. Adaptive learning is continuously present along this process because the student may, at any moment, adapt the path he/she is going through, also promoting his/her self-organization and self-assessment. Diverse ways of learning are respected. On the other hand, it also empowers active evaluation since the teacher will receive more individual information about a student’s learning progress.

In terms of adaptivity, an LG can be viewed as a micro-adaptive tool since the next task is assigned based on the performance on the previous task (cf. [89]). This task assignment is based on the subject didactic considerations of the LG creator, i.e., the educator. Thus, the process of task assignment using the LG concept requires thoughtful analysis of the subject at hand and of the students’ needs when working on the tasks. Therefore, the LG provides a technically simple method for a micro-adaptive task assignment process. However, the sequence in which students complete the support tasks or the challenge tasks is still linear in the LG: the order in which these tasks are solved is predetermined, and the tasks are not assigned by AI. Thus, the advantages of easy implementation of the LG goes hand in hand with its inherent limitation: the upcoming challenge or support task is not selected based on an AI analysis of the very individual needs of the student in that specific situation.

4. Theory-Based Design of Mathematics Online Environments

In the following sections, we identify the design requirements for tools aimed at online mathematics education (Section 4.1) They are based on the previous considerations and take into account the issues of COVID-19 distance learning, the requirements of the CoI model and e-pedagogy, and mobile learning approaches (Section 3.1, Section 3.2 and Section 3.3). Subsequently, the ASYMPTOTE system is presented as an example of technical development of an online learning tool in view of the COVID-19-pandemic (Section 4.2). In Section 4.3, we analyze to what extent it meets the identified design requirements.

4.1. Design Requirements

As described in detail in the interim conclusions of Section 2, the COVID-19-pandemic brought forth five major problems in the educational world, which we can summarize as follows:

• Loss of personal interactions, which are usually essential parts of the educational process, e.g., students–teacher interaction, communication among students;
• Lack of adequate formative assessment: diagnosis, evaluation of the learning process, individual support for different student contexts (lower-performing, students with special needs, etc.;
• Deficit in curricular resources for dealing, deeply and widely, with the distance learning context;
• Lack of technical equipment concerning the availability of devices, such as computers, smartphones, tablets, etc., and stable internet access, singularly affecting students with lower socioeconomic status; and
• Lack of digital competences in the school staff, of teachers, students, and parents.

Clearly, the design of online mathematics environments should, on the one hand, should take into consideration the existence of these major issues, as they frame the context where the new contributions will be developed. It is necessary to regard these problems as part of the initial circumstances, the starting conditions. On the other hand, the design should attempt to contribute to the solution of these problems.

4.1.1. Principles for Online Learning Activities by Garrison

Both the problematic context and the attempt to improve it are taken into consideration in the description of the different theoretical contributions that are described in Section 3. Thus, a key theoretical model that focuses on the design of digital educational environments is the CoI (Section 3.1), which emphasizes the role of social and cognitive interaction and perceived collaboration (even if just virtual) among the members of the online community in the learning process.

To establish social presence, Garrison [50] states the following seven principles:

• Plan for the creation of open communication and trust;
• Plan for critical reflection and discourse;
• Establish a community and cohesion;
• Establish inquiry dynamics (purposeful inquiry);
• Sustain respect and responsibility;
• Sustain inquiry that moves to resolution; and
• Ensure assessment is congruent with intended processes and outcomes.

These principles focus mainly on the learning activity. To also address e-pedagogy, the role of the teacher, and organizational issues (Section 3.2), we complement the CoI principles with principles for online instruction.

4.1.2. Principles for Online Teaching by Sorensen and Baylen

To take into account the teacher’s role, we refer to the seven principles for good practice in web-based environments proposed by Sorensen and Baylen [91]. Their teaching principles, based on [92], are as follows:

• Enabling student–teacher interaction;
• Facilitating cooperation among students;
• Empowering active learning;
• Providing prompt feedback;
• Managing time on task;
• Communicating high expectations; and
• Respecting diverse ways of learning.

As shown by Fiock [93], these seven principles for online teaching are in line with CoI and thus can considered to be coherent with the CoI principles stated above. Following the approach of [94], we use the principles proposed by Sorensen and Baylen [91] to derive design requirements for online environments.

The first and second principles of [91] strongly refer to the relevance of teacher–learner interaction and student collaboration. As a consequence, online environments should facilitate direct interaction and collaboration via synchronous distance learning, as it is considered that synchronous learning favors social interaction in distance math classes by [17]. Moreover, student–teacher interaction should enable the teacher to maintain a balanced role, sometimes guiding students while also allowing them to design and to conduct their own learning graph (third principle; Section 3.4).

The lack of adequate formative assessment tools and individual support for different student contexts, etc. that we identified previously can be addressed in the design of online resources by considering the fourth and seventh principles in the list above, highlighting the importance of providing prompt feedback and adaptive design of learning environments for students with special needs.

Finally, mobile learning (Section 3.3) should be taken into account in the design of mathematics online environments, as the high accessibility of mobile devices among students in Europe can represent a promising alternative for online learning that faces some fundamental problems, e.g., to address the lack of technical equipment or media competence (Section 4.1, fourth and fifth problems of distance learning).

4.2. The ASYMPTOTE System

ASYMPTOTE is an Erasmus+ project co-funded by the European Union. Seven institutions from Germany, Greece, Italy, Portugal, and Spain will work on the project until February 2023. The starting point for the project was, of course, the COVID-19-induced distance education (Section 2). To address its inherent issues, ASYMPTOTE follows a mobile learning approach, providing students with a smartphone app to support them to complete the assigned tasks. For teachers, a web portal, including a monitoring tool, is provided. The extent to which the ASYMPTOTE system meets the requirements for designing distance learning tools in mathematics is discussed in Section 4.3.

In the following section, ASYMPTOTE is presented as a system for online and distance learning in mathematics education. After the ASYMPTOTE idea is sketched, its three key functionalities: web portal, app, and digital classroom, are presented. The system will be launched in May 2022. Both the ASYMPTOTE web portal and the app will be free of charge and GDPR compliant. The ASYMPTOTE app will run on Android and iOS devices. All features described in the following section are still subject to changes in the course of its development.

With ASYMPTOTE, we aim to provide a system for teaching and learning mathematics from lower secondary school to university, i.e., a system that is not limited to a specific topic but provides tasks and learning graphs for a wide range of mathematical topics.

The ASYMPTOTE system can be used to deliver distance education or remote teaching learning activities. In addition, it can be applied to supplement face-to-face phases with individual or collaborative online activities or as a learning environment for self-guided homework.

4.2.1. The ASYMPTOTE Idea

The technical starting point of the ASYMPTOTE project was the already existing and successfully used MathCityMap (MCM) system. MCM was developed at Goethe University Frankfurt as a system for experiencing mathematics outdoors by so-called math trails [95]. The MCM concept comprises two components: (a) the student’s side uses a smartphone to experience math trails in a geocaching-like manner, and (b) the teacher’s side is supported by a web portal, which provides a workspace to design tasks and trails. These two components are connected via an interactive digital classroom, which is an online session, allowing an entire class to work on the same trail while the teacher can monitor the individual and collective progress in real-time [95].

The ASYMPTOTE project has been adapted the MCM system to meet the challenges of distance learning, new challenges that occurred in the ERT phase of COVID-19-induced distance education. In view of this ERT phase, ASYMPTOTE has transformed the concept of straight outdoor learning trails into a concept of branched adaptive online learning graphs while retaining the two-component idea: an app allows students to work through an interactive adaptive learning graph, whereas on the teacher’s side, a web portal provides all functionalities needed to create one of the latter. The digital classroom will be extended and improved to create an even more classroom-like atmosphere. These three features are introduced in the following. First, however, how ASYMPTOTE uses the learning graph concept described in Section 3.4.4 will be demonstrated.

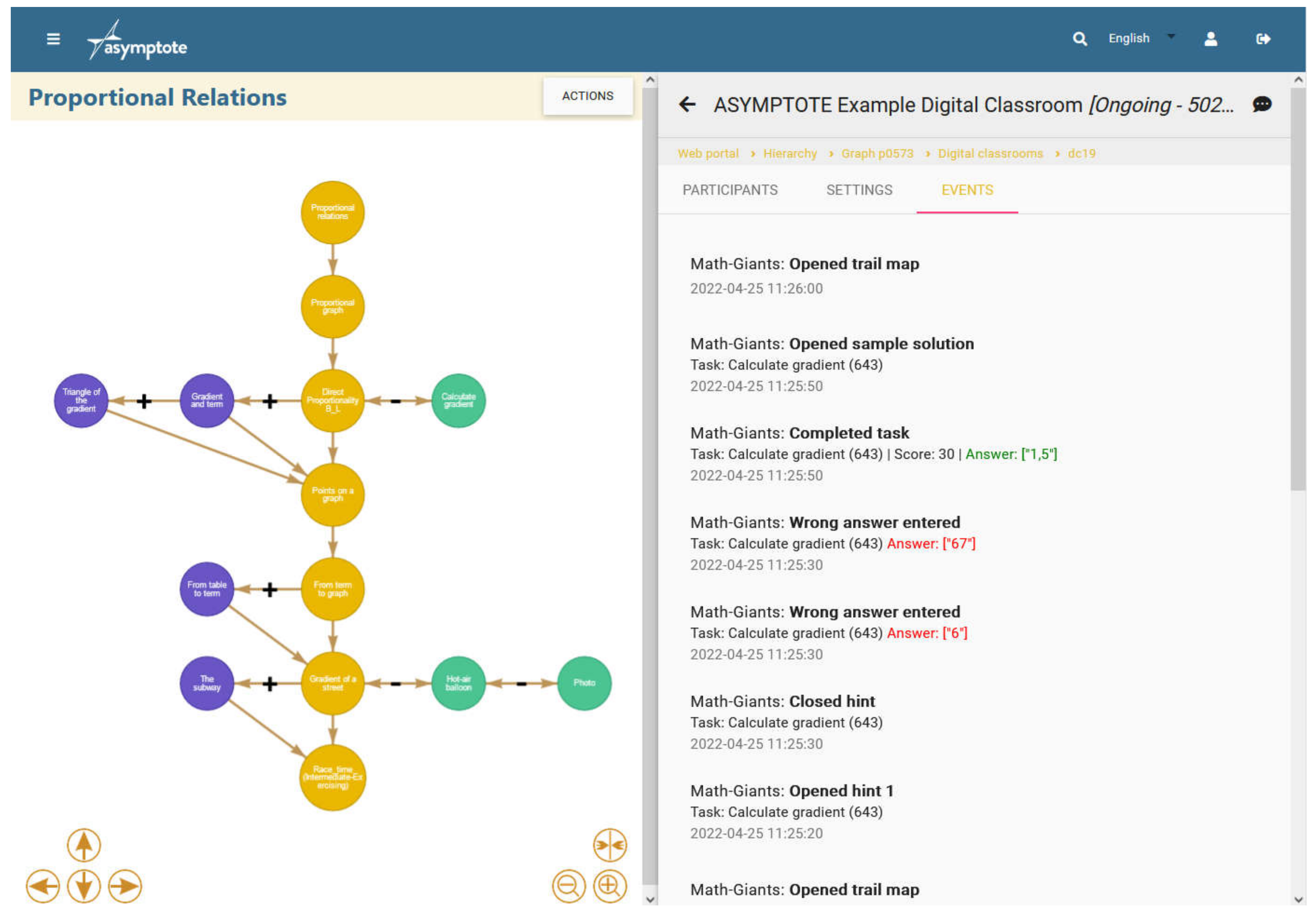
4.2.2. ASYMPTOTE Learning Graphs

On the one hand—as outlined in Section 2 and recalled in Section 4.1—students’ assessment and adequate feedback on their working progress was one major problem reported in the ERT phase [13,16,18,34]. Moreover, the higher degree of self-organization and the need for self-assessment by the students was identified as challenging [16,20,34]. On the other hand, according to [41,42], digital tools provide the potential for an adaptive allocation of tasks and a possibility for (self-)assessment.

Facing these challenges of distance education, ASYMPTOTE follows the concept of learning graphs (LG; Section 3.4.4) to provide an adaptive distance education system. An LG allocates the upcoming task based on the student’s performance in the previous task. Thus, ASYMPTOTE follows the idea of micro adaptivity, with ongoing measurement of the student’s work progress (cf. [89]). Hereby, the system validates the student’s entered solution, i.e., giving corrective feedback [96,97] and thus allocates the next task depending on its correctness. Consequently, the adaptive LG can be seen as a beneficial concept for online teaching in general, and for remote teaching activities. In addition, this adaptive functionality is provided by ASYMPTOTE following a low-barrier approach: ASYMPTOTE, considered as an intelligent tutoring system (ITS) as defined in [42], offers a user-friendly and intuitive authoring tool for ITS functionalities (i.e., task allocation, immediate feedback, adaptivity), addressing the needs of the students.

Moreover, the system can be used in various learning settings: for online and remote teaching and to supplement face-to-face teaching situations with online activities and to conduct self-guided homework, taking into account the individual performance level of the students.

Since the LG concept broadens the linear sequence of learning paths with additional easier or more difficult tasks (Section 3.4.4), three general task states emerge:

• Main tasks (yellow) are mandatory tasks and form the backbone of an LG. In a desirable scenario, each main task covers an aspect of the overall topic. Hence, a student who solved all main tasks encountered and learned the minimum requirements for this topic. This implies that students should solve as many main tasks as possible.
• Support tasks (green) are linked to the right side of a corresponding main task and provide related tasks on a lower level, which can help solve the main task afterward. This might be an easier version of the task, or a repetition of a topic needed in order to solve the main task. Multiple support tasks can be assigned to one main task and solving them will never pose any drawbacks for the students.
• Challenge tasks (purple) are located on the left side of the main task and are supposed to be more difficult than the latter, challenging those students who finish early or seek to dive even deeper into the topic. Challenge tasks are unlocked upon solving their respective main task or preceding challenge tasks since more than one challenge task can be associated with one main task.

A generic LG that includes all three types of tasks is presented in Figure 3. The tasks are represented by the vertices while the edges show the possible learning paths of the students.

In general, an LG in ASYMPTOTE is a collection of different tasks with varying difficulty concerning one mathematical topic. The aforementioned task state (main, support, or challenge task) is determined by the task location in the LG. Therefore, it is important to mention that a task can, for instance, be a support task in one but a challenge or main task in another LG. The edges connecting the tasks (vertices in the LG) indicate the possible workflow later in the ASYMPTOTE app (see Figure 3). Since the first main task of an LG is at the top and the last one at the bottom, the edges between the main tasks are always pointing downwards. Support tasks are connected by horizontal bidirectional arrows to highlight that the students can always return to the main task from any associated support task. Since a student can only solve challenge tasks after completing the corresponding main task, diagonal edges from all challenge tasks point downwards to the next main task.

Thanks to the combination of mandatory main tasks, optional challenge tasks, and individually selected support tasks, the ASYMPTOTE LG architecture ensures two core concepts. Firstly, the main tasks aim to cover the most important concepts of the mathematical topic, which, for instance, have been taught in the previous lesson in school. Thus, by solving as many main tasks as possible and resorting to support tasks, if necessary, students can train the underlying topic and achieve a profound understanding of it. Secondly, and most importantly, the entire learning process is self-guided and autonomous following the self-determination theory by Deci and Ryan [98].

The only mandatory target of an LG for students is to solve all main tasks. Everything else apart from this (support and challenge tasks) is optional. Eager students can strive to solve all available challenge tasks, whereas other students struggling with the main tasks can optionally visit and learn from support tasks and many other students likely choose one path in between. The possibility of invoking support tasks on demand can support lower-performing students in the online learning situation. Hence, what matters here is the fact that every student can choose a personal path through the LG, providing the opportunity for all students to work autonomously on tasks that meet their own performance level.

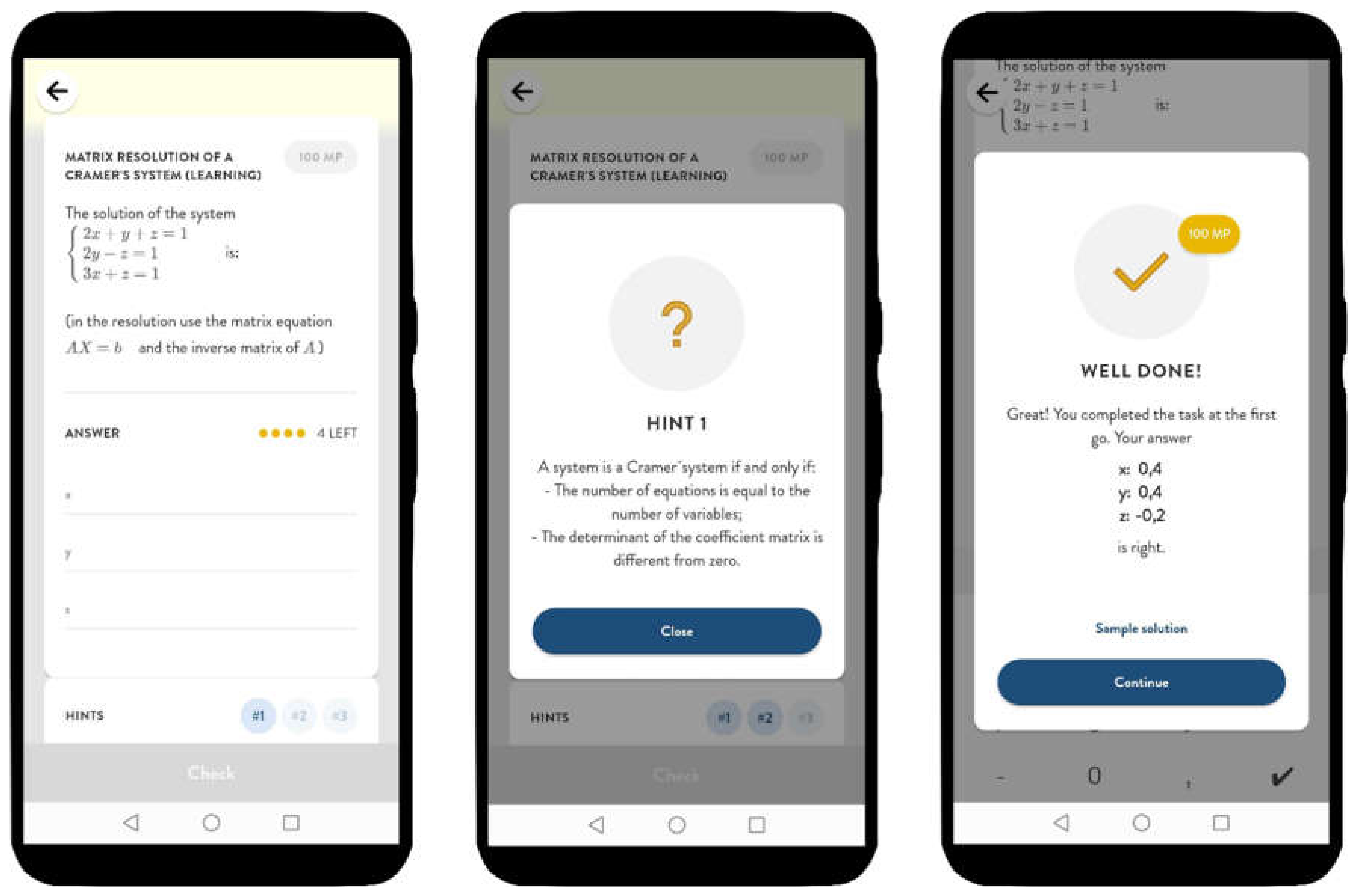
4.2.3. ASYMPTOTE Tasks

Tasks are the basic components of LG. They are created from a predefined task form, facilitating the ability to address as many different problems and topics as possible throughout all classes and skill levels. This form starts with a title and task instruction that precisely specifies what the task is about. The answer format is the core of each task. It determines the answer behavior in the ASYMPTOTE app. ASYMPTOTE currently provides eight different answer formats. Some are interdisciplinary, e.g., multiple-choice or closed texts, and some are particularly relevant for mathematical tasks, such as exact values, vectors, and sets. This list will be extended in the near future by, for instance, fractions and matrices. Supporting a self-guided working process, each task can and should be given a well-explained sample solution which not only displays the correct result but also describes all steps in between. A sample solution might contain text, image, and video files, which can later be viewed by the students after completing or failing the task. In line with the importance of immediate elaborate feedback [99,100], instant validation by the app and automatic feedback depending on the given answer format (e.g., whether the entered fraction is completely reduced or not) is available. Moreover, tasks can be equipped with a maximum of three stepped hints, ideally leading the students along the solution process. An example for a suitable succession of stepped hints could be (a) a different wording of the question, and then (b) an indication towards one possible formula followed by (c) providing the formula itself. Hints can include text, images, and videos, which follows the ideas of [101,102,103] in assisting multimedia material to foster the student’s learning progress. Independent of the task state (support/challenge/main), which is determined by its position in the respective LG, a task can indicate its general purpose by assigning a task category, namely learning, training, reasoning, and modelling.

One of the developments coming soon is the loop task. Loop tasks should provide a collection of permutations of the same task, allowing students to train their skills on a certain topic/task via repetition. Moreover, by presenting every student with a slightly different version of the same task, students should be less tempted to cheat. As an example, the teacher could type in the equation ax + b = c; specify the number space for a, b, c, and x; and choose the number of tasks, which are then automatically generated by the system. A mode to manually create multiple permutations of a text-based task is also planned.

4.2.4. The Web Portal: Teacher’s Side

With its design and implementation, the ASYMPTOTE web portal aims to meet the requirements of a fast editable LG and task creation platform. Teachers can choose to (a) either create their own tasks and LG tailored to the needs of their class or (b) select tasks and LG from a growing open database. Besides providing the system itself, the ASYMPTOTE project also aims to be available to teachers and students in all partner languages and beyond suitable distance education content. Furthermore, this collection will constantly be extended by a growing community. To achieve maximal accessibility and reusability in the ASYMPTOTE distance learning content, the web portal is equipped with the following features.

A large set of relevant content requires well-structured intuitive means for teachers to quickly find what they are looking for. Therefore, a European curriculum hierarchy related to the contents of the partner countries has been developed for mathematical topics from primary to university level. This hierarchy is built from four levels: namely, primary, lower secondary, upper secondary, and university, with each of them branching into their respective topic tree. Upon creation, the teacher is asked to assign a suitable hierarchy category to the task or LG. This allows other teachers to quickly find contents for the topic that is currently interesting. Moreover, it is possible to apply certain search and filter criteria to all items in the curriculum hierarchy to narrow down the content of interest.

The translation tool allows teachers to translate each task and LG into the languages of their choice. All available translations for one task or learning graph are then accessible in the ASYMPTOTE app. This feature not only allows teachers from around the globe to translate tasks into their language and use them but can also help, for instance, foreign students who are still learning the language to solve the tasks in their mother tongue. The LG created by the project team will be available in English and translated to the project languages German, Greek, Italian, Portuguese, and Spanish.

ASYMPTOTE will offer a way to make tasks and LG public. For a task to be public, a review by professionally trained reviewers is necessary beforehand. These reviewers check the completeness of the task instruction, obvious mistakes, the correctness of the calculation, the appropriateness of the chosen answer format, the presence of at least one supportive hint, the task category, and the curriculum hierarchy association. The resulting selection of high-quality tasks allows teachers to choose from their own and public tasks or those that were shared for them by other teachers via groups. It is important to note that teachers can use all of their own content without it being public. The public status also allows other teachers to easily use this content.

To make it easier for teachers to assess whether a task is relevant and suitable for their LG, several smaller assistive features are planned. A voting system will allow users to recommend a task they found to be useful. This voting will lead to a ranking of tasks of every topic, instantly displaying the most frequently used ones. Inspection of a task will also provide information about how often a task has been used as a support, challenge, or main task, and how often it has been used in total. A list of all public LGs this task has been used in will offer best-practice examples for this task’s usage. Finally, teachers will be provided with recommendations for other tasks that have most frequently been used with the current task. Together, all these features should provide quick and accurate insight into the quality and usefulness of a task.

4.2.5. The App—Student’s Side

The ASYMPTOTE app represents the student’s view on LG. Every LG starts with the first main task. Related support tasks are also available whereas an associated challenge task will only be unlocked after solving this first main task correctly.

Solving tasks is possible in an extra view (Figure 4). The student can view the task instructions, stepped hint buttons, and an input section depending on the answer format chosen by the teacher. The student’s answer is immediately validated, and direct corrective feedback is prompted (cf. [96,97]). Furthermore, a form of shallow gamification is implemented: students receive points for a successful task solving process (cf. [99,104]). When a task is completed, either by solving, failing, or giving up on it, the sample solution allows the student to see the solution of the teacher. While progressing in the LG, the student is always able to see the already achieved points and the status of their own progress in the LG. Every task that is unlocked but not yet completed (solved/failed/given up) can be attempted at any time. Finishing an LG enables a summary of all tasks, the given answers, and the received points. Once an LG is completed, it can be restarted, with the possibility of skipping tasks that were solved in a previous run to focus on those topics that are not yet completely understood.

Remote teaching tools are prone to students’ cheating since the teacher cannot observe the students. The ASYMPTOTE system will facilitate the characteristics of loop tasks, control features of the digital classroom (e.g., a live event log of all entered answers), and a future input section under every task in the ASYMPTOTE app where students could be asked to justify their solution in their own words. The possibility of cheating cannot be eliminated completely (neither in the online context nor in standard classroom exams), but our tools at least encourage students to face the evaluation tasks honestly.

In Figure 5, an exemplary working progress of a student is simulated. The student starts with main task 1 (M1) and solves it right away (step 0 + 1). He/she then encounters some problems at M2 and tries to solve a support task (S2.1, steps 2) first. After completing S2.1, the student manages to solve M2 and unlocks the first challenge task C2.1 (step 3). Motivated by this progress, the student also solves C2.1 and is presented with C2.2. However, he/she continues with M3, a tough task. The student requires the help of two support tasks S3.1 and S3.2 yet solves them (steps 6–9) and can then complete M3. M4 does not offer support tasks, but the student manages to solve it regardless (step 10). The same goes for M5, but he/she does not attempt the last challenge task C5.1 (step 11).

4.2.6. The Digital Classroom

The digital classroom is the connection between the web portal and the app, or rather the link between the student’s and the teacher’s side. In ASYMPTOTE, the digital classroom is supposed to promote a classroom-like atmosphere by allowing work on several LG for different topics, with more elaborate statistics during and after a session. Thus, a digital classroom can be open for a long time, e.g., over the current unit, several months, or the entire term. The three core features of the digital classroom are described in the following paragraph, including their current state and future improvements.

One of the main challenges in self-guided distance learning is the possibility of providing individual feedback as a teacher. Larmann et al. [105] showed that students using MCM with distance education tasks (MCM@home) used the chat to ask the teacher content questions without prior initiation. This observation highlights the importance and acceptance of this communication channel. Based on these experiences with the MathCityMap system, ASYMPTOTE offers a teacher-student chat too. Concerning the different types of feedback, the chat allows teachers to provide valuable evaluative and explanatory feedback (cf. [96,106]) in the synchronous online environment.

In the MathCityMap chat, teachers missed the possibility of communication among the students [105]. This finding is in line with CoI (Section 3.1), which highlights the importance of student collaboration in online environments. Since the use of a messenger app in schools for communication raises data protection issues and could harm the workflow and concentration, the digital classroom chat will be developed to a point where it can cover all necessary communication among students to work on an LG successfully. This so-called teamwork mode includes the support of images/screenshots and voice messages, and chatting in predefined teams, with the teacher having the ability to answer questions in each of these teams.

The individual progress display allows the teacher to monitor each student’s progress even from a distance. This includes the current state of the LG, all points earned so far, all hints utilized, and all entered answers for every task in the LG (Figure 6). The latter is especially important for the teacher to gain insights into the chosen approach and adjust it according to the precise feedback of the student. In the future, this progress display will also show the student’s individual learning path through the LG, comparable to the example in Figure 5 shown on the right side. This highlights the aspect of self-guided learning by visualizing the strategy that the student chose to complete the LG, e.g., by solving only the necessary main tasks or by seeking all challenge tasks or making use of every support task.

In the future, a class overview will summarize the individual progress data of the entire class on a well-structured analytic page. Every path chosen through the graph will be displayed in one LG, which will immediately show where the majority are heading, which challenge task is most appealing, and which main task is the most difficult one. More detailed statistics will cover the average time spent on each task, the average amount of points earned, the most popular answers, the average number of hints required, and many more parameters either for each task or the entire LG. Hence, this class overview has potential for an efficient LG improvement loop, e.g., by removing/improving support tasks that were never used, by editing hints in a way that targets the most common false inputs, by restructuring the LG to improve its workflow, and many more cases.

In summary, the digital classroom not only strives to create a distance learning environment with classroom-like features, such as team chats and direct contact with the teacher. It also offers teachers detailed analytic feedback that allows for pinpointed interventions and evaluation of individual answers, and the overall progress of the entire class. Moreover, this information allows for the improvement of specific tasks, intensifying the effort on a topic that was discovered to be lacking, and convenient long-term assessment of the learning process.

4.3. Analysis of the ASYMPTOTE System

In Section 4.1, we identified several design requirements based on the needs of distance learning during the ERT phase. In Section 4.2, the ASYMPTOTE system was presented. In the following, we combine both subsections and analyze the extent to which the ASYMPTOTE system meets the distance learning requirements.

The starting point for the development of the ASYMPTOTE system was the perceived challenges during the ERT phase in Spring 2020. Through a cross-national comparison among the partner countries, we were able to identify five major challenges that occurred in all five countries studied:

• Loss of personal interaction;
• Lack of adequate formative assessment;
• Deficit of curricular resources;
• Lack of technical equipment; and
• Lack of digital competencies.

In the following section, we analyze the ASYMPTOTE system. In doing so, we refer both to the already technically implemented features that will be available by May 2022 and to the upcoming further developments. Considering that this is a self-report of the state of the ASYMPTOTE project, we formulate 10 statements on how the system can address the challenges of distance education from our point of view. We start our analysis from a technical point of view.

4.3.1. Lack of Technical Equipment and Digital Competencies

Starting from a student’s perspective, based on challenges (d) and (e), we assume that a mobile learning approach with smartphones can overcome the problem of technical availability and handling. In terms of technical equipment, high and increasing access to smartphones has been observed [107]. Among European children, teenagers, and young adults, access to smartphones can even be assumed, as was shown in Germany [108]. Moreover, possession of a smartphone is significantly higher than possession of a computer [108]. Thus, the use of smartphones appears to be an essential basis for offering nearly all students the opportunity to participate in online and distance learning.

Regarding digital competencies, it can undoubtedly be assumed that students are familiar with the use of their smartphones—they use them in their daily life for entertainment and access to information [109]. Furthermore, mobile learning has been successfully used at all levels of education [109]. Other authors have emphasized the value of the portability and high computing power of mobile devices [67,110], and the possibility for interactivity and communication [68,111].

In addition to the general use of mobile devices, the technical development of ASYMPTOTE follows a low-barrier approach. The use of this system is free of costs and advertisement. It is in line with the European data protection strategy GDPR. To enable students with disabilities to participate in lessons with ASYMPTOTE, a zoom function for images and a read-out-loud function for text will be implemented.

Statement I.

ASYMPTOTE’s mobile learning approach can already be considered to be suitable for enabling almost all students to participate in online and distance learning. Further developments will lower participatory barriers even further, in particular for students with disabilities.

From the perspective of teachers, in order for students to work with the ASYMPTOTE app, educators must first familiarize themselves with the teacher workspace of ASYMPTOTE, namely the web portal. It can be accessed via a web browser. Therefore, no special equipment is required on the teacher’s side. Here, teachers can select or create their own tasks and digital learning graphs. In addition, they can create a session for their students in the web portal and use the digital classroom to assess the students’ work progress.

The structure of and the workflow in the ASYMPTOTE web portal are similar to the MathCityMap web portal. Since the latter has been successfully used by teachers all over the world [112], no major difficulties are expected after an initial familiarization phase. To facilitate the initial contact, information material on how to use the web portal and the app will be provided in tutorials. In addition, a free Massive Open Online Course (MOOC) for European student teachers and in-service teachers will be offered in autumn 2022. As the project team has good experience with an MOOC on MathCityMap [113], a substantial contribution to the project dissemination is expected.

Statement II.

No major technical problems are expected regarding teachers after an initial familiarization phase.

4.3.2. Deficit in Curricular Resources

As stated in the previous section, the ASYMPTOTE project not only aims to provide a tool for online learning from a technical point of view. It also aims to create appropriate content for mathematics lessons from the lower secondary to university levels. Thus, the project team will develop tasks and learning graphs for secondary schools and universities. These will be available in an open database, which will contain tasks for learning or training a topic at different levels of difficulty.

Since the majority of teachers focused on standard and reproduction tasks in the ERT phase [16,18] and rarely used modeling or reasoning tasks [17], the development of more complex task types seems to be particularly important. Therefore, the database will also include modeling or reasoning tasks.

It was not possible to provide a complete database for almost all mathematical topics relevant to schools or universities within the scope of this project. Therefore, the project team decided to create exemplary tasks on linear functions, quadratic functions and linear equations (secondary level), and matrices, inverse trigonometric functions, and integrals (university level). Geometric topics will be covered after the planned integration of dynamic geometry software (DGS) into ASYMPTOTE. This will allow manipulative and interactive tasks in the future.

Statement III.

During the project period, tasks for learning, training, modeling, and reasoning covering exemplary topics from lower secondary to university level were developed. Within the planned integration of DGS, it will also be possible to create manipulative and interactive tasks in the future.

The created tasks are pre-structured in learning graphs in a reasonable way. While the main tasks cover the main content of a topic, students can, on the one hand, receive help through support tasks or, on the other hand, challenge themselves by working on the available challenge tasks. To enable wide use of these elaborated learning graphs, they were created in English and translated into the project languages German, Greek, Italian, Portuguese, and Spanish.

Regarding Sorensen and Baylen’s principles for teaching in online environments [91] (Section 4.1), ASYMPTOTE can help address several of these principles through its available curricular resources.

Firstly, the student’s time on task can be fostered by the structure of learning graphs. Since the learning graph provides the opportunity to access challenge tasks or receive help through support tasks, students can work at their individual performance level, avoiding frustration or a loss of motivation. Furthermore, ASYMPTOTE respects mutual ways of learning, as the learning graph concept itself follows the idea of autonomous and self-directed learning (Section 3.4). This autonomous learning at a distance is contained, for example, in the possibility of retrieving hints or setting tasks if needed. In addition, lower-performing students can receive help through easier support tasks to ensure that they learn the basics of the topic.

Two additional criteria are addressed by the development of curriculum resources. In both traditional classroom and online settings, communicating high expectations and empowering active learning depends on the available task formats. Again, tasks for ASYMPTOTE will be created, with a special focus on modeling and reasoning. In addition, active learning can be fostered by interactive and manipulative tasks after implementing dynamic geometry software into ASYMPTOTE. Further, it can be fostered by students’ collaboration in the teamwork mode, which will contain a group chat (Section 4.2).

Statement IV.

For exemplary topics, ASYMPTOTE offers a selection of elaborated learning graphics, available in several languages and taking into account the main principles of online learning.

A limitation of the project is the number of topics for which tasks and learning graphs are provided. As mentioned above, the development of high-quality material during the project period is only possible for exemplary topics. In other words, even after the project’s end in February 2023, for many important school topics, no tasks will be provided by the project team.

To expand the database thereafter, it is planned that ASYMPTOTE will be a community project. Math teachers are encouraged to create tasks and learning graphs for their classes in the system. On the one hand, this will help to cover those topics that the project team did not select to be exemplary tasks. On the other hand, the possibility of self-created tasks and learning graphs has another positive aspect: it allows teachers to create tasks and learning graphs that meet the individual needs of their students and the learning level of their class. Thus, the ASYMPTOTE project allows teachers to modify and adapt the content to their own personalized program, which was recommended by [110].

After creating their own tasks and learning graphs, teachers can share the developed content with ASYMPTOTE users all around the world. To ensure the quality of the tasks, all tasks for which a publication is requested will be reviewed by members of the project team.

The decision regarding a community project is based on the technical origin of ASYMPTOTE, i.e., the MathCityMap system for outdoor mathematics. MathCityMap offered users more than 15,000 tasks in the summer of 2020, 4 years after the web portal was released [112]. Therefore, building the ASYMPTOTE project on a user community seems to be a promising approach for the near future of the system. The first activities required to build an active community are the already mentioned MOOC and the implementation of university courses and multiplier events for (student) teachers, starting in summer 2022.

Statement V.

At this stage, the project cannot fulfill the claim of providing a profound database for most curriculum topics. However, due to the community-based concept of ASYMPTOTE, an extensive open database is expected to be created in the medium term with the help of active users.

4.3.3. Lack of Adequate Formative Assessment

Providing appropriate formative assessment, which includes individualized support and feedback, was seen as a challenge during the ERT phase (Section 2). The need for assessment is also stated by Garrison [50] in his seventh CoI design principle: The teacher must ensure that the assessment is congruent with the intended processes and outcomes of the lesson. More specifically, Sorensen and Baylen [91] define the provision of prompt feedback as a core principle of online instruction.

Moreno [96] distinguishes between corrective and explanatory feedback. Following her guided feedback hypothesis, explanatory feedback promotes deeper learning processes than solely corrective feedback. This high value placed on explanatory feedback is in line with the meta-analysis of Hattie and Timperley [97]. Further, they state that feedback should be given immediately after the task has been completed.

In ASYMPTOTE, students receive automatic and systematic feedback on the correctness of the entered solution (Section 4.2). This corrective feedback is displayed immediately after entering a solution, as recommended by [97]. Additionally, as a shallow gamification, students receive up to 100 points for solving a task.

The possibility of viewing a sample solution seems to be promising if there is only one solution approach, i.e., in exercise tasks on a technical level (e.g., solving a linear equation). Here, students can easily compare their own solution with the provided sample solution. However, if a modeling and reasoning task is given, the prepared sample solution might be too specific and focused on one solution approach. Thus, the availability of a sample solution may not meet the need for explanatory feedback in every case.

Statement VI.

ASYMPTOTE provides immediate and gamified corrective feedback on the student’s solution. It is supplemented by a sample solution as explanatory feedback. However, the value of the feedback provided by the sample solution seems to depend on the type of task.

Furthermore, feedback can be provided by the chat tool via the Digital Classroom (Section 4.2.6). Here, direct interaction between the student and the teacher is enabled by text, audio, or image messages. To provide explanatory feedback, the teacher can either start a conversation with students who have made several incorrect entries using the individual progress display or respond in real time to questions from the students themselves (cf. [105]).

Statement VII.

The digital classroom chat allows teachers and students to provide explanatory feedback on the student’s individual needs. Together with the immediate systemic feedback and the possibility of invoking a sample solution, ASYMPTOTE will offer the possibility of providing both corrective and explanatory feedback at the time of its release in May 2022.

Providing effective feedback is one aspect of formative assessment. Other aspects, according to the theory of formative assessment by Black and Wiliam [114] concern (a) setting and understanding learning intentions and success criteria; (b) developing effective learning settings, such as classroom discussions or other tasks to elicit student understanding; (c) encouraging students to act as instructional resources for one another; and (d) promoting students to act as responsible agents for their own learning.

Based on (a), it can be argued that the structure of the learning graph can help to clarify the learning aims. The mandatory main tasks are located in the middle and represent the core of the topic while the support tasks provide help in solving the main tasks. The challenge tasks, on the other hand, can be completed by students voluntarily. Consequently, when learning with ASYMPTOTE, students must take greater responsibility for their learning as they have to make decisions independently, e.g., the use of the challenge tasks. This is consistent with (d), i.e., learners are encouraged to be responsible for their learning progress.

Within the development of the teamwork mode, students will, in addition, be able to interact with each other and discuss the assignments so that they can give feedback and advice to each other via the chat. This could help to encourage students to act as instructional resources (c). However, whether the chat can fulfill this claim needs to be proven by further research.

From the teacher’s perspective, the digital classroom offers both an individual progress display and a class overview. While the first feature is useful for retracing the student’s individual work progress, the second feature can provide the teacher with insight into which tasks are most challenging for the learners. Thus, the digital classroom provides the ability to monitor progress on a class and individual level. Consequently, it allows the teacher to promote students’ success in completing the tasks even at a distance. In addition, the digital classroom evaluation helps to prioritize follow-up discussion of tasks, e.g., via videoconferencing, thus assisting teachers in organizing fruitful discussion (b).

In addition, also concerning (b), the idea of the learning graph helps the teacher to develop online learning settings that fit the individual needs of their students. While the expected workflow—the learning trajectory—is represented as a sequence of mandatory main tasks, challenge and support tasks are additionally provided (Section 3.4.4). Adaptive task assignment forces learners to work on the support tasks after they have failed to solve a main task at least twice. Moreover, after successfully solving a main task, learners can independently decide whether to work on the more challenging task. Consequently, ASYMPTOTE learning graphs, which are based on a mixture of adaptive task assignment and autonomous task invocation, can provide effective learning environments for online instruction.

Statement VIII.

The ASYMPTOTE system will directly or immediately address the aspects of formative feedback stated by Black and William [114] in its forthcoming release. Further developments are planned for the immediate future. Within the learning graph, an effective learning setting can be provided at a distance. Moreover, the evaluation functions of the digital classroom can facilitate the design of an effective follow-up on the learning graph worked on.

4.3.4. Loss of Personal Interaction

Another major challenge during the ERT phase was the loss of personal interaction. As shown by research in many European countries (Section 2), personal contact between students was limited compared to face-to-face teaching. This, caused by the spatial separation during school closure, affected both teacher–student and student–student communication.

As Vygotsky [115] pointed out, learning is a social process. As a result, the loss of the personal dimension in the educational process has threatened the success of learning. The importance of social interaction is also highlighted by the CoI model for teaching and learning in online environments (Section 3.1). Social presence is described as the ability to position oneself as a real person in the online environment [49]. This requires open communication, the expression of emotions, and group cohesion in the online format [49].

In terms of group cohesion, ASYMPTOTE is used by students who have already formed a class community (this is less relevant for university students). Therefore, in most cases, it can be assumed that ASYMPTOTE users are already part of a community comprising their peers. This means that a sense of belonging to the group and an atmosphere of cooperation can be presumed. The challenge for the teacher, of course, is to maintain this group cohesion during online education. Here, ASYMPTOTE allows teachers to chat with all students at once or to conduct a one-to-one conversation with one student. In addition, the upcoming teamwork mode will allow students to stay in touch and work together in small groups. Thus, chat can be considered as one valuable component that maintains the group feeling; however, we are aware that it cannot maintain group cohesion during distance learning alone.

Regarding the expression of emotions, students are used to expressing their personal feelings daily via messenger services, such as WhatsApp. Moreover, our research on the use of the MathCityMap chat for distance learning showed that students themselves use the chat to personally contact the teacher, e.g., regarding questions about the teacher’s well-being [105]. Thus, we assume that the chat is a valuable tool for the expression of emotions, at least for the students.

The third requirement of social presence is the ability to engage in fruitful open communication (Garrison et al., 2000), which supports the individual construction of knowledge and metacognitive skills [46]. Again, ASYMPTOTE offers the possibility of targeted teacher support, with the teacher–student chat including text, audio, and image messages. As part of the teamwork mode, small group collaboration is realized via the chat. However, in view of Garrison’s principles for successful online teaching in terms of CoI [50] (Section 4.1), we are aware that a chat tool alone can only contribute to a limited extent to fulfill the requirements of open communication and fruitful group discussion. Therefore, we strongly recommend a follow-up activity that reflects on the students’ work process, both on a personal and a content level. In addition, in our opinion, the tasks with the highest failure rate should be discussed in class. To prepare for this online class discussion, the automated evaluation of the digital classroom can provide teachers valuable insight into the work process and the success of the students.

Statement IX.

The teacher–student chat of the ASYMPTOTE system helps to overcome the lack of face-to-face interaction to some extent. Moreover, in the teamwork mode, a tool for online collaboration among students will be developed. However, in order to fully meet the requirement of a face-to-face presence in terms of CoI, the teaching conducted with ASYMPTOTE should be followed by a class activity, e.g., via video conferencing.

Considering the CoI model (Section 3.1), the digital classroom provides the teacher with the possibility of direct instruction via the chat. Moreover, the teacher can use the systemic assessment to prepare a targeted follow-up of the lesson conducted with ASYMPTOTE. Consequently, ASYMPTOTE helps the teacher to meet the teaching presence requirements in terms of CoI.

The availability of appropriate digital tasks and the possibility of working at their own performance level in the learning graph promotes the cognitive presence of the students. Furthermore, the cognitive presence can be promoted by the discussion and reflection phase, which we propose as a follow-up to the work on the ASYMPTOTE learning graph.

Statement X.

Working on an ASYMPTOTE learning graph enhances the cognitive activation of the students. However, to fully meet the requirements of CoI, subsequent discussion and reflection is necessary, guided by the teacher using the digital classroom evaluation.

5. Final Remarks

Teaching and learning during the COVID-19-induced distance learning phase was a major challenge for both educators and students. Based on the experience of the ERT phase, this article provides a theoretical framework for distance learning tools and defines the requirements for designing these tools.

In addition, ASYMPTOTE was presented as an example of the development of a tool for distance education resulting from the COVID-19 pandemic. ASYMPTOTE takes a mobile learning approach that utilizes smartphones and aims to act as an adaptive system for synchronous online teaching that provides a profound evaluation function. This article analyzed the extent to which the ASYMPTOTE system meets the identified requirements for online learning tools.

In the following section, we briefly summarize the setup of a theoretical framework for distance learning tools and present the derived design requirements. Subsequently, the ASYMPTOTE system is finally analyzed.

5.1. Developing a Theoretical Framework for Online Education Tools

In this article, we identified five challenges in the ERT phase by comparing Germany, Greece, Italy, Portugal, and Spain.

Firstly, the loss of personal interaction, exacerbated by asynchronous teaching, was reported in view of student–teacher interaction and communication among students. This, secondly, made the formative assessment of a student’s learning progress at a distance more difficult. Thirdly, formative assessment was complicated by the lack of adequate curricular resources for online teaching. On a technical level, fourthly, a lack of technical equipment regarding digital devices for participation in distance education was observed. In addition, problems with technical implementation also concerned the handling of ICT: a lack of digital competencies among teachers and students was identified in all five states.

Starting with the need to enable face-to-face interaction in distance learning, the CoI model was introduced. This framework emphasizes the value of a social presence for online learning. In addition, to include the teacher’s perspective in designing and orchestrating distance education, we considered e-pedagogy and online teaching. To address the lack of technical equipment and digital competencies, this article proposes a mobile learning approach using smartphones. Finally, to enable teachers to conduct appropriate formative assessment, the concept of a learning graph was developed (Section 3.4.4). It comprises the individualization of learning in CBLE, the autonomous selection of tasks by the learner in learning paths, and the pre-selection of tasks by the teacher and their assessment, described in the concept of learning trajectories. Working on a learning graph thus supports individualization and at the same time is suitable for assessing the learner’s learning progress at a distance.

5.2. Development and Analysis of the ASYMPTOTE System

The ASYMPTOTE system of adaptive and synchronous online teaching was introduced in this article. This system consists of two components, namely a smartphone app for students and a web portal for teachers. As part of the digital classroom feature, the teacher can monitor the student’s work progress from a distance. A chat is also implemented to allow direct teacher–student interaction despite spatial separation. A teamwork mode that allows students to work and communicate together remotely will be developed in the next months. ASYMPTOTE, which is co-funded by the European Union through an Erasmus+ strategic partnership, is free of charge and advertising and in line with the GDPR. The system will be available in May 2022.

Regarding the five identified challenges of distance learning, the ASYMPTOTE system was analyzed (Section 4.3). Hereby, we referred to both already technically realized features and planned further developments. The 10 statements regarding teaching and learning with ASYMPTOTE are summarized below.

Statements I and II: Concerning the lack of technical equipment, a mobile learning approach with smartphones seems to be promising due to the high smartphone availability among students. The digital competencies required for handling a smartphone app on the students’ side can also be assumed. No major technical problems are expected to be encountered by the teachers after an initial training phase. Thus, the ASYMPTOTE system addresses the challenges of technical availability and handling reported in the ERT phase.

Statements III–V: ASYMPTOTE aims to address the lack of curricular resources by creating an open database of tasks and learning graphs from lower secondary school to university. However, for personal and monetary reasons, materials for school and university teaching can only be developed by the project team for some exemplary topics. Therefore, when the ASYMPTOTE system is released in May 2022, only a few available curriculum resources will be included in the open database.

In order to provide a comprehensive database in the medium term, ASYMPTOTE is designed to be a collaborative project, i.e., teachers from all over the world can develop and share self-created tasks and learning graphs in the ASYMPTOTE web portal. In summary, the ASYMPTOTE project cannot yet claim to provide a wide range of curriculum resources, but it is expected that it will provide a large open database of tasks and learning charts in the next few years.

Statements VI–VIII: The lack of adequate formative assessment is addressed in the ASYMPTOTE project in two ways. Firstly, corrective and gamified feedback is displayed to the students immediately after entering a solution. Furthermore, it is complemented by a sample solution, which seems to be an effective way to provide explanatory feedback for exercise tasks on a technical level. The teacher can also provide explanatory feedback via a chat that includes text, audio, and image messages.

Moreover, we were able to show that ASYMPTOTE takes into account further mutual aspects of formative assessment. In particular, the idea of the learning graph can be considered as a learning trajectory that is enriched with challenge and support tasks, allowing the student to follow an individual learning path, which has the potential to create effective distance learning settings. On the one hand, it enables students to set challenging tasks independently. On the other hand, the learning graph provides an adaptive element, i.e., the assignment of support tasks after failing twice on a main task.

In addition, the digital classroom feature can help teachers to design effective discussions as a follow-up to the lesson by providing automatic assessment of the lessons completed using ASYMPTOTE. Overall, we assume that the ASYMPTOTE system has the potential to overcome the lack of adequate formative assessment in online classes.

Statements IX–X: Moreover, the most difficult issue to address is the loss of face-to-face contact during COVID-19 distance learning. So far, ASYMPTOTE provides a chat for face-to-face interaction between teachers and learners. As our previous research has shown, the chat has been used independently by learners to ask the teacher for help or to start a conversation on a personal level with the teacher. In addition, a teamwork mode for collaborative group work will be implemented in ASYMPTOTE, offering a group chat. How this is adopted by students as a way of maintaining social interaction at a distance will be the subject of upcoming research.

We are aware that a chat alone cannot address the lack of face-to-face interaction in online classes. Therefore, we strongly recommend that lessons conducted with ASYMPTOTE are followed by class discussion and reflection, e.g., via video conferencing. As mentioned earlier, the automatic evaluation of the digital classroom can help teachers prioritize the debriefing of the lesson.

5.3. Outlook on the ASYMPTOTE System

In this paper, we self-reported the present status and the planned further developments of the ASYMPTOTE system. Ten statements were formulated to express how ASYMPTOTE meets the requirements of online learning from our point of view. As noted, we expect that it can provide a substantial contribution to online teaching in mathematics education.

However, this article is not based on empirical evidence, since our statements are not empirically proven. We see them as starting points for a detailed scientific evaluation of the ASYMPTOTE system, by ourselves and by other researchers in the field. Until the ASYMPTOTE system is released in May 2022 and until those research projects are realized, we agree with the following statement:

Final Statement.

Based on the previous considerations, we estimate that ASYMPTOTE will address most of the identified challenges of distance education. Moreover, since ASYMPTOTE has taken an adaptive, synchronous, and mobile approach to learning, it will meet the identified requirements for the design of online education tools. We consider ASYMPTOTE to be a low-tech-barrier tool for the teaching and learning of mathematics from lower secondary level to university: the system can be used for distance education or remote teaching activities. Further, it can be applied for self-guided homework or for supplementing face-to-face phases with individual or collaborative online activities. Consequently, we believe that ASYMPTOTE is a promising system for the preparation, delivery, and follow-up of online education.