A Structured AHP-Based Approach for Effective Error Diagnosis in Mathematics: Selecting Classification Models in Engineering Education

Abstract

Identifying and classifying mathematical errors is crucial to improving the teaching and learning process, particularly for first-year engineering students who often struggle with foundational mathematical competencies. This study aims to select the most appropriate theoretical framework for error classification by applying the Analytic Hierarchy Process (AHP), a multicriteria decision-making method. Five established classification models—Newman, Kastolan, Watson, Hadar, and Polya—were evaluated using six pedagogical criteria: precision in error identification, ease of application, focus on conceptual and procedural errors, response validation, and viability in improvement strategies. Expert judgment was incorporated through pairwise comparisons to compute priority weights for each criterion. The results reveal that the Newman framework offers the highest overall performance, primarily due to its structured approach to error analysis and its applicability in formative assessment contexts. Newman’s focus on reading, comprehension, transformation, and encoding addresses the most common errors encountered in the early stages of mathematical learning. The study demonstrates the utility of the AHP as a transparent and replicable methodology for educational model selection. It addresses a gap in the literature regarding evidence-based criteria for designing diagnostic instruments. These findings support the development of targeted pedagogical interventions in mathematics education for engineering programs.

1. Introduction

Mathematics teaching constitutes a fundamental pillar in the training of engineering students. Mathematics is essential for expressing physical, chemical, and engineering laws, providing the necessary tools to confront and solve technical problems (Harris et al., 2015; Sazhin, 1998). The ability to apply various mathematical techniques is key to academic success, both in the classroom and in professional engineering practice (Strum & Kirk, 1979). However, engineering students often perceive mathematical concepts as complex and abstract, complicating their understanding and application. This situation is exacerbated by a lack of motivation and the perception that mathematics is irrelevant, a common issue among engineering undergraduates (Brandi & Garcia, 2017; Harris et al., 2015; López-Díaz & Peña, 2021). Integrating practical examples and real-world problems can help students appreciate the relevance of mathematics in their field (Brandi & Garcia, 2017; Sazhin, 1998). Furthermore, collaboration between mathematics and engineering departments can significantly enhance the teaching and learning of mathematics (Jaworski & Matthews, 2011). Identifying and analyzing the mathematical errors committed by students is therefore crucial for improving the teaching–learning process, allowing instructors to intervene effectively at critical points in students’ learning trajectories (Hoth et al., 2022; Nuraini et al., 2018).

In the context of mathematics education, a mathematical error is generally defined as a deviation from the correct solution or process, often revealing underlying misconceptions or flawed reasoning (Makonye & Fakude, 2016). Educational research has categorized such errors into several types (Suciati & Sartika, 2023). Conceptual errors arise when students demonstrate incorrect or incomplete understanding of fundamental mathematical principles (Irham, 2020; Nurhayati & Retnowati, 2019; Roselizawati Hj Sarwadi & Shahrill, 2014; Sehole et al., 2023). These errors reflect failures in conceptualizing basic ideas, preventing students from correctly applying such concepts in problem-solving contexts. One example includes confusion regarding the notion of derivatives in calculus, which can lead to misinterpretation (Booth et al., 2013). Procedural errors, on the other hand, occur when students understand the underlying concept but fail to execute the necessary steps to solve a mathematical problem (Mosia et al., 2023; Rushton, 2018). These errors are common in algebraic operations, such as incorrect simplification or misuse of mathematical properties (Star & Rittle-Johnson, 2008). Interpretation errors constitute another important category, typically emerging when students misread problem statements or data, leading to misinterpretations of variable relationships or solving the problem using inappropriate logic (Chauraya & Mashingaidze, 2017; Hu et al., 2022; Kontrová et al., 2022; Resnick et al., 1989). These errors are frequent in word problems and require strong reading comprehension skills (Movshovitz-Hadar et al., 1987). Application errors reflect a student’s inability to transfer theoretical mathematical knowledge into practical or novel situations (Lobato, 2008; Mukuka et al., 2023), a critical competency in engineering education (Nakakoji & Wilson, 2020). Arithmetic or calculation errors, while seemingly trivial, may significantly impact the outcomes of more complex problem-solving scenarios (Engelbrecht & Harding, 2005). Lastly, systematic errors recur consistently, indicating deeply ingrained misunderstandings that must be addressed with targeted instructional strategies (Papadouris et al., 2024).

This review examines existing research on categorizing, qualifying, and quantifying mathematical errors, particularly in studies relevant to undergraduate engineering students. Although much of the literature focuses on other academic levels and disciplines, the methodologies and findings remain applicable to engineering education, where the improper use of mathematical concepts can hinder the development of essential competencies, particularly in mathematical modeling (Levey & Johnson, 2020), problem-solving (Wedelin et al., 2015) and the application of mathematics (Armstrong & Croft, 1999; Faulkner et al., 2019). This review aims to provide a comprehensive overview of the state of the art, offering a solid foundation for future research and the development of diagnostic tools to improve mathematics teaching and learning in engineering programs.

Despite notable advances in the study of mathematical errors, the literature indicates a lack of precise diagnostic tools that would enable instructors to identify common student errors early, categorize them appropriately, and design targeted pedagogical strategies to correct them (Hiebert & Grouws, 2007; Morgan, 1990). This gap is particularly evident in engineering degree programs, where students often lack foundational mathematical competencies. Thus, there is a pressing need to develop specific diagnostic tests and support strategies aimed at improving their academic performance (Junpeng et al., 2020).

In response to this problem, a critical step in constructing effective diagnostic instruments is selecting the most appropriate theoretical framework for classifying mathematical errors, especially one that aligns with first-year engineering students’ cognitive and curricular characteristics. While multiple theoretical models, such as those proposed by Polya, Newman, Kastolan, Watson, and Hadar, are widely cited, the literature shows that selection often relies on subjective or discipline-based preferences, rather than comparative, pedagogically informed processes. To overcome this limitation, a structured methodology is required to evaluate and prioritize such models.

Among the various multicriteria decision-making methods used in educational research, the Analytic Hierarchy Process (AHP), developed by Saaty, has emerged as one of the most robust and versatile methodologies for addressing complex decisions in educational settings. This approach enables the decomposition of a global objective, such as selecting a theoretical framework for classifying errors, into a hierarchical structure composed of criteria and alternatives evaluated through pairwise comparisons and weighted priorities (Chen et al., 2018). This makes AHP particularly valuable in studies involving qualitative and quantitative variables (Zhang & Wang, 2021), ensuring a comprehensive and integrative assessment approach.

The AHP has been widely applied to curriculum evaluation, institutional competitiveness, educational technology assessment, and strategic academic planning in higher education. For instance, it has been used to assess the effectiveness of curricular systems in technical and vocational institutions by identifying evaluation indicators through expert interviews and determining their respective weights (Chen et al., 2018) and to evaluate the pedagogical utility for training purposes (Hester & Bachman, 2009). Moreover, it has facilitated the prioritization of key criteria in developing institutional strategies, highlighting factors such as sustainability and leadership as central to enhancing higher education competitiveness (Yulmaini et al., 2020).

In faculty and program evaluation, the AHP has provided a systematic and quantifiable framework for assessing academic performance, offering a more objective method to evaluate instructional quality, including in fields such as computer-aided design education. (Chang, 2014; Do & Chen, 2013). It has also proven helpful in understanding the factors that influence students’ choices of undergraduate engineering institutions, allowing for prioritizing such factors based on structured pairwise comparisons (Mahendran et al., 2014).

The AHP has been integrated with other multicriteria decision-making (MCDM) techniques in educational technology to assess and select learning management systems (LMS). It has been particularly instrumental in identifying platforms like Moodle as optimal solutions due to their adaptability and capabilities for integrating adaptive learning tools (Smahi et al., 2024).

The primary benefits of the AHP in educational contexts include its ability to offer a structured and transparent framework for tackling multi-dimensional decision problems (Akram & Adeel, 2023; Ramík, 2020), its flexibility in incorporating both qualitative and quantitative expert judgments (Zhang & Wang, 2021), and its methodological transparency based on consistent and traceable comparison logic (Do & Chen, 2013; Mu & Nicola, 2019). Nevertheless, certain limitations must be acknowledged, such as the risk of inconsistency in individual assessments and the increasing cognitive load associated with a larger number of alternatives, which can make the comparison process cumbersome (Hester & Bachman, 2009; Mahendran et al., 2014).

Despite the extensive use of the AHP in curricular, technological, and institutional domains within the education system, a significant gap remains. There is a lack of studies that apply this methodology to compare and select theoretical frameworks for classifying mathematical errors in university students. This gap is especially critical in engineering education, where early and structured identification of mathematical mistakes can substantially impact teaching and learning effectiveness. In response, the present study proposes using the AHP to evaluate five theoretical frameworks and select the most appropriate one for developing a diagnostic instrument to identify and classify errors in first-year engineering students.

The need for this study arises from the annual repetition of the same mistakes made by first-semester engineering students in mathematics. This recurrence highlights a persistent problem in the teaching–learning process, leading teachers to feel the urgent need to intervene proactively by designing and implementing methodological strategies to mitigate this situation. In response to this problem, a comprehensive project has been proposed: “Development, implementation, and validation of a guide to the most frequent mathematical errors made by first-year engineering students at Universidad Politécnica Salesiana (UPS), Cuenca campus”. Although this initial exploratory study frequently refers to first-semester engineering students, they did not participate directly in this project phase. Instead, it will serve as the methodological basis for designing a diagnostic tool that will be applied to first-semester students in a subsequent phase of the project.

The main contributions of this study are as follows:

• To apply a structured and replicable AHP-based methodology for selecting theoretical frameworks in mathematics education.
• To identify the most appropriate classification model for diagnostic purposes in first-year engineering students.
• To provide a robust foundation for the future development of context-sensitive diagnostic tools and pedagogical intervention strategies.

This paper is organized as follows: Section 2 describes the adopted methodology and the application of the AHP model. Section 3 presents the analysis results, including visualizations and the final ranking. Section 4 discusses the findings in light of the reviewed literature. Finally, Section 5 presents the conclusions and outlines future research directions.

2. Materials and Methods

This section describes the procedures used to select and evaluate the criteria for categorizing mathematical errors. A detailed explanation of the methodological approach is provided, including the rationale behind choosing the Newman, Kastolan, Watson, Hadar, and Polya frameworks. The comparative evaluation was structured through a decision matrix, supplemented by a visual analysis using a radar chart to facilitate the comparison of the strengths and weaknesses of each framework. This approach offers a solid foundation for selecting the most appropriate criterion within the educational context of the Universidad Politécnica Salesiana, in Cuenca, Ecuador.

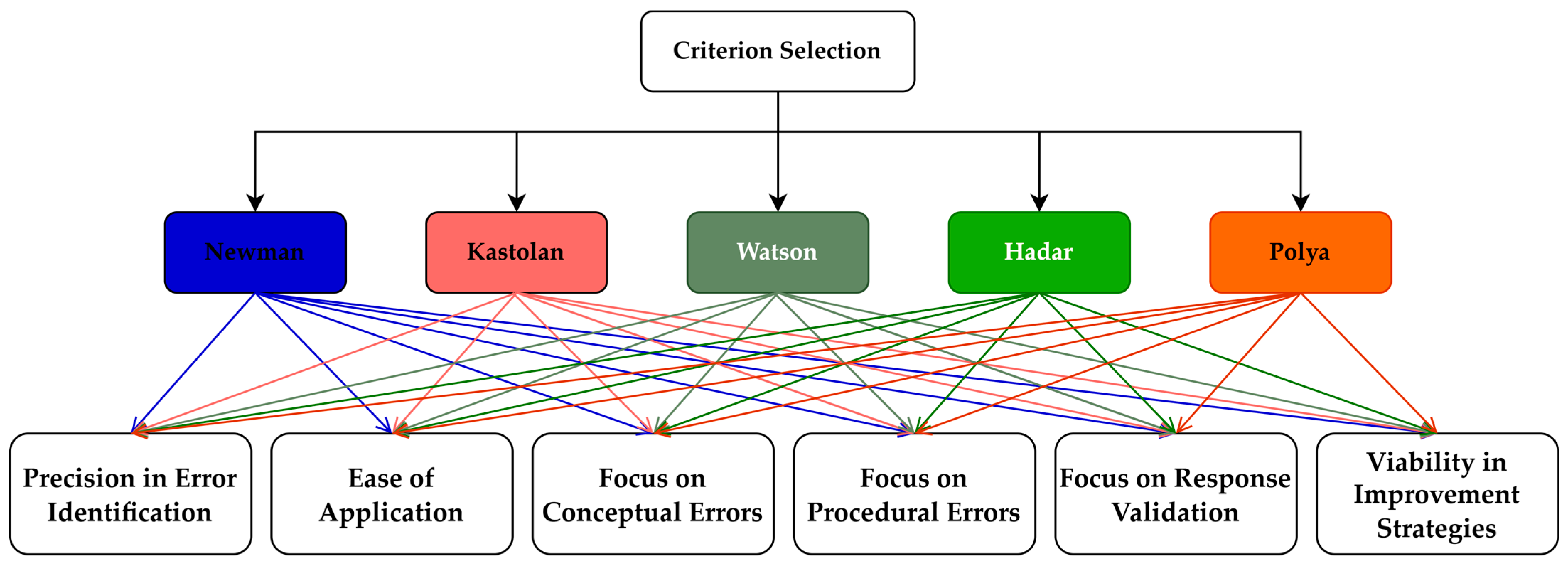
2.1. Criteria Selection and Justification

Various criteria and methodologies have been proposed to analyze mathematical errors, with the Newman Procedure being one of the most recognized. Developed in 1977 by Anne Newman, a renowned Australian mathematics educator (Noutsara et al., 2021), this procedure focuses on solving contextualized mathematical problems, also known as narrative or story-based problems (Arifin & Maryono, 2023). The Newman Procedure dissects the problem-solving process into five key stages: (1) reading errors, (2) comprehension errors, (3) transformation errors, (4) process skill errors, and (5) encoding errors (Nuryati et al., 2022). Each error type is associated with specific indicators that facilitate identifying and categorizing the most prevalent mistakes students make. These indicators help uncover students’ understanding and comprehension gaps and subsequent difficulties in correctly applying mathematical concepts. The classification of these errors is presented in

Table 1. Classification of mathematical errors according to the Newman criteria.

Error Type	Indicator of Error	Example
Reading error	Fails to identify key information in the problem	$\mathrm{A} \mathrm{train} \mathrm{leaves} \mathrm{station} A$$\mathrm{at} 3:00 \mathrm{p}.\mathrm{m}. \mathrm{and} \mathrm{arrives} \mathrm{at} \mathrm{station} B$$\mathrm{at} 5:00 \mathrm{p}.\mathrm{m}. \mathrm{Another} \mathrm{train} \mathrm{leaves} \mathrm{station} B$$\mathrm{at} 4:00 \mathrm{p}.\mathrm{m}. \mathrm{and} \mathrm{arrives} \mathrm{at} \mathrm{station} A$ at 6:00 p.m. At what time do the two trains cross paths? When reading the problem, the student does not correctly identify the departure and arrival times of the trains. He confuses the schedules and assumes that both trains leave at 3:00 p.m. and arrive at 6:00 p.m. Based on this incorrect information, he miscalculates that the trains cross at 4:30 p.m. (Arias Aristizábal, 2023)
	Incorrectly determines the known data	$\mathrm{The} \mathrm{student} \mathrm{confuses} \mathrm{the} \mathrm{independent} \mathrm{term} \mathrm{of} \mathrm{the} \mathrm{general} \mathrm{equation} \mathrm{of} \mathrm{the} \mathrm{line} 2x+3y+1=0$ as the ordinate to the origin (Saucedo, 2007).
	Uses self-created symbols without explaining their meaning	In a math problem, the task is to calculate the total construction cost of a building, knowing that the cost per square meter is 800,000 pesos and increases by 5% each year. The student writes the following expression: $\mathrm{“}C=\mathrm{800,000}\ast (1+0.05)^t\mathrm{”}$ $\mathrm{However}, \mathrm{the} \mathrm{student} \mathrm{does} \mathrm{not} \mathrm{explain} \mathrm{the} \mathrm{meaning} \mathrm{of} \mathrm{the} \mathrm{variables} \mathrm{“}C\mathrm{”}$$\mathrm{or} \mathrm{“}t\mathrm{”}$. Using these symbols without prior definition makes what they represent unclear, which could confuse the interpretation of the solution (Arroyo Valenciano, 2021).
Comprehension error	Responds incorrectly due to a lack of understanding or incomplete identification of problem elements	A water tank has a total capacity of 500 L. It currently holds 350 L. How long will the tank be full if water is added at 15 L per minute? The student incorrectly interprets what is to be solved. He assumes that he must calculate how long it takes to fill the tank from zero, ignoring that it already contains 350 liters (Winarso & Toheri, 2021).
	Writes a brief but unclear response, lacking sufficient argumentation when expressing what needs to be solved	A person has a rope 3 m long. He needs to cut the rope into 5 equal parts. How long will each part be? Student’s answer: Each part will be smaller than 3 m. The student writes something brief but unclear without providing a calculation or justifying his answer. He does not mention the necessary operation (division) or detail the procedure (Aksoy & Yazlik, 2017).
Transformation error	Inaccuracy in converting information into mathematical formulas	$\mathrm{It} \mathrm{poses} x(x+1)=y-2$ in the statement “A number plus its consecutive is equal to another minus 2”, erring in the conversion from natural language to mathematical language (Rodríguez-Domingo et al., 2015).
Process skill error	Error when using arithmetic operations	$\mathrm{The} \mathrm{student} \mathrm{poses} \mathrm{as} \mathrm{answer} \mathrm{the} \mathrm{sum} \mathrm{of} {\displaystyle \frac{7}{6}}+{\displaystyle \frac{1}{4}}+{\displaystyle \frac{3}{2}}$$: {\displaystyle \frac{11}{12}}$, adding numerators and denominators together (Booth et al., 2014).
	Incomplete procedures/steps	$\mathrm{In} \mathrm{the} \mathrm{equation} z(z^3+1)=0$$\mathrm{the} \mathrm{student} \mathrm{ignores} \mathrm{the} \mathrm{solution} z=0$$, \mathrm{posing} \mathrm{only} z^3+1=0$. (Agoiz, 2019)
Encoding error	Writing answers inappropriately	$\mathrm{In} \mathrm{the} \mathrm{equation} x^2-5x+6=0$$, \mathrm{the} \mathrm{student} \mathrm{obtains} \mathrm{the} \mathrm{solutions} x=3$$\mathrm{and} x=2$$; \mathrm{however}, \mathrm{he} \mathrm{indicates} \mathrm{that} \mathrm{the} \mathrm{roots} \mathrm{are} x=-3$$\mathrm{and} x=-2$. (Agoiz, 2019)
	Answers are not appropriate to the context	$\mathrm{In} \mathrm{an} \mathrm{analytical} \mathrm{geometry} \mathrm{problem}, \mathrm{the} \mathrm{student} \mathrm{is} \mathrm{asked} \mathrm{to} \mathrm{calculate} \mathrm{the} \mathrm{distance} \mathrm{between} \mathrm{points} A(2,3)$$\mathrm{and} B(5,7)$$\mathrm{in} \mathrm{the} \mathrm{Cartesian} \mathrm{plane}.$ $\mathrm{When} \mathrm{solving}, \mathrm{the} \mathrm{student} \mathrm{obtains} \mathrm{an} \mathrm{answer} \mathrm{of} d=-5$, which is inadequate because the distance between two points cannot be negative in any mathematical context (Checa & Martínez-Artero, 2010).
	Inaccurate or inconsistent conclusions	$\mathrm{The} \mathrm{student} \mathrm{is} \mathrm{asked} \mathrm{to} \mathrm{reduce} \mathrm{the} \mathrm{like} \mathrm{terms} \mathrm{of} \mathrm{the} \mathrm{expression} 3a-3b-3a+3b$$. \mathrm{The} \mathrm{student} \mathrm{concludes} \mathrm{that} \mathrm{the} \mathrm{result} \mathrm{is} 0a+0b$, an answer that makes no sense (Marpa, 2019).

, with accompanying examples for each error type. Including these examples is crucial, as they clarify the different error types, serving as a foundation for developing an evaluation tool based on the primary identified criteria. These examples significantly improve the precision of error identification, which will be indispensable in designing pedagogical strategies to address students’ specific needs. The primary contribution of the Newman criterion lies in its ability to reveal recurring error patterns during the problem-solving process (Arifin & Maryono, 2023). By identifying these patterns, errors can be corrected in real time and prevented by implementing targeted, proactive measures tailored to address students’ specific needs.

The Kastolan Criterion is widely acknowledged for its utility in analyzing mathematical errors, particularly in problems that are not of the narrative or contextual type (Suciati & Sartika, 2023). This criterion classifies errors into three main categories: conceptual, procedural, and technical (Mauliandri & Kartini, 2020). Conceptual errors refer to the incorrect application or misunderstanding of fundamental mathematical principles. These errors often stem from a lack of deep understanding of the underlying concepts, which may lead students to approach problems incorrectly. Procedural errors occur when students follow a correct sequence of steps but fail to correctly execute one or more parts of the procedure. These errors can be especially problematic in areas like algebra and calculus, where precise step-by-step reasoning is required. Technical errors are typically related to mechanical aspects of mathematics, such as incorrect arithmetic or improper notation. While these errors may seem trivial, they can significantly affect the final solution.

Each error type is associated with specific indicators that facilitate identification and analysis. This classification, summarized in

Table 2. Classification of mathematical errors according to the Kastolan criteria.

Error Type	Indicator of Error	Example
Conceptual Errors	Incorrect use of formulas or altered rules	$\mathrm{The} \mathrm{student} \mathrm{rewrites} {(4-x)}^2$$\mathrm{as} 16+x^2$$, \mathrm{incorrectly} \mathrm{modifying} \mathrm{the} \mathrm{special} \mathrm{product} \mathrm{rule} \mathrm{and} \mathrm{disregarding} \mathrm{the} \mathrm{middle} \mathrm{term}-8x$ (Agoiz, 2019).
	Selection of inappropriate formulas	The student uses the area formula to find the solution for the perimeter of a rectangle, failing to apply the correct perimeter formula.
Procedure Errors	Irregularity in problem-solving steps	$\mathrm{In} \mathrm{the} \mathrm{equation} x^2=16+y^2$$, \mathrm{the} \mathrm{student} \mathrm{isolates} \mathrm{the} \mathrm{variable} x$$\mathrm{by} \mathrm{individually} \mathrm{taking} \mathrm{each} \mathrm{term}’\mathrm{s} \mathrm{square} \mathrm{root} \mathrm{on} \mathrm{the} \mathrm{right-hand} \mathrm{side}, \mathrm{incorrectly} \mathrm{concluding} \mathrm{that} x=4+y$. (Agoiz, 2019).
	Inability to simplify	The given problem states that the sum of the first and the second numbers exceeds the third by two units; the second minus twice the first is ten units less than the third; and the sum of all three numbers is 24. The task is to determine the three numbers. The student sets up a 3 × 3 system of equations and solves it using Gaussian elimination, although a simple substitution method would suffice (Checa & Martínez-Artero, 2010).
	Interruption of the resolution process	$\mathrm{The} \mathrm{equation} 2x^2-6x=3$$\mathrm{is} \mathrm{presented} \mathrm{for} \mathrm{resolution}. \mathrm{The} \mathrm{student} \mathrm{correctly} \mathrm{completes} \mathrm{the} \mathrm{steps} \mathrm{and} \mathrm{obtains} \mathrm{the} \mathrm{solution} x={\displaystyle \frac{6\pm \sqrt{60}}{4}}$, but fails to simplify the final expression further (Pianda, 2018).
Technical Errors	Calculation errors	$\mathrm{In} \mathrm{the} \mathrm{equation} \sqrt{\sqrt[3]{5}}=\sqrt[5]{5}$, the student incorrectly adds the indices of the roots, leading to an invalid operation (Agoiz, 2019).
	Errors in notation or writing	$\mathrm{In} \mathrm{the} \mathrm{equation} -x-1=2y-6$$, \mathrm{the} \mathrm{student} \mathrm{incorrectly} \mathrm{rewrites} \mathrm{the} \mathrm{term} 2y$$\mathrm{and} \mathrm{reformulates} \mathrm{the} \mathrm{equation} \mathrm{as} -x+2y+5=0$, introducing an erroneous sign change (Agoiz, 2019).
	Inadequate substitution of values	$\mathrm{The} \mathrm{task} \mathrm{is} \mathrm{to} \mathrm{solve} \mathrm{the} \mathrm{equation} 3+\sqrt[3]{8x+1}=5$$. \mathrm{The} \mathrm{student} \mathrm{assumes} x=1$ and substitutes it incorrectly into the equation, leading to an invalid result (Caronía et al., 2008)

, offers valuable insights into common student mistakes, enabling educators to pinpoint areas where intervention may be necessary.

(Sari & Pujiastuti, 2022) emphasize the need for a comprehensive approach to reinforcing mathematical concepts and procedures in the classroom. By addressing these errors at their root, instructors can help enhance students’ overall mathematical competence and prevent the recurrence of these errors, often indicative of deeper learning gaps.

On the other hand, Watson, a psychologist known for his stimulus–response approach, developed a criterion aimed at facilitating the identification of specific errors in mathematical reasoning processes (Buhaerah et al., 2022). This approach, known as Watson’s Criterion, is used in the analysis of errors in solving mathematical problems and classifies these errors into eight main categories: (1) inadequate data, (2) inadequate procedures, (3) omitted data, (4) omitted conclusions, (5) conflicts at the response level, (6) undirected manipulation, (7) issues with the hierarchy of skills, and (8) errors outside these categories. While this criterion provides a clear structure for classification, its application may introduce elements of subjectivity (Musa et al., 2021).

Table 3. Classification of mathematical errors according to the Watson criteria.

Error Type	Indicator of Error	Example
Inappropriate Data	Data does not match.	$\mathrm{The} \mathrm{student} \mathrm{applies} {\left(a+b\right)}^2=a^2+b^2$$\mathrm{to} \mathrm{expand} {\left(x+3\right)}^2$, a common error in basic algebra (Booth et al., 2013)
	Misplaced data on the variable	$\mathrm{The} \mathrm{student} \mathrm{substitutes} x=3$$\mathrm{into} \mathrm{the} \mathrm{equation} y=2x+1$$\mathrm{and} \mathrm{calculates} y=2\left(4\right)+1=9$$, \mathrm{but} \mathrm{mistakenly} \mathrm{inputs} x=4$$\mathrm{leading} \mathrm{to} \mathrm{the} \mathrm{incorrect} \mathrm{calculation} \mathrm{of} y=9$ (Siegler & Lortie-Forgues, 2015).
	Assigns known data to incorrect variables	$\mathrm{The} \mathrm{student} \mathrm{treats} \mathrm{the} \mathrm{constant} \mathrm{term} \mathrm{as} \mathrm{if} \mathrm{it} \mathrm{were} \mathrm{the} \mathrm{coefficient} \mathrm{of} x$$\mathrm{in} 2x+5=0,$$\mathrm{incorrectly} \mathrm{solving} \mathrm{it} \mathrm{as} \mathrm{if} \mathrm{the} \mathrm{equation} \mathrm{were} 5x=0$ (Booth et al., 2013)
Inappropriate Procedure	Using the wrong formula	$\mathrm{The} \mathrm{student} \mathrm{attempts} \mathrm{to} \mathrm{solve} x^2-4=0$$\mathrm{using} \mathrm{the} “\mathrm{completing} \mathrm{the} \mathrm{square}” \mathrm{method} \mathrm{but} \mathrm{incorrectly} \mathrm{adds} \mathrm{a} \mathrm{term}: x^2+4x+4=4+4x+4$$\Rightarrow {\left(x+2\right)}^2=12$ (Ningsih & Retnowati, 2020).
	Do not write down the steps when solving problems	$\mathrm{The} \mathrm{student} \mathrm{introduces} \mathrm{an} \mathrm{unnecessary} \mathrm{multiplication} \mathrm{step} \mathrm{in} (x+2)(x-2)$$, \mathrm{writing}(x+2)(x-2)\cdot 1=x^2-4$, without providing justification. (Barbosa & Vale, 2021).
	Skipping essential steps	$\mathrm{The} \mathrm{student} \mathrm{omits} \mathrm{calculating} \mathrm{the} \mathrm{discriminant} \mathrm{before} \mathrm{applying} \mathrm{the} \mathrm{quadratic} \mathrm{formula} \mathrm{in} a{x}^2+bx+c=0$, which leads to incorrect conclusions about the nature of the solutions (Booth et al., 2013).
Missing Data	Omission of given data	$\mathrm{The} \mathrm{student} \mathrm{omits} \mathrm{the} \mathrm{constant} \mathrm{term} c$ $\mathrm{in} \mathrm{the} \mathrm{quadratic} \mathrm{equation} a{x}^2+bx+c=0$$, \mathrm{solving} \mathrm{it} \mathrm{as} \mathrm{if} c=0$, which leads to incorrect conclusions about the solutions (Siegler & Lortie-Forgues, 2015).
Omitted Conclusion	Fails to use the obtained data to draw conclusions	$\mathrm{The} \mathrm{student} \mathrm{finds} \mathrm{the} \mathrm{solutions} x=2$$\mathrm{and} x=-2$$\mathrm{for} x^2=4$$, \mathrm{but} \mathrm{fails} \mathrm{to} \mathrm{determine} \mathrm{which} \mathrm{solution} \mathrm{satisfies} \mathrm{the} \mathrm{context} \mathrm{of} \mathrm{the} \mathrm{problem} (\mathrm{e}.\mathrm{g}, x>0$) (Ningsih & Retnowati, 2020).
Response Level Conflict	Lack of readiness during the process	$\mathrm{The} \mathrm{student} \mathrm{obtains} \mathrm{a} \mathrm{value} \mathrm{of} x=-5$ or a length but fails to justify whether this solution should be accepted or discarded, neglecting to consider the contextual constraints of the problem. (Barbosa & Vale, 2021).
Indirect Manipulation	Application of arbitrary reasoning	$\mathrm{The} \mathrm{student} \mathrm{switches} \mathrm{between} \mathrm{factorization} \mathrm{methods} \mathrm{in} x^2+5x+6=0$ (Ningsih & Retnowati, 2020). $\mathrm{The} \mathrm{student} \mathrm{begins} \mathrm{solving}: x^2+5x+6=0$$\Rightarrow \left(x+2\right)\left(x-3\right)=0$ but interrupts the process, possibly due to uncertainty about the solution, and switches to completing the square method. They rewrite the equation as $x^2+5x+\left(missing term\right)=-6$ $\mathrm{To} \mathrm{complete} \mathrm{the} \mathrm{square}, \mathrm{the} \mathrm{student} \mathrm{adds} {\left({\displaystyle \frac{5}{2}}\right)}^2={\displaystyle \frac{25}{4}}$ to both sides, resulting in $x^2+5x+{\displaystyle \frac{25}{4}}=-6+{\displaystyle \frac{25}{4}}$ However, they simplify the right-hand side incorrectly, leading to an incorrect expression. This behavior exemplifies arbitrary reasoning and a lack of procedural consistency. The student alternates between methods without properly executing them, leading to repeated errors and unresolved confusion.
Skill Hierarchy Problem	Confusion in applying the hierarchy of mathematical operations	$\mathrm{The} \mathrm{student} \mathrm{incorrectly} \mathrm{solves} 3+5\times 2$$\mathrm{as} \left(3+5\right)\times 2=16$$, \mathrm{instead} \mathrm{of} \mathrm{applying} \mathrm{the} \mathrm{correct} \mathrm{order} \mathrm{of} \mathrm{operations} \mathrm{and} \mathrm{calculating} \mathrm{multiplication} \mathrm{first}, \mathrm{which} \mathrm{would} \mathrm{yield} 3+10=13$ (Sidney & Alibali, 2015)
Above Other	Inappropriate reformulation of the question	$\mathrm{The} \mathrm{student} \mathrm{attempts} \mathrm{to} \mathrm{solve} 3x-4=11$$\mathrm{but} \mathrm{incorrectly} \mathrm{reformulates} \mathrm{the} \mathrm{equation} \mathrm{as} 3x=11-4$$. \mathrm{While} \mathrm{solving}, \mathrm{they} \mathrm{write} x={\displaystyle \frac{11}{3}}-4$, improperly combining operations and leading to an incorrect result. (Booth et al., 2014)
	Omission of the response	$\mathrm{Given} \mathrm{the} \mathrm{problem} “\mathrm{Solve} \mathrm{the} \mathrm{equation} 4x+7=19$$”, \mathrm{the} \mathrm{student} \mathrm{correctly} \mathrm{follows} \mathrm{the} \mathrm{steps}: 4x=19-7$$; 4x=12$$; \mathrm{and} x=12/4$$. \mathrm{However}, \mathrm{they} \mathrm{fail} \mathrm{to} \mathrm{write} \mathrm{the} \mathrm{final} \mathrm{result} x=3$ as the solution, leaving the work incomplete without an explicit answer. (Lee et al., 2011)
	Disordered or inconsistent solution to the question	$\mathrm{The} \mathrm{student} \mathrm{simplifies} {\displaystyle \frac{6x^2+12x}{6x}}$$\mathrm{incorrectly} \mathrm{by} \mathrm{dividing} \mathrm{only} \mathrm{the} \mathrm{numerator} \mathrm{by} 6x$$, \mathrm{resulting} \mathrm{in} x+2x$$, \mathrm{and} \mathrm{presents} 3x$$\mathrm{as} \mathrm{the} \mathrm{final} \mathrm{answer}, \mathrm{which} \mathrm{does} \mathrm{not} \mathrm{match} \mathrm{the} \mathrm{correct} \mathrm{result} \mathrm{of} x+2$ (Mulungye, 2016)

summarizes the types of errors, their indicators, and representative examples. According to (Buhaerah et al., 2022) mathematical errors may vary depending on students’ predominant learning style, whether visual, auditory, or kinesthetic. This finding highlights the importance of adapting educational strategies to meet students’ individual needs to mitigate such errors. Similarly, (Rosita & Novtiar, 2021) recommend reinforcing fundamental concepts and providing more structured practices and exercises to reduce the incidence of mathematical errors.

Similarly, Hadar’s Criterion for the classification of mathematical errors was developed by Hadar, Zaslavsky, and Inbar in 1987 as an empirical model to categorize errors in mathematics at the secondary education level in Israel (Ganesan & Dindyal, 2014). This criterion identifies six types of errors that students may make when solving mathematical problems: (1) errors in data usage, (2) errors in language usage, (3) errors in the use of logic to conclude, (4) errors in the use of definitions or theorems, (5) errors due to failure to review the solution, and (6) technical errors (Fauzan & Minggi, 2024). The errors related to data usage occur when students fail to exactly copy or record the data given in the problem, as illustrated in

Table 4. Classification of mathematical errors according to the Hadar criteria.

Error Type	Indicator of Error	Example
Misused data	The student does not exactly copy data from the problem	In the problem: In 2020, the cow population in City A was 1600, and in City B, it was 500. Each month, the population in City A increases by 25, and in City B by 10. At some point, the population in City A triples that of City B. Determine the population of cows in City A at that moment. For this problem, the student records $I=\begin{array}{cc}A& B\\ 1600& 500\end{array}$ $A=1600 1625 1650$ $B=500 510 520 530 540 550$ Instead of correctly identifying the following: Initial population in City A: 1600. Initial population in City B: 500. Monthly increase in City A: 25. Monthly increase in City B: 10. The student failed to accurately record any required data from the problem and did not create an appropriate mathematical model (Fauzan & Minggi, 2024).
	Students add data that is not appropriate.	$\mathrm{The} \mathrm{student} \mathrm{rewrites} x^2-5x+6=0$$\mathrm{as} x^2-5x+6+y=0,$ $\mathrm{adding} \mathrm{an} \mathrm{unnecessary} \mathrm{term} y$ without justification (Ningsih & Retnowati, 2020).
	Ignores the data provided	$\mathrm{Students} \mathrm{fail} \mathrm{to} \mathrm{recognize} \mathrm{that} -\log 2$$\mathrm{and} \mathrm{ }\log {\displaystyle \frac{1}{2}}$ are equivalent (Ganesan & Dindyal, 2014)
	States a condition that is not needed	$\mathrm{To} \mathrm{verify} \mathrm{if} \mathrm{point} P(2,3)$ $\mathrm{lies} \mathrm{on} \mathrm{the} \mathrm{line} y=2x+1$$, \mathrm{the} \mathrm{student} \mathrm{unnecessarily} \mathrm{calculates} \mathrm{the} \mathrm{slope} \mathrm{of} \mathrm{the} \mathrm{line} \mathrm{through} \mathrm{the} \mathrm{origin} \mathrm{and} P$ and compares it with the given line’s slope (Mallart Solaz, 2014).
	Interpreting information that does not follow the actual text	$\mathrm{Students} \mathrm{assume} \mathrm{that} -\log {\displaystyle \frac{3}{4}}$ is a negative number. (Ganesan & Dindyal, 2014).
	Replacing the specified conditions with other inappropriate information	$\mathrm{For} \mathrm{the} \mathrm{problem} \mathrm{of} \mathrm{finding} \mathrm{the} \mathrm{equation} \mathrm{of} \mathrm{a} \mathrm{line} \mathrm{parallel} \mathrm{to} y=2x+3$$\mathrm{passing} \mathrm{through} P(1,4)$, the student unnecessarily assumes the line must also be perpendicular to another line instead of using the given slope (Mallart Solaz, 2014).
	Using the value of a variable for another variable	For the equation ${\left[{\log }_{5x-2}\left(x^2-8\right)\right]}^2-{\log }_{5x-2}\left(x^2-8\right)=0$ $\mathrm{the} \mathrm{student} \mathrm{assumes} y={\log }_{5x-2}\left(x^2-8\right)$, transforming it into $y^2-y=0$$⟹ y(y-1)=0$ $\mathrm{Solving} \mathrm{for} y$$, \mathrm{they} \mathrm{find} y=0$$\mathrm{and} y=1$$\mathrm{and} \mathrm{then} \mathrm{substitute} y=5x-2$$, \mathrm{leading} \mathrm{to} x={\displaystyle \frac{2}{5}}$$\mathrm{and} x={\displaystyle \frac{3}{5}}$. This demonstrates the misuse of one variable as another (Rafi & Retnawati, 2018).
Misinterpreted language	Students’ mistakes in translating mathematical symbols into everyday language	$\mathrm{To} \mathrm{solve} \mathrm{the} \mathrm{expression} 3a+2b$ $\mathrm{under} \mathrm{specific} \mathrm{conditions} \mathrm{by} \mathrm{assigning} \mathrm{numerical} \mathrm{values} \mathrm{to} a$$\mathrm{and} b$$, \mathrm{some} \mathrm{students} \mathrm{misinterpret} a$$\mathrm{and} b$$\mathrm{as} \mathrm{abbreviations} \mathrm{for} \mathrm{words} (\mathrm{e}.\mathrm{g}., a$$\mathrm{for} “\mathrm{animals}” \mathrm{and} b$ for “bags”) instead of treating them as mathematical variables. (Bolaños-González & Lupiáñez-Gómez, 2021).
	Writing symbols of a concept with other symbols that have different meanings	In inequalities, students confuse the meaning of the greater than (>) and less than (<) signs. (Huynh & Sayre, 2019).
Logically invalid inference	Mistakes are made when drawing incorrect conclusions from a problem	$\mathrm{While} \mathrm{expanding} \mathrm{the} \mathrm{binomial} {\left(x{y}^2+z^2\right)}^3$$\mathrm{the} \mathrm{student} \mathrm{incorrectly} \mathrm{writes} \mathrm{the} \mathrm{result} \mathrm{as} a^3{b}^5+b^5{a}^3{y}^5+b^5{y}^5$. $\mathrm{This} \mathrm{error} \mathrm{is} \mathrm{classified} \mathrm{as} \mathrm{a} \mathrm{reasoning} \mathrm{mistake}, \mathrm{as} \mathrm{the} \mathrm{student} \mathrm{introduces} \mathrm{variables} (a$$\mathrm{and} b$) that are not part of the original problem (Pazos & Salinas, 2012).
Distorted theorem or definition	Errors occur when students incorrectly apply formulas, theorems, or definitions that do not align with the problem.	$\mathrm{In} \mathrm{the} \mathrm{problem} {\log }_{25}5$$, \mathrm{the} \mathrm{student} \mathrm{attempts} \mathrm{to} \mathrm{apply} \mathrm{the} \mathrm{rule} {\log }_{a}a=1$$\mathrm{but} \mathrm{incorrectly} \mathrm{computes} {\log }_{5^2}5=2$. This error reflects a misapplication of logarithmic properties (Ganesan & Dindyal, 2014).
Unverified solution	Errors arise when students fail to verify each step against the final result, often because they rush through the problem without reviewing their work.	$\mathrm{For} \mathrm{the} \mathrm{equation} {\log }_x\left(2x+15\right)=2$$, \mathrm{the} \mathrm{student} \mathrm{accepts} x=5\mathrm{ }$$\mathrm{and} x=-3$, as solutions without verifying their validity (Ganesan & Dindyal, 2014).
Technical error	Calculation errors	$\mathrm{The} \mathrm{student} \mathrm{solves} 900+10n=3(1600+25n)$$\mathrm{and} \mathrm{obtains} n=20$$\mathrm{However}, \mathrm{the} \mathrm{correct} \mathrm{operation} \mathrm{yields} n=60$$, \mathrm{not} n=20$ (Fauzan & Minggi, 2024).
	Errors in quoting data	In the problem: In 2020, the cow population in City A was 1600, and in City B, it was 500. Each month, the population in City A increases by 25, and in City B by 10. At some point, the population in City A triples that of City B. Determine the population of cows in City A at that moment. The student records the data as (Fauzan & Minggi, 2024) $I=\begin{array}{cc}A& B\\ 1600& 500\end{array}$ $A=1600 1625 1650$ $B=500 510 520 530 540 550$ Instead of correctly applying the formula ${UA}_n=1600+(n-1)25$
	Errors in manipulating symbols	$\mathrm{The} \mathrm{student} \mathrm{formulates} \left(n-1\right)25=25n+25$ incorrectly (Fauzan & Minggi, 2024).

. For example, in a situation involving population growth in two cities, the student may incorrectly record the given data, such as mixing up values or omitting essential information, leading to confusion during problem-solving. The errors in language usage typically involve misinterpretation or improper use of mathematical terminology, which may result in incorrect problem formulation. In terms of logical reasoning, students may fail to draw proper inferences based on the given conditions of the problem, leading to faulty conclusions. Other errors may stem from misapplication of definitions or theorems, such as using an incorrect formula for area or volume.

The error analysis proposed by Hadar is particularly suitable for identifying students’ mistakes when solving contextualized mathematical problems. According to Hadar, errors may be influenced by key mathematical skills such as conceptual understanding, reasoning, connections, and mathematical communication (Suciati & Sartika, 2023).

Problem-solving is a fundamental skill that every student must master (Hadi & Radiyatul, 2014). One of the most recognized and widely used methods for teaching this skill is the one developed by George Polya, a distinguished 20th-century mathematics professor (Sukayasa, 2012). Polya proposed a structured problem-solving model consisting of four steps: (1) understand the problem, (2) devise a plan, (3) carry out the plan, and (4) look back (Winarso & Toheri, 2021).

This approach has been effectively used to analyze and classify mathematical errors. Errors in the first two phases of Polya’s model typically reflect conceptual difficulties and problems in understanding the mathematical fundamentals. In the third phase, errors are related to failures in processes and algorithms, while in the final phase, errors arise from a lack of review and verification of the obtained solutions (Suharti et al., 2021). According to Sulistyaningsih et al., the types of errors, organized by frequency, include reading, comprehension, transformation, process skill, and coding errors. (Sulistyaningsih et al., 2021).

Table 5. Classification of mathematical errors according to the Polya criteria.

Afgan wants to visit a total of 24 beaches with his three friends (Boy, Mondy, and Reva). Afgan can only take two friends per day. During the visits: Boy and Mondy visited 6 beaches together. Boy and Reva visited 4 beaches together. Mondy and Reva visited 8 beaches together. Determine how many beaches each friend visited using a linear system of three variables.
Error Type	Indicator of Error	Example
Understanding the problem	Students need to specify and identify what information is known, ask about the problem, and restate it in their own language.	$\mathrm{While} \mathrm{solving} \mathrm{the} \mathrm{problem}, \mathrm{the} \mathrm{student} \mathrm{incorrectly} \mathrm{writes} \mathrm{the} \mathrm{equations} \mathrm{as} a+b=6$$; a+c=4$$\mathrm{and} b+c=8$$, \mathrm{when} \mathrm{they} \mathrm{should} \mathrm{actually} \mathrm{be}: a+b-c=6$$; a+c-b=4$$\mathrm{and} b+c-a=8$.
Devising a plan	Students create a mathematical model, select an appropriate strategy that will be used, make estimates, and reduce things that are not related to the problem.	$\mathrm{The} \mathrm{student} \mathrm{attempts} \mathrm{to} \mathrm{represent} \mathrm{the} \mathrm{time} \mathrm{three} \mathrm{people} \mathrm{spend} \mathrm{visiting} \mathrm{beaches} \mathrm{using} \mathrm{variables} \mathrm{but} \mathrm{incorrectly} \mathrm{writes} {\displaystyle \frac{24}{x}}$ for each case, failing to relate it to the problem’s conditions.
Carrying out the plan	Students implement the plans and strategies chosen and arrange to solve the problem.	The number of beaches Boy visited in a day: $24 \mathrm{beaches} = x$ days $24 \mathrm{beaches} = x·1$ days ${\displaystyle \frac{24}{x}}$$\mathrm{beaches} = {\displaystyle \frac{x}{x}}$$\mathrm{days} = {\displaystyle \frac{24}{x}}$ days $\mathrm{The} \mathrm{student} \mathrm{incorrectly} \mathrm{assumes} \mathrm{that} x$ can be canceled on both sides without justification, leading to an erroneous result.
Looking back	Students review the solutions and results obtained from the problem-solving steps to avoid errors in their answers.	$\mathrm{After} \mathrm{solving} \mathrm{the} \mathrm{system} \mathrm{of} \mathrm{linear} \mathrm{equations}, \mathrm{the} \mathrm{student} \mathrm{fails} \mathrm{to} \mathrm{verify} \mathrm{whether} \mathrm{the} \mathrm{values} \mathrm{obtained} \mathrm{for} x, y$$, \mathrm{and} z$ satisfy the initial equations.

presents a detailed description of these steps and their application in identifying and analyzing mathematical errors. One example is used for this purpose. Polya’s model helps analyze students’ errors when solving contextualized or narrative-type problems (Suciati & Sartika, 2023). (Wiyah & Nurjanah, 2021) found that students make errors when modifying sentences into variables and creating mathematical models, highlighting the relevance of Polya’s approach to improving mathematics teaching and learning.

To determine which of the five criteria best suits the context of the Universidad Politécnica Salesiana, a multicriteria evaluation was conducted using the Analytic Hierarchy Process (AHP) described below.

2.2. Multicriteria Evaluation Procedure Using the Analytic Hierarchy Process (AHP)

This study adopts a quantitative approach with a multicriteria strategy, employing the Analytic Hierarchy Process (AHP) to select the most appropriate framework for classifying mathematical errors made by first-year engineering students. The objective is to develop an assessment instrument grounded in a rigorous theoretical review to identify, categorize, and pedagogically address the detected errors and deficiencies in mathematical competencies that hinder the teaching–learning process.

The methodological procedure was developed following the hierarchical logic of the Analytic Hierarchy Process (AHP) proposed by (Saaty, 2008), which has been widely applied in research on evaluation and complex decision-making in education (Alonso & Lamata, 2006; Anis & Islam, 2015; Gamboa-Cruzado et al., 2024; Ishizaka & Labib, 2011). It was structured into three hierarchical levels: the overall objective (selecting the optimal framework for error classification according to the study’s aims), the evaluation criteria, and the alternatives, which correspond to five theoretical approaches to the classification of mathematical errors: Newman, Kastolan, Watson, Hadar, and Polya. This process is visually summarized in Figure 1.

Additionally, Figure 2 presents the detailed methodological flow of the AHP used in this study, from the problem definition to the final ranking output.

The definition of the evaluation criteria represents a critical step in the methodology, as these criteria determine the aspects by which the alternatives will be assessed. Unlike traditional approaches that select criteria either directly or based solely on theoretical grounds, this study developed a multicriteria decision matrix that provides an objective basis for choosing the six subcriteria considered. To this end, the five aforementioned frameworks were analyzed by breaking each one down into its corresponding types of errors, which were then evaluated through six key dimensions: precision in error identification, ease of application, focus on conceptual errors, focus on procedural errors, focus on response validation, and viability in improvement strategies.

Based on this analysis, a qualitative matrix was constructed with textual descriptions in each cell, incorporating pedagogical evidence, teaching experience, and bibliographic references. To facilitate its integration into the AHP model, these descriptions were translated into a quantitative scale ranging from 1 to 5, supported by a semantic coding system based on the criteria detailed in

Table 6. Qualitative decision matrix.

Quantitative Value	Interpretation	Key Textual Indicators
5	High clarity, evidence, or applicability	“easy to identify”, “very easy”, “directly”, “evident”, “quickly recognized”
4	High, but with minor potential for confusion	“may be confused with…”, “quick but not direct”, “requires minimal analysis”
3	Moderate clarity or applicability; requires interpretation	“possibility of confusion”, “depends on the student”, “for the same reason”, “somewhat subjective”
2	Low clarity or applicability, though still identifiable	“difficult to identify”, “requires detailed analysis”, “not so clear”
1	Absent, not validated, or difficult to detect or apply	“not verified”, “not applicable”, “not focused”, “very difficult”, “unrelated to the concept”

:

This quantitative scale transformed the descriptive matrix into a numerical structure suitable for multicriteria analysis, resulting in a consolidated table of average scores by criterion and framework (see

Table 7. Decision matrix for selecting the most appropriate mathematical error classification criterion.

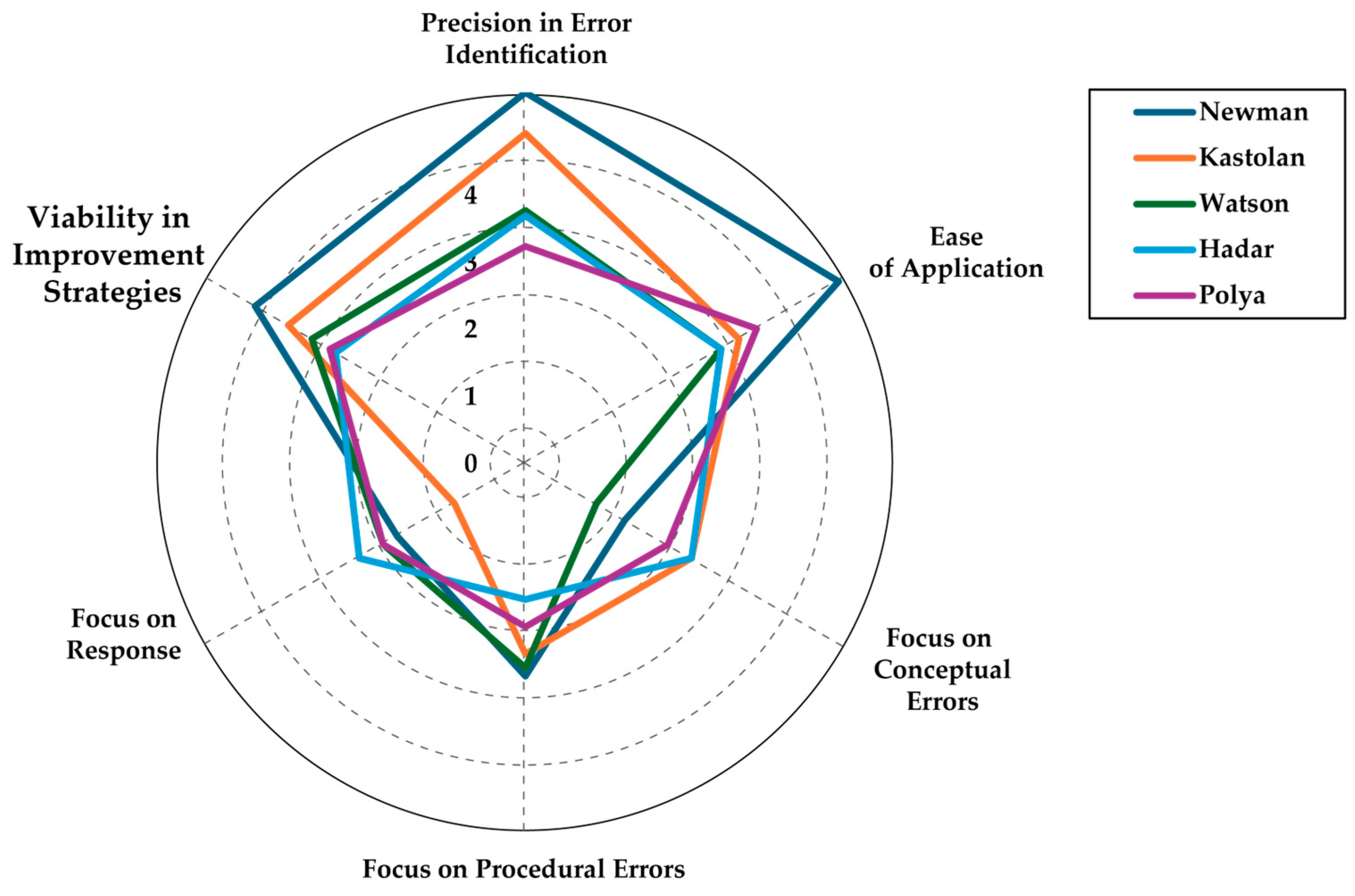
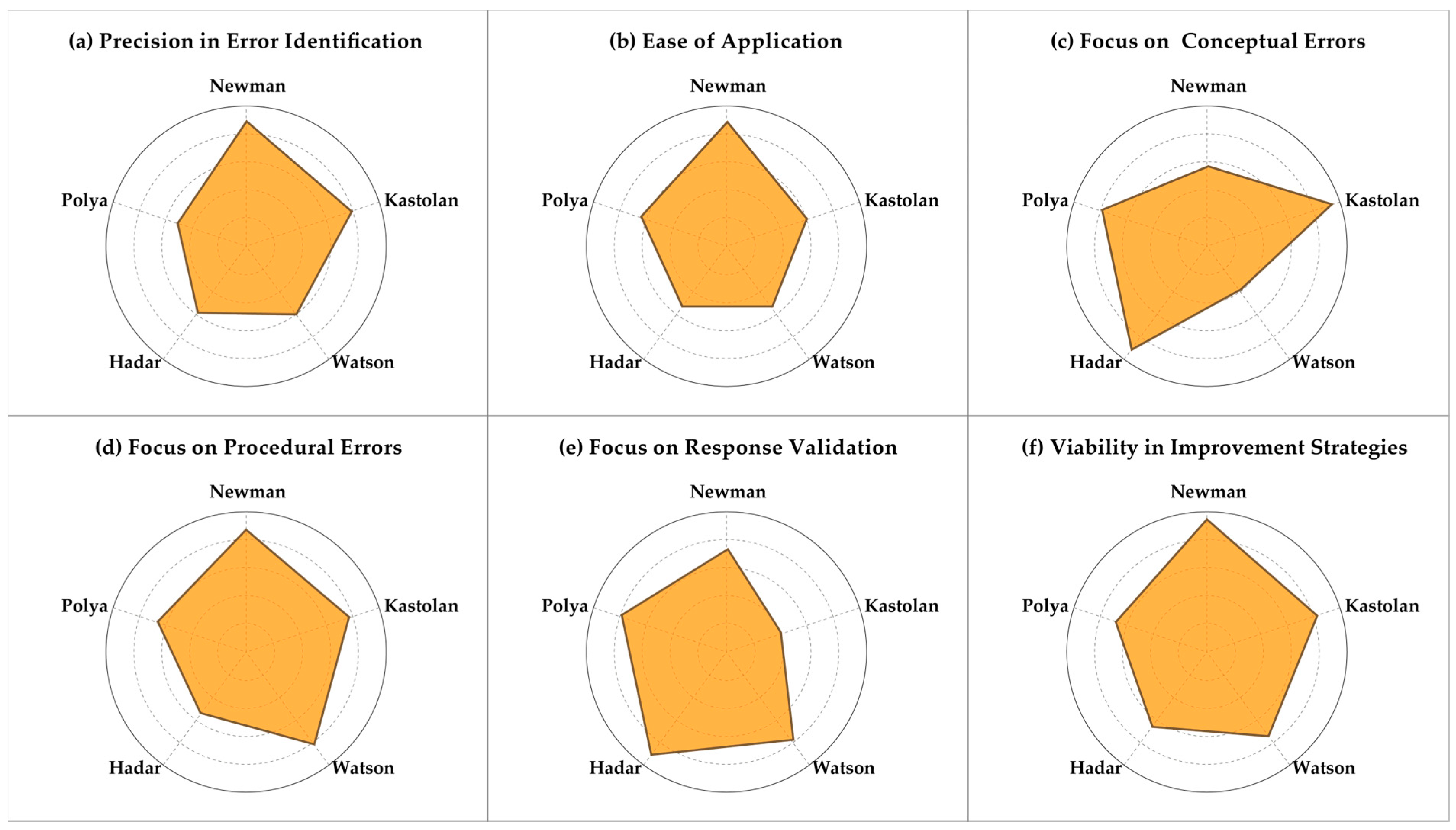
Criterion	Precision in Error Identification	Ease of Application	Focus on Conceptual Errors	Focus on Procedural Errors	Focus on Response Validation	Viability in Improvement Strategies	Average
Newman	4.5	4.4	1.4	1.8	1.8	3.8	3.1
Kastolan	4.0	3.0	2.3	2.3	1.0	3.3	2.7
Watson	3.1	2.8	1.0	2.5	2.0	3.0	2.4
Hadar	3.0	2.8	2.3	1.7	2.3	2.7	2.5
Polya	2.6	3.3	2.0	2.0	2.0	2.8	2.4

). A panel of five experts in mathematics education and engineering instruction was consulted to establish these scores. They all had over ten years of university-level teaching experience and had worked extensively with first-year engineering students. Among the participants, two held master’s degrees in mathematics education, while the remaining three were engineers with graduate studies in mathematics-related fields applied to engineering.

Each expert participated individually by completing a structured digital questionnaire in which they compared the five frameworks using six pedagogical criteria previously defined: (i) precision in error identification, (ii) ease of application, (iii) focus on conceptual errors, (iv) focus on procedural errors, (v) response validation, and (vi) viability for informing instructional improvement strategies.

The comparisons were made using Saaty’s fundamental scale of relative importance (ranging from 1 to 9). Each expert assigned scores based on their professional judgment, and the final values used in the matrix were calculated as the arithmetic mean for each cell. This grading process ensured a transparent and reproducible evaluation methodology. Additionally, responses were anonymized and processed in aggregate form to minimize potential group bias.

The decision to work with five experts aligns with methodological recommendations found in the specialized literature on the AHP in educational contexts, where the quality and diversity of expert judgment are prioritized over sample size, especially in exploratory or methodological studies (Hester & Bachman, 2009; Ishizaka & Labib, 2011). These authors suggest that between three and seven experts are sufficient, provided that (a) the participants are representative of the field, (b) logical consistency in judgments is achieved (consistency ratio, CR < 0.1), and (c) the selection process is justified correctly. In this study, all these criteria were satisfactorily fulfilled, ensuring the validity and rigor of the results obtained.

Once the key frameworks and dimensions were defined, a pairwise comparison matrix $A=\left[a_{ij}\right]$ was constructed using Saaty’s 1-to-9 scale. In this matrix, the element $a_{ij}$ represents the relative importance of criterion $i$ concerning criterion $j$, based on expert judgment from university faculty. The matrix is reciprocal, meaning that $a_{ji}=1/a_{ij}$ and $a_{ii}=1$. The resulting pairwise comparison matrix is presented in

Table 8. Pairwise comparison matrix ($A$).

Criterion	Precision in Error Identification	Ease of Application	Focus on Conceptual Errors	Focus on Procedural Errors	Focus on Response Validation	Viability in Improvement Strategies
Precision in Error Identification	1	7	8	2	9	3
Ease of Application	1/7	1	2	1/5	5	1/5
Focus on Conceptual Errors	1/8	1/2	1	1/7	3	1/7
Focus on Procedural Errors	1/2	5	7	1	7	2
Focus on Response Validation	1/9	1/5	1/3	1/7	1	1/8
Viability in Improvement Strategies	1/3	5	7	1/2	8	1

.

To obtain the weights of each criterion, the matrix was normalized by dividing each element by the sum of its corresponding column (Equation (1)). The priority vector ($w$) was then calculated by averaging each row of the normalized matrix (Equation (2)). The results are presented in

Table 9. Normalized matrix.

Criterion	Precision in Error Identification	Ease of Application	Focus on Conceptual Errors	Focus on Procedural Errors	Focus on Response Validation	Viability in Improvement Strategies	$\mathbf{Priority} \mathbf{Vector} \left(\mathit{w}\right)$
Precision in Error Identification	0.4520	0.3743	0.3158	0.5018	0.2727	0.4638	0.3967
Ease of Application	0.0646	0.0535	0.0789	0.0502	0.1515	0.0309	0.0716
Focus on Conceptual Errors	0.0565	0.0267	0.0395	0.0358	0.0909	0.0221	0.0453
Focus on Procedural Errors	0.2260	0.2674	0.2763	0.2509	0.2121	0.3092	0.2570
Focus on Response Validation	0.0502	0.0107	0.0132	0.0358	0.0303	0.0193	0.0266
Viability in Improvement Strategies	0.1507	0.2674	0.2763	0.1254	0.2424	0.1546	0.2028

.

$$a_{ij}^{\prime }={\displaystyle \frac{a_{ij}}{{\sum }_{i=1}^n{a}_{ij}}}$$

(1)

$$w_i={\displaystyle \frac{1}{n}}\sum _{j=1}^n{a}_{ij}^{\prime }$$

(2)

Subsequently, the AHP consistency check was applied to ensure the validity of the model by calculating the maximum eigenvalue ${\lambda }_{max}$ using Equation (3):

$${\lambda }_{max}={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\displaystyle \frac{{(A·w)}_i}{w_i}}$$

(3)

Then, the consistency index $\left(CI\right)$ and the consistency ratio $\left(CR\right)$ were calculated, as defined by Equations (4) and (5), respectively:

$$CI={\displaystyle \frac{{\lambda }_{max}-n}{n-1}}$$

(4)

$$CR={\displaystyle \frac{CI}{RI}}$$

(5)

where $RI$ is the Random Index, which for $n=6$ has a value of $1.24$ (Saaty, 2008). In this case,

$${\lambda }_{max}=6.3943; CI={\displaystyle \frac{6.3943-6}{5}}=0.0789; CR={\displaystyle \frac{0.0789}{1.24}}=0.0636$$

Since the consistency ratio (CR) was less than 0.10, the expert judgments are considered consistent and valid for decision-making purposes (Alonso & Lamata, 2006). Once the priority vector had been validated, the five mathematical error classification frameworks were evaluated using the six criteria outlined in Table 9. The weighted score for each framework was computed using Equation (6), which combines the performance value of each criterion with its corresponding weight:

$$Scor{e}_{method}=\sum _{i=1}^{6}Valu{e}_i·weigh{t}_i$$

(6)

Table 10. Decision matrix for selecting the most appropriate mathematical error classification framework.

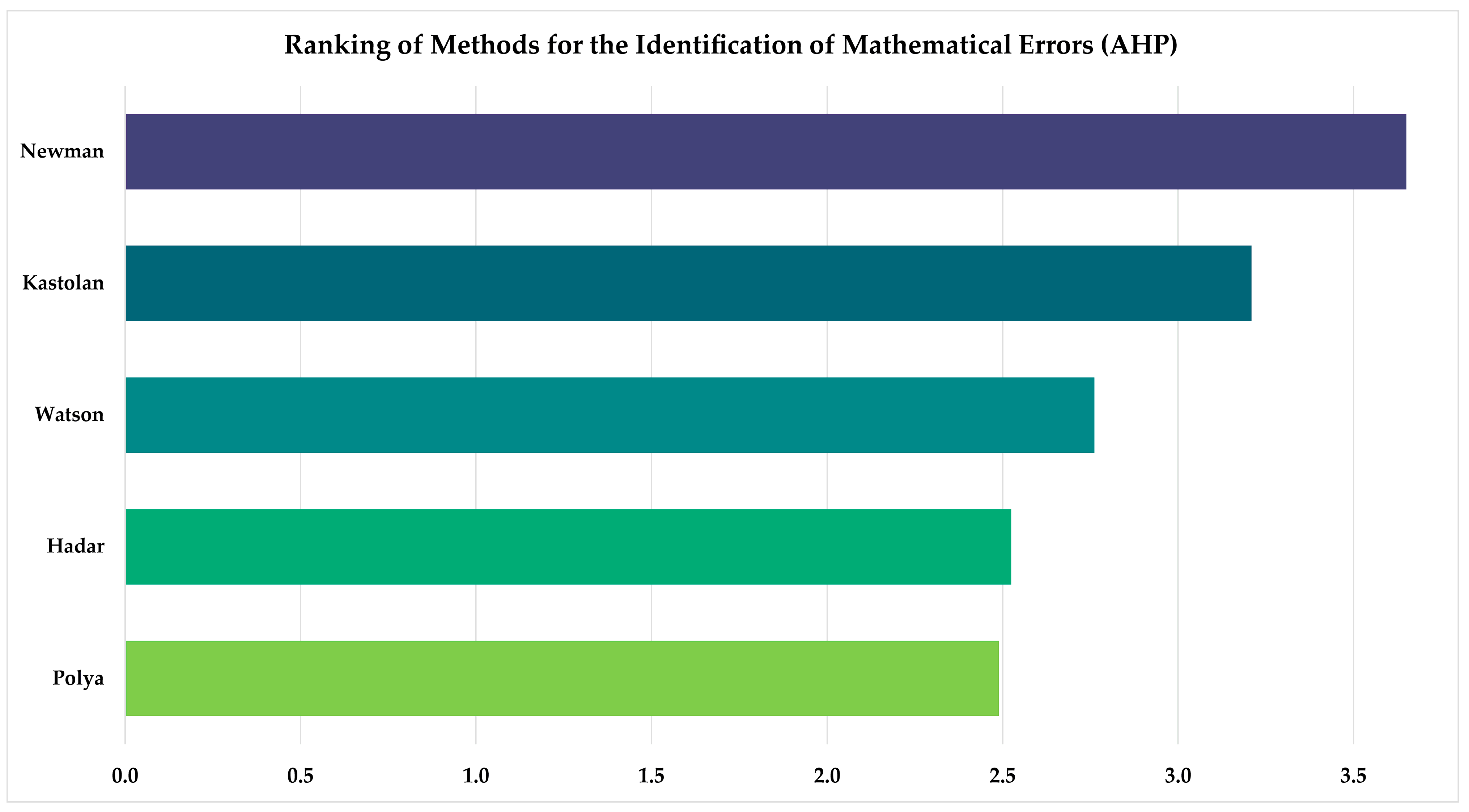
Criteria	Precision in Error Identification	Ease of Application	Focus on Conceptual Errors	Focus on Procedural Errors	Focus on Response Validation	Viability in Improvement Strategies	Score	Ranking
Newman	4.5	4.4	1.4	2.6	1.8	3.8	3.7	1
Kastolan	4.0	3.0	2.3	2.3	1.0	3.3	3.2	2
Watson	3.1	2.8	1.0	2.5	2.0	3.0	2.8	3
Hadar	3.0	2.8	2.3	1.7	2.3	2.7	2.5	4
Polya	2.6	3.3	2.0	2.0	2.0	2.8	2.5	5

presents the resulting weighted scores and corresponding rankings. Figure 3 provides a graphical representation of the final ranking, offering a comparative view of the five frameworks’ overall performance across the defined evaluation criteria.

3. Results

Applying the Analytic Hierarchy Process (AHP) enabled the structured prioritization of five theoretical frameworks to classify mathematical errors in educational contexts. The objective was to identify the most appropriate framework for designing a subsequent diagnostic instrument aimed at first-year engineering students at a polytechnic university. The theoretical models analyzed included Newman, Kastolan, Watson, Hadar, and Polya, which were evaluated against six criteria: accuracy in error identification, ease of application, focus on conceptual errors, procedural errors, response validation, and viability in improvement strategies.

First, the results obtained from the decision matrix show that the Newman framework achieved the highest average weighted score (3.7), followed by Kastolan (3.2), Watson (2.8), and both Hadar and Polya in the same position (2.5). These values are summarized in Table 7, which was constructed from a qualitative rating scale transformed into quantitative data and subsequently weighted using the priority vectors derived from the AHP model. The consistency of the model was verified through the consistency ratio (CR < 0.1), thereby ensuring the validity of the expert judgments.

The weights assigned to each criterion within the model highlight that accuracy in error identification carried the most significant weight (39.7%), followed by focus on procedural errors (25.7%) and viability in improvement strategies (20.3%). Together, these three criteria account for over 85% of the total weight, indicating that, within the scope of this study, which aims to diagnose mathematical errors in first-year engineering students, priority is given to clearly identifying the type of error, focusing on algorithmic procedures, and generating concrete pedagogical strategies for instructional intervention.

Figure 4 presents a comparative radar chart that simultaneously displays the performance of each framework across the six defined criteria. The chart clearly shows that the Newman framework outperforms the others in three key areas: accuracy in error identification (4.5), ease of application (4.4), and viability in improvement strategies (3.8). These results support its suitability as a foundation for developing diagnostic assessment tools within the educational context under study. Although Newman scores lower in focus on conceptual errors (1.4) and procedural errors (2.6), its structural design enables it to capture mistakes at various stages of the problem-solving process, particularly in contextualized tasks and narrative problems, which often reveal the most frequent errors among students with limited mathematical maturity.

It is worth noting that the ease of application of a framework becomes particularly relevant in the context of polytechnic universities, which often have large student groups, diverse prior educational backgrounds, and limited time for individualized feedback. In such environments, a diagnostic model that can be efficiently implemented and replicated in face-to-face and virtual settings, such as the Newman framework, becomes a highly valuable pedagogical tool. From an educational standpoint, this feature aligns with the principles of didactic usability and curricular operability, enabling instructors to promptly detect error patterns without requiring excessive time investment or specialized training.

Figure 5a illustrates the frameworks’ performance concerning the accuracy criterion in error identification. The Newman framework stands out with a score of 4.5. This value reflects the framework’s capacity to break down the problem-solving process into observable phases: reading, comprehension, transformation, execution of the procedure, and result encoding, thereby enabling a precise detection of where the error occurs. Such diagnostic precision is especially critical for first-year students, who often struggle to articulate their reasoning or recognize their mistakes.

Figure 5b shows that Newman also ranks highest in ease of application. This attribute is particularly significant considering that engineering faculty typically manage large student cohorts, and not all instructors have formal training in mathematics education. A framework that can be implemented through rubrics, guided questionnaires, or interview protocols, such as Newman’s, facilitates its institutional adoption and integration into continuous or formative assessment systems.

Regarding the focus on conceptual errors, represented in Figure 5c, the Kastolan and Hadar frameworks demonstrate greater sensitivity (scoring 2.3), as they incorporate categories related to incorrect definitions, invalid reasoning, or misinterpretations of mathematical theorems. With a score of 1.4, Newman does not directly address this type of error from a conceptual perspective within its theoretical structure, as its approach is oriented toward analyzing the problem-solving process rather than conceptual content per se. However, in practice, it does capture manifestations of such errors through categories like transformation and encoding, where distortions in the student’s logical–formal reasoning may be detected.

Far from being a disadvantage in the context of this study, this limitation proves to be beneficial: The objective of the instrument is to classify and characterize errors that hinder mathematical performance in the early stages of learning, particularly among first-semester engineering students. From this perspective, focusing on operational, reading, comprehension, or execution errors, as addressed by the Newman framework, is more relevant than providing an exhaustive classification of conceptual errors, which tend to emerge more clearly at advanced levels. Consequently, Newman’s theoretical limitations in addressing conceptual depth are reframed as practical strengths for the specific context of the diagnostic instrument’s application.

In Figure 5d, which corresponds to the criterion of procedural errors, the Newman (2.6) and Watson (2.5) frameworks show the highest scores, followed by Kastolan (2.3). This outcome aligns with the theoretical structures of these frameworks, which give priority to failures in algorithm execution, symbolic manipulation, and the logical sequence of operational steps. In particular, the Newman framework includes procedural skills, which identify common errors in applying formulas, algebraic properties, and incorrect mechanical procedures.

Its capacity to detect essential operational failures makes it especially relevant for first-semester students, who are still consolidating basic problem-solving techniques. In this regard, Newman’s simplified structure focuses on the types of errors that most hinder progress during the initial stages of university-level engineering education, thus making it an effective tool for early diagnosis aimed at implementing concrete pedagogical interventions.

Figure 5e shows the performance across the dimension of response validation, where the Hadar (2.3) and Watson (2.0) frameworks lead due to their emphasis on explicit result checking, logical coherence verification, and retrospective analysis of solutions. Although Newman scores slightly lower (1.8), it indirectly allows for identifying omissions or inconsistencies in student responses through encoding errors, understood as how the student presents or expresses the final result.

While validation is not an explicit component of its theoretical structure, detecting earlier errors, such as those related to comprehension or transformation, serves as an early filter that reduces the need for subsequent verification. Rather than being a limitation, this feature enhances its practical utility in settings where instructors must act on student errors without relying on extensive self-review. In contexts characterized by low metacognitive autonomy, such as introductory-level courses, this structure supports practical instructional guidance without demanding competencies that students have not yet developed.

Finally, Figure 5f presents the results for the viability criterion in improvement strategies, where the Newman framework achieves the highest score (3.8), significantly outperforming the other approaches. This result is particularly relevant, as one of the central goals of this study is to develop a diagnostic instrument that not only detects errors but also provides concrete pedagogical inputs to enhance academic performance.

The hierarchical structure of the Newman model, which divides the problem-solving process into sequential and observable stages, allows instructors to quickly and accurately identify the breakdown point in student performance. This, in turn, enables the design of targeted remedial tasks, differentiated feedback, and personalized intervention plans. Within this framework, the apparent simplicity of Newman becomes a strength, as it allows for pedagogical action without requiring an overly complex diagnostic process, making it especially suitable for contexts in which timely and precise responses are needed to support students whose learning is still in development.

The overall ranking objectively indicates that the Newman approach is the most suitable for adoption in the design of the diagnostic instrument, as it meets the essential requirements of diagnostic clarity, applicability in real educational settings, and potential to support corrective pedagogical actions. Its sequential structure, focused on contextualized tasks, is particularly valuable for students who struggle with mathematical reading, interpreting instructions, and symbolic encoding—areas that, according to various studies, represent major obstacles during the early stages of engineering education.

Kastolan, with a global average score of 3.2, emerges as a solid alternative, especially useful in more advanced courses requiring greater conceptual and technical discrimination. Watson and Hadar demonstrate strengths in specific dimensions, such as validation and logical reasoning. Still, their lower ease of application and overall accuracy position them as complementary rather than primary approaches. Polya, while beneficial for the structured teaching of problem solving, does not exhibit the robustness necessary to serve as the primary criterion for diagnostic classification in this context.

In conclusion, the results obtained through the AHP model provide a solid foundation for selecting the Newman approach as the primary criterion for designing the diagnostic instrument. Its simplicity, applicability, and diagnostic effectiveness make it an ideal tool for identifying common errors among first-year engineering students and guiding more effective teaching and learning processes responsive to the practical needs of polytechnic university classrooms.

4. Discussion

The results obtained through the Analytic Hierarchy Process (AHP) not only enabled the prioritization of five theoretical approaches for the classification of mathematical errors but also provided an objective and context-sensitive justification for selecting the Newman approach as the foundation for designing a diagnostic instrument targeted at first-semester engineering students. This choice is not solely based on numerical outcomes but rather on structural coherence with the pedagogical goals of the study and the practical demands of the polytechnic university context.

Several studies have noted that first-year engineering students often face difficulties interpreting mathematical problems, selecting appropriate solution strategies, and executing basic procedures (Hoth et al., 2022; Suciati & Sartika, 2023). These difficulties are not always the result of deep conceptual gaps, but frequently stem from deficiencies in transversal skills such as mathematical reading, contextual comprehension, and symbolic encoding (Berraondo et al., 2004; Booth et al., 2013). In this regard, the Newman approach, by breaking down the problem-solving process into observable phases: reading, understanding, transformation, procedure, and encoding, allows for a structured mapping of the breakdown points in student performance.

From a didactic perspective, this sequential structure aligns with the principles of cognitive constructivism and formative assessment, as it enables instructors to identify the precise moment when a student’s reasoning begins to deviate, thus allowing for more accurate and targeted feedback (Jaworski & Matthews, 2011; Rushton, 2018). Moreover, the ease of application associated with the Newman approach, strongly supported by the results obtained (4.4 out of 5), facilitates its institutional adoption in large-scale courses without requiring complex curricular adaptations or specialized teacher training in error analysis.

While approaches such as Kastolan and Watson offer greater depth in identifying conceptual and procedural errors, their implementation demands more abstraction from instructors and students. This may prove unfeasible in early stages, where the priority stabilizes foundational learning (Faulkner et al., 2019; Sazhin, 1998). In contrast, the Newman approach allows for identifying common error patterns and establishing direct correlations between error types and the corresponding pedagogical intervention, fostering its integration into continuous assessment models and academic leveling processes.

In addition, Newman’s high score (3.8) on the viability in improvement strategies criterion reinforces its potential as a practical input for pedagogical planning. Its structure supports a diagnostic–formative approach, in which each error is recorded and used to inform instructional adjustments. This perspective aligns with the recommendations of scholars such as Hiebert and Grouws (Hiebert & Grouws, 2007), who argue that mathematics teaching improves significantly when educators have access to detailed and specific information about the errors their students make.

Another key factor is the high weight assigned to the accuracy criterion in error identification (39.7%) within the AHP model. This underscores the need for approaches that not merely classify errors in general terms but also enable the precise detection of their origin and nature. In this respect, the Newman approach offers a significant advantage, as it facilitates the recognition of the error and its precise location within the resolution process, an essential aspect for designing targeted, non-generic remedial interventions.

Furthermore, the lower scores assigned to Newman in conceptual error detection and response validation should not be interpreted as a weakness in the context of this study, but rather as a theoretical delimitation consistent with its intended purpose. In the early stages of academic training, as is the case for first-semester students, difficulties are more likely to manifest in interpreting instructions, strategy selection, and execution of basic operations, rather than in abstract theoretical misconceptions that require advanced conceptual mastery (Morgan, 1990; Sulistyaningsih et al., 2021). Therefore, focusing the instrument on the dimensions in which errors are most frequent and most amenable to correction is a methodological decision and a pedagogical strategy supported by evidence.

In summary, the findings of this study confirm that although the Newman approach has limitations in detecting higher-order errors, it fully meets the functional requirements of the application context: high diagnostic precision, ease of implementation, and direct applicability in the design of pedagogical improvement strategies. Its adoption as the primary classification criterion in developing the proposed diagnostic instrument responds not to theoretical supremacy, but to practical relevance, grounded in technical and pedagogical criteria that are meaningful for engineering education at the university level.

These results offer concrete pedagogical implications for teachers facing the challenge of improving mathematics teaching in the early stages of engineering. The AHP methodology applied not only allowed for a justified selection of the theoretical framework for classifying errors, but also provides a replicable procedure for substantiating teaching decisions that are traditionally made intuitively or arbitrarily. In this sense, choosing the appropriate criteria for error detection is not a minor issue: It involves defining what type of difficulties are prioritized, how they are interpreted, and what pedagogical approach to take. In teaching practice, this translates into the possibility of designing more effective diagnostic tools aligned with first-semester students’ cognitive and curricular profiles. Likewise, the proposed methodology can be adapted to evaluate other relevant teaching decisions, such as the selection of teaching strategies, the creation of rubrics aligned with specific types of errors, support materials or evaluation criteria, reports on feedback and correction strategies based on standard error patterns, and guidance on curricular adjustments in fundamental mathematics courses. Thus, the study contributes to the development of diagnostic tools and promotes a culture of evidence-based decision-making within the engineering mathematics classroom.

5. Conclusions

This study applied the Analytical Hierarchy Process (AHP) to evaluate five theoretical frameworks used to classify mathematical errors. The objective was to identify the most suitable model for developing diagnostic instruments for first-year engineering students.

The AHP results ranked the Newman model as the most appropriate framework based on expert judgment and six pedagogical criteria. This finding provides a theoretically grounded basis for constructing tools to identify and address common mathematical errors at the undergraduate level.

The structured AHP-based approach used in this study offers a replicable methodology for supporting model selection in educational research. Future work will focus on designing and validating diagnostic instruments aligned with the selected framework and implementing classroom interventions that improve error recognition and remediation in early engineering education.

Two main lines of future research have been identified:

The first is the design, validation, and application of an assessment instrument based on the Newman approach. This stage will involve developing items aligned with the model’s five error categories (reading, comprehension, transformation, procedure, and encoding), validating them with experts, and conducting a pilot study with first-semester students. This research will be developed in an independent survey to offer an operational and transferable tool for other higher education institutions.

The second is implementing pedagogical strategies focused on acquiring and improving mathematical competencies based on the types of errors identified. Once the diagnostic instrument is consolidated, the next step will be to design, implement, and evaluate specific educational interventions according to the identified error types. This line of work will give rise to future research on the effectiveness of improvement strategies and their impact on knowledge retention, academic performance, and students’ mathematical self-awareness.

Both lines of inquiry will complete the diagnosis, intervention, and evaluation cycle and generate empirical evidence on using theoretical error classification frameworks as tools for enhancing mathematics teaching in higher education. In this way, the present study becomes a starting point for a broader research agenda committed to developing contextualized, effective, and sustainable educational solutions for the mathematical training of future engineers.