Using a Realistic Context to Motivate and Teach Engineering Students the Chain Rule

Abstract

Existing research shows that students struggle to understand and use the chain rule appropriately. Other research suggests instructors use more contextually rich problems in their teaching to allow the students to experience calculus through meaningful contexts. In response, this concept paper presents four tasks using the chain rule that we anticipate can be compatible with how students discern concepts, and which could enhance the students’ understanding of the chain rule. The setup is that the students learn the chain rule through the multiplication rule, demonstrated through four teaching tasks. Applying Tall’s three worlds of mathematics when designing mathematics tasks makes it possible to blend symbolic and embodied worlds, opening the door to the formal world, which is beneficial for engineering students.

1. Introduction

The chain rule is one of the key concepts in calculus, where it is a means to differentiate composite functions. Additionally, it is a basic component of several other calculus techniques and functions, such as implicit differentiation, differentiation of inverse functions, and integration by substitution. Mathematically, the chain rule states the following (Adams & Essex, 2010, p. 115):

“If $f\left(u\right)$ is differentiable at $u=g\left(x\right)$, and $g\left(x\right)$ is differentiable at $x$, then the composite function $\left(f\circ g\right)\left(x\right)=f\left(g\left(x\right)\right)$ is differentiable at x, and ${\left(f\circ g\right)}^{\prime }\left(x\right)=f^{\prime }\left(g\left(x\right)\right)\cdot g^{\prime }\left(x\right)$”.

Applying the Leibniz notation, the chain rule can be written as: ${\displaystyle \frac{dy}{dx}}={\displaystyle \frac{dy}{du}}·{\displaystyle \frac{du}{dx}}$.

The chain rule is taught in both upper secondary schools and at university to mathematics, science, and engineering students. However, students’ difficulties in understanding the chain rule have been documented in the research literature. For instance, Gordon (2005) states that the chain rule is among the most difficult topics for students. It is furthermore difficult to motivate the students to learn it, since it is not clear to the students where it comes from, and it is also hard to express in symbols. Also, when searching for previous research literature about teaching and learning the chain rule, it appears to be an under-researched area. One of the more recent of these studies, Rasmussen et al. (2014) concluded that, in general, for research in the learning of calculus, the mathematical branch to which the chain rule belongs, “considerably more progress is needed” (p. 512), and Clark et al. (1997) stated that “no studies were found on their [students’] understanding of the chain rule” (p. 348). However, what we do know from these previous studies is that, e.g., Clark et al. (1997) found that learning the chain rule implies that one is building a cognitive schema around this concept and that this schema must also contain a function schema containing composition and decomposition. This conclusion was confirmed by Cottrill (1999) and Maharaj (2013) in their studies of the relation between the students’ understanding of composite functions and their understanding of the chain rule. However, a study by Jojo (2011) directly disputed that claim, as the study found students who had an inadequate understanding of composition of functions, but who still performed well in the application of the chain rule. Further, this study found that students struggled with the manipulation of the algebraic terms but also concluded (with reference to Capistran’s (2005) dissertation) that most students do not like or understand the Leibniz notation. Kabael (2010) described a study in Turkey that concluded that most difficulties with the chain rule are related to symbolic or structural difficulties. Maharaj (2013) found that when teaching the chain rule, it is important to devote time to developing the mental structures at both the level of process, object, and schema. It is also essential to include both verbal and graphical approaches to the application of the concept. The benefits of visualization are also seen in the study by Uygur and Özdaş (2007), who, while to some extent building upon Thoo (1995), found that the arrow diagram has a significant effect on students’ calculation abilities with the chain rule. Lutzer (2003) argued for using students’ physical understanding of motion to help them develop an understanding of the chain rule. This was achieved using the calculation of a rate of change as a representation of the chain rule.

Tall (1992) indicated that “the Leibniz notation ${\displaystyle \frac{dy}{dx}}$ proves to be almost indispensable in calculus. Yet it causes serious conceptual problems. Is it a fraction, or a single indivisible symbol? What is the relationship between $dx$ in ${\displaystyle \frac{dy}{dx}}$ and the $dx$ in $\int f\left(x\right)dx?$ Can the $du$ be cancelled in the equation ${\displaystyle \frac{dy}{dx}}={\displaystyle \frac{dy}{du}}·{\displaystyle \frac{du}{dx}}$?” (p. 19). However, in a somewhat older paper, Thurston (1972) supported the Leibniz notation and stated that, “even if the teacher does not feel that ${\displaystyle \frac{dw}{dz}}·{\displaystyle \frac{dz}{dy}}·{\displaystyle \frac{dy}{dx}}={\displaystyle \frac{dw}{dx}}$ is immensely superior to ${\left(f\circ g\circ h\right)}^{\prime }\left(x\right)=f^{\prime }\left(g\left(h\left(x\right)\right)\right)\cdot g^{\prime }\left(h\right(x\left)\right)\cdot h^{\prime }\left(x\right)$ as a formula for the chain rule with two links, his students surely will” (p. 360). Thus, the Leibniz notation might be difficult, but it could be argued, is the lesser of “evils”.

Regarding the formal proof of the modern version of the chain rule, it seldom sheds light on the meaning of the chain rule since it uses an algebraic trick (Cottrill, 1999). For example, the proof given in Stewart (2016), which is a commonly used calculus textbook, is a purely symbolic explanation without a meaningful context that might otherwise have helped the students develop an image for the rule.

These are issues that illustrate the difficulties in learning the chain rule. Nevertheless, the chain rule is relevant, not only in various parts of calculus itself, but also in a variety of other disciplines, including physics, engineering, business, economics, biology, chemistry, and other natural sciences. So, the million dollars question is, perhaps, how can we teach it to enhance the students’ understanding of it? It is the goal of this paper to explore and discuss ways in which we can help the engineering students understand and use the Leibnitz chain rule.

2. Conceptual Framework: How Do Engineering Students Learn Math?

According to Maull and Berry (2000), engineering students are different from mathematics and physics students in ways that affect their learning styles, particularly in terms of what motivates them. For instance, mathematics and engineering students have different concept images, and engineering students’ growth in their understanding of mathematical terms was found to be linked to them seeing it, or having the term interpreted, in terms of the everyday world. In line with this, Sazhin (1998) states that when engineering students learn mathematics, they need to know why this mathematics is essential for their engineering profession. Furthermore, equations need to be illustrated by examples from praxis, and the students also need to have the necessary steps in algebraic manipulation highlighted. This focus on both the process and the praxis is in line with Tall’s (2013) theory of the three worlds of mathematics that provides a framework for the development of mathematical thinking, also for mathematics students. What is special about Tall’s three worlds is that his framework is based on how students perceive and carry out actions on objects and his framework considers three aspects of mathematics, namely, geometric, symbolic, and axiomatic.

The first world is that of conceptual embodiment, which is an object-based understanding of mathematics, and reflecting on using the senses to observe, describe, and deduce properties. The objects are not only physical objects but also mental images, pictures, and internal connections. This world involves students’ visual–spatial imagery. A square is, e.g., embodied as a plane figure with four equally straight lines, and four right angles. This mental image becomes a prototype for all squares. In this first world of conceptual-embodiment, students learn from observing the results of their actions on an object.

The second world is an action based proceptual–symbolic world, where symbols act either as concepts to think about or as processes to make calculations and perform symbolic manipulations with. Therefore, a symbol simultaneously denotes both a process and a concept. For example, the symbol ${\displaystyle \frac{dy}{dx}}$ both represents a process to be performed and the concept that is obtained through this process. Thus, it compresses action-schemas into thinkable concepts operating dually as processes and concepts (named procepts). The process begins with students being able to perform it step-by-step, then it becomes automatized, such that students can carry it out without paying attention to the technicalities. The brain is therefore able to switch from performing a process to thinking more abstractly about the concept.

The third is a property-based formal–axiomatic world of concept definitions and set-theoretical proofs. This world uses axioms, definitions in formal language, and logical deductions to develop axiomatic mathematics.

In Tall’s theory, learning is seen as dynamic, and takes place as a non-linear process, with students moving frequently back and forth between the three worlds.

Therefore, we anticipate that using a realistic context to motivate and teach all students is something that will benefit both engineering and mathematics students.

To meet “the challenge of the chain rule”, educators and researchers need to find alternative methods to facilitate students’ inquiries into it. For example, Borji and Martínez-Planell (2020) argue that special activities are needed for students taking introductory calculus to be able to understand the main ideas of implicit differentiation. In this regard, many studies, e.g., those of Uygur and Özdaş (2007) and Lutzer (2003), have pointed out that teaching the chain rule should be carried out in real contexts and that learning the chain rule should be connected to real-world situations. However, there have been few educational studies on incorporating real situations in teaching the chain rule to engineering students (Park & Lee, 2016). Our paper attempts to fill that gap.

3. Methods and Setting Up the Four Teaching Tasks

We propose presenting a series of tasks aimed at facilitating engineering students’ inquiries into the chain rule through an engineering context. The purpose of the tasks is to let the engineering students explore why the chain rule works and why it makes sense, thereby gaining a deeper, conceptual understanding of the rule. This is also based upon a study by Jukić and Dahl (2012) of various problems of learning derivatives among non-mathematics STEM students. The study showed students remembering procedures without understanding the concepts they involved or connecting these concepts to each other. Many students seemed to think that mathematics is about knowing the right procedure to use. Jukić and Dahl (2012) therefore suggested that educators giving tasks that do not just ask for the right answer may enable students to form better conceptualizations.

3.1. Interpretation of a Derivative

The tasks rely on infinitesimals in the interpretation of a derivative ${\displaystyle \frac{dy}{dx}}$ as representing how many times the infinitesimal change in $y$ is larger than an infinitesimal change in $x$. The reason for this is that, according to many researchers, defining the derivative as a difference arising from an infinitesimal change, is cognitively beneficial for the students (see, e.g., Ely (2017) and Jones (2015)). 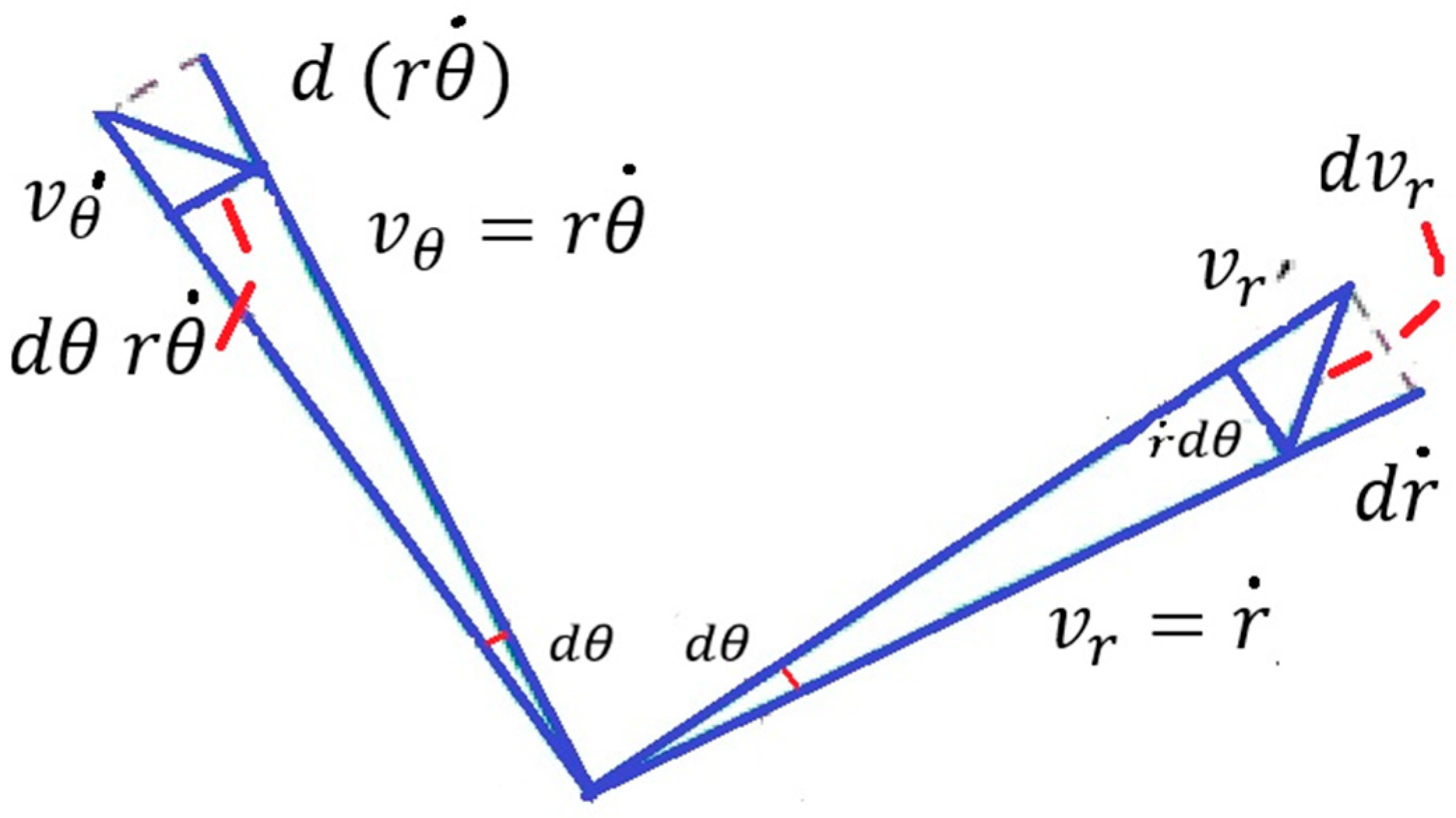Moreover, our use of infinitesimals is consistent with many modern engineering science textbooks, such as Cengel and Boles (2011) and Meriam and Kraige (2013), that still depend on them in deriving engineering formulas and equations. For example, the engineering dynamics textbook Meriam and Kraige (2013) uses geometry of the physical changes to derive the acceleration formula in polar coordinates (see Figure 1).

In our view, infinitesimals offer more obvious cognitive benefit in “thinking change”, than the modern rigorous theorem ${\left(f\circ g\right)}^{\prime }\left(x\right)=f^{\prime }\left(g\left(x\right)\right)\cdot g^{\prime }\left(x\right)$, which is also in line with the conclusion of Thurston (1972). As stated by Rodríguez and Lopez Fernandez: “It thus seems reasonable to suggest that when paradigms change in mathematics (as the change towards the theory of limits after the infinitesimal approach) they must have a cognitive advantage for dealing with pressing unsolved problems, but this advantage does not necessarily extend for mathematics education” (Rodríguez & Lopez Fernandez, 2010, p. 329).

3.2. The Engineering Students in Our Study

Our paper presents four tasks that we assume, based on the discussion above, would aid both the engineering students’ motivation to learn the chain rule and their understanding of it. In order to do a smaller study on how these tasks were received by students, the first author presented these tasks in Spring 2024 to the 2nd semester engineering students, enrolled in the undergraduate study program “Sustainable Design” at our university. The students had calculus during the first semester of the bachelor program. The first author of this paper is the instructor of the course. The name of the course is “Dynamics and Vibrations”. The textbook of the course is Engineering Mechanics: Dynamics, SI Units, 15th edition, by R. C. Hibbeler, Pearson, 2023. The number of students taking the course is 40, while 26 were present on this day. The teaching took place, as usual, in four-hours slots, starting with 1.5 h of lecture followed by students sitting in groups completing exercises for about two hours. The students spent around 1 h solving the four tasks. The trial took place at the very first session of the semester, and hence also functioned as repetition. The students were asked to write some comments regarding their experiences in solving the task on the back page of the tasks. The data collection, observation, and interviews shown below were carried out in an informal manner, among other things, to avoid creating too much disturbance from normal teaching, or creating stress. The students were made aware that this was not a formal test.

3.3. The Four Tasks About the Chain Rule

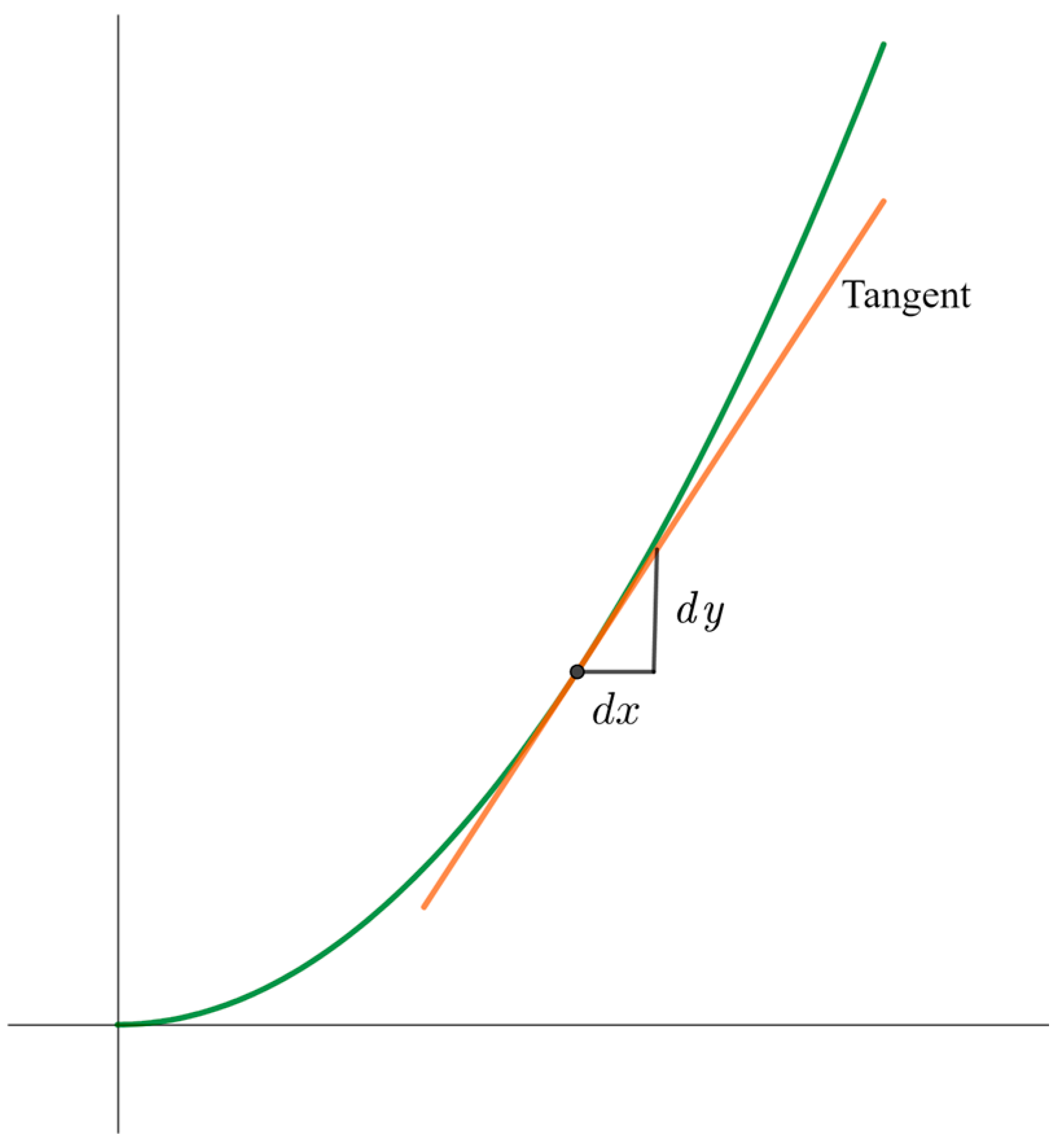
Before giving the tasks to the students, the first author reminded the students of the formal definition of the derivative and showed them a graph of a function having a tangent at a point (see Figure 2). The students were then asked to relate the derivative at a point with the slope of the tangent at that point. The purpose is to arrive at the relation $y^{\prime }\left(x\right)={\displaystyle \frac{dy}{dx}}$, using the commonly used formula of the slope of a straight line $a={\displaystyle \frac{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}{\mathrm{r}\mathrm{u}\mathrm{n}}}$. The difference between $dy$ and $\Delta y$ is also debated: $dy$ is defined as the infinitesimal change in $y$ when $x$ changes by an infinitesimal amount, with $dx\ne 0$, whereas $\Delta y$, which is related to the slope of a secant, can be a “large” difference.

In addition, the first author reminded the students of the formula of the chain rule, that they were introduced to, in their upper secondary mathematics course:

$${\left[f\left(g\left(x\right)\right)\right]}^{\prime }=f^{\prime }\left(g\left(x\right)\right)·g^{\prime }\left(x\right)$$

The following tasks were printed on a paper that is given to all students in the class. The purpose of the tasks was to help the students discern the multiplicative nature of the chain rule formula, as it is usually given in standard calculus texts. This rule is demonstrated by the four teaching tasks.

The students were asked to solve them individually, without support.

Task 1.

Suppose that the carbon monoxide pollution in the air is changing at the rate of 0.02 ppm (parts per million) for each person in a city whose population is growing at the rate of 1000 people per year. Find the rate at which the level of pollution is increasing with respect to time. Remember that the symbol ${\displaystyle \frac{dy}{dx}}$ stands for the derivative of $y$ with respect to $x,and$ represents the rate of change of $y$ with respect to $x$.

The purpose of this task is to allow the students to develop a concept image (Tall & Vinner, 1981) for the multiplicative nature of the chain rule, and obtain an equation like:

$${\displaystyle \frac{dL}{dt}}={\displaystyle \frac{dL}{dP}}·{\displaystyle \frac{dP}{dt}}$$

We also assumed that having a concrete context would make it possible for students to at least develop some conceptual embodiment as they may apply mental imagery on understanding the setup (Tall, 2013).

The first author observed that some students said they could not remember the way the chain rule was introduced in the upper secondary school, but this exercise was user-friendly and easy to understand.

Task 2.

Hanne runs twice as fast as Peter. Peter runs three times as fast as Mary. How much faster does Hanne run than Mary?

Though this task is very similar to Task 1, its aim is to develop a conceptual understanding beyond algebraic formulation of relationships among entities in a given problem situation, since the students’ problem-solving activities are not just copies or reductions of original problems, but rather, they can be decontextualized, integrated, and generalized from the concrete and the particular (Lesh & Doerr, 2003). It is also a task that can be perceived to fall within the first world of Tall, a conceptual embodiment as it involves well-known experience of running.

The first author noticed that a student mentioned that she “did use some sort of the chain rule” and that this exercise resembles “the upper secondary school method”.

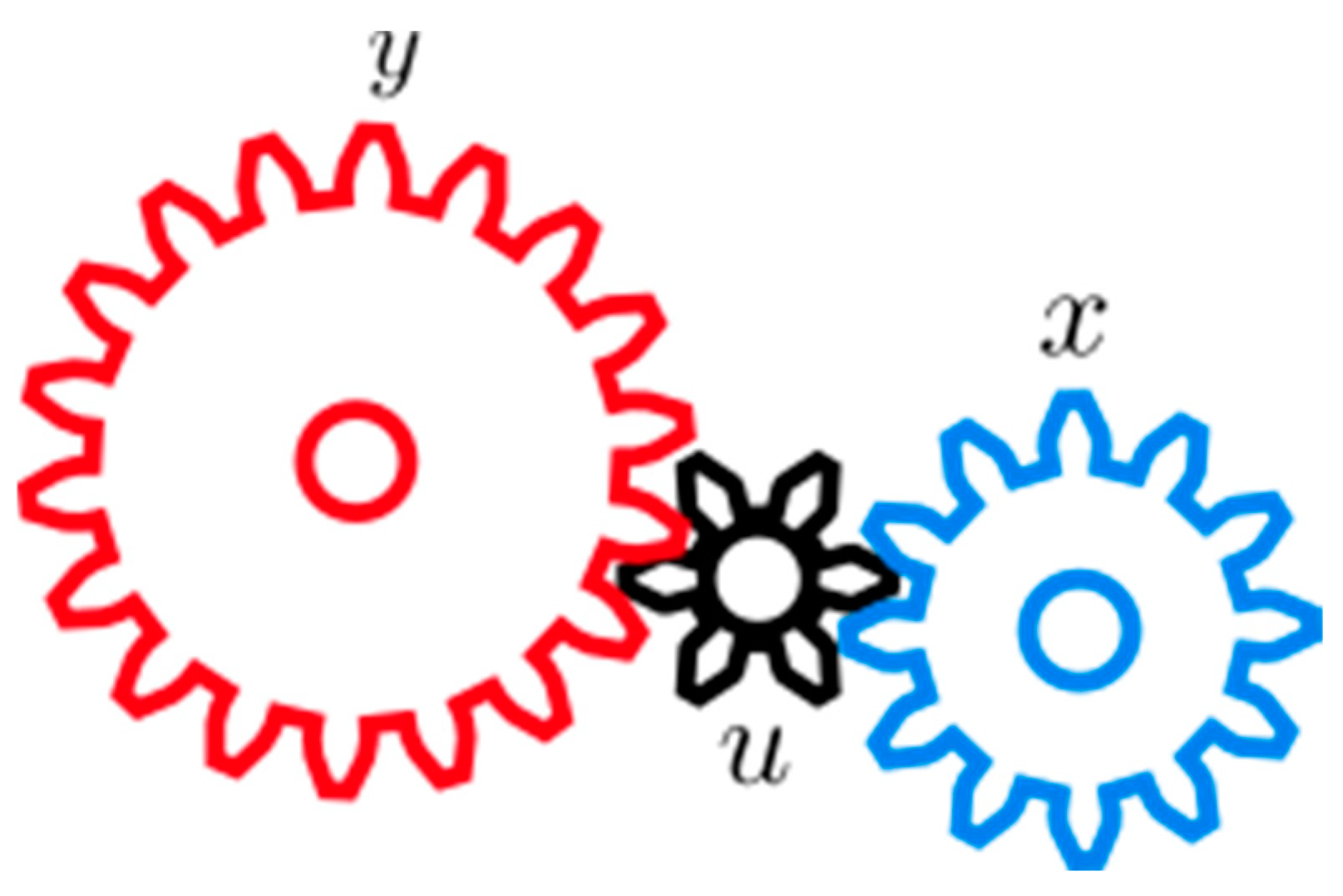
Task 3.

Given the gear train shown below in Figure 3. The number of teeth of the blue gear $x$ is 12, that of the black one $u$ is 6 and the number of teeth of the red gear $y$ is 18. How many times does gear $y$ spin for every one spin of gear $x$?

The purpose of this task is to help the students see both a composite function and the chain rule in action, by finding out that $u=2x$ and $y={\displaystyle \frac{1}{3}}u={\displaystyle \frac{2}{3}}x$, and realizing that for every one rotation of the blue gear, the black gear will spin twice, and for each rotation of the black gear, the red will spin ${\displaystyle \frac{1}{3}}$ turn. In Leibniz notation, ${\displaystyle \frac{du}{dx}}=2$ and ${\displaystyle \frac{dy}{du}}={\displaystyle \frac{1}{3}}$ and thus,

$${\displaystyle \frac{dy}{dx}}={\displaystyle \frac{dy}{du}}·{\displaystyle \frac{du}{dx}}={\displaystyle \frac{1}{3}}·2={\displaystyle \frac{2}{3}}$$

Some functions can be written as composite functions in different ways and, to confirm that this will not change the final derivative, the students can examine what happens when the size of the black gear is changed. For example, if the black gear has 24 teeth, then ${\displaystyle \frac{du}{dx}}={\displaystyle \frac{1}{2}}$ and ${\displaystyle \frac{dy}{du}}={\displaystyle \frac{4}{3}}$. Finding ${\displaystyle \frac{dy}{dx}}$, and thus confirming the chain rule, can again be carried out by visualizing the gears turning. Thus, ${\displaystyle \frac{dy}{dx}}={\displaystyle \frac{4}{6}}={\displaystyle \frac{2}{3}}$. As before,

$${\displaystyle \frac{dy}{dx}}={\displaystyle \frac{dy}{du}}·{\displaystyle \frac{du}{dx}}={\displaystyle \frac{4}{3}}·{\displaystyle \frac{1}{2}}={\displaystyle \frac{2}{3}}$$

Although this task is also from an engineering perspective, the illustration in Figure 3 is more idealized and a particular context is not mentioned. Also, we anticipate that such a task is one that all students can relate to. However, in actual teaching, a presentation of a context to the task, alongside pictures or perhaps even a physical model, is recommended. Nevertheless, it is easy to find real examples of gear trains. A physical model of a gear train may also be a way to stimulate the conceptual embodiment as well as the proceptual–symbolic world, as their extensive use of the Leibniz notation may aid this concept in becoming compressed, while the abstract notation is also an entry into the third world of mathematics (Tall, 2013).

When asked how they tackled this exercise, some students mentioned that “we mostly used our intuition”.

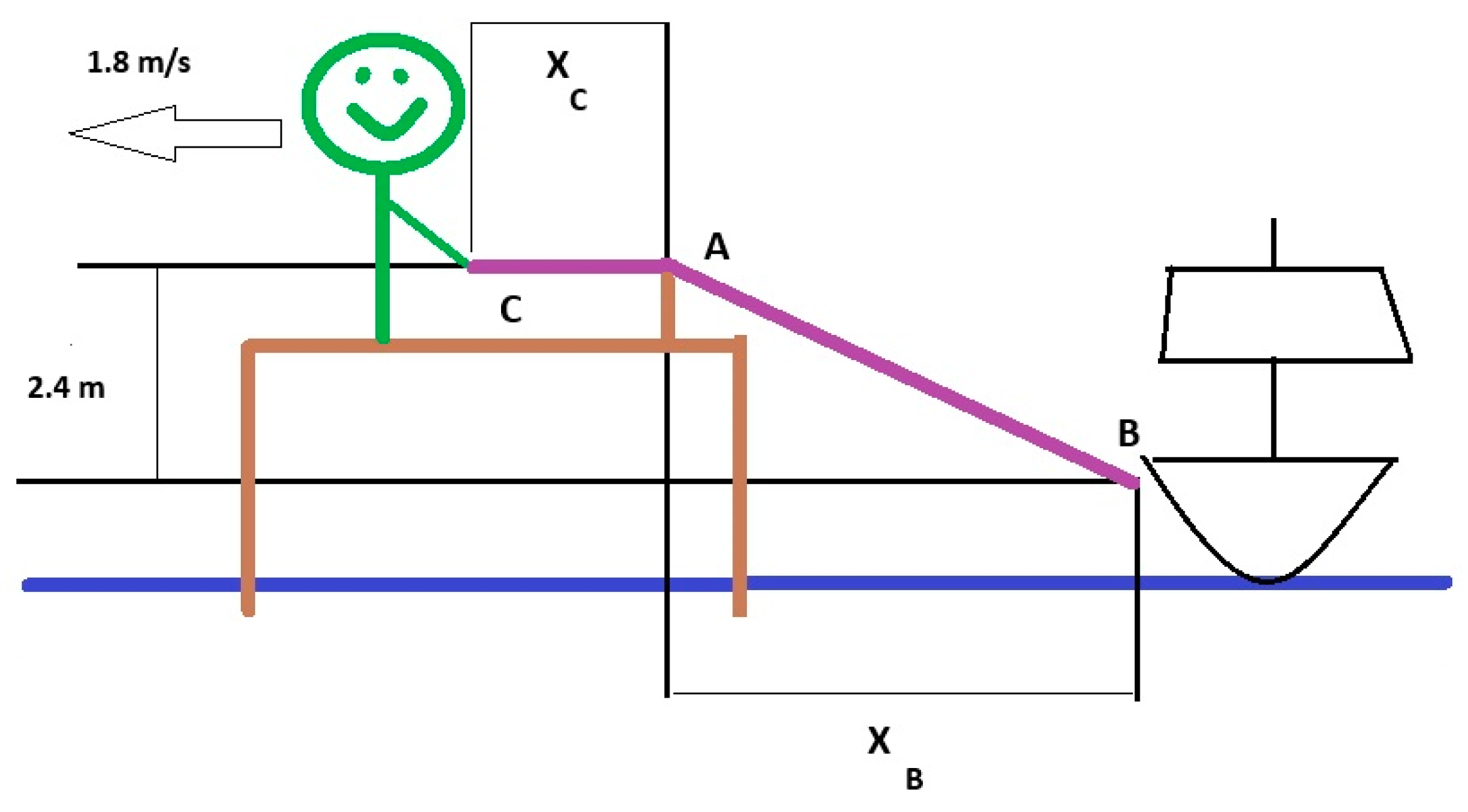
Task 4.

The girl at C stands near the edge of the pier (brown) and pulls in the rope (purple) horizontally at a constant speed of 1.8 m/s (Figure 4). Determine how fast the boat approaches the pier at the instant the rope length $AB$ is 15 m. Remember that the length of the whole rope  $BC$ is constant.

This task is a so-called related-rate problem in kinematics, as the students should first find a relation between the two variables $x_B$ and $x_C$ before they use the chain rule. This is, in addition, a task that is not very “engineering”-based, but something that we anticipate that mathematics students would also find relevant and motivating. Using the chain rule in a related-rate problem can help the students discover the relationship between the given and unknown rates in the problem (Infante, 2007). The sentence reminds the students that BC is a constant and it can be omitted, or not, depending on the level of the particular students in the class. Again, this task can build on the conceptual embodiment of the students, based on them being able to imagine the situation.

4. Results: Engineering Students’ Experiences of the Four Tasks

The first authors noted that a student wrote “I like this method. It’s more intuitive than the one we learnt in Gymnasium [Danish upper secondary school]”. Below (Figure 5), we present the comments of some students given at the end of the tasks’ session, regarding the “new” method of using the chain rule. Overall, we noticed students being positive towards this method as they use words such as “more intuitive”, “simpler”, “easier”, and “better”, although some also state that “it’s still difficult to take the real-life situation”.

When the time allocated to solving the tasks was over, the first author posed the question “Did your understanding of the chain rule improve after doing the tasks?” Many students asserted that the tasks were a good supplement to the method they learned from the upper secondary school, and the tasks gave an intuitive understanding that the usual method did not offer. Others said that, although this method is good to know, they preferred the way they the learned chain rule in upper secondary school.

5. Discussion: A Visual Proof of the Chain Rule

The culmination of these four tasks consists of giving the students an intuitive visual “proof” of the chain rule. If we let $y$ be a differentiable function of $u$ such that $u$ also is a differentiable function of $x$, then, since, $y^{\prime }\left(u\right)={\displaystyle \frac{dy}{du}}$, it follows that $dy=y^{\prime }\left(u\right)du$ and, similarly, $du=u^{\prime }\left(x\right)dx$. Consequently, $dy=y^{\prime }\left(u\right)u^{\prime }\left(x\right)dx$ and

$${\displaystyle \frac{dy}{dx}}={\displaystyle \frac{dy}{du}}·{\displaystyle \frac{du}{dx}}$$

This is the chain rule written in the Leibniz notation. According to Rodríguez and Lopez Fernandez (2010), the statement of the chain rule in the language of infinitesimals was so “evident” that it was not even mentioned explicitly in L’Hôpital’s and Euler’s analysis books: it did not require a proof or justification.

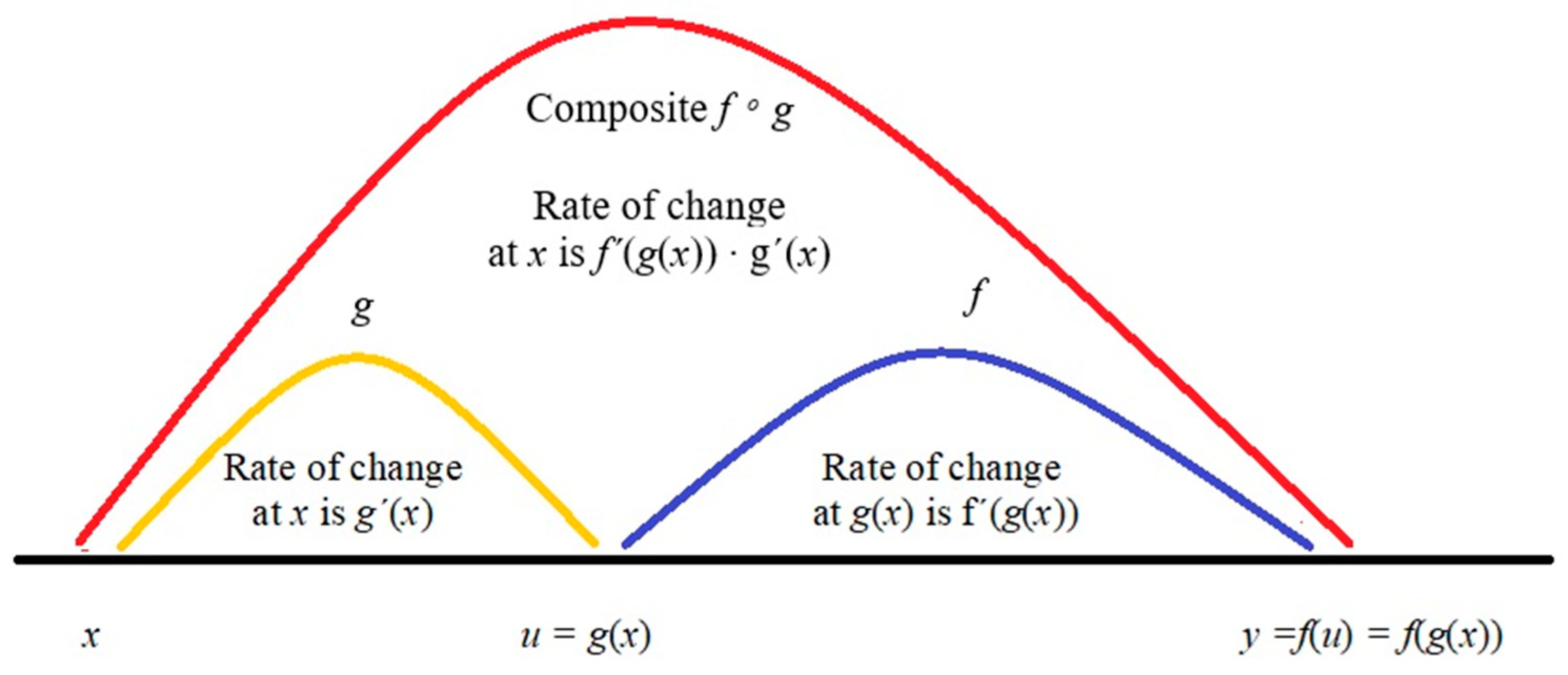
A visual illustration of the chain rule is shown in Figure 6 (Thomas et al., 2018, p. 143), where $u=g\left(x\right)$. The figure shows the multiplication of rates of change (derivatives), which the students use in the tasks. This “proof” may be sufficient for engineering students to understand and apply the chain rule in realistic situations. The purpose of the visual illustration of the chain rule is to let the students realize that the function $u=g\left(x\right)$ acts as a mediator between the input $x$ and the output $y$, as shown in the figure, and by observing the position of $du$ in the following formula:

$${\displaystyle \frac{dy}{dx}}={\displaystyle \frac{dy}{du}}·{\displaystyle \frac{du}{dx}}$$

Recognizing that the two du’s divide out may help the students to sharpen their intuition about the multiplicative nature of the chain rule. This observation can also help the students remember the chain rule when they regard the derivative ${\displaystyle \frac{dy}{dx}}$ as a fraction.

6. Conclusions and Application in Practice

In general, we know that an overemphasis on procedures and calculations can make it hard for students to make sense of mathematics and apply it appropriately to solve new tasks (Skemp, 2006). Our tasks focused on meaning: the meaning of derivatives, the multiplicative nature of the chain rule, and implicit functions. Therefore, a reason why students struggle to understand and appreciate the chain rule could, in part, be related to the fact that these students, whether in secondary school or in university, are required to put too much emphasis on procedures and manipulation of symbols, instead of focusing on the meaning to help them gain a conceptual understanding from the beginning. For instance, the textbook by Stewart (2016) introduces the chain rule as a procedure and does not provide opportunities for the student to explore why the chain rule works or why it makes sense. Therefore, the students still need to practice translating real-world problems into mathematical models and translating their solutions back into the context of the original problem.

Real-life problems on related rates can potentially be a beneficial way for students to experience the reasoning behind the chain rule before it is abstracted. This is the main goal of this article: To prepare students for the mathematics of the chain rule, using their previous experiences. We do not claim that our preliminary investigation is conclusive, given its small-scale nature especially, but rather, it is a steppingstone to build on in future research.

It can be a way for them to develop their conceptual images of the concept, thus improving their understanding and ability to apply the chain rule. This is something which was found in the study by (Dahl, 2017), which showed non-STEM students taking a calculus course being successful solving some calculus tasks without referencing definitions, but only applying their coherent concept images. This also follows Tall’s three worlds of mathematics (2013), suggesting that students first meet the first world, the conceptual embodiment, followed by the second world, which involves actions with the symbols, and from there becoming able to meet the third world, the formal–axiomatic world. A rather similar conclusion was made in the paper by (Jukić & Dahl, 2014) where a non-mathematics student’s struggle with other parts of calculus was studied and where it was concluded that Tall’s framework provides “a blend of the symbolic and embodied worlds, which gives rise to the formal world. … This will surely be beneficial for non-mathematics students who feel more confident in the embodied world since this will enable them to give a meaning to the actions they perform and allow them to perceive mathematical concepts in the physical or mental world, similar and closer to their field of interest” (p. 1204). This could also be argued based on our study. Therefore, we had this framework in mind when designing mathematics tasks or selecting to use tasks made by others (as seen in this paper).

We wish to argue that mathematics should be taught in meaningful contexts, through well-designed tasks that allow students to acquire genuine understanding of mathematical concepts (Abou-Hayt et al., 2019a), such as the limit of a function (Abou-Hayt et al., 2019b) and the chain rule. However, our point of view is not without its critics: one main criticism is that “it is often impossible to proceed from experientially real situations to mathematics” (Gravemeijer & Terwel, 2000, p. 792). Our response to that criticism is the following: designing a variety of learning tasks for a mathematical concept, such as the chain rule, can help students generalize their problem-solving activities from particular situations into a conceptual understanding of that concept. The conceptual meaning of the chain rule is to obtain a rate of change or derivative by using another mediatory variable through multiplication, and the tasks we are proposing are from situations enabling such generalizations, which, hence, foster learning.

Overall, our small-scale try-out of the four tasks showed that teaching the chain rule within a context improves the understanding of many of our students. Moreover, the authors claim that it will not take much teaching and preparation time to supplement the usual method of introducing the chain rule with real-life problems to help the students develop an intuitive understanding of the chain rule. We encourage instructors, who may be inspired by our tasks, to try them out or design their own tasks, which can lead to better conceptualization of the chain rule.