Supporting Multilingual Students’ Mathematical Discourse Through Teacher Professional Development Grounded in Design-Based Research: A Conceptual Framework
Abstract
1. Introduction
2. Literature Review
2.1. Design-Based Research
2.2. Teacher Professional Development
2.3. Honoring Teachers’ Expertise
2.4. Integrated English Language Development in Mathematics
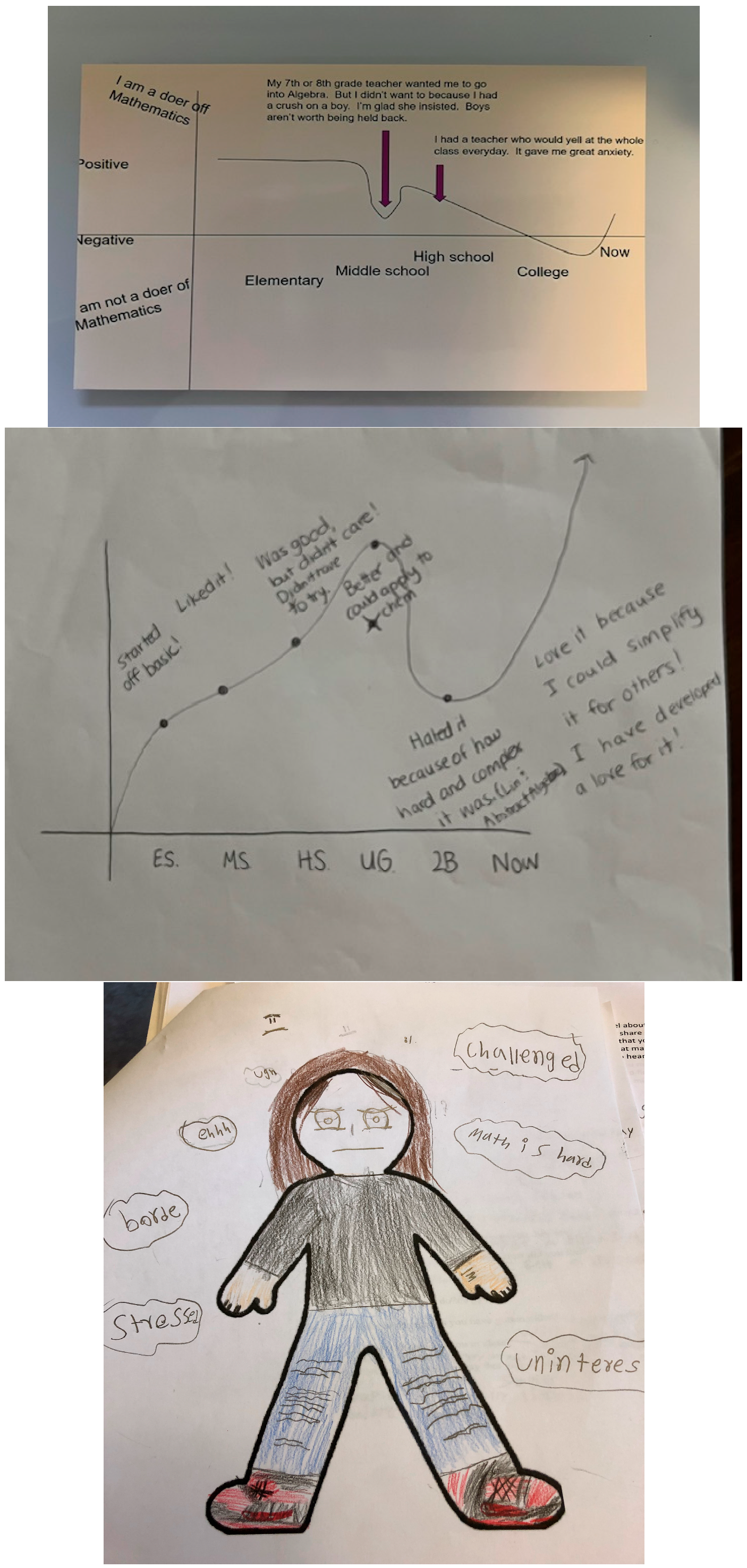
2.5. Mathematical Identity
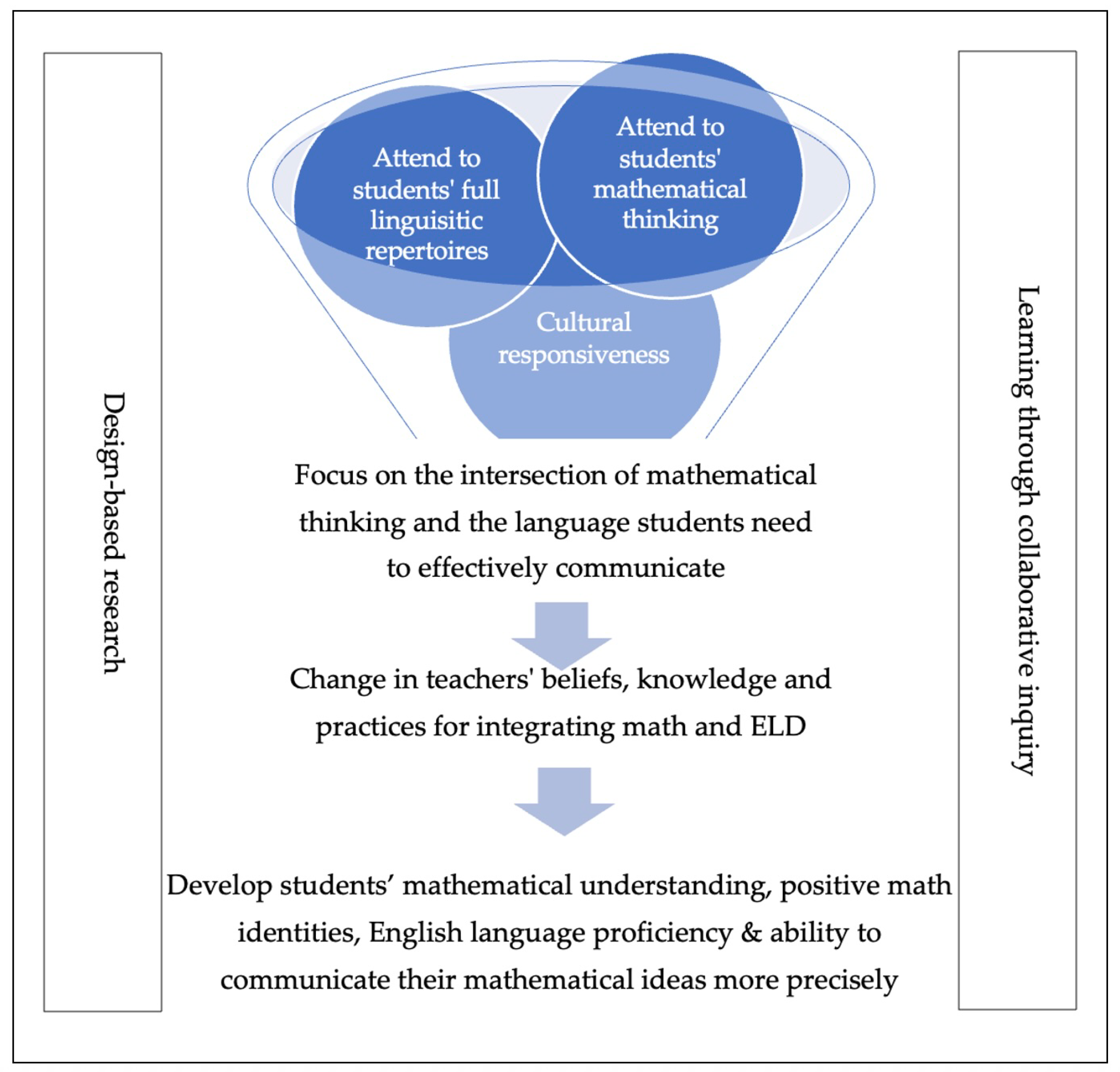
3. Conceptual Framework
3.1. Attending to Students’ Full Linguistic Repertoire
3.2. Attending to Students’ Mathematical Thinking
3.3. Cultural Responsiveness
4. Engaging and Supporting Practitioners’ Enactment of the ILMP Framework
4.1. Triple Track Agenda
4.2. Multilingual Language Learning Implementations
4.3. Mathematical Implementations
5. Challenges and Opportunities
5.1. Challenges
5.2. Opportunities
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdulrahim, N. A., & Orosco, M. J. (2020). Culturally responsive mathematics teaching: A research synthesis. The Urban Review, 52(1), 1–25. [Google Scholar] [CrossRef]
- Alam, A., & Mohanty, A. (2023). Cultural beliefs and equity in educational institutions: Exploring the social and philosophical notions of ability groupings in teaching and learning of mathematics. International Journal of Adolescence and Youth, 28(1), 2270662. [Google Scholar] [CrossRef]
- Allen, K., & Schnell, K. (2016). Developing mathematics identity. Mathematics Teaching in the Middle School, 21(7), 398–405. [Google Scholar] [CrossRef]
- Allen, L. B., & Crowley, K. (2017). From acquisition to inquiry: Supporting informal educators through iterative implementation of practice. In Preparing informal science educators: Perspectives from science communication and education (pp. 87–104). Springer. [Google Scholar]
- Andersson, A., Valero, P., & Meaney, T. (2015). “I am [not always] a maths hater”: Shifting students’ identity narratives in context. Educational Studies in Mathematics, 90, 143–161. [Google Scholar] [CrossRef]
- Armstrong, M., Dopp, C., & Welsh, J. (2020). Design-based research. In The students’ guide to learning design and research (pp. 1–6). Available online: https://edtechbooks.org/studentguide/design-based_research (accessed on 1 June 2025).
- Aronson, B., & Laughter, J. (2016). The theory and practice of culturally relevant education: A synthesis of research across content areas. Review of Educational Research, 86(1), 163–206. [Google Scholar] [CrossRef]
- Aşık, G., & Yılmaz, Z. (2017). Design-based research and teaching experiment methods in mathematics education: Differences and similarities. Journal of Theory and Practice in Education, 13(2), 343–367. [Google Scholar]
- Baird, A. S., Garrett, R., & August, D. (2020). Math and English language development: MELDing content and academic language for English learners. NABE Journal of Research and Practice, 10(1), 1–12. [Google Scholar] [CrossRef]
- Baker, K., Jessup, N. A., Jacobs, V. R., Empson, S. B., & Case, J. (2020). Productive struggle in action. Mathematics Teacher: Learning and Teaching PK-12, 113(5), 361–367. [Google Scholar] [CrossRef]
- Bakker, A. (2018). Design research in education. In Design research in education: A practical guide for early career researchers (Vol. 1, pp. 3–22). Routledge. [Google Scholar]
- Ball, D. L., & Cohen, D. K. (1999). Developing practice, developing practitioners: Toward a practice-based theory of professional education. In G. Sykes, & L. Darling-Hammond (Eds.), Teaching as the learning profession: Handbook of policy and practice (pp. 3–32). Jossey Bass. [Google Scholar]
- Banes, L. C., Ambrose, R. C., Bayley, R., Restani, R. M., & Martin, H. A. (2018). Mathematica classroom discussion as an equitable practice: Effects on elementary English learners’ performance. Journal of Language, Identity, & Education, 17(6), 416–433. [Google Scholar] [CrossRef]
- Bartell, T., Wager, A., Edwards, A., Battey, D., Foote, M., & Spencer, J. (2017). Toward a framework for research linking equitable teaching with the standards for mathematical practice. Journal for Research in Mathematics Education, 48(1), 7–21. [Google Scholar] [CrossRef]
- Bell, P. (2004). On the theoretical breadth of design-based research in education. Educational Psychologist, 39(4), 243–253. [Google Scholar] [CrossRef]
- Borko, H., Jacobs, J., & Koellner, K. (2010). Contemporary approaches to teacher professional development. International Encyclopedia of Education, 7(2), 548–556. [Google Scholar]
- Boylan, M., Adams, G., Perry, E., & Booth, J. (2023). Re-imagining transformative professional learning for critical teacher professionalism: A conceptual review. Professional Development in Education, 49(4), 651–669. [Google Scholar] [CrossRef]
- Brown, A. L. (1992). Design experiments: Theoretical and methodological challenges in creating complex interventions in classroom settings. The Journal of the Learning Sciences, 2(2), 141–178. [Google Scholar] [CrossRef]
- California Department of Education. (2023, July). Mathematics framework. Mathematics, Teaching and Learning, California Department of Education. Available online: https://www.cde.ca.gov/ci/ma/cf/ (accessed on 5 March 2025).
- Carpenter, T. P., Fennema, E., Franke, M. L., Levi, L., & Empson, S. B. (1999). Children’s mathematics: Cognitively guided instruction. Heinemann. ISBN 0325052874. [Google Scholar]
- Carpenter, T. P., & Franke, M. L. (2004). Cognitively guided instruction: Challenging the core of educational practice. In T. K. Glennan, S. J. Bodilly, J. R. Galegher, & K. A. Kerr (Eds.), Expanding the reach of education reforms: Perspectives from leaders in the scale-up of educational interventions (pp. 41–80). RAND Corporation. [Google Scholar]
- Civil, M. (2016). STEM learning research through a funds of knowledge lens. Cultural Studies of Science Education, 11(1), 41–59. [Google Scholar] [CrossRef]
- Clements, D. H., & Sarama, J. (2020). Learning and teaching early math: The learning trajectories approach. Routledge. [Google Scholar]
- Clements, D. H., Vinh, M., Lim, C. I., & Sarama, J. (2023). STEM for inclusive excellence and equity. In Developing culturally and developmentally appropriate early STEM learning experiences (pp. 148–171). Routledge. [Google Scholar]
- Cobb, P., Jackson, K., & Dunlap, C. (2015). Design research: An analysis and critique. In Handbook of international research in mathematics education (pp. 481–503). Routledge. [Google Scholar]
- Coburn, C. E., & Penuel, W. R. (2016). Research–practice partnerships in education: Outcomes, dynamics, and open questions. Educational Researcher, 45(1), 48–54. [Google Scholar] [CrossRef]
- Coburn, C. E., & Stein, M. K. (2010). Research and practice in education: Building alliances, bridging the divide. Rowman & Littlefield Publishers. [Google Scholar]
- Collins, A. (1992). Toward a design science of education (pp. 15–22). Springer. [Google Scholar]
- Cong-Lem, N. (2021). Teacher agency: A systematic review of international literature. Issues in Educational Research, 31(3), 718–738. [Google Scholar]
- Coulter, C., & Jiménez-Silva, M. (2017). Culturally sustaining and revitalizing pedagogies: Language, culture, and power. Emerald Publishing. [Google Scholar]
- Crespo, S. (2020). Learning to pose collaborative mathematics problems with secondary prospective teachers. International Journal of Educational Research, 102, 101430. [Google Scholar] [CrossRef]
- Cvencek, D., Nasir, N. I. S., O’Connor, K., Wischnia, S., & Meltzoff, A. N. (2015). The development of math–race stereotypes: “They say Chinese people are the best at math”. Journal of Research on Adolescence, 25(4), 630–637. [Google Scholar] [CrossRef]
- Dabbagh, N., & Castaneda, L. (2020). The PLE as a framework for developing agency in lifelong learning. Educational Technology Research and Development, 68(6), 3041–3055. [Google Scholar] [CrossRef]
- Darling-Hammond, L., & Richardson, N. (2009). Research review/teacher learning: What matters. Educational Leadership, 66(5), 46–53. [Google Scholar]
- Daro, P., & Asturias, H. (2019). Branching out: Designing high school math pathways for equity. Just Equations. [Google Scholar]
- Design-Based Research Collective. (2003). Design-based research: An emerging paradigm for educational inquiry. Educational Researcher, 32(1), 5–8. [Google Scholar] [CrossRef]
- Donohoo, J. (2017). Collective teacher efficacy research: Implications for professional learning. Journal of Professional Capital and Community, 2(2), 101–116. [Google Scholar] [CrossRef]
- Donohoo, J., & Velasco, M. (2016). The transformative power of collaborative inquiry: Realizing change in schools and classrooms. Corwin Press. [Google Scholar]
- Dweck, C. S. (2006). Mindset: The new psychology of success. Random house. [Google Scholar]
- Dweck, C. S., & Yeager, D. S. (2019). Mindsets: A view from two eras. Perspectives on Psychological Science, 14(3), 481–496. [Google Scholar] [CrossRef]
- Ecclestone, K. (2007). An identity crisis? The importance of understanding agency and identity in adults’ learning. Studies in the Education of Adults, 39(2), 121–131. [Google Scholar] [CrossRef]
- Empson, S., & Levi, L. (2011). Extending children’s mathematical thinking: Fractions and decimals: Innovations in cognitively guided instruction. Heinemann. ISBN 978-0-325-03053-1/0-325-03053-7/SKU E03053. [Google Scholar]
- Espinas, D. R., & Fuchs, L. S. (2022). The effects of language instruction on math development. Child Development Perspectives, 16(2), 69–75. [Google Scholar] [CrossRef]
- Faltis, C. J., & Valdés, G. (2016). Preparing teachers for teaching in and advocating for linguistically diverse classrooms: A vade mecum for teacher educators. In Handbook of research on teaching (pp. 549–592). MacMillan & Co., Ltd. [Google Scholar]
- Farrell, C. C., Penuel, W. R., Coburn, C. E., Daniel, J., & Steup, L. (2021). Practice partnerships in education: The state of the field. William T. Grant Foundation. [Google Scholar]
- Featherstone, H., Crespo, S., Jilk, L., Oslund, J., Parks, A., & Wood, M. (2011). Smarter together! Collaboration and equity in the elementary math classroom. National Council of Teachers of Mathematics. [Google Scholar]
- García, O., Johnson, S. I., Seltzer, K., & Valdés, G. (2017). The translanguaging classroom: Leveraging student bilingualism for learning (pp. v–xix). Caslon. [Google Scholar]
- Garet, M. S., Porter, A. C., Desimone, L., Birman, B. F., & Yoon, K. S. (2001). What makes professional development effective? Results from a national sample of teachers. American Educational Research Journal, 38(4), 915–945. [Google Scholar] [CrossRef]
- Gay, G. (2021). Culturally responsive teaching: Ideas, actions, and effects. In Handbook of urban education (pp. 212–233). Routledge. eBook ISBN 9780429331435. [Google Scholar]
- Goddard, R., Goddard, Y., Sook Kim, E., & Miller, R. (2015). A theoretical and empirical analysis of the roles of instructional leadership, teacher collaboration, and collective efficacy beliefs in support of student learning. American Journal of Education, 121(4), 501–530. [Google Scholar] [CrossRef]
- Gresalfi, M. S., & Cobb, P. (2006). Cultivating students’ discipline-specific dispositions as a critical goal for pedagogy and equity. Pedagogies, 1(1), 49–57. [Google Scholar] [CrossRef]
- Gutiérrez, R. (2017). Living mathematx: Towards a vision for the future. North American chapter of the international group for the psychology of mathematics education. Available online: https://eric.ed.gov/?id=ED581384 (accessed on 1 June 2025).
- Herbel-Eisenmann, B. A., Wagner, D., Johnson, K. R., Suh, H., & Figueras, H. (2015). Positioning in mathematics education: Revelations on an imported theory. Educational Studies in Mathematics, 89, 185–204. [Google Scholar] [CrossRef]
- Hill, H. C., Ball, D. L., & Schilling, S. G. (2008). Unpacking pedagogical content knowledge: Conceptualizing and measuring teachers’ topic-specific knowledge of students. Journal for Research in Mathematics Education, 39(4), 372–400. [Google Scholar] [CrossRef]
- Huang, B., Jong, M. S. Y., Tu, Y. F., Hwang, G. J., Chai, C. S., & Jiang, M. Y. C. (2022). Trends and exemplary practices of STEM teacher professional development programs in K-12 contexts: A systematic review of empirical studies. Computers & Education, 189, 104577. [Google Scholar] [CrossRef]
- Hunter, J. (2021). An intersection of mathematics educational values and cultural values: Pāsifika students’ understanding and explanation of their mathematics educational values. ECNU Review of Education, 4(2), 307–326. [Google Scholar] [CrossRef]
- Hunter, J., & Miller, J. (2022). Using a culturally responsive approach to develop early algebraic reasoning with young diverse learners. International Journal of Science and Mathematics Education, 20(1), 111–131. [Google Scholar] [CrossRef]
- Hunter, R., & Civil, M. (2021). Collaboration in mathematics: Taking a sociocultural perspective. Avances de Investigacion en Educacion Matematica, 19, 7–20. [Google Scholar] [CrossRef]
- Hunter, R., Hunter, J., & Bills, T. (2019). Enacting culturally responsive or socially response-able mathematics education. In Living culturally responsive mathematics education with/in Indigenous communities (pp. 137–154). Brill. [Google Scholar]
- Jacobs, V. R., Empson, S. B., Jessup, N. A., Dunning, A., Pynes, D. A., Krause, G., & Franke, T. M. (2024). Profiles of teachers’ expertise in professional noticing of children’s mathematical thinking. Journal of Mathematics Teacher Education, 27(3), 295–324. [Google Scholar] [CrossRef]
- Jones, M., & Charteris, J. (2017). Transformative professional learning: An ecological approach to agency through critical reflection. Reflective Practice, 18(4), 496–513. [Google Scholar] [CrossRef]
- Kelly, A. E. (2016). Design research in education: Yes, but is it methodological? In Design-based research (pp. 115–128). Psychology Press. [Google Scholar]
- Kibler, A. K., Walqui, A., & Bunch, G. C. (2015). Transformational opportunities: Language and literacy instruction for English language learners in the Common Core era in the United States. TESOL Journal, 6(1), 9–35. [Google Scholar] [CrossRef]
- Kolovou, M. (2023). Embracing culturally relevant education in mathematics and science: A literature review. The Urban Review, 55(1), 133–172. [Google Scholar] [CrossRef]
- Korthagen, F. (2016). Inconvenient truths about teacher learning: Towards professional development 3.0. Teachers and Teaching, 23(4), 387–405. [Google Scholar] [CrossRef]
- Kraft, M. A., Blazar, D., & Hogan, D. (2018). The effect of teacher coaching on instruction and achievement: A meta-analysis of the causal evidence. Review of Educational Research, 88(4), 547–588. [Google Scholar] [CrossRef]
- Ladson-Billings, G. (2014). Culturally relevant pedagogy 2.0: Aka the remix. Harvard Educational Review, 84(1), 74–84. [Google Scholar] [CrossRef]
- Lee, O. (2019). Aligning English language proficiency standards with content standards: Shared opportunity and responsibility across English learner education and content areas. Educational Researcher, 48(8), 534–542. [Google Scholar] [CrossRef]
- Lehrer, R. (2009). Designing to develop disciplinary dispositions: Modeling natural systems. American Psychologist, 64(8), 759. [Google Scholar] [CrossRef] [PubMed]
- Loyola Marymount University Center for Equity for English Learners and Californians Together. (2024, October 22). Elevating integrated English language development (iELD) in mathematics instruction for multilingual/English learners. Available online: https://drive.google.com/drive/folders/1_ZdikYvHkS4YX34nREv-XxZC6lWZl4M7 (accessed on 15 April 2025).
- Lucas, T., & Villegas, A. M. (2013). Preparing linguistically responsive teachers: Laying the foundation in preservice teacher education. Theory Into Practice, 52(2), 98–109. [Google Scholar] [CrossRef]
- Lynch, K., Hill, H. C., Gonzalez, K. E., & Pollard, C. (2019). Strengthening the research base that informs STEM instructional improvement efforts: A meta-analysis. Educational Evaluation and Policy Analysis, 41(3), 260–293. [Google Scholar] [CrossRef]
- Martin, D. B. (2012). Learning mathematics while Black. Educational Foundations, 26, 47–66. [Google Scholar]
- Miller-Cotto, D., & Lewis, N. A., Jr. (2020). Am I a “math person”? How classroom cultures shape math identity among Black and Latinx students. OSF Preprints. [Google Scholar]
- Miura, I. T., Okamoto, Y., Vlahovic-Stetic, V., Kim, C. C., & Han, J. H. (1999). Language supports for children’s understanding of numerical fractions: Cross-national comparisons. Journal of Experimental Child Psychology, 74(4), 356–365. [Google Scholar] [CrossRef]
- Mohamed, N. (2022, April 27). Using language portraits to explore student identities. TESOL International Association. Available online: https://www.tesol.org/blog/posts/using-language-portraits-to-explore-students-identities/ (accessed on 1 May 2025).
- Moll, L. (2014). L. S. Vygotsky and education. Routledge. [Google Scholar]
- O’Halloran, K. L. (2015). The language of learning mathematics: A multimodal perspective. The Journal of Mathematical Behavior, 40, 63–74. [Google Scholar] [CrossRef]
- Paris, D. (2012). Culturally sustaining pedagogy: A needed change in stance, terminology, and practice. Educational Researcher, 41(3), 93–97. [Google Scholar] [CrossRef]
- Paris, D., & Alim, H. S. (Eds.). (2017). Culturally sustaining pedagogies: Teaching and learning for justice in a changing world. Teachers College Press. [Google Scholar]
- Penuel, W. R., Fishman, B. J., Haugan Cheng, B., & Sabelli, N. (2011). Organizing research and development at the intersection of learning, implementation, and design. Educational Researcher, 40(7), 331–337. [Google Scholar] [CrossRef]
- Poehner, M. E., & Infante, P. (2017). Mediated development: A Vygotskian approach to transforming second language learner abilities. Tesol Quarterly, 51(2), 332–357. [Google Scholar] [CrossRef]
- Prediger, S., Kuzu, T., Schüler-Meyer, A., & Wagner, J. (2019). One mind, two languages—Separate conceptualisations? A case study of students’ bilingual modes for dealing with language-related conceptualisations of fractions. Research in Mathematics Education, 21(2), 188–207. [Google Scholar] [CrossRef]
- Reeves, T., & McKenney, S. (2012). 7 things you should know about educational design research. Educause 7 Things Series. Open Universiteit. Available online: https://core.ac.uk/download/390062948.pdf (accessed on 1 June 2025).
- Rittle-Johnson, B. (2024). Encouraging students to explain their ideas when learning mathematics: A psychological perspective. The Journal of Mathematical Behavior, 76, 1–8. [Google Scholar] [CrossRef]
- Sammons, L. (2018). Teaching students to communicate mathematically. Ascd. [Google Scholar]
- Sandoval, W. (2014). Conjecture mapping: An approach to systematic educational design research. Journal of the Learning Sciences, 23(1), 18–36. [Google Scholar] [CrossRef]
- Sancar, R., Atal, D., & Deryakulu, D. (2021). A new framework for teachers’ professional development. Teaching and Teacher Education 101, 1–12. [Google Scholar] [CrossRef]
- Sarkar, M., Gutierrez-Bucheli, L., Yip, S. Y., Lazarus, M., Wright, C., White, P. J., Ilic, D., Hiscox, T. J., & Berry, A. (2024). Pedagogical content knowledge (PCK) in higher education: A systematic scoping review. Teaching and Teacher Education, 144, 104608. [Google Scholar] [CrossRef]
- Short, D. J. (2017). How to integrate content and language learning effectively for English language learners. EURASIA Journal of Mathematics, Science and Technology Education, 13(7b), 4237–4260. [Google Scholar] [CrossRef]
- Shulman, L. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57(1), 1–23. [Google Scholar] [CrossRef]
- Silver, A. M., & Libertus, M. E. (2022). Environmental influences on mathematics performance in early childhood. Nature Reviews Psychology, 1(7), 407–418. [Google Scholar] [CrossRef]
- Smith, M., & Stein, M. K. (2018). 5 Practices for orchestrating productive mathematics discussion. National Council of Teachers of Mathematics. [Google Scholar]
- Swain, M. (2006). Languaging, agency and collaboration in advanced second language proficiency. In H. Byrnes (Ed.), Advanced language learning: The contribution of halliday and vygotsky, continuum, London (pp. 95–108). Continuum. [Google Scholar]
- Swartz, B. A., & DeRosa, K. (2023). Designing the supports for successful groupwork: How to make your task group-WORTHY. Middle School Journal, 54(5), 4–15. [Google Scholar] [CrossRef]
- Timperley, H., Wilson, A., Barrar, H., & Fung, I. (2007). Teacher professional learning and development. Best evidence synthesis iteration (BES). International Academy of Education. Available online: http://www.iaoed.org/downloads/EdPractices_18.pdf (accessed on 1 June 2025).
- Torrance, D., & Forde, C. (2017). Redefining what it means to be a teacher through professional standards: Implications for continuing teacher education. European Journal of Teacher Education, 40(1), 110–126. [Google Scholar] [CrossRef]
- Valdés, G., Bunch, G., Snow, C., Lee, C., & Matos, L. (2005). Enhancing the development of students’ language (s). In Preparing teachers for a changing world: What teachers should learn and be able to do (pp. 126–168). Jossey-Bass. [Google Scholar]
- Von Esch, K. S., & Kavanagh, S. S. (2018). Preparing mainstream classroom teachers of English learner students: Grounding practice-based designs for teacher learning in theories of adaptive expertise development. Journal of Teacher Education, 69(3), 239–251. [Google Scholar] [CrossRef]
- Voogt, J., Laferriere, T., Breuleux, A., Itow, R. C., Hickey, D. T., & McKenney, S. (2015). Collaborative design as a form of professional development. Instructional Science, 43, 259–282. [Google Scholar] [CrossRef]
- Vygotsky, L. S. (1987). The collected works (Vol. 3). Plenum Press. [Google Scholar]
- Wang, F., & Hannafin, M. (2005). Design-based research and technology-enhanced learning environments. Educational Technology Research and Development, 53(4), 5–23. [Google Scholar] [CrossRef]
- Wang, S. H., Lang, N., Bunch, G. C., Basch, S., McHugh, S. R., Huitzilopochtli, S., & Callanan, M. (2021). Dismantling persistent deficit narratives about the language and literacy of culturally and linguistically minoritized children and youth: Counter-possibilities. In Frontiers in education (Vol. 6, p. 641796). Frontiers Media SA. [Google Scholar] [CrossRef]
- Webster-Wright, A. (2009). Reframing professional development through understanding authentic professional learning. Review of Educational Research, 79(2), 702–739. [Google Scholar] [CrossRef]
- Wei, L. (2018). Translanguaging as a practical theory of language. Applied Linguistics, 39(1), 9–30. [Google Scholar] [CrossRef]
- Willis, J. (2010). Learning to love math: Teaching strategies that change student attitudes and get results. Association for Supervision and Curriculum Development. [Google Scholar]
- Zwiers, J., Dieckmann, J., Rutherford-Quach, S., Daro, V., Skarin, R., Weiss, S., & Malamut, J. (2017). Understanding Language/Stanford Center For Assessment, Learning, and Equity. Stanford. Available online: https://ul.stanford.edu/sites/default/files/resource/2021-11/Principles%20for%20the%20Design%20of%20Mathematics%20Curricula_1.pdf (accessed on 1 June 2025).
- Zwiers, J., O’Hara, S., & Pritchard, R. (2014). Common core standards in diverse classrooms: Essential practices for developing academic language and disciplinary literacy (1st ed.). Routledge. [Google Scholar] [CrossRef]


| 3 Pillars | Practitioners as Designers of Their Practice | Teaching Strategies |
|---|---|---|
| Attend to Students’ Full Linguistic Repertoires |
| Scaffolds:
|
| Attend to Students’ Math Ideas |
|
|
| Cultural Responsiveness |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiménez-Silva, M.; Martin, R.; Restani, R.; Abdelrahim, S.; Albano, T. Supporting Multilingual Students’ Mathematical Discourse Through Teacher Professional Development Grounded in Design-Based Research: A Conceptual Framework. Educ. Sci. 2025, 15, 778. https://doi.org/10.3390/educsci15060778
Jiménez-Silva M, Martin R, Restani R, Abdelrahim S, Albano T. Supporting Multilingual Students’ Mathematical Discourse Through Teacher Professional Development Grounded in Design-Based Research: A Conceptual Framework. Education Sciences. 2025; 15(6):778. https://doi.org/10.3390/educsci15060778
Chicago/Turabian StyleJiménez-Silva, Margarita, Robin Martin, Rachel Restani, Suzanne Abdelrahim, and Tony Albano. 2025. "Supporting Multilingual Students’ Mathematical Discourse Through Teacher Professional Development Grounded in Design-Based Research: A Conceptual Framework" Education Sciences 15, no. 6: 778. https://doi.org/10.3390/educsci15060778
APA StyleJiménez-Silva, M., Martin, R., Restani, R., Abdelrahim, S., & Albano, T. (2025). Supporting Multilingual Students’ Mathematical Discourse Through Teacher Professional Development Grounded in Design-Based Research: A Conceptual Framework. Education Sciences, 15(6), 778. https://doi.org/10.3390/educsci15060778








