Eye Tracking Characterization of Algebraic Fraction Simplifications

Abstract

Several major studies require that students understand and master the concepts and procedures of mathematics. More specifically, an area of mathematics such as algebra requires students to be able to simplify, operate with, or solve fractions. Many students entering university show numerous shortcomings and errors, especially when simplifying algebraic fractions. This is why we conducted a study using eye-tracking techniques to better understand how students process these types of exercises in attentional terms, comparing students who can handle them successfully against those who show errors in their procedures. For this purpose, we evaluated the eye movements of 64 students from different university majors to characterize the attentional–visual strategies they use to simplify four different algebraic fraction exercises. We found that each type of simplification exercise needs a specific strategy where some parts of the rational algebraic expressions are cognitively relevant. Students with correct answers tend to allocate attention to these elements. Students with incorrect answers tend to find similar expressions with the intention to cancel them out, without applying any metacognitive thinking. The rational algebraic expression needs to be taught in a more conceptual manner than procedural.

1. Introduction

Fractions serve as a foundational concept for algebra and higher mathematics (Booth & Newton, 2012; Brown & Quinn, 2007), and it is undeniable that college students continue to struggle with understanding fraction concepts and performing operations on both numerical and algebraic fractions.

Error patterns in basic operations on common fractions may lead to difficulties when applying fraction concepts to algebraic rational expressions (Lee & Boyadzhiev, 2020; Yakubu & Jungudo, 2023). Students often use rules without understanding and depending on cues (Skemp, 1978), which leads them to retrieve incomplete or wrong rules instead of having a rational understanding, which implies meaning and reasoning.

The fundamental principle of fractions states that multiplying or dividing both the numerator and denominator of a fraction by the same nonzero number or expression results in a fraction that is equal to the original fraction. Effectively simplifying fractions requires an understanding of the concept of factoring the entire numerator and denominator and cancelling out common factors—not terms—between them. The simplification of algebraic fractions has strong visual cues in recognizing like or identical terms or factors. It is important to note that terms are separated by addition or subtraction signs and cannot be cancelled directly. For this study, students must distinguish between terms and factors, as only factors can be simplified. Figueras et al. (2008) and Mhakure et al. (2014) identified and classified misconceptions in simplifying rational algebraic expressions: Cancellation Error, Partial Cancellation Error, De-fractionalization, Linearization, Like Term Error, and Equationalization. These errors, according to Baidoo et al. (2020), may be due to overgeneralization during the assimilation of new knowledge (Makonye & Stepwell, 2016).

However, it is not enough that the explanation that good “fraction simplifiers” have developed conceptual and procedural algebraic fractional knowledge and “non fraction simplifiers” have not. The lack of specificity does not explain the problem (see Ni & Zhou, 2005; Brizuela, 2006; Hecht & Vagi, 2010; Novianggraeni et al., 2019; Lenz et al., 2020 for further review). Thus, to better understand the difference, we have to resort to other techniques that provide more precise information about how the brain processes the simplification of algebraic fractions.

The use of the eye tracker (ET) in cognitive neuroscience is not new. It has been used to study many cognitive phenomena. The basic principle is that it measures the attentional allocation to a specific stimulus by measuring the movements of the eye; in other words, it measures where, how, and in what order gaze is being directed during a specific task (Carter & Luke, 2020). Nonetheless, the relation between the eye and the mind is more complex than that. The different variables of the movement and steadiness of the eye change the interpretation of the underlying cognitive processes for a given visual stimulus according to a given task. These variables are called “eye-tracking measures” of cognitive process (Liu & Cui, 2025).

A few studies that analyzed fixations during the comparison of fractions demonstrated that people use a componential processing strategy when comparing two fractions with common components or for which the decision-relevant components are easy to identify, and a holistic strategy if not, meaning that the strategy used is adaptive depending on the context and the numbers presented (Obersteiner et al., 2014; Huber et al., 2014; Obersteiner & Tumpek, 2016; Ischebeck et al., 2016; Miller Singley & Bunge, 2018). A study carried out by Miller Singley et al. (2020) found that when learning to compare fractions, children who had acquired the basic fraction rules made more eye movements than adults or less proficient children, and that correct responses were associated with a normative gaze pattern (the typical or expected way people direct their visual attention). Meaning that the student pays more attention to those relevant relationships of the numbers. In contrast, another eye-tracking study found that when adding fractions, participants processed the fraction components separately rather than the overall fraction magnitudes. The denominators are the ones that required more attention to adapt the strategy used to find the solution (Obersteiner & Staudinger, 2018).

As seen, there is scarce publication about the topic, and more investigation is needed.

This study aims to analyze and characterize eye movements and behaviour in areas of interest (AOIs) while simplifying algebraic fractions. Students with correct answers were compared to those with incorrect answers.

In this context, the present study addresses the following questions: (1) What are the main differences in the strategic simplification of four different algebraic fractions using ET analysis between the group of students with correct answers and the group with incorrect answers? (2) What are the main ET measurements of students with correct answers using the simplification strategy accurately, depending on the exercise?

2. Materials and Methods

Participants were 64 students of different university courses at Universidad Panamericana in Guadalajara, Mexico, aged between 17 and 21 years, with a mean age of 18.55 (SD = 0.90). The sample consisted of 37 women and 27 men, including 21 engineering students, 33 business administration students, and 10 students from psychology or pedagogy programmes. All participants signed an informed consent form.

None of the participants had any reported history of neurological or psychiatric illness. They were asked if they could see without any eye aid, like glasses, and if they had previously taken any drugs, coffee, tea, or alcohol. Also, they were asked to avoid using mascara or makeup, and they all reported having slept between 7 and 8 h the night before.

The exercises were displayed one by one on the screen, and the participants were required to perform the mental simplification or reduction in the fraction exercises. Once participants had obtained an answer, they were instructed to state it aloud.

The study consisted of the simplification of four different rational algebraic expressions, where the following data were recorded: answer correctness, duration time (D), fixation count (FC) on fraction components (areas of interest, AOIs), as well as saccades count (SC), revisit count (RC), and fixation sequences (TTFF sequence). The cognitive implications of the analyzed variables are summarized in

Table 1. Eye-tracking measurements.

Variable	Description
AOI	An AOI is a portion of stimuli that is utilized to analyze eye gaze metrics and associate eye movement indicators with the specific area of the stimuli examined (e.g., the duration spent observing a particular element within the stimulus) (Hessels et al., 2016).
Heatmaps	Heatmaps are visual tools that display the distribution of gaze points using a colour gradient over the stimulus, where red, yellow, and green indicate decreasing levels of visual attention. They provide both qualitative and quantitative insights into reading and viewing patterns. (Ghosh et al., 2021).
Fixation sequences TTFF	Fixation sequences show the path and order in which participants direct their gaze across AOIs, often starting at the centre due to fixation bias and then moving toward the most engaging elements. This order offers insights into attention patterns and underlying cognitive strategies. (Ying Tsang et al., 2010).
Fixation counts FC	Indicates the total number of gaze fixations performed to explore or interpret specific components within Areas of Interest (AOIs). (Rahal & Fiedler, 2019).
Revisits counts RC	Refers to the average number of times participants redirected their gaze back to a specific AOI. This metric captures how often attention returns to a particular area, which may occur due to visual appeal, cognitive dissonance, or emotional responses such as confusion or frustration. (RealEye, 2025).
Saccades count SC	Rapid, ballistic eye movements that swiftly redirect the point of fixation, typically aligning the line of sight with a desired target through a single, fluid motion. (Purves et al., 2001; Ramat et al., 2008).

. Heat maps were generated to compare differences between groups.

The eye-tracking measurements were performed using the Smart Eye AI-X 60 HZ mounted below the computer screen, with the participant seated directly in front of the eye tracker, approximately 60 cm from the screen. To capture eye tracking data, participants were required to follow a circle with their gaze as it moved around the screen for calibration. The iMotions screen-based eye-tracking module was used to process the data, allowing gaze location and duration to be overlaid on the gameplay footage. Gaze location was represented by circles, with the circle size increasing in proportion to fixation duration. The stimuli were presented in white text on a black background, with a resolution of 1920 × 1080 pixels, occupying 70% of the screen. The stimuli were presented on a Dell Intel^® Core™ i9-13900 computer. They were presented with no time limit; when the student had the answer, they had to say it out loud to the evaluator and then pass to the next exercise.

For data analysis, students were divided into two groups for each exercise: those with a correct answer (C) and those with an incorrect answer (IC), to conduct a comparative analysis of the group characteristics. The statistical analysis was performed using the software IBM SPSS Statistics (version 29, IBM Corp., Armonk, NY, USA).

Different statistical tests were employed to compare the metrics. For the duration (D) between C and IC, a Kolmogorov–Smirnov test, to analyze if the data have a normal distribution, and a Mann–Whitney test was conducted to compare the distributions of both groups. To compare FC, RC, and SC using the AOIs of each exercise, a Kruskal–Wallis test was performed to determine whether statistically significant differences existed between the medians of FC, RC, and SC concerning AOIs in each exercise.

The hypothesis for the different comparisons was as follows:

Duration

Null hypothesis (H0).

There is no difference between group distributions.

Alternative hypothesis (Ha).

Samples come from different populations, they have statistically different distributions.

FC, RC, and SC

The Kruskal–Wallis test:

Null hypothesis (H₀).

There is no statistically significant difference in the median values of FC, RC, and SC concerning AOIs across the exercises.

Alternative hypothesis (H₁).

At least one of the median values of FC, RC, and SC concerning AOIs differs significantly across the exercise.

If the alternative hypothesis is accepted—that at least one median value differs significantly from another—a post hoc pairwise comparison is performed using Dunn’s test with a Bonferroni correction to control for multiple comparisons, to identify which AOIs differ (Jamil & Khanam, 2024; Ortega, 2023; Dinno, 2015).

ITEMS

The study consisted of four simplifying exercises of algebraic fractions. With the next four simplifications of algebraic rational expressions proposed, a wide variety of errors can be analyzed, whether typical or singular. The sequence of these four algebraic fractions, thoroughly discussed, is important since they represent a gradual increment in the possibility of misconceptions in students’ procedures. Each exercise incorporates a minor variation from the preceding rational expression, with the specific aim of assessing students’ misconceptions. A detailed description of the procedure required for the simplification of each exercise is presented in

Table 2. Four rational algebraic expressions to be simplified.

Rational Algebraic Expression	Correct Answer	Important Facts Simplifying Each Expression
${\displaystyle \frac{(x+3)(x-5)}{(x+3)}}$	$x-5$	The first exercise was designed to analyze whether students know the concept of simplification or cancellation of identical factors in the numerator and denominator.
${\displaystyle \frac{x+3}{(x+3)(x-5)}}$	${\displaystyle \frac{1}{x-5}}$	The same concept should be applied in the second exercise, with the modification that the resulting factor appears in the denominator. Students have to remember the neutral elements “1”, when dividing the common factor (x + 3). A “1” prevails in the numerator.
${\displaystyle \frac{\left(x+3\right)+1}{x+3}}$	${\displaystyle \frac{x+4}{x+3}}$ or $1+{\displaystyle \frac{1}{x+3}}$	Students should observe that although the expression (x + 3) appears in both the numerator and the denominator, the presence of an addition operation sign (an addition of 1) indicates that these terms are not factors and therefore cannot be simplified, and addition in the numerator should be performed. On the other hand, the fraction can be split into two separate fractions; one could be simplified, and the other not.
${\displaystyle \frac{x\left(x+3\right)+(x+3)}{x+3}}$	$x+1$	The fourth and final exercise also includes an addition, so it can only be simplified if the term (x + 3) in the numerator is factored and then simplified. Alternatively, the expression can be split into two separate fractions and simplified individually, ultimately yielding the same result of x + 1. In this case, the brackets around (x + 3) may suggest a factorization of this expression in the numerator.

Elaboration: Authors.

.

For a better understanding, in

Table 3. The most common incorrect “simplifications” of the four rational algebraic expressions.

Rational Algebraic Expression	Incorrect Answer	Important Facts Simplifying Each Expression
${\displaystyle \frac{(x+3)(x-5)}{(x+3)}}$	${\displaystyle \frac{x^2-15}{x+3}}$ ${\displaystyle \frac{x^2-2}{x+3}}$ ${\displaystyle \frac{2x}{3x}}$	Expanding by multiplying the factors in the numerator may generate other mistakes and no simplification (EX) (1A) Only the first terms and last terms were multiplied (1B) The first terms were multiplied, and the second terms were added. (1C) Concatenation (CON), can be performed in several ways: 3x − −5x divided by 3x
${\displaystyle \frac{x+3}{(x+3)(x-5)}}$	${\displaystyle \frac{\mathrm{x}+3}{(x+3)(x-5)}}\ne x-5$	(2A) De-fractionalization error (DF), the “1” in the numerator is ignored, and the denominator is written as the numerator. Other errors align with the patterns observed in the first simplification exercise.
${\displaystyle \frac{\left(x+3\right)+1}{x+3}}$	${\displaystyle \frac{\left(x+3\right)+1}{x+3}}\ne 1$	(3A) Partial Cancellation Error (PCE) is the most common error
${\displaystyle \frac{x\left(x+3\right)+(x+3)}{x+3}}$	$2x+3$ $x^2+3x$	Partial Cancellation Errors (PCE) occur in two ways: (4A) The first expression (x + 3) in the numerator is cancelled (4B) The second expression (x + 3) is cancelled. These two error options yield different expressions.

Elaboration: Author.

, the various incorrect answers mentioned in the literature in simplifying algebraic rational expressions are presented. To illustrate the types of errors expected from the students in this study through the proposed simplification exercises. These errors are coded in accordance with the literature: Cancellation Errors (CE), Partial Cancellation Errors (PCE), De-fractionalization (DF), Linearization (LI), Like Term Error (LTE), Equationalization (E), Concatenation (CON), and Expansion (EX). (Eccius-Wellmann, 2008; Malle, 1993; Figueras et al., 2008; Mhakure et al., 2014; Ascencio & Eccius-Wellmann, 2019; Taban & Cadorna, 2018). Some are combined errors, and it may be challenging for the teacher to gain insight into the students’ cognitive processes.

As seen in Table 3, errors in simplifying algebraic fractions are mostly due to overgeneralization of cancellation methods, which means that students do not identify when an algebraic expression (in the numerator and denominator) is factored. Errors arise when they cancel out terms that are the same in the numerator and denominator.

3. Results and Discussion

Some errors are singular, meaning there is no specific pattern in how students simplify an algebraic fraction, leading to mistakes related to algebraic concepts, such as concatenation errors or misunderstandings of the meaning of a factor, or perhaps the need to perform operations between factors and make some mistakes when doing so. However, other errors committed by students are systematic, known as typical errors, occurring consistently among many students whenever they are presented with a similar exercise.

It would be beyond the scope of this study to explain each individual error, as some result from a combination of multiple error types. For example: the error 1A, was further interpreted as 2x − −15 in the numerator. Errors were classified by their first error, and subsequent errors were counted according to the corresponding original error (see Table 3). Percentages are reported with respect to the total number of participants. For example: exercise 1; Errors 1, 1A, and 1B: 11%

Error 1C: 7.8%

For exercise 2, Error 2: 20.3%, other errors have the same origin as 1.

For exercise 3, 48.4%

For exercise, Error 4A: 9.4%

Error 4B: 25%

For this study, no distinction was made between types of errors; students’ responses were classified as correct (C) or incorrect (IC).

In

Table 4. Exercise 1: Heatmaps, metrics with significant differences, and interpretation.

C Correct Answer	Metrics with Significant Differences (p Values in Brackets)	IC Incorrect Answer
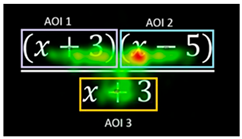	Exercise 1 Duration $ICD$ M = 13,399.29 ms, SD = 7328.63 CD M = 6980.28 ms, SD = 4693.66 Normal distributed different distributions p < 0.001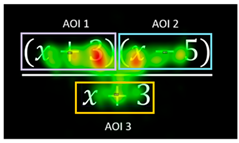
Percentage of C: 64% The heatmap shows a greater level of visual attention on AOI2. Correct respondents show less attention to AOI1 and AOI3.	For all AOI’s, C-FC < IC-FC; p < 0.001 C-RC AOI2 < IC-RC AOI2; p < 0.001 C-RC AOI3 < IC-RC AOI3; p < 0.001 C-RC AOI1 < IC-RC AOI1; p < 0.001 Both C and IC have significantly less SC on AOI2 than on AOI1, p < 0.001	Percentage of IC: 36% The heatmap shows a greater level of attention on AOI1, followed by attention on AOI2
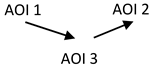	Order of TTFF time to first fixation: For C; AOI1→AOI3→AOI2 For IC; AOI1→AOI2→AOI3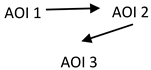
Analysis and interpretation Exercise 1:
D: The C respondents require less time to give their answer. This indicates that IC may have some difficulty processing information. TTFF sequence: The order in which they focus on the distinct AOIs is different; C respondents direct their attention first to the factor of the numerator (AOI1), then to the denominator factor (AOI3), and finally to the second factor of the numerator (AOI2). They stay longer on AOI2, which may be because AOI2 will prevail after the simplification. IC focuses sequentially from left to right, and then on the denominator. This may be due to the convention of reading from left to right, which might not facilitate the simplification of AOI1 and AOI3, because they will try to multiply the factors in the numerator. FC: The total number of gaze fixations on all AOIs (fixation count) was significantly less for C than for IC. C respondents need fewer fixations to explore or interpret specific components within the AOIs. This may suggest that IC respondents have difficulty recognizing the components. RC: Revisit counts on AOI2 and AOI3 were significantly less for C than for IC; IC may struggle with what to do with the second factor in the numerator. SC: Saccade counts on AOI2 for C and IC respondents are greater than SC on AOI1. For C, it might have a different interpretation than for IC respondents. For the first group (C), this may indicate that the AOI2 factor remains important even after simplification. Respondents in the IC group may believe they need to expand both factor AOI1 and factor AOI2 through multiplication, a process that is often carried out incorrectly.

Elaborated by the authors.

,

Table 5. Exercise 2: Heatmaps, metrics with significant differences, and interpretation.

C Correct Answer	Metrics with Significant Differences (p Values in Brackets)	IC Incorrect Answer
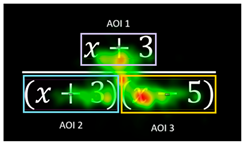	Exercise 2 Duration $ICD$ M = 28,297.77 ms, SD = 33,109.69 CD M = 11,727.77 ms, SD = 9988.79 different distributions p < 0.001
Percentage of C: 47% The heatmap shows more relative fixation time on AOI3; this factor is important because it is in the denominator.	C-FC-AOI 2 < C-FC-AOI 3 p = 0.031 C-FC-AOI2 < IC-FC-AOI2 p < 0.001 C-RC-AOI 2 < IC-RC-AOI 2 p = 0.029 C-SC-AOI 2 < C-SC-AOI 3 p = 0.004 C-SC-AOI 2 < IC-SC-AOI 2 p < 0.001	Percentage of IC: 53% More relative fixation on AOI2, little time fixation on AOI3, that is the important factor.
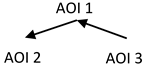	Order of TTFF time to first fixation: For C; AOI3→AOI1→AOI2 For IC; AOI2→AOI3→AOI1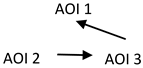
Analysis and interpretation Exercise 2
D: C respondents take less time to simplify the expression. TTFF sequence: C respondents look first at AOI3, the different factor (x − −5) from the others, and then at AOI1 and AOI2. The factor (x − 5) appears to be significant because of its placement in the denominator. IC respondents look from left to right in the denominator and afterwards on the numerator. This might be interpreted for IC that the larger expression in the denominator should be analyzed or operated on first. FC: For C, the intra fixation count on AOI3 is significantly greater than on the other AOIs. This may indicate increased attention and conscious recognition of the importance of AOI3. For IC, there is no significant difference between AOIs. RC: C has a significantly lower revisit count on AOI2 than IC. This probably means that C understands that AOI2 is important for simplification because it is a factor, but IC may have difficulties in understanding this part of the image (factor). SC: Intra-saccade count reveals that for C, AOI3 has a greater count; AOI3 may be important for C. But IC has a higher saccade count on AOI2 than C. This suggests that IC may place greater attentional conflict on AOI2.

Elaborated by the authors.

,

Table 6. Exercise 3: Heatmaps, metrics with significant differences, and interpretation.

C Correct Answer	Metrics with Significant Differences (p Values in Brackets)	IC Incorrect Answer
	Exercise 3 Duration $ICD$ M = 16,904.00 ms, SD = 13,987.2 CD M = 18,641.88 ms, SD = 9354.43 Normal distributed same distribution p = 0.196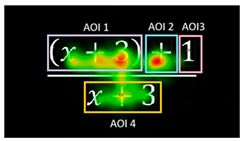
Percentage of C: 23% The heatmap shows an attention movement between AOI1 and AOI4, and a focus on the plus sign. Visual attention on the expression (x + 3) and the identification of the addition sign may indicate that the students know they cannot proceed with a cancellation shortcut.	C-FC-AOI1 > C-FC-AOI2, C-FC-AOI3, and C-FC-AOI4 p < 0.001 IC-FC-AOI1 > IC-FC-AOI2, IC-FC-AOI3, and IC-FC-AOI4 p < 0.001 IC-RC-AOI1 > IC-RC-AOI2, IC-RC-AOI3, and IC-RC-AOI4 p < 0.001 IC-SC-AOI1 > IC-SC-AOI2 p < 0.001 IC-SC-AOI1 > IC-SC-AOI4 p = 0.017	Percentage of IC: 77% The heatmap shows relatively higher attention on AOI1 and AOI2. The ‘1’ receives virtually no attention or is only perceived peripherally. The plus sign is probably the sign of their most common result, 1.
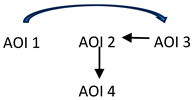	Order of TTFF time to first fixation: For C; AOI1→AOI3→AOI2 →AOI4 For IC; AOI1→AOI4→AOI2→ AOI3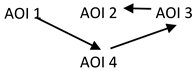
Analysis and interpretation Exercise 3
D: No statistically significant difference was found in the time taken by the groups to respond to the task. TTFF sequence: C respondents follow a sequence in which they analyze the components of the numerator, first skipping the addition sign, then returning to it immediately, and afterward moving on to the denominator. This sequence may suggest that C is conscious of the implications of the addition sign and the “1” before they look at the denominator to understand that the expressions (x + 3) in the numerator and denominator cannot be simplified or cancelled. IC respondents identify first the expressions (x + 3) in the numerator and denominator for a possible cancellation method and then analyze the addition sign and the “1”. FC: The fixation counts on AOI1 are the greatest for C and IC. RC: The revisit counts on all AOIs of C respondents have no statistical differences, but the revisit count on AOI1 of IC respondents is the greatest of all the AOIs. SC: There is no statistically significant difference in saccade count across all AOIs of the C group. The saccade count on AOI1 of IC is the greatest. This means that IC may be struggling with what to do with the first (x + 3) in the numerator. However, the TTFF sequence suggests that they want to cancel out this expression with the denominator, without considering the fact that the addition sign causes the numerator to consist of two distinct terms. SC: Intra-saccade count reveals that for C, AOI3 has a greater count; AOI3 may be important for C. But IC has a higher saccade count on AOI2 than C. This suggests that IC may place greater attentional conflict on AOI2.

Elaborated by the authors.

and

Table 7. Exercise 4: Heatmaps, metrics with significant differences, and interpretation.

C Correct Answer	Metrics with Significant Differences (p Values in Brackets)	IC Incorrect Answer
	Exercise 4 Duration $ICD$ M = 28,588.89 ms, SD = 20,007.48 CD M = 16,531.10 ms, SD = 6061.91 different distributions p < 0.001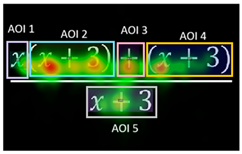
Percentage of C: 19% The heatmap shows greater visual attention on AOI3 (the addition sign is important in this exercise because simplification first involves factorization or fragmentation into two fractions with the same denominator. Therefore, paying attention to AOI3 may indicate awareness that cancellation cannot be applied without an algebraic transformation.	C-FC-AOI2 < C-FC-AOI1 p = 0.001 IC-FC-AOI2 > IC-FC-AOI1, IC-FC-AOI3, IC-FC-AOI4, IC-FC-AOI5 p < 0.001 IC-RC-AOI2 > IC-RC-AOI1, IC-RC-AOI3, IC-RC-AOI5 p = 0.004 IC-SC-AOI2 > IC-SC-AOI1, IC-SC-AOI3, IC-SC-AOI4, IC-SC-AOI5 p < 0.001	Percentage of IC: 81% The heatmap shows little attention to AOI3 (the addition sign that causes the numerator to have two terms). There is also relatively little attention to AOI5 compared with other similar expressions (AOI2 and AOI4). Most attention is focused on AOI2.
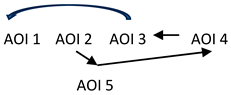	Order of TTFF time to first fixation: For C; AOI2→AOI5→AOI4→AOI3 →AOI1 For IC; AOI2→AOI4→AOI3→AOI5 →AOI1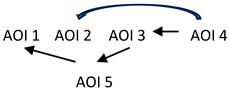
Analysis and interpretation Exercise 4
D: C respondents take statistically less time to simplify the expression. TTFF sequence: C respondents show a sequence where they identify all the expressions (x + 3) (AOI2, AOI15, and AOI4 in sequence), then focus on the addition sign (AOI3, with the greatest visual attention), which is important to recognize that the numerator has two terms. The sequence ends with AOI1. IC respondents focus their attention first on the two expressions (x + 3) in the numerator (AOI2 and AOI4, both with the greatest visual attention), then on the addition sign (AOI3), followed by the “x” (AOI1). This may indicate that the plus sign is less important to them. Another possibility is that IC is choosing which of the (x + 3) elements in the numerator can be cancelled out. FC, RC, and SC: IC-AOI2 has the highest intra-statistical values of SC, RC, and FC compared to AOI1, AOI3, AOI4, and AOI5. This indicates that IC focuses most on AOI2, the factor (x + 3) in the numerator. Students may need to pay more attention to process it. For C, there are no statistical differences between AOI’s.

Elaborated by the authors.

, AOIs were marked in different surrounding colours and correspond to the focuses of attention in the simplification of each exercise. The number after the acronyms and AOIs represents the area of interest number marked on the heatmaps. For example: C-FC-AOI 3 means: correct answer, fixation count at AOI 3 (third area of interest).

Also, the percentages of correct and incorrect answers are shown. The middle column of metrics will display only those with statistically significant differences. The heatmaps were interpreted below them. Ultimately, a possible interpretation of the differences in metrics between groups and within groups is presented. The analysis and interpretation of the results provide answers to the research questions.

Statistical analyses were performed at both intra- and inter-group levels. The prefix “intra-” denotes analyses within a single group across various eye-tracking measures of the AOIs, while “inter-” denotes comparisons between groups for a specific AOI.

4. Conclusions

Tasks on simplifying algebraic rational expressions were used to compare eye movements between students who provided a correct answer and those who made an error.

The percentage of correct answer respondents decreases from Exercise 1 to Exercise 4; this was expected because the difficulty of simplifying algebraic rational expressions increases. The first exercise, with a 64% correct answer rate, shows that students have studied the methods of cancelling and simplifying rational algebraic expressions. However, in the second exercise, the correct answer rate drops to 47%, with the majority committing a de-fractionalization error (DF) (students interpret a cancellation as an elimination, and the factor (x − −5) in the denominator is placed in the numerator). Exercises 3 and 4, which involve addition and do not allow for the direct simplification or cancellation of factors, are answered correctly by 23% and 19%, respectively. These errors are mainly Partial Cancellation Errors (PCE) (see Table 3). Apparently, when students do not recognize the important metacognitive aspect of distinguishing terms and factors, they tend to use an incorrect cancellation strategy.

The eye movement measurements allowed us to characterize the behaviour of respondents who provided a correct answer. Eye tracking may reflect the different modes of thinking, conceptual and non-conceptual thinking (Solstad et al., 2024). Students who rely on cancellation shortcuts without a conceptual understanding of factors or terms are less likely to succeed. Their problem-solving behaviour is marked by repetitive reexamination, as indicated by increased fixation, revisit, and saccade counts (Susac & Braeutigam, 2014). This pattern is further corroborated by the percentage of correct responses, which varies according to task difficulty.

We found that C respondents have a more efficient allocation of attention on the metacognitive aspects of the fraction, as Susac & Braeutigam (2014) stated. This distinction becomes more evident as the complexity of the exercise increases. In the first two exercises, attention was focused on the important factors when simplifying the expression. But, on exercises three and four, C focuses on the AOIs with the element (addition sign), which makes direct simplification impossible. C searches to identify the elements that allow a simplification or not.

On the other hand, IC respondents search for similar expressions in the numerator and denominator with the intention of a cancellation method, without understanding that it may not be possible to simplify. Overemphasis on cancellation exercises in algebraic fractions at prior educational levels may foster a long-term, unreflective use of the cross-out strategy. This results in a deficiency in metacognitive abilities.

The TTFF (time to first fixation) revealed the order of fixations on the different AOIs, which helps to understand how students first capture fraction information. A difference between C and IC respondents shows how the eye movements on the different elements affect the processing of information and the subsequent procedure for fraction simplification (see Table 4, Table 5, Table 6 and Table 7).

Heatmaps show differences in the levels of attention on certain AOIs. This means that the red spots were distributed differently between C and IC. It can be translated to the fact that C and IC focus on different aspects of the algebraic fraction and that consequently their processing and correct or incorrect procedures will vary.

We did not find common strategic patterns among C respondents across all the different simplification tasks, but their fixations on the crucial elements depended on the structure of the algebraic fraction. This means that fractions with similar structures have similar fixations. An example would be that in both cases of fractions that cannot be simplified directly because they have terms in the numerator, the fixation was on the addition sign that separated the terms.

In the first two tasks, C focused attention on the AOI that will prevail after cancellation. However, on task three, the addition sign makes the simplification not feasible. Task four can only be simplified with an algebraic transformation.

Considering the data collected on the heatmaps and TTFF sequence, we can conclude that each exercise needs a specific strategy for simplification, in which metacognition plays a significant role.

We found that the C group pays more attention to the more important conceptual elements. This means they engage in a more deliberate search and identification of the crucial parts of the rational algebraic expression.

In contrast, IC respondents tend to identify similar algebraic expressions in the numerator and denominator and cancel them out. Although they take longer to process the simplification exercises (except in exercise 3), they end up cancelling similar expressions, which is not always possible. It seems that when a student is facing a simplification exercise and does not recognize the metacognitive aspect, he or she may change to an erroneous cancellation strategy.

This study helps teachers to identify where students with correct answers and with incorrect answers fix their attention and then teach them to direct their attention to the important parts in simplifying rational algebraic expressions, depending on the types of simplification exercises.

This research emphasizes the importance of focusing on teaching both procedures and metacognitive aspects of the simplification of rational algebraic expressions. Procedures are specific steps for simplifying an expression; metacognition is “thinking about thinking”, in this sense, knowing when, how, and if one can apply a certain procedure (Malle, 1993).

The procedures and the corresponding metacognitive skills can be taught. For example, A teacher can think aloud while solving an exercise, commenting on how he or she reflects while solving it, and showing the important details in an exercise, translated into simplifications of algebraic fractions, the importance of the structure of the fractions, and whether they are simplifiable or not.