Next Article in Journal
Persistence of Conceptual Errors in First-Year University Physics Course and Its Possible Relationship with Learning Styles
Previous Article in Journal
Creating Transformative Research–Practice Partnership in Collaboration with School, City, and University Actors
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Education Sciences
Volume 14
Issue 4
10.3390/educsci14040400
education-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Enhancing Spatial Ability among Undergraduate First-Year Engineering and Architecture Students

by
Ronen Porat
1,2,* and
Ciprian Ceobanu
1
1
Faculty of Psychology and Educational Sciences, “Alexandru Ioan Cuza” University of Iasi, 700506 Iași, Romania
2
Shenkar College of Engineering, Design and Art, Ramat Gan 5252626, Israel
*
Author to whom correspondence should be addressed.
Educ. Sci. 2024, 14(4), 400; https://doi.org/10.3390/educsci14040400
Submission received: 26 February 2024 / Revised: 7 April 2024 / Accepted: 8 April 2024 / Published: 11 April 2024
Browse Figures
Versions Notes

Abstract

:
Spatial ability (SA) refers to the ability to generate, retain and manipulate abstract visual images in one’s head. Research of this ability conducted during the last few decades had shown that SA is an essential ability to the development of mathematical skills in children. Later studies addressed adult SA development and accordingly found that SA was a predictor of success in Science, Technology, Engineering and Mathematics (STEM) fields of academic studies. Recently, focus has also been directed to another related field which is architecture. This group has not been extensively researched in relation to its spatial thinking abilities. The current research examines the efficiency of a new training program aimed at improving engineering and architecture student’s SA abilities. This program was based on previous intervention programs but was innovative in its combination of both traditional and computer-based teaching methods and combining frontal learning, hands on model building and augmented reality (AR) tools, all in a short program of 20 h. We asked whether the training program will be effective in improving student’s SA ability and whether this improvement will remain across different factors such as gender, faculty and math level. The results showed a significant improvement in SA abilities among the students who took the training program, compared with the control group. These results were true for both engineering and architecture students. Moreover, the results showed the training program to be efficient regardless of gender or prior math level.

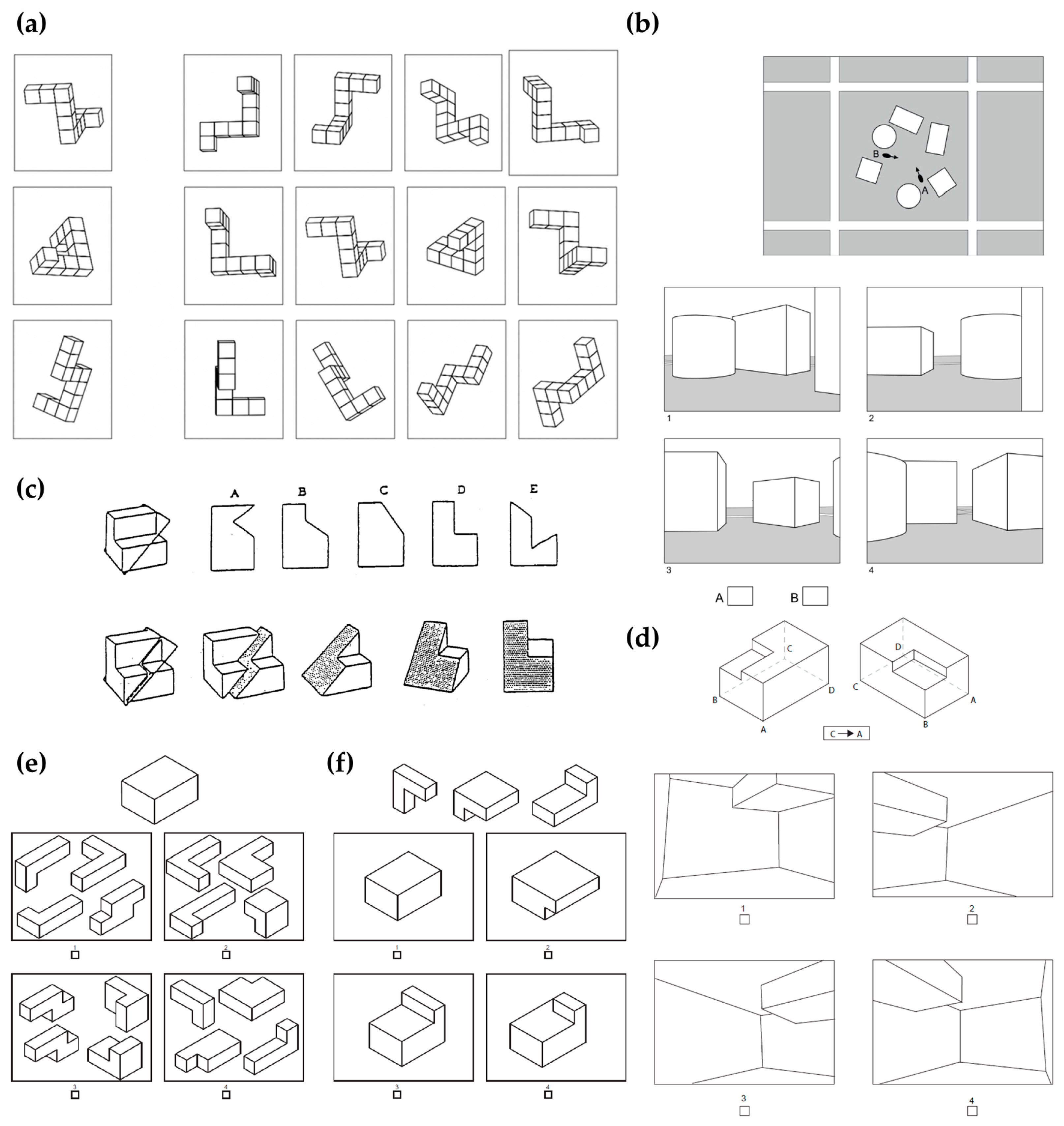
1. Introduction

Research in science has extensively explored human abilities, their development and their impact on performance [1]. Gardner [2], in his model of multiple intelligences, saw SA as one of the intelligences. According to his definition, SA is the ability to create a mental image of a spatial world and to imagine the motion of bodies or changes and processes occurring in them. This ability makes it possible to grasp the visual world accurately, change it and process it in the imagination.
Maier [3] further refined Gardner’s multiple intelligences model and theory when he distinguished between five types of SA and intelligence: Spatial perception is the horizontal and the vertical fixation of the direction regardless of disturbing information; Visualization is the ability to describe situations when the components are pleasant to each other; Mental rotation is the mental rotation of three-dimensional solids; Spatial relations is the ability to identify the relations between the parts of a solid and Spatial orientation is the ability to enter a given spatial state. Nowadays, the term spatial ability (SA) is commonly used, referring to spatial perception or visualization.
Buckley et al. [4] explored the origins and evolution of SA in the broader context of human intelligence, aiming to provide a refined contemporary definition. One of its main discussions is the Cattell–Horn–Carroll (CHC) theory [5,6]. The CHC theory is currently recognized as the principal framework describing individual differences in the structure of human intelligence. As the CHC theory suggests a contemporary framework of cognitive factors, it is most appropriate to define SA based on its factor structure within this framework. The hierarchical structure contains one third-order factor, general intelligence (g), and 16 s-order factors representing the primary mental abilities. SA is represented as a second-order factor; however, it is referred to as the Gv factor or visual processing. While these two terms both describe the same factor, SA is its more commonly used name. The Gv factor is defined as the ability to leverage mental imagery to address problems [6]. The CHC theory further breaks down SA into 11 first-order factors, which can be grouped into spatial skills, perceptual factors and memory factors. These first-order factors are described in Table 1. Sorby [7] offers a nuanced perspective, differentiating between innate spatial skills and learned spatial ability, a distinction that holds implications for educational strategies aiming to enhance SA.
Over the years, research shows SA to play a key role in the proper function of the environment in which we live and develop. Researchers and experts note that SA is not merely intuitive or genetically dictated, but is flexible and can be learned, acquired and improved [8].
In another aspect, recent studies have shown the neurological basis of SA, exploring how different regions of the brain are activated during spatial tasks [9,10]. This neurological perspective provides a deeper understanding of why certain training methods might be more effective than others. Another dimension of SA research has been the exploration of gender differences. There is a growing body of research examining gender differences in spatial abilities, which is crucial for creating inclusive training programs [11,12].
The influence of digital technology on SA has also been a topic of interest. With the rise of digital technology, researchers have been examining how interaction with digital devices might be influencing our inherent spatial abilities [13,14] and even reduces gender differences in spatial cognition [15]. Furthermore, with the immersive nature of virtual reality (VR) and augmented reality (AR), both are being explored as potent tools for enhancing spatial abilities, especially in educational settings. While VR provides a fully immersive environment, AR overlays digital information on the real world, offering a unique perspective that can be particularly beneficial for spatial tasks. Both technologies offer interactive experiences that can significantly aid in the understanding and manipulation of spatial constructs and improve learning immersion [16,17,18].
The research on SA began from studying the relationship between SA and children’s mathematical achievements and capabilities. These studies have shown that SA plays a major role in mathematical thinking [8,19,20]. Later studies have shown similar correlation in college students, showing SA to be among the cognitive factors that were identified as predictors of success in STEM fields [20,21]. Furthermore, large-scale studies show that SA can predict long term achievements in STEM, better than verbal and quantitative abilities [22]. One of the common theories about the way this effect occurs explains that mathematical thinking is supported by spatial–mental representations [23]. Thus, for example, some people create schematic representations of mathematical problems that include the spatial relationships described in the problems. Studies indicate that the solutions offered by these people are more correct on average [24].
Recent research mentioned the significant role of SA in the field of architecture [25]. Architects need good mathematical competence. It is essential for architects to possess strong mathematical skills, such as calculating the robustness of a structure or finding the optimal way of stabilizing a structure, and so on [26]. Furthermore, the architectural design process involves multistep stages and processes of spatial adjustments, switching between perspectives and so on [27]. Thus, the ability to visualize space is an integral skill in architecture [25]. Having said that, there were no studies found to show similar correlations between better SA and success in architecture studies. Some recent studies have shown that architecture students, as engineering students, get better at SA after the first year of academic studies [25]. Others found improved performance on SA tests among first-year students both in engineering and architecture after taking introductory engineering graphics course [28,29,30,31].
Although SA is a well-studied concept, there are but a few studies that have investigated the way training and improvement of the SA among students can enhance their performance in the field they have chosen. Maier, who introduced the five different types of SA, wrote the following: “The relevance of spatial ability leads to the following thesis as the approach for teaching: Based on psychological research findings, all five elements of spatial ability have to be specifically trained. The present conception of teaching space geometry does not come up to its cultural expectations.” [3]. The same author further introduced a modular construction system based on the traditional system where polygons were joined with rubber bands. Maier used real models, because in his view those were the most successful in improving students SA [3]. Although effective, this intervention is costly since it requires an expert teacher; it is also long and needs a lot of models if the students work individually [32].
Later there have been some computer-based suggested training programs [32,33,34] that seek to improve student’s spatial geometry ability and, according to the results, did so with success. Nevertheless, these interventions were mostly preliminary and limited in the kind of ability tested to improve geometry and in the number of subjects. Sorby [7] reports on a study conducted among engineering students, and examined what develops their spatial imagery ability. It was found that in courses where students were required to draw models by hand (rather than using a computer) and work with tangible models (rather than models on a computer monitor), there was a development in their spatial performance. More recently there were attempts to use virtual reality (VR), augmented reality (AR) and mixed reality (MR) training programs to help improve student’s SA; they also yielded some success but were only tried on a few of the SA subtypes (mental rotation, spatial visualization and spatial orientation) and on a very small group of subjects [35,36].
The current study describes the efficiency of a new training program aimed to develop student’s SA. It was designed to be a short, interactive and experiential program that would incorporate both traditional and technology-based teaching methods and thus would attract and engage students and facilitate learning.
Research hypothesis:
  • Students who will attend the intervention program will significantly improve their SA scores compared to students who will not attend it;
  • Improvements in SA scores will be gained across different factors, including faculty affiliation, gender and previous mathematical abilities;
  • Exploratory analysis: will gender, math level or math grades affect the level of effectiveness of the intervention.

2. Materials and Methods

2.1. Intervention Program

Through a series of practical and interactive activities, integrated with digital tools and collaborative learning experiences, the program aimed to develop and train student’s spatial thinking, visualization skills and spatial-problem-solving abilities. The training program extended over 20 academic hours within one month. It encompassed four sessions, each spanning four academic hours, along with two supplementary sessions, consisting of two academic hours each, dedicated to pre- and postprogram tests. The first session primarily involved traditional teaching methods, serving as a cornerstone for the intervention program by laying the groundwork for acquiring the fundamental knowledge and theory of SA. The other three sessions were composed of a combination of several teaching methods incorporating hands on model building, frontal teaching, computer-based learning (with SketchUp 2022 and GeoGebra programs) [37], augmented reality (AR) training and group work and discussions among teacher and students.

2.2. Participants

Sample: This study was conducted at Shenkar college in Israel, an academic institution for education and research in engineering, design and art. The sampling method employed the purposive/judgmental approach, by selecting students from Shenkar college who were in their first year of undergraduate study. These participants comprised two distinct groups: The first group included students beginning their studies in the faculty of engineering, from the departments of electrical and electronic engineering, software engineering and chemical engineering. The second group consisted of students beginning their studies in the faculty of design, specifically in the department of interior, structural and environmental design, and represents one of the research groups exemplifying architecture students.
Participation Criteria: To qualify for the research, participants needed to fulfill some specific requirements. They should be in their first year of engineering or architecture studies, be highly proficient in Hebrew, and they should not have learned any previous academic courses. Additionally, they must have finished 12 years of secondary schooling and been evaluated in mathematics and English according to Israel’s educational benchmarks. Respecting ethical guidelines, each participant was briefed on the research goals and provided their agreement to participate.
Sample Size: A total of 154 engineering and architecture students in their first year of study participated in this research, consisting of 79 engineering students and 75 architecture students. Among the engineering group, 47 students participated in the SA training program, while 32 others constituted the engineering control group who did not undergo the training and practice program. In architecture, the same program was delivered to 42 students and 33 architecture students were part of the control group that also did not undergo the program.
It should be noted that every student who participated in the program, whether from engineering or architecture, and regardless of whether they were in the group that was trained and practiced the intervention or in the control group, was tested in the SA test twice: SA pretest and post-test, under the same examination conditions and in an identical timeframe. The focus in this paper is mainly on the examination of its effectiveness while all the training program with its hybrid transfer methods are detailed in a separate article, now in press [38].

2.3. Measures

In order to assess SA among students, we used an SA test developed and tested by Berkowitz [25] to adjust the classical SA tests to the population of architecture students. This test was based on previous SA tests and on Maier’s five types of SA. The reliability (Alpha Cronbach), or construct validity, as mentioned by Berkowitz, of the 31-item scale was α = 0.71. The five SA tests were positively and moderately correlated, indicating a partial overlap in the measured abilities. Thus, each test has captured some unique skills, whereas other elements were common across the tests. A confirmatory factor analysis (CFA) on the five SA tests indicated that one-factor best fitted the data, thus confirming their validity as tests of SA (χ2 = 6.60, df = 5, p = 0.25; RMSEA = 0.02, 90% CI = 0.00–0.07; CFI = 0.997; SRMR = 0.02).
In our study, we relied on the exact SA test, adhering to its precise methodology, scoring system and allocated time for each subtest [25]. Since Berkowitz’s SA test is composed of both old and new subtests, measuring different aspects of SA, and this test was exclusively administered to students in their first year of undergraduate studies with no background knowledge, we decided it would fit both architecture and engineering students as a global tool for the measurement of SA. The SA test consists of five subtests. The two older subtests are the Mental Rotations Test (MRT) [39,40] and the Mental Cutting Test (MCT) [41]. Both established SA tests have been associated with achievements in STEM fields and have later been administered to architecture students. They are recognized measures of SA essential for various STEM disciplines. The three more recent subtests include the Urban Layout Test (ULT), the Indoor Perspective Test (IPT) and the Packing Test, which is further divided into two categories: ‘whole-to-parts’ (Packing-1) and ‘parts-to-whole’ (Packing-2). Figure 1 presents some examples from these five subtests.

2.4. Procedure

This study and its measures were approved by the Research, Development and Creation department of Shenkar college and were conducted under its authorization. All participating students gave their informed consent before engaging in the test and study. Testing took place in group settings within Shenkar classrooms. Test materials were presented in a paper-and-pencil format. Each test started with written instructions, complemented by examples. A trained experimenter provided general oral instructions prior to the beginning of the testing session. The MRT and MCT were administered following the standard procedures established for these tests and had received the necessary approvals from their respective owners. Students worked individually, and the order of tests remained the same for all participants.

3. Results

3.1. Sample and Descriptive Statistics

Table 2 summarizes sample size across study groups, age and gender. This study’s sample consisted of participants from two academic disciplines: architecture and engineering, each divided into control and intervention groups. In total, the architecture discipline comprised 75 participants, with 33 (44%) in the control group and 42 (56%) in the intervention group. The engineering discipline included 79 participants, with 32 (41%) in the control group and 47 (59%) in the intervention group. The average ages of participants were 22.7 years (SD = 2.5) and 22.2 years (SD = 2.9) in the architecture control and intervention groups, respectively, and 22.9 years (SD = 2.3) and 23.7 years (SD = 2.4) in the engineering control and intervention groups, respectively. The age range extended from 18 to 30 years in architecture and 19 to 28 years in engineering, indicating a predominantly young adult cohort. Notably, the proportion of women in the groups varied significantly, with the architecture discipline showing a higher female representation at 83% in the control group and 76% in the intervention group, compared to 47% in the engineering control group and 45% in the intervention group.
Table 3 summarizes and reflects the math background of incoming undergraduates in architecture and engineering, divided into control and intervention groups, to evaluate their foundational math skills. In architecture, fewer students had high-level math (5 units) experience, with 9% in the control and 5% in the intervention groups, while in engineering, this was more common, with 19% in the control and 17% in the intervention groups. Medium-level math (4 units) was studied by 36% and 31% in the architecture groups and by a majority of 53% in both engineering groups, indicating stronger initial math level in engineering. Low-level math (3 units) was predominant in architecture, with 55% in the control and 64% in the intervention groups, versus 28% and 30% in engineering, respectively.
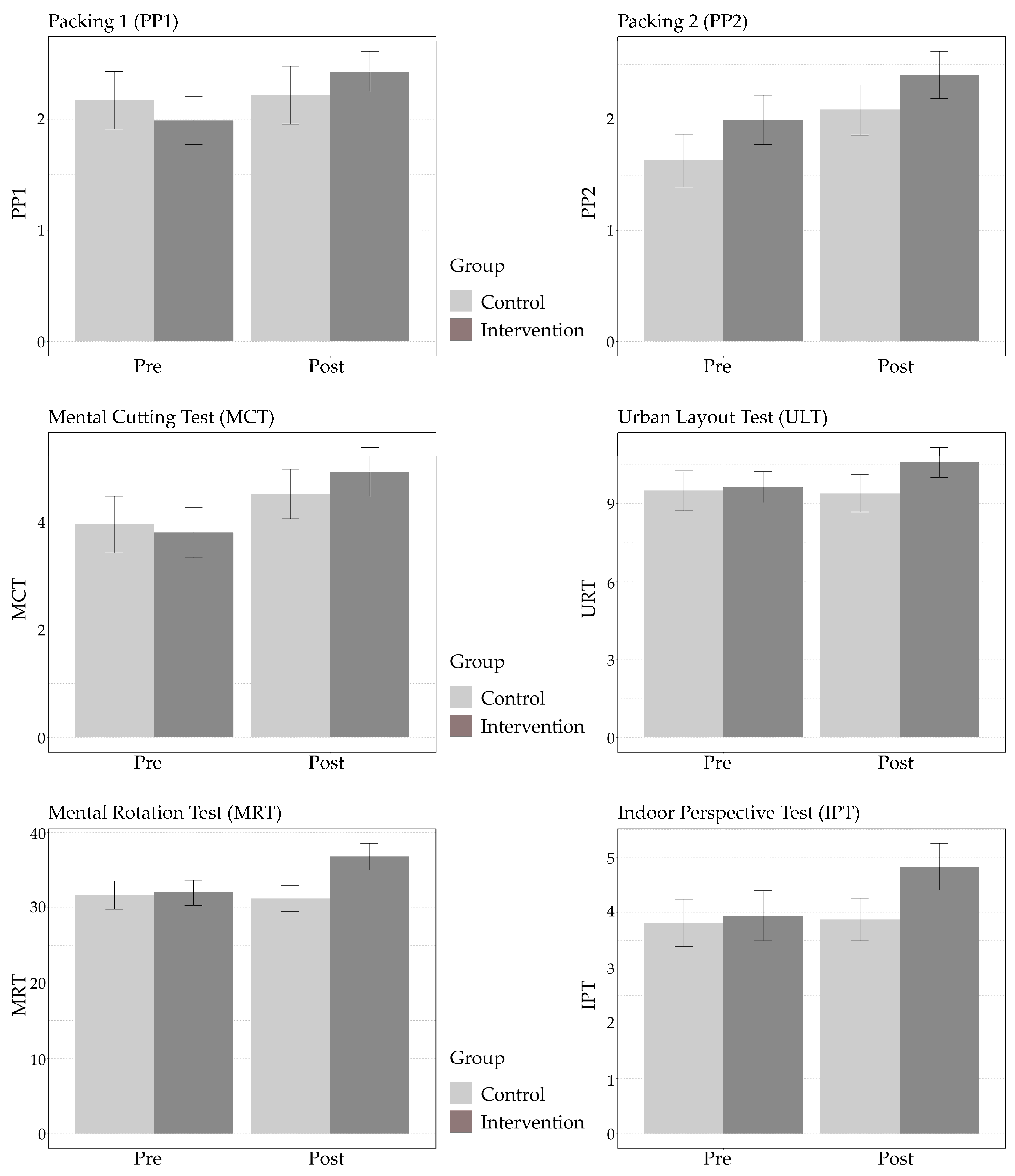
Table 4 presents descriptive statistics of the SA tests which were taken by the students before and after the intervention (i.e., dependent variable), employing subtests such as ULT, Packing-1, Packing-2, IPT, MCT and MRT.
In the architecture discipline, the control group’s ULT scores showed a slight decrease from pre- (Mean = 9.09, SD = 3.01) to postintervention (Mean = 8.79, SD = 2.93), while the intervention group demonstrated significant improvement, with scores rising from a preintervention mean of 9.29 (SD = 2.48) to a postintervention mean of 10.71 (SD = 2.41). The engineering discipline mirrored this positive trend, with the control group’s ULT scores marginally increasing from 9.94 (SD = 3.15) to 10.03 (SD = 2.78), and the intervention group’s scores improving from 9.96 (SD = 3.16) to 10.49 (SD = 3.12).
Packing tests further elucidated cognitive and spatial gains. For Packing-1, both control and intervention groups in architecture maintained or improved their scores slightly, with the intervention group notably advancing from a mean of 2.02 (SD = 1.09) to 2.50 (SD = 0.80). Engineering students also showed progress, especially in the intervention group, where scores increased from 1.96 (SD = 0.95) to 2.36 (SD = 0.94). Packing-2 results exhibited similar trends, with notable increases in the architecture intervention group from 1.88 (SD = 0.94) to 2.52 (SD = 0.92) and in the engineering intervention group from 2.11 (SD = 1.13) to 2.30 (SD = 1.10).
The IPT and MCT tests highlighted significant enhancements, particularly in the intervention groups. In architecture, IPT scores surged from 3.79 (SD = 1.85) preintervention to 4.90 (SD = 1.83) postintervention. Similarly, MCT scores in the same group improved from 3.60 (SD = 2.05) to 5.12 (SD = 2.09). Engineering students also exhibited growth in these areas, with IPT and MCT scores rising in the intervention group.
The MRT test showed substantial gains in the architecture intervention group, with mean scores escalating from 31.12 (SD = 7.65) to 35.52 (SD = 7.81). The engineering intervention group witnessed a remarkable increase from 32.83 (SD = 7.98) to 37.94 (SD = 8.72).
Overall, the total score, in line with the performance across tests, encapsulated the cumulative academic advancements. The architecture intervention group’s total score increased from a preintervention mean of 51.69 (SD = 12.48) to a postintervention mean of 61.29 (SD = 12.61). The engineering intervention group exhibited a similar trend, with the total score increasing from 54.91 (SD = 13.32) to 62.55 (SD = 14.86).

3.2. Intervention Effects

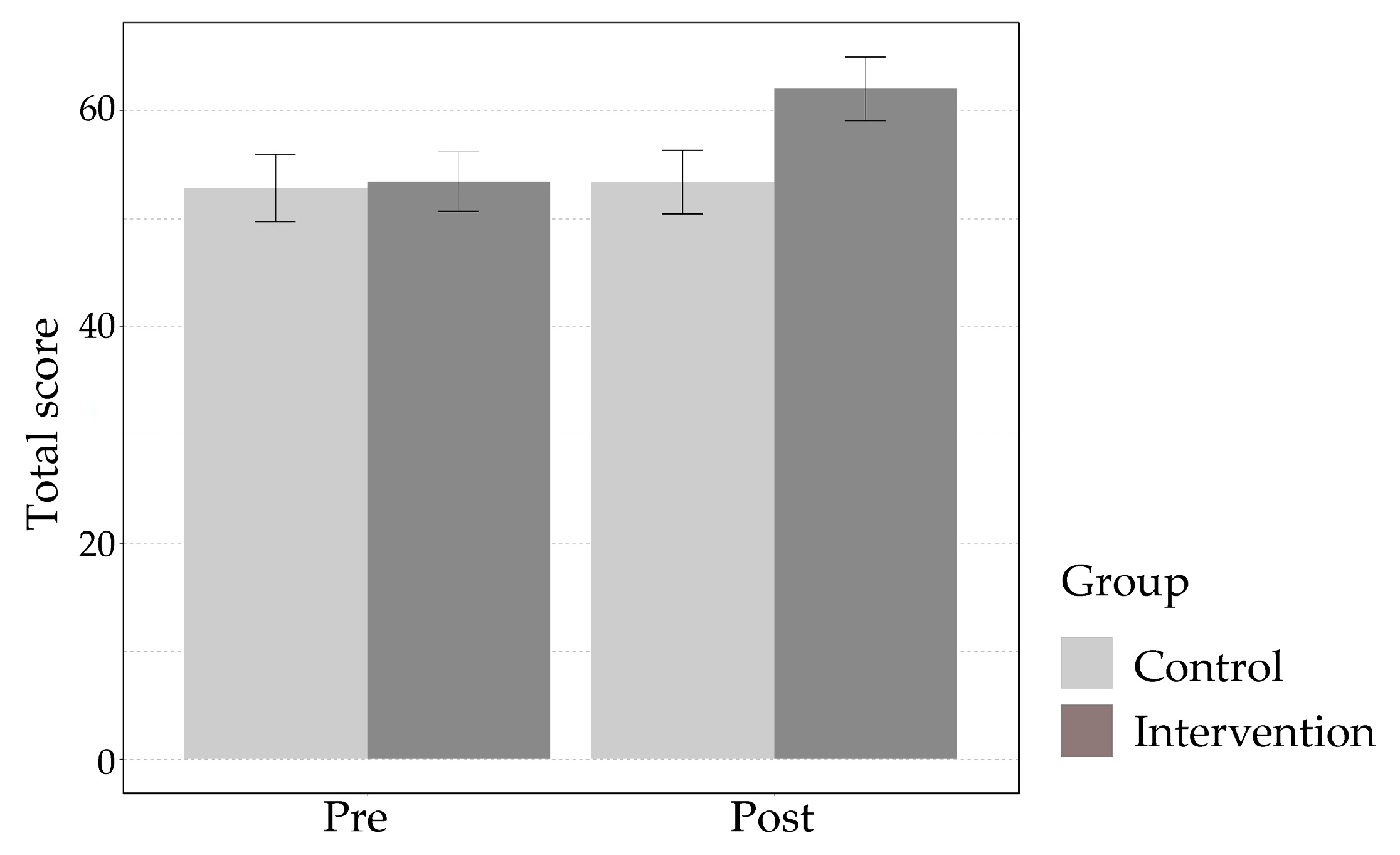
To assess the effect of intervention and compare pre–post group differences, we used an analysis of variance (ANOVA), with time (pre/post) as a within-subject factor and group (intervention/control) as a between-subject variable. Aggregated test scores (total score) served as the dependent variable. The model included two main effects and a time-by-group interaction. Results revealed significant effects for group (F(1,304) = 9.71, p = 0.002) and time (F(1,304) = 12.6, p < 0.001) and a significant time*group interaction (F(1,304) = 9.26, p = 0.007). To ensure the results’ robustness, we conducted an analysis of co-variance (ANCOVA), which included the following covariates: age, sex, high school major (arts/humanities/sciences), level of high-school math and English studies, final high school scores in these subjects, academic field (architecture/engineering) and whether the student works or not. Results remained significant after accounting for covariates, with higher p-values (all p < 0.0025). Post hoc analyses revealed significant improvement from pre to post among the intervention group (t(88) = 10.7, p < 0.0001, Cohen’s d = 1.14), while no significant improvement was observed in the control group (p = 0.21). While no group differences were observed preintervention (p = 0.76), the groups differed significantly postintervention (t(152) = 4.08, p < 0.0001, Cohen’s d = 0.66) with the intervention group presenting higher scores (mean ± SD = 61.96 ± 13.78 vs. 53.35 ± 11.67). The results are shown in Figure 2.

3.3. Intervention Effects among Architecture and Engineering Students

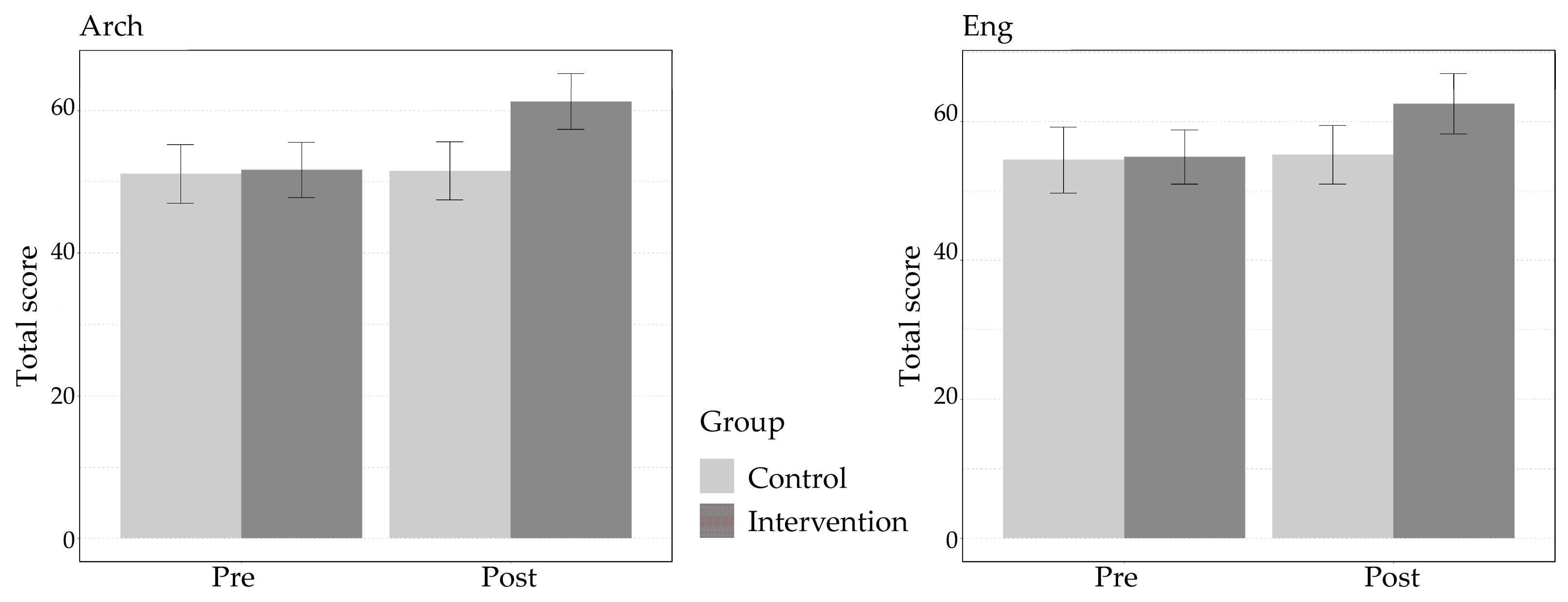
Next, we tested the intervention effects within the architecture and engineering student groups separately. Architecture and engineering students did not differ in SA scores at the pretest (mean score architecture: 51.4 + 12.0 and engineering: 54.7 + 13.2; t(152) = 1.62, p = 0.11, Cohen’s d = 0.26).
The architecture students group demonstrated similar effects as the primary analysis, with main effects for time (F(1,146) = 7.88, p = 0.006) and group (F(1,146) = 6.68, p = 0.011), and a significant time*group interaction (F(1,146) = 5.28, p = 0.022). Results held when accounting for multiple covariates in an ANCOVA. Similarly, the intervention group demonstrated significant improvement pre-to-post (t(41) = 8.04, p < 0.0001, Cohen’s d = 1.26), while the control group did not improve following intervention (p = 0.47).
Contrariwise, the engineering group only demonstrated a significant effect for group (F(1,154) = 5.12, p = 0.025) with only a marginal time effect (p = 0.08) and a nonsignificant effect for the time*group interaction (p = 0.12). Noteworthy is that testing the groups separately revealed similar patterns with significant improvement for the intervention group (t(46) = 7.08, p < 0.0001, Cohen’s d = 1.04) and no effect for the control group (p = 0.32). While these hypothesis-supporting effects did not translate into significant interactions in the ANOVA, possibly due to lack of statistical power, ANCOVA revealed a significant time*group interaction (F(1,137) = 4.41, p = 0.038), implying significant time-by-group differences while accounting for multiple covariates (Figure 3).

3.4. Intervention Effects on Subtests

Next, we tested whether time*group interactions existed in subtests using a similar statistical approach, with subtests scores as the dependent variable in each analysis. Results were controlled for multiple comparisons with Bonferroni correction. While descriptive measures showed anticipated patterns for all subtests, the only significant interaction was observed for the Mental Rotations Test (F(1,304) = 8.57, adjusted p = 0.022). The groups’ performance on subtests is depicted in Figure 4.

3.5. Exploratory Analysis

Our final analyses were of an exploratory nature, aiming to assess whether sex and math levels affected total score and whether these groups react differently to the intervention.
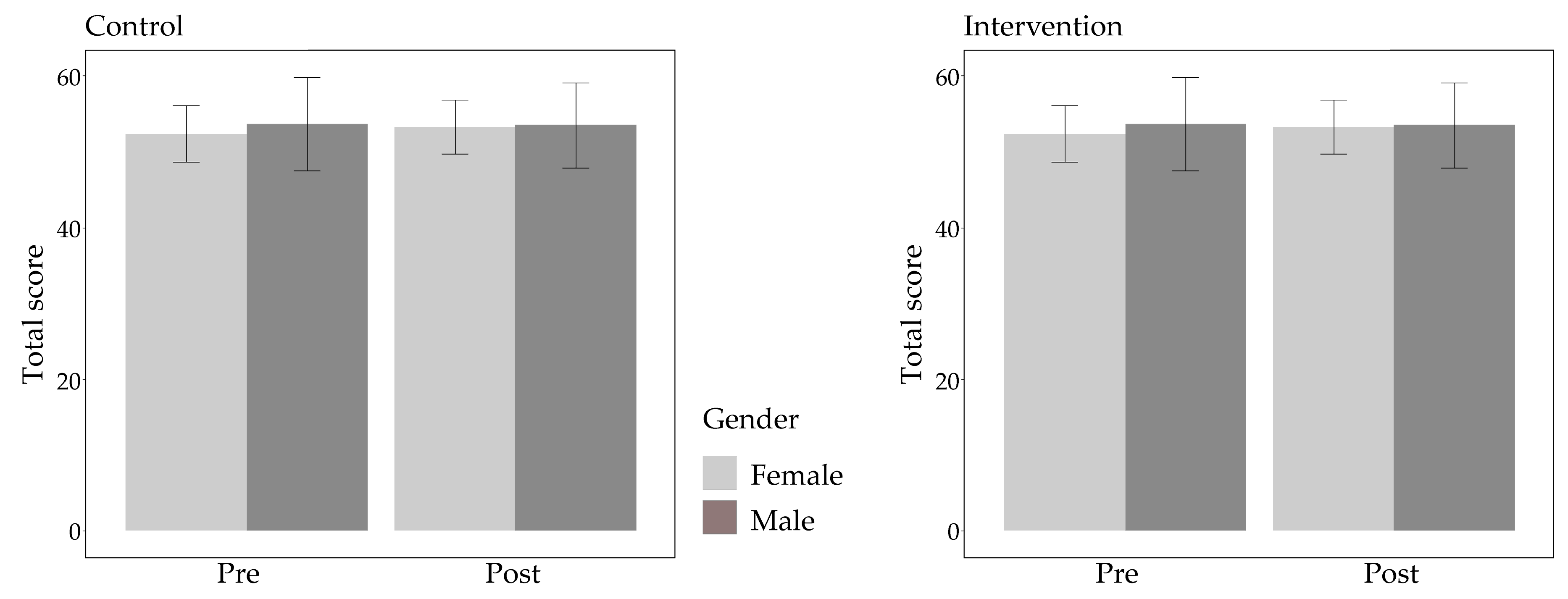
We conducted a t-test and ANOVA to compare males and females on total score. T-test revealed significant group differences (t(306) = 2.91, p = 0.004, Cohen’s d = 0.33), showing that males scored significantly higher than females (mean ± sd = 58.62 ± 14.27 for males vs. 54.07 ± 12.58 for females). However, nonsignificant time*group*sex interaction in ANOVA implied that both groups responded similarly to the intervention (Figure 5).
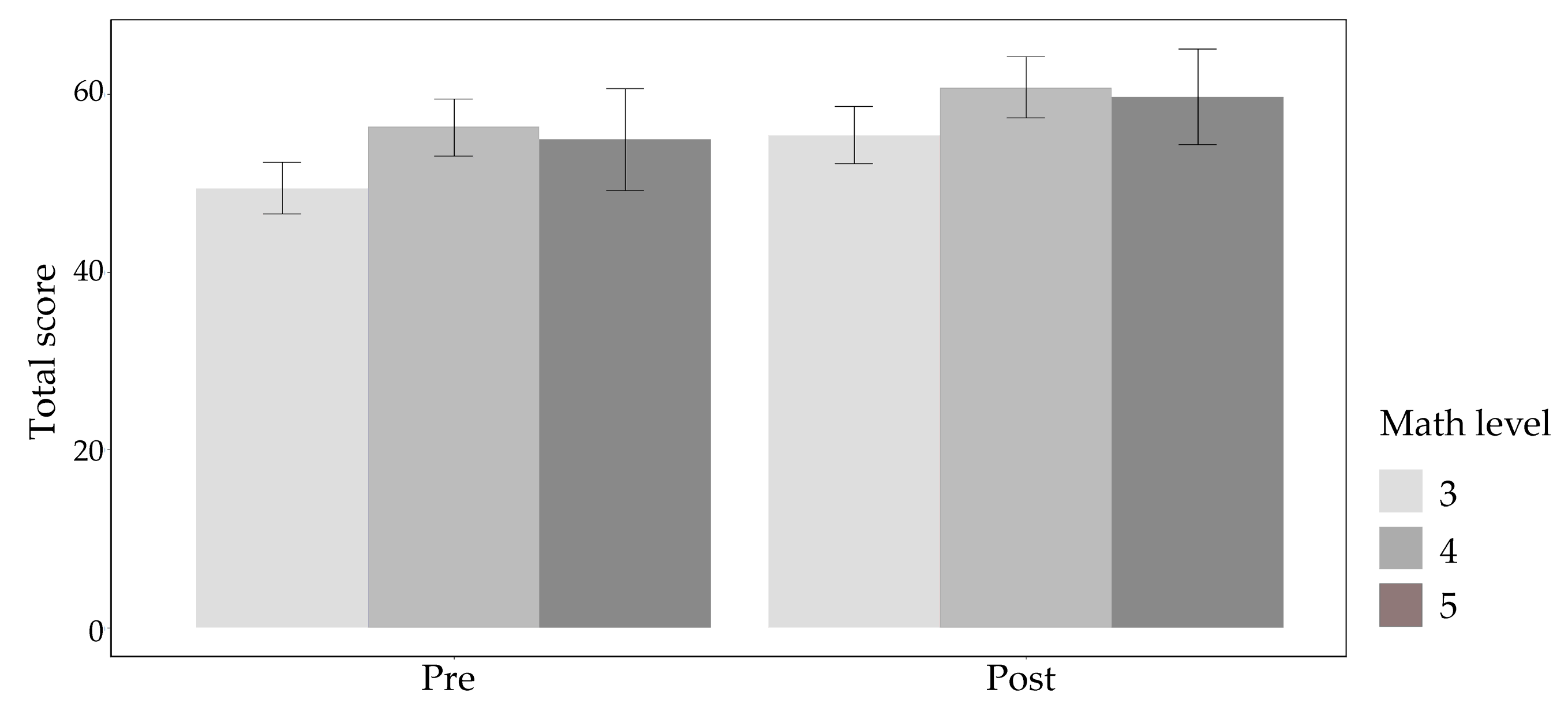
Finally, we conducted an ANOVA to test if math level affected total score. We conducted a similar analysis to the main one and added two additional independent variables: math level in high school final exams (either 3, 4 or 5 units of study, corresponding to the basic, intermediate and advanced levels of study appearing in the Israeli high-school diploma) and math scores in high school final exams (stratified to the following groups: 60–70, 71–80, 81–90 and 91–100, where 100 is the maximal score). We also included all possible interaction terms. Math level was significantly associated with total score (F(1,274) = 11.6, p = 0.0008), while only marginally significant effects emerged for math scores (p = 0.059) and math level by math score’s interaction (p = 0.053). A marginally significant effect also emerged for a quadruple time*group*math level*math scores interaction (p = 0.07). A post hoc analysis showed that students with low 3-unit level of math studies scored significantly lower on the test than students who had a 4-unit level math education (t(266) = 3.76, p = 0.0002, Cohen’s d = 0.46) and students with a 5-unit level math education (t(172) = 2.11, p = 0.036, Cohen’s d = 0.32). No significant differences were noted between students with 4- and 5-unit levels of math education (p = 0.62). Results are depicted in Figure 6.

4. Discussion

4.1. Effectiveness of the Intervention Program

The results of this study provide strong evidence supporting the effectiveness of the intervention program in enhancing SA among architecture and engineering students. Students who completed the intervention demonstrated substantial enhancements in their SA abilities compared to those who did not take the course.
The intervention program employed a range of teaching methods, including lectures, hands-on activities and interactive exercises, using 3D and VR, which allowed students to actively engage with spatial concepts and develop their skills. The concise, focused and innovative nature of the program ensured that students received targeted and effective instruction in spatial reasoning, enabling them to apply their newfound knowledge and skills to real-world architectural and engineering tasks. The cost-efficiency of the program made it accessible to a wide range of students, irrespective of their background. By offering a diverse set of teaching methods, the program catered to the varied learning styles and preferences of the students, ensuring maximum engagement and knowledge retention.
Overall, the intervention program successfully fulfilled its objectives of improving SA in architecture and engineering students.

4.2. Consistency across Different Factors

An important aspect of this study was the examination of the consistency of improvements in SA across different factors, including faculty affiliation, gender and previous mathematical abilities. The intervention program proved to be effective regardless of the participants’ background, indicating its potential applicability to a diverse student population. Architecture and engineering students, despite their different educational paths and curriculum content, both demonstrated significant improvements in SA. This suggests that the intervention program’s benefits extend beyond specific disciplines and can be adapted to various academic contexts.
The consistency of improvements across different factors indicates that the program targets foundational spatial reasoning skills that are crucial for success in architecture and engineering fields. However, it is worth noting that architecture students displayed more significant improvements in SA compared to their engineering counterparts. The reasons behind this discrepancy could be attributed to various factors, such as variations in teaching methods, curriculum content or the nature of spatial tasks encountered in each discipline. Architecture programs often emphasize design thinking and spatial visualization skills more explicitly, which could contribute to the observed differences. Furthermore, the limited statistical power of the current study suggests the need for future research with a larger sample size to provide a more comprehensive understanding of these differences and explore potential factors contributing to the varying improvements between architecture and engineering students.

4.3. Gender Differences in SA

Consistent with previous research conducted by Levine et al. [42], significant differences in SA abilities were found between male and female participants, with males generally outperforming females. These gender differences in SA have been observed across various age groups and educational settings. However, despite these gender differences, no significant interaction effects were observed among time, group (intervention vs. control) and gender in the present study. This suggests that the intervention program equally benefited both male and female students in improving their SA abilities, potentially contributing to the reduction of gender-based disparities in spatial cognition.
The findings indicate that targeted spatial intervention programs can provide a level playing field for both genders, empowering female students to develop their SA and bridge the existing gap. By addressing gender disparities in spatial cognition, the intervention program has the potential to enhance diversity and inclusivity in architecture and engineering fields. Educators and institutions can use these findings to design interventions that support female students in developing their spatial skills and create a more equitable learning environment.

4.4. Relationship between Math Level and SA Scores

This study also investigated the relationship between SA scores and math level (based on the mathematics matriculation exam in Israel, commonly known as the math Bagrut exam. The math Bagrut is the official certificate awarded to Israeli high school students who successfully complete their secondary education).
The results revealed a significant association between math level and total SA scores, indicating that students with a higher level of math education (4-unit level) during high school achieved higher SA scores compared to those with a lower level of math education (3-unit level). Mathematics and SA are closely intertwined, and proficiency in mathematics may correlate with spatial thinking and problem-solving skills. Therefore, incorporating spatial training alongside mathematics education could enhance students’ overall cognitive abilities in disciplines that heavily rely on spatial skills. This highlights the importance of integrating spatial reasoning tasks into mathematics curricula and providing opportunities for students to apply mathematical concepts in spatial contexts. By recognizing the synergistic relationship between mathematics and SA, educators can optimize the development of students’ cognitive skills in architecture and engineering.

4.5. Implications for Educational Practice

The findings of this study have significant implications for educational practice in architecture and engineering disciplines. The effectiveness of the intervention program in enhancing SA abilities among students highlights the importance of implementing targeted interventions to promote cognitive skill development.
Institutions can incorporate similar intervention programs into their curriculum to enhance SA among their students, fostering their problem-solving, design and visualization skills.
The program’s success across different demographic groups, including both male and female students, as well as individuals with varying mathematical backgrounds, highlights its inclusive nature. Institutions can leverage these findings to create a supportive and inclusive learning environment that values diversity and promotes equal opportunities for all students.
Additionally, the results call for a more integrated approach to curriculum design that recognizes the interplay between SA and mathematical proficiency. By incorporating spatial training alongside mathematics education, institutions can enhance students’ overall cognitive abilities and prepare them for the spatial demands of architecture and engineering disciplines.

4.6. Future Directions

The findings of this study open avenues for future research in the field of SA and education. Future research endeavors with larger sample sizes will enable a more comprehensive exploration of the factors contributing to the observed differential improvements between architecture and engineering students. Further investigation into the specific teaching methods, curriculum content and spatial tasks encountered in each discipline can provide insights into the factors influencing the varying improvements. Longitudinal studies assessing the long-term effects of the intervention program can shed light on the sustainability and durability of the acquired SA. Additionally, exploring the adaptability of the intervention program to diverse educational contexts and subgroups within the architecture and engineering student populations will yield valuable insights for the development of tailored interventions. Understanding the long-term effects and adaptability of the intervention program will guide the refinement and optimization of educational interventions targeting SA.
The discussion surrounding future directions regarding the expected correlation between SA scores in SA tests and students’ academic achievements is of great significance in educational research and should be the next study’s focus. This future study aims to uncover the potential relationship between students’ SA skills, as measured by the SA test, and their overall academic performance. Exploring this correlation can provide valuable insights into the role of SA competencies in students’ educational outcomes and pave the way for targeted interventions and support systems.
Another crucial future direction lies in examining the generalizability of the correlation between SA scores and academic achievements across diverse student populations and cultural contexts. It is essential to explore potential variations in this correlation among different demographics, including age groups, socioeconomic backgrounds, and cultural contexts. Such analysis ensures that interventions and educational practices are tailored to meet the unique needs and challenges of specific student groups. By acknowledging the diversity of students’ backgrounds and experiences, researchers and educators can develop more inclusive and effective strategies to support students’ social–emotional growth and academic success.

Author Contributions

Conceptualization, R.P. and C.C.; Methodology, R.P.; Formal analysis, R.P. and C.C.; Investigation, R.P. and C.C.; Writing—original draft, R.P. and C.C.; Writing—review and editing, R.P. and C.C.; Project administration, R.P. and CC. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

This study was conducted and approved by the Institutional Review Board of Shenkar College.

Informed Consent Statement

Informed consent was obtained from all subjects involved in this study.

Data Availability Statement

Available on request through the correspondence author.

Acknowledgments

The authors thank the Research and Development Authority, the Center for Teaching Excellence, the Core Sciences Unit in the Engineering Faculty and the Interior Building & Environment Design Department at Shenkar College of Engineering, Design and Art for their essential support in this research.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Porat, R.; Ceobanu, C. Spatial Ability: Understanding the Past, Looking into the Future. Eur. Proc. Educ. Sci. 2023, 6, 99–108. [Google Scholar] [CrossRef]
  2. Gardner, H. Frames of Mind: The Theory of Multiple Intelligences; Basic Books: New York, NY, USA, 1983. [Google Scholar]
  3. Maier, P.H. Spatial geometry and spatial ability—How to make solid geometry solid. In Selected Papers from the Annual Conference of Didactics of Mathematics; Gesellschaft für Didaktik der Mathematik (GDM): Osnabrueck, Germany, 1996; pp. 63–75. [Google Scholar]
  4. Buckley, J.; Seery, N.; Canty, D. A Heuristic Framework of Spatial Ability: A Review and Synthesis of Spatial Factor Literature to Support its Translation into STEM Education. Educ. Psychol. Rev. 2018, 30, 947–972. [Google Scholar] [CrossRef]
  5. McGrew, K.S. CHC theory and the human cognitive abilities project: Standing on the shoulders of the giants of psychometric intelligence research. Intelligence 2009, 37, 1–10. [Google Scholar] [CrossRef]
  6. Schneider, W.; McGrew, K. The CattellHornCarroll model of intelligence. In Contemporary Intellectual Assessment: Theories, Tests, and Issues; Guilford Press: New York, NY, USA, 2012; pp. 99–144. [Google Scholar]
  7. Sorby, S.A. Developing 3D spatial visualization skills. Eng. Des. Graph. J. 1999, 63, 21–32. [Google Scholar]
  8. Mix, K.S.; Levine, S.C.; Cheng, Y.-L.; Young, C.; Hambrick, D.Z.; Ping, R.; Konstantopoulos, S. Separate but correlated: The latent structure of space and mathematics across development. J. Exp. Psychol. Gen. 2016, 145, 1206–1227. [Google Scholar] [CrossRef]
  9. Murias, K.; Slone, E.; Tariq, S.; Iaria, G. Development of spatial orientation skills: An fMRI study. Brain Imaging Behav. 2019, 13, 1590–1601. [Google Scholar] [CrossRef] [PubMed]
  10. Hegarty, M. Chapter 7: Components of Spatial Intelligence. In The Psychology of Learning and Motivation; Academic Press: Cambridge, MA, USA, 2010; Volume 52, pp. 265–297. [Google Scholar] [CrossRef]
  11. Reilly, D.; Neumann, D.L.; Andrews, G. Gender Differences in Spatial Ability: Implications for STEM Education and Approaches to Reducing the Gender Gap for Parents and Educators. In Visual-Spatial Ability in STEM Education: Transforming Research into Practice; Khine, M.S., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 195–224. [Google Scholar] [CrossRef]
  12. Voyer, D.; Voyer, S.; Philip, B.M. Magnitude of sex differences in spatial abilities: A meta-analysis and consideration of critical variables. Psychol. Bull. 1995, 117, 250. [Google Scholar] [CrossRef]
  13. Di, X.; Zheng, X. A metaanalysis of the impact of virtual technologies on students’ spatial ability. Educ. Technol. Res. Dev. 2022, 70, 73–98. [Google Scholar] [CrossRef]
  14. Green, C.S.; Bavelier, D. Action-Video-Game Experience Alters the Spatial Resolution of Vision. Psychol. Sci. 2007, 18, 88–94. [Google Scholar] [CrossRef]
  15. Feng, J.; Spence, I.; Pratt, J. Playing an Action Video Game Reduces Gender Differences in Spatial Cognition. Psychol. Sci. 2007, 18, 850–855. [Google Scholar] [CrossRef]
  16. Dominguez, M.G.; MartinGutierrez, J.; Gonzalez, C.R.; Mato, C.M. Methodologies and Tools to Improve Spatial Ability. In Proceedings of the World Conference on Design, Arts and Education (DAE2012), Antalya, Turkey, 13 May 2012; Volume 51, pp. 736–744. [Google Scholar] [CrossRef]
  17. Bermejo, B.; Juiz, C.; Cortes, D.; Oskam, J.; Moilanen, T.; Loijas, J.; Govender, P.; Hussey, J.; Schmidt, A.L.; Burbach, R.; et al. AR/VR Teaching-Learning Experiences in Higher Education Institutions (HEI): A Systematic Literature Review. Informatics 2023, 10, 45. [Google Scholar] [CrossRef]
  18. Radu, I. Augmented reality in education: A metareview and cross-media analysis. Pers. Ubiquitous Comput. 2014, 18, 1533–1543. [Google Scholar] [CrossRef]
  19. Xie, F.; Zhang, L.; Chen, X.; Xin, Z. Is Spatial Ability Related to Mathematical Ability: A Meta-analysis. Educ. Psychol. Rev. 2019, 32, 113–155. [Google Scholar] [CrossRef]
  20. Wheatley, G.H. One Point of View: Spatial Sense and Mathematics Learning. Arith. Teach. 1990, 37, 10–11. [Google Scholar] [CrossRef]
  21. Newcombe, N.S. Harnessing Spatial Thinking to Support Stem Learning; OECD Education Working Paper, No. 161; OECD Publishing: Paris, France, 2017. [Google Scholar] [CrossRef]
  22. Wai, J.; Lubinski, D.; Benbow, C.P. Spatial ability for STEM domains: Aligning over 50 years of cumulative psychological knowledge solidifies its importance. J. Educ. Psychol. 2009, 101, 817–835. [Google Scholar] [CrossRef]
  23. Cheng, Y.-L.; Mix, K.S. Spatial Training Improves Children’s Mathematics Ability. J. Cogn. Dev. 2013, 15, 2–11. [Google Scholar] [CrossRef]
  24. Rittle-Johnson, B.; Zippert, E.L.; Boice, K.L. The roles of patterning and spatial skills in early mathematics development. Early Child. Res. Q. 2019, 46, 166–178. [Google Scholar] [CrossRef]
  25. Berkowitz, M.; Gerber, A.; Thurn, C.M.; Emo, B.; Hoelscher, C.; Stern, E. Spatial abilities for architecture: Cross sectional and longitudinal assessment with novel and existing spatial ability tests. Front. Psychol. 2021, 11, 4096. [Google Scholar] [CrossRef] [PubMed]
  26. Sergeeva, E.V.; Moskvina, E.A.; Torshina, O.A. The interaction between mathematics and architecture. IOP Conf. Ser. Mater. Sci. Eng. 2019, 675, 012018. [Google Scholar] [CrossRef]
  27. Cross, N. Design Thinking: Understanding How Designers Think and Work; Bloomsbury Publishing: London, UK, 2023. [Google Scholar]
  28. Leopold, C.; Gorska, R.A.; Sorby, S.A. International experiences in developing the spatial visualization abilities of engineering students. J. Geom. Graph. 2001, 5, 81–91. [Google Scholar]
  29. Sorby, S.A. Developing 3D spatial skills for engineering students. Australas. J. Eng. Educ. 2007, 13, 1–11. [Google Scholar] [CrossRef]
  30. Contero, M.; Naya, F.; Company, P.; Saorín, J.L.; Conesa, J. Improving visualization skills in engineering education. IEEE Comput. Graph. Appl. 2005, 25, 24–31. [Google Scholar] [CrossRef] [PubMed]
  31. Sorby, S.A.; Baartmans, B.J. The development and assessment of a course for enhancing the 3-D spatial visualization skills of first year engineering students. J. Eng. Educ. 2000, 89, 301–307. [Google Scholar] [CrossRef]
  32. Aszalos, L.; Bako, M. How can we improve the spatial intelligence. In Proceedings of the 6th International Conference on Applied Informatics, Eger, Hungary, 27–31 January 2004. [Google Scholar]
  33. Dilling, F.; Vogler, A. Fostering spatial ability through computeraided design: A case study. Digit. Exp. Math. Educ. 2021, 7, 323–336. [Google Scholar] [CrossRef]
  34. Panorkou, N.; Pratt, D. Using Google SketchUp to Develop Students’ Experiences of Dimension in Geometry. Digit. Exp. Math. Educ. 2016, 2, 199–227. [Google Scholar] [CrossRef]
  35. Roca-González, C.; Martín Gutiérrez, J.; García-Dominguez, M.; Mato Carrodeguas, M.D.C. Virtual Technologies to Develop Visual-Spatial Ability in Engineering Students. Eurasia J. Math. Sci. Technol. Educ. 2016, 13, 441–468. [Google Scholar] [CrossRef]
  36. Ho, S.; Liu, P.; Palombo, D.J.; Handy, T.C.; Krebs, C. The role of spatial ability in mixed reality learning with the HoloLens. Anat. Sci. Educ. 2022, 15, 1074–1085. [Google Scholar] [CrossRef] [PubMed]
  37. Yulian, V.; Wahyudin, W.; Anggrayani, L. The effect of GeoGebra-based learning on students’ spatial ability and motivation. In Proceedings of the 7th Mathematics, Science, and Computer Science Education International Seminar, Bandung, West Java, Indonesia, 12 October 2019; Volume 130. [Google Scholar]
  38. Porat, R.; Ciprian, C. Enhancing Spatial Abilities in Engineering and Architecture Students: An Integrated Hybrid Training Approach in a Mixed-Methods Framework. 2024, in press. [Google Scholar]
  39. Vandenberg, S.G.; Kuse, A.R. Mental Rotations, a Group Test of Three-Dimensional Spatial Visualization. Percept. Mot. Ski. 1978, 47, 599–604. [Google Scholar] [CrossRef] [PubMed]
  40. Peters, M.; Laeng, B.; Latham, K.; Jackson, M.; Zaiyouna, R.; Richardson, C. A redrawn Vandenberg and Kuse mental rotations test: Different versions and factors that affect performance. Brain Cogn. 1995, 28, 39–58. [Google Scholar] [CrossRef] [PubMed]
  41. CEEB. Special Aptitude Test in Spatial Relations; College Entrance Examination Board: New York, NY, USA, 1939. [Google Scholar]
  42. Levine, S.C.; Foley, A.; Lourenco, S.; Ehrlich, S.; Ratliff, K. Sex differences in spatial cognition: Advancing the conversation. Wiley Interdiscip. Rev. Cogn. Sci. 2016, 7, 127–155. [Google Scholar] [CrossRef] [PubMed]
Education 14 00400 g001
Figure 1. Example items from each subtest: (a) MRT; (b) ULT; (c) MCT; (d) IPT; (e) Packing-1 and (f) Packing-2.
Figure 1. Example items from each subtest: (a) MRT; (b) ULT; (c) MCT; (d) IPT; (e) Packing-1 and (f) Packing-2.
Education 14 00400 g001
Education 14 00400 g002
Figure 2. The effect of intervention and comparison of pre–post group differences.
Figure 2. The effect of intervention and comparison of pre–post group differences.
Education 14 00400 g002
Education 14 00400 g003
Figure 3. Intervention effects among the architecture (left) and engineering (right) groups.
Figure 3. Intervention effects among the architecture (left) and engineering (right) groups.
Education 14 00400 g003
Education 14 00400 g004
Figure 4. Group performances on subtests. Abbreviations: PP1 = Packing 1; PP2 = Packing 2; IPT = Indoor Perspective Test; MCT = Mental Cutting Test; ULT = Urban Layout Test and MRT = Mental Rotation Test.
Figure 4. Group performances on subtests. Abbreviations: PP1 = Packing 1; PP2 = Packing 2; IPT = Indoor Perspective Test; MCT = Mental Cutting Test; ULT = Urban Layout Test and MRT = Mental Rotation Test.
Education 14 00400 g004
Education 14 00400 g005
Figure 5. Test performance stratified by sex, pre and post intervention.
Figure 5. Test performance stratified by sex, pre and post intervention.
Education 14 00400 g005
Education 14 00400 g006
Figure 6. Test performance stratified by math level, pre and post intervention.
Figure 6. Test performance stratified by math level, pre and post intervention.
Education 14 00400 g006
Table 1. Spatial factors and their definitions from the CHC theory [4] (p. 7).
Table 1. Spatial factors and their definitions from the CHC theory [4] (p. 7).
FactorDefinition [6]
Visualization (Vz)The ability to perceive complex patterns and mentally simulate how they might look when transformed (e.g., rotated, changed in size or partially obscured).
Speeded rotation
(spatial relations) (SP)		The ability to solve problems quickly by using mental rotation of simple images.
Closure speed (CS)The ability to quickly identify a familiar and meaningful visual object from incomplete (e.g., vague, partially obscured or disconnected) visual stimuli, without knowing in advance what the object is.
Flexibility of closure (CF)The ability to identify a visual figure or pattern embedded in a complex, distracting or disguised visual pattern or array, when one knows in advance what the pattern is.
Visual memory (MV)The ability to remember complex images over short periods of time (less than 30 s).
Spatial scanning (SS)The ability to visualize a path out of a maze or a field with many obstacles.
Serial perceptual integration (PI)The ability to recognize an object after only parts of it are shown in rapid succession.
Length estimation (LE)The ability to visually estimate the length of objects.
Perceptual illusions (IL)The ability to not be fooled by visual illusions.
Perceptual alternations (PN)Consistency in the rate of alternating between different visual perceptions.
Imagery (IM)The ability to mentally produce very vivid images.
Table 2. Sample size across study groups, age and gender.
Table 2. Sample size across study groups, age and gender.
ArchitectureEngineering
ControlInterventionControlIntervention
Total Sample7579
Groups33
(44%)		42
(56%)		32
(41%)		47
(59%)
Average Age
(SD)		22.7
(2.5)		22.2
(2.9)		22.9
(2.3)		23.7
(2.4)
Min(max) Age18 (30)18 (29)19 (28)19 (28)
Women (%)28
(83%)		32
(76%)		15
(47%)		21
(45%)
Table 3. Mathematical background and previous grades among study groups.
Table 3. Mathematical background and previous grades among study groups.
ArchitectureEngineering
ControlInterventionControlIntervention
Math
5 units *
(Advanced)		N
(%)		 3268
(9%)(5%)(19%)(17%)
Grades
Level		90–1002123
80–900145
70–801000
60–700000
Math
4 units *
(Intermediate)		N
(%)		 12131725
(36%)(31%)(53%)(53%)
Grades
Level		90–1002758
80–90641012
70–802224
60–702001
Math
3 units *
(Basic)		N
(%)		 1827914
(55%)(64%)(28%)(30%)
Grades
Level		90–1005435
80–9031348
70–805721
60–705300
* Based on Israeli math grades on high school final exams called “Bagrut”, essential for academic eligibility. Math final grades are at 3 (basic), 4 (intermediate) or 5 (advanced) units.
Table 4. Pre- and postintervention scores on SA tests in study groups.
Table 4. Pre- and postintervention scores on SA tests in study groups.
TestScale RangeMeas.ArchitectureEngineering
ControlInterventionControlIntervention
PrePostPrePostPrePostPrePost
ULT0–16Mean9.098.799.2910.719.9410.039.9610.49
(SD)(3.01)(2.93)(2.48)(2.41)(3.15)(2.78)(3.16)(3.12)
Packing-10–4Mean2.002.002.022.502.342.441.962.36
(SD)(1.12)(1.06)(1.09)(0.80)(0.97)(1.01)(0.95)(0.94)
Packing-20–4Mean1.521.941.882.521.752.252.112.30
(SD)(0.87)(0.97)(0.94)(0.92)(1.05)(0.88)(1.13)(1.10)
IPT0–8Mean3.583.583.794.904.064.194.094.77
(SD)(1.62)(1.50)(1.85)(1.83)(1.85)(1.57)(2.38)(2.19)
MCT0–10Mean4.184.523.605.123.724.534.004.76
(SD)(1.72)(1.66)(2.05)(2.09)(2.48)(2.06)(2.39)(2.39)
MRT0–48Mean30.7630.7331.1235.5232.6631.7832.8337.94
(SD)(7.23)(6.83)(7.65)(7.81)(7.85)(6.91)(7.98)(8.72)
Total Score0–90Mean51.1251.5551.6961.2954.4755.2254.9162.55
(SD)(11.62)(11.53)(12.48)(12.61)(13.18)(11.69)(13.32)(14.86)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Porat, R.; Ceobanu, C. Enhancing Spatial Ability among Undergraduate First-Year Engineering and Architecture Students. Educ. Sci. 2024, 14, 400. https://doi.org/10.3390/educsci14040400

AMA Style

Porat R, Ceobanu C. Enhancing Spatial Ability among Undergraduate First-Year Engineering and Architecture Students. Education Sciences. 2024; 14(4):400. https://doi.org/10.3390/educsci14040400

Chicago/Turabian Style

Porat, Ronen, and Ciprian Ceobanu. 2024. "Enhancing Spatial Ability among Undergraduate First-Year Engineering and Architecture Students" Education Sciences 14, no. 4: 400. https://doi.org/10.3390/educsci14040400

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop