Persistence of Conceptual Errors in First-Year University Physics Course and Its Possible Relationship with Learning Styles
Abstract
1. Introduction
2. Literature Review of Previous Ideas and Learning Styles
- The conventional learning process cannot eliminate some prior (erroneous) ideas, as some of them persist even after students have graduated.
- Compared to American students, although Spanish university students have a better understanding of the concept of force, American students present a better performance in the FCI at the end of their studies.
3. Objectives and Research Questions
- Unraveling the existence of previous ideas among a group of freshmen university students.
- Analyze the persistence of the previously considered ideas at the end of the physics course.
- Check if the presence of previous ideas is larger among students with a lower university access qualification than among those with a better performance.
- Study possible relations between previous ideas and the Honey–Alonso learning styles.
4. Methodology
4.1. Physics Test to Identify Preconceptions
4.1.1. Analyzed Preconceptions
- Kinematics. Here, we consider concepts related to movement, such as position, velocity, and acceleration.
- Inertia. The study of understanding Newton’s first law when investigating the effect of forces on the movement of different objects.
- The second law of Newton. The effect of forces in different static and dynamic scenarios.
- Newton’s third law. The interaction between two objects, that is, the relationship between action/reaction forces and masses.
- Superposition principle. Analysis of the effect of various forces on an object.
- Active forces. Effect of an obstacle on a moving object.
- Resistant forces. Effect of forces that oppose the movement of an object.
- Gravitational forces. Forces exerted by masses due to the law of Universal Gravitation.
- Uncertainty. A way to correctly express experimental measurements (significant graphs, uncertainty, etc.).
- The center of mass: The concept of the center of mass and the way to calculate it.
- Rotatory motion. Effect of a change in the moment of inertia of a rotating object on its angular velocity. Relationship between angular and linear velocity.
4.1.2. Indicators Used in the Study of the Test on Conceptual Errors
Individual Characterization of Items According to the Classical Theory Indices
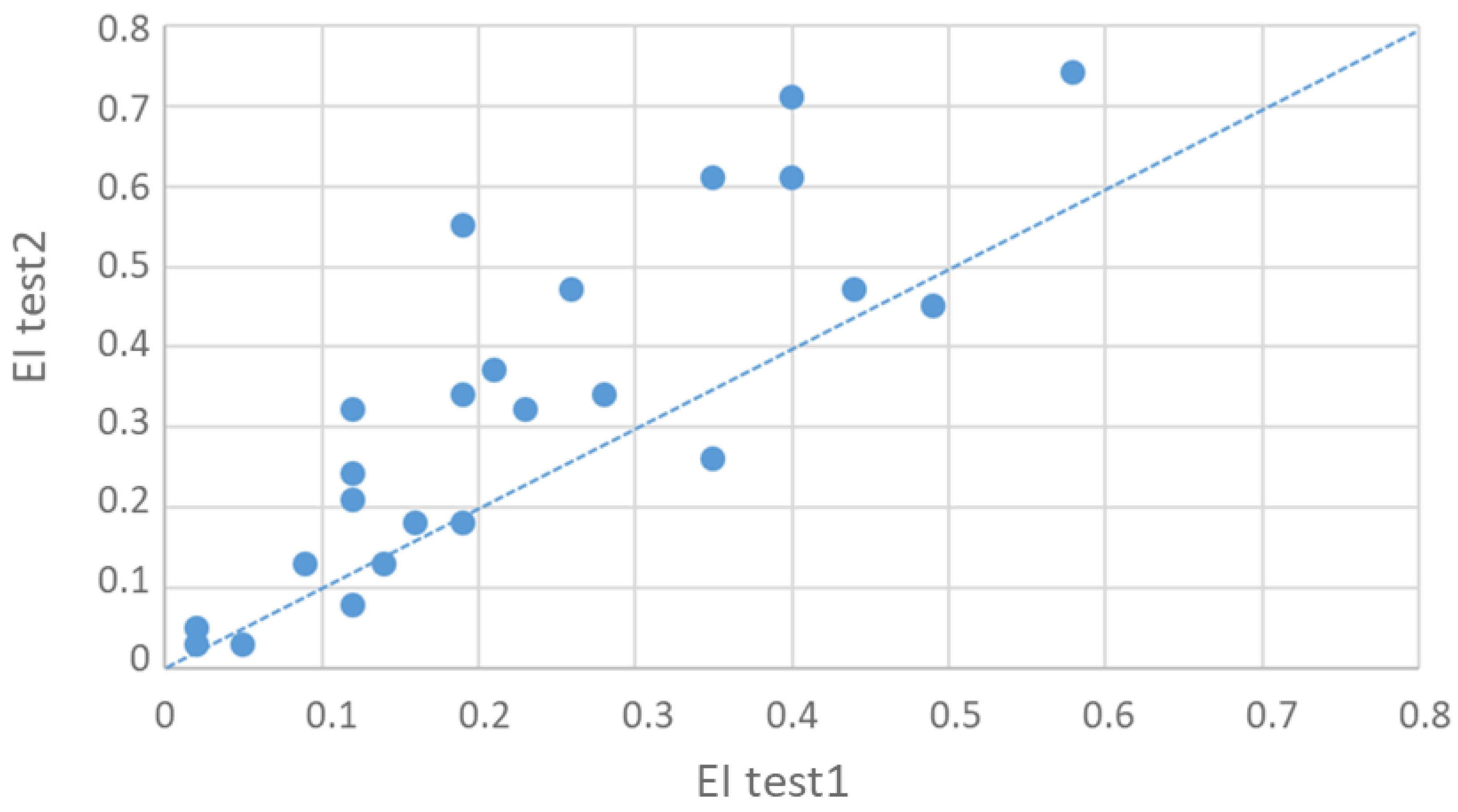
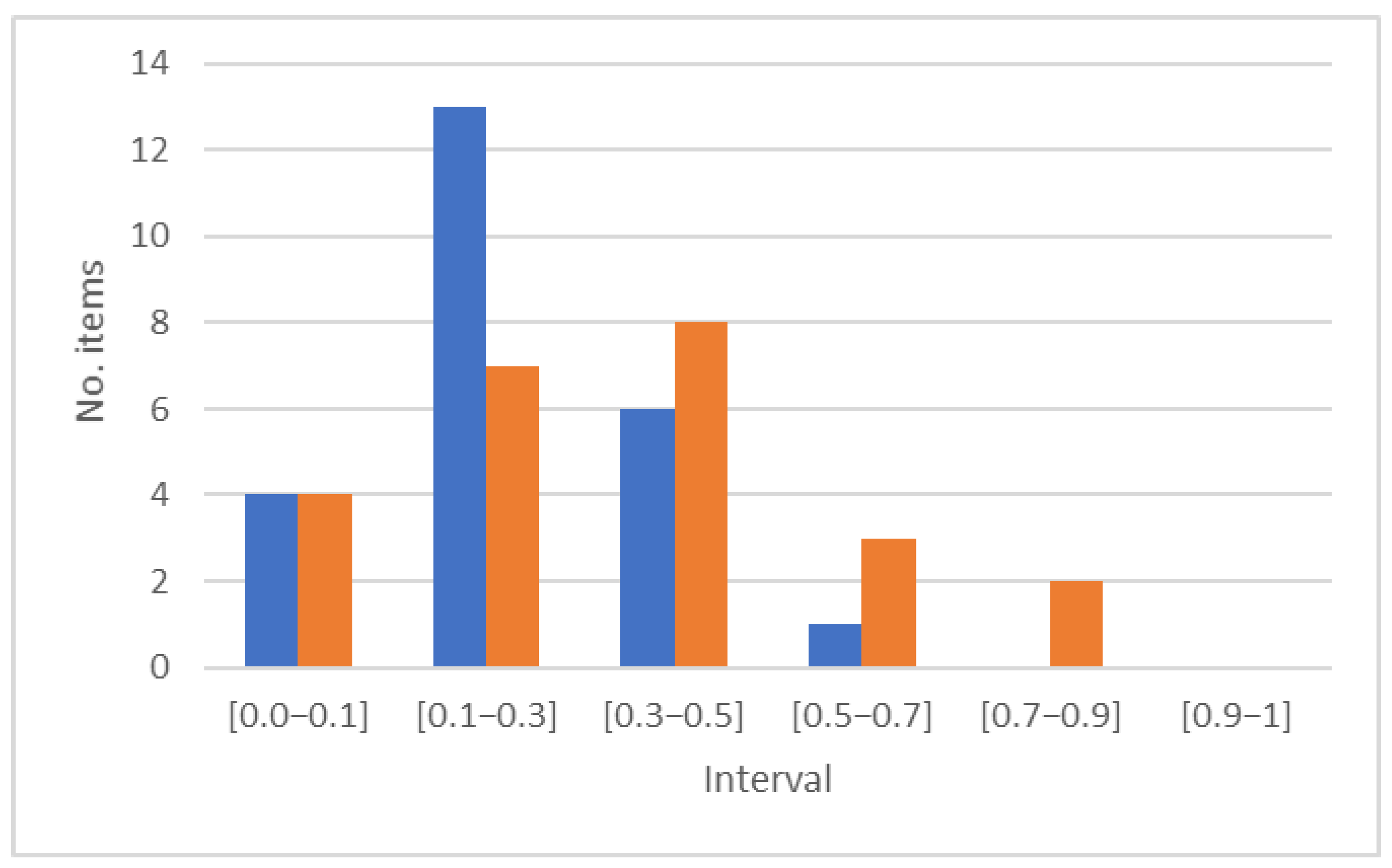
4.1.3. Global Characterization of Tests
4.2. The Honey–Alonso Learning-Styles Questionnaire
- Activist. Activist students prefer to learn through direct experimentation. These students like to try new experiences and opportunities, tackle multiple tasks, and work in groups. Contrarily, they do not like general topics with a lot of theory, care much about details, or repeat the same activity.
- Reflector. Reflector students like to perform direct observations and data collection. These students like to review what they have done, exchange opinions, investigate carefully, and think before acting. On the contrary, reflector students feel uncomfortable when acting as leaders and participating in situations that require action without previous planning.
- Theorist. Theorist students are attracted by abstract conceptualization. They like to work following a previously detailed plan and to methodically explore associations and relationships between ideas, events, and situations. Contrarily, they do not like to work on open problems or activities that lack a clear context and/or purpose.
- Pragmatist. Pragmatist students are hands-on individuals who like to apply (preferably as soon as possible) what they have learned. These students do not like to study general theories or concepts that are distant from reality and/or practical purposes.
5. Case Study and Results
5.1. Description of the Case Study
- Vector Calculus.
- Kinematics of a point particle.
- Kinematics of rigid solids.
- Relative kinematics.
- Point-particle dynamics.
- Dynamics of rigid solids.
- Static (equilibrium, center of gravity, and inertia moment).
5.2. Results
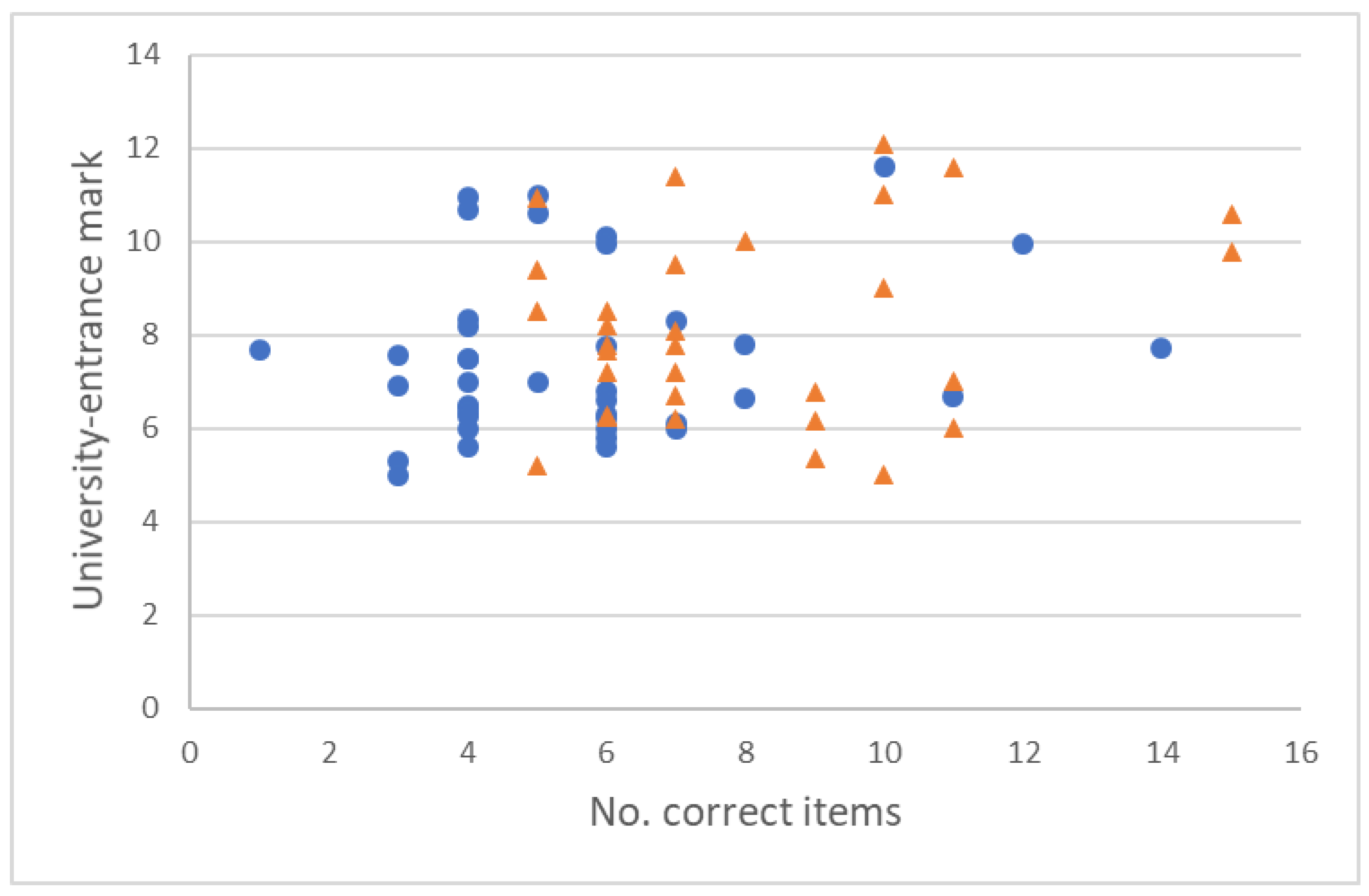
5.2.1. Analysis of Individual Items
5.2.2. Global Analysis of the Test
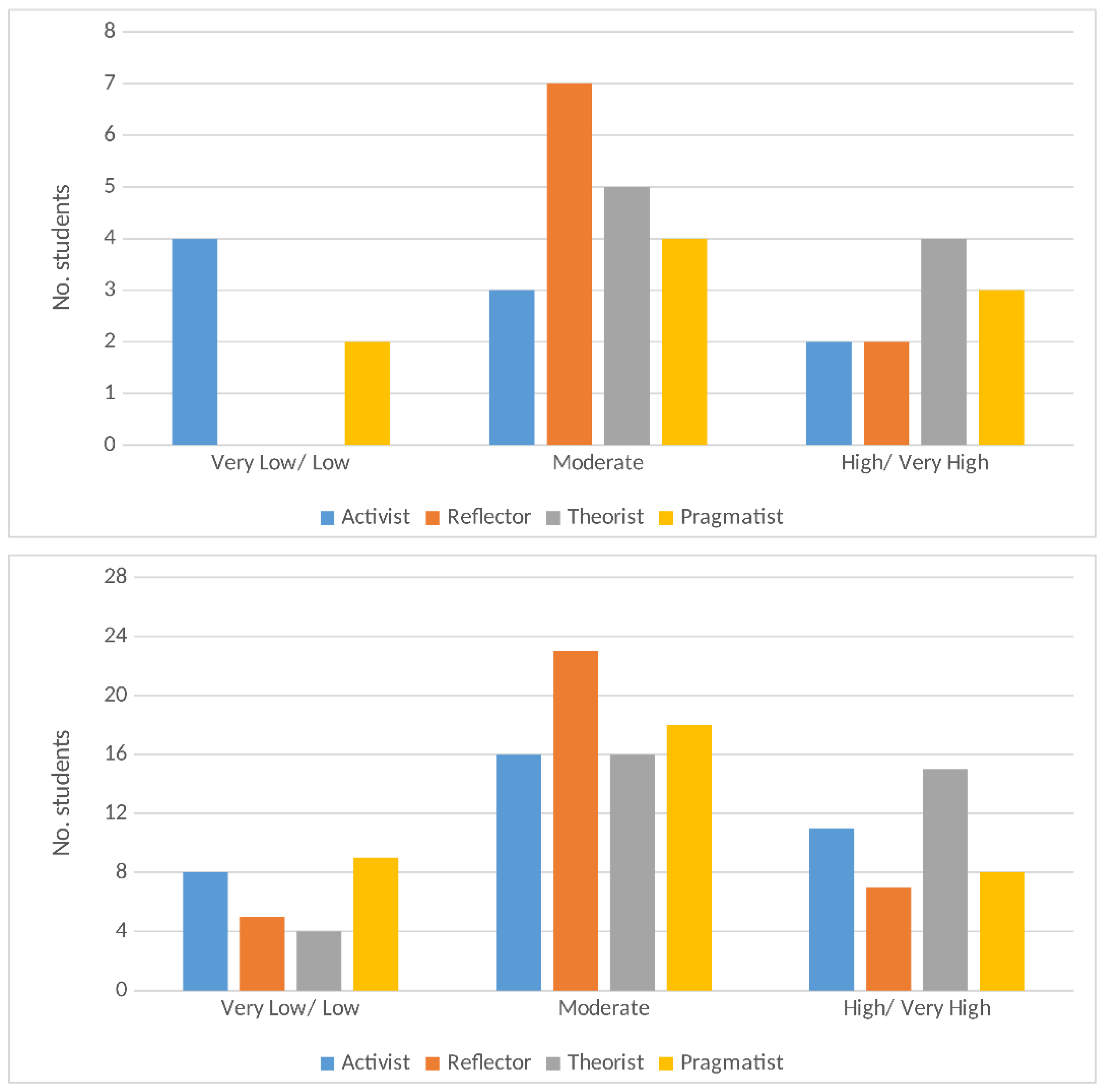
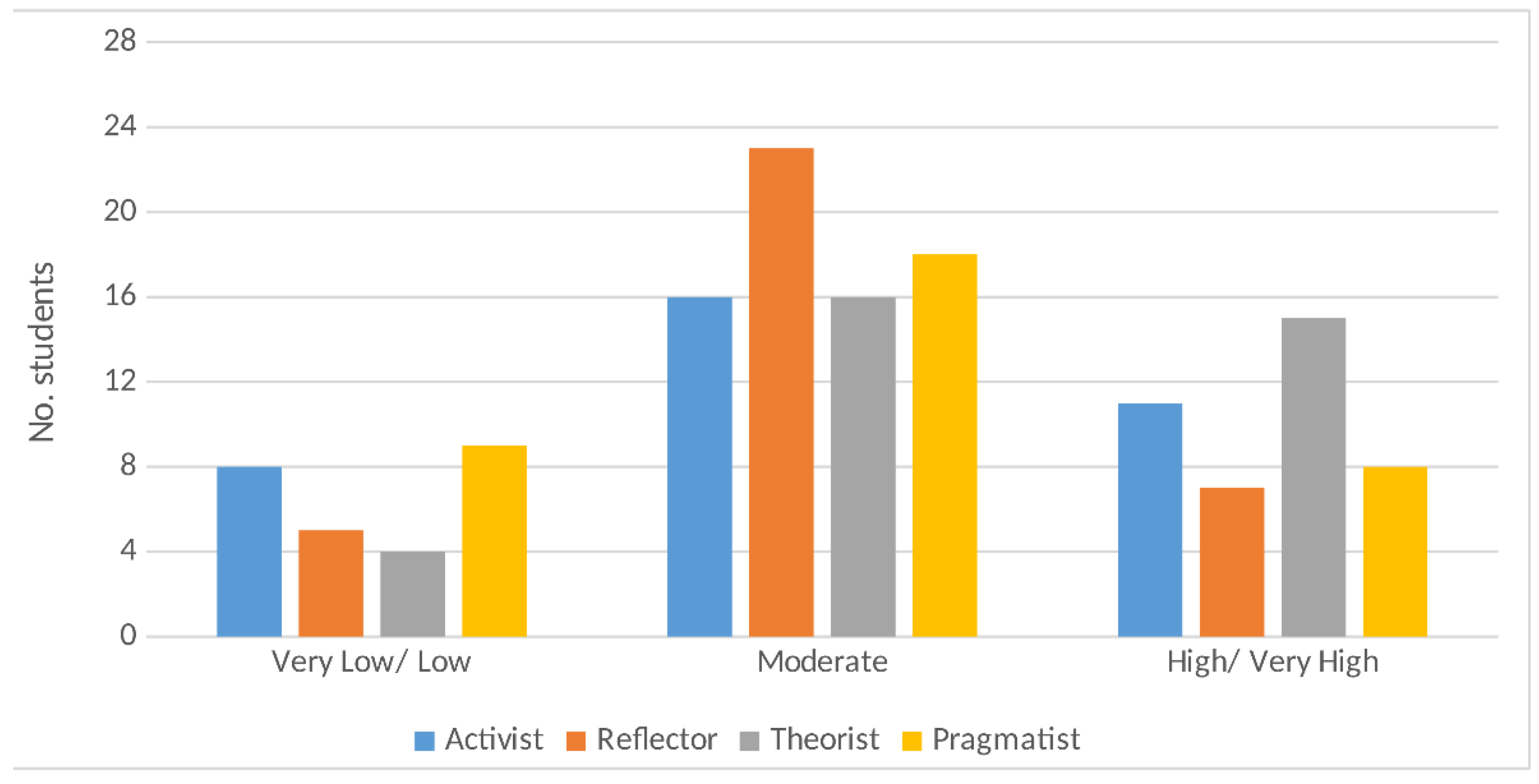
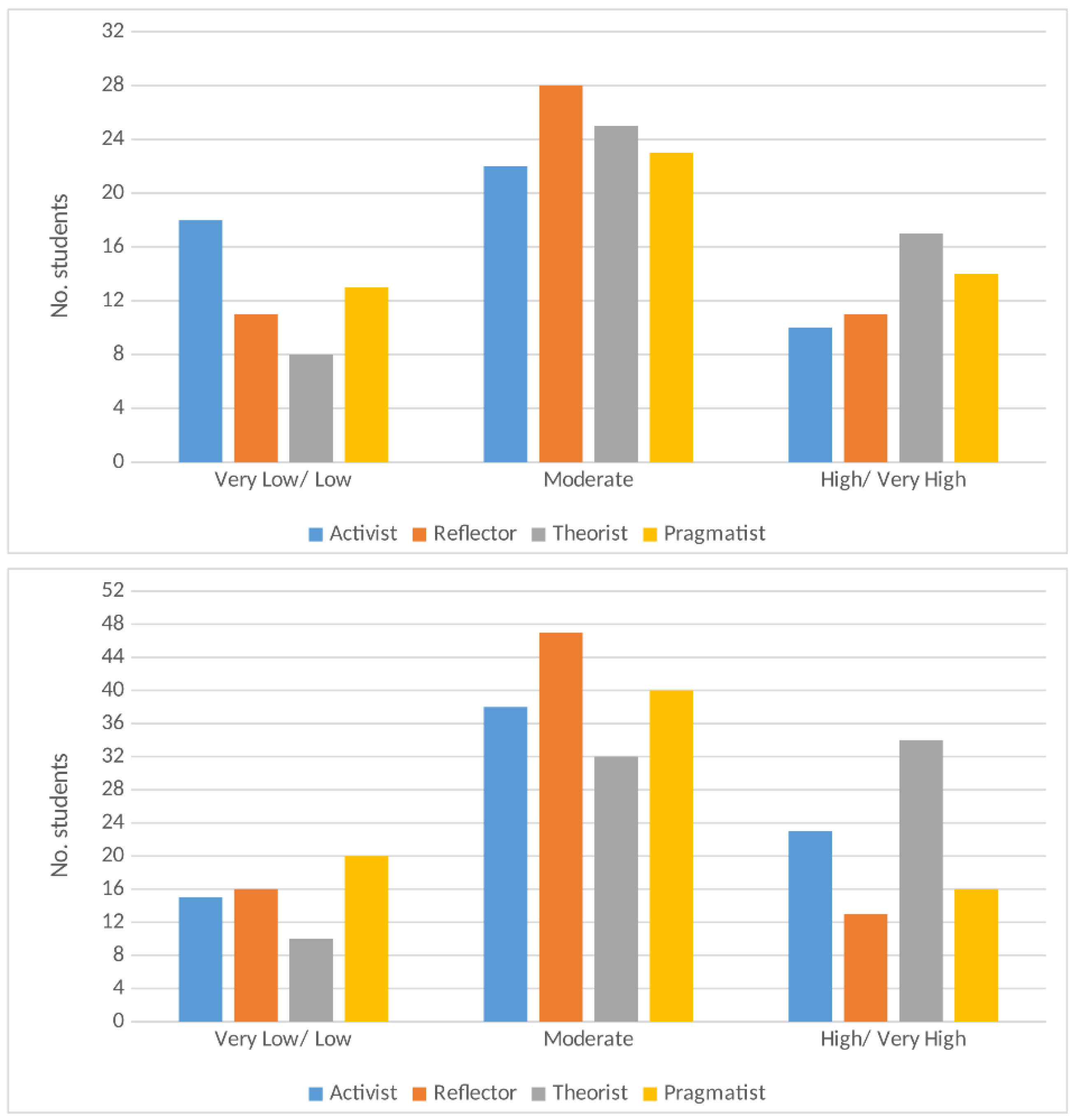
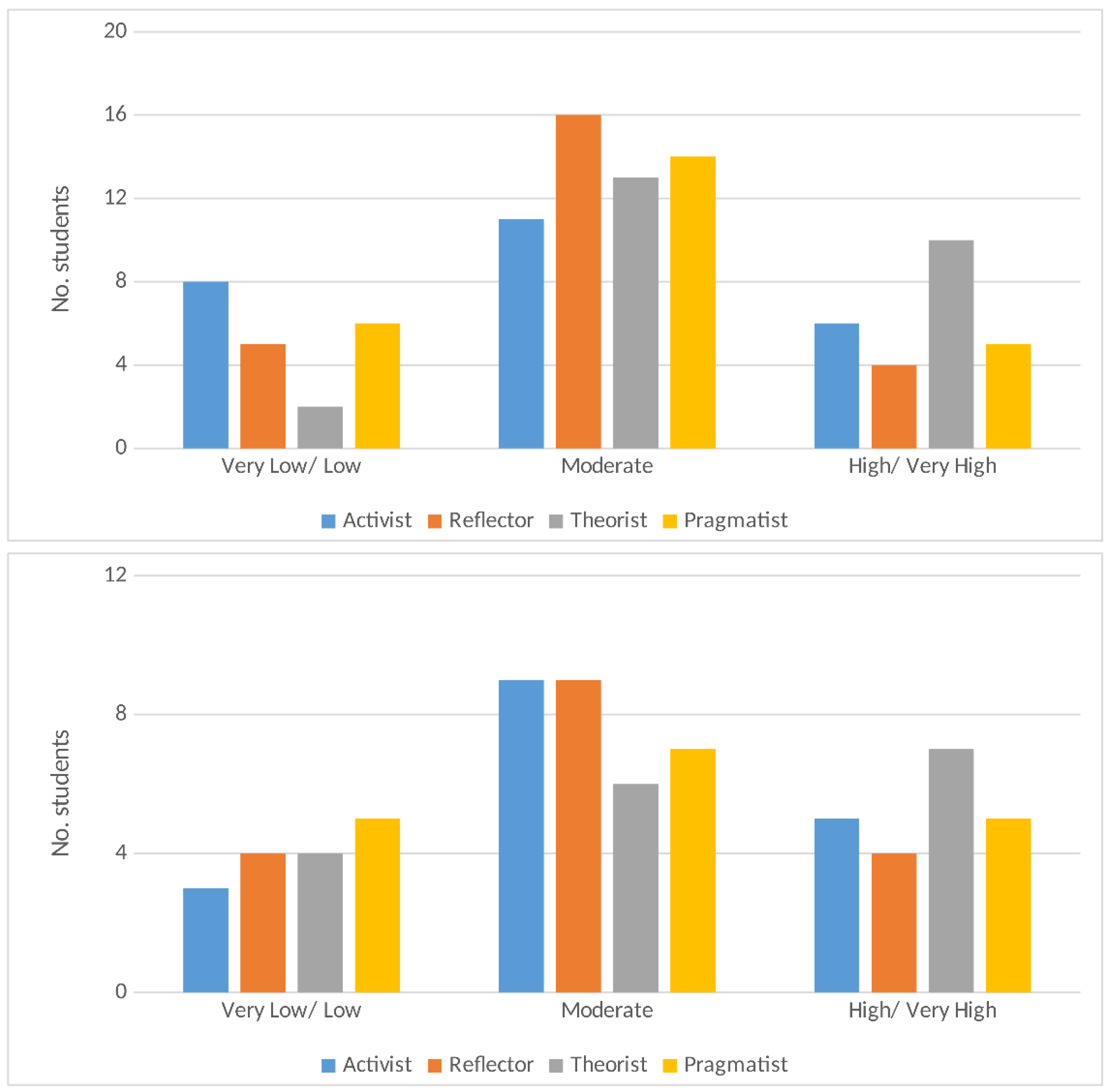
5.3. Learning Styles and Persistence of Conceptual Errors
6. Conclusions
- Difficulties when expressing the result of a measurement accompanied by its uncertainty and discerning the most precise measurement;
- Confusion between the concepts of speed and acceleration;
- The absence of movement implies the absence of forces;
- A body always moves in the same direction as the resultant force;
- There is no gravity in space;
- Only active bodies exert forces;
- The greatest force is what determines the movement;
- Inertia due to the effect of the blow;
- Loss or recovery of initial inertia;
- The last force to act is the one that determines the movement;
- Movement always occurs when the force acting is greater than the resistance;
- Speed is proportional to the force applied;
- A force causes acceleration to a maximum speed.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hattie, J. Visible Learning: A Synthesis of over 800 Meta-Analyses Relating to Achievement, 1st ed.; Routledge: London, UK, 2008. [Google Scholar] [CrossRef]
- Karagiannopoulou, E.; Entwistle, N. Students’ Learning Characteristics, Perceptions of Small-Group University Teaching, and Understanding through a “Meeting of Minds”. Front. Psychol. 2019, 10, 444. [Google Scholar] [CrossRef] [PubMed]
- Greca, I.M.; Moreira, M.A. The kinds of mental representations -models, propositions and images- used by college physics students regarding the concept of field. Int. J. Sci. Educ. 1997, 6, 711–724. [Google Scholar] [CrossRef]
- Bachelard, G.; McAllester, J.M. The Formation of the Scientific Mind: A Contribution to a Psychoanalysis of Objective Knowledge; Clinamen Press: Geneva, Switzerland, 2002. [Google Scholar]
- Gómez, M.A.; Pozo, J.I. Relationships between everyday knowledge and scientific knowledge: Understanding how matter changes. Int. J. Sci. Educ. 2004, 26, 1325–1343. [Google Scholar] [CrossRef]
- Reif, F.; Larkin, J.H. Cognition in scientific and everyday domains: Comparison and learning implications. J. Res. Sci. Teach. 1991, 28, 733–760. [Google Scholar] [CrossRef]
- Steinberg, M.S.; Brown, D.E.; Clement, J. Genius is not immune to persistent misconceptions: Conceptual difficulties impeding Isaac Newton and contemporary physics students. Int. J. Sci. Educ. 1990, 12, 265–273. [Google Scholar] [CrossRef]
- Baker, D.; Taylor, P.C.S. The effect of culture on the learning of science in non-western countries: The results of an integrated research review. Int. J. Sci. Educ. 1995, 17, 695–704. [Google Scholar] [CrossRef]
- Abrahams, I.; Homer, M.; Sharpe, R.; Zhou, M. A comparative cross-cultural study of the prevalence and nature of misconceptions in physics amongst English and Chinese undergraduate students. Res. Sci. Technol. Educ. 2015, 33, 111–130. [Google Scholar] [CrossRef]
- Niazi, H.K.; Dogar, S.R. A comparative study of misconceptions of physics curriculum among the students of O-level (University of Cambridge UK) and SSC level (Pakistani National Curriculum 2006). J. Res. Soc. Sci. 2016, 4, 28–53. [Google Scholar]
- Mora, C.; Herrera, D. A review of the previous ideas of the concept of force. Lat. Am. J. Phys. Educ. 2009, 3, 72–86. [Google Scholar]
- Clement, J. Students preconceptions in introductory mechanics. Am. J. Phys. 1982, 50, 66–71. [Google Scholar] [CrossRef]
- Camarazza, A.; McCloskey, M.; Green, B. Naive beliefs in sophisticated subjects: Misconceptions about trajectories of objects. Cognition 1981, 9, 117–123. [Google Scholar] [CrossRef]
- McDermott, L.C. Bridging the gap between teaching and learning: The role of research. AIP Conf. Proc. 1997, 399, 139–165. [Google Scholar] [CrossRef]
- Hestenes, D.; Wels, M.; Swackhamer, G. Force Concept Inventory. Phys. Teach. 1992, 30, 141–158. [Google Scholar] [CrossRef]
- Nelly, F.; Beleño, L.; Márquez, C.; Agudelo, J.d.J.; Muñiz, J.L. The conceptual evolution in the learning of physical concepts mediated by didactic units. Eng. Educ. Mag. 2019, 14, 1–8. [Google Scholar] [CrossRef]
- Alconchel, F.; Cámara, M.E.; Díaz, M.; Gámez, B.; Gámez, L.; Laguna, M.F.; Lávin, A.; Martín, P.; Ponce, A.; Seidel, L. Conceptual Quizzes in Physics: Assessment of Learning Outcomes and Misconceptions in Mechanics and Electromagnetism. In Proceedings of the III International Congress on Learning, Innovation and Competitiveness (CINAIC, 2015), Madrid, Spain, 14–16 October 2015; E.T.S.I. Industriales (UPM): Madrid, Spain, 2015. [Google Scholar]
- Covián, E.; Celemín, M. Ten years of evaluation of the teaching-learning of Newtonian mechanics in Spanish engineering schools. Academic performance and presence of preconceptions. Sci. Educ. 2008, 26, 23–42. [Google Scholar]
- Carrascosa, J. El problema de las concepciones alternativas en la actualidad (parte I). Análisis sobre las causas que las originan y/o mantienen. Rev. Eureka Sobre Enseñ. Divulg. Cienc. 2005, 2, 183–208. [Google Scholar] [CrossRef]
- McDaniel, M.A.; Stoen, S.M.; Frey, R.F.; Markow, Z.F.; Hynes, K.M.; Zhao, J.; Cahill, M.J. Dissociative conceptual and quantitative problem solving outcomes across interactive engagement and traditional format introductory physics. Phys. Rev. Phys. Educ. Res. 2016, 12, 020141. [Google Scholar] [CrossRef]
- Russell, T.; Martin, A.K. Learning to teach science. In Handbook of Research on Science Education; Routledge: London, UK, 2023; pp. 1162–1196. [Google Scholar]
- Pozo, J.I.; Gómez, M.A. Aprender y enseñar ciencia. In Del Conocimiento Cotidiano al Conocimiento Científico; Morata: Madrid, Spain, 1998; ISBN 978-8471124401. [Google Scholar]
- Picquart, M. What can we do to achieve meaningful learning in physics? Lat. Am. J. Phys. Educ. 2008, 2, 29–36. [Google Scholar]
- Engel-Clough, E.; Driver, R. A study of consistency in the use of students’ conceptual frameworks across different task contexts. Sci. Educ. 1986, 70, 473–496. [Google Scholar] [CrossRef]
- Helm, H. Misconceptions in physics among South African students. Phys. Educ. 1980, 15, 92–105. [Google Scholar] [CrossRef]
- Palmer, D.H. Exploring the link between students’ scientific and nonscientific conceptions. Sci. Educ. 1999, 83, 639–653. [Google Scholar] [CrossRef]
- Scott, T.F.; Schumayer, D. Conceptual coherence of non-Newtonian worldviews in Force Concept Inventory data. Phys. Rev. Phys. Educ. Res. 2017, 13, 010126. [Google Scholar] [CrossRef]
- Pinto, G.; Castro-Acuña, C.M.; López-Hernández, I.; Alcázar Montero, V. Learning Difficulties in the Interpretation of Matter at the Molecular Level by University Students—A Case Study: Dissolution of Oxygen in Water. Educ. Sci. 2023, 13, 781. [Google Scholar] [CrossRef]
- Rivera-Juárez, J.M.; Madrigal-Melchor, J.; Enciso-Muñoz, A.; López-Chávez, J. Persistence of previous ideas about Electricity of the students of the Physics degree at the Autonomous University of Zacatecas. Lat. Am. J. Phys. Educ. 2011, 5, 537–542. [Google Scholar]
- Fazio, C.; Battaglia, O.R.; Di Paola, B.; Persano Adorno, D. Analyzing the Conceptions on Modelling of Engineering Undergraduate Students: A Case Study Using Cluster Analysis. In Key Competences in Physics Teaching and Learning; Greczyło, T., Dębowska, E., Eds.; Springer Proceedings in Physics; Springer: Cham, Switzerland, 2017; Volume 190. [Google Scholar]
- Paniagua, M.A.; Swygert, K.A. How to Develop Questions for Written Assessments in the Area of Basic and Clinical Sciences; National Board of Medical Examiners: Philadelphia, PA, USA, 2016. [Google Scholar]
- Hestenes, D.; Halloun, I. Interpreting the Force Concept Inventory. A response to Huffman and Heller. Phys. Teach. 1995, 33, 502–506. [Google Scholar] [CrossRef]
- Hake, R. Interactive-engagement vs. Traditional methods: A six-thousand-student survey of mechanical test data for introductory physics courses. Am. J. Phys. 1998, 66, 64–74. [Google Scholar] [CrossRef]
- Henderson, C. Common concerns about the Force Concept Inventory. Phys. Teach. 2002, 40, 542–547. [Google Scholar] [CrossRef]
- Maries, A.; Singh, C. Teaching assistants’ performance at identifying common introductory student difficulties in mechanics revealed by the Force Concept Inventory. Phys. Rev. Phys. Educ. Res. 2016, 12, 010131. [Google Scholar] [CrossRef]
- Artamonova, I.; Mosquera, J.C.; Artamanov, J.D.M. Application of force concept inventory in Latin America for the evaluation of the understanding of the basic concepts of mechanics at the university level. Eng. Educ. Mag. 2017, 12, 56–63. [Google Scholar] [CrossRef]
- Abdelhadi, A.; Ibrahim, Y.; Nurunnabi, M. Investigating Engineering Student Learning Style Trends by Using Multivariate Statistical Analysis. Educ. Sci. 2019, 9, 58. [Google Scholar] [CrossRef]
- Kolb, D.A. Experiential Learning: Experience as the Source of Learning and Development, 2nd ed.; FT Press: Saddle River, NJ, USA, 2014; ISBN 978-0133892406. [Google Scholar]
- Alonso, C.; Gallego, D.; Honey, P. Los Estilos de Aprendizaje: Procedimientos de Diagnóstico y Mejora, 7th ed.; Mensajero: Bilbao, Spain, 2007; ISBN 978-84-271-1914-7. [Google Scholar]
- Estrada García, A. Estilos de aprendizaje y rendimiento académico. Rev. Bol. Redipe 2018, 7, 218–222. [Google Scholar]
- Smith, R.M. Learning How to Learn: Applied Theory for Adults, 1st ed.; Open University Press: Milton Keynes, UK, 1988; ISBN 9780335105854. [Google Scholar]
- Camarero Suárez, F.; Martín del Buey, F.; Herrero Diez, J. Estilos y estrategias de aprendizaje en estudiantes universitarios. Psicothema 2000, 12, 615–622. [Google Scholar]
- Keefe, J.W. Profiling and Utilizing Learning Style; NASSP Learning Style Series; ERIC: Stockholm, Sweden, 1988; ISBN 978-0882102078. [Google Scholar]
- Honey, P.; Mumford, A. The Manual of Learning Styles; Peter Honey Associates: Maidenhead, Berkshire, 1986; ISBN 978-0950844473. [Google Scholar]
- Pierart, C.G.A.; Pavés, F.R. Estilos de aprendizaje, género y rendimiento académico. Rev. Estilos Aprendiz. 2011, 4, 71–84. [Google Scholar] [CrossRef]
- Pashler, H.; McDaniel, M.; Rohrer, D.; Bjork, R. Learning Styles: Concepts and Evidence. Phycol. Sci. Public Interest 2008, 9, 105–119. [Google Scholar] [CrossRef]
- Lindsey, C.K.; Edwards, M.; Douglass Smith, M. Use of Learning Style Frameworks in Health Science Education. Am. J. Pharm. Educ. 2020, 84, 919–927. [Google Scholar] [CrossRef]
- Joswick, C.; Skultety, L.; Olsen, A.A. Mathematics, Learning Disabilities, and Learning Styles: A Review of Perspectives Published by the National Council of Teachers of Mathematics. Educ. Sci. 2023, 13, 1023. [Google Scholar] [CrossRef]
- Coffield, F.; Moseley, D.; Hall, E.; Ecclestone, K. Learning Styles and Pedagogy in Post-16 Learning: A Systematic and Critical Review; Learning and Skills Research Centre: London, UK, 2004. [Google Scholar]
- Rayner, S.; Cools, E. (Eds.) Style Differences in Cognition, Learning and Management; Routledge: New York, NY, USA, 2011; ISBN 9781136901638. [Google Scholar]
- Xu, W. Learning Styles and Their Implications in Learning and Teaching. Theory Pract. Lang. Stud. 2011, 1, 413–416. [Google Scholar] [CrossRef]
- Pantoja Ospina, M.A.; Duque Salazar, L.I.; Correa Meneses, J.S. Learning Styles Models: An upgrade for their revision and analysis. Rev. Colomb. Educ. 2013, 64, 79–105. [Google Scholar] [CrossRef]
- Owen, C.L. Understanding Design Research: Toward an Achievement of Balance. J. Jpn. Soc. Sci. Des. 1997, 5, 36–45. [Google Scholar] [CrossRef]
- Owen, C.L. Design Research: Building the Knowledge Base. Des. Stud. 1998, 19, 9–20. [Google Scholar] [CrossRef]
- Grasha, A.F.; Riechmann, S.W. Student Learning Styles Questionnaire; Faculty Resource Center, University of Cincinatti: Cincinatti, OH, USA, 1975. [Google Scholar]
- Ramanaiah, N.; Ribich, F.; Schmeck, R.R. Development of a Self-report Inventory for Assessing Individual Differences in Learning Processes. Appl. Psychol. Meas. 1977, 1, 413–431. [Google Scholar] [CrossRef]
- Marsick, V.J.; Watkins, K.E. Building the Learning Organization: A New Role for Human Resource Developers. Stud. Contin. Educ. 1992, 14, 115–129. [Google Scholar] [CrossRef]
- Entwistle, N.J. Styles of Learning and Teaching: An Integrated Outline of Educational Psychology for Student Teachers and Lecturers; David Fulton Publishers: London, UK, 1998. [Google Scholar]
- McCarthy, B. The 4MAT System: Teaching to Learning Styles with Right-Left Techniques; The Reading Teacher 35 (6) Barrington, Ill; Excel, Inc.: Lincolnton, NC, USA, 1987; ISBN 978-0960899203. [Google Scholar]
- Williams, L. Aprender Con Todo el Cerebro; Martínez Roca: Barcelona, Spain, 1986; ISBN 9788427010055. [Google Scholar]
- Myers, I.B. The Myers-Briggs Type Indicator: Manual; Consulting Psychologists Press: Washington, DC, USA, 1962. [Google Scholar]
- Argyris, C.; Schön, D.A. Organizational Learning: A Theory of Action Perspective; Addison-Wesley: Reading, MA, USA, 1978; ISBN 978-0201001747. [Google Scholar]
- McKee, D. An Organizational Learning Approach to Product Innovation. J. Prod. Innov. Manag. 1992, 9, 232–245. [Google Scholar] [CrossRef]
- Dunn, R.; Dunn, K. Teaching Students through Their Individual Learning Styles; Reston Publishing Company: Reston, VA, USA, 1978; ISBN 9780879098087. [Google Scholar]
- Fleming, N.D.; Mills, C. Not Another Inventory, rather a Catalyst for Reflection. Improv. Acad. 1992, 11, 137–155. [Google Scholar] [CrossRef]
- Fleming, N.D. Teaching and Learning Styles: VARK Strategies; N.D. Fleming: Christchurch, New Zealand, 2001; ISBN 9780473079567. [Google Scholar]
- Jolliffe, I.T.; Cadima, J. Principal Component Analysis, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Baladrón, J.; Curbelo, J.; Sánchez-Lasheras, F.; Romeo-Ladrero, J.M.; Villacampa, T.; Fernández-Somoano, A. Examination of the MIR exam. An approach to the structural validity through the classical test theory. FEM J. Med. Educ. Found. 2016, 19, 217–226. [Google Scholar]
- Crocker, L.; Algina, J. Introduction to Classical and Modern Test Theory; CBS College Publishing: New York, NY, USA, 1986. [Google Scholar]
- Backhoff, E.; Larrazolo, N.; Rosas, M. Difficulty level and discrimination power of the Basic Skills and Knowledge Examination (EXHCOBA). Redie Electron. J. Educ. Res. 2000, 2, 1–16. [Google Scholar]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation Coefficients: Appropriate Use and Interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
- García Cué, J.L.; Santizo Rincón, J.A.; Alonso García, C.M. Uso de las TIC de acuerdo a los estilos de aprendizaje de docentes y discentes. Rev. Iberoam. Educ. 2009, 48, 1–14. [Google Scholar] [CrossRef]
- Chistyakov, A.A.; Zhdanov, S.P.; Avdeeva, E.L.; Dyadichenko, E.A.; Kunitsyna, M.L.; Yagudina, R.I. Exploring the characteristics and effectiveness of project-based learning for science and STEAM education. Eurasia J. Math. Sci. Technol. Educ. 2023, 19, em2256. [Google Scholar] [CrossRef]
- Kokotsaki, D.; Menzies, V.; Wiggins, A. Project-based learning: A review of the literature. Improv. Sch. 2016, 19, 267–277. [Google Scholar] [CrossRef]
- Capraro, R.M.; Capraro, M.M.; Morgan, J.R. STEM Project-Based Learning: An Integrated Science, Technology, Engineering, and Mathematics (STEM) Approach; Sense: Rotterdam, The Netherlands, 2013; ISBN 978-94-6209-143-6. [Google Scholar]
- Battaglia, O.R.; Di Paola, B.; Persano Adorno, D.; Pizzolato, N.; Fazio, C. Evaluating the effectiveness of modelling-oriented workshops for engineering undergraduates in the field of thermally activated phenomena. Res. Sci. Educ. 2019, 49, 1395–1413. [Google Scholar] [CrossRef]
- Pizzolato, N.; Fazio, C.; Mineo, R.M.S.; Adorno, D.P. Open-inquiry driven overcoming of epistemological difficulties in engineering undergraduates: A case study in the context of thermal science. Phys. Rev. Spec. Top. Phys. Educ. Res. 2014, 10, 010107. [Google Scholar] [CrossRef]
- Battaglia, O.R.; Di Paola, B.; Fazio, C.; Pizzolato, N.; Adorno, D.P. A quantitative analysis of university student reasoning lines in the field of thermally activated phenomena. J. Phys. Conf. Ser. 2018, 1076, 012019. [Google Scholar] [CrossRef]
- Adorno, D.P.; Pizzolato, N.; Fazio, C. Long term stability of learning outcomes in undergraduates after an open-inquiry instruction on thermal science. Phys. Rev. Phys. Educ. Res. 2018, 14, 010108. [Google Scholar] [CrossRef]


| Preconception | Description | Incorrect Answers Associated with Erroneous Preconceptions |
|---|---|---|
| I. Kinematics | ||
| 1 | Misunderstanding of the concepts of velocity and acceleration | 4(a), 4(b), 4(d), 5(d), 6(a), 12(a), 12(b), 12(c) |
| II. Inertia | ||
| 2 | Inertia due to a hit | 20(d), 13(b), 13(c) |
| 3 | Loss or increment of initial inertia | 14(a), 16(a), 16(d) |
| 4 | Energy dissipation | 17(c), 20(b) |
| III. Newton’s second law | ||
| 5 | Only active bodies exert forces | 9(d), 11(d), 13(a) |
| 6 | Motion only takes place under the presence of a force | 20(a) |
| 7 | The absence of motion implies the absence of forces | 5(a), 9(d) |
| 8 | Velocity is proportional to the force applied | 15(a), 19(a) |
| 9 | Nonzero acceleration implies the existence of a variable force | 10(b) |
| 10 | Force induces acceleration up to a maximum value | 10(a), 15(d), 19(c) |
| 11 | A force acts until it is consumed | 15(c) |
| IV. Newton’s third law (action/reaction) | ||
| 12 | The larger the mass, the larger the force applied. | 8(a), 8(c) |
| V. Superposition principle | ||
| 13 | The largest force determines the movement | 11(a), 5(b) |
| 14 | Motion is determined by a combination of forces | 14(c) |
| 15 | The last force applied determines the motion | 14(b), 16(c) |
| VI. Active forces | ||
| 16 | Obstacles do not exert forces | 9(a), 8(b) |
| VII. Resistive forces | ||
| 17 | The mass of the self bodies makes them stop | 20(a), 20(b) |
| 18 | Motion occurs when the force acting is greater than the resistance | 18(b), 18(d), 19(b) |
| 19 | Resistance opposes force and inertia | 19(b) |
| VIII. gravitational forces | ||
| 20 | Air pressure enhances the action of gravity | 9(c), 10(d), 11(d) |
| 21 | Heavier objects fall down faster than lighter ones | 21(b), 21(d) |
| 22 | Gravity increases as bodies fall | 10(b) |
| 23 | There’s no gravity in space | 7(a), 7(c) |
| IX. Uncertainty | ||
| 24 | Lack of knowledge when expressing the result of a measurement accompanied by its uncertainty | 1(a), 1(b), 1(d), 2(a), 2(b), 2(d), 3(a), 3(b), 3(d) |
| X. Center of mass | ||
| 25 | Unclear understanding of the center of mass | 24(a), 24(b), 24(d) |
| XI. Rotational motion | ||
| 26 | A change in the moment of inertia does not affect the angular velocity of the rotating object | 22(a), 22(b), 22(d) |
| 27 | Unclear understanding between angular and linear velocity | 23(a), 23(b), 23(d) |
| Concepts | Correct Options |
|---|---|
| I. Kinematics | |
| Uniformly accelerated rectilinear motion | 4(c) |
| Distinction between velocity and acceleration | 12(d) |
| Parabolic motion means constant acceleration | 14(d) |
| Constant acceleration implies change in velocity | 15(b), 4(c) |
| II. Superposition principle | |
| Null resultant force implies rectilinear motion | 16(b) |
| Null resultant force implies constant velocity modulus | 17(a), 18(c), 11(b) |
| III. Newton’s second law | |
| Constant forces imply constant accelerations | 14(d), 15(b) |
| IV. Newton’s third law | |
| Newton’s third law for impulsive forces | 8(d) |
| V. Active forces | |
| Forces between solids in contact | 11(b), 6(c), 9(b), 19(d) |
| Frictional force | 20(c), 18(c) |
| VI. Resistive forces | |
| Air resistance | 13(d) |
| VII. Gravitational forces | |
| Force of gravity | 9(b), 13(d), 5(c), 6(c), 7(b), 10(c), 11(b) |
| Weight is independent acceleration | 21(a) |
| VIII. Uncertainty | |
| Correctly express the result of a measurement. Precision in measurements. | 1(c), 2(c), 3(c) |
| IX. Mass center | |
| Center-of-mass concept | 24(c) |
| X. Rotational movement | |
| Angular and linear velocity | 23(c) |
| Inertia moment | 22(c) |
| EI | Degree of Difficulty |
|---|---|
| 0 to 0.30 | Too difficult (discard) |
| 0.31 to 0.50 | Difficult |
| 0.51 to 0.70 | Moderate |
| 0.71 to 0.90 | Easy |
| 0.91 to 1 | Too easy (discard) |
| Learning Style | Very Low | Low | Moderate | High | Very High |
|---|---|---|---|---|---|
| Activist | 0–6 | 7–8 | 9–12 | 13–14 | 15–20 |
| Reflector | 0–10 | 11–13 | 14–17 | 18–19 | 20 |
| Theorist | 0–6 | 7–9 | 10–13 | 14–15 | 16–20 |
| Pragmatist | 0–8 | 9–10 | 11–13 | 14–15 | 16–20 |
| Test 1 | Test 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Item | EI | DI | Idiff | P | EI | DI | Idiff | P | |
| 1 | 31.5 | 0.40 * | 0.42 * | 0.60 * | 0.44 * | 0.71 | 0.37 | 0.29 * | 0.32 * |
| 2 | −2.0 | 0.05 | 0.09 | 0.95 | 0.52 | 0.03 | −0.05 | 0.97 | −0.05 |
| 3 | 15.5 | 0.58 | −0.14 | 0.42 | 0.09 | 0.74 | 0.11 | 0.26 | 0.27 |
| 4 | 2.1 | 0.16 | 0.14 | 0.84 | 0.09 | 0.18 | 0.16 | 0.82 | 0.21 |
| 5 | 0.3 | 0.02 | −0.05 | 0.98 | −0.09 | 0.03 | 0.05 | 0.97 | 0.13 |
| 6 | 21.8 | 0.26 | 0.23 | 0.74 | 0.08 | 0.47 | 0.11 | 0.53 | 0.28 |
| 7 | −0.8 | 0.14 | 0.09 | 0.86 | 0.29 | 0.13 | 0.26 | 0.87 | 0.51 |
| 8 | 6.3 | 0.28 | 0.09 | 0.72 | 0.33 | 0.34 | 0.26 | 0.66 * | 0.39 * |
| 9 | 21.0 | 0.40 * | 0.33 * | 0.60 * | 0.36 * | 0.61 | 0.16 | 0.39 * | 0.30 * |
| 10 | −4.1 | 0.49 | 0.23 | 0.51 * | 0.30 * | 0.45 | 0.05 | 0.55 | 0.29 |
| 11 | −3.7 | 0.12 | 0.05 | 0.88 | −0.07 | 0.08 | 0.05 | 0.92 | 0.06 |
| 12 | 9.4 | 0.12 | 0.14 | 0.88 | 0.19 | 0.21 | 0.21 | 0.79 | 0.06 |
| 13 | −0.2 | 0.19 | 0.09 | 0.81 | 0.19 | 0.18 | 0.16 | 0.82 | 0.06 |
| 14 | 36.7 | 0.19 | 0.09 | 0.81 | 0.19 | 0.55 | 0.16 | 0.45 | 0.02 |
| 15 | 8.3 | 0.23 | 0.28 | 0.77 | 0.28 | 0.32 | 0.21 | 0.68 * | 0.38 * |
| 16 | 3.9 | 0.09 | 0.09 | 0.91 | 0.31 | 0.13 | 0.16 | 0.87 | 0.43 |
| 17 | 3.2 | 0.44 * | 0.42 * | 0.56 * | 0.40 * | 0.47 * | 0.32 * | 0.53 * | 0.47 * |
| 18 | 12.1 | 0.12 | 0.14 | 0.88 | 0.07 | 0.24 | −0.05 | 0.76 | −0.08 |
| 19 | 2.9 | 0.02 | 0.05 | 0.98 | 0.09 | 0.05 | 0.11 | 0.95 | 0.36 |
| 20 | −8.6 | 0.35 * | 0.42 * | 0.65 * | 0.49 * | 0.26 | 0.53 | 0.74 | 0.48 |
| 21 | 15.6 | 0.19 | 0.00 | 0.81 | 0.40 | 0.34 | 0.05 | 0.66 | 0.15 |
| 22 | 15.9 | 0.21 | 0.05 | 0.79 | 0.10 | 0.37 * | 0.42 * | 0.63 * | 0.37 * |
| 23 | 25.6 | 0.35 * | 0.42 * | 0.65 * | 0.56 * | 0.61 | 0.05 | 0.39 | 0.28 |
| 24 | 20.0 | 0.12 | 0.14 | 0.88 | 0.41 | 0.32 | 0.11 | 0.68 * | 0.36 * |
| Mean value | 9.70 | 0.23 | 0.16 | 0.77 | 0.25 | 0.33 | 0.16 | 0.67 | 0.25 |
| Test 1 | Test 2 | |||||||
|---|---|---|---|---|---|---|---|---|
| Contents | Related Items | No. | % | EI | No. | % | EI | h |
| Kinematics | 4.12, 14.15 | 30 | 17.4 | 0.17 | 48 | 31.6 | 0.32 | 0.17 |
| Newton’s first law | 11, 13, 14, 15, 16, 17, 18, 20 | 74 | 21.5 | 0.22 | 85 | 28.0 | 0.28 | 0.08 |
| Second law of Newton | 5, 9, 10, 11, 14, 15, 19, 20 | 78 | 22.7 | 0.23 | 89 | 29.3 | 0.29 | 0.09 |
| Newton’s third law | 8 | 12 | 27.9 | 0.28 | 13 | 34.2 | 0.34 | 0.09 |
| Superposition principle | 5, 11, 14, 16, 18 | 23 | 10.7 | 0.11 | 39 | 20.5 | 0.21 | 0.11 |
| Types of forces | 5, 6, 7, 9, 10, 11, 13,18,19, 20, 21 | 98 | 20.7 | 0.21 | 108 | 25.8 | 0.26 | 0.06 |
| Expression of a measure | 1, 2, 3 | 44 | 34.1 | 0.34 | 56 | 49.1 | 0.49 | 0.23 |
| Mass center | 24 | 5 | 11.6 | 0.12 | 12 | 31.6 | 0.32 | 0.23 |
| Rotatory motion | 22, 23 | 24 | 27.9 | 0.28 | 37 | 48.7 | 0.49 | 0.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ablanque, J.; Revuelta, F.; Losada, J.C.; Benito, R.M. Persistence of Conceptual Errors in First-Year University Physics Course and Its Possible Relationship with Learning Styles. Educ. Sci. 2024, 14, 401. https://doi.org/10.3390/educsci14040401
Ablanque J, Revuelta F, Losada JC, Benito RM. Persistence of Conceptual Errors in First-Year University Physics Course and Its Possible Relationship with Learning Styles. Education Sciences. 2024; 14(4):401. https://doi.org/10.3390/educsci14040401
Chicago/Turabian StyleAblanque, Javier, Fabio Revuelta, Juan Carlos Losada, and Rosa M. Benito. 2024. "Persistence of Conceptual Errors in First-Year University Physics Course and Its Possible Relationship with Learning Styles" Education Sciences 14, no. 4: 401. https://doi.org/10.3390/educsci14040401
APA StyleAblanque, J., Revuelta, F., Losada, J. C., & Benito, R. M. (2024). Persistence of Conceptual Errors in First-Year University Physics Course and Its Possible Relationship with Learning Styles. Education Sciences, 14(4), 401. https://doi.org/10.3390/educsci14040401